中科大高等固体物理3尺度
《固体物理》复习大纲

«固体物理»复习大纲招生专业:凝聚态物理/材料物理与化学固体物理学的基本内容(专题除外), 主要有:晶体结构, 晶体结合, 晶格振动和晶体热学性质, 晶体的缺陷, 金属电子论和能带理论.主要参考书目: 1. 黄昆, 韩汝琦, 固体物理学, 高教出版社2. 陆栋, 蒋平, 徐至中, 固体物理学, 上海科技出版社3. 朱建国, 郑文琛等, 固体物理学, 科学出版社«新型功能材料»复习大纲招生专业:材料物理与化学/光学工程一、复习大纲1,材料、新材料的重要性;2,材料科学、材料工程、材料科学与工程的学科形成与学科内涵;3,材料科学与工程的“四要素”的内容;“四要素”间的相互关系(用图来表示);“四要素”在材料研究中的作用;(要求能结合具体材料事例予以说明)4,如何理解材料、特别是新材料是社会现代化的物质基础与先导;5,怎样区分结构材料和功能材料?新型功能材料的内涵是什么?6,了解新型功能材料中相关科学名词的解释,并能给出适当的例子,如:信息材料;光电功能材料;能源材料;高性能陶瓷;纳米材料;晶体材料;人工晶体(材料);压电材料;铁电材料;复合材料;梯度材料;智能材料与结构;材料设计;环境材料;低维材料;生物材料;非线形光学材料;光子晶体;半导体超晶格;等等;7,注意了解材料检测评价新技术的发展;注意了解材料的成分测定、结构测定、形貌观测的方法;材料无损检测评价新技术的发展概况;8,能结合具体的材料对象,给出材料的成分分析、原子价态分析、结构(含微结构)分析、形貌分析等所采用的主要技术,以及利用这些技术所得出的主要结果;9,对若干常用的分析技术,包括:X射线衍射分析(XRD),原子力显微镜分析(AFM),扫描电子显微镜分析(SEM),透射电子显微镜分析(TEM),俄歇电子能谱分析,X射线光电子能谱分析(XPS),核磁共振谱分析,等,能结合具体事例,阐述它们在材料物化结构分析中的作用和能解决的具体问题;10,材料科学技术是一门多学科交叉的前沿综合性学科;材料科学技术的学科内涵极为丰富;当代材料科学技术正在飞速发展,其主要发展趋势可以归纳为8个方面。
黄昆 固体物理 讲义 第二章

第二章 固体的结合晶体结合的类型 晶体结合的物理本质固体结合的基本形式与固体材料的结构、物理和化学性质有密切联系 § 2.1 离子性结合元素周期表中第I 族碱金属元素(Li 、Na 、K 、Rb 、Cs )与第VII 族的卤素元素(F 、Cl 、Br 、I )化合物(如 NaCl , CsCl ,晶体结构如图XCH001_009_01和XCH001_010所示)所组成的晶体是典型的离子晶体,半导体材料如CdS 、ZnS 等亦可以看成是离子晶体。
1. 离子晶体结合的特点以CsCl 为例,在凝聚成固体时,Cs 原子失去价电子,Cl 获得了电子,形成离子键。
以离子为结合单元,正负离子的电子分布高度局域在离子实的附近,形成稳定的球对称性的电子壳层结构;,,,Na K Rb Cs Ne Ar Kr Xe FClBrI++++−−−−⇒⇒⇒⇒离子晶体的模型:可以把正、负离子作为一个刚球来处理;离子晶体的结合力:正、负离子之间靠库仑吸引力作用而相互靠近,当靠近到一定程度时,由于泡利不相容原理,两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。
当排斥力和吸引力相互平衡时,形成稳定的离子晶体; 一种离子的最近邻离子为异性离子;离子晶体的配位数最多只能是8(例如CsCl 晶体);由于离子晶体结合的稳定性导致了它的导电性能差、熔点高、硬度高和膨胀系数小;大多数离子晶体对可见光是透明的,在远红外区有一特征吸收峰。
氯化钠型(NaCl 、KCl 、AgBr 、PbS 、MgO)(配位数6) 氯化铯型(CsCl 、 TlBr 、 TlI)(配位数8)离子结合成分较大的半导体材料ZnS 等(配位数4) 2. 离子晶体结合的性质 1)系统内能的计算晶体内能为所有离子之间的相互吸引库仑能和重叠排斥能之和。
以NaCl 晶体为例,r 为相邻正负离子的距离,一个正离子的平均库仑能:∑++−++321321,,2/122322222102)(4)1('21n n n n n n r n r n r n q πε ——遍及所有正负离子,因子1/2—库仑作用为两个离子所共有,一个离子的库伦能为相互作用能的一半。
中科大物理考研参考书

专业代码及名称培养单位代码招生类专业代码及名称培养单位代码招生类别070121★数学物理001 硕,博3 623 数学分析《数学分析教程》常庚哲中国科大出版社数学分析:极限、连续、微分、积分的概念及性质4 802 线性代数与解析几何《线性代数》李炯生中国科大出版社《空间解析几何简明教程》吴光磊高等教育出版社线性代数:行列式,矩阵,线性空间线性映射与线性变换,二次型与内积;解析几何:向量代数,平面与直线,常见曲面070201理论物理004 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070202粒子物理与原子核物理004 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070203原子与分子物理004 硕、博234 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 835 原子物理与量子力学《近代物理学》徐克尊高等教育出版社《原子物理学》杨福家高等教育出版社第三版《原子物理学》褚圣麟高等教育出版社《量子力学导论》曾谨言高等教育出版社原子结构和光谱、分子结构和光谱、量子力学概论070204等离子体物理004 硕、博4 808 电动力学A 《电动力学》郭硕鸿高等教育出版社第二版电磁现象的普遍规律,静电场和静磁场,电磁波的传播,电磁波的辐射(包括低速和高速运动带电粒子的辐射),狭义相对论4 872 等离子体物理导论《等离子体物理导论》F. F. Chen科学出版社1980《等离子体物理原理》马腾才胡希伟陈银华中国科大出版社1988 单粒子理论、等离子体平衡、等离子体波动、等离子体不稳定性070205凝聚态物理002 博203 硕3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 809 固体物理《固体物理》黄昆原著韩汝琦改编高等教育出版社晶体结构、晶体缺陷、晶体结合、晶体振动及热学性质、金属电子论、能带论、电导论4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁231 硕、博234 硕、博070207光学002 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070221★量子信息物理学234 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070301无机化学019 硕、博157 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 818 无机化学《无机化学》(上、下册)武汉大学、吉林大学等校编高等教育出版社第三版无机化学基本原理、理论及元素无机化学234 硕、博070302分析化学019 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 820 分析化学《分析化学》武汉大学主编高等教育出版社《定量分析化学》李龙泉等编著中国科大出版社误差与数据处理;酸碱滴定,配位滴定,氧化-还原滴定,沉淀滴定;重量分析;常用的分离方法与复杂物质分析070303有机化学019 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 819 有机化学《有机化学》伍越环编著中国科大出版社《有机化学实验》兰州大学、复旦大学编高等教育出版社伍越环编著的《有机化学》全部内容070304物理化学(含化学物理)003 硕、博231 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 815 结构化学《物质结构》潘道皑等人民教育出版社量子力学基础、原子分子电子结构、分子光谱、晶体结构4 818 无机化学《无机化学》(上、下册)武汉大学、吉林大学等校编高等教育出版社第三版无机化学基本原理、理论及元素无机化学以下为第2 组考试科目,共有 2 组考试科目,可任选一组3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程,一维定态问题、力学量算符与表象变换,对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁234 硕、博070305高分子化学与物理020 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 821 高分子化学与物理《高分子化学》潘才元中国科大出版社2001版;《高聚物的结构与性能》马德柱等科学出版社2003版考试范围包括指定参考书中所涉及的内容。
高等固体物理--非常好的ppt

独立完成
期末考试:闭卷
凝聚态物理
从微观角度出发,研究相互作用多粒子系统组成的凝聚态物质 (固体和液体)的结构和动力学过程, 及其与宏观物理性质之 间关系的一门科学.
凝聚态物理的重要性
(1)它为力学,流体力学,电子学,光学,冶金学及固态化学等经 典科学提供了量子力学基础.
(2)它为高技术的发展作出了巨大贡献. 如它是晶体管,超导 磁体,固态激光器, 高灵敏辐射能量探测器等重大技术革新的 源头. 对通信,计算以及利用能量所需的技术起着直接的作用, 对非核军事技术也产生了深刻的影响.
重要 重要 可能 密切 可能
科学的前沿: Before 80年代:天体物理、粒子物理 After 80年代:凝聚态物理 凝聚态物理已占整个物理学的半壁江山
Project 1
结合自己的专业列举和讨论某一子领域如何在经济社会各 方面发挥作用的.
第一章
1.1 1.2 1.3 1.4 范式
概论
固体物理的范式 量子化学的范式 凝聚态物理的范式
凝聚态物理表面上不同于其他学科, 内容显得多而杂, 有必要站在科学发展的高度, 审视其内在的规律. 科学史学家 Thomas Kuhn 强调范式在学科发展过程中的作用
/EDUCATION/mfp/Kuhnsnap.html
Thomas Kuhn (1922.7.18-1996.6.17) 在Harvard 大学读 理论物理研究生时 写的一本书
Hybrid orbitals • s + p + p + p = sp3 + sp3 + sp3+ sp3 • head on overlap produce sigma bonds • sideways overlap of unhybridized p orbitals produce pi bonds • How will this affect the character of s and p bonds?
物理学科简介

物理学是一级学科,是研究物质及 其相互作用和基本规律的科学,是 自然科学各学科的重要基础。
一级学科下属8个二级学科
070201 理论物理 070202 粒子物理与原子核物理 070203 原子与分子物理 070204 等离子体物理 070205 凝聚态物理 070206 声学 070207 光学 070208 无线电学
无线电
无线电是通过无线电波传播信号的技术。无线 电技术的原理在于,导体中电流强弱的改变会 产生无线电波。利用这一现象,通过调制可将 信息加载于无线电波之上。当电波通过空间传 播到达收信端,电波引起的电磁场变化又会在 导体中产生电流。通过解调将信息从电流变化 中提取出来,就达到了信息传递的目的。 (9KHz~300GHz,10KHz~300GHz)
宁夏大学、陕西师范大学、首都师范大学、 哈尔滨理工大学、宁波大学、南京师范大学、四川 师范大学、西南科技大学、广州大学、西南大学、 内蒙古科技大学、华南理工大学、扬州大学、 曲阜师范大学、云南大学、哈尔滨师范大学、 西北师范大学、东北大学、湖北大学、 西南交通大学、长春理工大学、吉首大学、 中国矿业大学、上海理工大学、长沙理工大学、 北京交通大学、南京理工大学、三峡大学、 青岛大学、天津理工大学、内蒙古大学、 福建师范大学、吉林师范大学、河海大学
现设有物理学一级学科博士、硕士研究生培养点;凝 聚态物理、理论物理、光学、等离子体物理4个二级学 科博士研究生培养点;凝聚态物理、理论物理、光学、 等离子体物理、无线电物理5个二级学科硕士研究生培 养点;材料工程、光学工程、集成电路工程3个专业学 位硕士研究生培养点。并设有物理学一级学科博士后 流动站。
报考需要注意事项
1、根据自己的实际情况来选择学校和方 向。 2、抓紧时间备考。 3、公共科目:英语 政治 方向科目:量子力学 普物 (高数 数理 方法 光学等 )
固体物理学_答案(黄昆 原著 韩汝琦改编)

《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
固体物理教学大纲课程名称固体物理课程性质专业必修课

固体物理教学⼤纲课程名称固体物理课程性质专业必修课《固体物理》教学⼤纲⼀、课程名称:固体物理⼆、课程性质:专业必修课三、课程教学⽬的:(⼀)课程⽬标:通过固体物理学课程的学习,使学⽣树⽴起晶体内原⼦、电⼦等微观粒⼦运动的物理图像及其有关模型,掌握晶体内微观粒⼦的运动规律及其与晶体宏观性能的物理联系,深刻理解晶体宏观性能的微观物理本质,为进⼀步学习和研究固体物理学各种专门问题及相关领域的内容建⽴初步的理论基础。
(⼆)教学⽬标:第⼀章晶体结构【教学⽬标】通过本章的教学,使学⽣了解晶格结构的实例、⾮晶态和准晶态的特征;理解和掌握晶体结构的周期性特征及其描述⽅法;理解和掌握晶体结构的对称性特征及其描述⽅法;理解和掌握倒格⼦的定义及其与正格⼦的关系;熟悉有关晶体结构的基本分析与计算。
借助于多媒体展⽰,使学⽣建⽴起晶体结构特征的直观图像。
第⼆章晶体的结合【教学⽬标】通过本章的教学,使学⽣了解晶体结合⼒的⼀般性质;掌握晶体的结合类型与特征;理解元素和化合物晶体结合的规律性;掌握离⼦晶体的结合能、体积弹性模量的计算;掌握范德⽡⽿斯晶体的结合能、体积弹性模量的计算。
在教学中,能够使学⽣认识到吸引与排斥的⽭盾的差别和对⽴统⼀是认识与理解固体的结合规律与性质的关键,培养学⽣的辩证思维能⼒。
第三章晶格振动与晶体的热学性质【教学⽬标】通过本章的教学,能够使学⽣理解简谐近似、格波概念、声⼦概念;理解玻恩-卡曼边界条件;了解三维格波的⼀般规律、晶格振动的⾮简谐效应;了解确定晶格振动谱的实验⽅法;掌握⼀维单原⼦、双原⼦晶格振动的格波解与⾊散关系;掌握晶格振动模式密度的计算⽅法;理解晶格热容量的量⼦理论、掌握爱因斯坦模型与德拜模型;理解格林爱森近似、掌握晶格状态⽅程。
结合例题分析和习题训练,提⾼学⽣分析问题和解决问题的能⼒。
第四章能带理论【教学⽬标】通过本章的教学,使学⽣能够了解晶体能带理论的基本假设和处理问题的基本思路;理解布洛赫定理及其推论的证明,掌握晶体能带的基本特征;熟悉克龙尼克—潘纳模型的求解与结论;熟悉布⾥渊区、费⽶⾯等基本概念;了解平⾯波⽅法、赝势⽅法;掌握近⾃由电⼦近似⽅法及其结论;掌握紧束缚近似⽅法的运⽤;掌握能态密度的计算⽅法。
材料基因组简介

材料基因组计划—第四次产业革命黄孙超hsunchao@中国科学院固体物理研究所2015.11.251国际背景长期以来欧美发达国家一直主导新材料的研发,进入21世纪以来,他们越发意识到传统科学直觉和试错法材料研发模式跟不上社会发展的脚步,成为限制社会发展进步的瓶颈。
为了维护自己的主导地位,他们纷纷提出了新材料的设计理念和新方法。
如美国的材料基因组计划、日本的玻璃、陶瓷、合金钢等领域材料数据库、知识库等,欧盟的高通量试验平台,德国的工业4.0。
2国内现状在1999年6月召开了以“发现和优化新材料的集成组合方法”为主题的香山会议,很多单位进行了相关尝试,但是由于各种问题,最后没有得到普及和开展。
当美国宣布材料基因组计划后,在国内引起了极大的响应,主要学术活动如下:2011年12月21-23日以“材料科学系统工程”为主题的香山会议;2013年3月14 日材料基因组咨询项目启动会;2013年12月15日“2013中国先进功能材料基因组技术高峰论坛”2014年4月18-20日第六届无机材料专题——材料基因组工程研究进展; 2014年科学院和工程院分别向国务院提交咨询报告;2015年9月17-20日的“材料基因组科学技术论坛”;2015年国家重点优先发展专项。
32011年12月21~23日香山科学会议学术讨论会,主题“材料科学系统工程”,旨在应对美国提出的材料基因组研究计划,对我国如何规划、开展实施自己的材料科学系统工程提出建议并进行深入的研讨。
国家自然科学基金委员会师昌绪研究员中国工程院徐匡迪教授清华大学顾秉林教授中科院物理所陈立泉研究员中科院金属所叶恒强研究员中科院化学所朱道本研究员北京有色金属研究总院屠海令研究员42013 年3 月14 日材料基因组”咨询项目启动会暨“材料基因组”•师昌绪、徐匡迪、陈难先、崔俊芝、干勇、葛昌纯、顾秉林、江东亮、黎乐民、南策文、屠海令、王崇愚、王鼎盛、王海舟、徐惠彬、薛其坤、杨裕生、叶恒强、张统一、张兴栋、周廉、朱静、祝世宁等23位中国科学院、中国工程院院士,近100 位知名专家参加了本次会议。
中科大固体物理

中科大固体物理
中科大固体物理专业是中科院固体物理研究所的研究生培养项目之一,该研究所成立于1982年3月,由国际著名物理学家、中国科学院院士葛庭燧先生创建。
经过三十多年的发展,现已成为凝聚态物理和材料科学基础研究的基地型研究所。
固体物理研究所是中科院材料物理重点实验室、安徽省纳米材料与技术重点实验室、安徽省特种金属材料工程实验室、安徽省纳米材料工程技术中心、中科院合肥物质科学研究院物质科学计算中心的依托单位,是凝聚态物理专业和材料物理与化学专业的硕士、博士学位培养基地,拥有物理学博士后流动站。
研究方向包括:纳米材料技术,新型功能材料,计算材料物理,内耗与固体缺陷,极端环境材料物理,核能工程材料,特种金属材料等。
1。
固体物理教学大纲

课程编号:011908 总学分:3学分固体物理(Solid-State Physics)课程性质:学科大类基础课适用专业:应用物理学专业学时分配:课程总学时:48学时。
其中:理论课学时:46学时(含演示学时);实验学时:0学时;上机学时:0学时;习题课学时:2学时。
先行、后续课程情况:先行课:高等数学、热力学与统计物理,;后续课:量子力学,原子物理。
教材:《固体物理学》,黄昆,韩汝琦,高等教育出版社参考书目:《固体物理学》,陆栋,上海科学技术出版社《固体物理基础》,阎守胜,北京大学出版社《固体物理简明教程》,蒋平,徐至中,复旦大学出版社一、课程的目的与任务固体物理学是应用物理和物理类各专业的一门必修基础课程,是继四大力学之后的一门基础且关键的课程,它的主要内容是研究固体的结构及组成粒子(原子、离子、电子等)之间的相互作用与运动规律,阐明固体的性能和用途,尤其以固态电子论和固体的能带理论为主要内容。
通过固体物理学的整个教学过程,使学生理解晶体结构的基本描述,固体电子论和能带理论,以及实际晶体中的缺陷、杂质、表面和界面对材料性质的影响等,掌握周期性结构的固体材料的常规性质和研究方法,了解固体物理领域的一些新进展,为以后的专业课学习打好基础。
二、课程的基本要求教学内容的基本要求分三级:掌握、理解、了解。
掌握:属于较高要求。
对于要求掌握的内容(包括定理、定律、原理等的内容、物理意义及适用条件)都应比较透彻明了,并能熟练地用以分析和计算有关问题,对于能由基本定律导出的定理要求会推导。
理解:属于一般要求。
对于要求理解的内容(包括定理、定律、原理等的内容、物理意义及适用条件)都应明了,并能用以分析和计算有关问题。
对于能由基本定律导出的定理不要求会推导。
了解:属于较低要求。
对于要求了解的内容,应该知道所涉及问题的现象和有关实验,并能对它们进行定性解释,还应知道与问题直接有关的物理量和公式等的物理意义。
三、课程教学内容绪论:了解固体的分类和固体物理学的研究内容;了解固体物理学的发展历史;了解固体物理学的研究方法。
中科大物理系培养方案

中科大物理系培养方案中科大物理系的培养方案那可是相当酷的。
一、基础课程阶段。
1. 数学基础。
首先呢,数学得学好。
像高等数学,这可是基石。
那里面的微积分啊,就像物理世界的魔法棒。
你想搞懂物理里的变化率之类的,没有微积分根本玩不转。
线性代数也不能少,矩阵啥的在处理物理中的多变量问题,比如量子力学里的态矢量表示,可太重要了。
还有数学物理方法,这门课就像是数学和物理的桥梁。
复变函数、偏微分方程的知识,在解物理中的各种场方程,像电磁场的麦克斯韦方程组的时候,那是必不可少的工具。
2. 物理基础。
普通物理肯定得学扎实啦。
力学部分,从牛顿定律到拉格朗日力学、哈密顿力学,就像一步步升级打怪。
你以为牛顿定律就够了?到了研究复杂系统的时候,拉格朗日和哈密顿的方法那是又简洁又强大。
热学也很有趣。
分子热运动、热力学定律,从微观的分子行为到宏观的热量传递、做功,这里面的学问可大了。
比如说为什么冰箱能制冷,这里面就全是热学的原理。
电磁学就更不用说了,电和磁的相互作用,从库仑定律到安培定律,再到麦克斯韦统一电磁场的伟大理论。
那电场、磁场就像看不见的魔法场,支配着电子的运动、电磁波的传播啥的。
光学也在这个阶段学。
光的反射、折射、干涉、衍射,这些现象不仅好看,背后的原理在很多高科技领域都有用,像光通信、激光加工啥的。
3. 实验技能。
普通物理实验是锻炼动手能力的好机会。
你得学会摆弄那些实验仪器,比如用游标卡尺精确测量物体的长度,用示波器看电信号的波形。
在实验里,你可能会遇到各种小状况,就像探险一样。
有时候仪器不听话,你就得像个小侦探一样去找出问题所在,是线路接错了,还是仪器本身有毛病?这个过程中,你就慢慢掌握了实验的技巧和物理量的测量方法。
二、专业课程阶段。
1. 核心物理理论。
量子力学那可是物理系的重头戏。
这里面的微观世界规则跟我们日常看到的完全不一样。
粒子可以同时处于多个状态,还有什么波粒二象性、量子纠缠。
就像进入了一个充满神秘和奇幻的微观世界,你得跟着薛定谔方程去探索粒子的状态变化,去理解那些奇奇怪怪的量子现象背后的数学逻辑。
中科大化学系物化方向培养计划

一
年
级
学时
120 40 60 40 80 80 60/60 80 80
学分
1 6 2 3 1 4 4
4 4 2
27/31 二
新课号
MA01002 PS01003 PE012* MA01003 PH01003 CH22002 CH22003 CH22702 PH01701 PH01009
小 年
老课号
001513 104007 103B01 001519 022153 019162 019123 019148 022162 022506 计 级
学分达到毕业要求。化学物理专业建议选修以下课程:
课程名称 *催化作用原理 *应用电化学 *单分子物理化学 *现代统计力学导论 *表面与胶体化学 *绿色化学 普通生物化学 电子线路 电子线路实验(1) 数据结构与数据库 机械制图(非机类)
微机原理与接口 四、主要课程关系结构图
学时 80 40 40 40 40 60 60 80 54
1 1 2 2 2 2 2 2 3 3 1 3 3 1 1 1 2 3 4
备注
两组选一 两组选一
两组选一 两组选一
学分小计
85/83
1.3 工科基础(4 学分)
5
计算机类 4
课程名称
计算机程序设计(B) 学分小计
学时 60/60
学分
4 4
开课学期 秋
建议年级 1 年级
2、专业部分:共计 18 学分
学时 120 120 80 60 40 40 40
80 80 80
80
80
80 60 60 60 60 80 40 80 40 80 80 80 60 60 80 60 60 40 80 80 80 80 80 80
中国科大物理学院培养方案

物理学院一、院系概况物理学院由物理系、近代物理系、光学与光学工程系和天文学系组成。
著名物理学家严济慈、赵忠尧、施汝为、钱临照、马大猷、吴有训、彭恒武、钱三强、朱洪元等曾在各系担任重要职务并执教多年。
现任院长为欧阳钟灿院士。
现有教职工232人,其中教授88人,副教授60人。
教授中有中科院院士8名,博士生导师80名,国家级教学名师2名,教育部长江学者4名,国家杰出青年基金获得者14名,中科院“百人计划”19名。
学院设有“严济慈大师讲席”和“赵忠尧大师讲席”,并聘请国内外近百名学者为兼职和客座教授。
物理学院内建有中国科学院重点实验室4个(量子信息重点实验室、基础等离子体物理重点实验室、核探测技术与核电子学重点实验室、星系与宇宙学重点实验室),省级重点实验室2个(光电子技术重点实验室、物理电子学重点实验室),同时,学院还紧密依托合肥微尺度物质科学国家实验室、国家同步辐射实验室开展科学研究。
物理学院的学科领域涵盖物理学、天文学、电子科学与技术、光学工程4个一级学科,包含光学、凝聚态物理、理论物理、粒子物理与原子核物理、等离子体物理、原子分子物理、天体物理、物理电子学、微电子与固体电子学、光学工程等10个二级学科。
物理学为国家一级重点学科,天体物理为国家二级重点学科,物理电子学、光学工程为省级重点学科。
物理学院以培养从事前沿和交叉科学的基础研究、应用研究和研制开发的领军人才为目标,注重对学生的物理素质和创新精神的培养。
学院的物理学和天文学均为国家理科基础科学研究和教学人才培养基地,物理实验教学中心为国家首批国家级示范教学中心。
本科生前期主要进行系统的基础理论教学和严格的实验动手能力训练,后期学生可根据自己的志趣和能力分别在10个二级学科范围内自主选择专业。
学院的本科毕业生约80%进入国内外大学或研究院所攻读研究生学位。
多年来,物理学院所属各系已经培养了一大批不同领域的杰出人才,包括10名中国科学院和中国工程院院士,多名从事国防事业的将军,以及活跃在国际科学研究前沿的年轻学者。
中科大高物名词解释Polymer Physics

Polymer Physics1.软物质:处于理想液体和理想固体这两个极端之间的中间带物质。
其间的弱连接性和密度低导致了它的“软”,并且外力作用主要不是能量效应而是熵的效应。
2.内聚能:1mol物质出去全部分子间作用力而使其内能增加的量。
3.内聚能密度:单位体积内某物质内聚能的大小,表征分子间作用力大小的物理量。
4.近程结构:是构成高聚物分子链最基本的结构,包括高聚合物的化学组成、结构单元的键接方式、结构单元的键接顺序、端基、支化与交联以及空间构型等。
5.远程结构:是指单个高分子链的大小和在空间存在的各种形状(形态、构象)例如:伸直链、无规线团、折叠链等,又称二级结构。
6.构型:由化学键所固定原子或原子团在空间的几何排列,这种排列是稳定的要改变构型必须通过化学键的断裂和重组。
7.等规度:是指高聚物中所含全同立构和间同立构在整个高聚物中所占的比例,也叫立构规整度。
8.全同指数:全同指数(IIP)是全同立构聚合物占聚合物总量的百分数。
9.自由内旋转:如果内旋转时完全不发生能量的变化,即分子中原子在空间中各种排布方式能量相同,这样的内旋转称之为自由内旋转。
10.受阻内旋转:实际的高分子链的内旋转不是自由的,因为C原子上所带的取代基在旋转过程中距离发生改变导致旋转时能量发生变化,内旋转受阻。
11.构象:是指分子中原子或是原子团由于单键内旋转而形成的在空间的排布称为构象,构象是不稳定的。
12.内旋转位垒:分子在内旋转时从最稳定的构象到最不稳定构象所需克服的能量。
13.内旋转异构体:对应位能曲线上不同深度位谷的相对稳定的构象即位能曲线上极小值点处的构象。
14.柔性:是指高分子链能够通过改变构象而无规卷曲的特性,柔性是长链高分子最主要的结构特征,是高聚物特有的结构层次。
15.刚性:与柔性相对的概念,之高分子链难以或不能改变其构象的性质。
16.持续长度:无限长的旋转链在第一个键方向上的投影平均值,是高分子链的刚性尺度。
固体物理教程答案

固体物理教程答案【篇一:黄昆固体物理课后习题答案4】>思考题1.设晶体只有弗仑克尔缺陷, 填隙原子的振动频率、空位附近原子的振动频率与无缺陷时原子的振动频率有什么差异?[解答]正常格点的原子脱离晶格位置变成填隙原子, 同时原格点成为空位,这种产生一个填隙原子将伴随产生一个空位的缺陷称为弗仑克尔缺陷. 填隙原子与相邻原子的距离要比正常格点原子间的距离小,填隙原子与相邻原子的力系数要比正常格点原子间的力系数大. 因为原子的振动频率与原子间力系数的开根近似成正比, 所以填隙原子的振动频率比正常格点原子的振动频率要高. 空位附近原子与空位另一边原子的距离, 比正常格点原子间的距离大得多, 它们之间的力系数比正常格点原子间的力系数小得多, 所以空位附近原子的振动频率比正常格点原子的振动频率要低.2.热膨胀引起的晶体尺寸的相对变化量?l/l与x射线衍射测定的晶格常数相对变化量?a/a存在差异,是何原因?[解答]la.3.kcl晶体生长时,在kcl溶液中加入适量的cacl2溶液,生长的kcl晶体的质量密度比理论值小,是何原因?[解答]2?2??由于ca离子的半径(0.99a)比k离子的半径(1.33a)小得不是太多, 所以caoo离子难以进入kcl晶体的间隙位置, 而只能取代k占据k离子的位置. 但ca一价, 为了保持电中性(最小能量的约束), 占据k离子的一个ca?2???2?比k高?将引起相邻的一个k?变成空位. 也就是说, 加入的cacl2越多, k?空位就越多. 又因为ca的原子量(40.08)?与k的原子量(39.102)相近, 所以在kcl溶液中加入适量的cacl2溶液引起k空位, 将导致kcl晶体的质量密度比理论值小.4.为什么形成一个肖特基缺陷所需能量比形成一个弗仑克尔缺陷所需能量低?[解答]形成一个肖特基缺陷时,晶体内留下一个空位,晶体表面多一个原子. 因此形成形成一个肖特基缺陷所需的能量, 可以看成晶体表面一个原子与其它原子的相互作用能, 和晶体内部一个原子与其它原子的相互作用能的差值. 形成一个弗仑克尔缺陷时,晶体内留下一个空位,多一个填隙原子. 因此形成一个弗仑克尔缺陷所需的能量, 可以看成晶体内部一个填隙原子与其它原子的相互作用能, 和晶体内部一个原子与其它原子相互作用能的差值. 填隙原子与相邻原子的距离非常小, 它与其它原子的排斥能比正常原子间的排斥能大得多. 由于排斥能是正值, 包括吸引能和排斥能的相互作用能是负值, 所以填隙原子与其它原子相互作用能的绝对值, 比晶体表面一个原子与其它原子相互作用能的绝对值要小. 也就是说, 形成一个肖特基缺陷所需能量比形成一个弗仑克尔缺陷所需能量要低.5.金属淬火后为什么变硬?[解答]我们已经知道晶体的一部分相对于另一部分的滑移, 实际是位错线的滑移, 位错线的移动是逐步进行的, 使得滑移的切应力最小. 这就是金属一般较软的原因之一. 显然, 要提高金属的强度和硬度, 似乎可以通过消除位错的办法来实现. 但事实上位错是很难消除的. 相反, 要提高金属的强度和硬度, 通常采用增加位错的办法来实现. 金属淬火就是增加位错的有效办法. 将金属加热到一定高温, 原子振动的幅度比常温时的幅度大得多, 原子脱离正常格点的几率比常温时大得多, 晶体中产生大量的空位、填隙缺陷. 这些点缺陷容易形成位错. 也就是说, 在高温时, 晶体内的位错缺陷比常温时多得多. 高温的晶体在适宜的液体中急冷, 高温时新产生的位错来不及恢复和消退, 大部分被存留了下来. 数目众多的位错相互交织在一起, 某一方向的位错的滑移,会受到其它方向位错的牵制, 使位错滑移的阻力大大增加, 使得金属变硬.6.在位错滑移时, 刃位错上原子受的力和螺位错上原子受的力各有什么特点?[解答]在位错滑移时, 刃位错上原子受力的方向就是位错滑移的方向. 但螺位错滑移时, 螺位错上原子受力的方向与位错滑移的方向相垂直.7.试指出立方密积和六角密积晶体滑移面的面指数.[解答]滑移面一定是密积面, 因为密积面上的原子密度最大, 面与面的间距最大, 面与面之间原子的相互作用力最小. 对于立方密积, {111}是密积面. 对于六角密积, (001)是密积面. 因此, 立方密积和六角密积晶体滑移面的面指数分别为{111}和(001).8.离子晶体中正负离子空位数目、填隙原子数目都相等, 在外电场作用下, 它们对导电的贡献完全相同吗?[解答]??由(4.48)式可知, 在正负离子空位数目、填隙离子数目都相等情况下, ab离子晶体的热缺陷对导电的贡献只取决于它们的迁移率?. 设正离子空位附近的离子和填隙离子的?a??a?ea?vi振动频率分别为和, 正离子空位附近的离子和填隙离子跳过的势垒高度分别为v????e?和ai, 负离子空位附近的离子和填隙离子的振动频率分别为bv和bi, 负离子空位附近e?e?的离子和填隙离子跳过的势垒高度分别bv为bi, 则由(4.47)矢可得?a??vea2?a?vkbte?e?av/kbt,i?a??iea2?a?kbtea2?b?ve?eai?/kbt, ?b??vkbtea2?b?ie?e?bv/kbt, ?b??ikbte?ebi?/kbt.由空位附近的离子跳到空位上的几率, 比填隙离子跳到相邻间隙位置上的几率大得多, 可e?e?以推断出空位附近的离子跳过的势垒高度, 比填隙离子跳过的势垒高度要低, 即avai,????????eb?eb???vi. 由问题1.已知, 所以有avai, bvbi. 另外, 由于a和b的离子半e??eb??a???b?径不同, 质量不同, 所以一般a, .?a???a???b???b?ivi也就是说, 一般v. 因此, 即使离子晶体中正负离子空位数目、填隙离子数目都相等, 在外电场作用下, 它们对导电的贡献一般也不会相同.9.晶体结构对缺陷扩散有何影响?[解答]扩散是自然界中普遍存在的现象, 它的本质是离子作无规则的布郎运动. 通过扩散可实现质量的输运. 晶体中缺陷的扩散现象与气体分子的扩散相似, 不同之处是缺陷在晶体中运动要受到晶格周期性的限制, 要克服势垒的阻挡, 对于简单晶格, 缺陷每跳一步的间距等于跳跃方向上的周期.10.填隙原子机构的自扩散系数与空位机构自扩散系数, 哪一个大? 为什么?[解答]填隙原子机构的自扩散系数1d2??02ae?(u2?e2)/kbt2,空位机构自扩散系数1d1??01ae?(u1?e1)/kbt2.自扩散系数主要决定于指数因子, 由问题4.和8.已知, u1u2,e1e2, 所以填隙原子机构的自扩散系数小于空位机构的自扩散系数.11.一个填隙原子平均花费多长时间才被复合掉? 该时间与一个正常格点上的原子变成间隙原子所需等待的时间相比, 哪个长?[解答]与填隙原子相邻的一个格点是空位的几率是n1/n, 平均来说, 填隙原子要跳n/n1步才遇到一个空位并与之复合. 所以一个填隙原子平均花费n1(u1?e2)/kbtt??2?en1?02的时间才被空位复合掉.由(4.5)式可得一个正常格点上的原子变成间隙原子所需等待的时间 1n2?21(u1?u2?e2)/kbt????epn1n2?02.由以上两式得ntn21.这说明, 一个正常格点上的原子变成间隙原子所需等待的时间, 比一个填隙原子从出现到被空位复合掉所需要的时间要长得多.12.一个空位花费多长时间才被复合掉?[解答]对于借助于空位进行扩散的正常晶格上的原子, 只有它相邻的一个原子成为空位时, ?eu2/kbt??它才扩散一步, 所需等待的时间是?1. 但它相邻的一个原子成为空位的几率是n1/n, 所以它等待到这个相邻原子成为空位, 并跳到此空位上所花费的时间n1(u1?e1)/kbtt??1?en1?01.13.自扩散系数的大小与哪些因素有关?[解答]填隙原子机构的自扩散系数与空位机构自扩散系数可统一写成11d??0a2e??/kbt??0a2e?n0?/rt22.可以看出, 自扩散系数与原子的振动频率?0, 晶体结构(晶格常数a), 激活能(n0?)三因素有关.14.替位式杂质原子扩散系数比晶体缺陷自扩散系数大的原因是什么? [解答]占据正常晶格位置的替位式杂质原子, 它的原子半径和电荷量都或多或少与母体原子半径和电荷量不同. 这种不同就会引起杂质原子附近的晶格发生畸变, 使得畸变区出现空位的几率大大增加, 进而使得杂质原子跳向空位的等待时间大为减少, 加大了杂质原子的扩散速度.15.填隙杂质原子扩散系数比晶体缺陷自扩散系数大的原因是什么?[解答]正常晶格位置上的一个原子等待了时间?后变成填隙原子, 又平均花费时间n?2n1后被空位复合重新进入正常晶格位置, 其中?2是填隙原子从一个间隙位置跳到相邻间隙位置所要等待的平均时间. 填隙原子自扩散系数反比于时间nt????2n1.因为所以填隙原子自扩散系数近似反比于?. 填隙杂质原子不存在由正常晶格位置变成填隙原子的漫长等待时间?, 所以填隙杂质原子的扩散系数比母体填隙原子自扩散系数要大得多.16.你认为自扩散系数的理论值比实验值小很多的主要原因是什么? [解答]目前固体物理教科书对自扩散的分析, 是基于点缺陷的模型, 这一模型过于简单, 与晶体缺陷的实际情况可能有较大差别. 实际晶体中, 不仅存在点缺陷, 还存在线缺陷和面缺陷, 这些线度更大的缺陷可能对扩散起到重要影响. 也许没有考虑线缺陷和面缺陷对自扩散系数的贡献是理论值比实验值小很多的主要原因.??17.ab离子晶体的导电机构有几种?[解答]??离子晶体导电是离子晶体中的热缺陷在外电场中的定向飘移引起的. ab离子晶体??????中有4种缺陷: a填隙离子, b填隙离子, a空位, b空位. 也就是说, ab离子晶体的导电机构有4种. 空位的扩散实际是空位附近离子跳到空位位置, 原来离子的位置变n?2n?1,????成了空位. ab离子晶体中, a空位附近都是负离子, b空位附近都是正离子. 由此可知, a空位的移动实际是负离子的移动, b空位的移动实际是正离子的移动. 因此, 在外电场作用下, a填隙离子和b空位的漂移方向与外电场方向一致, 而b填隙离子和?????a?空位的漂移方向与外电场方向相反.【篇二:黄昆版固体物理课后习题解答】>黄昆原著韩汝琦改编(陈志远解答,仅供参考)第一章晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
中科大、中科院试卷清单总汇

中科大、中科院试卷清单总汇许多试卷属中科院系统通用试卷,适用于中科院很多单位高等数学(甲)(中国科学院研究生院命题试卷)2006——2007高等数学(乙)(中国科学院研究生院命题试卷)2005(第1种),2005(第2种),2007高等数学(A)(中国科学院-中国科学技术大学联合命题试卷)2003——2008(2003——2008有答案)高等数学(B)(中国科学院-中国科学技术大学联合命题试卷)1993——2005(1993——2004有答案)高等数学(甲)(中国科学院-中国科学技术大学联合命题试卷)2001高等数学(丙)(中国科学院-中国科学技术大学联合命题试卷)2000——2002 高等数学(乙)(中国科学院-中国科学技术大学联合命题试卷)2000——2002(2000——2002有答案)普通物理(甲)(中国科学院研究生院命题试卷)2006——2007普通物理(乙)(中国科学院研究生院命题试卷)2007普通物理(A)(中国科学院-中国科学技术大学联合命题试卷)2003——2008(2003——2008有答案)普通物理(甲)(中国科学院-中国科学技术大学联合命题试卷)1997——1998,2000普通物理(B)(中国科学院-中国科学技术大学联合命题试卷)2003——2008(2004——2008有答案)普通物理(乙型)(中国科学院-中国科学技术大学联合命题试卷)1997——2002(1998,2000——2002有答案)量子力学(中国科学院研究生院命题试卷)2006——2007量子力学(中国科学院-中国科学技术大学联合命题试卷)2003——2008(2003——2008有答案)量子力学(实验型)(中国科学技术大学命题试卷)1990——1998(1997有答案)量子力学(实验型)(中国科学院命题试卷)1998——1999量子力学(实验型)(中国科学院-中国科学技术大学联合命题试卷)(2000——2002有答案)量子力学(理论型)(中国科学院-中国科学技术大学联合命题试卷)1990——2002 固体物理(中国科学院研究生院命题试卷)2007固体物理(B)(中国科学院研究生院命题试卷)2006——2007(2006——2007有答案)固体物理(中国科学技术大学命题试卷)1997——1999(1997有答案)固体物理(中国科学院命题试卷)1998,1999固体物理(中国科学院-中国科学技术大学联合命题试卷)2000——2008(2000——2008答案)电动力学(中国科学院研究生院命题试卷)2007电动力学(中国科学院命题试卷)1998电动力学(中国科学技术大学命题试卷)1999电动力学(中国科学院-中国科学技术大学联合命题试卷)2000——2002——2008有答案)电动力学(B)(中国科学院-中国科学技术大学联合命题试卷)2003——2005分析化学(中国科学院研究生院命题试卷)2007分析化学(中国科学院-中国科学技术大学联合命题试卷)1997,1997答案,1998,1998答案,1999,1999答案,2000A卷(第1种),2000A卷(第1种)答案,2000A卷(第2种),2000B卷,2000B卷答案,2001B卷(第1种),2001B卷(第1种)答案,2001B卷(第2种),2001B卷(第2种)答案,2002A卷,2002A卷答案,2002B卷(第1种),2002B卷(第2种),2002B卷(第2种)答案,2003A卷,2003A卷答案,2003B卷,2004,2004答案,2005B卷,2005B 卷答案,2006,2006答案,2007,2007答案,2008,2008答案物理化学(甲)(中国科学院研究生院命题试卷)2006——2008物理化学(乙)(中国科学院研究生院命题试卷)2007物理化学(中国科学院-中国科学技术大学联合命题试卷)1987,1995——2008(1995——2008有答案)物理化学(B)(中国科学院-中国科学技术大学联合命题试卷)2003——2008(2003——2008有答案)物理化学(C)(中国科学院-中国科学技术大学联合命题试卷)2004物理化学(合肥智能机械研究所命题试卷)2001——2004有机化学(中国科学院研究生院命题试卷)2006——2008有机化学(中国科学院命题试卷)1986——1990,1992——1998(1986,1988,1995——1998有答案)有机化学(中国科学技术大学命题试卷)1993,1998(1998有答案)有机化学(中国科学院-中国科学技术大学联合命题试卷)1999——2008(1999——2004,2006——2008有答案)无机化学(中国科学院研究生院命题试卷)2006——2007无机化学(中国科学院-中国科学技术大学联合命题试卷)1999——2008(2001,2003——2008有答案)高分子化学(中国科学院-中国科学技术大学联合命题试卷)1989,1991,1993——1998,2003——2005高分子化学与物理(中国科学院研究生院命题试卷)2007高分子化学与物理(中国科学院-中国科学技术大学联合命题试卷)1999——2002,2004(2001——2002有答案)高分子物理(中国科学院-中国科学技术大学联合命题试卷)1994高分子物理部分(中国科学院-中国科学技术大学联合命题试卷)2003(占总分值50%)高聚物的结构与性能(中国科学院-中国科学技术大学联合命题试卷)1996——1997,2001——2002普通化学(甲)(中国科学院研究生院命题试卷)2007普通化学(乙)(中国科学院研究生院命题试卷)2007普通化学(中国科学院-中国科学技术大学联合命题试卷)2001,2004——2008(2004,2006——2008有答案)综合化学(中国科学院命题试卷)1996综合化学(中国科学技术大学命题试卷)1999——2004有答案)基础化学(中国科学院-中国科学技术大学联合命题试卷)2008(2008有答案)化工原理(中国科学院研究生院命题试卷)2005,2007化学工程学(中国科学院-中国科学技术大学联合命题试卷)2003——2004(2004有答案)半导体物理(甲)(中国科学院研究生院命题试卷)2007半导体物理(乙)(中国科学院研究生院命题试卷)2007半导体物理(中国科学院、半导体研究所、中国科学技术大学联合命题试卷)1997——2002,2004(1997——2002有答案)半导体物理(中国科学院微电子中心命题试卷)2004半导体材料(半导体研究所命题试卷)1996,1998,2000——2001(1996,2000有答案)半导体材料物理(半导体研究所命题试卷)2002——2003半导体集成电路(中国科学院-中国科学技术大学联合命题试卷)2001——2002,2004(2002有答案)半导体模拟集成电路(中国科学技术大学、半导体研究所联合命题试卷)1995——1996,1998(1996,1998,1999有答案)模拟集成电路(中国科学技术大学、半导体研究所联合命题试卷)1997(1997有答案)材料力学(中国科学院研究生院命题试卷)2007——2008材料力学(中国科学院-中国科学技术大学联合命题试卷)2001,2003——2008(2001,2003——2007有答案)材料力学(等离子体物理研究所试卷)2004(2004有答案)大气科学导论(中国科学院-中国科学技术大学联合命题试卷)2005——2008(2005——2008有答案)地球化学(中国科学院研究生院命题试卷)2007地球化学(中国科学院-中国科学技术大学联合命题试卷)2000——2002,2004——2005地球物理学(中国科学院研究生院命题试卷)2007第四纪地质学(中国科学院研究生院命题试卷)2007电磁场理论(中国科学院-中国科学技术大学联合命题试卷)2003电路(中国科学院研究生院命题试卷)2007电子技术(中国科学院研究生院命题试卷)2007电子线路(中国科学院研究生院命题试卷)2007电子线路(中国科学院-中国科学技术大学联合命题试卷)1996——2008(1996——2001,2003——2008有答案)(注:2002年的试卷共12页,缺P2—P5)电子线路(电子所命题试卷)2002——2005(2002——2004有答案)电子线路(半导体研究所命题试卷)2002——2004信号与系统(中国科学院研究生院命题试卷)2006——2007信号与系统(中国科学技术大学命题试卷)1990——1999(1996——1999有答案)(另:有《信号与系统》期末考试试题11份,每份3元。
中科大化材学院研究生培养方案

无机化学(学科代码:070301)一、培养目标本学科培养德、智、体全面发展,具有坚实系统的无机化学理论基础,掌握现代化学实验技能,了解无机化学的国际前沿领域和发展动态,能在科学研究中作出创造性的成果,并能够适应我国经济、科技、教育发展需要,面向二十一世纪的从事无机化学研究和教育的高层次人才。
二、研究方向1.无机固体化学2.纳米化学3.仿生材料化学4.络合物化学5.生物无机化学6.新超导材料的设计和制备7.非线性光学材料8.分离提纯科学9.化学键理论三、学制及学分1、硕士生学制为2-3年,研究生在申请硕士学位前,必须取得总学分不低于35分。
其中公共必修课(英语、政治)为7学分;院定基础课获得的学分不低于10分,院定基础课和专业基础课获得的总学分不低于16分。
2、博士阶段学制为3-4年,研究生在申请博士学位前,必须取得总学分不低于10分。
其中公共必修课(英语、政治)为4学分;院定基础课(累计考核)为2学分;进展课至少2学分。
3、硕博连读生学制为5-6年,研究生在申请博士学位前,必须取得总学分不低于45分(包括硕士阶段)。
其中公共必修课(英语、政治)为11学分;院定基础课获得的学分不低于12分(包括累计考核2学分),院定基础课和专业基础课获得的总学分不低于16分;总学分中至少包含一门进展课2学分。
四、课程设置1、英语、政治等公共必修课和必修环节按研究生院统一要求。
2、专业课程分为院定基础课、专业基础课及专业选修课。
基础课和专业课如下所列。
院定基础课:累计考核(2)(博士生必修)纳米化学(3)CH16205团簇和团簇化学(2)CH25203分子光谱分析进展(3)CH25204近代电分析化学(3)CH25205分离科学与进展(3)CH35201高等有机化学(4)CH35202有机合成化学(4)CH34201有机结构分析(4)CH45208量子化学(4)CH44203反应动力学(4)CH44202分子光谱学(4)CH55201功能高分子(4)CH55202高分子凝聚态物理(4)CH55204聚合物研究方法(4)CH65205污染控制材料(2)CH65201膜科学与技术(3)CH65202环境生物技术原理(3)MS15203固体物理(4)MS15207固体材料结构(4)MS15201材料物理(4)MS25201热力学与相平衡(3)MS25202材料中的速率过程(3)MS25203材料合成化学(3)专业基础课:CH15201固体化学原理(3)CH15202结晶化学导论(3)CH15203相平衡及在材料科学中的应用(3)CH15204结构配位化学(3)CH15205高等无机化学(3)CH16207无机化学进展(3)专业选修课:CH15206生物无机化学(3)CH15207近代分离方法导论(3)CH45202催化作用原理(4)CH44206绿色化学(3)PH55220X射线衍射(3)PH55219透射电子显微学(2.5)PH55222物质结构的波谱能谱分析(3)CH16202高等配位化学(2)CH16206生物无机化学导论(2)说明:1、经导师同意,研究生可任选各学位点开出的进展课。
中科大2016年推免生拟录取名单
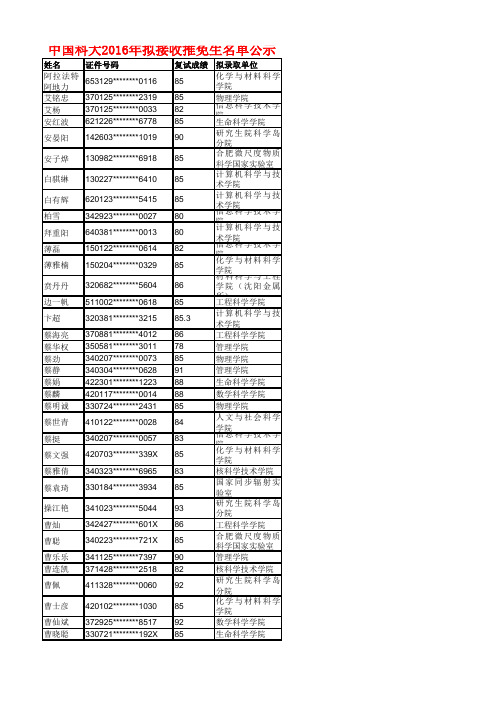
姓名证件号码复试成绩拟录取单位阿拉法特·阿地力653129********011685化学与材料科学学院艾铭忠370125********231985物理学院艾杨370125********003382信息科学技术学院安红波621226********677885生命科学学院安晏阳142603********101990研究生院科学岛分院安子烨130982********691885合肥微尺度物质科学国家实验室白骐綝130227********641085计算机科学与技术学院白有辉620123********541585计算机科学与技术学院柏雪342923********002780信息科学技术学院拜重阳640381********001380计算机科学与技术学院薄磊150122********061482信息科学技术学院薄雅楠150204********032985化学与材料科学学院贲丹丹320682********560486材料科学与工程学院(沈阳金属所)边一帆511002********061885工程科学学院卞超320381********321585.3计算机科学与技术学院蔡海亮370881********401286工程科学学院蔡华权350581********301178管理学院蔡劲340207********007385物理学院蔡静340304********062891管理学院蔡娟422301********122388生命科学学院蔡麟420117********001488数学科学学院蔡明诚330724********243185物理学院蔡世青410122********002884人文与社会科学学院蔡挺340207********005783信息科学技术学院蔡文强420703********339X 85化学与材料科学学院蔡雅倩340323********696583核科学技术学院蔡袁琦330184********393485国家同步辐射实验室操江艳341023********504493研究生院科学岛分院曹灿342427********601X 86工程科学学院曹聪340223********721X 85合肥微尺度物质科学国家实验室曹乐乐341125********739790管理学院曹连凯371428********251882核科学技术学院曹佩411328********006092研究生院科学岛分院曹士彦420102********103085化学与材料科学学院曹仙斌372925********851792数学科学学院曹晓聪330721********192X 85生命科学学院中国科大2016年拟接收推免生名单公示曹扬140123********023183材料科学与工程学院(沈阳金属所)曹伊人420682********202376信息科学技术学院曹原342923********002885化学与材料科学学院曹泽华320902********301385物理学院曾陈明420821********559588.5生命科学学院曾凯511524********061985物理学院曾令华510522********693686信息科学技术学院曾思韶120101********054481管理学院查君鹏340702********001087计算机科学与技术学院柴丽341281********104880信息科学技术学院常福莹120103********732090数学科学学院常敬腾320321********021491数学科学学院常静静341225********028389工程科学学院常力戈411002********152987工程科学学院常向廷411627********643186工程科学学院晁婷婷610322********454785化学与材料科学学院晁燕410502********500794研究生院科学岛分院车勇510703********291694研究生院科学岛分院陈斌430524********717490地球和空间科学学院陈斌340825********021790研究生院科学岛分院陈秉伦330782********003390化学与材料科学学院陈柄任210104********611583.3计算机科学与技术学院陈博文220102********181690地球和空间科学学院陈畅350102********155289信息科学技术学院陈朝阳411422********571882材料科学与工程学院(沈阳金属所)陈晨342623********146886化学与材料科学学院陈冲410221********991580计算机科学与技术学院陈冲520113********361191地球和空间科学学院陈春霖510623********301776信息科学技术学院陈纯缙332526********513985材料科学与工程学院(沈阳金属所)陈道敏342501********321480信息科学技术学院陈德康340603********105086国家同步辐射实验室陈迪350104********261686信息科学技术学院陈冬晓610521********001X 88化学与材料科学学院陈舫340825********021161信息科学技术学院陈放342422********081685化学与材料科学学院陈丰130984********091686生命科学学院陈福升652927********423185物理学院陈耿350122********211485核科学技术学院陈光610104********111685化学与材料科学学院陈国勇341281********461377信息科学技术学院陈涵510726********001493工程科学学院陈昊磊130503********091485物理学院陈浩340826********117380计算机科学与技术学院陈虹宇510722********705389工程科学学院陈华岳120113********003092地球和空间科学学院陈吉强140621********001379计算机科学与技术学院陈继明142430********311085物理学院陈嘉璐500102********081895化学与材料科学学院陈江军340827********181186化学与材料科学学院陈杰342625********283985工程科学学院陈金挺331081********761685物理学院陈炯玮330681********501189工程科学学院陈俊杰330381********751384地球和空间科学学院陈可511321********280594研究生院科学岛分院陈黎342401********698785工程科学学院陈丽丽342625********282387生命科学学院陈亮411322********003592信息科学技术学院陈璐430223********422693研究生院科学岛分院陈淼230602********362582地球和空间科学学院陈闽强352227********001681信息科学技术学院陈明博320582********851985物理学院陈楠341024********922480信息科学技术学院陈鹏340223********281885信息科学技术学院陈秋瑶450821********002977信息科学技术学院陈升430624********933385工程科学学院陈硕411121********054882信息科学技术学院陈思430181********501185合肥微尺度物质科学国家实验室陈腾飞340621********321185物理学院陈田田371525********002988数学科学学院陈务远422202********007187化学与材料科学学院陈翔340111********603478信息科学技术学院陈晓敏513821********220089.5生命科学学院陈心怡320482********730392信息科学技术学院陈欣冉340322********002584人文与社会科学学院陈新150402********132894数学科学学院陈新凯420704********057785物理学院陈星340121********581988研究生院科学岛分院陈旭松340121********703287信息科学技术学院陈宣良411123********003X 83材料科学与工程学院(沈阳金属所)陈雪雯420583********042880计算机科学与技术学院陈亚奇320112********041185物理学院陈阳341222********105X 85物理学院陈怡遐330681********178790工程科学学院陈以诺430304********127294工程科学学院陈玉文440711********572590管理学院陈玉莹340621********442688.3计算机科学与技术学院陈昱衡370302********751X 76信息科学技术学院陈煜章340123********451585工程科学学院陈远强342922********177689地球和空间科学学院陈昭昀420103********325085物理学院陈阵340322********009891信息科学技术学院陈振武342225********661X 90地球和空间科学学院陈震342423********207385合肥微尺度物质科学国家实验室陈志341226********101085化学与材料科学学院陈志鹏362525********331585合肥微尺度物质科学国家实验室陈竹340122********002680信息科学技术学院陈紫渝350881********077380信息科学技术学院陈自强411524********273686信息科学技术学院成博宇130984********003185物理学院成赢500101********331089生命科学学院承心怡320483********272785合肥微尺度物质科学国家实验室程彪340823********673385信息科学技术学院程春阳340406********321685物理学院程光340822********285890管理学院程慧茹340123********432185物理学院程慧媛340802********042685化学与材料科学学院程丽红341621********552390管理学院程龙灿429006********127388工程科学学院程梦卓362330********349674计算机科学与技术学院程铭410205********051X 85合肥微尺度物质科学国家实验室程普420111********661683信息科学技术学院程锐610581********260190管理学院程亦雨341202********051492数学科学学院程自强342426********361590数学科学学院储润润340824********502087化学与材料科学学院储艳清340824********004X 85化学与材料科学学院储宇奇342426********021390研究生院科学岛分院丛松宇210104********371774信息科学技术学院崔聪210781********403685材料科学与工程学院(沈阳金属所)崔笛340881********024892管理学院崔明明232101********283395管理学院崔硕530381********194085化学与材料科学学院崔巍410702********051985信息科学技术学院崔燕平510821********551885信息科学技术学院崔扬340721********242685信息科学技术学院崔艺文411481********454487工程科学学院笪良军340881********531778火灾科学国家重点实验室代白杨612501********001485合肥微尺度物质科学国家实验室代海涛341623********833489地球和空间科学学院代苑莹513822********020088信息科学技术学院戴德云340521********402875信息科学技术学院戴函320821********011992数学科学学院戴皓珽330106********401885物理学院戴立360424********001185信息科学技术学院戴维佳321283********301292信息科学技术学院戴智鑫320602********151580材料科学与工程学院(沈阳金属所)单传强341181********001080信息科学技术学院单翠翠342221********352785合肥微尺度物质科学国家实验室单小岩230605********181X 80信息科学技术学院单子涵220702********944590地球和空间科学学院邓贝贝420106********401787生命科学学院邓国强371428********053989材料科学与工程学院(沈阳金属所)邓家俊430111********073588信息科学技术学院邓维430621********043480管理学院丁超220582********091386地球和空间科学学院丁红鹤411481********423989国家同步辐射实验室丁佳晨610103********363082信息科学技术学院丁亮320611********342285化学与材料科学学院丁露锋430524********633X 85生命科学学院丁三潮421181********093883计算机科学与技术学院丁施清341225********014088国家同步辐射实验室丁小兵342623********443385信息科学技术学院丁旭340207********002985合肥微尺度物质科学国家实验室丁雅霖340111********452580管理学院丁治强450325********091377信息科学技术学院董菲342522********242687信息科学技术学院董芬芬340221********496287生命科学学院董浩340121********431076研究生院科学岛分院董华楠330621********690390数学科学学院董晶晶340621********202988国家同步辐射实验室董峻源511621********673280信息科学技术学院董若石210902********153085物理学院董天浩320923********421385物理学院董晓娟341221********902483信息科学技术学院董智慧341181********004992管理学院窦润东342423********005184信息科学技术学院杜博620422********432285物理学院杜德鑫371428********059785化学与材料科学学院杜海石210104********341682计算机科学与技术学院杜华140624********725081核科学技术学院杜坤420104********402488信息科学技术学院杜秋燕341222********102890地球和空间科学学院杜文文620503********171186计算机科学与技术学院杜祥慧370883********092389生命科学学院杜旭涛330206********031685合肥微尺度物质科学国家实验室杜毅620523********001185化学与材料科学学院杜志威429006********765285生命科学学院段贺211224********702678材料科学与工程学院(沈阳金属所)段隆宇360203********101384地球和空间科学学院段无瑕142603********104090生命科学学院段旭东371481********721290地球和空间科学学院段雪梅510182********062880信息科学技术学院樊连峰413026********061685合肥微尺度物质科学国家实验室樊奕510921********032087国家同步辐射实验室樊彧321081********781593管理学院范炜盛340123********259490研究生院科学岛分院方海涛422101********661285核科学技术学院方涵341002********141983信息科学技术学院方鸿强420104********121580火灾科学国家重点实验室方洁330227********754892管理学院方启林342622********063980信息科学技术学院方沁怡340403********262390管理学院方舒150429********002776信息科学技术学院方妍420116********460986工程科学学院方园342622********753183信息科学技术学院房亚男370282********302892材料科学与工程学院(沈阳金属所)房永峰340823********313490研究生院科学岛分院费乙洋511023********119790化学与材料科学学院冯超320623********001685合肥微尺度物质科学国家实验室冯晨510722********706X 85合肥微尺度物质科学国家实验室冯海军340123********729590管理学院冯绍文360203********153X 85合肥微尺度物质科学国家实验室冯爽342426********426088研究生院科学岛分院冯韬320382********191992研究生院科学岛分院冯万泉371502********031988数学科学学院冯晓云410181********752888信息科学技术学院冯宇超142431********005283材料科学与工程学院(沈阳金属所)冯玉杰412701********202183公共事务学院付景智342221********251782计算机科学与技术学院付生伟321324********301685合肥微尺度物质科学国家实验室付贤玲342401********528280火灾科学国家重点实验室付艳晴320322********472985火灾科学国家重点实验室付永旭372330********105485物理学院甘蕴久420606********001385合肥微尺度物质科学国家实验室高宝峰371623********413585核科学技术学院高飞亮410329********967685国家同步辐射实验室高峰360427********301980计算机科学与技术学院高健342423********785X 84工程科学学院高洁341126********022884公共事务学院高劲松340721********511094数学科学学院高婧婧340421********242990研究生院科学岛分院高军341622********151293.4材料科学与工程学院(沈阳金属所)高磊371323********912090地球和空间科学学院高梅君340121********792585信息科学技术学院高明230503********131676材料科学与工程学院(沈阳金属所)高潇330124********231090地球和空间科学学院高雅文340302********002890管理学院高岩370684********312383生命科学学院高仰刚362401********403685化学与材料科学学院高蕴智130982********752088化学与材料科学学院高志付340421********203088信息科学技术学院郜东方411123********601693数学科学学院葛殿龙341222********101890研究生院科学岛分院葛美红342531********282297研究生院科学岛分院葛鹏342601********061090研究生院科学岛分院葛维421222********001282信息科学技术学院葛阳洋320683********455988信息科学技术学院耿波涛341224********371180管理学院耿佳琪342201********084085物理学院宫帅340402********061480信息科学技术学院宫祥云321281********795992数学科学学院龚成431081********049493数学科学学院龚海华340826********003680计算机科学与技术学院龚鸣川342601********211593管理学院龚少博420982********321481核科学技术学院龚仕鹏411526********483285合肥微尺度物质科学国家实验室龚涛142727********601083信息科学技术学院龚玺421281********251285物理学院龚振342426********003980软件学院古健340222********101585化学与材料科学学院古雪姣420881********404290国家同步辐射实验室顾俊341221********151X 80信息科学技术学院顾守曦321324********141990研究生院科学岛分院顾玥320602********452X 89化学与材料科学学院关桥桥340621********820585化学与材料科学学院关圣楠340621********082685工程科学学院官润南360702********061990化学与材料科学学院桂永强413026********451583信息科学技术学院郭和茹342625********004490研究生院科学岛分院郭慧泉330702********321285物理学院郭佳佳321283********341985信息科学技术学院郭建320324********117283工程科学学院郭俊良610113********253083.3计算机科学与技术学院郭凯与210302********211291数学科学学院郭磊412824********681588信息科学技术学院郭明晓371526********402785材料科学与工程学院(沈阳金属所)郭晴艳330481********624183.3生命科学学院郭瑞妍410221********884285化学与材料科学学院郭文慧410221********762387工程科学学院郭文哲340322********243085物理学院郭晓慧370126********152X 88材料科学与工程学院(沈阳金属所)郭旭370725********041589工程科学学院郭宇430981********183X 90化学与材料科学学院郭昱君142601********972284生命科学学院郭钰340825********431385物理学院郭跃340102********251889化学与材料科学学院郭子颖421126********382781信息科学技术学院国健男210903********051480信息科学技术学院哈梦可341222********076085合肥微尺度物质科学国家实验室韩成成130182********243493信息科学技术学院韩春慧230521********111890研究生院科学岛分院韩丁丁412728********524089工程科学学院韩福洲341221********261878材料科学与工程学院(沈阳金属所)韩浩420922********423086信息科学技术学院韩江萍410305********054187信息科学技术学院韩凯341226********389585信息科学技术学院韩露341227********443885化学与材料科学学院韩守诚420323********051290地球和空间科学学院韩云飞341222********561480研究生院科学岛分院郝娅汝370102********372190人文与社会科学学院郝雨筱410522********814886工程科学学院何超华140602********551585合肥微尺度物质科学国家实验室何晨露341024********801085化学与材料科学学院何德威420984********663X 81信息科学技术学院何富冬340822********181185物理学院何泓川210404********211285化学与材料科学学院何俊江320681********521881火灾科学国家重点实验室何凯340603********021484生命科学学院何坤411503********501580火灾科学国家重点实验室何灵欣522221********121078火灾科学国家重点实验室何苗610326********166X 87化学与材料科学学院何迁迁340881********134279火灾科学国家重点实验室何声一340824********003992计算机科学与技术学院何天宇340204********261392信息科学技术学院何韦刚340811********631485合肥微尺度物质科学国家实验室何伟栋330282********001280计算机科学与技术学院何先婷340321********310593研究生院科学岛分院何異500381********732788研究生院科学岛分院何宇强321283********143279信息科学技术学院何泽洲342427********691492工程科学学院何子力420703********621285物理学院贺克宝342224********071285核科学技术学院贺丽萍140224********474285.4生命科学学院贺晓东430321********653X 87化学与材料科学学院贺云天340304********003892计算机科学与技术学院洪昌文340223********111085化学与材料科学学院洪阳411481********331290数学科学学院侯利410504********108885合肥微尺度物质科学国家实验室侯梦青370829********354085化学与材料科学学院侯明心411403********152X 88化学与材料科学学院侯晓天340102********101990管理学院侯耀平410329********154986工程科学学院侯颖亭513902********388889生命科学学院侯壮豪445222********355692化学与材料科学学院胡传真342201********281793工程科学学院胡代明430482********219290地球和空间科学学院胡继恒340321********439891地球和空间科学学院胡佳栋330902********741X 85物理学院胡军342601********185582化学与材料科学学院胡均毅330211********001380计算机科学与技术学院胡庆庆342425********002485信息科学技术学院胡若晨340103********305288信息科学技术学院胡淑萍360782********252289信息科学技术学院胡松341224********491288研究生院科学岛分院胡泰斗340826********225183生命科学学院胡涛362401********201493工程科学学院胡腾飞340621********033585信息科学技术学院胡腾飞411481********696890生命科学学院胡婷婷341227********762185化学与材料科学学院胡婉璐340702********052086工程科学学院胡万培130722********384785化学与材料科学学院胡维达429004********003985物理学院胡晓丹341002********144393研究生院科学岛分院胡亚敏142703********067485计算机科学与技术学院胡严敏340826********225585化学与材料科学学院胡逸飞340104********303480计算机科学与技术学院胡银雷410329********303492数学科学学院胡莹莹412326********724785物理学院胡永泉340202********201785信息科学技术学院胡月乔622102********002590地球和空间科学学院胡郅虬420704********031685化学与材料科学学院胡治江340103********303990工程科学学院华天鹏430623********481086化学与材料科学学院黄超明320401********343077信息科学技术学院黄冲420984********504580.5生命科学学院黄传力420105********361785火灾科学国家重点实验室黄东阳340123********789682生命科学学院黄渡342501********381290地球和空间科学学院黄革421102********323795研究生院科学岛分院黄建民342427********661689国家同步辐射实验室黄江雷622727********831283信息科学技术学院黄立航350205********001X 90工程科学学院黄林坤362424********161585化学与材料科学学院黄凌瑞340122********227785工程科学学院黄璐362425********322890研究生院科学岛分院黄猛341225********901186化学与材料科学学院黄桥422801********101990人文与社会科学学院黄睿奇211381********001985生命科学学院黄珊340824********142885化学与材料科学学院黄泰子362424********541690地球和空间科学学院黄彤彤370781********222489生命科学学院黄伟恒442000********095090国家同步辐射实验室黄伟哲360502********161785物理学院黄文环460004********527885合肥微尺度物质科学国家实验室黄文杰610113********213487信息科学技术学院黄新亚341125********546083.6生命科学学院黄炎340104********202084生命科学学院黄烨凯320681********163985化学与材料科学学院黄一桓450103********001285工程科学学院黄优421127********081485合肥微尺度物质科学国家实验室黄禹侨450103********251885管理学院黄仔452122********421480计算机科学与技术学院黄正薇342422********608092管理学院火清羿320105********101491数学科学学院霍庆海130924********353290数学科学学院霍延凯370681********401085工程科学学院霍姚远340104********301785合肥微尺度物质科学国家实验室季佳旭410781********042X 85物理学院季琴342623********682185信息科学技术学院冀伟安341281********207390工程科学学院郏乘帆331081********007682计算机科学与技术学院贾春妮653130********284787材料科学与工程学院(沈阳金属所)贾存磊130133********339984材料科学与工程学院(沈阳金属所)贾顿340602********243279火灾科学国家重点实验室贾翔宇341222********476488信息科学技术学院贾亚宁130582********482893研究生院科学岛分院贾宇宁140202********304988化学与材料科学学院简敏珍362204********304X 88化学与材料科学学院江晨辉340881********513985化学与材料科学学院江捷445122********503985物理学院江蒙411522********004085化学与材料科学学院江伟韬452223********203390化学与材料科学学院江兴何341623********321990计算机科学与技术学院江艳泓340881********522582公共事务学院姜佳静341024********802788工程科学学院姜丽华370613********104X 80火灾科学国家重点实验室姜毛毛342625********100191信息科学技术学院姜宁370681********002282火灾科学国家重点实验室姜世民140223********001086国家同步辐射实验室姜秀梅340322********162X 87工程科学学院姜雪莹650103********282274管理学院蒋立峰330621********151685化学与材料科学学院蒋鹏飞341221********487285信息科学技术学院蒋诗威362322********391185地球和空间科学学院蒋素会130432********132990地球和空间科学学院蒋一聪340102********152390管理学院蒋志猛362330********757886信息科学技术学院焦曼340803********278685物理学院焦庆磊320304********521X80信息科学技术学院焦瑞恒371203********351185物理学院焦阳612301********033290化学与材料科学学院矫德峰220282********261983生命科学学院接丹丹340603********024185人文与社会科学学院解春342425********471387国家同步辐射实验室解尧410402********563481核科学技术学院金斌斌330282********003X80计算机科学与技术学院金晶340824********002188地球和空间科学学院金效梅341225********012694研究生院科学岛分院金宇婷210211********434281材料科学与工程学院(沈阳金属所)晋忠孝140428********001184计算机科学与技术学院靳启祯410802********003587地球和空间科学学院靳宗梓510725********771987化学与材料科学学院井方铭210411********183985物理学院巨力610323********041285化学与材料科学学院康丽丽410727********092692研究生院科学岛分院康桥320106********361X94数学科学学院康卫敏429005********089887公共事务学院孔垂麟130202********271692工程科学学院孔繁羽340104********201886工程科学学院孔婕370911********402193数学科学学院孔维文410621********253785材料科学与工程学院(沈阳金属所)孔祥栋622624********239485化学与材料科学学院况志强362228********051490研究生院科学岛分院兰家欣142329********232992地球和空间科学学院兰荣亨350824********181180信息科学技术学院乐伟510181********461585核科学技术学院雷晶440204********392685化学与材料科学学院雷言言412727********004785工程科学学院雷泽灵350724********203588信息科学技术学院黎凌云342523********822691生命科学学院黎盛阳360403********151X80管理学院李冰410102********012783.5生命科学学院李博411522********693X 76火灾科学国家重点实验室李博文511623********573485国家同步辐射实验室李琛411402********002385化学与材料科学学院李传冰420103********441185核科学技术学院李传召372929********031385合肥微尺度物质科学国家实验室李春龙370303********761685物理学院李聪410621********001987生命科学学院李翠440803********342389化学与材料科学学院李丹130131********392983核科学技术学院李东君370784********582286化学与材料科学学院李栋130184********601291信息科学技术学院李奉誉341125********009385工程科学学院李国春370725********507482火灾科学国家重点实验室李国欣411422********123695研究生院科学岛分院李晗340881********331285计算机科学与技术学院李晗371524********303389工程科学学院李航420982********495X 85合肥微尺度物质科学国家实验室李浩宇230103********511488数学科学学院李亨370682********561285物理学院李宏广430405********451379信息科学技术学院李泓旻450481********381882信息科学技术学院李虎成511622********023788材料科学与工程学院(沈阳金属所)李辉410621********353485物理学院李慧平360782********131X 85物理学院李慧群421127********254X 89信息科学技术学院李济安340202********201690管理学院李佳341226********449067信息科学技术学院李佳惠370786********482290研究生院科学岛分院李家强340111********501990研究生院科学岛分院李嘉110102********112790管理学院李剑波500381********021992数学科学学院李杰341223********119785合肥微尺度物质科学国家实验室李洁370911********002X 91研究生院科学岛分院李结文340827********651090地球和空间科学学院李京京340104********202X 95管理学院李景新150429********292280.5生命科学学院李璟奭320283********323585化学与材料科学学院李娟612430********042693数学科学学院李军340827********471885信息科学技术学院李俊瑶610112********204285物理学院李凯362528********501980管理学院李可寒430602********401785物理学院李宽130421********601588工程科学学院李宽370705********051985化学与材料科学学院李磊340123********467X 85合肥微尺度物质科学国家实验室李立夫341102********081289国家同步辐射实验室李莉370481********604180信息科学技术学院李六六410822********557384核科学技术学院李曼370481********426080信息科学技术学院李梦涵370724********386X 92地球和空间科学学院李梦娜342224********094985化学与材料科学学院李梦婷511602********196994研究生院科学岛分院李敏511303********512X 85物理学院李敏412725********912792数学科学学院李明412822********202789工程科学学院李明洋341226********231085化学与材料科学学院李娜372922********740285国家同步辐射实验室李磐342221********743986核科学技术学院李盼盼341203********281081.1生命科学学院李鹏342423********047770信息科学技术学院李鹏程340123********469492信息科学技术学院李琴511123********456682生命科学学院李姗姗372922********900885工程科学学院李少华340322********563182信息科学技术学院李少炜350783********701985合肥微尺度物质科学国家实验室李诗昂342529********001492化学与材料科学学院李士博230604********411280信息科学技术学院李爽132930********356590数学科学学院李思宇130203********002185生命科学学院李檀372924********002379信息科学技术学院李腾130102********121983信息科学技术学院李铁强410402********561985合肥微尺度物质科学国家实验室李韦340521********545682计算机科学与技术学院李伟健420607********363085信息科学技术学院李伟祥441323********851392信息科学技术学院李伟泽450404********241985化学与材料科学学院李文涵372330********004184生命科学学院李文倩340103********102185生命科学学院李西川510922********765385化学与材料科学学院李小丹420117********632085信息科学技术学院李小喜342225********531688信息科学技术学院李晓帆370829********625X85物理学院李晓磊340104********201696地球和空间科学学院李晓齐652301********154591材料科学与工程学院(沈阳金属所)李笑笑372922********622872材料科学与工程学院(沈阳金属所)李星320305********243X90地球和空间科学学院李星悦321084********652578计算机科学与技术学院李旭东342623********501788信息科学技术学院李宣令140109********101285物理学院李璇431230********002187工程科学学院李雪341203********256785化学与材料科学学院李雪燕370502********044989地球和空间科学学院李雅倩341621********212294研究生院科学岛分院李亚祥420621********227585工程科学学院李娅宁620422********432888工程科学学院李阳342423********357780生命科学学院李洋360103********591X85物理学院李业422130********411283信息科学技术学院李伊薇340406********344990管理学院李勇341204********201492数学科学学院李游321023********022990管理学院李雨农350524********157185合肥微尺度物质科学国家实验室李雨倩411402********552182计算机科学与技术学院李玉芳340825********472785信息科学技术学院李玉巧622322********242289数学科学学院李沅锦371122********061585物理学院李远瞳362527********171989工程科学学院李悦220381********362X85合肥微尺度物质科学国家实验室李占科371581********313X85工程科学学院李兆锐210104********231685化学与材料科学学院李祯星411322********131881.5生命科学学院李政120102********261177管理学院李志彬341282********461975信息科学技术学院李忠锋412326********277985物理学院李子龙420105********081984火灾科学国家重点实验室李子味432501********002085物理学院廉超341226********041883核科学技术学院梁礼培362422********621684信息科学技术学院梁林波530322********103088国家同步辐射实验室梁澎军140322********213885物理学院梁爽429004********373182信息科学技术学院梁文韬320281********151985物理学院梁晓653021********021281信息科学技术学院廖凡430421********038X 85化学与材料科学学院廖晖510723********367285物理学院廖靓欢230604********414283.4生命科学学院廖赏举371322********223X 83材料科学与工程学院(沈阳金属所)廖文韬362422********001X 88数学科学学院廖星宇500112********041393数学科学学院林冰倩350125********332285生命科学学院林丰350525********001389信息科学技术学院林慧430281********202490管理学院林建平350825********411887信息科学技术学院林健明350824********001785物理学院林楠330283********001786.7计算机科学与技术学院林生富320981********597091地球和空间科学学院林盛然445221********161485物理学院林伟350182********295182信息科学技术学院林俣洁370305********042X 90火灾科学国家重点实验室林志宇350322********431085化学与材料科学学院林子欣340603********042690管理学院凌东亚342623********851984信息科学技术学院凌志成230102********431685工程科学学院刘冰370283********102985合肥微尺度物质科学国家实验室刘博371522********001X 72管理学院刘财兴420281********465490研究生院科学岛分院刘彩银342923********662780计算机科学与技术学院刘畅341125********002175信息科学技术学院刘超421202********571585物理学院刘晨370181********446X 88火灾科学国家重点实验室刘冲429004********803590计算机科学与技术学院刘川川341282********401685物理学院刘春波411081********635883核科学技术学院刘春能362329********163982公共事务学院刘大庆341322********005585信息科学技术学院刘德斌412301********401990数学科学学院刘凡凡342625********087585化学与材料科学学院刘芳睿420103********372885信息科学技术学院刘福宁230802********012988化学与材料科学学院刘富林371523********169382信息科学技术学院刘国庆321183********461983信息科学技术学院刘海伦412727********077487信息科学技术学院刘航340302********021585火灾科学国家重点实验室刘弘威362202********009088化学与材料科学学院刘红蕾362425********182084信息科学技术学院刘欢430421********851185化学与材料科学学院刘佳琦410302********203280计算机科学与技术学院刘家龙411503********231382火灾科学国家重点实验室刘建花321088********186982计算机科学与技术学院刘剑420625********351991数学科学学院刘健220282********561382材料科学与工程学院(沈阳金属所)刘健江420822********491990地球和空间科学学院刘精昌341225********005585计算机科学与技术学院刘景昊360732********533580信息科学技术学院刘静432503********082088化学与材料科学学院刘军明341181********503285计算机科学与技术学院刘君楠411329********191685计算机科学与技术学院刘君延532726********301185生命科学学院刘凯370403********761676火灾科学国家重点实验室刘凯冉371424********512693数学科学学院刘堃320829********001X 88信息科学技术学院刘磊340122********481580计算机科学与技术学院刘立岩211381********611090化学与材料科学学院刘琳琳341181********102X 97研究生院科学岛分院刘龙祥410611********703678火灾科学国家重点实验室刘璐410182********252080信息科学技术学院刘梦蜀450326********184290地球和空间科学学院刘鸣342221********105685物理学院刘鹏511623********731583信息科学技术学院刘倩342423********736289生命科学学院刘锐佳340121********520586地球和空间科学学院刘睿诚370213********201583计算机科学与技术学院刘世凯370214********401385物理学院。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学ppt
9
(b).正常金属中的Aharonov-Bohm(AB)效应
经典电磁学:
E,B 麦克斯韦方程 ( r, ),矢标 量A 量 (势 r)势
E 1A,BA;当,A 作 规 范 变 换 :
()2
n(qvF0)2
n(qvF0)2=Dq 2t,
2
DvF 20/2:二 维 扩 散 系
t n0为 电 子 k态从 被 散射 k态到 的 时 间
(qvF)2的 平 均(q值 vF)2为 /2(二 维 ) (qvF)2/3(三 维 )
电子回波产生的反向粒子流:
I k (2 1 )2
d2 Z q 1 ex D p 2 t) q (0 , k F lt
电子输运平均自由程
=
0
k
2 F
2
e2 kF
l
e2
2 2
kF l
00kF l
00 :电导量子
教学ppt
2
输运弛豫时间包含了各种相互作用的贡献:
电子-杂质,电子—声子,电子-电子
1 1 1 1 11
eimp eph ee
0
电 子 与 静 态 散 射 散中 射心 :的 弹 性 散 射 电 子 与 动 态 散 射 散中 射心 :的 非 弹 性 散 射
第三章 尺寸
3.1 介观体系 3.2 纳米体系 3.3 原子团簇
教学ppt
1
3.1 介观体系
1.电子波的干涉 金属的电导率
0
ne 2
m*
m* : 载流子(电子)的有效质量
n :电子浓度
:输运驰豫时间 处于某动量本征态的电子的平均寿命
在二维情况下:n
k
2 F
2
kF为费米波矢
l
vF
m*vF
m*
kF
m*
电导也将以括号内的因子减少:
n m 2 * 0 e [ 1 k 1 F lln 0 ]00l0n 00
为弱局域化电导修正
为0量 0 1级 - 0 6~ 1 , - 0 5S低的温电下导,率一0.般01金~属0.薄1S膜。
ln 在电子平均自由程较小的样品中容易观察到 0 这种现象:淬火薄膜或掺氧薄膜
教学ppt
3
简化的合理性:
X’
电子沿不同的布朗运动路径从X’
点到达X”点(假设所以路径上电子
经历的散射为弹性):
分波An: | An|expi(n) n为其相位
| A n|2 A n2 A nA m * 干涉效应
X”
n
n
n m
cosn(m)路 径 无 规 co, sn( 平 m)均 0
某些特殊条件下,干涉效应不为零:
K空间的态密度为: 2kF
l
圆环所包含的状态数: Z k F
2l
kk,kkq 都对相关散射有贡献
初态+末态的动量 q
能量差为: Eq v F
在一次散射时间间隔 0 内产生的相移: E 0 / q v F 0
教学ppt
7
中间态上的相移不同,位相平方相加,叠加n次散射后:
M
O
N
计及量子效应之后,电子似
乎更趋向于呆在原点
教学ppt
6
弱定域化引起的电导变化:
假定处于 k
该电子被散射到
态k的的电几子率可为能1/被Z散,射而到与费经米历面的上中的间态Z个散状射态
次数n无关。
电子处于动量本征态 k 的平均寿命 0
费米波矢的不确定量为: / l
l vF0 自由程
二维:不确定量构成的圆环面积:
相同
教学ppt
5
A+与A-具有相同的振幅,相同的相位:
|A A |2 |A |2 |A |2 2 R A A * e 4 A 2 虽然巨大数量的电子扩散路径的电子分波的干涉趋向于相互 抵消,但经过时间反演路径的电子波的干涉却相互增强。电 子回到途中某一点几率的增加,意味着观察点N发现电子的几 率下降,导致电导率的减小或电阻率的增加,呈现对经典电 导率的量子力学改正——弱定域化的物理图象,是量子力学 波函数叠加原理导致宏观可观察后果的独特范例。
->12->0 k,波函数为A+
4 35
等概率地:
k 态的电子从0点开始:0->12->11->10…
->1->0 k ,波函数为A-
k
2 1
0
12
|A+|=|A-|=A
k
6 7
8 10 9
11
这两个路径的顺序具有时间反演对称性,称之为时间反演路径
(time reversal path)
对 射所从有k散' 态射到为弹k"性态散和射从的情k形",态可到证明k,' 态电所子附受加相的同相的移杂质 散是
• 沿一闭合路径反向运动的两电子分波,具有时间反演对 称性。两电子分波的叠加在总平均中不抵消
• 电子散射的可能路径不是无限多,而是局限于若干个有 限路径时
教学ppt
4
(a).弱局域化电导修正
闭合路径:电子在固体中扩散运动时以一定的概率返回
它的出发点,这种路径称之为闭合路径。
k 态的电子从0点开始:0->1->2->3…
较纯金属:杂质散射贡献较小,电子-电子相互作用由于传 导电子的屏蔽效应而变得很弱。在温度较高时,声子散射起 主要作用,它决定了电导率随温度变化的规律。随温度的降 低,声子浓度不断减少,而杂质的数量不变,因此电导将趋 于常数(剩余电阻).
电子被看作粒子,各种相互作用都被纳入相应的驰豫时间, 电子作为波的运动特征-相位被完全忽略了。
B
A C
F 经典物理:电子束通路上没有磁场, 没有磁力作用在电子上,螺线管中
磁场不会产生任何影响。
量子力学:电子将感受到与磁通量相联系的矢势存在,波函数 将附加一与矢势A有关,依赖于路径的相位。
c t
AA'A(r,t),'1 (r,t)
ct
E和B都不改变 任。 意 物理观测量与 规 之范 无不 关变性
量子力学: 电磁场中运动的粒子方程
i[ 1 (pqA)2q],
t 2m c
A 物理上的实
教学ppt
10
i[ 1(pqA)2q]
t 2m c
规范变换
A A ' A (r ,t) , ' 1 (r ,t) c t iq 'e c
1 I k~ t
若一个电子在t=0时处于k态,根据驰豫时间近似,其动量 k
以特征时间 0 指数衰减,而由于干涉回波产生的反向动量k
则随时间的倒数衰减,且在 t 时消失,那么这个电子
对于平均动量的贡献为:
k [0 et0d t0 k F 教0l学pd ptt ] tk0 [1 k 1 F lln 0]8
