第七讲 等熵过程及压气机热力过程综述
热力学四个基本过程

热力学四个基本过程
热力学是研究能量转换和能量传递的物理学分支,其中包括四个基本过程:
1. 等容过程(Isochoric Process):在等容过程中,系统的体积保持不变,即系统在过程中不发生体积变化。
在等容过程中,系统对外界做功为零,因为体积没有变化,但系统可以通过热量的吸收或放出来改变其内能。
2. 等压过程(Isobaric Process):在等压过程中,系统的压力保持不变,即系统在过程中不发生压力变化。
在等压过程中,系统对外界做功由于体积的变化而存在,同时也可以通过热量的吸收或放出来改变其内能。
3. 等温过程(Isothermal Process):在等温过程中,系统的温度保持不变,即系统在过程中不发生温度变化。
在等温过程中,系统对外界做功由于体积的变化而存在,同时也有热量的吸收或放出,以保持系统的温度不变。
4. 绝热过程(Adiabatic Process):在绝热过程中,系统与外界没有热量的交换,即系统在过程中不吸收也不放
出热量。
在绝热过程中,系统对外界做功主要是由于体积的变化,以保持系统的内能不变。
这四个基本过程描述了热力学系统中能量的转换和传递方式。
它们在不同的情况下具有不同的特点和应用,对于理解和研究热力学系统的行为和性质非常重要。
制冷剂等熵指标简介

制冷剂等熵指标简介制冷剂等熵指标简介1. 引言在制冷和空调系统中,制冷剂是起到传热媒体的重要角色。
而制冷剂的性能评估指标中,等熵指标是其中一个重要参数。
本文将对制冷剂的等熵指标进行简要介绍,包括其定义、计算方法以及在制冷系统中的应用。
2. 等熵过程的概念在热力学中,等熵过程指的是在这个过程中熵保持不变的状态变化。
也就是说,在等熵过程中,热量的增减不会引起系统熵的改变。
等熵过程一般发生在绝热条件下,即系统与外界没有热量交换。
在制冷和空调系统中,制冷剂在蒸发和压缩过程中通常可以近似看作是等熵过程。
3. 等熵指标的定义等熵指标是用来评估制冷剂在等熵过程中性能表现的参数。
等熵指标通常包括等熵膨胀系数(Isentropic Expansion Coefficient)和等熵压缩系数(Isentropic Compression Coefficient)两个方面。
3.1 等熵膨胀系数等熵膨胀系数描述了制冷剂在等熵膨胀过程中的性能表现。
具体而言,等熵膨胀系数是指制冷剂在等熵膨胀过程中的膨胀比,表示了在等熵过程中制冷剂的压力和密度之间的关系。
计算等熵膨胀系数可以利用热力学基本关系式和制冷剂的物性数据。
3.2 等熵压缩系数等熵压缩系数则描述了制冷剂在等熵压缩过程中的性能表现。
同样,等熵压缩系数表示了在等熵过程中制冷剂的压力和密度之间的关系。
计算等熵压缩系数同样可以利用热力学基本关系式和制冷剂的物性数据。
4. 等熵指标的计算方法计算等熵指标需要利用到制冷剂的热力学性质和基本的热力学关系式。
一般而言,可以通过制冷剂的压力、温度、比热容等基本性质来计算等熵指标。
对于不同的制冷剂,其等熵指标的计算方法可能存在差异,需要根据具体的制冷剂性质来确定。
5. 等熵指标在制冷系统中的应用等熵指标作为制冷剂性能的重要评估参数,在制冷系统中具有广泛的应用。
等熵指标可以用于评估制冷剂在压缩机中的性能,确定最佳的工作参数,从而提高能效和制冷效果。
热力学理想气体的等容和等压过程

热力学理想气体的等容和等压过程热力学是研究能量转化关系的分支学科,而理想气体是热力学中用于研究理想气体状态变化的模型。
在热力学中,等容和等压过程是两种常见的状态变化方式。
本文将重点讨论热力学理想气体在等容和等压过程中的特性和数学表达。
一、等容过程等容过程是指在恒定体积下,理想气体发生的状态变化过程。
在等容过程中,气体的体积保持不变,但其他变量如压力、温度和物质量等可能发生变化。
1. 等容过程的特性在等容过程中,理想气体的体积保持不变,即V = 常数。
根据理想气体状态方程PV = nRT,其中P为气体的压力,V为气体的体积,n 为气体的物质量,R为气体常数,T为气体的温度,可得等容过程的数学表达式为:P/T = 常数。
2. 等容过程的图像在P-T坐标系中,等容过程表示为一条垂直线。
由于等容过程中气体的体积保持不变,所以气体只能在等容线上移动。
当温度增加时,气体的压力也会增加;当温度减少时,气体的压力也会减少。
二、等压过程等压过程是指在恒定压力下,理想气体发生的状态变化过程。
在等压过程中,气体的压力保持不变,但其他变量如体积、温度和物质量等可能发生变化。
1. 等压过程的特性在等压过程中,理想气体的压力保持不变,即P = 常数。
根据理想气体状态方程PV = nRT,其中P为气体的压力,V为气体的体积,n 为气体的物质量,R为气体常数,T为气体的温度,可得等压过程的数学表达式为:V/T = 常数。
2. 等压过程的图像在V-T坐标系中,等压过程表示为一条水平线。
由于等压过程中气体的压力保持不变,所以气体只能在等压线上移动。
当温度增加时,气体的体积也会增加;当温度减少时,气体的体积也会减少。
结论:通过对热力学理想气体的等容和等压过程的讨论,可以得出以下结论:1. 等容过程中,理想气体的体积保持不变,而等压过程中,理想气体的压力保持不变。
2. 在等容过程中,气体的压力与温度成正比;在等压过程中,气体的体积与温度成正比。
简述常见的热力学过程

简述常见的热力学过程热力学是研究热、功、能量转换关系的学科。
在热力学中,物质的状态可以通过温度、压力、体积、内能等物理量来描述。
物质在不同的环境下,会经历各种不同的热力学过程,下面我们来简述一些常见的热力学过程。
1. 等温过程等温过程是指物质在恒定温度下的热力学过程。
在等温过程中,物质的体积会发生变化,但是温度保持不变。
根据理想气体定律,等温过程中,气体的压强与体积呈反比关系,即PV=常数。
等温过程通常在恒温条件下进行,比如说在恒温箱中。
2. 绝热过程绝热过程是指物质在没有热量交换的情况下的热力学过程。
在绝热过程中,物质的内能保持不变,但是温度、压力和体积会发生变化。
绝热过程通常在绝热容器中进行,比如说热瓶。
3. 等压过程等压过程是指物质在恒定压力下的热力学过程。
在等压过程中,物质的体积与温度成正比关系。
根据理想气体定律,等压过程中,气体的体积与温度呈正比关系,即V/T=常数。
等压过程通常在恒压条件下进行,比如说在恒压热源中。
4. 等体积过程等体积过程是指物质在恒定体积下的热力学过程。
在等体积过程中,物质的压力与温度成正比关系。
等体积过程通常在恒容器中进行,比如说在恒容热源中。
5. 等焓过程等焓过程是指物质在恒定焓下的热力学过程。
焓是热力学中的一个重要物理量,表示系统的内能和对外界所做的功的和。
在等焓过程中,物质的压力、体积和温度会发生变化,但是焓保持不变。
等焓过程通常在恒焓条件下进行,比如说在恒热源中。
以上就是常见的热力学过程,它们在热力学中具有重要的应用价值。
通过对这些过程的研究,我们可以更好地理解热力学的基本原理,从而应用于实际的工程和科学研究中。
燃气轮机热力循环原理
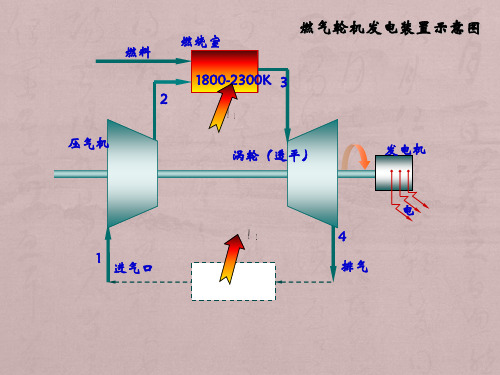
• 热耗率 机组每输出产生l kW·h的功需要多
少焦耳的热量。
• 油耗 每产生lkW·h的功所消耗的标准燃
油(是指发热量为43124kJ/kg的燃油) 的克数。
燃气轮机理想简单循环性能分析
理想简单循环比功
w G Tcp T 1 * [(1 m ) (m 1 )]
推导上式
压气机耗功的计算:
3 T
w ch 2h 1cp(T 2T 1)
单机功率
• 合同额定功率 指在事先确定的运行工况下连续运行,
发电机能够保证的出力。
单机功率
• 现场额定功率 指在燃气轮机发电厂所处的当前环境
的条件下,诸如大气压、大气温度、压力 损失等条件下的最大持续功率。
单机功率
• 尖峰功率 在规定的运行条件下,保持一个约定
的短时间内,燃气轮机以高于连续额定功 率安全运行的最大功率。
k1
cpT1TT12
1cpT1
p2 p1
k
1
p 4
2 p
1
k1
cpT1( k 1)
s
燃气轮机作功量的计算:
w Th 3h 4cp(T 3T 4)
k1
k1
cpT 4 T T 4 31 cpT 4 p p4 3 k
1 cpT 4 p p1 2 k
1
一般来说,T3*每提高 100℃,机组比功大约增加 20%~40%,热效率增加 2%~5%
7压气机的热力过程解析

一、工作原理
f-1为进气过程,是气体 的移动过程; 1-2为压缩过程; 2-g为排气过程,是气体 的移动过程。
g
p p2 2
f 0
p1
1 V2 V1 V Wsh Wc
压缩过程的类型:
(1)绝热压缩过程; (2)定温压缩过程; (3)实际过程是n介于1与k之间的多变压缩过程。
Vc / Vh 和n确定,则 ,V 。
确定,则 Vc / Vh ,V 。
2、理论耗功
n 1 n 1 n n n p2 n p V p3 1 WC p1V1 1 n 1 4 4 n 1 p1 p4
可见,不但余隙容积本身不起压气作用,而且 使另一部分气缸容积也不起压缩作用。
分析:
(1)容积效率(volumetric efficiency):有效吸气容 积与气缸排量之比,即
V
V Vh
在相同的余隙容积下,若 增压比增大,则有效吸气容积 减少,容积效率降低,达到某 一极限时将完全不能进气。
7.3 多级压缩和级间冷却
工程上需要高压气体,但压缩过程中压力越高温 度也越高,而V 下降。为使
T2 T2 , max
V V , min
多级压缩(multistage compression), 通常采用 级间冷却(intervening cooling)。
动 作 原 理 及 构 造
活塞式压气机 压 缩 气 叶轮式压气机 体 的 压 引射式压缩器 力
通风机0.01Mpa表压以下) 鼓风机(0.1~0.3Mpa表压) 压气机(0.3Mpa表压以上)
注意:压气机中进行的过程不是循环。
压气机等熵效率

压气机的等熵效率一、引言压气机,作为航空发动机和燃气轮机等热力机械的核心部件,其性能直接影响到整个系统的运行效率。
等熵效率是衡量压气机性能的一个重要参数,它反映了压气机在压缩过程中能量的损失情况。
本文将对压气机的等熵效率进行深入探讨,分析其影响因素、计算方法以及提高措施,以期为压气机的优化设计和运行维护提供理论支持。
二、等熵效率的定义与意义等熵效率,是指在压缩过程中,压气机实际消耗的功与理想等熵压缩过程所需的功之比。
理想等熵压缩过程是一个可逆过程,即压缩过程中没有能量损失。
因此,等熵效率越接近1,说明压气机的能量损失越小,性能越优越。
等熵效率的高低直接影响到压气机的功耗、温升以及整机性能。
三、影响等熵效率的因素1. 流动损失:压气机内部的气流流动受到各种因素的影响,如叶片形状、流道设计、进口条件等,这些因素都会导致气流在流动过程中的能量损失。
流动损失是影响等熵效率的主要因素之一。
2. 摩擦损失:压气机的叶片和流道壁面之间存在摩擦,这种摩擦会导致气流的能量损失。
摩擦损失与材料的选择、表面处理以及制造工艺等因素有关。
3. 泄漏损失:压气机在工作过程中,由于叶片间隙、密封结构等原因,会导致气体从高压区泄漏到低压区,从而造成能量损失。
泄漏损失是影响等熵效率的重要因素之一。
4. 激波损失:当气流在压气机内部遇到激波时,会产生能量损失。
激波损失与压气机的设计、运行条件以及气流状态等因素有关。
四、等熵效率的计算方法等熵效率的计算通常基于压气机的进出口参数,如压力、温度等。
通过测量或计算这些参数,可以得到压气机的实际压缩功和理想等熵压缩功,进而求得等熵效率。
计算方法可以采用经验公式、理论模型或数值模拟等方法。
其中,数值模拟方法能够较为准确地模拟压气机的内部流动和能量转换过程,因此在等熵效率计算中得到广泛应用。
五、提高等熵效率的措施为了提高压气机的等熵效率,可以采取以下措施:1. 优化叶片设计:通过改进叶片形状、减小叶片间隙、优化叶片排列等方式,降低流动损失和泄漏损失。
PHNIX压气机的热力过程基础学习

a
1
v
p
一、工作原理
a
1
v
p
2
一、工作原理
a
1
v
p
2
一、工作原理
同14
a
1
v
p
2
一、工作原理
a
1
v
p
2
一、工作原理
同 1 4
a
1
v
p
2
一、工作原理
a
1
v
同14
p
2
一、工作原理
a
1
v
同14 p b p2 2
一、工作原理
a-1:气体引入气缸 1-2:气体在气缸内进行压缩 2-b:气体流出气缸,输向储气筒
9-3 多级压缩和级间冷却
省功(减少压缩过程的多变指数) 避免单级压缩因增压比太高而影响容积效 率
一、两级压缩、中间冷却压气机
中间冷却器
冷却水
多级压缩、级间 冷却压气机装置 系统
p
p
3
2
p
1
高压缸
低压缸
多 级 压 缩 、 级 间 冷 却 压 气 机 装 置 系 统 图
多级压缩级间冷却的压气机
可见压气机耗功以技术功计。
对于理想气体:
Wp 11 V d Vp V c 22 p
1 2
活塞式压气机的理论压缩耗功
p b p2 2
1 ' 1 a 0 1 ' 1 2 2 ' 1 ' 1 2 b 0 2 ' 1
( 1 2 2 ' 1 ' 1 2 b 0 2 ' 1 ) 1 ' 1 a 0 1 '
第七讲 等熵过程及压气机热力过程

s
2
p2 s 1 Rg ln 0 p1
0
s
0
2
p2 s 1 Rg ln p1
0
由热力性质表查得温度T2
例题4.3
N2气体被可逆绝热压缩,初态p1=105Pa,T1=300K, 终态p1=8×105Pa。求终态温度T2及压缩5kmolN2气 体的压缩过程功和所需要的轴功。按(1)定值绝热指数; (2)平均绝热指数;(3)热力性质表。 解: (1) 定值绝热指数 由表3.2,CV,m=0.741×28=20.75J/mol· K;
多变过程膨胀功表达式中需要有多变指数
w
Rg n 1
(T1 T2 )
能量守恒:
q u w cv (T2 T1 ) Rg n 1 (T1 T2 ) (cv )(T2 T1 ) n 1 Rg
比热容的原始定义:
q c T
q1 380 c1 3.405 kJ/( kg K) T1 111.6 q2 210 c2 1.6733 kJ/( kg K) T2 125.5
3)压缩过程可逆。 满足上述条件的压气机称
理想压气机。
重要参数指标定义:
排气压力与进气压力之比 称增压比 π = p 2/ p 1
余隙容积
基本分析
全过程应包括有:吸气、压缩、排气三个过程,故是开口 系统,压缩机耗功应该是技术功。当进口动能差、位能差 忽略时即为轴功 吸气过程:由假设 2) 0—1:进气过程外界对压缩机作 功 p1(v1-0) 压缩过程:由假设3) 1—2:有三种情况:等熵、等温、 多变
解:1)按第一定律观点 Δ u=q+w Δ u1=380-300=80kJ/kg Δ u2=210-300=-90kJ/kg
等熵绝热过程

等熵绝热过程等熵绝热过程是热力学中的一个重要概念,也是理解物质在过程中的变化和性质的关键。
在等熵绝热过程中,系统的熵保持不变,即系统的熵增量为零。
这意味着系统在过程中不会发生热量的交换,熵的变化主要由于体积和压强的变化引起。
在等熵绝热过程中,系统的内能和温度会发生变化,但是熵保持不变。
根据热力学第一定律,系统的内能变化等于系统所吸收的热量与对外做功的总和。
在等熵绝热过程中,由于没有热量的交换,所以系统的内能变化主要由对外做功引起。
等熵绝热过程可以分为两种情况:等容绝热过程和等压绝热过程。
在等容绝热过程中,系统的体积保持不变,即系统的体积增量为零。
在这种情况下,由于没有体积的变化,所以对外做功为零。
根据热力学第一定律,系统的内能变化等于系统所吸收的热量。
由于等熵绝热过程中系统的熵保持不变,所以系统的内能变化也为零。
因此,在等容绝热过程中,系统既不吸收热量也不对外做功。
在等压绝热过程中,系统的压强保持不变,即系统的压强增量为零。
在这种情况下,对外做功等于系统所吸收的热量。
根据热力学第一定律,系统的内能变化等于系统所吸收的热量减去对外做功。
由于等熵绝热过程中系统的熵保持不变,所以系统的内能变化也为零。
因此,在等压绝热过程中,系统吸收的热量等于对外做功。
等熵绝热过程在自然界中广泛存在。
例如,在大气物理学中,空气上升时会发生等压绝热过程。
当空气上升到较高的高度时,由于气压降低,空气膨胀并且对外做功。
由于没有热量交换,空气上升过程中的温度减少。
另一个例子是理想气体的绝热膨胀和压缩过程。
当理想气体被压缩时,由于体积减小,气体对外做功,并且温度升高。
而当理想气体膨胀时,由于体积增大,气体对外做负功,并且温度降低。
等熵绝热过程在工程和科学领域中有着广泛的应用。
例如,在内燃机中,汽缸内的空气在发动机活塞上升时发生等压绝热过程。
这个过程中,空气被压缩并且温度升高,从而增加了发动机的效率。
在工业领域中,等熵绝热过程也被广泛应用于压缩机、涡轮机和喷气发动机等设备中。
工程热力学课件压气机热力过程

解 单级多变压缩时排气温度为
T 3T 1(p p1 3)nn 129 (0 6 .0 1)1.1 2 .2 157 .73 K 9
t3=300.790c 单级压缩时压气机消耗的功率为
N
Wc,n 3600
mn 3600n1RT1[1(
p3 p1
n1
)n ]
108.51.210.287290[1(
6
1.21
nn 1p 1 V 1 1 (p p 1 2)n n 1 - nn 1p 4 V 4 1 (p p 4 3)n n 1
p1p4,p2p3
W c,nnn 1p1(V1V4)1(p p1 2)nn 1
Wt,34=- Wt,43
p3Βιβλιοθήκη 241Vc
Vh V1-V4
W c,nnn 1p1(V1V4)1(p p1 2)nn 1
V
式中,V1 - V4= m’v1 , m’为有余隙 容积时进入气缸的气体质量
有余隙容积压缩机示功图
压缩1kg 气体所消耗的功为: W c,nW m c,'n nn 1p1v11(p p1 2)nn 1
无余隙容积时,压缩1kg 气体所消耗的功为:
W' c,n
nn1p1v11(pp12)nn1
有余隙容积和无余隙容积时,压缩1kg 气体所消耗的功是相同的
1V Vh c(p p1 2)1 n111 n1
1V Vh c(p p1 2)1 n111 n1
Vc Vh
p2 p1
称为压缩机的余隙比 称为压缩机的增压比
1
容积效率: V 1(n 1)
增大时,容积效率降低; 提高时,容积效率也降低。
3、增压比对容积效率的影响
p
第七讲等熵过程及压气机热力过程
Cp ,m=1.038×28=29.06 J/mol· K
p2 T2 T1 ( ) p1
k 1 k
8 105 1.4 300 ( ) 543.4 K 5 10
1.41
W nCv,m (T2 T1 ) 5 103 20.75 (543.4 300) 2.5277104 kJ
Ws kW 1.395 (2.531103 ) 3.531104 kJ
(3)按热力性质表 300K :
0 Sm 2
0 Sm .789J/(mol K) 1 191 5 p 8 10 0 2 Sm R ln 191.789 8.314 ln 208.97J/(mol K) 1 5 p1 10
多变过程
实际过程的多样性
实验:请课代表安排
4人一小组,每次2组
指数n叫多变指数
pv 定值
n
对一个过程,n值可以保持不变,不同的过程有不同的n 值;或一个过程中,在不同的局部中n是变化的 ln( p2 / p1 ) 多变指数n的确定原则: n ln(v2 / v1 ) 多变过程的参数关系 n 1 p2 v1 n T2 v1 n1 p2 n ( ) ( ) ( ) p1 v2 T1 v2 p1
c1 kcv 3.405 1.4 0.717 n1 0.893 c1 cv 3.405 0.717
c2 kcv 1.6733 1.4 0.717 n2 1.120 c 2 cv 1.6733 0.717
0
s
2
p2 s 1 Rg ln 0 p1
0
s
0
2
p2 s 1 Rg ln p1
0
由热力性质表查得温度T2
等熵过程温度和压强关系

等熵过程温度和压强关系
关系:一般气体受热膨胀,在体积有限的情况下,气体对容器壁的压强增大,由于受力面积不变,压力也会增大;温度降低时相反。
1、ΔH与T的关系:反应焓变会随着温度而变化。
等压条件下,焓随温度的变化率,即(əH/əT)p=Cp即等压热容,那么(əΔH/əT)p=ΔCp,即等压时焓变随温度的变化率为等压热容的变化值,等压热容的变化值一般由实验得出。
2、ΔH与p的关系:对于理想气体,H只决定于温度。
定温下ΔH也应该是定值,对于非理想气体ΔH=a(1/Vm,1-1/Vm,2)+Δ(pVm)a是范德华气体方程中的参数,Vm 是摩尔体积,1、2指体积变化的前后状态(体积变化由等温条件也可以求压强变化)。
含义
等熵过程又叫可逆绝热过程。
所谓绝热过程乃是气体在和外界没有热量交换的条件下进行的热力过程。
当过程进行的很快时,工质与外界还来不及与外界交换热量或是交换热量很少,则可近似地看作绝热过程。
涡轮喷气发动机的压气机内空气的压缩过程,燃气在涡轮内和尾喷管内进行的膨胀过程,都可近似地看作绝热过程。
压气机的热力过程

3。试分析,在增压比相同时,采用定温压缩和采用绝热压缩的 压气机的容积效率何者高?
4。试说明余隙容积对实际压气机消耗的轴功是否有影响?
8.983kJ/Kmin
IT0sis
oT0sN 2s298 3 .982 36.93k1 J min
4.8 3k7W
思考题
1。 如果多级压缩的分级越多,且每两级之间均设置中间冷却措 施,则压气机消耗的轴功将减少的越多,试问压气机消耗的轴功 是否存在最小的极限值?
p2
p2 p1p4
p2
2
3
p1
1
v
w 分 级nn 1RT 1[2(p p1 2)nn -1(p p2 4)nn -1]
最佳增压比的推导
w分级最小值,
p2 p1p4
p2 p1
最佳增压比
p2 p1
p4 p1
பைடு நூலகம்
p1 p4 p1
p终 p初
p4 p
p2
p4
p2
p1
可证明 若m级
1
Image
讨论:
a)当Vc,Vh确定 ;
v m生产量
b)当一定;
VcVcs vm生产 量
三.余隙容积对理论耗功的影响
W CW t12W t34
No n nn n 1 1p p1 V 11 V 1n V n 1 4 1 nn 1n n 11 p 4 V 4 n n 1 1 Imagenn1Vesp1nn11
采用中间冷却器,可降低压缩过程中气体的温度, 使压缩终了温度不致过高。也可以减少压气机所消耗
压气机的热力过程

f-1和2-g过程
不是热力过程,只是气体的移动过程,气体状 态不发生变化,缸内气体的数量发生变化
1-2过程
热力过程,气体的参数发 生变化。 过程耗功量可由图中过程 线1-2与V轴所包围的面 积表示。 有两种极限情况: 绝热过程1-2s 定温过程1-2T 实际压缩1-2n
二、压气机的理论耗功量
Vh为气缸排量:
Vh V1 V3
因为3-4为余隙容 积中剩余气体的膨胀过 程(多变过程),所以 4-1表示有效进气。
二、余隙容积的影响
生产量:
有效吸气容积:
V V1 V4
容积效率:
Vc V V 1 Vh Vh
1
1 n
余隙容积百分比Vc/Vh和多变指数n一定时,增压比越大,
(3)可逆定温压缩
wC ,T wt ,T v2 p1 Rg T1 ln Rg T1 ln v1 p2
二、压气机的理论耗功量
三种压缩过程耗功量
wC , s wC ,n wC ,T
T2,s T2,n T2,T
9-2 余隙容积的影响
一、余隙容积
当活塞运动到上死 点位置时,活塞顶面与 气缸盖间留有一定的空 隙,为余隙容积Vc
9-4 叶轮式压气机的工作原理
与活塞式压气机相比,叶轮式压气机结构紧
凑,输气量大,输气均匀且运转平稳,效率 高。缺点是增压比小。 叶轮式压气机分为离心式与轴流式两种型式。
一、叶轮式压气机工作原理
轴流式 离心式
二、叶轮式压气机分析
理想压缩过程
定熵压缩过程1-2s
wC h2 s h1 Aj 2T 2s m
第七讲 等熵过程及压气机热力过程

结果比较(1)543.4 (2)540.5 (3)541.3
多变过程
实际过程的多样性
实验:请课代表安排 4人一小组,每次2组
pvn 定值
指数n叫多变指数
对一个过程,n值可以保持不变,不同的过程有不同的n 值;或一个过程中,在不同的局部中n是变化的
210 1.6733 125 .5
kJ/( kg K)
n1
c1 kcv c1 cv
3.405 1.4 0.717 3.405 0.717
0.893
n2
c2 kcv c2 cv
1.6733 1.4 0.717 1.6733 0.717
1.120
图
0<n1<n2<k
4.5 压气机的热力过程分析
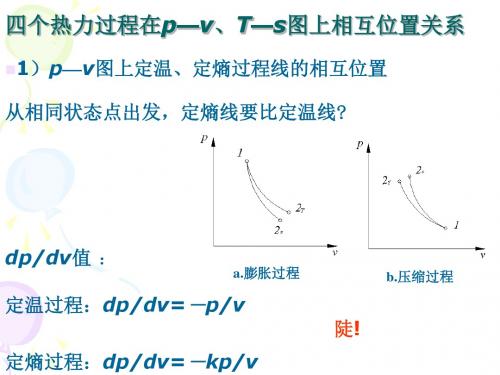
四个热力过程在p—v、T—s图上相互位置关系
1)p—v图上定温、定熵过程线的相互位置 从相同状态点出发,定熵线要比定温线?
dp/dv值 :
a.膨胀过程
定温过程:dp/dv=-p/v
定熵过程:dp/dv=-kp/v
b.压缩过程
陡!
2)T—s图上定容、定压过程线的相互位置 从相同状态点出发,定容线比定压线 ?
定熵过程 Δs=0
s02
s
0 1
Rg
ln
p2 p1
0
由热力性质表查得温度T2
s02
s
0 1
Rg
ln
p2 p1
例题4.3
N2气体被可逆绝热压缩,初态p1=105Pa,T1=300K,终 态p1=8×105Pa。求终态温度T2及压缩5kmolN2气体的压 缩过程功和所需要的轴功。按(1)定值绝热指数;(2) 平均绝热指数;(3)热力性质表。
压气机的热力过程概述和工作原理

二、余隙容积VC对理论耗功的影响
功=面积12341 =面积12561-面积43564
p 5
VC
3
2
设12和3 4两过程n相同
6
Wt
n n 1
p1V1
1
p2 p1
n1 n
4 V3
1 V
V1 V
n n 1
p14V4
1
p23 pp14
n1
n
p2 p3 p1 p4
Wt
n n 1
理想气体热力过程的p-v,T-s图
pT s v
T
sv
n0
p
n0 T
n 1
n 1
1 n k
p
nk
n
nvBiblioteka nk s可能的压气过程
(1)特别快,来不及换热 s n k
(2)特别慢,热全散走 T n 1 (3)实际压气过程 n 1 n k
p
p2
2T
2n
2s
p1
T
2n 2T
1 v
2s p2
p1
1 s
二、 理论耗功
以p1=0.1MPa,p2=2.5MPa, =0.04 计算。
单级压缩 二级压缩
1
1
V 1 n 1 1 0.04 251 1 0.04
l h
p2 5 p1
1 2
V V ,l V ,h 1 0.04 51 1 0.706
例题1
活塞式压气机把0.1MPa,298K的空气加压到2.5MPa。 试
1
0.525
二级压缩,中间冷却
若取 pa 0.2MPa
l
pa p1
0.2 0.1
热力学等压过程

热力学等压过程热力学等压过程是指在恒定的压力条件下,系统从一个初始状态变化到一个最终状态的过程。
在这个过程中,系统对外界做功并吸收热量,同时其体积也发生变化。
本文将探讨热力学等压过程的基本原理、特征以及应用。
一、基本原理热力学等压过程遵循以下基本原理:1. 压力恒定:在整个过程中,系统所受到的压力保持不变。
这意味着系统与外界保持了恒定的压强差,从而确保了等压过程的进行。
2. 系统对外界做功:在等压过程中,系统通过扩大或收缩体积对外界做功。
当系统从初始状态变化到最终状态时,系统内部发生了能量的转移和转化,一部分能量被转化为对外界做的功。
3. 吸热或放热:等压过程中,系统与外界交换热量。
若系统吸热,则热量从外界流入系统;若系统放热,则热量从系统流向外界。
热量的交换使得系统内部能量发生变化。
二、特征及计算热力学等压过程具有以下特征:1. 温度变化:等压过程中,系统温度通常会发生变化。
根据热力学第一定律,系统内部能量的增加等于吸收的热量与对外界做的功之和。
2. 体积变化:在等压过程中,系统的体积发生变化。
当系统对外界做功时,体积会增加;当系统从外界吸热时,体积会减小。
体积变化直接影响系统内部能量的变化。
3. 熵变:熵是刻画系统无序程度的物理量,等压过程中,系统熵通常会发生变化。
热力学第二定律指出,在等温等压过程中,系统熵增加的趋势是不可逆的。
针对等压过程的计算,可采用以下公式:1. 对外界做功的计算公式:\[ W = p(V_f - V_i) \]其中,W表示对外界做的功,p表示压力,V_f和V_i分别表示最终和初始状态下系统的体积。
2. 吸收/放出的热量的计算公式:\[ Q = nC_p\Delta T \]其中,Q表示吸热或放热的热量,n表示物质的摩尔数,C_p 表示物质在恒定压力下的摩尔定容热容,\Delta T表示温度变化。
三、应用热力学等压过程在工程领域有广泛的应用,例如:1. 内燃机工作过程:汽车等燃油发动机工作过程中,往往采用等压过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:1)按第一定律观点 Δ u=q+w Δ u1=380-300=80kJ/kg Δ u2=210-300=-90kJ/kg
查附表3 cv=0.717kJ/kg· K Rg=0.287 kJ/kg· K k=1.4 ΔT1=Δu1/cv=80/0.717=111.6K ΔT2=Δu2/cv=-90/0.717=-125.5K 2)多变指数 过程初终状态参数?
t2 t1
R 29.356 8.314 21.042 J/(mol K)
C p ,m C v ,m
t2 t1 t2 t1
1.395 1 1.395
29.356 1.395 21.042
540.5 K
8 105 T2 300 ( ) 5 10
t2
1
W nCv,m t (T2 T1 ) 5 103 21.042 (540.5 300) 2.531 104 kJ
附表9,得T2=541.3K
Hm1=8723.9 J/mol;Hm2=15806 J/mol Ws=-n(Hm2-Hm1)
=-5×103×(15806-8723)=-3.5415×104 kJ W= Ws /k= -3.5415×104/1.395=-2.5387×104 kJ 结果比较(1)543.4 (2)540.5 (3)541.3
Ws kW 1.4 (2.5277103 ) 3.5388104 kJ
(2) 按平均绝热指数:
在27℃ (300K)时
C p ,m
t1 0
(29.144- 29.115) 0.27 29.115 29.123 J/(mol K)
在267℃(540K)
C p ,m
dT/ds值 :
a.加热过程
b.冷却过程
定容过程dT/ds=T/cV 定压过程dT/ds=T/cp
陡!
定熵过程的变值比热容计算
适用情况:精度要求比较高的工程计算
1)平均绝热指数方法计算 过程方程:pvk=定值
k
cp cv
T2
T1
问题:当T2未知时,确定km值比较困难 2)按气体热力性质表数据计算 定熵过程 Δ s=0
c1 kcv 3.405 1.4 0.717 n1 0.893 c1 cv 3.405 0.717
c2 kcv 1.6733 1.4 0.717 n2 1.120 c 2 cv 1.6733 0.717
多变过程
实际过程的多样性
实验:请课代表安排
4人一小组,每次2组
指数n叫多变指数
pv 定值
n
对一个过程,n值可以保持不变,不同的过程有不同的n 值;或一个过程中,在不同的局部中n是变化的 ln( p2 / p1 ) 多变指数n的确定原则: n ln(v2 / v1 ) 多变过程的参数关系 n 1 p2 v1 n T2 v1 n1 p2 n ( ) ( ) ( ) p1 v2 T1 v2 p1
多变过程热力学能、焓、熵
Δ u=cvΔ T,Δ h=cpΔ T
T2 v2 s cv ln Rg ln T1 v1
例题4.4 1kg空气分两种情况进行热力过程,均作膨胀功300kJ。 一种情况下,吸热380kJ;另一种情况下吸热210kJ。 问两种情况下空气的热力学能变化多少?若两种过程都是 多变过程,求多变指数,并将两个过程在同一p—v图和 T—s图上绘出。(按定值比热容计算)
Cp ,m=1.038×28=29.06 J/mol· K
p2 T2 T1 ( ) p1
k 1 k
8 105 1.4 300 ( ) 543.4 K 5 10
1.41
W nCv,m (T2 T1 ) 5 103 20.75 (543.4 300) 2.5277104 kJ
Ws kW 1.395 (2.531103 ) 3.531104 kJ
(3)按热力性质表 300K :
0 Sm 2
0 Sm .789J/(mol K) 1 191 5 p 8 10 0 2 Sm R ln 191.789 8.314 ln 208.97J/(mol K) 1 5 p1 10
0
s
2ቤተ መጻሕፍቲ ባይዱ
p2 s 1 Rg ln 0 p1
0
s
0
2
p2 s 1 Rg ln p1
0
由热力性质表查得温度T2
例题4.3
N2气体被可逆绝热压缩,初态p1=105Pa,T1=300K, 终态p1=8×105Pa。求终态温度T2及压缩5kmolN2气 体的压缩过程功和所需要的轴功。按(1)定值绝热指数; (2)平均绝热指数;(3)热力性质表。 解: (1) 定值绝热指数 由表3.2,CV,m=0.741×28=20.75J/mol· K;
多变过程膨胀功表达式中需要有多变指数
w
Rg n 1
(T1 T2 )
能量守恒:
q u w cv (T2 T1 ) Rg n 1 (T1 T2 ) (cv )(T2 T1 ) n 1 Rg
比热容的原始定义:
q c T
q1 380 c1 3.405 kJ/( kg K) T1 111.6 q2 210 c2 1.6733 kJ/( kg K) T2 125.5
四个热力过程在p—v、T—s图上相互位置关系
1)p—v图上定温、定熵过程线的相互位置
从相同状态点出发,定熵线要比定温线?
dp/dv值 :
a.膨胀过程
b.压缩过程
定温过程:dp/dv=-p/v 陡! 定熵过程:dp/dv=-kp/v
2)T—s图上定容、定压过程线的相互位置
从相同状态点出发,定容线比定压线 ?
t1 0
(29.383 - 29.228) 0.67 29.228 29.332J/(m ol K)
近似平均值: t 29.332 267 29.123 27 C p ,m 29.356 J/(mol K) t 267 27
2 1
CV ,m
t2 t1
C p ,m
