2020初中奥数题及答案

合集下载

初中奥数题及答案

年初中奥数题及答案初中奥数题试题一一、选择题（每题分，共分）．如果，都代表有理数，并且＋，那么 ( )．，都是．，之一是．，互为相反数．，互为倒数答案：解析：令，－，满足(－)，由此、互为相反数。

．下面的说法中正确的是 ( )．单项式与单项式的和是单项式．单项式与单项式的和是多项式．多项式与多项式的和是多项式．整式与整式的和是整式答案：解析：²，都是单项式．两个单项式，²之和为²是多项式，排除。

两个单项式²，之和为是单项式，排除。

两个多项式与－之和为是个单项式，排除，因此选。

．下面说法中不正确的是 ( ). 有最小的自然数．没有最小的正有理数．没有最大的负整数．没有最大的非负数答案：解析：最大的负整数是，故错误。

．如果，代表有理数，并且＋的值大于－的值，那么 ( )．，同号．，异号．＞．＞答案：．大于－π并且不是自然数的整数有 ( )．个．个．个．无数个答案：解析：在数轴上容易看出：在－π右边的左边（包括在内）的整数只有－，－，－，共个．选。

．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

这四种说法中，不正确的说法的个数是 ( )．个．个．个．个答案：解析：负数的平方是正数，所以一定大于它本身，故错误。

．代表有理数，那么，和－的大小关系是 ( )．大于－．小于－．大于－或小于－．不一定大于－答案：解析：令，马上可以排除、、，应选。

．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( ) ．乘以同一个数．乘以同一个整式．加上同一个代数式．都加上答案：解析：对方程同解变形，要求方程两边同乘不等于的数，所以排除。

我们考察方程－，易知其根为．若该方程两边同乘以一个整式－，得(－)(－)，其根为及，不与原方程同解，排除。

同理应排除．事实上方程两边同时加上一个常数，新方程与原方程同解，对，这里所加常数为，因此选．．杯子中有大半杯水，第二天较第一天减少了，第三天又较第二天增加了，那么，第三天杯中的水量与第一天杯中的水量相比的结果是( )．一样多．多了．少了．多少都可能答案：解析：设杯中原有水量为，依题意可得，第二天杯中水量为×(－)；第三天杯中水量为()×()××；第三天杯中水量与第一天杯中水量之比为∶，所以第三天杯中水量比第一天杯中水量少了，选。

初中奥数20道经典奥数题及答案解析

初中奥数20道经典奥数题及答案解析1.已知一张桌子的价钱是一把椅子的10倍，又知一张桌子比一把椅子多288元，一张桌子和一把椅子各多少元？想：由已知条件可知，一张桌子比一把椅子多的288元，正好是一把椅子价钱的(10-1)倍，由此可求得一把椅子的价钱。

再根据椅子的价钱，就可求得一张桌子的价钱。

解：一把椅子的价钱：288÷(10-1)=32(元)一张桌子的价钱：32×10=320(元)答：一张桌子320元，一把椅子32元。

2、3箱苹果重45千克。

一箱梨比一箱苹果多5千克，3箱梨重多少千克？想：可先求出3箱梨比3箱苹果多的重量，再加上3箱苹果的重量，就是3箱梨的重量。

解：45+5×3=45+15=60(千克)答：3箱梨重60千克。

3、甲乙二人从两地同时相对而行，经过4小时，在距离中点4千米处相遇。

甲比乙速度快，甲每小时比乙快多少千米？想：根据在距离中点4千米处相遇和甲比乙速度快，可知甲比乙多走4×2千米，又知经过4小时相遇。

即可求甲比乙每小时快多少千米。

解：4×2÷4=8÷4=2(千米)答：甲每小时比乙快2千米。

4、李军和张强付同样多的钱买了同一种铅笔，李军要了13支，张强要了7支，李军又给张强0.6元钱。

每支铅笔多少钱？想：根据两人付同样多的钱买同一种铅笔和李军要了13支，张强要了7支，可知每人应该得(13+7)÷2支，而李军要了13支比应得的多了3支，所以又给张强0.6元钱，即可求每支铅笔的价钱。

解：0.6÷[13-(13+7)÷2]=0.6÷[13-20÷2]=0.6÷3=0.2(元)答：每支铅笔0.2元。

5、甲乙两辆客车上午8时同时从两个车站出发，相向而行，经过一段时间，两车同时到达一条河的两岸。

因为河上的桥正在维修，车辆禁止通行，两车需交换乘客，然后按原路返回各自出发的车站，到站时已是下午2点。

2020年简单的七年级奥数题3篇

2020年简单的七年级奥数题3篇2020年简单的七年级奥数题篇11.一块正方形的草地如果每边增加5米，扩大后仍为一块正方形草地，面积比原来正方形草地增多425平方米，求原来的正方形草地的边长。

2.植树节那天，小明、小红、小月和小康四位同学共种了120棵树，小明种的树是其他同学种树总数的一半，小红种的树是其他同学种树总数的三分之一，小月种的树是其他同学种树总数的四分之一，你知道小康同学种了多少棵树?3.一商店售出两件不同的衣服，售价都是240元，按成本计算，其中一件赚了五分之一，另一件亏了五分之一，售出衣服后，商店是赚了还是亏了?差额是多少?4.一项工程，甲队单独完成需要10天，乙队单独完成需要15天，丙队单独完成需要20天，开始时三个队一起工作，中途甲队撤走，由乙、丙两个队一起完成剩下的工程，最后共用6天时间完成该工程，那么甲队实际工作了多少天?5.小明早上从家步行去学校，走完一半路程时，爸爸发现小明的数学课本丢在家里，随即开车去给小明送书，赶上时，小明还有的路程未走完，小明随即上了爸爸的车，由爸爸送往学校，这样，小明比独自步行提早5分钟到校，小明从家到学校全部步行要多少时间?2020年简单的七年级奥数题篇21.一件工程，甲队单独做要15天完成，乙队单独做要20天完成。

两队合做要多少天完成?2.一件工作,甲单独做要6小时完成，乙单独做要4小时完成，丙单独做要3小时完成。

三人合做要几小时完成?3.一个水池，装有甲、乙、丙三个水管，甲乙为进水管，丙为出水管。

单开甲管2小时可将空水池注满，单开乙管3小时可将空水池注满，单开丙管4小时将满池水放完。

三管齐开，多少时间才能把空池注满?4.一项工程，甲独做8天可以完成，乙独做8天只能完成这项工程的4/5，如果甲、乙合做，多少时间才能完成这项工程?5.一批零件，甲独做12天完成，乙独做8天完成。

甲、乙先合作3天，余下的由乙独做，还要几天完成?2020年简单的七年级奥数题篇31.一项工程，甲队做10天，乙队做15天，均可完成工程的1/3，若甲乙两队合作完成工程的1/3后由甲队做完，共用时间多少天?2.一项工程，甲队做4天，又与乙队合作6天，完成工程的3/5，若两队一开始就合作则6天完成工程的2/5，问甲队独做多少天完成工程?3.一批零件，甲独做比乙独坐所需时间多1/4，如果两人合作，则完成任务时乙比甲多做40个零件，这批零件有多少个?4.一个水池有三根进水管，若单开甲管需12小时注满水池，单开乙管10小时注满水池，现在两管同时开了2小时，又打开丙管，三管又开了2小时方把水池注满。

2020初中奥数竞赛题及答案

选择题1. 数1 是()A. 最小整数B. 最小正数C. 最小自然数D. 最小有理数答案：C解析：整数无最小数，排除A;正数无最小数，排除B;有理数无最小数，排除D。

1是最小自然数，正确，故选Co2. a 为有理数，则一定成立的关系式是()A. 7a>aB. 7+a>aC. 7+a>7D. |a| >7答案：B解析：若a=0, 7X 0=0排除A;7+0=7排除C;|0|0，必有7+a>0+a=a选B。

33 1416 X 7.5944+3.1416 X (-的的值是)()A. 6.1632B. 6.2832C. 6.5132D. 5.3692答案：B解析：3.1416 X 7.5944+3.1416 X (-5.5944)=3.1416(7.5944-5.5944)=2 X 3.1416=6.2832，选B。

4. 在-4，-1，-2.5，-0.01 与-15这五个数中，的数与绝对值的那个数的乘积是()A. 225B. 0.15C. 0.0001D. 1答案：B解析：-4，-1，-2.5，-0.01 与-15中的数是-0.01，绝对值的数是-15，(0.01) X (-15)=0；!选B。

填空题1.计算：(-1)+(-1)-(-1) X (-1)宁(。

)=答案：(-1)+(-1)-(-1) X (-1) r-1)=(-2)-(-1)=-12. 求值：(-1991)-|3-|-31||=答案：(-1991)-|3-|-31||=-1991-28=-2019 。

3. n为正整数，1990n-1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009。

则n 的最小值等于答案：4解析：1990n 的末四位数字应为1991+8009的末四位数字.即为0000，即 1990n 末位至少要4个0,所以n 的最小值为4。

4.不超过 (-1.7)2的整数是答案： 2解析： (-1.7)2=2.89，不超过 2.89 的整数为 2。

2020年基础的七年级奥数题

2020年基础的七年级奥数题2020年基础的七年级奥数题篇一1、一件工作，甲独做10小时完成，乙独做12小时完成，丙独做15小时完成。

三人合做几小时能够完成工作的一半的一半？2、从甲地到乙地，慢车要行15小时，快车要行10小时，慢车从乙地开出5小时后，快车从甲地开出，再经过几小时两车相遇？3、一件工程，甲乙两人合作8天能够完成；乙丙两人合作6天能够完成；丙丁两人合作12天能够完成。

那么甲丁合作几天能够完成？4、有一批机器零件，甲单独制作需要八又二分之一天，比乙单独制作多用了1/2天，两人合作4天后，剩下210个零件，由甲单独去做，自始至终甲共制作了多少个零件？5、甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行。

现在已知甲走一圈的时间是70分钟，如果在出发后第45分钟甲、乙二人相遇，那么乙走一圈的时间是多少分钟？2020年基础的七年级奥数题篇二1、两辆汽车从两地同时出发，相向而行，已知甲车行完全程比乙车多用1.5小时，甲车每小时行40千米，乙车每小时行50千米，出发后多少小时两车相遇？2、甲车每小时行40千米，乙车每小时行60千米。

甲车从A地、乙车从B地同时出发相向而行。

两车相遇后4.5小时甲车到达B地，A、B两地相距多少千米？3、甲乙两车分别从相距306千米的两地同时开出，相向而行，4.5小时后相遇，甲乙两车的速度比为8：9，甲乙两车每小时各行多少千米？4、甲乙从同一地点向相反的方向行驶，甲下午6时出发每小时行40000米，乙第二天上午4时出发，经过10小时后两车相距1080千米。

乙车的时速是多少千米？5、客车由甲城开往乙城要10小时,货车由乙城开往甲城要15小时,两车同时从两城相向开出,相遇时客车比货车多行96千米,甲乙两城之间的公路长多少千米?2020年基础的七年级奥数题篇三1、一件工程，乙队先独做4天，继而甲、丙两队合作6天，剩下的工程甲队又独做9天才完成。

已知乙队完成的是甲队完成的1/3，丙队完成的是乙队完成的2倍。

初中数学奥林匹克竞赛题word版含答案

初中数学奥林匹克竞赛题及答案奥数题一一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么 ( )A．a，b都是0B．a，b之一是0C．a，b互为相反数D．a，b互为倒数答案：C解析：令a=2，b=－2，满足2+(－2)=0，由此a、b互为相反数。

2．下面的说法中正确的是 ( )A．单项式与单项式的和是单项式B．单项式与单项式的和是多项式C．多项式与多项式的和是多项式D．整式与整式的和是整式答案：D解析：x²，x3都是单项式．两个单项式x3，x²之和为x3+x²是多项式，排除A。

两个单项式x²，2x2之和为3x2是单项式，排除B。

两个多项式x3+x2与x3－x2之和为2x3是个单项式，排除C，因此选D。

3．下面说法中不正确的是 ( )A. 有最小的自然数B．没有最小的正有理数C．没有最大的负整数D．没有最大的非负数答案：C解析：最大的负整数是-1，故C错误。

4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么 ( )A．a，b同号B．a，b异号C．a＞0D．b＞0答案：D5．大于－π并且不是自然数的整数有 ( )A．2个B．3个C．4个D．无数个答案：C解析：在数轴上容易看出：在－π右边0的左边（包括0在内）的整数只有－3，－2，－1，0共4个．选C。

6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

这四种说法中，不正确的说法的个数是 ( )A．0个B．1个C．2个D．3个答案：B解析：负数的平方是正数，所以一定大于它本身，故C错误。

7．a代表有理数，那么，a和－a的大小关系是 ( )A．a大于－aB．a小于－aC．a大于－a或a小于－aD．a不一定大于－a答案：D解析：令a=0，马上可以排除A、B、C，应选D。

8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( )A．乘以同一个数B．乘以同一个整式C．加上同一个代数式D．都加上1答案：D解析：对方程同解变形，要求方程两边同乘不等于0的数，所以排除A。

初中数学奥林匹克竞赛题及答案

初中数学奥林匹克竞赛题及答案奥数题一一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么()A．a，b都是0B．a，b之一是0C．a，b互为相反数D．a，b互为倒数答案：C解析：令a=2，b=－2，满足2+(－2)=0，由此a、b互为相反数。

2．下面的说法中正确的是()A．单项式与单项式的和是单项式B．单项式与单项式的和是多项式C．多项式与多项式的和是多项式D．整式与整式的和是整式答案：D解析：x2，x3都是单项式．两个单项式x3，x2之和为x3+x2是多项式，排除A。

两个单项式x2，2x2之和为3x2是单项式，排除B。

两个多项式x3+x2与x3－x2之和为2x3是个单项式，排除C，因此选D。

3．下面说法中不正确的是()A.有最小的自然数B．没有最小的正有理数C．没有最大的负整数D．没有最大的非负数答案：C解析：最大的负整数是-1，故C错误。

4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么()A．a，b同号B．a，b异号C．a＞0D．b＞0答案：D5．大于－π并且不是自然数的整数有()A．2个B．3个C．4个D．无数个答案：C解析：在数轴上容易看出：在－π右边0的左边（包括0在内）的整数只有－3，－2，－1，0共4个．选C。

这四种说法中，不正确的说法的个数是()A．0个B．1个C．2个D．3个答案：B解析：负数的平方是正数，所以一定大于它本身，故C错误。

7．a代表有理数，那么，a和－a的大小关系是()A．a大于－aB．a小于－aC．a大于－a或a小于－aD．a不一定大于－a答案：D解析：令a=0，马上可以排除A、B、C，应选D。

8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边()A．乘以同一个数B．乘以同一个整式C．加上同一个代数式D．都加上1答案：D解析：对方程同解变形，要求方程两边同乘不等于0的数，所以排除A。

完整初二奥数题及答案

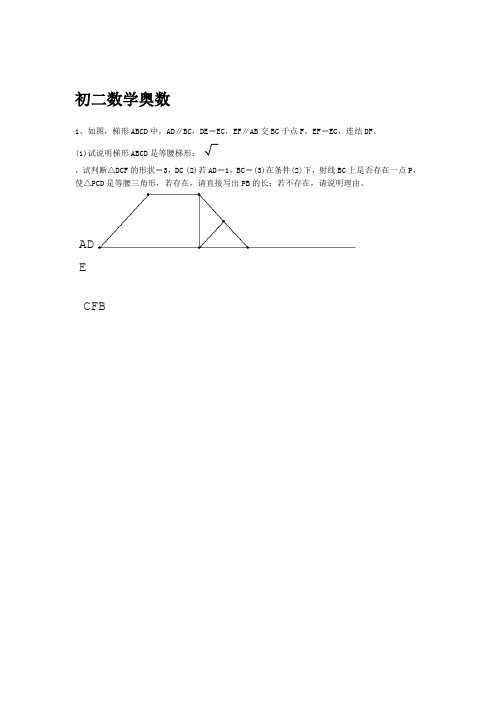
初二数学奥数1、如图，梯形ABCD中，AD∥BC，DE＝EC，EF∥AB交BC于点F，EF＝EC，连结DF。

(1)试说明梯形ABCD是等腰梯形；，试判断△DCF的形状＝3，DC (2)若AD＝1，BC＝(3)在条件(2)下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由。

ADECFB12、在边长为6的菱形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N.（1）如图25－1，当点M在AB边上时，连接BN.≌△ADNABN；①求证：△②若∠ABC = 60°，AM = 4，求点M到AD的距离；（2）如图25－2，若∠ABC = 90°，记点M运动所经过的路程为x（6≤x≤12）试问：x为何值时，△ADN为等腰三角形.2ONOMOMONMMMOONO，，点＝沿的方向运动到⊥左转弯继续运动到，且3、对于点，使、OM点完成一次“左转弯运动”这一过程称为点关于．CPPAPPBABCDPP左转左转弯运动到，，关于正方形关于和点，左转弯运动到点关于2211PADPPPP左转弯运动到左转弯运动到，，……．弯运动到，关于关于54334P）请你在图中用直尺和圆规在图中确定点的位置；（11ADP之间有怎样的关系？并说明理由。

△ABP与△、（2）连接PAPB，判断111y PADDAB两点的为在第二象限，为原点、直线轴建立直角坐标系，并且已知点、(3)以PPP、三点的坐标．1、，4）（1，），请你推断：、0坐标为（201020094ABOPNMCD1图2图34、如图1和2，在20×20的等距网个单位长）格（每格的宽和高均是1MABCA重合的位从点与点中，Rt△个单位长的速度先1置开始，以每秒BC边与网的底部重合向下平移，当时，继续同样的速度向右平移，当ABCPC停止Rt 点△与点重合时，QACx的秒，△移动.设运动时间为y.面积为CBAABCABC关向下平移到△的位置时，请你在网格中画出Rt△RtRt1（）如图1，当△111111QN 于直线成轴对称的图形；xyxABC的函数关系式，并说明当向下平移的过程中，请你求出△）如图（22，在Rt与y分别取何值时，取得最大值和最小值？最大值和最小值分别是多少？yxABC 取得最大值和最小值？最取何值时，△）在（3Rt向右平移的过程中，请你说明当大值和最值分别是多少？为什么？45、如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．(1)图中有几个等腰三角形?猜想：EF与BE、CF之间有怎样的关系，并说明理由．(2)如图②，若AB≠AC，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们．在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC 交AB于E，交AC于F．这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由。

初一数学奥林匹克竞赛题含答案

初一数学奥林匹克竞赛题（含答案）初一奥数题一甲多开支100元，三年后负债600元．求每人每年收入多少？S的末四位数字的和是多少？4．一个人以3千米/小时的速度上坡，以6千米/小时的速度下坡，行程12千米共用了3小时20分钟，试求上坡与下坡的路程．5．求和：6．证明：质数p除以30所得的余数一定不是合数．8．若两个整数x，y使x2+xy+y2能被9整除，证明：x和y能被3整除．9．如图1－95所示．在四边形ABCD中，对角线AC，BD的中点为M，N，MN的延长线与AB边交于P点．求证：△PCD的面积等于四边形ABCD的面积的一半．解答：所以x=5000(元)．所以S的末四位数字的和为1＋9＋9＋5=24．3．因为a-b≥0，即a≥b．即当b≥a＞0或b≤a＜0时，等式成立．4．设上坡路程为x千米，下坡路程为y千米．依题意则有由②有2x+y=20，③由①有y=12-x．将之代入③得 2x+12-x=20．所以x=8(千米)，于是y=4(千米)．5．第n项为所以6．设p=30q＋r，0≤r＜30．因为p为质数，故r≠0，即0＜r＜30．假设r 为合数，由于r＜30，所以r的最小质约数只可能为2，3，5．再由p=30q＋r 知，当r的最小质约数为2，3，5时，p不是质数，矛盾．所以，r一定不是合数．7．设由①式得(2p-1)(2q-1)=mpq，即(4-m)pq+1=2(p+q)．可知m＜4．由①，m＞0，且为整数，所以m=1，2，3．下面分别研究p，q．(1)若m=1时，有解得p=1，q=1，与已知不符，舍去．(2)若m=2时，有因为2p-1=2q或2q-1=2p都是不可能的，故m=2时无解．(3)若m=3时，有解之得故 p＋q=8．8．因为x2+xy+y2=(x-y)2+3xy．由题设，9｜(x2+xy＋y2)，所以3｜(x2＋xy ＋y2)，从而3｜(x-y)2．因为3是质数，故3｜(x-y)．进而9｜(x-y)2．由上式又可知，9｜3xy，故3｜xy．所以3｜x或3｜y．若3｜x，结合3(x-y)，便得3｜y；若3｜y，同理可得，3｜x．9．连结AN，CN，如图1－103所示．因为N是BD的中点，所以上述两式相加另一方面，S△PCD =S△CND＋S△CNP＋S△DNP．因此只需证明S△AND ＝S△CNP＋S△DNP．由于M，N分别为AC，BD的中点，所以S△CNP =S△CPM-S△CMN=S△APM-S△AMN=S△ANP．又S△DNP =S△BNP，所以S△CNP ＋S△DNP=S△ANP+S△BNP=S△ANB=S△AND．初一奥数题二1．已知3x2-x=1，求6x3+7x2-5x＋2000的值．2．某商店出售的一种商品，每天卖出100件，每件可获利4元，现在他们采用提高售价、减少进货量的办法增加利润，根据经验，这种商品每涨价1元，每天就少卖出10件．试问将每件商品提价多少元，才能获得最大利润？最大利润是多少元？3．如图1－96所示．已知CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1＋∠2=90°．求证：DA⊥AB．4．已知方程组的解应为一个学生解题时把c抄错了，因此得到的解为求a2＋b2＋c2的值．5．求方程｜xy｜-｜2x｜+｜y｜=4的整数解．6．王平买了年利率7.11％的三年期和年利率为7.86％的五年期国库券共35000元，若三年期国库券到期后，把本息再连续存两个一年期的定期储蓄，五年后与五年期国库券的本息总和为47761元，问王平买三年期与五年期国库券各多少？(一年期定期储蓄年利率为5.22％)7．对k，m的哪些值，方程组至少有一组解？8．求不定方程3x＋4y＋13z=57的整数解．9．小王用5元钱买40个水果招待五位朋友．水果有苹果、梨子和杏子三种，每个的价格分别为20分、8分、3分．小王希望他和五位朋友都能分到苹果，并且各人得到的苹果数目互不相同，试问他能否实现自己的愿望？解答：1．原式=2x(3x2-x)+3(3x2-x)-2x+2000 =2x×1＋3×1-2x+2000=2003．2．原来每天可获利4×100元，若每件提价x元，则每件商品获利(4＋x)元，但每天卖出为(100-10x)件．如果设每天获利为y元，则y ＝(4＋x)(100-10x)=400＋100x-40x-10x2=-10(x2-6x＋9)＋90＋400=-10(x-3)2＋490．所以当x=3时，y最大=490元，即每件提价3元，每天获利最大，为490元．3．因为CE平分∠BCD，DE平分∠ADC及∠1＋∠2=90°(图1－104)，所以∠ADC＋∠BCD=180°，所以AD∥BC．①又因为 AB⊥BC，②由①，② AB⊥AD．4．依题意有所以a2+b2+c2=34．5．｜x｜｜y｜-2｜x｜+｜y｜=4，即｜x｜(｜y｜-2)+(｜y｜-2)=2，所以(｜x｜+1)(｜y｜-2)=2．因为｜x｜＋1＞0，且x，y都是整数，所以所以有6．设王平买三年期和五年期国库券分别为x元和y元，则因为y=35000-x，所以 x(1＋0.0711×3)(1＋0.0522)2+(35000-x)(1+0.0786×5)=47761，所以 1.3433x＋48755-1.393x=47761，所以 0.0497x=994，所以 x=20000(元)，y=35000-20000=15000(元)．7．因为 (k－1)x＝m-4，①m为一切实数时，方程组有唯一解．当k=1，m=4时，①的解为一切实数，所以方程组有无穷多组解．当k=1，m≠4时，①无解．所以，k≠1，m为任何实数，或k=1，m=4时，方程组至少有一组解．8．由题设方程得z＝3m-y．x=19-y-4(3m-y)-m =19+3y-13m．原方程的通解为其中n，m取任意整数值．9．设苹果、梨子、杏子分别买了x，y，z个，则消去y，得12x-5z=180．它的解是x=90-5t，z=180-12t．代入原方程，得y=-230＋17t．故x=90-5t，y=-230+17t，z=180-12t．x=20，y=8，z=12．因此，小王的愿望不能实现，因为按他的要求，苹果至少要有1＋2＋3+4＋5＋6=21＞20个．初一奥数题三1．解关于x的方程2．解方程其中a＋b＋c≠0．3．求(8x3-6x2+4x-7)3(2x5-3)2的展开式中各项系数之和．4．液态农药一桶，倒出8升后用水灌满，再倒出混合溶液4升，再用水灌满，这时农药的浓度为72％，求桶的容量．5．满足[-1.77x]=-2x的自然数x共有几个？这里[x]表示不超过x的最大整数，例如[-5.6]=-6，[3]=3．6．设P是△ABC内一点．求：P到△ABC三顶点的距离和与三角形周长之比的取值范围．7．甲乙两人同时从东西两站相向步行，相会时，甲比乙多行24千米，甲经过9小时到东站，乙经过16小时到西站，求两站距离．8．黑板上写着三个数，任意擦去其中一个，将它改写成其他两数的和减1，这样继续下去，最后得到19，1997，1999，问原来的三个数能否是2，2，2？9．设有n个实数x1，x2，…，xn，其中每一个不是+1就是-1，且求证：n是4的倍数．解答：1．化简得6(a-1)x=3-6b+4ab，当a≠1时，2．将原方程变形为由此可解得x=a＋b+c．3．当x=1时，(8-6+4-7)3(2-1)2=1．即所求展开式中各项系数之和为1．依题意得去分母、化简得7x2-300x+800=0，即7x-20)(x-40)=0，5．若n为整数，有[n＋x]=n＋[x]，所以[-1.77x]=[-2x＋0.23x]=-2x+[0.23x]．由已知[-1.77x]=-2x，所以-2x=-2x+[0.23x]，所以 [0.23x]=0．又因为x为自然数，所以0≤0.23x＜1，经试验，可知x可取1，2，3，4，共4个．6．如图1－105所示．在△PBC中有BC＜PB＋PC，①延长BP交AC于D．易证PB＋PC＜AB＋AC．②由①，② BC＜PB＋PC＜AB+AC，③同理 AC＜PA＋PC＜AC＋BC，④AB＜PA＋PB＜AC＋AB．⑤③＋④＋⑤得AB＋BC＋CA＜2(PA＋PB＋PC)＜2(AB＋BC＋CA)．所以7．设甲步行速度为x千米/小时，乙步行速度为y千米/小时，则所求距离为(9x+16y)千米．依题意得由①得16y2=9x2，③由②得16y=24＋9x，将之代入③得即 (24＋9x)2=(12x)2．解之得于是所以两站距离为9×8＋16×6=168(千米)．8．答案是否定的．对于2，2，2，首先变为2，2，3，其中两个偶数，一个奇数．以后无论改变多少次，总是两个偶数，一个奇数(数值可以改变，但奇偶性不变)，所以，不可能变为19，1997，1999这三个奇数．。

2020年江苏省苏州市中考数学奥赛试题试卷附解析

2020年江苏省苏州市中考数学奥赛试题试卷学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上一、选择题1．下列图形中阴影部分面积相等的是（）A ．①②B ．②③C ．①④D ．③④2．已知△ABC 的三边长分别为6 cm ，7.5 cm ，9 cm ，△DEF 的一边长为4 cm ，当△DEF 的另两边长是下列哪一组时，这两个三角形相似（） A ．2 cm ，3 cm B ．4 cm ，5 cm C ．5 cm ，6 cm D ．6 cm ，7 cm3．若抛物线y=ax 2经过点P （l ，-2），则它也经过（）A ． P 1（-1，-2 ）B ． P 2（-l, 2 ）C ． P 3（ l, 2）D ． P 4（2, 1） 4．口ABCD 的周长为36 cm ，AB=BC=2cm ，则AD ，CD 的长度分别为（） A ．12 cm ，6 cmB ．8 cm ，10 cmC ．6 cm ，12 cmD ．10 cm ，8 cm5．下列命题是真命题的是（） A ．三角形、四边形不是多边形 B ．内角和等于外角和的多边形不存在 C ．若多边形的边数增加，则它的外角和也增加 D ．若多边形边数减少，则其内角和也减少 6．以3，-4为根的一元二次方程是（）A ．x x 2120+-= B ．x x 2120++= C ．x x 2120-+=D ． x x 2120--=7．某市为了申办2010年冬奥会决定改善城市容貌，绿化环境，计划经过两年时间，绿地面积增加44%，这两年平均绿地面积的增长率是（） A ．19% B ．20% C ．21%D ．22%8．小王只带2元和 5元两种面值的人民币，他买一件学习用品要支付27元，则付款的方式有（） A ． 1种B ． 2种C ．3种D ．4种9．不改变分式yx x 7.0213.1--的值，把它的分子、分母的系数化为整数，其结果正确的是（）A ．yx x 72113--B ．yx x 721013--C ．yx x 7201013--D ．yx x 720113--10．在数|3|-，2-+，(0.5)--，|0|+-中负数共有（） A ．1 个B ．2 个C ．3 个D ．4 个二、填空题11．请画出正四棱锥的俯视图．12．两圆的圆心距等于 1，半径R 、r 是方程27120x x -+=的两根，则这两圆的位置关系是．13．已知两个相似三角形的相似比为3：1，则它们的周长比为．14．某学校食堂现有存煤 200 吨．这些煤能烧的天数y 与平均每天的吨数x 之间的函数解析式为．15．在Rt △ABC 中，D 是斜边AB 上的中点, AC=1，BC=3，则CD= ．16．如图，长方形ABCD 中(AD ＞AB)，M 为CD 上一点，若沿着AM 折叠，点N 恰落在BC 上，∠ANB ＋∠MNC ＝____________．17．一箱水果售价 a 元，水果的总质量为b(kg)，则每kg 水果售价是元. 18．如图，点A 、B 、C 在直线l 上，则图中共有______条线段．19．用四舍五入法取l29543的近似值，保留3个有效数字，并用科学记数法表示是． 20．若a 满足2008(2006)1a -=，则a= ．21．对于加法，我们有 3+5=5+3，11112332+=+，(-3) +(-0.5) = (-0. 5)+(-3)，…，用字母可以表示成．三、解答题22．如图，直角三角形纸片ABC ，∠Ｃ＝90°，AC ＝6，BC ＝8，折叠△ABC 的一角，使点B 与点A 重合，展开得折痕DE ．（1）求证：△BED ∽△BCA ；（2）求BD 的长．FGEDCBA23．一个滑轮起重装置如图所示，滑轮的半径是10cm ，当重物上升10cm 时，滑轮的一条半径OA 绕轴心0 按逆时针方向旋转的角度约为多少呢(假设绳索与滑轮之间没有滑动，取 3.14，结果精确到1°)？24．如图EG ∥AF.请你从下面三个条件中，选择两个作为已知条件，另一个作为结论，推出一个正确的命题（只需要写出一种情况）. ①AB = AC ；②DE = DF ；③BE = CF. 已知：EG ∥AF ， = ， = . 求证： . 请证明上述命题.25．观察如图所示的四个图形，找出它们的共同特征并给以名称，再作出定义．26．在一块边长为1m 的正方形铁板上截出一个面积为800cm 2的矩形铁板，使长比宽多20cm ，问矩形铁板的长和宽各为多长?27．甲、乙两战士各打靶5次，命中环数如下：甲：5，9，8，10，8；乙：6，10，5，10，9．求：(1)两战士平均每枪分别命多少环? (2)你认为哪一个战士发挥比较稳定．28．如图①，在6×6的方格纸中，给出如下三种变换：P 变换，Q 变换，R 变换．将图形F 沿直线x 向右平移l 格得图形F 1，称为作1次P 变换；将图形F 沿直线y 翻折得图形F 2，称为作1次Q 变换；将图形F 绕坐标原点顺时针旋转90°得图形F 3，称为作1次R 变换．规定：PQ 变换表示先作1次Q 变换，再作1次P 变换；n R 变换表示作n 次R 变换．解答下列问题： (1)作R 4变换相当于至少作次Q 变换；(2)请在图②中画出图形F 作R 2007变换后得到的图形F 4；(3)PQ 变换与QP 变换是否是相同的变换?请在图③中画出PQ 变换后得到的图形F 5，在图④中画出QP 变换后得到的图形F 6．29．如图，AC ＝AE ，∠BAM ＝∠BND ＝∠EAC ，图中是否存在与△ABE 全等的三角形?并说明理由．ADM CBEN30．某校学生会在“暑假社会实践”活动中组织学生进行社会调查，并组织评委会对学生写出的调查报告进行了评比．学生会随机抽取了部分评比后的调查报告进行统计，如下表．请根据该表回答下列问题：某校暑假社会实践活动评比抽样统计表(1)(2)若等第A为优秀，则优秀率为；(3)学生会共收到调查报告1000份，估计该校调查报告的等第为E的有份．(4)根据表中信息，绘制条形统计图．【参考答案】学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．D2．C3．A4．B5．D6．A7．B8．C9．C10．A二、填空题12．内切13．3：114．200y x=15． 116．90°17．ab18． 319．1.30×10520．2007 或 200521．a+b=b+a三、解答题 22．（1）由题意得：∠DEB=∠BCA=90°，∠B=∠B ，∴△BED ∽△BCA （2）在Rt △ABC 中，由勾股定理得：AB 2210AC BC += ，BE ＝21AB ＝5 ∵△BDE ～△BAC ，∴AB BD BC BE =，即1085BD= 解得BD ＝425 ∴BD 的长为425． 23．旋转的角度约为：018010573.1410⨯≈⨯24．25．轴对称图形：把一个图形沿着一条直线对折，直线两旁的部分能够互相重合，这样的图形叫做轴对称图形．26．长 40 cm，宽 20 cm27．环；(2)甲发挥稳定(1)8==x x乙甲28．(1)2 (2)略(3)略29．存在△ABE≌△ADC，理由略30．(1)50 (2)16％ (3)40 (4)略。

初三数学奥数题及答案

初三数学奥数题及答案题目一：数列问题题目描述：已知数列 {a_n} 的前几项为 a_1 = 1, a_2 = 3, a_3 = 6, a_4 = 10, ... 求 a_5 的值以及数列的通项公式。

解题思路：观察数列的前几项，可以发现每一项与前一项的差值依次为 2, 3, 4, ... 这是一个等差数列的差值，差值为 1, 2, 3, ...。

因此，可以推断出数列 {a_n} 的通项公式为 a_n = 1 + n * (n - 1) / 2。

答案：根据通项公式，a_5 = 1 + 5 * (5 - 1) / 2 = 1 + 20 / 2 = 11。

题目二：几何问题题目描述：在三角形 ABC 中，已知 AB = 5, AC = 7, BC = 6。

求三角形 ABC 的面积。

解题思路：利用海伦公式，首先计算半周长 s = (AB + AC + BC) / 2 = (5 + 7 + 6) / 2 = 9。

然后根据海伦公式S = √(s * (s - AB) * (s - AC) * (s - BC)) 计算面积。

答案：S = √(9 * (9 - 5) * (9 - 7) * (9 - 6)) = √(9 * 4 * 2* 3) = 6√6。

题目三：组合问题题目描述：有 10 个不同的球，要将它们放入 3 个不同的盒子中，每个盒子至少放一个球。

求不同的放法总数。

解题思路：首先，将 10 个球分成 3 组，其中两组有 3 个球，另一组有 4 个球。

使用组合公式 C(n, k) 计算分组的方法数，然后将分组的结果分配到 3 个盒子中。

答案：首先计算分组的方法数，C(10, 3) = 120。

然后将 3 组分配到3 个盒子中，有 3! = 6 种方法。

因此，总的放法数为 120 * 6 = 720。

题目四：函数问题题目描述：已知函数 f(x) = x^2 - 6x + 8，求 f(x) 的最小值。

解题思路：观察函数 f(x)，可以看出它是一个开口向上的二次函数。

2020年简单的初中奥数题

2020年简单的初中奥数题2020年简单的初中奥数题（1）1、甲、乙两车分别从A、B两地出发，相向而行，4小时相遇。

相遇后，甲车继续行了3小时到达B地，乙每小时行24千米，AB 两地间的路程是多少千米？2、一队自行车运动员以每小时24千米的速度骑车从甲地到乙地,两小时后一辆摩托车以每小时56千米的速度也从甲地到乙地,在甲地到乙地距离的二分之一处追上了自行车运动员.问:甲乙两地相距多少千米?3、小爱和小清同时从A、B两城相向而行，在离A城35千米处相遇，到达对方城市后立即以原速沿原路返回，又在离A城15千米处相遇，两城相距多少千米？4、A、B、C三辆车同时从甲出发到乙地去，A、B两车速度分别为每小时50km和38km，有一辆迎面开来的卡车分别在他们出发后4小时、5小时、6小时先后与A、B、C三车相遇。

求C车的速度。

5、两名运动员在湖周围环形道上练习长跑，甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙，如果两人同时同地反向出发，经过多少分钟两人相遇？2020年简单的初中奥数题（2）1.李明看一本故事书，第一天看了全书的一半，第二天看了全书的三分之一，还剩下35页没有看，李明两天一共看了多少页?2.修一条路，甲队独修15天完成，乙队独修20天完成，甲队先修3天后，剩下的两队合修，大约要几天修完?3.长州电厂有一批煤，原计划每天烧5吨，可以烧60天，实际每天节约20%，这批煤实际可以烧多少天?(用比例解)4.甲车每小时行40千米，乙车每小时行60千米。

甲车从A 地、乙车从B地同时出发相向而行。

两车相遇后4.5小时甲车到达B地，A、B两地相距多少千米？5.甲乙两地相距258千米。

一辆汽车和一辆拖拉机同时分别从两地相对开出，经过4小时两车相遇。

已知汽车的速度是拖拉机速度的2倍。

相遇时，汽车比拖拉机多行多少千米？2020年简单的初中奥数题（3）1.一座下底面是边长为10米的正方形石台，它的一个顶点A 有一个虫子巢穴，虫甲每分钟爬6厘米，虫乙每分钟爬10厘米，甲沿正方形的边由A-B-C-D-A不停地爬行，甲先爬2厘米后，乙沿甲爬行过的路线追赶甲，当乙遇到甲后，乙就立即沿原路返回巢穴，然后乙再沿甲爬行的路线追赶甲，在甲爬行的一圈内，乙最后一次追上甲时，乙爬行了多长时间？2.有一群猴子，分一堆桃子，第一只猴子分了4个桃子和剩下桃子的1/10，第二只猴子分了8个桃子和这时剩下桃子的1/10，第三只猴子分了12个桃子和这时剩下桃子的1/10。

2020年浙江省绍兴市中考数学奥赛试题试卷附解析

2020年浙江省绍兴市中考数学奥赛试题试卷学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．如图，已知⊙O 的半径为5，点O 到弦AB 的距离为3，则⊙O 上到弦AB 所在直线的距离为2的点有（）A ．1个B ．2个C ．3个D ．4个2．二次函数(3)(2)y x x =-+的图象的对称轴是直线（）A ．x =3B ．x=2C ．12x =-D ．12x = 3．一个容量为50的样本，最大值是l35，最小值是40，取组距为10，则可以分（）A ．10组B ．9组C ．8组D ．7组 4．下列方程中是一元二次方程的是（）A ．2x ＋1=0B ．y 2＋x=1C ．x 2＋1＝0D ．112=+x x5．，（）A ．2 个B ．3 个C ．4 个D ．5 个 6．若点P （m ，2）与点Q （3，n ）关于y 轴对称，则m 、n 的值分别为（）A ． -3，2B ． 3，-2C ．-3，-2D ．3，2 7．对于数据3，3，2，3，6，3，10，3，6，3，2. 有以下结论：①这组数据的众数是3；②这组数据的众数与中位数的数值不等；③这组数据的中位教与平均数的数值相等；④这组数据的平均数与众数的数值相等.其中正确的有（）A ．1个B ． 2个C ．3个D ．4个8．已知下列说法：①数轴上原点右边的点所表示的数是正数；②数轴上的点都表示有理数；③非正数在教轴上所表示的点在原点左边；④所有的有理数都可以用数轴上的点来表示. 其中正确的有（）A ． 1 个B ．2 个C ．3 个D ．4 个二、填空题9．已知⊙O 的半径为5㎝，弦AB 的长为8㎝，则圆心O 到AB 的距离为㎝.10．用配方法把二次函数y=-2x 2+8x-5化成y=a(x+m)2+n 的形式，即y= . y=-2（x －2）2+311．△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于F ，若BF=AC ，则∠ABC= 度.12．在△ABC 中，∠C=90°，∠A=2∠B ，则A= 度． 13．如果y-1与x-3成正比例，且当x=4时，y=-1，那么y 关于x 的函数解析式是．14．妈妈做了一份美味可口的菜品，为了了解菜品的咸淡是否适合．于是妈妈取了一点品尝，这应该属于 (填“普查”或“抽样调查”)．15．在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为分.16．如图，1l ⊥2l , 3l ⊥2l ，则1l 3l ，理由是．17．若(1+x)(2x 2+mx+5)的计算结果中x 2项的系数为－3,则m= _．18．从 1 至 10 这 10 个数中任意取一个，则选中的数字是2 的倍数的可能性比选中的数字是质数的可能性．19．如图所示的五家银行行标中，是轴对称图形的有 (填序号)．三、解答题20．如图所示，海中有一小岛 P ，在距离P 处82海里范围内有暗礁，一轮船自西向东航行，它在A 处时测得小岛 P 位于北偏东 60°，且A 、P 之间的距离为 16 海里，若轮船继续向东航行，请计算轮船有无触礁的危险，如有危险，轮船自A 处开始至少东偏南多少度方向航行，才能安全通过这一海域？21．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为12． (1）试求袋中蓝球的个数；(2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．22．已知函数y ＝x 2－bx －1的图象经过点（3，2）(1）求这个函数的解析式；(2）当x>0时，利用图像求使y ≥2的x 的取值范围．（1）y ＝x ２－2x －1；（2）x ≥3．23．在如图所示的 4×4 方格内画三角形，使它的顶点都在格点上，三条边长分别为11255，4，2232 ．24．某礼堂共有30排座位，第1排共有20个座位，后面每一排比前一排多2个座位，则(1)第5排、第10排分别有几个座位?(2)若某一排有54个座位，则应是第几排?(3)写出每排的座位数m 与这排的排数n 之间的关系式，并指出这个问题中的常量和变量．25．在A市北方250 km处有B市，在A市北偏东30°方向100 km处有C市，在A市西北方向的l00 km处有D市，以A市为原点，东西方向的直线为x轴，南北方向为y轴，并取50 km为1个单位长度，画出直角坐标系和各城市，并求各城市的坐标．根据气象台预报，今年17号台风中心位置处在(8，6)，并以20 km／h的速度自东向西移动，台风影响范围半径为200 km，问经过12 h后，上述城市哪些已受到台风的影响?26．(1)在平面直角坐标系中，作出下列各点A(0，2)、B(1，O)、C(5，2)、D(2，4)；(2)求四边形ABCD的面积．27．解不等式：(1）1223ix xx+-<-；（2）22(2)12x x+->28．如图所示，四边形ABCD 中，AB=CD，BC=AD，请你添一条辅助线，把它分成两个全等的三角形．你有几种添法?分别说明理由．29．2008年十一黄金周期间，某市旅游收入再创历史新高，旅游消费呈现多样化，各项消费所占的比例如图所示，其中住宿费为3438.24万元.(1)求该市2008年十一黄金周期间旅游消费共多少亿元？(2)对于十一黄金周期间的旅游消费，如果该市2009年要达到2.28亿元的目标，那么2008~2009年的增长率是多少？30．有五条线段，长度分别为1、3、5、7、9，从中任取三条线段，一定能构成三角形吗？能构成三角形的概率是多少？【参考答案】学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．C2．D3．A4．C5．B6．A7．A8．B二、填空题9．310．11．12．6013．y=2x+714．抽样调查15．7116．∥；∠l=∠2=90°,同位角相等，两直线平行17．-518．大19．①②③三、解答题20．过P 作 PB ⊥AE 于B ，∠PAB= 30° ,18822PB PA ==< ∴继续航行有触栈的危险．设安全航向为 AD ，作 PC ⊥AD 于C ，82PC =，PA=16，2sin 2PC PAC PA ∠==, ∴∠PAC=45°，从而∠BAC= 15°故轮船自 A 开始，至少应沿东偏南15°的方向航行，才能安全通过这一个海域.21．（1）1个；（2）树状图略；P=61．23．如图所示24．(1)28个，38个；(2)18排；(3)m=20+2(n-1)(1≤n ≤30且n 为正整数)；常量为20，2，1；变量为m ，n25．图略 A(0，0)，B(0，5)，C(13，D(2-2，B 市会受到影响，A 、C 、D 三市不会受影响26．(1)略；(2)1027．(1)x<-1；(2)x>228．连结AC 或连结BD ，都是根据SSS 说明三角形全等29．(1)由图，知住宿消费为 3438.24万元，占旅游消费的22.62%，所以旅游消费共计3438.2422.62%=15200÷（万元)= 1.52(亿元)；(2)设2008年到2009年旅游消费的年平均增长率是x ，由题意，得1.52(1) 2.28x +=，解得0.5x =答：2008年到 2009年旅游消费的年平均增长率是50%.30．不一定能构成三角形，因为由树形图（图略）可知，从1，3，5，7，9中任取3个数，能组合成10种形式，能构成三角形的数字有（3,5,7）,(3,7,9),(5,7,9),所以从长度分别为1,3,5,7,9 的5条线段中任取三条能构成三角形的概率为310．。

初中奥数题目及答案大全

【导语】奥数对青少年的脑⼒锻炼有着⼀定的作⽤，可以通过奥数对思维和逻辑进⾏锻炼，对学⽣起到的并不仅仅是数学⽅⾯的作⽤,通常⽐普通数学要深奥些。

下⾯为⼤家分享⼀道题⽬。

初中奥数题及答案⼤全：⼀、选择题(每题1分，共10分) 1.下⾯的说法中正确的是() A.单项式与单项式的和是单项式 B.单项式与单项式的和是多项式 C.多项式与多项式的和是多项式 D.整式与整式的和是整式答案：D 解析：x2，x3都是单项式.两个单项式x3，x2之和为x3+x2是多项式，排除A。

两个单项式x2，2x2之和为3x2是单项式，排除B。

两个多项式x3+x2与x3-x2之和为2x3是个单项式，排除C，因此选D。

2.如果a，b都代表有理数，并且a+b=0，那么() A.a，b都是0 B.a，b之⼀是0 C.a，b互为相反数 D.a，b互为倒数答案：C 解析：令a=2，b=-2，满⾜2+(-2)=0，由此a、b互为相反数。

3.下⾯说法中不正确的是() A.有最⼩的⾃然数 B.没有最⼩的正有理数 C.没有的负整数 D.没有的⾮负数答案：C 解析：的负整数是-1，故C错误。

4.如果a，b代表有理数，并且a+b的值⼤于a-b的值，那么() A.a，b同号 B.a，b异号 C.a>0 D.b>0 答案：D 5.⼤于-π并且不是⾃然数的整数有() D.⽆数个答案：C 解析：在数轴上容易看出：在-π右边0的左边(包括0在内)的整数只有-3，-2， -1，0共4个.选C。

6.有四种说法：甲.正数的平⽅不⼀定⼤于它本⾝; ⼄.正数的⽴⽅不⼀定⼤于它本⾝; 丙.负数的平⽅不⼀定⼤于它本⾝; 丁.负数的⽴⽅不⼀定⼤于它本⾝。

这四种说法中，不正确的说法的个数是() A.0个 B.1个 C.2个 D.3个答案：B 解析：负数的平⽅是正数，所以⼀定⼤于它本⾝，故C错误。

7.a代表有理数，那么，a和-a的⼤⼩关系是() A.a⼤于-a B.a⼩于-a C.a⼤于-a或a⼩于-a D.a不⼀定⼤于-a 答案：D 解析：令a=0，马上可以排除A、B、C，应选D。

2020初中奥数题及答案

设蒸发变成含盐为40%的水重x克，
即60X30%=40%x
解得：x=45(千克)。
遇到这一类问题，我们要找不变量，本题中盐的含量是一个不变量，通过它列出等式进行计算。
三、解答题
1.甲乙两人每年收入相等，甲每年储蓄全年收入的-，乙每月比甲多开支100元,
5
三年后负债600元，求每人每年收入多少？
答案：解：设每人每年收入x元，甲每年开支4/5x元，依题意有：
A.2个
B.3个
C.4个
D.无数个
答案：C
解军析：在数轴上容易看出：在一n右边0的左边(包括0在内)的整数只有一3, —2, —1，0共4个.选C。
6．有四种说法：
甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。
这四种说法中，不正确的说法的个数是( )
多少元？
答案：原来每天可获利4X100元，若每件提价x元，则每件商品获利(4+x)元, 但每天卖出为(100-10x)件。
如果设每天获利为y元，
则y=(4+x)(100-10x)
2
=400+100x-40x-10x
=-10(x2-6x+9)+90+400
=-10(x-3)2+490。
所以当x=3时，y最大=490元，即每件提价3元，每天获利最大为490元。
=6.2832，选Bo
4.在-4,-1,-2.5,-0.01与-15这五个数中，最大的数与绝对值最大的那个数
的乘积是()
A.225
B.0.15
C.0.0001
D.1
答案：B
解析：-4,-1,-2.5,-0.01与-15中最大的数是-0.01,绝对值最大的数是-15,(-0.01)X(-15)=0.15,选Bo