2013高考试题解析

合集下载

2013年高考试题答案和解析

2013年普通高等学校招生全国统一考试语文本试题卷共8页，六大题23小题。

全卷满分150分。

考试用时150分钟。

注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。

2．选择题的作答：每小题选出答案后，用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

答在试题卷、草稿纸上无效。

3．非选择题的作答：用统一提供的签字笔直接答在答题卡上对应的答题区域内。

答在试题卷、草稿纸上无效。

4．考生必须保持答题卡的整洁。

考试结束后，请将本试题卷和答题卡一并上交。

一、语文基础知识（共15分，共5小题，每小题3分）1．下列各组词语中，加点字的注音全都正确的一组是A．踹（chuài）水竞（jìnɡ）赛蘸（zhàn）酒擂（léi）鼓助威B．跋涉（shè）陡（dǒu）峭攀登（dēnɡ）餐霜饮雪（xiě）C．善（shàn）良谦逊（sùn）璞（pú）玉不事雕琢（zhuó）D．荆棘（jí）飘泊（bó）青苔（tāi）红漆（qī）雕花2．下列各组词语中，没有错别字的一组是A．彷徨愁怨寂寥静默凄婉惆伥B．顾盼精捍步履稳健风神潇洒C．睿智禀赋崇高品质趋善避恶D．辩难商榷典藉满架旁稽博采3．依次填入下列横线处的词语，最恰当的一组是①宋人画雪常不用铅粉，把背景用墨衬黑，一层层，留出山头的白，树梢的白，甚至花蕾上的白，虚实映衬，意境悠远。

②因为睡不着，打开窗帘，遥望夜空，满天，斜月晶莹，薄雾似轻纱漫卷，。

我思念那个小山村，那个让我魂牵梦绕的地方！A．而是点染星汉如梦如幻B．总是浸染星云如诗如画C．却是绘染星光诗意盎然D．只是渲染星斗诗意朦胧4．下列各项中，没有语病的一项是A．《美丽中国》以歌舞为主，融入京剧演唱、茶艺表演、少林武术等元素，加上奇幻的灯光，震撼的音响，一幅美丽中国的大写意，声光舞影流溢着浓郁的中国情。

2013年高考试题及解析：语文(北京卷)

2013年普通高等学校招生全国统一考试语文(北京卷)本试卷共8页，150分。

考试时长150分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回。

一、本大题共5小题。

每小题3分，共15分。

1.下列词语，字形与加点字的注音全部正确的一项是（）A．养殖业与日剧增便笺（jiān）独辟蹊（xī）径B．醉醺醺席不暇暖泥淖（nào）向隅（yú）而泣C．滥摊子自由竞争卷帙（dié）运筹帷幄（wò）D．颤巍巍信笔涂鸭蠹（dù）虫湮（yīn）没无闻【参考答案】B【答案解析】本题综合考查字音、字形的识记与辨析，与日俱增、卷帙（zhì）、信笔涂鸦、湮（yān）没无闻【试题点评】本题在高考强化提高班讲座2第2讲《字音的识记与辨析》第3讲《字形的识记与辨析》中有详细讲解，所考词语视频中已全部复习讲解。

在高考强化提高班讲座1、寒假特训班、百日冲刺班中也均有涉及。

2.下列语句中，没有语病的一项是（）A．近几年，食品药品在安全方面出现的问题被媒体曝光，不同职能部门各管一段的监管模式也因此受到了社会的质疑。

B.第九届中国国际园林博览会在北京永定河西岸盛大开幕，对于513公顷的园博园，为了方便游客，专门开设了电瓶车专线。

C．据世界黄金协会分析，2013年春节前后中国黄金需求高涨的原因，主要由于消费者对中国经济前景充满信心所致。

D．日前，交通管理部门就媒体对酒驾事故的连续报道做出了积极回应，表示要进一步加大对交通违法行为的查处。

【参考答案】A【答案解析】本题考查病句的辨析及修改， B缺少主语，C重复，D搭配不当，加大……力度【试题点评】本题在高考强化提高班讲座2第6讲、第7讲、第8讲《病句的辨析与修改》中对以上几种病句类型有详细重点讲解，在高考强化提高班讲座1、寒假特训班、百日冲刺班中均有涉及。

3.依次填入句中横线处的词语，正确的一项是（）①文学艺术创造来源于生活，作家塑造的人物形象，往往是以现实生活中的真实人物为创作而形成的。

2013年高考语文试题及解析(安徽卷)

绝密★启用前2013年普通高等学校招生全国统一考试（安徽卷）语文本试卷分为第I卷（阅读题）和第II卷（表达题）。

全卷满分150分，考试时间150分钟。

考生注意事项：1．答题前，务必在试题卷、答题卡规定的地方填写自己的姓名、座位号，并认真核对答题卡上所粘贴的条形码中的姓名、座位号与本人姓名、座位号是否一致。

务必在答题卡背面规定的地方填写姓名和座位号后两位。

2．答选择题（第I卷1 ~ 6题，第II卷15 ~ 17题）时，每小题选出答案后，用2B 铅笔把答题卡上所对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

3．答非选择题（第I卷7 ~ 14题，第II卷18 ~ 21题）必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰。

作图题可先用铅笔在答题卡的规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚。

必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效。

4．考试结束后，务必将试题卷和答题卡一并上交。

第I卷（阅读题，共66分）一、（9分）阅读下面的文字，完成1 ~ 3题。

①科学所研究的是那些被认为是独立于研究者个人而存在的关系。

这也适用于把人本身作为研究对象的科学。

科学陈述的对象还可以是我们自己创造出来的概念，像在数学中就是那样。

我们不一定要假设这种概念是同外在世界显的任何客体相对应的。

但是，一切科学陈述和科学定律都有一个共用的特征：它们是“真的或者假的”（适当的或者不适当的）。

粗略地说来，我们对它们的反应是“是”或者是“否”。

②科学的思维方式还有另一个特征。

它为建立它的贯彻一致的所用到的概念用是不表达什么感情的。

对于科学家，只有“存在”，而没有什么愿望，没有什么价值，没有善，没有恶；也没什么目标。

只要我们逗留在科学本身的领域里，我们就绝不会碰到想“你不可以说谎”这样的事。

附带地说，这个特点是慢慢发展起来的，而且是现代西方思想所特有的。

2013年高考数学全国卷1(完整版试题+答案+解析)

2013年普通高等学校招生全国统一考试（全国卷）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共6页．考试时间120分钟．满分150分．答题前，考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ卷答题卡和第Ⅱ卷答题纸规定的位置．参考公式：样本数据n x x x ,,21的标准差nx x x x x x s n 22221)()()(-++-+-=其中x 为样本平均数球的面积公式24R S π=第Ⅰ卷（选择题共60分）注意事项：1．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上． 2．第Ⅰ卷只有选择题一道大题．一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1.复数ii++121（i 是虚数单位）的虚部是 A ．23 B ．21C ．3D ．1 2.已知R 是实数集，{}11,12+-==⎭⎬⎫⎩⎨⎧<=x y y N x xM ，则=M C N R A ．)2,1(B ．[]2,0C .∅D ．[]2,13.现有10个数，其平均数是4，且这10个数的平方和是200，那么这个数组的标准差是 A ．1 B ．2 C ．3 D ．44.设n S 为等比数列{}n a 的前n 项和，0852=-a a ，则=24S S A ．5 B ．8 C ．8- D ．15 5.已知函数)62sin()(π-=x x f ，若存在),0(π∈a ，使得)()(a x f a x f -=+恒成立，则a的值是A ．6π B ．3π C ．4π D ．2π 6.已知m 、n 表示直线，γβα,,表示平面，给出下列四个命题，其中真命题为（1）βααβα⊥⊥⊂=则,,,m n n m （2）m n n m ⊥==⊥则,,,γβγαβα （3）,,βα⊥⊥m m 则α∥β （4）βαβα⊥⊥⊥⊥则,,,n m n mA ．（1）、（2）B ．（3）、（4）C ．（2）、（3）D ．（2）、（4）7.已知平面上不共线的四点C B A O ,,,，若||,23BC AB OC OB OA -=等于A ．1B ．2C ．3D ．4 8.已知三角形ABC ∆的三边长成公差为2的等差数列，且最大角的正弦值为23，则这个三角形的周长是A ．18B ．21C ．24D ．15 9.函数xx x f 1lg )(-=的零点所在的区间是 A ．(]1,0 B ．(]10,1 C ．(]100,10 D ．),100(+∞ 10.过直线y x =上一点P 引圆22670x y x +-+=的切线，则切线长的最小值为A ．22 B ． 223 C ．210 D ．211.已知函数b ax x x f 2)(2-+=.若b a ,都是区间[]4,0内的数，则使0)1(>f 成立的概率是A ．43 B ．41 C ．83D ．8512.已知双曲线的标准方程为116922=-y x ，F 为其右焦点，21,A A 是实轴的两端点，设P 为双曲线上不同于21,A A 的任意一点，直线P A P A 21,与直线a x =分别交于两点N M ,,若0=⋅FN FM ,则a 的值为A ．916 B ．59 C ．925 D ．516题图第13第Ⅱ卷（非选择题共90分）注意事项：1．请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置．书写的答案如需改动，要先划掉原来的答案，然后再写上新答案．2．不在指定答题位置答题或超出答题区域书写的答案无效．在试题卷上答题无效． 3．第Ⅱ卷共包括填空题和解答题两道大题．二、填空题：本大题共4小题，每小题4分，共16分． 13.如图所示的程序框图输出的结果为__________.14. 若一个底面是正三角形的三棱柱的正视图如下图所示，其在一个球面上，则该球的表面积为__________.15.地震的震级R 与地震释放的能量E 的关系为)4.11(lg 32-=E R ．2011年3月11日，日本东海岸发生了9.0级特大地震，2008年中国汶川的地震级别为8.0级，那么2011年地震的能量是2008年地震能量的倍． 16.给出下列命题： ①已知,,a b m都是正数，且bab a >++11，则a b <； ②已知()f x '是()f x 的导函数，若,()0x R f x '∀∈≥，则(1)(2)f f <一定成立； ③命题“x R∃∈，使得2210x x -+<”的否定是真命题； ④“1,1≤≤y x 且”是“2≤+y x ”的充要条件.其中正确命题的序号是 .(把你认为正确命题的序号都填上)第14题图三、解答题：本大题共６小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知向量),2cos 2sin 3()2cos ,1(y xx b x a +==→→与共线，且有函数)(x f y =．（Ⅰ）若1)(=x f ，求)232cos(x -π的值；（Ⅱ）在ABC ∆中，角C B A ,,,的对边分别是c b a ,,，且满足b c C a 2cos 2=+，求函数)(B f 的取值范围.18．（本小题满分12分）已知等差数列{}n a 的前n 项和为n S ，公差,50,053=+≠S S d 且1341,,a a a 成等比数列．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设⎭⎬⎫⎩⎨⎧n n a b 是首项为1，公比为3的等比数列，求数列{}n b 的前n 项和n T .已知四棱锥BCDE A -，其中1====BE AC BC AB ，2=CD ，ABC CD 面⊥，BE∥CD ，F 为AD 的中点. （Ⅰ）求证：EF ∥面ABC ；（Ⅱ）求证：面ACD ADE 面⊥；（III ）求四棱锥BCDE A -的体积.20.（本小题满分12分）在某种产品表面进行腐蚀性检验，得到腐蚀深度y 与腐蚀时间x 之间对应的一组数据：现确定的研究方案是：先从这6组数据中选取2组，用剩下的4组数据求线性回归方程，再对被选取的2组数据进行检验．（Ⅰ）求选取的2组数据恰好不相邻的概率；（Ⅱ）若选取的是第2组和第5组数据，根据其它4组数据，求得y 关于x 的线性回归方程26139134ˆ+=x y，规定由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．AB CDEF已知函数1)(2++=x bax x f 在点))1(,1(--f 的切线方程为03=++y x . （Ⅰ）求函数()f x 的解析式；（Ⅱ）设x x g ln )(=，求证：)()(x f x g ≥在),1[+∞∈x 上恒成立.22.（本小题满分14分）实轴长为34的椭圆的中心在原点，其焦点1,2,F F 在x 轴上.抛物线的顶点在原点O ，对称轴为y 轴，两曲线在第一象限内相交于点A ,且12AF AF ⊥，△12AF F 的面积为3. （Ⅰ）求椭圆和抛物线的标准方程；（Ⅱ）过点A 作直线l 分别与抛物线和椭圆交于C B ,,若AB AC 2=,求直线l 的斜率k .参考答案及评分标准一．选择题（本大题共12小题，每小题5分，共60分．）B D B A D B B D BC C B二．填空题（本大题共4小题，每小题4分，共16分．）13．2 14.π31915. 2310 16. ①③三．解答题17．（本小题满分12分）解：（Ⅰ）∵→a 与→b 共线∴yxx x 2cos 2cos2sin 31=+21)6sin()cos 1(21sin 232cos 2cos 2sin 32++=++=+=πx x x x x x y …………3分∴121)6sin()(=++=πx x f ，即21)6sin(=+πx …………………………………………4分211)6(sin 21)3(cos 2)3(2cos )232cos(22-=-+=--=-=-ππππx x x x…………………………………………6分（Ⅱ）已知b c C a 2cos 2=+由正弦定理得：CA C A C C A C ABC C A sin cos 2cos sin 2sin cos sin 2)sin(2sin 2sin cos sin 2+=++==+∴21cos =A ，∴在ABC ∆中 ∠3π=A …………………………………………8分 21)6sin()(++=πB B f∵∠3π=A ∴320π<<B ,6566πππ<+<B …………………………………………10分∴1)6sin(21≤+<πB ,23)(1≤<B f ∴函数)(B f 的取值范围为]23,1( …………………………………………12分18．（本小题满分12分）解：（Ⅰ）依题意得⎪⎩⎪⎨⎧+=+=⨯++⨯+)12()3(5025452233112111d a a d a d a d a …………………………………………2分解得⎩⎨⎧==231d a ， …………………………………………4分 1212)1(23)1(1+=+=-+=-+=∴n a n n d n a a n n 即，．……………………………6分(Ⅱ)13-=n nna b ，113)12(3--⋅+=⋅=n n n n n a b …………………………………………7分 123)12(37353-⋅+++⋅+⋅+=n n n T n n n n n T 3)12(3)12(3735333132⋅++⋅-++⋅+⋅+⋅=- ……………………9分n n n n T 3)12(3232323212+-⋅++⋅+⋅+=--nnn n n 323)12(31)31(3231⋅-=+---⋅+=- ∴nn n T 3⋅= …………………………………………12分19．（本小题满分12分）解：（Ⅰ）取AC 中点G,连结FG 、BG ， ∵F,G 分别是AD,AC 的中点∴FG ∥CD,且FG=21DC=1 ．∵BE ∥CD ∴FG 与BE 平行且相等∴EF ∥BG ． ……………………………2分ABC BG ABC EF 面面⊂⊄,∴EF ∥面ABC ……………………………4分（Ⅱ）∵△ABC 为等边三角形 ∴BG ⊥AC 又∵DC ⊥面ABC,BG ⊂面ABC ∴DC ⊥BGABCDEF G∴BG 垂直于面ADC 的两条相交直线AC,DC ，∴BG ⊥面ADC ． …………………………………………6分 ∵EF ∥BG ∴E F ⊥面ADC∵EF ⊂面ADE ，∴面ADE ⊥面ADC ． …………………………………………8分（Ⅲ）连结EC,该四棱锥分为两个三棱锥E －ABC 和E －ADC ．43631232313114331=+=⨯⨯+⨯⨯=+=---ACD E ABC E BCDE A V V V ．………………………12分另法：取BC 的中点为O ，连结AO ，则BC AO ⊥，又⊥CD 平面ABC ,∴C CD BC AO CD =⊥ , , ∴⊥AO 平面BCDE ，∴AO 为BCDE A V -的高，43232331,2321)21(,23=⨯⨯=∴=⨯+==-BCDE A BCDE V S AO ． 20．（本小题满分12分）解：（Ⅰ）设6组数据的编号分别为1,2,3,4,5,6.设抽到不相邻的两组数据为事件A ，从6组数据中选取2组数据共有15种情况：（1,2）（1,3）（1,4）（1,5）（1,6）（2,3）（2,4）（2,5）（2,6）（3,4）（3,5）（3,6）（4,5）（4,6）（5,6），其中事件A 包含的基本事件有10种． …………………………………………3分所以321510)(==A P ．所以选取的2组数据恰好不相邻的概率是32． ………………………6分(Ⅱ) 当10=x 时，;2|1026219|,262192613910134ˆ<-=+⨯=y……………………………………9分当30=x 时，;2|1626379|,263792613930134ˆ<-=+⨯=y所以，该研究所得到的回归方程是可靠的． …………………………………………12分 21．（本小题满分12分）解：（Ⅰ）将1-=x 代入切线方程得2-=y ∴211)1(-=+-=-ab f ，化简得4-=-a b ． …………………………………………2分 222)1(2)()1()(x xb ax x a x f +⋅+-+='12424)(22)1(-===-+=-'bb a b a f ． …………………………………………4分解得：2,2-==b a∴122)(2+-=x x x f ． …………………………………………6分（Ⅱ）由已知得122ln 2+-≥x x x 在),1[+∞上恒成立化简得22ln )1(2-≥+x x x即022ln ln 2≥+-+x x x x 在),1[+∞上恒成立． …………………………………………8分设22ln ln )(2+-+=x x x x x h ，21ln 2)(-++='xx x x x h ∵1≥x ∴21,0ln 2≥+≥xx x x ，即0)(≥'x h ． …………………………………………10分 ∴)(x h 在),1[+∞上单调递增，0)1()(=≥h x h∴)()(x f x g ≥在),1[+∞∈x 上恒成立． …………………………………………12分22．（本小题满分14分）解（1）设椭圆方程为22221(0)x y a b a b+=>>，12,AF m AF n ==由题意知⎪⎪⎩⎪⎪⎨⎧==+=+6344222mn n m c n m …………………………………………2分解得92=c ，∴39122=-=b ．∴椭圆的方程为131222=+y x …………………………………………4分 ∵3=⨯c y A ，∴1=A y ,代入椭圆的方程得22=A x ，将点A 坐标代入得抛物线方程为y x 82=． …………………………………………6分（2）设直线l 的方程为)22(1-=-x k y ，),(),,(2211y x C y x B2013年高考数学全国卷1(完整版试题+答案+解析)- 11 - / 11 由AB AC 2= 得)22(22212-=-x x ，化简得22221=-x x …………………………………………8分联立直线与抛物线的方程⎪⎩⎪⎨⎧=-=-yx x k y 8)22(12，得0821682=-+-k kx x ∴k x 8221=+① …………………………………………10分联立直线与椭圆的方程⎪⎩⎪⎨⎧=+-=-124)22(122y x x k y 得0821632)2168()41(2222=--+-++k k x k k x k ∴22241821622kk k x +-=+② …………………………………………12分 ∴2222418216)228(222221=++---=-kk k k x x 整理得：0)4121)(2416(2=+--k k k ∴42=k ，所以直线l 的斜率为42 ． …………………………………………14分。

2013四川高考生物试题含答案(含详细解析)

2013四川8.（11分）将玉米的PEPC酶基因导入水稻后，测的光照强度对转基因水稻和原种水稻的气孔导度及光合速率的影响结果，如下图所示。（注：气孔导度越大，气孔开放程度越高）
（1）水稻叶肉细胞进行光合作用的场所是
，
捕获叶光绿能体的色素中含量最多的
。叶绿素 a
（2）CO2 通过气孔进入叶肉细胞后，首先与 C5 结合而被固定，固定产物的还原需要光反
为达到筛选目的，平板内的固体培养基应以____淀___粉_____
作为唯一碳源。②、③过程需要重复几次，目的是
_进__一__步__筛__选__纯__化_。获得分解淀粉能力强的酵母菌（2）某同学尝试过程③的操作，其中一个平板经培养后的菌落分布如图乙所示。该同学的接种方法是_稀_释__涂__布_平__板__法__________；推测该同学接
2013四川4.下列所采取的措施，不涉及 “降低化学反应活化能”原理的是：
A.利用果胶酶提高水果的出汁率 B.滴加肝脏研磨液促使过氧化氢的分解 C.滴加 FeCl3溶液提高过氧化氢的分解速率
D.利用水浴加热提高胡萝卜素的萃取效率
【答案】D
【解析】本题考查的为酶的相关知识。“降低反应活化能”的原理描述的是催化剂的作用原理，A、B 项中的两种酶和 C 项中的 FeCl3均为催化剂，所以均能降低反应活化能。利用水浴加热提高胡萝卜素的萃取效率则是利用温度升高提高胡萝卜素的溶解度的原理， D项错误。
应提供 [H]和 AT。P
（3）光照强度低于 8×102μmol·s-1时，影响转基因水稻光合速率的主要因素是光照强；度光照强度
为 10~14×102μmol·s-1时，原种水稻的气孔导度下
降但光合速率基本不变，可能的原因

2013年高考语文新课标全国卷Ⅱ及答案详细解析

2013年普通高等学校招生全国统一考试（新课标全国卷Ⅱ）语文试题第Ⅰ卷阅读题甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题20世纪后期，陕西凤雏村出土了刻有“凤”字的甲骨四片，这些“凤”字的形体大致相同，均为头上带有象征神权或王权的抽象化了的毛角的短尾鸟。

东汉许慎《说文解字》云：“鸑鷟，凤属，神鸟也。

……江中有鸑鷟，似兔而大，赤目。

”据此，古代传说中鸣于岐山、兆示周王朝兴起的神鸟凤凰，其原型应该是一种形象普通、类似水鸭的短尾水鸟。

那么，普通的短尾鸟“凤”为何在周代变为华冠长尾、祥瑞美丽的神鸟了呢？我们看到，在商代早期和中期的青铜器纹饰中，只有鸟纹而没有凤纹，真正的凤形直到殷商晚期才出现，而且此时是华冠短尾鸟和华丽而饰有眼翎的长尾鸟同时出现，可见“凤”是由鸟演变而来的。

综观甲骨文和商代青铜器，凤鸟的演变应该是鸟在先，凤在后，贯穿整个商代的不是凤而是鸟。

“天命玄鸟，降而生商”，在商人的历史中鸟始终扮演着图腾始祖的重要角色。

《左传》记载郯子说：“我高祖少皞挚之立也，凤鸟适至，故纪于鸟，为鸟师而鸟名。

凤鸟氏历正也，……九扈为九农正。

”凤鸟氏成为“历正”之官，是由于它知天时，九扈成为“九农正”，也是由于它们带来了耕种、耘田和收获的信息。

殷人先祖之所以“鸟师而鸟名”，应该是由于这些随着信风迁批的鸟，给以少皞为首的商人的农业生产带来了四季节令的消息。

对凤鸟的崇拜起于商代，其鼎盛却在周代。

正是在周代，“凤”完成了其发展程序中最后也是最重要的环节：变为神鸟凤凰。

许多历史资料记载了周王室在克商前后对“天命”的重视。

《尚书》“周书”十二篇中大量出现的“命”字多指天命，“殷革夏命”也是常见的语句。

武王在甲子日牧野之战结束后，紧接着就“不革服”“格于庙”（来不及换衣服就到神庙参拜），这个“庙”自然不可能是周庙，而是商人的神庙。

这说明周王室急于把商人的正统接过来，成为中原合法的统治者。

周人之所以宣扬天命，归根结底在于强调“周改殷命”是出自天的意志和抉择。

2013年全国统一高考物理试卷(新课标ⅱ)(含解析版)

2013年全国统一高考物理试卷（新课标Ⅱ）一、选择题：本题共8小题，每小题6分．在每小题给出的四个选项中，第1～5题只有一项符合题目要求，第6～8题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分．1．（6分）一物块静止在粗糙的水平桌面上。

从某时刻开始，物块受到一方向不变的水平拉力作用。

假设物块与桌面间的最大静摩擦力等于滑动摩擦力。

以a 表示物块的加速度大小，F表示水平拉力的大小。

能正确描述F与a之间的关系的图象是（）A．B．C．D．2．（6分）如图，在固定斜面上的一物块受到一外力F的作用，F平行于斜面向上。

若要物块在斜面上保持静止，F的取值应有一定范围，已知其最大值和最小值分别为F1和F2．由此可求出（）A．物块的质量B．斜面的倾角C．物块与斜面间的最大静摩擦力D．物块对斜面的正压力3．（6分）如图，在光滑水平桌面上有一边长为L、电阻为R的正方形导线框；在导线框右侧有一宽度为d（d＞L）的条形匀强磁场区域，磁场的边界与导线框的一边平行，磁场方向竖直向下。

导线框以某一初速度向右运动。

t=0时导线框的右边恰与磁场的左边界重合，随后导线框进入并通过磁场区域。

下列v ﹣t图象中，可能正确描述上述过程的是（）A．B．C．D．4．（6分）空间有一圆柱形匀强磁场区域，该区域的横截面的半径为R，磁场方向垂直横截面。

一质量为m、电荷量为q（q＞0）的粒子以速率v0沿横截面的某直径射入磁场，离开磁场时速度方向偏离入射方向60°．不计重力，该磁场的磁感应强度大小为（）A．B．C．D．5．（6分）如图，在光滑绝缘水平面上，三个带电小球a、b和c分别位于边长为l的正三角形的三个顶点上；a、b带正电，电荷量均为q，c带负电。

整个系统置于方向水平的匀强电场中。

已知静电力常量为k。

若三个小球均处于静止状态，则匀强电场场强的大小为（）A．B．C．D．6．（6分）在物理学发展过程中，观测、实验、假说和逻辑推理等方法都起到了重要作用。

2013年全国统一高考真题数学试卷(理科)(新课标ⅰ)(含答案及解析)

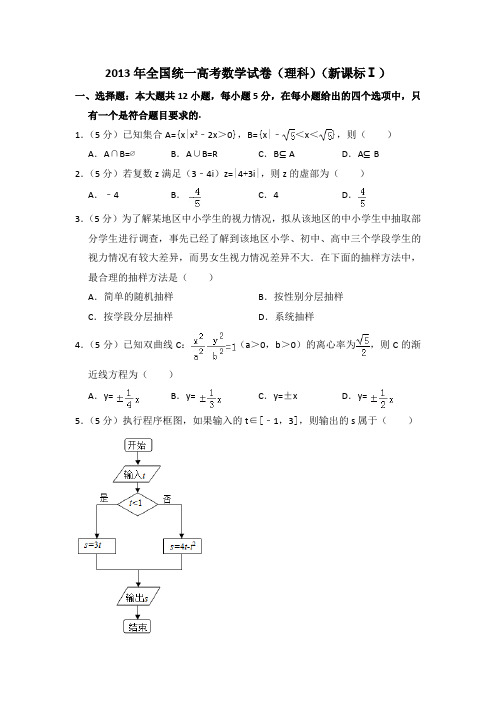
2013年全国统一高考数学试卷（理科）（新课标Ⅰ）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（）A．A∩B=∅B．A∪B=R C．B⊆A D．A⊆B2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4B．C．4D．3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（）A．简单的随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（）A．y=B．y=C．y=±x D．y=5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）A．[﹣3，4]B．[﹣5，2]C．[﹣4，3]D．[﹣2，5] 6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（）A．B．C．D．7．（5分）设等差数列{a n}的前n项和为S n，若S m﹣1=﹣2，S m=0，S m+1=3，则m=（）A．3B．4C．5D．68．（5分）某几何体的三视图如图所示，则该几何体的体积为（）A．16+8πB．8+8πC．16+16πD．8+16π9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（）A．5B．6C．7D．810．（5分）已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（）A．（﹣∞，0]B．（﹣∞，1]C．[﹣2，1]D．[﹣2，0] 12．（5分）设△A n B n C n的三边长分别为a n，b n，c n，△A n B n C n的面积为S n，n=1，2，3…若b1＞c1，b1+c1=2a1，a n+1=a n，，，则（）A．{S n}为递减数列B．{S n}为递增数列C．{S2n﹣1}为递增数列，{S2n}为递减数列D．{S2n﹣1}为递减数列，{S2n}为递增数列二.填空题：本大题共4小题，每小题5分.13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=．14．（5分）若数列{a n}的前n项和为S n=a n+，则数列{a n}的通项公式是a n=．15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=．16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．（1）若PB=，求PA；（2）若∠APB=150°，求tan∠PBA．18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．（Ⅰ）证明AB⊥A1C；（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．（Ⅰ）求这批产品通过检验的概率；（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P 的半径最长时，求|AB|．21．（12分）已知函数f（x）=x2+ax+b，g（x）=e x（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．（Ⅰ）求a，b，c，d的值；（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.22．（10分）（选修4﹣1：几何证明选讲）如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．（Ⅰ）证明：DB=DC；（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．（1）把C1的参数方程化为极坐标方程；（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．24．已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．（Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）的解集；（Ⅱ）设a＞﹣1，且当x∈[﹣，]时，f（x）≤g（x），求a的取值范围．2013年全国统一高考数学试卷（理科）（新课标Ⅰ）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）已知集合A={x|x2﹣2x＞0}，B={x|﹣＜x＜}，则（）A．A∩B=∅B．A∪B=R C．B⊆A D．A⊆B【考点】1D：并集及其运算；73：一元二次不等式及其应用．【专题】59：不等式的解法及应用；5J：集合．【分析】根据一元二次不等式的解法，求出集合A，再根据的定义求出A∩B和A∪B．【解答】解：∵集合A={x|x2﹣2x＞0}={x|x＞2或x＜0}，∴A∩B={x|2＜x＜或﹣＜x＜0}，A∪B=R，故选：B．【点评】本题考查一元二次不等式的解法，以及并集的定义，属于基础题．2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4B．C．4D．【考点】A5：复数的运算．【专题】5N：数系的扩充和复数．【分析】由题意可得z==，再利用两个复数代数形式的乘除法法则化简为+i，由此可得z的虚部．【解答】解：∵复数z满足（3﹣4i）z=|4+3i|，∴z====+i，故z的虚部等于，故选：D．【点评】本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，属于基础题．3．（5分）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（）A．简单的随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样【考点】B3：分层抽样方法．【专题】21：阅读型．【分析】若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样．【解答】解：我们常用的抽样方法有：简单随机抽样、分层抽样和系统抽样，而事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．了解某地区中小学生的视力情况，按学段分层抽样，这种方式具有代表性，比较合理．故选：C．【点评】本小题考查抽样方法，主要考查抽样方法，属基本题．4．（5分）已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（）A．y=B．y=C．y=±x D．y=【考点】KC：双曲线的性质．【专题】5D：圆锥曲线的定义、性质与方程．【分析】由离心率和abc的关系可得b2=4a2，而渐近线方程为y=±x，代入可得答案．【解答】解：由双曲线C：（a＞0，b＞0），则离心率e===，即4b2=a2，故渐近线方程为y=±x=x，故选：D．【点评】本题考查双曲线的简单性质，涉及的渐近线方程，属基础题．5．（5分）执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）A．[﹣3，4]B．[﹣5，2]C．[﹣4，3]D．[﹣2，5]【考点】3B：分段函数的解析式求法及其图象的作法；EF：程序框图．【专题】27：图表型；5K：算法和程序框图．【分析】本题考查的知识点是程序框图，分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算一个分段函数的函数值，由条件为t＜1我们可得，分段函数的分类标准，由分支结构中是否两条分支上对应的语句行，我们易得函数的解析式．【解答】解：由判断框中的条件为t＜1，可得：函数分为两段，即t＜1与t≥1，又由满足条件时函数的解析式为：s=3t；不满足条件时，即t≥1时，函数的解析式为：s=4t﹣t2故分段函数的解析式为：s=，如果输入的t∈[﹣1，3]，画出此分段函数在t∈[﹣1，3]时的图象，则输出的s属于[﹣3，4]．故选：A．【点评】要求条件结构对应的函数解析式，要分如下几个步骤：①分析流程图的结构，分析条件结构是如何嵌套的，以确定函数所分的段数；②根据判断框中的条件，设置分类标准；③根据判断框的“是”与“否”分支对应的操作，分析函数各段的解析式；④对前面的分类进行总结，写出分段函数的解析式．6．（5分）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（）A．B．C．D．【考点】LG：球的体积和表面积．【专题】11：计算题；5F：空间位置关系与距离．【分析】设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．【解答】解：设正方体上底面所在平面截球得小圆M，则圆心M为正方体上底面正方形的中心．如图．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质，得R2=（R﹣2）2+42，解出R=5，∴根据球的体积公式，该球的体积V===．故选：A．【点评】本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题．7．（5分）设等差数列{a n}的前n项和为S n，若S m﹣1=﹣2，S m=0，S m+1=3，则m=（）A．3B．4C．5D．6【考点】83：等差数列的性质；85：等差数列的前n项和．【专题】11：计算题；54：等差数列与等比数列．【分析】由a n与S n的关系可求得a m+1与a m，进而得到公差d，由前n项和公式及S m=0可求得a1，再由通项公式及a m=2可得m值．【解答】解：a m=S m﹣S m﹣1=2，a m+1=S m+1﹣S m=3，所以公差d=a m﹣a m=1，+1S m==0，m﹣1＞0，m＞1，因此m不能为0，得a1=﹣2，所以a m=﹣2+（m﹣1）•1=2，解得m=5，另解：等差数列{a n}的前n项和为S n，即有数列{}成等差数列，则，，成等差数列，可得2•=+，即有0=+，解得m=5．又一解：由等差数列的求和公式可得（m﹣1）（a1+a m﹣1）=﹣2，m（a1+a m）=0，（m+1）（a1+a m+1）=3，可得a1=﹣a m，﹣2a m+a m+1+a m+1=+=0，解得m=5．故选：C．【点评】本题考查等差数列的通项公式、前n项和公式及通项a n与S n的关系，考查学生的计算能力．8．（5分）某几何体的三视图如图所示，则该几何体的体积为（）A．16+8πB．8+8πC．16+16πD．8+16π【考点】L!：由三视图求面积、体积．【专题】16：压轴题；27：图表型．【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体，依据三视图的数据，得出组合体长、宽、高，即可求出几何体的体积．【解答】解：三视图复原的几何体是一个长方体与半个圆柱的组合体，如图，其中长方体长、宽、高分别是：4，2，2，半个圆柱的底面半径为2，母线长为4．∴长方体的体积=4×2×2=16，半个圆柱的体积=×22×π×4=8π所以这个几何体的体积是16+8π；故选：A．【点评】本题考查了几何体的三视图及直观图的画法，三视图与直观图的关系，柱体体积计算公式，空间想象能力9．（5分）设m为正整数，（x+y）2m展开式的二项式系数的最大值为a，（x+y）2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（）A．5B．6C．7D．8【考点】DA：二项式定理．【专题】5P：二项式定理．【分析】根据二项式系数的性质求得a和b，再利用组合数的计算公式，解方程13a=7b求得m的值．【解答】解：∵m为正整数，由（x+y）2m展开式的二项式系数的最大值为a，以及二项式系数的性质可得a=，同理，由（x+y）2m+1展开式的二项式系数的最大值为b，可得b==．再由13a=7b，可得13=7，即13×=7×，即13=7×，即13（m+1）=7（2m+1），解得m=6，故选：B．【点评】本题主要考查二项式系数的性质的应用，组合数的计算公式，属于中档题．10．（5分）已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．【考点】K3：椭圆的标准方程．【专题】5D：圆锥曲线的定义、性质与方程．【分析】设A（x1，y1），B（x2，y2），代入椭圆方程得，利用“点差法”可得．利用中点坐标公式可得x1+x2=2，y1+y2=﹣2，利用斜率计算公式可得==．于是得到，化为a2=2b2，再利用c=3=，即可解得a2，b2．进而得到椭圆的方程．【解答】解：设A（x1，y1），B（x2，y2），代入椭圆方程得，相减得，∴．∵x1+x2=2，y1+y2=﹣2，==．∴，化为a2=2b2，又c=3=，解得a2=18，b2=9．∴椭圆E的方程为．故选：D．【点评】熟练掌握“点差法”和中点坐标公式、斜率的计算公式是解题的关键．11．（5分）已知函数f（x）=，若|f（x）|≥ax，则a的取值范围是（）A．（﹣∞，0]B．（﹣∞，1]C．[﹣2，1]D．[﹣2，0]【考点】7E：其他不等式的解法．【专题】16：压轴题；59：不等式的解法及应用．【分析】由函数图象的变换，结合基本初等函数的图象可作出函数y=|f（x）|的图象，和函数y=ax的图象，由导数求切线斜率可得l的斜率，进而数形结合可得a的范围．【解答】解：由题意可作出函数y=|f（x）|的图象，和函数y=ax的图象，由图象可知：函数y=ax的图象为过原点的直线，当直线介于l和x轴之间符合题意，直线l为曲线的切线，且此时函数y=|f（x）|在第二象限的部分解析式为y=x2﹣2x，求其导数可得y′=2x﹣2，因为x≤0，故y′≤﹣2，故直线l的斜率为﹣2，故只需直线y=ax的斜率a介于﹣2与0之间即可，即a∈[﹣2，0]故选：D．【点评】本题考查其它不等式的解法，数形结合是解决问题的关键，属中档题．12．（5分）设△A n B n C n的三边长分别为a n，b n，c n，△A n B n C n的面积为S n，n=1，2，3…若b1＞c1，b1+c1=2a1，a n+1=a n，，，则（）A．{S n}为递减数列B．{S n}为递增数列C．{S2n﹣1}为递增数列，{S2n}为递减数列D．{S2n﹣1}为递减数列，{S2n}为递增数列【考点】82：数列的函数特性；8H：数列递推式．【专题】16：压轴题；54：等差数列与等比数列；55：点列、递归数列与数学归纳法．=a n可知△A n B n C n的边B n C n为定值a1，由b n+1+c n+1﹣【分析】由a n+12a1=及b1+c1=2a1得b n+c n=2a1，则在△A n B n C n中边长B n C n=a1为定值，另两边A n C n、A n B n的长度之和b n+c n=2a1为定值，由此可知顶点A n在以B n、C n为焦点的椭圆上，根据b n+1﹣c n+1=，得b n﹣c n=，可知n→+∞时b n→c n，据此可判断△A n B n C n的边B nC n的高h n随着n的增大而增大，再由三角形面积公式可得到答案．【解答】解：b1=2a1﹣c1且b1＞c1，∴2a1﹣c1＞c1，∴a1＞c1，∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1＞0，∴b1＞a1＞c1，又b1﹣c1＜a1，∴2a1﹣c1﹣c1＜a1，∴2c1＞a1，∴，由题意，+a n，∴b n+1+c n+1﹣2a n=（b n+c n﹣2a n），∴b n+c n﹣2a n=0，∴b n+c n=2a n=2a1，∴b n+c n=2a1，由此可知顶点A n在以B n、C n为焦点的椭圆上，﹣c n+1=，∴=a1﹣b n，又由题意，b n+1﹣a1=，∴b n﹣a1=，∴b n+1∴，c n=2a1﹣b n=，∴[][]=[﹣]单调递增（可证当n=1时＞0）故选：B．【点评】本题主要考查由数列递推式求数列通项、三角形面积海伦公式，综合考查学生分析解决问题的能力，有较高的思维抽象度，是本年度全国高考试题中的“亮点”之一．二.填空题：本大题共4小题，每小题5分.13．（5分）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=2．【考点】9H：平面向量的基本定理；9O：平面向量数量积的性质及其运算．【专题】5A：平面向量及应用．【分析】由于•=0，对式子=t+（1﹣t）两边与作数量积可得=0，经过化简即可得出．【解答】解：∵，，∴=0，∴tcos60°+1﹣t=0，∴1=0，解得t=2．故答案为2．【点评】熟练掌握向量的数量积运算是解题的关键．14．（5分）若数列{a n}的前n项和为S n=a n+，则数列{a n}的通项公式是a n=（﹣2）n﹣1．【考点】88：等比数列的通项公式．【专题】54：等差数列与等比数列．【分析】把n=1代入已知式子可得数列的首项，由n≥2时，a n=S n﹣S n﹣1，可得数列为等比数列，且公比为﹣2，代入等比数列的通项公式分段可得答案．【解答】解：当n=1时，a1=S1=，解得a1=1当n≥2时，a n=S n﹣S n﹣1=（）﹣（）=，整理可得，即=﹣2，故数列{a n}从第二项开始是以﹣2为首项，﹣2为公比的等比数列，故当n≥2时，a n=（﹣2）n﹣1，经验证当n=1时，上式也适合，故答案为：（﹣2）n﹣1【点评】本题考查等比数列的通项公式，涉及等比数列的判定，属基础题．15．（5分）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=﹣．【考点】GP：两角和与差的三角函数；H4：正弦函数的定义域和值域．【专题】16：压轴题；56：三角函数的求值．【分析】f（x）解析式提取，利用两角和与差的正弦函数公式化为一个角的正弦函数，由x=θ时，函数f（x）取得最大值，得到sinθ﹣2cosθ=，与sin2θ+cos2θ=1联立即可求出cosθ的值．【解答】解：f（x）=sinx﹣2cosx=（sinx﹣cosx）=sin（x﹣α）（其中cosα=，sinα=），∵x=θ时，函数f（x）取得最大值，∴sin（θ﹣α）=1，即sinθ﹣2cosθ=，又sin2θ+cos2θ=1，联立得（2cosθ+）2+cos2θ=1，解得cosθ=﹣．故答案为：﹣【点评】此题考查了两角和与差的正弦函数公式，同角三角函数间的基本关系，以及正弦函数的定义域与值域，熟练掌握公式是解本题的关键．16．（5分）若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为16．【考点】57：函数与方程的综合运用；6E：利用导数研究函数的最值．【专题】11：计算题；16：压轴题；51：函数的性质及应用；53：导数的综合应用．【分析】由题意得f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，由此求出a=8且b=15，由此可得f（x）=﹣x4﹣8x3﹣14x2+8x+15．利用导数研究f（x）的单调性，可得f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数，结合f（﹣2﹣）=f（﹣2+）=16，即可得到f（x）的最大值．【解答】解：∵函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣2对称，∴f（﹣1）=f（﹣3）=0且f（1）=f（﹣5）=0，即[1﹣（﹣3）2][（﹣3）2+a•（﹣3）+b]=0且[1﹣（﹣5）2][（﹣5）2+a•（﹣5）+b]=0，解之得，因此，f（x）=（1﹣x2）（x2+8x+15）=﹣x4﹣8x3﹣14x2+8x+15，求导数，得f′（x）=﹣4x3﹣24x2﹣28x+8，令f′（x）=0，得x1=﹣2﹣，x2=﹣2，x3=﹣2+，当x∈（﹣∞，﹣2﹣）时，f′（x）＞0；当x∈（﹣2﹣，﹣2）时，f′（x）＜0；当x∈（﹣2，﹣2+）时，f′（x）＞0；当x∈（﹣2+，+∞）时，f′（x）＜0∴f（x）在区间（﹣∞，﹣2﹣）、（﹣2，﹣2+）上是增函数，在区间（﹣2﹣，﹣2）、（﹣2+，+∞）上是减函数．又∵f（﹣2﹣）=f（﹣2+）=16，∴f（x）的最大值为16．故答案为：16．【点评】本题给出多项式函数的图象关于x=﹣2对称，求函数的最大值．着重考查了函数的奇偶性、利用导数研究函数的单调性和函数的最值求法等知识，属于中档题．三、解答题：解答应写出文字说明，证明过程或演算步骤.17．（12分）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．（1）若PB=，求PA；（2）若∠APB=150°，求tan∠PBA．【考点】HP：正弦定理；HR：余弦定理．【专题】58：解三角形．【分析】（I）在Rt△PBC，利用边角关系即可得到∠PBC=60°，得到∠PBA=30°．在△PBA中，利用余弦定理即可求得PA．（II）设∠PBA=α，在Rt△PBC中，可得PB=sinα．在△PBA中，由正弦定理得，即，化简即可求出．【解答】解：（I）在Rt△PBC中，=，∴∠PBC=60°，∴∠PBA=30°．在△PBA中，由余弦定理得PA2=PB2+AB2﹣2PB•ABcos30°==．∴PA=．（II）设∠PBA=α，在Rt△PBC中，PB=BCcos（90°﹣α）=sinα．在△PBA中，由正弦定理得，即，化为．∴．【点评】熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键．18．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．（Ⅰ）证明AB⊥A1C；（Ⅱ）若平面ABC⊥平面AA1B1B，AB=CB=2，求直线A1C与平面BB1C1C所成角的正弦值．【考点】LW：直线与平面垂直；LY：平面与平面垂直；MI：直线与平面所成的角．【专题】5F：空间位置关系与距离；5G：空间角．【分析】（Ⅰ）取AB的中点O，连接OC，OA1，A1B，由已知可证OA1⊥AB，AB ⊥平面OA1C，进而可得AB⊥A1C；（Ⅱ）易证OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立坐标系，可得，，的坐标，设=（x，y，z）为平面BB1C1C的法向量，则，可解得=（，1，﹣1），可求|cos ＜，＞|，即为所求正弦值．【解答】解：（Ⅰ）取AB的中点O，连接OC，OA1，A1B，因为CA=CB，所以OC⊥AB，由于AB=AA1，∠BAA1=60°，所以△AA1B为等边三角形，所以OA1⊥AB，又因为OC∩OA1=O，所以AB⊥平面OA1C，又A1C⊂平面OA1C，故AB⊥A1C；（Ⅱ）由（Ⅰ）知OC⊥AB，OA1⊥AB，又平面ABC⊥平面AA1B1B，交线为AB，所以OC⊥平面AA1B1B，故OA，OA1，OC两两垂直．以O为坐标原点，的方向为x轴的正向，||为单位长，建立如图所示的坐标系，可得A（1，0，0），A1（0，，0），C（0，0，），B（﹣1，0，0），则=（1，0，），=（﹣1，，0），=（0，﹣，），设=（x，y，z）为平面BB1C1C的法向量，则，即，可取y=1，可得=（，1，﹣1），故cos＜，＞==，又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值，故直线A1C与平面BB1C1C所成角的正弦值为：．【点评】本题考查直线与平面所成的角，涉及直线与平面垂直的性质和平面与平面垂直的判定，属难题．19．（12分）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为，且各件产品是否为优质品相互独立．（Ⅰ）求这批产品通过检验的概率；（Ⅱ）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．【考点】CG：离散型随机变量及其分布列；CH：离散型随机变量的期望与方差．【专题】5I：概率与统计．【分析】（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，由概率得加法公式和条件概率，代入数据计算可得；（Ⅱ）X可能的取值为400，500，800，分别求其概率，可得分布列，进而可得期望值．【解答】解：（Ⅰ）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品全是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A=（A1B1）∪（A2B2），且A1B1与A2B2互斥，所以P（A）=P（A1B1）+P（A2B2）=P（A1）P（B1|A1）+P（A2）P（B2|A2）==（Ⅱ）X可能的取值为400，500，800，并且P（X=800）=，P（X=500）=，P（X=400）=1﹣﹣=，故X的分布列如下：X 400 500 800P故EX=400×+500×+800×=506.25【点评】本题考查离散型随机变量及其分布列涉及数学期望的求解，属中档题．20．（12分）已知圆M：（x+1）2+y2=1，圆N：（x﹣1）2+y2=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P 的半径最长时，求|AB|．【考点】J3：轨迹方程；J9：直线与圆的位置关系．【专题】5B：直线与圆．【分析】（I）设动圆的半径为R，由已知动圆P与圆M外切并与圆N内切，可得|PM|+|PN|=R+1+（3﹣R）=4，而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，求出即可；（II）设曲线C上任意一点P（x，y），由于|PM|﹣|PN|=2R﹣2≤4﹣2=2，所以R ≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．分①l的倾斜角为90°，此时l与y轴重合，可得|AB|．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，设l与x轴的交点为Q，根据，可得Q（﹣4，0），所以可设l：y=k（x+4），与椭圆的方程联立，得到根与系数的关系利用弦长公式即可得出．【解答】解：（I）由圆M：（x+1）2+y2=1，可知圆心M（﹣1，0）；圆N：（x﹣1）2+y2=9，圆心N（1，0），半径3．设动圆的半径为R，∵动圆P与圆M外切并与圆N内切，∴|PM|+|PN|=R+1+（3﹣R）=4，而|NM|=2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，∴a=2，c=1，b2=a2﹣c2=3．∴曲线C的方程为（x≠﹣2）．（II）设曲线C上任意一点P（x，y），由于|PM|﹣|PN|=2R﹣2≤3﹣1=2，所以R≤2，当且仅当⊙P的圆心为（2，0）R=2时，其半径最大，其方程为（x﹣2）2+y2=4．①l的倾斜角为90°，则l与y轴重合，可得|AB|=．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与x轴不平行，设l与x轴的交点为Q，则，可得Q（﹣4，0），所以可设l：y=k（x+4），由l于M相切可得：，解得．当时，联立，得到7x2+8x﹣8=0．∴，．∴|AB|===由于对称性可知：当时，也有|AB|=．综上可知：|AB|=或．【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式等基础知识，需要较强的推理能力和计算能力及其分类讨论的思想方法．21．（12分）已知函数f（x）=x2+ax+b，g（x）=e x（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．（Ⅰ）求a，b，c，d的值；（Ⅱ）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．【考点】3R：函数恒成立问题；6H：利用导数研究曲线上某点切线方程．【专题】16：压轴题；53：导数的综合应用．【分析】（Ⅰ）对f（x），g（x）进行求导，已知在交点处有相同的切线及曲线y=f （x）和曲线y=g（x）都过点P（0，2），从而解出a，b，c，d的值；（Ⅱ）由（I）得出f（x），g（x）的解析式，再求出F（x）及它的导函数，通过对k的讨论，判断出F（x）的最值，从而判断出f（x）≤kg（x）恒成立，从而求出k的范围．【解答】解：（Ⅰ）由题意知f（0）=2，g（0）=2，f′（0）=4，g′（0）=4，而f′（x）=2x+a，g′（x）=e x（cx+d+c），故b=2，d=2，a=4，d+c=4，从而a=4，b=2，c=2，d=2；（Ⅱ）由（I）知，f（x）=x2+4x+2，g（x）=2e x（x+1）设F（x）=kg（x）﹣f（x）=2ke x（x+1）﹣x2﹣4x﹣2，则F′（x）=2ke x（x+2）﹣2x﹣4=2（x+2）（ke x﹣1），由题设得F（0）≥0，即k≥1，令F′（x）=0，得x1=﹣lnk，x2=﹣2，①若1≤k＜e2，则﹣2＜x1≤0，从而当x∈（﹣2，x1）时，F′（x）＜0，当x∈（x1，+∞）时，F′（x）＞0，即F（x）在（﹣2，x1）上减，在（x1，+∞）上是增，故F（x）在[﹣2，+∞）上的最小值为F（x1），而F（x1）=﹣x1（x1+2）≥0，x≥﹣2时F（x）≥0，即f（x）≤kg（x）恒成立．②若k=e2，则F′（x）=2e2（x+2）（e x﹣e﹣2），从而当x∈（﹣2，+∞）时，F′（x）＞0，即F（x）在（﹣2，+∞）上是增，而F（﹣2）=0，故当x≥﹣2时，F（x）≥0，即f（x）≤kg（x）恒成立．③若k＞e2时，F′（x）＞2e2（x+2）（e x﹣e﹣2），而F（﹣2）=﹣2ke﹣2+2＜0，所以当x＞﹣2时，f（x）≤kg（x）不恒成立，综上，k的取值范围是[1，e2]．【点评】此题主要考查利用导数研究曲线上某点切线方程，函数恒成立问题，考查分类讨论思想，解题的关键是能够利用导数工具研究函数的性质，此题是一道中档题．四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.22．（10分）（选修4﹣1：几何证明选讲）如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．（Ⅰ）证明：DB=DC；（Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径．【考点】NC：与圆有关的比例线段．【专题】5B：直线与圆．【分析】（I）连接DE交BC于点G，由弦切角定理可得∠ABE=∠BCE，由已知角平分线可得∠ABE=∠CBE，于是得到∠CBE=∠BCE，BE=CE．由已知DB⊥BE，可知DE为⊙O的直径，Rt△DBE≌Rt△DCE，利用三角形全等的性质即可得到DC=DB．（II）由（I）可知：DG是BC的垂直平分线，即可得到BG=．设DE的中点为O，连接BO，可得∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．得到CF⊥BF．进而得到Rt△BCF的外接圆的半径=．【解答】（I）证明：连接DE交BC于点G．由弦切角定理可得∠ABE=∠BCE，而∠ABE=∠CBE，∴∠CBE=∠BCE，BE=CE．又∵DB⊥BE，∴DE为⊙O的直径，∠DCE=90°．∴△DBE≌△DCE，∴DC=DB．（II）由（I）可知：∠CDE=∠BDE，DB=DC．故DG是BC的垂直平分线，∴BG=．设DE的中点为O，连接BO，则∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．∴CF⊥BF．∴Rt△BCF的外接圆的半径=．【点评】本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识，需要较强的推理能力、分析问题和解决问题的能力．23．已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ．（1）把C1的参数方程化为极坐标方程；（2）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．【考点】Q4：简单曲线的极坐标方程；QH：参数方程化成普通方程．【专题】11：计算题；35：转化思想；4R：转化法；5S：坐标系和参数方程．【分析】（1）曲线C1的参数方程消去参数t，得到普通方程，再由，能求出C1的极坐标方程．（2）曲线C2的极坐标方程化为直角坐标方程，与C1的普通方程联立，求出C1与C2交点的直角坐标，由此能求出C1与C2交点的极坐标．【解答】解：（1）将，消去参数t，化为普通方程（x﹣4）2+（y﹣5）2=25，即C1：x2+y2﹣8x﹣10y+16=0，将代入x2+y2﹣8x﹣10y+16=0，得ρ2﹣8ρcosθ﹣10ρsinθ+16=0．∴C1的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0．（2）∵曲线C2的极坐标方程为ρ=2sinθ．∴曲线C2的直角坐标方程为x2+y2﹣2y=0，。

2013年高考真题——理综(新课标I卷)解析版

1 课标卷Ⅰ理科综合生物试题解析（适用地区：河南、河北、山西、陕西、湖南、湖北、江西）必修部分分值分配统计分数分配比较合理，都接近平均分25分，与教学时数相统一。

知识点分布：选择题1．关蛋白质合成的基础知识；2. 有丝分裂和减数分裂；3. 植物细胞主动运输方式吸收所需矿质元素离子；4.免疫调节等；5. 生态学部分种群、群落和生态系统；6. 验证孟德尔分离定律。

非选择题29.物质鉴定及植物代谢（11分）30．血糖的调节（10分）31．基因分离定律的验证（12分）32．生态学群落演替和生态系统的稳定性（6分）选做题（15分）39．泡菜的制作40．基因工程、蛋白质工程、胚胎工程一、选择题（共6题，每题6分）1．关于蛋白质生物合成的叙述，正确的是（）A．一种tRNA可以携带多种氨基酸B．DNA聚合酶是在细胞核中合成的C．反密码子是位于mRNA上相邻的三个碱基D．线粒体中的DNA能控制某些蛋白质的合成【答案】D【解析】tRNA的一端有三个碱基外露为反密码子，与mRNA上的密码子进行碱基互补配对，另一端携带一种氨基酸到达核糖体上，通过发生脱水缩合形成肽健，合成多肽链。

所以A、C错误。

DNA聚合酶是蛋白质，在核糖体上合成，而细胞核内无核糖体，不能合成蛋白质，因而DNA聚合酶是在细胞质中合成的蛋白质类酶，通过核孔进入细胞核发挥作用。

B 错。

线粒体中不仅具有自己的DNA，而且还有核糖体，能够通过转录和翻译控制一部分蛋白质的合成，所以核糖体具有一定的独立性。

D正确。

【试题点评】本题不偏不难，正面考查了有关蛋白质合成的基础知识，DNA聚合酶是在细胞核内起催化作用的，部分考生可能会误选B。

本题主要涉及的知识点是化合物的本质及合成，基因控制蛋白质合成过程中有关概念及特点。

旨在考查考生对蛋白质合成过程中相关知识点的识记及初步分析问题的能力。

2．关于同一个体中细胞有丝分裂和减数第一次分裂的叙述，正确的是（）A．两者前期染色体数目相同，染色体行为和DNA分子数目不同B．两者中期染色体数目不同，染色体行为和DNA分子数目相同C．两者后期染色体行为和数目不同，DNA分子数目相同D．两者后期染色体行为和数目相同，DNA分子数目不同【答案】C【解析】有丝分裂和减数分裂分裂期过程的最大区别是染色体的行为不同。

2013 年高考真题及答案详解(四川省)

•
高考真题
• 5.下列关于明代花鸟画的表述，不符合原文意思的一项是（） • A.明宣宗时，宫廷画院花鸟画风格面貌多样，但意境与格调比宋代院体花鸟画略逊一筹。 • B."吴门四家"花鸟画在吸收前代大师成果基础上发展处鲜明个性特征，取得重大突破。 • C.陈淳的大写意花鸟画充分表达了笔墨的特性与画面的形式感，开写意花鸟一代新风。 • D.徐渭开创了大写意花鸟的新体派，其成就超越了早于他的陈淳，对后世影响深远。 • 答案：B • 【答案解析】B. 第二自然段结尾说的是"在美术史上颇有影响"，"取得重大突破"无中生有
• 今年的字音的考查与 11 年、12 年有一定区别，11、 12 年要求的是选出读音全部正确的一项是什么，而今年要求选出每对读音都不相同的一项是什么，难度要比前两年大一些，由以前考查 16 个词增加到 32 个词，但考查的词语本身难度不高，都是比较常见的，无生僻字。各项的读音分别读： • A. cù/cuì /zé、dùn/ tún、mi~n 、zì • B. qiào/xiāo、pī/pēi、fǔ /pú、ku /guī • C. bù/fù、chì /shè、bì 、zú/cù • D. shuò/sù、chēn、lào/luò、dú/shú • ACD 三项都有一组读音相同，只有 B 选项符合要求，故选 B。
【答案解析】
• 该题属于 B(理解)能力层级的题，考查的是关联词与成语的运用。 • （1）"不只" 和"还要"连用，故排除 AC； • （2）"坚不可摧"与"无坚不摧"的区分稍微要难一些，" 无坚不摧"多形容力量的强大，而"坚不可摧"指非常坚固，摧毁不了，这里说"什么样的战斗堡垒"所以最好用 "坚不可摧"； • （3）区分"自以为是"和"自行其是"，"自以为是"是指自己总认为自己是对的，形容主观不虚心，"自行其是"是指自己认为对的就做，不考虑别人的意见。句子说的是 "每当出现什么什么的苗头"出现的只是想法并没有去做，所以这里应该选"自以为是"。 • 故选 B。

2013年高考真题——地理(全国卷)(含答案和解析)

2013年普通高等学校招生全国统一考试(大纲卷)文综试题（地理部分）一、单项选择题(本大题共35小题，每小题4分，共140分。

在每题给出的四个选项中，只有一项是符合题目要求的。

下图示意某跨国公司的制造企业和研发中心在中国的分布。

读下图，完成1～2题。

1．该公司在中国多地投资建制造企业主要是为了()A．扩大市场份额B．分散投资风险C．建立营销网络D．利用廉价原料2．该公司研发中心选址考虑的首要因素是()A．交通B．人才C．市场D．资金在太行山南段东麓相邻的两条间歇性河流上分别建有甲、乙水库，它们的汇水面积大体相等。

2009年雨季，乙水库入库水量912万立方米，甲水库却几乎没有入库水量。

据此完成3～4题。

3．甲、乙两水库上游流域()A．河流以地下水补给为主B．自然植被为针阔叶混交林C．降水集中于7、8月份D．位于半干旱地区4．2009年雨季，甲水库无入库水量是因为其流域()A．几乎没有降水B．植被截留降水C．降水大量下渗D．人工拦截径流自20世纪90年代初，浙江温州的一些瓜农到海南岛承包土地，种植西瓜，产品销往全国各地。

他们每年8月底到海南岛种西瓜，次年5月中旬返回温州。

据此完成5～6题。

5．温州瓜农选择在海南岛种植西瓜，是因为海南岛()A．西瓜品种优B．种植成本低C．种植利润高D．市场需求大6．温州瓜农每年5～8月离开海南岛，主要原因是此期间()A．温州正值农忙季节B．海南岛不宜种植西瓜C．瓜地休耕以恢复肥力D．海南岛西瓜竞争力弱赤潮是某些浮游生物暴发性繁殖引起水色异常和水质恶化的现象。

赤潮的出现和人类活动排放的污染物有关。

据此完成7～9题。

7．引发赤潮的污染物主要为()A．重金属盐B．氮、磷营养物C．固体废弃物D．泄漏的石油8．赤潮暴发的海域一般()A．水温偏高、风力偏大B．水温偏低、风力偏大C．水温偏高、风力偏小D．水温偏低、风力偏小9．赤潮多发的海域位于()A．赤道附近B．大洋中部C．中、低纬近海D．高纬近海某种生物的种密度指单位面积该种生物的个体数量。

2013安徽高考试题语文卷详细答案

2013年普通高等学校招生全国统一考试（安徽卷）语文一1.【答案】D【解析】A项“不充分表达”应为“不表达”；B项“绝不会碰到”绝对化；C项“科学家”应加上“追求真理的”这一定语。

2.【答案】C【解析】A“推导出”错，另一个特征不是第一个特征推导出的；B③段承②段，说逻辑思维同伦理毫不相干；D伦理公理的建立和考验同科学的公理并无很大区别。

3.【答案】D【解析】文中说“人们会把它们作为自己在大量个人感情经验方面打好基础的东西而接受下来”，因此“被人们自觉接受并运用于打好知识基础等方面”错。

二4、【答案】：D【解析】：由，出于。

5、【答案】：D【解析】：D、用在动词前，形成所字短语。

A于是/因为；B目的连词，来/转折连词，却；C于是/竟然。

6.【答案】：B【解析】：“且南越君民同心”无中生有。

7.【答案】：（1）而现在您却一反中国人的习俗，丢弃衣冠巾带，想用只有弹丸之地的小小南越来和天子抗衡，成为敌国，那你的大祸也就要临头了。

（2）我不能在中原发迹起家，所以才在此称王。

假使我占据中国，我又哪里比不上汉王呢？解析：陆贾是楚国人，以幕僚宾客的身份随从高祖平定天下，当时人们都称他是很有口才的说客，所以伴随在高祖的身边常常出使各个诸侯国。

在高祖刚把中国平定的时候，尉佗也平定了南越，便在那里自立为王。

高祖考虑天下初定，中国劳苦，就没有诛杀尉佗，还派遣陆贾带着赐给尉佗的南越王之印前去任命。

陆生到了南越，尉佗梳着当地流行的一撮锥子一样的发髻，像簸箕一样地伸开两腿坐着，接见陆生。

陆生就此高尉佗说道：“您本是中国人，亲戚、兄弟祖先的坟墓都在真定。

而现在您却一反中国人的习俗，丢弃衣冠巾带，想用只有弹丸之地的小小南越来和天子抗衡，成为敌国，那你的大祸也就要临头了。

况且秦朝暴虐无道，诸侯豪杰都纷纷而起，只有汉王首先入关，占据咸阳。

项羽背叛盟约，自立为西楚霸王，诸侯们都归属于他，可以称得上是强大无比。

但是汉王从巴蜀出兵之后，征服天下，平定诸侯，杀死项羽，灭掉楚国。

2013高考全国2数学试卷及解析

2013年普通高等学校招生全国统一考试（Ⅱ）一．选择题（共12小题）1．已知集合M={x|（x﹣1）2＜4，x∈R}，N={﹣1，0，1，2，3}，则M∩N=（）A．{0，1，2}B．{﹣1，0，1，2}C．{﹣1，0，2，3}D．{0，1，2，3}2．设复数z满足（1﹣i）z=2i，则z=（）A．﹣1+i B．﹣1﹣i C．1+i D．1﹣i3．等比数列{a n}的前n项和为S n，已知S3=a2+10a1，a5=9，则a1=（）A．B．C．D．4．已知m，n为异面直线，m⊥平面α，n⊥平面β．直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则（）A．α∥β且l∥αB．α⊥β且l⊥βC．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l5．已知（1+ax）（1+x）5的展开式中x2的系数为5，则a=（）A．﹣4 B．﹣3 C．﹣2 D．﹣16．执行右面的程序框图，如果输入的N=10，那么输出的S=（）A．B．C．D．7．一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（）A．B．C．D．8．设a=log36，b=log510，c=log714，则（）A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c9．已知a＞0，实数x，y满足：，若z=2x+y的最小值为1，则a=（）A．2 B．1 C．D．10．已知函数f（x）=x3+ax2+bx+c，下列结论中错误的是（）A．∃x0∈R，f（x0）=0B．函数y=f（x）的图象是中心对称图形C．若x0是f（x）的极小值点，则f（x）在区间（﹣∞，x0）单调递减D．若x0是f（x）的极值点，则f′（x0）=011．设抛物线C：y2=2px（p＞0）的焦点为F，点M在C上，|MF|=5，若以MF为直径的圆过点（0，2），则C的方程为（）A．y2=4x或y2=8x B．y2=2x或y2=8xC．y2=4x或y2=16x D．y2=2x或y2=16x12．已知点A（﹣1，0），B（1，0），C（0，1），直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，则b的取值范围是（）A．（0，1）B．C．D．二．填空题（共4小题）13．已知正方形ABCD的边长为2，E为CD的中点，则•=．14．从n个正整数1，2，…，n中任意取出两个不同的数，若取出的两数之和等于5的概率为，则n=．15．设θ为第二象限角，若tan（θ+）=，则sinθ+cosθ=．16．等差数列{a n}的前n项和为S n，已知S10=0，S15=25，则nS n的最小值为．三．解答题（共7小题）17．△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB．（Ⅰ）求B；（Ⅱ）若b=2，求△ABC面积的最大值．18．如图，直棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=AB．（Ⅰ）证明：BC1∥平面A1CD（Ⅱ）求二面角D﹣A1C﹣E的正弦值．19．经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以x（单位：t，100≤x≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．（Ⅰ）将T表示为x的函数；（Ⅱ）根据直方图估计利润T不少于57000元的概率；（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x∈[100，110））则取x=105，且x=105的概率等于需求量落入[100，110）的频率，求T的数学期望．20．平面直角坐标系xOy中，过椭圆M：（a＞b＞0）右焦点的直线x+y﹣=0交M于A，B两点，P为AB的中点，且OP的斜率为．（Ⅰ）求M的方程（Ⅱ）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．21．已知函数f（x）=e x﹣ln（x+m）（Ι）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性；（Ⅱ）当m≤2时，证明f（x）＞0．22．已知动点P、Q都在曲线（β为参数）上，对应参数分别为β=α与β=2α（0＜α＜2π），M为PQ的中点．（1）求M的轨迹的参数方程；（2）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．2018年04月22日fago的高中数学组卷参考答案与试题解析一．选择题（共12小题）1．已知集合M={x|（x﹣1）2＜4，x∈R}，N={﹣1，0，1，2，3}，则M∩N=（）A．{0，1，2}B．{﹣1，0，1，2}C．{﹣1，0，2，3}D．{0，1，2，3}【分析】求出集合M中不等式的解集，确定出M，找出M与N的公共元素，即可确定出两集合的交集．【解答】解：由（x﹣1）2＜4，解得：﹣1＜x＜3，即M={x|﹣1＜x＜3}，∵N={﹣1，0，1，2，3}，∴M∩N={0，1，2}．故选：A．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．设复数z满足（1﹣i）z=2i，则z=（）A．﹣1+i B．﹣1﹣i C．1+i D．1﹣i【分析】根据所给的等式两边同时除以1﹣i，得到z的表示式，进行复数的除法运算，分子和分母同乘以分母的共轭复数，整理成最简形式，得到结果．【解答】解：∵复数z满足z（1﹣i）=2i，∴z==﹣1+i故选：A．【点评】本题考查代数形式的除法运算，是一个基础题，这种题目若出现一定是一个送分题目，注意数字的运算．3．等比数列{a n}的前n项和为S n，已知S3=a2+10a1，a5=9，则a1=（）A．B．C．D．【分析】设等比数列{a n}的公比为q，利用已知和等比数列的通项公式即可得到，解出即可．【解答】解：设等比数列{a n}的公比为q，∵S3=a2+10a1，a5=9，∴，解得．∴．故选：C．【点评】熟练掌握等比数列的通项公式是解题的关键．4．已知m，n为异面直线，m⊥平面α，n⊥平面β．直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则（）A．α∥β且l∥αB．α⊥β且l⊥βC．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l【分析】由题目给出的已知条件，结合线面平行，线面垂直的判定与性质，可以直接得到正确的结论．【解答】解：由m⊥平面α，直线l满足l⊥m，且l⊄α，所以l∥α，又n⊥平面β，l⊥n，l⊄β，所以l∥β．由直线m，n为异面直线，且m⊥平面α，n⊥平面β，则α与β相交，否则，若α∥β则推出m∥n，与m，n异面矛盾．故α与β相交，且交线平行于l．故选：D．【点评】本题考查了平面与平面之间的位置关系，考查了平面的基本性质及推论，考查了线面平行、线面垂直的判定与性质，考查了学生的空间想象和思维能力，是中档题．5．已知（1+ax）（1+x）5的展开式中x2的系数为5，则a=（）A．﹣4 B．﹣3 C．﹣2 D．﹣1【分析】由题意利用二项展开式的通项公式求得展开式中x2的系数为+a•=5，由此解得a的值．【解答】解：已知（1+ax）（1+x）5=（1+ax）（1+x+x2+x3+x4+x5）展开式中x2的系数为+a•=5，解得a=﹣1，故选：D．【点评】本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．6．执行右面的程序框图，如果输入的N=10，那么输出的S=（）A． B．C． D．【分析】从赋值框给出的两个变量的值开始，逐渐分析写出程序运行的每一步，便可得到程序框图表示的算法的功能．【解答】解：框图首先给累加变量S和循环变量i赋值，S=0+1=1，k=1+1=2；判断k＞10不成立，执行S=1+，k=2+1=3；判断k＞10不成立，执行S=1++，k=3+1=4；判断k＞10不成立，执行S=1+++，k=4+1=5；…判断i＞10不成立，执行S=，k=10+1=11；判断i＞10成立，输出S=．算法结束．故选：B．【点评】本题考查解决程序框图中的循环结构时，常采用写出前几次循环的结果，找规律．7．一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（）A．B．C．D．【分析】由题意画出几何体的直观图，然后判断以zOx平面为投影面，则得到正视图即可．【解答】解：因为一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），几何体的直观图如图，是正方体的顶点为顶点的一个正四面体，所以以zOx平面为投影面，则得到正视图为：故选：A．【点评】本题考查几何体的三视图的判断，根据题意画出几何体的直观图是解题的关键，考查空间想象能力．8．设a=log36，b=log510，c=log714，则（）A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c【分析】利用log a（xy）=log a x+log a y（x、y＞0），化简a，b，c然后比较log32，log52，log72大小即可．【解答】解：因为a=log36=1+log32，b=log510=1+log52，c=log714=1+log72，因为y=log2x是增函数，所以log27＞log25＞log23，∵，，所以log32＞log52＞log72，所以a＞b＞c，故选：D．【点评】本题主要考查不等式与不等关系，对数函数的单调性的应用，不等式的基本性质的应用，属于基础题．9．已知a＞0，实数x，y满足：，若z=2x+y的最小值为1，则a=（）A．2 B．1 C．D．【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即先确定z的最优解，然后确定a的值即可．【解答】解：作出不等式对应的平面区域，（阴影部分）由z=2x+y，得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点C时，直线y=﹣2x+z的截距最小，此时z最小．即2x+y=1，由，解得，即C（1，﹣1），∵点C也在直线y=a（x﹣3）上，∴﹣1=﹣2a，解得a=．故选：C．【点评】本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．10．已知函数f（x）=x3+ax2+bx+c，下列结论中错误的是（）A．∃x0∈R，f（x0）=0B．函数y=f（x）的图象是中心对称图形C．若x0是f（x）的极小值点，则f（x）在区间（﹣∞，x0）单调递减D．若x0是f（x）的极值点，则f′（x0）=0【分析】利用导数的运算法则得出f′（x），分△＞0与△≤0讨论，列出表格，即可得出．【解答】解：f′（x）=3x2+2ax+b．（1）当△=4a2﹣12b＞0时，f′（x）=0有两解，不妨设为x1＜x2，列表如下x（﹣∞，x1）x1（x1，x2）x2（x2，+∞）f′（x）+0﹣0+f（x）单调递增极大值单调递减极小值单调递增由表格可知：①x2是函数f（x）的极小值点，但是f（x）在区间（﹣∞，x2）不具有单调性，故C不正确．②∵+f（x）=+x3+ax2+bx+c=﹣+2c，=，∵+f（x）=，∴点P为对称中心，故B正确．③由表格可知x1，x2分别为极值点，则，故D正确．④∵x→﹣∞时，f（x）→﹣∞；x→+∞，f（x）→+∞，函数f（x）必然穿过x轴，即∃xα∈R，f（xα）=0，故A正确．（2）当△≤0时，，故f（x）在R上单调递增，①此时不存在极值点，故D正确，C不正确；②B同（1）中②正确；③∵x→﹣∞时，f（x）→﹣∞；x→+∞，f（x）→+∞，函数f（x）必然穿过x轴，即∃x0∈R，f（x0）=0，故A正确．综上可知：错误的结论是C．由于该题选择错误的，故选：C．【点评】熟练掌握导数的运算法则、中心得出的定义、单调性与极值的关系等基础知识与方法，考查了分类讨论的思想方法等基本方法．11．设抛物线C：y2=2px（p＞0）的焦点为F，点M在C上，|MF|=5，若以MF为直径的圆过点（0，2），则C的方程为（）A．y2=4x或y2=8x B．y2=2x或y2=8xC．y2=4x或y2=16x D．y2=2x或y2=16x【分析】根据抛物线方程算出|OF|=，设以MF为直径的圆过点A（0，2），在Rt△AOF 中利用勾股定理算出|AF|=．再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF，Rt△AMF中利用∠AMF的正弦建立关系式，从而得到关于p的方程，解之得到实数p的值，进而得到抛物线C的方程．【解答】解：∵抛物线C方程为y2=2px（p＞0），∴焦点F坐标为（，0），可得|OF|=，∵以MF为直径的圆过点（0，2），∴设A（0，2），可得AF⊥AM，Rt△AOF中，|AF|==，∴sin∠OAF==，∵根据抛物线的定义，得直线AO切以MF为直径的圆于A点，∴∠OAF=∠AMF，可得Rt△AMF中，sin∠AMF==，∵|MF|=5，|AF|=∴=，整理得4+=，解之可得p=2或p=8因此，抛物线C的方程为y2=4x或y2=16x．故选：C．方法二：∵抛物线C方程为y2=2px（p＞0），∴焦点F（，0），设M（x，y），由抛物线性质|MF|=x+=5，可得x=5﹣，因为圆心是MF的中点，所以根据中点坐标公式可得，圆心横坐标为=，由已知圆半径也为，据此可知该圆与y轴相切于点（0，2），故圆心纵坐标为2，则M点纵坐标为4，即M（5﹣，4），代入抛物线方程得p2﹣10p+16=0，所以p=2或p=8．所以抛物线C的方程为y2=4x或y2=16x．故选：C．【点评】本题给出抛物线一条长度为5的焦半径MF，以MF为直径的圆交抛物线于点（0，2），求抛物线的方程，着重考查了抛物线的定义与简单几何性质、圆的性质和解直角三角形等知识，属于中档题．12．已知点A（﹣1，0），B（1，0），C（0，1），直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，则b的取值范围是（）A．（0，1）B．C．D．【分析】解法一：先求得直线y=ax+b（a＞0）与x轴的交点为M（﹣，0），由﹣≤0可得点M在射线OA上．求出直线和BC的交点N的坐标，①若点M和点A重合，求得b=；②若点M在点O和点A之间，求得＜b＜；③若点M在点A的左侧，求得＞b＞1﹣．再把以上得到的三个b的范围取并集，可得结果．解法二：考查临界位置时对应的b值，综合可得结论．【解答】解：解法一：由题意可得，三角形ABC的面积为=1，由于直线y=ax+b（a＞0）与x轴的交点为M（﹣，0），由直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，可得b＞0，故﹣≤0，故点M在射线OA上．设直线y=ax+b和BC的交点为N，则由可得点N的坐标为（，）．①若点M和点A重合，则点N为线段BC的中点，故N（，），把A、N两点的坐标代入直线y=ax+b，求得a=b=．②若点M在点O和点A之间，此时b＞，点N在点B和点C之间，由题意可得三角形NMB的面积等于，即=，即=，可得a=＞0，求得b＜，故有＜b＜．③若点M在点A的左侧，则b＜，由点M的横坐标﹣＜﹣1，求得b＞a．设直线y=ax+b和AC的交点为P，则由求得点P的坐标为（，），此时，由题意可得，三角形CPN的面积等于，即•（1﹣b）•|x N﹣x P|=，即（1﹣b）•|﹣|=，化简可得2（1﹣b）2=|a2﹣1|．由于此时b＞a＞0，0＜a＜1，∴2（1﹣b）2=|a2﹣1|=1﹣a2 ．两边开方可得（1﹣b）=＜1，∴1﹣b＜，化简可得b＞1﹣，故有1﹣＜b＜．再把以上得到的三个b的范围取并集，可得b的取值范围应是，故选：B．解法二：当a=0时，直线y=ax+b（a＞0）平行于AB边，由题意根据三角形相似且面积比等于相似比的平方可得=，b=1﹣，趋于最小．由于a＞0，∴b＞1﹣．当a逐渐变大时，b也逐渐变大，当b=时，直线经过点（0，），再根据直线平分△ABC的面积，故a不存在，故b＜．综上可得，1﹣＜b＜，故选：B．【点评】本题主要考查确定直线的要素，点到直线的距离公式以及三角形的面积公式的应用，还考察运算能力以及综合分析能力，分类讨论思想，属于难题．二．填空题（共4小题）13．已知正方形ABCD的边长为2，E为CD的中点，则•=2．【分析】根据两个向量的加减法的法则，以及其几何意义，可得要求的式子为（）•（），再根据两个向量垂直的性质，运算求得结果．【解答】解：∵已知正方形ABCD的边长为2，E为CD的中点，则=0，故=（）•（）=（）•（）=﹣+﹣=4+0﹣0﹣=2，故答案为2．【点评】本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量垂直的性质，属于中档题．14．从n个正整数1，2，…，n中任意取出两个不同的数，若取出的两数之和等于5的概率为，则n=8．【分析】列出从n个正整数1，2，…，n中任意取出两个不同的数的所有取法种数，求出和等于5的种数，根据取出的两数之和等于5的概率为列式计算n的值．【解答】解：从n个正整数1，2，…，n中任意取出两个不同的数，取出的两数之和等于5的情况有：（1，4），（2，3）共2种情况；从n个正整数1，2，…，n中任意取出两个不同的数的所有不同取法种数为，由古典概型概率计算公式得：从n个正整数1，2，…，n中任意取出两个不同的数，取出的两数之和等于5的概率为p=．所以，即，解得n=8．故答案为8．【点评】本题考查了古典概型及其概率计算公式，考查了组合数公式，解答此题时既可以按有序取，也可以按无序取，问题的实质是一样的．此题是基础题．15．设θ为第二象限角，若tan（θ+）=，则sinθ+cosθ=﹣．【分析】已知等式利用两角和与差的正切函数公式及特殊角的三角函数值化简，求出tanθ的值，再根据θ为第二象限角，利用同角三角函数间的基本关系求出sinθ与cosθ的值，即可求出sinθ+cosθ的值．【解答】解：∵tan（θ+）==，∴tanθ=﹣，而cos2θ==，∵θ为第二象限角，∴cosθ=﹣=﹣，sinθ==，则sinθ+cosθ=﹣=﹣．故答案为：﹣【点评】此题考查了两角和与差的正切函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．16．等差数列{a n}的前n项和为S n，已知S10=0，S15=25，则nS n的最小值为﹣49．【分析】由等差数列的前n项和公式化简已知两等式，联立求出首项a1与公差d的值，结合导数求出nS n的最小值．【解答】解：设等差数列{a n}的首项为a1，公差为d，∵S10=10a1+45d=0，S15=15a1+105d=25，∴a1=﹣3，d=，∴S n=na1+d=n2﹣n，∴nS n=n3﹣n2，令nS n=f（n），∴f′（n）=n2﹣n，∴当n=时，f（n）取得极值，当n＜时，f（n）递减；当n＞时，f（n）递增；因此只需比较f（6）和f（7）的大小即可．f（6）=﹣48，f（7）=﹣49，故nS n的最小值为﹣49．故答案为：﹣49．【点评】此题考查了等差数列的性质，以及等差数列的前n项和公式，熟练掌握性质及公式是解本题的关键．三．解答题（共7小题）17．△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB．（Ⅰ）求B；（Ⅱ）若b=2，求△ABC面积的最大值．【分析】（Ⅰ）已知等式利用正弦定理化简，再利用两角和与差的正弦函数公式及诱导公式变形，求出tanB的值，由B为三角形的内角，利用特殊角的三角函数值即可求出B的度数；（Ⅱ）利用三角形的面积公式表示出三角形ABC的面积，把sinB的值代入，得到三角形面积最大即为ac最大，利用余弦定理列出关系式，再利用基本不等式求出ac的最大值，即可得到面积的最大值．【解答】解：（Ⅰ）由已知及正弦定理得：sinA=sinBcosC+sinBsinC①，∵sinA=sin（B+C）=sinBcosC+cosBsinC②，∴sinB=cosB，即tanB=1，∵B为三角形的内角，∴B=；（Ⅱ）S=acsinB=ac，△ABC由已知及余弦定理得：4=a2+c2﹣2accos≥2ac﹣2ac×，整理得：ac≤，当且仅当a=c时，等号成立，则△ABC面积的最大值为××=××（2+）=+1．【点评】此题考查了正弦、余弦定理，三角形的面积公式，两角和与差的正弦函数公式，以及基本不等式的运用，熟练掌握定理及公式是解本题的关键．18．如图，直棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=AB．（Ⅰ）证明：BC1∥平面A1CD（Ⅱ）求二面角D﹣A1C﹣E的正弦值．【分析】（Ⅰ）通过证明BC1平行平面A1CD内的直线DF，利用直线与平面平行的判定定理证明BC1∥平面A1CD（Ⅱ）证明DE⊥平面A1DC，作出二面角D﹣A1C﹣E的平面角，然后求解二面角平面角的正弦值即可．【解答】解：（Ⅰ）证明：连结AC1交A1C于点F，则F为AC1的中点，又D是AB中点，连结DF，则BC1∥DF，因为DF⊂平面A1CD，BC1⊄平面A1CD，所以BC1∥平面A1CD．（Ⅱ）因为直棱柱ABC﹣A1B1C1，所以AA1⊥CD，由已知AC=CB，D为AB的中点，所以CD⊥AB，又AA1∩AB=A，于是，CD⊥平面ABB1A1，设AB=2，则AA1=AC=CB=2，得∠ACB=90°，CD=，A1D=，DE=，A1E=3故A1D2+DE2=A1E2，即DE⊥A1D，所以DE⊥平面A1DC，又A1C=2，过D作DF⊥A1C于F，∠DFE为二面角D﹣A1C﹣E的平面角，在△A1DC中，DF==，EF==，所以二面角D﹣A1C﹣E的正弦值．sin∠DFE=．【点评】本题考查直线与平面平行的判定定理的应用，二面角的平面角的求法，考查空间想象能力与计算能力．19．经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以x（单位：t，100≤x≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．（Ⅰ）将T表示为x的函数；（Ⅱ）根据直方图估计利润T不少于57000元的概率；（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x∈[100，110））则取x=105，且x=105的概率等于需求量落入[100，110）的频率，求T的数学期望．【分析】（Ⅰ）由题意先分段写出，当x∈[100，130）时，当x∈[130，150）时，和利润值，最后利用分段函数的形式进行综合即可．（Ⅱ）由（I）知，利润T不少于57000元，当且仅当120≤x≤150．再由直方图知需求量X ∈[120，150]的频率为0.7，利用样本估计总体的方法得出下一个销售季度的利润T不少于57000元的概率的估计值．（Ⅲ）利用利润T的数学期望=各组的区间中点值×该区间的频率之和即得．【解答】解：（Ⅰ）由题意得，当x∈[100，130）时，T=500x﹣300（130﹣x）=800x﹣39000，当x∈[130，150）时，T=500×130=65000，∴T=．（Ⅱ）由（Ⅰ）知，利润T不少于57000元，当且仅当120≤x≤150．由直方图知需求量X∈[120，150]的频率为0.7，所以下一个销售季度的利润T不少于57000元的概率的估计值为0.7．（Ⅲ）依题意可得T的分布列如图，T4500053006100065000p0.10.20.30.4所以ET=45000×0.1+53000×0.2+61000×0.3+65000×0.4=59400．【点评】本题考查用样本的频率分布估计总体分布及识图的能力，求解的重点是对题设条件及直方图的理解，了解直方图中每个小矩形的面积的意义，是中档题．20．平面直角坐标系xOy中，过椭圆M ：（a＞b＞0）右焦点的直线x+y ﹣=0交M于A，B两点，P为AB的中点，且OP 的斜率为．（Ⅰ）求M的方程（Ⅱ）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．【分析】（Ⅰ）把右焦点（c，0）代入直线可解得c．设A（x1，y1），B（x2，y2），线段AB的中点P（x0，y0），利用“点差法”即可得到a，b的关系式，再与a2=b2+c2联立即可得到a，b，c．（Ⅱ）由CD⊥AB，可设直线CD的方程为y=x+t，与椭圆的方程联立得到根与系数的关系，即可得到弦长|CD|．把直线x+y﹣=0与椭圆的方程联立得到根与系数的关系，即可得到=即可得到关于t的表达式，利用二次函数的单调性弦长|AB|，利用S四边形ACBD即可得到其最大值．【解答】解：（Ⅰ）把右焦点（c，0）代入直线x+y﹣=0得c+0﹣=0，解得c=．设A（x1，y1），B（x2，y2），线段AB的中点P（x0，y0），则，，相减得，∴，∴，又=，∴，即a2=2b2．联立得，解得，∴M的方程为．（Ⅱ）∵CD⊥AB，∴可设直线CD的方程为y=x+t，联立，消去y得到3x2+4tx+2t2﹣6=0，∵直线CD与椭圆有两个不同的交点，∴△=16t2﹣12（2t2﹣6）=72﹣8t2＞0，解﹣3＜t＜3（*）．设C（x3，y3），D（x4，y4），∴，．∴|CD|===．联立得到3x2﹣4x=0，解得x=0或，∴交点为A（0，），B，∴|AB|==．===，∴S四边形ACBD∴当且仅当t=0时，四边形ACBD面积的最大值为，满足（*）．∴四边形ACBD面积的最大值为．【点评】本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程根与系数的关系、弦长公式、四边形的面积计算、二次函数的单调性等基础知识，考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力．21．已知函数f（x）=e x﹣ln（x+m）（Ι）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性；（Ⅱ）当m≤2时，证明f（x）＞0．【分析】（Ⅰ）求出原函数的导函数，因为x=0是函数f（x）的极值点，由极值点处的导数等于0求出m的值，代入函数解析式后再由导函数大于0和小于0求出原函数的单调区间；（Ⅱ）证明当m≤2时，f（x）＞0，转化为证明当m=2时f（x）＞0．求出当m=2时函数的导函数，可知导函数在（﹣2，+∞）上为增函数，并进一步得到导函数在（﹣1，0）上有唯一零点x0，则当x=x0时函数取得最小值，借助于x0是导函数的零点证出f（x0）＞0，从而结论得证．【解答】（Ⅰ）解：∵，x=0是f（x）的极值点，∴，解得m=1．所以函数f（x）=e x﹣ln（x+1），其定义域为（﹣1，+∞）．∵．设g（x）=e x（x+1）﹣1，则g′（x）=e x（x+1）+e x＞0，所以g（x）在（﹣1，+∞）上为增函数，又∵g（0）=0，所以当x＞0时，g（x）＞0，即f′（x）＞0；当﹣1＜x＜0时，g（x）＜0，f′（x）＜0．所以f（x）在（﹣1，0）上为减函数；在（0，+∞）上为增函数；（Ⅱ）证明：当m≤2，x∈（﹣m，+∞）时，ln（x+m）≤ln（x+2），故只需证明当m=2时f（x）＞0．当m=2时，函数在（﹣2，+∞）上为增函数，且f′（﹣1）＜0，f′（0）＞0．故f′（x）=0在（﹣2，+∞）上有唯一实数根x0，且x0∈（﹣1，0）．当x∈（﹣2，x0）时，f′（x）＜0，当x∈（x0，+∞）时，f′（x）＞0，从而当x=x0时，f（x）取得最小值．由f′（x0）=0，得，ln（x0+2）=﹣x0．故f（x）≥=＞0．综上，当m≤2时，f（x）＞0．【点评】本题考查了利用导数研究函数的单调性，利用导数求函数在闭区间上的最值，考查了不等式的证明，考查了函数与方程思想，分类讨论的数学思想，综合考查了学生分析问题和解决问题的能力．熟练函数与导数的基础知识是解决该题的关键，是难题．22．已知动点P、Q都在曲线（β为参数）上，对应参数分别为β=α与β=2α（0＜α＜2π），M为PQ的中点．（1）求M的轨迹的参数方程；（2）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．【分析】（1）利用参数方程与中点坐标公式即可得出；（2）利用两点之间的距离公式、三角函数的单调性即可得出．【解答】解：（1）依题意有P（2cosα，2sinα），Q（2cos2α，2sin2α），因此M（cosα+cos2α，sinα+sin2α）．M的轨迹的参数方程为为参数，0＜α＜2π）．（2）M点到坐标原点的距离d=（0＜α＜2π）．当α=π时，d=0，故M的轨迹过坐标原点．【点评】本题考查了参数方程与中点坐标公式、两点之间的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．23．【选修4﹣﹣5；不等式选讲】设a，b，c均为正数，且a+b+c=1，证明：（Ⅰ）（Ⅱ）．【分析】（Ⅰ）依题意，由a+b+c=1⇒（a+b+c）2=1⇒a2+b2+c2+2ab+2bc+2ca=1，利用基本不等式可得3（ab+bc+ca）≤1，从而得证；（Ⅱ）利用基本不等式可证得：+b≥2a，+c≥2b，+a≥2c，三式累加即可证得结论．【解答】证明：（Ⅰ）由a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca得：a2+b2+c2≥ab+bc+ca，由题设得（a+b+c）2=1，即a2+b2+c2+2ab+2bc+2ca=1，所以3（ab+bc+ca）≤1，即ab+bc+ca≤．（Ⅱ）因为+b≥2a，+c≥2b，+a≥2c，故+++（a+b+c）≥2（a+b+c），即++≥a+b+c．所以++≥1．【点评】本题考查不等式的证明，突出考查基本不等式与综合法的应用，考查推理论证能力，属于中档题．。

2013年高考真题——语文(江苏卷) 解析版含答案

2013年普通高考语文江苏卷详解详析第Ⅰ卷一、语言文字运用（15分）1。

【答案】D【命题立意】本题考查识记现代汉语普通话常用字的字音，能力层级为A。

【解析】A项“亢”与“伉”读（kàng）、“吭"读（háng)和“沆”读（hàng) ，B项“稂”、“锒"、“琅”读(láng)、“阆”读(làng),C项“孩”、“骸" 读（hái）、骇读（hài）、“赅”读（gāi）.本题考查词语信息量较大，有的两组词语之间联系不大，这就需要考生的复习备考要适当增加记忆积累的范围。

本题可以采用排除法来逐步缩小答题范围.2。

【答案】B【命题立意】本题考查正确使用成语，能力层级为E。

【解析】第一空根据语境应填“买椟还珠"，“买椟还珠" 用来比喻没有眼光取舍不当；第二空根据“儒、释、道哪一条路上行走”一句，所以选填“殊途同归”最为恰当，“殊途同归”指通过不同的途径,到达同一个目的地。

比喻采取不同的方法而得到相同的结果；第三空根据“他的危机感丝毫未减”，选填“如履薄冰”，“如履薄冰”指比喻行事极为谨慎，存有戒心.本题成语的考查数量虽然较多,但题干中明确的语境降低了解题的难度，三个空都可依据这一点3。

【答案】改变自己比改变环境（世界)更容易。

【命题立意】本题考查语言表达准确、鲜明、生动，能力层级为E。

【解析】题干中已明确答题的方向：画线句子的含义。

因此在答此题的时候要注意由点到面的思维，针对“穿鞋”上升到“改变自己”,针对“给全世界铺上地毯"上升到“改变世界”。

再组织恰当的语言表述.4. 【答案】大多数作家需要十年左右的创作积累,才能进入创作成熟期。

【命题立意】本题考查图表转述能力。

能力层级为E。

【解析】本题采用图表分析的形式,旨在考查考生的语言综合运用能力，尤其是图文转换能力。

图表分析题要求考生能够根据图表中的有关内容来分析有关材料，辨别、提取、挖掘其中隐含的信息，进而对材料进行综合性评价。

【语文】2013年高考真题——(全国卷)解析版

2013年普通高等学校招生全国统一考试语文注意事项：1. 本试卷分第Ⅰ卷（阅读题）和第Ⅱ卷（表达题）两部分。

第Ⅰ卷1至8页，第Ⅱ卷9至10页。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束，将本试题和答题卡一并交回。

第Ⅰ卷（30分）一、（12分，每小题3分）1．下列词语中加点的字，读音全都正确的一组是A．女红．（gōng）安土重．迁移（zhîng）商埠．(fǔ) 花团锦簇．（cù）B．莅．临（lì）大放厥．词（jué）挟．制（xié）蔫．头呆脑（yān）C．懦．弱（nuî）年高德劭．（shāo）两栖．（qī）沁．人心脾（qīn）D．遽．然（jù）精神抖擞．（sǒu）塌．陷（tā）一柱擎．天（qíng）【答案】C【解析】本题考查识记现代汉语普通话的字音的能力，能力层级为A级。

A项，“埠”应读“bu”；B项，“挟”应读“xia”；D项，“坍”应读“tan”。

2．下列各句中，加点的成语使用恰当的一项是A．客厅墙上挂着我们全家在桂林的合影，尽管照片有些褪色，但温馨和美的亲情历历．．在目．．。

B．为了完成在全国的市场布局，我们三年前就行动了，特别是在营销策略的制订上可谓处心积虑．．．．。

C．沉迷网络使小明学习成绩急剧下降，幸亏父母及时发现，并不断求全责备．．．．，他才戒掉了网瘾。

D．他在晚会上出神入化．．．．的近景魔术表演，不仅令无数观众惊叹不已，还引发了魔术道具的热销。

【答案】D【解析】本题考查正确使用词语（包括熟语）的能力，能力层级为D级。

A项，历历在目：指远方的景物看得清清楚楚，或过去的事情清清楚楚地重现在眼前。

这里用来形容“真情”，显然不当。

B项，处心积虑：形容蓄谋已久。

是一个贬义词，此处感情色彩用错。

C项，求全责备：对人或对人做的事情要求十全十美,毫无缺点。

2013年高考语文真题试题江西卷(解析版)

2013普通高等学校招生全国统一考试（江西卷）语文试题详解第Ⅰ卷（选择题共３６分）一、（１８分，每小题３分）1、下列词语中，加点的字读音全都正确的一组是A、衣着（zhuï）果脯（fǔ）给（gěi]养揆情度（duï）理B、蟊（máo）贼呵（hē）护湍（tuān）急模棱（léng）两可C、载（zài）体供（gîng）认涔（cén）涔呱（guā）呱坠地D、愠（yùn）色角（jiǎoj）色畏葸（xǐ）殒身不恤（xù）【答案】B【解析】A(jǐ)养——①所需物质和食物、饲料、燃料等的储备。

②供给军队人员的主食、副食、燃料和军用牲畜的饲料等的统称。

揆情度理kuí qíng duï lǐ——揆：估量揣测；度：猜想。

按照情和理估量，推测。

C、呱呱坠地gū gū zhuì dì——形容婴儿出生或事物问世。

D、角（jué）色。

殒身不恤yǔn shēn bú xù——殒：牺牲；恤：顾惜。

牺牲生命也不顾惜。

[出自]鲁迅《记念刘和珍君》2、下列词语中，没有错别字的一组是A、松驰回溯卫戍皇天后土B、辨认影牒荣膺残羹冷炙C、豆蔻聘礼修葺金壁辉煌D、城阙编纂恻隐亭亭玉立【答案】D。

【解析】【A、松驰（弛）B、影牒（碟）C、金壁辉煌（碧）】3、下列各句中，加点的词语使用恰当的一项是（1）家庭的使他从小对美就有敏锐的感悟，乡村丰富的色彩和生动的线条使他陶醉不已。

（2）那个时候的中国，社会动荡，经济秩序极为混乱，物价，人民苦不堪言。

（3）沈阳飞机制造公司全体职工都总经理罗阳献身国防事业的崇高精神打动。

A、熏陶青云直上为••而B、熏染青云直上为••而C、熏陶扶摇直上为••所D、熏染扶摇直上为••所【答案】C。

【解析】熏陶——人的思想行为因长期接触某些事物而受到好的影响。

2013年山东高考数学文科试卷带详解

2013年普通高等学校招生全国统一考试（山东卷）文科数学一．选择题:本题共12个小题，每题5分，共60分.1．复数2(2i)iz -=（i 为虚数单位），则z = ( )A ．25 B.41 C.5 D.5 【测量目标】复数的代数的四则运算，复数的基本概念（复数的模）. 【考查方式】给出复数的乘方与除法形式,求复数的模. 【参考答案】C【试题解析】利用复数的乘方和乘除运算计算出z ，进而求出z ，2222(2i)44i+i 34i =43i,z (4)(3)5i i iz ---===--∴=-+-=.2．已知集合,A B 均为全集{}=1,2,3,4U 的子集，且{}()4U A B = ð,{}=1,2B ,则U A B = ð ( )A.{3}B.{4}C.{3，4}D.∅【测量目标】集合间的基本运算.【考查方式】集合的表示(列举法),给出集合间的四则运算结果，去计算A B 与的补集的交集.【参考答案】A【试题解析】利用所给条件计算出A 和U B ð，进而求交集{}{}=1,2,3,4,()4U U A B = ，ð(步骤1) {}{}{}{}1,2,3.=123123.A B B A ∴=∴⊆⊆ 又，，，，(步骤2) 又{}{}=34,3.U UB A B ∴= ，痧(步骤3)3．已知函数()f x 为奇函数，且当0x >时()21f x x x=+，则()1f -= ( ) A ．2 B.1 C.0 D.-2【测量目标】函数奇偶性的综合运用.【考查方式】已知函数的部分解析式、利用函数的奇偶性，解决函数的求值问题. 【参考答案】D【试题解析】利用奇函数的性质()()f x f x -=-求解.当2210(),(1)11 2.x f x x f x>=+∴=+=时， ()f x 为奇函数.(1)(1)2f f ∴-=-=-4．一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如右图所示该四棱锥侧面积和体积分别是 ( ) A ．45,8 B.845,3C.84(51),3+ D. 8,8 【测量目标】由三视图求几何体表面积与体积.【考查方式】给出四棱锥的主视图，描述四棱锥棱的情况，求解四棱锥的侧面积与体积.【参考答案】B 【试题解析】有正视图知：四棱锥的底面是边长为2的正方形，四棱锥的高为2，21822.33V ∴=⨯⨯=四棱锥的侧面是全等的等腰三角形，底为2，高为15,=425=452S ∴⨯⨯⨯侧5．函数1()123xf x x =-++的定义域为 ( ) A.(-3，0] B. (-3，1] C. ()(],33,0-∞-- D. ()(],33,1-∞-- 【测量目标】函数的定义域.【考查方式】通过给定函数式，使每个部分有意义，求其定义域. 【参考答案】A【试题解析】求函数定义域就是是这个式子有意义的自变量x 的取值范围，由题意，自变量x 应满足120,30,x x ⎧-⎨+>⎩…解得0,303,x x x ⎧∴-<⎨>-⎩……6．执行右边的程序框图，若第一次输入的a 的值为-1.2，第二次输入的a 的值为1.2，则第一次、第二次输出的a 的值分别为 ( )A.0.2，0.2B. 0.2，0.8C. 0.8，0.2D. 0.8，0.8 【测量目标】循环结构的程序框图.【考查方式】给出具体的算法流程图，求输出的结果.【参考答案】C【试题解析】根据输入a 的值的不同而执行不同的程序.当 1.20, 1.210.2,0,a a a a =-<∴=-+=-< 时，0.210.8,0.0.81,a a =-+=>< 输出0.8.a =当 1.21, 1.210.2.a a a =∴=-=时，…0.21,< 输出0.2.a =7．ABC △的内角A B C 、、的对边分别是a b c 、、，若=2,=1,=3,B A a b 则c = ( )A. 23B. 2C.2D.1【测量目标】用正余弦定理判断三角形形状，勾股定理，二倍角.【考查方式】已知三角形的边角关系求边长，考查正弦定理、二倍角公式. 【参考答案】B【试题解析】先利用正弦定理，求出角A ,进而求出角B 和角C ，得出角C 为直角，从而用勾股定理求出边c 由正弦定理得,2,1,3,sin sin a bB A a b A B==== 13.sin 2sin cos A A A∴=（步骤1） A 为三角形的内角3sin 0.cos 2A A ∴≠∴=，.(步骤2)ππ0π,2.63A A B A <<∴=∴==又，(步骤3)ππ2C A B ABC ∴=--=∴，△为直角三角形由勾股定理得221(3) 2.c =+=（步骤4）8．给定两个命题q p ,，p ⌝是q 的必要而不充分条件，则p 是q ⌝ ( ) A ．充分而不必要条件 B.必要而不充分条件 C.充要条件 D.不充分也不必要条件【测量目标】充分、必要条件，四种命题之间的关系.【考查方式】根据逻辑连接词,来主要考查命题的基本关系及充分必要条件. 【参考答案】A【试题解析】借助原命题与逆否命题等价判断.若p ⌝是q 的必要不充分条件，则q p ⇒⌝但p q ⌝≠，其逆否命题为,p q q p p q ⇒⌝⌝≠∴⌝但是的充分不必要条件.9．函数cos sin y x x x =+的图象大致为 ( )A B C D【测量目标】函数奇偶性的综合运用，函数图象的阅读及处理. 【考查方式】通过给定的函数式，确定函数的大概图象.【参考答案】D【试题解析】结合给出的函数图象，带入特殊值，利用排除法求解.π10,C 2π,1,B 2π,π0 A.Dx y x y x y ==>=-=-==-<时，排除当排除当排除故选10．将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91，现场做的9个分数的茎叶图后来有一个数据模糊，无法辨认，在图中以x 表示：则7个剩余分数的方差为（）A.1169 B.367 C.36 D.677【测量目标】茎叶图、用样本数字特征估计总体数字特征（方差，平均数）.【考查方式】给定茎叶图，里面含有未知数，给定去高去低后的平均数，求剩余分数的方差.【参考答案】B【试题分析】利用平均数为91，求出x 的值，利用方差的定义，计算方差，根据茎叶图.[]22222222187+94909190(90)9191, 4.7136(8791)(9491)(9091)(9191)(9091)(9491)(9191)77x x s ++++++=∴=⎡⎤=-+-+-+-+-+-+-=⎣⎦11．抛物线211:()2C y x p p=>0的焦点与双曲线222:13x C y -=的右焦点的连线交1C 于第一象限的点M ，若1C 在点M 处的切线平行于2C 的一条渐近线，则p = （）A ．316 B.38 C.233 D.433【测量目标】双曲线、抛物线的简单几何性质，抛物线与直线的位置关系.【考查方式】给定两抛物线交点位置，交点处的切线与抛物线的关系，去求抛物线中的未知数.【参考答案】D【试题解析】做出草图，数形结合，建立方程求解.双曲线2223x C y -:=1,∴右焦点为F (2,0)，渐近线方程为33y x =±（步骤1）抛物线21102C y x p p=>：(),焦点为(0,).2p F '（步骤2）设200001.2M x y y x p=(,), 020001222,.2113,|.3MF FF x x p p x p k k x y x y x p p ''=-=∴=-''=∴== 得433p =（步骤3） 12．设正实数,,x y z 满足22340x xy y z -+-=，当zxy取得最大值时，2x y z +-的最大值为()A ．0 B.98 C.2 D.94【测量目标】基本不等式求最值.【考查方式】给定三个未知数满足的方程式，用基本不等式求式子的最大值. 【参考答案】B【试题解析】含三个参数,,x y z 消元，利用基本不等式及配方法求最值.222234(0,0,0),44323134z x xy y x y z xy xy x y x yz x xy y y x y x=-+>>>∴==+--=-+ …(步骤1) 当且仅当42x yx y y x==,时等号成立2222222223446422222242(1)2z x xy y y y y y x y z y y y y y y =-+=-+=∴+-=+-=-+=--+(步骤2)12y x y z ∴=+-,的最大值是2(步骤3)二．填空题：本大题共4小题，每小题4分，共16分13．过点(3，1)作圆22(2)(2)4x y -+-=的弦，其中最短的弦长为__________ 【测量目标】圆的简单几何性质.【考查方式】给定定点，与圆的标准方程，求过点的最短弦长. 【参考答案】22【试题解析】借助圆的几何性质，确定圆的最短弦位置，利用半径，弦心距及半弦长的关系求弦长.设A （3,1），可知圆心C （2,2），半径r =2，当弦过点A （3,1）且与CA 垂直时为最短弦22(23)(21)2CA =-+-=（步骤1）所以半弦长22=422r CA -=-=最短弦长为2214．在平面直角坐标系xOy 中，M 为不等式组2360200x y x y y +-⎧⎪+-⎨⎪⎩………所表示的区域上一动点，则直线OM 的最小值为_______【测量目标】二元线性规划求目标函数的最小值.【考查方式】给出约束条件，应用数形结合思想画出不等式组所表示的平面区域，求出线性规划目标函数的最小值．【参考答案】2 【试题解析】如图所示，M 为图中阴影部分的一个动点，由于点到直线的距离最短，所以OM 的最小值2==2215．在平面直角坐标系xOy 中，已知(1,),(2,2)OA t OB =-= ，若90ABO ∠=，则实数t 的值为______【测量目标】平面向量在平面几何中的应用，向量的坐标运算.【考查方式】给出两向量的坐标表示，两向量的垂直关系，求未知数t . 【参考答案】5【试题解析】利用向量垂直的充要条件，列方程求解.90,,0.ABO AB OB OB AB ∠=∴⊥∴=(2,2)(1,)(3,2),AB OB OA t t =-=--=-又(步骤1)(2,2)(3,2)62(2)0t t ∴-=+-= 5t ∴=(步骤2)16．定义“正对数”：()()0,01ln ln ,1x x x x +<<⎧⎪=⎨⎪⎩…，现有四个命题：①若0,a b >>0，则()lnlnba b a ++=；②若0,0a b >>，则ln ()ln ln ab a b +++=+ ③若0,0a b >>，则ln ln ln a a b b +++⎛⎫- ⎪⎝⎭… ④若0,0a b >>，则()lnln ln ln2a b a b ++++++…其中的真命题有____________(写出所有真命题的序号) 【测量目标】分段函数，对数的性质，不等式恒成立问题.【考查方式】给定分段函数，求所给的4个小命题的正确性，逐一论证. 【参考答案】○1○3○4【试题解析】本题是新定义型问题，解题时要严格按照所给定义，对每一个选项逐一论证或排除.○11,0,1,ln ()ln ln ln .bb b a b aa ab a b a ++>∴∴=== 当厖(步骤1)01,0,1,l n ()bba b a a +<<>∴<∴= 当(步骤2) ln 0,ln 0,ln ()ln ba b a a b a ++++=∴=∴=又(步骤3) 故○1正确. ○2112,,ln ()ln 0,42a b ab ++====当而ln ln 2,ln 0,ln ln ln 2a b a b ++++==∴+=(步骤4) 故○2不成立. ○3a.01,01,ln ln 0a b a b ++<<-=当剟而ln 0,ln ln ln a a a b b b ++++⎛⎫⎛⎫∴-⎪ ⎪⎝⎭⎝⎭厖(步骤5)b ．当+01,1,ln ln ln 0a b a b b ++<>-=-<…而+ln ()0,ln ()ln ln a a a b bb +++=∴-…(步骤6)c ．当1,01,1,aa b a b ><>剠(步骤7) ln ()ln()ln ln ln ln a a a a a b b b ++++∴===-…ln ()ln ln a a b b+++∴-… (步骤8)d ．当1,1,,ln ()0a a b a b b+>><=且 ln ln 0,ln ()ln ln a a b a b b+++++-<∴-…(步骤9)e ．当1,1,,1aa b a b b>>>>且时ln ()ln()ln ln ln ln a aa b a b b b +++∴==-=-(步骤10)综上：ln ()ln ln a a b b+++-…，故○3正确.○4a.01,01,01,ln ()0a b ab a b +<+<<∴+=当剟?ln ln ln 200ln 20a b ++++=++>+ln ()ln ln ln 2a b a b ++∴+<++(步骤11)b ．1,a b +>当分下列三种情况：（i ）当 11,12,a b a b b b b b <+++= 0，剠剟ln ()ln()ln 2ln ln ln 2a b a b b a b +++∴+=+=++…(步骤12) (ii)1,011+2,a b a b aa a a <++= 当时，厔剟+ln ()ln()ln 2ln ln 2ln ln ln 2a b a b a a a b ++∴+=+=+=++…(步骤13)(iii)01,012,ln 0,a ba b a +<<∴+=当时，且剟?ln 0.ln ()ln()ln 2ln ln ln 2b a b a b a b ++++=∴++=++剟(步骤14)综上：ln ()ln ln ln 2a b a b ++++++…，故○4正确.三．解答题：本大题共6小题，共74分， 17．(本小题满分12分) 某小组共有A B C D E 、、、、五位同学，他们的身高（单位:米）以及体重指标（单位:千克/米2）如下表所示：ABCDE身高 1.69 1.73 1.75 1.79 1.82 体重指标 19.225.118.523.320.9（1）从该小组身高低于1.80的同学中任选2人，求选到的2人身高都在1.78以下的概率（2）从该小组同学中任选2人，求选到的2人的身高都在1.70以上且体重指标都在[18.5，23.9)中的概率【测量目标】列举法、古典概型，随机事件与概率.【考查方式】给出五个学生的身高与体重，按照一定条件求概率.【试题分析】解（1）从身高低于1.80的同学中任选2人，其一切可能的结果组成的基本事件有（,A B ）,(,A C ),(,A D ),(,B C ),(,B D ),(,C D )共6个.(步骤1)由于每个人被选到的机会均等，因此这些基本事件的出现是均等的.选到的2人身高都在1.78以下的事件有(,A B ),(,A C ),(,B C ),共3人.(步骤2)因此选到的俩人身高都在1.78以下的概率为12p =(步骤3) （2）从该小组同学中人选两人，其组成成分有(,A B ),(,A C ),(,A D ),(,A E ),(,B C ),(,B D ),(,B E ),(,C D ),(,C E ),(,D E ),共10个(步骤4) 选到的2人的身高都在 1.70以上且体重指标都在[)18.5,23.9中的事件有(,C D ),(,C E ),(,D E ),共三个(步骤5)选到的2人的身高都在1.70以上且体重指标都在[)18.5,23.9中的概率310P =(步骤6) 18．(本小题满分12分)设函数23()3sin sin cos (0)2f x x x x ωωωω=-->，且()y f x =的图象的一个对称中心到最近的对称轴的距离为π4，（1）求ω的值. （2）求()f x 在区间3ππ,2⎡⎤⎢⎥⎣⎦上的最大值和最小值. 【测量目标】两角和与差的三角函数公式、二倍角公式、三角函数的图象与性质【考查方式】利用倍角公式化简函数式,数形结合求未知数ω再求函数在一段区间上的最值.【试题分析】（1）先利用倍角公式，两角和与差的三角公式把()f x 的解析式进行化简整理，再利用对称中心到最近的对称轴的距离为π4求出ω，（2）先根据x 的取值范围求出π23x -的取值范围，然后利用三角函数的图象，并结合其单调性求出()f x 的最值. 23()3sin sin cos 231cos 213sin 2222f x x x x x x ωωωωω=---=-- （1）31πcos 2sin 2sin 2223x x x ωωω⎛⎫=-=-- ⎪⎝⎭(步骤1) 因为图象的一个对称中心到最近的对称轴的距离为π4，又2ππ0,424ωω>∴=⨯ 因此1ω=(步骤2)（2）由（1）知π()sin 2.3f x x ⎛⎫=-- ⎪⎝⎭当3π5ππ8ππ,2.2333xx -剟剟 3πsin 2 1.23x ⎛⎫∴-- ⎪⎝⎭剟(步骤3) 因此31()2f x -剟故()f x 在区间3ππ,2⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为3,12-(步骤4) 19．(本小题满分12分)如图，四棱锥P ABCD -中，,,AB AC AB PA ⊥⊥,2,,,,,AB CD AB CD E F G M N = 分别为,,,,PB AB BC PD PC 的中点(Ⅰ)求证：CEPAD 平面；(Ⅱ)求证：EFG EMN ⊥平面平面【测量目标】线面平行的判定定理，线面垂直，面面垂直的判定定理，平行线的传递性.【考查方式】根据所给出的直线间的位置关系,用线线平行推导线面平行，根据线面垂直，去证明面面垂直.【试题分析】要证明线面平行，可考虑证明线线平行，也可先证明面面平行，进而转化为证线面平行，利用三角形的中位线或平行四边形的性质证明线线平行是证明平行问题首先要考虑的;要证明EFG EMN ⊥平面平面，可先考虑证明平面EMN 中的MN 垂直于平面EFG ,即转化为证明线面垂直，而要证明MN EFG ⊥平面，需要证明MN 垂直于平面EFG 中的两条相交直线(1):如图，取,PA H EH DH 的中点，连接E 为PB 的中点1,.2EH AB EH AB ∴= (步骤1)1,2AB CD CD AB =,.EH CD CD EH ∴= (步骤2)所以四边形DCEH 是平行四边形 (步骤3).CE DH ∴ (步骤4),DH PAD CE PAD ⊂又平面平面Ü CE PAD ∴平面 (步骤5)(2)因为,E F 分别为,PB AB 的中点，所以.,.EF PA AB PA AB EF ⊥∴⊥又 (步骤6)同理可证AB FG ⊥(步骤7),,EF FG F EF EFG FG =⊂⊂ 又平面平面EFGAB ⊥因此平面EFG (步骤8)又,M N 分别为,PD PC 的中点MN DC ∴ (步骤9) 又,,AB DC MN AB MN ∴∴⊥ 平面EFG (步骤10)MN ⊂又平面,EMN 所以平面EFG ⊥平面EMN (步骤11)20．(本小题满分12分)设等差数列{}n a 的前n 项和为n S ，且4224,21n n S S a a ==+. (Ⅰ)求数列{}n a 的通项公式 (Ⅱ)设数列{}n b 满足*12121...1,2n n n b b b n a a a +++=-∈N ，求{}n b 的前n 项和n T . 【测量目标】等差数列通项公式及前n 项和公式，错位相减法求和.【考查方式】已知{}n a 为等差数列，给定{}2n n S a 与进行逆推{}n a ，再由题给出的{}{}n n a b 与的关系式错位相减求出结果.【试题分析】（1）由于已知{}n a 是等差数列，因此可以考虑用基本量1,a d 表示已知等式，进而求出{}n a 的通项公式.（2）先求出nnb a ，进而求出{}n b 的通项公式，再用错位相减法求{}n b 的前n 项和.解：（1）设等差数列{}n a 的首项为1a ，公差为d . 由422421,n n S S a a ==+，11114684,(21)22(1)1a d a d a n d a n d +=+⎧⎨+-=+-+⎩ 解得112a d =⎧⎨=⎩(步骤1) 因此，*21,n a n n =-∈N (步骤2)*121211111,,211,;21112,11222n n n n n n n n b b b n a a a b n a b n a -++⋅⋅⋅+=-∈==⎛⎫=---= ⎪⎝⎭N (2)由已知当当…*1,.2n n n b n a ∴=∈N (步骤3) 由*21,,n a n n =-∈N （1）*21,2n nn b n -∴=∈N (步骤4) 2313521,2222n n n T -∴=+++⋅⋅⋅+23113232122222n n n n n T --=++⋅⋅⋅++(步骤5) 两式相减，得231111122221()2222223121,222n n n n n n T n +-+-=+++⋅⋅⋅+--=--2332n nn T +∴=-(步骤6)21．(本小题满分12分)已知函数2()ln (,)f x ax bx x a b =+-∈R , (Ⅰ)设0a …，求()f x 的单调区间(Ⅱ) 设0a >，且对于任意0,()(1)x f x f >….试比较ln a 与2b -的大小【测量目标】利用导数求函数的单调区间，利用导数解决不等式问题. 【考查方式】用导数求含参数函数的单调区间，利用导数证明不等式.【试题分析】（1）求()f x 的单调区间，需要对()f x 求导.当()0,()f x f x '>是增函数，()0,()f x f x '<是减函数，但是需要对参数,a b 进行讨论（2）()f x 的最小值为(1)f ，当()f x 有唯一极小值点时，极小值就是最小值，然后构造函数求解.解：由2()ln ,(0,),f x ax bx x x =+-∈+∞221()ax bx f x x +-'=(步骤1)11.0,().bx a f x x-'==a ．若0b …，当0x >，()0f x '<恒成立所以函数()f x 的单调递减区间是()0,+∞.(步骤2)1b.0,0,()0b x f x b'><<<若当函数()f x 单调递减1,(),x f x b'>函数()f x 单调递增(步骤3)所以函数()f x 的单调递减区间1(0,)b ，单调递增区间是1(,)b+∞（步骤4）2.当20,()0,210.a f x ax bx '>=+-=令得(步骤5) 由280b a +>得221288,44b b a b b ax x a a--+-++==(步骤6) 显然120,0.x x <>当20,()0,x x f x '<<<函数()f x 单调递减2,()0,x x f x '>>当函数()f x 单调递增(步骤7)所以函数()f x 的单调递减区间是280,4b b a a ⎛⎫-++ ⎪ ⎪⎝⎭，单调递增区间是28,4b b a a ⎛⎫-+++∞⎪ ⎪⎝⎭(步骤8) 综上所述，当0,0a b =…，函数()f x 的单调递减区间是()0,+∞当0,0a b =>，函数()f x 的单调递减区域是10,b ⎛⎫ ⎪⎝⎭，单调递增区域是1,b ⎛⎫+∞ ⎪⎝⎭当0a >，函数()f x 的单调递减区间是280,4b b a a ⎛⎫-++ ⎪ ⎪⎝⎭，单调递增区间是28,4b b a a ⎛⎫-+++∞⎪ ⎪⎝⎭.(步骤9) （2）由题意知函数()1f x x =在处取最小值，由284b b a a-++（1）知是()f x 的唯一极小值点(步骤10)故28=14b b a a-++.整理，21,a b +=即12.b a =-(步骤11)令14()24ln ,().xg x x x g x x-'=-+=则(步骤12) 令1()0,4g x x '==得(步骤13) 10,()0,()4x g x g x '<<>单调递增1,4x >()0g x '<,()g x 单调递减.(步骤13)因此11()()1ln 1ln 4044()0,24ln 2ln 0,g x g g a a a b a =+=-<<-+=+<即… 即ln 2a b <-(步骤14)22．(本小题满分14分)在平面直角坐标系xOy 中，已知椭圆C 的中心在原点O ，焦点在x 轴上，短轴长为2，离心率为22(I)求椭圆C 的方程(Ⅱ),A B 为椭圆C 上满足AOB △的面积为64的任意两点，E 为线段AB 的中点，射线OE 交椭圆C 与点P ，设OP tOE =，求实数t 的值.【测量目标】椭圆的标准方程及简单几何性质，直线与椭圆的位置关系，点到直线的距离公式，向量的线性运算，平面向量在平面几何中的应用.【考查方式】给出椭圆的位置情况，短轴及离心率，用待定系数法去求椭圆方程，（Ⅱ）中给出AOB △的面积及部分支线的几何位置，求满足向量方程的未知数. 【试题解析】（1）可用待定系数法求出,a b ，进而求出椭圆C 的方程.（2）设出直线AB 的方程，带入椭圆方程，设而不求，利用根与系数的关系转化，但要注意AB 与x 轴垂直时的情况.解：（1）设椭圆C 的方程为22221(0),x y a b a b+=>>由题意 2222,222a b c cab ⎧=+⎪⎪=⎨⎪=⎪⎩解得21a b ⎧=⎪⎨=⎪⎩ 因此椭圆C 的方程为 22 1.2x y +=(步骤1) （2）（i ）当,A B 两点关于x 轴对称，设直线AB 的方程为x m =. 由题意得20m <<-或02m <<(步骤2)将x m =带入椭圆方程22221,22x m y y -+==(步骤3) 226.24AOBm S m -∴== △解得223122m m ==或 ○1 (步骤4) 11()(2,0)(,0),22OP tOE t OA OB t m mt ==+==又P 为椭圆C 上一点212mt ∴=（） ○2 (步骤5)由○1○2，得22443t t ==或又230,23t t t >∴==或 (步骤6) （ii ）当,A B 两点关于x 轴不对称时，设直线AB 的方程为y kx h =+将其代入椭圆的方程2212x y +=，得 ()222124220.k xkhx h +++-=(步骤7)设1122(,),(,).A x y B x y 由判定式0∆>可得2212k h +>(步骤8)21212221212222121242,,12122()2,121()4kh h x x x x k khy y k x x h k AB k x x x x +=-=+++=++=+∴=+⨯+-222212221.12k h k k+-=⨯+⨯+(步骤9) 因为点O 到直线AB 的距离21h d k=+，2221122212AOBk h S AB d h k +-∴==⨯⨯+△(步骤10) 2221+262124k h h k -∴⨯⨯=+ ○3 (步骤11) 212,n k =+令代入○3整理得224316160n h n h -+= 解得22443n h n h ==或，即222241241+23k h k h +==或 ○4 (步骤12) 121211()(,)22OP tOE t OA OB t x x y y ==+=++222,1212khtht k k ⎛⎫=- ⎪++⎝⎭(步骤13) 又P 为椭圆C 上一点，2222212()121212kh h t k k ⎡⎤⎛⎫∴-+=⎢⎥ ⎪++⎝⎭⎢⎥⎣⎦即222112h t k=+ ○5(步骤13) 将○4代入○5，得22443t t ==或 (步骤14) 230,2.3t t t >==又故或(步骤15) 经检验,符合题意23i ii 23t t ==综合（）（），得或(步骤16)。

2013年高考英语试题浙江卷详细解析

2011年普通高等学校招生全国统一考试(浙江卷)解析英语第一部分英语知识运用（共两节，满分80分）从A B C D 四个选项中，选出可以填入空白处地最佳选项，并在答题卡上将该项涂黑。

1. -I’m sorry I didn’t make it to your party last night.-- ______, I know you’re busy these days.A. Of courseB. No kiddingC. That’s all nightD. Don’t mention it【答案】C【解析】情景交际今年首次出现在第一题，说明了高考重视应用的趋势。

完整的问句和答句的后半句都是提示信息：根据问句中的I’msorry…可以排除选项A、B；根据后半句―我知道你最近几天很忙‖可以排除选项D。

2. Experts think that ______recently discovered painting may be ______ Picsso.A. the ;不填B. a ;theC. a; 不填D. the; a【答案】D【解析】本题考点为冠词，每年必考一题，常为区分某名词是特指还是泛指。

根据句意―专家们认为这幅最近本发现的画作可能是一幅毕加索的作品。

‖可知前一空应该是表示特指的定冠词the；后一空用不定冠词a加上毕加索的名字（该单词学生在不认识的情况下，可以观察到其开头字母大写，应该是人名或地名类的专有名词，再由全句判断得出词义），表示其众多作品之一，泛指。

3. Bats are surprisingly long lived creatures some ______a life span of around 20 years.A. havingB. hadC. haveD. to have【答案】A【解析】本题的考点为独立主格结构，判断依据是逗号前后主语不同，前者是所有蝙蝠，而后者是某些蝙蝠（主语前后不一致又没有用连词引导的从句结构，这是少见的―独立主格‖标志）。