圆心角与圆周角能力提升训练(含答案)
初三数学上册圆心角与圆周角训练题

初三数学上册圆心角与圆周角训练题初三数学上册圆心角与圆周角的训练积累越多,学会越熟练。
下面是我们为大家带来的关于初三数学上册圆心角与圆周角的训练题,期望会给大家带来协助。
初三数学上册圆心角与圆周角训练题目一、选择题1.在同圆中,同弦所对的圆周角 A.相等 B.互补 C.相等或互补D.互余2.3-63所示,A,B,C,D在同一个圆上,四边形ABCD的两条对角线把四个内角分成的8个角中,相等的角共有 A.2对 B.3对 C.4对 D.5对3.3-64所示,⊙O的半径为5,弦AB,C是圆上一点,则ACB的度数是.4.四边形 ABCD内接于⊙O,若BOD=100,则DAB的度数为A.50B.80C.100D.1305.是中国共产主义年轻人团团旗上的案,点A、B、C、D、E五等分圆,则A+B+C+D+E的度数是A.180B.15 0C.135D.1206.下列命题中,正确的命题个数是①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④圆周角相等,则它们所对的弧也相等。
A、1个B、2个C、3个D、4个二、填空题7.3-65所示,在⊙O中,AOB=100,C为优弧ACB的中点,则CAB=8.3-66所示,AB为⊙O的直径,AB=6,CAD=30,则弦DC= .9.3-67所示,AB是⊙O的直径,BOC=120,CDAB,求ABD的度数.10.已知AB是⊙O的直径,AD ∥ OC弧AD的度数为80,则BOC=_________11.⊙O内接四边形ABCD中,AB=CD则中和1相等的角有______。
12.弦AB的长等于⊙O的半径,点C在AB上,则C的度数是________-.三、解答题13.3-68所示,在△ABC中,AB=AC,C=70,以AB为直径的半圆分别交AC,BC于D,E,O为圆心,求DOE的度数.14.已知⊙O的直径为10,点A,点B,点C在⊙O上,CAB的平分线交⊙O于点D.①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;②,若CAB=60,求BD的长.15.3-70所示,在⊙O中,AB是直径,弦AC=12 cm,BC=16 cm,ACB的平分线交⊙O于点D,求AD的长.16.3-71所示,AB是半圆O的直径,C是半圆上一点,D是AC的中点,DHAB,H是垂足,AC分别交BD,DH于E,F,试说明DF=EF.初三数学上册圆心角与圆周角训练题答案1.C2.C3.60[提示:3-72所示,作ODAB,垂足为D,则BDsinBODBOD=60,BOA=120,BCABOA=60.故填60.]4.剖析:由于BOD=100,所以C=50,所以A=130,由于圆内接四边形的对角互补。
圆的定义圆心角圆周角训练题(含答案)

圆的定义圆心角圆周角训练题一、单选题(共17题;共34分)1.(2020九上·江苏月考)下列说法错误的是()A. 长度相等的两条弧是等弧B. 直径是圆中最长的弦C. 面积相等的两个圆是等圆D. 半径相等的两个半圆是等弧2.(2019九上·台安期中)下列说法中,不正确的个数是()①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.A. 1个B. 2个C. 3个D. 4个3.(2019九上·沭阳月考)下列命题:①直径相等的两个圆是等圆;②等弧是长度相等的弧;③圆中最长的弦是通过圆心的弦;④一条弦把圆分为两条弧,这两条弧不可能是等弧.其中真命题是( )A. ①③B. ①③④C. ①②③D. ②④4.(2019九上·贾汪月考)下列说法中,错误的是()A. 半圆是弧B. 半径相等的圆是等圆C. 过圆心的线段是直径D. 直径是弦5.(2018九上·下城期末)下列命题中是真命题的为()A. 弦是直径B. 直径相等的两个圆是等圆C. 平面内的任意一点不在圆上就在圆内D. 一个圆有且只有一条直径6.(2020九上·浙江期中)如图,是的直径,,,则的度数是().A. 52°B. 57°C. 66°D. 78°7.(2019九上·柳江月考)如图,AB是⊙O的直径,,∠COD=34°,则∠AOE的度数是( )A. 51°B. 56°C. 68°D. 78°8.(2019九上·邯郸月考)如图,AB是O的直径, ,∠BOC=40°,则∠AOE的度数为()A. 30°B. 40°C. 50°D. 60°9.(2019九上·余杭期中)如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为()A. 45º-αB. αC. 45º+αD. 25º+α10.(2020九下·南召月考)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A. AB=ADB. BC=CDC.D. ∠BCA=∠DCA11.(2020九上·无锡月考)在半径为的圆中,长度等于的弦所对的弧的度数为()A. B. C. 或 D. 或12.(2020·西湖模拟)如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是()A. 36°B. 48°C. 72°D. 96°13.(2020·衢州模拟)如图,在⊙O中,=,∠A=40°,则∠B的度数是()A. 60°B. 40°C. 50°D. 70°14.(2020·乾县模拟)如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB 的度数是()A. 70°B. 80°C. 82°D. 85°15.(2019九上·龙湖期末)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )A. 40°B. 45°C. 50°D. 60°16.(2019九上·道外期末)如图,,是的直径,,若,则的度数是()A. 32°B. 60°C. 68°D. 64°17.(2019九上·光明期中)如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为()A. B. C. D.参考答案一、单选题1.【答案】A【解析】【解答】解:A、等弧就是指能完全重合的两段弧,所以长度相等的弧的度数不一定是等弧,故错误;B、直径是圆中最长的弦,正确;C、面积相等的两个圆是等圆,正确;D、半径相等的两个半圆是等弧,正确.故答案为:A.2.【答案】C【解析】【解答】在同圆或等圆中,优弧一定比劣弧长,所以①错误;面积相等的两个圆半径相等,则它们是等圆,所以②正确;能完全重合的弧是等弧,所以③错误;经过圆内一个定点可以作无数条弦,所以④正确;经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.故答案为:C.3.【答案】A【解析】【解答】解:①直径相等的两个圆能重合,所以是等圆,①是真命题;②长度相等的弧不一定能重合,所以不一定是等弧,②是假命题;③圆中最长的弦是直径,通过圆心的弦是直径,③是真命题;④一条弦把圆分成两条弧,这两条弧可以是半圆,所以可能是等弧,④是假命题.故答案为:A.4.【答案】C【解析】【解答】解:A、半圆是弧,所以A选项的说法正确;B、半径相等的圆是等圆,所以B选项的说法正确;C、过圆心的弦为直径,所以C选项的说法错误;D、直径是弦,所以D选项的说法正确.故答案为:C.5.【答案】B【解析】【解答】解:弦不一定是直径,A是假命题;直径相等的两个圆是等圆,B是真命题;平面内的任意一点在圆上、圆内或圆外,C是假命题;一个圆有无数条直径,D是假命题;故选:B.6.【答案】C【解析】【解答】解:∵AB是⊙O的直径,,∠COD=38°,∴∠BOC=∠COD=∠DOE=38°.∴∠BOE=114°,∴∠AOE=180°-114°=66°.故答案为:C.7.【答案】D【解析】【解答】解:∵,∠COD=34°,∴∠BOC=∠COD=∠DOE=34°,∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .故答案为:D.8.【答案】D【解析】【解答】解:∵,∠BOC=40°∴∠BOC=∠COD=∠EOD=40°∴∠BOE=120°∴∠AOE=180°-∠BOE=60°.9.【答案】A【解析】【解答】解:如图,连接CD,∵的度数为,∴∠DCE= ,∵BC=CD,∴∠CBD=∠BDC= ,∵∠C=90°,∴∠CBD+∠A=90°,∴,∴;故选择:A.10.【答案】B【解析】【解答】解:A.∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;B.∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;C.∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;D.∠BCA与∠DCA的大小关系不确定,故本选项错误。
圆周角 同步提升训练(附答案) 2021-2022学年苏科版九年级数学上册

2021-2022学年苏科版九年级数学上册《2.4圆周角》同步能力提升训练(附答案)1.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为()A.45°B.50°C.60°D.75°2.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为()A.80°B.100°C.110°D.130°3.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是()A.25°B.27.5°C.30°D.35°4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为()A.50°B.60°C.70°D.80°5.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为()A.15°B.28°C.29°D.34°7.如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为()A.5cm B.5cm C.5cm D.6cm8.如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是、上一点(不与端点重合),如果∠MNP=∠MNQ,下面结论:①∠1=∠2;②∠P+∠Q =180°;③∠Q=∠PMN;④PM=QM;⑤MN2=PN•QN.其中正确的是()A.①②③B.①③⑤C.④⑤D.①②⑤9.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为.10.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=°.11.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=.12.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为.13.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC 交AC于点D,连接MA,MC.(1)求⊙O半径的长;(2)求证:AB+BC=BM.14.如图,在△ABC中,CA=CB,E是边BC上一点,以AE为直径的⊙O经过点C,并交AB于点D,连接ED.(1)判断△BDE的形状并证明.(2)连接CO并延长交AB于点F,若BE=CE=3,求AF的长.15.如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.(1)求⊙O的半径;(2)求证:CE=BE.16.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=,AE=2,求⊙O的半径.17.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG与DC的延长线交于点F.(1)如CD=8,BE=2,求⊙O的半径长;(2)求证:∠FGC=∠AGD.18.已知△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于E,(1)如图①,若AB=6,CD=2,求CE的长;(2)如图②,当∠A为锐角时,使判断∠BAC与∠CBE的关系,并证明你的结论;(3)若②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与圆O相交于E.请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明,若不同,请说明理由.19.已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.(1)如图①,若BC为⊙O的直径,AB=6,求AC、BD、CD的长;(2)如图②,若∠CAB=60°,求BD的长.20.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.(1)求证:AC∥OD;(2)若OE=4,求AC的长.参考答案1.解:设∠ADC的度数=α,∠ABC的度数=β;∵四边形ABCO是平行四边形,∴∠ABC=∠AOC;∵∠ADC=β,∠ADC=α;而α+β=180°,∴,解得:β=120°,α=60°,∠ADC=60°,故选:C.2.解:连接OC,如图所示,∵OB=OC,∴∠OCB=∠OBC=40°,∴∠BOC=100°,∵∠1+∠BOC=360°,∴∠1=260°,∵∠A=∠1,∴∠A=130°.故选:D.3.解:∵∠A=60°,∠ADC=85°,∴∠B=85°﹣60°=25°,∠CDO=95°,∴∠AOC=2∠B=50°,∴∠C=180°﹣95°﹣50°=35°故选:D.4.解:∵∠BOD=100°,∴∠A=∠BOD=50°,∵∠B=60°,∴∠C=180°﹣∠A﹣∠B=70°.故选:C.5.解:连接BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选:C.6.解:根据圆周角定理可知:圆周角的度数等于它所对的弧的度数的一半,根据量角器的读数方法可得:(86°﹣30°)÷2=28°.故选:B.7.解:连接EC,由圆周角定理得,∠E=∠B,∠ACE=90°,∵∠B=∠EAC,∴∠E=∠EAC,∴CE=CA,∴AC=AE=5(cm),故选:B.8.解:延长MN交圆于点W,延长QN交圆于点E,延长PN交圆于点F,连接PE,QF ∵∠PNM=∠QNM,MN⊥AB,∴∠1=∠2(故①正确),∵∠2与∠ANE是对顶角,∴∠1=∠ANE,∵AB是直径,∴可得PN=EN,同理NQ=NF,∵点N是MW的中点,MN•NW=MN2=PN•NF=EN•NQ=PN•QN(故⑤正确),∴MN:NQ=PN:MN,∵∠PNM=∠QNM,∴△NPM∽△NMQ,∴∠Q=∠PMN(故③正确).故选:B.9.解:当GH为⊙O的直径时,GE+FH有最大值.当GH为直径时,E点与O点重合,∴AC也是直径,AC=14.∵∠ABC是直径上的圆周角,∴∠ABC=90°,∵∠C=30°,∴AB=AC=7.∵点E、F分别为AC、BC的中点,∴EF=AB=3.5,∴GE+FH=GH﹣EF=14﹣3.5=10.5.故答案为:10.5.10.解:如图,连接CE,∵五边形ABCDE是圆内接五边形,∴四边形ABCE是圆内接四边形,∴∠B+∠AEC=180°,∵∠CED=∠CAD=35°,∴∠B+∠E=180°+35°=215°.故答案为:215.11.解:∵∠A=55°,∠E=30°,∴∠EBF=∠A+∠E=85°,∵∠A+∠BCD=180°,∴∠BCD=180°﹣55°=125°,∵∠BCD=∠F+∠CBF,∴∠F=125°﹣85°=40°.故答案为40°.12.解:∵∠CBE=50°,∴∠ABC=180°﹣∠CBE=180°﹣50°=130°,∵四边形ABCD为⊙O的内接四边形,∴∠D=180°﹣∠ABC=180°﹣130°=50°,∵DA=DC,∴∠DAC==65°,故答案为:65°13.解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,∵∠ABC=120°,∴∠AMC=180°﹣∠ABC=60°,∴∠AOC=2∠AMC=120°,∴∠AOH=∠AOC=60°,∵AH=AC=,∴OA=2,故⊙O的半径为2.(2)证明:在BM上截取BE=BC,连接CE,如图2,∵∠ABC=120°,BM平分∠ABC,∴∠ABM=∠CBM=60°,∵BE=BC,∴△EBC是等边三角形,∴CE=CB=BE,∠BCE=60°,∴∠BCD+∠DCE=60°,∵∠ACM=60°,∴∠ECM+∠DCE=60°,∴∠ECM=∠BCD,∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,∴△ACM是等边三角形,∴AC=CM,∴△ACB≌△MCE,∴AB=ME,∵ME+EB=BM,∴AB+BC=BM.14.(1)证明:△BDE是等腰直角三角形.∵AE是⊙O的直径∴∠ACB=∠ADE=90°,∴∠BDE=180°﹣90°=90°.∵CA=CB,∴∠B=45°,∴△BDE是等腰直角三角形.(2)过点F作FG⊥AC于点G,则△AFG是等腰直角三角形,且AG=FG.∵OA=OC,∴∠EAC=∠FCG.∵BE=CE=3,∴AC=BC=2CE=6,∴tan∠FCG=tan∠EAC=.∴CG=2FG=2AG.∴FG=AG=2,∴AF=2.15.(1)解:∵OC为⊙O的半径,OC⊥BD,∴;∵DB=8,∴MB=4设⊙O的半径为r,∵CM=2,∴OM=r﹣2,在Rt△OMB中,根据勾股定理得(r﹣2)2+42=r2,解得r=5;(2)证明:方法一:连接AC、CB,∵AB是直径,∴∠ACB=90°.∴∠ACF+∠FCB=90°.又∵CF⊥AB,∴∠CAF+∠ACF=90°∴∠FCB=∠CAF(3分)∵OC为⊙O的半径,OC⊥BD,∴C是的中点,∴∠CAF=∠CBD.∴∠FCB=∠DBC.∴CE=BE;方法二:如图,连接BC,补全⊙O,延长CF交⊙O于点G;又∵CF⊥AB,AB为直径,∴=.∴OC为⊙O的半径,OC⊥BD.∴C是的中点,∴=.∴=.∴∠FCB=∠DBC.∴CE=BE.16.(1)证明:如图.∵OC=OB,∴∠BCO=∠B.∵∠B=∠D,∴∠BCO=∠D;(2)∵AB是⊙O的直径,且CD⊥AB于点E,∴CE=CD=×4=2,在Rt△OCE中,OC2=CE2+OE2,设⊙O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,∴r2=(2)2+(r﹣2)2,解得:r=3,∴⊙O的半径为3.17.(1)解:连接OC.设⊙O的半径为R.∵CD⊥AB,∴DE=EC=4,在Rt△OEC中,∵OC2=OE2+EC2,∴R2=(R﹣2)2+42,解得R=5.(2)证明:连接AD,∵弦CD⊥AB∴=,∴∠ADC=∠AGD,∵四边形ADCG是圆内接四边形,∴∠ADC=∠FGC,∴∠FGC=∠AGD.18.解:(1)连接AD.∵AB为直径,∴AD⊥BC.又∵AB=AC,∴BD=CD.又CD=2,∴BD=2.∴CE=.(2)∠BAC与∠CBE的关系是:∠BAC=2∠CBE.理由如下:由(1),得AD⊥BC.又AB=AC,∴∠1=∠2.又∠2=∠CBE,∴∠BAC=2∠CBE.(3)相同.理由如下:连接AD.∵AB为直径,∴AD⊥BC,又AB=AC,∴∠1=∠2,∵∠CAD是圆内接四边形AEBD的外角,∴∠2=∠CBE,∴∠CAB=2∠CBE.19.解:(1)如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.∵在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8.∵AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5;(2)如图②,连接OB,OD,∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5,∴BD=5.20.(1)证明:∵AD平分∠CAB,∴∠OAC=2∠OAD.∵∠BOD=2∠BAD,∴∠BOD=∠OAC,∴AC∥OD.(2)解:作OF⊥AC于点F,如图所示:则AF=AC,∵AC∥OD,∴∠DOE=∠OAF.在△DOE和△OAF中,,∴△DOE≌△OAF(AAS),∴OE=AF=AC,∴AC=2OE=8.。
湘教版九年级下册2.2.1圆心角练习(含答案)

湘教版九年级下册 2.2.1圆心角练习(含答案)2.2圆心角、圆周角2.2.1圆心角基础题知识点1认识圆心角1.下边四个图中的角,是圆心角的是()A. B.C. D.︵2.如图,已知AB为⊙O的直径,点D为半圆周上的一点,且AD所对圆心角的度数是则圆心角∠BOD的度数为____________.知识点2圆心角、弧、弦之间的关系3.以下说法中,正确的选项是() A.等弦所对的弧相等B.等弧所对的弦相等C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等︵BD所对圆心角度数的两倍,︵︵4.如图,在⊙O中,AB=AC,∠AOB=122°,则∠AOC的度数为()A.122°B.120°C.61°D.58°5.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为() A.AB>CD B.AB=CDC.AB<CD D.不可以确立︵︵6.如图,已知在⊙O中,BC是直径,AB=DC,∠AOD=80°,则∠ABC等于()A.40°B.65°C.100°D.105°1/6︵湘教版九年级下册 2.2.1圆心角练习(含答案)︵︵︵︵︵︵︵7.以下图,在⊙O中,AC,BC是弦,依据条件填空:︵若AC=BC,则________________________________________________________________________;︵若AC=BC,则________________________________________________________________________;若∠AOC=∠BOC,则________________________________________________________________________.︵8.如图,在⊙O中,点C是AB的中点,∠A=50°,则∠BOC等于____________度.︵︵9.以下图,在⊙O中,AB=AC,∠B=70°,则∠A=____________.︵︵︵10.(贵港中考改编)以下图,AB是⊙O的直径,BC=CD=DE,∠COD=34°,求∠AEO的度数.2/6湘教版九年级下册 2.2.1圆心角练习(含答案)中档题11.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA.则∠BCD等于()A.100°B.110°C.120°D.135°12.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则以下说法中正确的个数为()︵︵①∠DOE=∠AOB;②AB=DE;③OF=OC;④AC=EF.A.1 B.2 C.3 D.4︵︵︵︵13.已知AB,CD是同圆的两段弧,且AB=2CD,则弦AB与2CD之间的关系为()A.AB=2CD C.AB>2CD B.AB<2CDD.不可以确立︵14.如图,已知D,E分别为半径OA,OB的中点,C为AB的中点.试问CD与CE能否相等?说明你的原因.15.以下图,以?ABCD的极点A为圆心,AB为半径作圆,交AD,BC于E,F,延伸BA交⊙A于G,求证:3/6湘教版九年级下册 2.2.1圆心角练习(含答案)︵︵GE=EF.︵︵16.如图,AB是⊙O的直径,AC=CD,∠COD=60°.△AOC是等边三角形吗?请说明原因;(2)求证:OC∥BD.综合题4/6湘教版九年级下册 2.2.1圆心角练习(含答案)︵17.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AON=60°,点B为AN的中点,P是直径MN上的一个动点,求PA+PB的最小值.5/6湘教版九年级下册2.2.1圆心角 练习(含答案)参照答案1.D 2.60° 3.B 4.A 5.B 6.B ︵ ︵7.(1)AC =BC ,∠AOC =∠BOC (2)AC =BC ,∠AOC =∠BOC︵ ︵(3)AC =BC ,AC =BC 8.409.40°︵ ︵ ︵ 10.∵BC =CD =DE ,∠COD =34°,∴∠BOE =102°. OA =OE ,∴∠AEO =∠EAO =12∠BOE =51°. 11.C 12.D 13.B 14.相等.原因以下:连结 OC. ∵D ,E 分别为⊙O 半径OA ,OB 的中点, ∴OD =1AO ,OE = 1 B O. 2 2︵OA =OB ,∴OD =OE.∵C 是AB 的中点, ︵ ︵AC =BC.∴∠AOC =∠BOC.∴△DCO ≌△ECO(SAS).∴CD =CE.15.证明:连结 AF.∵四边形ABCD 为平行四边形 ,AD ∥BC.∴∠GAE =∠B ,∠EAF =∠AFB. 又∵AB =AF ,∴∠B =∠AFB. ︵ ︵∴∠GAE =∠EAF.∴GE =EF.︵ ︵16.(1)△AOC 是等边三角形.∵AC =CD ,∴∠AOC =∠DOC =60°.又∵OA =OC ,∴△AOC 是等边三角形.︵ ︵1∠AOD.(2)证明:∵AC =CD ,∴∠AOC =∠COD =2OD =OB.∴∠B =∠ODB =1∠AOD.2 ∴∠AOC =∠B.∴OC ∥BD.17.作点A 对于MN 的对称点 A ′,连结A ′B,交MN 于点P ,连结OA ′,OB ,PA ,AA ′.∵点A 与A ′对于MN 对称,点A 是半圆上的一个三平分点 ,∴∠A ′ON =∠AON =60°,PA =PA ′. ︵∵点B 是AN 的中点,∴∠BON =30°. ∴∠A ′OB =∠A ′ON +∠BON =90°. 又∵OA =OA ′=1,∴A ′B = 2.∴PA +PB =PA ′+PB =A ′B= 2.6/6。
北师大九年级下《3.4圆周角与圆心角的关系》强化训练含答案

《3.4圆心角与圆周角的关系》强化训练一、选择题1.如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是()第1小题图第2小题图第3小题图第4小题图A.150°B.140°C.130°D.120°2.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是()A.75°B.60°C.45°D.30°3.如图,BD是⊙O的直径,点A、C在⊙O上,AB BC,∠AOB=60°,则∠BDC的度数=是()A.60°B.45°C.35°D.30°4.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为()A.140°B.70°C.60°D.40°5.如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=()第5小题图第6小题图第7小题图第8小题图A .64°B .58°C .72°D .55° 6.如图,点A ,B ,C 在⊙O 上,∠A=36°,∠C=28°,则∠B=( ) A .100° B .72° C .64°D .36°7.如图,线段AB 是⊙O 的直径,弦CD ⊥AB ,∠CAB=40°,则∠ABD 与∠AOD 分别等于( ) A .40°,80°B .50°,100°C .50°,80°D .40°,100°8.如图,已知AB 是⊙O 的直径,∠D=40°,则∠CAB 的度数为( ) A .20° B .40°C .50°D .70°9.如图,把直角三角板的直角顶点O 放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M 、N ,量得OM=8cm ,ON=6cm ,则该圆玻璃镜的半径是( )第9小题图 第10小题图 第11小题图 第12小题图A B .5cm C .6cm D .10cm10.如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 为( )A .13B .CD 11.如图,点A 、B 、C 是圆O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于( ) A .12.5°B .15°C .20°D .22.5°12.如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则()A.DE=EB B C D.DE=OB二、填空题13.如图,AB为⊙O的直径,C,D为⊙O上的两点,若AB=6,BC=3,则∠BDC=度.第13小题图第14小题图第15小题图第16小题图14.如图,在⊙O中,AB是弦,C是 AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC 的大小为度.15.如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=度.16.如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC=.17.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=°.第17小题图第18小题图第19小题图第20小题图18.如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=.19.如图,A,B,C,D是⊙O上的四个点,∠C=110°,则∠BOD=140度.20.如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O 的直径,AB=BC=CD.连接PA、PB、PC,若PA=a,则点A到PB和PC的距离之和AE+AF=.三、解答题21.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.22.如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若EF=2CD的长.23.已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形(1)求证:△DFB是等腰三角形;(2)若,求证:CF⊥AB.24.在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP ⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.25.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且.DE BE(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.26.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;(2)若AB=4,CD的长.参考答案1.A2.D3.D4.B5.B6.C7.B8.C9.B 10.C 11.B 12.D13.30 14.30 15.35 16.35°17.62°18.65 19.140 20.21.(1)∵BC=DC,∴∠CBD=∠CDB=39°,∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°;(2)∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD,∵∠BAE=∠BDC=∠CBD,∴∠1=∠2.22.(1)证明:连接DE,∵BD是⊙O的直径,∴∠DEB=90°,∵E是AB的中点,∴DA=DB,∴∠1=∠B,∵∠B=∠F,∴∠1=∠F;(2)∵∠1=∠F,∴AE=EF=2,∴AB=2AE=4,在Rt△ABC中,AC=AB•sinB=4,∴BC==8,设CD=x,则AD=BD=8﹣x,∵AC2+CD2=AD2,即42+x2=(8﹣x)2,∴x=3,即CD=3.23.(1)∵AB是⊙O直径,∴∠ACB=90°,∵△AEF为等边三角形,∴∠CAB=∠EFA=60°,∴∠B=30°,∵∠EFA=∠B+∠FDB,∴∠B=∠FDB=30°,∴△DFB是等腰三角形;(2)过点A作AM⊥DF于点M,设AF=2a,∵△AEF是等边三角形,∴FM=EM=a,,在Rt△DAM中,,,∴DM=5a,∴DF=BF=6a,∴AB=AF+BF=8a,在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a,∵AE=EF=AF=2a,∴CE=AC﹣AE=2a,∵∠AEF=∠ECF +∠EFC=60°,∴∠CFE=30°, ∴∠AFC=∠AFE +∠EFC=60°+30°=90°, ∴CF ⊥AB .24. (1)连结OQ ,如图1,∵PQ ∥AB ,OP ⊥PQ , ∴OP ⊥AB ,在Rt △OBP 中,∵tan ∠B=OPOB,∴OP=3tan30°在Rt △OPQ 中,∵OQ=3,∴= (2)连结OQ ,如图2,在Rt △OPQ 中,=, 当OP 的长最小时,PQ 的长最大, 此时OP ⊥BC ,则OP=12OB=32,∴PQ 2=.25. (1)△ABC 为等腰三角形.理由如下:连结AE ,如图,∵ DEBE =, ∴∠DAE=∠BAE ,即AE 平分∠BAC , ∵AB 为直径,∴AE⊥BC,∴△ABC为等腰三角形;(2)∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=12BC=12×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE=,∵AB为直径,∴∠ADB=90°,∴12AE•BC=12BD•AC,∴BD=81248 105⨯=,在Rt△ABD中,∵AB=10,BD=485,∴145 =,∴sin∠ABD=14751025 ADAB==.26.(1)证明:∵ED=EC,∴∠EDC=∠C,∵∠EDC=∠B,∴∠B=∠C,∴AB=AC;(2)连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=12BC=,∵△CDE∽△CBA,∴CD CE CB AC=,∴CE•CB=CD•CA,AC=AB=4,,∴CD=32第11 页/ 共11 页。
圆周角—巩固练习(提高)含答案

C圆周角—巩固练习(提高)【巩固练习】一、选择题1.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()A、2个B、3个C、4个D、5个2.已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。
给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC。
其中正确的有()个A.5B.4C.3D.2第1题图第2题图第3题图3.如图,在⊙O中,弦AB的长是半径OA的3倍,为AB中点,AB、OC交于点P,则四边形OACB是() A.平行四边形B.矩形C.菱形D.正方形4.如图,设⊙O的半径为r,弦的长为a,弦与圆心的距离为d,弦的中点到所对劣弧中点的距离为h,下面说法或等式:①r=d+h②4r2=4d2+a2正确结论的序号是()③已知r、a、d、h中任意两个,可求其它两个。
其中A.仅①B.②③C.①②③D.①③5.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为()A.68°B.88°C.90°D.112°6.(2016黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为()A.cm B.3cm C.3cm D.6cm二、填空题7.如图所示,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD、CB的延长线相交于P,则∠P=________°.(第7题)(第9题)8.(2016青岛)如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=°.9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,BE=1,C D42,则∠AED=°.10.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.11.如图所示,在半径为3的⊙O中,点B是劣弧AC的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD=________.ABM O P N(第10题图)(第11题图)(第12题图)︵12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,点B为AN中点,P直径MN上的一个动点,则PA+PB的最小值是.13.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=.三、解答题14.如图,在⊙O中,AB=BC=CD,OB,OC分别交AC,BD于E、F,求证O E=OF15.如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.16.如图所示,AB是⊙O的直径,C为AE的中点,CD⊥AB于D,交AE于F,连接AC,求证:AF=CF.17.如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.【答案与解析】一、选择题1.【答案】D.【解析】与∠BCE相等的角有5个,∠DAE=∠AED=∠ABD,∠BAD=∠BAE+∠DAE=∠BAE+∠ABD=∠BCE,同理∠ADO=∠ODE=∠OED=∠BCE,且∠ACD=∠BCE.2.【答案】C.【解析】①②④正确.3.【答案】C.【解析】由弦AB的长是半径OA的3倍,C为AB中点,得∠AOC=60°,△AOC为等边三角形,所以AO=AC,进而得到OA=OB=BC=AC,故则四边形OACB是菱形.4.【答案】C.【解析】根据垂径定理及勾股定理可得①②③都是正确的.5.【答案】B.【解析】如图,∵AB=AC=AD,∴点B、C、D在以点A为圆心,以AB的长为半径的圆上;∵∠CBD=2∠BDC,∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,而∠BAC=44°,∴∠CAD=88°,故选B.6.【答案】A.【解析】连接CB.∵AB是⊙O的直径,弦CD⊥AB于点E,∴圆心O到弦CD的距离为OE;∵∠COB=2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB=30°,=∴∠COB=60°;在 △Rt OCE 中,OC=5cm ,∴OE= cm . 故选 A .二、填空题 7.【答案】40°;【解析】∵ ∠AOC =130°,∴ ∠ADC =∠ABC =65°, 又 AB ⊥CD ,∴ ∠PCD =90°-65°=25°,∴ ∠P =∠ADC -∠PCD =65°-25°=40°.8.【答案】62.【解析】∵AB 是⊙O 的直径,∴∠ACB=90°,∵∠BCD=28°,∴∠ACD=62°,由圆周角定理得,∠ABD=∠ACD=62°,故答案为:62.9.【答案】30°; 10.【答案】3;11.【答案】43;【解析】连结 OA 、OB ,交 AC 于 E ,因为点 B 是劣弧 AC 的中点,所以OB ⊥AC ,设 BE=x,则 OE=3-x ,由 AB 2-BE 2=OA 2-OE 2 得22-x 2=32-(3-x )2,解得 x = 2 4, CD = 2BE = .3 3AB CD 2 CD 4或连接 OA 、△O B , OAB ∽△BCD , , = , CD = . OA BC 3 2 312.【答案】;【解析】作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.(如图)此时PA+PB最小,且等于AC的长.连接OA,OC,根据题意得弧AN的度数是60°,则弧BN的度数是30°,根据垂径定理得弧CN的度数是30°,则∠AOC=90°,又OA=OC=1,则AC=.13.【答案】40°;【解析】∵∠A=55°,∠E=30°,∴∠EBF=∠A+∠E=85°,∵∠A+∠BCD=180°,∴∠BCD=180°﹣55°=125°,∵∠BCD=∠F+∠CBF,∴∠F=125°﹣85°=40°.三、解答题14.【答案与解析】如图,∵AB=BC=CD,∴AC=BD,∴AC=BD,∵B,C是AC,BD的中点,∴BF=CE=1AC,O B⊥AC,O C⊥BD, 2∴Rt OBF≌Rt OCE,∴OE=OF15.【答案与解析】证明:如图,在AE上截取AF=BD,连接CF,CD;在△ACF和△BCD中∴△ACF≌△BCD,∴CF=CD,∵CE⊥AD于E,∴EF=DE,∴AE=AF+EF=BD+DE.16.【答案与解析】证法一:连接BC,如图所示.∵AB是直径,∴∠ACB=90°,即∠ACF+∠BCD=90°.又∵CD⊥AB,∴∠B+∠BCD=90°,∴∠ACF=∠B.∵点C是AE的中点,∴AC=CE,∴∠B=∠CAE,∴∠ACF=∠CAE,∴AF=CF.证法二:如图所示,连接BC,并延长CD交⊙O于点H.∵AB是直径,CD⊥AB,∴AC=AH.∴点C是AE的中点,∴AC=CE,∴AH=CE.∵∠ACF=∠CAF,∴AF=CF.四边形ADBC =S17.【答案与解析】∵AB是直径,∴∠ACB=∠ADB=∠90°.在△R t ABC中,AB=6,AC=2,∴BC=AB2-AC2=62-22=42.∵∠ACB的平分线交⊙O于点D,∴∠DCA=∠BCD.∴AD=DB,∴AD=BD.∴在△R t ABD中,AD2+BD2=AB2=62,∴AD=BD=32.∴S∆ABC +S∆ABD=11A C BC+AD BD22=11⨯2⨯42+⨯(32)2=9+42.22。
(名师整理)最新人教版数学中考《垂径定理 圆心角 圆周角定理》专题精练(含答案解析)

垂径定理圆心角圆周角定理一选择题:1、如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是()A.42°B.48°C.52°D.58°2.如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )A.50° B.55° C.60° D.65°3.如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是()A.100° B.110° C.120°D.130°4.如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM取值范围是()A.3≤OM≤5B.3≤OM<5C.4≤OM≤5 D.4≤OM<55、如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()A.2个 B.3个 C.4个 D.5个6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B 的读数分别为86°、30°,则∠ACB的大小为( )A.15°B.28° C.29°D.34°7.如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中,AB、AC是弦,O在∠ABO的内部,,,,则下列关系中,正确的是()A. B. C. D.9.如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35º C.20º与40º D.30º与35º10.图中∠BOD的度数是()A.55° B.110° C.125° D.150°11.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为()(A)140°(B)125°(C)130°(D)110°12.如图,弦AB∥CD,E为上一点,AE平分,则图中与相等(不包括)的角共有()A.3个 B.4个 C.5个 D.6个13、如图,已知的半径为1,锐角内接于,于点,于点,则的值等于()A.的长 B.的长 C.的长 D.的长14.如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是()A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为()A. B. C.或 D.或或16.如图,,在以为直径的半圆上,,在上,为正方形,若正方形边长为1,,,则下列式子中,不正确的是()A. B. C. D.17.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为()A.4 B.5 C.6 D.718.如图,在△ABC中,AD是高,AE是直径,AE交BC于G,有下列四个结论:•①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的有()A.1个 B.2个 C.3个 D.4个19.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M,N,P,Q。
人教版 九年级数学上册 第24章 圆的概念及弧、弦、圆心角和圆周角 专题练习(含答案)

圆的概念及弧、弦、圆心角和圆周角专题练习(含答案)例1. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于()A.160°B.150°C.140°D.120°例2. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE CE=1.则弧BD 的长是()B C D例3.如图,已知A,B,C在⊙O上,ACB为优弧,下列选项中与∠AOB相等的是()A.2∠C B.4∠B C.4∠A D.∠B+∠C例4. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是()A.6 B.5 C.4 D.3巩固练习1.如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.2.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为________.3.⊙O中,∠AOB=100°,若C是AB上一点,则∠ACB等于( ).A.80°B.100°C.120°D.130°4.已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.5. 已知:如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为AD的中点,若∠BAD=20°,求∠ACO的度数6.如图,以ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC、AD于E、F,交BA的延长线于G,试说明弧EF和弧FG相等.7. ⊙O中,M为AB的中点,则下列结论正确的是( ).A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定8. 如图,⊙O中,AB为直径,弦CD交AB于P,且OP=PC,试猜想AD与CB之间的关系,并证明你的猜想.9. 如图,⊙O中,直径AB=15cm,有一条长为9cm的动弦CD在ANB上滑动(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.(1)求证:AE=BF;(2)在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明并求这个定值;若不是,请说明理由.10.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,∠ABE=______,∠ADC=______,∠ABC=______.10题图11题图12题图11.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,∠FAE=______,∠DAB=______,∠EFA=______.12.如图,ΔABC是⊙O的内接正三角形,若P是AB上一点,则∠BPC=______;若M是BC上一点,则∠BMC=______.13.在⊙O中,若圆心角∠AOB=100°,C是AB上一点,则∠ACB等于( ).A.80°B.100°C.130°D.140°14.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( ).A.13°B.79°C.38.5°D.101°15.如图,AC 是⊙O 的直径,弦AB ∥CD ,若∠BAC =32°,则∠AOD 等于( ).A .64°B .48°C .32°D .76°16.如图,弦AB ,CD 相交于E 点,若∠BAC =27°,∠BEC =64°,则∠AOD 等于( ).A .37°B .74°C .54°D .64°17.如图,四边形ABCD 内接于⊙O ,则x = 。
圆心角与圆周角能力提升训练(含答案)

松滋市实验中学九年级培优辅差《圆周角》训练题命题人:胡海洋题号一、选择题二、填空题三、简答题总分得分一、选择题1、如图,内接于,若,则的大小为()A.B. C.D.(第1题)(第2题)(第3题)(第4题)(第5题)2、如图,AB是的直径,点C、D在上,,则()A.70° B.60° C.50° D.40°3、如图,是的外接圆,已知,则的大小为()A.40° B.30° C.45°D.50°4、如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C= ( )A.180°B.90°C.45°D.30°5、如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35º C.20º与40º D.30º与35º6、. 如右图,A、B、C、D为⊙O的四等分点,若动点P从点C出发,沿C→D→O→C路线作匀速运动,设运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是A B CD二、填空题7、如图,在⊙O中,∠AOB=46º,则∠ACB=º.8、如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 º,那么∠B= º.(第7题)(第8题)(第9题)(第10题)(第11题)9、如图,AB是⊙0的直径,弦AC长为4a,弦BC长为5a,∠ACB的平分线交⊙0于点D,则CD的长为 .10、如图, ⊙P过O、、,半径PB⊥PA,双曲线恰好经过B点,则k的值是____________.11、如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____________.12、如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交BC于点D,连接DC,则∠DCB= 。
完整版)圆心角圆周角练习题

完整版)圆心角圆周角练习题知识点三:弧、弦、圆心角与圆周角1.定义圆心角为顶点在圆心的角。
2.在同圆或等圆中,弧、弦、圆心角之间的关系:两个圆心角相等,圆心角所对的弧相等(无论是优弧还是劣弧),圆心角所对的弦相等。
3.一个角是圆周角必须满足两个条件:(1)角的顶点在圆上;(2)角的两边都与圆有除顶点外的交点。
4.同一条弧所对的圆周角有两个。
5.圆周角定理:圆周角等于圆心角的一半。
6.圆周角定理的推论:(1)同弦或等弦所对的圆周角相等;(2)半圆或直径所对的圆周角相等;(3)90°的圆周角所对的弦是直径。
需要注意的是,“同弦或等弦”改为“同弧或等弧”结论就不一定成立了,因为一条弦所对的圆周角有两类,它们是相等或互补关系。
7.圆内接四边形定义为所有顶点都在圆上的多边形,圆心即为这个圆内接四边形的交点。
圆内接四边形的对角线相互垂直,且交点为对角线的中点。
夯实基础1.如果两个圆心角相等,则它们所对的弧相等,选项B正确。
2.不正确的语句为③,因为圆不一定是轴对称图形,只有圆上的任何一条直径所在直线才是它的对称轴。
3.错误的说法是D,相等圆心角所对的弦不一定相等。
4.根据圆心角的性质,∠A=2∠B,所以∠A=140°。
5.∠BAC与∠BCD互补,∠BCD与∠CBD相等,所以与∠BAC相等的角有2个,即∠CBD和∠ABD。
6.因为∠CAB为30°,所以∠ABC为60°,由正弦定理可得BC=5√3.7.根据圆周角定理,∠ACB=40°。
8.设∠A=3x,∠B=4x,∠C=6x,则∠D=360°-3x-4x-6x=120°。
9.∠DCE=∠A。
1、如图,AB是⊙O的直径,C,D是BE上的三等分点,∠AOE=60°,求证∠COE=80°。
证明:由三等分点的性质可知,BC=CD=DE,又∠AOE=60°,所以∠AOC=120°。
(完整版)圆心角圆周角的经典练习
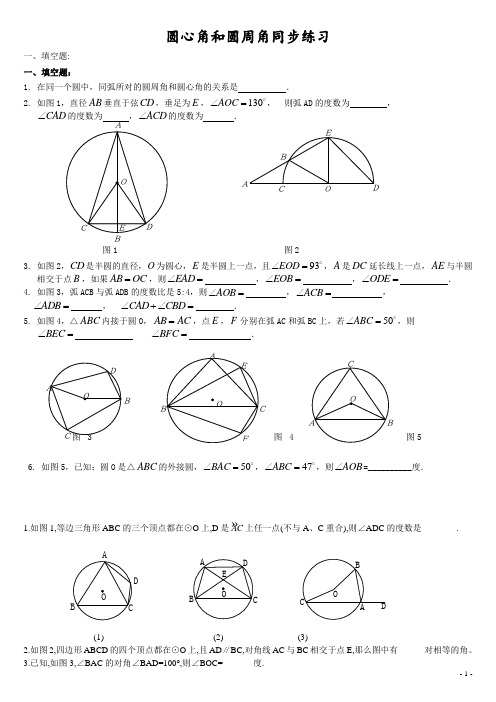
圆心角和圆周角同步练习一、填空题: 一、填空题:1. 在同一个圆中,同弧所对的圆周角和圆心角的关系是.2. 如图1,直径AB 垂直于弦CD ,垂足为E ,130AOC ∠=o, 则弧AD 的度数为 ,CAD ∠的度数为 ,ACD ∠的度数为 .图1 图23. 如图2,CD 是半圆的直径,O 为圆心,E 是半圆上一点,且93EOD ∠=o,A 是DC 延长线上一点,AE 与半圆相交于点B ,如果AB OC =,则EAD ∠= ,EOB ∠=,ODE ∠=.4. 如图3,弧ACB 与弧ADB 的度数比是5:4,则AOB ∠= ,ACB ∠=,ADB ∠= , CAD CBD ∠+∠= .5. 如图4,△ABC 内接于圆O ,AB AC =,点E ,F 分别在弧AC 和弧BC 上,若50ABC ∠=o,则BEC ∠= BFC ∠=.图图56. 如图5,已知:圆O 是△ABC 的外接圆,50BAC ∠=o,47ABC ∠=o,则AOB ∠=__________度.1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是»AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DDCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有______对相等的角。
3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.A4.如图4,A 、B 、C 为⊙O 上三点,若∠OAB=46°,则∠ACB=_______度.BAA(4) (5) (6)5.如图5,AB 是⊙O 的直径, »»BC BD =,∠A=25°,则∠BOD 的度数为________.6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DDCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对9.如图9,D 是»AC 的中点,则图中与∠ABD 相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个10.如图10,∠AOB=100°,则∠A+∠B 等于( )A.100°B.80°C.50°D.40°11.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( ) A.30° B.30°或150° C.60° D.60°或120°12.如图,A 、B 、C 三点都在⊙O 上,点D 是AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( ) A.40° B.50° C.70° D.110°三、解答题:13.如图,⊙O 的直径AB=8cm,∠CBD=30°,求弦DC 的长.BA14.如图,A 、B 、C 、D 四点都在⊙O 上,AD 是⊙O 的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC 的长.15.如图,在⊙O 中,AB 是直径,CD 是弦,AB ⊥CD.(1)P 是¼CAD上一点(不与C 、D 重合),试判断∠CPD 与∠COB 的大小关系, 并说明理由. (2)点P′在劣弧CD 上(不与C 、D 重合时),∠CP′D 与∠COB 有什么数量关系?请证明你的结论.16.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻.当甲带球部到A 点时,乙随后冲到B 点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)答案:1.120°2.3 13.160°4.44°5.50°7.A 8.C 9.B 10.C 11.B 12.C 13.连接OC 、OD,则OC=OD=4cm,∠COD=60°,故△COD 是等边三角形,从而CD= 4cm. 14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.∵AD 是直径,∴∠ACD=90°, ∴AC 2+CD 2=AD 2,即2AC 2=36,AC 2. 15.(1)相等.理由如下:连接OD,∵AB ⊥CD,AB 是直径,∴»»BCBD ,∴∠COB= ∠DOB. ∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)∠CP′D+∠COB=180°.理由如下:连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.16.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B,即∠B>∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.。
圆心角与圆周角专题练习

圆周角和圆心角的练习题一、选择题1.圆周角是24°,则它所对的弧是________ A.12°;B.24°;C.36°;D.48°.2.在⊙O中,∠AOB=84°,则弦AB所对的圆周角是________A.42°;B.138°;C.84°;D.42°或138°.3.如图,圆内接四边形ABCD的对角线AC,BD把四边形的四个角分成八个角,这八个角中相等的角的对数至少有___________.()A.1对;B.2对;C.3对;D.4对.4.如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥C D.如果∠BAC=32°,则∠AOD=___[ ] A.16°;B.32°;C.48°;D.64°.二、计算题6.如图,AD是△ABC外接圆的直径,AD=6cm,∠DAC=∠AB C.求AC的长.7.已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°(如图).求BD 的长.8.如图,半圆的直径AB =13cm ,C 是半圆上一点,CD ⊥AB 于D ,并且CD =6cm .求AD 的长.、9.如图,圆内接△ABC 的外角∠MAB 的平分线交圆于E ,EC =8cm .求BE 的长.10.已知:如图,AD 平分∠BAC ,DE ∥AC ,且AB =a .求DE 的长.11.如图,在⊙O 中,F ,G 是直径AB 上的两点,C ,D,E 是半圆上的三点,如果弧AC 的度数为60°,弧BE 的度数为20°,∠CFA =∠DFB ,∠DGA =∠EG B .求∠FDG 的大小.12.如图,⊙O 的内接正方形ABCD 边长为1,P 为圆周上与A ,B ,C ,D 不重合的任意点.求PA 2+PB 2+PC 2+PD 2的值.13.如图,在梯形ABCD 中,AD ∥BC ,∠BAD =135°,以A 为圆心,AB 为半径作⊙A 交AD ,BC 于E ,F 两14.如图,⊙O 的半径为R ,弦AB =a ,弦BC ∥OA ,求AC 的长.15.如图,在△ABC 中,∠BAC ,∠ABC ,∠BCA 的平分线交△ABC 的外接圆于D ,E 和F ,如果,,分别为m °,n °,p °,求△ABC 的三个内角.16.如图,在⊙O 中,BC ,DF 为直径,A ,E 为⊙O 上的点,AB =AC ,EF =21DF .求∠ABD +∠CBE 的值.17.如图,等腰三角形ABC 的顶角为50°,AB =AC ,以数.第二页18.如图,AB是⊙O的直径,AB=2cm,点C在圆周上,且∠BAC=30°,∠ABD=120°,CD⊥BD于D.求BD的长.19.如图,△ABC中,∠B=60°,AC=3cm,⊙O为△ABC的外接圆.求⊙O的半径.20.以△ABC的BC边为直径的半圆,交AB于D,交AC于E,EF⊥BC于F,AB=8cm,AE=2cm,BF∶FC=5∶1(如图).求CE的长.21.已知等腰三角形的腰长为13cm,底边长为10cm,求它的外接圆半径.22.如图,△ABC中,AD是∠BAC的平分线,延长AD交△ABC的外接圆于E,已知AB=a,BD=b,BE=c.求AE的长.23.如图,△ABC中,AD是∠BAC的平分线,延长AD交△ABC的外接圆于E,已知AB=6cm,BD=2cm,BE=2.4cm.求DE的长.24.如图,梯形ABCD内接于⊙O,AB∥CD,的度数为60°,∠B=105°,⊙O 的半径为6cm.求BC的长.25.已知:如图,AB是⊙O的直径,AB=4cm,E为OB的中点,弦CD⊥AB于E.求CD的长.26.如图,AB为⊙O的直径,E为OB的中点,CD为过E点并垂直AB的弦.求∠ACE的度数.27.已知:如图,在△ABC中,∠C=90°,∠A=38°,以C为圆心,BC为半径作圆,交AB于D,求的度数.第三页28.如图,△ABC内接于圆O,AD为BC边上的高.若AB=4cm,AC=3cm,AD=2.5cm,求⊙O的半径.29.设⊙O的半径为1,直径AB⊥直径CD,E是OB的中点,弦CF过E点(如图),求EF的长.30.如图,在⊙O中直径AB,CD互相垂直,弦CH交AB于K,且AB=10cm,CH=8cm.求BK∶AK的值.31.如图,⊙O的半径为40cm,CD是弦,A为的中点,弦AB交CD于F.若AF=20cm,BF=40cm,求O点到弦CD的弦心距.32.如图,四边形ABCD内接于以AD为直径的圆O,且AD=4cm,AB=CB=1cm,求CD的长.三、证明题33.如图,已知△ABC内接于半径为R的⊙O,A为锐角.求证:ABCsin =2R 34.已知:如图,在△ABC 中,AD ,BD 分别平分∠BAC 和∠ABC ,延长AD 交△ABC 的外接圆于E ,连接BE .求证:BE =DE .35.如图,已知D 为等边三角形ABC 外接圆上的上的一点,AD 交BC 边于E .求证:AB 为AD 和AE 的比例中项.36.已知:如图,在△ABC 中,AB =AC ,以AB 为直径的圆交BC 于D .求证:D 为BC 的中点.第四页37.已知:如图,⊙O 是△ABC 的外接圆,AD ⊥BC 于D ,AE 平分∠BAC 交⊙O 于E .求证:AE 平分∠OA D .38.已知:如图,△ABC 的AB 边是⊙O 的直径,另两边BC 和AC 分别交⊙O 于D ,E 两点,DF ⊥AB ,交AB 于F ,交BE 于G ,交AC 的延长线于H .求证:DF 2=HF ·GF .39.已知:如图,圆内接四边形ABCD 中,BC =C D .求证:AB ·AD +BC 2=AC 2.40.已知:如图,AB 是半圆的直径,AC 是一条弦,D 是中点,DE ⊥AB 于E ,交AC 于F ,DB 交AC 于G .求证:AF =FG .41.如图,AB 是⊙O 的弦,P 是AB 所对优弧上一点,直径CD ⊥AB ,PB 交CD 于E ,延长AP 交CD 的延长线于F .求证:△EPF ∽△EO A .42.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,M为上一点,AM的延长线交DC于F.求证:∠AMD=∠FM C.43.已知:如图,AB,AC分别为⊙O的直径与弦,CD⊥AB于D,E为⊙O外一点,且AE=AC,BE交⊙O于F,连结ED,CF.求证:∠ACF=∠AE D.44.如图,⊙O的半径OD,OE分别垂直于弦AB和AC,连结DE交AB,AC于F,G.求证:AF2=AG2=DF·GE.45.如图,△ABC内接于圆,D是AB上一点,AD=AC,E是AC延长线上一点,AE=AB,连接DE交圆于F,延长ED交圆于G.求证:AF=AG.第五页46.已知:如图,⊙O的两条直径AB⊥CD,E是OD的中点,连结AE,并延长交⊙O于M,连结CM,交AB于F.求证:OB=3OF.47.已知:如图,△ABC是等边三角形,以AC为直径作圆交BC于D,作DE⊥AC 交圆于E.(1)求证:△ADE是等边三角形;(2)求S△ABC∶S△ADE.48.已知:如图,半径都是5cm的两等圆⊙O1和⊙O2相交于点A,B,过A作⊙O1的直径AC与⊙O2交于点D,且AD∶DC=3∶2,E为DC的中点.(1)求证:AC⊥BE;(2)求AB的长.一、填空题:1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.4.如图4,A 、B 、C 为⊙O 上三点,若∠OAB=46°,则∠ACB=_______度.BAA(4) (5) (6)5.如图5,AB 是⊙O 的直径, BC BD ,∠A=25°,则∠BOD 的度数为________.第六页6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______. 二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对9.如图9,D 是AC 的中点,则图中与∠ABD 相等的角的个数是( )A.4个B.3个C.2个D.1个 10.如图10,∠AOB=100°,则∠A+∠B 等于( ) A.100° B.80° C.50° D.40°11.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )A.40°B.50°C.70°D.110°三、解答题:13.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.A14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.15.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值.16.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.第七页17.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素) 18.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢?。
圆心角与圆周角练习题

圆心角与圆周角练习题一、选择题(每题3分,共30分)1. 在同圆或等圆中,如果圆心角相等,那么对应的圆周角:A. 相等B. 不相等C. 无法确定D. 可能相等2. 已知圆的半径为5,圆心角为30°,求圆周角的度数:A. 15°B. 30°C. 45°D. 60°3. 在圆中,圆心角的度数是圆周角度数的:A. 2倍B. 1/2倍C. 1/4倍D. 4倍4. 如果一个圆周角的度数是60°,那么它所对的圆心角是:A. 120°B. 60°C. 30°D. 180°5. 在同圆或等圆中,圆心角和圆周角的关系是:A. 相等B. 互补C. 互余D. 没有固定关系6. 已知圆的半径为10,圆心角为45°,求圆周角的度数:A. 22.5°B. 45°C. 90°D. 无法确定7. 圆心角和圆周角的关系可以用以下哪个公式表示:A. 圆心角= 2 × 圆周角B. 圆周角= 2 × 圆心角C. 圆心角 = 圆周角D. 圆周角 = 圆心角 / 28. 如果一个圆周角的度数是90°,那么它所对的圆心角是:A. 45°B. 90°C. 180°D. 270°9. 在圆中,圆心角和圆周角的度数之和:A. 总是等于180°B. 总是等于360°C. 总是小于360°D. 总是大于360°10. 已知圆的半径为8,圆心角为60°,求圆周角的度数:A. 30°B. 60°C. 90°D. 120°二、填空题(每题2分,共20分)11. 在同圆或等圆中,如果圆心角是圆周角度数的2倍,那么圆周角的度数是圆心角的________倍。
12. 圆心角的度数是圆周角度数的________倍。
圆周角圆心角练习题

圆周角圆心角练习题一、选择题1. 圆周角定理指出,圆周角的度数是同弧所对圆心角的度数的______。
A. 1/2B. 2倍C. 3倍D. 4倍2. 若圆心角为40°,则同弧所对的圆周角为______。
A. 20°B. 40°C. 80°D. 120°3. 在圆中,若一条弦所对的圆心角为60°,则这条弦所对的圆周角是______。
A. 30°B. 45°C. 60°D. 90°4. 圆内接四边形ABCD中,若∠A=60°,则∠B的度数为______。
A. 60°B. 120°C. 180°D. 240°5. 已知圆的半径为5,圆心角为120°,那么这个圆心角所对的弧长为______。
A. 5πB. 10πC. 15πD. 20π二、填空题6. 若圆周角为45°,则同弧所对的圆心角为______。
7. 在圆中,若弦AB所对的圆心角为100°,则弦AB所对的圆周角为______。
8. 已知圆的半径为10,圆心角为150°,则这个圆心角所对的弧长为______。
9. 圆内接四边形ABCD中,若∠A=90°,则∠B的度数为______。
10. 若圆的半径为8,圆心角为90°,则这个圆心角所对的弧长为______。
三、简答题11. 解释什么是圆周角,并说明它与圆心角的关系。
12. 给出一个圆内接四边形的例子,并说明其对角互补的性质。
13. 解释如何计算一个圆心角所对的弧长。
14. 在圆中,如果知道圆周角的度数,如何计算同弧所对的圆心角的度数?15. 圆内接四边形的对角互补性质在实际问题中有哪些应用?四、解答题16. 已知圆的半径为6,圆心角为60°,求这个圆心角所对的弧长。
17. 在圆中,若弦AB所对的圆心角为120°,求弦AB所对的圆周角的度数。
2023学年北师大版九年级数学下册《3-4圆周角与圆心角的关系》假期同步提升练习题(附答案)

2022-2023学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》假期同步提升练习题(附答案)一.选择题(共10小题,满分30分)1.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB为()A.34°B.56°C.60°D.68°4.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为()A.35°B.38°C.40°D.42°5.如图,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,则∠BCD等于()A.75°B.95°C.100°D.105°6.如图,C,D在⊙O上,AB是直径,∠D=64°,则∠BAC=()A.64°B.34°C.26°D.24°7.如图,AB是⊙O的直径,弦CD⊥AB于点E.如果∠OCE=50°,那么∠ABD=()A.50°B.60°C.70°D.80°8.如图,点A、B、C、D、E均在⊙O上,∠BAC=20°,∠CED=40°,则∠BOD的度数为()A.30°B.60°C.100°D.120°17.圆中一条弦恰好等于圆的半径,则这条弦所对的圆周角的度数为()A.30°B.60°C.30°或150°D.60°或120°21.如图,已知⊙O的弦AB、DC的延长线相交于点E,∠AOD=128°,∠E=40°,则∠BDC的度数是()A.16°B.20°C.24°D.32°9.如图,点A、B、C、D、E都是⊙O上的点,=,∠D=130°,则∠B的度数为()A.130°B.128°C.115°D.116°10.如图,四边形ABCD内接于⊙O,DE是⊙O的直径,连接BD.若∠BCD=2∠BAD,则∠BDE的度数是()A.25°B.30°C.32.5°D.35°二.填空题(共8小题,满分24分)11.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为.12.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=.13.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4,CD=8,则AB =.14.如图,线段CD上一点O,以O为圆心,OD为半径作圆,⊙O上一点A,连结AC交⊙O于B点,连结BD,若BC=BD,且∠C=25°,则∠BDA=.15.如图,正方形ABCD四个顶点都在⊙O上,点P是在弧BC上的一点(P点与C点不重合),则∠CPD的度数是.16.如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E 两点,过点D作直径DF,连接AF,则∠DF A=.17.如图,AB是圆O的直径,∠A=30°,BD平分∠ABC,CE⊥AB于E,若CD=6,则CE的长为.18.如图,经过原点的⊙P与x轴,y轴分别交于A(3,0),B(0,4)两点,点C是上一点,且BC=2,则AC=.三.解答题(共7小题,满分66分)19.如图,已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.20.如图,⊙O的直径AB和弦CD相交于点E,AE=1cm,EB=5cm,∠DEB=60°,OF ⊥CD于F.(1)求EF的长;(2)求CD的长.21.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连接AC,OC,BC.(1)求证:∠1=∠2;(2)若BE=2,CD=6,求⊙O的半径长.22.如图,AB是⊙O的直径,点C在⊙O上且不与点A,B重合,∠ABC的平分线交⊙O 于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.(1)求证:FG=DE;(2)若AB=6,FG=6,求AG的长.23.如图,已知AB是⊙O的直径,∠ACD=30°.(1)求∠DAB的度数.(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求EF的长.24.如图,在△ABC中,AB=AC,以AB为直径作圆O,交BC于点D,交AC于点E.(1)求证:BD=CD.(2)若弧DE=50°,求∠C的度数.25.如图(1),已知AB是⊙O的直径,C是上的一个动点(点C与点A,B不重合),连接AC,D是的中点,作弦DE⊥AB于点F.(1)若点C和点E不重合,连接BC,CE和EB,当△BCE是等腰三角形时,求∠CAB 的度数;(2)若点C和点E重合,如图(2),探索AB与AC的数量关系并说明理由.参考答案一.选择题(共10小题,满分30分)1.解:∵∠C=34°,∴∠AOB=2∠C=68°.故选:D.2.解:连接CD,如图所示:∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ACD=90°﹣∠A=20°,∴∠DOE=2∠ACD=40°,故选:C.3.解:∵OD=OA,∴∠ODA=∠OAD,∵∠DOA=30°,∴∠OAD=×(180°﹣∠DOA)=75°,∵A、D、C、B四点共圆,∴∠BCD+∠OAD=180°,∴∠BCD=180°﹣75°=105°,故选:D.4.解:连接BC,∵∠D=64°,∴∠D=∠B=64°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠BAC=90°﹣∠B=26°,故选:C.5.解:连接OD,∵CD⊥AB,AB过O,∴=,∴∠COB=∠DOB,∵CD⊥AB,∴∠OEC=90°,∵∠OCE=50°,∴∠COB=90°﹣∠OCE=40°,∴∠DOB=40°,∵OB=OD,∴∠ABD=∠ODB=(180°﹣∠DOB)=(180°﹣40°)=70°,故选:C.6.解:连接OC,如图,∵∠BOC=2∠BAC=2×20°=40°,∠DOC=2∠CED=2×40°=80°,∴∠BOD=∠BOC+∠DOC=40°+80°=120°.故选:D.7.解:如图:AB=2AC,AB为⊙O的直径,连接BC,AD,CD,∴∠ACB=90°,∴∠B=30°,∵∠B+∠D=180°,∴∠D=150°,即这条弦所对的圆周角的度数为30°或150°,故选:C.8.解:∵∠ABD是所对的圆周角,∴∠ABD=∠AOD=×128°=64°,∵∠ABD是△BDE的外角,∴∠BDC=∠ABD﹣∠E=64°﹣40°=24°,故选:C.9.解:连接AC、CE,∵点A、C、D、E都是⊙O上的点,∴∠CAE+∠D=180°,∵∠D=130°,∴∠CAE=180°﹣130°=50°,∵=,∴∠ACE=∠AEC=×(180°﹣50°)=65°,∵点A、B、C、E都是⊙O上的点,∴∠AEC+∠B=180°,∴∠B=180°﹣65°=115°,故选:C.10.解:连接BE,∵四边形ABCD内接于⊙O,∴∠BCD+∠BAD=180°,∵∠BCD=2∠BAD,∴∠BAD=60°,由圆周角定理得:∠BED=∠BAD=60°,∵DE是⊙O的直径,∴∠EBD=90°,∴∠BDE=90°﹣60°=30°,故选:B.二.填空题(共8小题,满分24分)11.解:∵∠CBE=50°,∴∠ABC=180°﹣∠CBE=180°﹣50°=130°,∵四边形ABCD为⊙O的内接四边形,∴∠D=180°﹣∠ABC=180°﹣130°=50°,∵DA=DC,∴∠DAC==65°,故答案为:65°12.解:由相交弦定理得,AP•BP=CP•DP,则DP==6,故答案为:6.13.解:∵AB是⊙O的直径,弦CD⊥AB,CD=8,∴CP=4,根据相交弦定理得,16=AP×4AP,解得AP=2,∴AB=10.14.解:设CD与⊙O相交于点E,连接BE,∵BC=BD,∴∠C=∠BCDC=25°,∴∠CBD=180°﹣∠C﹣∠BDC=130°,∵ED是⊙O的直径,∴∠EBD=90°,∴∠BED=90°﹣∠BDC=65°,∵四边形ABED是⊙O的内接四边形,∴∠A=180°﹣∠BED=115°,∴∠BDA=∠CBD﹣∠A=15°,故答案为:15°.15.解:连接BD,∵四边形ABCD为正方形,∴∠DBC=45°,由圆周角定理得:∠CPD=∠DBC=45°,故答案为:45°.16.解:∵点C是半径OA的中点,∴OC=OD,∵DE⊥AB,∴∠CDO=30°,∴∠DOA=60°,∴∠DF A=30°,故答案为:30°.17.解:∵AB是直径,∴∠ACB=90°,∵∠A=30°,∴∠D=∠A=30°,∠ABC=60°,∵BD平分∠ABC,∴∠CBD=∠ABC=30°,∴∠D=∠CBD,∴CD=CB=6,∵CE⊥AB,∴∠CEB=90°,∴EC=3,故答案为3.18.解:连接AB.∵∠AOB=90°,∴AB是圆的直径.∵A的坐标是(3,0),B的坐标是(0,4),∴OA=3,OB=4,∴AB===5,∵AB是直径,∴∠C=90°,∴AC===.故答案是:.三.解答题(共7小题,满分66分)19.解:(1)连接AD、BC.∵∠A=∠C,∠D=∠B,∴△ADM∽△CBM∴即AM•MB=CM•MD.(2)连接OM、OC.∵M为CD中点,∴OM⊥CD在Rt△OMC中,∵OC=3,OM=2∴CD=CM===由(1)知AM•MB=CM•MD.∴AM•MB=•=5.20.解:(1)∵AE=1cm,EB=5cm,∴AB=1+5=6cm,AO=×6=3cm,∴EO=3﹣1=2cm.又∵∠DEB=60°,∴EF=EO•cos60°=2×=1cm.(2)∵OF⊥CD,∴CF=DF,设CE=x,则CF=DF=x+EF=x+1,根据相交弦定理,AE•EB=CE•ED,x(1+x+1)=1×5,解得:x=﹣1±,由于CE为正数,所以x=﹣1+,所以CD=2×(﹣1++1)=2.21.(1)证明:∵AB是⊙O的直径,CD⊥AB,∴=,∴∠A=∠2,又∵OA=OC,∴∠1=∠A,∴∠1=∠2.(2)∵AB为⊙O的直径,弦CD⊥AB,CD=6,∴∠CEO=90°,CE=ED=3,设⊙O的半径是R,EB=2,则OE=R﹣2,在Rt△OEC中,R2=(R﹣2)2+32,解得:,∴⊙O的半径是.22.(1)证明:∵BD平分∠ABC,∴∠ABD=∠CBD,∵∠E=∠CBD,∴∠E=∠ABD,∵DE⊥AB,∴DG=EG,∠BGD=90°,∵∠ABD+∠BDG=90°,∴∠E+∠FDE=90°,∴∠EFD=90°,∴GF=DE;(2)解:如图,连接OD,则OD=OA=AB=3,∵FG=DG=6,∴OG==3,∴AG=OA﹣OG=33.23.解:(1)连接BD.∵AB是直径,∴∠ADB=90°,∵∠ABC=∠ACD=30°,∴∠DAB=90°﹣∠ABD=60°;(2)连接OD.∵OA=OD,∠OAD=60°,∴△AOD是等边三角形,∴∠AOD=60°,OA=OD=2,∵AB⊥CD,∴DE=EF,∵DE=OD•sin60°=,∴EF=.24.(1)证明:连接AD.∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=DC;(2)解:连接OE,OD.∵的度数=50°,∴∠DOE=50°,∴∠DAC=∠DOE=25°,∵AD⊥BC,∴∠C=90°﹣25°=65°.25.解:(1)连接OC,当△BCE是等腰三角形时,分两种情况:①当CE=BC时,=,如图(1),设所对的圆心角的度数为x°,则所对的圆心角的度数=所对的圆心角的度数=x°,∴所对的圆心角的度数为2x°.∵DE⊥AB,AB为直径,∴所对的圆心角的度数=所对的圆心角的度数=2x°,∴所对的圆心角的度数为3x°,∴所对的圆心角的度数为6x°,∴所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数=2x°+3x°=5x°.∵所对的圆心角的度数=180°,∴5x=180,解得,x=36,∴∠BOC=36°,∴∠CAB=∠BOC=18°.②当CE=BE时,=,如图(2),设所对的圆心角的度数为y°,则所对的圆心角的度数为y°.∵DE为弦,AB为直径,DE⊥AB,∴所对的圆心角的度数=所对的圆心角的度数=y°,∴所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数+所对的圆心角的度数=3y°.∵D是的中点,∴所对的圆心角的度数为3y°,∴所对的圆心角的度数为6y°,∴所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数=y°+3y°=4y°.∵所对的圆心角的度数=180°,∴4y=180,解得,y=45,∴所对的圆心角的度数为90°,∴∠BOC=90°,∴∠CAB=45°.综上所述,当△BCE是等腰三角形时,∠CAB的度数是18°或45°.(2)AC=AB.理由:设所对的圆心角的度数为t°,则所对的圆心角的度数=所对的圆心角的度数=t°.∵D是的中点,∴所对的圆心角的度数=所对的圆心角的度数=2t°,∴所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数=t°+2t°=3t°.∵所对的圆心角的度数为180°,∴3t=180,解得,t=60°,∴∠A=30°.∵AB为⊙O的直径,在Rt△ABC中,BC=AB,∴AC==AB.。
圆周角练习题及答案

圆周角练习题及答案在平面几何课程中,圆周角是一个非常重要的概念。
学生通过练习圆周角的计算和解题,可以更好地理解和应用该概念。
本文将提供一些圆周角的练习题及其答案,旨在帮助学生加深对圆周角的理解和应用能力。
一、单选题1. 在圆的半径为r的两条弦之间所夹的圆周角是:A. 60度B. 90度C. 180度D. 360度答案:C. 180度2. 在相同圆上的两个圆周角,其中一个是另一个的两倍,那么它们的度数分别是:A. 60度和120度B. 90度和180度C. 120度和240度D. 150度和300度答案:C. 120度和240度二、填空题1. 在相同圆上的两个圆周角,它们的度数之和为________度。
答案:360度2. 在一个圆上,一个圆周角的度数是60度,那么它所对应的弧长为________。
答案:π/3(弧度)三、解答题1. 已知一个圆的半径为8cm,圆心角的度数为60度,求该圆内切正多边形的边长和面积。
解答:首先,由于圆心角度数为60度,所以切割的正多边形是六边形。
其次,由于圆的半径为8cm,因此可以通过正多边形的对称性得知,该六边形的边长为2r=16cm。
最后,可以通过将该六边形切割成等腰三角形,并计算其面积的一半来得到该多边形的面积。
所以,该六边形的边长为16cm,面积为(16*8*sin60°)/2=64√3 cm^2。
2. 若一个正八边形的外接圆的圆周角的度数为x度,求x的值。
解答:在一个正八边形中,通过连接圆心以及相邻的两个顶点,可以将该八边形分割为八个等腰三角形。
由于正八边形的圆心角度数为x 度,而圆心角是等腰三角形的内角,所以每个三角形的内角度数为x/2度。
根据三角形的内角和公式,可得(x/2)*8=180度,解得x=360度。
综上所述,圆周角练习题及答案提供了一些常见的练习题,通过对这些题目的解答,可以帮助学生更好地理解和应用圆周角的概念。
希望本文对学生们的学习有所帮助!。
《圆心角与圆周角》练习题及答案

《圆心角与圆周角》练习题1.下列说法中,正确的是( )A .等弦所对的弧相等 B. 等弧所对的弦相等C. 圆心角相等,它们所对的弦相等D. 弦相等,它们所对的圆心角相等2.如图,在⊙O 中,若C 是AB ︵的中点,∠A =50°,则∠BOC 的度数为( )A .40°B .45°C .50°D .60°(第2题) (第3题) (第4题)3.如图,在三个等圆上各自有一条劣弧AB ︵,CD ︵,EF ︵,如果AB ︵+CD ︵=EF ︵,那么AB +CD 与EF 的大小关系是( )A .AB +CD =EF B .AB +CD >EFC .AB +CD <EF D .不能确定4.如图,AB 为半圆O 的直径,C ,D ,E 为半圆弧上的点,CD ︵=DE ︵=EB ︵,若∠BOE =55°,则∠AOC 的度数为___.5.如图所示,AB ,CD ,EF 都是⊙O 的直径,且∠1=∠2=∠3,则⊙O 的弦AC ,BE ,DF 的大小关系是_______(第5题) (第6题) (第7题) (第8题)6.如图所示,在⊙O 中,AB ︵=AC ︵,∠B =70°,则∠A 的度数为________.7.如图,AB 是⊙O 的直径,AC ,CD ,DE ,EF ,FB 都是⊙O 的弦,且AC =CD =DE =EF =FB ,则∠AOC =________°,∠COF =________°.8.如图,AD ︵=BC ︵,若AB =3,则CD =________.9.如图,AB 是⊙O 的直径,C 、D 、E 是⊙O 上的点,则∠1+∠2等于( )A .90°B .45°C .180°D .60°(第9题) (第10题) (第11题) (第12题) (第13题)10.如图,在⊙O中,若C是BD的中点,则图中与∠BAC相等的角有()A.1个B.2 个C.3个D.4个11.如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数为( )A.90°B.60°C.45°D.30°12.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是()A.30°B.45°C.55°D.60°13.如图,OA、OB是⊙O的半径,点C在⊙O上,连接AC、BC,若∠A=20°,∠B=70°,则∠ACB的度数为()A.50° B.55° C.60° D.65°14.如图,AB、CD是⊙O的两条弦,连接AD、BC,若∠BAD=60°,则∠BCD的度数为()A.40°B.50°C.60°D.70°(第14题)(第15题)(第16题)(第17题)(第18题)15.如图,在△ABC中,AB为⊙O 的直径,∠B=60°,∠BOD=100°,则∠C的度数为()A.50° B.60° C.70° D.80°16.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于()A.12.5° B.15° C.20° D.22.5°17.如图,⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是()A.43°B.35°C.34°D.44°18.如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O 交于点P,点B与点O重合.将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )A.30≤x≤60 B.30≤x≤90 C.30≤x≤120 D.60≤x≤12019.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= .(第19题)(第20题)(第21题)(第22题)(第23题)20.如图,已知点E 是圆O 上的点,B ,C 是AD ︵的三等分点,∠BOC =46°,则∠AED 的度数为________.21.已知如图,四边形ABCD 内接于⊙O ,若∠A =60°,则∠DCE = .22.如图,在⊙O 中,AB=AC ,∠ABC=70°.∠BOC=________.23.如图,在⊙O 中,∠AOB 的度数为m ,C 是ACB ︵上一点,D ,E 是AB ︵上不同的两点(不与A ,B 两点重合),则∠D +∠E 的度数为24.如图,DC 是⊙O 的直径,弦AB ⊥CD 于点F ,连接BC ,DB ,则下列结论错误的是( )A. AD ︵=BD ︵ B .AF =BF C .OF =CF D .∠DBC =90°(第24题) (第25题) (第26题) (第27题) (第29题)25.已知AB ,CD 是⊙O 的两条直径,∠ABC =30°,那么∠BAD =( )A .45°B .60°C .90°D .30°26.如图,BC 是⊙O 的直径,A 是⊙O 上的一点,∠OAC =32°,则∠B 的度数是( )A .58°B .60°C .64°D .68°27.如图,已知BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=BC ︵,∠AOB =60°,则∠BDC 的度数是( )A .20°B .25°C .30°D .40°28.在⊙O 中,∠AOB =160°,则弦AB 所对的圆周角是( )A .80°B .320°C .160°D .80°或100°29.如图,▱ABCD 的顶点A ,B ,D 在⊙O 上,顶点C 在⊙O 的直径BE 上,连接AE ,∠E =36°,则∠ADC 的度数是( )A .44°B .54°C .72°D .53°30. 如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB ,COD ,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A .6B .8C .5 2D .53(第30题) (第31题) (第32题) (第33题) (第34题)31.如图是以△ABC 的边AB 为直径的半圆O ,点C 恰好在半圆上,过C 作CD ⊥AB 交AB 于点D.已知cos ∠ACD =35,BC =4,则AC 的长为( ) A .1 B.203 C .3 D.16332.如图,B ,C 是⊙A 上的两点,AB 的垂直平分线与⊙A 交于E ,F 两点,与线段AC 交于D 点.若∠BFC =20°,则∠DBC =( )A .30°B .29°C .28°D .20°33. 如图,在△ABC 中,∠ACB =90°,过B ,C 两点的⊙O 交AC 于点D ,交AB 于点E ,连接EO 并延长交⊙O 于点F ,连接BF ,CF ,若∠EDC =135°,CF =2 ,则AE 2+BE 2的值为( )A .8B .12C .16D .2034.如图,⊙O 的直径CB 的延长线与弦ED 的延长线交于点A ,∠A =20°,且CE ︵=BE ︵,则∠C 的度数是______.35.如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =55°,则∠BCD 的度数为________.(第35题) (第36题) (第37题) (第38题) (第39题)36.如图,△ABC 是⊙O 的内接三角形,AD 是⊙O 的直径,∠ABC =45°,AC =2 cm ,则AD =______cm.37. 如图,四边形ABCD 内接于⊙O ,DA =DC ,∠CBE =50°,则∠DAC 的大小为_________.38.如图,AB 为⊙O 的直径,C ,D 为⊙O 上的点,=.若∠CAB =40°,则∠CAD =________.39.如图,点A ,B ,C ,D 在⊙O 上,O 点在∠D 的内部,四边形OABC 为平行四边形,则∠OAD +∠OCD =_________.40.如图,在⊙O 中,CD ⊥AB 于E ,若∠B =60°,则∠A =________.(第40题) (第41题) (第42题) (第43题) (第44题)41.如图,点A ,B ,C 在⊙O 上,∠BAC =120°,AB =AC ,BD 为⊙O 的直径,AD =6,则DC =_________.42.如图,已知点A ,B ,C 在⊙O 上,ACB 为优弧,下列选项中与∠AOB 相等的是( )A .2∠CB .4∠BC .4∠AD .∠B +∠C43.如图,△ABC 的顶点A ,B ,C 均在⊙O 上,若∠ABC +∠AOC =90°,则∠AOC 的大小是( )A .30°B .45°C .60°D .70°44. 如图,⊙O 中,弦BC 与半径OA 相交于点D ,连接AB ,OC.若∠A =60°,∠ADC =85°,则∠C 的度数是( )A .25°B .27.5°C .30°D .35°45.如图,⊙O 的直径CD 过弦EF 的中点G ,∠DCF =20°,则∠EOD 等于( )A .10°B .20°C .40°D .80°(第45题) (第46题) (第47题) (第48题) (第49题)46. 如图,点A ,B ,C 均在⊙O 上,若∠A =66°,则∠OCB 的度数是( )A .24°B .28°C .33°D .48°47. 如图,⊙O 是△ABC 的外接圆,∠B =60°,⊙O 的半径为4,则AC 的长等于( )A .4 3B .6 3C .2 3D .848.如图,在⊙O 中,OC ⊥AB ,∠ADC =32°,则∠OBA 的度数是( )A .64°B .58°C .32°D .26°49. 如图,AB 是⊙O 的弦,OC ⊥AB ,交⊙O 于点C ,连接OA ,OB ,BC ,若∠ABC =20°,则∠AOB 的度数是( )A .40°B .50°C .70°D .80°50.如图,在⊙O 中,弦AC ∥半径OB ,∠BOC =50°,则∠OAB 的度数为( )A .25°B .50°C .60°D .30°(第50题) (第51题) (第52题) (第53题) (第54题)51.如图所示,AB 是⊙O 的直径,C ,D ,E 三点在⊙O 上,则∠1+∠2=__ __度.52.如图,正方形ABCD 内接于⊙O ,P 是AD ︵上任意一点,则∠ABP +∠DCP =_______.53. 如图,已知AB 是⊙O 的弦,半径OC 垂直AB ,点D 是⊙O 上一点,且点D 与点C 位于弦AB 两侧,连接AD ,CD ,OB ,若∠BOC =70°,则∠ADC =_________度.54.如图,在⊙O 的内接五边形ABCDE 中,∠CAD =35°,则∠B +∠E =_________°.55.如图,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD =34°,则∠AOE 的度数是( )A .51°B .56°C .68°D .78°56.下列四个命题:其中正确的命题有( )①圆心角是顶点在圆心的角; ②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等; ④等弧所对的圆心角相等.A .1个B .2个C .3个D .4个57.如图,在⊙O 中,AB ︵=AC ︵,∠A =30°,则∠B =( )A .150°B .75°C .60°D .15°(第57题) (第58题) (第60题) (第61题) (第62题)58.如图,在⊙O 中,若点C 是 AB ︵的中点,∠A =50°,则∠BOC =( )A .40°B .45°C .50°D .60°59. 在同圆中,下列四个命题:①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中真命题有( )A .①②③④B .①②④C .②③④D .②④60.如图,AB ,CD 分别为⊙O 的两条弦,OM ⊥AB 于点M ,ON ⊥CD 于点N ,且OM =ON ,则A .AB =CD B .∠AOB =∠COD C.AB ︵=CD ︵ D .以上结论都对61.如图,已知A ,B ,C ,D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有( )①AB ︵=CD ︵;②BD ︵=AC ︵;③AC =BD ;④∠BOD =∠AOC.A .1个B .2个C .3个D .4个62.如图,AB ,CD 是⊙O 的直径,AE ︵=BD ︵,若∠AOE =32°,则∠COE 的度数是( )A .32°B .60°C .64°D .68°63.如图,在⊙O 中,AB ︵=CD ︵,则下列结论:①AB =CD ;②AC =BD ;③∠AOC =∠BOD ;④AC ︵=BD ︵中,正确的有A .1个B .2个C .3个D .4个(第63题) (第64题) (第65题) (第66题)64.如图,AB 为⊙O 的直径,C ,D 分别为OA ,OB 的中点,CF ⊥AB ,DE ⊥AB ,下列结论:①CF =DE ;②AF ︵=FE ︵=EB ︵;③AE =2CF ;④四边形CDEF 为正方形.其中正确的是( )A .①②③B .①②④C .②③④D .①③④65.如图,点A 、B 、C 在⊙O 上,D 是的中点,若∠ACD =20°,则∠AOB 的度数为( ) A .60° B .70° C .80° D .90°66.如图,已知⊙O 是△ABD 的外接圆,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°,则∠BCD 等于( )A .116°B .32°C .58°D .64°67.如图,AB 是⊙O 的直径,点E 是半径OA 的中点,过点E 作DC ⊥AB ,交⊙O 于点C 、D ,过点D 作直径DF ,连接AF ,则∠DF A 的大小为( )A .25°B .30°C .35°D .40°(第67题) (第68题) (第69题) (第70题)68.如图,在平面直角坐标系中,⊙A 经过原点O ,并且分别与x 轴、y 轴交于B 、C 两点,已知B (8,0),C (0,6),则⊙A 的半径为( )A .3B .4C .5D .869.如图,⊙O 的半径为1,AB 是⊙O 的一条弦,且AB =,则弦AB 所对圆周角的度数为( )A .30°B .60°C .30°或150°D .60°或120° 70.如图A ,B ,C 是⊙O 上的三个点,若∠AOC =100°,则∠ABC 等于( )A .50°B .80°C .100°D .130°71.如图,AB 是⊙O 的弦,AB =10,点C 是⊙O 上的一个动点,且∠ACB =45°,若点M 、N 分别是BC 、AB 的中点,则MN 长的最大值是( )A .10B .5C .10D .2072.如图,⊙A 过原点O ,分别与x 轴、y 轴交于点C 和点D ,点B 在⊙A 上,已知∠B =30°,⊙A 的半径为2,则圆心A 的坐标是( )A .(,1)B .(1,)C .(,1)D .(1,)73.如图,AB ,CD 是⊙O 的弦,AB ⊥CD ,BE 是⊙O 的直径.若AC =3,则DE 的长是( )A .3B .3.5C .2D .1.5(第71题) (第72题) (第73题) (第74题)74.如图,点A ,B ,C ,D 为⊙O 上的四个点,AC 平分∠BAD ,AC 交BD 于点E ,CE =4,CD =6,则AE 的长为( )A .4B .5C .6D .775如图,点A ,B ,C 在⊙O 上,CO 的延长线交AB 于点D ,∠A =50°,∠B =30°,则∠ADC 的度数为 .(第75题) (第76题) (第77题) (第78题)76.如图,圆内接四边形ABCD 中两组对边的延长线分别相交于点E ,F ,且∠A =45°,∠E =30°,则∠F = .77.如图,⊙O 中两条弦AB 、CD 相交于点P ,已知P A =3,PB =4,PC =2,那么PD 长为 .78.如图,AB 是⊙O 的直径,E 是OB 的中点,过E 点作弦CD ⊥AB ,G 是弧AC 上任意一点,连结AG 、GD ,则∠G = .79.已知,如图:AB 为⊙O 的直径,AB =AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,∠BAC =45°.给出以下四个结论:①∠EBC =22.5°;②BD =DC ;③劣弧是劣弧 的2倍;④AE =BC .其中正确结论的序号是 .80.已知⊙O 的直径为10,点A 、点B 、点C 在⊙O 上,∠CAB 的平分线交⊙O 于点D .(1)如图①,若BC 为⊙O 的直径,AB =6,求AC 、BD 、CD 的长;(2)如图②,若∠CAB =60°,求BD 的长.答案1.B2.[解析] A ∵∠A =50°,OA =OB ,∴∠OBA =∠A =50°,∴∠AOB =180°-50°-50°=80°.∵C 是AB ︵的中点,∴∠BOC =12∠AOB =40°. 3.B 4.15 5.AC =BE =DF6.[答案] 40°[解析] ∵在⊙O 中,AB ︵=AC ︵,∴AB =AC.又∵∠B =70°,∴∠C =∠B =70°,∴∠A =180°-∠B -∠C =40°.7.36 108 8.39.A 10.C 11.B 12.D 13.A 14.C 15.C 16.B 17.B 18.A19.166° 20.690 21.600 22.800 23.1800-2m 24--28 CDACD 29--33 BBDAC34. 25° 35. 35° 36. 2 37.65° 38. 25° 39. 60° 40. 30° 41. 23 42--50 ACDC AADDA51. 90 52. 45° 53. 35 54. 21555--64 DBDAA DDCDA65--74. C .B .B .C .D .D .A .A .AB .75. 110°.76. 60°.77. 6.78. 60°.79.①②③.80.解:(1)如图①,∵BC 是⊙O 的直径,∴∠CAB =∠BDC =90°.∵在直角△CAB 中,BC =10,AB =6,∴由勾股定理得到:AC ===8. ∵AD 平分∠CAB ,∴=,∴CD =BD .在直角△BDC 中,BC =10,CD 2+BD 2=BC 2,∴易求BD =CD =5; (2)如图②,连接OB ,OD ,∵AD 平分∠CAB ,且∠CAB =60°,∴∠DAB =∠CAB =30°, ∴∠DOB =2∠DAB =60°.又∵OB =OD ,∴△OBD 是等边三角形,∴BD =OB =OD .∵⊙O 的直径为10,则OB =5,∴BD =5.。
北师大数学九年级下《4圆周角与圆心角的关系》强化训练含答案

综合与实践视力的变化同步练习1.若要了解全市范围内学生平均每周用电脑和写作业的时间,你将如何进行统计活动?设计一个调查方案.2.根据设计的调查方案,展开调查,根据收集的数据,你能提供哪些合理的建议?3.调查全校七、八、九年级的学生,分别记录他们的视力情况,并据此分析学生的视力状况随年龄的变化趋势.哪种方式更合算同步练习1.某商场进行促销活动,规定凡在商场一次性消费200元以上的顾客可以参加一次摸奖活动,摸奖规则如下:一个不透明的袋子里装有红(1个)、黄(2个)、绿(4个)、白(18个)除颜色外其余完全相同的小球,充分摇匀后,从中摸出一个小球,如果摸出的球是红、黄、绿色小球,顾客就可以分别获得150元、100元、50元的现金.如果不选择摸奖,则可以直接获得15元购物券,有一名顾客本次购物225元.(1)这名顾客能否参加摸奖,摸奖获得现金的概率是多少?(2)请通过计算说明选择哪种方式更合算?2.某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)该顾客最少可以得到多少元购物券?最多可以得到多少元购物券?(2)求出该顾客所获得购物券的金额不低于30元的概率.拓展延伸3.小亮看到路边上有人设摊玩“有奖掷币”游戏,规则是:交2元钱可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币正面朝上,奖金5元;如果是其他情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).小亮拿不定主意究竟是玩还是不玩,请同学们帮帮忙!(1)利用列表格或者画树状图,求出中奖的概率;(2)如果有100人,每人玩一次这种游戏,大约有___________人中奖,奖金共约是________元,则设摊者约获利_________元;(3)通过以上“有奖”游戏,你从中可得到什么启示?设计遮阳篷同步练习1.查阅有关资料,获得我们青岛地区的α和β相应数据,然后以小组为单位为某家的某个窗户设计一个遮阳篷(模型),你是如何设计的?2.南京冬至这一天正午时刻的太阳光与地平面的夹角为35︒,南京夏至这一天正午时刻的太阳光与地平面的夹角为81︒.如图设计一个直角遮阳篷BCD ,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,请求出CD 和BC 的长度.拓展延伸3.如图所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知 1tan 1.082θ≈,2tan 0.412θ≈.如果安装工人确定支架AB 高为25cm ,求支架CD 的高.(结果精确到1cm )综合练习题(一)一、选择题1. 如图,A 、B 、C 三点在正方形网格线的交点处,若将ABC △绕着点A 逆时针旋转得到''AC B △,则tan 'B 的值为()A.12 B.13 C.14 2.如图,O 的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD =,则直径AB 的长是() A.B. C. D.3.向上发射一枚炮弹,经x 秒后的高度为y 米,且高度()y 与时间()x 的关系式为2y ax bx =+.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的?()A.第8秒B.第10秒C.第12秒D.第15秒4.二次函数2365y x x =--+的图象的顶点坐标是()A.()1,8-B.()1,8C.()1,2-D.()1,4-5.如图是以ABC △的边AB 为直径的半圆O ,点C 恰好在半圆上,过C 作CD AB ⊥交AB 于D .已知3cos 5ACD ∠=,4BC =,则AC 的长为()A.1B.203C.3D.163 6.已知二次函数,()20y ax bx c a =++≠的图象如图,且关于x 的一元二次方程20ax bx c m ++-=没有实数根,有下列结论:①240b ac ->;②0abc <;③2m >.其中,正确结论的个数是().A.0B.1C.2D.3二、填空题7.在Rt ABC △中,90C ∠=︒,3AC =,4BC =,那么cos B =___________.8.在ABC △中,A ∠、B ∠均为锐角,且有(2tan 2sin 0B A +=,则ABC △的形状是___________三角形.9.一个人乘雪橇沿坡比为S (米)与时间t (秒)间的关系为2102S t t =+.若滑到坡底的时间为4秒,则此人下降的高度为______________.10.若二次函数22y ax =+的图象经过点()2,10-,则a =____________.11.已知O 的半径为3cm ,点O 到直线l 的距离5cm d =,则直线l 与O 的位置关系是__________. 12.如图为直径是52cm 圆柱形油槽,装入油后,油深CD 为16cm ,那么油面宽度AB =________cm .13.如图,在一帽长80cm ,宽50cm 的矩形风景画的四周外围镶一条金色纸边,制成一幅矩形挂画,设整个挂画总面积为2cm y ,金色纸边的宽为cm x ,则y 与x 的关系式是______________.14.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业,比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y (米)与水平距离x (米)之间满足关系22810999y x x =-++,则羽毛球飞出的水平距离为__________米.三、解答题15.如图,在Rt ABC △中,90BCA ∠=︒,CD 是中线,5cos 8B =,4CD =,求AC 的长.16.如图,在Rt ABC △中,90ACB ∠=︒.(1)先作ABC ∠的平分线交AC 边于点O ,再以点O 为圆心,OC 为半径作O (要求:尺规作图,保留作图痕迹,不写作法);(2)请你判断(1)中AB 与O 的位置关系,并证明你的结论.17.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台.为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.D CB AC BA(1)假设每台冰箱降价x 元,商场每天销售这种冰箱的利润是y 元,请写出y 与x 之间的函数表达式.(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?18.我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB ),放置在教学楼的顶部(如图所示).小明在操场上的点D 处用1米高的测角仪CD 进行测量,从点C 测得宣传牌的底部B 的仰角为37︒,然后向教学楼正方向走了4米到达点F 处,又从点E 测得宣传牌的顶部A 的仰角为45︒,已知教学楼高17BM =米,且点A 、B 、M 在同一直线上,求宣传牌AB 的高度.(结果精确到0.1米,1.73,sin 370.60︒≈,cos370.81︒≈,tan 370.75︒≈)19.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y (毫克/百毫升)与时间x (时)的关系可近似地用二次函数2200400y x x =-+刻画,1.5小时后(包括1.5小时)y 与x 可近似地用反比例函数()0k y k x=>刻画,如图所示.(1)根据上述数学模型计算:①喝酒后几小时血液中的酒精含量达到最大值?最大值为多少?②当5x =时,45y =,求k 的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.20.在平面直角坐标系xOy 中,过原点O 及点()0,2A ,()6,0C 作矩形OABC ,AOC ∠的平分线交AB于点D .点P 从点O OD 方向移动;同时点Q 从点O 出发,以每秒2个单位长度的速度沿x 轴正方向移动.设移动时间为t 秒.(1)当点P 移动到点D 时,求出此时t 的值;(2)当t 为何值时,PQB △为直角三角形.综合练习题(二)一、选择题1.如图,为了测量河流某一段的宽度,在河北岸选了一点A ,在河南岸选相距200米的B ,C 两点,分别测得60ABC ∠=︒,45ACB ∠=︒,则这段河的宽度为()米.A.B. C.(1003- D.(10032.如图,O 是ABC △的外接圆,已知60B ∠=︒,则CAO ∠的度数是()A.15︒B.30︒C.45︒D.60︒3.已知二次函数()20y ax bx c a =++≠的图象如图所示,给出以下结论:①0a >;②该函数的图象关于直线1x =对称;③当1x =-或3x =时,函数y 的值都等于0.其中正确结论的个数是().A.3B.2C.1D.04.图(1)是一个横断面为抛物线形状的拱桥,当水面在l 时,拱顶(拱桥洞的最高点)离水面2m ,水面宽4m .如图(2)建立平面直角坐标系,则抛物线的关系式是().A.22y x =-B.22y x =C.212y x =-D.212y x = 5.已知0a ≠,在同一直角坐标系中,函数y ax =与2y ax =的图象有可能()A.B.C.D.二、填空题 6.抛物线()212y x =-+的对称轴是___________,顶点坐标是_____________.7.如图,直角坐标系,α∠的顶点在原点,始边与x 轴的正半轴重合,终边经过点()3,4P ,则sin α=____________,tan α=___________.8.如图,AB 是O 的直径,弦CD AB ∥.若65ABD ∠=︒,则ADC ∠=___________.9.已知二次函数2y ax bx c =++中,函数y 与自变量x 的部分对应值如下表:10.如图,抛物线()20y ax bx c a =++>的对称轴是过点()1,0且平行于y 轴的直线,若点()4,0P 在该抛物线上,则42a b c -+的值为___________.11.如图,点A 、B 、C 都在圆O 上,如果84AOB ACB ∠+∠=︒,那么ACB ∠的大小是_______.12.如图,在ABC △中,30A ∠=︒,45B ∠=︒,AC =,则AB 的长为_________.三、解答题13.如图,在Rt ABC △中,90ACB ∠=︒,以AC 为直径作O 交AB 于点D ,连接CD .(1)求证:A BCD ∠=∠.(2)若M 为线段BC 上一点,试问:当点M 在什么位置时,直线DM 与O 相切?并说明理由. 14.如图,在一个坡角为40︒的斜坡上有一棵树BC ,树高4米.当太阳光AC 与水平线成70︒角时,该树在斜坡上的树影恰好为线段AB ,求树影AB 的长.(结果保留1位小数;参考数据:sin 200.34︒≈,tan 200.36︒≈,sin 300.50︒≈,tan 300.58︒≈,sin 400.64︒≈,tan 400.84︒≈,sin 700.94︒≈,tan 70 2.75︒≈)15.某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y (万件)与销售单价x (元)之间的关系可以近似地看作一次函数2100y x =-+.(利润=售价-制造成本) (1)写出每月的利润z (万元)与销售单价x (元)之间的函数解析式.(2)销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?(3)根据相关部门规定,这种电子产品的销售单价不得高于32元.如果厂商要获得每月不低于350万元的利润,那么制造这种产品每月的最低制造成本需要多少万元?16.某小学门口有一直线马路,为方便学生过一马路,交警在门口设有一定宽度的斑马线,斑马线的宽度为4米.为安全起见,规定车头距斑马线后端的水平距离CD 不得低于2米.现有一旅游车在路口遇红灯刹车停下,此时汽车里司机与斑马线前后两端的视角分别为16FAE ∠=︒和31FAD ∠=︒,司机距车头的水平距离为0.8米.(E 、D 、C 、B 四点在平行于斑马线的同一直线上)(1)旅游车高至少多少米?(2)该旅游车停车是否符合上述安全标准?(参考数据:sin 310.52︒≈,tan 310.60︒≈,sin160.27︒≈,tan160.28︒≈)17.我市某工艺厂为配合北京奥运,设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,猜想y 与x 的函数关系,并求出函数关系式.(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?18.已知:如图,在Rt ABC △中,90BCA ∠=︒,6cm AC =,8cm BC =,D 是AB 的中点,连接CD ,点P 从点C 出发,沿CD 方向,向点D 匀速运动,速度为1cm /s ;同时,点Q 从点B 出发,沿BA 方向,向点A 匀速运动,速度为2cm /s ,连接BP 、PQ ,设运动时间为()()05t s t ≤≤,PQB △的面积为()2cm y .解答下列问题:(1)过点C 作CE AB ⊥于E ,求CE 的长.(2)求y 与t 之间的函数关系式;当t 为何值时,y 有最大值,并求出y 的最大值.(3)是否存在某一时刻t ,使得PQD △为等腰三角形?若存在,求出此时t 的值;若不存在,请说明理由.综合与实践答案视力的变化略.哪种方式更合算 答案同步练习1.解:(1)能,124725252525++=. (2)1241501005022252525⨯+⨯+⨯=(元).2215>,∴选择摸奖更合算. 2.解:(1)最少可以得到10元购物券,最多可以得到50元购物券.(2)不低于30元的概率为23. 拓展延伸3.(1)解:掷两枚硬币出现的情况是(正,正)、(正,反)、(反,正)、(反,反),故出现两枚硬币都正面朝上的概率,即中奖的概率是14(表格、树状图略) (2)25,125,75.解析:由(1)可得:中奖的概率是14,则如果有100人,每人玩一次这种游戏,大约有1100254⨯=(人)中奖,奖金约255125⨯=(元).设摊者约获利为100212575⨯-=(元). (3)谨慎参加类似的活动(只要合理就行).设计遮阳篷答案同步练习1.略2.略拓展延伸3.解:过点A 作AE BC ∥,则2EAF CBG θ∠=∠=,且25cm EC AB ==.在Rt ADF △中,1tan DF AF θ=,在Rt EAF △中,2tan EF AF θ=,()12tan tan DE DF EF AF θθ∴=-=-.又140cm AF =,1tan 1.082θ≈,2tan 0.412θ≈,()()140 1.0820.41293.8cm DE ∴⨯-=≈.()93.825118.8119cm CD DE CE ∴=+=+=≈.答:支架CD 的高约为119cm .综合练习题(一)答案一、1.B 2.D 3.B 4.A 5.D 6.D二、7.458.等边 9.36米 10.2 11.相离 12.48 13.()()802502y x x =++ 14.5三、15.解:90BCA ∠=︒,CD 是中线,2AB CD ∴=.4CD =,8AB ∴=.5cos 8BC B AB==,5BC ∴=.由勾股定理可得AC16.解:(1)如图(1):O 即为所求.(2)AB 与O 相切.证明:作OD AB ⊥于D ,如图(2).BO 平分ABC ∠,90ACB ∠=︒,OD AB ⊥,OD OC ∴=,AB ∴与O 相切.17.解:(1)()2224002000842432005025x y x x x ⎛⎫=--+⨯=-++ ⎪⎝⎭. (2)当4800y =时,22243200480025x x -++=, 解得1100x =,2200x =.答:为使老百姓得到实惠,每台冰箱应降价200元.(3)当1502b x a=-=时,max 5000y =. 答:降价150元时,商场每天销售这种冰箱的利润最高,最高为5000元. 18.宣传牌AB 的高度约1.3m . 19.解:(1)①()222004002001200y x x x =-+=--+,∴喝酒后1小时血液中的酒精含量达到最大值,最大值为200毫克/百毫升. ②当5x =时,45y =,()0k y k x=>, 455225k xy ∴==⨯=.(2)不能驾车上班; 理由:晚上20:00到第二天早上7:00,一共有11小时,∴将11x =代入225y x =,则2252011y =>, ∴第二天早上7:00不能驾车去上班.20.解:(1)矩形OABC ,90AOC OAB ∴∠=∠=︒. OD 平分AOC ∠,45AOD DOQ ∴∠=∠=︒.∴在Rt AOD △中,45ADO ∠=︒,2AO AD ∴==,OD =2t ∴==. (2)要使PQB △为直角三角形,显然只有90PQB ∠=︒或90PBQ ∠=︒. 如图,作PG OC ⊥于点G .在Rt POG △中,45POQ ∠=︒,45OPG ∴∠=︒.2OP =,OG PG t ∴==,∴点P 坐标为(),t t .又()2,0Q t ,()6,2B ,()()22262PB t t ∴=-+-,()222622BQ t =-+, ()222222PQ t t t t =-+=.①若90PQB ∠=︒,则有222PQ BQ PB +=,()()()22222262262t t t t ⎡⎤∴+-+=-+-⎣⎦, 整理得2480t t -=,解得10t =(舍去),22t =. 2t ∴=.②若90PBQ ∠=︒,则有222PB BQ PQ +=,()()()22222626222t t t t ⎡⎤⎡⎤∴-+-+-+=⎣⎦⎣⎦,整理得210200t t -+=,解得5t =∴当2t =或5t =5t =PQB △为直角三角形. 综合练习题(二)答案一、1.C 2.B 3.B 4.C 5.C二、6.直线1x =,()1,2 7.45,438.25︒ 9.04x << 10.0 11.28︒ 12.33+三、13.(1)证明:AC 为直径,90ADC ∴∠=︒, 90A DCA ∴∠+∠=︒.90ACB ∠=︒,90DCB DCA ∴∠+∠=︒,A DCB ∴∠=∠.(2)解:当MC MD =(或点M 是BC 的中点)时,直线DM 与O 相切. 理由:如图,连接DO .DO CO =,12∴∠=∠.DM CM =,43∴∠=∠.2490∠+∠=︒,1390∴∠+∠=︒,∴直线DM 与O 相切.14.2.7米15.解:(1)()18z x =-()()218210021361800y x x x x =--+=-+-,z ∴与x 之间的函数解析式为221361800z x x =-+-. (2)由350z =,得235021361800x x =-+-, 解此方程,得125x =,243x =.∴销售单价应定为25元或43元,可获得350万元的利润.把221361800z x x =-+-配方,得()2234512z x =--+.因此,当销售单价为34元时,厂商每月能够获得最大利润,最大利润是512万元. (3)结合(2)及函数221361800z x x =-+-的图象(如图所示)可知,2543x ≤≤时,350z ≥.又由限价为32元,得2532x ≤≤.根据一次函数的性质,得2100y x =-+中y 随x 的增大而减小,∴当32x =时,每月制造成本最低.最低成本是()182********⨯-⨯+=(万元).因此,每月的最低制造成本需要648万元.16.解:16FAE ∠=︒,31FAD ∠=︒,16AEB FAE ∴∠=∠=︒,31ADB FAD ∠=∠=︒. 设CD x =.在Rt ABE △中,tan AB AEB BE ∠=,tan1640.8AB x︒=++, ()40.80.28AB x ∴++⨯≈.在Rt ABD △中,tan AB ADB DB ∠=,tan310.8AB x ︒=+, ()0.80.6AB x ∴+⨯≈.()()40.80.280.80.6x x ∴++⨯=+⨯.2.7x ∴=.(1)()()0.80.60.8 2.70.6 2.1AB x +⨯=+⨯=≈.答:旅游车高至少2.1米.(2) 2.72>,∴该旅游车停车符合上述安全标准.17.解:(1)画图如下图.由图可猜想y 与x 是一次函数关系,设这个一次函数为()0y kx b k =+≠.这个一次函数的图象经过()30,500,()40,400这两点,50030,40040,k b k b =+⎧∴⎨=+⎩,解得10,800,k b =-⎧⎨=⎩ ∴函数关系式是10800y x =-+.(2)设工艺厂试销该工艺品每天获得的利润是W 元,依题意得()()2010800W x x =--+210100016000x x =-+-()210509000x =--+,∴当50x =时,W 有最大值9000.∴销售单价定为50元/件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.(3)对于函数()210509000W x =--+,当45x ≤时,W 的值随着x 值的增大而增大,∴销售单价定为45元/件时,工艺厂试销该工艺品每天获得的利润最大.18.解:(1)Rt ABC △中,()10cm AB .1122ABC S AC BC AB CE =⋅=⋅△, 6810CE ∴⨯=⨯,()4.8cm CE ∴=. (2)过点P 作PF AB ⊥于F .ABC △为直角三角形,D 是AB 的中点,152CD AB ∴==. PF CE ∥,C E PDF D ∴∽△△,PD PF CD CE ∴=,55 4.8t PF -=, 2424525PF t ∴=-. 21124242424222525255y BQ PF t t t t ⎛⎫∴=⋅=⋅⋅-=-+ ⎪⎝⎭. 即22456252y t ⎛⎫=--+ ⎪⎝⎭. 0a <,∴图象开口向下,函数有最大值.因为顶点为5,62⎛⎫ ⎪⎝⎭,∴当52t =时,6y =最大. (3)当0t =时,PDQ △是等腰三角形. ①若PD QD =(如图(1)),则525t t -=-,103t ∴=. ②若PD PQ =,作PH DQ ⊥于H (如图(2)).B A BCEC ∽△△,BE BC BC AB∴=, 8810BE ∴=, 6.4BE ∴=. 6.45 1.4DE ∴=-=.PH CE ∥,C E PDH D ∴∽△△,DH PD DE CD∴=, 51.45DH t -∴=, ()7525DH t ∴=-. PDQ △为等腰三角形,PH DQ ⊥.2DQ DH ∴=,()7252525t t ∴-=⨯-,19564t ∴=. ③若DQ PQ =,作QF PD ⊥于F (如图(3)).D E DFQ C ∽△△,DF DQ DE CD ∴=,251.45DF t -∴=, ()72525DF t ∴=-. PDQ △为等腰三角形,QF PD ⊥,2PD DF ∴=,()7522525t t ∴-=⨯-, 17053t =. 综上所述,当0t =,103,19564或17053时,PQD △为等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
松滋市实验中学九年级培优辅差《圆周角》训练题
命题人:胡海洋
题号一、选择题二、填空题三、简答题总分
得分。
一、选择题
1、如图,内接于,若,则的大小为()
A.B. C.D.
)
(第1题)(第2题)(第3题)(第4题)(第5题)
2、如图,AB是的直径,点C、D在上,,则()A.70° B.60° C.50° D.40°
3、如图,是的外接圆,已知,则的大小为()
A.40° B.30° C.45°
D.50°
4、如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C= ( )
A.180°B.90°C.45°D.30°
¥
5、如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35º C.20º与40º D.30º与35º
6、. 如右图,A、B、C、D为⊙O的四等分点,若动点P从点C出发,沿C→D→O→C路线作匀速运动,设运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是
A B C
D
二、填空题
7、如图,在⊙O中,∠AOB=46º,则∠ACB=º.
8、如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 º,那么∠B= º.
—
(第7题)(第8题)(第9题)(第10题)(第11题)
9、如图,AB是⊙0的直径,弦AC长为4a,弦BC长为5a,∠ACB的平分线交⊙0于点D,则CD的长为 .
10、如图, ⊙P过O、、,半径PB⊥PA,双曲线恰好经过B点,则k的值是
____________.
11、如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____________.
12、如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交BC于点D,连接DC,则∠
DCB= 。
(第12题)(第13题)(第14题)
】
13、如图,为的直径,点为其半圆上任意一点(不含、),点为另一半圆上一定点,若
为度,为度.则与的函数关系是.
14、如图,是半圆的直径,为圆心,是半圆上一点,且,是延长线上一点,与半圆相交于点,如果,则,,.
三、简答题
15、AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连BC.若,求的度数.
`
16、已知AB、AC为⊙O的两条弦
(1)用直尺(没有刻度)和圆规作出弧BC的中点D;
(2)连接OD,则OD∥AC吗若成立,请证明;若不成立,请添加一个适当的条件,
使之成立,再证明.
}
17、如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长。
,BF和AD交于E,
18、.如图20-12,BC为⊙O的直径,AD⊥BC,垂足为D,AB AF
求证:AE=BE.。
19、在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
{
20、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知AD=6求圆心O到BD的距离.
21、如图,⊙ 0是ABC的外接圆,AD是⊙0的直径,DE⊥ BC于E,AF⊥BC于F
(1)求证BE=CF;
(2)作OG ⊥BC于G,若DE=BF=3,OG=1,求弦AC的长.
》
22、如右图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=10,求弦AC的长.
:
23、.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD。
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系请证明你的结论。
{
24、如图,⊙O为四边形的外接圆,圆心在上,∥。
(1)求证:AC平分;
(2)若AC = 8,AC:CD=2:1试求⊙C的半径;
(3)
%
`
¥
参考答案
一、选择题
{
1、D
2、D
3、A
4、B
5、B
6、C
二、填空题
¥
7、【考点】圆周角定理.
【分析】由⊙O中,∠AOB=46°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠ACB的度数.
【解答】解:∵⊙O中,∠AOB=46°,
∴∠ACB=1 2 ∠AOB=1 2 ×46°=23°.
故答案为:23.
【点评】此题考查了圆周角定理.此题比较简单,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用,注意数形结合思想的应用.
8、21°
9、
[
10、-4
11、65°
12、30度
13、
14、
三、简答题
15、证明:切⊙O于是⊙O的直径,
!
∴.
,∴.
∴.
16、解:(1)作图略……………………………………… 3分
(2) 不成立,添加:AB是直径…………… 2分
证明略……………………………… 3分
17、3
18、证明:连结AB,AC,
-
∠BAD=∠ABF AE=BE.
19、解:连接BD
∵AB⊙O是直径
∴BD⊥AD
又∵CF⊥AD
∴BD∥CF
∴∠BDC=∠C…………………………3分
(
又∵∠BDC=∠BOC
∴∠C=∠BOC
∵AB⊥CD
∴∠C=30°
∴∠ADC=60°…………………………………………………………………6分20、考点:圆周角定理;三角形内角和定理;垂径定理。
解答:解:(1)∵∠APD=∠C+∠CAB,
∴∠C=65°﹣40°=25°,
》
∴∠B=∠C=25°;
(2)作OE⊥BD于E,
则DE=BE,
又∵AO=BO,
∴,
圆心O到BD的距离为3.
21、(1)证明:延长DE交⊙0于B,
~
连接AH、BH.则四边形AHEF为矩形,
∴AF=EH,AH//EF,∴∠HAB=∠ABC,
∴BH =AC,∴ Rt△BEH≌ Rt△CFA,.∴ BE=CF;
(2)解:连接CD,连接FO并延长交DE于P点.
则AFO≌△DPO,∴ AF=DP,OF=OP,
∴OG= PE,∴PE=2,∴AF=DP=1
∵DE=BF=CE,∴∠BCD=45°
又∠ACD=90°,:. ∠ACB=45°.
∴AC=
22、解:∵BD为⊙O的直径,∴∠BAD=90°
,
23、(1)证明:连接OD,∵AB是直径,AB⊥CD,∴∠COB=∠DOB=。
又∵∠CPD=,∴∠CPD=∠COB。
(2)∠CP′D与∠COB的数量关系是:∠CP′D+∠COB=180°。
证明:∵∠CPD+∠CP′D=180°,∠CPD=∠COB,∴∠CP′D+∠COB=180°。
24、解:(1)∵OC//AB,∴∠BAC=∠ACO,
∵ OC=OA∴∠ACO =∠CAO
∴∠CAO=∠BAC即:AC平分∠DAB
(2)AC=8,弧AC与CD之比为2:1,
∴∠CAD=30°∵AD是直径,∴∠ACD=90°,
∴ AD=∴圆O的半径为
(3)∵点B为弧AC的中点∴∠BAC=∠BCA,
∴∠BAC=∠BCA=∠=OAC=∠OCA∴OA//BC
∴四边形ABCO是平行四边形∵ AO=CO ∴四边形ABCO为菱形。
