试验9不良导体导热系数的测定
物理实验报告测量不良导体的导热系数.docx

物理实验报告测量不良导体的导热系数.docx 摘要:本实验是测量不良导体的导热系数实验,主要目的是研究不同材料的导热性质,并通过实验方法测量导热系数。
实验过程中,先选取了两种不同的材料(石棉、灰铸铁)进行实验,然后分别利用导热仪和热传导仪测算材料的导热系数,并计算结果。
结果表明,两种材料的导热系数差别较大,石棉的导热系数远小于灰铸铁的导热系数。
本实验得到的结果对于进一步了解材料的物性能有重要意义。
关键词:导热系数,导热仪,热传导仪,试样,材料引言:导热系数是指在单位时间内,单位面积的材料温度梯度下,单位厚度内热量传递的能力。
导热系数是一个材料对热传导的基本反应,它是材料的一个基本物理参数,不同材料的导热系数大小差别较大,因此对于不同材料的导热系数进行测量具有重要意义。
实验项目:1.测量石棉的导热系数;实验原理:一、导热仪法导热仪法是利用导热仪来测量不同材料的导热系数。
导热仪是一种用于测量导热系数的仪器,利用它可以轻松地测量导热系数,而且测量结果比较精确。
导热仪分为静态导热仪和动态导热仪两种。
静态导热仪是指采用一定时间后的热平衡来测量材料的导热系数,它的原理是利用热传导平衡定理。
热传导平衡定理是指当物体的温度分布达到稳定状态时,所有点的温度分布相同,在每个点上的热流密度相等,因此可以根据热流密度和热传导系数的定义求得导热系数。
动态导热仪是指在一定时间内,通过测量目标材料表面和内部温度的变化来测量材料的导热系数。
动态导热仪具有快速、精确、稳定的特点,可以在室温下测量导热性能。
利用热传导仪测量材料的导热系数时,首先需要将试样放置在热源上,并使热源产生热量。
然后,利用热流计和温度计测量试样内外的温度差,从而计算出材料的导热系数。
实验步骤:1.选定两种不同材料(石棉、灰铸铁)作为试验样品;2.利用切割机将两种材料切割成长方形样品;5.利用计算机软件计算出试样的导热系数。
实验结果:(1)导热仪法:0.004 (W/mK)2.灰铸铁的导热系数:分析:通过实验结果可以看出,石棉的导热系数要小得多,而灰铸铁的导热系数则要大得多。
不良导体导热系数的测量 (9

热 导 系 数 的 测 量李索恒 PB07210395实验目的:了解热传导现象的物理过程,学习用稳态平板法测量不良导体的热传导系数并用作图法求冷却速率实验原理:1. 导热系数当物体内存在温度梯度时,热量从高温流向低温,传热速率正比于温差和接触面积,定义比例系数为热导系数:dQ dTdS dt dxλ=- 2. 不良导体导热系数的测量厚度为h 、截面面积为S 的样品盘夹在加热圆盘和黄铜盘之间。
热量由上方加热盘传入。
两面高低温度恒定为1T 和2T 时,传热速率为:S hT T dt dQ21--=λ 热平衡时,样品的传热速率与相同温度下盘全表面自由放热的冷却速率相等。
因此每隔30秒记录铜盘自由散热的温度,一直到其温度低于2T ,可求出铜盘在2T 附近的冷却速率dtdT。
铜盘在稳态传热时,通过其下表面和侧面对外放热;而移去加热盘和橡胶板后是通过上下表面以及侧面放热。
物体的散热速率应与它们的散热面积成正比:()()dtQ d h R R h R R dt dQ '++=222ππ 式中dtQ d '为盘自由散热速率。
而对于温度均匀的物体,有 dtdTmc di Q d =' 联立得:()()dtdT mc h R R h R R dt dQ 222++=ππ结合导热系数定义即可得出样品的导热系数表达式。
实验内容:1. 用卡尺测量A 、B 盘的厚度及直径(各测三次,计算平均值及误差)。
2. 按图连接好仪器。
3. 接通调压器电源,等待上盘温度缓慢升至1T =3.2~3.4mV4. 将电压调到125V 左右加热,来回切换观察1T 和2T 值,若十分钟基本不变(变化小于0.03)则认为达到稳态,记录下1T 和2T 的值5. 移走样品盘,直接加热A 盘,使之比2T 高10℃(约0.4 mV );调节变压器至零,再断电,移走加热灯和传热筒,使A 盘自然冷却,每隔30s 记录其温度,选择最接近2T 的前后各6个数据,填入自拟表格数据处理:样品盘质量898.5m g =上盘稳定温度1 3.17T mV =下盘稳定温度2 2.56T mV =样品盘比热容10.3709()c kJ kg K -=⋅⋅实验前室温=21.8C T ︒室 实验后室温=22.6C T '︒室几何尺寸均使用游标卡尺测量:自由散热降温时下盘温度:下面先处理几何数据:取0.95P =,3n = 则0.95 4.30t = 1.96p k =a) 对下盘厚度A h :0.768A h cm =0.002/0.001A A h u cm σ===游标卡尺测量:C =0.002cm ∆=仪 由于下盘∆估因较小而忽略0.002cm B ∆=∆=仪0.950.006U cm ===最后:(0.7680.006)Ah cm =±0.95P =b) 对下盘直径A D :12.954A D cm = /0.002/0.001AA D u cm σ===游标卡尺测量:C =0.002cm ∆=仪 考虑直径判断误差,取0.01cm ∆=估0.01cm B ∆==0.950.012U cm ===最后:(12.9540.012)AD cm =±0.95P =c) 对样品盘厚度B h :0.757B h cm = 0.002BA h u cm σ===游标卡尺测量:C =0.002cm ∆=仪 由于样品质地较软,取0.01cm ∆=估0.01cm B ∆==0.950.014U cm ===最后:(0.7570.014)Ah cm =±0.95P =d) 对下盘直径B D :12.995B D cm = /0.006/0.003BA D u cm σ===游标卡尺测量:C =0.002cm ∆=仪 考虑直径判断误差,且样品较软,取0.02cm ∆=估0.02cm B ∆==0.950.026U cm ===最后:(12.9950.026)BD cm =±0.95P =电压表测量:3C = 0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪0.95/ 1.960.005/30.003P B U k C mV =∆=⨯=最后:1(3.170.00)T mV =±0.95P =f)对下盘稳定温度2T :由于只测量了一次,因此只计算B 类不确定度电压表测量:3C =0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪0.95/ 1.960.005/30.003P B U k C mV =∆=⨯=最后:1(2.560.00)T mV =±0.95P =1. 逐差法将12个数据前后分成2组,然后对应相减:(对应组数据时间差630180t s s ∆=⨯=)0.25T mV ∆=0.02T mV σ= /0.02/0.008A T u mV σ===电压表测量:3C =0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪等效测量次数6n =,取0.95P =,则0.95 2.57t = 1.96p k =0.950.02U mV ===最后:(0.250.02)TmV ∆=±0.95P =得出逐差法降温速度:30.25 1.38910/180dT T mV s dt t -∆===⨯∆根据公式:()()21224()2B A A B A A mch D h dTdtD T T D h λπ+=⋅-+代入数据:()()323322320.8985(0.370910)(0.75710)12.95440.76810 1.389103.14(12.99510)(3.17 2.56)12.95420.76810λ-----⨯⨯⨯⨯⨯⨯+⨯⨯=⨯⨯⨯⨯⨯-⨯+⨯⨯得到:110.240W m K λ--=⋅⋅由不确定度传递公式:()()122ln lnln ln 42ln ln 2ln ln()B A A B A A mch D h D D h V V V tλπ=+++--++∆--∆ 求微分:()()121242()242A A A A B B B A A B A A d D h d D h dh dD d V V d d V h D h D D h V V V λλ++-∆=+--+-++∆- 合并同类项:1212122()(42)4242B B A A A A B B A A A A A A A A dh dD dD dD dh dh dV dV d d V h D D h D h D h D h V V V V V λλ∆=-+-+-+-+++++∆--转化成不确定度:12222222221212222()()()[][]()()()(4)(2)(4)(2)B B A A h D A D A h V V T B B A A A A A A A A U U h U D U U U U U h D D h D h D h D h T V V V V λλ∆=++++++++++∆--即:U λ=代入数据: U λ= 得:110.039U W m K λ--=⋅⋅0.95P =最后:2. 作图法先在2 2.56T mV =前后取点,再作一直线,使所取个点尽量均匀的分布在直线两边。
不良导体导热系数的测定

况。
由于热电偶冷端的温度为0℃,当温度θ变化范 围不太大时,其温差电动势ε与待测温度θ存在线性关 系,即有,所以可用测得的温差电动势ε代替温度θ。 将测得的数据作ε~t图,图中曲线在ε2处的斜率为, 求得铜盘A在θ2时的冷却速率为。
Q mc d (RA2 2RAhA )
t
dt 2(RA2 RAhA )
不良导体导热系数的测定
【预习要点】 了解导热系数的两种测量方法,即稳态法和动态
法。本实验采用稳态法测定不良导体的导热系数。
【实验目的】 1、学会用稳态平板法测定不良导体的导热系数 2、学习用作图法求散热速率。
【仪器用具】 导热系数测定仪、热电偶2副、直流数字电压表、
游标卡尺、天平、停表等。
【实验原理】 由傅里叶热传导方程可知,对于半径为RB、厚度
【思考题】 1、改变样品形状,采取一些措施,能否利用本
实验装置测量良导体的导热系数?为什么?
(2)
பைடு நூலகம்
由于物体的冷却速率与它的表面积成正比,则 稳态时,铜盘A的散热速率为
mc d (RA 2hA )
hB
(3)
dt 2(RA hA ) (1 2 )RB 2
式中ε1、ε2匙对应于温度θ1、θ2的电压表读数。
【实验内容】 导热系数测定仪主要由加热装置和散热铜盘组
成。待测样品应放在加热装置底盘和散热铜盘之间, 并紧密接触。当系统的加热功率等于散热功率时, 系统的温度分布将趋于稳定。利用稳态法测量样品 的导热系数就是在温度场的分布不随时间变化时, 测量样品上下表面的温度。这两个温度可用与样品 紧密接触的上下铜盘的温度代替。
为hB的圆盘样品,在单位时间内通过待测样品B任一 圆戒面的热流量为
δQ δt
不良导体导热系数的测定_3

不良导体导热系数的测定一、实验中,测量导热系数的公式为:)()(2)2(21εεπελ-++=B B A A A A R h h R h R dt d c m式中21,εε 是稳态时对应于加热铜盘C ,散热铜盘A 的温度分别为 21,θθ的电压表的读数。
dtd ε:铜盘A 在温度为2θ时的散热速率 m : 铜盘A 的质量 已知 g m 00.896=c :铜的比热已知 11385--⋅⋅=C Kg J cA R :铜盘A 的半径已知cm R A 00.132= A h :铜盘A 的厚度已知 cm h A 754.0= B h :待测样品B 的厚度 已知 cm h B 800.0= B R :待测样品B 的半径已知cm R B 00.132=二、实验步骤:1. 小心地将橡胶塞从杜瓦瓶里拔出,将它(连同两根玻璃管)斜靠在基座,如图(1)所示。
将杜瓦瓶装上适量的水和冰块,小心地把橡胶塞连同两根玻璃管塞入瓶中。
(1)2.将铜盘A放在三脚支架上并使之不与周围的三个金属柱接触。
然后,在铜盘A 上放上待测的橡胶盘B,如图(2)。
3.将红外加热装置连同加热铜盘C压在待测的橡胶盘B上。
把热电偶的热端分别插入铜盘C和铜盘A;将红外加热炉的防护罩罩好,如图(3)。
4.将电压表接好,并调零。
把拨动开关拨到上方,电源开关拨到220V,关风扇。
此时,电压表显示的是铜盘C 的温度。
如图(4)。
(2)(3)(4)铜盘A橡胶盘B 三脚支架热电偶热端5. 10分钟后,电源开关拨到110V ,开风扇。
此后,每隔2分钟记录一次上下铜盘的温度,直到连续的三次记录中,上盘的温度不变,同时下盘的温度也不变。
这时系统达到了稳态,将稳态时的温度值记为s s 21,εε 表格1:6. 关电源,关风扇,停止加热。
移去橡胶盘, 使铜盘C 直接接触铜盘A ,拨动开关拨到下方, 电源开关拨到220V 进行加热。
此时,电压表显 示的是铜盘A 的温度。
7. 铜盘A 的温度比稳态时的温度增加1mV ,停止加热。
不良导体导热系数的测量实验及改进

不良导体导热系数的测量实验及改进■闫钰龙201300121192(山东大学信息科学与工程学院电信一班)[摘要]以传热学相关理论及数学工具软件,对稳态法测量不良导体导热系数实验中的数据处理进行改进。
[关键词]导热系数;稳态法;牛顿冷却定律;回归分析1、引言导热系数是反映物质材料热传导能力的物理量,在理论研究和工程应用上有重要的价值。
其定义为在稳定传热条件下,1m厚的材料,两侧表面温差为1度(K或℃)时,1s内通过1㎡的的面积传递的热量,单位为W/(m·K)。
它与材料的组成、结构、密度、含水率、温度等影响因素有关。
而固体由自由电子和原子组成,原子被束缚在规律排列的晶格之中。
在这种构形下,热能传导主要通过自由电子的迁移和晶格的振动波实现。
金属之中,电子对热传导的贡献最大。
而本实验的不良导体中,晶格振动子起着主要作用。
由于导热系数牵涉了如此多的外部条件,所以具体材料的导热系数往往需要实验测定。
测量导热系数的方法分为稳态法和动态法两类,本次实验采用稳态法,通过加热和传热使得样品内部形成稳定的温度分布,从而测得样品的导热系数。
笔者在实验之余又对数据处理方式进行了些许改进,并写入了本文之中,使之更接近于真实值。
2、实验原理图1 热传导原理图导热系数的测定基于热传导的基本公式——傅里叶方程:⑴在方程中,表示在时间内通过面元传递的热量,是沿面元法向的温度梯度,即材料的导热系数,方程中的负号表示热流传递方向与温度梯度的方向相反。
实验所采用的样品盘厚度为,面积为,侧面绝热,当上下表面分别被加热到和时,在时间内传导的热量为,导热系数的表达式变为:⑵通过实验装置中的加热盘与散热盘分别对样品盘上下表面进行加热与散热,使之达到热稳定状态,而后撤去样品盘使之在左右自然散热。
结合散热盘的比热容与质量,并对有无样品盘覆盖时的散热盘散热面积进行修正,得到表达式:⑶温度通过热电偶与数字电表联合测得。
热电偶高温端与低温端温差为时,温差电动势为,冷端温度保持℃,则。
非良导体导热系数的测量实验
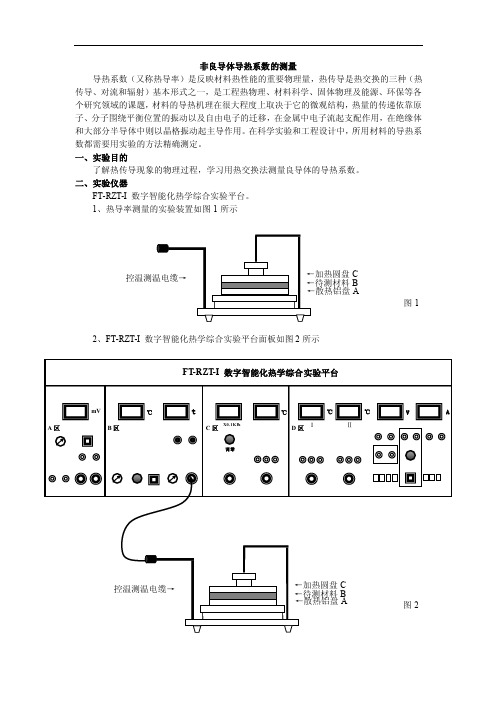
非良导体导热系数的测量导热系数(又称热导率)是反映材料热性能的重要物理量,热传导是热交换的三种(热传导、对流和辐射)基本形式之一,是工程热物理、材料科学、固体物理及能源、环保等各个研究领域的课题,材料的导热机理在很大程度上取决于它的微观结构,热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移,在金属中电子流起支配作用,在绝缘体和大部分半导体中则以晶格振动起主导作用。
在科学实验和工程设计中,所用材料的导热系数都需要用实验的方法精确测定。
一、实验目的了解热传导现象的物理过程,学习用热交换法测量良导体的导热系数。
二、实验仪器FT-RZT-I 数字智能化热学综合实验平台。
1、热导率测量的实验装置如图1所示2、FT-RZT-I 数字智能化热学综合实验平台面板如图2所示C B A图1三、实验原理1882年法国科学家傅立叶(J.Fourier )建立了热传导理论,目前各种测量导热系数的方法都是建立在傅立叶热传导定律的基础之上。
测量的方法可以分为两大类:稳态法和瞬态法,本实验采用的是稳态平板法测量不良导体的导热系数。
当物体内部有温度梯度存在时,就有热量从高温处传递到低温处,这种现象被称为热传导。
傅立叶指出,在dt 时间内通过dS 面积的热量dQ ,正比于物体内的温度梯度,其比例系数是导热系数,即:dS dxdTdt dQ -λ= (1) 式中dtdQ 为传热速率,dx dT 是与面积dS 相垂直的方向上的温度梯度,“-”号表示热量由高温区域传向低温区域,λ是导热系数,表示物体导热能力的大小,在SI 中λ的单位是W ·m -1·K -1。
对于各向异性材料,各个方向的导热系数是不同的(常用张量来表示)。
如图4所示,设样品为一平板,则维持上下平面有稳定的T 1和T 2(侧面近似绝热),即稳态时通过样品的传热速率为B BS h TT dt dQ 21-λ= (2) 式中h B 为样品厚度,S B =πR 2B 为样品上表面的面积,(T 1-T 2)为上、下平面的温度差,λ为导热系数。
试验9不良导体导热系数的测定

实验九不良导体导热系数的测量导热系数(热导率)是反映材料热性能的物理量,导热是热交换三种(导热、对流和辐射)基本形式之一,是工程热物理、材料科学、固体物理及能源、环保等各个研究领域的课题之一,要认识导热的本质和特征,需了解粒子物理而目前对导热机理的理解大多数来自固体物理的实验。
材料的导热机理在很大程度上取决于它的微观结构,热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移,在金属中电子流起支配作用,在绝缘体和大部分半导体中则以晶格振动起主导作用。
因此,材料的导热系数不仅与构成材料的物质种类密切相关,而且与它的微观结构、温度、压力及杂质含量相联系。
在科学实验和工程设计中所用材料的导热系数都需要用实验的方法测定。
(粗略的估计,可从热学参数手册或教科书的数据和图表中查寻)1882年法国科学家J?傅里叶奠定了热传导理论,目前各种测量导热系数的方法都是建立在傅里叶热传导定律基础之上,从测量方法来说,可分为两大类:稳态法和动态法,本实验采用的是稳态平板法测量材料的导热系数。
【实验目的】1•了解热传导现象的物理过程2 •学习用稳态平板法测量材料的导热系数3 •学习用作图法求冷却速率4 •掌握一种用热电转换方式进行温度测量的方法【实验仪器】YBF-3导热系数测试仪、冰点补偿装置、测试样品(硬铝、硅橡胶、胶木板)、塞尺等【实验原理】为了测定材料的导热系数,首先从热导率的定义和它的物理意义入手。
热传导定律指出:如果热量是沿着z方向传导,那么在z轴上任一位置z o处取一个垂直截面积ds,以dT表示在z处的温度梯度,以dQ表示在该处的传热速率(单位时间dz dt内通过截面积ds的热量),那么传导定律可表示成:.dTdQ=-:・()z0dsdt (9-1)dz式中的负号表示热量从高温区向低温区传导(即热传导的方向与温度梯度的方向相反)。
(9-1)式中比例系数'即为导热系数,可见热导率的物理意义:在温度梯度为一个单位的情况下,单位时间内垂直通过单位面积截面的热量。
不良导体导热系数的测量实验报告

不良导体导热系数的测量实验报告
实验目的:
1.了解不良导体的特性;
2.测量不良导体的导热系数。
实验原理:
不良导体是指导热性能较差的物质,如木材、塑料等。
导热系数是描述不良导体导热性能的一个物理量,它反映了单位面积、单位厚度、单位温度梯度下热量通过材料传导的能力。
导热系数越小,说明该材料导热性能越差。
实验仪器:
1.不良导体样品;
2.热绝缘材料;
3.热源;
4.温度计;
5.测量仪器。
实验步骤:
1.将热绝缘材料平铺在工作台上,摆放不良导体样品;
2.将热源放置在样品的一侧,使其与材料保持良好的接触;
3.在样品的另一侧放置温度计,用以测量温度变化;
4.开始记录温度的变化,记录一定时间内温度的变化曲线;
5.使用测量仪器测量材料的厚度和面积。
实验数据和结果:
根据记录到的温度数据,可以得到温度随时间的变化曲线。
根据这些数据,可以计算出材料的导热系数。
实验讨论:
在讨论中,可以对不良导体的导热性能进行评估,并分析不同因素对导热系数的影响。
实验总结:
通过本次实验,我们了解了不良导体的特性和导热系数的测量方法。
同时,我们也明白了导热系数与材料导热性能之间的关系。
这对于我们选择材料、设计热工设备等方面都具有重要意义。
《不良导体导热系数的测定》实验课件文字稿(精)

《不良导体导热系数的测定》实验课件文字稿一、实验目的1.感知热传导现象的物理过程。
2.学习用稳态法测量不良导体的导热系数。
3.学习测量冷却速率的方法4.学习用温差电偶测量温度的原理和方法。
二、实验仪器和用具导热系数测定仪(FD —TC —II )、橡皮圆板(待测样品)、温差电偶(2对)、保温杯、数字式电压表(FPZ —II )、9Q 连接线、电子秒表、游标卡尺、电子天平、冰块。
三、实验原理 1、傅里叶热传导方程导热系数(热导率)是反映材料导热性能的物理量。
测定材料的导热系数在设计和制造加热器、散热器、传热管道、冰箱、节能房屋等工程技术及很多科学实验中都有非常重要的应用。
如图(一)所示。
设一粗细均匀的圆柱体横截面积为S ,高为h 。
经加热后,上端温度为1T ,下端温度为2T ,12T T >,热量从上端流向下端。
若加热一段时间后,内部各个截面处的温度达到恒定,此时虽然各个截面的温度不等,但相同的时间内流过各截面的热量必然相等(设侧面无热量散失),这时热传递达到动态平衡,整个导体呈热稳定状态。
法国数学家,物理学家傅里叶给出了此状态下的热传递方程12T T QS t hλ-∆=∆ (1) Q ∆是t ∆时间内流过导体截面的热量,Qt∆∆叫传热速率。
比例系数λ就是材料的导热系数(热导率),单位是()wm K瓦米开。
在此式中,S 、h 和1T 、2T 容易测得,关键是如何测得传热速率Qt∆∆。
2、用稳态法间接测量传热速率如图二所示,将待测样品夹在加热盘与散热盘之间,且设热传导已达到稳态。
由(1)式可知,加热盘的传热速率为图(一)2T1TT T 加热铜盘 待测样品 散热铜盘图二22121212()144T T T T d T T Q S d t h h hλπλλπ---∆===∆ (2) d 为样品的直径,h 为样品的厚度。
散热盘的散热速率为2T T Q T Cm t t=∆∆=∆∆ (3)C 为散热盘材料的比热,m 为散热盘的质量,2T T Tt=∆∆表示散热盘在温度是2T 时的冷却速率。
物理实验报告 测量不良导体的导热系数

物理实验报告测量不良导体的导热系数摘要:本实验通过测量来确定不良导体的导热系数。
实验使用的样品是一只塑料杯,将水倒入塑料杯中,并在杯子的底部固定一块加热器,通过测量上部和下部温度的差异来计算导热系数。
实验结果表明,该杯的导热系数为0.14 W/(m·K),属于低导热材料。
引言:导热是一种物质从高温区域向低温区域传递热量的能力。
导体的导热系数是衡量导热能力的量。
不良导体在电学上电阻较大,而在导热方面具有低导热系数。
利用导热系数可以确定材料是否适合用于绝缘或隔热材料。
实验步骤:1.将约500毫升的水倒入小塑料杯中,然后固定一块加热器在杯底。
2.将导热计的探头插入杯底离加热器最近的位置,并在杯顶外侧的相同位置插入第二个探头。
3.等待一段时间,直到温度稳定后,读取两个探头的温度并记录下来。
4.重复以上步骤,在杯的不同位置多次测量温度。
5.根据测量结果和相应的方程计算出不良导体的导热系数。
实验结果:本实验测量了不良导体(即小塑料杯)的导热系数。
在测量过程中,使用了加热器和导热计两个重要的工具。
通过将温度探头置于加热器底部和杯顶部两个不同位置,得出了该杯的不同位置的温度分布。
通过分析温度差异,测量出不良导体的导热系数。
本实验得出的测量结果如下,小塑料杯的导热系数为0.14 W/(m·K)。
讨论:根据实验结果,可以看出不良导体在导热方面表现略差。
但是,在一些实际应用中,低导热的物质也具有一定的优势,例如用作绝缘材料、隔热材料等。
在这些应用场合中,导热系数较低的物质是非常重要的。
实验中还需要注意一些问题。
例如,在测量进行中,需要等待一定的时间使温度稳定,并且要确保温度探头与测试杯的接触良好。
此外,在实验前还需要对仪器进行了解,以保证实验过程的准确性和安全性。
不良导体热导率的测定实验报告

不良导热体一般用稳态热流法,条件符合的话也可以使用激光导热法,但是多次测试的结果差异较大。
使用平板法测量不良导体的导热系数,这是一种稳态法,实验中,样品制成平板状,其上端面与一个稳定的均匀发热体充分接触,下端面与一均匀散热体相接触。
由于平板样品的侧面积比平板平面小很多,可以认为热量只沿着上下方向垂直传递,横向由侧面散去的热量可以忽略不计,即可以认为,样品内只有在垂直样品平面的方向上有温度梯度,在同一平面内,各处的温度相同。
扩展资料:
注意事项:
1、注意各仪器间的连线正确,加热盘和散热盘的两个传感器要一一对应,不可互换。
2、温度传感器插入小孔时,要抹些硅油,并使传感器与铜盘接触良好。
3、导热系数测定仪铜盘下方的风扇做强迫对流换热用,可以减少样品侧面与底面的放热比,增加样品内部的温度梯度,从而减小误差,所以实验过程中,风扇一定要打开。
不良导体导热系数的测定

不良导体导热系数的测定[实验目的]1. 用稳定流动法测定橡皮的导热系数;2. 学习用温差电偶测量温度的方法。
[实验器材]导热系数测定仪,热电偶(铜-康铜),多量程数字电压表,橡皮样品,杜瓦瓶,游标卡尺,螺旋测微计。
[实验原理]有一粗细均匀的橡皮圆盘,上平面与发热盘接触(温度高),下平面与散热盘接触(温度低),则热量将从高温面流向低温面。
在加热一段时间后,若圆盘上各处的温度不变(但不同横截面的温度不同,存在温度差),而且向圆盘侧面散失的热量可以忽略时,则在相等的时间内,通过圆盘各横截面的热量应该相等。
当圆盘各截面有热量通过,但各处温度保持不变时,就称为达到了稳定流动状态。
在稳定流动状态下,橡皮圆盘与外界的热交换为零,即上平面从发热盘吸收的热量等于下平面向散热盘放出的热量。
由此,法国数学家、物理学家约瑟夫·傅立叶给出测定导热系数的导热方程。
该方程式指出,在物体内部垂直于导热方向上,二个相距为h ,面积为A ,温度分别为θ1、θ2的平行平面,在∆t 秒内,从一个平面传到另一个平面的热量∆Q ,满足下述表达式:hA t Q 21θθλ-⋅⋅=∆∆ (1) 式中λ定义为该物质的导热系数,亦称导热率。
由此可知,导热系数——表示物质热传导性能的物理量,其数值等于二相距单位长度的平行平面上,当温度相差一个单位时,在单位时间内,垂直通过单位面积所流过的热量。
对于样品橡皮圆盘,上平面传入的热量与由散热盘向周围环境散热的速率相等(即t Q t Q ∆∆=∆∆'),而tmc t Q ∆∆=∆∆θ',2 R A π=,所以 212 12θθπθλθθ-⋅⋅∆∆==h R t mc (2) 导热系数的SI 制单位(瓦特每米开尔文)的符号为:W/m •℃导热系数的量纲为:[][][][][][]13222--=⋅⋅⋅=∆=θθθλLMT T L L MT L t A h Q 导热系数过去常用的非SI 制单位是国际蒸汽表卡每秒厘米开(尔文):cal / (s ·cm ·℃),它与SI 单位的换算是:1cal / (s ·cm ·K )=418.68 w / (m ·K )材料的结构变化与杂质多寡对导热系数都有明显的影响。
不良导体导热系数的测定实验

(二)实验目的 1.掌握稳态法测定不良导体导热系数的方法。 2. 了解物体散热速率和传热速率的关系。
(三)科学家简介
傅里叶(Jean Baptiste Joseph Fourier, 1768~1830),法国数学家、物理学家。 1768年3月21日生于法国中部欧塞尔一 个裁缝家庭,1830年5月16日卒于巴黎。 9岁父母双亡,被当地教堂收养。12岁 由一主教送入地方军事学校读书。17岁 回乡教数学,1794到巴黎,成为高等 师范学校的首批学员, 次年到巴黎综合工科学校执教。1798年随拿破仑远征埃及时任 军中文书和埃及研究院秘书,1801年回国后任伊泽尔省地方长 官。由于对热传导理论的贡献于1817年当选为科学院院士, 1822年任该院终身秘书,后又任法兰西学院终身秘书和理工科 大学校务委员会主席。主要贡献是在研究热的传播时创立了一 套数学理论。
设定的温度
可以通过右边的三个 按键设置加热盘温度
注意测温元件 PT100的插
法
3、打开加热开关加热,等待稳定状态到来; 此过程需要耐心,等真正稳定了才进行测量,对 于所测温度存在小幅波动的情况,可在一段时间 测量多组数据进行平均。
4、记录达到稳定时,样品上下表面的温度;
5、去掉样品后,让散热铜 盘在稳定温度 θ20的基础上 升温若干度,然后让其在空 气中自然冷却,记录其温度 随时间降低的数据(每30秒 记录一次)。
1、彭担任,《稳态双平板法测定煤和岩石的导热系 数》,江苏煤炭,1993年第3期,22~26页。
2、刘淑琴,《用稳态法导热仪测定聚氨酯硬泡导 热系数》,化学推进剂与高分子材料,1990年第4 期,41~43页。
七、最新进展
(一)微细尺度传热学
随着科技的发展,人们对热传导的研究扩展到微细尺度(例如在 对超大规模集成电路的热设计和热控制、航天器内生命保障系统 的传热过程、生命过程中的热现象等的研究中),其研究对象的 特征尺度与载热体(分子、电子、声子、光子)等的平均自由程 处于同一量级甚至更低,导热的Fourier定律、流动的N-S方程已 不在适用,微结构表面的辐射性质也出现奇特的变化,已经不能 有效地用传统的传热传质理论及传统的实验方法加以解决,导致 了热现象由宏观研究到微观研究的历史性转变,促使微尺度传热 学这一学科的出现和形成。微尺度传热学致力于尺度微形化极限 情况的传热学规律研究:一个是空间尺度极限,其研究的几何尺 度可以到微米或微毫米级;再一个是时间尺度极限,即在微妙以 至微毫秒内瞬时传热规律的研究。
稳态法测量不良导体的导热系数实验报告

稳态法测量不良导体的导热系数实验报告实验报告:稳态法测量不良导体的导热系数实验实验目的:本实验旨在通过稳态法测量不良导体的导热系数,了解不良导体的导热性能,并进一步分析材料的热传导特性。
实验仪器:1. 实验台2. 电热器3. 铜棒样品4. 温度计5. 计时器6. 多用电表7. 导热油实验原理:稳态法测量导热系数是通过测量材料的温度梯度和热流量来计算导热系数的。
在实验过程中,首先将导热油倒入实验台中,使其充满整个实验空间。
然后,在台面上放置热源和试样,热源通过导热油将热量传递给试样,试样将热量传递给周围环境。
通过测量试样两端的温度差和热流量,可以计算出导热系数。
实验步骤:1. 准备工作: 将实验台内充填导热油,并使其达到温度平衡。
2. 将导热棒和试样一起放置在实验台上,使其与实验台接触良好。
3. 将电流通入电热器中,通过导热油将热量传递给试样,使热量在试样内传递。
4. 同时使用温度计测量试样两端的温度差,并通过多用电表测量电热器的电流和电压,计算出热流量。
5. 记录不同时间间隔的试样温度和热流量数据,并绘制温度与热流量的关系曲线。
6. 根据数据计算出导热系数。
实验结果:根据实验得到的温度-热流量关系曲线,可以通过线性拟合得到试样的斜率,即热流量值。
通过计算不同时间间隔内的温度差,可以得到导热系数的数值。
实验结论:根据实验结果,可计算出不良导体的导热系数。
导热系数是衡量材料导热性能的重要参数,通过实验可以了解不良导体的导热性能,并为材料的热传导特性分析提供参考。
实验注意事项:1. 实验过程中要注意安全,避免触电或烫伤等意外情况。
2. 导热油的量要足够充填实验台,且温度均匀平衡。
3. 实验前要对实验仪器进行检查,确保正常工作。
4. 实验操作要严格按照实验步骤进行,尽量减小误差产生。
5. 实验完成后要对实验环境进行清理和整理,保持实验台的整洁。
不良导体导热系数的测定实验报告-不良导体实验报告

非金属固体材料导热系数的测量2004/04用热线法测量不良导体导热系数是一种广泛使用的方法,国家对此制定了标准——“非金属固体材料导热系数的测定——热线法”(GB/T 10297-1998)。
基本原理如图1所示,在匀质均温的物体内部放置一电阻丝,即热线,对其以恒定功率加热时,热线及其附近试样的温度将随时间变化。
根据时间与温度的变化关系,可以确定该试样的导热系数。
[1][原理简述]由热传导理论[2]可知,恒定功率的热线对匀质物体进行热传导时,可以用一维柱坐标系的热传导方程对物体的温度场进行描述:r r rt ∂∂+∂∂=∂∂θθθα1122 (1) 边界条件为:00=r θ(t =0,r ≥0),0=∞r θ(t >0,r =),const.π0=∂∂-==r r q θλ(t >0,r =0)[3] (2) 根据热传导方程和边界条件得到解为:t t e q t tr r t d π4042⎰-=αλθ (3)其中各物理量含义为,t :热线的加热时间,单位为s ;r :距热线的距离,单位为m ;q :热线单位长度的加热功率,单位为W/m ;t r θ:加热时间t ,距离热线距离r 处的温升,单位为K ;α:试样的热扩散率,单位为m 2/s ;λ:试样的导热系数,单位为W/(m ·K ),对于非金属固体材料,该系数一般小于2 W/(m ·K )。
假设t r α42→0,即r →0或αt →∞,利用Euler 公式,忽略展开后二次项以后的各项。
如果在不同时间t 1、t 2,测的同一点r 处的温升为1t r θ、2t r θ,则:12ln π412t t q t t r r λθθ=- (4) 根据(4)可以得到试样的导热系数()()12121212ln πL 4ln π4t t t t r r r r t t IU t t q θθθθλ-=-= [4] (5)(5)式中,I 、U 分别热线的通电电流(单位为A )和电压(单位为V ),L 为有效加热长度(单位为m )。
不良导体热导率的测定实验报告

实验名称:不良导体导热系数的测定目的:1.学习一种测量不良导体热导率的方法。
2.学习导热系数实验仪。
为了准确测量加热板和散热器的温度,两个传感器应涂导热硅脂或硅油,以使传感器与加热板和散热板完全接触;另外,在加热橡胶样品时,为了达到稳定的传热效果,调节底部的三个微调螺丝,使样品与加热板和散热板紧密接触,注意不要有气隙。
在中间;并且不要将螺丝拧得太紧而影响样品的厚度。
2.导热系数实验仪的铜板下方的风扇用于强制对流传热,以减小样品侧面和底部之间的放热率,增加样品内部的温度梯度,从而减少实验误差。
因此,在实验期间必须打开风扇。
[实验原理]导热系数是表征材料导热系数的物理量。
材料结构的变化和杂质的不同对材料的热导率有明显的影响,因此材料的热导率经常需要通过实验来测量。
测量导热系数的实验方法一般分为两种:稳态法和动态法。
在稳态方法中,首先使用热源加热样品。
样品内部的温差使热量从高温传递到低温。
样品中每个点的温度都会随着加热速度和传热速度的变化而变化。
通过适当控制实验条件和参数,可以平衡加热和传热的过程。
可以在室内形成稳定的温度分布,据此可以计算出导热系数。
在动态方法中,样品中的最终温度分布会随时间变化,例如周期性变化。
变化的周期和幅度还受实验条件和加热速度的影响,并且与热导率有关。
在本实验中,通过稳态法测量了不良导体(橡胶样品)的热导率,并学习了通过物体的散热率计算出导热率的实验方法。
1898年首先通过平板方法(一种稳态方法)测量不良导体的热导率。
在实验中,将样品制成平板,其上端面与稳定的均匀加热体完全接触,而下端面与均匀的散热器接触。
由于板样品的侧面面积比板平面的侧面面积小得多,因此可以认为热量仅沿上下方向垂直传递,而从侧面散发的热量可以忽略不计。
也就是说,样品中样品平面的垂直方向上仅存在温度梯度,并且在同一平面中的各处温度都相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验九 不良导体导热系数的测量导热系数(热导率)是反映材料热性能的物理量,导热是热交换三种(导热、对流和辐射)基本形式之一,是工程热物理、材料科学、固体物理及能源、环保等各个研究领域的课题之一,要认识导热的本质和特征,需了解粒子物理而目前对导热机理的理解大多数来自固体物理的实验。
材料的导热机理在很大程度上取决于它的微观结构,热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移,在金属中电子流起支配作用,在绝缘体和大部分半导体中则以晶格振动起主导作用。
因此,材料的导热系数不仅与构成材料的物质种类密切相关,而且与它的微观结构、温度、压力及杂质含量相联系。
在科学实验和工程设计中所用材料的导热系数都需要用实验的方法测定。
(粗略的估计,可从热学参数手册或教科书的数据和图表中查寻)1882年法国科学家J•傅里叶奠定了热传导理论,目前各种测量导热系数的方法都是建立在傅里叶热传导定律基础之上,从测量方法来说,可分为两大类:稳态法和动态法,本实验采用的是稳态平板法测量材料的导热系数。
【实验目的】1.了解热传导现象的物理过程2.学习用稳态平板法测量材料的导热系数 3.学习用作图法求冷却速率4.掌握一种用热电转换方式进行温度测量的方法 【实验仪器】YBF-3导热系数测试仪、冰点补偿装置、测试样品(硬铝、硅橡胶、胶木板)、塞尺等 【实验原理】为了测定材料的导热系数,首先从热导率的定义和它的物理意义入手。
热传导定律指出:如果热量是沿着z 方向传导,那么在z 轴上任一位置0z 处取一个垂直截面积ds ,以dT dz 表示在z 处的温度梯度,以dQ dt表示在该处的传热速率(单位时间内通过截面积ds 的热量),那么传导定律可表示成: 0()z dTdQ ds dt dz λ=-⋅ (9-1) 式中的负号表示热量从高温区向低温区传导(即热传导的方向与温度梯度的方向相反)。
(9-1)式中比例系数λ即为导热系数,可见热导率的物理意义:在温度梯度为一个单位的情况下,单位时间内垂直通过单位面积截面的热量。
利用(9-1)式测量材料的导热系数λ,需解决的关键问题两个:一个是在材料内造成一个温度梯度dTdz,并确定其数值;另一个是测量材料内由高温区向低温区的传热速率dQdt。
1.关于温度梯度dT dz为了在样品内造成一个温度的梯度分布,可以把样品加工成平板状,并把它夹在两块良导体——铜板之间,使两块铜板分别保持在恒定温度1T 和2T ,就可能在垂直于样品表面的方向上形成温度的梯度分布。
样品厚度可做成h D <<(样品直径)。
这样,由于样品侧面积比平板面积小得多,由侧面散去的热量可以忽略不计,可以认为热量是沿垂直于样品平面的方向上传导,即只在此方向上有温度梯度。
由于铜是热的良导体,在达到平衡时,可以认为同一铜板各处的温度相同,样品内同一平行平面上各处的温度也相同。
这样只要测出样品的厚度h 和两块铜板的温度1T 、2T ,就可以确定样品内的温度梯度度12T T h-。
当然这需要铜板与样品表面的紧密接触(无缝隙),否则中间的空气层将产生热阻,使得温度梯度测量不准确。
为了保证样品中温度场的分布具有良好的对称性,把样品及两块铜板都加工成等大的圆形。
2、关于传热速率dQdt单位时间内通过一截面积的热量dQdt是一个无法直接测定的量,我们设法将这个量转化为较为容易测量的量,为了维持一个恒定的温度梯度分布,必须不断地给高温侧铜板加热,热量通过样品传到低温侧铜块,低温侧铜板则要将热量不断地向周围环境散出。
当加热速率、传热速率与散热速率相等时,系统就达到一个动态平衡状态,称之为稳态。
此时低温侧铜板的散热速率就是样品内的传热速率。
这样,只要测量低温侧铜板在稳态温度2T 下散热的速率,也就间接测量出了样品内的传热速率。
但是,铜板的散热速率也不易测量,还需要进一步作参量转换,我们已经知道,铜板的散热速率与其冷却速率(温度变化率/dT dt )有关,其表达式为:22dQ dTmc dt dt T T=- (9-2) 式中m 为铜板的质量,c 为铜板的比热容,负号表示热量向低温方向传递。
因为质量容易直接测量,c 为常量,这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
测量铜板的冷却速率可以这样测量:在达到稳态后,移去样品,用加热铜板直接对下金属铜板加热,使其的温度高于稳定温度2T (大约高出10℃左右)再让其在环境中自然冷却,直到温度低于2T ,测出温度在大于2T 到小于2T 区间中随时间的变化关系,描绘出T t -曲线,曲线在2T 处的斜率就是铜板在稳态温度时2T 下的冷却速率。
应该注意的是,这样得出的/dT dt 是在铜板全部表面暴露于空气中的冷却速率,其散热面积为222P P P R R h ππ+(其中P R 和P h 分别是下铜板的半径和厚度)然而在实验中稳态传热时,铜板的上表面(面积为2P R π)是样品覆盖的,由于物体的散热速率与它们的面积成正比,所以稳态时,铜板散热速率的表达式应修正为:22222p P Pp P PR R h dQ dT mc dt dt R R h ππππ+=-⋅+ (9-3) 根据前面的分析,这个量就是样品的传热速率。
将上式代入热传导定律表达式,并考虑到2ds R π=可以得到导热系数: 22122122P P T T P P h R h dTmc h R R T T dt λπ=+=-⋅⋅⋅+- (9-4)式中的R 为样品的半径、h 为样品的高度、m 为下铜板的质量、c 为铜块的比热容、P R 和P h 分别是下铜板的半径和厚度。
右式中的各项均为常量或直接易测量。
【实验步骤与要求】1.用自定量具测量样品、下铜板的几何尺寸和质量等必要的物理量,多次测量、然后取平均值。
其中铜板的比热容()0.385/c KJ K Kg =⋅2.加热温度的设定1)按一下温控器面板上设定键(S ),此时设定值(SV )后一位数码管开始闪烁。
2)根据实验所需温度的大小,再按设定键(S )左右移动到所需设定的位置,然后通过加数键(▲)、减数键(▼)来设定好所需的加热温度。
3)设定好加热温度后,等待8秒钟后返回至正常显示状态。
3.圆筒发热盘侧面和散热盘P 侧面,都有供安插热电偶的小孔,安放时此二小孔都应与冰点补偿器在同一侧,以免线路错乱。
热电偶插入小孔时,要抹上些硅脂,并插到洞孔底部,保证接触良好,热电偶冷端接到冰点补偿器信号输入端。
根据稳态法的原理,必须得到稳定的温度分布,这就需要较长的时间等待。
手动控温测量导热系数时,控制方式开关打到“手动”。
将手动选择开关打到“高”档,根据目标温度的高低,加热一定时间后再打至“低”档。
根据温度的变化情况要手动去控制“高”档或“低”档加热。
然后,每隔5分钟读一下温度示值(具体时间因被测物和温度而异),如在一段时间内样品上、下表面温度1T 、2T 示值都不变,即可认为已达到稳定状态。
自动PID 控温测量时,控制方式开关打到“自动”,手动选择开关打到中间一档,PID 控温表将会使发热盘的温度自动达到设定值。
每隔5分钟读一下温度示值,如在一段时间内样品上、下表面温度1T 、2T 示值都不变,即可认为已达到稳定状态。
4.记录稳态时1T 、2T 值后,移去样品,继续对下铜板加热,当下铜盘温度比2T 高出10℃左右时,移去圆筒,让下铜盘所有表面均暴露于空气中,使下铜板自然冷却。
每隔30秒读一次下铜盘的温度示值并记录,直至温度下降到2T 以下一定值。
作铜板的T t 冷却速率曲线(选取邻近的2T 测量数据来求出冷却速率)。
5.根据(9-4)计算样品的导热系数λ。
6.本实验选用铜-康铜热电偶测温度,温差100℃时,其温差电动势约4.0mV ,故应配用量程0~20mV ,并能读到0.01mV 的数字电压表(数字电压表前端采用自稳零放大器,故无须调零)。
由于热电偶冷端温度为0℃,对一定材料的热电偶而言,当温度变化范围不大时,其温差电动势(mV )与待测温度(0℃)的比值是一个常数。
由此,再用(9-4)计算时,可以直接以电动势值代表温度值。
【实验注意事项】1.稳态法测量时,要使温度稳定约要40分钟左右。
手动测量时,为缩短时间,可先将热板电源电压打在高档,一定时间后,毫伏表读数接近目标温度对应的热电偶读数,即可将开关拨至低档,通过调节手动开关的高档、低档及断电档,使上铜盘的热电偶输出的毫伏值在±0.03mV 范围内。
同时每隔30秒记下上、下圆盘A 和P 对应的毫伏读数,待下圆盘的毫伏读数在3分钟内不变即可认为已达到稳定状态,记下此时的1T V 和2T V 值。
2.测金属的导热系数的稳态值时,热电偶应该插到金属样品上的两侧小孔中;测量散热速率时,热电偶应该重新插到散热盘的小孔中。
1T 、2T 值为稳态时金属样品上下两侧的温度,此时散热盘P 的温度为3T ,因此测量P 盘的冷却速率应为:32121T T T h mctT T R λπ=∆=⋅⋅∆- 测3T 值时要在1T 、2T 达到稳定时,将上面测1T 或2T 的热电偶移下来插到金属下端的小孔中进行测量。
高度h 按金属样品上的小孔的中心距离计算。
3.样品圆盘B 和散热盘P 的几何尺寸,可用游标尺多次测量取平均值。
散热盘的质量m 约0.8㎏,可用药物天平称量。
4.本实验选用铜—康铜热电偶,温差100℃时,温差电动势约4.27mV ,故配用了量程0—20mV 的数字电压表,并能测到0.01mV 的电压。
备注:当出现异常报警时,温控器测量值显示:HHHH ,设置值显示:Err ,当故障检查并解决后可按设定键(S )复位和加数键(▲)、减数键(▼)键重设温度。
【预习思考题】1.稳态平板法测量导热系数实验中,稳态指的什么?根据什么条件判断是否达到稳态?2.实验中为什么要测量散热盘的冷却速率? 【课后作业】1.试述稳态法测不良导体导热系数的基本思想方法? 2.求冷却速率时,为什么要在散热盘稳态温度附近选值?3.稳态法测量导热系数,要求哪些实验条件?在实验中如何确定和保证? 4.热电偶测量温度是通过热电势与温度的关系得出温度值的,本实验中为什么不用确定热电势与温度的关系来得到温度值,而直接代入热电势计算即可? 【附录】一、YBF-3型导热系数测试仪使用说明导热系数(热导率)是反映材料导热性能的物理量,它不仅是评价材料的重要依据,而且是应用材料时的一个设计参数,在加热器、散热器、传热管道设计、房屋设计等工程实践中都要涉及这个参数。
因为材料的热导率不仅随温度、压力变化,而且材料的杂质含量、结构变化都会明显影响热导率的数值,所以在科学实验和工程技术中对材料的热导率常用实验的方法测定。
测量热导率的方法大体上可分为稳态法和动态法两类。
