画法几何(点线面)习题解答
点线面位置关系例题与练习含答案

点、线、面的位置关系●知识梳理(一).平面公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。
公理2:不共线的三点确定一个平面. ...推论1:直线与直线外的一点确定一个平面. 推论2:两条相交直线确定一个平面. 推论3:两条平行直线确定一个平面.公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面1.1平行线的传递公理:平行于同一条直线的两条直线互相平行。
1.2等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
1.3异面直线定义:不同在任何一个平面内的两条直线——异面直线;????,900??;1.4异面直线所成的角:(1)范围:(2)作异面直线所成的角:平移法.2.直线与平面的位置关系:包含,相交,平行3.平面与平面的位置关系:平行,相交(三)平行关系(包括线面平行,面面平行)1.线面平行:①定义:直线与平面无公共点.?//a?a//b??②判定定理:③性质定理:???a?//ba??//?aa???????b???b??2.线面斜交:①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面????,900??内射影的夹角。
范围:????//???;面面平行:①定义: 3.②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行;?????////?,b//,b?b,a?O,aa符号表述:????//?,a?a?.符号表述:判定2:垂直于同一条直线的两个平面互相平行.??//???//??????a//?ab//a?));(2③面面平行的性质:(1????a????b??(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。
???,?a?l?al?l.,则符号表述:若任意都有,且??,ba??O?ab????????l?l al?a,?l??(②判定:1();2)③性质:??al??b?l?????a//b?a?b,;3.2面面斜交①二面角:(1)定义:【如图】??的平面角?-lOA?l??AOB是二面角OB?l,?AOB?[0?,180?] 范围:②作二面角的平面角的方法:(1)定义法;(2)三垂线法(常用);(3)垂面法.?????l???90;的平面角为3.3面面垂直(1)定义:若二面角,则??a????? 2)判定定理:(???a???????ABa???????a??MON?90MON??,则②,二面角的一个平面角为(3)性质:①若;???a??ABa??●热点例析【例1】热点一有关线面位置关系的组合判断ababl,则( )β=.?α,?β若,,α是两条异面直线,α,β是两个不同平面,∩lab分别相交,A.与lab都不相交.,与 B lab中一条相交.,至多与 C lab中的一条相交.,至少与D lablalbababl至少与∥解析:假设与与,从而,是异面直线矛盾,故均不相交,则∥∥,,ab 中的一条相交.选,D.热点二线线、线面平行与垂直的证明ABCDABCDDDABCDABCDABADAD,-⊥平面=,底面中,【例2】如图,在四棱台2是平行四边形,11111ABBAD =60°. =,∠11BDAA⊥(1)证明:;1.BDCCA∥平面(2)证明:11BDDDDDABCDBDABCD. ⊥平面⊥,且方法一:因为,所以?平面 (1)11ABDADBADAB,∠中,由余弦定理得又因为=2=60°,在△2222ADADBDABADAB -23=·,+cos 60°=222DDADDADBDABADBD+∩=,.所以⊥=.所以又1ABDADD.⊥平面所以11BDAAADDAAA.又?平面,故⊥1111ABCDABCDBDDD,(方法二:因为如图⊥平面),且?平面1DDBD.所以⊥1DGGAB.)如图(,连接的中点取.ABDABADAGAD. 中,由得=2在△=BAD=60°,又∠ADGGDGB,所以△=为等边三角形,因此DBGGDB.故∠=∠AGDGDB=30°,=60°,所以∠又∠ADBADGGDB=60°+30°=90°,故∠+∠=∠BDAD.所以⊥ADDDDBDADDA. =又⊥平面∩,所以111AAADDAAABD. ⊥平面又,故?1111ACAC.(2)如图,连接,11EABDEAC.=∩设,连接11ABCDECAC.因为四边形=为平行四边形,所以2ABADABACECACEC,知由棱台定义及∥=2==2且111111AECC 为平行四边形.所以四边形11CCEA.因此∥11 ABDABDCCEA,,平面平面又因为?1111CCABD.∥平面所以11热点三面面平行与垂直的证明ABCDADBCABBCADBCPABCDPAPB,为平面==2,【例3】在直角梯形外一点,且中,=∥,4⊥,,PDPCNCD的中点.为,=ABCDPCD⊥平面;求证:平面(1)EABPPCENE点的位置;若不存上是否存在一点∥平面在线段使得?若存在,说明理由并确定(2) 在,请说明理由.MNPNMPMAB,连接,, (1)证明:取,中点CDABPNPM.,⊥则⊥ABMNBCABCDAB. 又,∴为直角梯形,⊥⊥PMNABMNMPM. =∩⊥平面,∴∵PNPMNABPN.,∴⊥又?平面ABCDPNABCD.与∵相交,∴⊥平面ABCDPCDPNPCD.⊥平面,∴平面平面?又.11PCPBEFBFBPCECPEFMFNE,=上分别取点,,使,连接=,,(2)解:假设存在.在,,443EFBCEFBC=则3.∥=且可求得4MNMNBCEFMNEFMN. ,∴且∵=3且∥∥=MNEFENFM. 为平行四边形,∴∴四边形∥FMPAB,?又∵平面1PCENEABPCEPC.∥平面∴在线段=上存在一点,此时使得 4热点四折叠问题?AB,中,AP//BC,AP例4如图所示,在直角梯形ABCP1AP?2?PCD、、,,沿CDCBGAB=BC=分别为PC的中点,将PD,D是AP的中点,E折起,使F2PD?平面ABCD得.(Ⅰ)求证:AP//平面EFG;PD?G?EF的大小.) (Ⅱ求二面角F P D AFEDAECBGG B C.AC,BD:连交于O点,连GO,FO,EO:解(Ⅰ)证明11CDCD GOGOEF?EF同理// //, 分别为PC,PD的中点,∴// ,∵E,F22?EO??平面EFOG.四边形EFOG是平行四边形, ?PA//EO,PC,AC的中点又在三角形PAC中,E,O分别为??EO平面EFOG,平面EFOG,PA?PA//平面EFOG,即PA//平面EFG.方法二)连AC,BD交于O点,连GO,FO,EO.11CDPB GEEF //,∴同理//,PC,PDE,F∵分别为的中点221AB CDEF?又//AB,// 2?B,EEG?EF?,PB?AB? PAB,平面EFG//平面?//PA?平面EFGPA又.平面PAB,xyz?D DPDA,DC,为方向向量建立空间直角坐标系为原点D,以.方法三)如图以:则有关点及向量的坐标为????????????.2,00,0,1,1C,0,2,0F,G1,2,0A,EP0,0,10,0,2,??????1,EG?10,1,,2,EF???0,1AP?,?2,0??zn?,x,y EFG的法向量为设平面?0?0?ynx?z?EF????.??????0??0yx?y?z???0EG?n????10n?,1,取.?AP?0?,?2n?0?0?1?2An??1, ∵?AP?平面又EFG.平面EFG.AP//DCAD??PD?ABCDABCD ,Ⅱ)由已知底面又∵是正方形面(DCD?PD?PD?AD?又?DDA0,2,0??AD?PCDPCD平面, ,的一个法向量向量=是平面??n01,,?EFG的法向量为又由(Ⅰ)方法三)知平面2Dn.?cosDA,n???222n?DA0.45DEF?G?结合图知二面角的平面角为热点五线线角线面角面面角●6ABCDABCD?PPA与底面中,侧棱例5正四棱锥所成角的正切值为。
点线面位置关系知识点梳理及经典例题带解析

【知识梳理】(1)四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈ ⇒ ∈且。
公理2:过不在一条直线上的三点,有且只有一个平面。
三个推论:① 经过一条直线和这条直线外一点,有且只有一个平面 ② 经过两条相交直线,有且只有一个平面 ③ 经过两条平行直线,有且只有一个平面它给出了确定一个平面的依据。
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)。
符号语言:,,P P l P l αβαβ∈∈⇒=∈且。
公理4:(平行线的传递性)平行与同一直线的两条直线互相平行。
符号语言://,////a l b l a b ⇒且。
(2)空间中直线与直线之间的位置关系1.概念 异面直线及夹角:把不在任何一个平面内的两条直线叫做异面直线。
已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b '',我们把a '与b '所成的角(或直角)叫异面直线,a b 所成的夹角。
(易知:夹角范围090θ<≤︒)定理:空间中如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等或互补。
(注意:会画两个角互补的图形)2.位置关系:⎧⎧⎪⎨⎨⎩⎪⎩相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点(3)空间中直线与平面之间的位置关系直线与平面的位置关系有三种://l l A l ααα⊂⎧⎪=⎧⎨⎨⎪⎩⎩直线在平面内()有无数个公共点直线与平面相交()有且只有一个公共点直线在平面外直线与平面平行()没有公共点(4)空间中平面与平面之间的位置关系平面与平面之间的位置关系有两种://l αβαβ⎧⎨=⎩两个平面平行()没有公共点两个平面相交()有一条公共直线直线、平面平行的判定及其性质 1.内容归纳总结 ,//b P a βα=⇒//,a bαββ⊂=,//a b a bγγ==⇒直线、平面平垂直的判定及其性质 1.内容归纳总结 (一)基本概念1.直线与平面垂直:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α垂直,记作l α⊥。
画法几何(点线面)习题解答

4′1′ ) (′ 2
′
34 2 ( ) 1
18页
3-17.作一水平线MN与H面相距15mm, 3-16。作直线MN,使它与直线AB平行, 并与直线CD、EF都相交 。 e 并与 、 相交。 c b a n n m d
m c n d c b a m b b
15
a a
d
f f
c d m
画法几何习题解答画法几何习题解答吉林建筑工程学院制图教研室点线面投影变换部分页号题号251页号题号10312133714381214383415391215393416310111631213173141831516退出退出页号题号18317181931913193194620320222032123203242521326223272822329302233132233333423335362433738243394026411226413426423页号题号34423344243542526365123653375453856739589退出退出点击题号进入题解页号题号274452746728481228483429491229493430495631410113141213324141532416173341834334193542036421373442223
( )
正垂线 (4) (5)
水平线 (6)
铅垂线
一般线
正平线
侧平线
13页
3-8.根据已知条件,求直线
的三面投影。 2)已知 为正平线及点 的两面投影, 点 在点 的右下方。
Z
(1)已知 为水平线及点 的两面投影, ,点 在点 的右后方,且在 面上。
Z
=30
a
a a Y
土木工程画法几何习题集习题解答

几何建模与计算能力
建模能力
能够根据实际问题的需求,建立合适的 几何模型,将实际问题转化为数学问题 。
VS
计算能力
能够运用数学方法和计算技巧,对几何模 型进行精确或近似的求解。
THANKS FOR WATCHING
感谢您的观看
05 解决实际问题的方法
空间想象与构思能力
空间想象能力
通过观察二维图形,能够想象出三维 物体的形状和结构。
构思能力
能够根据实际需求和条件,构思出合 理的空间结构和解决方案。
空间分析与推理能力
空间分析能力
能够分析物体的空间位置、方向、角度等几何属性,以及它们之间的关系。
推理能力
能够根据已知条件和规律,推导出未知的几何属性或关系。
平面的投影
平面的投影是平面在平面上的表示形式。
输入 标题
详细描述
平面的投影是将平面按照一定的投影方向投射到投影 面上,得到平面的平面表示。在土木工程中,平面的 投影主要用于确定结构物的形状和尺寸。
总结词
总结词
通过平面的投影,我们可以确定平面在空间中的位置 和形状,进一步解决空间几何问题,如求两平面的交
点的投影是将点按照一定的投影方向 投射到投影面上,得到点的平面坐标。 在土木工程中,点的投影主要用于确 定结构物的位置和形状。
详细描述
通过点的投影,我们可以确定点在空 间中的位置,进一步解决空间几何问 题,如求两点的距离、求点到直线的 距离等。
直线的投影
总结词
直线的投影是直线在平面上的表示形式。
总结词
04 工程形体的表达
视图的形成与投影关系
视图的形成
通过将物体放置在三个互相垂直的投 影面上,分别进行正投影,得到主视 图、俯视图和左视图。
点线面答案

参考答案一、选择题 1.D解析:当垂直于直线l 的两条直线与l 共面时,两条直线平行;当这两条直线与l 不共面时,两条直线平行或相交或异面.2.D解析:当将AD 1平移至BC 1,连接A 1C 1,∴∠A 1BC 1是异面直线A 1B 与AD 1所成的角. 在△A 1BC 1中,容易计算A 1B =BC 1=5,A 1C 1=2. ∴由余弦定理得cos ∠A 1BC 1=54. 3.A解析:当平面外两点的连线与此平面垂直时,经过这两点与这个平面平行的平面不存在. 4.C解析:依条件得EF ∥=21AC ,GH ∥=21AC ,∴ EF ∥=GH . 又EH ∥=21BD ,FG ∥=21BD ,∴ EH ∥=FG . ∵AB =BC ,∴EF =EH .∵ AC 与BD 所成角的大小为90°,∴ EF 与EH 所成角的大小为90°. ∴四边形EFGH 是正方形. 5.B解析:对于A ,满足条件的直线l 可以与m ,n 中一条相交;对于C ,若l 与m ,n 都不相交,∵ l 分别与m ,n 共面,∴ l ∥m ,l ∥n .∴ m ∥n .矛盾;对于D ,满足条件的直线可以与m ,n 都相交.6.A解析:若设AC ,BD 交于点O ,连接C 1O ,则BD ⊥CO ,BD ⊥C 1O . ∴ ∠COC 1是二面角C 1-BD -C 的平面角.tan ∠COC 1=BCCC 1=33.∴ ∠COC 1=30°.7.C解析:当A ,B 两点在 同侧时,直线AB 和平面 平行;当A ,B 两点在 异侧时,直线AB 和平面 相交.8.B解析:对于A , ⊥ ,m ⊥ ,n ∥ ,m ,n 可以不垂直; 对于C ,m ⊥ ,n ∥ ,m ⊥n , , 可以不垂直; 对于D , ⊥ , ∩ =m ,n ⊥m , n , 可以不垂直. 9.A解析:设A ,C ∈ ,B ,D ∈ ,① 若AB ,CD 共面,∵ ∥ ,∴ AC ∥BD . ∵ E ,F 分别为AB ,CD 的中点,∴ EF ∥AC ,且EF ⊄ ,AC ⊂ ,∴ EF ∥ .②若AB ,CD 为异面直线,则过点F 做直线MN ∥AB ,MN 交 于M ,交 于N ,则MC ∥ND .∴ F 为的MN 中点.∴EF ∥AM ,且EF ⊄ ,AM ⊂ ,∴ EF ∥ .10.A解析:连接AB ′,A ′B ,于是∠ABA ′=6π,∠BAB ′=4π. 设AB =a ,∴ A ′B =a cos6π=2a ,BB ′=a cos 4π=2a . ∴ A ′B ′=12a .∴ AB ∶A ′B ′=2∶1. 二、填空题 11.60°.解析:将展开图恢复为正方体时,点B ,D 重合,∴ AB ,CD ,AC 三条面对角线构成等边三角形,∴ 直线AB ,CD 所成角的大小为60°.12.5.如图,取A 1B 1的中点G ,连接FG ,EG , ∵FG =1,EG =2,∴ EF =5.(第10题)ABC A 1B 1C 1EFG(第12题)13.414a . 解析:如图过点A 作AB ⊥OC ,垂足为B ,连接A ′B , 点A 到直线OC 距离是AB .依条件得AA ′=23a ,A ′O =21a ,A ′B =42a .∴ AB =16243+a =414a . 14.60°.解析:依条件可知正四棱锥底面中心到一边的距离为1,侧面等腰三角形底边上的高为 2,∴ 侧面与底面所成的二面角的余弦值是21. ∴ 侧面与底面所成的二面角的大小是60°. 15.5.解析:依条件可知当a ∥ ,b ∥ 时,以上五种情况都有可能出现,因此五个结论都有可能成立. 三、解答题16. 证明:(1)∵ AA 1⊥AB ,AA 1⊥AD ,且AB ∩AD =A , ∴ AA 1⊥平面ABCD .又BD ⊂平面ABCD ,∴ AA 1⊥BD .又AC ⊥BD ,AA 1∩AC =A ,∴ BD ⊥平面ACC 1A 1. (2)∵ DD 1∥AA 1,AA 1⊂平面ACC 1A 1, ∴ DD 1∥平面ACC 1A 1.∴ 点P 到平面ACC 1A 1的距离即为直线DD 1到面ACC 1A 1的距离. 也就是点D 到平面ACC 1A 1的距离,设AC ∩BD =O ,则DO 的长度是点D 到平面ACC 1A 1的距离.容易求出DO =22a .∴ P 到平面ACC 1A 1的距离为22a . 17.证明:(1)连接EO ,∵ 四边形ABCD 为正方形, ∴ O 为AC 的中点.∵ E 是PC 的中点,∴ OE 是△APC 的中位线.∴ EO ∥P A .∵ EO ⊂平面BDE ,P A ⊂平面BDE ,∴P A ∥平面BDE .(2)∵ PO ⊥平面ABCD ,BD ⊂平面ABCD , ∴ PO ⊥BD .∵ 四边形ABCD 是正方形, ∴ AC ⊥BD .∵ PO ∩AC =O ,AC ⊂平面P AC ,PO ⊂平面P AC , ∴ BD ⊥平面P AC .18.(1)证明:∵ PD ⊥平面ABCD ,BC ⊂平面ABCD ,∴ PD ⊥BC . 由∠BCD =90°,得CD ⊥BC . 又PD ∩DC =D , PD ,DC ⊂平面PCD , ∴ BC ⊥平面PCD .∵ PC ⊂平面PCD ,故PC ⊥BC .(2)解:(方法一)分别取AB ,PC 的中点E ,F ,连DE ,DF , 则易证DE ∥CB ,DE ∥平面PBC ,点D ,E 到平面PBC 的距离相等. 又点A 到平面PBC 的距离等于点E 到平面PBC 的距离的2倍,由(1)知,BC ⊥平面PCD , ∴平面PBC ⊥平面PCD .∵ PD =DC ,PF =FC ,∴ DF ⊥PC .又 ∴ 平面PBC ∩平面PCD =PC , ∴ DF ⊥平面PBC 于F . 易知DF =22,故点A 到平面PBC 的距离等于2. (方法二):连接AC ,设点A 到平面PBC 的距离为h . ∵ AB ∥DC ,∠BCD =90°,∴ ∠ABC =90°. 由AB =2,BC =1,得△ABC 的面积S △ABC =1.由PD ⊥平面ABCD ,及PD =1,得三棱锥P -ABC 的体积V =31S △ABC ·PD =31.∵ PD ⊥平面ABCD ,DC ⊂平面ABCD ,∴ PD ⊥DC .ABCOA ′(第13题)A BC A 1B 1C 1P · DD 1O(第16题)POECDBA(第17题)(第18题)(第18题)又 ∴ PD =DC =1,∴ PC =22DC PD +=2. 由PC ⊥BC ,BC =1,得△PBC 的面积S △PBC =22. ∵ V A - PBC =V P - ABC ,∴31S △PBC ·h =V =31,得h =2. 故点A 到平面PBC 的距离等于2.19.(1)证明:∵ AC ⊥BD ,又BB 1⊥平面ABCD ,且AC ⊂平面ABCD , ∴ BB 1⊥AC . BD ∩BB 1=B ,∴ AC ⊥平面B 1 D 1DB . (2)证明:由(1)知AC ⊥平面B 1D 1DB , ∵ BD 1⊂平面B 1D 1DB ,∴ AC ⊥BD 1. ∵ A 1D 1⊥平面A 1B 1BA ,AB 1⊂平面A 1B 1BA , ∴ A 1D 1⊥AB 1.又 ∵ A 1B ⊥AB 1且A 1B ∩A 1D 1于A 1, ∴ AB 1⊥平面A 1D 1B . ∵ BD 1⊂平面A 1D 1B , ∴ BD 1⊥AB 1, 又 ∴ AC ∩AB 1=A , ∴ BD 1⊥平面ACB 1.(3)解:(方法1)C BB A ACB B V V 11=--=31×1×(21×1×1)=61.(方法2)1ACB B V -=21(31V 正方体)=61. 20.(1)证明:∵ AB ⊥平面BCD ,∴ AB ⊥CD . ∵ CD ⊥BC ,且AB∩BC =B ,∴ CD ⊥平面ABC .又AC AE =ADAF= (0< <1), ∴ 不论 为何值,恒有EF ∥CD , ∴ EF ⊥平面ABC . ABC . ∵ EF ⊂平面BEF , ∴不论 为何值总有平面BEF ⊥平面(2)解:由(1)知,BE ⊥EF ,又平面BEF ⊥平面ACD ,∴ BE ⊥平面ACD .∴ BE ⊥AC .∵ BC =CD =1,∠BCD =90°,∠ADB =60°,∴ BD =2,AB =6,AC =7.由△ABC ∽△AEB ,有AB 2=AE ·AC ,从而AE =76.∴ =AC AE =76.故当 =76时,平面BEF ⊥平面ACD .数列测试答案一、选择题1.A 解析:由等差数列的求和公式可得63S S =da da 1563311++=31,可得a 1=2d 且d ≠0所以126S S =da da 661215611++=d d 9027=103.2.B解析:解法1:设等比数列{a n }的公比为q ,等差数列{b n }的公差为d ,由a 6=b 7,即a 1q 5=b 7. ∵ b 4+b 10=2b 7,∴ (a 3+a 9)-(b 4+b 10)=(a 1q 2+a 1q 8)-2b 7 =(a 1q 2+a 1q 8)-2a 1q 5 =a 1q 2(q 6-2q 3+1) =a 1q 2(q 3-1)2≥0.(第20题)∴ a 3+a 9≥b 4+b 10. 解法2:∵ a 3·a 9=a 26,b 4+b 10=2b 7,∴ a 3+a 9-(b 4+b 10)=a 3+a 9-2b 7.又a 3+a 9-293a a ⋅=(3a -9a )2≥0, ∴ a 3+a 9≥293 a a ·.∵ a 3+a 9-2b 7≥293a a ⋅-2b 7=2a 6-2a 6=0, ∴ a 3+a 9≥b 4+b 10. 3.C解析:∵ a 1+a 2 008=a 1 003+a 1 006=a 1 004+a 1 005, 而a 1 003+a 1 004+a 1 005+a 1 006=18,a 1+a 2 008=9, ∴ S 2 008=21(a 1+a 2 008)×2 008=9 036,故选C . 4.B解析:∵ a ,b ,c 成等差数列,∴ 2b =a +c , 又S △ABC =21ac sin 30°=23,∴ ac =6, ∴ 4b 2=a 2+c 2+12,a 2+c 2=4b 2-12, 又b 2=a 2+c 2-2ac cos 30°=4b 2-12-63, ∴ 3b 2=12+63,b 2=4+23=(1+3)2. ∴ b =3+1. 5.A解析:题中所给圆是以(5,0)为圆心,5为半径的圆,则可求过(5,3)的最小弦长为8,最大弦长为10,∴ a k -a 1=2,即(k -1)d =2,k =d 2+1∈[5,7],∴ k ≠4.6.A解析:∵ a 7+a 9=a 4+a 12=16,a 4=1,∴ a 12=15. 7.A解析:∵ a 2+a 6=2a 4,a 5+a 10+a 15=3a 10,∴ 6a 4+6a 10=24,即a 4+a 10=4, ∴ S 13=2+13131)(a a =2+13104)(a a =26. 8.B解析:∵ ⎩⎨⎧78=++24=-++209118321a a a a a a∴ (a 1+a 20)+(a 2+a 19)+(a 3+a 18)=54, 即3(a 1+a 20)=54, ∴ a 1+a 20=18, ∴ S 20=2+20201)(a a =180. 9.C解析: 因数列{a n }为等比数列,则a n =2q n -1.因数列{a n +1}也是等比数列,则(a n +1+1)2=(a n +1)(a n +2+1)⇒21+n a +2a n +1=a n a n +2+a n +a n +2⇒a n +a n +2=2a n +1⇒a n (1+q 2-2q )=0⇒(q -1)2=0⇒q =1.由a 1=2得a n =2,所以S n =2n . 10.C解析:依题意a 2=a 1q =2,a 5=a 1q 4=41,两式相除可求得q =21,a 1=4,又因为数列{a n }是等比数列,所以{a n ·a n +1}是以a 1a 2为首项,q 2为公比的等比数列,根据等比数列前n 项和公式可得222111q q a a n-)-(=332(1-4-n ).二、填空题 11.-2.解析:当q =1时,S n +1+S n +2=(2n +3)a 1≠2na 1=2S n ,∴ q ≠1. 由题意2S n =S n +1+S n +2⇒S n +2-S n =S n -S n +1, 即-a n +1=a n +2+a n +1,a n +2=-2a n +1,故q =-2. 12.1.解析:方法一 ∵ S n -S n -1=a n ,又S n 为等差数列,∴ a n 为定值. ∴ {a n }为常数列,q =1-n n a a =1.方法二:a n 为等比数列,设a n =a 1q n -1,且S n 为等差数列,∴ 2S 2=S 1+S 3,2a 1q +2a 1=2a 1+a 1+a 1q +a 1q 2,q 2-q =0,q =0(舍)q =1. 所以答案为1. 13.256,377. 解析:a 9=28=256,S 9=(a 1+a 3+a 5+a 7+a 9)+(a 2+a 4+a 6+a 8) =(1+22+24+26+28)+(3+7+11+15) =341+36 =377. 14.74.解析:由{a n }是等比数列,S 10=a 1+a 2+…+a 10,S 20-S 10=a 11+a 12+…+a 20=q 10S 10,S 30-S 20=a 21+a 22+…+a 30=q 20S 10,即S 10,S 20-S 10,S 30-S 20也成等比数列,得(S 20-S 10)2=S 10(S 30-S 20),得(56-32)2=32(S 30-56),∴ S 30=3232-562)(+56=74. 15.21,211. 解析:将a 1+a 2+a 3=8,①2n -36=36(2n -1).a 4+a 5+a 6=-4.②两式相除得q 3=-21, ∴ a 13+a 14+a 15=(a 1+a 2+a 3) q 12=8·421-⎪⎭⎫ ⎝⎛=21,S 15=21+121--185⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛=211. 16.152.解析:由a n +2+a n +1=6a n 得q n +1+q n =6q n -1,即q 2+q -6=0,q >0,解得q =2,又a 2=1,所以a 1=21,S 4=2121214-)-(=152.三、解答题17.解析:设等差数列{a n }的公差为d ,由前n 项和的概念及已知条件得a 21=9(2a 1+d ),①4a 1+6d =4(2a 1+d ).②由②得d =2a 1,代入①有21a =36a 1,解得a 1=0或a 1=36. 将a 1=0舍去. 因此a 1=36,d =72, 故数列{a n }的通项公式a n =36+(n -1)·72=718.解析:(1)证明:因a 1,a 2,a 4成等比数列,故22a =a 1a 4,而{a n }是等差数列,有a 2=a 1+d ,a 4=a 1+3d ,于是(a 1+d )2=a 1(a 1+3d ), 即21a +2a 1d +d 2=21a +3a 1d . d ≠0,化简得a 1=d .(2)由条件S 10=110和S 10=10a 1+d 2910⨯,得到10a 1+45d =110, 由(1),a 1=d ,代入上式得55d =110,故d =2,a n =a 1+(n -1)d =2n . 因此,数列{a n }的通项公式为a n =2n (n =1,2,3,…).19.解析;由题意得22a =a 1a 4,即(a 1+d )2=a 1(a 1+3d ),d (d -a 1)=0, 又d ≠0,∴ a 1=d .又a 1,a 3,1k a ,2k a ,…,n a k ,…,成等比数列, ∴ 该数列的公比为q =13a a =dd 3=3, ∴ n a k =a 1·3n +1. 又n a k =a 1+(k n -1)d =k n a 1,∴ k n =3n +1为数列{k n }的通项公式.】、 20.解析:(1)由a 1=1,及S n +1=4a n +2,有a 1+a 2=4a 1+2,a 2=3a 1+2=5,∴ b 1=a 2-2a 1=3. 由S n +1=4a n +2 ①,则当n ≥2时,有S n =4a n -1+2. ② ②-①得a n +1=4a n -4a n -1,∴ a n +1-2a n =2(a n -2a n -1).又∵ b n =a n +1-2a n ,∴ b n =2b n -1.∴ {b n }是首项b 1=3,公比为2的等比数列. ∴ b n =3×2 n -1.(2)∵ c n =n n a 2,∴ c n +1-c n =112++n n a -n n a 2=1122++-n n n a a =12+n n b =11223+-⨯n n =43,c 1=21a =21,∴ {c n }是以21为首项,43为公差的等差数列.(3)由(2)可知数列⎭⎬⎫⎩⎨⎧nn a 2是首项为21,公差为43的等差数列. ∴nn a 2=21+(n -1)43=43n -41,a n =(3n -1)·2n -2是数列{a n }的通项公式. 设S n =(3-1)·2-1+(3×2-1)·20+…+(3n -1)·2n -2. S n =2S n -S n=-(3-1)·2-1-3(20+21+…+2n -2)+(3n -1)·2n-1=-1-3×12121---n +(3n -1)·2n -1=-1+3+(3n -4)·2n -1=2+(3n -4)·2n -1.∴ 数列{a n }的前n 项和公式为S n =2+(3n -4)·2n -1.。
点线面位置关系例题与练习(含答案)

点线⾯位置关系例题与练习(含答案)点、线、⾯的位置关系●知识梳理(⼀).平⾯公理1:如果⼀条直线上有两点在⼀个平⾯内,那么直线在平⾯内。
公理2:不共线...的三点确定⼀个平⾯. 推论1:直线与直线外的⼀点确定⼀个平⾯. 推论2:两条相交直线确定⼀个平⾯. 推论3:两条平⾏直线确定⼀个平⾯.公理3:如果两个平⾯有⼀个公共点,那么它们还有公共点,这些公共点的集合是⼀条直线(⼆)空间图形的位置关系1.空间直线的位置关系:相交,平⾏,异⾯平⾏线的传递公理:平⾏于同⼀条直线的两条直线互相平⾏。
等⾓定理:如果⼀个⾓的两边与另⼀个⾓的两边分别平⾏,那么这两个⾓相等或互补。
异⾯直线定义:不同在任何⼀个平⾯内的两条直线——异⾯直线;异⾯直线所成的⾓:(1)范围:(]0,90θ∈??;(2)作异⾯直线所成的⾓:平移法. 2.直线与平⾯的位置关系:包含,相交,平⾏ 3.平⾯与平⾯的位置关系:平⾏,相交(三)平⾏关系(包括线⾯平⾏,⾯⾯平⾏) 1.线⾯平⾏:①定义:直线与平⾯⽆公共点.②判定定理:////a b a a b ααα?③性质定理:////a a a b b αβαβ=? 2.线⾯斜交:①直线与平⾯所成的⾓(简称线⾯⾓):若直线与平⾯斜交,则平⾯的斜线与该斜线在平⾯内射影的夹⾓。
范围:[]0,90θ∈?? 3.⾯⾯平⾏:①定义://αβαβ=??;②判定定理:如果⼀个平⾯内的两条相交直线都平⾏于另⼀个平⾯,那么两个平⾯互相平⾏;符号表述:,,,//,////a b ab O a b ααααβ?=?判定2:垂直于同⼀条直线的两个平⾯互相平⾏.符号表述:,//a a αβαβ⊥⊥?.③⾯⾯平⾏的性质:(1)////a a αββα;(2)////a a b b αβαγβγ?==?(四)垂直关系(包括线⾯垂直,⾯⾯垂直)1.线⾯垂直①定义:若⼀条直线垂直于平⾯内的任意⼀条直线,则这条直线垂直于平⾯。
符号表述:若任意,a α?都有l a ⊥,且l α?,则l α⊥.②判定:,a b a b O l l l al b ααα=??⊥??⊥?⊥??③性质:(1),l a l a αα⊥??⊥;(2),//a b a b αα⊥⊥?;⾯⾯斜交①⼆⾯⾓:(1)定义:【如图】,OB l OA l AOB l αβ⊥⊥?∠-是⼆⾯⾓-的平⾯⾓范围:[0,180]AOB ∠∈??②作⼆⾯⾓的平⾯⾓的⽅法:(1)定义法;(2)三垂线法(常⽤);(3)垂⾯法. ⾯⾯垂直(1)定义:若⼆⾯⾓l αβ--的平⾯⾓为90?,则αβ⊥;(2)判定定理:a a ααββ??⊥?⊥?(3)性质:①若αβ⊥,⼆⾯⾓的⼀个平⾯⾓为MON ∠,则90MON ∠=?;②a AB a a a ABαβββα⊥??=?⊥⊥?●热点例析【例1】热点⼀有关线⾯位置关系的组合判断若a ,b 是两条异⾯直线,α,β是两个不同平⾯,a ?α,b ?β,α∩β=l ,则( ). A .l 与a ,b 分别相交 B .l 与a ,b 都不相交C .l ⾄多与a ,b 中⼀条相交D .l ⾄少与a ,b 中的⼀条相交解析:假设l 与a ,b 均不相交,则l ∥a ,l ∥b ,从⽽a ∥b 与a ,b 是异⾯直线⽭盾,故l ⾄少与a ,b 中的⼀条相交.选D.热点⼆线线、线⾯平⾏与垂直的证明【例2】如图,在四棱台ABCD -A 1B 1C 1D 1中,D 1D ⊥平⾯ABCD ,底⾯ABCD 是平⾏四边形,AB =2AD ,AD =A1B 1,∠BAD =60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平⾯A1BD.(1)⽅法⼀:因为D1D⊥平⾯ABCD,且BD?平⾯ABCD,所以D1D⊥BD. ⼜因为AB=2AD,∠BAD=60°,在△ABD中,由余弦定理得BD2=AD2+AB2-2AD·AB cos 60°=3AD2,所以AD2+BD2=AB2.所以AD⊥BD.⼜AD∩D1D=D,所以BD⊥平⾯ADD1A1.⼜AA1?平⾯ADD1A1,故AA1⊥BD.⽅法⼆:因为D1D⊥平⾯ABCD,且BD?平⾯ABCD(如图),所以BD⊥D1D.取AB的中点G,连接DG(如图).在△ABD中,由AB=2AD得AG=AD.⼜∠BAD=60°,所以△ADG为等边三⾓形,因此GD=GB,故∠DBG=∠GDB.⼜∠AGD=60°,所以∠GDB=30°,故∠ADB=∠ADG+∠GDB=60°+30°=90°,所以BD⊥AD.⼜AD∩D1D=D,所以BD⊥平⾯ADD1A1.⼜AA1?平⾯ADD1A1,故AA1⊥BD.(2)如图,连接AC,A1C1.设AC ∩BD =E ,连接EA 1.因为四边形ABCD 为平⾏四边形,所以EC =12AC .由棱台定义及AB =2AD =2A 1B 1知A 1C 1∥EC 且A 1C 1=EC ,所以四边形A 1ECC 1为平⾏四边形.因此CC 1∥EA 1.⼜因为EA 1?平⾯A 1BD ,CC 1 平⾯A 1BD ,所以CC 1∥平⾯A 1BD .热点三⾯⾯平⾏与垂直的证明【例3】在直⾓梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =4,P 为平⾯ABCD 外⼀点,且PA =PB ,PD =PC ,N 为CD 的中点.(1)求证:平⾯PCD ⊥平⾯ABCD ;(2)在线段PC 上是否存在⼀点E 使得NE ∥平⾯ABP ?若存在,说明理由并确定E 点的位置;若不存在,请说明理由.(1)证明:取AB 中点M ,连接PM ,PN ,MN ,则PM ⊥AB ,PN ⊥CD .⼜ABCD 为直⾓梯形,AB ⊥BC ,∴MN ⊥AB . ∵PM ∩MN =M ,∴AB ⊥平⾯PMN . ⼜PN ?平⾯PMN ,∴AB ⊥PN .∵AB 与CD 相交,∴PN ⊥平⾯ABCD .⼜PN ?平⾯ PCD ,∴平⾯PCD ⊥平⾯ABCD .(2)解:假设存在.在PC ,PB 上分别取点E ,F ,使BF =14BP ,CE =14CP ,连接EF ,MF ,NE ,则EF ∥BC 且可求得EF =34BC =3.∵MN =3且MN ∥BC ,∴EF ∥MN 且EF =MN . ∴四边形MNEF 为平⾏四边形,∴EN ∥FM . ⼜∵FM ?平⾯PAB ,∴在线段PC 上存在⼀点E 使得NE ∥平⾯ABP ,此时CE =14PC .热点四折叠问题例4如图所⽰,在直⾓梯形ABCP 中,AP ⊥221=AP PCD ?⊥PD D EF G --EF CD 211EO ∴?EO ?∴CAPGEFBDOEFCD 21GE 12PB CD EF ∴AB 21∴=?=?,,B AB PB E EF EG ?//PA ∴DP DC DA ,,xyz D -()()()()()()0,0,2,0,2,0,1,2,0,0,1,1,0,0,1,2,00.P C G E F A ()()()1,1,1,0,1,0,2,0,2-=-=-=()z y x ,,=.00000==??=-+=-?==∴y z x z y x y EF n ()1,0,1=()⊥∴=?+?+-?=?,0210021?AP ∴∴DC AD ⊥⊥PD PD AD ⊥∴D CD PD =?⊥∴AD∴()0,0,2()1,0,1=.22222cos ===∴nDA n DA D EF G --.450ABCD P -PA ABCD26PAD ABCD PAD ⊥BD AC ,O PA ABCD 2623PFO ∠PAD ABCD PFO ?3tan ==∠FO PO PFO 3π=∠PFO PAD ABCD 3πEO =//PD 21EOD ∠PDO ?2522=+=PO OD PD 45=EO BD AO ⊥PO AO ⊥⊥AO PBD EO AO ⊥AOE ?5102tan ==∠EO AO AEO 5102FO BC G PG H PG GH EH ,ABCD P -F AD G BC PG BC ⊥FG BC ⊥PFG BC ⾯⊥PBC PFG ⾯PG PF =3π=∠PFO PFG ?PGFH ⊥PBC FH ⾯⊥FK HE //FK HE =HEKF FH KE //PBC KE ⾯⊥,m n γβα,,m ⊥αn //αnm ⊥αβ//βγ//m ⊥αm ⊥γm //αn //αm n //αγ⊥βγ⊥//αβ,,a b c222a b c ++22212a b c ++22222a b c ++22232a b c ++A BCD-AC ⊥,,,,30BCD BD DC BD DC AC a ABC ⊥==∠=C ABD55a 15535a 153a 1111ABCD A B C D -E 11A C CE AC BD 1A D 11A D P ABC -PH H ABC ABCD AC 21ACDOPEFGHKA CD B--12133323S ABC -a ,E F SC AB EF SA 090060045030,A B α4cm 6cm AB Mα0601226P ABC -4,8AB PA ==A ,PB PC D E ?ADE1C (1)求证:BE =B 1E ;(2)若AA 1=A 1B 1,求平⾯A 1EC 与平⾯A 1B 1C 1所成⼆⾯⾓的⼤⼩.3如图,在四棱锥P -ABCD 中,PD ⊥平⾯ABCD ,底⾯ABCD 为矩形,PD =DC =4,AD =2,E 为PC 的中点.(1)求证:AD ⊥PC ;(2)求三棱锥A -PDE 的体积;(3)在AC 上是否存在⼀点M ,使得PA ∥平⾯EDM ?若存在,求出AM 的长;若不存在,请说明理由.答案⼀、选择题1. A ③若m //α,n //α,则m n //,⽽同平⾏同⼀个平⾯的两条直线有三种位置关系④若αγ⊥,βγ⊥,则//αβ,⽽同垂直于同⼀个平⾯的两个平⾯也可以相交 2.C 设同⼀顶点的三条棱分别为,,x y z ,则222222222,,x y a y z b x z c +=+=+=得2222221()2x y z a b c ++=++22222212()22a b c a b c ++=++3.B 作等积变换A BCD C ABD V V --=4.B BD 垂直于CE 在平⾯ABCD 上的射影5.C BC PA BC AH ⊥?⊥6.C 取AC 的中点E ,取CD 的中点F ,123,22EF BE BF ===3cos EF BF θ==7.C 取SB 的中点G ,则2aGE GF ==,在△SFC 中,22EF a =,045EFG ∠= ⼆、填空题1.5cm 或1cm 分,A B 在平⾯的同侧和异侧两种情况2.48 每个表⾯有4个,共64?个;每个对⾓⾯有4个,共64?个3.090 垂直时最⼤ 4. 60 度5. 11 沿着PA 将正三棱锥P ABC -侧⾯展开,则',,,A D E A 共线,且'//AA BC 三、解答题:略1.证明:(1)连接BD ,MO .在平⾏四边形ABCD 中,因为O 为AC 的中点,所以O 为BD 的中点.⼜M 为PD 的中点,所以PB ∥MO . 因为PB ?平⾯ACM ,MO ?平⾯ACM ,所以PB ∥平⾯ACM .(2)因为∠ADC =45°,且AD =AC =1,所以∠DAC =90°,即AD ⊥AC .⼜PO ⊥平⾯ABCD ,AD ?平⾯ABCD ,所以PO ⊥AD . ⽽AC ∩PO =O ,所以AD ⊥平⾯PAC .2[解析] (1)取A 1C 1中点F ,作EG ⊥⾯AC 1于G ,B 1F ∥EGB 1E ∥⾯AC 1?BE ∥FG ?B 1EGF 为平⾏四边形?FG ⊥A 1C 1?G 为A 1C 之中点.从⽽E 为BB 1之中点.∴BE =B 1E .(2)由(1)知G 为矩形ACC 1A 1的中⼼,过G 作直线平⾏于A 1C 1,交AA 1于点P ,交CC 1于Q 点,连结EP ,EQ ,则平⾯A 1B 1C 1∥平⾯PEQ ,即求平⾯AEC 与平⾯PEQ 所成的⾓,∵交线为EG ,∴其平⾯⾓为∠A 1GP ,因AA 1=A 1B 1,则ACC 1A 1为正⽅形,则∠A 1GP =45°.3.(1)证明:因为PD ⊥平⾯ABCD ,所以PD ⊥AD .⼜因为四边形ABCD 是矩形,所以AD ⊥CD .因为PD ∩CD =D ,所以AD ⊥平⾯PCD .⼜因为PC ?平⾯PCD ,所以AD ⊥PC . (2)解:由(1)知AD ⊥平⾯PCD ,所以AD 是三棱锥A -PDE 的⾼.因为E 为PC 的中点,且PD =DC =4,所以S △PDE =12S △PDC =12×? ??12×4×4=4. ⼜AD =2,所以V A -PDE =13AD ·S △PDE =13×2×4=83.(3)解:取AC 的中点M ,连接EM ,DM ,因为E 为PC 的中点,M 是AC 的中点,所以EM ∥PA .⼜因为EM ?平⾯DEM ,PA ?平⾯EDM ,所以PA ∥平⾯DEM .此时AM =12AC =12AD 2+DC 2=1222+42=5,即在AC 上存在⼀点M ,使得PA ∥平⾯EDM ,且AM 的长为 5.。
点线面关系练习题(有答案)复习进程

点线面关系练习题(有答案)点线面位置关系总复习二、平面与平面平行1.判定方法(1) 定义法:两平面无公共点a// 、b//(2)判定定理:a > //b a b P a r(3)其他方法:知识梳理一、直线与平面平行1.判定方法(1) 定义法:直线与平面无公共点a(2) 判定定 ba / /b 理:(3)其他方法:a"} a//a//2.性质定理:a卜 a//ba//1 卜// // J卜//a」// A2•性质定理: a a//bb、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直(2)判定方法①用定义•a b 、a c②判定定理:b c A abc 丿③推论:a"I ba//bJ(3)性质} a//b四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直a 〕(2)判定定理a」(3)性质①性质定理1>aa 1 J②>A lPPA 垂足为A jl3 PAPPA 」“转化思想”面面平行" 平行 "线线平行面面垂直垂直廿线线垂直求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2•在二面角'■'的棱上任取一点0,在两半平面内分别作射线0A丄l, OB丄l,则/ AOB叫做二面角「•'的平面角例1.如图,在三棱锥S-ABC中,SA 底面ABC , AB BC, DE垂直平分SC,且分别交AC于D,交SC于E,又SA=AB , SB=BC,求以BD为棱,以BDE和BDC为面的二面角的度数。
求线面夹角定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。
例1:在棱长都为1的正三棱锥S-ABC中,侧棱SA与底面ABC所成的角是_________________ .例2:在正方体ABCD -A1B1C1D1中,①BC1与平面AB1所成的角的大小是_____________ ;②BD1与平面AB1所成的角的大小是_____________ ;③CC1与平面BC1D所成的角的大小是____________ ;④BC1与平面A1BCD1所成的角的大小是______________ ;⑤BD1与平面BC1D所成的角的大小是_____________ ;例3:已知空间内一点0出发的三条射线0A、OB、OC两两夹角为60°,试求OA与平面BOC 所成的角的大小.求线线距离说明:求异面直线距离的方法有:(1)(直接法)当公垂线段能直接作出时,直接求•此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.(2)(转化法)把线线距离转化为线面距离,如求异面直线a、b距离,先作出过a且平行于b的平面,则b与距离就是a、b距离.(线面转化法).也可以转化为过a平行b的平面和过b平行于a的平面,两平行平面的距离就是两条异面直线距离.(面面转化法).(3)(体积桥法)利用线面距再转化为锥体的高用何种公式来求.(4)(构造函数法)常常利用距离最短原理构造二次函数,利用求二次函数最值来解.两条异面直线间距离问题,教科书要求不高(要求会计算已给出公垂线时的距离),这方面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.例:在棱长为a的正方体中,求异面直线BD和B1C之间的距离。
点线面位置关系例题与练习(含答案)

点、线、面的位置关系● 知识梳理 (一).平面公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。
公理2:不共线...的三点确定一个平面. 推论1:直线与直线外的一点确定一个平面. 推论2:两条相交直线确定一个平面. 推论3:两条平行直线确定一个平面.公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线 (二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面1.1平行线的传递公理:平行于同一条直线的两条直线互相平行。
1.2等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
1.3异面直线定义:不同在任何一个平面内的两条直线——异面直线;1.4异面直线所成的角:(1)范围:(]0,90θ∈︒︒;(2)作异面直线所成的角:平移法.2.直线与平面的位置关系: 包含,相交,平行3.平面与平面的位置关系:平行,相交(三)平行关系(包括线面平行,面面平行) 1.线面平行:①定义:直线与平面无公共点.②判定定理:////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭③性质定理:////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ 2.线面斜交: ①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角。
范围:[]0,90θ∈︒︒ 3.面面平行:①定义://αβαβ=∅⇒;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行; 符号表述:,,,//,////a b ab O a b ααααβ⊂=⇒判定2:垂直于同一条直线的两个平面互相平行.符号表述:,//a a αβαβ⊥⊥⇒.③面面平行的性质:(1)////a a αββα⎫⇒⎬⊂⎭;(2)////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。
工程制图-画法几何(点线面)习题解答

页号
9 9 9 9 9 10 13 14 14 15 15 16 16 17 18
题号
2-5(2) 2-5(3) 2-5(4) 2-5(5) 2-5 (6) 3-1、2 3-7 3-8(1、2) 3-8(3、4) 3-9(1、2) 3-9(3、4) 3-10、11 3-12、13 3-14 3-15、16
a″
a
b′ mm
b″
24页
4-1. 判别直线与平面,平面与平面是否平行 。
(1)
b e
a
(2)
f a
b f
e
b a
c
c
f
e
( 平行 )
c
b
f
e c
a
( 不平行 )
26页
4-1. 判别直线与平面,平面与平面是否平行 。
(3)
c
b
e
a
b a
d e
c d
( 平行 )
(4)
b
f a
e d
c
f
f a
b f
(1)
5页
2-2.根据物体的立体图画出三面投影图(尺寸由立体图中量 取)。
(2)
5页
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(1)
5
6页
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(2)
6页
3
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
( ) ( ) ( )
3-19. 判别两条直线是否垂直。 3-19。判别两直线是否垂直。
4
5c
c
b
b
点线面位置关系练习(有详细答案)

【空间中的平行问题】(1)直线与平面平行的判定及其性质①线面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。
(线线平行→线面平行)②线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(线面平行→线线平行)(2)平面与平面平行的判定及其性质两个平面平行的判定定理:①如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行(线面平行→面面平行) ②如果在两个平面内,各有两组相交直线对应平行,那么这两个平面平行。
(线线平行→面面平行) ③垂直于同一条直线的两个平面平行两个平面平行的性质定理:①如果两个平面平行,那么某一个平面内的直线与另一个平面平行。
(面面平行→线面平行) ②如果两个平行平面都和第三个平面相交,那么它们的交线平行。
(面面平行→线线平行)【空间中的垂直问题】(1)线线、面面、线面垂直的定义①两条异面直线的垂直:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。
②线面垂直:如果一条直线和一个平面内的任何一条直线垂直,就说这条直线和这个平面垂直。
③平面和平面垂直:如果两个平面相交,所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直。
(2)垂直关系的判定和性质定理①线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
②面面垂直的判定定理和性质定理判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。
【空间角问题】(1)直线与直线所成的角①两平行直线所成的角:规定为 ②两条相交直线所成的角:两条直线相交其中不大于直角的角,叫这两条直线所成的角。
画法几何(点线面)习题解答PPT课件
a'
b' k'
k b a
15页
43
3-10. 求直线AB的实长 及α、β角实形。
′ AB
β
′
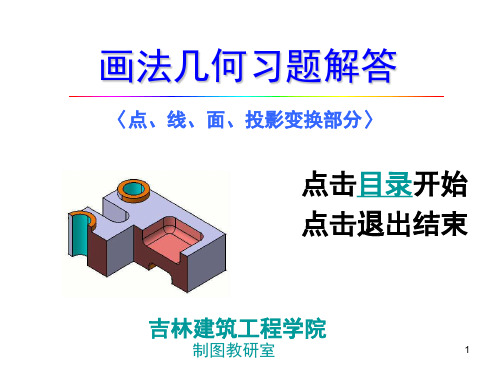
3-11.已知AB=35mm及a′和 ab,求a′b′。
′
′
α AB 35
16页
44
3-12.已知AB=30mm,β=30°及 a′b′的方向,点B在点A的右
前上方,求AB的V、H面投影。
3-13.已知直线AB及点C的两面投 影,在直线上AB上取一点D, 使AD=AC。
a Y
a Y
14页
40
3-8.根据已知条件,求直线 的三面投影。
(3)已知 为铅垂线及点 的两面投影, 点 在点 的上方, 的实长为15 。
Z
b'
b"
4)已知 为侧垂线及点 的两面投影, 点 在W面上。
Z
b
a
b" a"
a'
a"
X
YX
O
Y O
b(a)
b
a
Y
Y
14页
41
3-9.根据已知条件,求直线上点的投影。
35 4-20
36 4-21
37 34 4-22
页号 题号
34 4-23 34 4-24 35 4-25、26 36 5-1、2 36 5-3 37 5-4、5 38 5-6、7 39 5-8、9
退出
点击题号进入题解
3
2-1.根据物体的立体图画出三面投影图(尺寸由立体图中 量取)。
(1)
(2)
4页
点击题号进入题解
退出
2
目 录 (二)
画法几何点线面投影的习题
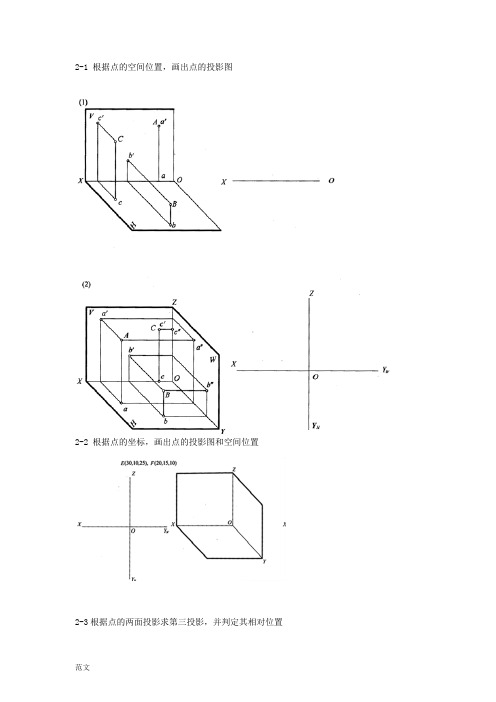
2-1 根据点的空间位置,画出点的投影图2-2 根据点的坐标,画出点的投影图和空间位置2-3根据点的两面投影求第三投影,并判定其相对位置2-4 已知点B 在点A 的正上方10,点C 在点B 的正左方10,求A 、B 、C 的三面投影,并标明其可见性。
b'b b”c'c” c( a” ) ( )ab”A AA BBB c ׳dC CCDD2-5 已知长方体的投影图,试判定棱线AB、AC、CD与投影面的相对位置,并标明其侧面投影。
2-6 注出三棱锥SABC各棱线的水平和正面投影,并判定它们属于哪类直线。
2-7求直线AB的第三投影。
2-8 分别求出直线CD和EF的实长及其倾角α和β。
2-9 已知直线AB与V面的倾角β=300,求其水平投影ab。
2-10 判定点K是否在直线AB上。
不在2-11 判定下列直线的相对位置(平行、相交、交叉)2-12 求点M到直线AB的距离。
2-13求一距H面为20的水平线,与两交叉直线AB、CD相交2-14判定两条交叉直线AB、CD对V、W面重影点的可见性2-15试求两条直线AB、CD之间的距离2-16已知正方形ABCD的对角线位于侧平线EF上,试完成该正方形的正面、侧面投影2-17求下列平面的第三投影,并判定它们与投影面的相对位置2-18试判定A、B两点是否在下列平面内2-19 完成平面五边形的正面投影2-20判定3条相互平行的直线是否在同一平面内通过作图可知:左边两条平行直线可确定一平面,右边的平行线没有过该平面上的某一点,所以三条平行线不在同一平面。
2-21已知直线CD在⊿ABC平面内,试求c′d′2-22试在⊿ABC内取一点K,使K距H面、V面均为20。
点线面位置关系例题及练习包括答案.doc

点、线、面的位置关系●知识梳理(一) .平面公理 1:如果一条直线上有两点在一个平面内,那么直线在平面内。
公理 2:不共线的三点确定一个平面....推论 1:直线与直线外的一点确定一个平面. 推论2:两条相交直线确定一个平面. 推论3:两条平行直线确定一个平面.公理 3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面平行线的传递公理:平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
异面直线定义:不同在任何一个平面内的两条直线——异面直线;异面直线所成的角:( 1)范围:0 ,90;(2)作异面直线所成的角:平移法.2.直线与平面的位置关系:包含,相交,平行3.平面与平面的位置关系:平行,相交(三)平行关系(包括线面平行,面面平行)1.线面平行:①定义:直线与平面无公共点.a //b a //②判定定理: a a// ③性质定理: a a // bb I b2.线面斜交:①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角。
范围:0 ,903.面面平行:①定义:I // ;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行;符号表述:a,b , a I b O ,a // ,b // //判定2:垂直于同一条直线的两个平面互相平行.符号表述: a , a // .////③面面平行的性质:( 1) a //;(2)I a a // baI b(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。
符号表述:若任意 a , 都有 l a ,且 l ,则 l .a,ba Ib O②判定: l l ③性质:( 1)l , a l a ;( 2 )l al ba ,b a // b ;面面斜交①二面角:( 1)定义:【如图】 OB l ,OA l AOB 是二面角- l 的平面角范围:AOB [0 ,180 ]②作二面角的平面角的方法:( 1)定义法;( 2)三垂线法(常用);( 3)垂面法 .面面垂直( 1)定义:若二面角l的平面角为90 ,则;a( 2)判定定理:a( 3)性质:①若a I ABa ,二面角的一个平面角为MON ,则 MON 90 ;②aa AB● 热点例析【例 1】热点一有关线面位置关系的组合判断若 a, b 是两条异面直线,α,β是两个不同平面, a? α, b? β,α∩β= l,则 ( ).A.l 与 a, b 分别相交B. l 与 a, b 都不相交C. l 至多与 a,b 中一条相交D. l 至少与 a, b 中的一条相交解析:假设 l 与 a,b 均不相交,则l∥ a,l∥ b,从而 a∥ b 与 a, b 是异面直线矛盾,故l 至少与 a,b 中的一条相交.选 D.热点二线线、线面平行与垂直的证明【例 2】如图,在四棱台 ABCD-A1 1 1 1 1B C D 中,D D⊥平面 ABCD,底面 ABCD是平行四边形, AB= 2AD,AD= A1B1,∠BAD=60°.(1)证明: AA1⊥BD;(2)证明: CC1∥平面 A1 BD.(1)方法一:因为D1 D⊥平面 ABCD,且 BD? 平面 ABCD,所以 D1D⊥ BD.又因为 AB= 2AD,∠BAD=60°,在△ ABD 中,由余弦定理得BD2= AD2+ AB2-2AD·ABcos 60 °=3AD2,所以 AD2+ BD2= AB2.所以 AD⊥ BD.又 AD∩D1D=D,所以 BD⊥平面 ADD1A1 .又AA1 ? 平面 ADD1 A1,故 AA1⊥ BD.方法二:因为D1D⊥平面 ABCD,且 BD? 平面 ABCD(如图 ),所以 BD⊥ D1D.取 AB 的中点 G,连接 DG(如图 ).在△ ABD 中,由 AB= 2AD 得 AG= AD.又∠ BAD= 60°,所以△ ADG为等边三角形,因此GD= GB,故∠ DBG=∠ GDB.又∠ AGD= 60°,所以∠GDB=30°,故∠ ADB=∠ ADG+∠ GDB= 60°+ 30°= 90°,所以 BD⊥ AD.又AD∩D1D= D,所以 BD⊥平面 ADD1A1.又AA1 ? 平面 ADD1 A1,故 AA1⊥ BD.(2)如图,连接 AC,A1C1.设AC∩BD= E,连接 EA1.1因为四边形ABCD为平行四边形,所以EC=2AC.由棱台定义及 AB=2AD= 2A1B1知 A1C1∥ EC且 A1C1=EC,所以四边形 A1 ECC1为平行四边形.因此 CC1∥EA1.又因为 EA1 ? 平面 A1BD,CC1平面A1BD,所以 CC1∥平面 A1BD.热点三面面平行与垂直的证明【例 3】在直角梯形ABCD中, AD∥ BC, AB⊥BC, AD= 2,BC= 4, P 为平面 ABCD外一点,且PA =PB, PD= PC, N 为 CD的中点.(1)求证:平面 PCD⊥平面 ABCD;(2)在线段 PC 上是否存在一点 E 使得 NE∥平面 ABP 若存在,说明理由并确定 E 点的位置;若不存在,请说明理由.(1)证明:取AB 中点 M ,连接 PM,PN,MN ,则PM⊥ AB, PN⊥ CD.又ABCD为直角梯形, AB⊥ BC,∴ MN ⊥AB.∵ PM∩MN =M ,∴ AB⊥平面 PMN.又PN? 平面 PMN,∴ AB⊥PN.∵AB 与 CD相交,∴ PN⊥平面 ABCD.又 PN? 平面PCD,∴平面PCD⊥平面 ABCD.1 1(2) 解:假设存在.在PC, PB 上分别取点E, F,使 BF=4BP, CE=4CP,连接 EF, MF, NE,3则 EF∥ BC 且可求得EF=4BC= 3.∵MN =3 且 MN ∥ BC,∴ EF∥ MN 且 EF= MN .∴四边形 MNEF 为平行四边形,∴ EN∥ FM.又∵ FM? 平面 PAB,1∴在线段PC上存在一点 E 使得 NE∥平面 ABP,此时 CE=4PC.热点四折叠问题例 4 如 图 所 示 , 在 直 角 梯 形 ABCP 中 ,PPA DFPPFEBGECHFEADEOBG C DA BDCG CGFOKBAAP1AP 2PCD PDG EF 1 1 EF GOEOEO2D EFCD GOCD22EF1CD GE 1PB CDEF1AB EGEF E, PB AB B,PA // DA, DC , DP2 22P 0,0,2 , C 0,2,0 , G 1,2,0 , E 0,1,1 , F 0,0,1 , A2,00 . D xyzAP2,0,2 , EF0, 1,0 , EG1,1, 1 nx, y, zn EF 0y 0x z.n EG0 x y z 0y 0 n1,0,1 n AP 12 0 0 1 2 0, nAP APADDC PDAD PD PD CD DADDA DA2,0,0 n 1,0,1cos DA, nDA n 2 22 .DA n22G EFD 450. PABCD PA ABCD6 PAD ABCD PADAC, BD O PA ABCD6 322 2PFO PAD ABCDPFO tan PFOPO 3PFO3PAD ABCD3 EO //1PDFO2EOD PDO PDOD 2PO25EO5 AO BD AO PO AOPBD AOEO24AOE tan AEOAO 2 10 2 10 FO BC G PG H PG EH ,GHPABCD F AD G BC EO55BCPG BCFG BC 面 PFG PBC 面 PFG PFPGPFO 3 PFG FHPGFH 面 PBC HE // FK HE FK HEKF KE // FH KE 面 PBC m, n , , mn / / m n / // /mmm/ /n / /m / /n//a,b,ca 2b 2c 2 1 a 2 b 2 c 22 a 2 b 2 c 23 a 2 b 2 c 2 A BCDAC222BCD , BDDC , BD DC , AC a, ABC300CABD5 a 15 a 3 a 15 a5553ABCD A 1B 1C 1D 1 E A 1C 1CE AC BD A 1 D A 1D 1 P ABC PH H ABC ABCD AC 2 1A CDB 1 1 3 2 S ABC a E, F SC AB EF SA 900 600 450 300 A, B 4cm 6cm AB M2 3 3 3600 12 2 6 P ABC AB 4, PA 8A PB, PC D E ADE1C(1)求证:BE=B1E;(2)若 AA1= A1B1,求平面 A1EC与平面 A1B1C1所成二面角的大小.3如图,在四棱锥 P- ABCD 中, PD⊥平面 ABCD,底面 ABCD 为矩形, PD=DC= 4, AD=2, E 为 PC 的中点.(1)求证: AD⊥ PC;(2)求三棱锥 A- PDE 的体积;(3)在 AC 上是否存在一点 M,使得 PA∥平面 EDM 若存在,求出 AM 的长;若不存在,请说明理由.答案一、选择题1. A ③若 m/ / , n / / ,则 m / / n ,而同平行同一个平面的两条直线有三种位置关系④若,,则// ,而同垂直于同一个平面的两个平面也可以相交2. C 设同一顶点的三条棱分别为x, y, z ,则x2 y2 a2 , y2 z2 b2 , x2 z2 c2得 x2 y2 z2 1 (a2 b2 c2 ) ,则对角线长为 1 ( a2 b2 c2 ) 2 a2 b2 c22 2 23. B 作等积变换 V A BCD V C ABD4. B BD 垂直于 CE 在平面 ABCD 上的射影5. C BC PA BC AH6. C 取 AC 的中点 E ,取 CD 的中点 F ,EF 1, BE2, BF3cos EF 3 2 2 2 BF 37. C 取 SB 的中点 G ,则 GE GF a,在△ SFC 中,EF2a ,EFG 4502 2二、填空题1. 5cm或1cm 分 A, B 在平面的同侧和异侧两种情况2. 48 每个表面有 4 个,共 6 4 个;每个对角面有 4 个,共 6 4 个3.900垂直时最大4.60 度5. 11沿着PA将正三棱锥P ABC 侧面展开,则A, D , E, A'共线,且 AA' // BC三、解答题:略1.证明: (1)连接 BD,MO .在平行四边形ABCD中,因为 O 为 AC 的中点,所以 O 为 BD 的中点.又 M 为 PD 的中点,所以 PB ∥ MO.因为 PB 平面 ACM , MO? 平面 ACM ,所以 PB ∥平面 ACM.(2) 因为 ∠ADC = 45°,且 AD = AC = 1, 所以 ∠ DAC = 90°,即 AD ⊥ AC.又 PO ⊥平面 ABCD , AD? 平面 ABCD ,所以 PO ⊥ AD. 而 AC ∩PO =O ,所以 AD ⊥平面 PAC.2[解析 ] (1)取 A 1C 1 中点 F ,作 EG ⊥ 面 AC 1 于 G ,B 1F ∥ EG? B 1EGF 为平行四边形 ? FG ⊥ A 1C 1? G 为 A 1C 之中点.B 1E ∥ 面 AC 1? BE ∥ FG从而 E 为 BB 1 之中点. ∴BE =B 1E.(2) 由 (1)知 G 为矩形 ACC 1A 1 的中心, 过 G 作直线平行于 A 1 C 1,交 AA 1 于点 P ,交 CC 1 于 Q 点,连结 EP ,EQ ,则平面 A B C ∥ 平面 PEQ ,即求平面 AEC 与平面 PEQ 所成的角,11 1∵ 交线为 EG , ∴其平面角为 ∠ A 1GP ,因 AA 1= A 1 B 1,则 ACC 1A 1 为正方形,则 ∠ A 1GP = 45°.3. (1) 证明:因为 PD ⊥平面 ABCD ,所以 PD ⊥ AD . 又因为四边形 ABCD 是矩形,所以 AD ⊥ CD . 因为 PD ∩CD = D ,所以 AD ⊥ 平面 PCD . 又因为 PC? 平面 PCD ,所以 AD ⊥ PC .(2) 解: 由(1)知 AD ⊥ 平面 PCD ,所以 AD 是三棱锥 A - PDE 的高.因为 E 为 PC 的中点,且 PD = DC = 4,所以 S △PDE1△ PDC 1 1= 2S = 2×2× 4×4=4.1 1 8 又 AD = 2,所以 V A -PDE = AD ·S △PDE = × 2×4= .3 33(3) 解: 取 AC 的中点 M ,连接 EM , DM ,因为 E 为 PC的中点, M 是 AC 的中点,所以 EM∥ PA.又因为 EM? 平面 DEM, PA?平面 EDM,所以 PA∥平面 DEM.1 1AD2+ DC2=122+ 42= 5,此时 AM = AC=2 22即在 AC 上存在一点M,使得 PA∥平面 EDM,且 AM 的长为 5.。
点线面关系知识总结和练习题(答案)

//a α//a b点线面位置关系复习知识梳理一、直线与平面平行 1.判定方法(1)定义法:直线与平面无公共点。
(2)判定定理:(3)其他方法://a αββ⊂2.性质定理://a a bαβαβ⊂⋂= 二、平面与平面平行 1.判定方法(1)定义法:两平面无公共点。
(2)判定定理:////a b a b a b Pββαα⊂⊂⋂= //αβ(3)其他方法:a a αβ⊥⊥ //αβ;////a γβγ//αβ2.性质定理://a bαβγαγβ⋂=⋂= 三、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法 ① 用定义.② 判定定理:a ba cbc A b c αα⊥⊥⋂=⊂⊂ a α⊥③ 推论://a a bα⊥ b α⊥//a b a b αα⊄⊂//a α//a b//a b(3)性质 ①a b αα⊥⊂ a b ⊥②a b αα⊥⊥ 四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理a a αβ⊂⊥ αβ⊥(3)性质①性质定理la a lαβαβα⊥⋂=⊂⊥ αβ⊥② l P P A A αβαβαβ⊥⋂=∈⊥垂足为 A l ∈④ l P PA αβαβαβ⊥⋂=∈⊥ PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直 练习巩固:一、选择题1.设 α,β为两个不同的平面,l ,m 为两条不同的直线,且l ⊂α,m ⊂β,有如下的两个命题:①若 α∥β,则l ∥m ;②若l ⊥m ,则 α⊥β.那么( ).A .①是真命题,②是假命题B .①是假命题,②是真命题C .①②都是真命题D .①②都是假命题2.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是( ). A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1角为60° 3.关于直线m ,n 与平面 α,β,有下列四个命题: ①m ∥α,n ∥β 且 α∥β,则m ∥n ; ②m ⊥α,n ⊥β 且 α⊥β,则m ⊥n ; ③m ⊥α,n ∥β 且 α∥β,则m ⊥n ;④m ∥α,n ⊥β 且 α⊥β,则m ∥n .(第2题)A.①②B.③④C.①④D.②③4.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线其中假.命题的个数是().A.1 B.2 C.3 D.45.下列命题中正确的个数是().①若直线l上有无数个点不在平面 α 内,则l∥α②若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都没有公共点A.0个B.1个C.2个D.3个6.两直线l1与l2异面,过l1作平面与l2平行,这样的平面().A.不存在B.有唯一的一个C.有无数个D.只有两个7.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为().A.90°B.60°C.45°D.30°8.下列说法中不正确的....是().A.空间中,一组对边平行且相等的四边形一定是平行四边形B.同一平面的两条垂线一定共面C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D.过一条直线有且只有一个平面与已知平面垂直9.给出以下四个命题:①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面③如果两条直线都平行于一个平面,那么这两条直线互相平行④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直A .4B .3C .2D .110.异面直线a ,b 所成的角60°,直线a ⊥c ,则直线b 与c 所成的角的范围为( ). A .[30°,90°] B .[60°,90°] C .[30°,60°] D .[30°,120°]二、填空题11.已知三棱锥P -ABC 的三条侧棱PA ,PB ,PC 两两相互垂直,且三个侧面的面积分别为S 1,S 2,S 3,则这个三棱锥的体积为 .12.如图,在正三角形ABC 中,D ,E ,F 分别为各边的中点,G ,H ,I ,J 分别为AF ,AD ,BE ,DE 的中点,将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为 .13.直线l 与平面 α 所成角为30°,l ∩α=A ,直线m ∈α,则m 与l 所成角的取值范围是 .14.棱长为1的正四面体内有一点P ,由点P 向各面引垂线,垂线段长度分别为d 1,d 2,d 3,d 4,则d 1+d 2+d 3+d 4的值为 .三、解答题15.在四面体ABCD 中,△ABC 与△DBC 都是边长为4的正三角形. (1)求证:BC ⊥AD ;(2)若点D 到平面ABC 的距离等于3,求二面角A -BC -D 的正弦值;(3)设二面角A -BC -D 的大小为 θ,猜想 θ 为何值时,四面体A -BCD 的体积最大.(不要求证明)16. 如图,在长方体ABCD —A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点,连结ED ,EC ,EB 和DB .(1)求证:平面EDB ⊥平面EBC ; (2)求二面角E -DB -C 的正切值.J(第12题)答案: 一、选择题1.D 解析:命题②有反例,如图中平面 α∩平面 β=直线n ,l ⊂α,m ⊂β,且l ∥n ,m ⊥n ,则m ⊥l ,显然平面 α 不垂直平面 β, (第1题) 故②是假命题;命题①显然也是假命题, 2.D 解析:异面直线AD 与CB 1角为45°.3.D 解析:在①、④的条件下,m ,n 的位置关系不确定.4.D 解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D . 5.B 解析:学会用长方体模型分析问题,A 1A 有无数点在平面ABCD 外,但AA 1与平面ABCD 相交,①不正确;A 1B 1∥平面ABCD ,显然A 1B 1不平行于BD ,②不正确;A 1B 1∥AB ,A 1B 1∥平面ABCD ,但AB ⊂平面ABCD 内,③不正确;l 与平面α平行,则l 与 α 无公共点,l 与平面 α 内的所有直线都没有公共点,④正确,应选B . (第5题)6.B 解析:设平面 α 过l 1,且 l 2∥α,则 l 1上一定点 P 与 l 2 确定一平面 β ,β 与 α 的交线l 3∥l 2,且 l 3 过点 P . 又过点 P 与 l 2 平行的直线只有一条,即 l 3 有唯一性,所以经过 l 1 和 l 3 的平面是唯一的,即过 l 1 且平行于 l 2 的平面是唯一的.7.C 解析:当三棱锥D -ABC 体积最大时,平面DAC ⊥ABC ,取AC 的中点O ,则△DBO 是等腰直角三角形,即∠DBO =45°.8.D 解析:A .一组对边平行就决定了共面;B .同一平面的两条垂线互相平行,因而共面;C .这些直线都在同一个平面内即直线的垂面;D .把书本的书脊垂直放在桌上就明确了.9.B 解析:因为①②④正确,故选B .10.A 解析:异面直线a ,b 所成的角为60°,直线c ⊥a ,过空间任一点 P ,作直线 a ’∥a , b ’∥b , c ’∥c . 若a ’,b ’,c ’ 共面则 b ’ 与 c ’ 成 30° 角,否则 b ’ 与 c ’ 所成的角的范围为(30°,90°],所以直线b 与c所成角的范围为[30°,90°] .二、填空题 11.313212S S S .解析:设三条侧棱长为 a ,b ,c .则21ab =S 1,21bc =S 2,21ca =S 3 三式相乘: ∴81a 2 b 2 c 2=S 1S 2S 3,∴ abc =23212S S S .∵ 三侧棱两两垂直,∴ V =31abc ·21=313212S S S .12.60°.解析:将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为60°.13.[30°,90°].解析:直线l 与平面 α 所成的30°的角为m 与l 所成角的最小值,当m 在 α 内适当旋转就可以得到l ⊥m ,即m 与l 所成角的的最大值为90°.14.36.解析:作等积变换:4331⨯×(d 1+d 2+d 3+d 4)=4331⨯·h ,而h =36. 三、解答题15.证明:(1)取BC 中点O ,连结AO ,DO . ∵△ABC ,△BCD 都是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O , ∴BC ⊥平面AOD .又AD ⊂平面AOD ,∴BC ⊥AD . (第17题)解:(2)由(1)知∠AOD 为二面角A -BC -D 的平面角,设∠AOD =θ,则过点D 作DE ⊥AD ,垂足为E . ∵BC ⊥平面ADO ,且BC ⊂平面ABC ,∴平面ADO ⊥平面ABC .又平面ADO ∩平面ABC =AO , ∴DE ⊥平面ABC .∴线段DE 的长为点D 到平面ABC 的距离,即DE =3. 又DO =23BD =23, 在Rt △DEO 中,sin θ=DODE =23,故二面角A -BC -D 的正弦值为23. (3)当 θ=90°时,四面体ABCD 的体积最大.16.证明:(1)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC =45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABC D -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D ,∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD ⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -D B -C 的平面角.利用平面几何知识可得OF =51,又OE =1,所以,tan ∠EFO =5.。
点线面位置关系例题与练习(含答案)之欧阳美创编

点、线、面的位置关系●知识梳理(一).平面公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。
公理2:不共线...的三点确定一个平面.推论1:直线与直线外的一点确定一个平面. 推论2:两条相交直线确定一个平面. 推论3:两条平行直线确定一个平面. 公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面1.1平行线的传递公理:平行于同一条直线的两条直线互相平行。
1.2等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
1.3异面直线定义:不同在任何一个平面内的两条直线——异面直线;1.4异面直线所成的角:(1)范围:(]θ∈︒︒;(2)作异面0,90直线所成的角:平移法.2.直线与平面的位置关系: 包含,相交,平行3.平面与平面的位置关系:平行,相交 (三)平行关系(包括线面平行,面面平行) 1.线面平行:①定义:直线与平面无公共点.②判定定理:////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭③性质定理:////a a a bb αβαβ⎫⎪⊂⇒⎬⎪=⎭2.线面斜交: ①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角。
范围:[]0,90θ∈︒︒3.面面平行:①定义://αβαβ=∅⇒;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行; 符号表述:,,,//,////a b ab O a b ααααβ⊂=⇒判定2:垂直于同一条直线的两个平面互相平行.符号表述:,//a a αβαβ⊥⊥⇒.③面面平行的性质:(1)////a a αββα⎫⇒⎬⊂⎭;(2)////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。
点线面关系练习题(有答案)

点线面位置关系总复习之阿布丰王创作知识梳理一、直线与平面平行1.判定方法(1)定义法:直线与平面无公共点。
(2)判定定理:(3)其他方法:2.性质定理:二、平面与平面平行1.判定方法(1)定义法:两平面无公共点。
(2)判定定理:(3)其他方法:;2.性质定理:三、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法①用定义.②判定定理:③推论:(3)性质①②四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理(3)性质①性质定理②3“转化思想”面面平行线面平行线线平行面面垂直线面垂直线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角的平面角例1.如图,在三棱锥SABC中,SA^底面ABC,AB^BC,DE垂直平分SC,且分别交AC于D,交SC于E,又SA=AB,SB=BC,求以BD为棱,以BDE和BDC为面的二面角的度数。
●求线面夹角定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。
例1:在棱长都为1的正三棱锥S-ABC中,侧棱SA与底面ABC所成的角是________.例2:在正方体ABCD-A1B1C1D1中,①BC1与平面AB1所成的角的大小是___________;②BD1与平面AB1所成的角的大小是___________;③CC1与平面BC1D所成的角的大小是___________;④BC1与平面A1BCD1所成的角的大小是___________;⑤BD1与平面BC1D所成的角的大小是___________;例3:已知空间内一点O出发的三条射线OA、OB、OC两两夹角为60°,试求OA与平面BOC所成的角的大小.●求线线距离说明:求异面直线距离的方法有:(1)(直接法)当公垂线段能直接作出时,直接求.此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.(2)(转化法)把线线距离转化为线面距离,如求异面直线、距离,先作出过且平行于的平面,则与距离就是、距离.(线面转化法).也可以转化为过平行的平面和过平行于的平面,两平行平面的距离就是两条异面直线距离.(面面转化法).(3)(体积桥法)利用线面距再转化为锥体的高用何种公式来求.(4)(构造函数法)经常利用距离最短原理构造二次函数,利用求二次函数最值来解.两条异面直线间距离问题,教科书要求不高(要求会计算已给出公垂线时的距离),这方面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.例:在棱长为的正方体中,求异面直线和之间的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题号
3-17、18 3-19(1-3) 3-19 (4-6) 3-20、22 3-21、23 3-24、25 3-26 3-27、28 3-29、30 3-31、32 3-33、34 3-35、36 3-37、38 3-39、40 4-1(1、2) 4-1(3、4) 4-2、3
5 5 6 6 6 6 6 6 6 6 8 8 8 8 8 8 9
b e c a a
22页
b
c d e
3-33. 已知五边形ABCDE的H面 3-34. 完成平面图形的H面投影 3-34.完成平面图形的H面投影 3-33.已知五边形ABCDE的H面投影,及和W面投影。 投影,及其另一边CD的V面投影, 和W面投影. 其一边CD的V面投影,并知BD为水平线, 并知BD为水平线,试完成其V面 投影。 试完成其V面投影.
AB=40mm,求V面投影。
a′
b′
n′ c′
b′ m′ n m a′ d′
b
a
a
c
b d
20页
3-25. 已知A D为等腰直角△ABC的高, 3-24. 以BC为底边作等腰三角形, 斜边BC在直线MN上,求△ABC的V、 高为底边的1/2,并与H面成 H面投影。 30°角。 a′ a′
b′
d′
c′
点击题号进入题解
退出
目
页号
27 27 28 28 29 29 30 31 31 32 32 33 33 33 34 34
录 (二)
页号
34 34 35 36 36 37 38 39
题号
4-4、5 4-6、7 4-8(1、2) 4-8(3、4) 4-9(1、2) 4-9(3、4) 4-9(5、6) 4-10、11 4-12、13 4-14、15 4-16、17 4-18 4-19 4-20 4-21 4-22
′
16页
3-14 判别两直线的相对位置。
(1)
a c c a c b d bd c a
b
(2)
a d
AB与CD 交错
c
AB与CD 相交
c a
d
b
(3)
a
d b
(4)
b a d c
d
b
c
a
b d
AB与CD 平行 17页
AB与CD 交错
判别交错两直线 的可见性。
′ ′ 3′
、
′
重影点
.已知平行四边形 中, 为水平线, 为正平线,求平行四边形 的两面投影。
(8)
6页
(1)
点击此处查看立体图
8页
返回
2-4. 补画形体的第三面投影。
(2)
点击此处查看立体图
8页
返回
2-4. 补画形体的第三面投影。
(3)
点击此处查看立体图
8页
返回
2-4. 补画形体的第三面投影。
(4)
点击此处查看立体图
8页
返回
2-4. 补画形体的第三面投影。
(5)
点击此处查看立体图
8页
返回
2-4. 补画形体的第三面投影。
(6)
点击此处查看立体图
8页
返回
2-5. 补画形体的第三面投影。
(1)
9页
2-5. 补画形体的第三面投影。
(2)
点击此处查看立体图
9页
返回
2-5. 补画形体的第三面投影。
(3)
点击此处查看立体图
9页
返回
2-5. 补画形体的第三面投影。
a′
c′
b
a′ c
b′
c a
a
b
24页
3-39.已知AB为平面对H面的最大斜度 线,平面的α=30,求作该平面的两面投 影. b′
3-40.已知△ABC平面的AB边为该平面相 对于V面的最大斜度线,并知点C比点A 高10mm,且距W面50mm,完成该平面的V、W 面投影.
′ c′ a
c′ b b′
4-5. 过点D作平面与△ABC平行。
b e d a b c c b a P H e d a c d b d a c
27页
4-6. 过点E作平面△EFG平行于两 平行线AB、CD所表示的平面。
4-7. 过直线AB作平面平行于 △DEF(a'b'∥c'd'f')。
a b c
g e f d a
b e d e a
(4)
6页
1
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(5)
6页
9
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(6)
4
6页
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(7)
6页
10
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
的三面投影。 4)已知 为侧垂线及点 的两面投影, 点 在W面上。 Z
b a b" a"
(3)已知 为铅垂线及点 的两面投影, 点 在点 的上方, 的实长为15 。
Z b' b"
a' X O
a"
Y
X O
Y
b(a)
b
a
Y
Y
14页
3-9.根据已知条件,求直线上点的投影。
(1)点K距H面20mm。
(2)点K距V、W面等距。
(2)
5页
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(1)
6页
5
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(2)
6页
3
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
(3)
6页
12
2-3.参照下一页的立体图填入对应的序号,并画出所缺的 投 影图。
m′
b′ d′
c′
n′
c
c d
n
d m a
20页
b
b
a
3-26. 补画各平面图形的第三面投影,并注明是何种位置平面。(21页)
(1) (2) (3)
侧垂面 (4) (5)
一般面 (6)
侧平面
水平面
正垂面 21页
正平面
3-27. 已知等腰直角△MNK∥V面, ∠M=90°,MN为一腰长,求 △MNK的三面投影。
( )
a
c
4
5
6
b
a
d b c d
a a
c d c b b
a
AB与CD
a
AB与 AC
19页
是
否
AB与 CD
是
3-20. 求A点到直线BC的距离。 3-22. 求两直线A B、CD之间的距离。
b′ a′
d′ a′
b′
c′
c′
d′
(d )
a
c(d)
b(c)
a b
20页
3-21. 求点M到直线AB的距离。 3-24. 已知直线A B与CD垂直相交,
b
b
e
e
c
c
f
a
22页
3-31.已知直线EF在△ABC平 3-32.完成平面图形AB 3-32. 完成平面图形ABCD的H 3-31. 已知直线EF在△ABC平 的H面投影. 面上,求直线EF的H面投影.面投影。 面上,求直线EF的H 面投影。 a′ b ′ e′ e ′ a′ ′ b d′ f′ c′ c′ f
题号
4-23 4-24 4-25、26 5-1、2 5-3 5-4、5 5-6、7 5-8、9
点击题号进入题解
退出
2-1.根据物体的立体图画出三面投影图(尺寸由立体图中量 取)。
(1) (2)
4页
2-2.根据物体的立体图画出三面投影图(尺寸由立体图中量 取)。
(1)
5页
2-2.根据物体的立体图画出三面投影图(尺寸由立体图中量 取)。
( )
n e
18页
( )
a
b
( )
c
3-19。判别两直线是否垂直。 2 1
( )
c
3
a
b b c
b
d
a a
d d
c
a
d
a
c AB与 BC 是 AB与 CD b c b AB与 CD 是
否
19页
3-19. 判别两条直线是否垂直。 3-19。判别两直线是否垂直。
( ) ( )
c
c b b c d
mm
c″
′ a
a″
c
a
b″
24页
4-1. 判别直线与平面,平面与平面是否平行 。 (1) (2)
f a e a e b f
b
c b c b a e a f
c f e c
( 平行 )
( 不平行 )
26页
4-1. 判别直线与平面,平面与平面是否平行 。 (3)
c b a d b a f c d e e f a d f f b d c e
( )
正垂线 (4) (5)
水平线 (6)
铅垂线
一般线
正平线
侧平线
13页
3-8.根据已知条件,求直线
的三面投影。 2)已知 为正平线及点 的两面投影, 点 在点 的右下方。
Z
(1)已知 为水平线及点 的两面投影, ,点 在点 的右后方,且在 面上。
Z
=30
a
a a Y
a Y
X
X
