数字PID的仿真实验例子
实验三 数字式PID调节器控制算法仿真

实验三 数字式PID 调节器控制算法仿真一、实验目的1、了解并掌握基本的数字PID 控制算法和常用的PID 控制改进算法。
2、掌握用Matlab 进行仿真的方法。
3、了解PID 参数整定的方法及参数整定在整个系统中的重要性。
二、实验设备PC 机(Matlab 软件)三、实验原理1、基本的PID 控制算法:基本的数字P0控制有三种算法:位置式、增量式和速率式,其中应用最为广泛的是增量式,因为增量式算法只与最近几次采样值有关,不需要累加;计算机输出增量,误差动作时影响小。
因此这里采用增量式PID 算法:)]1()1(2)([)()]1()([)(-+--++--=∆k e k e k e k k e k k e k e k k u d i p其中设)]1()([)(--=k e k e k k u p p)()(k e k k u i i =)]2()1(2)([)(-+--=k e k e k e k k u d d则)()()()(k u k u k u k u d i p ++=∆2、数字PID 调节器参数的整定:为使系统性能满足一定的要求,必须确定算法中各参数的具体值,这就是参数整定。
参数整定是十分重要的,调节系统参数整定的好坏直接影响调节品质。
要想快速、灵活的将参数整定好,首先应透彻理解这些参数对系统性能的影响:增大比例系数,一般将加快系统的响应,这在有静差系统中有利于减小静差,但过大会使系统有较大超调,并产生振荡,使稳定性变坏。
增大积分时间(积分作用减弱)有利于减小超调,减小振荡,使系统更加稳定,但系统静差消除的过程将随之减慢。
增大微分时间(微分作用增强)有利于加快系统响应,使超调减小,稳定性增加,但系统对扰动有较敏感的响应。
四、实验要求1、在Matlab 环境中,按照给定对象,构建仿真PID 控制系统。
2、调整PID 参数,观察各参数对系统响应的影响。
3、采用增量式PID 算法进行控制系统仿真,对各参数进行整定,观察系统响应曲线,直到获得满意的响应曲线。
PID仿真实验报告

PID仿真实验报告PID控制是一种经典的控制方法,被广泛应用于工业自动化控制系统中。
本次实验主要针对PID控制器的参数调整方法进行仿真研究。
实验目的:1.研究PID控制器的工作原理;2.了解PID参数调整的方法;3.通过仿真实验比较不同PID参数对系统控制性能的影响。
实验原理:PID控制器由比例(P)、积分(I)、微分(D)三个控制部分组成。
比例控制:输出与误差成比例,用来修正系统集成误差;积分控制:输出与误差的积分关系成比例,用来修正系统持续存在的静态误差;微分控制:输出与误差变化率成比例,用来修正系统的瞬态过程。
PID参数调整方法有很多种,常见的有经验法、Ziegler-Nichols法和优化算法等。
实验中我们使用经验法进行调整,根据系统特性来进行手动参数调整。
实验装置与步骤:实验装置:MATLAB/Simulink软件、PID控制器模型、被控对象模型。
实验步骤:1. 在Simulink中建立PID控制器模型和被控对象模型;2.设定PID控制器的初始参数;3.运行仿真模型,并记录系统的响应曲线;4.根据系统响应曲线,手动调整PID参数;5.重复第3步和第4步,直到系统的响应满足要求。
实验结果与分析:从图中可以看出,系统的响应曲线中存在较大的超调量和震荡,说明初始的PID参数对系统控制性能影响较大。
从图中可以看出,系统的响应曲线较为平稳,没有出现明显的超调和震荡。
说明手动调整后的PID参数能够使系统达到较好的控制效果。
总结与结论:通过本次实验,我们对PID控制器的参数调整方法进行了研究。
通过手动调整PID参数,我们能够改善系统的控制性能,提高系统的响应速度和稳定性。
这为工业自动化控制系统的设计和优化提供了参考。
需要注意的是,PID参数的调整是一个复杂的工作,需要结合具体的控制对象和要求进行综合考虑。
而且,不同的参数调整方法可能适用于不同的控制对象和场景。
因此,在实际应用中,需要根据具体情况选择合适的参数调整方法,并进行实验验证。
学生--PID控制MATLAB仿真实验

计算机控制技术实验指导书(MATLAB版)机电学院杨蜀秦编2012-11-19实验一 连续系统的模拟PID 仿真一、基本的PID 控制 在模拟控制系统中,控制器最常用的控制规律是PID 控制。
模拟PID 控制系统原理框图如图1-1所示。
图1-1 模拟PID 控制系统原理框图PID 控制规律为:⎪⎪⎭⎫⎝⎛++=⎰dt t de T dt t e T t e k t u DtI p )()(1)()(0或写成传递函数的形式⎪⎪⎭⎫ ⎝⎛++==s T s T k s E s U s G D I p 11)()()( Ex1 以二阶线性传递函数ss 251332+为被控对象,进行模拟PID 控制。
输入信号)2.0*2sin()(t t r π=,仿真时取3,1,60===d i p k k k ,采用ODE45迭代方法,仿真时间10s 。
仿真方法一:在Simulink 下进行仿真,PID 控制由Simulink Extras 节点中的PID Controller 提供。
仿真程序:ex1_1.mdl ,如图1-2所示。
图1-2 连续系统PID 的Simulink 仿真程序连续系统的模拟PID 控制正弦响应结果如图1-3所示。
图1-3 连续系统的模拟PID 控制正弦响应仿真方法二:在仿真一的基础上,将仿真结果输出到工作空间中,并利用m 文件作图。
仿真程序:ex1_2.mdl ,程序中同时采用了传递函数的另一种表达方式,即状态方程的形式,其中[]0,01,1330,25010==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=D C B A ,如图1-4所示。
m 文件作图程序:ex1_2plot.mclose all ;plot(t,rin,'k',t,yout,'k'); xlabel('time(s)'); ylabel('r,y');二、线性时变系统的PID 控制 Ex2 设被控对象为Jss Ks G +=2)(,其中)2sin(300400),6sin(1020t K t J ππ+=+=,输入信号为)2sin(5.0t π。
PID控制器MATLAB仿真

实验4 PID 控制器一、 实验目的1. 了解PID 控制器中P ,I ,D 三种基本控制作用对控制系统性能的影响。
2. 进行PID 控制器参数工程整定技能训练。
二、实验内容:题目1 了解P 、I 、D 三种控制器的作用:. )11(s T sT K G d i p c ++= 已知被控对象传递函数为3)1(1+sA 获取比例系数为1的系统阶跃响应曲线;实验步骤:在matlab 命令窗口中键入: clcclear allg0=tf(1,conv([1 2 1],[1 1])); kp=1;sys=feedback(kp*g0,1); step(sys);legend('Kp=1');grid on 运行得到的图象如图一:Step ResponseTime (sec)A m p l i t u d e图一B 调节比例系数,分析p K 过大和过小对系统动态性能(s p t t ,,σ)有何影响?稳态性能(稳定/ss e )的影响;实验步骤:在matlab 命令窗口中键入: clcclear allg0=tf(1,conv([1 2 1],[1 1])); kp=0.1:0.6:3;for i=1:length(kp)sys=feedback(kp(i)*g0,1); step(sys);legend('first','second','third','four','five'); grid on hold onend 运行之后得到的图象如图二:0246810121416180.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e图二分析:图二中绘制了Kp 从0.1到3时的系统单位阶跃响应曲线,可以看到,当比例作用增大时,闭环系统稳态误差变小,响应的震荡加剧,响应速度变快。
PID仿真实验报告

PID仿真实验报告PID控制算法是一种重要的控制算法,被广泛应用于工业控制系统中。
本文通过仿真实验的方式,对PID控制算法进行了验证和分析。
一、实验目的1.了解PID控制算法的基本原理和调节方法;2. 掌握MATLAB/Simulink软件的使用,进行PID控制实验仿真;3.验证PID控制算法的稳定性和性能。
二、实验内容本次实验选择一个常见的控制系统模型,以电感驱动的直流电机控制系统为例。
通过PID控制算法对该系统进行控制,观察系统的响应特性。
三、实验步骤1.搭建电感驱动的直流电机控制系统模型,包括电感、直流电机、PID控制器等组成部分;2.设置PID控制器的参数,包括比例增益Kp、积分时间Ti、微分时间Td等;3.进行仿真实验,输入适当的控制信号,观察系统的响应曲线;4.调节PID控制器的参数,尝试不同的调节方法,观察响应曲线的变化,寻找合适的参数。
四、实验结果与分析1.首先,设置PID控制器的参数为Kp=1,Ti=1,Td=0,进行仿真实验。
观察到系统的响应曲线,并记录与分析曲线的特点;2.其次,调整PID控制器的参数,如增大比例增益Kp,观察系统的响应曲线的变化;3.最后,调整积分时间Ti和微分时间Td,观察系统的响应曲线的变化。
通过实验结果与分析,可以得到以下结论:1.PID控制算法能够有效地控制系统,并实现稳定的控制;2.比例增益Kp对系统的超调量有较大的影响,增大Kp可以减小超调量,但也会增加系统的稳定时间;3.积分时间Ti对系统的稳态误差有较大的影响,增大Ti可以减小稳态误差,但也会增加系统的超调量;4.微分时间Td对系统的响应速度有较大的影响,增大Td可以增加系统的响应速度,但可能会引起系统的振荡。
五、实验总结通过本次实验,我深入理解了PID控制算法的原理和调节方法。
同时,通过对实验结果的分析,我也了解了PID控制算法的稳定性和性能。
在实际工程应用中,需要根据具体的控制对象,合理选择PID控制器的参数,并进行调节优化,以获得理想的控制效果。
《计算机控制技术》数字PID控制器设计与仿真实验报告
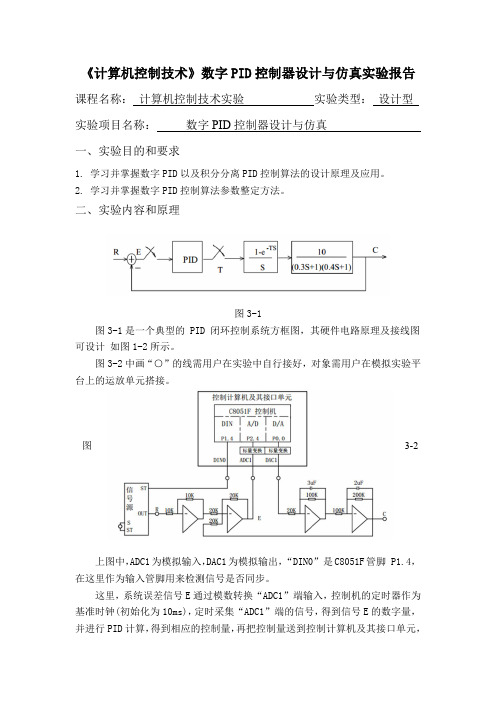
《计算机控制技术》数字PID控制器设计与仿真实验报告课程名称:计算机控制技术实验实验类型:设计型实验项目名称:数字PID控制器设计与仿真一、实验目的和要求1. 学习并掌握数字PID以及积分分离PID控制算法的设计原理及应用。
2. 学习并掌握数字PID控制算法参数整定方法。
二、实验内容和原理图3-1图3-1是一个典型的 PID 闭环控制系统方框图,其硬件电路原理及接线图可设计如图1-2所示。
图3-2中画“○”的线需用户在实验中自行接好,对象需用户在模拟实验平台上的运放单元搭接。
图3-2上图中,ADC1为模拟输入,DAC1为模拟输出,“DIN0”是C8051F管脚 P1.4,在这里作为输入管脚用来检测信号是否同步。
这里,系统误差信号E通过模数转换“ADC1”端输入,控制机的定时器作为基准时钟(初始化为10ms),定时采集“ADC1”端的信号,得到信号E的数字量,并进行PID计算,得到相应的控制量,再把控制量送到控制计算机及其接口单元,由“DAC1”端输出相应的模拟信号,来控制对象系统。
本实验中,采用位置式PID算式。
在一般的PID控制中,当有较大的扰动或大幅度改变给定值时,会有较大的误差,以及系统有惯性和滞后,因此在积分项的作用下,往往会使系统超调变大、过渡时间变长。
为此,可采用积分分离法PID控制算法,即:当误差e(k)较大时,取消积分作用;当误差e(k)较小时才将积分作用加入。
图3-3是积分分离法PID控制实验的参考程序流程图。
图3-3三、主要仪器设备计算机、模拟电气实验箱四、操作方法与实验步骤1.按照图3-2搭建实验仿真平台。
2.确定系统的采样周期以及积分分离值。
3.参考给出的流程图编写实验程序,将积分分离值设为最大值0x7F,编译、链接。
4.点击,使系统进入调试模式,点击,使系统开始运行,用示波器分别观测输入端R以及输出端C。
5.如果系统性能不满意,用凑试法修改PID参数,再重复步骤3和4,直到响应曲线满意,并记录响应曲线的超调量和过渡时间。
pid控制实验报告[最新版]
![pid控制实验报告[最新版]](https://img.taocdn.com/s3/m/ab6b0408640e52ea551810a6f524ccbff121ca13.png)
pid控制实验报告pid控制实验报告篇一:PID控制实验报告实验二数字PID控制计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID控制算法不能直接使用,需要采用离散化方法。
在计算机PID控制中,使用的是数字PID控制器。
一、位置式PID控制算法按模拟PID控制算法,以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID位置式表达式:Tu T ?kpeu=para; J=0.0067;B=0.1; dy=zeros= y= -+ = k*ts; %time中存放着各采样时刻rineu_1=uerror_1=error;%误差信号更新图2-1 Simulink仿真程序其程序运行结果如表2所示。
Matlab输出结果errori = error_1 = 表2 例4程序运行结果三、离散系统的数字PID控制仿真1.Ex5 设被控对象为G?num 仿真程序:ex5.m%PID Controller clear all; close all;篇二:自动控制实验报告六-数字PID控制实验六数字PID控制一、实验目的1.研究PID控制器的参数对系统稳定性及过渡过程的影响。
2.研究采样周期T对系统特性的影响。
3.研究I型系统及系统的稳定误差。
二、实验仪器1.EL-AT-III型自动控制系统实验箱一台 2.计算机一台三、实验内容1.系统结构图如6-1图。
图6-1 系统结构图图中 Gc(s)=Kp(1+Ki/s+Kds) Gh(s)=(1-e)/s Gp1(s)=5/((0.5s+1)(0.1s+1)) Gp2(s)=1/(s(0.1s+1))-TS 2.开环系统(被控制对象)的模拟电路图如图6-2和图6-3,其中图6-2对应GP1(s),图6-3对应Gp2(s)。
图6-2 开环系统结构图1 图6-3开环系统结构图2 3.被控对象GP1(s)为“0型”系统,采用PI控制或PID控制,可使系统变为“I型”系统,被控对象Gp2(s)为“I型”系统,采用PI控制或PID控制可使系统变成“II型”系统。
(完整word版)离散系统数字PID控制仿真

离散系统数字PID 控制仿真一、题目:用数字PID 控制传递函数为G(s)的被控对象:G(s)=523500/(s^3+87.35*s^2+10470*s)二、分析过程:1、对G(s)进行离散化即进行Z 变换得到Z 传递函数:G(Z)=(n1*z^3+n2*z^2+n3*z+n4)/(m1*z^3+m2*z^2+m3*z+m4)注:之所以为z 的三次式,这是通过matlab 进行z 变换后,观察num,den 的数据得到z 传递函数形式为z 的三次式,若为其他次数n ,则相应有n+1项。
2、分子分母除以z 的最高次数即除以z 的3次得到:Y(z)/U(z)=(n1+n2*z^-1+n3*z*^-2+n4*z^-3)/(m1+m2*z^-1+m3*z^-2+m4*z^-3) (m1+m2*z^-1+m3*z^-2+m4*z^-3) Y(z)= (n1+n2*z^-1+n3*z*^-2+n4*z^-3)* U(z)3、由z 的位移定理Z[e(t-kt)]=z^k*E(z)逆变换得到差分方程:m1*y(k)+m2*y(k-1)+m3*y(k-2)+m4*y(k-3)=n1*u(k)+n2*u(k-1)+n3*u(k-2)+n4*u(k-3) 通常m1=1得:y(k)+m2*y(k-1)+m3*y(k-2)+m4*y(k-3)=n1*u(k)+n2*u(k-1)+n3*u(k-2)+n4*u(k-3) y(k)=-m2*y(k-1)-m3*y(k-2)-m4*y(k-3)+n1*u(k)+n2*u(k-1)+n3*u(k-2)+n4*u(k-3)4、PID 编程实现P :△y = Kp* △ε I: D: 由于是仿真采样此处为数字式故采样时间为1ms ,时间很短,已经相当于微元化,所以可以按照以下程序实现PID 控制:x(1)=error(k); %数字控制器的P 编程实现 数字式控制器需要采样已经微元化 x(2)=(error(k)-error_1)/ts; %数字控制器的D 编程实现⎰⋅=∆dt T y I ε1dtd T y D ε=∆x(3)=error(k)*ts; %数字控制器的I编程实现三、程序清单clear all;close all;ts=0.001; %数字控制器的采样时间sys=tf(5.235e005,[1,87.35,1.047e004,0]); %写出控制对象的传递函数dsys=c2d(sys,ts,'z'); %被控对传递函数离散化[num,den]=tfdata(dsys,'v'); %离散化后的数据矩阵转化为Z传函u_1=0.0;u_2=0.0;u_3=0.0; %初始化差分方程的初始值y_1=0.0;y_2=0.0;y_3=0.0;x=[0,0,0]'; %PID的三个变量并赋予初值error_1=0; %作为偏差的前一时刻的变量for k=1:1:1500time(k)=k*ts;%设置输入信号类型和PID参数S=2;if S==1kp=0.50;ki=0.001;kd=0.001;rin(k)=1; %Step Signalelseif S==2kp=0.50;ki=0.001;kd=0.001;rin(k)=sign(sin(2*2*pi*k*ts)); %Square Wave Signalelseif S==3kp=1.5;ki=1.0;kd=0.01; %Sine Signalrin(k)=0.5*sin(2*2*pi*k*ts);endu(k)=kp*x(1)+kd*x(2)+ki*x(3); %PID控制器输出,作为被控对象的输入if u(k)>=10 %限制控制器的输出u(k)=10;endif u(k)<=-10u(k)=-10;end%*****************************************关键点*****************************************% yout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;%被控对象传递函数的输出与输入的关系,由Z变换的位移定理的逆变换得到%*****************************************关键点*****************************************%error(k)=rin(k)-yout(k);u_3=u_2;u_2=u_1;u_1=u(k); %参数反馈,差分方程得以继续y_3=y_2;y_2=y_1;y_1=yout(k);%*****************************************关键点*****************************************% x(1)=error(k); %数字控制器的P编程实现数字式控制器需要采样已经微元化x(2)=(error(k)-error_1)/ts; %数字控制器的D编程实现x(3)=error(k)*ts; %数字控制器的I编程实现%*****************************************关键点*****************************************% error_1=error(k); %得到当前的偏差作为PID运算中进行偏差运算endfigure(1);plot(time,rin,'k',time,yout,'k');xlabel('time(s)'),ylabel('rin,yout');grid on四、评价数字PID控制算法的缺点是,由于采用全量输出,所以每次的输出都与过去的状态有关,计算时要对error(k)量进行累加,计算机输出控制量u(k)对应的是执行机构的实际位置偏差,如果位置传感器出现故障,u(k)可能出现大幅度变化。
数字PID控制实验

4.5.1数字PID 控制实验 1 标准PID 控制算法1. 一. 实验要求2. 了解和掌握连续控制系统的PID 控制的原理。
3. 了解和掌握被控对象数学模型的建立。
4. 了解和掌握数字PID 调节器控制参数的工程整定方法。
观察和分析在标准PID 控制系统中, P.I.D 参数对系统性能的影响。
二. 实验内容及步骤 ⑴ 确立模型结构本实验采用二个惯性环节串接组成实验被控对象, T1=0.2S, T2=0.5S Ko=2。
S e T K s G τ-+⨯≈+⨯+=1S 110.2S 21S 5.01)(000⑵ 被控对象参数的确认被控对象参数的确认构成如图4-5-10所示。
本实验将函数发生器(B5)单元作为信号发生器, 矩形波输出(OUT )施加于被测系统的输入端R, 观察矩形波从0V 阶跃到+2.5V 时被控对象的响应曲线。
图4-5-10 被控对象参数的确认构成实验步骤: 注: 将‘S ST ’用‘短路套’短接!① 在显示与功能选择(D1)单元中, 通过波形选择按键选中‘矩形波’(矩形波指示灯亮)。
② B5的量程选择开关S2置下档, 调节“设定电位器1”, 使之矩形波宽度>2秒(D1单元左显示)。
③ 调节B5单元的“矩形波调幅”电位器使矩形波输出电压= 2.5V 左右(D1单元右显示)。
④ 构造模拟电路: 按图4-5-10安置短路套及测孔联线, 表如下。
(a )安置短路套 (b )测孔联线⑤ 运行、观察、记录:A)先运行LABACT 程序, 选择界面的“工具”菜单选中“双迹示波器”(Alt+W )项, 弹出双迹示波器的界面, 点击开始, 用虚拟示波器观察系统输入信号。
图4-5-11 被控对象响应曲线B) 在图4-5-112被控对象响应曲线上测得t1和t2。
通常取 , 要求从图中测得 ; 通常取 , 要求从图中测得 。
计算 和 : 0.84730.3567t -1.204t )]t (y 1[ln -)]t (y 1[ln )]t (y 1[ln t )]t (y 1[n t 0.8473t t )]t (y 1[ln -)]t (y 1[ln t t T 212010201102122010120==-----=-=---=τC) 求得数字PID 调节器控制参数P K 、I T 、D T (工程整定法))/0.2(1)/0.37()/0.6(1)/0.5()/2.5(]27.0)/(35.1[10000200000T T T T T T T T T T K K D I P ττττττ+⨯=++⨯=+=据上式计算数字PID 调节器控制参数P K 、I T 、D T⑶ 数字PID 闭环控制系统实验数字PID 闭环控制系统实验构成见图4-5-12, 观察和分析在标准PID 控制系统中, P.I.D 参数对系统性能的影响, 分别改变P.I.D 参数, 观察输出特性, 填入实验报告,模块号 跨接座号 1 A5 S5, S7, S102 A7 S2, S7, S9, P3 B5‘S-ST ’1 输入信号R B5(OUT )→A5(H1)2 运放级联 A5A (OUTA )→A7(H1)3 示波器联接 ×1档B5(OUT )→B3(CH1) 4A7A (OUTA )→B3(CH2)图4-5-12 数字PID 闭环控制系统实验构成实验步骤: 注: 将‘S ST ’用‘短路套’短接!① 在显示与功能选择(D1)单元中, 通过波形选择按键选中‘矩形波’(矩形波指示灯亮)。
PID控制算法matlab仿真实验
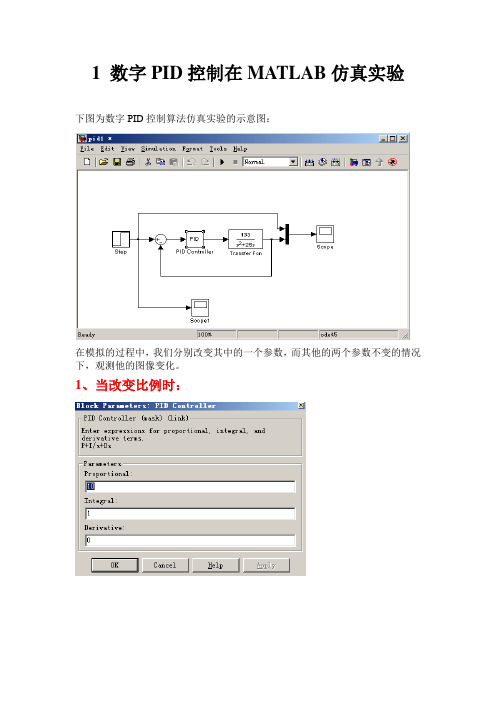
1 数字PID控制在MATLAB仿真实验下图为数字PID控制算法仿真实验的示意图:
在模拟的过程中,我们分别改变其中的一个参数,而其他的两个参数不变的情况下,观测他的图像变化。
1、当改变比例时:
分析结果:当只改变比例,积分和微分都不变的情况下,比例系数越大,调节作用越强,但是存在调节误差。
2、当只改变积分时
分析结果:当系统中只改变积分,而比例和微风都不变时,可以减少或消除误差,但响应慢。
3、当只改变微分时
分析结果:当系统中加入了微分环节时,改善了系统的稳定性能和动态性能,但是,它的响应比较慢。
基于MATLAB的数字PID控制器设计及仿真分析.

基于MATLAB的数字PID控制器设计及仿真分析摘要PID控制作为历史最为悠久,生命力最强的控制方式一直在生产过程自动化控制中发挥着巨大的作用。
PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛用于过程控制和运动控制中。
数字PID控制算法是将模拟PID离散化而得到的,各参数有着明显的物理意义,而且调整方便,所以PID控制器很受工程技术人员的喜爱。
本论文主要实现基于MATLAB的数字PID控制器设计及仿真。
首先介绍了传统的模拟PID控制方法,包括比例控制方法、比例积分控制方法、比例积分微分控制方法等。
接下来,介绍了数字PID控制。
随着时代的发展,科技的进步,传统的模拟PID控制方法不能满足人们的需求,数字PID控制的改进算法也便随之而来。
本文最后,应用MATLAB软件,在实验的环境下实现了其设计及仿真。
本次毕业设计用来完成数字PID控制器的设计,并通过MATLAB实现其仿真同时加以分析。
通过查阅文献得知,与传统模拟PID控制器相比较,该控制器具有良好的灵活性,而且可得到精确的数学模型。
另外,基于MATLAB的数字PID 控制器设计及仿真,充分的利用了MATLAB的实验环境,整个设计验证了数字PID的广泛可实现性及准确性。
关键词:PID控制;模拟PID控制器;数字PID控制器;MATLAB仿真;Design and simulation analysis of Digital PID ControllerMATLAB-basedAbstractAs the most age-old and powerful control mode, PID control always has had a great effect on the automatic control of the production process. PID control is one of the first developed control strategy, because of thesimple algorithm,great robust and high reliability, it is widely used in process control and motor control. Digital PID control algorithm is gotten by discreting the analog PID control, and the parameters have obvious physical meaning and facility adjustment, so PID controller is popular with engineering and technical personnel.In the paper, the main idea is to accomplish MATLAB-based digital PID controller design and simulation analysis. In the first place, the traditional analog PID control methods is introduced, including proportional control methods, proportional integral control and proportional integral differential control. In the second place, the digital PID control methods are offered. With the development of the times, the advancement of technology, traditional analog PID control method cannot make a satisfaction, then digital PID control is followed. At last,the application of MATLAB software to achieve their design and simulation is easy to accomplish.The graduation project is to complete the digital PID controller design and simulation through MATLAB simulation and analysis. It is known that through the literature, compare with traditional PID controller, the controller has good flexibility and precision of the mathematical models available. In addition, in the number of MATLAB-based PID controller design and simulation, the MATLAB experiment environment is used comprehensively. The entire design is confirmed the wide range and accuracy of digital PID controller.Key words:PID control;analog PID controller;digital PID controller;MATLAB simulatio目录摘要 (I)ABSTRACT (I)第1章绪论 (1)1.1课题目的及意义 (1)1.2数字PID控制器的研究现状 (2)第2章 PID控制器 (3)2.1传统PID控制器概述 (3)2.2PID控制器的基本原理 (4)2.2.1 比例(P)调节 (5)2.2.2 比例积分(PI)调节 (7)2.2.3 比例积分微分(PID)调节 (8)第3章数字PID控制器 (11)3.1数字PID控制系统 (11)3.2数字PID控制的基本算法 (11)3.2.1 位置式PID控制算法 (11)3.2.2 增量式PID控制算法 (13)3.2.3 位置算式与增量算式的比较 (14)第4章数字PID的改进算法 (15)4.1积分算法的改进 (16)4.1.1 积分分离法 (18)4.1.2 变速积分法 (20)4.1.3 遇限消弱积分法 (21)4.1.4 梯形积分法 (22)4.2微分算法的改进 (22)4.2.1 不完全微分PID控制算法 (23)4.2.2 微分先行PID控制算法 (25)4.3带死区的PID控制算法 (27)第5章基于MATLAB的数字PID控制器设计及仿真 (28)5.1位置式PID控制算法仿真实例 (29)5.2增量式PID控制算法仿真实例 (30)参考文献 (31)谢辞 (32)第1章绪论1.1 课题目的及意义PID控制器又称为PID调节器,是按偏差的比例P、积分I、微分进行控制的调节器的简称,它主要针对控制对象来进行参数调节。
控制系统pid参数整定方法的matlab仿真实验报告

控制系统pid参数整定方法的matlab仿真实验报告一、引言PID控制器是广泛应用于工业控制系统中的一种常见控制算法。
PID 控制器通过对系统的误差、误差积分和误差变化率进行调节,实现对系统的稳定性和动态性能的控制。
而PID参数的整定是保证系统控制性能良好的关键。
本实验旨在利用Matlab仿真,研究控制系统PID参数整定的方法,探讨不同整定策略对系统稳定性和动态性能的影响,为工程实际应用提供理论依据。
二、控制系统模型本实验采用了以二阶惯性环节为例的控制系统模型,其传递函数为:G(s) = K / (s^2 + 2ξω_ns + ω_n^2)其中,K为系统增益,ξ为阻尼比,ω_n为自然频率。
三、PID参数整定方法实验中我们探讨了几种典型的PID参数整定方法,包括经验法、Ziegler-Nichols方法和遗传算法。
1. 经验法经验法是一种简单粗糙的PID参数整定方法,根据实际系统的性质进行经验性调试。
常见的经验法包括手动调整法和试探法。
在手动调整法中,我们通过调整PID参数的大小,观察系统的响应曲线,从而找到满足系统性能要求的参数。
这种方法需要操作者有一定的经验和直觉,且对系统有一定的了解。
试探法是通过试验和试验的结果来确定PID参数的值。
在试探过程中,我们可以逐渐逼近最佳参数,直到满足系统性能要求。
2. Ziegler-Nichols方法Ziegler-Nichols方法是一种广泛应用的PID参数整定方法。
该方法通过系统的临界增益和临界周期来确定PID参数。
首先,在开环状态下,逐渐增加系统增益,当系统开始出现振荡时,记录下此时的增益值和周期。
然后根据临界增益和临界周期的数值关系,计算出PID参数。
3. 遗传算法遗传算法是一种基于生物进化原理的优化算法,可以用于自动化调整PID参数。
该方法通过对参数的种群进行进化迭代,逐渐找到最优的PID参数。
四、实验结果与分析我们利用Matlab进行了控制系统的PID参数整定仿真实验,并得到了不同整定方法下的系统响应曲线。
控制仿真PID实验报告

自动化1103
张天赐
201123910415
实验内容;控制系统设计与仿真(根轨迹,伯德图,PID)
实验步骤:
例4-8已知晶闸管直流调速系统的结构图如图,分析PID控制器的P、I和D对调速系统性能的影响
实验截图:
随着Kp的增大,系统的在增加,过渡过程时间变大,但响应初期的速度变大;系统的ess随着Kp的增大而减小。
绘制矫正后曲线
可得校正后系统的单位阶跃响应,曲线校正后系统是稳定的
例4-11某单位反馈控制系统的开环传递函数为:
校正后
4-12某单位反馈控制系统的开环传递函数为
校正前图像
未校正系统稳定,但响应速度较慢
校正后
校正后系统稳定,性能为
例4-4
未校正时的伯德图为
校正装置的传函为
校正后为
性能满足要求
实验心得:通过本次实验,了解了如何通过PID控制,波特图来判断是否系统处于稳定状态,并如何进行校正使之满足性能上的要求。
(2)积分作用分析,令,,,
绘制系统单位阶跃响应曲线,程如下
随着Kp的增大,系统的在增加,过渡过程时间变大,但响应初期的速度变大;系统的ess随着Kp的增大而减小。
微分作用分析
随着TD的增大,系统的在增大,过渡过程时间变大,响应初期的速度变小
例4-9程序为
其次,绘制根轨迹图,找到临界稳定增益
求取PID的参数kp=0.024,ti=0.98,td=0.25
PID实验报告(实验一)
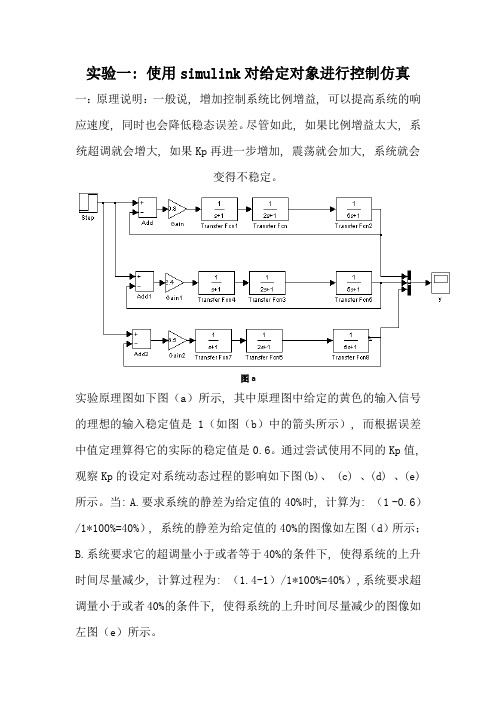
实验一: 使用simulink对给定对象进行控制仿真一:原理说明:一般说, 增加控制系统比例增益, 可以提高系统的响应速度, 同时也会降低稳态误差。
尽管如此, 如果比例增益太大, 系统超调就会增大, 如果Kp再进一步增加, 震荡就会加大, 系统就会变得不稳定。
图a实验原理图如下图(a)所示, 其中原理图中给定的黄色的输入信号的理想的输入稳定值是1(如图(b)中的箭头所示), 而根据误差中值定理算得它的实际的稳定值是0.6。
通过尝试使用不同的Kp值, 观察Kp的设定对系统动态过程的影响如下图(b)、 (c) 、(d) 、(e)所示。
当: A.要求系统的静差为给定值的40%时, 计算为: (1 -0.6)/1*100%=40%), 系统的静差为给定值的40%的图像如左图(d)所示;B.系统要求它的超调量小于或者等于40%的条件下, 使得系统的上升时间尽量减少, 计算过程为: (1.4-1)/1*100%=40%),系统要求超调量小于或者40%的条件下, 使得系统的上升时间尽量减少的图像如左图(e)所示。
一: 当给定KP 分别为 0.8、2.4、3.5 :Kp 的设定对系统动态过程的影响图像如左图(b )所示:1_1: 当调节KP 分别为1.3.5:Kp 的设定对系统动态过程的影响图像如左图(c )所示:1_2: 当调节KP 分别为 1.5.3.5 : 图(b )图(c )系统的静差为给定值40%(注: (1-0.6)/1*100%=40%)的图像如左图(d)所示:图(d)对于单位负反馈, 静差E(S)=R(S)-C(S), 其中输入信号为1(t)根据终值定理可知当KP取1.5时, 系统的静差刚好为给定值的40%。
1_3: 当调节KP分别为7、3.5:➢系统要超调量小于或40%((1.4-1)/1*100%=40%)条件下, 使系统上升时间尽量减少如图(e)所示:➢总结: 联系上图(b)、(c)、(d)、(e)可知, KP由0.8一直增大到7可以看出, 增大比例系数KP可以加快系统的响应, 在有静差的时候有助于减小静差。
数字PID控制器的MATLAB仿真

江苏科技大学电子信息学院实验报告实验名称:数字PID控制器的MATLAB仿真学号:1345733203 姓名:胡文千班级:完成日期:2015年11 月16日一、实验目的(1)掌握用SIMULINK对系统进行仿真的基本方法。
(2)对PID数字控制器进行仿真。
二、实验内容1、基本的PID控制在模拟控制系统中,控制器最常用的控制规律是PID控制。
模拟PID控制系统原理框图如图1-1所示。
比例微分积分被控对象r(t)-y(t)u(t)e(t)++图1-1 模拟PID控制系统原理框图PID控制规律为:⎪⎪⎭⎫⎝⎛++=⎰dt t deTdtt eTt ektuDtIp)()(1)()(或写成传递函数的形式⎪⎪⎭⎫⎝⎛++==sTsTksEsUsGDIp11)()()(仿真1以二阶线性传递函数ss251332+为被控对象,进行模拟PID控制。
输入信号)2.0*2sin()(ttrπ=,仿真时取3,1,60===dipkkk,采用ODE45迭代方法,仿真时间10s。
仿真方法:在Simulink下进行仿真,PID控制由Simulink Extras节点中的PID Controller 提供。
仿真程序:ex1_1.mdl,如图1-2所示。
图1-2 连续系统PID的Simulink仿真程序将该连续系统的模拟PID 控制正弦响应结果截图后至于下面的空白处: 连续系统的模拟PID 控制正弦响应如图1-3所示。
图1-3 连续系统的模拟PID 控制正弦响应2、连续系统的数字PID 控制仿真计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用,需要采用离散化方法。
在计算机PID 控制中,使用的是数字PID 控制器。
按模拟PID 控制算法,以一系列的采样时刻点kT 代表连续时间t ,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID 位置式表达式:∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=kj di p kj DIp Tk e k e k T j e k k e k k e k e T T j e T T k e k k u 0)1()()()())1()(()()()(式中,D p d Ip i T k k T k k ==,,e 为误差信号(即PID 控制器的输入),u 为控制信号(即控制器的输出)。
PID仿真实验

PID仿真实验实验1 闭环控制系统仿真实验——PID 控制算法仿真⼀、实验⽬的1.掌握PID 控制规律及控制器实现。
2.掌握⽤Simulink 建⽴PID 控制器及构建系统模型与仿真⽅法。
⼆、实验设备计算机、MATLAB 软件三、实验原理在模拟控制系统中,控制器中最常⽤的控制规律是PID 控制。
PID 控制器是⼀种线性控制器,它根据给定值与实际输出值构成控制偏差。
PID 控制规律写成传递函数的形式为s K sKiK s T s T K s U s E s G d p d i p ++=++==)11()()()( 式中,P K 为⽐例系数;i K 为积分系数;d K 为微分系数;ip i K K T =为积分时间常数;pdd K K T =为微分时间常数;简单来说,PID 控制各校正环节的作⽤如下:(1)⽐例环节:成⽐例地反映控制系统的偏差信号,偏差⼀旦产⽣,控制器⽴即产⽣控制作⽤,以减少偏差。
(2)积分环节:主要⽤于消除静差,提⾼系统的⽆差度。
积分作⽤的强弱取决于积分时间常数i T ,i T 越⼤,积分作⽤越弱,反之则越强。
(3)微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差信号变得太⼤之前,在系统中引⼊⼀个有效的早期修正信号,从⽽加快系统的动作速度,减少调节时间。
四、实验过程1、在MA TLAB 命令窗⼝中输⼊“simulink ”进⼊仿真界⾯。
2、构建PID 控制器:(1)新建Simulink 模型窗⼝(选择“File/New/Model ”),在Simulink Library Browser 中将需要的模块拖动到新建的窗⼝中,根据PID 控制器的传递函数构建出如下模型:各模块如下:Math Operations 模块库中的Gain 模块,它是增益。
拖到模型窗⼝中后,双击模块,在弹出的对话框中将‘Gain ’分别改为‘Kp ’、‘Ki ’、‘Kd ’,表⽰这三个增益系数。
Continuous 模块库中的Integrator 模块,它是积分模块;Derivative 模块,它是微分模块。
第6章 PID例子

4
•
小明终于喘了一口,但任务的要求突然严了,水位控制的及时性要求大大提高,一旦 水位过高,必须立即将阀门开大,水降到到要求位置,而且不能低太多,反之亦然。 否则不给工钱。小明又为难了!于是他又开动脑筋,终于想到一个办法:通过观察水 面的变化,发现开大阀门后,大约10分钟后水面才开始下降,于是他就不再等到水面 低于要求之后才关阀门,而在第一次发现水面开始下降后就提前关闭阀门,经过一段 时间,小明总结出了一套水面变化速度与提前动作时间之间的一个关系,这个变化速 度与时间的关系就称为“微分时间”——D。
由于前方没有车辆,采用速度控制的方法进行控制, 使自车平稳地达到并保持巡航速度。仿真结果见图所示。
图13 仿真实验一:速度、时间响应曲线
20
自车以 vc 18m / s 速度行驶,突然前方一速度为 v p 20m / s 的车拐入本车道,两车实际距离 d r 25m。
在该种工况下,纵向控制系统检测到同一车道 的前方车辆
5
例1、汽车纵向闭环控制系统
对汽车模型进行了简化,得到了一个近似的线性系统, 其传递函数为 C ( s) 10 G( s) R( s) s 2 1.6s 1
6
⑴闭环控制系统: 速度闭环系统 控制逻辑实现切换 距离闭环系统(小于安全距离) 距离速度闭环系统 ⑵主要针对高速公路的交通环境 高速行驶的车辆速度调节 节气门(油门)控制器 复杂交通环境停-走 节气门(油门)控制器和制动器
汽车安全辅助驾驶系统的PID控制
智能交通运输系统 (Intelligent Transportation Systems,ITS)
利用现代信息技术、传感技术来扩展驾驶人员的感知能力, 将感知技术获取的外界信息(车速,其它障碍物距离等)传递给 驾驶人员,同时在路况与车况的综合信息中识别是否构成安全隐 患,在不安全情况下,自动采取措施控制汽车,使汽车能主动避 开危险,保障汽车安全。 三大安全辅助驾驶系统: 1.车辆避撞报警(Collision Warning,CW)下面的例子 2.具有避撞功能的车辆自适应巡航控制系统 (Adaptive Cruise Control,ACC) 3.交通环境的车辆智能控制系统(ACC+Stop and Go)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K)p ,
T由i 大到小,直
(使3)调稍KT微p:d若提系升统一动点态,特由性小不到好大,,则直加到入动,T态d同满时 意。
工程实际中,以上几步反复操作,直到满意 为止。常见被调量的PID调节器参数选择范围 如下表:
被调量 流量
特点 对象时间常数并有噪声
Kp
T(i m)
(m)
Td
1~2.5
0.1~1
(1)先调 :让系统闭环,使积分和微分不起作 用( ,K p ),观察系统的响应,若反映 快、超调Ti 小 ,静Td 差 0满足要求,则就用纯比例 控制器。
(2)调 T:i 若静差太大,则加入 ,Ti 且同时使 略K p 下降(如降至原来的80%,因加入积分会使
系统稳定性下降,故减小 到满足静差要求。
仿真中对象输出端加幅值为0.01的随机信号.输 入信号为阶跃信号.对象在不完全微分PID和 标 准 PID 作 用 下 的 输 出 响 应 分 别 见 仿 真 程 序 D_partial.m和partialD.mdl
二、微分先行 e80s
仿真举例:设被控对象为 G0 (s) 6s 1
输入信号为带有高频干扰的方波信号:
仿真实例3:设被控对象为G0 (s)
s2
54 18s
1
输入信号是脉宽20s、周期50s的脉冲信号。假
设常规PID控制器为:
D(s) 0.51 1 2s 3.5s
采用微分先行PID控制器,并设其中的r 0.5
系统采用两种控制器的原理图如下:
仿真实例4:设被控对象为
400 G0 (s) s2 50s
(1
z 1)
400 s2 (s 50)
G0 ( z)
(1
z 1 )
Z
8 s 2
0.16 s
0.16 s 50
z
1 z
8Tz ( z 1)2
0.16 z z 1
0.16 z z e 50T
G(z)
z
z
1
(
8Tz z 1)
2
0.16z z 1
0.16z z e50T
设常规PID控制器为:
D(s) 0.51 1 2s 3.5s
采用微分先行PID控制器,并设其中的r 0.5
系统采用两种控制器的原理图如下:
系统采用两种控制器的输出响应波形如下:
四、 试凑法
试凑法试一种凭借经验整定参数的方法, 让系统闭环,改变给定值以给系统施加干扰 信号,一边按 K p Ti 顺序T调d 节,一边观察 过渡过程,直到满意为止。其过程如下:
0.0001968z 1 0.0001936z2 11.9512z 1 0.9512z 2
G(z)
Y (z) U (z)
0.0001968z1 0.0001936z2 11.9512z1 0.9512z2
U (z)(0.0001968z1 0.0001936z2 ) Y (z)(11.9512z1 0.9512z2 )
if u(k)>=110 u(k)=110; end
if u(k)<=-110 u(k)=-110; end
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k); y_3=y_2;y_2=y_1;y_1=yout(k); error_2=error_1; error_1=error(k); end
rin(t) 1.0sign(sin(0.0005t)) 0.05sin(0.03t)
对象在微分先行PID作用和标准PID控制器作用下输 入输出见仿真程序D_advance.m
通过结构图的仿真见advanceD.mal
举例2:设被控对象为
G0 (s)
s2
54 18s
1
输入信号是脉宽20s、周期50s的脉冲信号。假
0.0001968z1U (z) 0.0001936z2U (z) Y (z) 1.9512z1Y (z) 0.9512z2Y (z)
0.0001968u(k 1) 0.0001936u(k 2) y(k) 1.9512 y(k 1) 0.9512 y(k 2)
y(k) 1.9512 y(k 1) 0.9512 y(k 2) 0.0001968u(k 1) 0.0001936u(k 2)
y(k) den(2) y(k 1) den(3) y(k 2) num(2)u(k 1) num(3)u(k 2)
脚本:
clear all; close all;
ts=20; sys=tf([1],[60,1],'inputdelay',80);
dsys=c2d(sys,ts,'zoh'); [num,den]=tfdata(dsys,'v'); u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
温度
多容系统,有较大滞后
1.6~5
3~10 0.5~3
压力
多容系统,滞后不大
1.4~3.5 0.4~3
液位
允许有静差,
1.25~5
对F(s)部分分式展开:F (s)
2s3 9s 1 s3 s2 4s
4
b=[2 0 9 1];
a=[1 1 4 4];
[r,p,k]=residue(b,a)
展开后得:
F (s) 2 2 0.25 j 0.25 j s 1 s 2 j s 2 j
求f(t)=1-e-at的Z变换:
x=sym(‘1-exp(-a*t)');
X=ztrans(x)
求F(z)的反变换:
F(z)
z3
z2 4z2
5z
2
X=sym('z^2/(z^3-4*z^2+5*z-2)'); x=iztrans(X)
对
G0 (s)
1用0 零阶保持器,在采样周
s(s 1)
期Ts=1s下离散化求G(z)
sys=tf(10,[1 1 0]); dsys=c2d(sys,1,‘zoh’) [z,p,k]=tf2zp(num,den)
y_1=0;y_2=0;y_3=0; error_1=0;error_2=0;
ei=0; for k=1:1:200 time(k)=k*ts; yout(k)=-den(2)*y_1+num(2)*u_5;
%I separation
rin(k)=40;
error(k)=rin(k)-yout(k);
利用增量式PID,采用脚本编程实现对上面对象
的控制,并整定PID参数
被控对象为
400 G0 (s) s2 50s
采用零阶保持器离散化,采样时间取0.001s,离 散化得:
G0 (z)
ZOH
400 s2 50s
1 eTs s
400 s2 50s
G0 (z)
(1
z 1)
400 s(s2 50s)
elseif abs(error(k))>=10&abs(error(k))<=20
beta=0.9;
else
beta=1.0;
end
elseif M==2
beta=1.0;
kp=0.80; ki=0.005;
kd=3.0; u(k)=kp*error(k)+kd*(error(k)-
error_1)/ts+beta*ki*ei;
figure(1); plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel('rin,yout');
figure(2); plot(time,u,'r'); xlabel('time(s)');ylabel('u');
2、抗积分饱和法
ei=ei+error(k)*ts;
M=1;
if M==1
%Using integration
separation
if abs(error(k))>=30&abs(error(k))<=40
beta=0.3;
elseif abs(error(k))>=20&abs(error(k))<=30
beta=0.6;
结果如P123:G(z):
仿真实例1:G(s)
s2
10 2s
1
利用simulink中的比例、积分、微分,自 己搭建连续PID控制器,实现对上述对象的 控制,修改PID参数观察其阶跃响应曲线变 化,掌握PID各个部分对系统性能的影响。
仿真实例2:G(s) e80s
60s 1
利用simulink中的PID控制器实现对上述 对象的控制,修改PID参数观察其阶跃响应 曲线变化。
算法:
当u(k) 00H时, 取u(k )=00H
当u(k ) FFH时, 取u(k )=FFH
仿真实例:
G(s)
s3
523500 87.35s2 10470s
二、不完全微分 仿真实验,采用图(b)结构的不完全微分,对象为
G(s)
பைடு நூலகம்
e 80 s 60s+1
Df
(s)
1 180s
1 ,Ts
20ms
背景:PID控制器的输出由于积分作用不断累 加而加大,从而导致执行机构达到极限位置(如 阀门全开),若控制器输出继续增大,阀门开度不 可能再增大,此时就称计算机输出超出了正常 运行范围而进入了饱和区.系统进入饱和后, 饱和越深,退饱和时间越长,系统超调就越大。
措施:对输出进行限幅,同时切除积分作用。
