异方差性习题及答案
异方差练习题参考解答

异方差练习题参考解答练习题1.设消费函数为i i i i u X X Y +++=33221βββ式中,i Y 为消费支出;i X 2为个人可支配收入;i X 3为个人的流动资产;i u 为随机误差项,并且222)(,0)(ii i X u Var u E σ==(其中2σ为常数)。
试回答以下问题: (1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
2.由表中给出消费Y 与收入X 的数据,试根据所给数据资料完成以下问题:(1)估计回归模型u X Y ++=21ββ中的未知参数1β和2β,并写出样本回归模型的书写格式; (2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性; (3)选用合适的方法修正异方差。
Y X Y X Y X 5580 152 220 95 140 65 100 144 210 108 145 70 85 175 245 113 150 80 110 180 260 110 160 79 120 135 190 125 165 84 115 140 205 115 180 98 130 178 265 130 185 95 140 191 270 135 190 90 125 137 230 120 200 75 90 189 250 140 205 74 105 55 80 140 210 110 160 70 85 152 220 113 150 75 90 140 225 125 165 65 100 137 230 108 145 74 105 145 240 115 180 80 110 175 245 140 225 84 115 189 250 120 200 79 120 180 260 145 240 90 125 178 265 130185981301912703.表中的数据是美国1988研究与开发(R &D )支出费用(Y )与不同部门产品销售量(X ).试根据资料建立一个回归模型,运用Glejser 方法和White 方法检验异方差,由此决定异方差的表现形式并选用适当方法加以修正。
应用回归分析,第4章课后习题参考答案

第4章违背基本假设的情况思考与练习参考答案4.1 试举例说明产生异方差的原因。
答:例4.1:截面资料下研究居民家庭的储蓄行为Y i=β0+β1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例4.2:以某一行业的企业为样本建立企业生产函数模型Y i=A iβ1K iβ2L iβ3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
4.2 异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果:1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
异方差性自相关性和多重共线性思考与练习

第二章异方差性、自相关性和多重共线性思考与练习参考答案2.1参考答案答:随机误差项方差随观察单位而变的现象为异方差。
影响:(1)尽管OLS估计仍无偏,但起方差不再有效(即最小方差性不具备),且模型误差项方差估计有偏.(2)t检验、F 检验失效,从而对参数、模型整体的显著性判断不可靠.(3)预测精度低,模型的应用失效.2.2参考答案答:G---Q检验原理:(1)假定随机误差项方差σ2t 与某一解释变量Xti成正(负)相关;(2)对样本观察值按Xi升序排列后去除中间的部分样本值;(3)分别以剩下的两部分样本值为子样,利用OLS法计算各自的方差估计值;(4)以两子样的方差估计值构造F统计量,判断两子样的方差是否差异显著。
若显著,则存在异方差;否则反之。
White检验原理:通过构造辅助回归模型e2t =β+tipiix∑=1β+tjpjitiijxx∑=1,β来判断零假设H0:①E(Ut)=2σ(t=1,2,3……N) ,并且②模型设定Y=XB+U正确若检验显著,则否定零假设,从而认为存在异方差或者模型设定错误;若检验不显著,则接受零假设。
White、Park和Glecses检验均使用辅助回归模型来探测住回归方程系数显著性检验来探测异方差性。
其间区别在于:Park和Glecses检验是通过辅助回归方程系数显著性来探测异方差;而White检验则是通过辅助回归方程整体显著性来检验探测主回归模型是否存在异方差性或者设定误差。
2.3参考答案答:WLS发实质上为模型变换法.考虑回归模型Y t =b 0+b 1x t +U t ,假设其存在异方差性并且Var(U t )=2t σ=K 2其中K 为常数,对远模型使用权数为W t =1/)/(t x t 的WLS 法进行估计时,实质上是对原模型作了变换,变换后的形式为:)(t tx f Y =)(0t x f b +)(1t tx f x b +)(t tx f v经过转换后,模型的异方差性被清除了。
计量经济学课后答案第五章 异方差性汇总

第五章课后答案5.1(1)因为22()i i f X X =,所以取221iiW X =,用2i W 乘给定模型两端,得 312322221i i ii i i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数,即22221()()i i i iu Var Var u X X σ==(2)根据加权最小二乘法,可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=-- ()()()()()()()***2****22232322322*2*2**2223223ˆi i i i i i i i i i i i i i i i i iW y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii ii i i iii i i ii i i i i iW y x W x W y x W x x Wx W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,iii i i i iiiW XW X W Y X X Y WWW ===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y=-=-=- 5.2(1)2222211111 ln()ln()ln(1)1 u ln()1Y X Y X Yu u X X X u ββββββββββ--==+≈=-∴=+[ln()]0()[ln()1][ln()]11E u E E u E u μ=∴=+=+=又(2)[ln()]ln ln 0 1 ()11i i iiP P i i i i P P i i E P E μμμμμμμ===⇒====∑∏∏∑∏∏不能推导出所以E 1μ()=时,不一定有E 0μ(ln )= (3) 对方程进行差分得:1)i i βμμ--i i-12i i-1lnY -lnY =(lnX -X )+(ln ln 则有:1)]0i i μμ--=E[(ln ln5.3(1)该模型样本回归估计式的书写形式为:Y = 11.44213599 + 0.6267829962*X (3.629253) (0.019872)t= 3.152752 31.5409720.944911R =20.943961R = S.E.=9.158900 DW=1.597946 F=994.8326(2)首先,用Goldfeld-Quandt 法进行检验。
异方差练习题参考解答

异方差练习题参考解答练习题1.设消费函数为i i i i u X X Y +++=33221βββ式中,i Y 为消费支出;i X 2为个人可支配收入;i X 3为个人的流动资产;i u 为随机误差项,并且222)(,0)(i i i X u Var u E σ==(其中2σ为常数)。
试回答以下问题:(1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
2.由表中给出消费Y 与收入X 的数据,试根据所给数据资料完成以下问题: (1)估计回归模型u X Y ++=21ββ中的未知参数1β和2β,并写出样本回归模型的书写格式;(2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性; (3)选用合适的方法修正异方差。
Y X Y X Y X 55 80 152 220 95 140 65 100 144 210 108 145 70 85 175 245 113 150 80 110 180 260 110 160 79 120 135 190 125 165 84 115 140 205 115 180 98 130 178 265 130 185 95 140 191 270 135 190 90 125 137 230 120 200 75 90 189 250 140 205 74 105 55 80 140 210 110 160 70 85 152 220 113 150 75 90 140 225 125 165 65 100 137 230 108 145 74 105 145 240 115 180 80 110 175 245 140 225 84 115 189 250 120 200 79 120 180 260 14524090125178265130185981301912703.表中的数据是美国1988研究与开发(R&D)支出费用(Y)与不同部门产品销售量(X)。
异方差性习题及答案

异⽅差性习题及答案异⽅差性⼀、单项选择1.Goldfeld-Quandt ⽅法⽤于检验()A.异⽅差性B.⾃相关性C.随机解释变量D.多重共线性2.在异⽅差性情况下,常⽤的估计⽅法是()A.⼀阶差分法B.⼴义差分法C.⼯具变量法D.加权最⼩⼆乘法3.White 检验⽅法主要⽤于检验()A.异⽅差性B.⾃相关性C.随机解释变量D.多重共线性4.Glejser 检验⽅法主要⽤于检验()A.异⽅差性B.⾃相关性C.随机解释变量D.多重共线性5.下列哪种⽅法不是检验异⽅差的⽅法()A.⼽德菲尔特——匡特检验B.怀特检验C.⼽⾥瑟检验D.⽅差膨胀因⼦检验6.当存在异⽅差现象时,估计模型参数的适当⽅法是()A.加权最⼩⼆乘法B.⼯具变量法C.⼴义差分法D.使⽤⾮样本先验信息7.加权最⼩⼆乘法克服异⽅差的主要原理是通过赋予不同观测点以不同的权数,从⽽提⾼估计精度,即()A.重视⼤误差的作⽤,轻视⼩误差的作⽤B.重视⼩误差的作⽤,轻视⼤误差的作⽤C.重视⼩误差和⼤误差的作⽤D.轻视⼩误差和⼤误差的作⽤8.如果⼽⾥瑟检验表明,普通最⼩⼆乘估计结果的残差i e 与i x 有显著的形式i i i v x e +=28715.0的相关关系(i v满⾜线性模型的全部经典假设),则⽤加权最⼩⼆乘法估计模型参数时,权数应为() A. i x B. 21i x C. i x 1 D. i x 19.如果⼽德菲尔特——匡特检验显著,则认为什么问题是严重的()A.异⽅差问题B.序列相关问题C.多重共线性问题D.设定误差问题10.设回归模型为i i i u bx y +=,其中i i x u Var 2)(σ=,则b 的最有效估计量为() A. ∑∑=2?x xy b B. 2 2)(?∑∑∑∑∑--=x x n y x xy n b C. x y b =? D. ∑=x y n b 1?⼆、多项选择1.下列计量经济分析中那些很可能存在异⽅差问题()A.⽤横截⾯数据建⽴家庭消费⽀出对家庭收⼊⽔平的回归模型B.⽤横截⾯数据建⽴产出对劳动和资本的回归模型C.以凯恩斯的有效需求理论为基础构造宏观计量经济模型D.以国民经济核算帐户为基础构造宏观计量经济模型E.以30年的时序数据建⽴某种商品的市场供需模型2.在异⽅差条件下普通最⼩⼆乘法具有如下性质()A 、线性B 、⽆偏性C 、最⼩⽅差性D 、精确性E 、有效性3.异⽅差性将导致A 、普通最⼩⼆乘法估计量有偏和⾮⼀致B 、普通最⼩⼆乘法估计量⾮有效C 、普通最⼩⼆乘法估计量的⽅差的估计量有偏D 、建⽴在普通最⼩⼆乘法估计基础上的假设检验失效E 、建⽴在普通最⼩⼆乘法估计基础上的预测区间变宽4.下列哪些⽅法可⽤于异⽅差性的检验()A 、DW 检验B 、⽅差膨胀因⼦检验法C 、判定系数增量贡献法D 、样本分段⽐较法E 、残差回归检验法5.当模型存在异⽅差现象进,加权最⼩⼆乘估计量具备()A 、线性B 、⽆偏性C 、有效性D 、⼀致性E 、精确性6.下列说法正确的有()A 、当异⽅差出现时,最⼩⼆乘估计是有偏的和不具有最⼩⽅差特性B 、当异⽅差出现时,常⽤的t 和F 检验失效C 、异⽅差情况下,通常的OLS 估计⼀定⾼估了估计量的标准差D 、如果OLS 回归的残差表现出系统性,则说明数据中不存在异⽅差性E 、如果回归模型中遗漏⼀个重要变量,则OLS 残差必定表现出明显的趋势三、名词解释1.异⽅差性2.格德菲尔特-匡特检验3.怀特检验4.⼽⾥瑟检验和帕克检验四、简答题1.什么是异⽅差性?试举例说明经济现象中的异⽅差性。
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第12章 时间序列回归中的序列相关和异方差性

第12章时间序列回归中的序列相关和异方差性12.1复习笔记一、含序列相关误差时OLS 的性质1.无偏性和一致性在时间序列回归的前3个高斯—马尔可夫假定(TS.1~TS.3)之下,OLS 估计量是无偏的。
特别地,只要解释变量是严格外生的,无论误差中的序列相关程度如何,ˆjβ都是无偏的。
这类似于误差中的异方差不会造成ˆjβ产生偏误。
把严格外生性假定放松到()|0t t E u X =,并证明了当数据是弱相关的时候,ˆj β仍然是一致的(但不一定无偏)。
这一结论不以对误差中序列相关的假定为转移。
2.效率和推断高斯—马尔可夫定理要求误差的同方差性和序列无关性,所以,在出现序列相关时,OLS 便不再是BLUE 的了。
通常的OLS 标准误和检验统计量也不再确当,而且连渐近确当都谈不上。
假定误差存在序列相关,1,1,2,...,ρ-=+=tt t u u e t n ,1ρ<。
其中e t 是均值为0方差为2e σ满足经典假定的误差,对于简单回归模型:01ββ=++t t ty x u 假定x t 的样本均值为零,于是1111ˆn x t t i SST x u ββ-==+∑其中21n x t i SST x ==∑,计算1ˆβ的方差,()()22221111ˆ/2/n n n t j x t t x x t t j i i j Var SST Var x u SST SST x x βσσρ--+===⎛⎫==+ ⎪⎝⎭∑∑∑其中()2σ=t Var u 由1ˆβ的方差表达形式可知,第一项为2/xSST σ,为经典假定条件下的简单回归模型中参数的方差,所以当模型中的误差项存在序列相关时,按照OLS 估计的方差是有偏的。
在出现序列相关的时候,使用通常的OLS 标准误就不再准确。
因此,检验单个假设的t 统计量也不再正确。
因为较小的标准误意味着较大的t 统计量,所以当ρ﹥0时,通常的t 统计量常常过大。
用于检验多重假设的通常的F 统计量和LM 统计量也不再可靠。
计量经济学 第五章习题答案
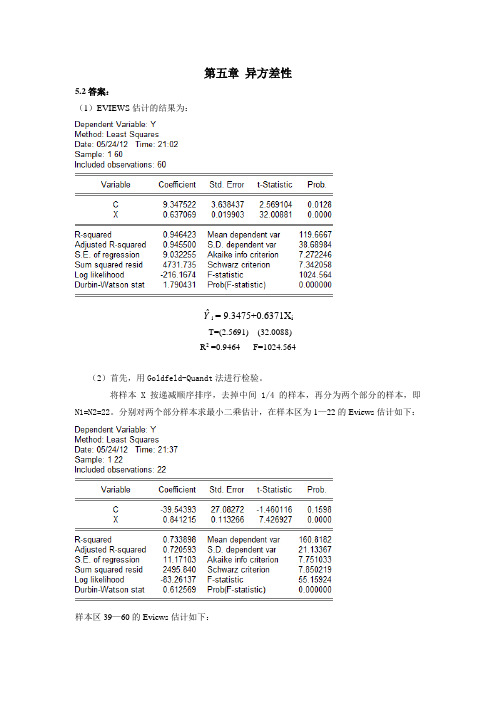
第五章异方差性5.2答案:(1)EVIEWS估计的结果为:Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564(2)首先,用Goldfeld-Quandt法进行检验。
将样本X按递减顺序排序,去掉中间1/4的样本,再分为两个部分的样本,即N1=N2=22。
分别对两个部分样本求最小二乘估计,在样本区为1—22的Eviews估计如下:样本区39—60的Eviews估计如下:得到两个部分各自的残差平方和,即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为: F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05,查F 分布表,得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值,有F =4.1390>F 0.05=(20,20)=2.12,说明该模型的随机误差项存在异方差。
其次,用White 法进行检验结果如下:给定α=0.05,在自由度为2下查卡方分布表,得χ2=5.9915。
比较临界值与卡方统计量值,即nR2=10.8640>χ2=5.9915,同样说明模型中的随机误差项存在异方差。
(2)用权数W1=1/X,作加权最小二乘估计,得如下结果用White法进行检验得如下结果:F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。
比较临界值与卡方统计量值,即nR2=5.9519<χ2=5.9915,说明加权后的模型中的随机误差项不存在异方差。
其估计的结果为:Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案:(1)EVIEWS估计结果:Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 (2)利用White方法检验异方差,则White检验结果见下表:由上述结果可知,该模型存在异方差。
异方差性

例5-1 -我国制造业利润函数模型表5-1列出了1998年我国主要制造工业销售收入Y与销售利润X的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
表5-1 我国制造工业1998年销售利润与销售收入情况(1) 参数估计进入EViews软件包,确定时间范围;编辑输入数据;选择估计方程菜单,估计样本回归函数如下估计结果为9322.1528547.0)367.12()6165.0(1044.00335.12ˆ2==+=F R X yi i括号内为t 统计量值。
(2) 检验异方差性①图形分析检验A. 观察销售利润(Y )与销售收入(X )的相关图(图5-1):SCAT XY图5-3 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
B. 残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids 按钮就可以得到模型的残差分布图(或建立方程后在Eviews 工作文件窗口中点击resid 对象来观察)。
图5-4 我国制造业销售利润回归模型残差分布图5-4显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
②Goldfeld-Quant 检验A. 将样本按解释变量排序(SORT X )并分成两部分(分别有1到10共10个样本合19到28共10个样本)B. 利用样本1建立回归模型1,其残差平方和为1RSS =2579.587。
C. 利用样本2建立回归模型2,其残差平方和为2RSS =63769.67。
D. 计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72。
取05.0=α时,查F 分布表得44.3)210,210(05.0=--F ,44.372.2405.0=>=F F ,所以存在异方差性③White 检验A. 建立回归模型:LS Y C X ,回归结果如图5-5。
计量经济学第四章习题

地区 农业总产 农作物种植
值
面积
湖北 921.6 省
7155.9
湖南 874.0 省
7886.2ຫໍສະໝຸດ 广东 960.0 省4808.0
广 西 623.1
6368.2
海南 省
重庆 市
四川 省
贵州 省
云南 省
西藏
170.9 333.0 987.7 317.7 516.9 26.6
826.9 3435.3 9387.5 4695.0 5890.0 231.2
试问:
(1) 当设定模型为 相关?
时,是否存在序列
(2) 若按一阶自相关假设,试用杜宾两步法与广义最小 二乘法估计原模型。
(3) 采用差分形式与作为新数据,估计模型,该模型是 否存在序列相关?
15. 对于线性回归模型:,已知为一阶自回归形式:,要 求:证明的估计值为:
16. 某上市公司的子公司的年销售额与其总公司年销售额的 观测数据如下:
1550
2400
24350
10
1500
2600
26860
11. 2004年全国31个省市自治区农业总产值(亿元)和农作物 播种面积(万亩)数据(数据来源:《中国统计年鉴 2005》)如下表所示:
地区
北京 市
天津 市
河北 省
山西 省
内蒙 古
辽宁 省
吉林 省
黑龙 江
上海 市
江苏 省
浙江 省
安徽 省
农业总产 值
(1) (2)
(3)
19. 为研究劳动力在制造业中所占比率的变动趋势,根据美 国1949~1964年的年度数据,得以下两种回归模型结 果:
模型A: 模型B: 其中:Y为劳动力比率,t为时间。括号中的数字是t检验 值。要求:
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第8章 异方差性【圣才出品】

第8章异方差性8.1复习笔记一、异方差性对OLS 所造成的影响1.异方差性对无偏性的影响多元线性回归模型表达式为:01122k k y x x x uββββ=+++⋅⋅⋅+异方差性并不会导致j β的OLS 估计量出现偏误或产生不一致性,但诸如省略一个重要变量之类的情况出现则具有这种影响。
2.异方差性对拟合优度的影响对拟合优度指标R 2和2R 的解释不受异方差性的影响。
通常的R 2和调整2R 都是估计总体R 2的不同方法,而总体R 2无非就是221/u y σσ-(因为2/11/SSR SSR n R SST SST n=-=-),其中2u σ是总体误差方差,2y σ是y 的总体方差。
关键是,由于总体R 2中这两个方差都是无条件方差,所以总体R 2不受()1Var | k u x x ⋅⋅⋅,,中出现异方差性的影响。
无论()1Var | k u x x ⋅⋅⋅,,是否为常数,SSR/n 都一致地估计了2u σ,SSR/n 也一致地估计了2y σ。
当使用自由度调整时,依然如此。
因此,无论同方差假定是否成立,R 2和2R 都一致地估计了总体R 2。
3.估计量的方差()ˆVar jβ在没有同方差假定的情况下,估计量的方差ˆ()jVar β是有偏的。
由于OLS 标准误直接以这些方差为基础,所以它们都不能用来构造置信区间和t 统计量。
4.对统计检验的影响在出现异方差性的情况下,在高斯-马尔可夫假定下用来检验假设的统计量都不再成立。
(1)在出现异方差性时,通常普通最小二乘法的t 统计量就不具有t 分布,使用大样本容量也不能解决这个问题。
(2)F 统计量也不再是F 分布。
(3)LM 统计量也不服从渐近2χ分布。
二、OLS 估计后的异方差—稳健推断1.单个自变量模型01i i iy x u ββ=++假定前4个高斯-马尔可夫假定成立。
如果误差包含异方差性,那么()2Var |i i iu x σ=其中,给2σ加上下标i,表示误差方差2i σ不再是固定的值,而是随着x i 的不同而不同。
异方差性习题与答案(精品).doc

第五章异方差性习题与答案1、产生异方差的后果是什么?2、下列哪种情况是异方差性造成的结果?(1)OLS估计量是有偏的(2)通常的t检验不再服从t分布。
(3)OLS估计量不再具有最佳线性无偏性。
3、已知模型:乙=0o+0]X”+02X2i+"i式中,乙为某公司在第i个地区的销售额;X“为该地区的总收入;X2,为该公司在该地区投入的广告费用(£=0,1,2……,50)。
(1)由于不同地区人口规模乙可能影响着该公司在该地区的销售,因此有理由怀疑随机误差项g是异方差的。
假设b,依赖于总体£•的容量,逐步描述你如何对此进行检验。
需说明:A、零假设和备择假设;B、要进行的回归;C、要计算的检验统计值及它的分布(包括自由度);D、接受或拒绝零假设的标准。
(2)假设q =陋-逐步描述如何求得BLUE并给出理论依据。
4、下表数据给出按学位和年龄划分的经济学家的中位数工薪:表1经济学家的工资表中位数工薪(以千美元计算)年龄硕士博士25-29&08.830-349.29.635-3911.011.040-4412.812.545-4914.213.650-5414.714.355-5914.515.060—6413.515.065-6912.015.0(1)有硕士学位和有博士学位经济学家的中位数工薪的方差相等么?(2)如果相等,你会怎样检验两组平均中位数工薪相等的假设?(3)在年龄35至5岁之间的经济学家,有硕士学位的比有博士学位的赚更多的钱,那么你会怎样解释这一发现?5、为了解美国工作妇女是否受到歧视,可以用美国统计局的“当前人口调查” 中的截面数据,研究男女工资有没有差别。
这项多元回归分析研究所用到的变量有:W—雇员的工资率(美元/小时)1表示雇员为女性,0表示女性意外的雇员。
ED:受教育的年数。
AGE:年龄对124名雇员的样本进行的研究得到回归结果为:(括号内为估计的t值)W = -6.41 -2.76sex + 0.99ED + 0.12AGE R2 -0.867 E = 23.2求:(1)该模型调整后的决定系数艮2 (2)各估计值的标准差为多少?(3)检验美国工作妇女是否受到歧视,为什么?(4)按此模型预测一个30岁受教育16年的美国男性的平均每小时的工作收入为多少美元?6、下表给出了2000年中国部分省市城镇居民每个家庭平均全年可支配收入X 与消费支出Y的统计数据。
应用回归分析,第4章课后习题参考答案

第4章违背基本假设的情况思考与练习参考答案试举例说明产生异方差的原因。
答:例:截面资料下研究居民家庭的储蓄行为Y i=?0+?1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例:以某一行业的企业为样本建立企业生产函数模型Y i=A i?1K i?2L i?3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果:1、参数估计量非有效2、变量的显着性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
这样对残差所提供信息的重要程度作一番校正,以提高参数估计的精度。
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
计量经济学课后习题答案汇总

计量经济学练习题第一章导论一、单项选择题⒈计量经济研究中常用的数据主要有两类:一类是时间序列数据,另一类是【 B 】A 总量数据B 横截面数据C平均数据 D 相对数据⒉横截面数据是指【A 】A 同一时点上不同统计单位相同统计指标组成的数据B 同一时点上相同统计单位相同统计指标组成的数据C 同一时点上相同统计单位不同统计指标组成的数据D 同一时点上不同统计单位不同统计指标组成的数据⒊下面属于截面数据的是【D 】A 1991-2003年各年某地区20个乡镇的平均工业产值B 1991-2003年各年某地区20个乡镇的各镇工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇工业产值⒋同一统计指标按时间顺序记录的数据列称为【B 】A 横截面数据B 时间序列数据C 修匀数据D原始数据⒌回归分析中定义【 B 】A 解释变量和被解释变量都是随机变量B 解释变量为非随机变量,被解释变量为随机变量C 解释变量和被解释变量都是非随机变量D 解释变量为随机变量,被解释变量为非随机变量二、填空题⒈计量经济学是经济学的一个分支学科,是对经济问题进行定量实证研究的技术、方法和相关理论,可以理解为数学、统计学和_经济学_三者的结合。
⒉⒊现代计量经济学已经形成了包括单方程回归分析,联立方程组模型,时间序列分析三大支柱。
⒋⒌经典计量经济学的最基本方法是回归分析。
计量经济分析的基本步骤是:理论(或假说)陈述、建立计量经济模型、收集数据、计量经济模型参数的估计、检验和模型修正、预测和政策分析。
⒍⒎常用的三类样本数据是截面数据、时间序列数据和面板数据。
⒏⒐经济变量间的关系有不相关关系、相关关系、因果关系、相互影响关系和恒等关系。
三、简答题⒈什么是计量经济学?它与统计学的关系是怎样的?计量经济学就是对经济规律进行数量实证研究,包括预测、检验等多方面的工作。
计量经济学是一种定量分析,是以解释经济活动中客观存在的数量关系为内容的一门经济学学科。
计量经济学第二版孙敬水主编习题答案

计量经济学第二版孙敬水主编习题答案1《计量经济学》思考与练习参考答案第1章引论一、单项选择题1.B2.C3.C4.B5.B6.A7.D8.B9.A 10.A 11.B 12.A 13.B 二、多项选择题1.ABCDE2.CD3.ABCD4.ACD5.ABCD6.ABCD7.BDE8.BCE9.ABC 10.ABCDE 11.ABC第2章一元线性回归模型一、单项选择题1.A2.D3.A4.B5.D6.C7.D8.D9.B 10.C 11.B 12.D 13.B 14.D15.D 16.A 17.B 18.C 19.D 20.D 21.A 22.C 23.B 24.B 25.B 26.C 27.A 28.B 29.C 30.D 31.D 二、多项选择题1.ACD2.ABCDE3.ABC4.BE5.AC6.CDE7.ABCDE8.BCDE9.ABCDE 10.ABDE 11.CDE 12.ABCDE 13.ABCDE 14.ABCDE 第3章多元线性回归模型一、单项选择题1.C2.D3.D4.C5.B6.B7.A8.B9.C 10.A 11.A 12.A 13.D 14.B 15.C 16.C 17.B 18.D 19.A 20.C 21.A 22.C 23.B 24.C 25.D 二、多项选择题1.BCD2.ACDE3.BCD4.AD5.BC6.ACDE7.ABC8.ABCD9.ABC 10.ABCDE 三、简答题、分析与计算题3.决定系数2R与总体线性关系显著性F检验之间的关系;在多元线性回归分析中,F检验与t检验有何不同?在一元线性回归分析中二者是否有等价的作用? 2参考答案:(1)在多元线性回归分析中,可决系数2R是指解释变差占总变差的比重,用来表述解释变量对被解释变量的解释程度,它与总体线性关系显著性检验统计量F关系如下: F=2211RRkkn. . .. 或FkknFkR.+.. . = )1( 2可决系数是用于检验回归方程的拟和优度的,F检验是用于检验回归方程总体显著性的。
应用回归分析,第4章课后习题参考答案

第4章违背基本假设的情况思考与练习参考答案试举例说明产生异方差的原因。
答:例:截面资料下研究居民家庭的储蓄行为Y i=0+1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例:以某一行业的企业为样本建立企业生产函数模型Y i=A i1K i2L i3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果:1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
这样对残差所提供信息的重要程度作一番校正,以提高参数估计的精度。
伍德里奇《计量经济学导论》(第6版)复习笔记和课后习题详解-时间序列回归中的序列相关和异方差性

第12章时间序列回归中的序列相关和异方差性12.1复习笔记考点一:含序列相关误差时OLS 的性质★★★1.无偏性和一致性当时间序列回归的前3个高斯-马尔可夫假定成立时,OLS 的估计值是无偏的。
把严格外生性假定放松到E(u t |X t )=0,可以证明当数据是弱相关时,∧βj 仍然是一致的,但不一定是无偏的。
2.有效性和推断假定误差存在序列相关,即满足u t =ρu t-1+e t ,t=1,2,…,n,|ρ|<1。
其中,e t 是均值为0方差为σe 2满足经典假定的误差。
对于简单回归模型:y t =β0+β1x t +u t 。
假定x t 的样本均值为零,因此有:1111ˆn x t tt SST x u -==+∑ββ其中:21nx t t SST x ==∑∧β1的方差为:()()122221111ˆ/2/n n n t j xt t x x t t j t t j Var SST Var x u SST SST x x ---+===⎛⎫==+ ⎪⎝⎭∑∑∑βσσρ其中:σ2=Var(u t )。
根据∧β1的方差表达式可知,第一项为经典假定条件下的简单回归模型中参数的方差。
因此,当模型中的误差项存在序列相关时,OLS 估计的方差是有偏的,假设检验的统计量也会出现偏差。
3.拟合优度当时间序列回归模型中的误差存在序列相关时,通常的拟合优度指标R 2和调整R 2便会失效;但只要数据是平稳和弱相关的,拟合优度指标就仍然有效。
4.出现滞后因变量时的序列相关(1)在出现滞后因变量和序列相关的误差时,OLS 不一定是不一致的假设E(y t |y t-1)=β0+β1y t-1。
其中,|β1|<1。
加上误差项把上式写为:y t =β0+β1y t-1+u t ,E(u t |y t-1)=0。
模型满足零条件均值假定,因此OLS 估计量∧β0和∧β1是一致的。
误差{u t }可能序列相关。
虽然E(u t |y t-1)=0保证了u t 与y t-1不相关,但u t-1=y t -1-β0-β1y t-2,u t 和y t-2却可能相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
异方差性一、单项选择1.Goldfeld-Quandt 方法用于检验( )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.Glejser 检验方法主要用于检验( )A.异方差性B.自相关性C.随机解释变量D.多重共线性 5.下列哪种方法不是检验异方差的方法 ( )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 6.当存在异方差现象时,估计模型参数的适当方法是 ( ) A.加权最小二乘法 B.工具变量法C.广义差分法D.使用非样本先验信息7.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即 ( )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用8.如果戈里瑟检验表明,普通最小二乘估计结果的残差i e 与i x 有显著的形式ii i v x e +=28715.0的相关关系(i v满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为 ( )A. i xB. 21i x C. i x 1D. i x 19.如果戈德菲尔特——匡特检验显著,则认为什么问题是严重的 ( ) A.异方差问题 B.序列相关问题 C.多重共线性问题 D.设定误差问题 10.设回归模型为ii i u bx y +=,其中ii x u Var 2)(σ=,则b 的最有效估计量为( )A.∑∑=2ˆx xy bB. 22)(ˆ∑∑∑∑∑--=x x n y x xy n bC.x y b=ˆ D. ∑=xy n b 1ˆ二、多项选择1.下列计量经济分析中那些很可能存在异方差问题( ) A.用横截面数据建立家庭消费支出对家庭收入水平的回归模型 B.用横截面数据建立产出对劳动和资本的回归模型C.以凯恩斯的有效需求理论为基础构造宏观计量经济模型D.以国民经济核算帐户为基础构造宏观计量经济模型E.以30年的时序数据建立某种商品的市场供需模型 2.在异方差条件下普通最小二乘法具有如下性质()A 、线性B 、无偏性C 、最小方差性D 、精确性E 、有效性 3.异方差性将导致A 、普通最小二乘法估计量有偏和非一致B 、普通最小二乘法估计量非有效C 、普通最小二乘法估计量的方差的估计量有偏D 、建立在普通最小二乘法估计基础上的假设检验失效E 、建立在普通最小二乘法估计基础上的预测区间变宽 4.下列哪些方法可用于异方差性的检验()A 、DW 检验B 、方差膨胀因子检验法C 、判定系数增量贡献法D 、样本分段比较法E 、残差回归检验法5.当模型存在异方差现象进,加权最小二乘估计量具备( )A 、线性B 、无偏性C 、有效性D 、一致性E 、精确性 6.下列说法正确的有()A 、当异方差出现时,最小二乘估计是有偏的和不具有最小方差特性B 、当异方差出现时,常用的t 和F 检验失效C 、异方差情况下,通常的OLS 估计一定高估了估计量的标准差D 、如果OLS 回归的残差表现出系统性,则说明数据中不存在异方差性E 、如果回归模型中遗漏一个重要变量,则OLS 残差必定表现出明显的趋势 三、名词解释1.异方差性2.格德菲尔特-匡特检验3.怀特检验4.戈里瑟检验和帕克检验 四、简答题1.什么是异方差性?试举例说明经济现象中的异方差性。
2.产生异方差性的原因及异方差性对模型的OLS 估计有何影响。
3.检验异方差性的方法有哪些?4.异方差性的解决方法有哪些?5.什么是加权最小二乘法?它的基本思想是什么?6.样本分段法(即戈德菲尔特——匡特检验)检验异方差性的基本原理及其使用条件。
五、计算题 1.设消费函数为01i i i y b b x u =++,其中i y 为消费支出,i x 为个人可支配收入, i u 为随机误差项,并且22()0,()i i i E u Var u x σ==(其中2σ为常数)。
试回答以下问题:(1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
2.检验下列模型是否存在异方差性,列出检验步骤,给出结论。
0112233t t t t t y b b x b x b x u =++++样本共40个,本题假设去掉c=12个样本,假设异方差由1i x 引起,数值小的一组残差平方和为10.46617RSS E =-,数值大的一组平方和为20.3617RSS E =-。
0.05(10,10) 2.98F =3.假设回归模型为:ii y a u =+,其中:2(0,);()0,i i i j u N x E u u i j σ=≠:;并且ix 是非随机变量,求模型参数b 的最佳线性无偏估计量及其方差。
4.现有x 和Y 的样本观测值如下表:假设y对x 的回归模型为01i i i ,且()i i Var u x σ=,试用适当的方法估计此回归模型。
5.某人根据某区的有关资料作如下的回归模型,结果为:i i 2ˆlnY =10.0930.239X t = (54.7) (12.28) R =0.803ˆ t = (47.87) (15.10)----其中,Y 表示人口密度,X 表示离中心商业区的距离(英里)(1)如果存在异方差,异方差的结构是什么?(2)从变换后的(WLS )回归函数中,你如何知道异方差已被消除或减弱了?(3)你如何解释回归结果?它是否有经济意义?答案一、单选A D A A D ABC A C 二、多选1.ABCDE2.AB3.BCDE4.DE5.ABCDE6.BE 三、名词解释1.异方差性:在线性回归模型中,如果随机误差项的方差不是常数,即对不同的解释变量观测值彼此不同,则称随机项i u具有异方差性。
2.戈德菲尔特-匡特检验:该方法由S.M.Goldfeld 和R.E.Quandt 于1965年提出,用对样本进行分段比较的方法来判断异方差性。
3.怀特检验:该检验由White 在1980年提出,通过建立辅助回归模型的方式来判断异方差性。
4.戈里瑟检验和帕克检验:该检验法由戈里瑟和帕克于1969年提出,其基本原理都是通过建立残差序列对解释变量的(辅助)回归模型,判断随机误差项的方差与解释变量之间是否存在着较强的相关关系,进而判断是否存在异方差性。
四、简答题1. 异方差性是指模型违反了古典假定中的同方差假定,它是计量经济分析中的一个专门问题。
在线性回归模型中,如果随机误差项的方差不是常数,即对不同的解释变量观测值彼此不同,则称随机项i u 具有异方差性,即常数≠=2)var(t i u σ (t=1,2,……,n )。
例如,利用横截面数据研究消费和收入之间的关系时,对收入较少的家庭在满足基本消费支出之后的剩余收入已经不多,用在购买生活必需品上的比例较大,消费的分散幅度不大。
收入较多的家庭有更多可自由支配的收入,使得这些家庭的消费有更大的选择范围。
由于个性、爱好、储蓄心理、消费习惯和家庭成员构成等那个的差异,使消费的分散幅度增大,或者说低收入家庭消费的分散度和高收入家庭消费得分散度相比较,可以认为牵着小于后者。
这种被解释变量的分散幅度的变化,反映到模型中,可以理解为误差项方差的变化。
2.产生原因:(1)模型中遗漏了某些解释变量;(2)模型函数形式的设定误差;(3)样本数据的测量误差;(4)随机因素的影响。
产生的影响:如果线性回归模型的随机误差项存在异方差性,会对模型参数估计、模型检验及模型应用带来重大影响,主要有:(1)不影响模型参数最小二乘估计值的无偏性;(2)参数的最小二乘估计量不是一个有效的估计量;(3)对模型参数估计值的显著性检验失效;(4)模型估计式的代表性降低,预测精度精度降低。
3.检验方法:(1)图示检验法;(2)戈德菲尔德—匡特检验;(3)怀特检验;(4)戈里瑟检验和帕克检验(残差回归检验法);(5)ARCH 检验(自回归条件异方差检验) 4.解决方法:(1)模型变换法;(2)加权最小二乘法;(3)模型的对数变换等 5.加权最小二乘法的基本原理:最小二乘法的基本原理是使残差平方和∑2t e 为最小,在异方差情况下,总体回归直线对于不同的t t e x ,的波动幅度相差很大。
随机误差项方差2t σ越小,样本点t y 对总体回归直线的偏离程度越低,残差t e 的可信度越高(或者说样本点的代表性越强);而2t σ较大的样本点可能会偏离总体回归直线很远,t e 的可信度较低(或者说样本点的代表性较弱)。
因此,在考虑异方差模型的拟合总误差时,对于不同的2t e 应该区别对待。
具体做法:对较小的2t e 给于充分的重视,即给于较大的权数;对较大的2t e 给于充分的重视,即给于较小的权数。
更好的使∑2t e 反映)var(i u 对残差平方和的影响程度,从而改善参数估计的统计性质。
6. 样本分段法(即戈德菲尔特—匡特检验)的基本原理:将样本分为容量相等的两部分,然后分别对样本1和样本2进行回归,并计算两个子样本的残差平方和,如果随机误差项是同方差的,则这两个子样本的残差平方和应该大致相等;如果是异方差的,则两者差别较大,以此来判断是否存在异方差。
使用条件:(1)样本容量要尽可能大,一般而言应该在参数个数两倍以上;(2)t u 服从正态分布,且除了异方差条件外,其它假定均满足。
六、计算题1. 解:(一)原模型:01i i i y b b x u =++ (1)等号两边同除以i x ,新模型:011i i i i i y u b b x x x =++(2) 令**1,,i i i i i i i iy u y x v x x x === 则:(2)变为**10i i i y b b x v =++此时22221()()()i i i i iu Var v Var x x x σσ===新模型不存在异方差性。
(二)对**10i i i y b b x v =++进行普通最小二乘估计****0*2*2**10()()i i i i i i i i n x y x y b n x x b y b x ⎧-=⎪-⎨⎪=-⎩∑∑∑∑∑ 其中**1,i ii i iy y x x x ==(进一步带入计算也可)2.解:(1)01:; :;t t H u H u 为同方差性为异方差性(2)120.466171.290.3617RSS E F RSS E -===- (3)0.05(10,10) 2.98F =(4)0.05(10,10)F F ≤,接受原假设,认为随机误差项为同方差性。
