comsol内置函数
comsol算符大全

circint(r,expr),
circavg(r,expr),
diskint(r,expr),
diskavg(r,expr),
sphint(r,expr),
sphavg(r,expr),
test(expr)
试函数
用于方程弱形式的算符,test(F(u,∇u))等价于:
var(expr,fieldname1,
fieldname2, ...)
变异算子
用于弱形式,它和test算符功能相同,但是仅用于某些特定的场中;
如var(F(u,∇u, v,∇v),a),变量u是a场的变量,而v不是。
linsol
调用标准解,如linpoint或lintotal
linzero
计算表达式的根
linper
标记一个荷载项用于线性扰动求解器
ppr
精确的派生修复
用polynomial-preserving recovery计算表达式中所有用lagrange形函数差分的变量,如e=ux+vy
ppr(e^2)=(ppr(ux)+ppr(vy))^2
pd和d的区别:
d(u+x,x)=ux+1,d(u,t)=ut,u和x,t等有关
pd(u+x,x)=1,pd(u,t)=0,u是独立的和x,t无关
dtang(f,x)
边界上f对x的切向微分
在边界上d(u,x)不能定义,但是可以使用dtang(u,x),dtang付出基本的微分法则,如乘积法则和链式法则,但是需要指出的是,dtang(x,x)不一定等于1。
如果解没有线性化点,那么会报错;
comsol内置参数变量函数
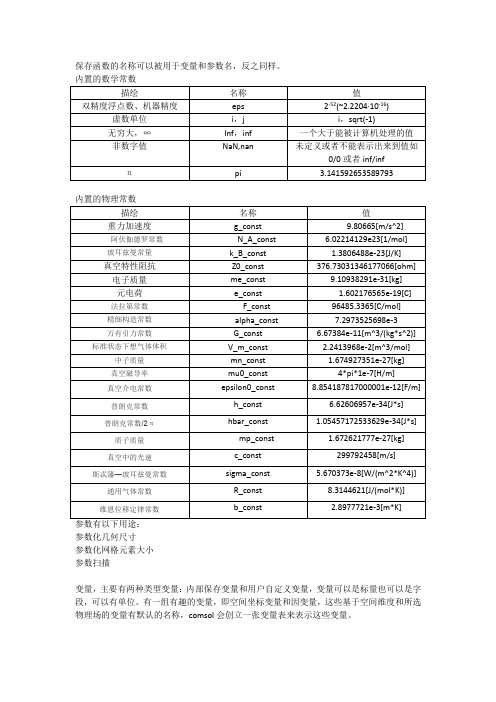
保存函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数参数有以下用途:参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保存变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创立一张变量表来表示这些变量。
内置变量用户定义和自动消费的变量T表示在2D空间维度时的温度,按时间传热的模型。
x、y是空间坐标的名称。
所以可以消费以下变量:Tx,Ty,Txx,Txy,Tyx,Tyy,Tt,Txt,Tyt,Txxt,Txyt,Tyxt,Tyyt,Ttt,Txtt,Tytt,Txxtt,Txytt,Tyxtt,Tyytt。
其中Tx是T对x的导数,Ttt是T对t的二阶导数。
假设空间坐标有其他的名字,同理置换相应变量。
内置数学函数下面的函数不能用于表达式定义参数:acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli, besselk,erf,gamma,和psi。
内置操作函数:这些内置的函数不同于内置的数学函数,详细见用户指南。
用户定义消费的函数:表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
Comsol内置参数变量函数

C o m s o l内置参数变量
函数
Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
Comsol 内置表达式:参数、变量、函数
表达式:?
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
?
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
?
函数?
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数
变量:主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创建一张变量表来表示这些变量。
称。
所以可以生产下列变量:Tx、Ty、Txx、Txy
Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T 对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli,bes selk,
erf,gamma,和psi。
内置操作函数:。
COMSOL_Multiphysics中各常用内置参量

Summary of Built-In Variables With Reserved NamesThis section is an overview of the built-in elements of the following categories as defined by the underlying COMSOL language:•C onstants•V ariables•F unctionsThese language elements are built-in or user-defined. In addition there are operators that cannot be user-defined, and expressions, which are always user-defined.具有保留名称的内置变量摘要本节概述了由基础COMSOL语言定义的以下类别的内置元素:•常量•变量•功能这些语言元素是内置的或用户定义的。
此外,还有不能由用户定义的运算符,以及始终由用户定义的表达式。
ABOUT RESERVED NAMES关于预留名称Built-in variables have reserved names, names that cannot be redefined by the user. It is not recommended to use a reserved variable name for a user-defined variable, parameter, or function. For some of the most common reserved variable names, such as pi, i, and j, the text where you enter the name turns orange and you get a tooltip message if you select the text string. Reserved function names are reserved only for function names, which means that such names can be used for variable and parameter names, and vice versa. The following tables list most built-in elements and hence those reserved names.内置变量具有保留名称,用户无法重新定义。
Comsol内置参数变量函数

Comsol 内置表达式:参数、变量、函数
表达式:?
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
?
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
?
函数?
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的数学常数
内置的物理常数
变量:主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol 会创建一张变量表来表示这些变量。
内置变量
称。
所以可以生产下列变量:Tx、Ty、Txx、Txy
Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
内置数字函数
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli,bes selk,
erf,gamma,和psi。
内置操作函数:
这些内置的函数不同于内置的数学函数,详细见用户指南。
comsol内置参数变量函数

保存函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数参数有以下用途:参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保存变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创立一张变量表来表示这些变量。
内置变量用户定义和自动消费的变量T表示在2D空间维度时的温度,按时间传热的模型。
x、y是空间坐标的名称。
所以可以消费以下变量:Tx,Ty,Txx,Txy,Tyx,Tyy,Tt,Txt,Tyt,Txxt,Txyt,Tyxt,Tyyt,Ttt,Txtt,Tytt,Txxtt,Txytt,Tyxtt,Tyytt。
其中Tx是T对x的导数,Ttt是T对t的二阶导数。
假设空间坐标有其他的名字,同理置换相应变量。
内置数学函数下面的函数不能用于表达式定义参数:acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli, besselk,erf,gamma,和psi。
内置操作函数:这些内置的函数不同于内置的数学函数,详细见用户指南。
用户定义消费的函数:表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
comsol内置参数变量函数

保存函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数参数有以下用途:参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保存变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创立一张变量表来表示这些变量。
内置变量用户定义和自动消费的变量T表示在2D空间维度时的温度,按时间传热的模型。
x、y是空间坐标的名称。
所以可以消费以下变量:Tx,Ty,Txx,Txy,Tyx,Tyy,Tt,Txt,Tyt,Txxt,Txyt,Tyxt,Tyyt,Ttt,Txtt,Tytt,Txxtt,Txytt,Tyxtt,Tyytt。
其中Tx是T对x的导数,Ttt是T对t的二阶导数。
假设空间坐标有其他的名字,同理置换相应变量。
内置数学函数下面的函数不能用于表达式定义参数:acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli, besselk,erf,gamma,和psi。
内置操作函数:这些内置的函数不同于内置的数学函数,详细见用户指南。
用户定义消费的函数:表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
COMSOL_Multiphysics中各常用内置参量

COMSOL_Multiphysics中各常⽤内置参量Summary of Built-In Variables With Reserved NamesThis section is an overview of the built-in elements of the following categories as defined by the underlying COMSOL language:C onstantsV ariablesF unctionsThese language elements are built-in or user-defined. In addition there are operators that cannot be user-defined, and expressions, which are always user-defined.具有保留名称的内置变量摘要本节概述了由基础COMSOL语⾔定义的以下类别的内置元素:常量?变量?功能这些语⾔元素是内置的或⽤户定义的。
此外,还有不能由⽤户定义的运算符,以及始终由⽤户定义的表达式。
ABOUT RESERVED NAMES关于预留名称Built-in variables have reserved names, names that cannot be redefined by the user. It is not recommended to use a reserved variable name for a user-defined variable, parameter, or function. For some of the most common reserved variable names, such as pi, i, and j, the text where you enter the name turns orange and you get a tooltip message if you select the text string. Reserved function names are reserved only for function names, which means that such names can be used for variable and parameter names, and vice versa. The following tables list most built-in elements and hence those reserved names.内置变量具有保留名称,⽤户⽆法重新定义。
Comsol 内置参数变量函数

Comsol 内置表达式:参数、变量、函数
表达式:
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数
数扫描。
变量:主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创建一张变量表来表示这些变量。
间坐标的名称。
所以可以生产下列变量:Tx、Ty、Txx、Txy Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt 是T对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli,besselk, erf,gamma,和psi。
内置操作函数:。
comsol表示一阶修正贝塞尔函数

comsol表示一阶修正贝塞尔函数bellel函数简介从事暖通空调行业的人都知道,在夏季制冷工况下,室内盘管温度低于空气露点温度时,室内湿空气会有水分凝结在盘管表面,此时称盘管为湿盘管。
相对应室外侧盘管因温度较高无水分凝结,称为干盘管。
湿盘管的存在使得换热器的设计计算变得更加复杂,例如在计算换热器翅片效率时,考虑凝结水膜的换热后湿翅片效率计算公式为:I0=零阶的第一种修正Bessel函数(modified,zero-order Bessel function of the first kind)I1=一阶的第一种修正Bessel函数(modified,first-orderBessel function of the first kind) K0=零阶的第二种修正Bessel函数(modified,zero-orderBessel function of the second kind) K1=一阶的第二种修正Bessel函数(modified,first-orderBessel function of the second kind) rc=圆管的管外半径,若管外翅片有翻边,则要包含翅片厚度re=包含翅片高度的管半径,若翅片型式不是圆型而是连续型,需采用等效面积法以req来取代re贝塞尔函数(Bessel Function),是数学上的一类特殊函数的总称,是贝塞尔方程的解(无法用初等函数系统表示),一般贝塞尔函数是下列常微分方程(一般称为贝塞尔方程)的标准解函数y(x):贝塞尔函数的具体形式随着方程中实数参数α变化,且α被称为贝塞尔函数的阶数。
实际应用中常见α为整数n,对应n阶贝塞尔函数。
利用matlab绘制贝塞尔函数曲线代码如下所示:clearformat longx=(0:0.1:20):y_O=besselj(0,x);%0阶第1类贝塞尔函数y_1=besselj(1,x):%1阶第1类贝塞尔函数y_2=besselj(2,x):%2阶第1类贝塞尔函数figureh=plot(x,y_0,'',x,y_1,'',x,y_2,');grid on;%绘制贝塞尔曲线axis([0,20,-1,1]):xlabel(Variable X):ylabel(Variable Y):%坐标轴及名称title("besselj curve graph");legend(0, 1, 2) ;绘制出来0阶、1阶和2阶第一类贝塞尔函数曲线图:贝塞尔函数的求解十分复杂,我们可以借助现成工具来完成求解,下面介绍两种求解Bessel函数的方法一、excel求解法在Excel中提供了4个与贝塞尔(Bessel)相关的函数,分别是BesselJ和BesselY、BesselL和BesselK。
comsol算符大全

subst(hmnf.nutildeinit,p,pin_stat)
circint(r,expr),
circavg(r,expr),
diskint(r,expr),
diskavg(r,expr),
sphint(r,expr),
sphavg(r,expr),
ballint(r,expr),
差分一个变量使用的单元级数
prev(expr,i)
在i步前计算表达式
向后Euler法:(u-prev(u,1))/timestep
bdf(expr,i)
应用级数为i的向后差分公式
bdf(u,1) = (u-prev(u,1))/timestep
subst(expr,
expr1_orig, ,
expr1_subst,...)
特别的:当f线性依赖于解,那么lindev(f)=f,如果不依赖则lindev(f)=0;
如果解没有线性化点,那么会报错;
lintotal
调用线性化点的和和线性扰动
lintotalavg
在各相中计算平均lintotal
lintotalrms
在各相中计算lintotal的RMS
lintotalrms(f)=sqrt(lintotalavg(abs(f)^2))
test(expr)
试函数
用于方程弱形式的算符,test(F(u,∇u))等价于:
var(expr,fieldname1,
fieldname2, ...)
nojac(expr)
up(expr)
down(expr)
mean(expr)
depends(expr)
isdefined(variable)
Comsol-内置参数变量函数
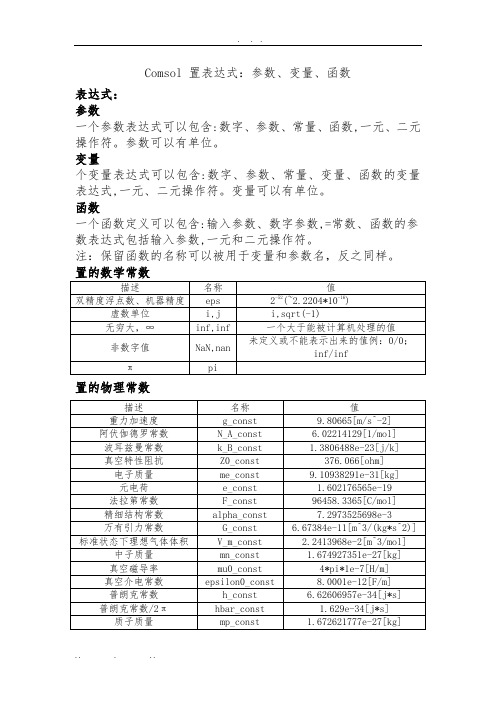
Comsol 置表达式:参数、变量、函数
表达式:
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
置的物理常数
数扫描。
变量:主要有两种类型变量:部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创建一变量表来表示这些变量。
坐标的名称。
所以可以生产下列变量:Tx、Ty、Txx、Txy Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,bes seli,besselk,
erf,gamma,和psi。
置操作函数:。
Comsol-内置参数变量函数

Comsol-内置参数变量函数Comsol 内置表达式:参数、变量、函数表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的数学常数描述名称值双精度浮点数、机器精度eps 2-52(~2.2204*10-16)虚数单位i,j i,sqrt(-1)无穷大,∞inf,inf 一个大于能被计算机处理的值非数字值NaN,nan未定义或不能表示出来的值例:0/0;inf/infπpi内置的物理常数描述名称值重力加速度g_const9.80665[m/s^-2]阿伏伽德罗常数N_A_const 6.02214129[1/mol]波耳兹曼常数k_B_const 1.3806488e-23[j/k]真空特性阻抗Z0_const 376.73031346177066[ohm] 电子质量me_const 9.10938291e-31[kg]元电荷e_const 1.602176565e-19 法拉第常数F_const 96458.3365[C/mol]精细结构常数alpha_const 7.2973525698e-3万有引力常数G_const 6.67384e-11[m^3/(kg*s^2)]标准状态下理想气体体积V_m_const 2.2413968e-2[m^3/mol] 中子质量mn_const 1.674927351e-27[kg]真空磁导率mu0_const 4*pi*1e-7[H/m]真空介电常数epsilon0_const 8.854187817000001e-12[F/m]普朗克常数h_const 6.62606957e-34[j*s]普朗克常数/2πhbar_const 1.05457172533629e-34[j*s] 质子质量mp_const 1.672621777e-27[kg] 真空中的光速c_const 299792458[m/s]斯忒潘—波耳兹曼常数sigma_const 5.670373e-8[W/(m^2*k^4)] 通用气体常数R_const 8.3144621[j/(mol*k)] 维恩位移定律常数b_const 2.8977721e-3[m*k]参数有以下用途:参数化几何尺寸、参数化网格元素大小、参数扫描。
COMSOL软件使用技巧-内置常数和参数说明

COMSOL 软件使用技巧:内置常数和参数说明
为了方便用户的建模操作,COMSOL 软件中预置了很多常用的变量、物理常数,以及函数,并提供很多自定义函数。
《COMSOL Multiphysics 简介》附录说明将向大家介绍这些预置功能,希望能够提高大家的建模使用经验。
访问COMSOL 官网“产品文档”页面(comsol/documentation)或点击文末“阅读原文”,可查看本系列全部内容。
今天将介绍系列说明的第一部分:常数和参数。
常数和参数
可以从“模型开发器”访问三种不同类型的常数:内置的数学和数值常数、
内置物理常数及参数。
参数是用户定义的常数,可随参数扫描而发生变化。
常数是标量值。
下表列出了内置的数学和数值常数,以及内置物理常数。
常
数和参数可以有单位。
comsol内置参数变量函数

保存函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数参数有以下用途:参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保存变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创立一张变量表来表示这些变量。
内置变量用户定义和自动消费的变量T表示在2D空间维度时的温度,按时间传热的模型。
x、y是空间坐标的名称。
所以可以消费以下变量:Tx,Ty,Txx,Txy,Tyx,Tyy,Tt,Txt,Tyt,Txxt,Txyt,Tyxt,Tyyt,Ttt,Txtt,Tytt,Txxtt,Txytt,Tyxtt,Tyytt。
其中Tx是T对x的导数,Ttt是T对t的二阶导数。
假设空间坐标有其他的名字,同理置换相应变量。
内置数学函数下面的函数不能用于表达式定义参数:acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli, besselk,erf,gamma,和psi。
内置操作函数:这些内置的函数不同于内置的数学函数,详细见用户指南。
用户定义消费的函数:表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
comsol内置参数变量函数

保留函数的名称可以被用于变量和参数名,反之同样。
描述名称值双精度浮点数、机器精度eps2-52(~2.2204·10-16)虚数单位i,j i,sqrt(-1)无穷大,∞Inf,inf一个大于能被计算机处理的值非数字值NaN,nan未定义或者不能表示出来到值如0/0或者inf/infπpi 3.141592653589793描述名称值重力加速度g_const9.80665[m/s^2]阿伏伽德罗常数N_A_const 6.02214129e23[1/mol]玻耳兹曼常量k_B_const1.3806488e-23[J/K]真空特性阻抗Z0_const376.73031346177066[ohm]电子质量me_const9.10938291e-31[kg]元电荷e_const 1.602176565e-19[C]法拉第常数F_const96485.3365[C/mol]精细结构常数alpha_const7.2973525698e-3万有引力常数G_const 6.67384e-11[m^3/(kg*s^2)]标准状态下想气体体积V_m_const 2.2413968e-2[m^3/mol]中子质量mn_const 1.674927351e-27[kg]真空磁导率mu0_const4*pi*1e-7[H/m]真空介电常数epsilon0_const8.854187817000001e-12[F/m]普朗克常数h_const 6.62606957e-34[J*s]普朗克常数/2πhbar_const 1.05457172533629e-34[J*s]质子质量mp_const 1.672621777e-27[kg]真空中的光速c_const299792458[m/s]斯忒藩—玻耳兹曼常数sigma_const 5.670373e-8[W/(m^2*K^4)]通用气体常数R_const8.3144621[J/(mol*K)]维恩位移定律常数b_const 2.8977721e-3[m*K]参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
comsol内置函数

comsol内置函数算符d(f,x) f对x⽅向的微分1. 使⽤d算符来计算⼀个变量对另⼀个变量的导数,如:d(T,x)指变量T对x求导,⽽d(u^2,u)=2*u等;2. 如果模型中含有任何独⽴变量,建模中使⽤d算符会使模型变为⾮线性;3. 在解的后处理上使⽤d算符,可以使⽤⼀些预置的变量,如:uxx,d(ux,x),d(d(u,x),x)都是等效的;4. pd算符与d算符类似,但对独⽴变量不使⽤链式法则;5. d(E,TIME)求解表达式E的时间导数;6. dtang算符可以计算表达式在边界上的切向微分(d算符⽆法计算),在求解域上使⽤dtang等价于d,dtang只求解对坐标变量的微分,但需要注意的是并不是所有的量都有切向微分。
pd(f,x) f对x⽅向的微分pd和d的区别:d(u+x,x)=ux+1,d(u,t)=ut,u和x,t等有关pd(u+x,x)=1,pd(u,t)=0,u是独⽴的和x,t⽆关dtang(f,x) 边界上f对x的切向微分在边界上d(u,x)不能定义,但是可以使⽤dtang(u,x),dtang付出基本的微分法则,如乘积法则和链式法则,但是需要指出的是,dtang(x,x)不⼀定等于1。
test(expr) 试函数⽤于⽅程弱形式的算符,test(F(u,?u))等价于:var(expr,fieldname1,fieldname2, ...)变异算⼦⽤于弱形式,它和test算符功能相同,但是仅⽤于某些特定的场中;如var(F(u,?u, v,?v),a),变量u是a场的变量,⽽v不是。
试函数之只作⽤于变量u。
nojac(expr) 对Jacobian矩阵没有贡献将表达式排除在Jacobian计算外,这对那些对Jacobian贡献不⼤,但是计算消耗很⼤的变量是否有效;k-e 湍流模型就是利⽤nojac算符来提⾼计算性能的例⼦。
up(expr) 上邻近估算表达式up,down,mean算符只能⽤在边界上,对于⼀个表达式或变量在边界处两边不连续,COMSOL通常显⽰边界的平均值,使⽤up,down可计算某个⽅向上的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算符
d(f,x) f对x方向的微分
1. 使用d算符来计算一个变量对另一个变量的导数,如:d(T,x)指变
量T对x求导,而d(u^2,u)=2*u等;
2. 如果模型中含有任何独立变量,建模中使用d算符会使模型变为
非线性;
3. 在解的后处理上使用d算符,可以使用一些预置的变量,如:
uxx,d(ux,x),d(d(u,x),x)都是等效的;
4. pd算符与d算符类似,但对独立变量不使用链式法则;
5. d(E,TIME)求解表达式E的时间导数;
6. dtang算符可以计算表达式在边界上的切向微分(d算符无法计
算),在求解域上使用dtang等价于d,dtang只求解对坐标变量的微分,
但需要注意的是并不是所有的量都有切向微分。
pd(f,x) f对x方向的微分
pd和d的区别:
d(u+x,x)=ux+1,d(u,t)=ut,u和x,t等有关
pd(u+x,x)=1,pd(u,t)=0,u是独立的和x,t无关
dtang(f,x) 边界上f对x的切向微分
在边界上d(u,x)不能定义,但是可以使用dtang(u,x),dtang付出基本的
微分法则,如乘积法则和链式法则,但是需要指出的是,dtang(x,x)不一
定等于1。
test(expr) 试函数
用于方程弱形式的算符,test(F(u,∇u))等价于:
var(expr,fieldnam
e1,
fieldname2, ...)
变异算子
用于弱形式,它和test算符功能相同,但是仅用于某些特定的场中;
如var(F(u,∇u, v,∇v),a),变量u是a场的变量,而v不是。
试函数之只作用于变量u。
nojac(expr) 对Jacobian矩阵没有贡献
将表达式排除在Jacobian计算外,这对那些对Jacobian贡献不大,但是
计算消耗很大的变量是否有效;
k-e 湍流模型就是利用nojac算符来提高计算性能的例子。
up(expr) 上邻近估算表达式
up,down,mean算符只能用在边界上,对于一个表达式或变量在边界
处两边不连续,COMSOL通常显示边界的平均值,使用up,down可计
算某个方向上的值。
down(expr) 下邻近估算表达式
mean(expr) 邻近边界上的平均值
depends(expr) 查看某个表达式是否依赖于求解结果
isdefined(variable
)
变量是否定义
dest(expr) 在目标端计算积分耦合表达式
dest算符强制将source points上的表达式用在destination points上。
例如:u/((dest(x)-x)^2+(dest(y)-y)^2)
if(cond,expr1,expr 2) 条件表达式
例如:if(x==0,1,sin(x)/x)
isinf(expr) 表达式的值是否是无穷大
islinear(expr) 解是否是线性函数
isnan(expr) 表达式是否是非数
with 调用某个解
例如with(3,u^2)指调用解3的u^2用于本次求解;
with只能用于解的后处理,不能用于建模;
at 调用解的某个时间
例如:at,u)
timeint 表达式的时间积分
timeint(t1,t2,expr,tol,minlen),t1,t2需要是实数,expr是表达式,tol是容
差,默认大小为1e-8,minlen设置积分的最短路径,它需要是正数,默
认长度为1e-6。
timeint只能用于解的后处理,不能用于建模;
timeavg 表达式的时间积分平均值
timeavg(t1,t2,expr,tol,minlen)
linpoint 调用线性化点
lindev 计算在线性化点的表达式
当解存储了一个线性化点,那么表达式在线性化点上先线性化,然后用
当前的解来计算;
特别的:当f线性依赖于解,那么lindev(f)=f,如果不依赖则lindev(f)=0;
如果解没有线性化点,那么会报错;
lintotal 调用线性化点的和和线性扰动
lintotalavg 在各相中计算平均lintotal
lintotalrms 在各相中计算lintotal的RMS
lintotalrms(f)=sqrt(lintotalavg(abs(f)^2))
lintotalpeak 在各相中计算lintotal的最大值
linsol 调用标准解,如linpoint或lintotal
linzero 计算表达式的根
linper 标记一个荷载项用于线性扰动求解器
ppr 精确的派生修复
用polynomial-preserving recovery计算表达式中所有用lagrange形函数差
分的变量,如e=ux+vy
range函数的用法
range( a,(b-a)/(n-1),b)
10^range(-3,3) 产生:10-3, 10-2, …, 103 1^range(1,10) 产生10个1。
