西安电子科技大学 研究生 电磁场数值分析期末考试题
西电电磁场与电磁波试卷

《电磁场与电磁波》模拟试卷6一、 填空题(本大题共10小题,每小题3分,共30分)1. 设x y z r xe ye ze ==++r ,r ∇⨯ = ,2(1/)r ∇= 。
2.. 在国际单位制中电场强度E 的单位是/V m ,磁场强度H 的单位是__________,传导电流密度矢量J 的单位是__________,位移电流密度矢量D J 的单位是__________。
3. 无限长直导线(沿z 轴放置)上有线电荷l ρ,则线外任一点电场强度的大小为,方向为。
4. 电磁波的相移常数β的单位为 , 在自由空间与相波长的关系为。
5. 电磁波等相位面移动的速度称为,电磁波能量传播的速度称为,对于TME 波两个速度的关系为。
6.任一线极化波都可分解为两个振幅、旋向的圆极化波,任一圆极化波都可分解为两个振幅、相互且相位的线极化波。
7.半径为a 的接地导体球外距球心d 处放置一点电荷q ,则镜像电荷q '-=,距球心b = 。
8. 已知介质的电参数为9,4,0r r μεσ===,则波阻抗η=。
9. 均匀平面波由空气向9r ε=的理想介质垂直入射时,媒质界面处的反射系数Γ=,透射系数τ=,驻波比ρ=。
10.若接收点距离发射天线1km 处,用电基本阵子做发射天线,要求接收点的场强值至少为30/mV m 时,天线的辐射功率至少为。
二、 单项选择题(本大题共10小题,每小题3分,共30分)1. 电磁波的极化特性由决定。
A.磁场强度B.电场强度C.电场强度和磁场强度D. 矢量磁位2. 已知静磁场中的矢位函数为77x y xy yx =+A e e ,那么磁感应强度B = A. 77z z y x -e e B.77z z y x +e e C.77x y x y +e e D. 77y x x y +e e3. 下述关于介质中静电场的基本方程正确的是 。
A.0∇⨯=E ,Sqd ε⋅=⎰E S B. ∇⨯=E J ,Sqd ε⋅=⎰E SC.ρ∇⋅=D ,0Cd ⋅=⎰E l D.Sqd ε⋅=⎰E S ,0Cd ⋅=⎰E l4. 一半径为a 的圆环(环面法矢z =n e )通过电流I ,则圆环中心处的磁感应强度B 为A.02r Iaμe B.02Iaφμe C.02z Iaμe D.02z Iaμπe 5. 下列关于电力线的描述正确的是A.是表示电子在电场中运动的轨迹B. 只能表示E 的方向,不能表示E 的大小C. 曲线上各点E 的量值是恒定的D. 既能表示E 的方向,又能表示E 的大小 6. 0∇⋅=E 说明A.静电场是无散场B.空间不存在电荷C.空间不存在电流D. 以上都不是7. 恒定电场的基本方程可由下面D 式推导而来。
西电电磁场与电磁波15年期末试题知识讲解

西电电磁场与电磁波15年期末试题15《电磁场与电磁波》期末考试题答案(A 卷)(120分钟)一、 简答题. (40分)1求标量函数23u x yz =的梯度u ∇;以及矢量函数x y z A xe ye ze =++v v v v的散度A∇⋅v 及旋度A ∇⨯v ;(其中,,x y z e e e v v v为x , y , z 为三个方向单位矢量)(6分)解:3232223x y z x y z u u u u e e e e xyz e x z e x yz x y z∂∂∂∇=++=++∂∂∂v v v v v v (2分)3y x z A A AA x y z ∂∂∂∇⋅=++=∂∂∂r (2分)0xy z x y z xyz e e e e e e A x y z x y z A A A xyz∂∂∂∂∂∂∇⨯===∂∂∂∂∂∂v v v v vv v (2分)2 写出均匀各向同性媒质中时域麦克斯韦方程组的微分形式、本构关系及边界条件;(8分) 解:麦克斯韦方程组0D H J t B E t B D ρ⎧∂∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩vv v vv vv (4分) 本构关系D EB H JEεμσ⎧=⎪=⎨⎪=⎩v v vv v v (2分) 边界条件()()()()21212121ˆ0ˆˆˆ0S s n E E nD D nH H J n B B ρ⎧⨯-=⎪⎪⋅-=⎪⎨⨯-=⎪⎪⋅-=⎪⎩v v v v v v v v v (2分) 3 将下面复数形式表示的场矢量变换为瞬时值,或做相反的变换;(4分)1)0jkzx E e jE e -=v v , 2)0sin()y E e E t kz ω=+v v解:1){}/200(t)Re cos(/2)j jkz j t x x E e E e e e e E t kz πωωπ-==-+v v v (2分)2)时域:0cos(/2)y E e E t kz ωπ=+-v v复数形式:0jkzy E e jE e =-v v (2分)4 描述平面电磁波极化概念,可分为哪三种极化状态?(4分)解: 在空间任一固定点上电磁波的电场强度矢量的空间取向(矢端)随时间的变化方式(轨迹)称之为极化 (1分) 线极化、圆极化、椭圆极化(3分)5 给出驻波比的数学表达式,同时解释其为行波,驻波和行驻波的三种情况;(4分)解:max min 11E S E +Γ==-Γ(1分) 当|Γ| = 0、S = 1时,为行波状态;(1分) 当|Γ| = 1、S = ∞时,为驻波状态;(1分) Γ= -1 ~ 1, S =1 ~ ∞,为行驻波状态;(1分)6 已知平面电磁波在良导体中传播,写出集肤深度及表面阻抗的表达式;(2分)解:集肤深度 1δα===(1分)表面阻抗1)(1)S Z j j σδ=+=+ (1分) 7 对于非磁性介质,写出斜入射的均匀平面波产生全反射及全透射的条件;(6分)解: 对于非磁性媒质,产生全透射的条件是:① 均匀平面电磁波平行极化斜入射; ② 入射角等于布儒斯特角,即θi =θB ;arctanB θ=或 B θ=(3分) 对于非磁性媒质,斜入射的均匀平面电磁波产生全反射的条件是: ① 入射波自媒质1向媒质2斜入射,且ε2 <ε1; ② 入射角等于或大于临界角,即θc ≤θi ≤90°c θ=(3分)8计算长度0.1dl λ=的电基本振子的辐射电阻以及电流振幅值为2mA 时的辐射功率。
电子科技大学数值分析研究生期末考试习题二

习 题 二请尽可能提供程序1、假设)(x f 在[]b a ,上连续,求)(x f 的零次最佳一致逼近多项式。
2、选择常数a ,使得ax x x -≤≤310max 达到极小,又问这个解是否唯一?3、如何选取r ,使r x x p +=2)(在[]1,1-上与零偏差最小?r 是否唯一?4、设在[]1,1-上543238401653841524381211)(x x x x x x -----=ϕ,试将)(x ϕ降低到3次多项式.求a 、b 使⎰-+202]sin [πdx x b ax 为最小。
5、设{}x span ,11=ϕ,{}1011002,x x span =ϕ,分别在21,ϕϕ上求一元素,使其为]1,0[2C x ∈的最佳平方逼近,并比较其结果。
6、用最小二乘法求一个形如2bx a y +=的经验公式,使它与下列数据相拟合,并求均方误差。
i x 19 25 31 38 44i y19.0 32.3 49.0 73.3 97.87、确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度。
)()0()()(101h f A f A h f A dx x f hh++-≈--⎰8、用辛普森公式求积分1x e dx -⎰并估计误差。
9、求近似求积公式)]43(2)21()41(2[31)(10f f f dx x f +-≈⎰的代数精度。
10、用三个节点(2=n )的Gauss 求积公式计算积分)2(14112π=+=⎰-dx x I 。
11、试确定常数A ,B ,C 和α,使得数值积分公式)()0()()(22ααCf Bf Af dx x f ++-=⎰-为Gauss 型公式。
12、用三点公式求2)1(1)(x x f +=在1.1,0.1=x 和1.2处的导数值,并估计误差,)(x f 的值由下表给出:X1.0 1.11.2 1.3 1.4)(x f0.2500 0.2268 0.2066 0.1890 0.173613、就初值问题0)0(,=+='y b ax y 分别导出欧拉方法和改进的欧拉方法的近似解的表达式,并与准确解bx ax y +=221相比较。
西电研究生数值分析试题A答案

答 案一. 填空题1、① x θ=2、②331()(53)2P x x x =- ③ 110,()()2,21n m n m P x P x dx n m n -≠⎧⎪=⎨=⎪+⎩⎰3、④ n ⑤ 04、⑥f f ⎛+ ⎝ ⑦ 1 ⑧ n+1 5、⑨02ω<< 6、⑩ 1()()k k k k f x cx x f x +-=-'二. 解:问题等价于求()f x =[1,1]-上关于权函数()x ρ=佳平方逼近多项式。
故选取切比雪夫基函数2012121===-,,T T x T x .001122(,),(,)(,)2T T T T T T ππ===1011111122211(,)1,(,)0,(,)(21)(21)0f T f T x f T x x x dx ----=====-=-=⎰⎰⎰⎰()f x =220(,)1()(,)j j j j j T f P x T T T π===∑由此得到参数10,0,a b c π===.而最小值(,,)I a b c 即是平方误差.即222(,,)(,)(,)I a b c f f f P δ==-2212211(,)(1(,)jj j jT fx xT T-==--∑⎰10.07448ππ=-≈三.证明:(1)若函数充分光滑,则有(1)1()()()()()(1)!nni i niff x f x l x xnξω++==++∑式中101()()()()n nx x x x x x xω+=---当()1f x≡时,有001()()()0()n ni i ii if x f x l x l x====+=∑∑(2)如果求积公式至少具有n次代数精度,则它对于n次多项式()njkj k jj kx xl xx x=≠-=-∏精确成立,即有()()nbk i k iail x dx Al x==∑⎰注意到()k i kil xδ=,故()()nbk i k i kail x dx Al x A===∑⎰即()0,1,2,,bk kaA l x dx k n==⎰ .解:(3) 插值节点为0121.0, 1.1 1.2.x x x===,步长100.1h x x=-=由三点公式()1021()()2f x f x f xh'=-+⎡⎤⎣⎦[]10.25000.206620.10.217=-+⨯=-另解(3)()()()()nn i iif x L x l x f x='''≈=∑当1 x x =时,110()()()ni i i f x l x f x =''≈∑三点的插值基函数为:1200102()()()()()1( 1.1)( 1.2)0.02x x x x l x x x x x x x --=--=--01()(2 2.3)0.02l x x '=-0211012()()()()()1(1)( 1.2)0.01x x x x l x x x x x x x --=--=--- 11()(2 2.2)0.01l x x '=-- 0122021()()()()()1(1)( 1.1)0.02x x x x l x x x x x x x --=--=-- 21()(2 2.1)0.02l x x '=- 将1 x x =代入,得:01()5l x '=-,11()0l x '=, 21()5l x '=(1.1)5(1.0)0(1.1)5(1.2)f f f f '∴=-⋅+⋅+⋅50.250050.20660.217=-⨯+⨯=-四. 解:(1) 令26x f (x)e -=,则212x f (x)xe -'=-,()221221x f (x)ex-''=-,()222432001xf (x)x(x )e x ,-'''=-≠∈,当01x ≤≤时,0f (x)'''>,所以1112f (x)f ()e -''''≤=f (x)''在[0,1]上为单调函数,因此[]()()(){}()0101012x ,max f x max f ,f f ∈''''''''===由于复化梯形公式的离散误差为()()()20112n h b a E f f ,-''-ξ<ξ<因此 ()()[]()20112n x ,h b a E f max f x ∈-''≤要使 ()610n E f-≤,则只要()[]()26011012x ,h b a max f x -∈-''≤即 ()22612101012h h --=≤因此310h -≤,故可取步长310h -=,由于1b a h n n-==,因此得310n =, 故节点数至少取1001.(2)将1,x 分别代入求积公式,使得1=2=a b +⎰;1021=35a b =+⎰. 由此的51,33a b ==.对应的求积公式为1511()(1)353f f ≈+⎰,将2x代入等式21251153253==+⎰恒成立,将3x代入等式31226775=≠⎰不成立, 故该求积公式的代数精度为2.五. (1) 解:由算式1111111111(1,2,3,4),/(2,3,4),(2,3,4;2,3,4),()/(2,3,4;3,4).jj i i k kj kj km mj m k ik ik im mk kk m u a j l a u i u a l u k j l a l u u k i -=-=⎧⎪====⎪⎪=-==⎨⎪⎪=-==⎪⎩∑∑得10004215210003001210002130410001A LU ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦b Ly =→(1,3,2,8)Ty =-y Ux =→(9,1,5,8)T x =--(2) 因为10042211001220091212A LU ⎡⎤⎢⎥-⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥--⎣⎦, 所以有200211110012123003TA LL -⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦b Ly =→(5,0,3)Ty =T L x y =→(22,1)T x =,六. (1) 解:雅可比迭代矩阵为1022101220--⎡⎤⎢⎥=-+=-⎢⎥⎢⎥⎣⎦()B D L U因为3-=-det()B I λλ,所以123===0λλλ,从而0=()B ρ,故雅可比迭代收敛。
西安电子科技大学微波技术基础07期末考试考题

d a] 工0 西安电子科技大学考试时间120分钟试 题(A )题号1 .五 总分分数1.考试形式:闭卷;2.本试卷共 五 大题,总分值100分。
班级 学号 姓名 任课教师一、简答题(每题3分,共45分)1、传输线解为侬+4〃鱼,上面公式中哪个表示+z 方向传输波? 哪个表示-z 方向传输波?为什么?2、假设传输线接容性负载(2乙=勺+户:<0),那么其行驻波分布离 负载端最近的是电压波节点,还是电压波腹点?3、如图三个两端口网络级联,各自的A 参数分别是Ai, A2和A3,写出其 组成网络的A 参数\ ________________________________ □4、如图单枝节匹配,可调参数为两段传输线的长度/和d,简要说明其工 作原理和两段传输线的作用。
5、矩形波导和圆波导的方圆转换中各自的工作模式是什么?6、带线宽度W,上下板距离b,当W/b增大时,带线特性阻抗如何变化?为什么?7、微带或者带线的开口端是否相当于开路端?为什么?如果不是,如何等效?8、一段矩形波导,尺寸Qxb, TEio模的散射矩阵如下,写出其传输TE20 模时的散射矩阵。
「I「0 e-je~9、金属圆波导的模式TEmnp和TMmnp,下标m, n, p各自代表什么含义?10、写出如图双口网络的输入反射系数「讥的表达式。
11、环行器的端口定义和散射矩阵如下,该环行器环行方向是顺时针还是逆时针?0 0 1S= 1 0 00 1 012、说明下列图E面T的工作特点13、写出如图理想两端口隔离器的S矩阵。
一二一①14、写出谐振腔品质因数Q 的普遍定义式。
15、 与低频LC 谐振回路相比,微波谐振腔的主要特点是什么? 、(10分)如图传输线中求Z 为何值时可使输入阻抗Z 加=50。
匹配, Z, =250。
l J>1题二图传输线匹配问题 a.(15分)证明:在任意负载条件下,传输线上反射系数和输入阻抗有下 列关系:1、r (z ) = -「(Z ± 〃4)2、Z 讥(z )/Z0 =Z0/Z,“(z±〃4)(其中,Z0为特性阻抗,4为工作波长) 四、(15分)证明无耗网络匹配定理,即下列图中IQJW1,采用无耗网络[S ]予以 匹配,其条件是 Z, =25。
电磁场数值分析期末

《电磁场数值分析》(期末作业)--- 2019学年 ---学院:学号:姓名:联系方式:任课教师:2019年5月作业1模拟真空中二维TM 电磁波的传播,边界设置为一阶Mur 吸收边界,观察电磁波的传播过程。
波源为正弦函数:sin()sin(2)25z t cE t n t ωπ==∆代码: clc clear close allxmesh =150; ymesh =150;mu0=4*pi*1.0E-7; eps0=8.85E-12;C= 3.0E8; dx=1.0; dt=0.7*dx/C; timestep=150; ez( 1:xmesh+1,1:ymesh+1 ) = 0.0; hx( 1:xmesh+1,1:ymesh ) = 0.0; hy( 1:xmesh,1:ymesh+1 ) = 0.0;coef1 = dt/( mu0 * dx ); coef2 =dt/( eps0 * dx );coef3=(C*dt-dx)/(C*dt+dx); ez1=ez;for now = 1 : timestephx = hx - coef1 * ( ez( :, 2 : ymesh+1 ) - ez( :, 1 : ymesh ) ); hy = hy + coef1 * ( ez(2 : xmesh+1, : ) - ez(1 : xmesh, : )); ez( 2 : xmesh , 2 : ymesh ) = ez( 2 : xmesh , 2 : ymesh ) - ... coef2 * ( hx( 2 : xmesh, 2 : ymesh ) - hx( 2 : xmesh , 1 :ymesh - 1) ) + ...coef2 * ( hy( 2 : xmesh ,2 : ymesh ) - hy( 1 : xmesh - 1,2 : ymesh) );ez(1,:)=ez1(2,:)+coef3*(ez(2,:)-ez1(1,:));ez(xmesh+1,:)=ez1(xmesh,:)+coef3*(ez(xmesh,:)-ez1(xmesh+1 ,:));ez(:,1)=ez1(:,2)+coef3*(ez(:,2)-ez1(:,1));ez(:,ymesh+1)=ez1(:,ymesh)+coef3*(ez(:,ymesh)-ez1(:,ymesh +1));ez( xmesh/2+1, ymesh/2+1) = sin( now * dt * 2 * pi * C / 25.0 ); mesh(ez);pause(0.05)ez1=ez;end结果与分析:第10时间步第100时间步第150时间步作业2基于Pocklington方程用MoM分析半波对称振子天线:观察天线线径和分段数目分别取不同值对天线阻抗和辐射特性的影响(半径分别取0.001λ,0.0001λ,0.00001λ,分段数取11,21,31,可列表说明)代码:clear all; close all; clc;% 初始化参数c=3e8; % 光速r=1 % 波长f=c/r; % 频率w=2*pi*f; % 角频率e0=8.85e-12; % 介电常数u0=4*pi*1e-7; % 磁导率a=0.00001*r; % 半径L=0.5*r; % 振子长度k=2*pi/r; % 波数N=11; % 分段数(奇数段)dl=L/(N+1); % 每段长度(分母中+1 为两头半段之和)l=L/2-dl/2; % 两头空出半段,满足电流为0的边界条件lz=-l:dl:l;lzs=lz(1:N); % 每一小段的起点坐标lzm=lz(1:N)+dl/2; % 每一小段的中点坐标lze=lz(2:N+1); % 每一小段的终点坐标%阻抗矩阵元素求解fi=log(dl/a)/(2*pi*dl)-k/(4*pi)*1i;fi_1=exp(-k*dl*1i)/(4*pi*dl);fi_2=exp(-k*2*dl*1i)/(8*pi*dl);z=ones(N,N);for m=1:Nfor n=1:Nif m==nfi1=fi;fi2=fi_1;fi3=fi_1;z(m,n)=((k^2*dl^2-2)*fi1+fi2+fi3);elseif abs(m-n)==1fi1=fi_1;fi2=fi;fi3=fi_2;z(m,n)=((k^2*dl^2-2)*fi1+fi2+fi3);elsefi1=exp(-k*abs(m-n)*dl*1i)/(4*pi*abs(m-n)*dl);fi2=exp(-k*abs(m+1-n)*dl*1i)/(4*pi*abs(m+1-n)*dl); fi3=exp(-k*abs(n+1-m)*dl*1i)/(4*pi*abs(n+1-m)*dl); z(m,n)=((k^2*dl^2-2)*fi1+fi2+fi3);endendend%电压矩阵求解V=zeros(N,1);V((N+1)/2)=-1*(1i*w*e0);% 计算电流系数矩阵I=z\V;% 计算输入阻抗Z_in=1/I((N+1)/2);disp(['输入阻抗 = ',num2str(Z_in)]);% 计算振子上归一化电流分布I_amp=abs(I); Max=max(I_amp);Iunit2=[0;I_amp/Max(1);0]; % 两端零电流figure(1);h=0:dl/r:L/r;Ithe=sin(pi*h*r/L); % 半波振子电流解析值plot(h,Iunit2,'b',h,Ithe,'r','linewidth',2);legend('pocklinton','解析值');grid on;xlabel('电长度L/\lambda');ylabel('归一化电流');% 画方向图theta=0:0.01:2*pi;abs_f=zeros(1,length(theta));for n=1:1:Nabs_f=abs_f+I(n)*exp(k*(n*dl-L/2)*cos(theta)*1i);endabs_f=abs(sin(theta)*dl.*abs_f);Max_f=abs(sum(I)*dl);Far_patten2=abs_f/Max_f(1);theta_2=0:0.1:2*pi;Far_theory=abs((cos(k*(L/2)*cos(theta_2))-cos(k*L/2))./si n(theta_2));figure(2);polar(theta,Far_patten2,'-b');hold on;polar(theta_2,Far_theory,'or');hold off;legend('pocklinton','解析值');title('半波振子天线E面方向图');figure(3);polar(theta,ones(1,length(theta)),'-b');title('半波振子天线H面方向图');% 半波振子增益I_in=I((N+1)/2);A=(w*u0)^2/(4*pi*sqrt(u0/e0)*real(Z_in)*(abs(I_in))^2); G_theta=A*abs_f.^2;Max_gain=max(G_theta)Max_gain_dB=10*log10(Max_gain);disp(['半波振子增益 = ',sprintf('%.4fdBi', Max_gain_dB)]); 结果与分析:作业3基于电场积分方程用MoM分析对称振子天线:计算振子总长度分别为0.25λ ,0.5λ,λ,1.5λ时,振子的输入阻抗和E面方向图。
电子科技大学2016数值分析研究生期末考试

《数值分析》复习题
Ex1.证明方程 1 – x – sin x = 0 在区间[0,1]上有一 根。使用二分法求误差不大于0.5×10-4的根需二分 多少次?
Ex2. 对于二元方程G(x,y)=0,已知(x0,y0)满 足方程。如果在点x0附近有函数y =y(x),则根据隐 函数存在定理,对于接近于x0的自变量x,试构造 牛顿迭代法计算隐函数值的迭代格式。
初值问题?
15/15
第五章 思考题 1. 代数插值问题的存在唯一性定理是如何叙述的 2. 拉格朗日插值和牛顿插值方法各有何特点? 3. Runge反例主要说明一个什么样的问题? 第六章 思考题
1. 多项式拟合与代数插值问题有何差异?拟合函数 有何特点?
2. 曲线拟合的最小二乘法有何特点? 3. 求一个超定方程组的最小二乘解有哪些主要方法?
Ex 27 将积分上限函数
f ( x) exp( x2 ) x exp( t 2 )dt 0
转化为常微分方程初值问题。并确定一种可求解的二 阶方法
11/15
第一章 思考题
1.在科学计算中,一般误差的来源有几种?列出部分 数值分析课中主要讨论误差。
2.有效数字的概念是如何抽象而来的,简单给予叙述 3.什么样的算法被称为是不稳定的算法?试举一个例
Ex 18.已知实验数据如下: x1 2 3 4
y 10 30 50 80
求二次多项式拟合函数P(x) = a + b x2 Ex 19 利用数据表 t –2 –1 0 1 2
y yk-2 yk-1 yk
yk+1 yk+2
数值分析期末考试题之经典例题

题型一:有效数字1,确定113的首位数字x 1,要使113的近似值x *的相对误差不超过0.5×10-5,至少要保留几位有效数字.(2010-2011)1*1151211||10100.5102226n n r x n e x n ---=≤⨯=⨯≤⨯⨯≥=解答:设至少要保留位有效数字,则有解得, n 5.7取位有效数字.2,要使112的相对误差不超过0.5×10-4,至少要保留几位有效数字?(2009-2010) 3,已知21.787654为有效数,确定其绝对误差界与相对误差界.(2007-2008)*6*118711||102111||1010102224n r e e x ----=⨯=⨯=⨯=⨯⨯解答:4,已知30.49876为有效数,确定其绝对误差界.(2006-2007B)5,设有效数x=12.4567,确定x 的绝对误差界.(2004-2005)题型二:插值多项式1,已知f(x)的函数值:f(0)=-2, f(1)=1, f(2)=5, 用反插值法求f(x)=0在[0,2]内的近似根x *.(2010-2011)11111202012012010210122021()()()()()()()()()()()()()()()()()(2)(5)(2)(1)012(12)(15)(52)(51)2991422884y y y y y y y y y y y y y L y f y f y f y y y y y y y y y y y y y y y y y y ----------=⋅+⋅+⋅------+-+-=+⨯+⨯+-+-=+-解答:对y=f(x)的反函数x=f 进行二次插值2*229(0)42y x L ≈=故,2,已知f(x)的如下函数值及导数值:f(-1)=1, f(0)=2, f ’(0)=3, f(1)=7; (1),建立不超过3次的埃尔米特插值多项式H 3(x);(2),x ∈[-1,1], 确定用H 3(x)代替f(x)的误差界(已知|f (4)(x)|≤M 4,x ∈[-1,1]).(2010-2011)32001001201232233)),(0,1,2)()()[,]()[,,]()()1(1)2(1)(0)232()()(1)(0)(1)232()'(i i H x f x i N x f x f x x x x f x x x x x x x x x x x x H x N x k x x x x x k x x H ===+-+--=++++-=++=++--=+++-解答:(1),满足插值条件((的二次插值多项式为:也可用拉格朗日插值法满足题设插值条件的插值多项式为:2323(4)23443)43(31)'(0)'(0)3()232()(2),(1)(0)(1),(1,1)4!1||=4!496x x k x H f H x x x f R x x x M M R ζζ=++-===+++--∈-≤⨯由得:k=0故:误差(x)=则误差界(x)3,已知f(x)的函数值:f(0)=2, f(1)=4, f(2)=9, 写出二次拉格朗日插值多项式及余项.(2009-2010) 4,已知f(x)的如下函数值及导数值:f(1)=1, f(2)=2, f ’(1)=3, f(3)=9; (1),建立不超过3次的埃尔米特插值多项式;(2)计算f(1.6)的近似值;若M 4=0.5,估计f(1.6)的误差界.(已知|f (4)(x)|≤M 4).(2009-2010)5,写出满足条件H(0)=1, H(1)=0, H ’(1)=1, H(2)=1的三次插值多项式,并给出误差估计式.(2008-2009B)6,已知一组数据,求函数f(x)=0的根.(2008-2009B)x i -1 0 2 3 f(x i )-7-1177,已知f(x)的如下函数值及导数值:f(0)=1, f(1)=3, f ’(1)=1, f(2)=9, (1),建立不超过3次的埃尔米特插值多项式,写出误差估计式;(2),计算f(1.8)的近似值:若M 4=1,估计f(1.8)的误差界.(已知|f (4)(x)|≤M 4).(2007-2008) 8,已知f(x)的如下函数值及导数值:f(1)=2, f(2)=4, f ’(2)=5, f(3)=8, (1),建立不超过3次的埃尔米特插值多项式;(2),计算f(2.5)的近似值:若M 4=0.5,估计f(2.5)的误差界.(已知|f (4)(x)|≤M 4).(2006-2007) 9,已知f(x)的如下函数值表x i 0.1 0.2 0.3 0.4 f(x i )1.122.652.811.68选取合适的插值节点,用二次插值多项式计算f(0.35)的近似值.(2005-2006) 10,已知f(x)=sinx 的如下函数值表x i 1.0 1.5 2.0 sinx i0.84150.99750.9093用插值多项式计算sin1.8, 并估计误差界.(2004-2005)11,用f(x)的关于互异节点集112{}{}n ni i i i x x -==和的插值多项式g(x)和h(x)构造出关于节点集1{}ni i x =的插值多项式.(2005-2006)(课后习题)-11111121111{}(),()(){}(),()()()()))()())]()n n i i i i n n n n n n n n n n n n n n q x q x g x x x x x x x x x g A x x g x ==------=----=-解答:法一:设关于节点集x 的插值多项式为则与有共同插值节点x ,则设:q(x)=g(x)+Aw w f(x (x )由q(x )=f(x 得,w w 故:q(x)=g(x)+[f(x (x )w 法二:设q(x)=g(x)+1-122311111()()(){}()()()()(),01()=()[()()]()[()()]()()()()()()[()()]=-n n i i n n n n n n n n n n x g x h x B g x h x B x x x x x x B x x x g x h x BAx x g x h x Bq x f x h x Ah x g x x x g x h x BA B -=---=---≠----===+--Aw 由于和有共同插值节点x ,则存在常数,使得则,w 故:q(x)=g(x)+由得得1111()[()()]()n n x x x x h x g x x x ----则:q(x)=g(x)+12,(1),已知f(x)的如下函数值:f(0)=1,f(1)=3,f(3)=5,写出二次拉格朗日插值多项式L 2(x); (2),若同时已知:f ’(1)=1,用待定系数法求埃尔米特插值多项式H 3(x); (3),当(3)(4)1|()|2|()|4,[0,3]fx fx x ≤≤≤≤∈及3时,x 不取节点,[0,3]x ∈,求32()()||()()f x H x f x L x --的上界.(2011-2012)题型三:最佳平方逼近多项式及最小二乘法1,已知函数值表:x -2 -1 0 1 2 y121用二次多项式y=C 0+C 1X+C 2X 2按最小二乘法拟合改组数据,并求平方逼近误差.(2010-2011)(2005-2006)()000102030410111213142021222324012()()()()()11111()()()()()21012()()()()()4101401210,5010010010034T T T T x x x x x A x x x x x x x x x x y A AC A y c c c ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎛⎫⎛⎫ ⎪ ⎪==-- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭==⎛⎫⎛ ⎪ ⎪ ⎪⎝⎭⎝解答:法一:线性拟合的法方程组为:即()()01222*20000100011402583,0,3575833570581358||||=(y,y)-Y 01210402023531701(,)0,(,)(T c c y x C x xx δϕϕϕαϕαϕϕϕα⎫⎛⎫⎪ ⎪=⎪ ⎪⎪ ⎪⎭⎝⎭===-=-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪=-=⎪ ⎪ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭====解得:c 则平方逼近误差:法二:构造首项系数为的正交多项式:(x)=1(x)=x-111211021100002*22022220,)0(,)(,)2,()()2(,)(,)46583()()0(2)(,)514357(,)8||||=(y,y)-(,)35i i i i i i i i i x x y x x x x y ϕϕϕϕϕβααϕβϕϕϕϕϕϕϕϕϕδϕϕ======----==++-=-=∑∑(x)(x)=x 则,平方逼近误差:2,求21()1f x x=+在区间[0,1]上的一次最佳平方逼近多项式及平方逼近误差(去权函数ρ(x)=x).(2009-2010) 3,通过实验获得以下数据:x i 0 1 2 3 y i13610请用最小二乘法求形如y=a+bx 2的经验公式.(2008-2009)T T A AC A y =解析:4,利用正交多项式的性质构造首项系数为1的正交多项式1{()}i i g x ∞=,有下列公式:010111()1()()()()(),(1,2,...)k k k k k g x g x x g x x g x g x k ααβ+--==-=--=其中:111(,),(0,1,2...)(,)(,),(1,2...)(,)k k k k k k k k k k xg g k g g g g k g g αβ---====(1),求[0,1]上首项系数为1的正交多项式(权函数ρ(x)=1),g 0(x),g 1(x),g 2(x)(2),以上述正交多项式为基,求sinx 在区间[0,1]上的二次最佳平方逼近多项式,并求平方逼近误差.(2008-2009B)(2004-2005)010000110001201111211021102110000*010001(1),()1(,)11,()(,)221()(,)121(,)2()2(,)11,()()()()(,)126(,)(,)(2),()(,)(g x xdx xg g g x x x g g dx x x dx xg g g g x dx g g g x x g x g x x x g g g f g f x g g g g αααβαβϕ=====-=--===-===--=-+=+⎰⎰⎰⎰解答:21212211120020111222000222*220(,),)(,)11()sin ()sin sin 11621()()1126()()260.00746 1.09130.23546(,)||||(,)0.000623.(,)i i i i g f g g g g g x x xdx x xdx xdx x x x dx x dx x x dx x x f g f f f g g ϕ=+-+-=⋅+⋅-+⋅-+--+=-+--=-=⎰⎰⎰⎰⎰⎰∑平方逼近误差:5,以正交多项式为基,求函数21()1f x x=+在区间[0,1]上的二次最佳平方逼近多项式,并求平方逼近误差.(2007-2008)(权函数ρ(x)=x,(2011-2012))20120122201201()1,(),(),111()2,()1,()2242211112234211113454111112224561.0656,0.503x x x x x f In f f In C F In c c c In ϕϕϕπϕϕϕπ=====-=-=⎛⎫⎛⎫⎪ ⎪⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⋅=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭==-解答:法一:取解得,,,正规方程组为:H 即:解得:c c 2*222*00001000111110110002,0.07423() 1.06560.503020.07423=(f,f)-F 0.000029041()11(,)223,()1(,)332(,)8(,)1,(,)15(,)T n p x x x C g x xg g g x x x g g xg g g g g g g g δαααβ=-=--======-=-====c 故二次最佳平方逼近多项式:平方逼近误差:法二:构造首项系数为的正交多项式:221100*201220120011222*1882163()()()()()()15318510(,)(,)(,)()()()() 1.06560.503020.07423(,)(,)(,)=(f,f)-F 0.00002904T n g x x g x g x x x x x f g f g f g p x g x g x g x x x g g g g g g C αβδ=--=---=-+=++=--=则:平方逼近误差:6,通过实验获得以下数据:u i 0 1 9 16 v i11/21/31/4请用最小二乘法求形如011v c c u=+的经验公式,并求平方误差.(2006-2007)011:c c u v=+解答转化题型四:代数精确度1,确定参数α,使求积公式20()[(0)()]['(0)'()]2hhf x dx f f h h f f h α≈++-⎰的代数精确度尽可能高,并求其代数精确度.(2010-2011)23322442320()1,,()1(),=121()()(0)(03)2121()()0+)(04)212()[(0)()]['(0)'()]2h h h f x x f x f x x h f x x f x dx h h h h f x x f x dx h h h hf x dx f f h h f f h αα====++-=≠+-≈++-⎰⎰⎰解答:令显然成立令得又时:时:(故具有三次代数精确度.2,确定参数A 1,A 2,使求积公式12()()(0)()3hhhf x dx A f h A f f h -≈-++⎰的代数精确度尽可能高,并求其代数精确度.(2009-2010) 3,建立高斯型求积公式1211221()()()x f x dx A f x A f x -≈+⎰.(2009-2010)231212113112211224112211335112211212000010001,23025031,53()1(,)0,()(,)x A A x dx A x A x x dx A x A x x dx A x A x x dx x A A g x xg g g x x xg g ααα----+==+==+==+===-=-======-=⎰⎰⎰⎰解答:法一:已知求积公式有3次代数精确度,令f(x)=1,x,x 得解上述方程组得:x 法二:构造二次正交多项式11110110022110021211222112111221121(,)(,)30,(,)(,)53()()()()53()0,511,33133()[()()]355xg g g g g g g g g x x g x g x x g x x x x x x A x dx A x dx x x x x x f x dx f f βαβρ---=====--=-==-=---=⋅==⋅=--≈-+⎰⎰⎰令得高斯点: x 故高斯型求积公式为:方法三:设[-1,1]上权(x)2221221122122121122221122331122212121().223()0,+0,5352()0,0,053().52:3250()()(),(g x x ax b b x g x dx b a x xg x dx a g x x A A A x A x A x A x A x A x x x x x x x c x c x ϕϕ--=++===-⋅====-+=+=+=+==--=++⎰⎰=x ,首项系数为1的二次正交多项式为则有:即即所以剩下步骤同法二.法四显然222221122111122212211221112221222332211122211221112221122112)()0()()()()()()()2230,535()()()()()20,053(),5x A x A x A x c x c A x c x c A x A x c A x A x c A A c c A x x A x x A x A x c A x A x c A x A x c c x x ϕϕϕϕϕϕ==+=+++++=+++++=+==-+=+++++====-剩下步骤同法二.4,确定求积公式()()(0)()hhf x dx Af h Bf Cf h -≈-++⎰中的参数A,B,C ,使其代数精度尽量高,并指出其代数精确度.(2008-2009B) 5,确定求积公式1211123()()()()343234f x dx f f f ≈-+⎰的代数精确度.(2006-2007B) 6,确定下列求积公式中的参数,使求积公式的代数精确度尽可能高,并求出代数精确度10120113()()()()424f x dx A f A f A f ≈++⎰.(2005-2006)7,确定下列求积公式中的参数,使求积公式的代数精确度尽可能高,并求出代数精确度101()()(0)()hhf x dx A f h A f A f h --≈-++⎰.(2004-2005)8,已知h>0,建立高斯型求积公式:21122()()()hhx f x dx A f x A f x -≈+⎰.(2011-2012)题型五:求积公式的最少节点数1,设定积分32x e dx -⎰,问用复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数为多少?(2010-2011)(4)2244(4)461(),()16301[]||()|101801801696017.0519.x xS f x e fx eb a h f h f h b ahη---==--=-≤⋅=<-=解答:复化辛普森公式截断误差:|R 解得:h<0.176,n>故应取个节点2,设定积分13x edx -⎰,问用复化梯形求积公式进行计算,要求误差小于10-6,所需要的最少节点数为多少?(2009-2010)(2)3322(2)261(),()9101[]||()|10121891622.8.x x T f x e f x e b a h f h f h b ahη---==--=-≤⋅=<-=解答:复化梯形公式截断误差:|R 解得:h<0.357,n>故应取4个节点3,给定积分2cos2xdx ⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少?(注:2(2)4(4)[](),[](),[,]122880T S b a b a R f h f R f h f a b ηηη--=-=-∈)(2008-2009B) 4,给定积分14x edx -⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少?(2007-2008) 5,给定积分21Inxdx ⎰,问用复化梯形求积公式和复化辛普森(Simpson)求积公式进行计算,要求误差小于10-6,所需要的最少节点数各为多少? (已知:2(2)4(4)1212[](),[](),,(,)12180T S b a b a R f h f R f h f a b ηηηη--=-=-∈)(2006-2007) 6,用积分82122dx In x=⎰计算In2,要使所得近似值具有7位有效数字,问用复化辛普森求积公式至少需要取多少个节点?(2005-2006)4(4)8(4)52(4)-744(4)4-7[](),[2,8]18011122,(),()223|()|,[2,8]817[]102631[]||()|101801808802820.04472,S S S b a R f h f In dx f x f x x x xf x x R f b a h R f h f h h n hηηη-=-∈===≤∈≤⨯-=-≤⋅=≤⨯-≤≥=⎰解答:复化辛普森公式截断误差公式:则使所得的近似值具有位有效数字,即令:|134.2137故至少需要取个节点.7,用积分6213dx In x=⎰计算In3,要使所得近似值具有5位有效数字,问用复化梯形求积公式至少需要取多少个节点?(2004-2005) 8,对于定积分1()If x dx =⎰,当M 2=1/8,M 4=1/32,用11点的复化辛普森(Simpson)求积公式求I 的截断误差为R s [f],用n 个节点的复化梯形求积公式求I 的截断误差为R T [f],要使R T [f]≤R s [f],n 至少是多少?(M 2=max|f ”(x)|,M 4=max|f (4)(x)|,[0,1]x ∈).(2011-2012)题型六:Doolittle 分解及方程组求解1,求矩阵212454635⎛⎫ ⎪ ⎪ ⎪-⎝⎭的Doolittle 分解.(2010-2011) 212100212454210030635321001LU ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪== ⎪ ⎪⎪ ⎪ ⎪⎪---⎝⎭⎝⎭⎝⎭解答:A=2,求矩阵114103241⎛⎫ ⎪- ⎪ ⎪⎝⎭的Doolittle 分解.(2009-2010) 3,设线性方程组123410135114152410162116x x x x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪⋅= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ (1),对方程组的系数矩阵A 作Doolittle 分解;(2),用所得的Doolittle 分解求该线性方程组的解.(2007-2008&2005-2006)1234123410001013101311000132114124100013224101119162116210001313191,,,)(5,0,11,)13,,,)(1,1,1,1).T TT T A LU LY b y y y UX Y x x x --⎛⎫⎛⎫--⎛⎫ ⎪⎪- ⎪ ⎪⎪-⎪=== ⎪⎪--- ⎪ ⎪⎪ ⎪ ⎪⎪-- ⎪⎪⎝⎭⎝⎭⎝⎭==---==--解答:由得:(y 由得:(x4,设线性方程组123411415101312410762118x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪⎪ ⎪⋅=⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ (1),对方程组的系数矩阵A 作Doolittle 分解;(2),用所得的Doolittle 分解求该线性方程组的解.(2006-2007)5,设线性方程组:12312312323153478113x x x x x x x x x ++=+-=-++=-(1),对方程组的系数矩阵A 作Doolittle 分解;(2),利用上述分解结果求解该线性方程组.(2004-2005)6,用高斯顺序消去法求解线性方程组:13241234242532431737x x x x x x x x x x +=+=+++=+=.(2010-2011)432110205102051020*******101301013=124317022312002160103701037000242,2,1, 1.x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪→→⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭====解答:增广矩阵回代求解:x 7,用高斯顺序消去法求解线性方程组:1231231233472212320x x x x x x x x x -+=-+-=---=.(2009-2010)题型七:条件数及范数1,求线性方程组1212391078981510x x x x x --=+==的系数矩阵A 的条件数cond 1(A),并说明其含义.(2010-2011)1111191008900015910089010015()||||||||19193611A A cond A A A A b ----⎛⎫ ⎪= ⎪⎪⎝⎭⎛⎫ ⎪-- ⎪= ⎪⎪⎪⎝⎭==⨯=解答:系数矩阵条件数远大于,这说明当和有小扰动时会引起解的较大误差,即该方程组是病态的.2,设矩阵15000910089A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,求cond ∞(A).(2009-2010) 3,设三阶对称矩阵A 的特征值分别为:-2,1,3,求||A||2及cond 2(A).(2007-2008)222max max max 111-122-12max max max 1222||||()()()3||||(())()=()=1()|||||||| 3.T T A A A A A A A A A A cond A A A λλλλλλ----========解答:()则:4,若n 元线性方程组Ax=b 为病态的,可以得到关于系数矩阵A 的什么性质.(2006-2007)5,若111123124A ⎛⎫⎪= ⎪ ⎪⎝⎭,求cond 1(A).(2005-2006)求cond ∞(A).(2004-2005) 6,设1231032475A -⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭,求1||||||||A A ∞与.(2007-2008)7,若1234A ⎛⎫= ⎪⎝⎭,求谱半径()A ρ.(2005-2006)5332ρ+解答:最大特征值:(A)=题型八:雅可比迭代与高斯-赛德尔迭代1,写出求解方程组1231231237321241021534818x x x x x x x x x -+=--=--=的雅可比迭代公式,并说明其收敛性.(2010-2011)(1)()()123(1)()()213(1)()()312(0)1(3212)71(4215)101(3418)87324102348.k k k k k k k k k J x x x x x x x x +++=-+=--++=--++-⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭解答:雅可比迭代公式为:x 雅可比迭代法迭代矩阵:B 严格对角占优,故求解该方程组的雅可比迭代法关于任意初始向量x 收敛2,设有方程组:132********2112212x x x x x x x -=+=-++=,讨论用雅可比迭代法和高斯-赛德尔迭代法解此方程组的收敛性.(2010-2011)112330200030000202100002000121221000200020031()002110211||0,=0=-=-12J J J L D U B D L U E B B λλλλρ---⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=++=++ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫ ⎪ ⎪⎪=-+=- ⎪ ⎪⎪- ⎪⎝⎭-=解答:A=雅可比迭代矩阵:得,()<1,故用雅可比迭代法解答此方程组对任意(0)1123(0)20031-()00211001211||0,=012-S S S B D L U E B B λλλλρ-⎛⎫ ⎪ ⎪⎪=-+=- ⎪ ⎪⎪ ⎪⎝⎭-===初始向量x 都收敛.高斯赛德尔迭代矩阵:得,()<1,故用高斯赛格尔迭代法解答此方程组对任意初始向量x 都收敛.3,写出求解方程组:123123123532124721535818x x x x x x x x x -+=--=--=的高斯-赛德尔迭代公式,并说明收敛性.(2009-2010)4,用雅可比迭代法求解以313132323A ⎛⎫⎪= ⎪ ⎪-⎝⎭为系数矩阵的线性方程组时,确定其收敛性.(2009-2010)5,设线性方程组123123123221162222x x x x x x x x x -+=-+-=--+=-,讨论分别用雅可比迭代法和高斯-赛德尔迭代法解此线性方程组的收敛性,若收敛,请给出迭代格式.(2008-2009B)6,设线性方程组:1231231232215202225x x x x x x x x x +-=-++=++=-(1),证明求解该方程组的雅可比迭代法关于任意初始向量收敛;相应的高斯-赛德尔迭代法不是关于任意初始向量收敛;(2),取(0)(0,0,0)T x =,用雅可比迭代法进行求解,要求(1)()5||||10k k xx +--<.(2007-2008)11231123022()101220||0,===0)1022()023002||0,0,2,)1-J J J S S S D L U E B D L U E λλλλρλλλλρ---⎛⎫ ⎪=-+=-- ⎪⎪--⎝⎭-=<-⎛⎫⎪=-+=- ⎪⎪⎝⎭-====>解答:(1):B B 解得:,(B B 解得:(B 所以用雅可比迭代法解此方程组对任意初始向量都收敛,而用高斯赛德尔迭代法解此方程组不是对任意初始向量都收敛.(2):(1)()()123(1)()()213(1)()()312(0)(1)(2)(3)(4)2215202225(0,0,0)(15,20,25)(105,60,35)(205,160,65)(205,160,65)k k k k k k k k k T T T TTx x x xx x x x x x x x x +++=-+-=--+=---==--=--=-=-雅可比迭代公式:x 当时,计算得:(精确解).7,设线性方程组:123123123821027325431111x x x x x x x x x ++=--++=-+=-(1),写出求解该方程组的雅可比迭代法的迭代公式和高斯-赛德尔迭代法的迭代公式,并确定其收敛性; (2),取(0)(0,0,0)T x=,用高斯-赛德尔迭代法计算x(3).(2006-2007)8,设线性方程组Ax=b 的系数矩阵232131t A t t ⎛⎫⎪= ⎪ ⎪-⎝⎭,其中t<0,问t 取何值时雅可比迭代法关于任意初始向量都收敛.(2006-2007)12122223021()0310422||()0=0=-,=)12||<1,t<-2,or t>20, 2.J J J t t D L U t t t t E B t t ttt t λλλλλλρ-⎛⎫-- ⎪ ⎪ ⎪=-+=-- ⎪ ⎪ ⎪- ⎪⎝⎭-=-=<<<-解答:雅可比迭代矩阵B 得,,雅可比迭代法对于任意初始向量都收敛,则(B 即:得又故9,1),设线性方程组:121232343243430424x x x x x x x +=+-=-+=-写出求解该方程组的雅可比迭代法的迭代公式,并确定该迭代法的收敛性;2),设线性方程组:123123123104413410811481025x x x x x x x x x ++=++=++=写出求解该方程组的高斯-赛德尔迭代法的迭代公式,并确定该迭代法的收敛性.(2004-2005)10,给定方程组:1231231232251223x x x x x x x x x +-=++=++=(1),用三角分解法解此方程组;(2),写出解此方程组的雅可比迭代公式,说明收敛性;取初始向量x 0=(0,0,0)T,当21||||10k kx x -+-<时,求其解.(2011-2012)11,设()21253sin 3421sincos 4134tan 5k k k k k k k Ak k k kkk⎛⎫- ⎪+ ⎪ ⎪= ⎪+ ⎪ ⎪+ ⎪⎝⎭,求()lim k k A →∞.(2007-2008)()020lim 021205K k A →∞⎛⎫⎪= ⎪ ⎪⎝⎭解答:12,若()()11,lim 1sin sin k k k k k k AA k k k k →∞⎛⎫⎪+=⎪ ⎪⎪⎝⎭求.(2004-2005)()01lim 10K k A→∞⎛⎫= ⎪⎝⎭解答: 题型九:非线性迭代1,设计一个算法求125的值.(2008-2009B)101125(),0.2k k kx x x +=+>解答:牛顿迭代公式:x2,给出用牛顿法求6170的近似值的迭代公式,并确定初值的取值范围.(2010-2011)6661556'5"4"*600066601050517017001701170[5]66()170,()60,()300170()()0,.1170170170(5)17061170()(5)6k k k k k kx x x x x x x x f x x f x x f x x x f x f x x x x x x g x x x +=-=-=-=+=-=>=>>⋅><-=+-=+-解答:转化为方程的正根.由牛顿迭代法得迭代公式:当时,故此时收敛到当0<时,设66'6666611*60170,(0,170)1850()(5)0,(0,170),()(170)0,6:1700,170,(0,170),.0.x g x x g x g xx x x x x ∈=-<∈>=->>∈>故故回到前段.所以当迭代公式也收敛到综上:3,给出用牛顿法求5140近似值的迭代公式,并给出初值的取值范围.(2009-2010)解答:方法同上.4,设φ(x)=x+c(x 2-5),当c 为何值时,x k+1=φ(x k ),(k=0,1,2…)产生的序列{x k }收敛于5;又c 为何值时收敛最快?(2010-2011)2''**1**'*5),||<1,||<1110,=50;51.25k k cx x c ϕϕϕϕϕ+-=-<<-<<解答:(x)=x+c(x (x)=1+2cxx (x )收敛,则有(x )即1+2cx 又,则当(x )=0,即c=-时,收敛最快5,设2()(3)x x c x ϕ=+-,应如何选取常数c 才能使迭代1(),(0,1,2)k k x x k ϕ+==具有局部收敛性?C 取何值时,这个迭代收敛最快?取x 0=2,123c =-计算()x ϕ的不动点,要求当61||10k k x x -+-<时结束迭代.(2004-2005)****21*2'****'**1(),(3)3,()(3)()|133|12|1,11,3,-0,,0.333(2),()0+0,636(3),k k k x x x x c x x x x c x x cx cx x c or c x x ϕϕϕϕ++==+-=±=+-<+<-<<=±<<<<==±±解答:(1),令x 收敛于则故要局部收敛,即|又得根据收敛阶定理,当时,迭代至少二阶收敛,即12cx 得c=故c=时,迭代收敛最快.迭代公式为:2012346*431(3)2321.7113248651.7319268031.7320508041.732050808|10,: 1.732050808.k k x x x x x x x x x x -=--=====-<=又因为|故6,方程x 3-3x-1=0在x=2附近有一根,构造一个局部收敛的不动点迭代法,并说明收敛的理由.(2009-2010)3'3223132(1.5) 1.765174168,(2.5) 2.040827551[1.5,2.5]()[1.5,2.5]11()|||0.33,(13) 5.5xx x x x x ϕϕϕϕϕ+===∈∈=≤<+解答:(x)=取的邻域[1.5,2.5]当时,又因为|故迭代在[1.5,2.5]上整体收敛.7,已知方程42()440f x x x =-+=有一个两重根02x =,请以初值x 0=1.5,用m 重根的牛顿迭代法计算其近似值,要求51||10k k x x -+-<.(2008-2009B)(P204例7.7)8,(1),已知方程240xex +-=在0.6附近有一根x ,迭代法214,0,1,2kx k x ek +=-=是否局部收敛?如果不收敛,试构造一个局部收敛的不动点迭代法,并说明收敛的理由.(2),取x 0=0.6,用你所构造的不动点迭代法求解该方程,迭代至x 5. (3),给出牛顿法求120的近似值的迭代公式,并给出初值的取值范围.(2007-2008)2'2'**1'''1(1):()4,()2|()|1,(0),1(4)211(4),()22(4)1(0)2,(1)3()[0,1]21()||(1)|161(4)2x xk k k k x e x e x x x In x In x x x In In x x x In x ϕϕϕϕϕϕϕϕϕϕ++=-=->>=---=-==∈≤=<=-解答:故该迭代公式不是局部收敛的.构造:理由:取邻域[0,1](x)=故又|故迭代式在[0,1]上整体收敛11021324354101(2),(4),21(4)0.61188771521(4)0.61013645921(4)0.61039483321(4)0.61035672221(4)0.61036234421120(3),(),0.2k k k k kx In x x In x x In x x In x x In x x In x x x x x ++=-=-==-==-==-==-==+>.则9,给定方程x 2+x-2=0,[0,2]x ∈,采用迭代公式xk+1=x k +c(x k 2+x k -2),(k=0,1,2…)求其根,问当c 为何值时,迭代法收敛?又当c 为何值时,迭代法收敛最快?(2011-2012)*2'''1,()(2)()1(21)2(1)||1(21)|1,-0.31(1)=03x x x c x x x c x c c ϕϕϕϕ==++-=++=++<<<解答:当|即时,线性收敛当,即c=-时收敛最快.10,给定方程230x xe -=,[3,4]x ∈(1),构造一种线性收敛的不动点迭代公式求该方程的根(含迭代公式,初值取何值或何区间,迭代法收敛的原因); (2),构造一种二次收敛的不动点迭代公式求该方程的根(含迭代公式,初值取何值或何区间,迭代法收敛的原因).(2011-2012)21111'12102'"0(1),()(3),3.29(3)()(4) 3.8712(),[3,4]23(3),(0,1,2,)[3,4].(2),()3,[3,4](3)0,(4)0()60,()60,[3,4]3k k x x x x In x x x x In x k x f x x e x f f f x x e f x e x x ϕϕϕϕϕ+==≤≤=≤≤∈==∈=-∈><=-<=-<∈=解答:故不动点迭代公式:x 对于任意初值收敛取初值时,牛顿213.6kkx kk k x k x ex x x e+-=--迭代法:收敛,且二次收敛11,方程x 3-x 2-1=0在x=1.5附近有根,建立一个收敛的迭代公式,并证明其收敛性.(2004-2005)122''33312111.51()1(1.3) 1.591715976,(1.6) 1.390625[1.3,1.6]()[1.3,1.6]222(),|()|||0.921.311k k k kx x x x x x x x x x x x x ϕϕϕϕϕϕ++=+==+==∈∈=-=-≤<=+解答:取的邻域[1.3,1.6]故当时,又故迭代公式:在[1.3,1.5]上整体收敛.12,(1),已知方程1020x e x +-=在0.09附近有一根x,迭代法1(210),(0,1,2)k k x In x k +=-=是否局部收敛?如果不收敛,请构造一个局部收敛的不动点迭代法,并说明收敛的理由;(2),取x 0=0.09,用局部收敛的迭代法计算x 5; (3),用牛顿法求3234的近似值,并给出初值的取值.(2006-2007)'''*1''5(1),()(210),()15|()|1,[0,1],|()|>1.11510111(),()51010(0)0.1,(0.12)0.087250323[0,0.12]()[0,0.12]()|kx k x xx In x x xx x x x e x e x e x x x ϕϕϕϕϕϕϕϕϕϕ+-=-=->∈=-=-=-==∈∈≤解答:显然故该迭代公式不是局部收敛的构造:因为取[0,0.12]邻域考察故当时,又|'0.12110.09010.09058257820.09051881530.0905241|(0.12)|||0.1131101151011(2),510110.09,0.090582578510110.090518815510110.09052579651011510k kx k x k e x e x e x x e x e x e x e ϕ++=-<<=-=-==-==-==-==-故迭代公式:在[0,0.12]上整体收敛.57960.09052503151200.090525031110.0905251155102117(3),()30.k k k x e x x x +==-==+>使用迭代公式:进行求解.初值:x13,设方程x 3-3x-1=0在x=2附近有根;1),证明该方程在区间[1.5,2.5]内有唯一根x *;2),确定迭代函数φ(x).当初始值x 0在何区间取值时,迭代公式x k+1=φ(x k ),(k=0,1,2…)收敛到x *,并说明理由. 3),写出求解该方程组的牛顿法迭代公式,当初始值x 0在何区间取值时,牛顿法迭代公式收敛到x,并说明理由.取x 0=1.8,用牛顿法迭代公式计算x,要求(1)()4||||10k k x x +--<.4),写出求解该方程的弦截法迭代公式,当初始值在何区间取值时,弦截法迭代公式收敛到x,并说明理由.(2005-2006)3'2'331223(1),()31,()33(1.5) 2.125,(2.5)7.125(1.5)(2.5)0,()0()0,[1.5,2.5][1.5,2.5].(2),3121(3),,3333()3k k k k k k k f x x x f x x f f f f f x f x x x x x x x x x f x x +=--=-=-=⋅<=>∈--+=-=--=-解答:证明:故在[1.5,2.5]内有根.又故方程在区间内有唯一根牛顿法迭代公式:'2"1,()33,()6x f x x f x x-=-=题型十:稳定算法1,对给定的x ,下列两式能否直接计算,说明理由;如果不能,请给出变换算式:(1)21x x +-,x 很大;(2)311x +-,|x|很小.(2010-2011)223331(1):1111=.1+1x x x x x x x +-=+++-+解答:不能直接计算,因为两个相近的数相减,会产生较大的误差:;2,为了提高计算精度,当正数x 很大时,计算1x x +-时应转化成什么形式.(2005-2006)3,给出计算积分1,(0,1,2,10)10nnx I dx n x ==+⎰的递推稳定算法和初值.(2010-2011) 1111111000-11110002010101101010101=101011111)11101010(1)11121[].2111)101)220(1)n n n n n n n n n n x x dx x dx x dx I I x x nn n x x x dx dx dx n x n n n n ----+-===-=-++-=<<=+++=+=+++⎰⎰⎰⎰⎰⎰解:I 该算法不稳定,变形得:I 因为(取初值I ((4,设计一种求1x n nI e x dx =⎰(n 为非负整数)稳定的递推算法,包括递推公式,初值的确定;当初值201221e I =⋅时,利用上述稳定的递推公式计算三个连续的积分值.(2011-2012)题型十一:部分证明题1,利用差分的性质证明:12+22+…n 2=n(n+1)(2n+1)/6222()12,g n n n =++证明:设函数对任意的建立差分表:g(n)(n+1)22n+3 2 g(n+1) (n+2)2 2n+5 2 g(n+2) (n+3)2 2n+7 g(n+3) (n+4)2 g(n+4)函数g(n)的三阶差分是与n 无关的非零常数,故g(n)是n 的三次多项式:3(1)1,(2)5,(3)14,(4)30111()()14521231(1)(2)(1)(2)(3)(1)(21)14521!2!3!6g g g g n n n g n N n n n n n n n n n n ====---⎛⎫⎛⎫⎛⎫==+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭------++=+⋅+⋅+⋅=按等距节点牛顿向前插值公式建立三次插值多项式,则2,证明:n+1个互异节点的插值型求积公式的代数精确度至少为n.(2010-2011)(1)0()(),.(1)!n nbi ai f x x dx n ζ+=-+∏⎰证明:截断误差R[f]=易证 3,若0{()}ni i l x =是关于互异节点0{}ni i x =的拉格朗日插值基函数组,函数0011()()()(),(1)n n f x x l x x l x x l x n =++≥,证明:f(x)≡x.(2009-2010)00110()()()()()()()()n n i i n n i f x L x f x l x x l x x l x x l x f x x=≈==+++≡∑证明:故:4,证明:0101'()[()()]"()2hf x f x f x f h ζ=--,其中h=x 1-x 0,01(,)x x ζ∈.(2009-2010)"'20000"'211001010'"010())()()()2!(),())()()()2!1()[()()]()2f f x x x x x f x x f x f x x x x x hf x f x f x f h ζζζ+-+-==+-+-=--证明:由泰勒公式得f(x)=f(x 令则f(x 整理得: 5,证明:关于互异节点0{}ni i x =的拉格朗日插值基函数0{()}ni i l x =满足恒等式012()()()()1n l x l x l x l x +++≡.(2008-2009B)(2006-2007B)(2004-2005)120(1)(1)1010()1,(),,1=L ()()()()()()()1,()0,()()0(1)!()()()()1n n n n i n i n n n n ni n i f x f x x x x x R x l x f x R x f f x fx R x W x n l x l x l x l x ζ=+++==+=+=≡==+=+++≡∑∑证明:令对在上进行拉格朗日插值,有因故故:6,证明求积公式()[()()]2bab af x dx f a f b -≈+⎰的截断误差:3"()[](),12f R f b a ηη=--∈其中:(a,b).(2007-2008) (1)001(2)(2)(2)33()()(1)!1,,()()()1"()()()()()()()2!2!2!612n nb i ai b b aa f x x dx n n x a xb f f f f x a x b dx x a x b dx a b b a ζζηηη+=-+===--=--=⋅-=--∏⎰⎰⎰证明:插值型求积公式截断误差R[f]=R[f]=7,设矩阵A 为可逆上三角阵,证明A -1仍为上三角阵,并导出求逆算法.(2006-2007B)8,设x k =a+kh(k=0,1,2;h>0),f(x)的三阶导数连续,证明:2(3)102021'()[()()](),(,)26h f x f x f x f x x h ζζ=-+-∈其中为中值.(2011-2012)001122120201201201021012202112020101222,),,),,)()()()()()()()()()()()()()()()()()()()()()()()()(22x y x y x y x x x x x x x x x x x x x f x f x f x x x x x x x x x x x x x x x x x x x x x x x x x f x f x f x h h h ------=++------------=-+证明:过(((的拉格朗日插值多项式为:L 12'2102(3)201202(3)'''1210122'(3)10202)1()[()()]2()()()()()(),(,)3!()()()[()()()]3!1()[()()](),(,)26x x L x f x f x hf f x L x x x x x x x x x f f x L x x x x x x x h f x f x f x f x x h ηηηζζ==-+-=---∈-=---=-+-∈又故:。
电子科技大学数值分析研究生期末考试习题一

电子科技大学数值分析研究生期末考试习题一习题请尽可能提供程序1.用二分法求方程012=--x x 的正根,要求误差05.0<。
2. 为求方程0123=--x x 在5.10=x 附近的一个根,设将方程改写成下列等价形式,并建立相应的迭代公式:1)2/11x x +=,迭代公式21/11k k x x +=+;2)231x x +=,迭代公式3211k k x x +=+;3)112-=x x ,迭代公式1/11-=+k k x x ;4)132-=x x ,迭代公式131-=+k k x x 。
试分析每种迭代公式的收敛性。
3. 给定函数)(x f ,设对一切x ,)(x f '存在且M x f m ≤'≤<)(0,证明对于范围M /20<<λ内的任意定数λ,迭代过程)(1k k k x f x x λ-=+均收敛于)(x f 的根*x 。
4.设a 为正整数,试建立一个求a1的牛顿迭代公式,要求在迭代公式中不含有除法运算,并考虑公式的收敛性。
请提供程序。
5.用Gauss 消去法求解方程组:-=????? ??????? ??----503121312111321x x x (请提供程序)用列主元Gauss 消去法求解下列方程组:(1)=????? ??????? ??13814142210321321x x x (请提供程序)6.用追赶法解三对角方程组b Ax =,其中--------=2100012100012100012100012A ,=00001b 。
7.设n n R P ?∈且非奇异,又设x 为n R 上一向量范数,定义Px xp =。
试证明px 是n R 上向量的一种范数。
8.用平方根法(Cholesky 分解)求解方程组:=????? ??????? ??7351203022323321x x x9.用改进的平方根法(T LDL 分解)求解方程组:=????? ??????? ??3016101795953533321x x x 。
电子科技大学 数值分析研究生期末考试

1 0 2 0
1
A
0 1
1 2
0 4
1
3
,
b
0 4
0
1
0
3
2
计算矩阵 A 的 LU 分解,并求出方程的解.
解:矩阵 A 的 LU 分解为
1
1 0 2 0
A
LU
0 1
1 2
1
1
0
1
2 1
0
1
0
1
2
方程组的精确解为 x (1,-1,1,1)T .
4. 给定求积公式 1 f (x)dx Af (0) Bf (0.5) Cf (0) ,试确定 A, B, C ,使其代数精度尽可能的高,并 0
指明此时求积公式的代数精度.
解:分别将 f (x) 1, x, x2 ,代入求积公式,可得
1
A B
1
2
B 1B 4
C
1 0
1 dx 1,
解:由于高斯求积公式为
1
f (x)dx
1
n
Ak
k 0
f (xk ) ,其中 xk 是 Pn1 (x) 的零点.
首先将积分区间转化
为[1,1] .令 x t 2 则 x [1,3] 时 t [1,1] .而
I 3 e x sin xdx 1 et2 sin(t 2)dt 令 g(t) et2 sin(t 2)
yn1
yn
h[f 2
(xn ,
yn )
f
(xn1, yn1)]
是二阶的,并求出局部截断误差的主项.
证:局部截断误差为
Tn1
y(xn1)
y(xn )
西安电子科技大学数值分析
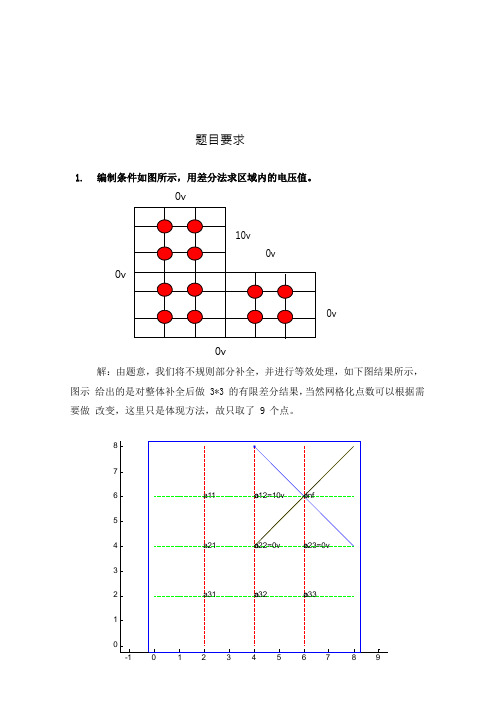
题目要求1. 编制条件如图所示,用差分法求区域内的电压值。
0v10v0v0v0v0v解:由题意,我们将不规则部分补全,并进行等效处理,如下图结果所示,图示给出的是对整体补全后做3*3 的有限差分结果,当然网格化点数可以根据需要做改变,这里只是体现方法,故只取了 9 个点。
876 a11o a12=10v o-inf54 a21o a22=0v o a23=0v32 a31o a32o a331-1 0 1 2 3 4 5 6 7 8 9根据拉普拉斯 5 点差分原理,可知得到关于电压变量 a(i, j 1, 2, 3) 的i , j方程如下:4a 1,1 a 2,110;a 1,1 4a 2,1 a 3,1 0; a 2,1 4a 3,1 a 3,2 0; a 3,1 4a 3,2 a 3,3 0; a 3,2 4a 3,30.4 1 0 0 0 10 1 4 1 00 0 写成矩阵的形式: Ax b ; 其中, A 0 1 4 10 , b 0 。
0 0 1 41 0编写程序可以求得0 01 4a , a , a , a , a , 2.6790.7180.1920.0513 0.0132. 在区域一边有个源,边界为 PML 边界,用 FDTD 法求所研究区域的场分布。
建模说明:二维 TE 波在空间传播,采用 PML 边界吸收,点辐射源验证。
FDTD 基本差分方程Yee 采用矩形网格进行空间离散,将每个节点进行编号,节点的编号和其空 间坐标位置按照下面的方式对应起来()(),,,,i j k i x j y k z =∆∆∆ (2-1) 而该点的任意函数()x,y,z,F t 在时刻n t ∆的值可以表示为:()(),,,,,n F i j k F i x j y k z n t =∆∆∆∆ (2-2)式中x ∆、y ∆、z ∆分别为沿,,x y z 方向上离散的空间步长,t ∆是时间步长。
西安电子科技大学数值分析往年题1

,,}n e 是Hilbert ,}n e ,则对于 .1x xe =-,则求f .21012A a ⎡⎤⎢⎥=⎢⎥,当cholesky 分解LL ()'⎰baf x ()'⎰baf x 问它们是否构成内积?说明理由分)设()f x C ∈使得求积公式 2(2)Cf +⎰答 案一. 填空题1、① 5 ② 5 ③6.62、④ 13、⑥1(,)niii x e e =∑4、⑦11kx k k k kx e x x x -+-=-+5、⑧||a 或a <<或(a ∈ 6、⑨ 07、⑩ 02ω<<二. 答:1.不构成内积,举反例说明.2.按定义(,)f g 构成内积验证:(1)正定性 22(,)()()0baf f f x dx f a '=+≥⎰而()0()(,)0()0()0f x f x cf f f x f a '=⇒=⎧=⇔⇒=⎨=⎩ (2)共轭对称性 由于(,)()()()()baf g f x g x dx f a g a ''=+⎰而(,)()()()()b ag f g x f x dx g a f a ''=+⎰()()()()bag x f x dx g a f a ''=+⎰()()()()b af xg x dx f a g a ''=+⎰所以 (,)(,)f g g f =.(3)第一变元线性性()()121212(,)()()baf fg ff g dx f f a g a αβαβαβ''+=+++⎰()1212()()()()baf g f g dx f a g a f a g a αβαβ''''=+++⎰12(,)(,)f g f g αβ=+综上,按定义(,)f g 构成内积.三. 解:设求积公式至少满足二次代数精度,则有方程组20220232220;012;012;x dx A B C x dx A B C x dx A B C ⎧=++⎪⎪=⨯+⨯+⨯⎨⎪⎪=⨯+⨯+⨯⎩⎰⎰⎰求此方程组得 04323A B C ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩则求积公式为242()(1)(2);33xf x dx f f ≈+⎰当3()f x x =时,522053≠,所以该求积公式是二次代数精度的。
电子科技大学数值分析研究生期末考试

、已知方程 exp x gsin x 1
1、确定方程全部正根的隔根区间。
2、设最小正根为x *,取猜测值X o ,写出x *的牛顿迭代法计算格式。
1 1 1
2 3
1 1 1
2 3
1、求雅可比迭代矩阵h (I 1)1A 的范数G。
2、写出高斯-赛德尔迭代矩阵。
3、判定是否有R f''(x *)
2f'(x *
) 1求成立,并解释其意义。
的LU 分解,并求出用“込范数”计算矩阵 U 的条件数
1
Cond(U)。
四、给点数表
用最小二乘法确定线性拟合函数 x C 0 C 1x
五、根据等距结点:为1,X j ,X j 1 (满足X j 1 X j X j X j 1 h ),写出二次拉格朗日插值
三、求A 1
基函数:I j 1 X ,I j X ,I j ! x 。
求:
f k x xI k' x ' ,(k j 1,j,j 1) 在x X j处的值
六、将积分上限函数
x
y x exp x t exp t dt转换为一阶常微分方程初值冋题,取
1
h ,记x jh
n
j 0,1,2,..., n,写出用Euler方法计算y 1的计算公式。
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
(完整word)西安电子科技大学电磁场期末试卷()
ee 《电磁场理论》期末考试题(120分钟 )一、 概念题。
(5⨯8=40分)1 写出电介质中静电场基本方程的微分形式和积分形式;2 写出磁感应强度B和磁矢位A 的关系式,并写出有源及无源空间磁矢位A 满足的方程; 3 写出时变电磁场的边界条件的矢量形式;4 写出麦克斯韦方程组和电流连续性方程的瞬时值微分形式;5 写出正弦电磁场的复坡印亭矢量S和复坡印亭定理;6 写出电磁波极化的定义以及平面电磁波的极化形式;7 对于非磁性介质,写出斜入射的均匀平面波产生全反射的条件; 对于非磁性介质,斜入射的均匀平面波产生全反射的条件是:8 计算长度λ10.=dl 的电基本振子的辐射电阻以及电流振幅值为mA 2时的辐射功率。
二、 一个半径为a 的均匀带电圆盘,电荷面密度为s ρ,求轴线上任意一点的电位.(10分)第二题用图三、内、外半径分别为a 、b 的无限长空心圆柱中均匀分布着轴向电流I ,求柱内外的磁感应强度。
(10 分)ab=l第三题用图四、一个截面如图所示的长槽,向y 方向无限延伸,两侧边的电位为零,槽内∞→y ,0=ϕ,底部电位为00U x =),(ϕ,求槽内电位。
(12分)=ϕ第四题用图五、从麦克斯韦方程组出发,推导各向同性、均匀、无耗介质中,无源区正弦电磁场的波动方程。
六.已知均匀平面电磁波的电场强度为)cos(ˆ)sin(ˆkz t E a kz t E aE y x i -+-=ωω00,将其作为入射波由空气向理想介质平面(0=z )垂直入射,坐标系如图(a )所示,介质的电磁参数为02029μμεε==,,计算:1、反射电磁波电场强度r E 和透射电磁波电场强度t E的复数值表达式;2、反射电磁波磁场强度r H 和透射电磁波磁场强度t H 的瞬时值表达式),(t z H r 和),(t z H t;3、判断入射电磁波、反射电磁波和透射电磁波是何种极化波;4、计算反射功率的时间平均值r av S , 和透射功率的时间平均值t av S ,;5、如果在理想介质分界面处加入厚度为d 的电磁介质如图(b )所示,试求交界面(0=z )无反射时,插入介质层的厚度d 以及相对介电常数r ε。
电子科大数值分析期末试卷及评分细则2

一、填空题:(30分,每空3分)1. 迭代公式11,01n n n p p λλ-=<<,设01p =,若0p 有误差,按照迭代公式生成的数列误差随着n的增大而_____增大2. 线性方程组Ax b =,其中410141014A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,565b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,如果采用Jacobi 迭代法解该线性方程组,其迭代矩阵为00.2500.2500.2500.250-⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦3.一个问题是否病态与 问题本身 有关4.当1,3,4x =时,()3,6,2f x =,则()f x 的二次拉格朗日插值多项式2()L x =21153246x x -+- 5. 矩阵123635301⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦的1l 范数等于 10 6. 三次样条插值具有 2 阶光滑性7. 如果插值求积公式()()1n b k k a k f x dx A f x =≈∑⎰为高斯公式,那么其求积公式具有 2n+1 次代数精度。
8. 线性方程组Ax b =中,1203A ⎡⎤=⎢⎥-⎣⎦,则()A ρ= 3 9. 对于插值型积分公式,其积分节点越多,积分精度 不确定 。
(越高,越低,不确定)10.对于微分方程初值问题()2,01y xy y '=-=,取步长0.1h =,则其显式Euler 方法的计算公式为()10.201n n n n y y x y y +=-⎧⎨=⎩二、判断题:错误用“×”、正确用“√”示意(10分,每小题2分)1. 解线性方程组Ax b =的迭代法收敛的充分必要条件为()1A ρ< ( × )2. 如果线性方程组Ax b =中矩阵A 为严格对角占优矩阵,那么对于任意迭代格式都是收敛的。
( × )3. 只要插值节点是互异的,则一定存在唯一的插值多项式满足插值条件。
( √ )4. 曲线拟合比三次样条插值好的一个原因是曲线拟合的计算量小。
西安电子科技大学-研究生-电磁场数值分析期末考试题

西安电子科技大学何超电磁场数值分析考点1: 矩量法的一般过程(算子方程、离散化过程、选配过程、矩阵方程求解)。
给定算子方程和基函数,采用伽略金法,计算阻抗矩阵和激励电压矩阵,从而求得电流系数矩阵,即得到方程的近似解. (矩阵维数一般为2×2,或3×3,便于计算)。
1http://wenku.baidu。
com/link?url=oRwkn_6gajdEKC3YUFvvipOKLuZJXnVk43odUwyDWYRaonT1SlZLKEq9PCQba5xPYg _7mXpK8pZW0R—_RfT5EOXLvj0BKqKmQ6cfXMuW8P7有3个矩量法例题考点2:ScaLAPACK 的矩阵分布方式.给定进程网格,矩阵分块大小,要求能写出按ScaLAPACK矩阵分布方式,每个进程对应的矩阵元素。
?1 并行矩阵填充在PC集群系统中MPI并行矩量法研究36 37考点3:temporary block column 对active block column 分解产生的影响.对于当前活动列块(即正在进行LU分解的列块),要能够分析其左侧临时列块对其LU分解所产生的影响。
?英文书写得很详细了啊45-—55有lu分解将系数矩阵A转变成等价两个矩阵L和U的乘积,其中L和U分别是下三角和上三角矩阵。
当A 的所有顺序主子式都不为0时,矩阵A可以分解为A=LU,且当L的对角元全为1时分解唯一.其中L是下三角矩阵,U是上三角矩阵。
4阶矩阵的LU分解[1]高斯消元法见数值分析教材考点4:积分方程的建立要求掌握EFIE 、MFIF 、PMCHW(电场、磁场、表面积分方程)根据等效原理建立的过程,即对于给定的问题(PEC (理想导体)或介质)能根据等效原理建立积分方程(不要求写出场的位函数表达式,主要考察方程建立的思想).看矩量法的书那个英文书只有EFIE等效原理EFIE考点 5:RWG 基函数考察 RWG 基函数的 表达式,以及其 特点,对于给定的一个三角形网格图要能够标出哪些地方( 公共边上) 存在基函数。
《电磁场与电磁波》西安科技大学期末考试试题

西安科技大学《电磁场与电磁波》期末考试试题A 卷一:(16分)简答以下各题:1. 写出均匀、理想介质中,积分形式的无源(电流源、电荷源)麦克斯韦方程组;(4分)d d d d d 0d 0l S l S S S t t ∂⎧⋅=⋅⎪∂⎪∂⎪⋅=-⋅⎪∂⎨⎪⋅=⎪⎪⋅=⎪⎩⎰⎰⎰⎰⎰⎰D H l S B E l S D S B S2. 假设两种理想介质间带有面密度为S ρ的自由电荷,写出这两种介质间矢量形式的交变电磁场边界条件;(4分)()()()()12121212000S ρ⋅-=⎧⎪⋅-=⎪⎨⨯-=⎪⎪⨯-=⎩n D D n B B n E E n H H3. 矩形金属波导中采用TE 10模(波)作为传输模式有什么好处(3点即可);(4分)4. 均匀平面波从媒质1(ε1,μ1=μ0,σ1=0)垂直入射到与媒质2(ε2,μ2=μ0,σ2=0)的边界上。
当ε1与ε2的大小关系如何时,边界上的电场振幅大于入射波电场振幅?当ε1与ε2的大小关系如何时,边界上的电场振幅小于入射波电场振幅?(4分)答:(1)电场在边界上振幅与入射波振幅之比是1+R,所以问题的关键是判的R 的正负.第一问答案ε1 < ε2 ,第二问答案 ε1〉 ε2二、(16分)自由空间中平面波的电场为:()120e j t kx z ω+=πE e ,试求:1。
与之对应的H ;(5分)2。
相应的坡印廷矢量瞬时值;(5分)3. 若电场存在于某一均匀的漏电介质中,其参量为(0ε, 0μ,σ),且在频率为9kHz 时其激发的传导电流与位移电流幅度相等,试求电导率σ。
(6分)解:1.容易看出是均匀平面波,因此有()()()j j 01120e e 120t kx t kx x x z y ωωπηπ++⎛⎫-=⨯=-⨯⋅= ⎪⎝⎭e H E e e e (A/m)或者直接利用麦克斯韦方程也可以求解:()j 0e j t kx y ωωμ+∇⨯==-E H e 2.若对复数形式取实部得到瞬时值,则()120cos z t kx =πω+E e ,()cos y t kx =ω+H e ,()()()2120cos cos 120cos z y x t kx t kx t kx πωωπω⎡⎤=⨯=+⨯+=-+⎡⎤⎣⎦⎣⎦S E H e e e (W/m 2)。
电子科技大学研究生数值分析期末试卷

电子科技大学研究生数值分析期末试卷一、(15分)(1)牛顿迭代法的主要思想是什么?如何将其推广到二维问题的求解? (2)求证:迭代公式x k+1=x k (x k 2+3a 2)3x k2+a 2,a>0,是计算a 的三阶方法。
二、(15分)已知实验数据如下:(1) 求二次拟合函数y (x )=ax 2+bx +c 。
(2) 请简单叙述插值、拟合、函数逼近三者之间的区别与联系。
三、(15分)(1)拉格朗日插值与牛顿插值有何异同? (2)已知函数f(0)=1,f(1)=3,f(2)=9,f(3)=25,求3次插值多项式P 3(x),并计算P 3(0.5)。
四、(10分)用列主元高斯消元法求解下面的线性方程组:{x 1− x 2 + x 3=−45x 1−4x 2+3x 3=−122x 1+ x 2 + x 3=11五、(15分)给定求积公式∫f (x )dx 10=Af (0)+Bf (0.5)+Cf ′(0),试确定A 、B 、C ,使其代数精度尽可能的高,并指明此时求积公式的代数精度。
六、(15分)给定方程组{x 1+ 2x 2−2x 3 =5x 1+ x 2+ x 3 =12x 1+ 2x 2 + x 3=3(1) 用LU 分解法求此方程组;(2) 写出解此方程组的雅克比迭代公式,说明收敛性;并取初始向量x 0=(0,0,0)T ,求其满足‖x k+1−x k ‖<10−1的近似解。
七、(15分)设微分方程{y′′′=6y 2y′y (0)=1,y ′(0)=−1,y ′′(0)=2(1) 把该微分方程写为一阶常微分方程的初值问题; (2) 写出用二阶R-K 法:K 1=f(x n ,y n ),K 2=f(x n +ℎ,y n +ℎK 1),y n+1=y n +ℎ2(K 1+K 2)求解的迭代公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安电子科技大学何超
电磁场数值分析
考点1:矩量法的一般过程(算子方程、离散化过程、选配过程、矩阵方程求解)。
给定算子方程和基函数,采用伽略金法,计算阻抗矩阵和激励电压矩阵,从
而求得电流系数矩阵,即得到方程的近似解。
(矩阵维数一般为2×2,或3×3,
便于计算)。
1
/link?url=oRwkn_6gajdEKC3YUFvvipOKLuZJXnVk43odUwyDWYRao nT1SlZLKEq9PCQba5xPYg_7mXpK8pZW0R-_RfT5EOXLvj0BKqKmQ6cfXMuW8P7
有3个矩量法例题
考点2:ScaLAPACK 的矩阵分布方式。
给定进程网格,矩阵分块大小,要求能写出按ScaLAPACK矩阵分布方式,每个进程对应的矩阵元素。
?
1 并行矩阵填充在PC集群系统中MPI并行矩量法研究36 37
考点3:temporary block column 对active block column 分解产生的影响.对于当前活动列块(即正在进行LU分解的列块),要能够分析其左侧临时列块对其LU分解所产生的影响。
?英文书写得很详细了啊45--55有
lu分解
将系数矩阵A转变成等价两个矩阵L和U的乘积,其中L和U分别是下三角和上三角矩阵。
当A 的所有顺序主子式都不为0时,矩阵A可以分解为A=LU,且当L的对角元全为1时分解唯一。
其中L是下三角矩阵,U是上三角矩阵。
4阶矩阵的LU分解[1]
高斯消元法见数值分析教材
考点4:积分方程的建立
要求掌握EFIE 、MFIF 、PMCHW(电场、磁场、表面积分方程)根据等效原理建立的过程,即对于给定的问题(PEC (理想导体)或介质)能根据等效原理建立积分方程(不要求写出场的位函数表达式,主要考察方程建立的思想)。
看矩量法
的书那个英文书只有EFIE 等效原理
EFIE
考点 5:RWG 基函数
考察 RWG 基函数的 表达式,以及其 特点,对于给定的一个三角形网格图要能够标出哪些地方( 公共边上) 存在基函数。
书上都有啊
RWG 基函数用共边的三角形对作为基本的面元形式,如图2所示,第n 条边对应的电流基函数表示为
)
6(022⎪⎪⎩
⎪⎪⎨⎧∈∈=-
-++
-+otherwise T r T r f n
n A l n
n A l n n
n n
n
ρρ
考点6:解矩阵方程的迭代方法-CG 迭代方法
要求掌握RCG 和RPCG 的计算流程,二者中考一个。
书上有啊只有RCG
考点7:并行性能评测
Wall clock time 、并行加速比、并行效率、可扩展性。
其中Wall clock time
由哪几部分时间组成。
时钟时间(墙上时钟时间wall clock time):从进程从开始运行到结束,时钟走过的时间,这其中包含了进程在阻塞和等待状态的时间。
进程的三种状态为阻塞、就绪、运行。
Wall clock time由哪几部分时间组成? 时钟时间=阻塞时间+就绪时间+运行时间
用户CPU时间=就是用户的进程获得了CPU资源以后,在用户态执行的时间。
系统CPU时间= 用户进程获得了CPU资源以后,在内核态的执行时间。
用户CPU时间+系统CPU时间=运行时间。
并行算法的评价方法 .
1.加速比(speedup),是同一个任务在单处理器系统和并行处理器系统中运行消耗的时间的比率,
Sp=T1/Tp
Sp是加速比,T1是单处理器下的运行时间,Tp是在有P个处理器并行系统中的运行时间。
该评测指标,如果能够随着P保持一个线性的增长,则表示,多台机器能够很好的缩短所需时间
2.并行效率也是评价并行性能的重要指标之一,它其实是“每个进程”的加速比:
线性加速比相当于并行效率p/p=1.0,通常,效率都小于1。
3.scaleup可扩展性
评测scaleup的方法是,在扩大数据的同时,增加计算机的数目。
scaleup计算方法如下:
scaleup(DB,m)=使用1台电脑在DB上运行算法使用的时间/使用m台电脑在m*DB上运行算法使用的时间。
如果scaleup值随着m的改变,一直在1.0附近,或者更低,则表示该算法,对数据集的大小有很好的适应性。
考点8:并行矩量法的调优方法
调优参数:Block size 、process grid 、in-core buffer(核外而言)。
要掌握一些基本的结论。
197--199 170--176
出了矩量法基本原理
和积分方程那一块可能没有就说这些参数怎么影响性能的
1 对于Intel CPU,当问题规模增加时,Block size为104表现优于Block size为112.
2 The matrix solving time decreases to approximately 70% of the original time after the process grid is changed from 1*64 to 8*8.
Using more CPU cores does not guarantee faster simulation unless the code is executed with a properly designed process grid.
The choice of 2*32 process grid is better than the choice of the 4*16 process grid.
The choice of the optimum process grid changes with the hardware configuration.
Properly choosing the number of cores and the shape of the process grid is the key to attaining the best performance.
3
但是积分方程应该就考简单的EFIF
Block size 是ScaLAPACK 矩阵循环分布时矩阵分块的大小
process grid过程网格
in-core buffer 内核的缓冲区
评价算法优劣的标准是?
①时间复杂度:同样的输入规模(问题规模)花费多少时间
②空间复杂度:同样的输入规模花费多少空间(主要是内存)
以上两点越小越好
③稳定性:不会因为输入的不同而导致不稳定的情况发生
④算法思路是否简单:越简单越容易实现越好
程序优化方法
1 程序尽量采用多线程机制,利用平行处理的观念,
2充分利用CPU时间片;尽量减少数据的搬移操作。
3优化耗时比较大的环节
4使用软件流水技术
5尽量少进行函数调用
6尽量使用逻辑运算代替乘除运算
7 增加CACHE高速缓存的使用
电场积分方程是对于金属问题根据电场满足的边界条件建立的方程
MPI 消息传递互动
进程一段程序的执行过程
RCS 雷达散射截面
介绍计算电磁学中的几种典型算法。
