若当标准形介绍
若当标准型求解

• 方法步骤:
由特征值i 对应的线性无关的特征向量的个数确定 J(i) 中 Jordan 块的个数 由特征值i 的代数重数确定主对角线元素是的 i 的 Jordan 矩阵J(i ) 的阶数。 由特征向量求得的Jordan 链条的长度确定Jordan块的阶数 链条中的向量合起来构成可逆矩阵P,Jordan块构成JA
另外,注意的选择。观察上面的公式可以发现
R(( A i I )nj1) N ( A iI )
2 1
例 A
20 2 2
,求可逆矩阵P使得A相似
2 3
2
于Jordan 标准型。
解:可计算A的包含阶数为2和3的两个Jordan块。可计算得:
0 1
00
A2I
0 2
0 3
0
2. 矩阵的化简
方阵A的Jordan 标准形变换矩阵P的求法
• 目标:求可逆矩阵P和Jordan矩阵JA ,使AP=PJA • 求法与步骤:根据前面的计算求出初等因子组
f ( ) I A ( 1 )k1 ( 2 )k2 ( s )ks
矩阵A和JA的特征值相等
APi Pi Ji( i )
先求二阶Jordan对应的特征向量和广义特征向量。显然取
p1 R(( A 2 I )) N ( A 2 I ), p1 (a,0,b,0,0)T , a 0或b 0
这时
p2 (x, a, z, b / 2, 0)T (x, 0, z, 0, 0)T (0, a, 0, b / 2, 0)T
2
1
g( A ) P 15 23 P1
15
关于Jordan标准形的计算
由于计算涉及的内容偏多,有兴趣或需要的可以 参见教材。另外很多定理的证明可参见北京大学 出版社出版的<<高等代数>>教材的相关内容即可。
复矩阵若当标准形的性质与应用

莆田学院数学与应用数学系“高等代数选讲”课程论文题目:复矩阵若当标准形的性质与应用姓名:廉换霞学号:410401143莆田学院数学与应用数学系数学与应用数学专业2004级2007年6 月 25 日复矩阵若当标准形的性质与应用数本041 廉换霞 410401143摘要:若当标准形有广泛的应用。
本文首先给出了若当形矩阵的定义和若当标准形的一些性质及相关例题。
然后讲到其应用。
若当标准形在“矩阵分解论”、“矩阵方程论”,在解线性递推关系式等等中都有它的应用,我们通过一些例题来说明。
最后,利用若当标准形的性质给出了哈密尔顿——凯莱定理的另一种证法。
关键词:若当形矩阵 若当标准形 初等因子 可逆阵 哈密尔顿——凯莱定理一、 定义及性质1、若当形矩阵的定义 形式为1(,)1t tJ t λλλλ⨯⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 的矩阵称为若当块,其中λ是复数。
由若干个若当块组成的准对角矩阵称为若当形矩阵。
特别地一级若当块就是一级矩阵,因此若当形矩阵包括对角矩阵。
2、若当标准形的性质性质一 若当形矩阵除去其中若当块排列次序外,被它的初等因子惟一决定。
此性质可用于求矩阵的若当标准形。
例1 求矩阵126103114A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭的若当标准形解:首先求E A λ-的初等因子2221260132100130110111141140132100100011010002100(1)E A λλλλλλλλλλλλλλλλλλλλλ⎛⎫+--+-+-⎛⎫⎛⎫⎪ ⎪ ⎪-=-→--+→--+ ⎪ ⎪ ⎪⎪ ⎪ ⎪---+-+-⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪→--+→- ⎪ ⎪ ⎪ ⎪-+--⎝⎭⎝⎭因此,A 的初等因子是1λ-,2(1)λ-,A 的若当标准形是100010011J ⎛⎫ ⎪= ⎪ ⎪⎝⎭性质二 一个若当形矩阵的全部初等因子就是它的全部若当块的初等因子的汇集。
例2、设复准对角12S A A A A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭其中i A 是i n 阶方阵,1,2,,i s = 。
高等代数 第9章矩阵的标准型 9.6 若当标准型

T
再由第三个方程解出一个特解为
,那么所求相似变换矩阵为
0 4 1 P X 1, X 2 , X 3 1 3 0 0 2 0
例 2 求方阵
1 2 6 A 1 0 3 1 1 4
J 0 3 1 0 0 3
或
3 1 0 J 0 3 0 0 0 1
例 2 用矩阵秩的方法求出矩阵
1 0 A 0 0
的Jordan标准形。
2 1 0 0
3 2 1 0
4 3 2 1
解:首先求出其特征值,显然其特征多项式为
矩阵的Jordan标准形 定义: 称 n 阶矩阵
ai Ji
1 ai
1 1 ai ni ni
为Jordan块。设 J1, J 2 ,, J s 为Jordan块, 称准对角形矩阵
J1 J
J2
Js
X 3 2, 0, 1
T
T
再由第三个方程解出一个特解为
,那么所求相似变换矩阵为
1 2 2 P X 1, X 2 , X 3 1 1 0 0 1 1
从而有
1 0 0 1 P AP 0 1 1 0 0 1
故 A 的Jordan标准形为
0 0 0 J 0 0 0 0 0 2
或
0 0 0 J 0 2 0 0 0 0
求Jordan标准形的另一种方法:特征矩阵秩 的方法. 具体操作步骤: (1)先求出该矩阵的特征多项式及其特征 值 A (2)其Jordan标准形的主对角线上都是 i 在主对角线上出 的特征值,并且特征值 现的次数等于 i 作为特征根的重数。对于每 i ,求出以它为主对角元的各级 个特征值 Jordan 块的数目N (i ) ,首先求出
若当(JORDAN)标准形

8.6 若当标准形的理论推导
编辑ppt
19
A 的若当标准形为
1 0
1 1
10
11
10
11
1
1
i
1i
i 1
i
8.6 若当标准形的理论推导
编辑ppt
20
练习: 求矩阵A的若当标准形
1 1 1
A
3 2
3 2
3 2
1 0 0
答案: E A0 0 0 0 2
( 1 ) k 1 ,( 2 ) k 2 , ,( s ) k s .
8.6 若当标准形的理论推导
编辑ppt
8
可见,每个若当形矩阵的全部初等因子就是它 的全部若当块的初等因子构成的. 由于每个若当块 完全被它的级数与主对角线上的元素 0 所刻划,
而这两个数都反应在它的初等因子 ( 上0).n
第八章 λ─矩阵
§1 λ-矩阵 §2 λ-矩阵的
标准形
§3 不变因子
§4 矩阵相似的条件 §5 初等因子
§6 若当(Jordan)标准形 的理论推导
小结与习题
编辑ppt
1
§8.6 若当标准形的理论推导
一、若当块的初等因子 二、若当形矩阵的初等因子 三、若当标准形存在定理
8.6 若当标准形的理论推导
0 0
0 0
0 2
.
8.6 若当标准形的理论推导
编辑ppt
18
例2、已知12级矩阵A的不变因子为
1 , 1 ,, 1 ,( 1 ) 2 ,( 1 ) 2 1 , 1 2 1 (2 1 ) 2
9 个
求A的若当标准形.
解:依题意,A的初等因子为
高等代数_若当标准形
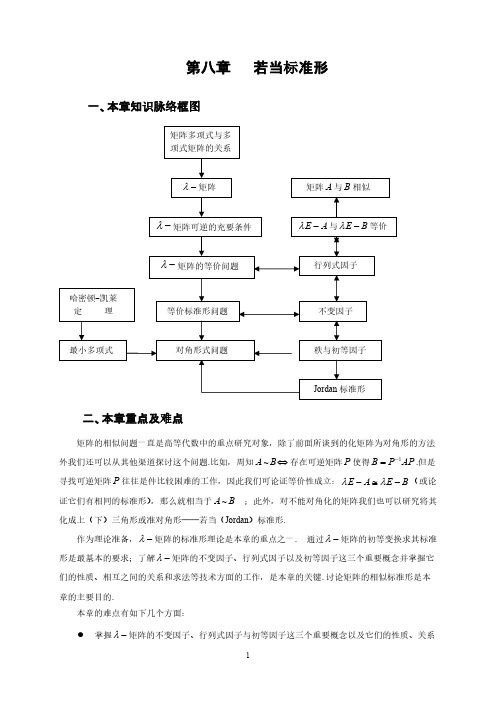
第八章 若当标准形一、本章知识脉络框图二、本章重点及难点矩阵的相似问题一直是高等代数中的重点研究对象,除了前面所谈到的化矩阵为对角形的方法外我们还可以从其他渠道探讨这个问题.比如,周知~存在可逆矩阵使得.但是A ⇔B P 1B P AP -=寻找可逆矩阵往往是件比较困难的工作,因此我们可论证等价性成立:(或论P E A E B λλ-≅-证它们有相同的标准形),那么就相当于~ ;此外,对不能对角化的矩阵我们也可以研究将其A B 化成上(下)三角形或准对角形──若当(Jordan )标准形.作为理论准备,矩阵的标准形理论是本章的重点之一. 通过矩阵的初等变换求其标准-λ-λ形是最基本的要求;了解矩阵的不变因子、行列式因子以及初等因子这三个重要概念并掌握它-λ们的性质、相互之间的关系和求法等技术方面的工作,是本章的关键.讨论矩阵的相似标准形是本章的主要目的. 本章的难点有如下几个方面:掌握矩阵的不变因子、行列式因子与初等因子这三个重要概念以及它们的性质、关系-λ和求法;●理解并掌握两个数字矩阵与相似的充分必要条件,以及数字矩阵与对角矩阵相似A B A 的充分必要条件;●充分发挥最小多项式的性质在讨论矩阵的相似标准形中的作用;●掌握矩阵的Jordan 标准形的求法、性质及其应用.三、本章的基本知识要点 (一)矩阵的概念和性质λ-1.设是一个数域,是一个文字,如果矩阵的每个元素都是的多项式,即 F λn m ⨯()A λλ=,那么,就是一个关于的多项式矩阵,简称为矩阵.如果 ,()A λ(())ij m n a λ⨯()A λλ-λn m =则称为阶矩阵.()A λn -λ2. 如果在矩阵中,有一个阶子式不为零,一切阶子式(如果存在)全-λ()A λ(1)r r ≥1r +为零,则称的秩为,记为.()A λr (())r A r λ=注意:① ;(())0r A λ=⇔()0A λ=② 若是一个数字阶矩阵,则必有.A n ()r E A n λ-=3. 设是阶矩阵,若存在阶矩阵使得()A λn -λn -λ()B λ ()()()()A B B A E λλλλ==则称是可逆的,并称是的逆矩阵,记为.()A λ()B λ()A λ1()()B A λλ-=4.注意:(1)一个阶矩阵是可逆的充要条件为行列式:.n -λ()A λ()0A c λ=≠(2)若是可逆时,则有,其中是伴随矩阵.()A λ)(|)(|1)(*1λλλA A A =-()A λ*()A λ(3)在数字矩阵中,阶矩阵是可逆的充分必要条件是行列式(即是满秩矩阵),但n A ||0A ≠A 对于矩阵来说,当矩阵的行列式时,矩阵未必是可逆的,即满秩的矩阵未-λ|()|0A λ≠()A λ-λ必是可逆的. (二)初等矩阵λ-1、由阶单位矩阵经过一次矩阵的初等变换得到的阶矩阵称为初等矩阵.其n E -λn -λ-λ有三种不同的类型,分别是、与,而且都是可逆矩阵,且逆矩阵仍是(,)P i j (())P i k (,(()))P i j ϕλ同类的初等矩阵.-λ2、对的矩阵进行一次初等行变换,相当于在的左边乘上相应的阶初等m n ⨯()A λ()A λm 矩阵;而对进行一次初等列变换,就相当于在的右边乘上相应的阶初等矩阵.-λ()A λ()A λn -λ3.矩阵可逆的充分必要条件是可表成一系列初等矩阵的乘积. -λ()A λ()A λ-λ4.注意:(1) 由于在矩阵的第二类型的初等变换中,不允许用一个非常数的多项式去乘或除矩-λ()ϕλ阵的某一行(列),这导致了矩阵的初等变换与数字矩阵的初等变换在性质上有些区别,这请读λ-者充分注意.(2) 等价的矩阵具有相同的秩、行列式因子、不变因子和初等因子.-λ(三)矩阵的标准形λ-1.矩阵不变因子λ-设的矩阵的秩为,那么可经过一系列的初等变换化成对角矩阵m n ⨯-λ()A λr ()A λ, ()11()()(),,(),0,,000r r d d diag d d λλλλ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ()*即存在阶可逆矩阵和阶可逆矩阵,使m ()P λn ()Q λ,()()()P A Q λλλ=()1(),,(),0,,0r diag d d λλ= 其中是首一多项式,且()i d λ(1,2,,)i r = .1()(),(1,2,,1)j j d d j r λλ+=- 并称※式为矩阵的标准形.其中称为的不变因子.-λ()A λ12(),(),,()r d d d λλλ ()A λ注意:若是一个阶数字矩阵,则的特征多项式必有A n A (1);12()()()()A n f E A d d d λλλλλ=-= (2)所有不变因子的次数之和.1(())n i i d n λ=∂==∑2、矩阵的行列式因子λ-(1)设的矩阵的秩为,那么对于正整数的全部阶子式m n ⨯-λ()A λr ,1,k k r ≤≤()A λk 的首项系数为1的最大公因式,称为的阶行列式因子,记为.()A λk ()k D λ(2)不变因子与行列式因子之间的关系是:12(),(),,()r d d d λλλ 12(),(),,()r D D D λλλ ,,……, (I )11()()D d λλ=212()()()D d d λλλ=12()()()()r r D d d d λλλλ= (3)两个矩阵等价的充分必要条件是它们具有相同的不变因子或相同的各阶行列式因子.-λ(4)阶可逆矩阵的各阶行列式因子是,进一步,n -λ()A λ12()()()1n D D D λλλ====的不变因子是()A λ,12()()()1n d d d λλλ==== 从而知道矩阵的标准形是单位矩阵.即可逆的矩阵的标准形是单位矩阵,反过来,如果()A λE -λ矩阵与单位矩阵等价,那么一定是一个可逆矩阵.-λ()A λ()A λ3. 矩阵的初等因子与阶数字矩阵的初等因子λ-n (1)把矩阵的每个次数大于零的不变因子分解成互不相同的一次因式的方幂的乘积,-λ()A λ所有这些一次因式的方幂(相同的必须按出现的次数计算),称为的初等因子.()A λ特别地,如果为阶数字矩阵,的特征矩阵的初等因子习惯上称为的初等因子.A n A E A λ-A (2)设为阶数字矩阵,若特征矩阵等价于下列的对角形矩阵(不一定是标准形)A n E A λ-,1()()()n h B h λλλ⎛⎫ ⎪= ⎪ ⎪⎝⎭ 其中都是首一多项式. 那么将分解成互不相同的一次因式的方幂(相同的必须按出现的()i h λ()i h λ次数计算)就是的全部初等因子.A 4. 不变因子、行列式因子与初等因子之间的关系矩阵的不变因子、行列式因子与初等因子之间存在有密切关系,它们之间可以互相-λ()A λ导出.(1)如果已知不变因子,直接使用定义可得到初等因子,利用上面的12(),(),,()r d d d λλλ 关系式(I )可导出行列式因子.12(),(),,()r D D D λλλ (2)如果已知行列式因子,同样可以利用关系式(I )导出不变因子12(),(),,()r D D D λλλ ,从而得出初等因子.12(),(),,()r d d d λλλ (3)如果已知矩阵的秩及其初等因子,这时可以将全部初等因子按不可约因子的方幂()A λr 降幂排列,同一个不可约因子的方幂排成一行.如果不可约因子的方幂的个数不足个,则在后面r 用1补足,这时全体不可约因子的方幂排成下列的形式:11121212221211122212(),(),,(),(),(),,(),0(1,2,,)(),(),,(),r r s s sr t t t t t t i i ir t t t s s s P P P P P P t t t i s P P P λλλλλλλλλ≥≥≥≥= 那么,矩阵的不变因子是()A λ,12112()()()()sr r r t t t s d P P P λλλλ= ,11121212()()()()s r r r tt t s d P P P λλλλ---= ……………… 1112112()()()()s t t t r s d P P P λλλλ= 依此就可以得到矩阵的行列式因子.12(),(),,()r D D D λλλ 下图列出了矩阵及其标准形,不变因子,行列式因子以及秩与初等因子之间的关系.在计算过程中,读者可以根据具体情况采用适当的步骤进行.(四)矩阵的等价、数字方阵相似和对角化的条件λ-1.设与都是的矩阵,那么有下列等价条件:()A λ()B λm n ⨯-λ(1)与等价与有相同的标准形; ()A λ()B λ⇔()A λ()B λ(2)与等价与有相同的不变因子;()A λ()B λ⇔()A λ()B λ(3)与等价与有相同的行列式因子;()A λ()B λ⇔()A λ()B λ(4)与等价与有相同的秩和初等因子;()A λ()B λ⇔()A λ()B λ(5)与等价存在一系列初等矩阵和使得()A λ()B λ⇔-λ12,,,s P P P 12,,,t Q Q Q ;1212()()s t PP P A Q Q Q B λλ= (6)与等价存在可逆矩阵和使得.()A λ()B λ⇔-λ()P λ()Q λ()()()()P A Q B λλλλ=注意:两个阶数一样的矩阵仅是初等因子相同时,不能保证它们等价.例如矩阵-λ如的初等因子相同,但它们不等价.10()01A λλλ-=+⎛⎫ ⎪⎝⎭(1)(1)0()00B λλλ-+=⎛⎫ ⎪⎝⎭2.设都是阶数字矩阵,那么有下列关于矩阵相似的等价条件:,A B n (1)~与等价;A ⇔B E A λ-E B λ-(2)~与有相同的标准形;A ⇔B E A λ-E B λ-(3)~与有相同的不变因子;A ⇔B E A λ-E B λ-(4)~与有相同的行列式因子;A ⇔B E A λ-E B λ-(5)~与有相同的初等因子(或者与有相同的初等因子);A ⇔B E A λ-E B λ-A B (6)~与有相同的若当标准形.A ⇔B A B 3.设是阶数字复矩阵,那么有下列等价条件:A n (1)与对角矩阵相似的充分必要条件是的不变因子没有重根;A E A λ-(2)与对角矩阵相似的充分必要条件是的初等因子都是一次的;A A (3)与对角矩阵相似的充分必要条件是的最小多项式没有重根;A A (4)与对角矩阵相似的充分必要条件是每个特征根的代数重数等于几何重数.A A (五)数字矩阵的若当标准形与有理标准形 从前面所谈论的化矩阵为对角形矩阵可知,并不是所有的阶数字矩阵都能相似对角化,虽然n 如此,但对于实数域上的阶对称矩阵,即实对称矩阵是一定与一个实对角矩阵相似的.于R n A A 是,我们自然会提出这样一个有待解决的重要问题:当一个矩阵不与对角矩阵相似时,能否退而求其次,使相似于一个比对角矩阵稍为复杂,但仍能给计算和研究带来便利的某种标准形呢?这就A 是我们下面要介绍的矩阵的若当标准形与有理标准形.1.矩阵的若当标准形(1)设是一个复数,形式为0λ0000000001000(,)00100001t tJ t λλλλλ⨯⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ 的矩阵称为若当(Jordan )块. 而由若干个若当块组成的准对角矩阵(分块对角矩阵)(,)i i J t λ1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 称为若当形矩阵,其中参数可以是相等,也可以是不相等.12,,,s λλλ (2)由于若当块的特征矩阵的各阶行列式因子是0(,)J t λ0(,)E J t λλ-,1210()()()1,()()t t t D D D D λλλλλλ-=====- 因此,它的不变因子是.1210()()()1,()()t t t d d d d λλλλλλ-=====- 由此即得,的初等因子是,也就是若当块的初等因子.由于若当块0(,)E J t λλ-0()t λλ-0(,)J t λ完全被它的级数与主对角线上的元素所刻划,而这两个数都反映在它的初等因子0(,)J t λt 0λ中.因此,若当块是由它的初等因子唯一决定的.0()t λλ-(3)类似地,我们可以求得若当形矩阵1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 的初等因子是.1212(),(),,()s t t t s λλλλλλ--- 也就是说,每个若当形矩阵的全部初等因子是由它的全部若当块的初等因子构成的.而每个若当块是由其初等因子来决定的,由此可见,若当形矩阵除去其中的若当块排列的次序外,是被它的初等因子唯一决定的.(4)若当形矩阵的主要结论是:复数域上任一个阶矩阵都相似于一个若当形矩阵C n A ,1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 这个若当形矩阵称为的若当标准形.A (5)设是一个阶矩阵,是的若当标准形,那么A n J A ●存在可逆矩阵,使得;T 1T AT J -=●与有相同的秩与行列式;A J ●与有相同的特征多项式与最小多项式;A J ●特征矩阵与有相同的行列式因子;E A λ-E J λ-●与(或者与)有相同的不变因子与初等因子.E A λ-E J λ-A J (6)对于复数域上的维线性空间的任一个线性变换,在中必存在有一组基C n V σV ,使得在此基下的矩阵是一个若当形的.12,,,n ααα σ(7)每个阶的复数矩阵都与一个下(或上)三角形矩阵相似,其主对角线上的元素刚好n A 是矩阵的全部特征值. 即存在可逆矩阵,使A T (下三角形矩阵),110*n T AT λλ-⎛⎫ ⎪= ⎪ ⎪⎝⎭ 其中是矩阵的全部特征值.如果是一个多项式,则的全部特征值是1,,n λλ A ()g λ()g A,即1(),,()n g g λλ .11()0()*()n g T g A T g λλ-⎛⎫ ⎪= ⎪ ⎪⎝⎭ 2.矩阵的有理标准形在上面我们讨论了复数域上任何一个阶矩阵可相似于一个若当形矩阵,下面我们将在任意C n 一个数域上来讨论类似的问题,而且证明了上任意一个阶矩阵必相似于一个有理标准形矩F F n 阵.(1)对于数域上的一个多项式F ,12121(),1n n n n n f a a a a n λλλλλ---=+++++≥ 称矩阵122100001000010000100001n n n a a a A a a ---⎛⎫ ⎪- ⎪ ⎪-= ⎪ ⎪ ⎪- ⎪ ⎪-⎝⎭ 是多项式的伴侣阵.()f λ多项式的伴侣阵的不变因子(即是的不变因子)是()f λA E A λ-,.121()()()1n d d d λλλ-==== ()()n d f λλ=(2)设阶矩阵的不变因子是n A 121,,1,(),(),,()k k n d d d λλλ++ 其中的次数大于等于1,并且假设分别是的()k i d λ+12,,,n k N N N - 12(),(),,()k k n d d d λλλ++ 伴侣阵,这时我们称分块对角矩阵12n k N N F N -⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭是矩阵的有理标准形.A (3)数域上的任意一个阶矩阵必相似于它的有理标准形(因为它们具有相同的初等因F n A 子).注意:若当标准形在复数域上是一定存在的,而有理标准形在任何数域上都是存在的.(六)最小多项式及其性质 1.零化多项式与最小多项式设是一个数域,是上的阶数字矩阵,如果数域上的多项式使得,F A F n F ()f x ()0f A =则称以为根或为的零化多项式.()f x A ()f x A 在以为根的多项式中,次数最低且首一的多项式称为的最小多项式,记为.A A ()A m λ2、哈密顿─凯莱定理设是一个数域,是上的阶数字矩阵,记的特征多项式为F A F n A12121()n n n A n n f E A a a a a λλλλλλ---=-=+++++ 那么 12121()0n n n A n n f A A a A a A a A a E ---=+++++= 即的特征多项式是的零化多项式.同时,还有A A *12231211211()()()()n n n n n n E A A a A a a A a a E λλλλλλ-------=++++++++++ 3、最小多项式的性质设是数域上的阶数字矩阵,为的最小多项式.A F n ()A m λA (1)最小多项式是唯一的;(2)设,则的充分必要条件是;特别地,矩阵的最小()[]g F λλ∈()0g A =()()A m g λλA 多项式是的特征多项式的一个因式.()A m λA ()A f E A λλ=-(3)若是一个阶数字矩阵,且的特征多项式为A n A 12()()()()A n f E A d d d λλλλλ=-= 那么;()()A n m d λλ=1()()A n f D λλ-=(4)的特征根都是根.A ()A m λ(5)设都是阶数字矩阵,如果相似,即~;,AB n ,A B A ⇔B ()()A B m m λλ=(6)设是准对角形,且分别是的最小多项式,那么1s A A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭ ()i m λi A ;()A m λ12[(),(),,()]s m m m λλλ= (7)阶若当块t0000000001000(,)00100001t t J t λλλλλ⨯⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ 的最小多项式.0()()t J m λλλ=-(六)主要定理与结论定理1 假设都是阶数字矩阵,如果存在阶数字矩阵满足,A B n n 00,P Q 00()E A P E B Q λλ-=-则矩阵与相似.A B 作为矩阵多项式,矩阵也有下列的带余除法定理.-λ定理2 设是数域上的两个阶矩阵,其中(),()A B λλF n -λ1011(),(),0,1,,.m m m m i n B B B B B B M F i m λλλλ--=++++∈= 如果可逆,则存在矩阵及,满足0B -λ(),()L L Q R λλ(),()R R Q R λλ,,()()()()L L A B Q R λλλλ=+()()()()R R A Q B R λλλλ=+其中分别是零或者,且满足上述条件的(),()L R R R λλ(())(()),(())(())L R R B R B λλλλ∂<∂∂<∂及是唯一的.表示矩阵中所有元素的最高次数.(),()L L Q R λλ(),()R R Q R λλ(())A λ∂()A λ如果把定理2的矩阵分别改成数字矩阵的特征矩阵,那么定理2变成下列的()B λA E A λ-定理.定理3 对于任何不是零的阶数字矩阵,以及矩阵与,一定存在矩阵n A -λ()U λ()V λ-λ与以及数字矩阵与使得()Q λ()R λ0U 0V ,.0()()()U E A Q U λλλ=-+0()()()V R E A V λλλ=-+定理3的一个常用推论是下面的定理4 设,则存在唯一的矩阵使得()[],()n f F A M F λλ∈∈-λ()Q λ.()()()()()()()f E E A Q f A Q E A f A λλλλλ=-+=-+证明:存在性的验证. 假设多项式1011()m m m m f c c c c λλλλ--=++++ 那么,1011()m m m m f E c E c E c E c E λλλλ--=++++ 1011()m m m m f A c A c A c A c E--=++++ 取120121()m m m m Q D D D D λλλλ----=++++ 其中10110,0,1,, 1.kk i k k k i k k i D c A c A c A c A c k m ---===++++=-∑ 代入定理中,可以验证等式成立.唯一性的证明. 假设还存在有另一个矩阵使得-λ1()Q λ11()()()()()()()f E E A Q f A Q E A f A λλλλλ=-+=-+只要把两个等式相减,可以得到11(()())(()())Q Q A Q Q λλλλλ-=-再通过比较等式两边的次数,即可得到.■λ1()()Q Q λλ=定理5 阶数字矩阵的最大不变因子等于的所有初等因子的最小公倍式.n A ()n d λA 证明: 因为,将矩阵全部初等因子按不可约因子的方幂降幂排列,同一()r E A n λ-=A 个不可约因子的方幂排成一行,不足个的在后面用1补足. 排列的形式如下:n 11112221221*********(),(),,(),(),(),,(),0(1,2,,)(),(),,(),n n s s sn t t t t t t i i in t t t s s s P P P P P P t t t i s P P P λλλλλλλλλ≥≥≥≥=那么,不变因子 ,也就是等于所有初等因子的最小公倍式. ■1112112()()()()s tt t n s d P P P λλλλ= 定理6设阶矩阵的最小多项式为,证明:,其中是n A ()m λ()()n m d λλ=()n d λ的最后一个不变因子.E A λ-证明:设的全部初等因子是A 1111211121111112112(),(),,(),(),(),,(),r sr s s s sn n n rn n n s s s s s sr n n n n n n λλλλλλλλλλλλ⎧---≤≤≤⎪⎪⎨⎪---≤≤≤⎪⎩其中两两不同.这时 .12,,,s λλλ 121212()()()()sr r r sn n n n s d λλλλλλλ=--- 其次,由于相似于若当标准形A ,1112srs n n n J J J J ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭1,1,2,,.1,2,,.1ij i i n s i J i s j r λλλ⎛⎫ ⎪⎪=== ⎪ ⎪⎝⎭ 由于对角分块矩阵的最小多项式等于各分块矩阵最小多项式的最小公倍式,而且相似矩阵有相同的最小多项式,所以1111111()(),,(),,(),,()sr r s s n nn n s s m λλλλλλλλλ⎡⎤=----⎣⎦.■111()()()sr r s n ns n d λλλλλ=--= 定理7设是准对角形,且分别是的最小多项式,证明:1s A A A ⎛⎫⎪= ⎪ ⎪⎝⎭()i m λi A ,其中表示的最小公倍式.()A m λ1[(),,()]s m m λλ= 1[(),,()]s m m λλ 1(),,()s m m λλ 证明:因为 ,所以,,1()()0()A A A s m A m A m A ⎛⎫⎪== ⎪ ⎪⎝⎭1()()0A A s m A m A === 即是矩阵零化多项式,因此,故是()A m λ1,,s A A )(|)(,,)(|)(1λλλλA s A m m m m ()A m λ的一个公倍式.1(),,()s m m λλ 另一方面,任取的一个公倍式,则有,1(),,()s m m λλ )(λh 1()()0()s h A h A h A ⎛⎫⎪== ⎪ ⎪⎝⎭可见是矩阵的一个零化多项式,所以,. 再因为的首项系数为1,因)(λh A ()|()A m h λλ()A m λ此. ■()A m λ1[(),,()]s m m λλ= 定理8 相似矩阵具有相同的最小多项式.证明:设阶矩阵与相似,即存在可逆矩阵,使得.又设分n A B T 1B T AT -=12(),()m m λλ别是矩阵,的最小多项式,且设A B 12110()s s s m b b b λλλλ--=++++ 那么,我们有121100()s s s m B B b B b B b E--==++++ 1111102()().s s s T A b A b A b E T T m A T ----=++++= 所以,,是的零化多项式,而是的最小多项式,因此,2()0m A =2()m λA 1()m λA .12()|()m m λλ类似可以证明,.再从的首项系数为1,即可得到.■21()|()m m λλ12(),()m m λλ12()()m m λλ=四、基本例题解题点击1.矩阵的基本概念与计算λ-【例1】设有矩阵,-λ2222123(),()1253A B λλλλλλλλλλλ⎛⎫-⎛⎫== ⎪ ⎪++++⎝⎭⎝⎭计算:(1);(2).()2()A B λλ-()()A B λλ⋅【提示及点评】矩阵的运算法则与数字矩阵的运算法则相同.-λ【例2】设,求.21()12A λλλλλ⎛⎫=⎪+++⎝⎭1()A λ-【提示及点评】可以按数字矩阵求逆的方法进行计算.【例3】设,求.00()1001A λλλλ=⎛⎫ ⎪ ⎪ ⎪⎝⎭()nA λ【解】因为00100000()1001010001001010A EB λλλλλλ==+=+⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭而,所以可以应用牛顿二项式定理来进行计算.EB BE B ==0111222()()n nnk n k k n n n n n n n k A E B C E B C E C B C B λλλλλλ---==+=⋅=++∑. ■1(1)21200nn nn n n n n n n λλλλλλ----⎛⎫⎪= ⎪ ⎪⎝⎭【知识扩展提示】题目可以扩充为对任意阶数的若当块,0000000001000(,)00100001t tJ t λλλλλ⨯⎛⎫⎪⎪ ⎪=⎪⎪ ⎪⎝⎭求.0(,)nJ t λ【例4】设有矩阵-λ2221211111()2211,()2131221023A B λλλλλλλλλλλλλλλλ-+-+-+--+=-+++=---+---⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭试求矩阵使得(),()L L Q R λλ,()()()()L L A B Q R λλλλ=+其中或者.()0L R λ=(())(())L R B λλ∂<∂【提示及点评】此例子主要介绍矩阵的带余除法定理.-λ【解】首先把矩阵表示成矩阵多项式的形式:(),()A B λλ22012100120111()010121211002101012A A A A λλλλλ---=++-=++--⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭01101111()010*********B B B λλλ--=+--=+--⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭然后借助于多项式除以多项式的运算,我们有01B B λ+2012A A A λλ++100()L Q B A λλ-=210100A B B A λλ-+1101100()B A B B A --+-111002()A B B A A λ--+1111100101100()()A B B A B B A B B A λ----+-112101100()()L R A B B A B B A λ--=--所以,,1110001100211()()134002L Q B A B A B B A λλλλλ-----⎛⎫ ⎪=+-=-+ ⎪ ⎪+⎝⎭.■112101100250()()169205L R A B B A B B A λ--⎛⎫ ⎪=--= ⎪ ⎪-⎝⎭【知识扩展提示】题目如果是求矩阵使得,则在-λ(),()R R Q R λλ()()()()R R A Q B R λλλλ=+做多项式除法的时候,注意矩阵与相乘时的左右方向即可.01B B λ+()R Q λ2.求矩阵的标准形、行列式因子、不变因子与初等因子λ-(1)行列式因子的计算方法一:直接使用行列式因子的定义进行计算.【例5】设有矩阵-λ,2221211()2211122A λλλλλλλλλλλ⎛⎫-+-+- ⎪=-+++ ⎪ ⎪-+-⎝⎭试求其行列式因子.【解】由于矩阵的元素中含有非零常数1,所以一阶行列式因子.或者是由于下列()A λ1()1D λ=所有多项式{}2221,21,1,2,21,1,,1,22λλλλλλλλλλ-+-+--+++-+-的最大公因式是1,所以.1()1D λ=对于二阶行列式因子. 由于的2阶子式一共有9个,一一计算比较麻烦,我们只2()D λ()A λ要找出特别的几个出来,看它们是否互素即行. 由于2阶子式与22211λλλλ-++-2211211λλλλ-+-+++是互素的,即最大公因式是1,所以二阶行列式因子.2()1D λ=最后计算三阶行列式因子,由于矩阵的3阶子式只有1个,所以3()D λ()A λ. ■65432311()|()|(2338385)2D A a λλλλλλλλ==++--+-【注意】由于使用定义的方法求行列式因子的计算过程比较麻烦,因此一般很少用,除非是矩阵比较简单.()A λ方法二:先用初等变换化简矩阵,一般情况是化简成为标准形或者对角形,再对简化后的-λ矩阵求行列式因子.-λ【例6】设有矩阵-λ111()2131023B λλλλλ+--+=----⎛⎫⎪ ⎪ ⎪⎝⎭试求其行列式因子.【解】由于(1)(3)1111023()2132131023111B λλλλλλλλλ↔+--+--=------+--+⎛⎫⎛⎫ ⎪ ⎪−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭32100010002447λλλ-→→--+-⎛⎫⎪ ⎪ ⎪⎝⎭因此,所求的行列式因子是,. ■12()()1D D λλ==3237()222D λλλλ=-+-方法三:对于特殊类型的矩阵(如对角形、上下三角形等等),可以先求出阶数大的行列-λ式因子,再利用的关系,求出阶数低的行列式因子.1()|()k k D D λλ-【例7】设有下列矩阵-λ①;②1221000100010()0000001n n n a a a A a a λλλλλλ--⎛⎫ ⎪- ⎪⎪-= ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭31104101()0021001A λλλλλ--⎛⎫ ⎪+ ⎪= ⎪+- ⎪⎝⎭试求它们的行列式因子.【解】① 由于矩阵的行列式()A λ12121|()|n n n n nA a a a a λλλλλ---=+++++ 所以,,12121()n n n n n n D a a a a λλλλλ---=+++++ 又由于在中有一个阶的子式,故,于是,()A λ1n -110001(1)0000001n λλλ---=--1()1n D λ-=.231()()()1n n D D D λλλ--==== ② 显然,2243121()(1)(1)411D λλλλλλλ--+-==-++又其中的一个3阶子式,11010123021λλλ-+=++-由于三阶行列式因子并且还有,因此可见,于是3()|(23)D λλ+34()|()D D λλ3()1D λ=. ■21()()1D D λλ==(2)矩阵的标准形、不变因子与初等因子的计算-λ方法一:直接使用矩阵的初等变换,求矩阵的标准形,进而可以得到不变因子.-λ【例8】用初等变换求下列矩阵的标准形、不变因子与初等因子.-λ.222223222213()2322A λλλλλλλλλλλλλλλλλ⎛⎫- ⎪=--+-- ⎪ ⎪+++⎝⎭【提示及点评】在使用初等变换来求矩阵的标准形时,第一步应将矩阵左上角的元素变成-λ能够整除矩阵的所有元素,第二步才能消去矩阵的第一行与第一列的其余元素,重复这个过程即可把矩阵化其标准形. 关键的一步是在矩阵的所有元素中直接找出一个或者经过加减运算后找出-λ一个元素,使其能够整除矩阵的所有元素.【解】2222222322232(1)(2)(1)2222212112()23222322022A λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ+⋅-⎛⎫⎛⎫-- ⎪ ⎪=--+--−−−−→--+-- ⎪ ⎪⎪ ⎪+++++⎝⎭⎝⎭1000(1)000(1)(1)λλλλλ⎛⎫⎪→→+ ⎪⎪+-⎝⎭于是,的不变因子,从而得出矩阵的初()A λ123()1,()(1),()(1)(1)d d d λλλλλλλλ==+=+-等因子是.■,,1,1, 1.λλλλλ++-方法二:对于一些形如上(下)三角形、对角形等特殊的矩阵,可以先求其行列式因子-λ(或者初等因子),再利用不变因子与行列式因子的关系,求出不变因子,进而得到矩阵的标准形.【例9】求下列矩阵的标准形与不变因子.-λ①;②21000210()00210002A λλλλλ+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭22220(1)00(1)000()000100(1)0A λλλλλλλλ⎛⎫+ ⎪- ⎪= ⎪- ⎪ ⎪+⎝⎭【解】① 显然,行列式因子,而且矩阵有一个3阶子式44()|()|(2)D A λλλ==+)(λA ,所以有,故的不变因子是 1002101021λλ+=+321()()()1D D D λλλ===)(λA ,,即的标准形是. 123()()()1d d d λλλ===44()(2)d λλ=+)(λA 410000100001000(2)λ⎛⎫⎪⎪⎪ ⎪+⎝⎭② 虽然矩阵不是对角形,但可用初等变换化成对角形:)(λA 220(1)00(1)000λλλλ⎛⎫⎛⎫+-由此可得矩阵的初等因子是,而矩阵的)(λA 222,,,(1),(1),1,1,1λλλλλλλλ+++--秩=4,据此可知不变因子是,2123()1,()(1),()(1)(1)d d d λλλλλλλλ==+=+-,故矩阵的标准形是224()(1)(1)d λλλλ=+- . ■22210000(1)0000(1)(1)0000(1)(1)λλλλλλλλ⎛⎫ ⎪+ ⎪ ⎪+- ⎪+-⎝⎭(3)有关数字矩阵的初等因子的计算【例10】求下列数字矩阵的初等因子(以及不变因子,相应特征矩阵的行列式因子)...308316205A ⎛⎫⎪=- ⎪ ⎪--⎝⎭【提示及点评】对于计算数字矩阵的初等因子,其实其过程与求矩阵的若当标准形一样. 计算方法与求一般矩阵的初等因子是一样的.-λ【解】因为(2)(3)1308308316111205205E A λλλλλλλλ+⋅----⎛⎫⎛⎫ ⎪ ⎪-=-+-−−−−→-+- ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭210002(1)000(1)/2λλ-⎛⎫⎪→→+ ⎪⎪-+⎝⎭因此,所求的初等因子是,不变因子是,2(1),1λλ++2123()1,()1,()(1)d d d λλλλλ==+=+行列式因子是. ■3123()1,()1,()(1)D D D λλλλλ==+=+3.有关矩阵等价的判断与证明λ-【例11】判断下列两个矩阵是否等价?,010001()000000A λαλαλλαλα+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭010100()000000B λαλαλλαλα+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭【提示及点评】利用矩阵等价的6个方法之一进行判断.-λ【解】易见,矩阵与的行列式因子都是)(λA )(λB 241234()()1,()(),()()D D D D λλλλαλλα===+=+因此,矩阵与是等价的. ■)(λA )(λB 【例12】对于任意的阶矩阵,证明与等价.n -λ)(λA )(λA )(/λA 【提示及点评】可以证明它们有相同的行列式因子或者有相同的标准形.【解】假设矩阵的标准形是)(λA ()1()(),,(),0,,0r D diag d d λλλ= 因此,存在可逆矩阵使得,两边取转置得到)(,)(λλQ P )()()()(λλλλD Q A P =,从而知道与有相同的标准形,所以与)()()()()(////λλλλλD D P A Q ==)(λA )(/λA )(λA 等价.■)(/λA 4.有关数字矩阵的特征矩阵(特征多项式、凯莱定理)的应用A E A λ-【例13】设有矩阵,求,其中是正整数.130240121A -=---⎛⎫ ⎪ ⎪ ⎪⎝⎭nA n 【提示及点评】利用哈密顿-凯莱定理及带余除法进行计算.【解】设是矩阵的特征多项式,那么计算可得()||f E A λλ=-A 322()452(2)(1)f λλλλλλ=-+-=--再根据计算的要求,取多项式,并令(带余除法)nA ()ng λλ=2()()()n g f q a b cλλλλλλ==+++分别把代入,得到 .又因为是特征多项式2,1λλ==422,1na b c a b c ++=++=1λ=的2重根,所以,对上式两边求导后有()f λ///1()()()()()2n g f q f q a b n λλλλλλλ-=+++=再代入得到,.求解上面关于的联立方程组,我们可以得到1λ=2a b n +=,,a b c 121,223,22n n n a n b n c n+=--=-+=-因此,.■12323(12)02(12)23206(12)799271n n n n n n n A aA bA cE n n +⎛⎫--+ ⎪=++=--+-+⋅ ⎪ ⎪-+--⋅+⎝⎭【注意】关键是如何利用矩阵A 的特征值,找到关于的联立方程组.,,a b c 【例14】设有矩阵,及多项式,求130240121A -⎛⎫ ⎪=- ⎪ ⎪--⎝⎭119653()461f λλλλλλλ=-+--+-.1()f A -【提示及点评】利用哈密顿-凯莱定理及带余除法进行计算.【解】因为特征多项式,再由带余除法得到32()||452g E A λλλλλ=-=-+-2()()()(759933)f g q λλλλλ=+-+-因此,由哈密顿—凯莱定理得到,22433780()75993325238703997779f A A A E -⎛⎫ ⎪=-+-=- ⎪ ⎪--⎝⎭再求其逆,得到. ■43141354512811355511469113513590()0f A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭【注意】此题型的计算量比较大,关键是掌握其计算的方法与技巧.【例15】如果是一个阶可逆矩阵,导出使用哈密顿—凯莱定理求逆矩阵的公式.A n 1-A 【解】假定矩阵的特征多项式是A 12121()||n n n n nf E A a a a a λλλλλλ---=-=+++++ 则由凯莱定理知道,121210n n n n n A a A a A a A a E ---+++++= 而,因此,(1)||0n na A =-≠1231211()n n n n nA A a A a A a E E a -----⋅++++= 即矩阵的逆矩阵A . ■11231211()n n n n nA A a A a A a E a ------=++++ 【知识扩展提示】题目可以改成:证明存在一个实系数多项式,使得.)(x g )(1A g A=-【例16】设是任意一个阶矩阵,且A n 12121()||n n n n nf E A a a a a λλλλλλ---=-=+++++ 证明:的伴随矩阵是的多项式,并且A *A A .*1123121(1)()n n n n n A A a A a A a E -----=-++++ 【证明】由上例知道,123121(1)()n n n n n A A a A a A a E a E----⋅-++++= 而,代入上述,可以得到||(1)||nn a A A =-=-1123121(1)()||n n n n n A A a A a A a E A E-----⋅-++++=所以,.■*1123121(1)()n n n n n A A a A a A a E -----=-++++ 5.相似矩阵的判断与证明【例16】判断下列矩阵3253212610,222123365A B --⎛⎫⎛⎫ ⎪ ⎪=-=- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭是否相似.【提示及点评】要判断两个矩阵是否相似,通常的方法是先求出它们的不变因子(或行列式因子、或初等因子),如果它们相同,则相似,否则不相似.当然,如果两个矩阵的秩,行列式,特征多项式或最小多项式有一个不相等,则它们一定不相似.要注意的是,即使它们的秩,行列式,特征多项式或最小多项式都相等,仍然不能确定它们是否相似.许多学生往往根据两个矩阵的特征多项式相同,就断定这两个矩阵相似,这是初学者常犯的一个错误,请读者给予充分的注意.【解】由于2325100261002012300(2)E A λλλλλλ--⎛⎫⎛⎫ ⎪ ⎪-=--→→- ⎪ ⎪⎪ ⎪--+-⎝⎭⎝⎭ 232110022202036500(2)E B λλλλλλ--⎛⎫⎛⎫ ⎪ ⎪-=-+-→→- ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭ 从而,与有相同的不变因子,故与相似.■A B A B 【例17】假设多项式有个不同的根12121()n n n n n f a a a a λλλλλ---=+++++ n ,证明矩阵12,,,n λλλ 与 相似.1210000100001000001n n n a a A a a ---⎛⎫⎪- ⎪ ⎪=- ⎪⎪ ⎪-⎝⎭12n B λλλ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 【提示及点评】验证两个矩阵的不变因子相同即行.■【例18】下列形式的矩阵1100a b ⎛⎫⎪(其中称为上对角元素)称为海森伯格矩阵.试证明:两个上对角元素全非零的海森伯格矩阵相j b 似的充分必要条件是它们有相同的特征多项式.【提示及点评】计算特征矩阵的行列式因子,再依此进行证明.H E -λ【证明】由于特征矩阵112231000*n n a b a b E H a b a λλλλλ---⎛⎫⎪--⎪⎪-=- ⎪- ⎪ ⎪-⎝⎭如果,由于有一个阶的子式0(1,2,,1)jb j n ≠=- H E -λ1-n 1221121100(1)0n n n b a b b b b b λ------=-≠- 所以的行列式因子.由此得,的行列式因子是H E -λ1()1n D λ-=H E -λ.121()()()1,()()||n n H D D D D f E H λλλλλλ-======- 于是,两个上对角元素全非零的海森伯格矩阵相似于与有相同的1H 2H ⇔1H E -λ2H E -λ行列式因子. ■⇔)()(21λλH H f f =6.求矩阵的Jordan 标准形和有理标准形【例19】求下列数字矩阵的若当(Jordan )标准形和有理标准形.(1); (2).308316205A ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭230002000042013A ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭【提示及点评】可以先求出矩阵的初等因子,然后由初等因子写出矩阵的若当标准形及有理标准形.【解】(1)由于2308308100316112401020520500(1)E A λλλλλλλλλλ----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=-+-→++→+ ⎪ ⎪ ⎪⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭所以,初等因子是,因此矩阵的若当标准形与有理标准形分别是21,(1)λλ++A J F,.100010011J -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭100001012F -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭(2)容易算得,矩阵的初等因子是,所以,若当标准形与有理标A 25,2,(2)λλλ---J 准形分别是F ,. ■52212J ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭520414F ⎛⎫⎪⎪= ⎪ ⎪-⎝⎭【知识扩展提示】从上面的例子可以看出,矩阵的若当标准形 = 有理标准形的充分必要A J F 条件是:矩阵的初等因子都是一次的.A 【例20】设. 求可逆矩阵,使得成为若当标准形.308316205A ⎛⎫⎪=- ⎪ ⎪--⎝⎭T 1T AT -【提示及点评】这是求相似变换矩阵的问题. 可先求出若当标准形,然后通过求解线性方程组来求可逆矩阵.T 【解】由例19知道,矩阵的若当标准形是A .100010011J -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭设有可逆矩阵,使得,则.令,其中是列T 1T AT J -=AT TJ =()123,,T ααα=123,,ααα向量组,那么1122333,,,A A A ααααααα=-=-+=-所以,是的属于特征值的特征向量,且满足.13,ααA 1λ=-23,αα23()A E αα+=下面先求向量,因,所以是齐次线性方程组2α223()()0A E A E αα+=+=2α2()0A E X +=的非零解,并且满足()0A E X +≠又因为,所以每一个非零向量都是的非零解. 取2()0A E +=2()0A E X +=,则()/21,1,1α=/32()(12,9,6)0.A E αα=+=-≠再从齐次线性方程组()0A E X +=求出一个属于特征值的特征向量,此时取矩阵1λ=-/1(2,0,1)α=-()1232112,,019116T ααα-==-⎛⎫ ⎪ ⎪ ⎪⎝⎭则可逆,且T ■1100010011.T AT J --==--⎛⎫ ⎪ ⎪ ⎪⎝⎭7.矩阵最小多项式的计算及在证明中的应用求阶方阵的最小多项式,通常采用如下三种方法:n A ()A m λ方法一试探法:首先求出的特征多项式,然后写出中包含的所A ()||f E A λλ=-()f λA 有互异特征值的因式,最后验证这些因子是否是的零化多项式,其中次数最低的首一多项式即是A .()A m λ方法二 求出的若当标准形,再利用A 1212()()()()tr r r A t m λλλλλλλ=--- 其中是的若当标准形中以为对角元的若当块的最高阶数.i r A J i λ方法三 当的阶行列式因子易于求得,利用求最小多项式.A 1-n 1()n D λ-1()()()A n f m D λλλ-=【例21】求下列矩阵的最小多项式.(1); (2);(3)2300020000420013A ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭2123021200210002A ⎛⎫⎪⎪=⎪ ⎪⎝⎭308316205A ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭【解】(1)因为,其包含的所有互异的特征值的因式有:3()||(2)(5)f E A λλλλ=-=--A ,直接计算有23(2)(5),(2)(5),(2)(5)λλλλλλ------,(2)(5)0A E A E --≠2(2)(5)0A E A E --=从而的最小多项式.A 2()(2)(5)A m λλλ=--(2) 显然可以求得的三阶行列式因子,而特征多项式,所E A λ-3()1D λ=4()(2)f λλ=-以最小多项式.443()()()(2)()A f m d D λλλλλ===-(3) 由例19知道,矩阵的不变因子是,所以最小A 2123()1,()1,()(1)d d d λλλλλ==+=+多项式是.■2()(1)A m λλ=+【例22】求指定的数字矩阵的最小多项式A (1) 4阶矩阵的元素均是1;A (2) ;123331313;3;31333J J J ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3) 已知3阶矩阵的特征值分别是1,-1,2,B 325A B B =-(4) 的充分必要条件是什么?()()A A f m λλ=(5) 若的特征值都是单根,那么对吗?A ()()A A f m λλ=【解】(1)由于,而计算知道,所以最小多项式是3()||(4)A f E A λλλλ=-=-(4)0A E A -=.()(4)A m λλλ=-【知识扩展提示】题目可扩充为如果阶矩阵的所有元素都是且不为零,求其最小多项式.n A a (2) 可以把矩阵看作若当标准形矩阵,其最小多项式由各个若当块的最小多项式的最小公倍式组成. 因此,3个矩阵的最小多项式分别是;;1()[3,3,3]3J m λλλλλ=---=-222()[(3),3](3)J m λλλλ=--=-333()[(3)](3)J m λλλ=-=-(3) 由于,而且矩阵的特征值分别是1,-1,2,由此,可以求得矩阵的特325A B B =-B A 征值分别是-4,-6,-12.故的特征多项式,由此得到的最小多A ()(4)(6)(12)A f λλλλ=+++A 项式是.()(4)(6)(12)A m λλλλ=+++(4)对于阶数字矩阵,的充分必要条件是的行列式因子n A ()()A A f m λλ=E A λ-. 这可从计算公式得到.1()1n D λ-=1()()()A n f m D λλλ-=(5) 若的特征值都是单根,那么矩阵与一对角矩阵相似,从而知道最小多项式没A A ()A m λ有重根,再根据特征多项式与含有相同的的特征值,因此有. ■()A f λ()A m λA ()()A A f m λλ=【例23】求矩阵的全体零化多项式集.2300020000420013A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭【提示及点评】求一个矩阵的零化多项式集,其实是求矩阵的最小多项式,再转化成一种零化。
若当矩阵幂的若当标准形

戤 + l , …, ( 1 ) = ‘ ( )
i, 、 ki , 、 + 1,
可得
。 的秩为 n 一 1 , 因此可知 的若当标准形
=
( 1 J = 口 。 ( 1 ) =
收 稿 日期 : 2 0 1 2 —1 2 —2 1
基金项 目: 山西省教育科学规划项 目 G H 一 1 1 1 0 3 。 作者简介 : 王慧群 ( 1 9 7 2 一 ) , 男, 山西长子人 , 副教授 , 主要从事有 限群及其表示理论研究 。
,
J r } , 那 么 的幂 的若 当标准形归结为最终归结
为若当块 的幂 的若当标准形 。
对 于复 数 A的 凡阶 若 尔 当块 为 J ( a, n ) , 分 两
种 情况 :
则 可视 为 上 的线 性变 换 , 令 = , 则 丁为线 性
空 间 的变换 , 且
丁 ( 1 , s 2 , …, ) : ( 1 , , …, 占 ) A,
为 证 明定 理 中的 结论 , 只 需证 明存 在 另 结论 l A≠O时 , 若 当块 J ( A, n ) 的 次 幂 的 其 中 A= 外一组基 , 使得 丁在该基下 的矩阵恰好是 d i a g { J  ̄ , 若 当标 准形 为 , n ) , 因此 A, n ) 的 k次 幂 的初 ) 即可 , 事 实上 可 以通 过构 造 的 k个 丁 一 等 因子仅有 ( 一 ) “ . 子空 间完 成证 明 . 记。 ( A, ) , 注意 到 l , 的特 征 根 为 A( 重 数 为 首先 , 构 造子 空 间 , 取一 组基 :
・
31 ・
长 治 学 院 学 报
记L : ( s , 丁 ( ) , ( ) , …, 丁 ( ) ) . 可记 丁 = I , J ,
若当标准型求解

P ( p1, p2 , p3 , p4 , p5 )
a
0
0
0
0
a
0
0
b
0
c
0
0
b 2
0
c 2
0
0
0
0
0
0
0
0
c 6
从前面的计算可以看出,如果先取a=0,那么后面的计 算将无法进行。因此我们应该在求Jordan块对应特征
值的时候先求阶数比较高的,然后在同阶数的可以随 便进行。依此类推。可总结如下
I I I
) 0 ) y2
) y3 y2
特征向量
( A Biblioteka i I ) yn j yn j 1 广义特征向量
注意:这里使用的是 ( A i I ) yi1 yi 教材上使用的是 (i I Ai ) yi1 yi
另外,注意的选择。观察上面的公式可以发现
J( )
1
1
rr
g(
)
g( ) g( )
g( )
2! g( )
g( r1)( )
( r 1)!
g( J )
mr
g( )
g( )
2! g( )
g( )
15
关于Jordan标准形的计算
由于计算涉及的内容偏多,有兴趣或需要的可以 参见教材。另外很多定理的证明可参见北京大学 出版社出版的<<高等代数>>教材的相关内容即可。
【论文】矩阵的若当标准形的计算方法及其应用

摘 要矩阵的若当标准形的求解方法在代数中有着极其重要的作用,在计算行列式、求矩阵的方幂、矩阵的分解、解微分方程等问题中都有重要的应用.此外,矩阵的若当标准形理论在力学和计算方法中是一个非常重要的工具.但是,在众多的教科书及包含矩阵理论的著作中,对矩阵的若当标准形的求解方法及其相似变换矩阵的介绍并不全面,所以显得这部分内容比较的简单,不容易被学生所重视.本论文首先阐述了矩阵的若当标准形的求解方法的背景、意义、研究现状、相关概念和性质定理,然后对矩阵的若当标准形的求解方法进行归纳和总结,并给出具体例题以便详细说明每一种解法的步骤与特点.同时,对各种方法进行比较,指出各种方法的优缺点和适应性,以期待能够帮助读者在解决与矩阵的若当标准形的求解有关题目时能够选择使用适当的方法,从而提高解题的效率;最后,鉴于矩阵的若当标准形在“矩阵方程论”、“矩阵函数论”以及“常微分方程”和“现代控制论”中都有广泛的应用,所以对矩阵的若当标准形的应用进行总结,并给出具体实例,强调理论联系实际的重要性.此外,利用所总结的矩阵的若当标准形的求解方法及其应用,教学者能更深刻地向学生展示数学方法的多样性与统一性,进一步培养学生的发散性思维,使学生能更深刻地理解数学之美.关键词:矩阵,若当标准形,计算方法,应用AbstractHow to get the Jordan Canonical form of a matrix has an extremely important role in the algebra. The Jordan Canonical form of a matrix can be used in calculating the determinant, the power of matrices, the decomposition of matrices, the solution of differential equations and so on. In addition, the Jordan Canonical form of a matrix is also a very important tool in mechanics and computational methods. However, the methods to get the Jordan Canonical form of a matrix are not elaborated in many textbooks and books include matrix theory. In this paper, the background, the significance of research, the nature of the relevant concepts and theorems with respect to the Jordan Canonical form of a matrix are given firstly. And then, the methods to get the Jordan Canonical form of a matrix are summarized and concluded, and there is a specific example of each method to help the readers understand the method. At the same time, comparisons of various methods are given. Finally, in view of the Jordan Canonical form of a matrix is wide used in the "matrix equation"、 " matrix function of "、" Ordinary Differential Equations "and" modern control theory ", the application of the Jordan Canonical form of a matrix are summarized. Furthermore, this paper can be used to help teachers show students the diversity and unity of mathematical methods and the beauty of mathematics.Key words:Matrix,Jordan Canonical form,solution,application目 录第一章 前言 (1)1.1 矩阵的若当标准形的计算方法及其应用的背景及意义 (1)1.2 矩阵的若当标准形的计算方法及其应用的研究现状 (1)1.3 论文的结构安排 (2)第二章 矩阵的若当标准形的相关概念与结论 (3)2.1 基本概念的介绍 (3)2.2 若当块、若当标准形的定义和性质 (4)2.3 矩阵的若当标准形的基本定理 (5)第三章 矩阵的若当标准形的计算方法 (6)3.1 初等因子方法一 (6)3.2 初等因子方法二 (7)3.3 特征值方法一 (8)3.4 特征值方法二 (10)3.5 行列互逆初等变换法 (11)3.6 λ-矩阵初等变换法 (12)3.7 初等相似变换法 (14)3.8 幂零矩阵的若当标准形求法 (16)3.9 可分块矩阵的若当标准形的求法 (17)第四章 矩阵的若当标准形的应用 (19)4.1 在计算矩阵多项式中的应用 (19)4.2 在矩阵的高次幂计算中的应用 (20)4.3 在证明过程中的应用 (22)4.4 在解线性微分方程组中的应用 (25)第五章 总结 (27)参考文献 (28)致 谢 (29)声 明 (30)第一章 前 言1.1 矩阵的若当标准形的计算方法及其应用的背景及意义在高等代数和线性代数中,矩阵的理论与方法贯穿于行列式、线性方程组、线性空间、线性变换、二次型等各个方面,高等代数的许多问题都可以转化为相应的矩阵问题来处理.同时矩阵也是许多其他数学分支和学科中研究问题的重要工具.若当标准形定理是矩阵标准形理论的一个重要定理.矩阵的若当标准形在计算行列式、求矩阵的方幂、矩阵的分解、求解微分方程等数学问题中都有重要的应用.此外,矩阵的若当标准形理论在力学及其计算方法中也是一个非常重要的工具.鉴于矩阵的若当标准形在各个领域的重要性,讨论、归纳和总结矩阵的若当标准形的计算方法及矩阵的若当标准形的应用是有必要的,且具有一定的理论和实际意义.希望通过对若当标准形的的多种计算方法的总结和比较,加深笔者和读者对矩阵的若当标准形的理解和认识,进一步培养笔者和读者的发散性思维,从而有助于今后更好地利用该方法解决各类实际问题.1.2 矩阵的若当标准形的计算方法及其应用的研究现状若当标准形是矩阵理论中不可缺少的部分,在研究矩阵若当标准形的过程中,大多是以矩阵若当标准形的基本定理[1]出发,即:每个n阶的复数矩阵A都与一个若当形矩阵相似,这个若当形矩阵除去其中若当块的排列次序外是被矩阵A唯一确定的,它称为A的若当标准形.这个定理是计算矩阵的若当标准形各种方法的理论基础.根据这个基本定理和其他定理,能够得出其他的推论[2,3],如:复数矩阵A与对角矩阵相似的充分必要条件是,A的初等因子全为一次的.求解矩阵的若当标准形的最常见的方法是初等因子法、特征值法和初等变换法.初等因子方法是最为基础的求解矩阵若当标准形的计算方法.[4]中介绍了两种初等因子法求矩阵若当标准形的详细步骤,并给出简单的例子进行说明.文献[4~7]中介绍的求矩阵的若当标准形的方法是特征值法,该方法也是比较基础的计算方法.两种方法都是先求出矩阵的特征值,之后再根据不同的方法来求解矩阵的若当标准形。
数学代数方法T矩阵若儿当标准型

(即初等变换不改变 -矩阵的秩与行列式因子)
2)若 矩阵 A( ) 的标准形为
d1( )
O
D(
)
dr ( )
0
O
0
其中 d1( ),L dr ( ) 为首1多项式,且
di ( ) di1( ), i 1,2,L r 1,
行列式因子的定 义:
设 A为(一) 个 阶 n矩阵,对于任意的正整数
k
1 k r必A有(非) 零的 阶子式k, 的全A部() 阶子式的k首
一最大公因子称为 的 阶行A(列)式因k子。记为:
Dk ()
规定: D0( ) 1
显然,如果 rank( A()) r ,则行列式因子一共有r 个
例1 求
3、在一个线性变换 的若当标准形中,主对角线 上的元素是 的特征多项式的全部根(重根按多数
计算).
λ-矩阵的概念 λ-矩阵的秩 可逆λ-矩阵
λ-矩阵的概念
定义:
设P是一个数域, 是一个文字,P[]是多项式环, 若矩阵A的元素是 的多项式,即 P[] 的元素,则 称A为 ―矩阵,并把A写成 A( ).
例 用初等变换化λ―矩阵为标准形.
1 2 1
A( )
2
1 2 3 1 2
解:
1 2 1 1
A(
)
[31 ]
1
2
2 3 1
0 1
1 2 1 1
[1,3 ]
0 1
2 3 1
1 2 1 3 2
行列式因子
1. 定义:
设 -矩阵 A( )的秩为 r ,对于正整数 k,1 k r, A( )中必有非零的 k 级子式, A( )中全部 k级子式 的首项系数为1的最大公因式 Dk ( ), 称为 A( ) 的
方阵的若当标准型(最简洁版)

的m阶方阵称为m阶Jordan J d 快,其中 是复数。 当 是某一矩阵A的特征值时,称Jm ( ) 为A 的特征值 的Jordan块。
例6.
1 1 0 J 3 ( 1) ) 0 1 1 0 0 1
1 2 i 0 0 0 0 1 2 i 0 0 0 0 1 2 i 0 0 0 0 1 2 i
Dk 1 ( )k det Tk Dk 1 ( ) Aij ( j 1, 2, k ) 从而:
而Dk ( )是A( ) 的所有的k 阶子式中首一的 最大公因式,所以: D ( ) D ( )
k 1 k
定义3 设 A( )为 n 阶 矩阵, D ( ) 是 A( ) 的 k k 阶行列式因子,则称: Dk ( ) dk k 1,2, , n A( ) 为 的不变因子 Dk 1 ( ) 定理3 任意一个非零秩为 r 的n阶 A( )阵都等价 于一个对角矩阵,即:
d 1 ( ) 1, d 2 ( ) , d 3 ( ) ( 1)
为不变因子
d 2 ( 1 ) ( 2 ) ( s )
e21 e22
d1 ( 1 )e11 ( 2 )e12 ( s )e1 s
f ( )与 g ( )分别是 A( ) 与 B( )的 k 级行列式因子.
下证 f ( ) g ( ) 以下分三种情形:
定理2 设 A( )为n 阶 矩阵, Dk ( ) 是 A( ) 的 k 阶行列式因子,则: Dk 1 ( ) Dk ( ) 证明 设 Tk ( t ij )k k 为 A( )的任意一个 k 阶子矩阵, 则有:det Tk t11 A11 t12 A12 t1k A1k 其中,A1 j 为 t1 j 的代数余子式。显然
矩阵论3-3.方阵的若当标准型

2 1 0 1 0 0 λ +λ ≅ 3 2 3 2 ≅ 0 −λ − λ + λ −λ 0 −λ − λ + λ −λ 0 −λ4 − λ3 − λ −λ2 0 −λ4 − λ3 − λ −λ2
Department of Mathematics
Department of Mathematics
B ( λ ) = P ( λ ) A( λ )Q ( λ )
行列式因子的定 义: 矩阵, 设 A(λ )为一个 n 阶 λ 矩阵,对于任意的正整数 k 阶子式, A 1 ≤ k ≤ r A( λ ) 必有非零的 k 阶子式, (λ) 的全部 k 阶 行列式因子。 子式的首一最大公因子称为 A( λ ) 的k 阶行列式因子。 规定: 规定 D0 (λ) = 1 记为: 记为: D (λ) 显然, 显然,如果 rank ( A(λ )) = r ,则行列式因子一共有r 个 例1 求
λ ( λ + 1) A( λ ) =
Department of Mathematics
λ
2 ( λ + 1)
λ ( λ + 1) A( λ ) =
λ
2 ( λ + 1)
≅ ≅
λ ( λ + 1) λ λ ( λ + 1) 2 λ ( λ + 1) λ λ −λ ( λ + 2) 1
k
1− λ A(λ ) = λ 1 + λ 2
λ λ 的各阶行列式因子。 λ −λ 的各阶行列式因子。 λ 2 −λ 2
2
Department of Mathematics
3-3.方阵的若当标准型

其中,每个初等因子 (i )kti 对应J 的若当
子块 J it
Department of Mathematics
33
例6: 求矩阵 1 1 0
A
4
3
0
1 0 2 的Jordan标准形。
解: 先求出 A 的初等因子。对I A 运用初等
变换可以得到
所以 A 的初等
J
s
其中
Ji1
Ji
Ji2
J isi
mi mi
为A的特征值 i 的若当块, m i 为 i 的代数重复度
Department of Mathematics
31
而:
i 1
i 1
J it
i
1
i kti kti
为A的特征值 i 的若当子块,
t 1 ,2 , si ,i 1 ,2 , , .
换,相当于用相应的 m 阶初等矩阵左乘 A ( ) 。对A ( )
的列作初等列变换,相当于用相应的 n 阶初等矩阵 右
乘 A( ) 定义4 如果 A经( 过) 有限次的初等变换之后变成
B,( 则) 称 与A ( ) 等价B (, )记之为
A()B()
定理2: A ( ) 与 B ( ) 等价的充要条件是存在两个可逆
为不变因子
Department of Mathematics
13
练习1
(1)
A()
(1)2
将其化成Smith标准形。
解:
(1)
A()
(1)2
Department of Mathematics
14
(1)
A()
(1)2
( 1)
( 1)
3-2.埃尔米特二次形及若当标准型

Department of Mathematics
解:
(1)
0 i 1 x1 x1 , x2 , x3 −i 0 0 x2 f ( x1 , x2 , x3 ) = 1 0 0 x3
i 1 + i x1 1 f ( x1 , x2 , x3 ) = x1 , x2 , x3 −i 0 1 x2 1 − i 1 2 x3
(1) (2)
f ( x1 , x2 , x3 ) = i x1 x2 + x1 x3 − ix1 x2 + x1 x3 f ( x1 , x2 , x3 ) = x1 x1 + i x1 x2 + (1 + i ) x1 x3 − i x2 x1 + x2 x3 + (1 − i ) x3 x1 + x3 x1 + 2 x3 x3
f ( x) = xH Ax = y1 + y2 +L+ yp − yp+1 − yp+2 −L− yr
2 2 2 2 2 2
称为 f (x)的规范型
Department of Mathematics
写出下面Hermite二次型的 例1: 写出下面 二次型的 矩阵表达式,并用酉线性替换将其化为标准形 矩阵表达式 并用酉线性替换将其化为标准形. 并用酉线性替换将其化为标准形
由此可以看出:H-阵 的正 负惯性指数即为A 的正、 N 1 由此可以看出 I 阵A的正、负惯性指数即为 N1 p
其中: 其中
λ1 N1 =
O
我们记
Ip H A = N V1 − Ir− p 于是VV ∈ C n n×n ,且: 于是: 且 V = U N2 O I n− r
若当标准型

都是若当块.
第六章 线性空间
例7.8.1 以下若当形矩阵是由哪几个若当块组成?
1 1 0 A= 0 0 0
解:
0 0 0 0 0 1 0 0 0 0 0 i 0 0 0 0 1 i 0 0 0 0 0 0 0 0 0 0 1 0
, A3
1 0 其中 A1 = J (1, 2) = , 1 1 0 0 A3 = J (0, 2) = 1 0
§7.8 若当(Jordan)标准形介绍
§7.8 若当(Jordan)标准形介绍
一,若当(Jordan)形矩阵 二,若当(Jordan)标准形
第六章 线性空间
一,若当(Jordan)形矩阵
λ 1 定义1 形如 J ( λ , t ) = 0 0 0 0 0 1 0 0 0
λ
0 0
λ
1
0 0 的矩阵称为 0 λ t ×t
为若当(Jordan)块.
第六章 线性空间
λ
1 0 0
0 0 0 0 0 0 0 λ 1 0 0 λ t ×t
�
A1 A=
A2
i 0 A2 = J ( i , 2) = , 1 i
第六章 线性空间
二,若当(Jordan)标准形
对于复数域上线性空间V上的线性变换 σ 来说,可以在V中 找到一个基,使 σ 在这个基下的矩阵为若当形,这就是下面的 定理,它回答了前面提出的问题. 定理7.8.1 设 σ 是C上n维线性空间V的一个线性变换,在V 中必存在一个基,使 σ 在这个基下的矩阵是若当形矩阵,且这 个若当形矩阵除去其中若当块的排列次序外,是由 σ 唯一决定 的,这个矩阵称为 σ 的若当标准形. 这个结论用矩阵的语言可叙述为: 定理7.8. 1′ 每个n阶复数矩阵A都与一个若当形矩阵相似, 这个若当形矩阵除去其中若当块的排列次序外被矩阵A唯一确 定,它称为A的若干标准形.
第三章矩阵对角化、若当标准型

第三章 矩阵的对角化、若当标准型§ 矩阵对角化线性变换在基下的矩阵若为对角阵,则向量在基下的表示将非常简单,而线性变换在两个基下的矩阵相似,故线性变换在基下矩阵为对角阵问题即为矩阵对角化问题。
一、特征值、特征向量性质定义1 设n n A ⨯∈C ,称A 的全体特征值为A 的谱。
下面定理1是显然的。
定理1 相似矩阵有相同的特征多项式,从而有相同的谱。
由于矩阵A 的不同特征值对应的特征子空间的和是直和,故有下面定理2。
定理2 设n n A ⨯∈C ,则A 的不同特征值对应的特征向量线性无关。
定义2设n n A ⨯∈C ,i λ为A 的特征值,称A 的特征多项式中i λ的重根数i m 为iλ的代数重复度,称特征子空间i V λ的维数i α为i λ的几何重复度。
由定义2即知A 的特征值i λ的几何重复度i α为A 对应于特征值i λ的线性无关特征向量的个数。
定理3 设n n A ⨯∈C ,i λ为A 的特征值,i α为i λ的几何重复度,则rank()i i n n I A αλ=--证明 特征子空间{|,}i n i V x Ax x x λλ==∈C ,所以dim dim ()ii i n V N I A λαλ==-dim ()i n n R I A λ=-- rank()i n n I A λ=--例1 求123323001A ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦的谱,及相异特征值的代数重复度和几何重复度。
解 123det()32301I A λλλλ----=---+ 2(1)(4)λλ=+-所以A 的谱为11,1λ=--,24λ=,12,λλ的代数重复度分别为122,1m m ==。
1λ的几何重复度113rank()I A αλ=--2233rank 3331000---⎡⎤⎢⎥=----=⎢⎥⎢⎥⎣⎦2λ的几何重复度223rank()I A αλ=--3233rank 3231005--⎡⎤⎢⎥=---=⎢⎥⎢⎥⎣⎦定理4 设n n A ⨯∈C ,i λ为A 的特征值,i m 为i λ的代数重复度,i α为i λ的几何重复度,则i i m α≤。
若当(Jordan)标准形介绍

• 矩阵
• 的最小多项式是: (x-1)2 的最小多项式是: (x-
1 1 1 0 0 0 0 1 0 0 矩阵A = 与矩阵B = 0 0 0 1 0 0 0 0 0 2 的最小多项式都是( x − 1) 2 ( x − 2).
1
0 1 0 0 0 2 0 0 0 2 0
矩阵A与B的最小多项式 相同但它们的特征值不 同(特征多项式不同),从 而A和B不是相似矩阵
引理3.设A是一个准对角矩阵
A1 A= A 2
如果A1的最小多项式是g1(x),A2的最小多 项式是g2(x),则A的最小多项式是g1(x)和 g2(x)的最小公倍式[g1(x),g2(x)]. 推论: 推论:准对角矩阵的最小多项式是个块矩 阵最小多项式的最小公倍式. 阵最小多项式的最小公倍式.
用最小多项式判断一个矩阵能否对角化的 问题 引理1.矩阵A的最小多项式是唯一的. 引理1.矩阵A的最小多项式是唯一的. 1.矩阵 证明: d(x)与g(x)都是矩阵A 证明:设d(x)与g(x)都是矩阵A的最小多项 都是矩阵 g(x)且 |d(x),从而 式,则d(x)| g(x)且g(x) |d(x),从而 d(x)= g(x). 引理2.设 是矩阵A的最小多项式, 引理2.设g(x)是矩阵A的最小多项式,那么 2. 为根的充分必要条件是g( f(x)以A为根的充分必要条件是g(x)整除 f(x).
关于约旦形矩阵的主要结论: 关于约旦形矩阵的主要结论:
设A是复数域上n维线性空间V的线性变换. 是复数域上n维线性空间V的线性变换. 中必定存在一组基, 在V中必定存在一组基,使A在这组基下的 矩阵是若当形矩阵,并且这Jordan Jordan形矩阵 矩阵是若当形矩阵,并且这Jordan形矩阵 除去其中Jordan块的排列次序外,是被A Jordan块的排列次序外 除去其中Jordan块的排列次序外,是被A 唯一决定的-称为矩阵A Jordan标准形 标准形. 唯一决定的-称为矩阵A的Jordan标准形.
方阵的若当标准型

( j )eij ,eij 0,i 1,L , r, j 1,L , s
称为 矩阵A() 的初等因子
例4 如果 矩阵A() 的不变因子为
d1 1
则A() 的初等因子为
d2 ( 1) d3 ( 1)2( 1)2 d4 2( 1)3( 1)3( 2)
( 1)2 1
A3()
2
2
那么
A1() 0
0
A(
)
0
A2 ()
0
0
0 A3()
对于 A3() ,其初等因子为, 1, 1
由上面的定理可知 A() 的初等因子为
,,, 1, 1, 1
A() 的不变因子为
d4 ( 1)( 1), d3 ( 1),
d2 , d1 1
Dk ()
规定: D0( ) 1
显然,如果 rank( A()) r ,则行列式因子一共有r
例个1 求
1 2
A(
)
的各阶行列式因子。
1 2 2 2
由于 (1 , ) 1 ,所以D1() 1 。
1 2 (2 1) f ()
1 2 3( 1) g()
2 1 2
所以:At1 [t1 , t2 , , tn ] j1 At2 [t1 , t2 , , tn ] j2 解方程并选择适当的
t1 , t2 , , tn 即得。
Atn [t1 , t2 , , tn ] jn
称T 为相似变换矩阵。对于相似变换矩阵的
一般理论我们不作过多的讨论,只通过具体的例题
A( ) B( )
定理2: A() 与B() 等价的充要条件是存在两个可
逆
P() Q()
Jordon标准型介绍

3、在一个线性变换 的若当标准形中,主对角线 上的元素是 的特征多项式的全部根(重根按多数 计算). (1、2、3的证明将在第八章给出)
§7.8 λ─矩阵介绍
附:有时也规定形式为
0 J ( , t ) 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 t t
0 0 4 0 0 0
0 0 0 i 1 0
0 0 0 0 i 1
0 J (1,2) 0 0 J (4,1) 0 0 J ( i ,3) i
注:一级若当块就是一级矩阵,从而对角矩阵都是 若当形矩阵.
§7.8 λ─矩阵介绍
§7.8 λ─矩阵介绍
2 0 0 0 如: 1 2 0 , 1 0 1 2 0 0
1 1 0 0 0 0
0 0 1 0
0 0 0 1
0 0, 0 0
i 0 都是若当块; 1 i
而下面的准对角形则是一个若当形矩阵.
0 1 0 0 0 0
的矩阵为若当(Jordan)块.
§7.8 λ─矩阵介绍
二、若当(Jordan)标准形
1、设 是复数域C上n维线性空间的一个线性变换, 在V中必存在一组基,使 在这组基下的矩阵是若当 形矩阵,并是除若当块的排列次序外,该若当形由
唯一决定,称之为 的若当标准形.
2、任一n级复矩阵A总与某一若当形矩阵相似, 并且除若当块的排列次序外,该若当形矩阵由矩阵 A唯一决定,称之为矩阵A的若当标准形.
§7.8 Jordon标准型介绍
一、若当(Jordan)形矩阵
二、若当(Jordan)标准形
第二章 特征值与特征向量 若当标准型

degg ( ) degm1 ( ) 且 g ( A) O ,这与
m1 ( ) 是最小多项式矛盾. 所以唯一.
证毕 定理2.6 矩阵A 的最小多项式 m( ) 与其特 征多项式 ( ) 的零点(即A的特征值)相同 (不计重数).
证ቤተ መጻሕፍቲ ባይዱ设
0
是 ( ) 的零点,即A的特征值,
i i
例7.设 A C 66 的特征多项式是
( ) det(I A) ( 2)( 1)
定理2.4 n阶矩阵A是其特征多项式的根(零 点),即令
( ) det(I A) n an1n1 a0
则
( A) A an1 A a0 I O
n n 1
利用此结论,计算n阶矩阵A的高次幂可以用小 于n的次幂来表示,从而简化矩阵运算。 证明 改写 ( ) 为 ( ) ( 1 )( 2 )( n )
3 ( ) 解 因为 ,所以A 的最小多项式可
能是 , , 之一,由于 A2 0 ,所以A 的最
2 3
小多项式是 m( ) 2 另解:因为 ( ) ,而
3
2 2 0 2 E A 4 2 0 2 2 中各元素的最大公因式为 d ,所以A
1 因为 2 1 P AP n 1 1 1 ( P AP ) ( P AP I ) ( P AP n ) 于是 1 0 2 1 n 1
定理2.2 相似矩阵有相同的特征多项式,因此 有相同的特征值,相同的迹和行列式值。 定理2.3 设 A1 , A2 ,, Am 均为方阵,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明 参见文献 [1] 349 页定理 10.
史莹晶. 若当标准形专题
11/19
电子
学 大
qn ~ y 科 技
U e STC
2 2. 数字矩阵的若当标准形 2.2. 若当标准形的求解
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
1956
【注】 用初等变换化特征矩阵 sI − A 为对角形式, 然后将主
2 数字矩阵的若当标准形
10
2.1 若当标准形的定义 . . . . . . . . . . . . . . . . . 10
2.2 若当标准形的求解 . . . . . . . . . . . . . . . . . 12
2.3 若当标准形的变换矩阵 . . . . . . . . . . . . . . . 14
组成的准对角型矩阵. 不难算出若当块
J 0 = s000
1 s0 0
0 1 s0
所对应的特征矩阵 sI − J 0 的初等因子是 (s − s0)4.
史莹晶. 若当标准形专题
电子
学 大
qn ~ y 科 技
U e STC
2 2. 数字矩阵的若当标准形 2.1. 若当标准形的定义
史莹晶. 若当标准形专题
1 s 矩阵的 Smith 标准形
1.1 Smith 标准形的存在性
定义 1.1 由单位矩阵 I 经过一次初等变换得到的矩阵称为初等 矩阵。
定义 1.2 矩阵 A 与 B 称为等价的,如果 B 可以由 A 经过一 系列初等变换得到。
定义 1.3 如果 m × n 阶矩阵 A(s) 的所有元素 ai,j = ai,j(s) 均 为变量 s 的实系数多项式,则称 A(s) 为一个关于 s 的 m × n 阶实数域上的多项式矩阵,其全体记为 Rm×n[s]。
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
1956
因为数字矩阵与其特征矩阵一一对应, 因此数字矩阵确定,
[ A(λ) = f1(λ)g1(λ)
0 [ B(λ) = f2(λ)g1(λ)
0
] 0
f2(λ)g2(λ) ]
0
f1(λ)g2(λ)
(1.3) (1.4)
如果多项式 f1(λ), f2(λ) 都与 g1(λ), g2(λ) 互素, 则 A(λ) 和 B(λ) 具有相同的各级行列式因子, 即 A(λ) 和 B(λ) 等价.
唯一确定的.
事实上, 如果两个同级的数字矩阵有相同的初等因子, 则它
们就有相同的不变因子, 因而它们相似. 反之, 如果两个矩阵相
似, 则它们有相同的不变因子, 因而它们有相同的初等因子.
史莹晶. 若当标准形专题
7/19
电子
学 大
qn ~ y 科 技
U e STC
1 1. S 矩阵的 SMITH 标准形 1.3. SMITH 标准形的求解
ϕ(s) 为一个多项式。 和数字矩阵的初等变换一样,可以引进初等矩阵,使得对一个
矩阵的初等行(列)变换可以通过适当的初等矩阵左(右)乘
该矩阵来完成。
定义 1.4 如果可以用一系列初等变换将多项式矩阵 A(s) 化为
多项式矩阵 B(s),则称多项式矩阵 A(s) 和 B(s) 相互等价。
史莹晶. 若当标准形专题
1956
数量矩阵 A 的特征矩阵 sI − A 为关于 s 的多项式矩阵。
与数字矩阵类似,多项式矩阵亦有初等变换。 所谓多项式
矩阵的初等行(列)变换,是指下列三种典型操作:
1. 矩阵的两行(列)互换位置。 2. 矩阵的某一行(列)乘以非零的常数 c。 3. 矩阵的某一行(列)加上另一行(列)的 ϕ(s) 倍,此处
1956
定义 1.7 把矩阵 A 的每个次数大于零的不变因子分解成互不
相同的一次因式方幂的乘积, 所有这些一次因式方幂(相同的必
须按出现的次数计算)称为矩阵 A 的初等因子.
例题 1.1 设 12 级矩阵的不变因子是
1, 1, · · · , 1, (λ − 1)2, (λ − 1)2(λ + 1), (λ − 1)2(λ + 1)(λ2 + 1)2
2/19
电子
学 大
qn ~ y 科 技
U e STC
1 1. S 矩阵的 SMITH 标准形 1.1. SMITH 标准形的存在性
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
Q[2, 3]
0
s−2
0
0 s−2
0
0 0
(s − 2)2
0 0
s−2
0 0
s−2
其不变因子为 1, s − 2, (s − 2)2. 初等因子为 s − 2, (s − 2)2.
史莹晶. 若当标准形专题
9/19
2 数字矩阵的若当标准形
2.1 若当标准形的定义
若当 (Jordan) 标准形是数字矩阵的一种结构, 是由若当块
史莹晶. 若当标准形专题
3/19
电子
学 大
qn ~ y 科 技
U e STC
1 1. S 矩阵的 SMITH 标准形 1.2. SMITH 标准形的唯一性
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
1956
sI
−
A
=
s
− 0
2
−3 s−2
0 0
−P−[2−(−−3→)]
1956
1.2 Smith 标准形的唯一性
为了说明 s 矩阵的 Smith 标准形是唯一的, 引入行列式因 子定义.
定义 1.5 设 s 矩阵 A(s) 的秩为 r, 对于正整数 k, 1 ≤ k ≤ r, A(s) 中必有非零的 k 级子式. A(s) 中全部 k 级子式的首项系 数为 1 的最大公因式 Dk(s) 称为 A(s) 的 k 级行列式因子.
1 1. S 矩阵的 SMITH 标准形 1.3. SMITH 标准形的求解
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
对角线上的元素分解成互不相同的一次因式方幂的乘积, 则所有
这些一次因式的方幂(相同的按出现的次数计算)就是 A 的全
部初等因子.
例题 1.2 已知
A = 20
3 2
00
002
求其特征矩阵的 Smith 标准形.
(1.6)
史莹晶. 若当标准形专题
8/19
电子
学 大
qn ~ y 科 技
U e STC
1 1. S 矩阵的 SMITH 标准形 1.3. SMITH 标准形的求解
史莹晶. 若当标准形专题
电子
学 大
qn ~ y 科 技
U e STC
1 1. S 矩阵的 SMITH 标准形 1.1. SMITH 标准形的存在性
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
1956
我们注意不变因子有一个除尽一个的性质, 即
di(s)|di+1(s), i = 1, 2, · · · , n − 1
(1.5)
因此, 在 di(s), i = 1, 2, · · · , n 的分解式中, 属于同一个一次因式 的方幂的指数有递升的性质, 同一个一次因式的方幂作成的初等
因子中, 方次最高的必定出现在 dn(s) 的分解中, 方次次高的必 定出现在 dn−1(s) 的分解中. 如此顺推下去, 可知属于同一个一 次因式的方幂的初等因子在不变因子的分解式中出现的位置是
School of Automation Engineering. University of Electronic Science and Technology of China. School of Automation Engineering.
1956
1.3 Smith 标准形的求解
