2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形剖析

合集下载

全国各地中考数学试卷解析分类汇编(第1期)专题18 图形的展开与叠折

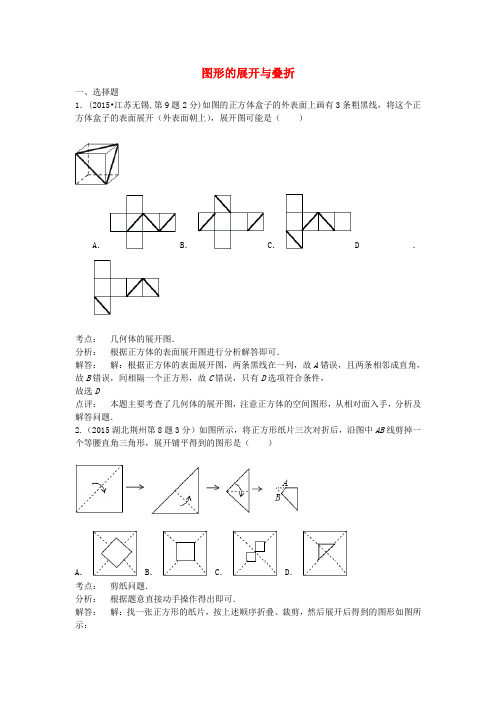
图形的展开与叠折一、选择题1．(2015•江苏无锡,第9题2分)如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（）A ．B ．C ．D ．考点：几何体的展开图．分析：根据正方体的表面展开图进行分析解答即可．解答：解：根据正方体的表面展开图，两条黑线在一列，故A 错误，且两条相邻成直角，故B 错误，间相隔一个正方形，故C 错误，只有D 选项符合条件，故选D点评：本题主要考查了几何体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．2.（2015湖北荆州第8题3分）如图所示，将正方形纸片三次对折后，沿图中AB 线剪掉一个等腰直角三角形，展开铺平得到的图形是（）A ．B ．C ．D ．考点：剪纸问题．分析：根据题意直接动手操作得出即可．解答：解：找一张正方形的纸片，按上述顺序折叠、裁剪，然后展开后得到的图形如图所示：故选A．点评：本题考查了剪纸问题，难点在于根据折痕逐层展开，动手操作会更简便．3.（2015湖北鄂州第8题3分）如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF =（）A．B．C．D．【答案】D.考点：翻折问题.4.（2015•四川资阳,第9题3分）如图5，透明的圆柱形容器（容器厚度忽略不计）的高为12cm ，底面周长为10cm ，在容器内壁离容器底部3 cm 的点B 处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3 cm 的点A 处，则蚂蚁吃到饭粒需爬行的最短路径是 A ．13cmB．CD．考点：平面展开－最短路径问题．.分析：将容器侧面展开，建立A 关于EF 的对称点A ′，根据两点之间线段最短可知A ′B 的长度即为所求．解答：解：如图：∵高为12cm ，底面周长为10cm ，在容器内壁离容器底部3cm 的点B 处有一饭粒，此时蚂蚁正好在容器外壁，离容器上沿3cm 与饭粒相对的点A 处，∴A ′D =5cm ，BD =12﹣3+AE =12cm ，∴将容器侧面展开，作A 关于EF 的对称点A ′，连接A ′B ，则A ′B 即为最短距离，A ′B ===13（Cm ）．故选：A ．点评：本题考查了平面展开﹣﹣﹣最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．5、（2015•四川自贡,第10题4分）如图，在矩形ABCD 中，AB 4AD 6==，,E 是AB 边的中点，F 是线段BC 边上的动点，将△EBF 沿EF 所在直线折叠得到△'EB F ,连接'B D ‘,则'B D ‘的最小值是（）A. 2 B .6 C.2 D .4图5EB考点：矩形的性质、翻折（轴对称）、勾股定理、最值.分析：连接EA 后抓住△DEB 中两边一定，要使'DB 的长度最小即要使'DEB ∠最小(也就是使其角度为0°)，此时点'B 落在DE 上, 此时''D B D E EB =-略解：∵E 是AB 边的中点，AB 4= ∴1AE EB AB 22===∵四边形ABCD 矩形 ∴A 90∠=o∴在Rt △DAE 根据勾股定理可知：222DE AE AD =+又∵AD 6= ∴ED =根据翻折对称的性质可知'EB EB 2==∵△DEB 中两边一定，要使'DB 的长度最小即要使'DEB ∠最小(也就是使其角度为0°)，此时点'B 落在DE 上（如图所示）. ∴''DB DE EB 2=-= ∴'DB 的长度最小值为2. 故选A6. （2015•绵阳第12题，3分）如图，D 是等边△ABC 边AB 上的一点，且AD ：DB =1：2，现将△ABC 折叠，使点C 与D 重合，折痕为EF ，点E ，F 分别在AC 和BC 上，则CE ：CF =（）A ．B ．C ．D ．考点：翻折变换（折叠问题）．.分析：借助翻折变换的性质得到DE =CE ；设AB =3k ，CE =x ，则AE =3k ﹣x ；根据余弦定理分别求出CE 、CF 的长即可解决问题．解答：解：设AD =k ，则DB =2k ； ∵△ABC 为等边三角形，EB∴AB=AC=3k，∠A=60°；设CE=x，则AE=3k﹣x；由题意知：EF⊥CD，且EF平分CD，∴CE=DE=x；由余弦定理得：DE2=AE2+AD2﹣2AE•AD•cos60°即x2=（3k﹣x）2+k2﹣2k（3k﹣x）cos60°，整理得：x=，同理可求：CF=，∴CE：CF=4：5．故选：B．点评：主要考查了翻折变换的性质及其应用问题；解题的关键是借助余弦定理分别求出CE、CF的长度（用含有k的代数式表示）；对综合的分析问题解决问题的能力提出了较高的要求．7. （2015•浙江省台州市，第8题）如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（）A.8cmB.C.5.5cmD.1cm8．(2015·贵州六盘水，第4题3分)如图2是正方体的一个平面展开图，原正方体上两个“我”字所在面的位置关系是（）A．相对 B．相邻 C．相隔 D．重合考点：专题：正方体相对两个面上的文字．.分析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．解答：解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“我”与“国”是相对面， “我”与“祖”是相对面， “爱”与“的”是相对面．故原正方体上两个“我”字所在面的位置关系是相邻．故选B ．点评：本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．9. （2015•浙江宁波，第10题4分）如图，将△ABC 沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的A 1处，称为第1次操作，折痕DE 到BC 的距离记为1h ；还原纸片后，再将△ADE 沿着过AD 中点D 1的直线折叠，使点A 落在DE 边上的A 2处，称为第2次操作，折痕D 1E 1到BC 的距离记为2h ；按上述方法不断操作下去，经过第2015次操作后得到的折痕D 2014E 2014到BC 的距离记为2015h ，若1h =1，则2015h 的值为【】A . 201521B . 201421C .2015211-D .2014212-【答案】D . 【考点】探索规律题（图形的变化类）；折叠对称的性质；三角形中位线定理.【分析】根据题意和折叠对称的性质，DE 是△ABC 的中位线，D 1E 1是△A D 1E 1的中位线，D 2E 2是△A 2D 2E 1的中位线，…∴21111122h =+=-，32211111222h =++=-，42331111112222h =+++=-，…20152201420141111112222h =+++⋅⋅⋅+=-.故选D .10.（2015•江苏泰州,第4题3分）一个几何体的表面展开图如图所示，则这个几何体是A .四棱锥B .四棱柱C .三棱锥D .三棱柱【答案】A . 【解析】试题分析：根据四棱锥的侧面展开图得出答案. 试题解析：如图所示：这个几何体是四棱锥. 故选A .考点：几何体的展开图.11. （2015•四川广安，第4题3分）在市委、市府的领导下，全市人民齐心协力，将广安成功地创建为“全国文明城市”，为此小红特制了一个正方体玩具，其展开图如图所示，原正方体中与“文”字所在的面上标的字应是（）A ．全B ．明C ．城D ．国考点：专题：正方体相对两个面上的文字．.分析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．解答：解：由正方体的展开图特点可得：与“文”字所在的面上标的字应是“城”．故选：C．点评：此题考查了正方体相对两个面上的文字的知识；掌握常见类型展开图相对面上的两个字的特点是解决本题的关键．12. （2015•浙江金华，第9题3分）以下四种沿AB折叠的方法中，不一定能判定纸带两条边线，互相平行的是【】A. 如图1，展开后，测得∠1=∠2B. 如图2，展开后，测得∠1=∠2，且∠3=∠4C. 如图3，测得∠1=∠2D. 如图4，展开后，再沿CD折叠，两条折痕的交点为O，测得OA=OB，OC=OD【答案】C.【考点】折叠问题；平行的判定；对顶角的性质；全等三角形的判定和性质.【分析】根据平行的判定逐一分析作出判断：A. 如图1，由∠1=∠2，根据“内错角相等，两直线平行”的判定可判定纸带两条边线，互相平行；B. 如图2，由∠1=∠2和∠3=∠4，根据平角定义可得∠1=∠2=∠3=∠4=90°，从而根据“内错角相等，两直线平行”或“同旁内角互补，两直线平行”的判定可判定纸带两条边线，互相平行；C. 如图3，由∠1=∠2不一定得到内错角相等或同位角相等或同旁内角互补，故不一定能判定纸带两条边线，互相平行；D. 如图4，由OA=OB，OC=OD，得到，从而得到，进而根据“内错角相等，两直线平行”的判定可判定纸带两条边线，互相平行.故选C.13. （2015•山东潍坊第11 题3分）如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（）A．cm2 B．cm2 C．cm2 D．cm2考点：二次函数的应用；展开图折叠成几何体；等边三角形的性质．.分析：如图，由等边三角形的性质可以得出∠A=∠B=∠C=60°，由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK，根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK，四边形ODEP、四边形PFGQ、四边形QHKO为矩形，且全等．连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°，设OD=x，则AO=2x，由勾股定理就可以求出AD= x，由矩形的面积公式就可以表示纸盒的侧面积，由二次函数的性质就可以求出结论．解答：解：∵△ABC为等边三角形，∴∠A=∠B=∠C=60°，AB=BC=A C．∵筝形ADOK≌筝形BEPF≌筝形AGQH，∴AD=BE=BF=CG=CH=AK．∵折叠后是一个三棱柱，∴DO=PE=PF=QG=QH=OK，四边形ODEP、四边形PFGQ、四边形QHKO都为矩形．∴∠ADO=∠AKO=90°．连结AO，在Rt△AOD和Rt△AOK中，，∴Rt△AOD≌Rt△AOK（HL）．∴∠OAD=∠OAK=30°．设OD=x，则AO=2x，由勾股定理就可以求出AD= x，∴DE=6﹣2 x，∴纸盒侧面积=3x（6﹣2 x）=﹣6 x2+18x，=﹣6 （x﹣）2+ ，∴当x= 时，纸盒侧面积最大为．故选C．点评：本题考查了等边三角形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，矩形的面积公式的运用，二次函数的性质的运用，解答时表示出纸盒的侧面积是关键．二、填空题1. （2015•浙江嘉兴，第14题5分）如图，一张三角形纸片ABC，AB=AC=5.折叠该纸片使点A落在边BC的中点上，折痕经过AC上的点E，则线段AE的长为____▲____.考点：翻折变换（折叠问题）．.分析：如图，D为BC的中点，AD⊥BC，因为折叠该纸片使点A落在BC的中点D上，所以折痕EF垂直平分AD，根据平行线等分线段定理，易知E是AC的中点，故AE=2.5．解答：解：如图所示，∵D为BC的中点，AB=AC，∴AD⊥BC，∵折叠该纸片使点A落在BC的中点D上，∴折痕EF垂直平分AD，∴E是AC的中点，∵AC=5∴AE=2.5．故答案为：2.5．点评：本题考查了折叠的性质，等腰三角形的性质以及平行线等分线段定理，意识到折痕EF垂直平分AD，是解决问题的关键．2. （2015•四川省内江市，第14题，5分）如图，在四边形ABCD中，AD∥BC，∠C=90°，E为CD上一点，分别以EA，EB为折痕将两个角（∠D，∠C）向内折叠，点C，D恰好落在AB边的点F处．若AD=2，BC=3，则EF的长为．考点：翻折变换（折叠问题）．.分析：先根据折叠的性质得DE=EF，CE=EF，AF=AD=2，BF=CB=3，则DC=2EF，AB=5，再作AH⊥BC于H，由于AD∥BC，∠B=90°，则可判断四边形ADCH为矩形，所以AH=DC=2EF，HB=BC﹣CH=BC﹣AD=1，然后在Rt△ABH中，利用勾股定理计算出AH=2，所以EF=．解答：解∵分别以AE，BE为折痕将两个角（∠D，∠C）向内折叠，点C，D恰好落在AB 边的点F处，∴DE=EF，CE=EF，AF=AD=2，BF=CB=3，∴DC=2EF，AB=5，作AH⊥BC于H，∵AD∥BC，∠B=90°，∴四边形ADCH为矩形，∴AH=DC=2EF，HB=BC﹣CH=BC﹣AD=1，在Rt△ABH中，AH==2，∴EF=．故答案为：．点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理．3. （2015•浙江滨州,第17题4分）如图，在平面直角坐标系中，将矩形AOCD沿直线AE 折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8），则点E的坐标为 .【答案】（10,3）考点：折叠的性质，勾股定理4. （2015•浙江杭州,第16题4分）如图，在四边形纸片ABCD中，AB=BC，AD=CD，∠A=∠C=90°，∠B=150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平，若铺平后的图形中有一个是面积为2的平行四边形，则CD=_______________________________【答案】24+【考点】剪纸问题；多边形内角和定理；轴对称的性质；菱形、矩形的判定和性质；含30度角直角三角形的性质；相似三角形的判定和性质；分类思想和方程思想的应用.【分析】∵四边形纸片ABCD中，∠A=∠C=90°，∠B=150°，∴∠C=30°.如答图，根据题意对折、裁剪、铺平后可有两种情况得到平行四边形：如答图1，剪痕BM、BN，过点N作NH⊥BM于点H，第16题A易证四边形BMDN 是菱形，且∠MBN =∠C =30°.设BN =DN =x ，则NH =12x.根据题意，得1222x x x ⋅=⇒=，∴BN =DN =2， NH =1.易证四边形BHNC 是矩形，∴BC =NH =1. ∴在Rt BCN ∆中，CN∴CD=2+如答图2，剪痕AE 、CE ，过点B 作BH ⊥CE 于点H ，易证四边形BAEC 是菱形，且∠BCH =30°.设BC =CE =x ，则BH =12x.根据题意，得1222x x x ⋅=⇒=，∴BC =CE =2， BH =1.在Rt BCH ∆中，CHEH=2.易证BCD EHB ∆∆∽，∴CD BC HB EH =，即1CD =∴224CD +==+.综上所述，CD =2+4+5. （2015•四川省宜宾市，第15题，3分）如图，一次函数的图象与x 轴、y 轴分别相交于点A 、B ，将△AOB 沿直线AB 翻折，得△ACB .若C (32，32)，则该一次幽数的解析式为 .y =+yxCBAO三、解答题1. （2015•浙江金华，第23题10分）图1，图2为同一长方体房间的示意图，图2为该长方体的表面展开图.（1）蜘蛛在顶点A'处①苍蝇在顶点B 处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线；②苍蝇在顶点C 处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD 爬行的最近路线A 'GC 和往墙面BB'C'C 爬行的最近路线A 'HC ，试通过计算判断哪条路线更近？（2）在图3中，半径为10dm 的⊙M 与D 'C '相切，圆心M 到边CC'的距离为15dm ，蜘蛛P 在线段AB 上，苍蝇Q 在⊙M 的圆周上，线段PQ 为蜘蛛爬行路线。

中考数学真题分类汇编套专题三十四·矩形菱形正方形

一、选择题1．2010江苏苏州如图,在菱形ABCD 中,DE ⊥AB,3cos 5A =,BE=2,则tan ∠DBE 的值是 A ．12B ．2C ．52D ．55答案B2．2010湖南怀化如图２,在菱形ABCD 中, 对角线AC=4,∠BAD=120°, 则菱形ABCD 的周长为A ．20B ．18C ．16D ．15 答案C3．2010安徽芜湖下列命题中是真命题的是A ．对角线互相垂直且相等的四边形是正方形B ．有两边和一角对应相等的两个三角形全等C ．两条对角线相等的平行四边形是矩形D ．两边相等的平行四边形是菱形答案C4．2010甘肃兰州如图所示,菱形ABCD 的周长为20cm ,DE ⊥AB,垂足为E,sin A=53,则下列结论正确的个数有①cm DE 3= ②cm BE 1= ③菱形的面积为215cm ④cm BD 102= A ． 1个 B ． 2个 C ． 3个 D ． 4个答案C5．2010江苏南通如图,菱形ABCD 中,AB = 5,∠BCD = 120°,则对角线AC 的长是A ．20B ．15C ．10D ．5答案D6．2010江苏盐城如图所示,在菱形ABCD 中,两条对角线AC ＝6,BD ＝8,则此菱形的边长为 A ．5B ．6C ．8D ．10答案A7．2010 浙江省温州下列命题中,属于假命题的是▲A ．三角形三个内角的和等于l80°B ．两直线平行,同位角相等C ．矩形的对角线相等D ．相等的角是对顶角．答案D8．2010 浙江省温州如图,AC ；BD 是矩形ABCD 的对角线,过点D 作DE ／／AC 交BC 的延长线于E,则图中-与AABC 全等的三角形共有．▲A ．1个B ．2个C ．3个D ．4个答案D9．2010 浙江义乌下列说法不正确．．．的是 ▲ A ．一组邻边相等的矩形是正方形 B ．对角线相等的菱形是正方形 C ．对角线互相垂直的矩形是正方形 D ．有一个角是直角的平行四边形是正方形答案D10．2010 重庆已知：如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE ．过点A 作AE 的垂线交ED 于点P ．若1AE AP ==, 5PB =．下列结论：①△APD ≌△AEB ；②点B 到直线AE 2； ③EB ED ⊥；④16APD APB S S ∆∆+=46ABCD S =+正方形ABCD第6题BACD第8题其中正确结论的序号是A ．①③④B ．①②⑤C ．③④⑤D ．①③⑤ 答案D11．2010山东聊城如图,点P 是矩形ABCD 的边AD 的一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P到矩形的两条对角线AC 和BD 的距离之和是A ．125B ．65C ．245D ．不确定答案A12．2010 福建晋江如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作；然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作；再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作；...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是 .A. 669B. 670 D. 672答案B13．2010 山东济南如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2010厘米后停下,则这只蚂蚁停在点．答案C14．2010 江苏连云港如图,四边形ABCD 的对角线AC 、BD 互相垂直,则下列条件能判定四边形ABCD 为菱形的是CAFDB G第7题图10题图A PEDCBA ．BA ＝BCB ．AC 、BD 互相平分 C ．AC ＝BD D ．AB ∥CD 答案B15．2010福建宁德如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是 . A ．2＋10 B ．2＋210 C ．12 D ．18 答案B16．2010江西如图,已知矩形纸片ABCD,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸片折叠,使点B 落在纸片上的点H 处,连接AH,则与∠BEG 相等的角的个数为 A ．4 B ．3 C ．2 D ．1答案B17．2010 山东滨州如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为° ° °° 答案C18．2010山东潍坊如图,已知矩形ABCD ,一条直线将该矩形ABCD 分割成两个多边形含三角形,若这两个多边形的内角和分别为M 和N ,则M ＋N 不可能是．BAG CDHE第8题图B C D第7题① ② 3 4答案D19．2010北京若菱形两条对角线的长分别为6和8,则这个菱形的周长为A．20 B．16 C．12 D． 10答案A20．2010 浙江省温州下列命题中,属于假命题的是▲A．三角形三个内角的和等于l80° B．两直线平行,同位角相等C．矩形的对角线相等 D．相等的角是对顶角．答案D21．2010 浙江义乌下列说法不正确．．．的是▲A．一组邻边相等的矩形是正方形B．对角线相等的菱形是正方形C．对角线互相垂直的矩形是正方形D．有一个角是直角的平行四边形是正方形答案D22．2010陕西西安若一个菱形的边长为2,则这个菱形两条对角线长的平方和为A．16 B．8 C．4 D．1答案A23．2010江西省南昌如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,︒BEG,现沿直线EG将纸片折叠,使点B落在约片上的点H处,∠60>∠相等的角的个数为连接AH,则与BEGB. 3C.2第10题答案B24．2010湖北襄樊下列命题中,真命题有1邻补角的平分线互相垂直2对角线互相垂直平分的四边形是正方形3四边形的外角和等于360°4矩形的两条对角线相等A．1个B．2个C．3个D．4个答案C25．2010湖北襄樊菱形的周长为8cm,高为1cm,则菱形两邻角度数比为A．3：1 B．4：1 C．5：1 D．6：1答案C26．2010 四川泸州如图1,四边形ABCD是正方形,E是边CD上一点,若△AFB经过逆时针旋转角θ后与△AED重合,则θ的取值可能为A．90°B．60°C．45°D．30°答案A27．2010 山东淄博如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置．若∠AMD′＝36°,则∠NFD ′等于A144° B126°C108° D72° 答案B28．2010 天津下列命题中正确的是A 对角线相等的四边形是菱形B 对角线互相垂直的四边形是菱形C 对角线相等的平行四边形是菱形D 对角线互相垂直的平行四边形是菱形答案D29．2010 湖南湘潭下列说法中,你认为正确的是A ．四边形具有稳定性B ．等边三角形是中心对称图形C ．任意多边形的外角和是360oD ．矩形的对角线一定互相垂直答案C30．2010 福建泉州南安已知四边形ABCD 中,90A B C ===∠∠∠,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是． A ．90D =∠ B ．AB CD = C ．AD BC = D ．BC CD = 答案D31．2010 四川自贡边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB ′C ′D ′,两图叠成一个“蝶形风筝”如图所示阴影部分,则这个风筝的面积是 ;A ．2－33B ．332 C ．2－43D ．2答案A32．2010 山东荷泽如图,矩形纸片ABCD 中,AB ＝4,AD ＝3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,记与点A重合点为A ＇,则△A ＇B G 的面积与该矩形的面积比为BCD ′NF 第10题A ．121 B ．91C ．81D ．61答案C33．2010 山东荷泽如图,菱形ABCD 中,∠B ＝60°,AB ＝2㎝,E 、F 分别是BC 、CD 的中点,连结AE 、EF 、AF ,则△AEF 的周长为A ．32㎝B ．33㎝C ．34㎝D ．3㎝答案B34．2010青海西宁矩形ABCD 中,E 、F 、M 为AB 、BC 、CD 边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM 的长为 A ．5 B ．25 C ．6 D ．26答案B35．2010广西南宁正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK ∆ 的面积为：A10 B12 C14 D16答案D36．2010广东茂名如图,边长为1的正方形ABCD 绕点A 逆时针旋转45度后得到正方形'''D C AB ,边''C B 与DC 交于点O,则四边形OD AB '的周长．．是 A ．22 B ．3 C ．2 D ．21+8题图ABC DEFA BCDGA ＇答案A37．2010广西柳州如图4,在正方形ABCD 的外侧作等边△ADE ,则∠AEB 的度数为 A ．10° B ．° C ．15° D ．20°答案C38．2010广西柳州如图6,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A对应点为A ',且C B '=3,则AM 的长是A ．B ．2C ．D ．答案B39．2010湖北宜昌如图,菱形ABCD 中,AB=15,120ADC ∠=°,则B 、D 两点之间的距离为 ; 40．2010广西河池如图5是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边x y >,下列四个说法：①2249x y +=,②2x y -=,③2449xy +=,④9x y +=. 其中说法正确的是A ．①② B. ①②③ C. ①②④ D. ①②③④A BCDMNA 'B '图6第10题图OC 'B 'D D答案B41．2010广东肇庆菱形的周长为4,一个内角为60°,则较短的对角线长为A ．2B ．错误!C ．1D ．错误! 答案C42．2010吉林如图,在矩形ABCD 中,AB=12cm,BC=6cm,点E 、F 分别在AB 、CD 上,将矩形ABCD 沿EF 折叠,使点A 、D 分别落在矩形ABCD 外部的点A’,D’处,则整个阴影部分图形的周长．．为 A ．18cmB ．36cmC ．40cmD ．72cm答案BB.15323答案A二、填空题1．2010江苏盐城小明尝试着将矩形纸片ABCD 如图①,AD >CD 沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE 如图②；再沿过D 点的直线折叠,使得C 点落在DA 边上的点N 处,E 点落在AE 边上的点M 处,折痕为DG 如图③．如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD 长与宽的比值为 ▲ ．答案错误!2．2010山东威海从边长为a 的大正方形纸板中间挖去一个边长为b 的小正方形后,将其截成四个相同的等腰梯形﹙如图①﹚,可以拼成一个平行四边形﹙如图②﹚．现有一平行四边形纸片ABCD ﹙如图③﹚,已知∠A ＝45°,AB ＝6,AD ＝4．若将该纸片按图②方式截成四个相同的等腰梯形,然后按图①方式拼图,则得到的大正方形的面积为．yx图5A第13题A BCDABDF① ②B C G MN ③答案2611+．3．2010浙江嘉兴如图,已知菱形ABCD 的一个内角︒=∠80BAD ,对角线AC 、BD 相交于点O ,点E 在AB 上,且BO BE =,则EOA ∠= ▲ 度．答案254．2010年上海已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1如图4所示把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为___________.E DCBAFF答案CF=1或55．2010山东青岛把一张矩形纸片矩形ABCD 按如图方式折叠,使顶点B 和点D 重合,折痕为EF ．若AB = 3 cm,BC =5 cm,则重叠部分△DEF 的面积是 cm 2．答案6．2010 福建德化已知菱形的两对角线长分别为6㎝和8㎝,则菱形的面积为㎝2.答案247．2010湖南邵阳如图九在等腰梯形ABCD 中,AB ∥DC ,AD=BC=CD ,点E 为AB 上一点,连结CE ,请添加一个你认为合适的条件 ,使四边形AECD 为菱形．图4第15题D图 ② 图 ①a A图 ③BC第18题图A BCFE 'A 第13题图 'B DAE DCB图九答案AE ＝CD 或AD ∥CE 或CE=BC 或∠CEB ＝∠B 的任意一个都可8．2010山东临沂正方形ABCD 的边长为a ,点E 、F 分别是对角线BD 上的两点,过点E 、F 分别作AD 、AB 的平行线,如图所示,则图中阴影部分的面积之和等于 .答案212a9．2010四川宜宾如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论：①AP =EF ；②AP ⊥EF ；③△APD 一定是等腰三角形；④∠PFE =∠BAP ；⑤PD = 错误!EC ．其中正确结论的序号是．答案①、②、④、⑤．10．2010 江苏连云港矩形纸片ABCD 中,AB ＝3,AD ＝4,将纸片折叠,使点B 落在边CD 上的B ’处,折痕为AE ．在折痕AE 上存在一点P 到边CD 的距离与到点B 的距离相等,则此相等距离为________．答案11．2010 黄冈如图矩形纸片ABCD,AB ＝5cm,BC ＝10cm,CD 上有一点E,ED ＝2cm,AD 上有一点P,PD ＝3cm,过P 作PF ⊥AD 交BC 于F,将纸片折叠,使P 点与E 点重合,折痕与PF 交于Q 点,则PQ 的长是____________cm.第18题 A BCB ’ D E P A BCD EF MN Q P第18题图答案3412．2010 河北把三张大小相同的正方形卡片A,B,C 叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示．若按图10-1摆放时,阴影部分的面积为S 1；若按图10-2摆放时,阴影部分的面积为S 2,则S 1 S 2填“＞”、“＜”或“=”．答案=13．2010 山东省德州在四边形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,如果四边形EFGH 为菱形,那么四边形ABCD 是只要写出一种即可．答案答案不唯一：只要是对角线相等的四边形均符合要求．如：正方形、矩形、等腰梯形等． 14．2010 广东珠海如图,P 是菱形ABCD 对角线BD 上一点,PE ⊥AB 于点E,PE ＝4cm, 则点P 到BC 的距离是_____cm.答案415．2010 四川巴中如图5所示,已知□ABCD,下列条件：①AC=BD,②AB=AD,③∠1=∠2,④AB ⊥BC 中,能说明□ABCD 是矩形的有填写番号;答案①④ 16．2010江苏淮安已知菱形ABCD 中,对角线AC=8cm,BD=6cm,在菱形内部包括边界任取一点P,使△A CP 的面积大于6cm 2的概率为．２１ＤＣＢA图5图10-1 ACBCBA图10-2答案1417．2010 湖南株洲如图,四边形ABCD 是菱形,对角线AC 和BD 相交于点O ,4AC cm =,8BD cm =,则这个菱形的面积是 2cm ．答案1618．2010广东中山如图1,已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形1111D C B A ；把正方形1111D C B A 边长按原法延长一倍得到正方形2222D C B A 如图2；以此下去,则正方形n n n n D C B A 的面积为．答案62519．2010江苏苏州如图,四边形ABCD 是正方形,延长AB 到E, 使AE=AC,则∠BCE 的度数是 ▲ °．答案20．2010湖北恩施自治州如图,在矩形ABCD 中,AD =4,DC =3,将△ADC 按逆时针方向绕点A 旋转到△AEF 点A 、B 、E 在同一直线上,连结CF ,则CF = .答案5221．2010山东泰安如图,将矩形纸片ABCD 沿EF 折叠,使D 点与BC 边的中点D /重合,若BC=8,CD=6,则CF= .O DCBA第14题图答案35 22．2010云南楚雄如图,在□ABCD 中,对角线AC 与BD 相交于点O ,在不添加任何辅助线和字母的情况下,请添加一个条件,使得□ABCD 变为矩形,需要添加的条件是．写出一个即可答案AC ＝BD 或∠ABC ＝90°等．23．2010湖北随州如图矩形纸片ABCD,AB ＝5cm,BC ＝10cm,CD 上有一点E,ED ＝2cm,AD 上有一点P,PD ＝3cm,过P 作PF ⊥AD 交BC 于F,将纸片折叠,使P 点与E 点重合,折痕与PF 交于Q 点,则PQ 的长是____________cm.答案3424．2010黑龙江哈尔滨如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C '处,折痕为EF,若20=∠ABE ,那么C EF '∠的度数为度;答案12525．2010广东东莞如图⑴,已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1；把正方形A 1B 1C 1D 1边长按原法延长一倍后得到正方形A 2B 2C 2D 2如图⑵；以此下去…,则正方形A 4B 4C 4D 4的面积为．ADO答案62526．2010 四川绵阳已知菱形ABCD 的两条对角线相交于点O ,若AB = 6,∠BDC = 30,则菱形的面积为．答案18327．2010 广东汕头如图1,已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1；把正方形A 1B 1C 1D 1边长按原法延长一倍得到正方形A 2B 2C 2D 2如图2；以此下去···,则正方形A 4B 4C 4D 4的面积为__________答案62528．2010 山东淄博在一块长为8、宽为32的矩形中,恰好截出三块形状相同、大小不等的直角三角形,且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是．答案229．2010 天津如图,已知正方形ABCD 的边长为3,E 为CD 边上一点,1DE =．以点A 为中心,把△ADE 顺时针旋转90︒,得△ABE ',连接EE ',则EE '的长等于．第13题图1 1B 1C 1D 1A BC D D 2A 2B 2C 2D 1C 1B 1A 1A BC D 第13题图2ABC D A 1B 1C 1D 1第10题图1CDA 1B 1C 1D 1 A BA 2B 2C 2D 2第10题图2答案2530．2010 甘肃如图,在ABC △中,点D 、E 、F 分别在边AB 、BC 、CA 上,且DE CA ∥,DF BA ∥．下列四种说法： ①四边形AEDF 是平行四边形；②如果90BAC ∠=,那么四边形AEDF 是矩形； ③如果AD 平分BAC ∠,那么四边形AEDF 是菱形；④如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形. 其中,正确的有 .只填写序号答案①②③④31．2010 福建泉州南安如图,大正方形网格是由25个边长为1的小正方形组成, 把图中阴影部分剪下来,用剪下来的阴影部分拼成一个正方形, 那么新正方形的边长是．答案532．2010广西梧州如图3,边长为6的正方形ABCD 绕点B 按顺时针方向旋转30°后得到正方形EB G F ,E F 交CD 于点H ,则F H 的长为______结果保留根号;图3ABCDFE HG第16题图ＡＦＣＤＢＥ第18题图第14题AE ' C答案6-2333．2010广西河池如图2,矩形ABCD 中,AB ＝8cm,BC ＝4cm,E 是DC 的中点,BF ＝41BC ,则四边形DBFE 的面积为 2cm ．答案1034．2010贵州铜仁已知菱形的两条对角线的长分别为5和6,则它的面积是________．答案1535．2010云南曲靖如图,活动衣帽架由三个菱形组成,利用四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩,当菱形的边长为18cm,α=1200时,A 、B 两点的距离为 cm.答案5436．2010黑龙江绥化如图所示,E 、F 是矩形ABCD 对角线AC 上的两点,试添加一个条件： ,使得△ADF ≌△CBE ．答案AF=CE 或AE=CF 或DF ∥BE 或∠ABE=∠CDF 等37．2010黑龙江绥化如图,在平面直角坐标系中,边长为1的正方形OA 1B 1C 的对角线 A 1C 和OB 1交于点M 1；以M 1A 1为对角线作第二个正方形A 2A 1B 2M 1,对角线A 1M 1和A 2B 2交于点M 2；以M 2A 1为对角线作第三个正方形A 3A 1B 3M 2,对角线A 1M 2和A 3B 3交于点M 3；……依此类推,这样作的第n 个正方形对角线交点M n 的坐标为 .答案111,22nn ⎛⎫-⎪⎝⎭38．2010内蒙呼和浩特如图,矩形ABCD 沿着直线BD 折叠,使点C 落在C '处,C B '交AD 于点E ,AD = 8,AB = 4,则DEEB图2的长为．答案5三、解答题1．2010安徽省中中考如图,AD ∥FE,点B 、C 在AD 上,∠1＝∠2,BF ＝BC ⑴求证：四边形BCEF 是菱形⑵若AB ＝BC ＝CD,求证：△ACF ≌△BDE 答案2．10湖南益阳如图7,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E ．1 求∠ABD 的度数； 2求线段BE 的长．答案解:⑴ 在菱形ABCD 中,AD AB =,︒=∠60A∴ABD ∆为等边三角形∴︒=∠60ABD ……………………………4分⑵由1可知4==AB BD又∵O 为BD 的中点∴2=OB ……………………………6分又∵AB OE ⊥,及︒=∠60ABD ∴︒=∠30BOE∴1=BE ……………………………8分D ABO607图3．10湖南益阳我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度．．相等．．. 一条直线l 与方形环的边线有四个交点M 、'M 、'N 、N ．小明在探究线段'MM 与N N ' 的数量关系时,从点'M 、'N 向对边作垂线段E M '、F N ',利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：⑴当直线l 与方形环的对边相交时如图18-,直线l 分别交AD 、D A ''、C B ''、BC 于M 、'M 、'N 、N ,小明发现'MM 与N N '相等,请你帮他说明理由；⑵当直线l 与方形环的邻边相交时如图28-,l 分别交AD 、D A ''、C D ''、DC 于M 、'M 、'N 、N ,l 与DC 的夹角为α,你认为'MM 与N N '还相等吗若相等,说明理由；若不相等,求出NN MM ''的值用含α的三角函数表示.答案⑴解: 在方形环中,∵AD BC F N AD E M ,',⊥⊥'∥BC∴NF N M EM FN N EM M F N E M ',90','∠='∠=∠='∠='︒∴△E MM '≌△F NN '∴N N M M '=' ……………………………5分⑵解法一：∵α='∠='∠︒='∠='∠M M E N FN M ME N NF ,90 ∴N NF '∆∽EM M '∆ ……………………………8分∴NFEM N N M M '='' ∵F N E M '='∴αtan ''='=NFFN N N MM 或ααcos sin ……………………………10分 ①当︒=45α时,tan α=1,则N N M M '=' ②当︒≠45α时,N N M M '≠' 则αtan =''N N M M 或ααcos sin ……………………………12分解法二：在方形环中,︒=∠90D又∵CD F N AD E M ⊥⊥'', ∴E M '∥E M F N DC '=', ∴α=∠='∠NF N E M M ' 在F N N Rt '∆与E M M Rt '∆中,B18-图28-图MM EM N N F N ''='=ααcos ,'sin N N M M E M M M N N F N ''=''⋅'=='cos sin tan ααα 即 αtan =''N N M M 或ααcos sin ……………………………10分 ①当︒=45α时,N N M M '=' ②当︒≠45α时,N N M M '≠' 则αtan =''N N M M 或ααcos sin ……………………………12分 4．2010江苏南京8分如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止,连接EM 并延长交射线CD 于点F,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG;1设AE=x 时,△EGF 的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围； 2P 是MG 的中点,请直接写出点P 的运动路线的长;答案5．2010辽宁丹东市如图,已知矩形ABCD 中,E 是AD 上的一点,F 是AB 上的一点,EF ⊥EC ,且EF =EC ,DE =4cm,矩形ABCD的周长为32cm,求AE 的长．答案解：在Rt△AEF 和Rt△DEC 中, ∵EF ⊥CE , ∴∠FEC =90°,∴∠AEF +∠DEC =90°,而∠ECD +∠DEC =90°,∴∠AEF =∠ECD ． ····················· 3分又∠FAE =∠EDC =90°．EF =EC ∴Rt△AEF ≌Rt△DCE ． ····················· 5分 AE =CD ． ····················· 6分 AD =AE +4．∵矩形ABCD 的周长为32 cm, ∴2AE +AE +4=32． ······················· 8分解得, AE =6 cm ． 10分6．2010山东济宁数学课上,李老师出示了这样一道题目：如图1,正方形ABCD 的边长为12,P 为边BC 延长线上的一点,E 为DP 的中点,DP 的垂直平分线交边DC 于M ,交边AB 的延长线于N .当6CP =时,EM 与EN 的比值是多少经过思考,小明展示了一种正确的解题思路：过E 作直线平行于BC 交DC ,AB 分别于F ,G ,如图2,则可得：DF DEFC EP=,因为DE EP =,所以DF FC =.可求出EF 和EG 的值,进而可求得EM 与EN 的比值.1 请按照小明的思路写出求解过程.2 小东又对此题作了进一步探究,得出了DP MN =的结论.你认为小东的这个结论正确吗如果正确,请给予证明；如果不正确,请说明理由. 答案1解：过E 作直线平行于BC 交DC ,AB 分别于点F ,G ,则DF DE FC EP =,EM EFEN EG=,12GF BC ==. ∵DE EP =,∴DF FC =. ······························································· 2分∴116322EF CP ==⨯=,12315EG GF EF =+=+=. ∴31155EM EF EN EG ===. ································································· 4分 2证明：作MH ∥BC 交AB 于点H , ····························································· 5分则MH CB CD ==,90MHN ∠=︒. ∵1809090DCP ∠=︒-︒=︒, ∴DCP MHN ∠=∠.∵90MNH CMN DME CDP ∠=∠=∠=︒-∠,90DPC CDP ∠=︒-∠, ∴DPC MNH ∠=∠.∴DPC MNH ∆≅∆. ········································ 7分第20题图BCA EDF 第22题∴DP MN =. ··········································································· 8分7．2010山东青岛已知：如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF ．1求证：BE = DF ；2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM ．判断四边形AEMF 是什么特殊四边形并证明你的结论．答案证明：1∵四边形ABCD 是正方形,∴AB ＝AD ,∠B = ∠D = 90°． ∵AE = AF ,∴Rt Rt ABE ADF △≌△． ∴BE ＝DF ． ·························· 4分 2四边形AEMF 是菱形．∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC ．∵BE ＝DF ,∴BC －BE = DC －DF . 即CE CF =．∴OE OF =．∵OM = OA ,∴四边形AEMF 是平行四边形． ∵AE = AF ,∴平行四边形AEMF 是菱形． ·························· 8分8．2010山东日照如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,∠AEF =90o ,且EF 交正方形外角的平分线CF 于点F ． 1证明：∠BAE =∠FEC ； 2证明：△AGE ≌△ECF ； 3求△AEF 的面积．第22题H B CDE M NA PA DB E F O CM 第21题图DCBAOE答案1证明：∵∠AEF =90o ,∴∠FEC +∠AEB =90o ．………………………………………1分在Rt △ABE 中,∠AEB +∠BAE =90o ,∴∠BAE =∠FEC ；……………………………………………3分 2证明：∵G ,E 分别是正方形ABCD 的边AB ,BC 的中点,∴AG=GB=BE=EC ,且∠AGE =180o －45o =135o ．又∵CF 是∠DCH 的平分线,∠ECF =90o +45o =135o ．………………………………………4分在△AGE 和△ECF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠=FEC GAE ECF AGE EC AG o,135, ∴△AGE ≌△ECF ； …………………………………………6分 3解：由△AGE ≌△ECF ,得AE=EF ．又∵∠AEF =90o ,∴△AEF 是等腰直角三角形．………………………………7分由AB=a ,BE =21a ,知AE =25a ,∴S △AEF =85a 2．…………………………………………………9分 9．2010四川眉山如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD ．1试判断四边形OCED 的形状,并说明理由； 2若AB =6,BC =8,求四边形OCED 的面积．答案解：1四边形OCED 是菱形．…………2分∵DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形,…………3分又在矩形ABCD 中,OC =OD ,∴四边形OCED 是菱形．…………………4分 2连结OE ．由菱形OCED 得：CD ⊥OE , …………5分 ∴OE ∥BC 又 CE ∥BD∴四边形BCEO 是平行四边形∴OE =BC =8……………………………………………7分∴S 四边形OCED =11862422OE CD ⋅=⨯⨯=……………8分DCBAOE10．2010浙江宁波如图1,有一张菱形纸片ABCD ,AC =8, BD =6. 1请沿着AC 剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图2中用实线画出你所拼成的平行四边形；若沿着BD 剪开,请在图3中用实线画出拼成的平行四边形.并直接写出这两个平行四边形的周长.2沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4中用实线画出拼成的平行四边形.注：上述所画的平行四边形都不能与原菱形全等答案解：11分周长为26 2分3分周长为22 4分 26分注:画法不唯一.11．2010浙江绍兴 1 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF ＝90°. 求证：BE ＝CF .第21题图2 图3 图4周长为 ▲ 周长为 ▲图12 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH ＝90°, EF ＝4.求GH 的长.3 已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH ＝90°,EF ＝4. 直接写出下列两题的答案：①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长；②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长用n 的代数式表示.答案1 证明：如图1,∵ 四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°, ∴ ∠EAB +∠AEB =90°. ∵ ∠EOB =∠AOF ＝90°, ∴ ∠FBC +∠AEB =90°,∴ ∠EAB =∠FBC , ∴ △ABE ≌△BCF , ∴ BE =CF ． 2 解：如图2,过点A 作第23题图 1第23题图2第23题图3第23题图1第23题图2O ′NMAM 1证明：△AB E ≌△DAF ；2若∠AGB =30°,求EF 的长.答案解：1∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB ∴△ABE ≌△DAF -----------------------4分2∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分在正方形ABCD 中, AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中,∠AFD=900AD=2∴AF=3 DF =----------------------------8分由1得△ABE ≌△ADF ∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分14．2010山东聊城如图,在等边△ABC 中,点D 是BC 边的中点,以AD 为边作等边△ADE ．1求∠CAE 的度数；2取AB 边的中点F ,连结CF 、CE ,试证明四边形AFCE 是矩形．ABDEF 1423题图24答案1在等边△ABC 中,∵点D 是BC 边的中点,∴∠DAC ＝30o,又∵等边△ADE ,∴∠DAE ＝60o,∴∠CAE ＝30o 2在等边△ABC 中,∵F 是AB 边的中点,D 是BC 边的中点,∴CF ＝AD ,∠CF A ＝90o,又∵AD ＝AE ,∴AE ＝CF ,由1知∠CAE ＝30o,∴∠EAF ＝60o+30o ＝90o,∴∠CF A ＝∠EAF ,∴CF ∥AE ,∵AE ＝CF ,∴四边形AFCE 是平行四边形,又∵∠CF A ＝90o,∴四边形AFCE 是矩形．15．2010湖南长沙在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED 1求证：△BEC ≌△DEC ；2延长BE 交AD 于F,当∠BED ＝120°时,求EFD 的度数．答案解：1∵四边形ABCD 是正方形, ∴BC ＝DC又∵AC 为对角线,E 为AC 上一点, ∴∠BCE ＝∠DCE ＝45°． ∵EC ＝EC,∴△BEC ≌△DECSAS ；2∵△BEC ≌△DEC, ∠BED ＝120°, ∴∠BEC ＝∠DEC ＝60°． ∵∠DAC ＝45°, ∴∠ADE ＝15°∴∠EFD ＝∠BED －∠ADE ＝120°－15°＝105°16．2010浙江金华本题12分如图,把含有30°角的三角板ABO 置入平面直角坐标系中,A ,B 两点坐标分别为3,0和3动点P 从A 点开始沿折线AO-OB-BA 运动,点P 在AO ,OB ,BA 上运动的速度分别为3长度单位/秒﹒一直尺的上边缘l 从x 轴的位置开始以错误! 长度单位/秒的速度向上平行移动即移动过程中保持l ∥x 轴,且分别与OB , AB 交于E ,F 两点﹒设动点P 与动直线l 同时出发,运动时间为t 秒,当点P 沿折线 AO -OB -BA 运动一周时,直线l 和动点P 同时停止运动．请解答下列问题：1过A ,B 两点的直线解析式是 ▲ ；2当t ﹦4时,点P 的坐标为 ▲ ；当t ﹦ ▲ ,点P 与点E 重合； 3① 作点P 关于直线EF 的对称点P′. 在运动过程中,若形成的四边形PEP′F 为菱形,则t 的值是多少第22题图F C② 当t ﹦2时,是否存在着点Q ,使得△FEQ ∽△BEP 若存在, 求出点Q 的坐标；若不存在,请说明理由．答案解：1333+-=x y ； 20,3,29=t ； 3①当点P 在线段AO 上时,过F 作FG ⊥x 轴,G 为垂足如图1∵FG OE =,FP EP =,∠=EOP ∠=FGP 90° ∴△EOP ≌△FGP ,∴PG OP =﹒又∵t FG OE 33==,∠=A 60°,∴t FG AG 3160tan 0== 而t AP =,∴t OP -=3,t AG AP PG 32=-=由t t 323=-得 59=t ；当点P 在线段OB 上时,形成的是三角形,不存在菱形；当点P 在线段BA 上时,过P 作PH ⊥EF ,PM ⊥OB ,H 、M 分别为垂足如图2∵t OE 33=,∴t BE 3333-=,∴3360tan 0t BE EF -==∴6921tEF EH MP -===, 又∵)6(2-=t BP 在Rt △BMP 中,MP BP =⋅060cos 即6921)6(2tt -=⋅-,解得745=t ．②存在﹒理由如下：图1y∵2=t ,∴332=OE ,2=AP ,1=OP 将△BEP 绕点E 顺时针方向旋转90°,得到 △EC B '如图3∵OB ⊥EF ,∴点B '在直线EF 上, C 点坐标为332,332－1 过F 作FQ ∥C B ',交EC 于点Q ,则△FEQ ∽△EC B '由3=='=QE CE FE E B FE BE ,可得Q 的坐标为－32,33根据对称性可得,Q 关于直线EF 的对称点Q '－32,3也符合条件;17．2010江苏泰州如图,四边形ABCD 是矩形,∠EDC =∠CAB ,∠DEC =90°．1求证：AC ∥DE ；2过点B 作BF ⊥AC 于点F ,连结EF ,试判断四边形BCEF 的形状,并说明理由．答案⑴在矩形ABCD 中,AC ∥DE ,∴∠DCA =∠CAB ,∵∠EDC =∠CAB , ∴∠DCA =∠EDC ,∴AC ∥DE ； ⑵四边形BCEF 是平行四边形．理由：由∠DEC =90°,BF ⊥AC ,可得∠AFB =∠DEC =90°, 又∠EDC =∠CAB ,AB=CD ,∴△DEC ≌△AFB ,∴DE =AF ,由⑴得AC ∥DE ,∴四边形AFED 是平行四边形,∴AD ∥EF 且AD =EF , ∵在矩形ABCD 中,AD ∥BC 且AD =BC , ∴EF ∥BC 且EF =BC ,∴四边形BCEF 是平行四边形． 18．2010江苏无锡1如图1,在正方形ABCD 中,M 是BC 边不含端点B 、C 上任意一点,P 是BC 延长线上一点,N 是∠DCP 的平分线上一点．若∠AMN =90°,求证：AM =MN ．下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明．证明：在边AB 上截取AE =MC ,连ME ．正方形ABCD 中,∠B =∠BCD =90°,AB =BC ． ∴∠NMC =180°—∠AMN —∠AMB =180°—∠B —∠AMB =∠MAB =∠MAE ．下面请你完成余下的证明过程2若将1中的“正方形ABCD ”改为“正三角形ABC ”如图2,N 是∠ACP 的平分线上一点,则当∠AMN =60°时,结论AM=MN 是否还成立请说明理由．3若将1中的“正方形ABCD ”改为“正n 边形ABCD ……X ”,请你作出猜想：当∠AMN = °时,结论AM =MN 仍然成立．直接写出答案,不需要证明答案解：1∵AE=MC ,∴BE=BM , ∴∠BEM=∠EMB=45°, ∴∠AEM =135°,∵CN 平分∠DCP ,∴∠PCN=45°,∴∠AEM=∠MCN=135°在△AEM 和△MCN 中：∵,,=CMN,AEM MCN AE MC EAM ∠=∠=∠∠⎧⎪⎨⎪⎩∴△AEM ≌△MCN ,∴AM=MN2仍然成立．在边AB 上截取AE=MC,连接ME ∵△ABC 是等边三角形, ∴AB=BC ,∠B=∠ACB=60°, ∴∠ACP=120°． ∵AE=MC,∴BE=BM ∴∠BEM=∠EMB=60° ∴∠AEM=120°．∵CN 平分∠ACP ,∴∠PCN =60°, ∴∠AEM =∠MCN =120°∵∠CMN=180°—∠AMN —∠AMB =180°—∠B —∠AMB=∠BAM ∴△AEM ≌△MCN,∴AM=MN3(2)180n n-︒19．2010山东临沂如图1,已知矩形ABCD ,点C 是边DE 的中点,且2AB AD =. 1判断ABC ∆的形状,并说明理由；2保持图1中的ABC ∆固定不变,绕点C 旋转DE 所在的直线MN 到图2中的位置当垂线段AD 、BE 在直线MN 的同侧.试探究线段AD 、BE 、DE 长度之间有什么关系并给予证明；3保持图2 中的ABC ∆固定不变,继续绕点C 旋转DE 所在的直线MN 到图3中的位置当垂线段AD 、BE 在直线MN 的异侧.试探究线段AD 、BE 、DE 长度之间有什么关系并给予证明.答案解：1△ABC 是等腰直角三角形; 如图1在矩形ABED 中, 因为点C 是边DE的中点,且AB=2AD, 所以MNPCBA图2M NPDCEBA 图1 E D CB A 图1E D C B A 图2MN NM 图3A B CD E。

2016年全国中考数学真题分类相似形及应用(习题解析)

2016年全国中考数学真题分类相似形及应用一、选择题1．（2016安徽，8，4分）如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为（）A．4 B．4C．6 D．4【考点】相似三角形的判定与性质．【分析】根据AD是中线，得出CD=4，再根据AA证出△CBA∽△CAD，得出=，求出AC即可．【解答】解：∵BC=8，∴CD=4，在△CBA和△CAD中，∵∠B=∠DAC，∠C=∠C，∴△CBA∽△CAD，∴=，∴AC2=CD•BC=4×8=32，∴AC=4；故选B．2．（2016甘肃定西，7，3分）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16 B．1：4 C．1：6 D．1：2【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答即可．【解答】解：∵两个相似三角形的面积比是1：4，∴两个相似三角形的相似比是1：2，∴两个相似三角形的周长比是1：2，故选：D ．【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方是解题的关键．3. （2016浙江杭州，2,3分）如图，已知直线a ∥b ∥c ，直线m 交直线a ，b ，c 于点A ,B ,C ，直线n 交直线a ，b ，c 于点D ,E ,F ,若12AB BC=,则DE EF=（）FE D CB A cb a nmA. 13B.12C. 23D.1 【答案】B4．（2016新疆生产建设兵团，7，5分）如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，下列说法中不正确的是（）A ．DE=BCB ． =C ．△ADE ∽△ABCD ．S △ADE ：S △ABC =1：2【考点】相似三角形的判定与性质；三角形中位线定理．【分析】根据中位线的性质定理得到DE ∥BC ，DE=BC ，再根据平行线分线段成比例定理和相似三角形的性质即可判定．【解答】解：∵D 、E 分别是AB 、AC 的中点， ∴DE ∥BC ，DE=BC ， ∴=，△ADE ∽△ABC ，∴，∴A，B，C正确，D错误；故选：D．【点评】该题主要考查了平行线分线段成比例定理和相似三角形的性质即可判定；解题的关键是正确找出对应线段，准确列出比例式求解、计算、判断或证明．5.（2016河北，15，2分）如图，△ABC中，∠A=78°，AB=4，AC=6.将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似．．．的是（ C ）第15题图答案：Ｃ解析：只要三个角相等，或者一角相等，两边成比例即可。

2016年江西省中考数学试卷(解析版)

2016年江西省中考数学试卷参考答案与试题解析一、选择题（本大题共6小题，每小题3分，满分18分，每小题只有一个正确选项）1．（3分）（2016•江西）下列四个数中，最大的一个数是（）A．2 B．C．0 D．﹣2【考点】实数大小比较．【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【解答】解：根据实数比较大小的方法，可得﹣2＜0＜＜2，故四个数中，最大的一个数是2．故选：A．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．2．（3分）（2016•江西）将不等式3x﹣2＜1的解集表示在数轴上，正确的是（）A．B．C．D．【考点】解一元一次不等式；在数轴上表示不等式的解集．【分析】先解出不等式3x﹣2＜1的解集，即可解答本题．【解答】解：3x﹣2＜1移项，得3x＜3，系数化为1，得x＜1，故选D．【点评】本题考查解一元一次不等式\在数轴上表示不等式的解集，解题的关键是明确解一元一次不等式的方法．3．（3分）（2016•江西）下列运算正确的是（）A．a2+a2=a4B．（﹣b2）3=﹣b6C．2x•2x2=2x3D．（m﹣n）2=m2﹣n2【考点】单项式乘单项式；合并同类项；幂的乘方与积的乘方；完全平方公式．【分析】结合选项分别进行合并同类项、积的乘方、单项式乘单项式、完全平方公式的运算，选出正确答案．【解答】解：A、a2+a2=2a2，故本选项错误；B、（﹣b2）3=﹣b6，故本选项正确；C、2x•2x2=4x3，故本选项错误；D、（m﹣n）2=m2﹣2mn+n2，故本选项错误．故选B．【点评】本题考查了合并同类项、积的乘方、单项式乘单项式、完全平方公式，掌握运算法则是解答本题的关键．4．（3分）（2016•江西）有两个完全相同的正方体，按下面如图方式摆放，其主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据主视图的定义即可得到结果．【解答】解：其主视图是C，故选C．【点评】此题考查了三视图的作图，主视图、左视图、俯视图是分别从物体正面、侧面和上面看所得到的图形．5．（3分）（2016•江西）设α、β是一元二次方程x2+2x﹣1=0的两个根，则αβ的值是（）A．2B．1C．﹣2D．﹣1【考点】根与系数的关系．【分析】根据α、β是一元二次方程x2+2x﹣1=0的两个根，由根与系数的关系可以求得αβ的值，本题得以解决．【解答】解：∵α、β是一元二次方程x2+2x﹣1=0的两个根，∴αβ=，故选D．【点评】本题考查根与系数的关系，解题的关键是明确两根之积等于常数项与二次项系数的比值．6．（3分）（2016•江西）如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（）A．只有②B．只有③C．②③D．①②③【考点】相似三角形的判定与性质；三角形中位线定理．【分析】利用相似三角形的判定和性质分别求出各多边形竖直部分线段长度之和与水平部分线段长度之和，再比较即可．【解答】解：假设每个小正方形的边长为1，①：m=1+2+1=4，n=2+4=6，则m≠n；②在△ACN中，BM∥CN，∴=，∴BM=，在△AGF中，DM∥NE∥FG，∴=，=，得DM=，NE=，∴m=2+=2.5，n=+1++=2.5，∴m=n；③由②得：BE=，CF=，∴m=2+2++1+=6，n=4+2=6，∴m=n，则这三个多边形中满足m=n的是②和③；故选C．【点评】本题考查了相似多边形的判定和性质，对于有中点的三角形可以利用三角形中位线定理得出；本题线段比较多要依次相加，做到不重不漏．二、填空题（本大题共6小题，每小题3分，满分18分）7．（3分）（2016•江西）计算：﹣3+2=﹣1．【考点】有理数的加法．【分析】由绝对值不等的异号加减，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0，即可求得答案．【解答】解：﹣3+2=﹣1．故答案为：﹣1．【点评】此题考查了有理数的加法．注意在进行有理数加法运算时，首先判断两个加数的符号：是同号还是异号，是否有0，从而确定用哪一条法则．在应用过程中，要牢记“先符号，后绝对值”．8．（3分）（2016•江西）分解因式：ax2﹣ay2=a（x+y）（x﹣y）．【考点】提公因式法与公式法的综合运用．【分析】应先提取公因式a，再对余下的多项式利用平方差公式继续分解．【解答】解：ax2﹣ay2，=a（x2﹣y2），=a（x+y）（x﹣y）．故答案为：a（x+y）（x﹣y）．【点评】本题主要考查提公因式法分解因式和平方差公式分解因式，需要注意分解因式一定要彻底．9．（3分）（2016•江西）如图所示，△ABC中，∠BAC=33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为17°．【考点】旋转的性质．【分析】先利用旋转的性质得到∠B'AC'=33°，∠BAB'=50°，从而得到∠B′AC的度数．【解答】解：∵∠BAC=33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，∴∠B'AC'=33°，∠BAB'=50°，∴∠B′AC的度数=50°﹣33°=17°．故答案为：17°．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．10．（3分）（2016•江西）如图所示，在▱ABCD中，∠C=40°，过点D作AD的垂线，交AB 于点E，交CB的延长线于点F，则∠BEF的度数为50°．【考点】平行四边形的性质．【分析】由“平行四边形的对边相互平行”、“两直线平行，同位角相等”以及“直角三角形的两个锐角互余”的性质进行解答．【解答】解：∵四边形ABCD是平行四边形，∴DC∥AB，∴∠C=∠ABF．又∵∠C=40°，∴∠ABF=40°．∵EF⊥BF，∴∠F=90°，∴∠BEF=90°﹣40°=50°．故答案是：50°．【点评】本题考查了平行四边形的性质．利用平行四边形的对边相互平行推知DC∥AB是解题的关键．11．（3分）（2016•江西）如图，直线l⊥x轴于点P，且与反比例函数y1=（x＞0）及y2=（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2=4．【考点】反比例函数与一次函数的交点问题；反比例函数系数k的几何意义．【分析】由反比例函数的图象过第一象限可得出k1＞0，k2＞0，再由反比例函数系数k的几何意义即可得出S△OAP=k1，S△OBP=k2，根据△OAB的面积为2结合三角形之间的关系即可得出结论．【解答】解：∵反比例函数y1=（x＞0）及y2=（x＞0）的图象均在第一象限内，∴k1＞0，k2＞0．∵AP⊥x轴，∴S△OAP=k1，S△OBP=k2．∴S△OAB=S△OAP﹣S△OBP=（k1﹣k2）=2，解得：k1﹣k2=4．故答案为：4．【点评】本题考查了反比例函数与一次函数的交点问题已经反比例函数系数k的几何意义，解题的关键是得出S△OAB=（k1﹣k2）．本题属于基础题，难度不大，解决该题型题目时，根据反比例函数系数k的几何意义用系数k来表示出三角形的面积是关键．12．（3分）（2016•江西）如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是5\sqrt{2}或4\sqrt{5}或5．【考点】矩形的性质；等腰三角形的性质；勾股定理．【分析】分情况讨论：①当AP=AE=5时，则△AEP是等腰直角三角形，得出底边PE=AE=5即可；②当PE=AE=5时，求出BE，由勾股定理求出PB，再由勾股定理求出等边AP即可；③当PA=PE时，底边AE=5；即可得出结论．【解答】解：如图所示：①当AP=AE=5时，∵∠BAD=90°，∴△AEP是等腰直角三角形，∴底边PE=AE=5；②当PE=AE=5时，∵BE=AB﹣AE=8﹣5=3，∠B=90°，∴PB==4，∴底边AP===4；③当PA=PE时，底边AE=5；综上所述：等腰三角形AEP的对边长为5或4或5；故答案为：5或4或5．【点评】本题考查了矩形的性质、等腰三角形的判定、勾股定理；熟练掌握矩形的性质和等腰三角形的判定，进行分类讨论是解决问题的关键．三、解答题（本大题共5小题，每小题3分，满分27分）13．（3分）（2016•江西）（1）解方程组：．（2）如图，Rt△ABC中，∠ACB=90°，将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．求证：DE∥BC．【考点】翻折变换（折叠问题）；解二元一次方程组．【分析】（1）根据方程组的解法解答即可；（2）由翻折可知∠AED=∠CED=90°，再利用平行线的判定证明即可．【解答】解：（1），①﹣②得：y=1，把y=1代入①可得：x=3，所以方程组的解为；（2）∵将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．∴∠AED=∠CED=90°，∴∠AED=∠ACB=90°，∴DE∥BC．【点评】本题考查的是图形的翻折变换，涉及到平行线的判定，熟知折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．14．（6分）（2016•江西）先化简，再求值：（+）÷，其中x=6．【考点】分式的化简求值．【分析】先算括号里面的，再算除法，最后把x=6代入进行计算即可．【解答】解：原式=÷=÷=•=，当x=6时，原式==﹣．【点评】本题考查的是分式的化简求值，分式中的一些特殊求值题并非是一味的化简，代入，求值．许多问题还需运用到常见的数学思想，如化归思想（即转化）、整体思想等，了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助．15．（6分）（2016•江西）如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=．（1）求点B的坐标；（2）若△ABC的面积为4，求直线l2的解析式．【考点】两条直线相交或平行问题；待定系数法求一次函数解析式；勾股定理的应用．【分析】（1）先根据勾股定理求得BO的长，再写出点B的坐标；（2）先根据△ABC的面积为4，求得CO的长，再根据点A、C的坐标，运用待定系数法求得直线l2的解析式．【解答】解：（1）∵点A（2，0），AB=∴BO===3∴点B的坐标为（0，3）；（2）∵△ABC的面积为4∴×BC×AO=4∴×BC×2=4，即BC=4∵BO=3∴CO=4﹣3=1∴C（0，﹣1）设l2的解析式为y=kx+b，则，解得∴l2的解析式为y=x﹣1【点评】本题主要考查了两条直线的交点问题，解题的关键是掌握勾股定理以及待定系数法．注意：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解，反之也成立．16．（6分）（2016•江西）为了了解家长关注孩子成长方面的状况，学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查，调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目，并随机抽取甲、乙两班共100位学生家长进行调查，根据调查结果，绘制了如图不完整的条形统计图．（1）补全条形统计图．（2）若全校共有3600位学生家长，据此估计，有多少位家长最关心孩子“情感品质”方面的成长？（3）综合以上主题调查结果，结合自身现状，你更希望得到以上四个项目中哪方面的关注和指导？【考点】条形统计图；用样本估计总体．【分析】（1）用甲、乙两班学生家长共100人减去其余各项目人数可得乙组关心“情感品质”的家长人数，补全图形即可；（2）用样本中关心孩子“情感品质”方面的家长数占被调查人数的比例乘以总人数3600可得答案；（3）无确切答案，结合自身情况或条形统计图，言之有理即可．【解答】解：（1）乙组关心“情感品质”的家长有：100﹣（18+20+23+17+5+7+4）=6（人），补全条形统计图如图：（2）×3600=360（人）．答：估计约有360位家长最关心孩子“情感品质”方面的成长；（3）无确切答案，结合自身情况或条形统计图，言之有理即可，如：从条形统计图中，家长对“情感品质”关心不够，可适当关注与指导．【点评】本题主要考查条形统计图，条形统计图能清楚地表示出每个项目的数据，熟知各项目数据个数之和等于总数，也考查了用样本估计总体．17．（6分）（2016•江西）如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．（1）在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；（2）在图2中画出线段AB的垂直平分线．【考点】作图—应用与设计作图．【分析】（1）根据等腰直角三角形的性质即可解决问题．（2）根据正方形、长方形的性质对角线相等且互相平分，即可解决问题．【解答】解：（1）如图所示，∠ABC=45°．（AB、AC是小长方形的对角线）．（2）线段AB的垂直平分线如图所示，点M是长方形AFBE是对角线交点，点N是正方形ABCD的对角线的交点，直线MN就是所求的线段AB的垂直平分线．【点评】本题考查作图﹣应用设计、正方形、长方形、等腰直角三角形的性质，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．四、（本大题共4小题，每小题8根，共32分）18．（8分）（2016•江西）如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交于点F，交过点C的切线于点D．（1）求证：DC=DP；（2）若∠CAB=30°，当F是的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．【考点】切线的性质；垂径定理．【分析】（1）连接OC，根据切线的性质和PE⊥OE以及∠OAC=∠OCA得∠APE=∠DPC，然后结合对顶角的性质可证得结论；（2）由∠CAB=30°易得△OBC为等边三角形，可得∠AOC=120°，由F是的中点，易得△AOF与△COF均为等边三角形，可得AF=AO=OC=CF，易得以A，O，C，F为顶点的四边形是菱形．【解答】（1）证明：连接OC，∵∠OAC=∠ACO，PE⊥OE，OC⊥CD，∴∠APE=∠PCD，∵∠APE=∠DPC，∴∠DPC=∠PCD，∴DC=DP；（2）解：以A，O，C，F为顶点的四边形是菱形；∵∠CAB=30°，∴∠B=60°，∴△OBC为等边三角形，∴∠AOC=120°，连接OF，AF，∵F是的中点，∴∠AOF=∠COF=60°，∴△AOF与△COF均为等边三角形，∴AF=AO=OC=CF，∴四边形OACF为菱形．【点评】本题主要考查了切线的性质、圆周角定理和等边三角形的判定等，作出恰当的辅助线利用切线的性质是解答此题的关键．19．（8分）（2016•江西）如图是一根可伸缩的鱼竿，鱼竿是用10节大小不同的空心套管连接而成．闲置时鱼竿可收缩，完全收缩后，鱼竿长度即为第1节套管的长度（如图1所示）：使用时，可将鱼竿的每一节套管都完全拉伸（如图2所示）．图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图．已知第1节套管长50cm，第2节套管长46cm，以此类推，每一节套管均比前一节套管少4cm．完全拉伸时，为了使相邻两节套管连接并固定，每相邻两节套管间均有相同长度的重叠，设其长度为xcm．（1）请直接写出第5节套管的长度；（2）当这根鱼竿完全拉伸时，其长度为311cm，求x的值．【考点】一元一次方程的应用．【分析】（1）根据“第n节套管的长度=第1节套管的长度﹣4×（n﹣1）”，代入数据即可得出结论；（2）同（1）的方法求出第10节套管重叠的长度，设每相邻两节套管间的长度为xcm，根据“鱼竿长度=每节套管长度相加﹣（10﹣1）×相邻两节套管间的长度”，得出关于x的一元一次方程，解方程即可得出结论．【解答】解：（1）第5节套管的长度为：50﹣4×（5﹣1）=34（cm）．（2）第10节套管的长度为：50﹣4×（10﹣1）=14（cm），设每相邻两节套管间重叠的长度为xcm，根据题意得：（50+46+42+…+14）﹣9x=311，即：320﹣9x=311，解得：x=1．答：每相邻两节套管间重叠的长度为1cm．【点评】本题考查了一元一次方程的应用，解题的关键是：（1）根据数量关系直接求值；（2）根据数量关系找出关于x的一元一次方程．本题属于基础题，难度不大，解决该题型题目时，根据数量关系找出不等式（方程或方程组）是关键．20．（8分）（2016•江西）甲、乙两人利用扑克牌玩“10点”游戏，游戏规则如下：①将牌面数字作为“点数”，如红桃6的“点数”就是6（牌面点数与牌的花色无关）；②两人摸牌结束时，将所摸牌的“点数”相加，若“点数”之和小于或等于10，此时“点数”之和就是“最终点数”；若“点数”之和大于10，则“最终点数”是0；③游戏结束前双方均不知道对方“点数”；④判定游戏结果的依据是：“最终点数”大的一方获胜，“最终点数”相等时不分胜负．现甲、乙均各自摸了两张牌，数字之和都是5，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4，5，6，7．（1）若甲从桌上继续摸一张扑克牌，乙不再摸牌，则甲获胜的概率为\frac{1}{2}；（2）若甲先从桌上继续摸一张扑克牌，接着乙从剩下的扑克牌中摸出一张牌，然后双方不再摸牌．请用树状图或表格表示出这次摸牌后所有可能的结果，再列表呈现甲、乙的“最终点数”，并求乙获胜的概率．【考点】列表法与树状图法．【分析】（1）由现甲、乙均各自摸了两张牌，数字之和都是5，甲从桌上继续摸一张扑克牌，乙不再摸牌，甲摸牌数字是4与5则获胜，直接利用概率公式求解即可求得答案；（2）首先根据题意画出树状图，然后根据树状图列出甲、乙的“最终点数”，继而求得答案．【解答】解：（1）∵现甲、乙均各自摸了两张牌，数字之和都是5，甲从桌上继续摸一张扑克牌，乙不再摸牌，∴甲摸牌数字是4与5则获胜，∴甲获胜的概率为：=；故答案为：；（2）画树状图得：则共有12种等可能的结果；列表得：∴乙获胜的概率为：．【点评】此题考查了列表法或树状图法求概率．注意根据题意列出甲、乙的“最终点数”的表格是难点．用到的知识点为：概率=所求情况数与总情况数之比．21．（8分）（2016•江西）如图1是一副创意卡通圆规，图2是其平面示意图，OA是支撑臂，OB是旋转臂，使用时，以点A为支撑点，铅笔芯端点B可绕点A旋转作出圆．已知OA=OB=10cm．（1）当∠AOB=18°时，求所作圆的半径；（结果精确到0.01cm）（2）保持∠AOB=18°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与（1）中所作圆的大小相等，求铅笔芯折断部分的长度．（结果精确到0.01cm）（参考数据：sin9°≈0.1564，cos9°≈0.9877，sin18°≈0.3090，cos18°≈0.9511，可使用科学计算器）【考点】解直角三角形的应用．【分析】（1）根据题意作辅助线OC⊥AB于点C，根据OA=OB=10cm，∠OCB=90°，∠AOB=18°，可以求得∠BOC的度数，从而可以求得AB的长；（2）由题意可知，作出的圆与（1）中所作圆的大小相等，则AE=AB，然后作出相应的辅助线，画出图形，从而可以求得BE的长，本题得以解决．【解答】解：（1）作OC⊥AB于点C，如右图2所示，由题意可得，OA=OB=10cm，∠OCB=90°，∠AOB=18°，∴∠BOC=9°∴AB=2BC=2OB•sin9°≈2×10×0.1564≈3.13cm，即所作圆的半径约为3.13cm；（2）作AD⊥OB于点D，作AE=AB，如下图3所示，∵保持∠AOB=18°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与（1）中所作圆的大小相等，∴折断的部分为BE，∵∠AOB=18°，OA=OB，∠ODA=90°，∴∠OAB=81°，∠OAD=72°，∴∠BAD=9°，∴BE=2BD=2AB•sin9°≈2×3.13×0.1564≈0.98cm，即铅笔芯折断部分的长度是0.98cm．【点评】本题考查解直角三角形的应用，解题的关键是明确题意，作出合适的辅助线，找出所求问题需要的条件．五、（本大题共10分）22．（10分）（2016•江西）如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．【探究证明】（1）请在图1和图2中选择其中一个证明：“叠弦三角形”（△AOP）是等边三角形；（2）如图2，求证：∠OAB=∠OAE′．【归纳猜想】（3）图1、图2中的“叠弦角”的度数分别为15°，24°；（4）图n中，“叠弦三角形”是等边三角形（填“是”或“不是”）（5）图n中，“叠弦角”的度数为60°﹣\frac{180°}{n}（用含n的式子表示）【考点】几何变换综合题．【分析】（1）先由旋转的性质，再判断出△APD≌△AOD'，最后用旋转角计算即可；（2）先判断出Rt△AEM≌Rt△ABN，在判断出Rt△APM≌Rt△AON 即可；（3）先判断出△AD′O≌△ABO，再利用正方形，正五边形的性质和旋转的性质，计算即可；（4）先判断出△APF≌△AE′F′，再用旋转角为60°，从而得出△PAO是等边三角形；（5）用（3）的方法求出正n边形的，“叠弦角”的度数．【解答】解：（1）如图1，∵四ABCD是正方形，由旋转知：AD=AD'，∠D=∠D'=90°，∠DAD'=∠OAP=60°，∴∠DAP=∠D'AO，∴△APD≌△AOD'（ASA）∴AP=AO，∵∠OAP=60°，∴△AOP是等边三角形，（2）如图2，作AM⊥DE于M，作AN⊥CB于N．∵五ABCDE是正五边形，由旋转知：AE=AE'，∠E=∠E'=108°，∠EAE'=∠OAP=60°∴∠EAP=∠E'AO∴△APE≌△AOE'（ASA）∴∠OAE'=∠PAE．在Rt△AEM和Rt△ABN中，∠AEM=∠ABN=72°，AA AE=AB ∴Rt△AEM≌Rt△ABN （AAS），∴∠EAM=∠BAN，AM=AN．在Rt△APM和Rt△AON中，AP=AO，AM=AN∴Rt△APM≌Rt△AON （HL）．∴∠PAM=∠OAN，∴∠PAE=∠OAB∴∠OAE'=∠OAB （等量代换）．（3）由（1）有，△APD≌△AOD'，∴∠DAP=∠D′AO，在△AD′O和△ABO中，，∴△AD′O≌△ABO，∴∠D′AO=∠BAO，由旋转得，∠DAD′=60°，∵∠DAB=90°，∴∠D′AB=∠DAB﹣∠DAD′=30°，∴∠D′AD=∠D′AB=15°，同理可得，∠E′AO=24°，故答案为：15°，24°．（4）如图3，∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形，∴∠F=F′=120°，由旋转得，AF=AF′，EF=E′F′，∴△APF≌△AE′F′，∴∠PAF=∠E′AF′，由旋转得，∠FAF′=60°，AP=AO∴∠PAO=∠FAO=60°，∴△PAO是等边三角形．故答案为：是（5）同（3）的方法得，∠OAB=[（n﹣2）×180°÷n﹣60°]÷2=60°﹣故答案：60°﹣．【点评】此题是几何变形综合题，主要考查了正多边形的性质旋转的性质，全等三角形的判定，等边三角形的判定，解本题的关键是判定三角形全等．六、（本大题共12分）23．（12分）（2016•江西）设抛物线的解析式为y=ax2，过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点B2（，0）作x轴的垂线，交抛物线于点A2；…；过点B n （（）n﹣1，0）（n为正整数）作x轴的垂线，交抛物线于点A n，连接A n B n+1，得Rt△A n B n B n+1．（1）求a的值；（2）直接写出线段A n B n，B n B n+1的长（用含n的式子表示）；（3）在系列Rt△A n B n B n+1中，探究下列问题：①当n为何值时，Rt△A n B n B n+1是等腰直角三角形？②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△A k B k B k+1与Rt△A m B m B m+1相似？若存在，求出其相似比；若不存在，说明理由．【考点】二次函数综合题．【分析】（1）直接把点A1的坐标代入y=ax2求出a的值；（2）由题意可知：A1B1是点A1的纵坐标：则A1B1=2×12=2；A2B2是点A2的纵坐标：则A2B2=2×（）2=；…则A n B n=2x2=2×[（）n﹣1]2=；B1B2=1﹣=，B2B3=﹣==，…，B n B n+1=；（3）因为Rt△A k B k B k+1与Rt△A m B m B m+1是直角三角形，所以分两种情况讨论：根据（2）的结论代入所得的对应边的比列式，计算求出k与m的关系，并与1≤k＜m≤n（k，m均为正整数）相结合，得出两种符合条件的值，分别代入两相似直角三角形计算相似比．【解答】解：（1）∵点A1（1，2）在抛物线的解析式为y=ax2上，∴a=2；（2）A n B n=2x2=2×[（）n﹣1]2=，B n B n+1=；（3）由Rt△A n B n B n+1是等腰直角三角形得A n B n=B n B n+1，则：=，2n﹣3=n，n=3，∴当n=3时，Rt△A n B n B n+1是等腰直角三角形，②依题意得，∠A k B k B k+1=∠A m B m B m+1=90°，有两种情况：i）当Rt△A k B k B k+1∽Rt△A m B m B m+1时，=，=，=，所以，k=m（舍去），ii）当Rt△A k B k B k+1∽Rt△B m+1B m A m时，=，=，=，∴k+m=6，∵1≤k＜m≤n（k，m均为正整数），∴取或；当时，Rt△A1B1B2∽Rt△B6B5A5，相似比为：==64，当时，Rt△A2B2B3∽Rt△B5B4A4，相似比为：==8，所以：存在Rt△A k B k B k+1与Rt△A m B m B m+1相似，其相似比为64：1或8：1．【点评】本题考查了二次函数的综合问题，这是一个函数类的规律题，把坐标、二次函数和线段有机地结合在一起，以求线段的长为突破口，以相似三角形的对应边的比为等量关系，代入计算解决问题，综合性较强，因为本题小字标较多，容易出错．2016年江西省中考数学试卷一、选择题（本大题共6小题，每小题3分，满分18分，每小题只有一个正确选项）1．（3分）（2016•江西）下列四个数中，最大的一个数是（）A．2B．C．0D．﹣22．（3分）（2016•江西）将不等式3x﹣2＜1的解集表示在数轴上，正确的是（）A．B．C．D．3．（3分）（2016•江西）下列运算正确的是（）A．a2+a2=a4B．（﹣b2）3=﹣b6C．2x•2x2=2x3D．（m﹣n）2=m2﹣n24．（3分）（2016•江西）有两个完全相同的正方体，按下面如图方式摆放，其主视图是（）A．B．C．D．5．（3分）（2016•江西）设α、β是一元二次方程x2+2x﹣1=0的两个根，则αβ的值是（）A．2B．1C．﹣2D．﹣16．（3分）（2016•江西）如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（）A．只有②B．只有③C．②③D．①②③二、填空题（本大题共6小题，每小题3分，满分18分）7．（3分）（2016•江西）计算：﹣3+2=．8．（3分）（2016•江西）分解因式：ax2﹣ay2=．9．（3分）（2016•江西）如图所示，△ABC中，∠BAC=33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为．10．（3分）（2016•江西）如图所示，在▱ABCD中，∠C=40°，过点D作AD的垂线，交AB 于点E，交CB的延长线于点F，则∠BEF的度数为．11．（3分）（2016•江西）如图，直线l⊥x轴于点P，且与反比例函数y1=（x＞0）及y2=（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2=．12．（3分）（2016•江西）如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．三、解答题（本大题共5小题，每小题3分，满分27分）13．（3分）（2016•江西）（1）解方程组：．（2）如图，Rt△ABC中，∠ACB=90°，将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．求证：DE∥BC．14．（6分）（2016•江西）先化简，再求值：（+）÷，其中x=6．15．（6分）（2016•江西）如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=．（1）求点B的坐标；（2）若△ABC的面积为4，求直线l2的解析式．16．（6分）（2016•江西）为了了解家长关注孩子成长方面的状况，学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查，调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目，并随机抽取甲、乙两班共100位学生家长进行调查，根据调查结果，绘制了如图不完整的条形统计图．（1）补全条形统计图．（2）若全校共有3600位学生家长，据此估计，有多少位家长最关心孩子“情感品质”方面的成长？（3）综合以上主题调查结果，结合自身现状，你更希望得到以上四个项目中哪方面的关注和指导？17．（6分）（2016•江西）如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．（1）在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；（2）在图2中画出线段AB的垂直平分线．四、（本大题共4小题，每小题8根，共32分）18．（8分）（2016•江西）如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交于点F，交过点C的切线于点D．（1）求证：DC=DP；（2）若∠CAB=30°，当F是的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．19．（8分）（2016•江西）如图是一根可伸缩的鱼竿，鱼竿是用10节大小不同的空心套管连接而成．闲置时鱼竿可收缩，完全收缩后，鱼竿长度即为第1节套管的长度（如图1所示）：使用时，可将鱼竿的每一节套管都完全拉伸（如图2所示）．图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图．已知第1节套管长50cm，第2节套管长46cm，以此类推，每一节套管均比前一节套管少4cm．完全拉伸时，为了使相邻两节套管连接并固定，每相邻两节套管间均有相同长度的重叠，设其长度为xcm．（1）请直接写出第5节套管的长度；（2）当这根鱼竿完全拉伸时，其长度为311cm，求x的值．20．（8分）（2016•江西）甲、乙两人利用扑克牌玩“10点”游戏，游戏规则如下：①将牌面数字作为“点数”，如红桃6的“点数”就是6（牌面点数与牌的花色无关）；②两人摸牌结束时，将所摸牌的“点数”相加，若“点数”之和小于或等于10，此时“点数”之和就是“最终点数”；若“点数”之和大于10，则“最终点数”是0；。

2014年全国中考数学试题分类汇编25 矩形菱形与正方形(含解析)

矩形菱形与正方形一、选择题1. （2014•安徽省,第10题4分）如图，正方形ABCD的对角线BD长为2，若直线l满足：①点D到直线l的距离为；②A、C两点到直线l的距离相等．则符合题意的直线l的条数为（）A． 1 B． 2 C． 3 D． 4考点：正方形的性质．菁优网分析：连接AC与BD相交于O，根据正方形的性质求出OD=，然后根据点到直线的距离和平行线间的距离相等解答．解答：解：如图，连接AC与BD相交于O，∵正方形ABCD的对角线BD长为2，∴OD=，∴直线l∥AC并且到D的距离为，同理，在点D的另一侧还有一条直线满足条件，故共有2条直线l．故选B．点评：本题考查了正方形的性质，主要利用了正方形的对角线互相垂直平分，点D到O 的距离小于是本题的关键．2. （2014•福建泉州，第5题3分）正方形的对称轴的条数为（）3. （2014•珠海，第2题3分）边长为3cm的菱形的周长是（）4.（2014•广西玉林市、防城港市，第6题3分）下列命题是假命题的是（）5.（2014•毕节地区，第8题3分）如图，菱形ABCD中，对角线AC、BC相交于点O，H 为AD边中点，菱形ABCD的周长为28，则OH的长等于（）AAB6.（2014•襄阳，第12题3分）如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（）PE===7.（2014•孝感，第9题3分）如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（）8．（2014·台湾，第12题3分）如图，D 为△ABC 内部一点，E 、F 两点分别在AB 、BC 上，且四边形DEBF 为矩形，直线CD 交AB 于G 点．若CF ＝6，BF ＝9，AG ＝8，则△ADC 的面积为何？( )A ．16B ．24C ．36D ．54分析：由于△ADC ＝△AGC ﹣△ADG ，根据矩形的性质和三角形的面积公式计算即可求解．解：△ADC ＝△AGC ﹣△ADG ＝12×AG ×BC ﹣12×AG ×BF＝12×8×(6＋9)﹣12×8×9＝60﹣36＝24．故选：B ．点评：考查了三角形的面积和矩形的性质，本题关键是活用三角形面积公式进行计算． 9．（2014·台湾，第27题3分）如图，矩形ABCD 中，AD ＝3AB ，O 为AD 中点，是半圆．甲、乙两人想在上取一点P ，使得△PBC 的面积等于矩形ABCD 的面积其作法如下： (甲) 延长BO 交于P 点，则P 即为所求；(乙) 以A 为圆心，AB 长为半径画弧，交于P 点，则P 即为所求．对于甲、乙两人的作法，下列判断何者正确？( )A ．两人皆正确B ．两人皆错误C ．甲正确，乙错误D ．甲错误，乙正确分析：利用三角形的面积公式进而得出需P甲H＝P乙K＝2AB，即可得出答案．解：要使得△PBC的面积等于矩形ABCD的面积，需P甲H＝P乙K＝2A B．故两人皆错误．故选：B．点评：此题主要考查了三角形面积求法以及矩形的性质，利用四边形与三角形面积关系得出是解题关键．10．（2014•浙江宁波，第6题4分）菱形的两条对角线长分别是6和8，则此菱形的边长是（）===511．（2014•浙江宁波，第11题4分）如图，正方形ABCD和正方形CEFG中，点D在CG 上，BC=1，CE=3，H是AF的中点，那么CH的长是（）．．=，=3，===2，=AF=×2=．11.（2014•呼和浩特，第9题3分）已知矩形ABCD的周长为20cm，两条对角线AC，BD 相交于点O，过点O作AC的垂线EF，分别交两边AD，BC于E，F（不与顶点重合），则以下关于△CDE与△ABF判断完全正确的一项为（）=12. （2014•湘潭，第7题，3分）以下四个命题正确的是（）13. （2014•株洲，第7题，3分）已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）14. （2014年江苏南京，第6题，2分）如图，在矩形AOBC中，点A的坐标是（﹣2，1），点C的纵坐标是4，则B、C两点的坐标分别是（）（第3题图）A．（，3）、（﹣，4）B．（，3）、（﹣，4）C．（，）、（﹣，4）D．（，）、（﹣，4）考点：矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质。

2016年中考数学试题分类解析汇编(第一辑)(29份)_3

2016年全国各地中考数学试题分类解析汇编（第一辑）第13章轴对称一．选择题（共20小题）1．（2016•台湾）若下列选项中的图形均为正多边形，则哪一个图形恰有4条对称轴？（）A．B．C．D．2．（2016•成都）平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标为（）A．（﹣2，﹣3）B．（2，﹣3）C．（﹣3，﹣2）D．（3，﹣2）3．（2016•巴中）在一些美术字中，有的汉字是轴对称图形，下列四个汉字中，可以看作轴对称图形的是（）A．B．C．D．4．（2016•深圳）下列图形中，是轴对称图形的是（）A．B．C．D．5．（2016•西宁）在一些汉字的美术字中，有的是轴对称图形．下面四个美术字中可以看作轴对称图形的是（）A．B．C．D．6．（2016•重庆）下列交通指示标识中，不是轴对称图形的是（）A．B．C．D．7．（2016•桂林）下列图形一定是轴对称图形的是（）A．直角三角形B．平行四边形C．直角梯形D．正方形8．（2016•泸州）下列图形中不是轴对称图形的是（）A．B．C．D．9．（2016•菏泽）以下微信图标不是轴对称图形的是（）A ．B ．C ．D ．10．（2016•北京）甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（）A ．B ．C ．D ．11．（2016•绍兴）我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化，窗框一部分如图2，它是一个轴对称图形，其对称轴有（）A ．1条B ．2条C ．3条D ．4条12．（2016•重庆）下列图形中是轴对称图形的是（）A ．B ．C ．D ．13．（2016•邵阳）下面四个手机应用图标中是轴对称图形的是（）A ．B ．C ．D ．14．（2016•漳州）下列图案属于轴对称图形的是（）A ．B ．C ．D ．15．（2016•舟山）在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（）A ．B ．C ．D ．16．（2016•南充）如图，直线MN 是四边形AMBN 的对称轴，点P 时直线MN 上的点，下列判断错误的是（）A．AM=BM B．AP=BN C．∠MAP=∠MBP D．∠ANM=∠BNM17．（2016•河北）如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（）A．1个B．2个C．3个D．3个以上18．（2016•内江）已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为（）A．B．C．D．不能确定19．（2016•雅安）如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE 垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．320．（2016•邵阳）如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（）A．AC＞BC B．AC=BC C．∠A＞∠ABC D．∠A=∠ABC2016年全国各地中考数学试题分类解析汇编（第一辑）第13章轴对称参考答案与试题解析一．选择题（共20小题）1．（2016•台湾）若下列选项中的图形均为正多边形，则哪一个图形恰有4条对称轴？（）A．B．C．D．【分析】直接利用轴对称图形的性质分析得出符合题意的答案．【解答】解：A、正三角形有3条对称轴，故此选项错误；B、正方形有4条对称轴，故此选项正确；C、正六边形有6条对称轴，故此选项错误；D、正八边形有8条对称轴，故此选项错误．故选：B．【点评】此题主要考查了轴对称图形，正确把握轴对称图形的定义是解题关键．2．（2016•成都）平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标为（）A．（﹣2，﹣3）B．（2，﹣3）C．（﹣3，﹣2）D．（3，﹣2）【分析】直接利用关于x轴对称点的性质，横坐标不变，纵坐标互为相反数，进而得出答案．【解答】解：点P（﹣2，3）关于x轴对称的点的坐标为（﹣2，﹣3）．故选：A．【点评】此题主要考查了关于x轴对称点的性质，正确记忆横纵坐标的关系是解题关键．3．（2016•巴中）在一些美术字中，有的汉字是轴对称图形，下列四个汉字中，可以看作轴对称图形的是（）A．B．C．D．【分析】利用轴对称图形定义判断即可．【解答】解：在一些美术字中，有的汉字是轴对称图形，下列四个汉字中，可以看作轴对称图形的是，故选D．【点评】此题考查了轴对称图形，熟练掌握轴对称图形的定义是解本题的关键．4．（2016•深圳）下列图形中，是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念求解．【解答】解：A、不是轴对称图形，故本选项错误；B、是轴对称图形，故本选项正确；C、不是轴对称图形，故本选项错误；D、不是轴对称图形，故本选项错误．故选B．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．5．（2016•西宁）在一些汉字的美术字中，有的是轴对称图形．下面四个美术字中可以看作轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可．【解答】解：四个汉字中只有“善”字可以看作轴对称图形，故选D．【点评】考查了轴对称图形的知识，掌握轴对称图形的意义，判断是不是轴对称图形的关键是找出对称轴，看图形沿对称轴对折后两部分能否完全重合．6．（2016•重庆）下列交通指示标识中，不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解．【解答】解：A、是轴对称图形，故本选项错误；B、是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项正确；D、是轴对称图形，故本选项错误．故选C．【点评】本题考查了轴对称图形，掌握中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．7．（2016•桂林）下列图形一定是轴对称图形的是（）A．直角三角形B．平行四边形C．直角梯形D．正方形【分析】根据轴对称图形的概念，结合选项求解即可．【解答】解：A、直角三角形中只有等腰直角三角形为轴对称图形，本选项错误；B、平行四边形不是轴对称图形，本选项错误；C、直角梯形不是轴对称图形，本选项错误；D、正方形是轴对称图形，本选项正确．故选D．【点评】本题考查了轴对称图形的知识，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．8．（2016•泸州）下列图形中不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念求解．【解答】解：根据轴对称图形的概念可知：A，B，D是轴对称图形，C不是轴对称图形，故选：C．【点评】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．9．（2016•菏泽）以下微信图标不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念求解，看图形是不是关于直线对称．【解答】解：A、是轴对称图形；B、是轴对称图形；C、是轴对称图形；D、不是轴对称图形．故选D．【点评】本题主要考查了轴对称的概念，轴对称的关键是寻找对称轴，两边图象折叠后可重合．10．（2016•北京）甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（）A．B．C．D．【分析】根据轴对称图形的概念求解．【解答】解：A、是轴对称图形，故本选项错误；B、是轴对称图形，故本选项错误；C、是轴对称图形，故本选项错误；D、不是轴对称图形，故本选项正确．故选D．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．11．（2016•绍兴）我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化，窗框一部分如图2，它是一个轴对称图形，其对称轴有（）A．1条B．2条C．3条D．4条【分析】直接利用轴对称图形的定义分析得出答案．【解答】解：如图所示：其对称轴有2条．故选：B．【点评】此题主要考查了轴对称图形的定义，正确把握定义是解题关键．12．（2016•重庆）下列图形中是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A、不是轴对称图形，不符合题意；B、不是轴对称图形，不符合题意；C、不是轴对称图形，不符合题意；D、是轴对称图形，对称轴有两条，符合题意．故选：D．【点评】此题主要考查了轴对称图形，确定轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．13．（2016•邵阳）下面四个手机应用图标中是轴对称图形的是（）A．B．C．D．【分析】分别根据轴对称图形与中心对称图形的性质对各选项进行逐一分析即可．【解答】解：A、既不是轴对称图形，也不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项错误；C、既不是轴对称图形，也不是中心对称图形，故本选项错误；D、是轴对称图形，故本选项正确．故选D．【点评】本题考查的是轴对称图形，熟知轴对称图形是针对一个图形而言的，是一种具有特殊性质图形，被一条直线分割成的两部分沿着对称轴折叠时，互相重合是解答此题的关键．14．（2016•漳州）下列图案属于轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的定义，寻找四个选项中图形的对称轴，发现只有，A有一条对称轴，由此即可得出结论．【解答】解：A、能找出一条对称轴，故A是轴对称图形；B、不能找出对称轴，故B不是轴对称图形；C、不能找出对称轴，故B不是轴对称图形；D、不能找出对称轴，故B不是轴对称图形．故选A．【点评】本题考查了轴对称图形，解题的关键是分别寻找四个选项中图形的对称轴．本题属于基础题，难度不大，解决该题型题目时，通过寻找给定图象有无对称轴来确定该图形是否是轴对称图形是关键．15．（2016•舟山）在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念进行判断即可．【解答】解：A、不是轴对称图形，故选项错误；B、是轴对称图形，故选项正确；C、不是轴对称图形，故选项错误；D、不是轴对称图形，故选项错误．故选：B．【点评】本题考查的是轴对称图形的概念，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．16．（2016•南充）如图，直线MN是四边形AMBN的对称轴，点P时直线MN上的点，下列判断错误的是（）A．AM=BM B．AP=BN C．∠MAP=∠MBP D．∠ANM=∠BNM【分析】根据直线MN是四边形AMBN的对称轴，得到点A与点B对应，根据轴对称的性质即可得到结论．【解答】解：∵直线MN是四边形AMBN的对称轴，∴点A与点B对应，∴AM=BM，AN=BN，∠ANM=∠BNM，∵点P时直线MN上的点，∴∠MAP=∠MBP，∴A，C，D正确，B错误，故选B．【点评】本题考查了轴对称的性质，熟练掌握轴对称的性质是解题的关键．17．（2016•河北）如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（）A．1个B．2个C．3个D．3个以上【分析】如图在OA、OB上截取OE=OF=OP，作∠MPN=60°，只要证明△PEM≌△PON 即可推出△PMN是等边三角形，由此即可对称结论．【解答】解：如图在OA、OB上截取OE=OF=OP，作∠MPN=60°．∵OP平分∠AOB，∴∠EOP=∠POF=60°，∵OP=OE=OF，∴△OPE，△OPF是等边三角形，∴EP=OP，∠EPO=∠OEP=∠PON=∠MP N=60°，∴∠EPM=∠OPN，在△PEM和△PON中，，∴△PEM≌△PON．∴PM=PN，∵∠MPN=60°，∴△POM是等边三角形，∴只要∠MPN=60°，△PMN就是等边三角形，故这样的三角形有无数个．故选D．【点评】本题考查等边三角形的判定和性质、全等三角形的判定和性质、角平分线的性质等知识，解题的关键是正确添加辅助线，构造全等三角形，属于中考常考题型．18．（2016•内江）已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为（）A．B．C．D．不能确定【分析】作出图形，根据等边三角形的性质求出高AH的长，再根据三角形的面积公式求出点P到三边的距离之和等于高线的长度，从而得解．【解答】解：如图，∵等边三角形的边长为3，∴高线AH=3×=，S△AB C=B C•AH=AB•PD+BC•PE+AC•PF，∴×3•AH=×3•PD+×3•PE+×3•PF，∴PD+PE+PF=AH=，即点P到三角形三边距离之和为．故选：B．【点评】本题考查了等边三角形的性质，根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键，作出图形更形象直观．19．（2016•雅安）如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE 垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．3【分析】过A作AF⊥BC于F，根据等腰三角形的性质得到∠B=∠C=30°，得到AB=AC=2，根据线段垂直平分线的性质得到BE=AE，即可得到结论．【解答】解：过A作AF⊥BC于F，∵AB=AC，∠A=120°，∴∠B=∠C=30°，∴AB=AC=2，∵DE垂直平分AB，∴BE=AE，∴AE+CE=BC=2，∴△ACE的周长=AC+AE+CE=AC+BC=2+2，故选：A．【点评】本题考查了线段垂直平分线性质，三角形的内角和定理，等腰三角形的性质，含30度角的直角三角形性质等知识点，主要考查运用性质进行推理的能力．20．（2016•邵阳）如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（）A．AC＞BC B．AC=BC C．∠A＞∠ABC D．∠A=∠ABC【分析】根据等腰三角形的两个底角相等，由AD=BD得到∠A=∠ABD，所以∠ABC ＞∠A，则对各C、D选项进行判断；根据大边对大角可对A、B进行判断．【解答】解：∵AD=BD，∴∠A=∠ABD，∴∠ABC＞∠A，所以C选项和D选项错误；∴AC＞BC，所以A选项正确；B选项错误．故选A．【点评】本题考查了等腰三角形的性质：等腰三角形的两腰相等；等腰三角形的两个底角相等；等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．。

中考数学_专项_矩形、菱形、正方形考点及题型

【中考数学】矩形、菱形、正方形的5大考点及题型汇总矩形、菱形、正方形是八年级下册特殊平行四边形这一章节的重要组成部分。

他们都是基于平行四边形的性质衍生出来的其基本的性质都和平行四边形是一样的。

所以大家在进行学习和记忆的时候只需要紧抓其特殊部分，就能把他们都区分出来。

熟练掌握矩形，菱形，正方形的性质，定义和判定是这部分学习的重点，同时这部分也是中考数学几何部分的重要考点。

只有把这些性质和判定融会贯通。

那么在遇到综合题或者是类似题型的几何才能应对自如，尽快的形成自己的解题思路。

今天就给大家分享初中数学矩形、菱形、正方形的5大考点及题型，同学们赶紧来查漏补缺。

一、矩形、菱形、正方形的性质1.矩形的性质①具有平行四边形的一切性质；②矩形的四个角都是直角；③矩形的对角线相等；④矩形是轴对称图形，它有两条对称轴；⑤直角三角形斜边上的中线等于斜边的一半。

2.菱形的性质①具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，每条对角线所在的直线都是它的对称轴；⑤菱形的面积＝底×高＝对角线乘积的一半。

3.正方形的性质: 正方形具有平行四边形，矩形，菱形的一切性质①边：四边相等，对边平行；②角：四个角都是直角；③对角线：互相平分；相等；且垂直；每一条对角线平分一组对角，即正方形的对角线与边的夹角为45度；④正方形是轴对称图形，有四条对称轴。

例1 矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为（）A．360 B．90C．270 D．180例2 如图，矩形ABCD中，AE⊥BD于点E，对角线AC与BD相交于点O，BE：ED ＝1：3，AB＝6cm，求AC的长。

例3 如图， O是矩形ABCD 对角线的交点， AE平分∠BAD，∠AOD=120°，求∠AEO 的度数。

例4 菱形的周长为40cm，两邻角的比为1:2，则较短对角线的长________ 。

2016年甘肃省兰州市临夏州武威市平凉市张掖市白银市定西市中考数学试卷(word解析版)

甘肃省兰州市2016 年中考试题数学（A）注意事项：1.本试卷满分150 分，考试用时120 分钟。

2.考生必须将姓名、准考证号、考场、座位号等个人信息填（涂）在答题卡上。

3.考生务必将答案直接填（涂）写在答题卡的相应位置上。

一、选择题：本大题共15 小题，每小题4 分，共60 分，在每小题给出的四个选项中仅有一项是符合题意的。

1.如图是由5 个大小相同的正方体组成的几何体，则该几何体的主视图是（）。

（A）（B）（C）（D）【答案】A【解析】主视图是从正面看到的图形。

从正面看有两行，上面一行最左边有一个正方形，下面一行有三个正方形，所以答案选A。

【考点】简单组合体的三视图2.反比例函数的图像在（）。

（A）第一、二象限（B）第一、三象限（C）第二、三象限（D）第二、四象限【答案】B【解析】反比例函数的图象受到的影响，当k 大于0 时，图象位于第一、三象限，当k小于0 时，图象位于第二、四象限，本题中k ＝2 大于0，图象位于第一、三象限，所以答案选B。

【考点】反比例函数的系数k 与图象的关系3.已知△ABC ∽△DEF，若△ABC与△DEF的相似比为3／4，则△ABC与△DEF对应中线的比为（）。

（A）3／4（B）4／3（C）9／16（D）16／9【答案】A【解析】根据相似三角形的性质，相似三角形的对应高线的比、对应中线的比和对应角平分线的比都等于相似比，本题中相似三角形的相似比为3／4，即对应中线的比为3／4，所以答案选A。

【考点】相似三角形的性质4.在Rt △ABC中，∠C＝90°，sinA＝3／5，BC＝6，则AB＝（）。

（A）4 （B）6 （C）8 （D）10【答案】D【解析】在Rt △ABC中，sinA＝BC／AB＝6／AB＝3／5，解得AB＝10，所以答案选D。

【考点】三角函数的运用5.一元二次方程的根的情况（）。

（A）有一个实数根（B）有两个相等的实数根（C）有两个不相等的实数根（D）没有实数根【答案】B【解析】根据题目，∆＝＝0, 判断得方程有两个相等的实数根，所以答案选B。

2016年中考数学试卷分类汇编解析：矩形菱形与正方形

矩形菱形与正方形一、选择题1．（2016·黑龙江大庆）下列说法正确的是（）A．对角线互相垂直的四边形是菱形B．矩形的对角线互相垂直C．一组对边平行的四边形是平行四边形D．四边相等的四边形是菱形【考点】矩形的性质；平行四边形的判定；菱形的判定．【分析】直接利用菱形的判定定理、矩形的性质与平行四边形的判定定理求解即可求得答案．【解答】解：A、对角线互相垂直且平分的四边形是菱形；故本选项错误；B、矩形的对角线相等，菱形的对角线互相垂直；故本选项错误；C、两组组对边分别平行的四边形是平行四边形；故本选项错误；D、四边相等的四边形是菱形；故本选项正确．故选D．【点评】此题考查了矩形的性质、菱形的判定以及平行四边形的判定．注意掌握各特殊平行四边形对角线的性质是解此题的关键．2. （2016·湖北鄂州）如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q 是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点为A′，当CA′的长度最小时，CQ的长为（）13A. 5B. 7C. 8D.2【考点】菱形的性质，梯形，轴对称（折叠），等边三角形的判定和性质，最值问题．【分析】如下图所示，由题意可知，△ABC为等边三角形；过C作CH⊥AB，则AH=HB；连接DH；要使CA′的长度最小，则梯形APQD沿直线PQ折叠后A的对应点A′应落在CH上，且对称轴PQ 应满足PQ ∥DH ；因为BP=3，易知HP=DQ=1，所以CQ=7.【解答】解：如图，过C 作CH ⊥AB ，连接DH ；∵ABCD 是菱形，∠B=60° ∴△ABC 为等边三角形； ∴AH=HB=28=4； ∵BP=3， ∴HP=1要使CA ′的长度最小，则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CH 上，且对称轴PQ 应满足PQ ∥DH ；由作图知，DHPQ 为平行四边形 ∴DQ=HP= 1， CQ=CD-DQ=8-1=7. 故正确的答案为：B ．【点评】本题综合考查了菱形的性质，梯形，轴对称（折叠），等边三角形的判定和性质，最值问题．本题作为选择题，不必直接去计算，通过作图得出答案是比较便捷的方法。

全国181套中考数学试题分类汇编44矩形、菱形、正方形

44矩形、菱形、正方形一、选择题1.（浙江舟山、嘉兴3分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（A ）48cm（B ）36cm （C ）24cm （D ）18cm 【答案】A 。

【考点】菱形的性质，平行四边形的性质。

【分析】根据①②③④四个平行四边形面积的和为14cm2，四边形ABCD 面积是11cm2，从图可求出⑤的面积： 2ABCD 1S S S 2cm ⑤四边形①+②+③+④=-=11-7=4。

从而可求出菱形的面积：2EFGH S S 14418cm ==+=①+②+③+④+⑤菱形。

又∵∠EFG=30°，∴菱形的边长为6cm 。

从而根据菱形四边都相等的性质得：①②③④四个平行四边形周长的总和=2（AE+AH+HD+DG+GC+CF+FB+BE ） =2（EF+FG+GH+HE ）=48cm 。

故选A 。

2.（浙江温州4分）如图，在矩形ABCD 中，对角线AC ，BD 交与点O ．已知∠AOB=60°，AC=16，则图中长度为8的线段有A 、2条B 、4条C 、5条D 、6条【答案】D 。

【考点】矩形的性质。

等边三角形的判定和性质。

【分析】因为矩形的对角线相等且互相平分，AC=16，所以AO=BO=CO=DO=8；又由∠AOB=60°，所以三角形AOB 是等边三角形，所以AB=AO=8；又根据矩形的对边相等得，CD=AB=AO=8．从而可求出线段为8的线段有6条。

故选D 。

3.（辽宁大连3分）如图，矩形ABCD 中，AB ＝4，BC ＝5，AF 平分∠DAE，EF⊥AE，则CF 等于A ．23B ．1C ．32D ．2【答案】C 。

4.（黑龙江哈尔滨3分）如图，矩形ABCD 中，对角线AC 、BD 相交于点O ，∠AOB=600，AB=5，则AD 的长是．（A)53 （B ）52 （C ）5 (D)10【答案】A 。

2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形

矩形菱形与正方形一、选择题1．（2016·黑龙江大庆）下列说法正确的是（）A ．对角线互相垂直的四边形是菱形B ．矩形的对角线互相垂直C ．一组对边平行的四边形是平行四边形D ．四边相等的四边形是菱形2. （2016·湖北鄂州）如图，菱形ABCD 的边AB=8，∠B=60°，P 是AB 上一点，BP=3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点为A ′，当CA ′的长度最小时，CQ 的长为（） A. 5 B. 7 C. 8 D. 213 4. (2016·四川资阳)如图，矩形ABCD 与菱形EF GH 的对角线均交于点O ，且E G ∥B C ，将矩形折叠，使点C 与点O 重合，折痕M N 恰好过点G 若AB=，EF =2，∠H=120°，则DN 的长为（）A ．B ．C ．﹣D ．2﹣ 5. （2016·四川广安·3分）下列说法：①三角形的三条高一定都在三角形内 ②有一个角是直角的四边形是矩形③有一组邻边相等的平行四边形是菱形 ④两边及一角对应相等的两个三角形全等⑤一组对边平行，另一组对边相等的四边形是平行四边形其中正确的个数有（）A ．1个 B ．2个 C ．3个 D ．4个7．（2016·山东枣庄）如图，四边形ABCD 是菱形，8=AC ，6=DB ，AB DH⊥于H ，则DH 等于A ．524 B ．512 C ．5 D ．4 8．（2016·江苏苏州）矩形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标为（3，4），D 是OA 的中点，点E 在AB 上，当△CDE 的周长最小时，点E 的坐标为（）A ．（3，1）B ．（3，）C ．（3，）D ．（3，2）9．（2016·江苏无锡）下列性质中，菱形具有而矩形不一定具有的是（）A ．对角线相等B ．对角线互相平分C ．对角线互相垂直D ．邻边互相垂直第9题 B CH10．（2016·江苏省宿迁）如图，把正方形纸片ABCD 沿对边中点所在的直线对折后展开，折痕为MN ，再过点B 折叠纸片，使点A 落在MN 上的点F 处，折痕为BE ．若AB 的长为2，则FM 的长为（） A ．2 B ． C ． D ．111．（2016·江苏省扬州）如图，矩形纸片ABCD 中，AB=4，BC=6．将该矩形纸片剪去3个等腰直角三角形，所有剪法中剩余部分面积的最小值是（）A ．6 B ．3 C ．2.5 D ．212．（2016•浙江省舟山）如图，矩形ABCD 中，AD=2，AB=3，过点A ，C 作相距为2的平行线段AE ，CF ，分别交CD ，AB 于点E ，F ，则DE 的长是（）A ． B ． C ．1 D ．13．（2016•呼和浩特）如图，面积为24的正方形ABCD 中，有一个小正方形EFGH ，其中E 、F 、G 分别在AB 、BC 、FD 上．若BF=，则小正方形的周长为（）A ．B ．C ．D ．14.(2016兰州，14,4分)如图，矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE ∥BD, DE ∥AC , AD ＝ , DE ＝2,则四边形 OCED 的面积为（）15.广东，如图，正方形ABCD 的面积为1，则以相邻两边中点连接EF 为边的正方形EFGH 的周长为（）AB、 C1+ D、1+2. 如图，在矩形ABCD 中，AB=3，对角线AC ，BD 相交于点O ，AE 垂直平分OB 于点E ，则AD 的长为． 3．如图，延长矩形ABCD 的边BC 至点E ，使CE=BD ，连结AE ，如果∠ADB=30°，则∠E= 度．16. （2016年浙江省如图，点P 在矩形ABCD 的对角线AC 上，且不与点A ，C 重合，过点P 分别作边AB ，AD 的平行线，交两组对边于点E ，F 和G ，H ．（1）求证：△PHC ≌△CFP ；（2）证明四边形PEDH 和四边形PFBG 都是矩形，并直接写出它们面积之间的关系．4. （2016吉林长春，12，3分）如图，在平面直角坐标系中，正方形ABCD 的对称中心与原点重合，顶点A 的坐标为（﹣1，1），顶点B 在第一象限，若点B 在直线y=kx+3上，则k 的值为．5.（2016·广东广州）如图5，正方形ABCD 的边长为,AC 、BD 是对角线，将△DCB 绕点D 顺时针旋转450得到△DGH ，HG 交AB 于点E ，连接DE 交AC 于点F ，连接FG ，则下列结论：①四边形AEGF 是菱形②△AED ≌△GED ③∠DFG ＝112.5 ④BC ＋FG ＝1.5 其中正确的结论是 .（填写所有正确结论的序号）6.（2016·广东茂名）已知矩形的对角线AC 与BD 相交于点O ，若AO=1，那么BD= ．8. (2016年浙江省丽水市)如图，在菱形ABCD 中，过点B 作BE ⊥AD ，BF ⊥CD ，垂足分别为点E ，F ，延长BD 至G ，使得DG=BD ，连结EG ，FG ，若AE=DE ，则= ．图513．（2016.山东省青岛市,3分）如图，在正方形ABCD 中，对角线AC 与BD 相交于点O ，E 为BC 上一点，CE=5，F 为DE 的中点．若△CEF 的周长为18，则OF 的长为．14．（2016.山东省泰安市，3分）如图，矩形ABCD 中，已知AB=6，BC=8，BD 的垂直平分线交AD 于点E ，交BC 于点F ，则△BOF 的面积为．15. （2016·江苏南京）如图，菱形ABCD 的面积为120，正方形AECF 的面积为50，则菱形的边长为_______.17．（2016·江苏省宿迁）如图，在矩形ABCD 中，AD=4，点P 是直线AD 上一动点，若满足△PBC 是等腰三角形的点P 有且只有3个，则AB 的长为．19．（2016•辽宁沈阳）如图，在Rt △ABC 中，∠A=90°，AB=AC ，BC=20，DE 是△ABC 的中位线，点M 是边BC 上一点，BM=3，点N 是线段MC 上的一个动点，连接DN ，ME ，DN 与ME 相交于点O．若△OMN是直角三角形，则DO的长是．1．（2016·湖北十堰）如图，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F．（1）判断四边形CEGF的形状，并证明你的结论；（2）若AB=3，BC=9，求线段CE的取值范围．5. （2016·四川达州·10分）△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．（1）如图1，当点D在线段BC上时，①BC与CF的位置关系为：．②BC，CD，CF之间的数量关系为：；（将结论直接写在横线上）（2）如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2，CD=BC，请求出GE的长．19．（2016•江苏省扬州如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．（1）求证：四边形AECF是平行四边形；（2）若AB=6，AC=10，求四边形AECF的面积．。

2016年河北省中考数学试卷附详细答案(原版+解析版)

2016年河北省中考数学试卷一、（本大题共16小题，共42分，1-10小题各3分，11-16小题各2分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）计算：﹣（﹣1）=（）A．±1 B．﹣2 C．﹣1 D．12．（3分）计算正确的是（）A．（﹣5）0=0 B．x2+x3=x5C．（ab2）3=a2b5D．2a2•a﹣1=2a3．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．4．（3分）下列运算结果为x﹣1的是（）A．1﹣B．•C．÷D．5．（3分）若k≠0，b＜0，则y=kx+b的图象可能是（）A．B．C．D．6．（3分）关于▱ABCD的叙述，正确的是（）A．若AB⊥BC，则▱ABCD是菱形B．若AC⊥BD，则▱ABCD是正方形C．若AC=BD，则▱ABCD是矩形D．若AB=AD，则▱ABCD是正方形7．（3分）关于的叙述，错误的是（）A．是有理数B．面积为12的正方形边长是C．=2D．在数轴上可以找到表示的点8．（3分）图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能围成正方体的位置是（）A．①B．②C．③D．④9．（3分）如图为4×4的网格图，A，B，C，D，O均在格点上，点O是（）A．△ACD的外心B．△ABC的外心C．△ACD的内心D．△ABC的内心10．（3分）如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C为圆心，CA为半径画弧①；步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；步骤3：连接AD，交BC延长线于点H．下列叙述正确的是（）A．BH垂直平分线段AD B．AC平分∠BADC．S△ABC=BC•AH D．AB=AD11．（2分）点A，B在数轴上的位置如图所示，其对应的数分别是a和b．对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：＞0其中正确的是（）A．甲乙B．丙丁C．甲丙D．乙丁12．（2分）在求3x的倒数的值时，嘉淇同学误将3x看成了8x，她求得的值比正确答案小5．依上述情形，所列关系式成立的是（）A．=﹣5 B．=+5 C．=8x﹣5 D．=8x+513．（2分）如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）A．66°B．104°C．114°D．124°14．（2分）a，b，c为常数，且（a﹣c）2＞a2+c2，则关于x的方程ax2+bx+c=0根的情况是（）A．有两个相等的实数根B．有两个不相等的实数根C．无实数根D．有一根为015．（2分）如图，△ABC中，∠A=78°，AB=4，AC=6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．16．（2分）如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（）A．1个B．2个C．3个D．3个以上二、填空题（本大题有3小题，共10分.17-18小题各3分；19小题有2个空，每空2分.把答案写在题中横线上）17．（3分）8的立方根是．18．（3分）若mn=m+3，则2mn+3m﹣5mn+10=．19．（4分）如图，已知∠AOB=7°，一条光线从点A出发后射向OB边．若光线与OB边垂直，则光线沿原路返回到点A，此时∠A=90°﹣7°=83°．当∠A＜83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2，易知∠1=∠2．若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A=°．…若光线从A点出发后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值=°．三、解答题（本大题有7个小题，共68分.解答应写出必要的文字说明、证明过程或演算步骤）20．（9分）请你参考黑板中老师的讲解，用运算律简便计算：（1）999×（﹣15）（2）999×118+999×（﹣）﹣999×18．21．（9分）如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC．（1）求证：△ABC≌△DEF；（2）指出图中所有平行的线段，并说明理由．22．（9分）已知n边形的内角和θ=（n﹣2）×180°．（1）甲同学说，θ能取360°；而乙同学说，θ也能取630°．甲、乙的说法对吗？若对，求出边数n．若不对，说明理由；（2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x．23．（9分）如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B；…设游戏者从圈A起跳．（1）嘉嘉随机掷一次骰子，求落回到圈A的概率P1；（2）淇淇随机掷两次骰子，用列表法求最后落回到圈A的概率P2，并指出她与嘉嘉落回到圈A的可能性一样吗？24．（10分）某商店通过调低价格的方式促销n个不同的玩具，调整后的单价y （元）与调整前的单价x（元）满足一次函数关系，如表：第1个第2个第3个第4个…第n个调整前的单价x（元）x1x2=6x3=72x4…x n调整后的单价y（元）y1y2=4y3=59y4…y n已知这个n玩具调整后的单价都大于2元．（1）求y与x的函数关系式，并确定x的取值范围；（2）某个玩具调整前单价是108元，顾客购买这个玩具省了多少钱？（3）这n个玩具调整前、后的平均单价分别为，，猜想与的关系式，并写出推导过程．25．（10分）如图，半圆O的直径AB=4，以长为2的弦PQ为直径，向点O方向作半圆M，其中P点在上且不与A点重合，但Q点可与B点重合．发现：的长与的长之和为定值l，求l：思考：点M与AB的最大距离为，此时点P，A间的距离为；点M与AB的最小距离为，此时半圆M的弧与AB所围成的封闭图形面积为；探究：当半圆M与AB相切时，求的长．（注：结果保留π，cos35°=，cos55°=）26．（12分）如图，抛物线L：y=﹣（x﹣t）（x﹣t+4）（常数t＞0）与x轴从左到右的交点为B，A，过线段OA的中点M作MP⊥x轴，交双曲线y=（k ＞0，x＞0）于点P，且OA•MP=12，（1）求k值；（2）当t=1时，求AB的长，并求直线MP与L对称轴之间的距离；（3）把L在直线MP左侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最高点的坐标；（4）设L与双曲线有个交点的横坐标为x0，且满足4≤x0≤6，通过L位置随t变化的过程，直接写出t的取值范围．2016年河北省中考数学试卷参考答案与试题解析一、（本大题共16小题，共42分，1-10小题各3分，11-16小题各2分。

2016届中考数学真题类编-知识点028 矩形、菱形、正方形和梯形2016A

一、选择题1.（2016山东东营，10，3分）如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠A．4个B．3个C．2个D．1个【答案】B【逐步提示】本题考查矩形的性质，相似三角形的判定与性质，平行四边形的判定与性质，锐角三角函数的定义等．综上所述，①②③正确，而无法判断④正确，故选B．【解后反思】【一题多解】③取BC的中点M，连接DM，FM，∴FM=CM．∵E是AD的中点，∴DE=BM，又∵DE∥BM，∴四边形BMDE是平行四边形，∴DM∥BE，∴DM⊥CF，∴DM是线段CF的垂直平分线，∴DF=DC．【关键词】矩形的性质；相似三角形的判定与性质；平行四边形的判定与性质；锐角三角函数的定义2.（2016山东泰安，23，3分）如图，矩形ABCD中，已知AB＝6，BC＝8，BD的垂直平分线交AD于点E，交BC于点F，则△BOF的面积为．【逐步提示】本题考查了矩形的性质、勾股定理、相似三角形的判定与性质，解题的关键是相似三角形面积比等于相似比的平方的性质的应用．与因为已知AB ＝6，BC ＝8，所以可以求出△BDC 的面积，因为EF 垂直平分BD ，可知∠BOF ＝90°，所以△BOF 与△BCD 相似．利用勾股定理可以求出BD 的长，也就知道了OB 的长度，根据相似三角形面积比等于相似比的平方，可以计算出△BOF 的面积．【详细解答】解：∵四边形ABCD 是矩形，∴AB ＝CD ＝6，∠C ＝90°，∵BC ＝8，∴由勾股定理得10BD ，168242BCD S ∆⨯⨯＝＝，∵EF 垂直平分BD ，∴∠BOF ＝90°，152OB BD ＝＝．∵∠OBF ＝∠DBC ，∠BOF ＝∠C＝90°，∴△BOF ∽△BCD ，∴222525864BOF BCD S OB S BC ∆∆⎛⎫ ⎪⎝⎭＝＝＝，∴257524648BOFS ∆⨯＝＝．【解后反思】由于所求的△BOF 是直角三角形，所以有的同学可能直接用12S OB OF ∆⨯⨯＝来计算三角形的面积，这样解决起来就很繁琐．实际上本题是考查相似三角形的性质：两个相似三角形面积的比等于相似比的平方．所以认真审题，理清脉络很关键．【关键词】矩形的性质；勾股定理；垂直平分线；相似三角形的性质．3. （ 2016山东省枣庄市，9，3分）如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于H ，则DH 等于（） A ．245B ．125 C ．5 D ．4【答案】A ．【逐步提示】本题考查了菱形的性质，及面积公式，解题的关键是灵活运用菱形的性质．根据菱形对角线互相垂直且平分，求出菱形的边长，再利用菱形的面积公式即可求出高线DH ．【详细解答】解：设AC 、BD 交于点O ．∵四边形ABCD 是菱形，∴AO ＝12AC ＝4，BO ＝12DB ＝3，∠AOB ＝90°，∴AB＝5，∵S 菱形ABCD ＝12AC ·DB ＝AB ·DH ，∴DH ＝12AC BD AB ⋅＝18625⨯⨯＝245，故选择A .ABDCHOAEDBFC第23题图【解后反思】本题考查了菱形的性质及面积公式．菱形的性质：①菱形的四条边相等；②菱形的对角线互相垂直平分，且每一条对角线平分一组对角；③S 菱形ABCD ＝12AC ·DB ＝底×高．本题在解答时，还可以利用△BDH ∽△BAO ，BD DHBA AO=求解．【关键词】勾股定理；菱形的性质；菱形的面积；4. （2016山东淄博，8，4分）如图，正方形ABCD 的边长为10， AG =CH =8，BG =DH =6，连接GH . 则线段GH 的长为（）A.C. 145D. 10－【答案】B【逐步提示】本题考查正方形，勾股定理及逆定理的知识，解题关键是能灵活添加辅助线，将问题转化为已知问题解决. 延长BG 交CH 于点E ，根据正方形的性质证明ABG ≌△CDH≌△BCE ，可得GE =BE ﹣BG =2、HE =CH ﹣CE =2、∠HEG =90°，由勾股定理可得GH 的长．【详细解答】解：法一：如图，延长BG 交CH 于点E ，∵AG =CH =8，BG =DH =6，AB =CD =10，∴△ABG ≌△CDH （SSS ）. ∵22AG BG +=2286+=210=2AB ，∴△ABG 是直角三角形，∠AGB =90°. 同理△DHC 是直角三角形，∠DHC =90°. ∵∠1=∠5，∠2=∠6，∠AGB =∠CHD =90°， ∴∠1+∠2=90°，∠5+∠6=90°，又∵∠2+∠3=90°，∠4+∠5=90°， ∴∠1=∠3=∠5，∠2=∠4=∠6，∵AB =BC ，∴△ABG ≌△BCE （ASA ）.∴BE =AG =8，CE =BG =6，∠BEC =∠AGB =90°. ∴GE =BE －BG =8－6=2. 同理可得HE =2GE .在RT △GHE 中，GH.故选择B.ABDCHO法二：过点G 作EF ⊥AB 于点EF ，过点H 作HF ∥AB .∵22AG BG +=2286+=210=2AB ，∴△ABG 是直角三角形，∠AGB =90°. 同理△DHC 是直角三角形，∠DHC =90°. ∴EG =6810⨯=4.8. ∴GF =10－2×4.8=0.4. ∵BE =6610⨯=3.6，∴HF =10－2×3.6=2.8. ∴HG. 故选择B.【解后反思】添加辅助线，构造直角三角形求解是解题关键. 【关键词】正方形，勾股定理及逆定理5. (2016天津，10，3分)如图，把一张矩形纸片ABCD 沿对角线AC 折叠，点B 的对应点为B ′，AB ′与DC 相交于点E ，则下列结论正确的是()A ．∠DAB′=∠CAB ′ B ．∠ACD=∠B′CDC ．AD =AE D ． AE =CE 【答案】D【逐步提示】本题是一道有关折叠的问题，应根据折叠的性质求解．根据折叠得到△ABC 与△AB′C 全等，得到∠BAC =∠B′AC ,然后利用矩形的性质将∠ACE 转化到∠CAB′.【解析】根据折叠得到△ABC ≌△AB ′C ，∴=BAC B AC '∠∠，又∵AB ∥CD ，∴∠BAC =∠DCA ，∴∠EAC =∠DCA ，∴EA =E C.故选择D .【解后反思】折叠问题是属于轴对称变换，折叠后图形的形状和大小不变，三角形折叠后得到的三角形与原三角形全等，对应边和对应角相等.【关键词】折叠问题；等腰三角形；全等三角形(2016浙江宁波，12，4分)如图是一个由 5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S 1 ,另两张直角三角形纸片的面积都为 S 2,中间一张正方形纸片的面积为S 3,则这个平行四边形的面积一定可以表示为( )A. 4S 1B. 4S 2C. 4S 2+ S 3D. 3S 1+ 4S 3E F【答案】A【逐步提示】本题考查了平行四边形性质、直角三角形性质、整式的加减运算，解题的关键是引入字母找出S 1 、S 2、S 3 之间的关系.设等腰直角三角形纸片的直角边长为a, 中间一张正方形纸片的边长为m,从而可以表示出面积为S 2的直角三角形纸片两条直角边长，进而得出S 1 、S 2、S 3 之间的关系.【解析】设等腰直角三角形纸片的直角边长为a, 中间一张正方形纸片的边长为m,则2112S a =，23S m =，∴22213111()()()(2)222S a m a m a m S S =-+=-=-,即31222S S S =-，∴这个平行四边形的面积=123121212222(22)4S S S S S S S S ++=++-=，故选择A . 【解后反思】此类问题常常通过引入字母，再结合图形把所求的面积具体化，找出三个面积之间的等量关系，就可以求得问题的解.【关键词】等腰三角形与直角三角形；平行四边形；平方差公式；整式的加减6.(2016浙江舟山，9，3分)如图，矩形ABCD 中，AD =2，AB =3，过点A ．C 作相距为2的平行线段AE 、CF ，分别交CD ．AB 于点E 、F ，则DE 的长是( )A ． 5B ．136C ．1D ．56【答案】D【逐步提示】本题考查了矩形、平行四边形、全等三角形的性质与判定，解题的关键是用DE 的代数式表示AE 的长度. 过点F 作FH ⊥AE ，交AE 于点H ，根据平行线间的距离的概念，得FH =2=AD .设DE =x .先说明四边形AECF 为平行四边形，由矩形、平行四边形的性质可得DE =BF =x ，即F A =3－x .再证△ADE ≌△FHA ，得AE =F A =3－x ，然后在Rt △ADE 中利用勾股定理构造关于x 的方程，解方程求出x 的值，即得DE 的长.【解析】设DE=x.过点F 作FH ⊥AE ，交AE 于点H ，∵AE 、CF 是平行线段，∴FH=2=AD ，AE ∥CF.∵四边形ABCD 是矩形，∴AB ∥CD ，AB=CD ，∴.四边形AECF 为平行四边形，∴AF=CE ，∴DE=BF=x ，即FA=3－x. 在矩形ABCD 中，∠BAD=∠D=90°，∴∠D=∠AHF=90°，∠DAE=AFH ，∴△ADE ≌△FHA ，∴AE=FA=3－x.因此在Rt △ADE 中，由“AD 2+DE 2=AE 2”得“22+x 2=(3－x)2”，解得x=56，即DE=56，故选择D .【解后反思】本题较综合地考查了部分特殊四边形的性质与判定，全等三角形的识别与性质等知识，设DE=x后，利用上述知识，用x的代数式表示AE的长度是解答本题的关键，再结合勾股定理，利用方程求解，充分体现了方程思想在求解几何图形相关问题的重要功能.【关键词】矩形的性质；平行四边形的判定；全等三角形的识别与性质；勾股定理；方程思想.7.（2016四川省广安市，8，3分）下列说法：①三角形的三条高一定都在三角形内；②有一个角是直角的四边形是矩形；③有一组邻边相等的平行四边形是菱形；④两边及一角对应相等的两个三角形全等；⑤一组对边平行，另一组对边相等的四边形是平行四边形．其中正确的个数有（）A．1个B．2个C．3个D．4个【答案】A【逐步提示】本题考查了三角形的中线、高线、角平分线的概念，矩形的判定，菱形的判定，全等三角形的判定，平行四边形的判定等，解题的关键是掌握这些概念、定理等．因为直角三角形与钝角三角形的三条高不都在三角形内，故①错；至少有三个角是直角的四边形是才是矩形，故②错；③是菱形的定义，正确；满足④的条件时有可能形成“边边角”的情况，故错误；等腰梯形满足“一组对边平行，另一组对边相等”，但它不是平行四边形，故⑤错误．【详细解答】解：只有③正确，故选择A.【解后反思】要理解三角形“三线”的概念，掌握三角形、平行四边形、矩形、菱形的判定方法，这是正确解题的基础．能画图举反例，以排除不符合条件情形，也是解这类题的基本功，要多思考，勤积累．类似的问题还有：判断下列说法是否正确：（1）一组对边相等且一组对角相等的四边形是平行四边形.解：错误．如图1，作△ABC，使AB＝AC，在BC上取一点D（D点不与B、C重合且BD≠CD），连接AD.再以A为顶点，AD为一边，作∠EAD，使∠EAD＝∠ADC，且AE＝DC，连接DE.由上述画图方法，可知△ADC≌△DAE（SAS）.所以DE＝AC＝AB，∠AED＝∠C＝∠B.即四边形ABCD有一组对边相等（DE＝AB）、一组对角相等（∠AED＝∠B），但却不是平行四边形（另一组对边AE和BD不平行也不相等）.（2）一组对边相等，且一条对角线平分另一条对角线的四边形是平行四边形.解：错误．如图2，画两条相交直线，交点为O，在其中一条直线上截取OA＝OC，分别过A、C两点向另一条直线作垂线，垂足分别为E、F.在线段OF上取一点D（D点不与O、F重合），连接CD.再在线段OE的延长线上取一点B，使EB＝FD，连接AB.由上述画图方法，易知△COF≌△AOE（AAS），则CF＝AE，由“SAS”可判定△CFD≌△AEB，则CD＝AB .连接AD 、BC ，则四边形ABCD 满足条件，却不是平行四边形.（3）一组对角相等，且连接这一组对角的顶点的对角线被另一条对角线平分的四边形是平行四边形.解：错误．如图，画一个“筝形”ABCD ，其中AB ＝AD ，BC ＝DC 且AO ≠OC ，则该“筝形”满足条件，但它不是平行四边形.【关键词】中线、高线、角平分线；矩形的判定；菱形的判定；全等三角形的判定；平行四边形的判定 8. （ 2016四川泸州，10，3分）如图，矩形ABCD 的边长AD=3,AB=2,E 为AB 的中点，F 在边BC 上，且BF=2FC ，AF 分别与DE 、DB 相交于点M ，N ，则MN 的长为（）A.5B.20C.4D.5【答案】B ，9 （ 2016四川省绵阳市，11，3分）如图，点E ，点F 分别在菱形ABCD 的边AB ，AD 上，且AE ＝DF ，BF 交DE 于点G ，延长BF 交CD 的延长线于H ，若AF DF ＝2，则HFBG的值为 ········ （） A ．23 B ．712C ．12D ．512【答案】B ．【逐步提示】本题考查了相似三角形的判定和性质．由菱形ABCD 知AB ∥CD ，AD ∥BC ，可知图中存在多个相似三角形中的基本图形：“A ”型“与”X “型．由基本图形得HF FB ＝DF AF ＝12，所以HF ＝13HB ①．类似地，HD ＝12AB ，又BE ＝23AB ，所以HD BE ＝34．由基本图形得BG HG ＝BE HD ＝43，所以BG ＝47HB ②，由①②可求HFBG的比值．【详细解答】解：设菱形ABCD 的边长为3a ．因为四边形ABCD 是菱形，AFDF＝2，AE ＝DF ，所以AE ＝DF ＝a ，AF ＝BE ＝2a ，AB ∥CD ，所以HF FB ＝HD AB ＝DF AF ＝12，所以HD ＝12AB ＝32a ，HF ＝13HB ．因为AB∥CD ，所以BG HG ＝BE HD ＝232a a ＝43，所以BG ＝47HB ．所以HF BG ＝1347HBHB 712，故答案为B ．【解后反思】（1）求线段的比通常利用平行线或相似三角形得到比例线段，然后再进行转化得到所求两线段的比．（2）遇到平行线，要联想到以下两个常用的基本图形（“A ”型“与”X “型）．【关键词】菱形的性质；相似三角形的判定；转化思想．10 （ 2016四川南充，8，3分）如图，对折矩形纸片ABCD ，使AB 与DC 重合得到折痕EF ，将纸片展平，再一次折叠，使点D 落到EF 上G 点处，并使折痕经过点A ，展平纸片后∠DAG 的大小为（）E CDFGHABA．30°B．45°C．60°D．75°【答案】C【逐步提示】本题主要考查了翻折变换的性质以及平行线的性质，正确得出∠2=∠4是解题关键．直接利用翻折变换的性质以及直角三角形的性质得出∠2=∠4，再利用平行线的性质得出∠1=∠2=∠3，进而得出答案．【详细解答】解：如图所示：由题意可得：∠1=∠2，AN=MN，∠MGA=90°，则NG=12AM，故AN=NG，则∠2=∠4，∵EF∥AB，∴∠4=∠3，∴∠1=∠2=∠3=13×90°=30°，∴∠DAG=60°．故选择C．【解后反思】本题还可以采用如下方法求解。

广东省中考数学第一部分考点研究第五章四边形第二节矩形、菱形和正方形试题

第五章四边形第二节矩形、菱形和正方形玩转广东省卷6年中考真题（2011～2016）命题点1 矩形的判定与计算(省卷6年3考)1. (2016省卷15，4分)如图，矩形ABCD中，对角线AC＝23，E为BC边上一点，BC ＝3BE.将矩形ABCD沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB＝____．第1题图2. (2013省卷22，8分)如图，矩形ABCD中，以对角线BD为一边构造一个矩形BDEF，使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1，Rt△BFC的面积为S2，Rt△DCE 的面积为S3，则S1_____S2＋S3(用“＞”、“＝”、“＜”填空)；(2)写出图中的三对相似三角形，并选择其中一对进行证明．第2题图3. (2012省卷21，9分)如图，在矩形纸片ABCD中，AB＝6，BC＝8.把△BCD沿对角线BD折叠，使点C落在C′处，B C′交AD于点G，E、F分别是C′D和BD上的点，线段EF 交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．(1)求证：△ABG≌△C′DG；(2)求tan∠ABG的值；(3)求EF的长．第3题图命题点2 菱形的判定与计算(省卷6年3考)4. (2015省卷12，4分)如图，菱形ABCD的边长为6，∠ABC＝60°，则对角线AC的长是______．第4题图【拓展猜押】如图，在菱形ABCD中，AC＝8，BD＝6，则△ABD的周长等于( )拓展猜押题图A. 18B. 16C. 15D. 14命题点3 正方形的性质与计算(省卷6年2考)5. (2016省卷5，3分)如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边的正方形EFGH的周长为( )第5题图A. 2B. 2 2C. 2＋1D. 22＋1【答案】1. 3 【解析】设BE＝x，AB＝y，则B′E＝x，CE＝2x，AB′＝y，∴B′C＝23－y，∵AB2＋BC2＝AC2，B′C2＋EB′2＝EC2，∴()(()()222222322y xy x x⎧+=⎪⎨⎪-+=⎩，解得1xy=⎧⎪⎨=⎪⎩或0xy=⎧⎪⎨=⎪⎩舍去)，故AB＝ 3.2.解：(1)＝；…………………………………………………(3分)【解法提示】设矩形BDEF的长和宽分别为x，y，则S1＝12xy，S2＋S3＝12·FC·y＋12·EC·y ＝12(FC＋EC)y＝12xy, ∴S1＝S2＋S3.(2)△BCF∽△CDE；△BCF∽△DBC；△BDC∽△DCE.……(5分)选△BCF∽△CDE，证明：∵在矩形ABCD中，∠BCD＝90°，且点C在边EF上，∴∠BCF＋∠DCE＝90°，∵在矩形BDEF中，∠F＝∠E＝90°，∴在Rt△BCF中，∠CBF＋∠BCF＝90°，∴∠CBF＝∠DCE，∴△BCF∽△CDE.……………………………………………(8分)或选△BCF∽△DBC，证明：∵BD∥FC，∴∠DBC＝∠BCF，又∵∠BFC＝∠DCB＝90°，∴△BCF∽△DBC. …………………………………………(8分)或选△BDC∽△DCE，证明：∵BD∥CE，∴∠DBC＝180°－∠BCE＝180°－(∠BCD＋∠DCE)＝180°－90°－∠DCE＝90°－∠DCE，∴∠DBC＋∠DCE＝90°，∵在△DCE中，∠E＝90°，∴∠DCE＋∠CDE＝90°，∴∠DBC＝∠CDE，又∵∠BCD＝∠E＝90°，∴△BDC∽△DCE. …………………………………………(8分)3．(1)证明：∵四边形ABCD是矩形，∴AB＝CD，∠BAG＝∠C＝90°，∵把△BCD沿对角线BD折叠得到△BC′D，∴∠C′＝∠C＝∠BAG＝90°，C′D＝AB，……………………(1分)∵∠AGB＝∠C′GD，∴△ABG≌△C′DG(AAS)；…………………………………(3分)(2)解：设AG＝x，则有DG＝BG＝8－x，∴(8－x )2＝62＋x 2，解得x ＝74，………………………………(4分) ∴tan ∠ABG ＝AG AB ＝746＝724；…………………………………(6分) (3)解：∵把△FDE 沿EF 折叠，使点D 落在点D ′，点D ′恰好与点A 重合， ∴EF ⊥AD ，DH ＝AH ＝4，∴EF ∥AB ，∴HF 是△ABD 的中位线，∴HF ＝3，………………………………………………………(7分)由(1)中的△ABG ≌△C ′DG 可知，∠ABG ＝∠C ′DG ，∴HE ＝DH ·tan ∠C ′DG ＝DH ·tan ∠ABG ＝4×724＝76，………(8分) ∴EF ＝HF ＋HE ＝3＋76＝256.…………………………………(9分) 4．6 【解析】∵四边形ABCD 是菱形，∴AB ＝BC ＝6，∵∠ABC ＝60°，∴AC ＝AB ＝BC ＝6.【拓展猜押】 B 【解析】∵四边形ABCD 是菱形，∴BO ＝OD ＝12BD ＝3，AO ＝OC ＝12AC ＝4，∴AB ＝5，∴△ABD 的周长为：5＋5＋6＝16.5．B 【解析】∵正方形ABCD 的面积为1，∴BC ＝CD ＝1，∵点E 、F 分别是边BC 、CD的中点，∴CE ＝CF ＝12，∴EF＝＝22，∴正方形EFGH 的周长为4×22＝2 2.。

全国各地2014年中考数学试卷解析版分类汇编矩形菱形与正方形

矩形菱形与正方形一、选择题1. （2014•某某，第6题4分）如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）A．△ABD与△ABC的周长相等B．△ABD与△ABC的面积相等C．菱形的周长等于两条对角线之和的两倍D．菱形的面积等于两条对角线之积的两倍考点：菱形的性质．分析：分别利用菱形的性质结合各选项进而求出即可．解答：解：A、∵四边形ABCD是菱形，∴AB=BC=AD，∵AC＜BD，∴△ABD与△ABC的周长不相等，故此选项错误；B、∵S△ABD=S平行四边形ABCD，S△ABC=S平行四边形ABCD，∴△ABD与△ABC的面积相等，故此选项正确；C、菱形的周长与两条对角线之和不存在固定的数量关系，故此选项错误；D、菱形的面积等于两条对角线之积的，故此选项错误；故选：B．点评：此题主要考查了菱形的性质应用，正确把握菱形的性质是解题关键．2. （2014•某某枣庄，第7题3分）如图，菱形ABCD的边长为4，过点A、C作对角线AC的垂线，分别交CB和AD的延长线于点E、F，AE=3，则四边形AECF的周长为（）A．22 B．18 C．14 D．11考点：菱形的性质分析：根据菱形的对角线平分一组对角可得∠BAC=∠BCA，再根据等角的余角相等求出∠BAE=∠E，根据等角对等边可得BE=AB，然后求出EC，同理可得AF，然后判断出四边形AECF是平行四边形，再根据周长的定义列式计算即可得解．解答：解：在菱形ABCD中，∠BAC=∠BCA，∵AE⊥AC，∴∠BAC+∠BAE=∠BCA+∠E=90°，∴∠BAE=∠E，∴BE=AB=4，∴EC=BE+BC=4+4=8，同理可得AF=8，∵AD∥BC，∴四边形AECF是平行四边形，∴四边形AECF的周长=2（AE+EC）=2（3+8）=22．故选A．点评：本题考查了菱形的对角线平分一组对角的性质，等角的余角相等的性质，平行四边形的判定与性质，熟记性质并求出EC的长度是解题的关键．3. （2014•某某某某，第6题3分）如图，在菱形ABCD中，M，N分别在AB，CD上，且AM=，MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC的度数为（）A．28°B．52°C．62°D．72°考点：菱形的性质，全等三角形．分析：根据菱形的性质以及AM=，利用ASA可得△AMO≌△O，可得AO=CO，然后可得BO⊥AC，继而可求得∠OBC的度数．解答：∵四边形ABCD为菱形，∴AB∥CD，AB=BC，∴∠MAO=∠NCO，∠AMO=∠O，在△AMO和△O中，∵，∴△AMO≌△O（ASA），∴AO=CO，∵AB=BC，∴BO⊥AC，∴∠BOC=90°，∵∠DAC=28°，∴∠BCA=∠DAC=28°，∴∠OBC=90°﹣28°=62°．故选C．点评：本题考查了菱形的性质和全等三角形的判定和性质，注意掌握菱形对边平行以及对角线相互垂直的性质．4.（2014•某某聊城，第9题，3分）如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（）A．2B．3C．6D．考点：矩形的性质；菱形的性质．分析：根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°，AB=BO=3，因为四边形BEDF是菱形，所以BE，AE可求出进而可求出BC的长．解解：∵四边形ABCD是矩形，答：∴∠A=90°，即BA⊥BF，∵四边形BEDF是菱形，∴EF⊥BD，∠EBO=∠DBF，∴AB=BO=3，∠ABE=∠EBO，∴∠ABE=∠EBD=∠DBC=30°，∴BE==2，∴BF=BE=2，∵EF=AE+FC，AE=CF，EO=FO∴CF=AE=，∴BC=BF+CF=3，故选B．点评：本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半，解题的关键是求出∠ABE=∠EBD=∠DBC=30°．5. （2014•某某某某，第5题，3分）下列命题中，正确的是（）A．梯形的对角线相等B．菱形的对角线不相等C．矩形的对角线不能相互垂直D．平行四边形的对角线可以互相垂直考点：命题与定理．专常规题型．题：分析：根据等腰梯形的判定与性质对A进行判断；根据菱形的性质对B进行判断；根据矩形的性质对C进行判断；根据平行四边形的性质对D进行判断．解答：解：A、等腰梯形的对角线相等，所以A选项错误；B、菱形的对角线不一定相等，若相等，则菱形变为正方形，所以B选项错误；C、矩形的对角线不一定相互垂直，若互相垂直，则矩形变为正方形，所以C选项错误；D、平行四边形的对角线可以互相垂直，此时平行四边形变为菱形，所以D选项正确．故选D．点评：本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式；有些命题的正确性是用推理证实的，这样的真命题叫做定理．6.(2014年某某黔东南10．（4分）)如图，在矩形ABCD中，AB=8，BC=16，将矩形ABCD沿EF 折叠，使点C与点A重合，则折痕EF的长为（）A． 6 B．12 C．2 D． 4考点：翻折变换（折叠问题）．分析：设BE=x，表示出CE=16﹣x，根据翻折的性质可得AE=CE，然后在Rt△ABE中，利用勾股定理列出方程求出x，再根据翻折的性质可得∠AEF=∠CEF，根据两直线平行，内错角相等可得∠AFE=∠CEF，然后求出∠AEF=∠AFE，根据等角对等边可得AE=AF，过点E作EH⊥AD于H，可得四边形ABEH是矩形，根据矩形的性质求出EH、AH，然后求出FH，再利用勾股定理列式计算即可得解．解答：解：设BE=x，则CE=BC﹣BE=16﹣x，∵沿EF翻折后点C与点A重合，∴AE=CE=16﹣x，在Rt△ABE中，AB2+BE2=AE2，即82+x2=（16﹣x）2，解得x=6，∴AE=16﹣6=10，由翻折的性质得，∠AEF=∠CEF，∵矩形ABCD的对边AD∥BC，∴∠AFE=∠CEF，∴∠AEF=∠AFE，∴AE=AF=10，过点E作EH⊥AD于H，则四边形ABEH是矩形，∴EH=AB=8，AH=BE=6，∴FH=AF﹣AH=10﹣6=4，在Rt△EFH中，EF===4．故选D．点评：本题考查了翻折变换的性质，矩形的判定与性质，勾股定理，熟记各性质并作利用勾股定理列方程求出BE的长度是解题的关键，也是本题的突破口．7.（2014•某某9．（3分））如图，边长为2的正方形ABCD中，P是CD 的中点，连接AP并延长交BC的延长线于点F，作△CPF的外接圆⊙O，连接BP并延长交⊙O于点E，连接EF，则EF的长为（）A．B．C．D．考点：相似三角形的判定与性质；正方形的性质；圆周角定理分析：先求出CP 、BF 长，根据勾股定理求出BP，根据相似得出比例式，即可求出答案．解答：解：∵四边形ABCD是正方形，∴∠ABC=∠PCF=90°，CD∥AB，∵F为CD的中点，CD=AB=BC=2，∴CP=1，∵PC∥AB，∴△FCP∽△FBA，∴==，∴BF=4，∴CF=4﹣2=2，由勾股定理得：BP==，∵四边形ABCD是正方形，∴∠BCP=∠PCF=90°，∴PF是直径，∴∠E=90°=∠BCP，∴△BCP∽△BEF，∴=，∴=，∴EF=，故选D．点评：本题考查了正方形的性质，圆周角定理，相似三角形的性质和判定的应用，主要考查学生的推理能力和计算能力，题目比较好，难度适中．8.（2014•某某9．（3分））如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC 交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE 的长为（）A．2B．C．2D．考点：勾股定理；等腰三角形的判定与性质；直角三角形斜边上的中线．分析：根据直角三角形斜边上的中线的性质可得DG=AG，根据等腰三角形的性质可得∠GAD=∠GDA，根据三角形外角的性质可得∠CGD=2∠GAD，再根据平行线的性质和等量关系可得∠ACD=∠CGD，根据等腰三角形的性质可得CD=DG，再根据勾股定理即可求解．解答：解：∵AD∥BC，DE⊥BC，∴DE⊥AD，∠CAD=∠ACB ∵点G为AF的中点，∴DG=AG，∴∠GAD=∠GDA，∴∠CGD=2∠CAD，∴∠ACD=∠CGD，∴CD=DG=3，在Rt△CED中，DE==2．故选：C．点评：综合考查了勾股定理，等腰三角形的判定与性质和直角三角形斜边上的中线，解题的关键是证明CD=DG=3．9. （2014•某某某某,第7题3分）若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（）A．矩形B．等腰梯形C．对角线相等的四边形D．对角线互相垂直的四边形考点：中点四边形．分析：首先根据题意画出图形，由四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，利用三角形中位线的性质与菱形的性质，即可判定原四边形一定是对角线相等的四边形．解答：解：如图，根据题意得：四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，∴EF=FG=CH=EH，BD=2EF，AC=2FG，∴BD=AC．∴原四边形一定是对角线相等的四边形．故选C．点评：此题考查了菱形的性质与三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．10. （2014•某某某某,第9题4分）如图，ABCD是正方形场地，点E在DC的延长线上，AE 与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A﹣B﹣F﹣C的路径行走至C，乙沿着A﹣F﹣E﹣C﹣D的路径行走至D，丙沿着A﹣F﹣C﹣D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（）A．甲乙丙B．甲丙乙C．乙丙甲D．丙甲乙考点：正方形的性质；线段的性质：两点之间线段最短；比较线段的长短．分析：根据正方形的性质得出AB=BC=CD=AD，∠B=∠ECF，根据直角三角形得出AF＞AB，EF ＞CF，分别求出甲、乙、丙行走的距离，再比较即可．解答：解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=90°，甲行走的距离是AB+BF+CF=AB+BC=2AB；乙行走的距离是AF+EF+EC+CD；丙行走的距离是AF+FC+CD，∵∠B=∠ECF=90°，∴AF＞AB，EF＞CF，∴AF+FC+CD＞2AB，AF+FC+CD＜AF+EF+EC+CD，∴甲比丙先到，丙比乙先到，即顺序是甲丙乙，故选B．点评：本题考查了正方形的性质，直角三角形的性质的应用，题目比较典型，难度适中．11．（2014•某某某某,第9题4分）如图，在正方形ABCD的外侧，作等边三角形ADE. AC，BE相交于点F，则∠BFC为【】A．45°B．55° C．60° D．75°12．（2014•某某某某,第7题4分）下列命题中正确的是（）A．有一组邻边相等的四边形是菱形B．有一个角是直角的平行四边形是矩形C．对角线垂直的平行四边形是正方形D．一组对边平行的四边形是平行四边形考点：命题与定理．分析：利用特殊四边形的判定定理对个选项逐一判断后即可得到正确的选项．解答：解：A、一组邻边相等的平行四边形是菱形，故选项错误；B、正确；C、对角线垂直的平行四边形是菱形，故选项错误；D、两组对边平行的四边形才是平行四边形，故选项错误．故选B ．点评：本题考查了命题与定理的知识，解题的关键是牢记特殊的四边形的判定定理，难度不大，属于基础题．13．（2014•某某,第8题3分）将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，（）．（A）（B）2 （C）（D ）图2-① 图2-②【考点】正方形、有内角的菱形的对角线与边长的关系【分析】由正方形的对角线长为2可知正方形和菱形的边长为，当=60°时，菱形较短的对角线等于边长，故答案为．【答案】A14．（2014•某某,第10题3分）如图3，四边形、都是正方形，点在线段上，连接，和相交于点．设，（）．下列结论：①；②；③；④．其中结论正确的个数是（）．（A）4个（B）3个（C）2个（D）1个【考点】三角形全等、相似三角形【分析】①由可证，故①正确；②延长BG交DE于点H，由①可得，（对顶角）∴=90°，故②正确；③由可得，故③不正确；④，等于相似比的平方，即，∴，故④正确．【答案】B7.8.二、填空题1. （2014•某某，第18题4分）如图，已知在矩形ABCD中，点E在边BC上，BE=2CE，将矩形沿着过点E的直线翻折后，点C、D分别落在边BC下方的点C′、D′处，且点C′、D′、B在同一条直线上，折痕与边AD交于点F，D′F与BE交于点G．设AB=t，那么△EFG的周长为2t （用含t的代数式表示）．考点：翻折变换（折叠问题）分析：根据翻折的性质可得CE=C′E，再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°，然后求出∠BGD′=60°，根据对顶角相等可得∠FGE=∠∠BGD′=60°，根据两直线平行，内错角相等可得∠AFG=∠FGE，再求出∠EFG=60°，然后判断出△EFG是等边三角形，根据等边三角形的性质表示出EF，即可得解．解答：解：由翻折的性质得，CE=C′E，∵BE=2CE，∴BE=2C′E，又∵∠C′=∠C=90°，∴∠EBC′=30°，∵∠FD′C′=∠D=90°，∴∠BGD′=60°，∴∠FGE=∠∠BGD′=60°，∵AD∥BC，∴∠AFG=∠FGE=60°，∴∠EFG=（180°﹣∠AFG）=（180°﹣60°）=60°，∴△EFG是等边三角形，∴AB=t，∴EF=t÷=t，∴△EFG的周长=3×t=2t．故答案为：2t．点评：本题考查了翻折变换的性质，直角三角形30°角所对的直角边等于斜边的一半，等边三角形的判定与性质，熟记性质并判断出△EFG是等边三角形是解题的关键．2. （2014•某某枣庄，第17题4分）如图，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处．若AE=BE，则长AD与宽AB的比值是．考点：翻折变换（折叠问题）分析：由AE=BE，可设AE=2k，则BE=3k，AB=5k．由四边形ABCD是矩形，可得∠A=∠ABC=∠D=90°，CD=AB=5k，AD=BC．由折叠的性质可得∠EFC=∠B=90°，EF=EB=3k，CF=BC，由同角的余角相等，即可得∠DCF=∠AFE．在Rt△AEF中，根据勾股定理求出AF==k，由cos∠AFE=cos∠DCF得出CF=3k，即AD=3k，进而求解即可．解答：解：∵AE=BE，∴设AE=2k，则BE=3k，AB=5k．∵四边形ABCD是矩形，∴∠A=∠ABC=∠D=90°，CD=AB=5k，AD=BC．∵将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处，∴∠EFC=∠B=90°，EF=EB=3k，CF=BC，∴∠AFE+∠DFC=90°，∠DFC+∠FCD=90°，∴∠DCF=∠AFE，∴cos∠AFE=cos∠DCF．在Rt△AEF中，∵∠A=90°，AE=2k，EF=3k，∴AF==k，∴=，即=，∴CF=3k，∴AD=BC=CF=3k，∴长AD与宽AB的比值是=．故答案为．点评：此题考查了折叠的性质，矩形的性质，勾股定理以及三角函数的定义．解此题的关键是数形结合思想与转化思想的应用．3. （2014•某某某某,第13题3分）已知正方形ABCD的对角线AC=，则正方形ABCD的周长为 4 ．考点：正方形的性质．分析：根据正方形的对角线等于边长的倍求出边长，再根据正方形的周长公式列式计算即可得解．解答：解：∵正方形ABCD的对角线AC=，∴边长AB=÷=1，∴正方形ABCD的周长=4×1=4．故答案为：4．点评：本题考查了正方形的性质，比较简单，熟记正方形的对角线等于边长的倍是解题的关键．4. （2014•某某某某,第17题3分）如图，在矩形ABCD中，=，以点B为圆心，BC长为半径画弧，交边AD于点E．若AE•ED=，则矩形ABCD的面积为 5 ．考点：矩形的性质；勾股定理．分析：连接BE，设AB=3x，BC=5x，根据勾股定理求出AE=4x，DE=x，求出x的值，求出AB、BC，即可求出答案．解答：解：如图，连接BE，则BE=BC．设AB=3x，BC=5x ，∵四边形ABCD是矩形，∴AB=CD=3x，AD=BC=5x，∠A=90°，由勾股定理得：AE=4x，则DE=5x﹣4x=x，∵AE•ED=，∴4x•x=，解得：x=（负数舍去），则AB=3x=，BC=5x=，∴矩形ABCD的面积是AB×BC=×=5，故答案为：5．点评：本题考查了矩形的性质，勾股定理的应用，解此题的关键是求出x的值，题目比较好，难度适中．5. （2014•某某某某,第15题4分）已知▱ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD成为一个菱形，你添加的条件是AD=DC ．考点：菱形的判定；平行四边形的性质．专题：开放型．分析：根据菱形的定义得出答案即可．解答：解：∵邻边相等的平行四边形是菱形，∴平行四边形ABCD的对角线AC、BD相交于点O，试添加一个条件：可以为：AD=DC；故答案为：AD=DC．点评：此题主要考查了菱形的判定以及平行四边形的性质，根据菱形的定义得出是解题关键．6．（2014•某某某某，第12题，3分）菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线长度是 5cm．考点：菱形的性质；特殊角的三角函数值分析：根据菱形的对角线互相垂直且平分各角，可设较小角为x，因为邻角之和为180°，∴x+2x=180°，所以x=60°，画出其图形，根据三角函数，可以得到其中较长的对角线的长．解答：解：∵菱形的周长为20cm∴菱形的边长为5cm∵两邻角之比为1：2∴较小角为60°画出图形如下所示：∴∠ABO=30°，AB=5cm，∵最长边为BD，BO=AB•cos∠ABO=5×=∴BD=2BO=．点评：本题考查了菱形的对角线互相垂直且平分各角，特殊三角函数的熟练掌握．7．（2014•某某凉山州，第14题，4分）顺次连接矩形四边中点所形成的四边形是菱形．学校的一块菱形花园两对角线的长分别是6m和8m，则这个花园的面积为24m2．考点：菱形的判定与性质；中点四边形分析：因为题中给出的条件是中点，所以可利用三角形中位线性质，以及矩形对角线相等去证明四条边都相等，从而说明是一个菱形．根据菱形的面积公式求出即可．解答：解：连接AC、BD，在△ABD中，∵AH=HD，AE=EB∴EH=BD，同理FG=BD，HG=AC，EF=AC，又∵在矩形ABCD中，AC=BD，∴EH=HG=GF=FE，∴四边形EFGH为菱形；这个花园的面积是×6m×8m=24m2，故答案为：菱形，24m2．点评：本题考查了菱形的判定和菱形的面积，三角形的中位线的应用，注意：菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义，②四边相等，③对角线互相垂直平分．8．（2014•某某某某、某某,第17题4分）如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为．考中心对称；菱形的性质．点：分根据菱形的面积等于对角线乘积的一半求出面积，再根据中心对称的性质判断出阴影析：部分的面积等于菱形的面积的一半解答．解答：解：∵菱形的两条对角线的长分别为6和8，∴菱形的面积=×6×8=24，∵O是菱形两条对角线的交点，∴阴影部分的面积=×24=12．故答案为：12．点评：本题考查了中心对称，菱形的性质，熟记性质并判断出阴影部分的面积等于菱形的面积的一半是解题的关键．9．（2014•某某某某,第17题4分）如果菱形的两条对角线的长为a和b，且a，b满足（a﹣1）2+=0，那么菱形的面积等于．考点：菱形的性质；非负数的性质：偶次方；非负数的性质：算术平方根．分析：根据非负数的性质列式求出a、b，再根据菱形的面积等于对角线乘积的一半列式计算即可得解．解答：解：由题意得，a﹣1=0，b﹣4=0，解得a=1，b=4，∵菱形的两条对角线的长为a和b，∴菱形的面积=×1×4=2．故答案为：2．点评：本题考查了非负数的性质，菱形的性质，主要利用了菱形的面积等于对角线乘积的一半，需熟记．6.7.8.三、解答题1. （2014•某某某某，第28题10分）如图，在四边形ABCD中，点H是BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连结BE，CF．（1）请你添加一个条件，使得△BEH≌△CFH，你添加的条件是，并证明．（2）在问题（1）中，当BH与EH满足什么关系时，四边形BFCE是矩形，请说明理由．考点：矩形的判定．分析：（1）根据全等三角形的判定方法，可得出当EH=FH，BE∥CF，∠EBH=∠FCH时，都可以证明△BEH≌△CFH，（2）由（1）可得出四边形BFCE是平行四边形，再根据对角线相等的平行四边形为矩形可得出BH=EH时，四边形BFCE是矩形．解答：（1）答：添加：EH=FH，证明：∵点H是BC的中点，∴BH=CH，在△△BEH和△CFH中，，∴△BEH≌△CFH（SAS）；（2）解：∵BH=CH，EH=FH，∴四边形BFCE是平行四边形（对角线互相平分的四边形为平行四边形），∵当BH=EH时，则BC=EF，∴平行四边形BFCE为矩形（对角线相等的平行四边形为矩形）．点评：本题考查了全等三角形的判定和性质以及平行四边形的判定，是基础题，难度不大．2. （2014•某某威海，第24题11分）猜想与证明：如图1摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM、ME，试猜想DM与ME的关系，并证明你的结论．拓展与延伸：（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为DM=DE．（2）如图2摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明（1）中的结论仍然成立．考点：四边形综合题分析：猜想：延长EM交AD于点H，利用△FME≌△AMH，得出HM=EM，再利用直角三角形中，斜边的中线等于斜边的一半证明．（1）延长EM交AD于点H，利用△FME≌△AMH，得出HM=EM，再利用直角三角形中，斜边的中线等于斜边的一半证明，（2）连接AE，AE和EC在同一条直线上，再利用直角三角形中，斜边的中线等于斜边的一半证明，解答：猜想：DM=ME证明：如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=EM，∴DM=HM=ME，∴DM=ME．（1）如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=EM，∴DM=HM=ME，∴DM=ME，故答案为：DM=ME．（2）如图2，连接AE，∵四边形ABCD 和ECGF 是正方形， ∴∠FCE =45°，∠FCA =45°， ∴AE 和EC 在同一条直线上，在RT △ADF 中，AM =MF ， ∴DM =AM =MF ，在RT △AEF 中，AM =MF ， ∴AM =MF =ME ，∴DM =ME ．点评：本题主要考查四边形的综合题，解题的关键是利用正方形的性质及直角三角形的中线与斜边的关系找出相等的线段．3. （2014•某某潍坊，第22题12分）如图1，在正方形ABCD 中，E 、F 分别为BC 、CD 的中点，连接AE 、BF ，交点为G ． (1)求证：AE ⊥BF ；(2)将△BCF 沿BF 对折，得到△BPF （如图2），延长FP 交BA 的延长线于点Q ，求sin ∠BQP 的值；(3)将△ABE 绕点A 逆时针方向旋转，使边AB 正好落在AE 上，得到△AHM （如图3），若AM 和BF 相交于点N ，当正方形ABCD 的面积为4时，求四边形GHMN 的面积．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；解直角三角形．分析：（1）由四边形ABCD 是正方形，可得∠ABE =∠BCF =90°，AB =BC ，又由BE =CF ，即可证得△ABE ≌△BCF ,可得∠BAE =∠CBF ，由∠ABF +∠CBF =900可得∠ABF +∠BAE =900，即AE ⊥BF ；（2）由△BCF ≌△BPF , 可得CF =PF ,BC =BP ,∠BFE =∠BFP ，由CD ∥AB 得∠BFC =∠ABF ,从而QB =QF ，设PF 为x ,则BP 为2x ,在Rt △QBF 中可求 QB 为25x ，即可求得答案；（3）由2)(AMAN AHM AGN =∆∆可求出△AGN 的面积，进一步可求出四边形GHMN 的面积．解答：(1)证明：∵E 、F 分别是正方形ABCD 边BC 、CD 的中点，∴CF =BE ，∴Rt △ABE ≌Rt △BCF ∴∠BAE =∠CBF 又∵∠BAE +∠BEA =900，∴∠CBF +∠BEA =900， ∴∠BGE =900， ∴AE ⊥BF(2)根据题意得：FP =FC ，∠PFB =∠BFC ，∠FPB =900， ∵CD ∥AB , ∴∠CFB =∠ABF ，∴∠ABF =∠PFB ．∴QF =QB 令PF =k （k >O ），则PB =2k ，在Rt △BPQ 中，设QB =x ， ∴x 2=(x －k )2+4k 2, ∴x =25k ，∴sin ∠BQP =54252==k k QP BP(3)由题意得：∠BAE =∠EAM ,又AE ⊥BF , ∴AN =AB =2, ∵ ∠AHM =900, ∴GN //HM , ∴2)(AM AN AHM AGN =∆∆ ∴54)52(12==ΛAGN ∴ 四边形GHMN =SΔAHM－SΔAGN =1一54= 54答：四边形GHMN 的面积是54.点评：此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质以及三角函数等知识．此题综合性较强，难度较大，注意掌握旋转前后图形的对应关系，注意数形结合思想的应用．4. （2014•某某某某，第25题10分）在正方形ABCD 中，动点E ，F 分别从D ，C 两点同时出发，以相同的速度在直线DC ，CB 上移动．（1）如图①，当点E 自D 向C ，点F 自C 向B 移动时，连接AE 和DF 交于点P ，请你写出AE 与DF 的位置关系，并说明理由；（2）如图②，当E ，F 分别移动到边DC ，CB 的延长线上时，连接AE 和DF ，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）（3）如图③，当E ，F 分别在边CD ，BC 的延长线上移动时，连接AE ，DF ，（1）中的结论还成立吗？请说明理由；（4）如图④，当E，F分别在边DC，CB上移动时，连接AE和DF交于点P，由于点E，F 的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD=2，试求出线段CP 的最小值．考点：全等三角形，正方形的性质，勾股定理，运动与变化的思想.分析：（1）AE=DF，AE⊥DF．先证得△ADE≌△DCF．由全等三角形的性质得AE=DF，∠DAE=∠CDF，再由等角的余角相等可得AE⊥DF；（2）是．四边形ABCD是正方形，所以AD=DC，∠ADE=∠DCF=90°，DE=CF，所以△ADE≌△DCF，于是AE=DF，∠DAE=∠CDF，因为∠CDF+∠ADF=90°，∠DAE+∠ADF=90°，所以AE⊥DF；（3）成立．由（1）同理可证AE=DF，∠DAE=∠CDF，延长FD交AE于点G，再由等角的余角相等可得AE⊥DF；（4）由于点P在运动中保持∠APD=90°，所以点P的路径是一段以AD为直径的弧，设AD的中点为O，连接OC交弧于点P，此时CP的长度最小，再由勾股定理可得OC的长，再求CP即可．解答：（1）AE=DF，AE⊥DF．理由：∵四边形ABCD是正方形，∴AD=DC，∠ADC=∠C=90°．∵DE=CF，∴△ADE≌△DCF．∴AE=DF，∠DAE=∠CDF，由于∠CDF+∠ADF=90°，∴∠DAE+∠ADF=90°．∴AE⊥DF；（2）是；（3）成立．理由：由（1）同理可证AE=DF，∠DAE=∠CDF延长FD交AE于点G，则∠CDF+∠ADG=90°，∴∠ADG+∠DAE=90°．∴AE⊥DF；（4）如图：由于点P在运动中保持∠APD=90°，∴点P的路径是一段以AD为直径的弧，设AD的中点为O，连接OC交弧于点P，此时CP的长度最小，在Rt△ODC中，OC=，∴CP=OC﹣OP=．点评：本题主要考查了四边形的综合知识．综合性较强，特别是第（4）题要认真分析．5. （2014•某某某某，第22题，12分）菱形ABCD的对角线AC，BD相交于点O，AC=4，BD=4，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．（1）用含x的代数式分别表示S1，S2；（2）若S1=S2，求x的值．考四边形综合题；菱形的性质；轴对称的性质；轴对称图形；特殊角的三角函数值点：专题：综合题；动点型；分类讨论．分析：（1）根据对称性确定E、F、G、H都在菱形的边上，由于点P在BO上与点P在OD上求S1和S2的方法不同，因此需分情况讨论．（2）由S1=S 2和S1+S2=8可以求出S1=S2=4．然后在两种情况下分别建立关于x的方程，解方程，结合不同情况下x的X围确定x的值．解答：解：（1）①当点P在BO上时，如图1所示．∵四边形ABCD是菱形，AC=4，BD=4，∴AC⊥BD，BO=BD=2，AO=AC=2，且S菱形ABCD=BD•AC=8．∴tan∠ABO==．∴∠ABO=60°．在Rt△BFP中，∵∠BFP=90°，∠FBP=60°，BP=x，∴sin∠FBP===sin60°=．∴FP=x．∴BF=．∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，∴S△BFP=S△BGP=S△DEQ=S△DHQ．∴S1=4S△BFP=4××x•=．∴S2=8﹣．②当点P在OD上时，如图2所示．∵AB=4，BF=，∴AF=AB﹣BF=4﹣．在Rt△AFM中，∵∠AFM=90°，∠FAM=30°，AF=4﹣．∴tan∠FAM==tan30°=．∴FM=（4﹣）．∴S△AFM=AF•FM=（4﹣）•（4﹣）=（4﹣）2．∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，∴S△AFM=S△AEM=S△CHN=S△CGN．∴S2=4S△AFM=4×（4﹣）2=（x﹣8）2．∴S1=8﹣S2=8﹣（x﹣8）2．综上所述：当点P在BO上时，S1=，S2=8﹣；当点P在OD上时，S1=8﹣（x﹣8）2，S2=（x﹣8）2．（2）①当点P在BO上时，0＜x≤2．∵S1=S2，S1+S2=8，∴S1=4．∴S1==4．解得：x1=2，x2=﹣2．∵2＞2，﹣2＜0，∴当点P在BO上时，S1=S2的情况不存在．②当点P在OD上时，2＜x≤4．∵S1=S2，S1+S2=8，∴S2=4．∴S2=（x﹣8）2=4．解得：x1=8+2，x2=8﹣2．∵8+2＞4，2＜8﹣2＜4，∴x=8﹣2．综上所述：若S1=S2，则x的值为8﹣2．点评：本题考查了以菱形为背景的轴对称及轴对称图形的相关知识，考查了菱形的性质、特殊角的三角函数值等知识，还考查了分类讨论的思想．6.（2014•某某14．（3分））如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD 及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是①（只填写序号）．考点：菱形的判定．分析：首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形，然后结合菱形的判定得到答案即可．解答：解：由题意得：BD=CD，ED=FD，∴四边形EBFC是平行四边形，∵邻边相等或对角线垂直的平行四边形是菱形，∴选择BE⊥EC，故答案为：①．点评：本题考查了菱形的判定，解题的关键是了解菱形的判定定理，难度不是很大．7．（3分）（2014•某某）如图，要使平行四边形ABCD是矩形，则应添加的条件是∠ABC=90°或AC=BD（不唯一）（添加一个条件即可）．考点：矩形的判定；平行四边形的性质专题：开放型．分析：根据矩形的判定定理：①对角线相等的平行四边形是矩形，②有一个角是直角的平行四边形是矩形，直接添加条件即可．解答：解：根据矩形的判定定理：对角线相等的平行四边形是矩形，有一个角是直角的平行四边形是矩形故添加条件：∠ABC=90°或AC=BD．故答案为：∠ABC=90°或AC=BD．点评：本题主要应用的知识点为：矩形的判定．①对角线相等且相互平分的四边形为矩形．②一个角是90度的平行四边形是矩形．8. (2014年某某某某24．（12分）)如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．。

2016全国各地中考数学分类汇编：矩形菱形与正方形(含解析)

矩形菱形与正方形一、选择题1. （2016·云南省昆明市·4分）如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若=，则3S△EDH=13S△DHC，其中结论正确的有（）A．1个 B．2个 C．3个 D．4个【考点】正方形的性质；全等三角形的判定与性质．【分析】①根据题意可知∠ACD=45°，则GF=FC，则EG=EF﹣GF=CD﹣FC=DF；②由SAS证明△EHF≌△DHC，得到∠HEF=∠HDC，从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=180°；③同②证明△EHF≌△DHC即可；④若=，则AE=2BE，可以证明△EGH≌△DFH，则∠EHG=∠DHF且EH=DH，则∠DHE=90°，△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2．【解答】解：①∵四边形ABCD为正方形，EF∥AD，∴EF=AD=CD，∠ACD=45°，∠GFC=90°，∴△CFG为等腰直角三角形，∴GF=FC，∵EG=EF﹣GF，DF=CD﹣FC，∴EG=DF，故①正确；②∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF≌△DHC（SAS），∴∠HEF=∠HDC，∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°，故②正确；③∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF≌△DHC（SAS），故③正确；④∵=，∴AE=2BE，∵△CFG为等腰直角三角形，H为CG的中点，∴FH=GH，∠FHG=90°，∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，在△EGH和△DFH中，，∴△EGH≌△DFH（SAS），∴∠EHG=∠DHF，EH=DH，∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°，∴△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，如图所示：设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2，∴3S△EDH=13S△DHC，故④正确；故选：D．2．（2016·山东省东营市·3分）如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为点F ，连接DF ，分析下列四个结论：①△AEF ∽△CAB ；②CF ＝2AF ；③DF ＝DC ；④tan ∠CAD ＝2．其中正确的结论有( )A.4个 B ．3个 C ．2个 D ．1个第10题图F DA【知识点】特殊平行四边形——矩形的性质、相似三角形——相似三角形的判定与性质、锐角三角函数——锐角三角函数值的求法【答案】B.【解析】∵矩形ABCD 中，∴AD ∥BC .∴△AEF ∽△CAB ….......................①正确；∵△AEF ∽△CAB ，∴AF CF ＝AE BC ＝12，∴CF ＝2AF ……………………………②正确；过点D 作DH ⊥AC 于点H .易证△ABF ≌△CDH (AAS ).∴AF ＝CH . ∵EF ∥DH ,∴AF FH ＝AE ED＝1.∴AF ＝FH .∴FH ＝CH . ∴DH 垂直平分CF .∴DF ＝DC . ……………………………………………③正确；第10题答案图GHF DA设EF ＝1，则BF ＝2.∵△ABF ∽△EAF .∴AF EF ＝BF AF .∴AF ＝EF •BF ＝1×2＝ 2. ∴tan ∠ABF ＝AF BF ＝22.∵∠CAD ＝∠ABF ，∴tan ∠CAD ＝tan ∠ABF ＝22.…………④错误. 故选择B.【点拨】本题考查了矩形的性质、相似三角形的判定和性质，图形面积的计算，锐角三角函数值的求法，正确的作出辅助线是解本题的关键．3．（2016·山东省菏泽市·3分）在▱ABCD 中，AB=3，BC=4，当▱ABCD 的面积最大时，下列结论正确的有（）①AC=5；②∠A+∠C=180°；③AC ⊥BD ；④AC=BD ．A ．①②③B ．①②④C ．②③④D ．①③④【考点】平行四边形的性质．【分析】当▱ABCD 的面积最大时，四边形ABCD 为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD ，根据勾股定理求出AC ，即可得出结论．【解答】解：根据题意得：当▱ABCD 的面积最大时，四边形ABCD 为矩形，∴∠A=∠B=∠C=∠D=90°，AC=BD ，∴AC==5， ①正确，②正确，④正确；③不正确；故选：B ．【点评】本题考查了平行四边形的性质、矩形的性质以及勾股定理；得出▱ABCD 的面积最大时，四边形ABCD 为矩形是解决问题的关键．4．（2016贵州毕节3分）如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC=2：1，则线段CH 的长是（）A ．3B ．4C ．5D ．6【考点】正方形的性质；翻折变换（折叠问题）．【分析】根据折叠的性质可得DH=EH ，在直角△CEH 中，若设CH=x ，则DH=EH=9﹣x ，CE=3cm ，可以根据勾股定理列出方程，从而解出CH 的长．【解答】解：由题意设CH=xcm，则DH=EH=（9﹣x）cm，∵BE：EC=2：1，∴CE=BC=3cm∴在Rt△ECH中，EH2=EC2+CH2，即（9﹣x）2=32+x2，解得：x=4，即CH=4cm．故选（B）5．（2016海南3分）如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）A．30° B．45° C．60° D．75°【考点】矩形的性质；平行线的性质．【分析】首先过点D作DE∥a，由∠1=60°，可求得∠3的度数，易得∠ADC=∠2+∠3，继而求得答案．【解答】解：过点D作DE∥a，∵四边形ABCD是矩形，∴∠BAD=∠ADC=90°，∴∠3=90°﹣∠1=90°﹣60°=30°，∵a∥b，∴DE∥a∥b，∴∠4=∠3=30°，∠2=∠5，∴∠2=90°﹣30°=60°．故选C．【点评】此题考查了矩形的性质以及平行线的性质．注意准确作出辅助线是解此题的关键．6.(2016河北3分）关于ABCD的叙述，正确的是（）A．若AB⊥BC，则是菱形B．若AC⊥BD，则ABCD是正方形C．若AC=BD，则ABCD是矩形D．若AB=AD，则ABCD是正方形答案：B解析：A项应是矩形；B项应是菱形；D项应是菱形。

2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形剖析

全国各地中考数学试卷解析分类汇编(第1期)专题18 图形的展开与叠折

中考数学真题分类汇编套专题三十四·矩形菱形正方形

2016年全国中考数学真题分类相似形及应用(习题解析)

2016年江西省中考数学试卷(解析版)

2014年全国中考数学试题分类汇编25 矩形菱形与正方形(含解析)

2016年中考数学试题分类解析汇编(第一辑)(29份)_3

中考数学_专项_矩形、菱形、正方形考点及题型

2016年甘肃省兰州市临夏州武威市平凉市张掖市白银市定西市中考数学试卷(word解析版)

2016年中考数学试卷分类汇编解析：矩形菱形与正方形

最新各地中考解析版试卷分类汇编(第2期)矩形菱形与正方形.doc

全国181套中考数学试题分类汇编44矩形、菱形、正方形

2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形

2016年河北省中考数学试卷附详细答案(原版+解析版)

2016届中考数学真题类编-知识点028 矩形、菱形、正方形和梯形2016A

广东省中考数学第一部分考点研究第五章四边形第二节矩形、菱形和正方形试题

全国各地2014年中考数学试卷解析版分类汇编矩形菱形与正方形

2016全国各地中考数学分类汇编：矩形菱形与正方形(含解析)

2016全国各地中考数学分类汇编：矩形菱形与正方形(含解析)解读

2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形剖析

全国各地中考数学试卷解析分类汇编(第1期)专题18 图形的展开与叠折

中考数学真题分类汇编套专题三十四·矩形菱形正方形

2016年全国中考数学真题分类 相似形及应用(习题解析)

2016年江西省中考数学试卷(解析版)

2014年全国中考数学试题分类汇编25 矩形菱形与正方形(含解析)

2016年中考数学试题分类解析汇编(第一辑)(29份)_3

中考数学_专项_矩形、菱形、正方形考点及题型

2016年甘肃省兰州市临夏州武威市平凉市张掖市白银市定西市中考数学试卷(word解析版)

2016年中考数学试卷分类汇编解析：矩形菱形与正方形

最新各地中考解析版试卷分类汇编(第2期)矩形菱形与正方形.doc

全国181套中考数学试题分类汇编44矩形、菱形、正方形

2016年各地中考数学解析版试卷分类汇编：矩形菱形与正方形

2016年河北省中考数学试卷附详细答案(原版+解析版)

2016届中考数学真题类编-知识点028 矩形、菱形、正方形和梯形2016A

广东省中考数学 第一部分 考点研究 第五章 四边形 第二节 矩形、菱形和正方形试题

全国各地2014年中考数学试卷解析版分类汇编 矩形菱形与正方形

2016全国各地中考数学分类汇编：矩形菱形与正方形(含解析)

2016全国各地中考数学分类汇编：矩形菱形与正方形(含解析)解读

2016年全国中考数学真题分类相似形及应用(习题解析)

广东省中考数学第一部分考点研究第五章四边形第二节矩形、菱形和正方形试题

全国各地2014年中考数学试卷解析版分类汇编矩形菱形与正方形