DSP定点运算-Q格式
DSP的定点运算

DSP的定点运算DSP的定点运算技术2007-06-29 09:45:14阅读82评论0字号:大中小许DSP芯片只支持整数运算,如果现在这些芯片上进行小数运算的话,定点小数运算应该是最佳选择了,此外即使芯片支持浮点数,定点小数运算也是最佳的速度选择。
在DSP世界中,由于DSP芯片的限制,经常使用定点小数运算。
所谓定点小数,实际上就是用整数来进行小数运算。
下面先介绍定点小数的一些理论知识,然后以C语言为例,介绍一下定点小数运算的方法。
在TI C5000 DSP系列中使用16比特为最小的储存单位,所以我们就用16比特的整数来进行定点小数运算。
先从整数开始,16比特的储存单位最多可以表示0x0000到0xffff,65536种状态,如果它表示C语言中的无符号整数的话,就是从0到65535。
如果需要表示负数的话,那么最高位就是符号位,而剩下的15位可以表示32768种状态。
这里可以看出,对于计算机或者DSP芯片来说,符号并没有什么特殊的储存方式,其实是和数字一起储存的。
为了使得无论是无符号数还是符号数,都可以使用同样的加法减法规则,符号数中的负数用正数的补码表示。
我们都知道-1+1=0,而0x0001表示1,那么-1用什么来表示才能使得-1+1=0呢?答案很简单:0xffff。
现在就可以打开Windows的计算器,用16进制计算一下0xffff+0x0001,结果是0x10000。
那么0x10000和0x0000等价么,我们刚才说过用16比特来表达整数,最高位的1是第17位,这一位是溢出位,在运算寄存器中没有储存这一位,所以结果是低16位,也就是0x0000。
现在我们知道负数的表达方式了。
举个例子:-100。
首先我们需要知道100的16进制,用计算器转换一下,可以知道是0x0064,那么-100就是0x10000-0x0064,用计算器算一下得0xff9c。
还有一种简单的转换符号的方法,就是取反加一:把数x写成二进制格式,每位0变1,1变0,最后把结果加1就是-x了。
DSP芯片的定点运算

浮点数 x=0.5,定标 Q=15, 则定点数=0.5*32768=16384
SuQian College
Q表示、S表示及数值范围
QHale Waihona Puke 示 Q15 Q14. . . . . .
Q1 Q0
S表示 S0.15 S1.14
. . . . . .
S14.1 S15.0
十进制数表示范围 -1≤X≤0.9999695 -2≤X≤1.9999390
. . . . . .
-16384≤X≤16383.5 -32768≤X≤32767
1 定点的基本概念
SuQian College
1、数的定标
在定点DSP芯片中,采用定点数进行数值运算, 其操作数一般采用整型数来表示
DSP芯片的数以2的补码形式表示 数的定标:Q表示法和S表示法 对定点数而言,数值范围与精度是一对矛盾, 一个变量要想能够表示比较大的数值范围,必须 以牺牲精度为代价。
SuQian College
Q表示法16进制数2000H
Q0表示为8192
SuQian College
0010000000000000
符
号 位 Q15表示为0.25
小数点的位置
0010000000000000
小数点的位置
浮点数与定点数的转换关系
浮点数转换为定点数
xq int x 2Q
定点数转换为浮点数
Q格式运算讲解

第3章 DSP 芯片的定点运算3.1 数 的 定 标在定点DSP 芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP 芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP 芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,1则表示数值为负。
其余15位表示数值的大小。
因此二进制数0010000000000011b =8195 二进制数1111111111111100b =-4对DSP 芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP 芯片是如何处理小数的呢?应该说,DSP 芯片本身无能为力。
那么是不是说DSP 芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q 表示法和S 表示法两种。
表3.1列出了一个16位数的16种Q 表示、S 表示及它们所能表示的十进制数值范围。
从表3.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如:16进制数2000H =8192,用Q0表示 16进制数2000H =0.25,用Q15表示但对于DSP 芯片来说,处理方法是完全相同的。
从表3.1还可以看出,不同的Q 所表示的数不仅范围不同,而且精度也不相同。
Q 越大,数值范围越小,但精度越高;相反,Q 越小,数值范围越大,但精度就越低。
例如,Q0的数值范围是-32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为 1/32768 = 0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想提高精度,则数的表示范围就相应地减小。
一种新的定点DSP Q格式数乘法运算方法

Q=L×,y×3276辫‘×g+‘×Q+(Q×g)>>15
=3 10743=0x0004BDD'/
Z=(float)(Q:X 2‘15)=9.483124
(1善xl。)<215
214
213
故只要保证
= +
用该方法处理Q15
格式的乘法,其计算结果基本正确。 该方法与将石和),按比例缩小或使用定标数小于15 的Q格式算法相比,该方法精度更高,并且可以从 根本上解决乘法运算的溢出问题。
f
x▲l恸
= +
5结论
f
y▲I恸
本文运用乘法运算和加法运算结合使用,Q0 格式和Q15格式整型数结合使用的方法提出一种新
(天津理工大学自动化学院
摘要TI公司最新推出了32位定点DSPTMS320F2812,并提出一种将浮点数转换成为Q格 式定标整型数进行运算的算法,解决了定点DSP无法直接处理浮点数的问题,提高了DSP运算 的速度.通常使用QO和Q15格式,但Q15格式数据阋的乘法运算极容易发生结果溢出的问题, 使得运算结果不准确.本文针对此问题提出一种新的Q15乘法运算算法,该算法从根本上解决了 Q15格式整型数相乘结果溢出的问题. 关键词:定点DSP A New Compute Q格式 结果溢出 of
该方法可以从根本上防止乘法运算时的溢出问 题,如上例,
y=2.57=3+0.57 Z=xxy=9.4833 ,,=2 y=3.69=3+0.69 【6】 【5】
苏奎峰.吕强.耿庆锋等.TMS320F2812原理与开 发.北京:电子工业出版社,2005 李其林.基于DSP的电机故障监测与数据传输技术. 天津理工大学.2006
212
2)变量定义为整型变量类型(int和long型), 采用放大若干倍数来表示小数。比如要表达精度达 到O.01Hz的频率变量f,就将变量f放大100,一 个初级程序员常常这样做,但这是一个比较僵硬的 做法。例如,当频率精度重新定义为O.001Hz时, 整个程序要全部重新编写,以防止溢出。 3)变量仍定义为整型变量类型(int和long型), 采用定标法来确定小数。整数定标本质上并不复 杂,简单而言,就是通过假定小数点位于哪一位, 从而确定小数的精度。 常用Q格式来表示数的定标。当假定小数点位 于第0位的右侧时,为Qo:当把小数点定位于第 15位的右侧时,为Q15,例如: 16进制数2000h=8192,用QO表示。 16进制数2000h=O.25,用Q15表示。 浮点数和定点数之间的转换公式如下: 浮点数xf转换为定点数xq时,
一DSP定点算数运算 1 数的定标 在定点DSP芯片中,采用...

一DSP定点算数运算1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,l则表示数值为负。
其余15位表示数值的大小。
因此,二进制数0010000000000011b=8195 二进制数1111111111111100b= -4 对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表1.1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。
从表1.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如,16进制数2000H=8192,用Q0表示16进制数2000H=0.25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表1.1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0 的数值范围是一32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为1/32768=0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想精度提高,则数的表示范围就相应地减小。
DSP与Q格式

DSP_Q 格式
1、Q 格式
就是将一个小数放大若干倍后,用整数来表示小数。
用这个放大的整数来进行中间过程的计算,最后把计算得出的结果又移位缩小为 原本的小数。
具体的Q 值是指小数点位于内存存储单元的第几位的右侧,把存储 单元分成整数和小数两部分。
2、Q 格式的定标
在定点DSP 处理器中,其数据结构一般用整型来表示,用定点的方式进行各种运 算,整型变量在内存中所占的自己数根据平台的不同而不同,一般情况下整型变 量占4个字节的存储单元。
如果我们要在定点DSP 中处理浮点数,那么我们就需要 通过Q 格式把浮点数表示成整型进行运算。
浮点数在内存单元中时分部存储,分 成符号位、数字、指数三个部分。
通过整型来表示浮点数进行存储,就是在内存 单元中利用小数点的位置将内存单元划分为两个部分,来分别表示整数和小数部 分。
这就是嵌入式浮点处理中所谓的数的定标。
3、Q 格式的运算
1> 定点加减法:须转换成相同的Q 格式才能加减
2> 定点乘法:不同Q 格式的数据相乘,相当于Q 值相加
3> 定点除法:不同Q 格式的数据相除,相当于Q 值相减
4> 定点左移:左移相当于Q 值增加
5> 定点右移:右移相当于Q 减少
4、Q 值的确定
设变量的绝对值的最大值为|max|,注意|max|必须小于或等于32767。
取一个整 数n ,使满足
12max 2n n -<<则有
2-Q=2-15*2n=2-(15-n)
Q=15-n
例如,某变量的值在-1至+1之间,即|max|<1,因此n=0,Q=15-n=15。
DSP-定点和浮点数格式解析

① 小数乘小数(n、m≠0,m≤ n) ② 整数乘小数(n≠0、m=0) ③ 整数乘整数(n=m=0)
① 小数乘小数(n、m≠0,m≤ n)
例:两个8位数相加,有溢出 进位位与最高位(MSB)不同 运算结果发生溢出,8位字长已不能正确地表示结果
10110000b( -80) + 10111111b( -65) 非饱和模式:101101111bቤተ መጻሕፍቲ ባይዱ-145)
00101001b( 41) + 01110011b(115) 非饱和模式:010011100b(156)
2)数值范围与精度
给定字长N,采用Qn格式表示小数
2 N 1 2 N 1 1 数值范围: n ~ 2 2n
精
度:
1
2n
16位字长Qn格式的数值范围与精度
Qn格式 Q15 数值范围 -1~0.999969482421875 精度 0.000030517578125
Q14
饱和模式:110000000b(-128)
饱和模式:001111111b(127)
溢出是由于字长有限,运算结果超出数值的表示范围引 起的
饱和模式
定点数减法运算的原理与加法运算相同
2)定点数的乘法运算
DSP处理器都有硬件乘法器和乘法指令,可实现单周期乘 法运算 二进制乘法运算包含一系列的移位和加法运算 定点数乘法运算不要求相乘数有相同的Qn格式 两个相乘数分别为Qn和Qm格式,字长为N,结果为 Q(n+m)格式,字长为2N 根据n和m的不同取值,定点数乘法运算可以分成三种情况
DSP 运算基础
• 1、 DSP的数据表示
• 2、定点数的格式与运算 • 3、浮点数的格式与运算
DSP的Q定标

一DSP定点算数运算1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,l则表示数值为负。
其余15位表示数值的大小。
因此,二进制数0010000000000011b=8195二进制数1111111111111100b= -4对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表1.1列出了一个16位数的16种Q 表示、S表示及它们所能表示的十进制数值范围。
从表1.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如,16进制数2000H=8192,用Q0表示16进制数2000H=0.25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表1.1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0 的数值范围是-32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为1/32768=0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想精度提高,则数的表示范围就相应地减小。
DSP-定点和浮点数格式

0.0625 0.125 0.25
0.5 1
3)动态范围
动态范围:数据表示格式中可以表示的最大值与最小值之比
N位定点数的动态范围:
DR
=
fix
(2N
1
1
1) / 2n
/
2n
2N 1 1
用分贝表示为:
DRfix=20 log10 2N1 1 6.02(N 1) dB
00001000b - 00000110b 商数:00001101 余数:00000010b
⑥ ⑦
00000100b - 00000110b 余数(丢弃):11111110b 商数:00011010 余数:00000100b
00001000b - 00000110b 商数: 00110101 余数:00000010b
① 小数乘小数(n、m≠0,m≤ n)
例:两个相乘数分别为Q7和Q6格式,8位字长
两个定点小数作乘法运算,结果左移一位,保存高位得到 运算结果,结果为Qm(m≤ n)格式
0.1000000b(0.5 Q7 )
01.100000b(1.5 Q6 )
000.1100000000000b(0.75 Q13)
对于负数(最高位MSB为1),要先把它转化为无符号二进制数,再进 行计算,最后加上负号
位
7 MSB
6
5
4
3
2
1
0 LSB
二进制补码 0
1
0
1
0
0
1
1
Q0
符号 26
252423源自222120
Q4
符号 22
21
20
Q格式定标
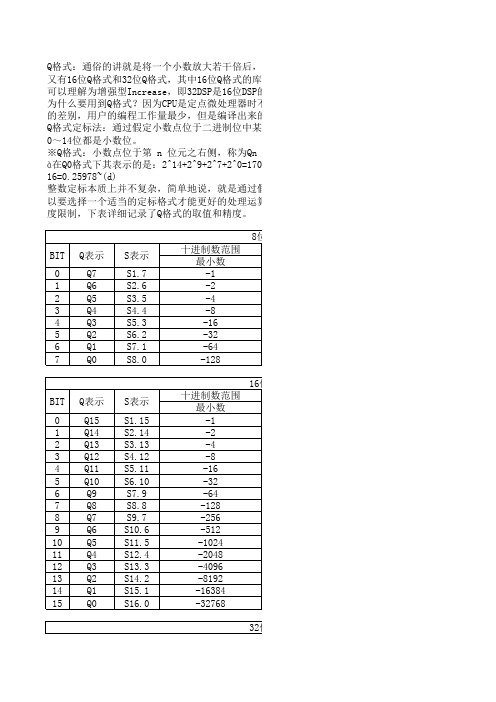
Q格式:通俗的讲就是将一个小数放大若干倍后,用整又有16位Q格式和32位Q格式,其中16位Q格式的库为<Qmath.h>,32位Q格式的库为<IQmath.h>。
那个字母可以理解为增强型Increase,即32DSP是16位DSP的增强型,然后32位的就用IQ表示。
为什么要用到Q格式?因为CPU是定点微处理器时不能直接处理小数,C语言中的自动调用运行时的函数来的差别,用户的编程工作量最少,但是编译出来的代码很庞大,在嵌入式应用中很多情况下,float型几Q格式定标法:通过假定小数点位于二进制位中某位的右侧,从而确定小数的精度。
Q0:小数点在第0位0~14位都是小数位。
※Q格式:小数点位于第 n 位元之右侧,称为Qn 格式。
例如;16位元二进位数:0100 0010 1000 0001à在Q0格式下其表示的是:2^14+2^9+2^7+2^0=17025(d);à在Q8格式下其表示的是:2^6+2^1+2^-1+2^-8 16=0.25978~(d)整数定标本质上并不复杂,简单地说,就是通过假定小数点位于哪一位。
从而确定小数精度。
实际应用以要选择一个适当的定标格式才能更好的处理运算。
DSP定点运算处理器运算浮点数时,对浮点数转换为度限制,下表详细记录了Q格式的取值和精度。
,用整数来表示小数。
其中Q是定点格式,浮点数进行定点数运算处理时一般有Q格式和S格式,位Q格式的库为<Qmath.h>,32位Q格式的库为<IQmath.h>。
那个字母I表示32位的DSP的标号,16位的DSP前面没有字母是16位DSP的增强型,然后32位的就用IQ表示。
微处理器时不能直接处理小数,C语言中的自动调用运行时的函数来处理浮点数(float型),C语言中抹平了定点处理是编译出来的代码很庞大,在嵌入式应用中很多情况下,float型几乎不能去想,所以才会要用到Q格式定标法。
Q格式_dsp定点和浮点数学运算规则

Q格式有符号数的表示法,机器数(出现在电脑的二进位数值)有3个特点,无符号或符号转换成数值来表示,没有+10101这样的资料,而是以010101来表示,只表示单纯的整数或小数,小数点的位置预设在一定的位置而较少变动,它的长度受到电脑硬体的限制,而不能无限增长。
Q格式,就是将一个小数放大若干倍后,用整数来表示小数。
Q格式前提无符号数:当参与运算的数值没有负数且运算的结果也没有负数时,则所有字元都可以表示数值,这种没有符号的数,称为无符号数(如记忆体储存位址),有符号数:数值中有某位数值代表符号,通常最高位作为符号位,0代表正,1代表负。
真值:有符号数所代表的数值,例如:110所代表的值是-2 而非6,有符号数只要去除符号位就可以获得该数的大小,在运算时,它的符号位可参与运算。
但在加减运算时,必须将它分离出来,才能进行运算。
有时,还要确定哪个有符号数的真值比较大,才能确定结果的符号。
为了达到这些功能,电路的设计就相当复杂。
所以很多电脑系统不直接使用有符号数,而使用有符号数的1’s补数或2’s补数表示法作为编码系统正弦脉波宽度调变(SPWM)之控制方法经Q 格式乘法器转换成振幅与频率可变V/F 控制,当成其单相感应马达的输入信号,藉由控制责任周期的大小,以达到变电压相对改变频率的效果。
DSP1.实现数位系统的第一步在自然世界中,所有的物理量包括时间、电压、质量、位移等等,都是类比的、连续的。
可是在数位系统中,讯号是在不连续的时间点取样,物理量或讯号的大小也不再是连续,而是被量化(Quantized)。
在数位系统中,只能用有限字元长度的数字去表示数量的大小,而不能以无限精确的数值(实数)去表示。
为了实现数位系统;使用了定数数与浮点数的表示法。
a)定点数(Fixed Point Number):指一个数字的表示,其小数点是在固定的位置(位元)。
b)浮点数(Floating Point Number):使用假数以及指数两部分来表示数值。
DSP定点运算-Q格式

DSP芯片的定点运算---Q格式(转)2008-09-03 15:47DSP芯片的定点运算1.数据的溢出:1>溢出分类:上溢(overflow):下溢(underflow)2>溢出的结果:MaxMin上溢在圆圈上按数据逆时针移动;下溢在圆圈上顺时钟移动。
例:signed int :32767+1=-32768;-32768-1=32767unsigned char:255+1=0;0-1=2553>为了避免溢出的发生,一般在DSP中可以设置溢出保护功能。
当发生溢出时,自动将结果设置为最大值或最小值。
2.定点处理器对浮点数的处理:1>定义变量为浮点型(float,double),用C语言抹平定点处理器和浮点处理器的区别,但是程序的代码庞大,运算速度也慢。
2>放大若干倍表示小数。
比如要表示精度为0.01的变量,放大100倍去运算,运算完成后再转化。
但是这个做法比较僵硬,如要将上面的变量重新定义成0.001精度,又需要放大1000倍,且要重新编写整个程序,考虑溢出等问题。
3>定标法:Q格式:通过假定小数点位于哪一位的右侧,从而确定小数的精度。
Q0:小数点在第0位的后面,即我们一般采用的方法Q15 小数点在第15位的后面,0~14位都是小数位。
转化公式:Q=(int)(F×pow(2,q))F=(float)(Q×pow(2,-q))3.Q格式的运算1>定点加减法:须转换成相同的Q格式才能加减2>定点乘法:不同Q格式的数据相乘,相当于Q值相加3>定点除法:不同Q格式的数据相除,相当于Q值相减4>定点左移:左移相当于Q值增加5>定点右移:右移相当于Q减少4.Q格式的应用格式实际应用中,浮点运算大都时候都是既有整数部分,也有小数部分的。
所以要选择一个适当的定标格式才能更好的处理运算。
一般用如下两种方法:1>使用时使用适中的定标,既可以表示一定的整数复位也可以表示小数复位,如对于2812的32位系统,使用Q15格式,可表示-65536.0~65535.999969482区间内的数据。
DSP数的表示:定点小数Q格式表示和加法

DSP数的表示:定点小数Q格式表示和加法•DSP数的表示:定点小数Q 格式表示和加法o在低开销DSP上表示小数o Q格式o小数点位置选择o Q格式举例o符号扩展o Q格式加法o使用保护位(guard bit)防止溢出o总结本文翻译自定点表示是的我们可以在低开销的整数硬件上使用小数运算。
本文首先介绍小数表示方法Q格式,然后给一些定点加法的例子。
在低开销DSP上表示小数为了降低开销,很多数字信号处理器都设计成只能进行整数算术运算。
为了在这些处理器上表示小数,我们可以使用隐含小数点。
例如,8bit字a=010101102a=010101102,单被当做整数时表示86108610。
然而,我们可以假设存在一个隐含的小数点,并把该数理解为一个小数。
假设小数点在第4和第5个bit之间,例如,a=0101.01102a=0101.01102。
我们可以通过以下公式得到该数等价的十进制的值:a=0×23+1×22+0×21+1×20+0×2−1+1×2−2+1×2−3+0×2−4=5.375a=0×23+1×22+0×21+1×20+0×2−1+1×2−2+1×2−3+0×2−4=5.375在这个例子中,我们用4bit表示整数部分,4bit表示小数部分。
从这个例子我们可以看到,小数点右边第一个bit的系数为0.5,第二个为0.25,以此类推。
需要注意这个隐含的小数点并没有在硬件上表达,程序猿需要假设一个合适的缩放因子来正确的解释计算结果。
在上面的例子中,硬件上只存储8bit数a=010101102a=010101102。
如果程序员想要用a表示5.375,就需要记住使用a进行的任何运算结果,都需要乘以一个缩放因子2−42−4。
Q格式小数点位置不同,同一个二进制数可以表示不同的值。
DSP芯片的定点运算

第3章 DSP 芯片的定点运算3.1 数 的 定 标在定点DSP 芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP 芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP 芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,1那么表示数值为负。
其余15位表示数值的大小。
因此二进制数=8195 二进制数11111=-4对DSP 芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP 芯片是如何处理小数的呢?应该说,DSP 芯片本身无能为力。
那么是不是说DSP 芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q 表示法和S 表示法两种。
表列出了一个16位数的16种Q 表示、S 表示及它们所能表示的十进制数值范围。
从表可以看出,同样一个16位数,假设小数点设定的位置不同,它所表示的数也就不同。
例如:16进制数2000H =8192,用Q0表示 16进制数2000H =,用Q15表示但对于DSP 芯片来说,处理方法是完全相同的。
从表还可以看出,不同的Q 所表示的数不仅范围不同,而且精度也不相同。
Q 越大,数值范围越小,但精度越高;相反,Q 越小,数值范围越大,但精度就越低。
例如,Q0的数值范围是-32768到+32767,其精度为1,而Q15的数值范围为-1到,精度为。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比拟大的数值范围,必须以牺牲精度为代价;而想提高精度,那么数的表示范围就相应地减小。
在实际的定点算法中,为了到达最正确的性能,必须充分考虑到这一点。
第3章DSP芯片的定点运算

第3章DSP芯片的定点运算3.1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,1则表示数值为负。
其余15位表示数值的大小。
因此二进制数0010000000000011b = 8195二进制数1111111111111100b = -4对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表3.1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。
从表3.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如:16进制数2000H = 8192,用Q0表示16进制数2000H = 0.25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表3.1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0的数值范围是-32768到+32767,其精度为1,而Q15的数值范围为-1到0.9999695,精度为1/32768 = 0.00003051。
因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想提高精度,则数的表示范围就相应地减小。
5 DSP Q格式概论

1) 很多数值可以离线设定。也就说,先离线计算出13653ห้องสมุดไป่ตู้ 然后赋值即可
2) 从50Hz转换到13653的设定过程,绝大多数情况下对时间 要求不苛刻,可以放在主程序或优先级低的任务中
3) 必须在线设定且对时间一起苛刻时,一个变通的方法是设 定常数MAXF为2的n次幂,比如MAXF=128,即可把除法 转换为右移。
当用一个16位的字来表示Q15格式时,在MSB(最高位)的右 边有一个小数点,而MSB表示符号位。
所以Q15的表示数字可表示范围从+1(以+0.99996表示)到-1 的值。
浮点数和定点数之间的转换公式如下
浮点数xf转换为定点数xq时, xq (int) xf 2Q
定点数xq转换为浮点数xf时, xf (int) xq 2Q
例:设定一个常数MAXF=120,那么频率变量f=50Hz的Q15表 示为: #define MAXF 120 unsigned int f; f=((unsigned long)50<<15)/MAXF; 频率变量f等于13653;
频率f代表的是百分比数值,且精度也很高。
1.2 Q15格式
上述计算用到了除法“/”,而除法运算是比较费时的,解决 方
EXAMPLE1:Current Sensing and Scaling
The two phase currents are sampled simultaneously by means of the DSP Controller by using one channel of each ADC module per current. In this application channel 1 (ADCIN0) and channel 9 (ADCIN8) are used to sample the phase currents. Below is the code that waits for the LEM output to be converted and then transforms the conversion result into a 4.12 representation of one phase current (attention :it may be wrong!).
DSP芯片的定点运算

DOC.第3章 DSP 芯片的定点运算3.1 数的定标在定点DSP 芯片中,采用定点数进展数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示X 围取决于DSP 芯片所给定的字长,一般为16位或24位。
显然,字长越长,所能表示的数的X 围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP 芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,1那么表示数值为负。
其余15位表示数值的大小。
因此二进制数00011b =8195 二进制数11100b =-4对DSP 芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP 芯片是如何处理小数的呢?应该说,DSP 芯片本身无能为力。
那么是不是说DSP 芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q 表示法和S 表示法两种。
表3.1列出了一个16位数的16种Q 表示、S 表示与它们所能表示的十进制数值X 围。
从表3.1可以看出,同样一个16位数,假设小数点设定的位置不同,它所表示的数也就不同。
例如:16进制数2000H =8192,用Q0表示 16进制数2000H =0.25,用Q15表示但对于DSP 芯片来说,处理方法是完全一样的。
从表3.1还可以看出,不同的Q 所表示的数不仅X 围不同,而且精度也不一样。
Q 越大,数值X 围越小,但精度越高;相反,Q 越小,数值X 围越大,但精度就越低。
例如,Q0的数值X 围是-32768到+32767,其精度为1,而Q15的数值X 围为-1到0.9999695,精度为 1/32768 = 0.00003051。
因此,对定点数而言,数值X 围与精度是一对矛盾,一个变量要想能够表示比拟大的数值X 围,必须以牺牲精度为代价;而想提高精度,那么数的表示X 围就相应地减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DSP芯片的定点运算---Q格式(转)
2008-09-03 15:47
DSP芯片的定点运算
1.数据的溢出:
1>溢出分类:
上溢(overflow):
下溢(underflow)
2>溢出的结果:
Max
Min
上溢在圆圈上按数据逆时针移动;下溢在圆圈上顺时钟移动。
例:signed int :32767+1=-32768;-32768-1=32767
unsigned char:255+1=0;0-1=255
3>为了避免溢出的发生,一般在DSP中可以设置溢出保护功能。
当发生溢出时,自动将结果设置为最大值或最小值。
2.定点处理器对浮点数的处理:
1>定义变量为浮点型(float,double),用C语言抹平定点处理器和浮点处理器
的区别,但是程序的代码庞大,运算速度也慢。
2>放大若干倍表示小数。
比如要表示精度为0.01的变量,放大100倍去运算,
运算完成后再转化。
但是这个做法比较僵硬,如要将上面的变量重新定义成
0.001精度,又需要放大1000倍,且要重新编写整个程序,考虑溢出等问题。
3>定标法:Q格式:通过假定小数点位于哪一位的右侧,从而确定小数的精度。
Q0:小数点在第0位的后面,即我们一般采用的方法
Q15 小数点在第15位的后面,0~14位都是小数位。
转化公式:Q=(int)(F×pow(2,q))
F=(float)(Q×pow(2,-q))
3.Q格式的运算
1>定点加减法:须转换成相同的Q格式才能加减
2>定点乘法:不同Q格式的数据相乘,相当于Q值相加
3>定点除法:不同Q格式的数据相除,相当于Q值相减
4>定点左移:左移相当于Q值增加
5>定点右移:右移相当于Q减少
4.Q格式的应用格式
实际应用中,浮点运算大都时候都是既有整数部分,也有小数部分的。
所以要选择
一个适当的定标格式才能更好的处理运算。
一般用如下两种方法:
1>使用时使用适中的定标,既可以表示一定的整数复位也可以表示小数复位,如
对于2812的32位系统,使用Q15格式,可表示-65536.0~65535.999969482
区间内的数据。
2>全部采用小数,这样因为小数之间相乘永远是小数,永远不会溢出。
取一个极
限最大值(最好使用2的n次幂),转换成x/Max的小数(如果Max是取的2的n次幂,就可以使用移位代替除法)。
5.Ti的qmath.lib库说明:
见TI的文档C28x IQMath Library (SPRC087a).zip的详细说明。
TI公司给出了一个Q格式的数学库qmath.lib
注意Q格式函数使用的时序和空间要求,尽量避重就轻。
