随机事件及其概率(知识点总结)Word版

合集下载

随机事件与概率知识点总结

随机事件与概率知识点总结随机事件与概率是概率论中的重要概念，用于描述和分析实际生活中的不确定性事件。

在这篇文章中，我们将对随机事件与概率的相关知识点进行总结和讨论。

一、随机事件的概念随机事件指的是在一定条件下可能发生也可能不发生的事件，其结果是不确定的。

例如掷骰子的结果、抽取扑克牌的花色等都属于随机事件。

二、样本空间和事件样本空间是指一个随机试验的所有可能结果的集合。

例如掷一枚骰子的样本空间为{1, 2, 3, 4, 5, 6}。

事件是样本空间的一个子集，表示某个结果的集合。

例如事件“A”表示掷骰子的结果是偶数，其包含的样本点为{2, 4, 6}。

三、概率的定义概率是描述随机事件发生可能性大小的数值，一般用P(A)表示事件A发生的概率。

概率的取值范围在0到1之间，其中0表示不可能发生，1表示一定发生。

四、概率的计算方法1. 经典概率法：适用于样本空间中的每个样本点出现的可能性相等的情况。

概率P(A)等于事件A包含的样本点数目除以样本空间的样本点数目。

2. 频率概率法：通过实验或观察来估计概率。

概率P(A)等于事件A 在一系列独立重复试验中发生的频率。

3. 主观概率法：基于个人主观判断来估计概率。

例如根据经验或直觉来估计某个事件发生的可能性。

五、概率的性质1. 非负性：概率值始终大于等于0，即P(A) >= 0。

2. 规范性：对于样本空间中的所有样本点的事件，它们的概率之和等于1，即P(S) = 1，其中S表示样本空间。

3. 可列可加性：对于两个互斥事件A和B，它们的概率之和等于它们各自的概率之和，即P(A∪B) = P(A) + P(B)。

六、条件概率条件概率是指在已知某一事件发生的条件下，另一事件发生的概率。

条件概率用P(A|B)表示，读作“在B发生的条件下A发生的概率”。

条件概率的计算公式为P(A|B) = P(A∩B) / P(B)。

七、独立事件独立事件是指两个事件A和B相互之间没有影响，即事件A的发生与否不会影响事件B的发生概率。

概率论与数理统计知识点总结!-知识归纳整理

《概率论与数理统计》第一章随机事件及其概率§1.1 随机事件一、给出事件描述，要求用运算关系符表示事件：二、给出事件运算关系符，要求判断其正确性： §1.2 概率古典概型公式：P （A ）=所含样本点数所含样本点数ΩA 实用中经常采用“罗列组合”的想法计算补例1：将n 个球随机地放到n 个盒中去，问每个盒子恰有1个球的概率是多少？解：设A ：“每个盒子恰有1个球”。

求：P(A)=？Ω所含样本点数：n n n n n =⋅⋅⋅...Α所含样本点数：!1...)2()1(n n n n =⋅⋅-⋅-⋅n n n A P !)(=∴补例2：将3封信随机地放入4个信箱中，问信箱中信的封数的最大数分别为1、2、3的概率各是多少？解：设A i ：“信箱中信的最大封数为i”。

(i =1,2,3)求：P(A i )=？Ω所含样本点数：6444443==⋅⋅A 1所含样本点数：24234=⋅⋅836424)(1==∴A PA 2所含样本点数：363423=⋅⋅C1696436)(2==∴A PA 3所含样本点数：4433=⋅C161644)(3==∴A P注：由概率定义得出的几个性质：知识归纳整理1、0<P （A ）<12、P(Ω)=1，P(φ) =0 §1.3 概率的加法法则定理：设A 、B 是互不相容事件（AB=φ），则： P （A ∪B ）=P （A ）+P （B ）推论1：设A 1、 A 2、…、 A n 互不相容，则 P(A 1+A 2+...+ A n )= P(A 1) + P(A 2) +…+ P(A n )推论2：设A 1、 A 2、…、 A n 构成完备事件组，则 P(A 1+A 2+...+ A n )=1推论3： P （A ）=1－P （A ）推论4：若B ⊃A ，则P(B －A)= P(B)－P(A) 推论5（广义加法公式）：对任意两个事件A 与B ，有P(A ∪B)=P(A)+P(B)－P(A B) 补充——对偶律：nnAA A A A A ⋂⋂⋂=⋃⋃⋃ (2)121nnAA A A A A ⋃⋃⋃=⋂⋂⋂ (2)121§1.4 条件概率与乘法法则条件概率公式：P(A/B)=)()(B P AB P （P(B)≠0）P(B/A)= )()(A P AB P （P(A)≠0）∴P （AB ）=P （A /B ）P （B ）= P （B / A ）P （A ）有时须与P （A+B ）=P （A ）+P （B ）－P （AB ）中的P （AB ）联系解题。

概率论知识点

第一章随机事件及其概率§1.1 随机事件及其运算随机现象：概率论的基本概念之一。

是人们通常说的偶然现象。

其特点是,在相同的条件下重复观察时,可能出现这样的结果,也可能出现那样的结果,预先不能断言将出现哪种结果.例如,投掷一枚五分硬币,可能“国徽”向上,也可能“伍分”向上;从含有5件次品的一批产品中任意取出3件,取到次品的件数可能是0,1,2或3.随机试验：概率论的基本概念之一.指在科学研究或工程技术中,对随机现象在相同条件下的观察。

对随机现象的一次观察(包括试验、实验、测量和观测等),事先不能精确地断定其结果,而且在相同条件下可以重复进行,这种试验就称为随机试验。

样本空间: 概率论术语。

我们将随机试验E 的一切可能结果组成的集合称为E 的样本空间,记为Ω。

样本空间的元素,即E 的每一个结果,称为样本点。

随机事件：实际中,在进行随机试验时,人们常常关心满足某种条件的那些样本点所组成的集合.称试验E 的样本空间Ω的子集为E 的随机事件,简称事件.在每次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件发生.特别,由一个样本点组成的单点集,称为基本事件.样本空间Ω包含所有的样本点,它是Ω自身的子集,在每次试验中它总是发生的,称为必然事件.空集Ø不包含任何样本点,它也作为样本空间的子集,它在每次试验中都不发生,称为不可能事件.互斥事件（互不相容事件）: 若事件A 与事件B 不可能同时发生，亦即ΦB A = ，则称事件A 与事件B 是互斥(或互不相容)事件。

互逆事件: 事件A 与事件B 满足条件ΦB A = ，Ω=B A ,则称A 与B 是互逆事件，也称A 与B 是对立事件,记作A B =（或B A =）。

互不相容完备事件组：若事件组n A A A ,,21满足条件ΦA A j i = ，（n 1,2j i, =），Ω== n 1i i A,则称事件组n A A A ,,21为互不相容完备事件组(或称n A A A ,,21为样本空间Ω的一个划分)。

10.5 随机事件的概率 Microsoft Word 文档

10.5随机事件的概率一、明确复习目标1.了解随机事件的发生存在着规律性和随机事件概率的意义;2.了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率.二．建构知识网络1.事件的定义：随机事件：在一定条件下可能发生也可能不发生的事件；必然事件：在一定条件下必然发生的事件；不可能事件：在一定条件下不可能发生的事件.2.随机事件的概率：一般地，在大量重复进行同一试验时，事件A 发生的频率m n 总是接近某个常数，在它附近摆动，这时就把这个常数叫做事件A 的概率，记作P(A).3.概率的性质：(由定义知,0≤m ≤1,01mn≤≤) ∴ 0()1P A ≤≤; 必然事件的概率为1,不可能事件的概率为0.必然事件和不可能事件看作随机事件的两个极端情形.4.等可能性事件：如果一次试验中有n 个可能的结果——称为基本事件，且每个基本事件出现的可能性都相等，即每个基本事件的概率都是1n，这种事件叫等可能性事件. 5.等可能性事件的概率：在等可能事件中,如果事件A 包含m 个结果，那么事件A 的概率()mP A n=.6.求概率的方法:(1)等可能性事件的概率,步骤:①明确事件A 的意义,确定是否等可能性事件. ②求出一次实验可能出现的结果的总数n;求m,n 时,要注意是否与顺序、位置有关，是“有放回”还是“无放回”抽取，正确排列、组合公式或计数原理求出分母n 和分子m;(分子、分母可以与顺序同时有关或无关，解题时可以灵活处理)。

③用等可能性事件概率公式P =nm求出概率值. (2)通过进行大量的重复试验，用这个事件发生的频率近似地作为它的概率. 三、双基题目练练手1.(2005广东)先后抛掷两枚均匀的正方体骰子（它们的六个面分别标有点数1、2、3、4、5、6），骰子朝上的面的点数分别为X 、Y ，则1log 2=Y X 的概率为（）A ．61B ．365 C ．121 D ．21 2. (2006安徽)在正方体上任选3个顶点连成三角形，则所得的三角形是直角非等腰．．．三角形的概率为（）A ．17B ．27C ．37 D ．473.（2006江西）将7个人(含甲、乙)分成三个组，一组3人，另两组各2人，不同的分组数为a ，甲、乙分在同一组的概率为P ，则a 、P 的值分别为（）A ．5105,21a P ==B . 4105,21a P ==C . 5210,21a P ==D . 4210,21a P ==4. (2004辽宁)口袋内装有10个相同的球，其中5个球标有数字0，5个球标有数字1，若从袋中摸出5个球，那么摸出的5个球所标数字之和小于2或大于3的概率是 .5．在两个袋中各装有分别写着0，1，2，3，4，5的6张卡片.今从每个袋中任取一张卡片，则取出的两张卡片上数字之和恰为7的概率为________.6.将1，2，…，9这9个数平均分成三组，则每组的三个数都成等差数列的概率为________;7.把4个不同的球任意投入4个不同的盒子内（每盒装球数不限），则恰有一个空盒的概率等于_______.◆练习简答:A; 3. a=C 73C 42÷2=105, 1235452510521C C C p ÷+==，选A 4.数字和可是0、1、4、5，概率为14415555510111363C C C C C +++= ; 5. P =1616C C 4⋅=91. 6.分母为33963!C C ⋅÷，求分子时先确定一组有:（123），（135），（147），（159），再定另两组…,答:561. 7.选一盒空C 41种，把4球分三组C 42种,再把三组放入三盒有A 33种,故恰有一个空盒的结果数为C 41C 42A 33,所求概率P （A ）=1234434C C A 4=169.四、经典例题做一做【例1】一个口袋里共有2个红球和8个黄球，从中随机地接连取3个球，每次取一个.设{恰有一个红球}=A ，{第三个球是红球}=B .求在下列条件下事件A 、B 的概率.（1）不返回抽样；（2）返回抽样. 解：（1）不返回抽样, P （A ）=310281312A A C C =157, (与顺序有关),或1228310715C C C = (与顺序无关) P （B ）=3102912A A C =51. （2）返回抽样, P （A ）=C 13102（108）2=12548, P （B ）=32121010C ⨯= 51.【例2】某油漆公司发出10桶油漆，其中白漆5桶，黑漆3桶，红漆2桶.在搬运中所有标签脱落，交货人随意将这些标签重新贴上，问一个定货3桶白漆、2桶黑漆和1桶红漆的顾客，按所定的颜色如数得到定货的概率是多少？解：随意贴上的标签等于没贴标签,从10桶油漆中随意取.P （A ）=610122335C C C C =72. 答：顾客按所定的颜色得到定货的概率是72. 【例3】将甲、乙两颗骰子先后各抛一次,a 、b 分别表示抛掷甲、乙两颗骰子所出现的点数.（1）若a+b<4的事件记为A ,求事件A 的概率;（2）若点P （a ,b ）落在直线x +y=m （m 为常数）上,且使此事件的概率最大,求m 的值.解：（1）基本事件总数为6×6=36. 当a =1时,b =1,2,3;当a =2时,b =1,2;当a =3时,b =1.共有（1,1）,（1,2）,（1,3）,（2,1）,（2,2）,（3,1）6个点适合题设,∴P （A ）=366=61. （2）由表可知,m=7所含的基本事件最多,发生的概率最大此时P =366= 61最大.【例4】（2004全国Ⅱ）已知8支球队中有3支弱队，以抽签方式将这8支球队分为A 、B 两组，每组4支.求：（1）A 、B 两组中有一组恰有两支弱队的概率；（2）A 组中至少有两支弱队的概率.解:（1）A 组中恰有两支弱队,或一只弱队,概率为2213353548C C 6C 7C C +=,(也可按对立事件求: 11548C 62C 7-⨯=) （2）解法一：A 组中至少有两支弱队的概率为2231353548C C 1C 2C C += (也可分为互斥的的两部分算: 482523C C C +481533C C C =21) 解法二：A 、B 两组有一组至少有两支弱队的概率为1，由于对A 组和B 组来说，至少有两支弱队的概率是相同的，所以A 组中至少有两支弱队的概率为21. 【研讨.欣赏】（1）从0、2、4、6、8这五个数字中任取2个，从1、3、5、7、9这五个数字中任取1个。

随机事件与概率知识点总结

随机事件与概率知识点总结概率是我们日常生活中经常用到的概念，它与随机事件密切相关。

在这篇文章中，我们将总结一些关于随机事件与概率的重要知识点。

一、随机事件的定义与表示方式随机事件是指在相同的随机试验中可能发生的某个结果或某些结果的集合。

我们可以用事件的名称或符号来表示随机事件。

例如，事件A表示“掷一枚硬币正面朝上”，事件B表示“掷一枚硬币反面朝上”。

二、随机事件的分类随机事件可以分为互斥事件和非互斥事件。

1. 互斥事件互斥事件指的是两个事件不能同时发生。

例如，事件A表示“掷一枚硬币正面朝上”，事件B表示“掷一枚硬币反面朝上”。

在同一次试验中，事件A和事件B是互斥事件，因为硬币不能同时正反面朝上。

2. 非互斥事件非互斥事件指的是两个事件可以同时发生。

例如，事件C表示“掷一颗六面骰子，点数为偶数”，事件D表示“掷一颗六面骰子，点数为3”。

在同一次试验中，事件C和事件D是非互斥事件，因为骰子可能同时满足偶数和点数为3这两个条件。

三、概率的定义与性质概率是一个表示事件发生可能性的数值，通常用0到1之间的实数表示。

概率的性质包括：1. 非负性任何事件的概率都不小于0，即P(A)≥0。

2. 规范性样本空间Ω中的事件A的概率为1，即P(Ω)=1。

3. 可列可加性如果事件A1、A2、A3...两两互斥，那么这些事件的概率之和等于它们的并集的概率，即P(A1∪A2∪A3...)=P(A1)+P(A2)+P(A3)+...。

四、概率的计算方法计算概率的方法有频率法、古典概型法和几何概型法。

1. 频率法频率法是通过实验来估计事件发生的概率。

当我们进行大量试验时，事件发生的频率趋近于事件发生的概率。

例如，我们翻一枚硬币100次，正面朝上的次数为60次，那么事件“掷一枚硬币正面朝上”的概率可以估计为60/100=0.6。

2. 古典概型法古典概型法适用于样本空间有限、各个结果概率相等的情况。

例如，掷一枚骰子，点数为1、2、3、4、5、6的概率都相等，即P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=1/6。

随机事件及其概率(知识点总结)

随机事件及其概率一、随机事件1、必然事件在一定条件下，必然会发生的事件叫作必然事件.2、不可能事件在一定条件下，一定不会发生的事件叫作不可能事件.3、随机事件在一定条件下，可能发生，也可能不发生的事件叫作随机事件，一般用大写字母A，B，C来表示随机事件.4、确定事件必然事件和不可能事件统称为相对于随机事件的确定事件.5、试验为了探索随机现象发生的规律，就要对随机现象进行观察或模拟，这种观察或模拟的过程就叫作试验.【注】（1）在一定条件下，某种现象可能发生，也可能不发生，事先并不能判断将出现哪种结果，这种现象就叫作随机现象. 应当注意的是，随机现象绝不是杂乱无章的现象，这里的“随机”有两方面意思：①这种现象的结果不确定，发生之前不能预言；②这种现象的结果带有偶然性. 虽然随机现象的结果不确定，带有某种偶然性，但是这种现象的各种可能结果在数量上具有一定的稳定性和规律性，我们称这种规律性为统计规律性. 统计和概率就是从量的侧面去研究和揭示随机现象的这种规律性，从而实现随机性和确定性之间矛盾的统一.（2）必然事件与不可能事件反映的是在一定条件下的确定性现象，而随机事件反映的则是在一定条件下的随机现象.（3）随机试验满足的条件：可以在相同条件下重复进行；所有结果都是明确可知的，但不止一个；每一次试验的结果是可能结果中的一个，但不确定是哪一个. 随机事件也可以简称为事件，但有时为了叙述的简洁性，也可能包含不可能事件和必然事件.二、基本事件空间1、基本事件在试验中不能再分的最简单的随机事件，而其他事件都可以用它们进行描述，这样的事件称为基本事件.2、基本事件空间所有基本事件构成的集合称为基本事件空间，常用大写字母Ω来表示，Ω中的每一个元素都是一个基本事件，并且Ω中包含了所有的基本事件.【注】基本事件是试验中所有可能发生的结果的最小单位，它不能再分，其他的事件都可以用这些基本事件来表示；在写一个试验的基本事件空间时，应注意每个基本事件是否与顺序有关系；基本事件空间包含了所有的基本事件，在写时应注意不重复、不遗漏.三、频率与概率1、频数与频率在相同条件S 下进行了n 次试验，观察某一事件A 是否出现，则称在n 次试验中事件A 出现的次数A n 为事件A 出现的频数；事件A 出现的比例()A n n f A n =为事件A 出现的频率.对于给定的随机事件A ，如果随着试验次数n 的增加，事件A 发生的频率()n f A 稳定在某个常数上，则把这个常数称为事件A 的概率，简称为A 的概率，记作()P A .3、频率与概率的关系（1）频率虽然在一定程度上可以反映事件发生的可能性的大小，但频率并不是一个完全确定的数. 随着试验次数的不同，产生的频率也可能不同，所以频率无法从根本上刻画事件发生的可能性的大小，但人们从大量的重复试验中发现：随着试验次数的无限增加，事件发生的频率会稳定在某一固定的值上，即在无限次重复试验下，频率具有某种稳定性.（2）概率是一个常数，它是频率的科学抽象. 当试验次数无限多时，所得到的频率就会近似地等于概率. 另外，概率大，并不表示事件一定会发生，只能说明事件发生的可能性大，但在一次试验中却不一定会发生.四、事件的关系与运算1、包含关系一般地，对于事件A 与事件B ，如果事件A 发生时，事件B 一定发生，则我们称事件B 包含事件A （或称事件A 包含于事件B ），记作B A ⊇（或A B ⊆）.2、相等关系一般地，对于事件A 与事件B ，如果事件A 发生时，事件B 一定发生，并且如果事件B 发生时，事件A 一定发生，即若B A ⊇且A B ⊇，则我们称事件A 与事件B 相等，记作A B =.3、并事件如果某事件发生当且仅当事件A 或事件B 发生，则我们称该事件为事件A 与事件B 的并事件（或和事件），记作A B ⋃（或A B +）.如果某事件发生当且仅当事件A发生且事件B也发生，则我们称该事件为事件A 与事件B的交事件（或积事件），记作A B⋅）.⋂（或A B5、互斥事件如果事件A与事件B的交事件A B⋂=∅），则我们称事⋂为不可能事件（即A B件A与事件B互斥，其含义是：事件A与事件B在任何一次试验中都不会同时发生.6、对立事件如果事件A与事件B的交事件A B⋂=∅），而事件A与⋂为不可能事件（即A B事件B的并事件A B⋃=Ω），则我们称事件A与事件B互⋃为必然事件（即A B为对立事件，其含义是：事件A与事件B在任何一次试验中有且仅有一个发生.【注】事件的关系与运算可以类比集合的关系与运算. 例如，事件A包含事件B 类比集合A包含集合B；事件A与事件B相等类比集合A与集合B相等；事件A 与事件B的并事件类比集合A与集合B的并集；事件A与事件B的交事件类比集合A与集合B的交集……五、互斥事件与对立事件互斥事件与对立事件是今后考察的重点，因此关于互斥事件与对立事件，我们很有必要再作进一步的说明.1、互斥事件与对立事件的关系互斥事件与对立事件都反映的是两个事件之间的关系. 互斥事件是不可能同时发生的两个事件，而对立事件除了要求这两个事件不同时发生以外，还要求这两个事件必须有一个发生. 因此，对立事件一定是互斥事件，而互斥事件不一定是对立事件. 例如，掷一枚骰子，事件：“出现的点数是1”与事件：“出现的点数是偶数”是互斥事件，但不是对立事件；而事件：“出现的点数是奇数”与事件：“出现的点数是偶数”既是互斥事件，也是对立事件.2、互斥事件的概率加法公式（1）两个互斥事件的概率之和如果事件A 与事件B 互斥，那么()()()P A B P A P B ⋃=+；（2）有限多个互斥事件的概率之和一般地，如果事件1A ，2A ，…，n A 两两互斥，那么事件“12n A A A ⋃⋃⋃L 发生”（指事件1A ，2A ，…，n A 中至少有一个发生）的概率等于这n 个事件分别发生的概率之和，即1212()()()()n n P A A A P A P A P A ⋃⋃⋃=+++L L .【注】上述这两个公式叫作互斥事件的概率加法公式. 在运用互斥事件的概率加法公式时，一定要首先确定各事件是否彼此互斥（如果这个条件不满足，则公式不适用），然后求出各事件分别发生的概率，再求和.3、对立事件的概率加法公式对于对立的两个事件A 与B 而言，由于在一次试验中，事件A 与事件B 不会同时发生，因此事件A 与事件B 互斥，并且A B ⋃=Ω，即事件A 或事件B 必有一个发生，所以对立事件A 与B 的并事件A B ⋃发生的概率等于事件A 发生的概率与事件B 发生的概率之和，且和为1，即()()()()1P P A B P A P B Ω=⋃=+=，或()1()P A P B =-.【注】上述这个公式为我们求事件A 的概率()P A 提供了一种方法，当我们直接求()P A 有困难时，可以转化为先求其对立事件B 的概率()P B ，再运用公式()1()P A P B =-即可求出所要求的事件A 的概率()P A .4、求复杂事件的概率的方法求复杂事件的概率通常有两种方法：一种是将所求事件转化为彼此互斥的事件的和，然后再运用互斥事件的概率加法公式进行求解；另一种是先求其对立事件的概率，然后再运用对立事件的概率加法公式进行求解. 如果采用方法一，一定要准确地将所求事件拆分成若干个两两互斥的事件，不能有重复和遗漏；如果采用方法二，一定要找准所求事件的对立事件，并准确求出对立事件的概率.六、概率的基本性质1、任何事件的概率都在01:之间，即对于任一事件A ，都有0()1P A ≤≤.2、必然事件的概率为1，不可能事件的概率为0.3、若事件A 与事件B 互斥，则()()()P A B P A P B ⋃=+.4、两个对立事件的概率之和为1，即若事件A 与事件B 对立，则()()1P A P B +=.。

(完整版)概率论知识点总结

概率论知识点总结第一章随机事件及其概率第一节基本概念随机实验：将一切具有下面三个特点：（1）可重复性（2）多结果性（3）不确定性的试验或观察称为随机试验，简称为试验，常用 E 表示。

随机事件：在一次试验中，可能出现也可能不出现的事情（结果）称为随机事件，简称为事件。

不可能事件：在试验中不可能出现的事情，记为Ф。

必然事件：在试验中必然出现的事情，记为Ω。

样本点：随机试验的每个基本结果称为样本点，记作ω.样本空间：所有样本点组成的集合称为样本空间. 样本空间用Ω表示.一个随机事件就是样本空间的一个子集。

基本事件—单点集，复合事件—多点集一个随机事件发生，当且仅当该事件所包含的一个样本点出现。

事件的关系与运算（就是集合的关系和运算）包含关系：若事件 A 发生必然导致事件B 发生，则称B 包含A ，记为A B ⊇或B A ⊆。

相等关系：若A B ⊇且B A ⊆，则称事件A 与事件B 相等，记为A ＝B 。

事件的和：“事件A 与事件B 至少有一个发生”是一事件，称此事件为事件A 与事件B 的和事件。

记为 A ∪B 。

事件的积：称事件“事件A 与事件B 都发生”为A 与B 的积事件，记为A∩ B 或AB 。

事件的差：称事件“事件A 发生而事件B 不发生”为事件A 与事件B 的差事件,记为 A －B 。

用交并补可以表示为B A B A =-。

互斥事件：如果A ，B 两事件不能同时发生，即AB ＝Φ，则称事件A 与事件B 是互不相容事件或互斥事件。

互斥时B A ⋃可记为A ＋B 。

对立事件：称事件“A 不发生”为事件A 的对立事件（逆事件），记为A 。

对立事件的性质：Ω=⋃Φ=⋂B A B A ,。

事件运算律：设A ，B ，C 为事件，则有（1）交换律：A ∪B=B ∪A ，AB=BA（2）结合律：A ∪(B ∪C)=(A ∪B)∪C=A ∪B ∪C A(BC)=(AB)C=ABC（3）分配律：A ∪(B∩C)＝(A ∪B)∩(A ∪C) A(B ∪C)＝(A∩B)∪(A∩C)= AB ∪AC （4）对偶律（摩根律）：B A B A ⋂=⋃ B A B A ⋃=⋂第二节事件的概率概率的公理化体系：（1）非负性：P(A)≥0；（2）规范性：P(Ω)＝1（3）可数可加性： ⋃⋃⋃⋃n A A A 21两两不相容时++++=⋃⋃⋃⋃)()()()(2121n n A P A P A P A A A P概率的性质：（1）P(Φ)＝0（2）有限可加性：n A A A ⋃⋃⋃ 21两两不相容时)()()()(2121n n A P A P A P A A A P +++=⋃⋃⋃当AB=Φ时P(A ∪B)＝P(A)＋P(B) （3）)(1)(A P A P -=（4）P(A －B)＝P(A)－P(AB)（5）P （A ∪B ）＝P(A)＋P(B)－P(AB)第三节古典概率模型1、设试验E 是古典概型, 其样本空间Ω由n 个样本点组成,事件A 由k 个样本点组成.则定义事件A 的概率为nk A P =)( 2、几何概率：设事件A 是Ω的某个区域，它的面积为 μ(A)，则向区域Ω上随机投掷一点，该点落在区域 A 的概率为)()()(Ω=μμA A P 假如样本空间Ω可用一线段，或空间中某个区域表示，则事件A 的概率仍可用上式确定，只不过把μ理解为长度或体积即可.第四节条件概率条件概率：在事件B 发生的条件下，事件A 发生的概率称为条件概率，记作 P(A|B).)()()|(B P AB P B A P =乘法公式：P(AB)=P(B)P(A|B)＝P(A)P(B|A)全概率公式：设n A A A ,,,21 是一个完备事件组，则P(B)=∑P(i A )P(B|i A ) 贝叶斯公式：设n A A A ,,,21 是一个完备事件组,则∑==)|()()|()()()()|(jj i i i i A B P A P A B P A P B P B A P B A P第五节事件的独立性两个事件的相互独立：若两事件A 、B 满足P(AB)= P(A) P(B)，则称A 、B 独立，或称A 、B 相互独立.三个事件的相互独立：对于三个事件A 、B 、C ，若P(AB)= P(A) P(B)，P(AC)= P(A)P(C)，P(BC)= P(B) P(C)，P(ABC)= P(A) P(B)P(C)，则称A 、B 、C 相互独立三个事件的两两独立：对于三个事件A 、B 、C ，若P(AB)= P(A) P(B)，P(AC)= P(A)P(C)，P(BC)= P(B) P(C)，则称A 、B 、C 两两独立独立的性质：若A 与B 相互独立，则A 与B ，A 与B ，A 与B 均相互独立总结：1.条件概率是概率论中的重要概念，其与独立性有密切的关系，在不具有独立性的场合，它将扮演主要的角色。

随机事件及其概率(知识点总结)

随机事件及其概率一、随机事件1、必然事件在一定条件下，必然会发生的事件叫作必然事件.2、不可能事件在一定条件下，一定不会发生的事件叫作不可能事件.3、随机事件在一定条件下，可能发生，也可能不发生的事件叫作随机事件，一般用大写字母A，B，C来表示随机事件.4、确定事件必然事件和不可能事件统称为相对于随机事件的确定事件.5、试验为了探索随机现象发生的规律，就要对随机现象进行观察或模拟，这种观察或模拟的过程就叫作试验.【注】（1）在一定条件下，某种现象可能发生，也可能不发生，事先并不能判断将出现哪种结果，这种现象就叫作随机现象. 应当注意的是，随机现象绝不是杂乱无章的现象，这里的“随机”有两方面意思：①这种现象的结果不确定，发生之前不能预言；②这种现象的结果带有偶然性. 虽然随机现象的结果不确定，带有某种偶然性，但是这种现象的各种可能结果在数量上具有一定的稳定性和规律性，我们称这种规律性为统计规律性. 统计和概率就是从量的侧面去研究和揭示随机现象的这种规律性，从而实现随机性和确定性之间矛盾的统一.（2）必然事件与不可能事件反映的是在一定条件下的确定性现象，而随机事件反映的则是在一定条件下的随机现象.（3）随机试验满足的条件：可以在相同条件下重复进行；所有结果都是明确可知的，但不止一个；每一次试验的结果是可能结果中的一个，但不确定是哪一个. 随机事件也可以简称为事件，但有时为了叙述的简洁性，也可能包含不可能事件和必然事件.二、基本事件空间1、基本事件在试验中不能再分的最简单的随机事件，而其他事件都可以用它们进行描述，这样的事件称为基本事件.2、基本事件空间所有基本事件构成的集合称为基本事件空间，常用大写字母Ω来表示，Ω中的每一个元素都是一个基本事件，并且Ω中包含了所有的基本事件.【注】基本事件是试验中所有可能发生的结果的最小单位，它不能再分，其他的事件都可以用这些基本事件来表示；在写一个试验的基本事件空间时，应注意每个基本事件是否与顺序有关系；基本事件空间包含了所有的基本事件，在写时应注意不重复、不遗漏.三、频率与概率1、频数与频率在相同条件S 下进行了n 次试验，观察某一事件A 是否出现，则称在n 次试验中事件A 出现的次数A n 为事件A 出现的频数；事件A 出现的比例()A n n f A n=为事件A 出现的频率.对于给定的随机事件A ，如果随着试验次数n 的增加，事件A 发生的频率()n f A 稳定在某个常数上，则把这个常数称为事件A 的概率，简称为A 的概率，记作()P A .3、频率与概率的关系（1）频率虽然在一定程度上可以反映事件发生的可能性的大小，但频率并不是一个完全确定的数. 随着试验次数的不同，产生的频率也可能不同，所以频率无法从根本上刻画事件发生的可能性的大小，但人们从大量的重复试验中发现：随着试验次数的无限增加，事件发生的频率会稳定在某一固定的值上，即在无限次重复试验下，频率具有某种稳定性.（2）概率是一个常数，它是频率的科学抽象. 当试验次数无限多时，所得到的频率就会近似地等于概率. 另外，概率大，并不表示事件一定会发生，只能说明事件发生的可能性大，但在一次试验中却不一定会发生.四、事件的关系与运算1、包含关系一般地，对于事件A 与事件B ，如果事件A 发生时，事件B 一定发生，则我们称事件B 包含事件A （或称事件A 包含于事件B ），记作B A ⊇（或A B ⊆）.2、相等关系一般地，对于事件A 与事件B ，如果事件A 发生时，事件B 一定发生，并且如果事件B 发生时，事件A 一定发生，即若B A ⊇且A B ⊇，则我们称事件A 与事件B 相等，记作A B =.3、并事件如果某事件发生当且仅当事件A 或事件B 发生，则我们称该事件为事件A 与事件 B 的并事件（或和事件），记作A B ⋃（或A B +）.如果某事件发生当且仅当事件A发生且事件B也发生，则我们称该事件为事件A 与事件B的交事件（或积事件），记作A B⋂（或A B⋅）.5、互斥事件如果事件A与事件B的交事件A B⋂=∅），则我们称事⋂为不可能事件（即A B件A与事件B互斥，其含义是：事件A与事件B在任何一次试验中都不会同时发生.6、对立事件如果事件A与事件B的交事件A B⋂=∅），而事件A与⋂为不可能事件（即A B事件B的并事件A B⋃=Ω），则我们称事件A与事件B互⋃为必然事件（即A B为对立事件，其含义是：事件A与事件B在任何一次试验中有且仅有一个发生.【注】事件的关系与运算可以类比集合的关系与运算. 例如，事件A包含事件B 类比集合A包含集合B；事件A与事件B相等类比集合A与集合B相等；事件A 与事件B的并事件类比集合A与集合B的并集；事件A与事件B的交事件类比集合A与集合B的交集……五、互斥事件与对立事件互斥事件与对立事件是今后考察的重点，因此关于互斥事件与对立事件，我们很有必要再作进一步的说明.1、互斥事件与对立事件的关系互斥事件与对立事件都反映的是两个事件之间的关系. 互斥事件是不可能同时发生的两个事件，而对立事件除了要求这两个事件不同时发生以外，还要求这两个事件必须有一个发生. 因此，对立事件一定是互斥事件，而互斥事件不一定是对立事件. 例如，掷一枚骰子，事件：“出现的点数是1”与事件：“出现的点数是偶数”是互斥事件，但不是对立事件；而事件：“出现的点数是奇数”与事件：“出现的点数是偶数”既是互斥事件，也是对立事件.2、互斥事件的概率加法公式（1）两个互斥事件的概率之和如果事件A 与事件B 互斥，那么()()()P A B P A P B ⋃=+；（2）有限多个互斥事件的概率之和一般地，如果事件1A ，2A ，…，n A 两两互斥，那么事件“12n A A A ⋃⋃⋃发生”（指事件1A ，2A ，…，n A 中至少有一个发生）的概率等于这n 个事件分别发生的概率之和，即1212()()()()n n P A A A P A P A P A ⋃⋃⋃=+++.【注】上述这两个公式叫作互斥事件的概率加法公式. 在运用互斥事件的概率加法公式时，一定要首先确定各事件是否彼此互斥（如果这个条件不满足，则公式不适用），然后求出各事件分别发生的概率，再求和.3、对立事件的概率加法公式对于对立的两个事件A 与B 而言，由于在一次试验中，事件A 与事件B 不会同时发生，因此事件A 与事件B 互斥，并且A B ⋃=Ω，即事件A 或事件B 必有一个发生，所以对立事件A 与B 的并事件A B ⋃发生的概率等于事件A 发生的概率与事件B 发生的概率之和，且和为1，即()()()()1P P A B P A P B Ω=⋃=+=，或()1()P A P B =-.【注】上述这个公式为我们求事件A 的概率()P A 提供了一种方法，当我们直接求()P A 有困难时，可以转化为先求其对立事件B 的概率()P B ，再运用公式()1()P A P B =-即可求出所要求的事件A 的概率()P A .4、求复杂事件的概率的方法求复杂事件的概率通常有两种方法：一种是将所求事件转化为彼此互斥的事件的和，然后再运用互斥事件的概率加法公式进行求解；另一种是先求其对立事件的概率，然后再运用对立事件的概率加法公式进行求解. 如果采用方法一，一定要准确地将所求事件拆分成若干个两两互斥的事件，不能有重复和遗漏；如果采用方法二，一定要找准所求事件的对立事件，并准确求出对立事件的概率.六、概率的基本性质1、任何事件的概率都在01之间，即对于任一事件A，都有0()1≤≤.P A2、必然事件的概率为1，不可能事件的概率为0.3、若事件A与事件B互斥，则()()()⋃=+.P A B P A P B4、两个对立事件的概率之和为1，即若事件A与事件B对立，则()()1+=.P A P B。

概率论必备知识点

概率论与数理统计知识点：第一章随机事件及其概率1、随机试验、样本空间与随机事件（1）随机试验：具有以下三个特点的试验称为随机试验，记为E .1）试验可在相同的条件下重复进行；2）每次试验的结果具有多种可能性，但试验之前可确知试验的所有可能结果； 3）每次试验前不能确定哪一个结果会出现.（2）样本空间：随机试验E 的所有可能结果组成的集合称为E 的样本空间，记为Ω；试验的每一个可能结果，即Ω中的元素，称为样本点，记为e .（3）随机事件：在一次试验中可能出现也可能不出现的事件称为随机事件，简称事件，常用A 、B 、C 等大写字母表示；可表述为样本空间中样本点的某个集合，分为复合事件和简单事件，还有必然事件（记为Ω）和不可能事件（记为Φ）. 2、事件的关系与运算（1）包含关系与相等：“事件A 发生必导致B 发生”，记为B A ⊂或A B ⊃；B A B A ⊂⇔=且A B ⊂.（2）和事件（并）：“事件A 与B 至少有一个发生”，记为B A ⋃. （3）积事件（交）：“ 事件A 与B 同时发生”，记为B A ⋂或AB .（4）差事件、对立事件(余事件)：“事件A 发生而B 不发生”，记为A －B 称为A 与B 的差事件；B B =-Ω称为B 的对立事件；易知：B A B A =-.（5）互不相容性：φ=AB ；B A 、互为对立事件Ω=⋃⇔B A 且Φ=AB . （6）事件的运算法则：1) 交换律：A B B A ⋃=⋃，BA AB = ； 2) 结合律：C B A C B A ⋃⋃=⋃⋃)()(，)()(BC A C AB =； 3) 分配律：BC AC C B A ⋃=⋃)(，))(()(C B C A C AB ⋃⋃=⋃；4) 对偶(De Morgan)律：B A B A =⋃，B A AB ⋃=，可推广kkkkkkkkAA A A ==,.3、频率与概率（1）频率的定义：事件A 在n 次重复试验中出现A n 次，则比值nn A称为事件A 在n 次重复试验中出现的频率，记为)(A f n ，即n n A f An =)(. （2）统计概率：当∞→n 时，频率)()(A P nnA f A n →=.当n 很大时，)()(A f P A P n ≈=称为事件A 的统计概率.（3）古典概率：若试验的基本事件数为有限个，且每个事件发生的可能性相等，则试验对应古典概型（等可能概型），事件A 发生的概率为：nA k n k A A P )()(＝＝中样本点总数中所含样本点数Ω=.（4）几何概率：若试验基本事件数无限，随机点落在某区域g 的概率与区域g 的测度(长度、面积、体积等)成正比，而与其位置及形状无关，则试验对应几何概型，“在区域Ω中随机地取一点落在区域g 中”这一事件g A 发生的概率为：的测度的测度＝Ωg A P g )(.（5）概率的公理化定义：设(F ,Ω)为可测空间，在事件域F 上定义一个实值函数),(A P F A ∈，满足：1) 非负性：0)(≥A P ，对任意F A ∈；2) 规范性：1)(=ΩP ；3) 可列可加性：若有一列,,2,1, =∈i F A i i Φ=j i A A ，使得∑∞=∞==11)()(j jj jA P A P ，则称),(A P F A ∈为σ域F 上的概率测度，简称“概率”． 4、概率的基本性质（1）不可能事件概率零：)(ΦP ＝0.（2）有限可加性：设n A A A ,,,21 是n 个两两互不相容的事件，即j i A A ＝Φ，（j i ≠）n j i ,2,1,,=，则有)(21n A A A P ⋃⋃⋃ ＝)(1A P ＋)()(2n A P A P ++ .（3）单调不减性：若事件B ⊃A ，则P (B )≥P (A )，且P (B －A )＝P (B )－P (A ).（4）互补性：P (A )＝1－P (A )，且P (A )≤1.（5）加法公式：对任意两事件B A 、，有=⋃)(B A P )()(B P A P +－)(AB P ；此性质可推广到任意n 个事件n A A A ,,,21 的情形.（6）可分性：对任意两事件B A 、，有)()()(B A P AB P A P +=. 5、条件概率与乘法公式（1）条件概率：设B A 、是Ω中的两个事件，即F B A ∈、，则)()()|(A P AB P A B P =称为事件A 发生的条件下事件B 发生的条件概率．（2）乘法公式：设F B A ⊂、，则)|()()|()()(B A P B P A B P A P AB P == 称为事件A 、B 的概率乘法公式.6、全概率公式与贝叶斯(Bayes)公式（1）全概率公式：设n A A A ,,,21 是Ω的一个划分，且0)(>i A P ，),,2,1(n i =，则对任何事件F B ∈，有∑=ni iiA B P A P B P 1)|()()(＝，称为全概率公式.（2）贝叶斯(Bayes)公式：设n A A A ,,,21 是Ω的一个划分，且0)(>i A P ),,2,1(n i =，则对任何事件F B ∈，有),,1(,)|()()|()()|(1n j A B P A P A B P A P B A P ni iij j j ==∑=，称为贝叶斯公式或逆概率公式. 7、事件的独立性（1）两事件的独立：设),,(P F Ω为一概率空间，事件F B A ∈、，且0)(>A P ，若)|()(A B P B P =，则称事件A 与B 相互独立；等价于：)()()(B P A P AB P =.（2）多个事件的独立：设n A A A ,,,21 是n 个事件，如果对任意的)1(n k k ≤<，任意的n i i i k ≤<<<≤ 211，具有等式)()()()(2121k k i i i i i i A P A P A P A A A P =，称n 个事件n A A A ,,,21 相互独立． 8、贝努里(Bernoulli)概型（1）只有两个可能结果的试验称为贝努里试验，常记为E ．E 也叫做“成功—失败”试验,“成功”的概率常用)(A P p =表示，其中A ＝“成功”.（2）把E 重复独立地进行n 次，所得的试验称为n 重贝努里试验，记为nE ．（3）把E 重复独立地进行可列多次，所得的试验称为可列重贝努里试验，记为∞E ．以上三种贝努里试验统称为贝努里概型．（4）nE 中成功k 次的概率是：)0(,)1(n k q p C p p C k n k k n k n k k n ≤≤=---其中1=+q p .第二章随机变量及其分布1、随机变量设Ω是随机试验的样本空间，如果对于试验的每一个可能结果Ω∈ω，都有唯一的实数)(ωX 与之对应，则称)(ωX 为定义在Ω上的随机变量，简记为X .随机变量通常用大写字母Z Y X 、、等表示. 2、分布函数及其性质设X 为随机变量，x 为任意实数，函数)}({)(+∞<<-∞≤=x x X P x F 称为随机变量X 的分布函数.分布函数完整地描述了随机变量取值的统计规律性，具有以下性质：（1）)(1)(0+∞<<-∞≤≤x x F ；（2）如果21x x <，则)()(21x F x F ≤；（3）)(x F 为右连续，即)()0(x F x F =+；（4）1)(lim ,0)(lim ==+∞→-∞→x F x F x x ；（5）)()(}{}{}{121221x F x F x X P x X P x X x P -=≤-≤=≤<. 3、离散型随机变量及其概率分布如果随机变量X 只能取有限个或可列个可能值，则称X 为离散型随机变量.如果X 的一切可能值为 ,,21x x ，并且X 取k x 的概率为k p ，则称),3,2,1}({ ===k x X P p k k 为离散型随机变量X 的概率函数（概率分布或分布律）.列成表格形式，也称为分布列(表2-1)：表2-1其中1,0=≥∑iii pp .常见的离散型随机变量的分布有：（1）0-1分布，记为)10(~-X ，概率函数10,1,0,)1(}{1<<=-==-p k p p k X P k k ；（2）二项分布，记为),(~p n B X ，概率函数10,,,1,0,)1(}{<<=-==-p n k p p C k X P k n kk n ；（3）泊松分布，记为)(~λP X ，概率函数0,,1,0,!}{>===-λλλ k k e k X P k ；泊松定理设0>λ是一常数，n 是任意正整数，设λ=n np ，则对于任一固定的非负整数k ，有!)1(lim k e p p C k kn n k nkn n λλ--∞→=-.当n 很大且p 很小时，二项分布可以用泊松分布近似代替，即!)1(k e p p C k kn k k nλλ--≈-，其中np =λ.（4）超几何分布，记为),,(~N M n H X ，概率函数),min(,,1,0,}{M n k C C C k X P nNk n MN k M ===--，其中M N n 、、为正整数，且N n N M ≤≤,.当N 很大，且Nn p =较小时，有k n k k n nN k n MN k M p p C C C C ----≈)1(.] （5）几何分布，记为)(~p G X ，概率函数10,,1,0,)1(}{1<<=-==-p k p p k X P k .4、连续型随机变量及其概率分布如果对于随机变量X 的分布函数)(x F ，存在非负函数)(x f ，使对于任一实数x ，有⎰∞-=xdt t f x F )()(，则称X 为连续型随机变量.函数)(x f称为X 的概率密度函数.概率密度函数具有以下性质：（1）0)(≥x f ；（2）1)(=⎰+∞∞-dt t f ；（3）⎰=≤<21)(}{21x x dt t f x X x P ；（4）0}{1==x X P ；（5）如果)(x f 在x 处连续，则)()(x f x F ='. 常见的连续型随机变量的分布有：（1）均匀分布，记为),(~b a U X ，概率密度为⎪⎩⎪⎨⎧≤≤-=其它,0,,1)(b x a a b x f .相应的分布函数为⎪⎩⎪⎨⎧>≤≤--<=b x b x a a b a x a x x F ,1,,0)(；（2）指数分布，记为)(~λE X ，概率密度为⎩⎨⎧≥=-其它,0,0,)(x e x f λλ.相应的分布函数为⎩⎨⎧<≥-=-0,00,1)(x x e x F x λ；（3）正态分布，记为),(~2σμN X ，概率密度为+∞<<-∞=--X ex f x ,21)(222)(σμπ，相应的分布函数为⎰∞---=xx dt ex F 222)(21)(σμπ；当1,0==σμ时，即)1,0(~N X 时，称X 服从标准正态分布.这时分别用)(x ϕ和)(x Φ表示X 的密度函数和分布函数，即⎰∞---=Φ=x t x dt e x ex 222221)(,21)(ππϕ.具有性质：)(1)(x x Φ-=-Φ.一般正态分布),(~2σμN X 的分布函数)(x F 与标准正态分布的分布函数)(x Φ有关系：)()(σμ-Φ=x x F .5、随机变量函数的分布（1）离散型随机变量函数的分布设X 为离散型随机变量，其分布列为(表2-2)：表2-2则)(X g Y =任为离散型随机变量，其分布列为(表2-3)：表2-3i y 有相同值时，要合并为一项，对应的概率相加.（2）连续型随机变量函数的分布设X 为离散型随机变量，概率密度为)(x f X ，则)(X g Y =的概率密度有两种方法可求.1）定理法：若)(x g y =在X 的取值区间内有连续导数)(x g '，且)(x g 单调时，)(X g Y =是连续型随机变量，其概率密度为⎩⎨⎧<<'=其它,0,)()]([)(βαy y h y h f y f X Y . 其中)()}.(),(max{)},(),(min{y h g g g g +∞-∞=+∞-∞=βα是)(x g 的反函数.2）分布函数法：先求)(X g Y =的分布函数∑⎰∆=≤=≤=k y xY k dx x fy X g P y Y P y F )()(})({}{)(，然后求])([)('=y F y f Y Y .第三章多维随机变量及其分布1、二维随机变量及其联合分布函数设X ，Y 为随机变量，则称它们的有序数组（Y X ,）为二维随机变量. 设（Y X ,）为二维随机变量，对于任意实数x 、y ，称二元函数},{),(y Y x X P y x F ≤≤=为（Y X ,）的联合分布函数.联合分布函数具有以下基本性质：（1）),(y x F 是变量x 或y 的非减函数；（2）1),(0≤≤y x F 且1),(0),(0),(0),(=+∞+∞=-∞-∞=-∞=-∞F F x F y F ，　，　，；（3）),(y x F 关于x 右连续，关于y 也右连续；（4）对任意点),(),,(2211y x y x ，若2121,y y x x <<，则0),(),(),(),(11211222≥+--y x F y x F y x F y x F .上式表示随机点),(Y X 落在区域],[2121y Y y x X x ≤<≤<内的概率为：},{2121y Y y x X x P ≤<≤<.2、二维离散型随机变量及其联合分布律如果二维随机变量),(Y X 所有可能取值是有限对或可列对，则称),(Y X 为二维离散型随机变量.设),(Y X 为二维离散型随机变量,它的所有可能取值为 ,2,1,),,(=j i y x j i 将),2,1,(},{ ====j i p y Y x X P ij j i 或表3.1称为),(Y X 的联合分布律.表3.1联合分布律具有下列性质：（1）0≥ij p ；（2）111=∑∑∞=∞=i j ijp.3、二维连续型随机变量及其概率密度函数如果存在一个非负函数),(y x p ,使得二维随机变量),(Y X 的分布函数),(y x F 对任意实数y x ,有 ⎰⎰∞-∞-=x ydy dx y x p y x F ),(),(，则称),(Y X 是二维连续型随机变量，称),(y x p 为),(Y X 的联合密度函数（或概率密度函数）.联合密度函数具有下列性质：（1）对一切实数y x ,，有0),(≥y x p ；（2）1),(=⎰⎰+∞∞-+∞∞-dy dx y x p ；（3）在任意平面域D 上，),(Y X 取值的概率⎰⎰=∈Ddxdy y x p D Y X P ),(}),{(；（4）如果),(y x p 在),(y x 处连续，则),(),(2y x p yx y x F =∂∂∂. 4、二维随机变量的边缘分布设),(Y X 为二维随机变量，则称},{)(+∞<<-∞≤=Y x X P x F X ，},{)(y Y X P y F Y ≤+∞<<-∞=分别为),(Y X 关于X 和关于Y 的边缘分布函数.当),(Y X 为离散型随机变量，则称),2,1(),2,1(1.1. ====∑∑∞=∞=j p p i p p i ij j j ij i 分别为),(Y X 关于X 和关于Y的边缘分布律.当),(Y X 为连续型随机变量，则称⎰⎰+∞∞-+∞∞-==dx y x p y p dy y x p x p Y X ),()(,),()( 分别为),(Y X 关于X 和关于Y 的边缘密度函数.5、二维随机变量的条件分布（1）离散型随机变量的条件分布设),(Y X 为二维离散型随机变量，其联合分布律和边缘分布律分别为),2,1,(}{,}{,},{.. ========j i p y Y P p x X P p y Y x X P j j i i ij j i ，则当j 固定，且0}{.>==j j p y Y P 时，称,2,1,}{},{}|{.========i p p y Y P y Y x X P y Y x X P jij j j i j i 为j y Y =条件下随机变量X的条件分布律.同理，有 ,2,1,}|{.====j p p x X y Y P i ij i j（2）连续型随机变量的条件分布设),(Y X 为二维连续型随机变量，其联合密度函数和边缘密度函数分别为：)(),(),,(y p x p y x p Y X .则当0)(>y p Y 时，在),(y x p 和)(x p X 的连续点处，),(Y X 在条件y Y =下，X 的条件概率密度函数为：)(),()|(|y p y x p y x p Y Y X =.同理，有)(),()|(|x p y x p y x p X X Y =.6、随机变量的独立性设),(y x F 及)()(y F x F Y X 、分别是),(Y X 的联合分布函数及边缘分布函数.如果对任何实数y x ,有)()(),(y F x F y x F Y X ⋅=则称随机变量X 与Y 相互独立.设),(Y X 为二维离散型随机变量，X 与Y 相互独立的充要条件是),2,1,(.. ==j i p p p j i ij .设),(Y X 为二维连续型随机变量，X 与Y 相互独立的充要条件是对任何实数y x ,，有)()(),(y p x p y x p Y X =.7、两个随机变量函数的分布设二维随机变量),(Y X 的联合概率密度函数为),(y x p ，),(Y X Z ϕ=是Y X ,的函数，则Z 的分布函数为dxdy y x p z F zy x Z ⎰⎰≤=),(),()(ϕ.（1）Y X Z +=的分布若),(Y X 为离散型随机变量，联合分布律为ij p ，则Z 的概率函数为：∑-=ii k i k Z x z x p z P ),()(或∑-=jj k j k Z y z y p z P ),()(.若),(Y X 为连续型随机变量，概率密度函数为),(y x p ，则Z 的概率函数为：dy y y z p dx x z x p z p Z ⎰⎰+∞∞-+∞∞--=-=),(),()(.（2）YXZ =的分布若),(Y X 为连续型随机变量，概率密度函数为),(y x p ，则Z 的概率函数为：⎰+∞∞-=dy y yz p y z p Z ),()(.第四章随机变量的数字特征1、随机变量的数学期望设离散型随机变量X 的分布律为 ,2,1,}{===k p x X P k k ，如果级数∑∞=1k k kp x绝对收敛，则称级数的和为随机变量X 的数学期望.设连续型随机变量X 的密度函数为)(x p ，如果广义积分⎰+∞∞-dx x xp )(绝对收敛，则称此积分值⎰+∞∞-=dx x xp X E )()(为随机变量X 的数学期望.数学期望有如下性质：（1）设C 是常数，则C C E =)(；（2）设C 是常数，则)()(X CE CX E =；（3）若21X X 、是随机变量，则)()()(2121X E X E X X E +=+；对任意n 个随机变量n X X X ,,,21 ，有)()()()(2121n n X E X E X E X X X E +++=+++ ；（4）若21X X 、相互独立，则)()()(2121X E X E X X E =；对任意n 个相互独立的随机变量n X X X ,,,21 ，有)()()()(2121n n X E X E X E X X X E =.2、随机变量函数的数学期望设离散型随机变量X 的分布律为 ,2,1,}{===k p x X P k k ，则X 的函数)(X g Y =的数学期望为 2,1,)()]([1==∑∞=k p x g x g E k k k ，式中级数绝对收敛.设连续型随机变量X 的密度函数为)(x p ，则X 的函数)(X g Y =的数学期望为⎰+∞∞-=dx x p x g x g E )()()]([，式中积分绝对收敛.3、随机变量的方差设X 是一个随机变量，则})]({[)()(2X E X E X Var X D -==称为X 的方差.)()(X X D σ=称为X 的标准差或均方差.计算方差也常用公式22)]([)()(X E X E X D -=. 方差具有如下性质：（1）设C 是常数，则0)(=C D ；（2）设C 是常数，则)()(2X D C CX D =；（3）若21X X 、相互独立，则)()()(2121X D X D X X D +=+；对任意n 个相互独立的随机变量n X X X ,,,21 ，有)()()()(2121n n X D X D X D X X X D +++=+++ ；（4）0)(=X D 的充要条件是：存在常数C ，使))((1}{X E C C X P ===. 4、几种常见分布的数学期望与方差（1）)1()(,)().10(~p p X D p X E X -==-；（2）)1()(,)().,(~p np X D np X E p n B X -==；（3）)1())(()(,)().,,(~2---==N N n N M N nM X D N nM X E N M n H X ；（4）λλλπ==)(,)().(~X D X E X ；（5）2/)1()(,/1)().(~p p X D p X E p G X -==；（6）12/)()(,2/)()().,(~2a b X D b a X E b a U X -=+=；（7）2/1)(,/1)().(~λλλ==X D X E e X ；（8）22)(,)().,(~σμσμ==X D X E N X . 5、矩设X 是随机变量，则 ,2,1),(==k X E k k α称为X 的k 阶原点矩.如果)(X E 存在，则 ,2,1},)]({[=-=k X E X E k k μ称为X 的k 阶中心矩. 设),(Y X 是二维随机变量，则 ,2,1,),(==l k Y X E l k kl α称为),(Y X 的l k +阶混合原点矩； ,2,1,},)]([)]({[=-⋅-=l k Y E Y X E X E l k kl μ称为),(Y X 的l k +阶混合中心矩.5、二维随机变量的数字特征(1) ),(Y X 的数学期望)](),([),(Y E X E Y X E =；若),(Y X 是离散型随机变量，则∑∑∞=∞==11)(i j ijipx X E ，∑∑∞=∞==11)(i j ijipy Y E .若),(Y X 是连续型随机变量，则⎰⎰+∞∞-+∞∞-=dxdy y x xp X E ),()(，⎰⎰+∞∞-+∞∞-=dxdy y x yp Y E ),()(.这里，级数与积分都是绝对收敛的.（2）),(Y X 的方差)](),([),(Y D X D Y X D =若),(Y X 是离散型随机变量，则∑∑∞=∞=-=112)]([)(i j ij ip X E xX D ，∑∑∞=∞=-=112)]([)(i j ij i p Y E y Y D .若),(Y X 是连续型随机变量，则⎰⎰+∞∞-+∞∞--=dxdy y x p X E x X D ),()]([)(2，⎰⎰+∞∞-+∞∞--=dxdy y x p Y E y Y D ),()]([)(2.这里，级数与积分都是绝对收敛的.6、协方差与相关系数随机变量),(Y X 的协方差为)]}()][({[),cov(Y E Y X E X E Y X --=.它是1+1阶混合中心矩，有计算公式：)()()(),cov(Y E X E XY E Y X -=.随机变量),(Y X 的相关系数为DYDX Y X XY ),cov(=ρ.相关系数具有如下性质：（1）1≤XY ρ；（2）⇔=1XY ρ存在常数b a ,，使}{b aX Y P +==1，即X 与Y 以概率1线性相关；（3）若Y X ,独立，则0=XY ρ，即Y X ,不相关.反之，不一定成立.第五章大数定律和中心极限定理1、切贝雪夫不等式设随机变量X 的数学期望μ=)(X E ，方差2)(σ=X D ，则对任意正数ε，有不等式22}{εσεμ≤≥-X P 或221}{εσεμ-><-X P 成立.2、大数定律（1）切贝雪夫大数定理:设 ,,,,21n X X X 是相互独立的随机变量序列，数学期望)(i X E 和方差)(i X D 都存在，且C X D i <)(),2,1( =i ，则对任意给定的0>ε，有1}|)]([1{|lim 1=<-∑=∞→εni i i n X E X n P . （2）贝努利大数定理:设A n 是n 次重复独立试验中事件A 发生的次数，p 是事件A 在一次试验中发生的概率，则对于任意给定的0>ε，有1}|{|lim =<-∞→εp nn P An . 贝努利大数定理给出了当n 很大时，A 发生的频率A n A /依概率收敛于A 的概率，证明了频率的稳定性. 3、中心极限定律（1）独立同分布中心极限定理:设 ,,,,21n X X X 是独立同分布的随机变量序列，有有限的数学期望和方差，μ=)(i X E ，),2,1(0)(2 =≠=i X D i σ.则对任意实数x ，随机变量σμσμn n Xn XY ni ini in ∑∑==-=-=11)(的分布函数)(x F n 满足⎰∞--∞→∞→=≤=xtn n n n dt e x Y P x F 2/221}{lim )(lim π.（2）李雅普诺夫定理:设 ,,,,21n X X X 是不同分布且相互独立的随机变量，它们分别有数学期望和方差：i i X E μ=)(,),2,1(0)(2=≠=i X D i i σ .记 ∑==ni inB 122σ,若存在正数δ，，使得当∞→n 时，有0}{1122→-∑=++ni ii nX E Bδδμ, 则随机变量nni ini ini i ni i ni in B X X D X E XZ ∑∑∑∑∑=====-=-=11111)()(μ的分布函数)(x F n 对于任意的x ，满足⎰∑∑∞--==∞→∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤-=x t n ni i n i i n n n dt e x B X x F 2/11221lim )(lim πμ.当n 很大时,),(~),1,0(~12.1.∑∑==ni n i ni in B N XN Z μ.（3）德莫佛—拉普拉斯定理:设随机变量),2,1( =n n η服从参数为)10(,<<p p n 的二项分布，则对于任意的x ，恒有⎰∞--∞→=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤--x t n n dt e x p np np P 2/221)1(lim πη.第六章数理统计的基本概念1、总体与样本在数理统计中，将研究对象的全体称为总体；组成总体的每个元素称为个体.从总体中抽取的一部分个体，称为总体的一个样本；样本中个体的个数称为样本的容量. 从分布函数为)(x F 的随机变量X 中随机地抽取的相互独立的n 个随机变量，具有与总体相同的分布，则n X X X ,,,21 称为从总体X 得到的容量为n 的随机样本.一次具体的抽取记录n x x x ,,,21 是随机变量n X X X ,,,21 的一个观察值，也用来表示这些随机变量. 2、统计量设n X X X ,,,21 是总体X 的一个样本，则不含未知参数的样本的连续函数),,,(21n X X X f 称为统计量.统计量也是一个随机变量，常见的统计量有（1）样本均值 ∑==ni i X n X 11；（2）样本方差 ][11)(11122122∑∑==--=--=ni in i i X n X n X X n S ；（3）样本标准差 2S S =；（4）样本k 阶原点矩 ,2,1,11==∑=k X n A n i ki k ；（5）样本k 阶中心矩 ,2,1,)(11=-=∑=k X X n B k ni i k .2、经验分布函数设n x x x ,,,21 是总体X 的一组观察值将它们按大小顺序排列为：**2*1n x x x ≤≤≤ ，称它为顺序统计量.则称⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<=+**1**2*1*1,1,,1,0)(nk k n x x x x x nkx x x n x x x F 为经验分布函数（或样本分布函数）. 3、一些常用统计量的分布（1）2χ分布设)1,0(~N X ，n X X X ,,,21 是X 的一个样本，则统计量∑==ni i X 122χ服从自由度为n 的2χ分布，记作)(~22n χχ.（2）t 分布设)1,0(~N X ，)(~2n Y χ，且Y X ,相互独立，则随机变量nY X t /=服从自由度为n 的t 分布，记作)(~n t t .t 分布又称为学生分布.（3）F 分布设)(~12n X χ，)(~22n Y χ，且Y X ,相互独立，则随机变量21//n Y n X F =服从自由度为),(21n n 的F 分布，记作),(~21n n F F . 4、正态总体统计量的分布设),(~2σμN X ，n X X X ,,,21 是X 的一个样本，则（1）样本均值X 服从正态分布，有),(~2nN X σμ或)1,0(~/2N nX U σμ-=；（2）样本方差)1(~)1(222--n S n χσ；（3）统计量)1(~/--n t nS X μ.设),(~),,(~222211σμσμN Y N X ，1,,,21n X X X 是X 的一个样本，2,,,21n Y Y Y 是Y 的一个样本，两者相互独立.则（1）统计量)1,0(~//)()(22212121N n n Y X σσμμ+---；（2）当21σσ=时，统计量)2(~/2/1)()(212121-+⋅+---n n t S n n Y X wμμ，其中2)1()1(21222211-+-+-=n n S n S n S w ；（3）统计量 )1,1(~//2122222121--n n F S S σσ；（4）统计量),(~/)(/)(2112221222112121n n F n n yx n j jn i i⋅--∑∑==σμσμ.第七章参数估计1、参数的点估计及其求法根据总体X 的一个样本来估计参数的真值称为参数的点估计. （1）估计量根据总体X 的一个样本n X X X ,,,21 构造的用其观察值来估计参数θ真值的统计量),,,(ˆ21n X X X θ称为估计量，),,,(ˆ21nx x x θ称为估计值. (2)矩估计法用样本矩作为相应的总体矩估计来求出估计量的方法.其思想是：如果总体中有k 个未知参数，可以用前k 阶样本矩估计相应的前k 阶总体矩，然后利用未知参数与总体矩的函数关系，求出参数的估计量.（3）极大似然估计法设总体X 的密度函数为),(θx p ，其中θ为未知参数， n X X X ,,,21 是取自总体X 的样本，n x x x ,,,21 为一组样本观测值，则总体X 的联合密度函数称为似然函数，记作∏==n i i x p L 1),(θ，取对数 ∑==ni i x p L 1),(ln ln θ，由0ln =θd Ld ，求得似然函数L 的极大值θˆ，即为未知参数θ的极大似然估计.其思想是：在已知总体X 概率分布时，对总体进行n 次观测，得到一个样本，选取概率最大的θ值θˆ作为未知参数θ的真值的估计是最合理的. （4）估计量的优劣标准1）无偏性.设)ˆ(),,,,(ˆˆ21θθθE X X X n=存在，且θθ=)ˆ(E ，则称值θˆ是θ的无偏估计量.否则称为有偏估计量.2）有效性.设1ˆθ和2ˆθ均为参数θ的无偏估计量，如果)ˆ()ˆ(21θθD D <，则称估计量1ˆθ比2ˆθ有效. 3）一致性（相合性）.设θˆ为θ的估计量，θˆ与样本容量n 有关，记为nθθˆˆ=，对于任意给定的0>ε，都有 1}ˆ{lim =<-∞→εθθnn P ，则称θˆ为参数θ的一致估计量.2、参数的区间估计设总体X 的分布);(θx F 中含有未知参数θ，若存在样本的两个函数),,,(21n X X X θ和),,,(21n X X X θ，使对于给定的)10(<<αα，有αθθθ-=<<1}{P ，则随机区间（θθ,）称为参数θ的置信度为α-1的双侧置信区间.若有αθθ-=<1}{P 或αθθ-=<1}{P ，则定义),(∞θ或),(θ-∞为θ的置信度为α-1的单侧置信区间.（1）单个正态总体均值与方差的置信区间（见表7-1）表7-1（2）两个正态总体均值差与方差比的置信区间（见表7-2）表7-2第八章假设检验1、假设检验的基本概念（1）假设检验对总体的分布提出某种假设，然后利用样本所提供的信息，根据概率论的原理对假设作出“接受”还是“拒绝”的判断，这一类统计推断问题统称为假设检验. 假设检验所依据的原则是：小概率事件在一次试验中是不该发生的. （2）两类错误在根据样本作推断时，由于样本的随机性，难免会作出错误的决定.当原假设0H 为真时，而作出拒绝0H 的判断，称为犯第一类错误；当原假设0H 不真时，而作出接受0H 的判断，称为犯第二类错误.控制犯第一类错误的概率不大于一个较小的数)10(<<αα称为检验的显著性水平. （3）假设检验的基本步骤 1）建立原假设0H ；2）根据检验对象，构造合适的统计量；3）求出在假设0H 成立的条件下，该统计量服从的概率分布； 4）选择显著性水平α，确定临界值；5）根据样本值计算统计量的观察值，由此作出接受或拒绝0H 的结论. 2、单个正态总体的假设检验设总体),(~2σμN X .关于均值μ的检验（见表8-1）表8-1（2）关于方差2σ的检验（见表8-2）表8-13、两个正态总体的假设检验设总体),(~211σμN X ，样本容量为1n ；),(~222σμN Y ，样本容量为2n . （1）两个正态总体均值的检验（见表8-3）表8-3（2）两个正态总体方差的检验（见表8-4）。

随机事件与概率的计算知识点总结

随机事件与概率的计算知识点总结随机事件与概率是数学中的重要概念，在许多实际应用中得到广泛的运用。

下面将对随机事件与概率的计算知识点进行总结。

一、随机事件的基本概念随机事件指的是在一定条件下，结果具有不确定性的事件。

随机事件可以用集合论中的概念进行描述，即事件是样本空间中的一个子集。

二、事件的概率计算事件的概率是指某个事件发生的可能性大小。

概率的计算可以通过频率和几何概率方法进行。

1. 频率法频率指的是在重复实验中，某一事件发生的次数与总实验次数之比。

频率法计算概率的基本步骤是：进行大量实验，记录事件发生的次数，然后计算事件发生的频率。

2. 几何概率法几何概率是指事件发生的可能性与样本空间中所有可能事件的比值。

几何概率计算的基本原理是：事件发生的可能性与事件所占的样本空间的面积成正比。

三、常用概率计算公式在概率计算中，有一些常用的公式可以帮助我们计算事件的概率。

1. 事件的互斥与对立事件互斥事件指的是两个事件不能同时发生，对立事件则指的是两个事件中一个事件发生时，另一个事件一定不发生。

对于互斥事件，可以使用加法法则计算概率；对于对立事件，可以使用减法法则计算概率。

2. 事件的独立性与条件概率事件的独立性指的是两个事件的发生与否互不影响，可以独立计算概率。

条件概率指的是在另一个事件已经发生的条件下，某一事件发生的概率。

四、排列与组合的计算在随机事件与概率的计算中，常常需要用到排列与组合的计算方法。

1. 排列排列是指从若干个元素中取出一部分并按照一定的顺序排列的方式。

排列的计算可以使用阶乘的方法进行。

2. 组合组合是指从若干个元素中取出一部分并不考虑顺序的方式。

组合的计算可以使用组合数的方法进行。

五、事件的加法与乘法规则在复杂事件的计算中，我们需要使用事件的加法与乘法规则。

1. 加法规则加法规则指的是对于两个不互斥事件的概率，可以通过将两个事件的概率相加来计算它们的并集概率。

2. 乘法规则乘法规则指的是对于两个独立事件的概率，可以通过将两个事件的概率相乘来计算它们的交集概率。

第一章随机事件及其概率总结

第一章随机事件及其概率总结随机事件是指在一定条件下，可能发生也可能不发生的现象或结果。

在任何随机事件中，我们都可以通过概率来描述它发生的可能性。

概率是一个在0到1之间的数字，表示一些随机事件发生的可能性大小。

以下是关于随机事件及其概率的总结。

1.随机事件的分类随机事件可以分为两类：简单事件和复合事件。

简单事件是指只有一个结果的随机事件，而复合事件是指有多个结果的随机事件。

例如，抛一枚硬币的结果可以是正面或反面，这就是一个简单事件；而抛两枚硬币的结果可以是两个正面、两个反面或一个正面一个反面，这就是一个复合事件。

2.样本空间样本空间是指一些随机事件所有可能结果的集合。

通过样本空间，我们可以计算概率。

例如，抛一枚硬币的样本空间为{正面，反面}，抛两枚硬币的样本空间为{正正，正反，反正，反反}。

3.事件的概率事件的概率是指一些事件发生的可能性大小。

概率可以通过以下公式计算：概率=事件的可能数/样本空间的总数。

例如，抛一枚硬币出现正面的概率为1/2，即0.5；抛两枚硬币出现两个正面的概率为1/4，即0.254.组合事件的概率组合事件是指由两个或多个简单事件组成的事件。

组合事件的概率可以通过以下公式计算：概率=简单事件1的概率×简单事件2的概率×……×简单事件n的概率。

例如，从一副扑克牌中抽出一张红心和一张方块的概率为(26/52)×(13/51)=1/85.互斥事件和对立事件互斥事件是指两个事件不能同时发生的事件。

对立事件是指一个事件的发生排除了另一个事件的发生。

互斥事件的概率可以通过简单事件的概率之和计算；对立事件的概率可以通过1减去事件的概率计算。

6.大数定律大数定律是指随着试验次数的增加，事件的相对频率趋近于事件的概率。

也就是说，如果一个事件的概率为p，那么在进行n次独立的重复试验后，事件发生的频率将会接近于np。

例如，抛1000次硬币，正面出现的频率将会接近于500次。

(完整版)数学随机事件与概率知识点归纳

数学随机事件与概率知识点归纳一、随机事件主要掌握好(三四五)(1)事件的三种运算：并(和)、交(积)、差；注意差A-B可以表示成A与E 的逆的积。

(2)四种运算律：交换律、结合律、分配律、德莫根律。

(3)事件的五种关系：包含、相等、互斥(互不相容)、对立、相互独立。

二、概率定义(1)统计定义：频率稳定在一个数附近，这个数称为事件的概率；(2)古典定义：要求样本空间只有有限个基本事件，每个基本事件出现的可能性相等，则事件A所含基本事件个数与样本空间所含基本事件个数的比称为事件的古典概率；(3)几何概率：样本空间中的元素有无穷多个，每个元素出现的可能性相等，则可以将样本空间看成一个几何图形，事件A看成这个图形的子集，它的概率通过子集图形的大小与样本空间图形的大小的比来计算；(4)公理化定义：满足三条公理的任何从样本空间的子集集合到[0, 1]的映射。

三、概率性质与公式(1)加法公式：P(A+B)=p(A)+P(B)-P(AB),特别地，如果A与B互不相容，则P(A+B)=P(A)+P(B);(2)差：P(A-B)=P(A)-P(AB)，特别地，如果B包含于A,贝U P(A-B)=P(A)-P(B);(3)乘法公式：P(AB)=P(A)P(B|A)或P(AB)=P(A|B)P(B)，特别地，如果A 与B相互独立，则P(AB)=P(A)P(B);(4)全概率公式：P(B)=刀P(Ai)P(B|Ai).它是由因求果，贝叶斯公式：P(Aj|B)=P(Aj)P(B|Aj)/ 刀P(Ai)P(B|Ai). 它是由果索因；如果一个事件E可以在多种情形(原因) A1,A2,....,A n 下发生，则用全概率公式求E发生的概率；如果事件E已经发生，要求它是由A j引起的概率，则用贝叶斯公式.(5)二项概率公式：Pn(k)=C(n,k)pAk(1-pF(n-k),k=0,1,2,•…,n.当一个问题可以看成n重贝努力试验(三个条件：n次重复，每次只有A与A的逆可能发生，各次试验结果相互独立)时，要考虑二项概率公式.。

随机事件及其概率知识点整理

随机事件及其概率知识点整理1. 什么是随机事件？随机事件是指在某个试验或观察中，可能发生或不发生的事件。

例如，抛一枚硬币，正面朝上和反面朝上都是可能的结果。

2. 随机事件的分类随机事件可以分为互斥事件和非互斥事件。

- 互斥事件：两个事件不能同时发生。

例如，抛硬币时，正面和反面是互斥事件。

- 非互斥事件：两个事件可以同时发生。

例如，掷骰子时，得到奇数和得到小于等于3的数是非互斥事件。

3. 概率的定义概率是用来描述随机事件发生可能性的数值。

概率的范围在0到1之间，其中0表示不可能事件，1表示必然事件。

4. 概率的计算方法根据事件的性质和条件，可以使用以下概率计算方法：- 经典概率：对于等可能的事件，经典概率可以通过事件的数量比上总的可能性数量来计算。

- 相对频率概率：通过观察事实事件发生的频率来计算概率。

- 主观概率：基于主观估计和判断来计算概率。

5. 概率的性质概率具有一些重要的性质，包括：- 加法法则：对于互斥事件，概率可以通过事件的概率求和来计算。

- 乘法法则：对于独立事件，概率可以通过事件的概率相乘来计算。

6. 条件概率条件概率是指在已知某一事件发生的条件下，另一个事件发生的概率。

条件概率可以通过将事件的交集概率除以条件事件的概率来计算。

7. 贝叶斯定理贝叶斯定理是用于计算逆条件概率的定理。

它通过已知条件发生的条件下，计算另一个事件发生的概率。

8. 期望值期望值是一个随机变量可能取值的加权平均值。

它可以通过将每个可能值乘以其概率，然后求和来计算。

以上是对随机事件及其概率知识点的简要整理，希望能对您有所帮助。

如有更多问题，请随时提问。

随机事件的概率知识点总结

随机事件的概率知识点总结事件的分类 1、确定事件必然发生的事件：当A 是必然发生的事件时，P （A ）=1 不可能发生的事件：当A 是不可能发生的事件时，P （A ）=0 2、随机事件：当A 是可能发生的事件时，０＜P （A ）＜１概率的意义一般地，在大量重复试验中，如果事件A 发生的频率mn会稳定在某个常数p 附近，那么这个常数p 就叫做事件A 的概率。

概率的表示方法一般地，事件用英文大写字母A ，B ，C ，…，表示事件A 的概率p ，可记为P （A ）=P 概率的求解方法１．利用频率估算法：大量重复试验中，事件A 发生的频率mn会稳定在某个常数p 附近，那么这个常数p 就叫做事件A 的概率（有些时候用计算出Ａ发生的所有频率的平均值作为其概率）．２．狭义定义法：如果在一次试验中，有n 种可能的结果，并且它们发生的可能性都相等，考察事件A 包含其中的m 中结果，那么事件A 发生的概率为P （A ）=nm３．列表法：当一次试验要设计两个因素，可能出现的结果数目较多时，为不重不漏地列出所有可能的结果，通常采用列表法．其中一个因素作为行标，另一个因素作为列标．特别注意放回去与不放回去的列表法的不同．如：一只箱子中有三张卡片，上面分别是数字１、２、３，第一抽出一张后再放回去再抽第二次，两次抽到数字为数字１和２或者２和１的概率是多少？若不放回去，两次抽到数字为数字１和２或者２和１的概率是多少？放回去 P （１和２）=92 不放回去P （１和２）=62(3,3)(3,2)(3,1)3(2,3)(2,2)(2,1)2(1,3)(1,2)(1,1)1第一次结果321第二次(3,2)(3,1)3(2,3)(2,1)2(1,3)(1,2)1第一次结果321第二次４．树状图法：当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．注意：求概率的一个重要技巧：求某一事件的概率较难时，可先求其余事件的概率或考虑其反面的概率再用１减——即正难则反易．概率的实际意义对随机事件发生的可能性的大小即计算其概率．一方面要评判一些游戏规则对参与游戏者是否公平，就是要看各事件发生概率．另一方面通过对概率的学习让我们更加理智的对待一些买彩票抽奖活动．。

(完整版),概率论公式总结,推荐文档

P( Ai Aj Ak ) (1)n1 P( A1 A2 An )
i 1
i 1
1i jn
1i jk n
3．条件概率 PB A P(AB) 乘法公式 P(AB) P(A)PB A (P(A) 0) P( A)
P( A1 A2 An ) P( A1 )P A2 A1 P An A1 A2 An1
(P( A1 A2 An1 ) 0)
n
全概率公式 P(A) P(ABi ) i 1
n
P(Bi ) P( A
i 1
Bi ) Bayes 公式 P(Bk
A) P( ABk ) P( A)
P(Bk )P( A Bk ) n P(Bi )P( A Bi ) i 1
4．随机变量及其分布
分布函数计算 P(a X b) P(X b) P(X a)
f (x, y)dx
fY X ( y x) f X (x)dx
fX Y (x y)
f (x, y) fY ( y)
fY X ( y x) fX (x) fY ( y)
fY X ( y x)
f (x, y) fX (x)
fX Y (x y) fY ( y) fX (x)
10. 随机变量的数字特征
E ( X E( X ))k (Y E(Y ))l
E(X kY l )
X ,Y 的 k + l 阶混合中心矩
X ,Y 的二阶混合原点矩 E(XY ) X ,Y 的二阶混合中心矩 X ,Y 的协方差 E( X E( X ))(Y E(Y ))
X ,Y 的相关系数
E
(X
E( X ))(Y E(Y D( X ) D(Y )
f (x, v)dv
8. 连续型二维随机变量 (1) 区域 G 上的均匀分布，U ( G )

概率论与数理统计期末复习知识点

fZ(z)
f (z y, y)dy
f (x, z x)dx
当X 和Y 相互独立:卷积公式
fZ (z) f X ( x) fY (z x)dx
f X (z y) fY ( y)dy
(2) 当X 和Y 相互独立时:
M = max(X,Y ) 的分布函数
Fmax(z) P{M z} FX (z)FY (z)
E(Y ) E[g( X )] g( xk )pk k 1
(1-3)设( X,Y ) 离散型随机变量. 分布律为：
P{X xi , Y y j } pij i, j 1,2,
若 Z=g(X,Y)（g为二元连续函数）
则 E(Z ) E[g( X ,Y )]
g( xi , y j )pij
(2) 连续型随机变量的分布函数的定义
x
F ( x) f (t)dt
f(x)的性质
1. f (x) 0
2. f ( x)dx 1
3. P{x1 X x2}
x2 f ( x)dx
x1
4. F( x) f ( x)，在f ( x)的连续点.
⁂ 三种重要的连续型随机变量
(一)均匀分布
pi1
p•1
pi2
p•2
pij pi•
p• j 1
性质：
1 0 pij 1
2
pij 1.
j 1 i1
2.边缘分布律
3. 独立性
pij pi• p• j , ( i, j 1,2, )
4.分布函数 ( x, y) R2
F ( x, y) pij xi x yjy
n
n
则
Ai Ai
Ai Ai
i 1

(完整word版)概率公式总结

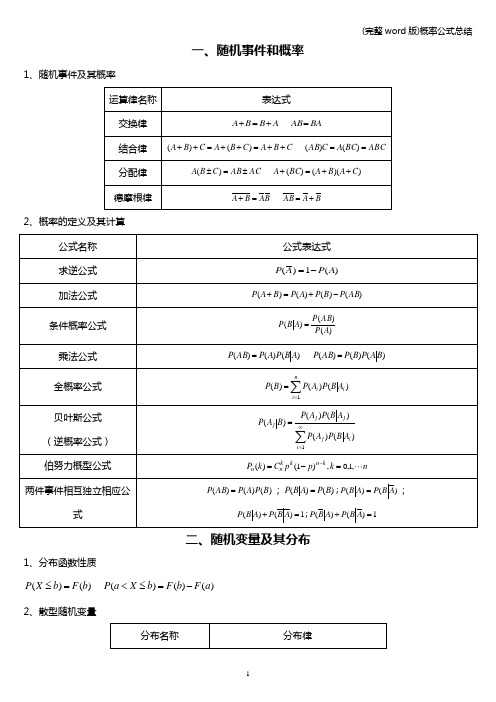
一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质)()(b F b X P =≤ )()()(a F b F b X a P -=≤< 2、散型随机变量3、续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布∑∑======⋅jjijjii i py Y x X P x X P p ),()(∑∑======⋅iiijjij j py Y x X P y Y P p ),()(2、离散型二维随机变量条件分布2,1,)(),()(=========⋅i P p y Y P y Y x X P y Y x X P p j ij j j i j i j i2,1,)(),()(=========⋅j P p x X P y Y x X P x X y Y P p i ij i j i i j i j3、连续型二维随机变量( X ,Y ）的分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),(4、连续型二维随机变量边缘分布函数与边缘密度函数分布函数：⎰⎰∞-+∞∞-=x X dvdu v u f x F ),()( 密度函数：⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=yY dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(5、二维随机变量的条件分布+∞<<-∞=y x f y x f x y f X X Y ,)(),()( +∞<<-∞=x y f y x f y x f Y Y X ,)(),()( 四、随机变量的数字特征1、数学期望离散型随机变量：∑+∞==1)(k k k p x X E 连续型随机变量：⎰+∞∞-=dx x xf X E )()(2、数学期望的性质(1)为常数C ,)(C C E = )()]([X E X E E = )()(X CE CX E =(2))()()(Y E X E Y X E ±=± b X aE b aX E ±=±)()( )()()(1111n n n n X E C X E C X C X C E +=+ (3)若XY 相互独立则:)()()(Y E X E XY E = (4))()()]([222Y E X E XY E ≤ 3、方差：)()()(22X E X E X D -= 4、方差的性质(1)0)(=C D 0)]([=X D D )()(2X D a b aX D =± 2)()(C X E X D -<(2)),(2)()()(Y X Cov Y D X D Y X D ±+=± 若XY 相互独立则：)()()(Y D X D Y X D +=± 5、协方差：)()(),(),(Y E X E Y X E Y X Cov -= 若XY 相互独立则：0),(=Y X Cov 6、相关系数：)()(),(),(Y D X D Y X Cov Y X XY ==ρρ 若XY 相互独立则：0=XY ρ即XY 不相关7、协方差和相关系数的性质(1))(),(X D X X Cov = ),(),(X Y Cov Y X Cov =(2)),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+ ),(),(Y X abCov d bY c aX Cov =++ 8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ξ有2)(})({ξξX D X E X P ≤≥-或2)(1})({ξξX D X E X P -≥<-2、大数定律：若n X X 1相互独立且∞→n 时，∑∑==−→−ni iDni i X E nX n11)(11（1）若n X X 1相互独立，2)(,)(i i i i X D X E σμ==且M i ≤2σ则：∑∑==∞→−→−ni iPni i n X E nX n11)(),(11(2）若n X X 1相互独立同分布，且i i X E μ=)(则当∞→n 时：μ−→−∑=Pn i i X n 113、中心极限定理（1）独立同分布的中心极限定理：均值为μ，方差为02>σ的独立同分布时，当n 充分大时有：)1,0(~1N n n XY nk kn −→−-=∑=σμ(2)拉普拉斯定理：随机变量),(~)2,1(p n B n n =η则对任意x 有： ⎰∞--+∞→Φ==≤--xt n x x dtex p np npP )(21})1({lim 22πη(3)近似计算：)()()()(11σμσμσμσμσμn n a n n b n n b n n Xn n a P b Xa P nk knk k-Φ--Φ≈-≤-≤-=≤≤∑∑==六、数理统计1、总体和样本总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k nk n x F x x x F =∏=2、统计量（1)样本平均值：∑==ni i X nX 11(2）样本方差：∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11（3）样本标准差:∑=--=ni i X X n S 12)(11（4）样本k 阶原点距： 2,1,11==∑=kXn A ni ki k（5)样本k 阶中心距：∑==-==ni k ik k k X XnM B 13,2,)(1（6）次序统计量：设样本),(21n X X X 的观察值),(21n x x x ，将n x x x 21,按照由小到大的次序重新排列，得到)()2()1(n x x x ≤≤≤ ，记取值为)(i x 的样本分量为)(i X ，则称)()2()1(n X X X ≤≤≤ 为样本),(21n X X X 的次序统计量。

(完整word版)概率统计公式大全

如果同时有，，则称事件A与事件B等价，或称A等于B：A=B。
A、B中至少有一个发生的事件：A B，或者A+B。
属于A而不属于B的部分所构成的事件，称为A与B的差，记为A-B，也可表示为A-AB或者，它表示A发生而B不发生的事件。
A、B同时发生：A B，或者AB。A B=Φ，则表示A与B不可能同时发生，称事件A与事件B互不相容或者互斥。基本事件是互不相容的。
1° ,
2° ,
3° ,
4° 。
（3）
离散与连续型随机变量的关系
积分元在连续型随机变量理论中所起的作用与在离散型随机变量理论中所起的作用相类似。
（4）
若事件、相互独立，且，则有
若事件，相互独立，则可得到与，与，与也都相互独立。
必然事件和不可能事件Φ与任何事件都相互独立。
Φ与任何事件都互斥。
②多个事件的独立性
设A，B，C是三个事件，如果满足两两独立的条件，
P(AB)=P(A)P(B)；P(BC)=P(B)P(C)；P(CA)=P(C)P(A)
1° 0≤P(A)≤1，
2° P(Ω) =1
3° 对于两两互不相容的事件，，…有
常称为可列（完全）可加性。
则称P(A)为事件的概率。
（8）
古典概型
1° ，
2° 。
设任一事件，它是由组成的，则有
P(A)=P =
（9）
几何概型
若随机试验的结果为无限不可数并且每个结果出现的可能性均匀，同时样本空间中的每一个基本事件可以使用一个有界区域来描述，则称此随机试验为几何概型。对任一事件A，
条件概率是概率的一种，所有概率的性质都适合于条件概率。
例如：P(Ω/B)=1 P( /A)=1-P(B/A)