专题训练(二) 平行线与“拐点”模型(优秀经典公开课比赛课件)
平行线中的几何探究--'拐点'问题(优秀课件)

再见!
华东师大版七年级上册第五章《相交线与平行线》
知识奠基
对顶角、邻补角
相
交
线
垂线及直角
平
判定
行
线
性质
找找感觉
1.如图,AB∥EF,CD⊥EF于点D.若 ∠ABC=40°,则∠BCD的度数为(130°)
引入探究
如图,AB∥CD,探讨下面四个图形中∠APC与 ∠PAB,∠PCD的数量关系.
探究1:自主探究
探究2:深入探究
如图,AB∥CD,在下面图形中,选择一个探 讨∠APC与∠PAB,∠PCD的数量关系.
小组汇报
如图,AB∥CD,你选择哪一个图形探讨∠APC与∠PAB, ∠PCD的数量关系.
方法小结
图形中探讨角的数量关系,方法或思想上有什么共同点?
寻找(构造)角所在的基本图形,通过基本图形中的数量关系, 实现角的等量转化。
【升华感觉】
1、如图1,已知a∥b,∠1=130°,∠2=90°,则 ∠3=_______.
(图1)
(图2)
2、如图2,将两张长方形纸片如图摆放,使其中一张 纸片的一个顶点恰好落在另一张纸片的一条边上,则 ∠1+∠2=________.
【升华感觉】
3、如图3,已知AB∥ED,∠B=58°,∠C=35°,则∠D 的度数为 .
(2)如图②,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+ ∠7还有类似的数量关系吗?若有,请直接写出,并将它们推广 到一般情况,用一句话写出你的结论.
【课后延伸】
2.如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,P为直线l3上 一点,A、B分别是直线l1、l2上的不动点.其中PA与l1相交为∠1,PA、 PB相交为∠2,PB与l2相交为∠3. (1)若P点在线段CD(C、D两点除外)上运动,问∠1、∠2、∠3之间 的关系是什么?这种关系是否变化? (2)若P点在线段CD之外时,∠1、∠2、∠3之间的关系有怎样?说明理 由.
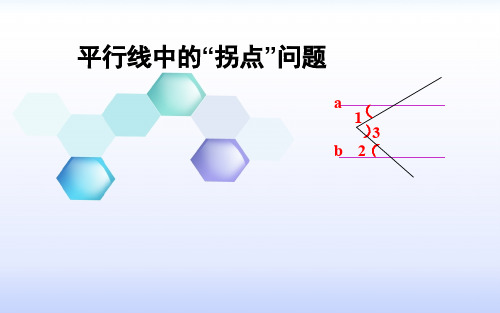
平行线中的拐点(拐角)问题专题

证明: 过点E作EF,使得EF∥AB
B
A
∵AB∥CD
1
F
E
∴EF∥CD
2
∴∠A+∠1=180°,∠C+∠2=180°
D
C
∵∠1+∠2=∠AEC ∴∠A+∠C+∠AEC=∠A+∠1+∠C+∠2=360°
②已知:∠AEC+∠A+∠C=360°,结论:AB∥CD
B
A 证明: 过点E作EF,使得EF∥AB
∴∠A=∠1
E1
F
2
∵∠AEC=∠1+∠2 ,且∠AEC=∠A+∠C ∴∠2=∠C
D
C
∴EF∥CD
∴AB∥CD
模型1:平行线间的“M”模型(猪手)
模型1:平行线间的“M”模型(猪手)
模型1:平行线间的“M”模型(猪手)
模型2:平行线间的“铅笔”模型(子弹头)
B
A
证明: 过点E作EF,使得EF∥AB
∵AB∥CD
D
C
∴EF∥CD
E
F ∴∠A=∠AEF,∠C=∠CEF ∵∠AEC=∠CEF-∠AEF
∴∠AEC=∠C-∠A
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
第二章 相交线与平行线
平行线中的拐点问题
模型1:平行线间的“M”模型(猪手)
①已知:AB∥CD,结论:∠AEC=∠A+∠C
B
A 证明: 过点E作EF,使得EF∥AB
七年级下册数学课件:平行线中的拐点问题

∴∠A=∠AEC+∠C
C
D
思考3:你能类比之前的构造辅助线的方法,想到其他证明方法吗?
新课授知
思考3:你能类比之前的构造辅助线的方法,想到其他证明方法吗?
E
解:延长EA交CD于点
∵AB//CD
∴∠AFD=∠EAB
∵∠AEC+∠C+∠EFC=180°
A
B
∵∠AFD+∠EFC=180°
∴∠AFD=∠AEC+∠C
拓展探索
思考2:还有其他方法吗?
A
B
A
1 E
F 2
C
E
2
D
13
F
C
A
B
B
1 2
E3
D
4 5
D
C
拓展探索
2、如图,AB∥CD,试求∠A、∠AEF、∠EFC、∠C有何关系?
A
B
E
M
F
N
C
D
新课授知
二、猪蹄型
3.如图,已知:AB∥CD,点E是平面内一点,那么∠AEC与∠A、 ∠C之间的数量关系是什么呢?
2023最新整理收集 do something
课题:5.3.3平行线中的拐点问题
复习回顾
两线 四角
相 交 线
三线 八角
一般情况
邻补角 对顶角
邻补角互补 对顶角相等
特殊
垂线
存在性和唯一性 垂线段最短 点到直线的距离
同位角 内错角 同旁内角
平
行 线
平行公理及其推论
平行线的判定 平行线的性质
典例探究
例1:已知如图,AB//CD;若线段AC是拉直的橡皮筋,在AC上任取一点E, 若向不同的方向拉动点E,动点E与两平行线的位置有哪几种?∠A,∠C, ∠AEC之间有何关系呢?
平行线中的“拐点”问题 优课教学课件
A
B
P
C
D
9
知识点二:‘凹’进去的模型
学以致用
2、如图,有一块含有45°角的三角尺放在直尺上,如果
∠2=20°,那么∠1= 25°。
1 2
10
知识点三:“猪手图”模型
新知究
F
1
1
解:过点P作PF∥AB,则PF∥CD(
)
∴∠CPF+∠C=180°∠1+∠A=180°( )
∴∠CPF=180°-∠C ,∠1=180°-∠A
A
B
解:过点E作EF//AB ∵AB//CD,EF//AB(已知)
1
E2
F
∴ CD // EF 。(平行于同一直线的两直线平行) C
D
∴∠A+∠1 =180o,∠C+∠2 =180o(两直线平行,同旁内角互补)
又∵∠A=100°,∠C=110°(已知)
∴ ∠ 1 = 80 °, ∠2 =70 ° (等量代换)
b2
判定:已知角的关系得平行的关系. 性质:已知平行的关系得角的关系.
平行线的判定与性质的关系图
判定 同位角相等
性质 同位角相等
内错角相等
两直线平行 内错角相等
同旁内角互补
同旁内角互补
(数量关系) (位置关系) (数量关系)
数形转化
学习目标
1.熟练运用平行线的判定与性质探究关于“ 拐点”问题的常规解法;
学以致用
例3:已知AB∥CD,∠ABE和∠CDE的平 110°
分线相交于F,∠E = 140º,则∠F= 。(1) 由基本图形二,你能得到∠F与∠1+∠3的关系吗? (2)由基本图形一,你能得到∠ABE+∠CDE的值吗? (3)由BF和DF分别平分∠ABE和∠CDE,你能得到
课件七年级数学人教版下册平行线中的拐点(拐角)问题专题

∴A.∠A1E2C0°=∠C-∠BA.130° C.140° D.150°
83.如图,所直示线,a若∥AbB,∥则CD∠,AB则D∠的A度,数∠D是,(∠E之)间的度数关系是( )
3(.3)如图利所用示上,述若结论AB解∥决CD问,题则:∠如A,图∠④D,,A∠BE∥之C间D,的∠度A数BE关和系∠是CD(E的平)分线相交于点F,∠E=140°,求∠BFD的度数.
10.如图,桌面上有木条b、c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
过点E作EF,使得EF∥AB
如图②,MA1∥NA3,则∠A1+∠A2+∠A3=
,请你说明理由;
3.如图所示,若AB∥CD,则∠A,∠D,∠E之间的度数关系是( )
A.72° B.68° C.63° D.18°
(A.2)340如°.图③如,BM.图A315∥°,NA4A,CD则.∠∥4A01°C+∠BA2+,D∠.A34∠+5∠°DA4==43°; ,∠B=25°,则∠DEB的度数为(
)
7.如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
如图AB∥CD,∠1=140°,∠2=90°,则∠3的度数是( )
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
小结
问题1:关于平行线中“拐角”问题,如何添加辅助线? 问题2:如何寻找动角之间的数量关系?
课后检测
1.如图,已知AB∥DE,∠B=20°,∠D=130°,那么∠BCD等于( ) A.60° B.70° C.80° D.90° 2.如图AB∥CD,∠1=140°,∠2=90°,则∠3的度数是( )
模型2:平行线间的“铅笔”模型(子弹头)
平行线与拐点问题公开课获奖课件百校联赛一等奖课件

教材母题(教材P23第7(2)题)
假如AB∥CD∥EF, 那么∠BAC+∠ACE+∠CEF=( )
(A)180°(B)270°(C)360°(D)540°
A
B
C
D
E
F
措施指导
(1)铅笔型
如图1,已知:AB∥CD,点E是平 面内一点,那么∠BED与∠B、∠D之 间旳数量关系是什么呢?
B
G
F
E
H
C
D
解:过点E作EG∥AB,过点F作FH∥AB, ∵AB∥CD ∴AB||CD||EG||FH ∴∠A=∠1,∠2=∠3,∠4=∠D ∴∠A+∠3+∠4=∠1+∠2+∠D ∴∠A+∠EFD=∠AEF+∠D
若左边有n个角,右边有m个角;你能找到规律吗?
A
F1 F2 Fn
B E1
E2
Em
C
D
①点在两平行线之间
A
B
E
C
D
图1
②点在两平行线之外
E
A
B
A
B
C 图3
D
C
D
图4 E
A
C
图2
B E
D
E
A
A
B
B
C
D
图5
C
D
图6
E
措施指导
(2)燕尾型(或M型) 如图2,已知:AB∥CD,点E是平面内
一点,那么∠BED与∠B、∠D之间旳数量 关系是什么呢?
A
B
E
C
图1
专题02 平行线中的拐点模型之铅笔头模型(解析版)

专题02 平行线中的拐点模型之铅笔头模型平行线中的拐点模型在初中数学几何模块中属于基础工具类问题,也是学生必须掌握的一块内容,熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题就平行线中的拐点模型(铅笔头模型)进行梳理及对应试题分析,方便掌握。
拐点(平行线)模型的核心是一组平行线与一个点,然后把点与两条线分别连起来,就构成了拐点模型,这个点叫做拐点,两条线的夹角叫做拐角。
通用解法:见拐点作平行线;基本思路:和差拆分与等角转化。
模型2:铅笔头模型图1 图2 图3如图1,①已知:AM∥BN,结论:∠1+∠2+∠3=360°;②已知:∠1+∠2+∠3=360°,结论:AM∥BN.如图2,已知:AM∥BN,结论:∠1+∠2+∠3+∠4=540°如图3,已知:AM∥BN,结论:∠1+∠2+…+∠n=(n-1)180°.【模型证明】在图1中,过P作AM的平行线PQ,∵AM∥BN,∴PQ∥BN,∴∠1+∠APQ=180°,∠3+∠BPQ=180°,∴∠1+∠2+∠3=360°;在图2中,过P1作AM的平行线P1C,过点P2作AM的平行线P2D,∵AM∥BN,∴AM∥P1C∥P2D∥BN,∴∠1+∠AP1C=180°,∠P2P1C+∠P1P2D=180°,∠BP2D+∠4=180°,∴∠1+∠2+∠3+∠4=540°;在图3中,过各角的顶点依次作AB的平行线,根据两直线平行,同旁内角互补以及上述规律可得:∠1+∠2+∠3+…+∠n=(n﹣1)180°.例1.(2023·江苏南通·校考二模)如图,已知//AB CD ,140A Ð=°,120E Ð=°,则C Ð的度数是( )A .80°B .120°C .100°D .140°【答案】C 【分析】过E 作直线MN //AB ,根据两直线平行,同旁内角互补即可求出∠1,进而可求出∠2,然后根据平行于同一条直线的两直线平行可得MN //CD ,根据平行线性质从而求出∠C .【详解】解:过E 作直线MN //AB ,如下图所示,∵MN //AB ,∴∠A +∠1=180°(两直线平行,同旁内角互补),∴∠1=180°﹣∠A =180°﹣140°=40°,∵12120AEC Ð=Ð+Ð=°,∴211204080AEC Ð=Ð-Ð=°-°=°∵MN //AB ,AB //CD ,∴MN //CD ,∴∠C +∠2=180°(两直线平行,同旁内角互补),∴∠C =180°﹣∠2=180°﹣80°=100°,故选:C .【点睛】此题考查的是平行线的判定及性质,掌握构造平行线的方法是解决此题的关键.例 2.(2023·山西吕梁·校联考模拟预测)如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.若132Ð=°,262Ð=°,则3Ð的度数为( )A .118°B .148°C .150°D .162°【答案】C 【分析】过点B 作BA ∥工作篮底部,根据平行线的性质及角的和差求解即可.【详解】解:如图,过点B 作BA ∥工作篮底部,3180MBA \Ð+Ð=°,Q 工作篮底部与支撑平台平行,BA ∥工作篮底部BA \∥支撑平台,132ABN \Ð=Ð=°,2ABN MBA Ð=Ð+ÐQ ,262Ð=°,30MBA \Ð=°,3150\Ð=°,故选:C .【点睛】此题考查了平行线的性质,熟记“两直线平行,内错角相等”、“两直线平行,同旁内角互补”是解题的关键.例3.(2023下·江苏·七年级专题练习)如图,AB //ED ,α=∠A +∠E , β=∠B +∠C +∠D ,则β与α的数量关系是( )A .2β=3αB .β=2αC .2β=5αD .β=3α【答案】B 【分析】作CF //ED ,利用平行线的性质求得β与α,再判断β与α的数量关系即可.【详解】解:如图,作CF //ED , ∵AB //ED ,∴∠A +∠E =180°= α ,∵ED //CF , ∴∠D +∠DCF =180°,∵AB //ED ,ED //CF ,∴AB //CF ,∴∠B +∠BCF =180°,∴∠D +∠DCF +∠B +∠BCF =180°+180° 即 ∠B +∠C +∠D =360°= β , ∴ β=2α . 故选B .【点睛】本题考查了平行线的性质,熟悉运用平行线的性质是解题的关键.例4.(2023下·广西南宁·七年级校考期末)如图,如果AB EF ∥,那么ABC BCD CDE DEF Ð+Ð+Ð+Ð=A .270°B .360°【答案】C 【分析】利用平行线的性质,结合所作的辅助线,可以得出答案.【详解】解:过点C 作CM AB ∥∵AB EF ∥,∴AB CM DN EF ∥∥∥,∴1180ABC Ð+Ð=°,23180Ð+Ð=°,Ð∴540ABC BCD CDE DEF Ð+Ð+Ð+Ð=【点睛】本题考查了平行线的性质及判定的相关知识点,掌握知识点是解答此题的关键.例5.(2023下·湖北武汉·七年级期末)如图,【答案】60°/60度【分析】根据平角定义可求出,∴180ABC BCM Ð+Ð=°,180MCF EFC +Ð=°,BCM Ð∴360ABC FCB EFC Ð+Ð+а,∵120FCB Ð=°,∴360360ABC EFC FCB Ð=-Ð=°-∵14ABP ABC Ð=Ð, 14EFP EFC Ð=Ð,A .2360P Q Ð+Ð=°B .2【答案】A 【分析】过点P 作PM AB ∥,EPM AEP FPM CFP Ð=ÐÐ=Ð进而得到12EQF Ð=Ð+Ð,再由角平分线的定义可得()2122PEB PFD EQF Ð+Ð=Ð+Ð=Ð,即可求解.【详解】解:如图,过点P 作PM AB ∥,过点Q 作QN AB ∥,∵AB CD P ,∴PM AB CD QN ∥∥∥,∴,EPM AEP FPM CFP Ð=ÐÐ=Ð,1,2EQN FQN Ð=ÐÐ=Ð,180,180PEB EPM PFD FPM Ð+Ð=°Ð+Ð=°,∴12EQF Ð=Ð+Ð,∵PEB Ð和PFD Ð的平分线交于点Q ,∴21,22PEB PFD Ð=ÐÐ=Ð,∴()()21222PEB PFD EQN FQN EQF Ð+Ð=Ð+Ð=Ð+Ð=Ð,∵180,180PEB EPM PFD FPM Ð+Ð=°Ð+Ð=°,∴2360EPF EQF AEP CFP PEB PFD Ð+Ð=Ð+Ð+Ð+Ð=°.故选:A .【点睛】本题考查了平行线的性质,平行公理的推论,角平分线的定义,熟练掌握平行线的性质是解题的关键.例7.(2023下·江苏南京·七年级统考期中)从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解.(1)如图1,AB CD ∥,点E 为AB 、CD 之间的一点.求证:12360MEN Ð+Ð+Ð=°.(2)如图2,AB CD ∥,点E 、F 、G 、H 为AB 、CD 之间的四点.则123456Ð+Ð+Ð+Ð+Ð+Ð=______.(3)如图3,AB CD ∥,则123n Ð+Ð+Ð++Ð=L ______.【答案】(1)证明见详解;(2)900°;(3)()1801°-n ;【分析】(1)过点E 作OE ∥A B ,可得OE AB CD ∥∥,根据平行线的性质可得1180MEO Ð+Ð=°,2180OEN Ð+Ð=°,再计算角度和即可证明;(2)分别过点E 、F 、G 、H 作AB 的平行线,在两相邻平行线间利用两直线平行同旁内角互补求得两角度和后,再将所有角度相加即可解答;(3)由(2)解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和,结合图3找出n 和线段条数的关系便可解答;【详解】(1)证明:如下图,过点E 作OE ∥A B ,∵AB CD ∥,OE ∥A B ,∴P OE CD ,根据两直线平行同旁内角互补可得:1180MEO Ð+Ð=°,2180OEN Ð+Ð=°,∴12360MEO OEN Ð+Ð+Ð+Ð=°,∴12360MEN Ð+Ð+Ð=°;(2)解:如下图,分别过点E 、F 、G 、H 作1O E AB ∥,2O F AB ∥,3O G AB ∥,4O H AB ∥,结合(1)解答在两相邻平行线间可得:1180AME MEO Ð+Ð=°,12180O EF EFO Ð+Ð=°,23180O FG FGO Ð+Ð=°,34180O GH GHO Ð+Ð=°,4180O HN HNC Ð+Ð=°,将所有角度相加可得:1234561805900Ð+Ð+Ð+Ð+Ð+Ð=°´=°;(3)解:由(2)解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和,由图3可知:当AB 、CD 之间有2条线段时,3n =,当AB 、CD 之间有3条线段时,4n =,当AB 、CD 之间有4条线段时,5n =,当AB 、CD 之间有5条线段时,6n =,…,当AB 、CD 之间有()1n -条线段时,n n =,∴()1231801n n Ð+Ð+Ð++Ð=°-L ;【点睛】本题考查了平行线公理的推论,平行线的性质,归纳总结的解题思路,通过作辅助线将角度按组计算是解题关键.例8.(2023下·江苏苏州·七年级校考期中)当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等例如:在图①、图中②,都有12Ð=Ð,3=4ÐÐ,设镜子AB 与BC 的夹角αABC Ð=.(1)如图①,若α90=°,判断入射光线EF 与反射光线GH 的位置关系,并说明理由.(2)如图②,若90α180°<<°,入射光线EF 与反射光线GH 的夹角βFMH Ð=,探索α与β的数量关系,并说明理由.(3)如图③,若α120=°,设镜子CD 与BC 的夹角γ(90γ180)BCD Ð=°<<°,入射光线EF 与镜面AB 的夹角1(090)m m Ð=°<<°,已知入射光线EF 从镜面AB 开始反射,经过(n n 为正整数,且3)n £次反射,当第n 次反射光线与入射光线EF 平行时,请直接写出γ的度数(可用含有m 的代数式表示).【答案】(1)EF GH ∥,见解析(2)2180b a =-°,见解析(3)90m °+或150°【分析】(1)在BEG V 中,23α180ÐÐ++=°,α90=°,可得2390Ð+Ð=°,根据入射光线、反射光线与镜面所夹的角对应相等可得,180FEG EGH Ð+Ð=°,进而可得//EF GH ;(2)在BEG V 中,23α180ÐÐ++=°,可得23180αÐÐ+=°-,根据入射光线、反射光线与镜面所夹的角对应相等可得,22MEG ÐÐ=,23MGE ÐÐ=,在MEG V 中,β180MEG MGE ÐÐ++=°,可得α与β的数量关系;(3)分两种情况画图讨论:①当3n =时,根据入射光线、反射光线与镜面所夹的角对应相等,及GCH △内角和,可得γ90.m =°+②当2n =时,如果在BC 边反射后与EF 平行,则α90=°,与题意不符;则只能在CD 边反射后与EF 平行,根据三角形内角和定理推出,可得γ60G Ð=-°,由EF HK ∥,且由(1)的结论可得,γ150=°.【详解】(1)EF GH ∥,理由如下:在BEG V 中,23α180ÐÐ++=°,α90=°,2390\Ð+Ð=°,12Ð=ÐQ ,3=4ÐÐ,1234180Ð+Ð+Ð+Ð=\°,12180FEG ÐÐÐ++=°Q ,34180EGH ÐÐÐ++=°,180FEG EGH \Ð+Ð=°,EF GH \∥;(2)β2α180=-°,理由如下:在BEG V 中,23α180ÐÐ++=°,23180αÐÐ\+=°-,12Ð=ÐQ ,1MEB Ð=Ð,2\Ð=ÐMEB ,22\Ð=ÐMEG ,同理可得,23MGE ÐÐ=,在MEG V 中,β180MEG MGE ÐÐ++=°,()β180MEG MGE ÐÐ\=°-+()1802223ÐÐ=°-+()180223ÐÐ=°-+()1802180α=°-°-2α180=-°;1BEG m ÐÐ==Q ,18012060BGE CGH m m ÐÐ\==°-°-=°-,180211802FEG m ÐÐ\=°-=°-(1802180260EGH BGE Ð=°-=°-°EF HK Q ∥,360FEG EGH GHK \Ð+Ð+=°,则120GHK Ð=°,则30GHC Ð=,由GCH △内角和得γ90m =°+.②当2n =时,如果在BC 边反射后与EF 平行,由(1)可知α90=°,与题意不符;则只能在CD 边反射后与EF 平行,如下图所示,设AB 与DC 的延长线交于点【答案】(1)110°(2)3603APC AQC Ð=°-Ð;(3)11n n -+【分析】(1)过点P 作PQ AB ∥,则PQ AB CD ∥∥,根据平行线的性质即可求解;(2)过点P 作PM AB ∥,过点Q 作QN AB ∥,则PM AB CD ∥∥,QN C AB D ∥∥,结合22QAP QAB QCP QCD Ð=ÐÐ=Ð,,即可得到结论;(3)过点P 作PE AB ∥,则PE ∥∵130PAB Ð=°,∴13050APQ Ð=-°=°,∵120APC Ð=°,∴5070CPQ Ð=°-°=°,∴18070110PCD Ð=°-°=°;(2)解:过点P 作PM ∥,过点Q 作QN AB ∥,则PM AB CD ∥,QN C AB D ∥∥∴180180PAB APM PCD CPM Ð+Ð=°Ð+Ð=°,,,即()360APC PAB PCD Ð=°-Ð+Ð,同理:AQC BAQ Ð=Ð课后专项训练1.(2023下·江苏苏州·七年级校考期中)如图,在五边形ABCDE 中,AE BC ∥,则C D E Ð+Ð+Ð=( )A .540°B .360°C .270°D .180°【答案】B 【分析】首先过点D 作DF AE ∥,交AB 于点F ,由AE BC ∥,可证得AE DF BC ∥∥,然后由两直线平行,同旁内角互补可知180E EDF Ð+Ð=°,180CDF C Ð+Ð=°,继而证得结论.【详解】解:过点D 作DF AE ∥,交AB 于点F ,AE BC Q ∥,AE DF BC \∥∥,180E EDF \Ð+Ð=°,180CDF C Ð+Ð=°,360C CDE E \Ð+Ð+Ð=°.故选:B .【点睛】此题考查了平行线的性质,注意掌握辅助线的作法,注意数形结合思想的应用.2.(2023上·四川绵阳·八年级统考开学考试)如图,一束光线AB 先后经平面镜OM ,ON 反射后,当35ABM Ð=°时,DCN Ð的度数为( )A .55°B .70°C .60°D .35°【答案】A 【分析】根据入射角等于反射角以及“两直线平行,同旁内角互补”解答即可.【详解】解:∵35ABM Ð=°,ABM OBC Ð=Ð,∴35OBC Ð=°,∴1801803535110ABC ABM OBC Ð=°-Ð-Ð=°-°-°=°,∵CD AB ∥,∴180ABC BCD Ð+Ð=°,∴18070BCD ABC Ð=°-Ð=°,A.115°B.120°【答案】A【分析】直接利用平移的性质结合平行线的性质得出答案.【详解】解:过B 作h m ∥,由题意可得:m n ∥,∴h n ∥,∴1180ABD Ð+Ð=°,∴3DBC Ð=Ð,180118065115ABD Ð=°-Ð=°-°=°,∴232115DBC ABD Ð-Ð=Ð-Ð=Ð=°.故选:A .【点睛】此题主要考查了平移的性质以及平行线的性质,正确转化角的关系是解题关键.5.(2023·安徽安庆·八年级统考期中)一把直尺与一块直角三角板按如图方式摆放,若146Ð=°,则2Ð=( )A .46°B .44°C .42°D .40°【答案】B 【分析】本题考查平行线的性质,掌握两直线平行,同位角相等是解题的关键,过三角板的直角顶点作直尺两边的平行线,根据平行线的性质可得1346Ð=Ð=°,24ÐÐ=,再结合角的和差关系可得答案.【详解】解:过三角板的直角顶点作直尺两边的平行线,∵直尺两边互相平行,∴1346Ð=Ð=°,24ÐÐ=,∵490344Ð=°-Ð=°,∴2444Ð=Ð=°,故选:B .6.(2023下·山东烟台·七年级统考期末)如图,按虚线剪去长方形纸片的相邻两个角,并使1160Ð=°,AB BC ^,则2Ð的度数为( )A .100°B .110°C .120°D .130°【答案】B 【分析】过点B 作BE AD ∥,然后根据两直线平行,同旁内角互补得出12360ABE CBE Ð+Ð+Ð+Ð=°,再解答即可.【详解】解:过点B 作BE AD ∥,∴1360ABE Ð+Ð=°∵CF AD ∥,∴CF BE AD ∥∥,∴2360CBE Ð+Ð=°∴12360ABE CBE Ð+Ð+Ð+Ð=°,∴12360ABC Ð+Ð+Ð=°,∵AB BC ^∴90ABC Ð=°∵1160Ð=°,∴2Ð的度数为110°.故选:B .【点睛】本题主要考查了平行线的性质,加辅助线,然后利用平行线的性质求解是解此题的关键.7.(2023下·广东中山·七年级校联考期中)如图,已知:,115,135AB CD B D Ð=°Ð=°∥,则E Ð= ( )A .105°B .110°C .115°D .120°【答案】B 【分析】过点E 作ME AB ∥,根据平行线的性质得出180B BEM Ð+Ð=°,180D DEM Ð+Ð=°,再根据角的和差求解即可.AB CD ∥Q ,ME AB CD \∥∥115B Ð=°Q ,135D Ð=°,\Ð110BED BEM DEM \Ð=Ð+Ð=A .40°B .50°【答案】C 【分析】利用多边形的内角和公式求得五边形的内角和,再由平行线性质求得BAE ABC BCD Ð+Ð+Ð,最后利用角的和差即可求得答案.【详解】解:∵四边形ABCDE 为五边形,【答案】540°/540度【分析】可过点B ,【详解】解:如图,过点AE DF ∥Q ,AE BM CN \∥∥则180A ABM Ð+Ð=°,MBC ÐA ABM MBC BCN =Ð+Ð+Ð+Ð【点睛】本题主要考查平行线的判定与性质,平行公理的推论,掌握两直线平行,同旁内角互补是解决此【答案】1402n °+°【分析】首先过点E 作EF AB ∥,由平行线的传递性得得出B C D A B C n Ð=Ð=°,BAD Ð=由两直线平行,内错角相等得出BEF Ð∥Q AB CD ,∴B C D A B C n Ð=Ð=°,Ð又∵BE 平分ABC Ð,DE 平分ADC Ð,∵AB EF CD ∥∥,∴12BEF ABE n Ð=Ð=° ∴1402BED FED BEF n Ð=Ð+Ð=°+°,故答案为:【答案】50【分析】先根据平行公理判定【详解】解:如图,过点∵CM EF ∥,AB EF ∥,∵155A Ð=°,105E Ð=°∵CD 平分ACE Ð,ACD \Ð【答案】150【分析】过点B 作BF AE P ,根据平行线的性质可得90BAE Ð=°,则90ABF Ð=°,可求出CBF Ð=【详解】解:过点B 作BF AE P ,∵CD AE ∥,∴BF AE CD ∥∥∵BA AE ^,∴90BAE Ð=°,∵120ABC Ð=°,∴30CBF Ð=【点睛】本题主要考查了平行线的性质和判定,解题的关键是掌握:平行于同一直线的两直线互相平行;【答案】3b a =/13a =【点睛】本题考查平行线的性质,关键是过点平行线的性质即可解决问题.14.(2023下·贵州安顺=540°,根据以上的规律求【答案】140【分析】过点E作EM Q AB CD∥,EM AB∥Q的平分线与ABFÐ1\Ð=ÐÐ,ABE ABF【答案】①②③④【分析】根据平行公理判断到212180Ð+Ð=°,2+4=90ÐÐ得到2123360Ð+Ð=°,根据【点睛】本题考查了平行线的判定和性质,熟练应用判定定理和性质定理是解题的关键,平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.【答案】(1)55°;(2)140°【点睛】本题考查平行线的性质和三角形外角的性质,掌握两直线平行,同旁内角互补,是解题的关键.18.(2023下·江苏南京·七年级校联考期末)珠江某河段两岸安置了两座可旋转探照灯示,假如河道两岸是平行的,PQ MN ∥,且(1)填空:BAN Ð= °;(2)若灯B 射线先转动30秒,灯A 射线才开始转动,在灯A 灯转动几秒,两灯的光束互相平行?(3)如图3,若两灯同时转动,在灯A 射线到达的射线AC 与BC 交于点C ,过C 作ACD Ð交PQ 于点D ,且120ACD Ð=°,则在转动过程中,与BCD Ð的数量关系,并说明理由.①当090t <<时,如图1,PQ MN Q ∥,PBD BDA \Ð=ÐAC BD Q P ,CAM BDA \Ð=Ð,CAM PBD \Ð=Ð2t \=②当90150t <<时,如图2,PQ MN Q ∥,PBD BDA \Ð+ÐAC BD Q P ,CAN BDA \Ð=Ð180PBD CAN \Ð+Ð=°1802CAN t Ð=°-Q ,\Ð又120ABC t Ð=°-Q ,(1)如图①,点C 是夹在AB 和DE 之间的一点,当AC CD ^时,垂足为C ,你知道(2)如图②,点1C ,2C 是夹在AB 和DE 之间的两点,请想一想:12A C C Ð+Ð+Ð(3)如图③,随着AB 与DE 之间点的增加,那么121n A C C C D -Ð+Ð+Ð++Ð+ÐL 的度数为必说明理由)【答案】(1)270°(2)540°(3)()180n °【分析】(1)如图所示,过点C 作AB 的平行线CF ,则CF DE AB ∥∥,由平行线的性质得到180A ACF Ð+Ð=°,180DCF D Ð+Ð=°,进而得到360A ACD D Ð+Ð+Ð=°,再由AC CD ^,即可得到270A D Ð+Ð=°.(2)如图所示,过点2C 作2C F AB ∥,则2C AB DE ∥∥,由平行线的性质得到2180D FC D +=°∠∠,同(1)可得112360A C C C F ++=°∠∠∠,112540A C C C D D +++=°∠∠∠∠;(3)由(1)(2)可知,AD DE、之间每多增加一个点,那么所得角度之和就会增加180°,据此规律求解即可.【详解】(1)解:如图所示,过点C 作AB 的平行线CF .∵AB DE ∥,∴CF DE ∥,∴180A ACF Ð+Ð=°,180DCF D Ð+Ð=°,∴1802360A ACD D Ð+Ð+Ð=°´=°.又∵AC CD ^,∴36090270A D Ð+Ð=°-°=°.(2)解:如图所示,过点2C 作2C F AB ∥,∵AB DE ∥,∴2C F AB DE ∥∥,∴2180D FC D +=°∠∠,同(1)可得112360A C C C F ++=°∠∠∠,∴1122540A C C C F D FC D ++++=°∠∠∠∠∠,∴112540A C C C D D +++=°∠∠∠∠,故答案为:540°;(3)解:由(1)(2)可知,AD DE 、之间每多增加一个点,那么所得角度之和就会增加180°,∴()121180n A C C C D n -Ð+Ð+Ð++Ð+Ð=°L ,故答案为:()180n °.【点睛】本题主要考查了平行线的性质,图形类的规律探索,熟知平行线的性质是解题的关键.20.(2023下·江苏·七年级专题练习)已知AB CD ∥,连接A ,C 两点.(1)如图1,CAB Ð与ACD Ð的平分线交于点E ,则AEC Ð等于(2)如图2,点M 在射线AB 反向延长线上,点N 在射线CD 4570AMN ACN Ð=°Ð=°,,求MEC Ð的度数;(3)如图3,图4,M ,N 分别为射线AB ,射线CD 上的点,()AMN ACN a b a b Ð=Ð=¹,,请直接写出图中MEC Ð的度数(用含【答案】(1)90(2)57.5°(3)1118022a b °-+或1118022b a °-+【分析】(1)根据平行线的性质得到180BAC ACD Ð+Ð=°90CAE ACE Ð+Ð=°,即可求出答案;(2)过点E 作EF ∥∵,ME CE 分别平分BMN ACD Ð,,∴122.52BME BMN Ð=Ð=°,∴3557.5MEC MEF CEF Ð=Ð+Ð=+°=°;(3)①如图3,过点E 作AB ,∵AB CD ∥,∴EF CD ∥,∵11AME AMN a Ð=Ð=,11802MEF a =°-,∵AB CD ∥,∴EF CD ∥,∴Ð∵1122ECD ACD b Ð=Ð=,∴Ð【点睛】此题考查了平行线的性质及角平分线的定义,解题的关键是正确掌握平行线的性质:两直线平行同旁内角互补,两直线平行内错角相等.【答案】(1)80°(2)36012P Ð=°-Ð-Ð;证明见详解(3)140°【分析】(1)过点P 作MN AB ∥,利用平行的性质就可以求角度,解决此问;(2)利用平行线的性质求位置角的数量关系,就可以解决此问;(3)分别过点P 、点G 作MN AB ∥、KR AB ∥,然后利用平行线的性质求位置角的数量关系即可.【详解】(1)解:如图过点P 作MN AB ∥,∵AB CD ∥,∴AB MN CD ∥∥.∴1180EPN Ð+Ð=°,2180FPN Ð+Ð=°.∵1130Ð=°,2150Ð=°,∴12360EPN FPN Ð+Ð+Ð+Ð=° ∴36013015080EPN FPN Ð+=°-°-°=°.∵P EPN FPN Ð=Ð+Ð,∴∠P =80°.故答案为:80°;(2)解:36012P Ð=°-Ð-Ð,理由如下:如图过点P 作MN AB ∥,∵AB CD ∥,∴AB MN CD ∥∥.∴1180EPN Ð+Ð=°,2180FPN Ð+Ð=°.∴12360EPN FPN Ð+Ð+Ð+Ð=°∵EPN FPN P Ð+Ð=Ð,36012P Ð=°-Ð-Ð.(3)如图分别过点P 、点G 作MN AB ∥、KR AB∥(1)如图2,AB CD P ,点M 是AEF Ð和FGC Ð平分线的交点,EFG Ð(2)如图3,AB CD P ,GM 平分CGF Ð,EM GM ^,EF 平分BEM ÐCGF Ð的度数是________.【答案】EFG BEF DGF Ð=Ð+Ð,360;(1)117°;(2)124°【答案】(1)60OFD Ð=°(2)见解析(3)2760n <<【分析】(1)过点O 作AB OH ∥,易得AB CD OH ∥P ,利用平行线的性质可求解;(2)延长EG 交CD 于Z ,由于EG 平分AEO Ð,所以AEG OEG Ð=Ð,根据此条件表示可求出两角的关系;(3)过点O 作AB OK MP NQ P P P ,设2AEG x Ð=,MNF MNG FNG Ð=Ð+Ð,求出n ,m 之间的关系,利用已知条件n m >,求出【详解】(1)解:证明:过点O 作AB OH ∥,∵AB CD ∥,∴AB CD OH ∥P ,∴AEO Ð又∵150AEO а=,90EOF а=,∴EOH Ð(2)解:GFO Ð与CFG Ð相等,理由如下:延长∵AB CD ∥,∴180AEG CZG Ð+аÐ=,∵135EGF а=,且CZG ZGF ZFG Ð=Ð+Ð又∵90EOF а=,∴在四边形EOFG 中,∵EG 平分AEO Ð,∴AEG OEG Ð=Ð,∴∵AB CD ∥,∴AB CD OK MP NQ ∥P P P ∴90EOF BEO OFD Ð=Ð+Ð=°,即180又∵3EMN n а=,5MNH m а=,∴MNF Ð∴322MNF MNQ FNQ n x Ð=Ð+Ð=°-+(1)【特例探究】如图1,90C Ð=°.①CED CGF Ð+Ð=______度;②若CED Ð与CGF Ð的角平分线相交于点P ,则EPG Ð=______度;(2)【一般探索】如图2,C a Ð=,EPG b Ð=.①若13DEP CED Ð=Ð,13FGP CGF Ð=Ð,求a 与b 的关系;②若1DEP CED nÐ=Ð,1FGP CGF n Ð=Ð(2n ³且n 为整数),直接写出a 与b 的关系;∴180DEC ECM Ð+Ð=°,∴DEC ECM MCG Ð+Ð+Ð∵ECM MCG ECG Ð+ÐÐ=∴DEC ECG FGC Ð+Ð+Ð=②∵CED Ð与CGF Ð的角平分线相交于点∴1DEP CED Ð=Ð,FGP Ð∵12l l ∥, ∴2CM l P ,PN ∥∴180DEC ECM Ð+Ð=°,Ð∴DEC ECM MCG Ð+Ð+Ð+即DEC ECG FGC Ð+Ð+Ð=∵13DEP CED Ð=Ð,FGP Ð。
平行线中的拐点问题经典实用

•平行线中的拐点问题
蓦然回首
对自己说,你有什么收获? 对同学说,你有什么温馨提示? 对老师说,你还有什么困惑?
•平行线中的拐点问题
•17
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
•平行线中的拐点问题
•13
思维导图
平行线性 质与判定
“拐点” 问题
‘凸’出来的模型 ‘凹’进去的模型 “猪手图”模型
•平行线中的拐点问题
•14
综合应用
如图所示,已知CD∥EF,∠C+∠F=∠ABC,求 证:AB∥GF.
•平行线中的拐点问题
•15
综合应用
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F. 当∠PEQ=70°时,请求出∠PFQ的度数.
)
∴∠CPF=180°-∠C ,∠1=180°-∠A
∴∠APC=∠CPF-∠1
=(180°-∠C)-(180°-∠A)=∠A-∠C
•平行线中的拐点问题
B D
F
•7
知识点三:“猪手图”模型
新知究
A
B
C
D
P
∠APC=∠A-∠C
P
A
B
C
D
∠APC=∠C-∠A
•平行线中的拐点问题
•8
知识点三:“猪手图”模型
M
1
a
P
2 3
b
N
•平行线中的拐点问题
•2
知识点一:‘凸’出来的模型
人教版七年级下册数学《平行线—平行线中的拐点问题》课件

【拓展延伸】
已知:如图,AB//CD,试解决下列问题:(1)∠1+∠2
=
+∠3+∠4=
;(4)
试探究∠1+∠2+∠3+∠4+…+∠n =
;
总结归纳: ①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线 ② A1 A2 An1 An 180 (n 1【) n-2个拐点】
【巩固练习】
4.如图,a∥b,∠1=55°,∠2=130°,则∠3=( )
A.100° B.105° C.110° D.115°5.某小区
地下停车场入口了栏杆的平面示意图如图所示,BA垂直地
面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC
=
°.
6.如图,直线m∥n,AB⊥BC,∠1=35°,∠2=62°,则
7题图
8题图
9题图
类型四、综合型
例4:①如图1,若AB∥CD,∠B,∠C,∠D之间有什么关系?请 证②明如. 图2,若AB∥CD,∠B,∠C,∠D之间有什么关系?请证 明.
【巩固练习】
10.如图,如果AB∥CD,那么角α,β,γ之间的关系式为( )
A.α+β+γ=360°
B.α﹣β+γ=180°
【巩固练习】
7.如图,BD∥EF,AE与BD交于点C,∠B=30°,∠A=75°, 则∠E的度数为( ) A.135° B.125° C.115° D.105° 8.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若 ∠BCD=100°,∠CDE=15°,则∠DEF的度数是( ) A.110° B.115° C.120° D.125° 9.如图,已知直线a∥b,则∠1、∠2、∠3的关系是( ) A.∠1+∠2+∠3=360° B.∠1+∠2﹣∠3=180° C.∠1﹣∠2+∠3=180° D.∠1+∠2+∠3=180°
平行线的性质 —平行线间的“拐点”问题说课课件 2023-2024学年人教版七年级数学下册

例1:已知:如图,AB//EF,请你猜想 ∠BAC、∠ACE、∠CEF它们之间的数量 关系,并说明理由。
A
B
C
1 2
D
E
F
学生易错点:1.添加辅助线叙 述错误,如:过点C作AB、EF 的平行线CD。 2、推理过程不严谨:如过点C 作CD//AB, 所以∠A+∠1=180° 又因为CD//EF, 所以∠2+∠E=180°。
M
1
a
P 23 N
b
(第1题图)
D
E
(第2题图)
笃行
3. 如图,有一块含有45°角的三角尺放在直尺上,如果∠2=20°, 那么∠1= ( ) A .15°B.20° C.25° D .30°
C
1 2
建模思想
笃行
4.如图,直线AB、EF,点C是直线AB上一点,点D是直线AB外一 点,若∠BCD=95°,∠CDE=25°,则∠DEF=( C )
时间 安排
0 3
从时间分配上来看,由于前面一题 多解上用时有点多,导致后面两种 模型的研究有些匆忙。
设计思路
A
B
C
E
F
7.教学反思
Fresh and simple teacher's lecture
通过一个基本图形,延伸到三种基本图形,启发 学生如何从题目中提炼出基本模型。渗透特殊到 一般、类比、转化等数学思想。引导学生善于观 察分析题目的内在联系,做到做一题、懂一类、 会一片的目的。
设计意图:分层布置作业,A组题让全体学生对今天的学习有练习,有巩固; B组题让学有余力的学生有探究,有提高。同时把数学的研究深入到课后,体
现深度学习的理念。
6.板书设计
2024七年级数学下册提练第2招巧解平行线中的“拐点”问题习题课件新版浙教版

(3)如图③,点P在直线CD下方,∠BAP与∠DCP的平分 线相交于点K,∠AKC与∠APC有何数量关系?并说 明理由.
【解】∠AKC=12∠APC. 理由:如图③,过点 K 作 KE∥AB, 则∠BAK=∠AKE, ∵AB∥CD,∴KE∥CD,∴∠DCK=∠CKE, ∴∠AKC=∠AKE-∠CKE=∠BAK-∠DCK.
【解】如图①,过点P作PE∥AB, 则∠APE=∠BAP. ∵AB∥CD,∴PE∥CD, ∴∠CPE=∠DCP, ∴∠APC=∠APE+∠CPE= ∠BAP+∠DCP=60°+20°=80°.
(2)如图②,点P在直线AB,CD之间,∠BAP与∠DCP的 平分线相交于点K,∠AKC与∠APC有何数量关系?并 说明理由.
【解】如图,过点C作CF∥AB, 则∠ABC+∠FCB=180°, ∴∠FCB = 180° - ∠ABC = 60° , ∴∠DCF=∠BCD-∠FCB= 80°-60°=20°. 由 题 意 可 得 DE∥AB , ∴CF∥DE , ∴∠CDE=∠DCF=20°.
4. 如图,已知AB∥CD,∠B=135°,∠D=30°,求 ∠BED的度数.
(1)MD和NE平行吗?为什么? 【解】MD∥NE.理由如下: 如图①,过点A作AF∥MD, 则∠MBA+∠BAF=180°. 又∵∠MBA+ ∠BAC+∠NCA=360°, ∴∠FAC+∠NCA=180°, ∴AF∥NE,∴MD∥NE.
(2)若∠ABD= 70° ,∠ACE= 36°, BP和CP分 别平 分 ∠ABD,∠ACE,求∠BPC的度数. 【解】如图②,过点P作PQ∥MD. ∵BP 和 CP 分 别 平 分 ∠ABD , ∠ACE , ∠ABD=70°,∠ACE=36°,
【解】∠AKC=12∠APC. 理由:如图②,过点 K 作 KE∥AB, 则∠AKE=∠BAK. ∵AB∥CD,∴KE∥CD,∴∠CKE=∠DCK, ∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK.
人教版七年级数学下第五章相交线与平行线专题二 平行线中的折线问题——过拐点作平行线习题课件

Hale Waihona Puke 年级 数学 下册 人教版解:(1)当 P 点在线段 CD 上运动时,∠APB=∠PAC+∠PBD. 理由:过点 P 在∠APB 的内部作 PE∥l1, ∵l1∥l2, ∴PE∥l2∥l1, ∴∠PAC=∠APE,∠PBD=∠BPE, ∴∠APB=∠APE+∠BPE=∠PAC+∠PBD.
七年级 数学 下册 人教版
七年级 数学 下册 人教版
5.如图,AB∥DE,∠1=25°,∠2=110°,求∠BCD 的度数. 解:过点 C 在∠BCD 的内部作 CM∥AB, 则∠BCM=∠1=25°, 又∵AB∥DE, ∴CM∥DE,∴∠DCM+∠2=180°, ∴∠DCM=180°-∠2=70°, ∴∠BCD=∠BCM+∠DCM=95°.
七年级 数学 下册 人教版
2.如图,点 E 在线段 AC 上,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE. 证明:过点 E 在∠BED 的内部作 EM∥AB,则∠B=∠BEM, ∵∠1=∠B,∴∠1=∠BEM, 又∵AB∥CD,∴EM∥CD,∴∠D=∠DEM, ∵∠2=∠D,∴∠DEM=∠2, ∵∠1+∠BEM+∠DEM+∠2=180°, ∴∠BEM+∠DEM=90°,即∠BED=90°, ∴BE⊥DE.
七年级 数学 下册 人教版
8.如图,已知∠MBA+∠BAC+∠NCA=360°. (1)求证:MD∥NE; (2)若∠ABD=70°,∠ACE=36°,BP,CP 分别 平分∠ABD,∠ACE,求∠BPC 的度数. (1)证明:过 A 在∠BAC 的内部作 AG∥MD.则∠MBA+∠BAG=180°, ∵∠MBA+∠BAC+∠NCA=360°, 即∠MBA+∠BAG+∠CAG+∠NCA=360°, ∴∠CAG+∠NCA=180°,∴AG∥NE,∴MD∥NE.
