2015数字图像处理实验一 基础实验
数字图像处理实验报告

数字图像处理实验报告数字图像处理实验报告1一. 实验内容:主要是图像的几何变换的编程实现,具体包括图像的读取、改写,图像平移,图像的镜像,图像的转置,比例缩放,旋转变换等.具体要求如下:1.编程实现图像平移,要求平移后的图像大小不变;2.编程实现图像的镜像;3.编程实现图像的转置;4.编程实现图像的比例缩放,要求分别用双线性插值和最近邻插值两种方法来实现,并比较两种方法的缩放效果;5.编程实现以任意角度对图像进行旋转变换,要求分别用双线性插值和最近邻插值两种方法来实现,并比较两种方法的旋转效果.二.实验目的和意义:本实验的目的是使学生熟悉并掌握图像处理编程环境,掌握图像平移、镜像、转置和旋转等几何变换的方法,并能通过程序设计实现图像文件的读、写操作,及图像平移、镜像、转置和旋转等几何变换的程序实现.三.实验原理与主要框架:3.1 实验所用编程环境:Visual C++(简称VC)是微软公司提供的基于C/C++的应用程序集成开发工具.VC拥有丰富的功能和大量的扩展库,使用它能有效的创建高性能的Windows应用程序和Web应用程序.VC除了提供高效的C/C++编译器外,还提供了大量的可重用类和组件,包括著名的微软基础类库(MFC)和活动模板类库(ATL),因此它是软件开发人员不可多得的开发工具.VC丰富的功能和大量的扩展库,类的重用特性以及它对函数库、DLL库的支持能使程序更好的模块化,并且通过向导程序大大简化了库资源的使用和应用程序的开发,正由于VC具有明显的优势,因而我选择了它来作为数字图像几何变换的开发工具.在本程序的开发过程中,VC的核心知识、消息映射机制、对话框控件编程等都得到了生动的体现和灵活的应用.3.2 实验处理的对象:256色的BMP(BIT MAP )格式图像BMP(BIT MAP )位图的文件结构:具体组成图: BITMAPFILEHEADER位图文件头(只用于BMP文件) bfType=”BM” bfSize bfReserved1bfReserved2bfOffBitsbiSizebiWidthbiHeightbiPlanesbiBitCountbiCompressionbiSizeImagebiXPelsPerMeterbiYPelsPerMeterbiClrUsedbiClrImportant单色DIB有2个表项16色DIB有16个表项或更少256色DIB有256个表项或更少真彩色DIB没有调色板每个表项长度为4字节(32位)像素按照每行每列的顺序排列每一行的字节数必须是4的整数倍BITMAPINFOHEADER 位图信息头 Palette 调色板 DIB Pixels DIB图像数据1. BMP文件组成BMP文件由文件头、位图信息头、颜色信息和图形数据四部分组成.2. BMP文件头BMP文件头数据结构含有BMP文件的类型(必须为BMP)、文件大小(以字节为单位)、位图文件保留字(必须为0)和位图起始位置(以相对于位图文件头的偏移量表示)等信息.3. 位图信息头BMP位图信息头数据用于说明位图的尺寸(宽度,高度等都是以像素为单位,大小以字节为单位, 水平和垂直分辨率以每米像素数为单位) ,目标设备的级别,每个像素所需的位数, 位图压缩类型(必须是 0)等信息.4. 颜色表颜色表用于说明位图中的颜色,它有若干个表项,每一个表项是一个RGBQUAD类型的结构,定义一种颜色.具体包含蓝色、红色、绿色的亮度(值范围为0-255)位图信息头和颜色表组成位图信息5. 位图数据位图数据记录了位图的每一个像素值,记录顺序是在扫描行内是从左到右,扫描行之间是从下到上.Windows规定一个扫描行所占的字节数必须是4的倍数(即以long为单位),不足的以0填充.3.3 BMP(BIT MAP )位图的显示:①一般显示方法:1. 申请内存空间用于存放位图文件2. 位图文件读入所申请内存空间中3. 在函数中用创建显示用位图, 用函数创建兼容DC,用函数选择显示删除位图但以上方法的缺点是: 1)显示速度慢; 2) 内存占用大; 3) 位图在缩小显示时图形失真大,(可通过安装字体平滑软件来解决); 4) 在低颜色位数的设备上(如256显示模式)显示高颜色位数的图形(如真彩色)图形失真严重.②BMP位图缩放显示 :用视频函数来显示位图,内存占用少,速度快,而且还可以对图形进行淡化(Dithering )处理.淡化处理是一种图形算法,可以用来在一个支持比图像所用颜色要少的设备上显示彩色图像.BMP位图显示方法如下:1. 打开视频函数,一般放在在构造函数中2. 申请内存空间用于存放位图文件3. 位图文件读入所申请内存空间中4. 在函数中显示位图5. 关闭视频函数 ,一般放在在析构函数中以上方法的优点是: 1)显示速度快; 2) 内存占用少; 3) 缩放显示时图形失真小,4) 在低颜色位数的设备上显示高颜色位数的图形图形时失真小; 5) 通过直接处理位图数据,可以制作简单动画.3.4 程序中用到的访问函数Windows支持一些重要的DIB访问函数,但是这些函数都还没有被封装到MFC中,这些函数主要有:1. SetDIBitsToDevice函数:该函数可以直接在显示器或打印机上显示DIB. 在显示时不进行缩放处理.2. StretchDIBits函数:该函数可以缩放显示DIB于显示器和打印机上.3. GetDIBits函数:还函数利用申请到的内存,由GDI位图来构造DIB.通过该函数,可以对DIB的格式进行控制,可以指定每个像素颜色的位数,而且可以指定是否进行压缩.4. CreateDIBitmap函数:利用该函数可以从DIB出发来创建GDI 位图.5. CreateDIBSection函数:该函数能创建一种特殊的DIB,称为DIB项,然后返回一个GDI位图句柄.6. LoadImage函数:该函数可以直接从磁盘文件中读入一个位图,并返回一个DIB句柄.7. DrawDibDraw函数:Windows提供了窗口视频(VFW)组件,Visual C++支持该组件.VFW中的DrawDibDraw函数是一个可以替代StretchDIBits 的函数.它的最主要的优点是可以使用抖动颜色,并且提高显示DIB的速度,缺点是必须将VFW代码连接到进程中.3.5 图像的几何变换图像的几何变换,通常包括图像的平移、图像的镜像变换、图像的转置、图像的缩放和图像的旋转等.数字图像处理实验报告2一、实验的目的和意义实验目的:本实验内容旨在让学生通过用VC等高级语言编写数字图像处理的一些基本算法程序,来巩固和掌握图像处理技术的基本技能,提高实际动手能力,并通过实际编程了解图像处理软件的实现的基本原理。
数字图像处理实验一图像的基本操作和基本统计指标计算实验报告.doc

实验一图像的基本操作和基本统计指标计算一、实验目的熟悉MATLAB图像处理工具箱,在掌握MATLAB基本操作的基础上,本课程主要依靠图像处理工具箱验证和设计图像处理算法。
对于初学者来说,勤学多练、熟悉MATLAB图像处理工具箱也是学号本课程的必经之路。
了解计算图像的统计指标的方法及其在图像处理中的意义。
了解图像的几何操作,如改变图像大小、剪切、旋转等。
二、实验主要仪器设备(1)台式计算机或笔记本电脑(2)MATLAB(安装了图像处理工具箱,即Image Processing Toolbox(IPT))(3)典型的灰度、彩色图像文件三、实验原理(1)将一幅图像视为一个二维矩阵。
(2)利用MATLAB图像处理工具箱读、写和显示图像文件。
①调用imread函数将图像文件读入图像数组(矩阵)。
例如“I=imread(‘tire.tif’);”。
其基本格式为:“A=imread(‘filename.fmt’)”,其中,A为二维矩阵,filename.为文件名,fmt 为图像文件格式的扩展名。
②调用imwrite函数将图像矩阵写入图像文件。
例如“imwrite(A,’test_image.jpg’);”。
其基本格式为“imwrite(a,filename.fmt)”。
③调用imshow函数显示图像。
例如“imshow(‘tire.tif’);”。
其基本格式为:I为图像矩阵,N为显示的灰度级数,默认时为256。
(3)计算图像有关的统计参数。
四、实验内容(1)利用MATLAB图像处理工具箱和Photoshop读、写和显示图像文件。
(2)利用MATLAB计算图像有关的统计参数。
五、实验步骤(1)利用“读图像文件I/O”函数读入图像Italy.jpg。
(2)利用“读图像文件I/O”的iminfo函数了解图像文件的基本信息:主要包括Filename(文件名)、FileModDate(文件修改时间)、Filesize(文件尺寸)、Format(文件格式)、FormatVersion (格式版本)、Width(图像宽度)、Height(图像高度)、BitDepth(每个像素的位深度)、ColorType (彩色类型)、CodingMethod(编码方法)等。
数字图像处理—实验一

数字图像处理—实验一一.实验内容:图像灰度变换二.实验目的:学会用Matlab 软件对图像灰度进行变换;感受各种不同的灰度变换方法对最终图像效果的影响。
三.实验步骤:1.获取实验用图像:Fig3.10(b).jpg. 使用imread 函数将图像读入Matlab 。
2.产生灰度变换函数T1,使得:0.3rr < 0.35s = 0.105 + 2.6333(r – 0.35) 0.35 ≤ r ≤ 0.651 + 0.3(r – 1)r > 0.65用T1对原图像Fig3.10(b).jpg 进行处理,打印处理后的新图像。
3.产生灰度变换函数T2,使得:s =用T2对原图像Fig3.10(b).jpg 进行处理,打印另一处理后的新图像。
4.分别用 s = r 0.6; s = r 0.4; s = r 0.3 对Fig3.08(a).jpg 图像进行处理。
为简便起见,请使用Matlab 中的imadjust 函数。
5.对Fig3.04(a).jpg 图像实施反变换(Negative Transformation )。
s =1-r; 6.对Fig3.10(b).jpg 图像实施灰度切片(Gray-level slicing )。
具体要求如下:当0.2 ≤ r ≤ 0.4时,将r 置为0.6, 当r 位于其他区间时, 保持其灰度与原图像一样。
四.实验报告要求:用imshow, plot 等函数生成各类图像,提交原图像和各种变换函数的曲线,以及按各种变换函数处理后的图像。
实验报告上的其他内容,按常规实验报告要求办。
胡小平2005-10-27。
实验报告-图像锐化

lWidth=m_BmpInfo.bmiHeader.biWidth;
lHeight=m_BmpInfo.bmiHeader.biHeight;
//分配内存,以保存新DIB
hDIB=GlobalAlloc(GHND,nBytePerLine*lHeight);
//判断是否内存分配失败
if(hDIB==NULL)
3.编写图像锐化的彩色图像灰度化,Sobel算法锐化,图像二值化处理相关的程序代码。
4.对程序进行相关调试,修改程序,去除其中的BUG。
5.利用自己准备的图像的文件和编写的程序,进行图像锐化处理。
6.截屏,保留实验结果,进行实验结果分析,并撰写实验报告。
三、相关背景知识
(写你自己觉得比较重要的与本实验相关的背景知识)
+ 0*val21+ 0*val22+ 0*val32
+ 1.0*val11+ 2.0*val12+ 1.0*val13;
//计算梯度的大小
Sobel=sqrt(gx*gx+gy*gy);
*(pImageDataNew+j*nBytePerLine+i* 3 + 0) =int(Sobel);
*(pImageDataNew+j*nBytePerLine+i* 3 + 1) =int(Sobel);
lHeight=m_BmpInfo.bmiHeader.biHeight;
for(intj= 0 ;j<lHeight;j++)
{
for(inti= 0 ;i<lWidth;i++)
{
//灰度化临时值
图像处理基本实验

实验一 图像的基本操作1.读取并显示一幅tif 格式的图像,并将新图像存存储成bmp, png 格式并显示出来.所用图片像素为264x264I=imread('dog_gray.tif'); % 读取tif 图像 [m,n]=size(I) % 显示图像规模imwrite(I,'dog_gray.bmp');% 图像保存为bmp 格式 imwrite(I,'dog_gray.png');% 图像保存为png 格式 I1=imread('dog_gray.bmp'); %读取bmp 图像 I2=imread('dog_gray.png'); %读取png 图像subplot(1,3,1),imshow(I);% 在1x3子屏中的第1个子图显示为dog_gray.tif title('dog_gray.tif');% 显示图像标题subplot(1,3,2),imshow(I1); %在1x3子屏中的第2个子图显示为dog_gray.bmp title('dog_gray.bmp');% 显示图像标题subplot(1,3,3),imshow(I2); % 在1x3子屏中的第2个子图显示为dog_gray.png title('dog_gray.png');% 显示图像标题m = 264 n = 264dog g ray.tif dog g ray.bmp dog g ray.png2 读取一幅RGB 彩色图像,在同一窗口输出原图像及R, G, B 三个分量图像.所用图片大小为352x351RGB=imread('fruits.tif'); %读取图像 [m,n,p]=size(RGB) % 矩阵大小 R=RGB(:,:,1); % 显示R 分量 G=RGB(:,:,2); %显示G 分量 B=RGB(:,:,2); %显示B 分量subplot(2,2,1),image(RGB); % 在2x2子屏中的第1个子图显示原图 title('原图'); % 显示标题subplot(2,2,2),image(R); % 在2x2子屏中的第2个子图显示R 分量图像 title('R 分量'); % 显示标题subplot(2,2,3),image(G); % 在2x2子屏中的第3个子图显示G 分量图像 title('G 分量'); % 显示标题subplot(2,2,4),image(B); % 在2x2子屏中的第4个子图显示B 分量图像 title('B 分量'); % 显示标题m = 352 n = 351 p = 31002003001002003001002003001002003001002003001002003001002003001002003003 & 4读取一幅RGB彩色图像,将其转换为灰度图像保存为tif格式,并在同一窗口显示原图像与灰度图像.将4中得到灰度图像转化为二值图像,并对其进行取反操作,在同一窗口显示灰度图所用图像像素为264x352RGB=imread('flower-0170.jpg'); % 读取图像[m,n,p]=size(RGB) %矩阵大小I=rgb2gray(RGB); % 真彩色图像转换为灰度图像I1=im2bw(I); % 灰色图像二值画I2=~I1; %对二值图像取反imwrite(I,'flower-0170.tif') % 将图像保存为tif格式subplot(1,2,1),imshow(RGB);%在1x2子屏的第1个子屏中显示原图title('flower-0170.jpg'); %显示标题subplot(1,2,2),imshow(I); % 在1x2子屏的第1个子屏中显示灰度图像title('flower-0170.tif'); %显示标题figure % 新建个图形窗口subplot(1,3,1),imshow(I); %在1x3子屏的第1个子屏中显示灰度图像subplot(1,3,2),imshow(I1); %在1x3子屏的第2个子屏中显示二值图像subplot(1,3,3),imshow(I2); %在1x3子屏的第3个子屏中显示二值图像取反后的图像m =264n =352p =3flower-0170.jpg flower-0170.tif5读取两幅图像,进行加,减,乘,除运算,并显示原图像与运算结果.所用图片像素为512x512I1=imread('baboon.tif'); % 读取图像I2=imread('barbara.tif'); % 读取图像[m1,n1]=size(I1)% I1的大小[m2,n2]=size(I2) % I2的大小 ADD=imadd(I1,I2); %两个图像相加 SUB=imsubtract(I1,I2);%两个图像相减 MUL=immultiply(I1,I1);%两个图像相乘 DIV=imdivide(I1,I2);%两个图像相除subplot(2,3,1),imshow(I1); %在2x3子屏的第1个子屏中显示baboon.tif title('baboon.tif');subplot(2,3,2),imshow(I2); %在2x3子屏的第2个子屏中显示barbara.tif title('barbara.tif');subplot(2,3,3),imshow(ADD); %在2x3子屏的第3个子屏中显示ADD title('ADD 图像');subplot(2,3,4),imshow(SUB); %在2x3子屏的第4个子屏中显示SUB title('SUB 图像');subplot(2,3,5),imshow(MUL); %在2x3子屏的第5个子屏中显示MUL title('MUL 图像');subplot(2,3,6),imshow(DIV); %在2x3子屏的第6个子屏中显示DIV title('DIV 图像');m1 = 512 n1 = 512 m2 = 512 n2 = 512baboon.tifbarbara.tifADD 图像SUB 图像MUL 图像DIV 图像6验证教材2.7节(点运算)中对图像的线性变换(例2-1),非线性变换(例2-2)及直方图均衡化实验.%图像线性变换a=imread('cameraman.tif'); % 读入cameraman图像figure(1);imshow(a);b1=a+45; % 图像灰度值增加45figure(2);imshow(b1);b2=1.2*a; % 图像对比度增大figure(3);imshow(b2);b3=0.65*a; % 图像对比度减少figure(4);imshow(b3);b4=-double(a)+225; %图像求补figure(5);imshow(uint8(b4));%用函数对cameraman图像进行非线性变换a=imread('cameraman.tif') ; %读取原始图像figure(1);imshow(a);xlabel('(a)原始图像');x=1:225;y=x+x.*(255-x)/255;figure(2);plot(x,y); %绘制函数图像xlabel('(b)函数的曲线图');b1=double(a)+0.006*double(a).*(255-double(a)); figure(3);imshow(uint8(b1)); %显示非线性图像xlabel('(c)非线性处理效果');(a)原始图像(c)非线性处理效果% 对cameraman进行直方图均衡化histgram=zeros(1,256); % 生成直方图数组cdf=zeros(1,256);[cm,map]=imread('cameraman.tif'); [a,b]=size(cm);for i=1:afor j=1:bk=cm(i,j);histgram(k)=histgram(k)+1;endend % 得到直方图cdf(1)=histgram(1);for i=2:256cdf(i)=cdf(i-1)+histgram(i);endfor i=1:afor i=1:bk=cm(i,j);cm_equ(i,j)=cdf(k)*256/(a*b); endendimshow(uint8(cm_equ));figure(2);imhist(uint8(cm_equ));050100150200250%对tire.tif图像进行均衡化处理I=imread('tire.tif');J=histeq(I);H=adapthisteq(I);figure(1);imshow(I);xlabel('原始图像');figure(2);imshow(J);xlabel('histeq均衡化');figure(3);imshow(H);xlabel('adapthisteq均衡化');原始图像histeq均衡化adapthisteq均衡化彩色图像和灰度图像中包含的信息内容有什么区别?彩色图像,每个像素通常是由红(R)、绿(G)、蓝(B)三个分量来表示的,分量介于(0,255)。
数字图像处理实验报告(五个实验全)

数字图像处理实验报告(五个实验全)实验⼀ Matlab图像⼯具的使⽤1、读图I=imread('lena.jpg');imshow(I);2、读⼊⼀幅RGB图像,变换为灰度图像和⼆值图像,并在同⼀个窗⼝内分成三个⼦窗⼝来分别显⽰RGB图像和灰度图像。
a=imread('lena.jpg')i = rgb2gray(a)I = im2bw(a,0.5)subplot(3,1,1);imshow(a);subplot(3,1,2);imshow(i);subplot(3,1,3);imshow(I);原图像灰度图像⼆值图像实验⼆图像变换1、对⼀幅图像进⾏平移,显⽰原始图像与处理后图像,分别对其进⾏傅⾥叶变换,显⽰变换后结果,分析原图的傅⾥叶谱与平移后傅⾥叶频谱的对应关系。
s=imread('beauty.jpg');i=rgb2gray(s)i=double(i)j=fft2(i);k=fftshift(j); 原图像原图的傅⾥叶频谱l=log(abs(k));m=fftshift(j);RR=real(m);II=imag(m);A=sqrt(RR.^2+II.^2);A=(A-min(min(A)))/(max(max(A)))*255;b=circshift(s,[800 450]);b=rgb2gray(b)b=double(b) 平移后的图像平移后的傅⾥叶频谱c=fft2(b);e=fftshift(c);l=log(abs(e));f=fftshift(c);WW=real(f);ZZ=imag(f);B=sqrt(WW.^2+ZZ.^2);B=(B-min(min(B)))/(max(max(B)))*255;subplot(2,2,1);imshow(s);subplot(2,2,2);imshow(uint8(b));subplot(2,2,3);imshow(A);subplot(2,2,4);imshow(B);2、对⼀幅图像进⾏旋转,显⽰原始图像与处理后图像,分别对其进⾏傅⾥叶变换,显⽰变换后结果,分析原图的傅⾥叶谱与旋转后傅⾥叶频谱的对应关系。
数字图像处理实验

4. medfilt2:中值滤波函数 中值滤波函数 L=medfilt2(J,[3 5]);
%1、利用低通邻域平均模板进行平滑: 、利用低通邻域平均模板进行平滑: clc clear close all I=imread('cameraman.tif'); subplot(1,3,1);imshow(I);title('原图 原图'); 原图 J=fspecial('average'); J1=filter2(J,I)/255; subplot(1,3,2);imshow(J1);title('3*3滤波 滤波'); 滤波 K=fspecial('average',9); K1=filter2(K,I)/255; subplot(1,3,3);imshow(K1);title('9*9滤波 滤波'); 滤波
利用模板进行图象增强就是进行模板卷积。 利用模板进行图象增强就是进行模板卷积。 1、 利用二个低通邻域平均模板(3×3和9×9)对一幅 、 利用二个低通邻域平均模板( × 和 × ) 图象进行平滑,验证模板尺寸对图象的模糊效果的影响。 图象进行平滑,验证模板尺寸对图象的模糊效果的影响。 2、 利用一个低通模板对一幅有噪图象(GAUSS白噪声) 、 利用一个低通模板对一幅有噪图象( 白噪声) 白噪声 进行滤波,检验两种滤波模板(分别使用一个5× 的 进行滤波,检验两种滤波模板(分别使用一个 ×5的 线性邻域平均模板和一个非线性模板: × 中值滤波 线性邻域平均模板和一个非线性模板:3×5中值滤波 对噪声的滤波效果。 器)对噪声的滤波效果。 3、 选择一个经过低通滤波器滤波的模糊图象,利用 、 选择一个经过低通滤波器滤波的模糊图象,利用sobel 水平边缘增强高通滤波器( 和prewitt水平边缘增强高通滤波器(模板)对其进行高 水平边缘增强高通滤波器 模板) 通滤波图象边缘增强,验证模板的滤波效果。 通滤波图象边缘增强,验证模板的滤波效果。 4、 选择一幅灰度图象分别利用 一阶 一阶Sobel算子和二阶 、 算子和二阶 Laplacian算子对其进行边缘检测,验证检测效果。 算子对其进行边缘检测, 算子对其进行边缘检测 验证检测效果。
数字图像处理实验

目录实验1 数字图像处理的MATLAB基础................. 错误!未定义书签。
实验2 灰度图像增强.. (2)实验3 空域滤波 (4)实验4 图像的二维傅里叶变换和频谱 (6)实验5 图像频域增强 (8)实验6 图像复原.................................. 错误!未定义书签。
实验7 彩色图像变换. (11)实验8 彩色图像滤波 (13)实验9 图像边缘检测 (15)附录一图像数据文件格式 (17)附录二实验报告格式 (20)实验2 灰度图像增强一、实验目的通过本实验使学生掌握使用MATLAB对灰度图像进行空域增强的目的,加深对空域图像增强的理解。
二、实验原理本实验是基于数字图像处理课程中的图像变换和增强理论来设计的。
本实验的准备知识:教材第三章,空域图像增强方法。
重点如下:1、直方图和直方图均衡通过实验领悟图像的直方图的含义,加深对图像直方图概念的理解,并且能够掌握直方图均衡的方法和效果。
画图像的直方图命令, imhist(A)直方图均衡命令, Aeq=histeq(A)2、基本灰度变换3、同屏显示图像的函数图形窗口分区的命令为 subplot, 例如subplot (2,2,1) 是将图形窗分为2×2的4个区,在第1个区画图。
示例figuresubplot(1,2,1) imshow(A);subplot(1,2,2) imshow(Aeq);将图形窗口分为两个区,分别显示图像A和Aeq。
三、实验内容(一)直方图均衡1、读入lena_gray.tif图像文件,画出其直方图,并解释之;2、对该图像进行直方图均衡,显示均衡后的图像及其直方图,并解释之;3、将均衡后的图像存为lena_gray_1.tif文件。
4、再将lena_gray_1.tif文件读入并重复上述过程,说明增强效果并解释之。
(二)图像灰度变换读入lena_gray.tif文件,对其灰度进行下列调整,并显示图像:(1)将图像的灰度降低70%,同屏显示原图像和灰度调整后图像;(2)将图像灰度加上一个值(如50),使图像变亮,编程,同屏显示原图像和灰度调整后图像。
人体骨骼认识实验报告

人体骨骼认识实验报告骨骼图像增强实验报告骨骼图像增强实验报告——数字图像处理第一次作业实验总体思路:原图像是人体骨骼核扫描图像,我们的目的是通过图像锐化突出骨骼的更多细节来增强图像。
由于图像灰度的动态范围很窄并且有很高的噪声内容,所以很难对其进行增强。
对此我们采取的策略是,首先用拉普拉斯法突出图像中的小细节,然后用梯度法突出其边。
平滑过的梯度图像将用于掩蔽拉普拉斯图像。
最后,我们将试图试用灰度变换来增强图像的灰度动态范围。
实验处理具体步骤:(图像可拉伸放大)1、此为图2,。
2、此为图3,。
(而这个时候看到图2的噪声水平,将图1和图2相加之后也必然会有很多的噪声。
拉普拉斯操作作为一种二阶微分算子,能很好的增强细节,但也产生更多的噪声。
而降低噪声的一种方法就是使用中值滤波器,但属于非线性滤波器的中值滤波器有可能改变图像的性质,所以不可取。
所以采取另一种方法,使用原图像梯度操作的平滑形式所形成的一个模板。
)3、此为图4,。
(梯度变换在灰度斜坡或台阶的平均相应要比拉普拉斯操作的更强烈,而对噪声和小细节的响应要比拉普拉斯操作的相应弱,而且可以通过均值滤波器对其进行平滑处理可以进一步降低,此时看(来自: 写论文网:人体骨骼认识实验报告)图像中的边缘要比拉普拉斯图像(即图3)中的边缘要突出许多)4、此为图5,。
(图4,5要比图2亮表明具有重要边缘内容的梯度图像的值一般要比拉普拉斯图像的值高)5、此为图6,。
(此时看到强边缘的优势和可见噪声的相对减少,用平滑后的梯度图像来掩蔽拉普拉斯图像的目的达到了)6、此为图7,(与原图像相比,该图像中大部分细节的清晰度的增加都很明显,所以我们才需要综合多种的方法对图像进行处理,单独使用一种方法根本不可能达到这么好的效果,只需要看相对应的图像进行对比即可知道)7、此为图8,(此时需要增大锐化后图像的动态范围,即使有很多种这样效果的灰度变换函数,但是用幂率变换处理更好,直方图均衡和规定化的效果都不太好)(此时人体的轮廓的清晰度虽然还是不高,因为扩大的灰度动态范围的同时也增大了噪声,但是相比原图还是有相当大幅度的提高的,看下图原图与最终图像对比)实验心得与收获:在本次的图像处理编程中,我首次对图像处理的众多方法有了一个感性的理解,图像处理并不是简简单单的应用几个函数即可获得理想的效果,还需要分析得出要得到相应的效果就需要不同的方法,使是知道了对应的图像处理方法也是不足的,在图像处理的编程方法上也必须要熟悉,这一次的例子中因为总体上的方法都已经给出了,因此大部分的工作量就落在了如何选择对应的matlab函数了,所以这一次收获较大的就是在图像处理函数的原型跟使用细节的认识上,还有在例子的理解过程中,也将之前所学的图像处理方法复习熟悉了一遍,在这一个阶段的学习上收获到的帮助很大。
数字图像处理实验(1)

3)存储该图像(文件名用同学们的本名); 4)、制作标准像的硬拷贝;打印两张,一张
上交(附在实验报告中),一张自己保留;
五、撰写实验报告 1)、实验目的叙述; 2)、实验环境描述; 3)、实验项目及内容; 4)、操作步骤详细描述;包括:系统的激 活方法,菜单的运用等;
5)、记录实验结果。 6)、基本原理介绍; 7)、实验现象描述; 8)、实验结果分析;
谢谢
软件: 操作系统:WINDOWS XP 应用软件: 数字图像处理演示软件。
三、实验内容:
1)、图像信息获取; 2)、图像存储; 3)、观察直方图均衡化处理的效果; 4)、观察图像边缘增强处理效果; 5)、拍摄自己的标准像。
四、实验步骤: 1、图像信息的获取: 1)、激活软件; 2)、调整摄像机的光圈和聚焦,
数字图像处理实验
(一)
一、实验目的
1)、了解“数字图像处理系统”的基本组 成结构;
2)、掌握微型数字图像处理系统的基本 操作方法;
3)、体验主要数字图像处理内容的效果。
二、实验的软、硬件平台:
硬件: 微型图像处理系统, 包括:主机, PC机; 摄像机:Logitech 130万像素, 分辨率:640×480 最高分辨率:1280×960 手动聚焦调整.
摄取一张明暗合适的图像;
ห้องสมุดไป่ตู้
3)、存储图像;
4)、调出该图像,验证是否成功存储了该 图像。
2、观察图像均衡化处理效果 1)、激活图像处理软件; 2)、调整摄像机光圈,摄取一张偏暗的图像 并存储该图像;
3)、调用演示程序中的直方图统计功 能,观察直方图形状;
4)、调用直方图均衡化处理功能,观察 处理结果,同时调用直方图统计功 能,观察直方图形状;
计算机图像处理实验报告(数字图像处理基本操作)

计算机图像处理实验报告(数字图像处理基本操作)课程名称:计算机图像处理实验名称:实验一数字图像处理基本操作一、实验目的(1)掌握MATLAB软件的运用,熟练掌握建立、保存、运行、调试m文件的方法。
(2)了解MATLAB软件中图像处理工具箱的使用方法。
(3)熟练掌握图像文件(黑白、灰度、索引色和彩色图像)的读取及显示方法。
(4)熟悉常用的图像文件格式和格式转换。
二、实验内容(包括源程序和程序运行结果)(1)编写matlab程序对灰度图像pout.tif、索引图像canoe.tif、真彩色图像peppers.png实现读取、显示和保存。
源程序:clearclcI=imread('pout.tif');subplot(131),imshow(I),title('灰度图像');[I1,map]=imread('canoe.tif');I2=ind2rgb(I1,map);subplot(132),imshow(I2),title('索引图像');I3=imread('peppers.png');subplot(133),imshow(I3),title('真彩色图像')imwrite(I,'newpout.bmp');imwrite(I2,'newcano.bmp');imwrite(I3,'newpeppers.bmp');程序运行结果:(2)matlab图像文件夹中的mri.mat是一个包含27帧、图像尺寸为128*128的多帧索引图像。
编写matlab程序对请将前20帧图像顺序读入到一个数组中并显示出来,转换成影像显示。
源程序:clearclcload mri;figure;subplot(4,5,1),imshow(D(:,:,:,1));subplot(4,5,2),imshow(D(:,:,:, 2));subplot(4,5,3),imshow(D(:,:,:,3));subplot(4,5,4),imshow(D(:,:,:,4));subplot(4,5,5),imshow(D(:,:,:,5));subplot(4,5,6),imshow(D(:,:,:,6));subplot(4,5,7),imshow(D(:,:,:,7));subplot(4,5,8),imshow(D(:,:,:, 8));subplot(4,5,9),imshow(D(:,:,:,9));subplot(4,5,10),imshow(D(:,:,:,10));subplot(4,5,11),imshow(D( :,:,:,11));subplot(4,5 ,12), imshow(D(:,:,:,12));subplot(4,5,13),imshow(D(:,:,:,13));subplot(4,5,14),imshow(D( :,:,:,14));subplot(4,5 ,15), imshow(D(:,:,:,15));subplot(4,5,16),imshow(D(:,:,:,16));subplot(4,5,17),imshow(D( :,:,:,17));subplot(4,5 ,18), imshow(D(:,:,:,18));subplot(4,5,19),imshow(D(:,:,:,19));subplot(4,5,20),imshow(D( :,:,:,20));mov=immovie(D,map);implay(mov)程序运行结果:(3)通过图像点运算减弱图像pout.tif的对比度。
数字图像处理实验一

《数字图像处理》实验报告实验一:Matlab编程基础实验姓名:xx班级:xx学号:xx一、实验目的1.了解MATLAB 程序设计语言的基本特点,熟悉MATLAB软件运行环境,了解MATLAB的函数库及应用。
2.熟悉管理、创建、保存、打开文件及数据的方法,设置文件路径的方法。
3.掌握变量、函数等有关概念,具备初步的将一般数学问题转化为对应计算机模型并进行处理的能力。
二、实验仪器1.计算机一台。
2.MATLAB图像处理工具箱。
三、实验内容1. 打开Matlab,熟悉Matlab环境在命令区键入如下命令,观察程序执行情况。
显示图像。
I=imread('FigP0606.tif ' );imshow(I);创建矩阵A=ones(3,5);2. 学习m文件的建立、保存、打开、运行方法t=0:0.1:2*pi;y1=sin(t);h_line1=plot(t,y1,':');hold ony2=cos(t);h_line2=plot(t,y2,'*');h_label=xlabel('Time(0~2\pi)','FontWeigh' , 'bold'); h_textl =text(pi,0,'\leftarrowsin wave');h_text2=text(pi/2,0,'\leftarrowcos wave');3. 练习图像文件的打开、处理、显示操作,运行并观察实验结果。
I=imread('10.pgm');imshow(I);4. 练习调用MATLAB函数imread,imshow,imopen, imsubtract,imadjust ,stretchlim,分析函数功能。
(1)imread:读取图片(2)imshow: 显示图片示例:i=imread('bacteria.bmp');imshow(i);(3)imopen:开运算,作用是:可以使边界平滑,消除细小的尖刺,断开窄小的连接,保持面积大小不变等。
数字图像处理实验报告

数字图像处理实验报告数字图像处理实验报告第一章总论数字图像处理是计算机图形学、数字信号处理等学科交叉的一门学科。
它是基于数字计算机对图像信号进行数字处理的一种方法。
数字图像处理技术已广泛应用于医学影像诊断、遥感图像处理、图像识别、安防监控等领域,在当今社会中具有不可替代的重要作用。
本次实验主要介绍了数字图像处理的基本方法,包括图像采集、图像增强、图像恢复、图像分割、图像压缩等几个方面。
在实验过程中,我们采用了一些常用的数字图像处理方法,并通过 Matlab 图像处理工具箱进行实现和验证。
第二章实验过程2.1 图像采集在数字图像处理中,图像采集是一个重要的步骤。
采集到的图像质量直接影响到后续处理结果的准确性。
本次实验使用的图像是一张 TIF 格式的彩色图像,通过 Matlab 读取图像文件并显示,代码如下:```Matlabim = imread('test.tif');imshow(im);```执行代码后,可以得到如下图所示的图像:2.2 图像增强图像增强是指利用某些方法使图像具有更好的视觉效果或者变得更适合某种应用。
本次实验我们主要采用直方图均衡化、灰度变换等方法进行图像增强。
2.2.1 直方图均衡化直方图均衡化是一种常用的增强方法,它可以增加图像的对比度和亮度,使图像更加清晰。
代码实现如下:```Matlabim_eq = histeq(im);imshow(im_eq);```执行代码后,会得到直方图均衡化后的图像,如下图所示:可以看出,经过直方图均衡化处理后,图像的对比度和亮度得到了明显提高。
2.2.2 灰度变换灰度变换是一种用于调整图像灰度级别的方法。
通过变换某些像素的灰度级别,可以增强图像的视觉效果。
本次实验我们采用对数变换和幂函数变换两种方法进行灰度变换。
实验一 数字图像处理实验报告
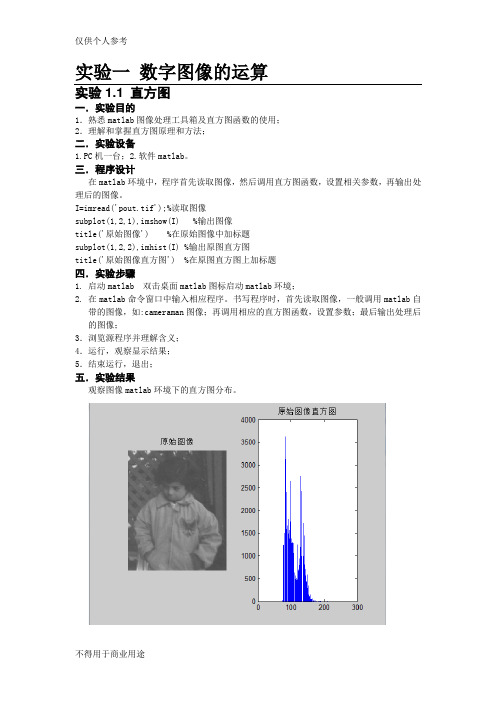
实验一数字图像的运算实验1.1 直方图一.实验目的1.熟悉matlab图像处理工具箱及直方图函数的使用;2.理解和掌握直方图原理和方法;二.实验设备1.PC机一台;2.软件matlab。
三.程序设计在matlab环境中,程序首先读取图像,然后调用直方图函数,设置相关参数,再输出处理后的图像。
I=imread('pout.tif');%读取图像subplot(1,2,1),imshow(I) %输出图像title('原始图像') %在原始图像中加标题subplot(1,2,2),imhist(I) %输出原图直方图title('原始图像直方图') %在原图直方图上加标题四.实验步骤1. 启动matlab 双击桌面matlab图标启动matlab环境;2. 在matlab命令窗口中输入相应程序。
书写程序时,首先读取图像,一般调用matlab自带的图像,如:cameraman图像;再调用相应的直方图函数,设置参数;最后输出处理后的图像;3.浏览源程序并理解含义;4.运行,观察显示结果;5.结束运行,退出;五.实验结果观察图像matlab环境下的直方图分布。
实验1.2 3*3均值滤波一.实验目的1.熟悉matlab图像处理工具箱及均值滤波函数的使用;2.理解和掌握3*3均值滤波的方法和应用;二.实验设备1.PC机一台;2.软件matlab;三.程序设计在matlab环境中,程序首先读取图像,然后调用图像增强(均值滤波)函数,设置相关参数,再输出处理后的图像。
I = imread('pout.tif');figure,imshow(I);J=filter2(fspecial('average',3),I)/255;figure,imshow(J);四.实验步骤1. 启动matlab双击桌面matlab图标启动matlab环境;2. 在matlab命令窗口中输入相应程序。
数字图像处理实验报告图像复原实验

实验报告课程名称数字图像处理导论专业班级_______________姓名_______________学号_______________电气与信息学院和谐勤奋求是创新2.对加入噪声图像选用不同的平滑(低通)模板做运算,对比不同模板所形成的效果,要求在同一窗口中显示。
I=imread('moon.tif');H = fspecial('sobel');subplot(2,2,1)imshow(I);title(' Qriginal Image ');Sobel = imfilter(I,H,'replicate');subplot(2,2,2)imshow(Sobel);title(' Sobel Image ')H = fspecial('laplacian',0.4);lap = imfilter(I,H,'replicate');subplot(2,2,3)imshow(lap);title(' Laplacian Image ')H = fspecial('gaussian',[3 3],0.5);gaussian = imfilter(I,H,'replicate');subplot(2,2,4)imshow(gaussian);title(' Gaussian Image ')3.使用函数imfilter时,分别采用不同的填充方法(或边界选项,如零填充、’replicate’、’symmetric’、’circular’)进行低通滤波,显示处理后的图像。
originalRGB = imread('trees.tif');subplot(3,2,1)imshow(originalRGB);title(' Qriginal Image ');h = fspecial('motion', 50, 45); %motion blurredfilteredRGB = imfilter(originalRGB, h);subplot(3,2,2)imshow(filteredRGB);title(' Motion Blurred Image ');boundaryReplicateRGB = imfilter(originalRGB, h, 'replicate');subplot(3,2,3)imshow(boundaryReplicateRGB);title(' 0-Padding');boundary0RGB = imfilter(originalRGB, h, 0);subplot(3,2,4)imshow(boundary0RGB);title('Replicate');boundarysymmetricRGB = imfilter(originalRGB, h, 'symmetric'); subplot(3,2,5)imshow(boundarysymmetricRGB);title(' Symmetric ');boundarycircularRGB = imfilter(originalRGB, h, 'circular'); subplot(3,2,6)imshow(boundarycircularRGB);title(' Circular');5.对加入椒盐噪声的图像分别采用均值滤波法,和中值滤波法对有噪声的图像做处理,要求在同一窗口中显示结果。
数字图像处理实验

《数字图像处理》实验报告学院:信息工程学院专业:电子信息工程学号:姓名:2015年6月18日目录实验一图像的读取、存储和显示 (2)实验二图像直方图分析 (6)实验三图像的滤波及增强 (15)实验四噪声图像的复原 (19)实验五图像的分割与边缘提取 (23)附录1 MATLAB简介 (27)实验一图像的读取、存储和显示一、实验目的与要求1.熟悉及掌握在MATLAB中能够处理哪些格式图像。
2.熟练掌握在MATLAB中如何读取图像。
3.掌握如何利用MATLAB来获取图像的大小、颜色、高度、宽度等等相关信息。
4.掌握如何在MATLAB中按照指定要求存储一幅图像的方法。
5.图像的显示。
二、实验原理一幅图像可以被定义为一个二维函数f(x,y),其中x和y是空间(平面)坐标,f 在任何坐标处(x,y)处的振幅称为图像在该点的亮度。
灰度是用来表示黑白图像亮度的一个术语,而彩色图像是由单个二维图像组合形成的。
例如,在RGB彩色系统中,一幅彩色图像是由三幅独立的分量图像(红、绿、蓝)组成的。
因此,许多为黑白图像处理开发的技术适用于彩色图像处理,方法是分别处理三副独立的分量图像即可。
图像关于x和y坐标以及振幅连续。
要将这样的一幅图像转化为数字形式,就要求数字化坐标和振幅。
将坐标值数字化成为取样;将振幅数字化成为量化。
采样和量化的过程如图1所示。
因此,当f的x、y分量和振幅都是有限且离散的量时,称该图像为数字图像。
三、实验设备(1) PC计算机(2) MatLab软件/语言包括图像处理工具箱(Image Processing Toolbox)(3) 实验所需要的图片四、实验内容及步骤1.利用imread( )函数读取一幅图像,假设其名为flower.tif,存入一个数组中;2.利用whos 命令提取该读入图像flower.tif的基本信息;3.利用imshow()函数来显示这幅图像;4.利用imfinfo函数来获取图像文件的压缩,颜色等等其他的详细信息;5.利用imwrite()函数来压缩这幅图象,将其保存为一幅压缩了像素的jpg文件设为flower.jpg语法:imwrite(原图像,新图像,‘quality’,q), q取0-100。
数字图像处理实验

4理解和掌握图像的平移、垂直镜像变换、水平镜像变换、缩放和旋转的原理和应用;
二、实验原理
1初始坐标为( , )的点经过平移( , ),坐标变为( , ),两点之间的关系为: ,以矩阵形式表示为:
2图像的镜像变换是以图象垂直中轴线或水平中轴线交换图像的变换,分为垂直镜像变换和水平镜像变换,两者的矩阵形式分别为:
3 a).调入、显示“实验一”获得的图像;图像存储格式应为“.gif”;
b)对这三幅图像做FFT并利用自编的函数显示其频谱;
c)讨论不同的图像内容与FFT频谱之间的对应关系。
4对频谱分别进行高斯、巴特沃兹、高斯高通和低通滤波,比较其锐化和平滑效果
5记录和整理实验报告。
四、实验仪器
1计算机;
2 MATLAB程序;
垂直镜像变换
DM642Programs\2.ImageProcess\SEED202_VertTranspose\VertTransposeloop2.pjt
水平镜像变换
DM642Programs\2.ImageProcess\SEED203_horizTranspose\HorizTransposeloop2.pjt
3移动式存储器(软盘、U盘等)。
4记录用的笔、纸。
五、实验报告内容
1叙述实验过程;
2提交实验的原始图像和结果图像,并对结果进行比较。
六、思考题
1.傅里叶变换有哪些重要的性质?
2.图像的二维频谱在显示和处理时应注意什么?
实验三、图像的几何变换
一、实验目的
1熟悉CCS集成开发环境的操作和基本功能;
2熟悉视频显示程序的运行过程、控制过程,搞清数据处理、传输途径;
数字图像处理 实验一.

数字图像处理实验一一、 实验目的1、 学习时域平滑滤波器的概念及原理,观察并比较由不同模版3×3,5×5,7×7模版处理后的图像。
2、 学会使用Robert 梯度算法寻找图像边界及其相关的原理。
3、 学习锐化处理,使用laplace 算子对图像实现锐化处理,不断尝试寻找不同的KI 观察其效果二、 实验原理1、 平滑空间滤波器平滑滤波器用于模糊处理和减小噪声,我们学习的平滑线性空间滤波器的输出响应是包含在滤波模版邻域内像素的简单平均值,也称均值滤波器,属于低通滤波器。
平滑滤波器用滤波模版确定的邻域内像素的平均灰度值去代替图像每个像素点的值,这种处理减小了图像灰度的尖锐化,同时也会带来一些负面的影响,比如的处理完之后带来图像会更加的模糊,尤其是当模版越大的时候越明显。
模版大致有两种,一是邻域平均,一是加权平均。
本次实验中使用加权平均的方式,简单的进行加权平均表示成:∑==nZi R i n2121注意滤波器模板的所有系数均为1,可保证输出图仍在原来的灰度值范围,计算也更有效。
在处理的时候,应该注意边界的处理必要的时候可以扩展一下边界。
补0或者是使用最外圈的数据扩展。
2、 Robert 梯度算法梯度法是基于一阶微分寻找边界的方法。
实际实现算法的过程中经常会使用绝对值(街区距离)来替代平方根(欧氏距离)运算近似求梯度。
为得出合适的滤波模版,Robert 定义了交叉差分算法,给出了梯度的近似算法如下:[(,)](,)(1,1)(1,)(,1)G f x y f x y f x y f x y f x y =-++++-+可以看出是两个3×3的模版对图像处理之后的相加。
模版分别为:000_010001h x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦与 000_011010h y ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦两个模版3.图像增强锐化——拉普拉斯算子使用二阶微分梯度在图像增强处理中的应用,边缘增强是要突出图像边缘,抑制图像中非边缘信息,使图像轮廓更加清晰。
数字图像处理实验

数字图像处理实验数字图像处理实验实验⼀:图像⾊彩编辑器⼀、图像⾊彩编辑器(ColorPicker)是⼀个基于对话框的应⽤程序,它具有以下功能:1、⾊彩编辑功能⽤户可以通过可以调整R、G、B的值来编辑颜⾊,亦可通过调整H、S、V的值来选取颜⾊。
颜⾊编辑的结果会马上反馈到颜⾊⾯板和颜⾊预览框中。
2、RGB颜⾊空间和HSV颜⾊空间的转换当改变RGB值,会得到相应的HSV值,并进⾏显⽰,反之亦然。
3、取⾊功能取⾊功能包含“⾯板取⾊”和“屏幕取⾊”。
⾯板取⾊就是⽤户可以在颜⾊⾯板中单击⿏标左键,选取⽬标点所表⽰的某种颜⾊。
屏幕取⾊则是允许⽤户获取整个屏幕上的任意⼀点的颜⾊值。
⽤户可以将⿏标移动到需要获取颜⾊的地⽅,然后按a键或A键即可以获取该点颜⾊值。
⼆、实验步骤1、创建新项⽬打开VC6.0,选择菜单中的[⽂件]——[新建]项⽬,在弹出的“新建项⽬”对话框中选择“MFC应⽤程序”模板,并在名称中输⼊“ColorPicker”,然后单击“确定”。
在“MFC 应⽤程序向导”的应⽤程序类型中选择“基本对话框”,其他选项采⽤系统默认设置,最后⽣成项⽬。
2、对话框设计设计对话框将解决各种控件的数量、摆放的位置和使⽤的名称等问题。
打开资源视图(ColorPicker Resources),点击对话框(Dialog),找到名为“IDD_COLORPICKER_DIALOG”的对话框资源,双击它进⼊编辑状态,并按照下图所⽰的图和表对该对话框进⾏编辑。
3、完成实例编程12 3 4 5 678 9 1011 12 13这⾥介绍⼀下组成ColorPicker 应⽤程序的每个⽂件的作⽤:(1)ColorPicker.vcproj这是使⽤应⽤程序向导⽣成的VC++ 项⽬的主项⽬⽂件。
它包含⽣成该⽂件的Visual C++ 的版本信息,以及有关使⽤应⽤程序向导选择的平台、配置和项⽬功能的信息。
(2)ColorPicker.h这是应⽤程序的主要头⽂件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一:
6、已知序列图像中相邻两幅图像A(up.jpg)、B(down.jpg) ,其坐标分别为(u,v)及(x,y),试求其图像变换校 正二阶拟合方程式系数K。要求用最小二乘法求解,变换 模型为: x = k100+ k110u + k101v+ k120u2+ k102v2+ k111uv y = k200+ k210u + k201v+ k220u2+ k202v2+ k211uv 提示:up.jpg不动, down.jpg做变换、旋转,图中给出大 于7个以上标记点,坐标自己读出。 7、编程实现大津阈值分割算法,对给定待分割图像进行 阈值分割。 8、对一幅灰度图像实现压缩编码,要求在Huffman码、 行程编码、变换编码等中至少选择两种方式编程实现。
傅立叶变换
噪 声
傅立叶变换
FFT 原始图像 显示:频谱图
求模 复数(实部+虚部)
去噪时:应当对傅立叶变换后的复数进行修改 (即,实部和虚部的数值都需要修改)
傅立叶变换
“transform.cpp”: 在void fft2D(unsigned char* imgBuf, int width, int height)中直接修改频谱 //频域数据保存至fftBuf fftBuf=buf; //带阻去噪 for (i=height/2-5; i<=height/2+5;i++){ for (j=width/2-10; j<= width/2-5;j++){ *(fftBuf+i*width*2+j*2+0)=0; *(fftBuf+i*width*2+j*2+1)=0; } for(j=width/2+5; j<= width/2+10;j++){ *(fftBuf+i*width*2+j*2+0)=0; *(fftBuf+i*width*2+j*2+1)=0; } } *(fftBuf+i*width*2+j*2+0) =*(fftBuf+i*width*2+j*2+0)/10; *(fftBuf+i*width*2+j*2+1) =*(fftBuf+i*width*2+j*2+1)/10;
加噪声
增强噪声频谱
傅立叶变换
傅立叶变换
高通滤波
高频:细节描述(边缘, 噪声)
傅立叶变换
低频:轮廓部分
低通滤波
思考题
1. 观察laplace、Roberts、Sobel、Kirch等算子 对边界检测的特点; 2. 如何实现彩色图像的边缘检测? 3. 傅里叶变换有哪些重要的性质,讨论图像的边 缘与频率的关系? 4. 当图像不满足N*N时,如何对图像补0,实现 其快速傅立叶变换?
f f
T
2 2 12 f ( x, y ) mag (f ( x, y )) (G x Gy )
梯度的方向: ( x, y ) arctan(G y G x ) 在离散域中,用差分代替微分来实现:
f ( x , y ) f x, y f x 1, y f x, y f x, y 1
边缘检测
边缘检测
//获取文档类中m_dib的指 针,访问当前DIB数据 //获取图像宽、高、每像素所占位数 //输入的图像每行像素所占字节数,必须为4的倍数
Doc文档,负责内存数据与磁盘的交互:读入,写盘。 View视图,负责内存数据与用户的交互:数据的显示、用户操作的响应(如菜单 的选取、鼠标的响应等等)
2
1 2 2
边缘检测
常用边缘检测算子: a) Roberts算子
ቤተ መጻሕፍቲ ባይዱ
gi, j f i, j f i 1, j 1 f i 1, j f i, j 1
2
1 2 2
近似式:
f (i, j ) f (i 1, j 1) f (i 1, j ) f (i, j 1)
傅立叶变换
void CDemoView::OnFft() { CDemoDoc *pDoc=GetDocument(); HDIB dib=pDoc->GetHDIB(); LPSTR lpDIB = (LPSTR) ::GlobalLock((HGLOBAL) dib); LPBITMAPINFOHEADER phead=(LPBITMAPINFOHEADER)lpDIB; int w = phead->biWidth; int h = phead->biHeight; int b = phead->biBitCount/8; if(b==3) { ::MessageBox(0,“只处理灰度图象! ",NULL,MB_OK); ::GlobalUnlock(dib); return; } int lineByte=(w * b+3)/4*4; unsigned char *lpDIBBits =(unsigned char *)::FindDIBBits(lpDIB); int bufLong=w; if(h>bufLong) bufLong=h; unsigned char *buf=new unsigned char[bufLong*bufLong]; int i, j; for(i=0;i<h;i++){ for(j=0;j<w;j++) buf[i*w+j]=*(lpDIBBits+i*lineByte+j); for(j=w;j<bufLong;j++) buf[i*w+j]=0; } for(i=h;i<bufLong;i++){ for(j=w;j<bufLong;j++) buf[i*w+j]=0; } fft2D(buf, bufLong, bufLong); for(i=0;i<h;i++){ for(j=0;j<w;j++){ *(lpDIBBits+i*lineByte+j)=buf[i*bufLong+j]; } } delete []buf; ::GlobalUnlock(dib); ifft2D(buf, bufLong, bufLong); Invalidate(); }
transform.cpp、transform.h
面向过程的DIB读写访问
傅立叶变换
将傅立叶变换函数加入所建立的工程 建立菜单项 注意:头文件是否包含进去
例如,用已有傅立叶变换函数做FFT变换时, 需要在DemoView.cpp里添加如下头文件
#include"math.h" #include "MainFrm.h" #include "transform.h"
抑制 噪声频谱
去噪
傅立叶变换
存储傅立叶变换后的数据 transform.cpp: float *buf1=new float[n*2]; 另一种方法 FFT.cpp: //复数类型结构体 struct ComplexNumber { float imag; // imaginary虚部 float real; //实部 }; //傅立叶变换缓冲区 ComplexNumber *m_pFFTBuf; //去噪 for(…;…;…){ for(…;…;…){ m_pFFTBuf[i*width+j].imag=0; m_pFFTBuf[i*width+j].real=0; } … }
边缘检测
1. 在已有函数中加入边缘检测算子,观察图像处理前后的 变化; 2.自己尝试加入新的菜单并映射函数,实现新的边缘检 测算子;
边缘检测
边缘检测
Message Maps选项卡: 是ClassWizard对话框中最重要的 选项卡,主要完成创建新类、添加、 删除消息处理函数等任务。
边缘检测
傅立叶变换
傅立叶变换
//加正弦波 for(j=width/2-5; j<= width/2+5;j++){ for(i=height/2-25; i<=height/2-20;i++){ *(fftBuf+i*width*2+j*2+0)=*(fftBuf+i*width*2+j*2+0)*30; *(fftBuf+i*width*2+j*2+1)=*(fftBuf+i*width*2+j*2+1)*30; } for(i=height/2+20; i<=height/2+25;i++){ *(fftBuf+i*width*2+j*2+0)=*(fftBuf+i*width*2+j*2+0)*30; *(fftBuf+i*width*2+j*2+1)=*(fftBuf+i*width*2+j*2+1)*30; } }
实验一:
独立完成以下8道题的编程实现: 1、实现laplace算子、Roberts算子、Sobel算子、Kirch算 子等边缘检测算子中的任何两个,对灰度图像处理。 2、对一幅有规则噪声的灰度图像(grid.bmp)作快速付立 叶变换,在频谱上去除规则噪声的频带,然后作快速付立叶 反变换恢复原图像,观察去噪效果,尝试自己生成噪声。 3、对一幅彩色图像进行近邻、双线性、三次立方卷积放大 ,放大倍数2、3、4倍。 4、用3*3,5*5,7*7模板实现均值和中值图像平滑,测试 效果和处理速度。 5、对一幅灰度图像进行直方图均衡、线性拉伸等变换。
