机械振动与噪声学习题集与答案
振动噪声课后习题答案

振动噪声课后习题答案振动噪声课后习题答案在学习振动噪声的课程中,习题是非常重要的一部分,通过解答习题可以帮助我们巩固所学知识,提高解决问题的能力。
下面是一些振动噪声课后习题的答案,希望能对大家的学习有所帮助。
1. 什么是振动噪声?振动噪声是指由于机械系统的振动引起的噪声。
当机械系统发生振动时,会产生声音,这种声音就是振动噪声。
振动噪声可以对人体健康和环境造成不良影响。
2. 振动噪声的主要来源有哪些?振动噪声的主要来源包括机械设备、交通工具、建筑物、电器设备等。
机械设备的运转会产生振动,交通工具在行驶过程中也会产生振动,建筑物和电器设备的使用也会引起振动噪声。
3. 如何评价振动噪声的强度?振动噪声的强度可以通过声级来评价。
声级是一种用于表示声音强度的单位,通常用分贝(dB)来表示。
振动噪声的强度越大,声级也就越高。
4. 振动噪声对人体健康有哪些影响?振动噪声对人体健康有很多不良影响。
长期暴露在高强度的振动噪声下会导致听力受损、心理压力增加、睡眠质量下降等问题。
此外,振动噪声还会引起头痛、胃痛、消化不良等身体不适。
5. 如何减少振动噪声的传播?减少振动噪声的传播可以采取多种措施。
首先,可以通过减少振动源的振动来降低振动噪声的产生。
其次,可以在振动源和传播路径之间设置隔振措施,如橡胶垫、减震器等。
此外,还可以通过改善建筑结构、增加隔音材料等方式来减少振动噪声的传播。
6. 如何评价振动噪声的影响?评价振动噪声的影响可以从两个方面来考虑。
一方面是对人体健康的影响,如对听力、心理状态、睡眠等的影响。
另一方面是对环境的影响,如对动植物的生长、生活质量等的影响。
7. 如何进行振动噪声的监测和控制?振动噪声的监测可以通过安装振动传感器等设备来实现。
控制振动噪声可以采取技术措施和管理措施相结合的方式。
技术措施包括减振、隔振等方法,管理措施包括制定噪声限制标准、加强监督检查等。
8. 振动噪声的治理需要政府和企业共同努力。
大学 机械振动 课后习题和答案(1~4章 总汇)

1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3 设有两个刚度分别为1k ,2k 的线性弹簧如图T —1.3所示,试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 满足:21111k k k eq +=解:1)对系统施加力P ,则两个弹簧的变形相同为x ,但受力不同,分别为:1122P k xP k x=⎧⎨=⎩由力的平衡有:1212()P P P k k x =+=+故等效刚度为:12eq Pk k k x ==+2)对系统施加力P ,则两个弹簧的变形为: 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩,弹簧的总变形为:121211()x x x P k k =+=+故等效刚度为:122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ,2t k 。
解:对系统施加扭矩T ,则两轴的转角为: 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为:121211()t t T k k θθθ=+=+,12111()eq t t k T k k θ==+故等效刚度为:12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ,2c ,试计算总粘性阻尼系数eq c1)在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P ,则两个减振器的速度同为x ,受力分别为:1122P c x P c x =⎧⎨=⎩ 由力的平衡有:1212()P P P c c x =+=+故等效刚度为:12eq P c c c x ==+ 2)对系统施加力P ,则两个减振器的速度为:1122P x c Px c ⎧=⎪⎪⎨⎪=⎪⎩,系统的总速度为:121211()x x x P c c =+=+ 故等效刚度为:1211eq P c x c c ==+1.6 一简谐运动,振幅为0.5cm,周期为0.15s,求最大速度和加速度。
机械振动试题(含答案)

机械振动试题(含答案)一、机械振动选择题1.沿某一电场方向建立x轴,电场仅分布在-d≤x≤d的区间内,其电场场强与坐标x的关系如图所示。
规定沿+x轴方向为电场强度的正方向,x=0处电势为零。
一质量为m、电荷量为+q的带点粒子只在电场力作用下,沿x轴做周期性运动。
以下说法正确的是()A.粒子沿x轴做简谐运动B.粒子在x=-d处的电势能为12-qE0dC.动能与电势能之和的最大值是qE0dD.一个周期内,在x>0区域的运动时间t≤2mdqE2.如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘在一起,且摆动平面不便.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后A56TB65TC.摆球最高点与最低点的高度差为0.3hD.摆球最高点与最低点的高度差为0.25h3.下列说法中不正确的是( )A.将单摆从地球赤道移到南(北)极,振动频率将变大B.将单摆从地面移至距地面高度为地球半径的高度时,则其振动周期将变到原来的2倍C .将单摆移至绕地球运转的人造卫星中,其振动频率将不变D .在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变4.如图为某简谐运动图象,若t =0时,质点正经过O 点向b 运动,则下列说法正确的是( )A .质点在0.7 s 时的位移方向向左,且正在远离平衡位置运动B .质点在1.5 s 时的位移最大,方向向左,在1.75 s 时,位移为1 cmC .质点在1.2 s 到1.4 s 过程中,质点的位移在增加,方向向左D .质点从1.6 s 到1.8 s 时间内,质点的位移正在增大,方向向右5.甲、乙两单摆的振动图像如图所示,由图像可知A .甲、乙两单摆的周期之比是3:2B .甲、乙两单摆的摆长之比是2:3C .t b 时刻甲、乙两摆球的速度相同D .t a 时刻甲、乙两单摆的摆角不等 6.如图所示,质量为m 的物块放置在质量为M 的木板上,木板与弹簧相连,它们一起在光滑水平面上做简谐振动,周期为T ,振动过程中m 、M 之间无相对运动,设弹簧的劲度系数为k 、物块和木板之间滑动摩擦因数为μ,A .若t 时刻和()t t +∆时刻物块受到的摩擦力大小相等,方向相反,则t ∆一定等于2T 的整数倍 B .若2T t ∆=,则在t 时刻和()t t +∆时刻弹簧的长度一定相同 C .研究木板的运动,弹簧弹力充当了木板做简谐运动的回复力 D .当整体离开平衡位置的位移为x 时,物块与木板间的摩擦力大小等于m kx m M+ 7.如图所示,将小球甲、乙、丙(都可视为质点)分别从A 、B 、C 三点由静止同时释放,最后都到达竖直面内圆弧的最低点D ,其中甲是从圆心A 出发做自由落体运动,乙沿弦轨道从一端B 到达最低点D ,丙沿圆弧轨道从C 点运动到D ,且C 点很靠近D 点,如果忽略一切摩擦阻力,那么下列判断正确的是( )A .丙球最先到达D 点,乙球最后到达D 点B .甲球最先到达D 点,乙球最后到达D 点C .甲球最先到达D 点,丙球最后到达D 点D .甲球最先到达D 点,无法判断哪个球最后到达D 点8.如图所示的弹簧振子在A 、B 之间做简谐运动,O 为平衡位置,则下列说法不正确的是( )A .振子的位移增大的过程中,弹力做负功B .振子的速度增大的过程中,弹力做正功C .振子的加速度增大的过程中,弹力做正功D .振子从O 点出发到再次回到O 点的过程中,弹力做的总功为零9.如图所示,在一条张紧的绳子上悬挂A 、B 、C 三个单摆,摆长分别为L 1、L 2、L 3,且L 1<L 2<L 3,现将A 拉起一较小角度后释放,已知当地重力加速度为g ,对释放A 之后较短时间内的运动,以下说法正确的是( )A .C 的振幅比B 的大B .B 和C 的振幅相等 C .B 的周期为2L gD .C 的周期为1L g10.如图所示,PQ 为—竖直弹簧振子振动路径上的两点,振子经过P 点时的加速度大小为6m/s 2,方向指向Q 点;当振子经过Q 点时,加速度的大小为8m/s 2,方向指向P 点,若PQ 之间的距离为14cm ,已知振子的质量为lkg ,则以下说法正确的是( )A.振子经过P点时所受的合力比经过Q点时所受的合力大B.该弹簧振子的平衡位置在P点正下方7cm处C.振子经过P点时的速度比经过Q点时的速度大D.该弹簧振子的振幅一定为8cm11.如图所示,在水平地面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,现将一个质量也为m的物体C从A的正上方一定高度处由静止释放,C和A相碰后立即粘在一起,之后在竖直方向做简谐运动。
机械振动试题(含答案)

机械振动试题(含答案)一、机械振动 选择题1.如图所示为某物体系统做受迫振动的振幅A 随驱动力频率f 的变化关系图,则下列说法正确的是A .物体系统的固有频率为f 0B .当驱动力频率为f 0时,物体系统会发生共振现象C .物体系统振动的频率由驱动力频率和物体系统的固有频率共同决定D .驱动力频率越大,物体系统的振幅越大2.某同学用单摆测当地的重力加速度.他测出了摆线长度L 和摆动周期T ,如图(a)所示.通过改变悬线长度L ,测出对应的摆动周期T ,获得多组T 与L ,再以T 2为纵轴、L 为横轴画出函数关系图像如图(b)所示.由此种方法得到的重力加速度值与测实际摆长得到的重力加速度值相比会( )A .偏大B .偏小C .一样D .都有可能3.用图甲所示的装置可以测量物体做匀加速直线运动的加速度,用装有墨水的小漏斗和细线做成单摆,水平纸带中央的虚线在单摆平衡位置的正下方。
物体带动纸带一起向左运动时,让单摆小幅度前后摆动,于是在纸带上留下如图所示的径迹。
图乙为某次实验中获得的纸带的俯视图,径迹与中央虚线的交点分别为A 、B 、C 、D ,用刻度尺测出A 、B 间的距离为x 1;C 、D 间的距离为x 2。
已知单摆的摆长为L ,重力加速度为g ,则此次实验中测得的物体的加速度为( )A .212()x x gLπ- B .212()2x x gLπ- C .212()4x x gLπ- D .212()8x x gLπ- 4.如图所示,弹簧的一端固定,另一端与质量为2m 的物体B 相连,质量为1m 的物体A 放在B 上,212m m =.A 、B 两物体一起在光滑水平面上的N 、N '之间做简谐运动,运动过程中A、B之间无相对运动,O是平衡位置.已知当两物体运动到N'时,弹簧的弹性势能为pE,则它们由N'运动到O的过程中,摩擦力对A所做的功等于()A.p E B.12pE C.13pE D.14pE5.如图所示,弹簧下面挂一质量为m的物体,物体在竖直方向上做振幅为A的简谐运动,当物体振动到最高点时,弹簧正好处于原长,弹簧在弹性限度内,则物体在振动过程中A.弹簧的弹性势能和物体动能总和不变B.物体在最低点时的加速度大小应为2gC.物体在最低点时所受弹簧的弹力大小应为mgD.弹簧的最大弹性势能等于2mgA6.如图甲所示,一个有固定转动轴的竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架的下面系着一个由弹簧和小球组成的振动系统.圆盘静止时,让小球做简谐运动,其振动图像如图乙所示.圆盘匀速转动时,小球做受迫振动.小球振动稳定时.下列说法正确的是()A.小球振动的固有频率是4HzB.小球做受迫振动时周期一定是4sC.圆盘转动周期在4s附近时,小球振幅显著增大D.圆盘转动周期在4s附近时,小球振幅显著减小7.在“用单摆测定重力加速度”的实验中,用力传感器测得摆线的拉力大小F随时间t变化的图象如图所示,已知单摆的摆长为l,则重力加速度g为( )A .224l t πB .22l t πC .2249l t π D .224l tπ8.公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T .取竖直向上为正方向,以t =0时刻作为计时起点,其振动图像如图所示,则A .t =14T 时,货物对车厢底板的压力最大 B .t =12T 时,货物对车厢底板的压力最小 C .t =34T 时,货物对车厢底板的压力最大 D .t =34T 时,货物对车厢底板的压力最小 9.如图所示,在一条张紧的绳子上悬挂A 、B 、C 三个单摆,摆长分别为L 1、L 2、L 3,且L 1<L 2<L 3,现将A 拉起一较小角度后释放,已知当地重力加速度为g ,对释放A 之后较短时间内的运动,以下说法正确的是( )A .C 的振幅比B 的大 B .B 和C 的振幅相等 C .B 的周期为2π2L g D .C 的周期为2π1L g10.沿某一电场方向建立x 轴,电场仅分布在-d ≤x ≤d 的区间内,其电场场强与坐标x 的关系如图所示。
噪声与振动复习题及答案

噪声与振动复习题及参考答案(40题)参考资料1、杜功焕等,声学基础,第一版(1981),上海科学技术出版社。
2、环境监测技术规范(噪声部分),1986年,国家环境保护局。
3、马大猷等,声学手册,第一版(1984),科学技术出版社。
4、噪声监测与控制原理(1990),中国环境科学出版社。
一、填空题1.在常温空气中,频率为500Hz的声音其波长为。
答:0.68米(波长=声速/频率)2.测量噪声时,要求风力。
答:小于5.5米/秒(或小于4级)3.从物理学观点噪声是由;从环境保护的观点,噪声是指。
答:频率上和统计上完全无规的振动人们所不需要的声音4.噪声污染属于污染,污染特点是其具有、、。
答:能量可感受性瞬时性局部性5.环境噪声是指,城市环境噪声按来源可分为、、、、。
答:户外各种噪声的总称交通噪声工业噪声施工噪声社会生活噪声其它噪声6.声压级常用公式Lp= 表示,单位。
答:Lp=20 LgP/P°dB(分贝)7.声级计按其精度可分为四种类型:O型声级计,是;Ⅰ型声级计为;Ⅱ型声级计为;Ⅲ型声级计为,一般用于环境噪声监测。
答:作为实验室用的标准声级计精密声级计普通声级计调查声级计不得8.用A声级与C声级一起对照,可以粗略判别噪声信号的频谱特性:若A声级比C声级小得多时,噪声呈性;若A声级与C声级接近,噪声呈性;如果A声级比C声级还高出1-2分贝,则说明该噪声信号在Hz 范围内必定有峰值。
答:低频性高频性2000-50009.倍频程的每个频带的上限频率与下限频率之比为。
1/3倍频程的每个频带的上限频率与下限频率之比为;工程频谱测量常用的八个倍频程段是Hz。
答:2 2-1/3 63,125,250,500,1K,2K,4K,8K10.由于噪声的存在,通常会降低人耳对其它声音的,并使听阈,这种现象称为掩蔽。
答:听觉灵敏度推移11.声级计校准方式分为校准和校准两种;当两种校准方式校准结果不吻合时,以校准结果为准。
大学机械振动考试题目及答案

大学机械振动考试题目及答案一、选择题(每题2分,共10分)1. 在简谐振动中,振幅与振动的能量关系是()。
A. 无关B. 成正比C. 成反比D. 振幅越大,能量越小答案:B2. 下列哪个不是机械振动系统的自由度?()。
A. 转动B. 平动C. 振动D. 形变答案:C3. 一个单自由度系统在受到初始条件激励后,其振动形式是()。
A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案:D4. 在阻尼振动中,如果阻尼系数增加,振动的振幅将()。
A. 增加B. 不变C. 减小D. 先增加后减小答案:C5. 对于一个二自由度振动系统,其振动模态数量是()。
A. 1B. 2C. 3D. 4答案:B二、填空题(每题2分,共10分)6. 一个物体做自由振动时,其频率称为______。
答案:固有频率7. 当外力的频率与系统的固有频率相等时,系统发生的振动称为______。
答案:共振8. 阻尼力与速度成正比的阻尼称为______阻尼。
答案:线性9. 振动系统的动态响应可以通过______分析法求解。
答案:傅里叶10. 在转子动力学中,临界转速是指转子发生______振动的转速。
答案:自激三、简答题(每题5分,共20分)11. 简述什么是简谐振动,并说明其运动方程的形式。
答案:简谐振动是一种周期性的振动,其加速度与位移成正比,且方向相反。
在数学上,简谐振动的运动方程可以表示为:x(t) = A * cos(ωt + φ)其中,A 是振幅,ω 是角频率,t 是时间,φ 是初相位。
12. 解释什么是阻尼振动,并说明其特点。
答案:阻尼振动是指在振动系统中存在能量耗散,导致振幅随时间逐渐减小的振动。
其特点包括振幅逐渐衰减,振动频率可能会随着振幅的减小而发生变化,且阻尼力通常与振动速度成正比。
13. 描述什么是受迫振动,并给出其稳态响应的条件。
答案:受迫振动是指系统在周期性外力作用下的振动。
当外力的频率接近系统的固有频率时,系统将发生共振,此时振幅会显著增大。
机械振动现象练习题(含答案)

机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体,在弹簧下端受到一个向下的力2 sin(10t) N,其中t为时间(秒)。
求物体的振动方程。
根据牛顿第二定律,可以得到物体的振动方程为:m * x'' + k * x = F(t)其中,m是物体的质量,x是物体的位移,x''是位移对时间的二阶导数,k是弹簧的常数,F(t)是作用在物体上的外力。
根据题目中给出的数据,代入上述公式,我们可以得到:0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。
2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动,已知质点的质量为0.5 kg。
求质点的角频率和振动周期。
根据振动方程的形式,我们可以知道物体的振动频率和周期与力的形式有关。
在这个题目中,我们可以看出力的形式为cos(3t),它是一个正弦函数。
如果将cos(3t)函数展开,我们可以得到下面的表达式:F(t) = a cos(wt)其中,a是振幅,w是角频率。
根据题目中给出的数据,我们可以得到:a = 0.1 N,w = 3 rad/s由于振动的频率与角频率之间是有关联的,振动的周期T可以表示为:T = 2π/w代入上述数据,我们可以得到:T = 2π/3 s这就是质点的振动周期。
3. 一个质点质量为0.3 kg,在一竖直方向上的弹簧中振动,弹簧的劲度系数为2000 N/m。
当质点受到一个外力F(t) = 0.5 cos(5t) N时,求质点的振动方程。
根据题目中给出的数据,我们可以得到:m = 0.3 kg,k = 2000 N/m,F(t) = 0.5 cos(5t)代入振动方程的一般形式,我们可以得到:0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。
《机械振动与噪声学》习题集与答案

《机械振动噪声学》习题集1-1 阐明下列概念,必要时可用插图。
(a) 振动;(b) 周期振动和周期;(c) 简谐振动。
振幅、频率和相位角。
1-2 一简谐运动,振幅为0.20 cm,周期为0.15 s,求最大的速度和加速度。
1-3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g,求其振动的振幅。
1-4 一简谐振动频率为10 Hz,最大速度为4.57 m/s,求其振幅、周期和最大加速度。
1-5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即:A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' ),并讨论φ=0、π/2 和π三种特例。
1-6 一台面以一定频率作垂直正弦运动,如要求台面上的物体保持与台面接触,则台面的最大振幅可有多大?1-7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象,求其振幅和拍频。
1-8 将下列复数写成指数A e i θ形式:(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i ) 2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8 ]2-1 钢结构桌子的周期τ=0.4 s,今在桌子上放W = 30 N 的重物,如图2-1所示。
已知周期的变化∆τ=0.1 s。
求:( a ) 放重物后桌子的周期;( b )桌子的质量和刚度。
2-2 如图2-2所示,长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住,求杆绕O点微幅振动的微分方程。
2-3 如图2-3所示,质量为m、半径为r的圆柱体,可沿水平面作纯滚动,它的圆心O 用刚度为k的弹簧相连,求系统的振动微分方程。
机械振动学(参考答案).docx

机械振动学试题(参考答案)一、判断题:(对以下论述,正确的打“J”,错误的打“X”,每题2 分,共20分)1、多自由度振动系统的运动微分方程组中,各运动方程间的耦合,并不是振动系统的固有性质,而只是广义坐标选用的结果。
(丁)2、一个单盘的轴盘系统,在高速旋转时,由于盘的偏心质量使轴盘做弓形回旋时,引起轴内产生交变应力,这是导致在临界转速时,感到剧烈振动的原因。
(X)3、单自由度线性无阻尼系统的自由振动频率由系统的参数确定,与初始条件无关。
(丁)4、当激振力的频率等于单自由度线性阻尼系统的固有频率时,其振幅最大值。
(X)5、一个周期激振力作用到单自由度线性系统上,系统响应的波形与激振力的波形相同,只是两波形间有一定的相位差。
(X)6、当初始条件为零,即*产;=0时,系统不会有自由振动项。
(X)7、对于多自由度无阻尼线性系统,其任何可能的自由振动都可以被描述为模态运动的线性组合。
(丁)8、任何系统只有当所有自由度上的位移均为零时,系统的势能才可能为零。
(X )9、隔振系统的阻尼愈大,则隔振效果愈好。
(X)10、当自激振动被激发后,若其振幅上升到一定程度并稳定下来,形成一种稳定的周期振动,则这种振幅自稳定性,是由于系统中的某些非线性因素的作用而发生的。
(J)二、计算题:1、一台面以f频率做垂直正弦运动。
如果求台面上的物理保持与台面接触,则台面的最大振幅可有多大?(分)解:台面的振动为:x = X sin(tyZ - cp)x = —a>2X sin(or —cp)最大加速度:无max = "X如台面上的物体与台面保持接触,贝U :九《=g (9・81米/秒2)。
所以,在f 频率(/=仝)时,最大振幅为:2nX max =x< g/4^72= 9.81/4* 严(米)2、质量为ni 的发电转子,它的转动惯量J 。
的确定采用试验方法:在转子经向Ri 的 地方附加一小质量mi 。
试验装置如图1所示,记录其振动周期。
机械振动与噪声学答案

机械振动与噪声学答案1. 机械振动的基本概念及分类机械振动是指机械运动中出现的周期性变化,通常包括以下几个方面:•振幅:振动系统的最大偏移量,是振动的主要特征之一。
•周期:振动系统经过一个完整的振动过程所需的时间。
•频率:振动系统在单位时间内所完成的振动次数。
•相位:用来描述振动状态的相对时间位置,是一种相对概念,通常用弧度来表示。
•谐振:振动系统的固有频率与外界激励频率相等时产生的现象,通常会引起振幅的急剧增加。
•非谐振:振动系统的固有频率与外界激励频率不等时产生的现象,随着激励频率的不同,振幅和相位也会不同。
根据机械振动的性质和机械结构的不同,可以将机械振动分为以下几类:•自由振动:振动系统在没有外界干扰的情况下,按照固有频率自行振动的过程。
•强迫振动:振动系统受到外界周期性的激励,按照外界激励的频率发生振动,通常比自由振动更为复杂。
•阻尼振动:振动系统因为受到摩擦力的作用而逐渐减弱的振动过程。
•维持振动:振动系统受到外界持续的激励时能够保持稳定的振动状态。
2. 声波的基本概念及特性噪声是指那些会引起人类不适的声音,它的特点是声强大、频率广泛,通常会对人的身体产生负面影响。
声波是一种在空气、水、固体等介质中传播的机械波,声波的基本概念包括以下几个方面:•音量:声音的强度,是声波与人耳之间的相对力度比较。
它通常用分贝(dB)来表示。
•频率:声波的频率表示了声音的音高,是声波波形中的周期性变化。
•色调:不同频率的声波会产生不同的音色,通常用人耳可以感知的不同声音来描述。
•声速:声波在介质中传播的速度,通常用米/秒来表示。
•声源:产生声波的物体或者振动体。
•声波强度:单位时间内声波传播时单位面积上的能量。
噪声的基本特性包括以下几个方面:•声压级:噪声的声压级决定了噪声的强度,通常用分贝dB来表示。
•频谱特性:噪声的频率分布情况,不同的噪声具有不同的频率分布特性。
•时间特性:噪声的音量随时间的变化,通常用峰值、持续时间来描述。
机械振动与噪声习题答案(1) 部分

振动与噪声习题解答(1)1-4 一简谐振动频率为10Hz ,最大速度为4.57m/s, 求其振幅、周期和最大加速度。
解:简谐振动的一般形式为: x (t )=Asin(ωt +φ) 速度:ẋ(t )=Aωcos(ωt +φ) 其最大速度为Aω=4.57,A =4.57ω=0.7273 周期T=1/f=0.1s, ẍ(t )=−Aω2sin(ωt +φ)ẍ(t )max =4.57ω=287.14 m/s 21-6 一台面以一定频率做垂直正弦运动,如要求台面上的物体保持与台面接触,则台面的最大振幅可有多大?解: 台面上的物体受力分析如下根据牛顿第二定律: mg −F =mẍ(t )=−mAω2sin(ωt +φ) 保持接触,则F ≥0,ẍ(t )max ≤g →A max =g ω21-7 计算两简谐运动x1=Xcos (ωt ),x2=Xcos(ω+ε)t 之和,其中ε≪ω。
如果发生拍振现象,求其振幅和拍频。
解:设x =x1+x2=X [cos (ωt )+cos (ω+ε)t ]=2Xcos (ε2)t cos (ω+ε2)t 上式可以看做是一个余弦函数,由于ε≪ω,频率可近似为ω:x ≈2Xcos (ε2)t cosωt振幅为可变振幅 2Xcos (ε2)t ,当t: 0→ πε →2πε, 振幅从 2X → 0 →2X , 每隔2πε时间重复一次,所以振幅的周期T =2πε,拍频为:T =ε2π 1-11 阐明振动与声的关系和区别答:声波是有振动引起的,这是声与振动的联系;声与振动的区别:振动量是时间t 的函数,而声波的波动量则不仅是时间t 的函数,同时还是空间s 的函数,声波波动量存在的空间称为声场。
2-3. 如图2-33所示,质量为m 、半径为r 的圆柱体,可以沿水平面做纯滚动,它的圆心O 用刚度为k 的弹簧相连,求系统的振动微分方程。
解:采用能量法1) 建立广义坐标。
取质量元件沿水平方向的位移作为广义坐标。
机械振动与噪声学 赵玫 课后习题答案(部分)

衰减为4F /k 。( F 是摩擦力 ) 3-9 求图3-9所示系统的固有频率和主振型。( 杆为刚性,不计质量。) 3-10 选图3-10所示均质杆的质心C 点向下移动的位移 x 及杆顺时针方向转角 为广义 坐标,求系统的固有圆频率和主振型。
图 3- 9
图3-10 求系统的固有频率
3-11 图3-11所示扭转振动系统中, k1 = k2 = k ,J1 = 2 J2 = 2 J。 (a)
图2-1
图2-2
图2-3
2-4 如图2-4所示,质量为 m、半径为 R 的圆柱体,可沿水平面作纯滚动,与圆心O距 离为 a 处用两根刚度为 k 的弹簧相连,求系统作微振动的微分方程。 2-5 求图2-5所示弹簧-质量-滑轮系统的振动微分方程。
图2-4 图2-5 2-6 图2-6所示系统垂直放置,L2 杆处于铅垂位置时系统静平衡,求系统作微振动的微 1
3-12 求图3-10所示系统的振型矩阵 [u]、正则化振型矩阵u 和主坐标。
(0) (0) 0 ,求系统对 和主振型;(b) 设: 1 (0) = 1 rad, 2 (0) = 2 rad, 1 2 初始条件的响应。
3-13 求图3-13所示系统的振型矩阵 [u]、正则化振型矩阵u 和主坐标。 3-14 设图3-14所示系统中, 轴的抗弯刚度为 EI,它的惯性矩不计,圆盘的转动惯量 J 2 = mR /4,R = L/4,静平衡时轴在水平位置。求系统的固有频率。
图2-13
图2-14
图2-15
图2-16
2-17 如图2-17所示,系统中 k 1 = k2 = k3 = k ,m1 = m2 = m,r1 = r2 = r ,J1 = J2 = J。求 2
系统的振动微分方程。 2-18 图2-18为行车载重小车运动的力学模型,小车质量 m1 ,受到两根刚度为 k 弹簧 的约束,悬挂物品质量为 m2 ,悬挂长度为 L,摆角 很小,求系统的振动微分方 程。
机械振动与噪声学 赵玫 课后习题答案(部分)

3-12 求图3-10所示系统的振型矩阵 [u]、正则化振型矩阵u 和主坐标。
(0) (0) 0 ,求系统对 和主振型;(b) 设: 1 (0) = 1 rad, 2 (0) = 2 rad, 1 2 初始条件的响应。
3-13 求图3-13所示系统的振型矩阵 [u]、正则化振型矩阵u 和主坐标。 3-14 设图3-14所示系统中, 轴的抗弯刚度为 EI,它的惯性矩不计,圆盘的转动惯量 J 2 = mR /4,R = L/4,静平衡时轴在水平位置。求系统的固有频率。
衰减为4F /k 。( F 是摩擦力 ) 3-9 求图3-9所示系统的固有频率和主振型。( 杆为刚性,不计质量。) 3-10 选图3-10所示均质杆的质心C 点向下移动的位移 x 及杆顺时针方向转角 为广义 坐标,求系统的固有圆频率和主振型。
图 3- 9
图3-10 求系统的固有频率
3-11 图3-11所示扭转振动系统中, k1 = k2 = k ,J1 = 2 J2 = 2 J。 (a)
分方程。 2-7 求图2-7所示系统的振动微分方程。 2-8 试用能量法确定图2-8所示系统的振动微分方程。(假定 m 系统的静平衡位置。)
2
>
m 1 ,图示位置是
图2-6
图2-7
图2-8
2-9 试确定图2-9所示弹簧系统的等效刚度。 2-10 求跨度为 L 的均匀简支梁在离支承点 L 3 处的等效刚度系数。 2-11 求图2-11所示系统对于广义坐标 x 的等效刚度。 2-12 一质量为 m、长度为 L 的均匀刚性杆,在距左端 O为 n L 处设一支承点,如图2 -12所示。求杆对O点的等效质量。
图3-11
图3-13
图3-14
3-15 用 Rayleigh 法和 Dunkerley 公式估算图 2-16 所示系统中质点在铅垂平面中作垂 直于绳索微振动时的基频,并与精确解相比较。 4-1 如图4-1所示,一质量为 m 的油缸与刚度为 k 的弹簧相连,通过阻尼系数为 c 的 粘性阻尼器以运动规律 y = A sin t 的活塞给予激励,求油缸运动的振幅以及它相 对于活塞的相位。 4-2 试导出图4-2所示系统的振动微分方程,并求系统的稳态响应。 4-3 求图4-3所示弹簧-质量系统在库仑阻尼和简谐激励力 F 0 sin t 作用下的振幅。 在什么条件下运动能继续?
机械振动与噪声学答案
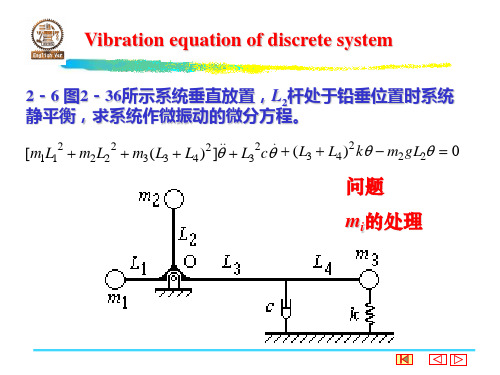
2-6 图2-36所示系统垂直放置,L2杆处于铅垂位置时系统 静平衡,求系统作微振动的微分方程。 [m1L12 m2L22 m3(L3 L4)2] L32c (L3 L4)2 k m2gL2 0
问题 mi的处理
柔度阵
L 2 1 3T 1 2
m2 L 3T
2 1
1 2 2 0
0 1
x x
1 2
x x
1 2
0 0
Vibration equation of discrete system
2-17 如图2-46所示,系统中 k1 = k2 = k3 = k,m1 = m2 = m,r1 = r2 = r ,J1 = J2 = J。求系统的振动微分方程。
1 2
k r2 , 1, { [ -1, 1 ] }
J
3 k r2 J , 1, { [ 1, 1 ] }
J1
0
0 J2
12
k1
k2 k2r2
r
2
k2
k2r2 k3
r
2
12
0 0
Vibration equation of discrete system
2-17 如图2-46所示,系统中 k1 = k2 = k3 = k,m1 = m2 = m,r1 = r2 = r ,J1 = J2 = J。求系统的振动微分方程。
1
4
f n 2π m( 1 1 1 1 )
4k 1 4k 2 k 3 k 4
详细推导
Free Vibration
1
k3 k1
k4 k2
? ke
Free Vibration
机械振动与噪声学 赵玫 课后习题答案(部分)

图4-9
图4-10
图4-11
4-12 一弹簧-质量系统,从t = 0时,突加一个F 0 力,以后该力保持不变。试用Duhamel 积分求系统的响应,并概略图示之。(图4-12) 4-13 一弹簧-质量系统,从t = 0开始作用一不变的F 0 力,作用时间为t0 (图4-13)。求 系统在t t0 和 t t0 两种情况下的响应,并找出 t t0 时最大位移与 t0 / 的关系。如 果 t0 与系统自振周期 相比很小,最大位移为多少? 请与脉冲响应函数比较。 4-14 一单自由度无阻尼弹簧-质量系统,受到图4 -14所示力的激励,请用Duhamel积 分求系统在 t < t1 和 t > t1 两种情况下的响应,并概略图示之。 4-15 求弹簧-质量系统在图4-15所示激励下的响应。
图2-9
图2-11
图2-12
2-13 如图 2-13 所示,悬臂梁长度为 L,弯曲刚度为EI,质量不计。求系统的等效刚度 和等效质量。 2 - 14 图2 - 14 是固定滑车力学模型。起吊物品质量为 m,滑轮绕中心 O 的转动惯量为 J0 ,假定绳索与滑轮间无滑动,求系统的振动微分方程。 2-15 用视察法建立图2-15所示链式系统的振动微分方程。 2-16 如图2-16所示,绳索上有两个质量 m1 和 m2 ( m1 = 2 m2 ),各段绳索中的张力均 为T ,用柔度法建立系统作微振动的微分方程。
分方程。 2-7 求图2-7所示系统的振动微分方程。 2-8 试用能量法确定图2-8所示系统的振动微分方程。(假定 m 系统的静平衡位置。)
2
>
m 1 ,图示位置是
图2-6
图2-7
图2-8
2-9 试确定图2-9所示弹簧系统的等效刚度。 2-10 求跨度为 L 的均匀简支梁在离支承点 L 3 处的等效刚度系数。 2-11 求图2-11所示系统对于广义坐标 x 的等效刚度。 2-12 一质量为 m、长度为 L 的均匀刚性杆,在距左端 O为 n L 处设一支承点,如图2 -12所示。求杆对O点的等效质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《机械振动噪声学》习题集1-1 阐明下列概念,必要时可用插图。
(a) 振动; (b) 周期振动和周期;(c) 简谐振动。
振幅、频率和相位角。
1-2 一简谐运动,振幅为 0.20 cm,周期为 s,求最大的速度和加速度。
1-3 一加速度计指示结构谐振在 82 Hz 时具有最大加速度 50 g,求其振动的振幅。
1-4 一简谐振动频率为 10 Hz,最大速度为 4.57 m/s,求其振幅、周期和最大加速度。
1-5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即:A cos n t +B cos (n t + ) =C cos (n t + ' ),并讨论=0、/2和三种特例。
1-6 一台面以一定频率作垂直正弦运动,如要求台面上的物体保持与台面接触,则台面的最大振幅可有多大?1-7 计算两简谐运动x1 = X1 cos t和x2 = X2 cos ( + ) t之和。
其中<< 。
如发生拍的现象,求其振幅和拍频。
1-8 将下列复数写成指数A e i 形式:(a) 1 + i3 (b) 2 (c) 3 / (3 - i ) (d) 5 i (e) 3/ (3 - i ) 2(f) (3 + i ) (3 + 4 i ) (g) (3 - i ) (3 - 4 i ) (h)( 2 i ) 2 + 3 i + 82-1 钢结构桌子的周期= s,今在桌子上放W = 30 N 的重物,如图2-1所示。
已知周期的变化= s。
求:( a ) 放重物后桌子的周期;( b )桌子的质量和刚度。
2-2 如图2-2所示,长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住,求杆绕O点微幅振动的微分方程。
2-3 如图2-3所示,质量为m、半径为r的圆柱体,可沿水平面作纯滚动,它的圆心O用刚度为k的弹簧相连,求系统的振动微分方程。
图2-1 图2-2 图2-32-4 如图2-4所示,质量为m、半径为R的圆柱体,可沿水平面作纯滚动,与圆心O距离为a 处用两根刚度为k的弹簧相连,求系统作微振动的微分方程。
2-5 求图2-5所示弹簧-质量-滑轮系统的振动微分方程。
图2-4 图2-52-6 图2-6所示系统垂直放置,L2杆处于铅垂位置时系统静平衡,求系统作微振动的微分方程。
2-7 求图2-7所示系统的振动微分方程。
2-8 试用能量法确定图2-8所示系统的振动微分方程。
(假定m 2 > m 1,图示位置是系统的静平衡位置。
)图2-6 图2-7 图2-82-9 试确定图2-9所示弹簧系统的等效刚度。
2-10 求跨度为L 的均匀简支梁在离支承点L 3 处的等效刚度系数。
2-11 求图2-11所示系统对于广义坐标x 的等效刚度。
2-12 一质量为m、长度为L 的均匀刚性杆,在距左端O为n L 处设一支承点,如图2-12所示。
求杆对O点的等效质量。
图2-9 图2-11 图2-122-13 如图2-13所示,悬臂梁长度为L,弯曲刚度为EI,质量不计。
求系统的等效刚度和等效质量。
2-14 图2-14是固定滑车力学模型。
起吊物品质量为m,滑轮绕中心O的转动惯量为J0,假定绳索与滑轮间无滑动,求系统的振动微分方程。
2-15 用视察法建立图2-15所示链式系统的振动微分方程。
2-16 如图2-16所示,绳索上有两个质量m1和m2 ( m1 = 2 m2 ),各段绳索中的张力均为T,用柔度法建立系统作微振动的微分方程。
图2-13 图2-14 图2-15 图2-162-17 如图2-17所示,系统中k1 = k2 = k3 = k,m1 = m2 = m,r1 = r2 = r,J1 = J2 = J。
求系统的振动微分方程。
2-18 图2-18为行车载重小车运动的力学模型,小车质量m1,受到两根刚度为k弹簧的约束,悬挂物品质量为m2,悬挂长度为L,摆角很小,求系统的振动微分方程。
图2-17 图2-18 图3-13-1 如图3-1所示,杆 a 与弹簧k1和k2相连,弹簧k3置于杆 a 的中央,杆 b 与弹簧k3和k4相连,质量m置于杆 b 的中央。
设杆 a 和杆 b 为质量和转动惯矩可忽略的刚性杆,并能在图示平面内自由移动和转动。
求质量m 上、下振动的固有频率。
3-2 如图3-2所示,一薄长板条被弯成半圆形,在水平面上摇摆。
用能量法求它摇摆的周期。
3-3 如图3-3所示,一长度为L、质量为m 的均匀刚性杆铰接在O点,并以弹簧和粘性阻尼器支承。
求:(a) 系统作微振动的微分方程;(b) 系统的无阻尼固有频率;(c) 系统的临界阻尼。
3-4 系统参数和几何尺寸如图3-4所示,刚性杆质量可忽略。
求:(a) 系统作微振动的微分方程;(b) 临界阻尼系数;(c) 有阻尼固有频率。
3-5 如图3-5所示,质量为m1的重物悬挂在刚度为k 的弹簧上并处于静平衡位置,质量为m2的重物从高度为h 处自由降落到m1 上而无弹跳,求系统的运动规律。
图3-2 图3-3 图3-4 图3-53-6 弹簧-质量-粘性阻尼器系统中,质量m = 10 kg·s2/m,弹簧刚度k = 1000 kg/m,初始条件为x0 = 0.01 m, x= 0。
求:系统的阻尼比分别为=0、和三种情况下系统对初始条件的响应,并给出概略简图。
3-7 图3-7所示带有库仑阻尼的系统中,质量 m = 9 kg ,弹簧刚度 k = 7 kN/m ,摩擦系数 = ,初始条件是x x 00250==mm,&。
求:(a) 位移振幅每周衰减; (b) 最大速度;(c) 速度振幅每周衰减;(d) 物体 m 停止的位置。
3-8 对只有库仑阻尼的弹簧-质量系统,用能量观点证明:对于自由振动,每周期振幅衰减为4F /k 。
( F 是摩擦力 )3-9 求图3-9所示系统的固有频率和主振型。
( 杆为刚性,不计质量。
)3-10 选图3-10所示均质杆的质心C 点向下移动的位移 x 及杆顺时针方向转角 为广义坐标,求系统的固有圆频率和主振型。
图3-9 图3-10 3-11 图3-11所示扭转振动系统中, k 1 = k 2 = k ,J 1 = 2 J 2 = 2 J 。
(a) 求系统的固有频率和主振型;(b) 设:)0(1θ = 1 rad ,)0(2θ = 2 rad ,0)0()0(21==θθ&&,求系统对初始条件的响应。
3-12 求图3-10所示系统的振型矩阵 [u]、正则化振型矩阵[]u 和主坐标。
3-13 求图3-13所示系统的振型矩阵 [u]、正则化振型矩阵[]u 和主坐标。
3-14 设图3-14所示系统中, 轴的抗弯刚度为 EI ,它的惯性矩不计,圆盘的转动惯量 J= mR 2/4,R = L /4,静平衡时轴在水平位置。
求系统的固有频率。
图3-7图3-11 图3-13 图3-143-15 用 Rayleigh 法和 Dunkerley 公式估算图2-16所示系统中质点在铅垂平面中作垂直于绳索微振动时的基频,并与精确解相比较。
4-1 如图4-1所示,一质量为m 的油缸与刚度为k 的弹簧相连,通过阻尼系数为c 的粘性阻尼器以运动规律y = A sin t 的活塞给予激励,求油缸运动的振幅以及它相对于活塞的相位。
4-2 试导出图4-2所示系统的振动微分方程,并求系统的稳态响应。
4-3 求图4-3所示弹簧-质量系统在库仑阻尼和简谐激励力 F 0 sin t 作用下的振幅。
在什么条件下运动能继续?图4-1 图4-2 图4-34-4 一重物悬挂在刚度k = 3 kN/m 的弹簧下,测得系统振动的准周期为 1 s,系统阻尼比为,当外力F = 20 cos 3t (N) 作用于系统上时,求系统稳态振动的振幅和相位。
4-5 带结构阻尼的单自由度系统,若刚度用复数形式k = k0 e i 2 表示。
求系统在简谐激励下的响应。
4-6 具有粘性阻尼的弹簧-质量系统在简谐力作用下作强迫振动。
求加速度幅值达到最大值时的频率比、放大因子和Q因子。
4-7 具有粘性阻尼的弹簧-质量系统在简谐力作用下作强迫振动。
求速度幅值达到最大值时的频率比、放大因子和Q因子。
4-8 具有粘性阻尼的弹簧-质量系统在简谐力作用下作强迫振动。
求位移幅值达到最大值时的频率比、放大因子和Q因子。
4-9 如图4-9所示,弹性支承的车辆沿高低不平的道路运行。
试求出车辆振幅与运行速度v之间的关系,并确定最不利的运行速度。
4-10 图4-10所示系统中,集中质量m = 20 kg,弹簧刚度k = kN/m,阻尼器的粘性阻尼系数为c = kN s /m,凸轮的转速为 60 rpm,行程为 0.01 m。
试求系统的稳态响应x (t)。
4-11 如图4-11所示,一个弹簧-质量系统从倾斜角为30的光滑斜面下滑。
求弹簧从开始接触挡板到脱开挡板的时间。
图4-9 图4-10 图4-114-12 一弹簧-质量系统,从t = 0时,突加一个F 0力,以后该力保持不变。
试用Duhamel积分求系统的响应,并概略图示之。
(图4-12)4-13 一弹簧-质量系统,从t = 0开始作用一不变的F 0力,作用时间为t0 (图4-13)。
求系统在t t0和t t0两种情况下的响应,并找出t t0时最大位移与t0 / 的关系。
如果t0与系统自振周期相比很小,最大位移为多少? 请与脉冲响应函数比较。
4-14 一单自由度无阻尼弹簧-质量系统,受到图4-14所示力的激励,请用Duhamel积分求系统在t < t1和t > t1两种情况下的响应,并概略图示之。
4-15 求弹簧-质量系统在图4-15所示激励下的响应。
图4-12 图4-13 图4-14 图4-154-16 对弹簧-质量系统,从t = 0开始施加按直线变化的力,即f (t) = a t ( a = const )。
请用Duhamel积分求系统的响应,并概略图示之。
4-17 试用拉普拉斯变换方法解题4-12。
4-18 试用拉普拉斯变换方法解题4-13。
4-19 求图4-19所示系统的稳态响应。
4-20 转动惯量为J的飞轮通过四个刚度为k的弹簧与转动惯量为J d并能在轴上自由转动的扭转减振器相联,见图4-20。
试建立系统作扭转振动的微分方程。
若在飞轮上作用一简谐变化的扭矩T sin t,求:(a)系统的稳态响应;(b)飞轮不动时J d的固有频率;(c)J d / J 的比值,使联接减振器后系统的固有频率为激振频率的倍。
4-21 求图4-21所示系统的稳态响应。
图4-19 图4-20 图4-215-1 具有粘性阻尼的弹簧-质量系统,使质量偏离平衡位置然后释放。
如果每一循环振幅减小 5 ,那么系统所具有的等效粘性阻尼系数占临界阻尼系数的百分之几?5-2 一振动系统具有下列参数:质量m = 17 5 kg,弹簧刚度k = N/cm,粘性阻尼系数 c = N s/cm。
