2012新课标高考数学试题及答案
2012年高考真题试卷理科数学(新课标卷)答案解析版(1)

2012年普通高等学校招生全国统一考试理科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
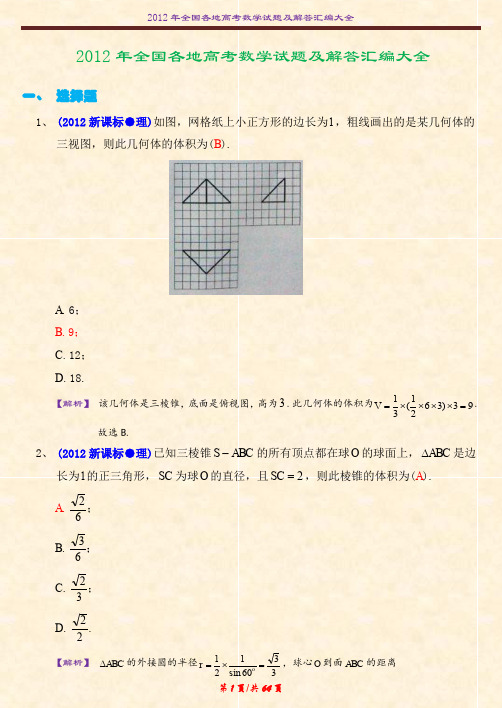
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第一卷一.选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素的个数为( )()A 3 ()B 6()C 8 ()D 10【解析】选D5,1,2,3,x y ==,4,1,2,3x y ==,3,1,2x y ==,2,1x y ==共10个 (2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种 ()B 10种()C 9种 ()D 8种【解析】选A甲地由1名教师和2名学生:122412C C =种(3)下面是关于复数21z i=-+的四个命题:其中的真命题为( )1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【解析】选C 22(1)11(1)(1)iz i ii i--===---+-+--1:2p z =,22:2p z i =,3:p z 的共轭复数为1i -+,4:p z 的虚部为1-(4)设12F F 是椭圆2222:1(0)x y E a b ab+=>>的左、右焦点,P 为直线32a x =上一点,∆21F P F 是底角为30 的等腰三角形,则E 的离心率为( )()A 12()B23()C 34()D 45【解析】选C∆21F P F 是底角为30 的等腰三角形221332()224cP F F F a c c e a ⇒==-=⇔==(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )()A 7 ()B 5()C -5 ()D -7【解析】选D472a a +=,56474784,2a a a a a a ==-⇒==-或472,4a a =-=471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-(6)如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则( )()A A B +为12,,...,n a a a 的和 ()B 2A B +为12,,...,n a a a 的算术平均数()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A 和B 分别是12,,...,n a a a 中最小的数和最大的数【解析】选C(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6 ()B 9 ()C 12 ()D 18【解析】选B该几何体是三棱锥,底面是俯视图,高为3 此几何体的体积为11633932V =⨯⨯⨯⨯=(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,43AB =;则C 的实轴长为( )()A 2 ()B 22 ()C 4 ()D 8【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(4,23)A -(4,23)B -- 得:222(4)(23)4224a a a =--=⇔=⇔=(9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
2012年高考理科数学试题及答案-全国卷2

2012年高考数学试题(理) 第1页【共10页】2012年普通高等学校招生全国统一考试(新课标Ⅱ卷)理 科 数 学第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合A ={1, 2, 3, 4, 5},B ={(x ,y )| x ∈A , y ∈A , x —y ∈A },则B 中所含元素的个数为( )A 。
3B. 6C. 8D 。
102. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有( ) A. 12种B. 10种C 。
9种D 。
8种3。
下面是关于复数iz +-=12的四个命题中,真命题为( )P 1: |z |=2, P 2: z 2=2i , P 3: z 的共轭复数为1+i , P 4: z 的虚部为-1 。
A 。
P 2,P 3B 。
P 1,P 2C 。
P 2,P 4D. P 3,P 44。
设F 1,F 2是椭圆E : 12222=+b y a x )0(>>b a 的左右焦点,P 为直线23ax =上的一点,12PF F △是底角为30º的等腰三角形,则E 的离心率为( ) A 。
21B 。
32 C.43 D 。
54 5。
已知{a n }为等比数列,a 4 + a 7 = 2,a5 a6 = 8,则a 1 + a 10 =( )A. 7B. 5C. —5D. —76. 如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1, a 2,…,a N ,输入A 、B ,则( ) A 。
A +B 为a 1, a 2,…,a N 的和B 。
2B A +为a 1, a 2,…,a N 的算术平均数C 。
A 和B 分别是a 1, a 2,…,a N 中最大的数和最小的数D 。
A 和B 分别是a 1, a 2,…,a N 中最小的数和最大的数 7. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )2012年高考数学试题(理) 第2页【共10页】A 。
2012 年全国各地高考数学试题及解答汇编大全
3、 (2012 全国卷大纲版●理)将字母 a,a,b,b,c,c 排成三行两列, 要求每行的字母 互不相同,每列的字母也互不相同,则不同的排列方法共有(A). A. 12 种; B. 18 种; C. 24 种; D. 36 种. 4、 (2012 全国卷大纲版●理)正方形 ABCD 的边长为 1,点 E 在边 AB 上,点 F 在边 BC 上, AE BF
2、 (2012 新课标●理)已知三棱锥 S ABC 的所有顶点都在球 O 的球面上, ABC 是边 长为 1 的正三角形, SC 为球 O 的直径,且 SC 2 ,则此棱锥的体积为(A). A. B. C. D.
2 ; 6
3 ; 6 2 ; 3
2 . 2
【解析】 ABC 的外接圆的半径 r 1 1 o 3 ,球心 O 到面 ABC 的距离 2 sin 60 3 第 1 页/共 64 页
1 1 1 1 f ( y),即 y f 1 ( x) g ( x) 知, y f (2 x) 的 2 2 2
反函数是 y 1 g ( x) ,故函数 y f (2 x) 与 y 1 g ( x) 的图像也关于直线 y x 对称;正 2 2 确. ③ f ( x) f (2 x) f ( x 2) f [2 ( x 2)] f (4 x) f ( x 4) .故 f ( x) 是周期为 4 的函数. 故选 C.
由对称性知, y x,y 1 , ( x 1) 2 ( y 1) 2 1 围成的面积与 x
1 y x,y , ( x 1)2 ( y 1)2 1 围成的面积相等. x
故 A B 所表示的平面图形的面积为 y x , ( x 1)2 ( y 1)2 1 围成的面积
2012新课标高考数学试卷真题(理科)

2012年普通高等学校招生全国统一考试理科数学注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第I卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第II卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所含元素的个数为A.3B.6C.8D.102.将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组有1名教师和2名学生组成,不同的安排方案共有A.12种B.10种C.9种D.8种(3)下面是关于复数z=-1+i/2的四个命题P1:|Z|=2 p2: Z2=2ioOo-OP3:z的共轭复数为1+I P4 :z的虚部为-1其中真命题为A P2 ,P3B P1 ,P2C P2,P4D P3 P4(4)设F1,F2是椭圆E:a2/x2+b2/y2=1 (a>b>0)的左、右焦点,P为直线x=3/2a上的一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为A 2/1B 3/2C 4/3D 5/4(5)已知{an}为等比数列,a4+a1=2 a5a6=-8 则a1+a10 =A.7B.5 C-5 D.-7(6)如果执行右边的程序图,输入正整数N(N≥2)和实数a1.a2,…a n,输入A,B,则A)A+B为a1a2,…,an的和(B)2/A+B为a1a2.…,an的算式平均数(C)A和B分别是a1a2,…a n中最大的数和最小的数(D)A和B分别是a1a2,…a n中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A)6 (B)9 (C)12 (D)18(8)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y²=16x 的准线交于A,B两点,|ab|=4/3,则C的实轴长为(A)(B)(C)4(D)8(9)已知w>0,函数f(x)=sin(wx+4/r)在单调递减,则w的取值范围是(A)|2/1,4/5|(B)|2/1*4/3||(C)0,2/1(D)(0,2](10)已知函数,f(x)=in(x+1)-x/1则y=f(x)的图像大致为(11)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为O的直径,且SC=2,则此棱锥的体积为(12)设点P在曲线上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为(A)1-ln2(B)(C)1+ln2(D)第Ⅱ卷本卷包括必考题和选考题两部分。
2012年高考新课标全国卷文科数学试题(附答案)

2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.(1)已知集合A={x |x 2−x −2〈0},B={x |−1〈x 〈1},则(A )A 错误!B (B )B 错误!A (C )A=B (D )A ∩B=∅(2)复数z =32i i -++的共轭复数是 (A )2i + (B )2i - (C )1i -+ (D )1i --(3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为(A)−1 (B)0 (C )错误! (D )1 (4)设1F ,2F 是椭圆E :2222x y a b+=1(a >b >0)的 左、 右焦点,P 为直线32a x =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为(A )12 (B )23 (C )34 D 。
45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC内部,则z x y =-+的取值范围是(A)(1-错误!,2) (B )(0,2) (C )(错误!-1,2) (D )(0,1+错误!)(6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数1a ,2a ,…,N a ,输出A ,B ,则(A)A +B 为1a ,2a ,…,N a 的和(B)2A B +为1a ,2a ,…,N a 的算术平均数 (C )A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数(D)A 和B 分别为1a ,2a ,…,N a 中的最小数和最大数(7)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A )6(B )9(C )12(D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为错误!,则此球的体积为(A )错误!π (B)4错误!π (C )4错误!π (D)6错误!π(9)已知ω〉0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=(A )错误! (B )错误! (C)错误! (D )错误!(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A 、B 两点,||AB =43,则C 的实轴长为(A )2 (B )22 (C )4 (D )8(11)当0〈x ≤错误!时,4log x a x <,则a 的取值范围是(A )(0,错误!) (B )(错误!,1) (C )(1,错误!) (D )(错误!,2)(12)数列{n a }满足1(1)21n n n a a n ++-=-,则{n a }的前60项和为(A )3690 (B)3660 (C)1845 (D)1830二.填空题:本大题共4小题,每小题5分。
2012年新课标数学高考试题(理科数学理科数学高考试题,word教师版【免费下载】)

2012年普通高等学校招生全国统一考试(新课标) 理科数学第一卷一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素的个数为( )()A 3()B 6 ()C 8 ()D 10【解析】选D5,1,2,3,x y ==,4,1,2,3x y ==,3,1,2x y ==,2,1x y ==共10个 (2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种()B 10种 ()C 9种()D 8种【解析】选A甲地由1名教师和2名学生:122412C C =种 (3)下面是关于复数21z i=-+的四个命题:其中的真命题为( )1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【解析】选C 22(1)11(1)(1)iz i ii i --===---+-+--1:p z =22:2p z i =,3:p z 的共轭复数为1i -+,4:p z 的虚部为1-(4)设12F F 是椭圆2222:1(0)x y E a b ab+=>>的左、右焦点,P 为直线32a x =上一点,∆21F P F 是底角为30 的等腰三角形,则E 的离心率为( )()A 12()B23()C 34()D 45【解析】选C ∆21F P F 是底角为30的等腰三角形221332()224c P F F F a c c e a ⇒==-=⇔==(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )()A 7()B 5 ()C -5()D -7【解析】选D472a a +=,56474784,2a a a a a a ==-⇒==-或472,4a a =-= 471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-(6)如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则( )()A A B +为12,,...,n a a a 的和()B 2A B +为12,,...,n a a a 的算术平均数()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A和B 分别是12,,...,n a a a 中最小的数和最大的数【解析】选C(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6()B 9 ()C 12 ()D 18【解析】选B该几何体是三棱锥,底面是俯视图,高为3 此几何体的体积为11633932V =⨯⨯⨯⨯=(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =C 的实轴长为( )()A ()B ()C 4 ()D 8【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(4,A -(4,B --得:222(4)4224a a a =--=⇔=⇔=(9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
2012年全国高考(新课标-)文科数学试卷及参考答案-2
2012年普通高等学校招生全国统一考试 (新课标文科数学试卷及参考答案)第Ⅰ卷一、选择题1.已知集合A={x |x 2-x -2<0},B={x |-1<x <1},则( )(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅ 2.复数z =-3+i2+i的共轭复数是 ( )(A )2+i (B )2-i (C )-1+i (D )-1-i 3.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为 ( )(A )-1 (B )0 (C )12(D )14.设F 1、F 2是椭圆E :x 2a 2+y 2b2=1(a >b >0)的左、右焦线x =3a2上一点,△F 1PF 2是底角为30°的等腰三角E 的离心率为( )(A )12 (B )23 (C )34 (D )455.已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 象限,若点(x ,y )在△ABC 内部,则z=-x+y 的取值是( )(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3)6.如果执行右边的程序框图,输入正整数N(N ≥2)和数a 1,a 2,…,a N ,输出A,B ,则( ) (A )A+B 为a 1,a 2,…,a N 的和(B )A +B 2为a 1,a 2,…,a N 的算术平均数(C )A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的(D )A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的7.如图,网格纸上小正方形的边长为1,粗线画出的何体的三视图,则此几何体的体积为( ) (A )6 (B )9 (C )12 (D )188.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为 ( )(A )6π (B )43π (C )46π (D )63π9.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x 条相邻的对称轴,则φ=( )(A )π4 (B )π3 (C )π2 (D )3π410.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB|=43,则C 的实轴长为( )(A ) 2 (B )2 2 (C )4 (D )811.当0<x ≤12时,4x<log a x ,则a 的取值范围是 ( )(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2) 12.数列{a n }满足a n +1+(-1)na n =2n -1,则{a n }的前60项和为( ) (A )3690 (B )3660 (C )1845 (D )1830 第Ⅱ卷二.填空题13.曲线y =x (3ln x +1)在点(1,1)处的切线方程为________14.等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =_______ 15.已知向量a ,b 夹角为45°,且|a |=1,|2a -b |=10,则|b |=16.设函数f (x )=(x +1)2+sin xx 2+1的最大值为M ,最小值为m ,则M+m =____三、解答题17.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,c = 3a sinC -c cosA (1) 求A(2) 若a =2,△ABC 的面积为3,求b ,c 18.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。
2012年高考理科数学全国卷1(含答案解析)
绝密★启用前2012年普通高等学校招生全国统一考试(全国新课标卷1)数学(理科)适用地区:海南、宁夏、黑龙江、吉林、山西、河南、新疆、云南、河北、内蒙古 注息事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3. 回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.4. 考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{1,2,3,4,5}A =,{(,)|,,}B x y x A y A x y A =∈∈-∈,则B 中所含元素的个数为( )A . 3B . 6C . 8D . 102. 将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )A . 12种B . 10种C . 9种D . 8种3. 下面是关于复数21iz =-+的四个命题: 1:||2p z =;22:2i p z =;3:p z 的共轭复数为1i +;4:p z 的虚部为1-.其中的真命题为( )A . 23,p pB . 12,p pC . 24,p pD . 34,p p4. 设1F ,2F 是椭圆E :22221(0)x y a b a b +=>>的左、右焦点,P 为直线32ax =上一点,21F PF △是底角为30的等腰三角形,则E 的离心率为( )A . 12B . 23C . 34D . 455. 已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( ) A . 7 B . 5 C . 5-D . 7-6. 如果执行右边的程序框图,输入正整数(2)N N ≥和实数1a ,2a ,,N a ,输出A ,B ,则( )A . AB +为1a ,2a ,,N a 的和B .2A B+为1a ,2a ,,N a 的算术平均数C . A 和B 分别是1a ,2a ,,N a 中最大的数和最小的数D . A 和B 分别是1a ,2a ,,N a 中最小的数和最大的数7. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A . 6B . 9C . 12D . 188. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A ,B 两点,||43AB =,则C 的实轴长为( )A .2B . 22C . 4D . 89. 已知0ω>,函数π()sin()4f x x ω=+在π(,π)2上单调递减,则ω的取值范围是 ( ) A . 15[,]24B . 13[,]24C . 1(0,]2D . (0,2] 10. 已知函数1()ln(1)f x x x=+-,则()y f x =的图象大致为( )ABCD11. 已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )A . 26B . 36C . 23D . 2212. 设点P 在曲线1e 2x y =上,点Q 在曲线ln(2)y x =上,则||PQ 的最小值为( )A . 1ln2-B . 2(1ln 2)-C . 1ln2+D .2(1ln 2)+第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13. 已知向量a ,b 夹角为45,且||1=a ,2|10-=|a b ,则|=|b _________.14. 设x ,y 满足约束条件1300x y x y x y --⎧⎪+⎪⎨⎪⎪⎩≥,≤,≥,≥,则2z x y =-的取值范围为_________.姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------15. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布2(1 000,50)N ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1 000小时的概率为_________.16. 数列{}n a 满足1(1)21nn n a a n ++-=-,则{}n a 的前60项和为_________.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,cos 3sin 0a C a C b c +--=. (Ⅰ)求A ;(Ⅱ)若2a =,ABC △的面积为3,求b ,c .18.(本小题满分12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花做垃圾处理.(Ⅰ)若花店一天购进16枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,n ∈N )的函数解析式;(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n 14 15 16 17 18 19 20 频数10201616151310以100天记录的各需求量的频率作为各需求量的概率.(ⅰ)若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差;(ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.19.(本小题满分12分)如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,1DC BD ⊥. (Ⅰ)证明:1DC BC ⊥;(Ⅱ)求二面角11A BD C --的大小.20.(本小题满分12分)设抛物线C :22(0)x py p =>的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B ,D 两点.(Ⅰ)若90BFD ∠=,ABD △的面积为42,求p 的值及圆F 的方程;(Ⅱ)若A ,B ,F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值.21.(本小题满分12分)设函数121()(1)e(0)2x f x f f x x -'=-+.(Ⅰ)求()f x 的解析式及单调区间;(Ⅱ)若21()2f x x ax b ++≥,求(1)a b +的最大值.请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4—1:几何证明选讲如图,D ,E 分别为ABC △边AB ,AC 的中点,直线DE 交ABC △的外接圆于F ,G 两点.若CF AB ∥,证明: (Ⅰ)CD BC =; (Ⅱ)BCD GBD △∽△.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线1C 的参数方程是2cos ,3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2ρ=,正方形ABCD 的顶点都在2C 上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为π(2,)3. (Ⅰ)求点A ,B ,C ,D 的直角坐标;(Ⅱ)设P 为1C 上任意一点,求2222||||||||PA PB PC PD +++的取值范围.24.(本小题满分10分)选修4—5:不等式选讲已知函数()|||2|f x x a x =++-.(Ⅰ)当3a =-时,求不等式()3f x ≥的解集;(Ⅱ)若()4|f x x -≤|的解集包含[1,2],求a 的取值范围.FGDE AB C2012年普通高等学校招生全国统一考试(全国新课标卷1)理科数学答案解析可知:该程序的作用是:求出12naa a,,,中最大的数和最小的数其中A为12naa a,,,中最大的数,B为12naa a,,,中最小的数【提示】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出12na a a,,中最大的数和最小的数.【考点】循环结构.7.【答案】B【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为3;,12ω>∴,验证三角函数的角的范围,排除选项,得到结的范围即可.的部分图象确定其解析式.22222(2)44|a b|a b a a b b-=-=-+224||4||||cos45||a ab b=-︒+24|||10b b=-+=,解得||32b=【提示】由已知可得,2||||cos45||2ba ab b=︒=,代入2222(2)44a b|ab a a b b-=-=-+242||||10b b=-+=可求【考点】平面向量数量积的运算,平面向量数量积的坐标表示、模、夹角.14.【答案】[]3,3-【解析】画出可行域,易知当直线2z x y=-经过点(1,2)时,z取最小值z x=-经过点(3,0)时,60(a++-(1117++=315959(()a a a a=++++奇177********S S=+=+⨯=奇偶141n nb a++=142242n na a++++++--{}na的前60sin0C>,0πA<<,由余弦定理可得222a b caab+-,22a b+-cos1A=,0πA<<ππ66=A∴(2)ABCS=△,2a A=,222a b c∴=+-.解得b c=【提示】(Ⅰ)由正弦定理及两角和的正弦公式可得sin cos sin sin cosA C A C++整理可求AX 的数学期望()550.1650.2750.16850.5476.4E X =⨯+⨯+⨯+⨯=,因为76.4>76,所以,直三棱柱,又1DC BD ⊥1DC D =2AB a =BDC ,1DC ∴(Ⅱ)由(Ⅰ)知,12DC a =Rt ABD △3,90a AD =AB ∴2AC BC +AC BC ∴⊥1BDA ,连结30. 30.轴,CB 为建立空间直角坐标系1(,0,2,0)(,0,A a a D a ,(,,DB a a =--1(,0,DC a =-11(,n x y =111100n DB ax az n DC ax ⎧=--=⎪⎨=-=⎪⎩,不妨令,故可取1(1,2,1)n =同理,可求得平面1DBA 的一个法向量2(1,1,0)n =设1n 与2n 的夹角为θ,则1212cos ||||6n n n n =⨯30.由图可知,二面角的大小为锐角,故二面角1A -.【提示】(Ⅰ)证明只需证明1DC DC ⊥⊥,(Ⅱ)证明BC ⊥BC AC ⊥取A 重合且C DO ∠()e h x '=x →-∞时,(2)当a (3)当a ()0f x '>10a +>CF ABCF AD,=∴=CD AF∥CF AB(Ⅱ)由(Ⅰ)知,BCD∴△∽△【提示】(Ⅰ)角,即可得到结论;(Ⅱ)证明两组对应角相等,即可证得。
2012年高考新课标全国卷文科数学试题(附答案)

2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={x |x 2−x −2<0},B={x |−1<x <1},则(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅ (2)复数z =32ii-++的共轭复数是 (A )2i + (B )2i - (C )1i -+ (D )1i --(3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为(A )−1 (B )0 (C )12(D )1(4)设1F ,2F 是椭圆E :2222x y a b+=1(a >b >0)的左、 右焦点,P 为直线32ax =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为 (A )12 (B )23 (C )34 D .45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC内部,则z x y =-+的取值范围是(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3) (6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数1a ,2a ,…,N a ,输出A ,B ,则 (A )A +B 为1a ,2a ,…,N a 的和 (B )2A B+为1a ,2a ,…,N a 的算术平均数 (C )A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数(D )A 和B 分别为1a ,2a ,…,N a 中的最小数和最大数 (7)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π (9)已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=(A )π4 (B )π3 (C )π2 (D )3π4(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A 、B 两点,||AB =43,则C 的实轴长为(A )2 (B )22 (C )4 (D )8 (11)当0<x ≤12时,4log xa x <,则a 的取值范围是(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2) (12)数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为(A )3690 (B )3660 (C )1845 (D )1830二.填空题:本大题共4小题,每小题5分。
2012年新课标全国高考数学卷(理)-附详解

绝密*启用前2012年普通高等学校招生全国统一考试理科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第一卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1. 已知集合{1,2,3,4,5},{(,)|,,}A B x y x A Y A X Y A ==∈∈-∈,则B 中所含元素的个数为A .3B .6C .8D .10【答案】D【解析】{(5,4),(5,3),(5,2),(5,1),(4,3),(4,2),(4,1),(3,2),(3,1),(2,1)}B =,所含元素个数为10.2. 将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有A .12种B .10种C .9种D .8种【答案】A【解析】122412C C ⋅=种安排方案。
3. 下面是关于复数21z i=-+的四个命题: 1P :||2z =; 2P :22z i =;3P :z 的共轭复数为1i +; 4P : z 的虚部为-1.其中的真命题为A .2P ,3PB .1P , 2PC .2P ,4PD .3P ,4P【答案】C【解析】211z i i==---+,则||z 1P 是假命题;22(1)2z i i =--=,2P 是真命题;1z i =-+,3P 是假命题;z 的虚部为-1,4P 是真命题。
故选C 。
4. 设12,F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32a x =上一点,21F PF ∆是底角为30°的等腰三角形,则E 的离心率为A .12B .23C .34D .45【答案】C【解析】设P 在x 轴上的射影为Q 。
2012年高考理科数学试题及答案-全国卷2

2012年普通高等学校招生全国统一考试(新课标Ⅱ卷)理 科 数 学第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合A ={1, 2, 3, 4, 5},B ={(x ,y )| x ∈A , y ∈A , x -y ∈A },则B 中所含元素的个数为( )A. 3B. 6C. 8D. 102. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有( ) A. 12种B. 10种C. 9种D. 8种3. 下面是关于复数iz +-=12的四个命题中,真命题为( )P 1: |z |=2, P 2: z 2=2i ,P 3: z 的共轭复数为1+i ,P 4: z 的虚部为-1 .A. P 2,P 3B. P 1,P 2C. P 2,P 4D. P 3,P 44. 设F 1,F 2是椭圆E : 12222=+b y a x )0(>>b a 的左右焦点,P 为直线23ax =上的一点,12PF F △是底角为30º的等腰三角形,则E 的离心率为( ) A.21B.32 C.43 D.54 5. 已知{a n }为等比数列,a 4 + a 7 = 2,a5 a6 = 8,则a 1 + a 10 =( )A. 7B. 5C. -5D. -76. 如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1, a 2,…,a N ,输入A 、B ,则( ) A. A +B 为a 1, a 2,…,a N 的和B.2B A +为a 1, a 2,…,a N 的算术平均数C. A 和B 分别是a 1, a 2,…,a N 中最大的数和最小的数D. A 和B 分别是a 1, a 2,…,a N 中最小的数和最大的数 7. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( ) A. 6B. 9C. 12D. 188. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=34,则C 的实轴长为( ) A.2B. 22C. 4D. 89. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是( )A. 15[,]24B. 13[,]24C. 1(0,]2D. (0,2]10. 已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为( )A.B.C.D.11. 已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.62B. 63C. 32D. 22 12. 设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则||PQ 的最小值为( ) A. 2ln 1-B.)2ln 1(2-C. 2ln 1+D. )2ln 1(2+第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:(本大题共4小题,每小题5分,共20分.)13. 已知向量a ,b 夹角为45º,且1=||a ,102=-||b a ,则=||b .14. 设x ,y 满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+-≥-0031y x y x y x ,则2z x y =-的取值范围为 . 15. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作. 设三个电子元件的使用寿命(单位:小时)服从正态分布N (1000,502),且各元件能否正常工作互相独立,那么该部件的使用寿命超过1000小时的概率为 .16. 数列}{n a 满足12)1(1-=-++n a a n n n ,则}{n a 的前60项和为 . 三、解答题:(解答题应写出文字说明,证明过程或演算步骤.)17. (本小题12分)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,0sin 3cos =--+c b C a C a .(Ⅰ)求A ;(Ⅱ)若a =2,△ABC 的面积为3,求b ,c .18. (本小题12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花做垃圾处理. (Ⅰ)若花店某天购进16枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,n ∈N )的函数解析式;(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:以(i )若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差;(ii )若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.19. (本小题12分)如图,直三棱柱ABC -A 1B 1C 1中,121AA BC AC ==,D 是棱AA 1的中点,DC 1⊥BD . (Ⅰ)证明:DC 1⊥BC ;(Ⅱ)求二面角A 1-BD -C 1的大小.20. (本小题满分12分)设抛物线:C py x 22=)0(>p 的焦点为F ,准线为l ,A 为C 上的一点,已知以F 为圆心,F A 为半径的圆F 交l 于B ,D 两点. (Ⅰ)若∠BFD =90º,△ABD 面积为24,求p 的值及圆F 的方程;(Ⅱ)若A 、B 、F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 的距离的比值.C BADC 1A 1B 121. (本小题12分)已知函数121()(1)(0)2x f x f e f x x -'=-+.(Ⅰ)求)(x f 的解析式及单调区间;(Ⅱ)若b ax x x f ++≥221)(,求b a )1(+的最大值. 请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一题评分,做答时请用2B 铅笔在答题卡上将所选题目对应的题号方框涂黑. 22. (本小题10分)【选修4-1:几何证明选讲】如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交于△ABC 的外接圆于F ,G 两点,若CF // AB ,证明: (Ⅰ)CD = BC ; (Ⅱ)△BCD ∽△GBD .23. (本小题10分)【选修4-4:坐标系与参数方程】已知曲线C 1的参数方程是2cos 3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ = 2. 正方形ABCD 的顶点都在C 2上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为)3,2(π.(Ⅰ)点A ,B ,C ,D 的直角坐标;(Ⅱ)设P 为C 1上任意一点,求|P A |2 + |PB |2 + |PC |2 + |PD |2的取值范围.24. (本小题10分)【选修4-5:不等式选讲】 已知函数f (x ) = |x + a | + |x -2|.(Ⅰ)当a =-3时,求不等式f (x ) ≥ 3的解集;(Ⅱ)若f (x ) ≤ | x -4 |的解集包含[1, 2],求a 的取值范围.G2012年普通高等学校招生全国统一考试(新课标Ⅱ卷)理 科 数 学【参考答案】一、选择题: 1.【答案:D 】解析:要在1,2,3,4,5中选出两个,大的是x ,小的是y ,共2510C =种选法. 2.【答案:A 】解析:只需选定安排到甲地的1名教师2名学生即可,共有1224C C 种安排方案. 3.【答案:C 】解析:经计算2221,||(1)21z i z z i i i==--∴==---+ =,复数z 的共轭复数为1i -+,z 的虚部为1-,综上可知P 2,P 4正确.4.【答案:C 】解析:由题意可得,21F PF △是底角为30º的等腰三角形可得212PF F F =,即32()22a c c -=, 所以34c e a ==. 5.【答案:D 】解析:472∵a a +=,56478a a a a ==-,4742a a ∴==-,或4724a a =-=,,14710∵,,,a a a a 成等比数列,1107a a ∴+=-.6.【答案:C 】解析:由程序框图判断x >A 得A 应为a 1,a 2,…,a N 中最大的数,由x <B 得B 应为a 1,a 2,…,a N 中最小的数. 7.【答案:B 】解析:由三视图可知,此几何体为底面是斜边为6的等腰直角三角形(俯视图),高为3的三棱锥,故其体积为113932V =⨯⨯=. 8.【答案:C 】解析:抛物线的准线方程是x =4,所以点A (4,-在222x y a -=上,将点A 代入得24a =,所以实轴长为24a =.9.【答案:A 】 解析:由322,22442k k k ππππππωπωπ+≤+<+≤+∈Z 得,1542,24k k k ω+≤≤+∈Z ,15024∵,∴ωω>≤≤.10.【答案:B 】解析:易知ln(1)0y x x =+-≤对(1,0)(0,)x ∈-+∞恒成立,当且仅当0x =时,取等号,故的值域是(-∞, 0). 所以其图像为B. 11.【答案:A 】解析:易知点S 到平面ABC 的距离是点O 到平面ABC 的距离的2倍.显然O -ABC 是棱长为113O ABC V -==,2S ABC O ABC V V --==. 12.【答案:B 】 解析:因为12xy e =与ln(2)y x =互为反函数,所以曲线12x y e =与曲线ln(2)y x =关于直线y =x 对称,故要求|PQ |的最小值转化为求与直线y =x 平行且与曲线相切的直线间的距离,设切点为A ,则A 点到直线y =x 距离的最小值的2倍就是|PQ |的最小值. 则11()122x x y e e ''===,2x e ∴=,即ln 2x =,故切点A 的坐标为(ln 2,1),因此,切点A 点到直线y =x距离为d ==,所以||2ln 2)PQ d ==-. 二、填空题: 13.【答案:解析:由已知得222222|2|(2)444||4||||cos45||a b a b a a b b a a b b -=-=-⨯+=-⋅+24|||10b b =-+=,解得||32b =.14.【答案:[3,3]-】解析:画出可行域,易知当直线2Z x y =-经过点(1,2)时,Z 取最小值-3;当直线2Z x y =-经过点(3,0)时,Z 取最大值3. 故2Z x y =-的取值范围为[3,3]-. 15.【答案:38】解析:由已知可得,三个电子元件使用寿命超过1000小时的概率均为12,所以该部件的使用寿命超过1000小时的概率为2113[1(1)]228--⨯=. 16.【答案:1830】解析:由1(1)21nn n a a n ++-=-得2212124341①②k k k k a a k a a k -+-=-⎧⎪⎨+=-⎪⎩,由②-①得,21212k k a a +-+=③ 由①得, 2143656059()()()()奇偶S S a a a a a a a a -=-+-+-++-(1117)30159********+⨯=++++==.由③得, 3175119()()()奇S a a a a a a =++++++5957()21530a a ++=⨯=,所以60()217702301830奇奇奇偶偶S S S S S S =+=-+=+⨯=.三、解答题:17.解析:(Ⅰ)由cos sin 0a C C b c --=及正弦定理可得sin cos sin A C A Csin sin 0B C --=,sin cos sin sin()sin 0A C A C A C C -+-=sin cos sin A C A C -sin 0C -=,sin 0C >,cos 10A A --=,2sin()106A π∴--=,1sin()62A π-=,0A π<<,5666A πππ∴-<-<,66A ππ∴-=,3A π∴=.(Ⅱ)ABCS=,1sin 24bc A ∴==4bc ∴=,2,3a A π==,222222cos 4a b c bc A b c bc ∴=+-=+-=,228b c ∴+=,解得2b c ==.18.解析:(Ⅰ)当n ≥16时,y =16×(10-5)=80,当n ≤15时,y =5n -5×(16-n )=10n -80,得1080,(15)()80,(16)n n y n N n -≤⎧=∈⎨≥⎩ .(Ⅱ)(ⅰ)X 可能取60,70,80. P (X =60)=0.1,P (X =70)=0.2,P (X =80)=0.7, X 的分布列为:X X 的方差D (X ) =(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44. (ⅱ)若花店计划一天购进17枝玫瑰花,X 的分布列为X因为76.4>76,所以应购进17枝玫瑰花. 19.解析:(Ⅰ) 证明:设112AC BC AA a ===,直三棱柱111C B A ABC -,1DC DC ∴==, 12CC a =,22211DC DC CC∴+=,1DC DC ∴⊥.又1DC BD ⊥,1DC DC D =,1DC ∴⊥平面BDC . BC ⊂平面BDC ,1DC BC ∴⊥.(Ⅱ)由 (Ⅰ)知,1DC =,1BC =,又已知BD DC ⊥1,BD ∴=. 在Rt ABD △中,BD =,,90AD a DAB =∠=,AB ∴=. 222AC BC AB ∴+=,C BADC 1 A 1 B 1AC BC ∴⊥.法一:取11A B 的中点E ,则易证1C E ⊥平面1BDA ,连结DE ,则1C E ⊥BD ,已知BD DC ⊥1,BD ∴⊥平面1DC E ,BD ∴⊥DE ,1C DE ∴∠是二面角11C BD A --平面角. 在1Rt C DE △中,1111sin 2C E C DE C D ∠===,130C DE ∴∠=. 即二面角11C BD A --的大小为30.法二:以点C 为坐标原点,为x 轴,CB 为y 轴,1CC 为z 轴,建立空间直角坐标系C xyz -.则()()()()11,0,2,0,,0,,0,,0,0,2A a a B aD a a C a . (),,DB a a a =--,()1,0,DC a a =-,设平面1DBC 的法向量为1111(,,)n x y z =,则1111110n DB ax ay az n DC ax az ⎧⋅=-+-=⎪⎨⋅=-+=⎪⎩,不妨令11x =,得112,1y z ==,故可取1(1,2,1)n =.同理,可求得平面1DBA 的一个法向量2(1,1,0)n =. 设1n 与2n 的夹角为θ,则12123cos ||||6n n n n θ⋅===⋅⨯, 30θ∴=. 由图可知,二面角的大小为锐角,故二面角11C BD A --的大小为30.20.解析:(Ⅰ) 由对称性可知,BFD △为等腰直角三角形,斜边上的高为p ,斜边长2BD p =. 点A 到准线l 的距离d FB FD===.由ABD S =△得,11222BD d p ⨯⨯=⨯= 2p ∴=. 圆F 的方程为22(1)8x y +-=. (Ⅱ) 由对称性,不妨设点(,)A A A x y 在第一象限,由已知得线段AB 是圆F 的在直径,90oADB ∠=,2BDp ∴=,32A y p ∴=,代入抛物线:C py x22=得A x =.直线m 的斜率为AF k ==.直线m 的方程为02x +=. 由pyx 22= 得22x y p=,x yp '=. 由3x y p '==得, x p =.故直线n 与抛物线C的切点坐标为)6p,直线n的方程为0x -=. 所以坐标原点到m ,n 3=.21.解析:(Ⅰ) 1()(1)(0)x f x f e f x -''=-+,令x =1得,f (x )=1,再由121()(1)(0)2x f x f e f x x -'=-+,令0x =得(1)f e '=. 所以)(x f 的解析式为21()2xf x e x x =-+,∴()1xf x e x '=-+,易知()1xf x e x '=-+是R 上的增函数,且(0)0f '=.所以()00f x x '>⇔>,()00f x x '<⇔<,所以函数)(x f 的增区间为(0,)+∞,减区间为(,0)-∞.(Ⅱ) 若b ax x x f ++≥221)(恒成立,即21()()(1)02x h x f x x ax b e a x b =---=-+-≥ 恒成立,()(1)x h x e a '=-+.(1)当10a +<时,()0h x '>恒成立,()h x 为R 上的增函数,且当x →-∞时,()h x →-∞,不合题意;(2)当10a +=时,()0h x >恒成立,则0b ≤,(1)0a b +=;(3)当10a +>时,()(1)xh x e a '=-+为增函数,由()0h x '=得ln(1)x a =+,故()0ln(1)f x x a '>⇔>+,()0ln(1)f x x a '<⇔<+,当ln(1)x a =+时,()h x 取最小值(ln(1))1(1)ln(1)h a a a a b +=+-++-. 依题意有(ln(1))1(1)ln(1)0h a a a a b +=+-++-≥,即1(1)ln(1)b a a a ≤+-++,10a +>,22(1)(1)(1)ln(1)a b a a a ∴+≤+-++,令22()ln 0u x x x x x =-> (),则()22ln (12ln )u x x x x x x x '=--=-,()00()0u x x u x ''>⇔<<<x ⇔>x =()u x取最大值2eu =.故当1a b +==(1)a b +取最大值2e. 综上,若b ax x x f ++≥221)(,则 b a )1(+的最大值为2e .22.解析:(Ⅰ) ∵D ,E 分别为△ABC 边AB ,AC 的中点,∴DE //BC . ∵CF //AB ,DF //BC ,∴CF //BD 且CF =BD ,∵又D 为AB 的中点,∴CF //AD 且CF =AD ,∴CD =AF . ∵CF //AB ,∴BC =AF ,∴CD =BC . (Ⅱ)由(Ⅰ)知,BC //GF ,∴GB =CF =BD ,∠BGD =∠BDG =∠DBC =∠BDC ,∴△BCD ∽△GBD .23.解析:(Ⅰ)依题意,点A ,B ,C ,D 的极坐标分别为5411(2,),(2,),(2,),(2,)3636ππππ. 所以点A ,B ,C ,D的直角坐标分别为、(、(1,-、1)-. (Ⅱ) 设()2cos ,3sin P ϕϕ,则222222||||||||(12cos )3sin )PA PB PC PD ϕϕ+++=-+222222(2cos )(13sin )(12cos )(3sin )2cos )(13sin )ϕϕϕϕϕϕ++-+--+++--[]22216cos 36sin 163220sin 32,52ϕϕϕ=++=+∈.所以2222||||||||PD PC PB PA +++的取值范围为[]32,52.G24.解析:(Ⅰ) 当3a =-时,不等式3)(≥x f ⇔|3||2|3x x -+-≥()()2323x x x ≤⎧⎪⇔⎨----≥⎪⎩或()()23323x x x <<⎧⎪⎨-++-≥⎪⎩或()()3323x x x ≥⎧⎪⎨-+-≥⎪⎩⇔或4x ≥. 所以当3a =-时,不等式3)(≥x f 的解集为{1x x ≤或}4x ≥.(Ⅱ)()|4|f x x ≤-的解集包含]2,1[,即|||2||4|x a x x ++-≤-对[]1,2x ∈恒成立,即||2x a +≤对[]1,2x ∈恒成立,即22a x a --≤≤-对[]1,2x ∈恒成立,所以2122a a --≤⎧⎨-≥⎩,即30a -≤≤. 故a 的取值范围为[]3,0-.。
2012年高考新课标全国卷文科数学试题附答案
学习资料收集于网络,仅供参考 2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题分,在每小题给同的四个选项中,只有一项是符一、选择题:本大题共12小题,每小题5 合题目要求的。
2 |?1<x<1},则?x?2<0},B={xx|A={(1)已知集合x??∩B=?(D)A (C)A=B (A)AA B (B)B??i?3?=的共轭复数是(2)复数z i2?i1???i1?i?2?i2 C ())(D(A)(B)不全相等)的,xx,x,…,…,(x,y)(n≥2,,(3)在一组样本数据(x,y),(xy)n121nn12211y??x 上,则这组样本)(i=1,2,…,n)都在直线,散点图中,若所有样本点(xy ii2数据的样本相关系数为11)(D )0 (C)B?(A)1 (222yxa b?FFE是椭圆>:0=1((4)设)的,>2122baa3PFF?x P上一点,△为直线左、右焦点,122030E的离心率为的等腰三角形,则是底角为4231D.(B)C(A))(5423ABC在第一象限,若点(x,y)在△)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C(5y??x?z内部,则的取值范围是3) (0,1+ (D)(C)(3-1,2) 2) B (1(A),-32) ()(0,NN和实2)≥(6)如果执行右边的程序框图,输入正整数(aaaBA,输出,数,,则,…,N12aaa BA+的和为,,…,(A)N12BA?aaa,…,B(),的算术平均数为N122aaa BA中的最大数,…,)(C和分别为,N12和最小数学习资料.学习资料收集于网络,仅供参考aaaBA,(D)中的最小数和最大数和,…,分别为N12,粗线画出的是)如图,网格上小正方形的边长为1(7某几何体的三视图,则此几何体的体积为(A)6B)9 ()12 (C18(D)??,则此球的体积2到平面(8)平面的距离为截球O的球面所得圆的半径为1,球心O 为(D)π6C()346π(A()6πB)43π??5?????xx)x?f(?x?)?sin(0图像的两条=是函数,直线9)已知和>0,=(44?=相邻的对称轴,则3ππππ(D))(C A()(B)44322x CC x16y?A、的中心在原点,焦点在轴上,的准线交于与抛物线(10)等轴双曲线C34|AB|B两点,=,则的实轴长为2228 D))((C)4 (A)(B1x xxlog4?,则a的取值范围是(11)当0<时,≤2a222) ,)( (D1) ,(C)2(1(A)(0,,) (B)2) (22n aa1n??1)a?2a?(项和为的前,则{60}(12)数列{}满足nnn1n?1830 D)()(C1845 (A)3690 (B)36605分。
2012年高考理科数学全国卷1-答案

2012年普通高等学校招生全国统一考试(全国新课标卷1)理科数学答案解析【解析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序, 可知:该程序的作用是:求出12n a a a ,,,中最大的数和最小的数 其中A 为12n a a a ,,,中最大的数,B 为12n a a a ,,,中最小的数【提示】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出12n a a a ,,中最大的数和最小的数. 【考点】循环结构.7.【答案】B【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为3; 底面三角形斜边长为6,高为3的等腰直角三角形,,12ω>∴,验证三角函数的角的范围,排除选项,得到结果.的范围即可.【解析】由已知得22222(2)44|a b|a b a a b b -=-=-+224||4||||cos45||a a b b =-︒+24|||10b b =-+=,解得||32b =【提示】由已知可得,2||||cos45||2b a a b b =︒=,代入 2222(2)44a b|a b a a b b -=-=-+242||||10b b =-+=可求14.【答案】[]3,3-60(a ++-117++=59(a +++,sin 0C >,0πA <<π5π66A -<法二:由正弦定理可得sin a 222a b c a ab+-,0πA <<)ABC S =△,2a A =,,直又1DC BD ⊥1DC D =2AB a =,1DC ∴(Ⅱ)由(Ⅰ)知,12DC a =90AB ∴30. 30.x 轴,(,DB a =-,1(,0,DC a =-的法向量为11(,n x y =111n DB ax n DC ax ⎧=-⎪⎨=-⎪⎩,故可取1(1,2,1)n =的一个法向量2(1,1,0)n =设1n 与2n 的夹角为1212||||6n n n n =⨯30.由图可知,二面角的大小为锐角,故二面角1A -'=h x()eh x→-∞()(2)当aa+>,10,所以当x ∥CF AB∥CF AB(Ⅱ)由(Ⅰ)知,∴△∽△BCD。
2012年高考数学试题及答案(全国卷理数2套)

一、选择题:本大题共 12 小题,每小题 5 分,在每小题给同的四个选项中,只有一项是符
合题目要求的.
1.(5 分)(2012•新课标)已知集合 A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x﹣y∈A}, 则 B 中所含元素的个数为( )
A.
B.
C.
D.
12.(5 分)(2012•新课标)设点 P 在曲线
上,点 Q 在曲线 y=ln(2x)上,则|PQ|
最小值为( )
A.1﹣ln2
B.
C.1+ln2
二.填空题:本大题共 4 小题,每小题 5 分.
13.(5 分)(2012•新课标)已知向量
夹角为 45°,且
=
.
D. ,则
14.(5 分)(2012•新课标)设 x,y 满足约束条件:
A.A+B 为 a1,a2,…,an 的和 B. 为 a1,a2,…,an 的算术平均数
C.A 和 B 分别是 a1,a2,…,an 中最大的数和最小的数 D.A 和 B 分别是 a1,a2,…,an 中最小的数和最大的数 7.(5 分)(2012•新课标)如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的 三视图,则此几何体的体积为( )
21.(12 分)(2012•新课标)已知函数 f(x)满足 f(x)=f′(1)ex﹣1﹣f(0)x+ x2;
(1)求 f(x)的解析式及单调区间;
(2)若
,求(a+1)b 的最大值.
四、请考生在第 22,23,24 题中任选一题作答,如果多做,则按所做的第一题计分,作答 时请写清题号. 22.(10 分)(2012•新课标)如图,D,E 分别为△ABC 边 AB,AC 的中点,直线 DE 交△
2012年新课标高考数学试题(理数)

3 c 3 ∆ F2 PF1 是底角为 30� 的等腰三角形 ⇒ PF2 = F2 F1 = 2( a − c ) = 2c ⇔ e = = 2 a 4
(5)已知 {an 为等比数列, a4 + a7 = 2 , a5 a6 = −8 ,则 a1 + a10 = (
}
)
( A) 7
【解析】选 D
( B) 5
� �
�
� �
�
�
� � � � �2 � � 2a − b = 10 ⇔ (2a − b)2 = 10 ⇔ 4 + b − 4 b cos 45° = 10 ⇔ b = 3 2 ⎧ x, y ≥ 0 ⎪ (14) 设 x, y 满足约束条件: ⎨ x − y ≥ −1 ;则 z = x − 2 y 的取值范围为 ⎪ x+ y ≤3 ⎩
(10) 已知函数 f ( x ) =
1 ;则 y = f ( x ) 的图像大致为( ln( x + 1) − x
)
【解析】选 B
x 1+ x ⇒ g ′( x ) > 0 ⇔ −1 < x < 0, g ′( x ) < 0 ⇔ x > 0 ⇒ g (x ) < g (0) = 0 g ( x ) = ln(1 + x) − x ⇒ g ′( x) = −
由图象关于 y = x 对称得: PQ 最小值为 2d min =
第Ⅱ卷
本卷包括必考题和选考题两部分。第 13 题~第 21 题为必考题,每个试题考生都必须作答, 第 22-第 24 题为选考题,考生根据要求做答。 二.填空题:本大题共 4 小题,每小题 5 分。 (13)已知向量 a, b 夹角为 45° ,且 a = 1, 2a − b = 10 ;则 b = _____ 【解析】 b = _____ 3 2
2012年高考数学试题

2012年全国统一高考数学试卷(新课标版)(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x﹣y∈A},则B中所含元素的个数为()A.3B.6C.8D.10考点:元素与集合关系的判断.专题:计算题.分析:由题意,根据集合B中的元素属性对x,y进行赋值得出B中所有元素,即可得出B中所含有的元素个数,得出正确选项解答:解:由题意,x=5时,y=1,2,3,4,x=4时,y=1,2,3,x=3时,y=1,2,x=2时,y=1综上知,B中的元素个数为10个故选D点评:本题考查元素与集合的关系的判断,解题的关键是理解题意,领会集合B中元素的属性,用分类列举的方法得出集合B中的元素的个数2.(5分)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种D.8种考点:排列、组合及简单计数问题.专题:计算题.分析:将任务分三步完成,在每步中利用排列和组合的方法计数,最后利用分步计数原理,将各步结果相乘即可得结果解答:解:第一步,为甲地选一名老师,有=2种选法;第二步,为甲地选两个学生,有=6种选法;第三步,为乙地选1名教师和2名学生,有1种选法故不同的安排方案共有2×6×1=12种故选A点评:本题主要考查了分步计数原理的应用,排列组合计数的方法,理解题意,恰当分步是解决本题的关键,属基础题3.(5分)下面是关于复数的四个命题:其中的真命题为(),p1:|z|=2,,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p4考点:复数的基本概念;命题的真假判断与应用.专题:计算题.分析:由z===﹣1﹣i,知,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,由此能求出结果.解答:解:∵z===﹣1﹣i,∴,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,故选C.点评:本题考查复数的基本概念,是基础题.解题时要认真审题,仔细解答.4.(5分)设F1、F2是椭圆的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.考点:椭圆的简单性质.专题:计算题.分析:利用△F2PF1是底角为30°的等腰三角形,可得|PF2|=|F2F1|,根据P为直线x=上一点,可建立方程,由此可求椭圆的离心率.解答:解:∵△F2PF1是底角为30°的等腰三角形∴|PF2|=|F2F1|∵P为直线x=上一点∴∴故选C.点评:本题考查椭圆的几何性质,解题的关键是确定几何量之间的关系,属于基础题5.(5分)已知{a n} 为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=()A.7B.5C.﹣5 D.﹣7考点:等比数列的性质;等比数列的通项公式.专题:计算题.分析:由a4+a7=2,及a5a6=a4a7=﹣8可求a4,a7,进而可求公比q,代入等比数列的通项可求a1,a10,即可解答:解:∵a4+a7=2,由等比数列的性质可得,a5a6=a4a7=﹣8∴a4=4,a7=﹣2或a4=﹣2,a7=4当a4=4,a7=﹣2时,,∴a1=﹣8,a10=1,∴a1+a10=﹣7当a4=﹣2,a7=4时,q3=﹣2,则a10=﹣8,a1=1∴a1+a10=﹣7综上可得,a1+a10=﹣7故选D点评:本题主要考查了等比数列的性质及通项公式的应用,考查了基本运算的能力.6.(5分)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a n,输出A,B,则()A.A+B为a1,a2,…,a n的和B.为a1,a2,…,a n的算术平均数C.A和B分别是a1,a2,…,a n中最大的数和最小的数D.A和B分别是a1,a2,…,a n中最小的数和最大的数考点:循环结构.专题:计算题.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出a1,a2,…,a n 中最大的数和最小的数.解答:解:解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是:求出a1,a2,…,a n中最大的数和最小的数其中A为a1,a2,…,a n中最大的数,B为a1,a2,…,a n中最小的数故选C.点评:本题主要考查了循环结构,解题的关键是建立数学模型,根据每一步分析的结果,选择恰当的数学模型,属于中档题.7.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12 D.18考点:由三视图求面积、体积.专题:计算题.分析:通过三视图判断几何体的特征,利用三视图的数据求出几何体的体积即可.解答:解:该几何体是三棱锥,底面是俯视图,三棱锥的高为3;底面三角形斜边长为6,高为3的等腰直角三角形,此几何体的体积为.故选B.点评:本题考查三视图与几何体的关系,考查几何体的体积的求法,考查计算能力.8.(5分)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,,则C的实轴长为()A.B.C.4D.8考点:圆锥曲线的综合.专题:计算题.分析:设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,由C与抛物线y2=16x的准线交于A,B两点,,能求出C的实轴长.解答:解:设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,∵C与抛物线y2=16x的准线l:x=﹣4交于A,B两点,∴A(﹣4,2),B(﹣4,﹣2),将A点坐标代入双曲线方程得=4,∴a=2,2a=4.故选C.点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.9.(5分)(2012•黑龙江)已知ω>0,函数在上单调递减.则ω的取值范围是()A.B.C.D.(0,2]考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:计算题.分析:法一:通过特殊值ω=2、ω=1,验证三角函数的角的范围,排除选项,得到结果.法二:可以通过角的范围,直接推导ω的范围即可.解答:解:法一:令:不合题意排除(D)合题意排除(B)(C)法二:,得:.故选A.点评:本题考查三角函数的单调性的应用,函数的解析式的求法,考查计算能力.10.(5分)已知函数;则y=f(x )的图象大致为()A.B.C.D.考点:对数函数图象与性质的综合应用;对数函数的图像与性质.专题:计算题.分析:考虑函数f(x )的分母的函数值恒小于零,即可排除A,C,D,这一性质可利用导数加以证明解答:解:设则g′(x)=∴g(x)在(﹣1,0)上为增函数,在(0,+∞)上为减函数∴g(x)<g(0)=0∴f(x)=<0得:x>0或﹣1<x<0均有f(x)<0排除A,C,D故选B点评:本题主要考查了函数解析式与函数图象间的关系,利用导数研究函数性质的应用,排除法解图象选择题,属基础题11.(5分)已知三棱锥S﹣ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为()A.B.C.D.考点:球内接多面体;棱柱、棱锥、棱台的体积.分析:先确定点S到面ABC的距离,再求棱锥的体积即可.解答:解:∵△ABC是边长为1的正三角形,∴△ABC的外接圆的半径,∵点O到面ABC的距离,SC为球O的直径∴点S到面ABC的距离为∴棱锥的体积为故选A.点评:本题考查棱锥的体积,考查球内角多面体,解题的关键是确定点S到面ABC的距离.12.(5分)设点P在曲线上,点Q在曲线y=ln(2x)上,则|PQ|最小值为()A.1﹣ln2 B.C.1+ln2 D.考点:点到直线的距离公式;反函数.专题:计算题.分析:由于函数与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数上的点到直线y=x的距离为的最小值,设g(x)=,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求解答:解:∵函数与函数y=ln(2x)互为反函数,图象关于y=x对称函数上的点到直线y=x的距离为设g(x)=,(x>0)则由≥0可得x≥ln2,由<0可得0<x<ln2∴函数g(x)在(0,ln2)单调递减,在[ln2,+∞)单调递增∴当x=ln2时,函数g(x)min=1﹣ln2由图象关于y=x对称得:|PQ|最小值为故选B点评:本题主要考查了点到直线的距离公式的应用,注意本题解法中的转化思想的应用,根据互为反函数的对称性把所求的点点距离转化为点线距离,构造很好二.填空题:本大题共4小题,每小题5分.13.(5分)(2012•黑龙江)已知向量夹角为45°,且,则=3.考点:平面向量数量积的运算;平面向量数量积的坐标表示、模、夹角.专题:计算题.分析:由已知可得,=,代入|2|====可求解答:解:∵,=1∴=∴|2|====解得故答案为:3点评:本题主要考查了向量的数量积定义的应用,向量的数量积性质||=是求解向量的模常用的方法14.(5分)设x,y满足约束条件:;则z=x﹣2y的取值范围为[﹣3,3].考点:简单线性规划.专题:计算题.分析:先作出不等式组表示的平面区域,由z=x﹣2y可得,y=,则﹣表示直线x﹣2y﹣z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围解答:解:作出不等式组表示的平面区域由z=x﹣2y可得,y=,则﹣表示直线x﹣2y﹣z=0在y轴上的截距,截距越大,z越小结合函数的图形可知,当直线x﹣2y﹣z=0平移到B时,截距最大,z最小;当直线x﹣2y﹣z=0平移到A 时,截距最小,z最大由可得B(1,2),由可得A(3,0)∴Z max=3,Z min=﹣3则z=x﹣2y∈[﹣3,3]故答案为:[﹣3,3]点评:平面区域的范围问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.15.(5分)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为.考点:正态分布曲线的特点及曲线所表示的意义.专题:计算题.分析:先根据正态分布的意义,知三个电子元件的使用寿命超过1000小时的概率为,而所求事件“该部件的使用寿命超过1000小时”当且仅当“超过1000小时时,元件1、元件2至少有一个正常”和“超过1000小时时,元件3正常”同时发生,由于其为独立事件,故分别求其概率再相乘即可解答:解:三个电子元件的使用寿命均服从正态分布N(1000,502)得:三个电子元件的使用寿命超过1000小时的概率为设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时时,元件3正常}C={该部件的使用寿命超过1000小时}则P(A)=,P(B)=P(C)=P(AB)=P(A)P(B)=×=故答案为点评:本题主要考查了正态分布的意义,独立事件同时发生的概率运算,对立事件的概率运算等基础知识,属基础题16.(5分)数列{a n}满足,则{a n}的前60项和为1830.考点:数列递推式;数列的求和.专题:计算题.分析:令b n+1=a4n+1+a4n+2+a4n+3+a4n+4,则b n+1=a4n+1+a4n+2+a4n+3+a4n+4=a4n﹣3+a4n﹣2+a4n﹣2+a4n+16=b n+16可得数列{b n}是以16为公差的等差数列,而{a n}的前60项和为即为数列{b n}的前15项和,由等差数列的求和公式可求解答:解:∵,∴令b n+1=a4n+1+a4n+2+a4n+3+a4n+4则b n+1=a4n+1+a4n+2+a4n+3+a4n+4=a4n﹣3+a4n﹣2+a4n﹣2+a4n+16=b n+16∴数列{b n}是以16为公差的等差数列,{a n}的前60项和为即为数列{b n}的前15项和∵b1=a1+a2+a3+a4=10∴=1830点评:本题主要考查了由数列的递推公式求解数列的和,等差数列的求和公式的应用,解题的关键是通过构造等差数列三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知a,b,c分别为△ABC三个内角A,B,C的对边,(1)求A;(2)若a=2,△ABC的面积为;求b,c.考点:解三角形.专题:计算题.分析:(1)由正弦定理及两角和的正弦公式可得sinAcosC+sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC,整理可求A(2)由(1)所求A及S=可求bc,然后由余弦定理,a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA 可求b+c,进而可求b,c解答:解:(1)∵acosC+asinC﹣b﹣c=0∴sinAcosC+sinAsinC﹣sinB﹣sinC=0∴sinAcosC+sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC∵sinC≠0∴sinA﹣cosA=1∴sin(A﹣30°)=∴A﹣30°=30°∴A=60°(2)由由余弦定理可得,a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA即4=(b+c)2﹣3bc=(b+c)2﹣12∴b+c=4解得:b=c=2点评:本题综合考查了三角公式中的正弦定理、余弦定理、三角形的面积公式的综合应用,诱导公式与辅助角公式在三角函数化简中的应用是求解的基础,解题的关键是熟练掌握基本公式18.(12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n 14 15 16 17 18 19 20频数10 20 16 16 15 13 10以100天记录的各需求量的频率作为各需求量发生的概率.(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.考点:概率的应用;离散型随机变量的期望与方差.专题:综合题.分析:(1)根据卖出一枝可得利润5元,卖不出一枝可得赔本5元,即可建立分段函数;(2)(i)X可取60,70,80,计算相应的概率,即可得到X的分布列,数学期望及方差;(ii)求出进17枝时当天的利润,与购进16枝玫瑰花时当天的利润比较,即可得到结论.解答:解:(1)当n≥16时,y=16×(10﹣5)=80;当n≤15时,y=5n﹣5(16﹣n)=10n﹣80,得:(2)(i)X可取60,70,80P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7X的分布列为X 60 70 80P 0.1 0.2 0.7EX=60×0.1+70×0.2+80×0.7=76DX=162×0.1+62×0.2+42×0.7=44(ii)购进17枝时,当天的利润为y=(14×5﹣3×5)×0.1+(15×5﹣2×5)×0.2+(16×5﹣1×5)×0.16+17×5×0.54=76.4 ∵76.4>76,∴应购进17枝点评:本题考查分段函数模型的建立,考查离散型随机变量的期望与方差,考查学生利用数学知识解决实际问题的能力.19.(12分)如图,直三棱柱ABC﹣A1B1C1中,,D是棱AA1的中点,DC1⊥BD(1)证明:DC1⊥BC(2)求二面角A1﹣BD﹣C1的大小.考点:二面角的平面角及求法;空间中直线与直线之间的位置关系.专题:综合题.分析:(1)证明DC1⊥BC,只需证明DC1⊥面BCD,即证明DC1⊥DC,DC1⊥BD;(2)证明BC⊥面ACC1A1,可得BC⊥AC取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,C1H,可得点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角,由此可求二面角A1﹣BD﹣C1的大小.解答:(1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°同理:∠A1DC1=45°,∴∠CDC1=90°∴DC1⊥DC,DC1⊥BD∵DC∩BD=D∴DC1⊥面BCD∵BC⊂面BCD∴DC1⊥BC(2)解:∵DC1⊥BC,CC1⊥BC,DC1∩CC1=C1,∴BC⊥面ACC1A1,∵AC⊂面ACC1A1,∴BC⊥AC取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,OH∵A1C1=B1C1,∴C1O⊥A1B1,∵面A1B1C1⊥面A1BD,面A1B1C1∩面A1BD=A1B1,∴C1O⊥面A1BD∵OH⊥BD,∴C1H⊥BD,∴点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角设AC=a,则,,∴sin∠C1DO=∴∠C1DO=30°即二面角A1﹣BD﹣C1的大小为30°点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定,正确作出面面角,属于中档题.20.(12分)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l 于B,D两点;(1)若∠BFD=90°,△ABD的面积为;求p的值及圆F的方程;(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.考点:圆锥曲线的综合;圆的标准方程;抛物线的简单性质.专题:综合题.分析:(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p点A到准线l的距离,由△ABD 的面积S△ABD=,知=,由此能求出圆F的方程.(2)由对称性设,则点A,B关于点F对称得:,得:,由此能求出坐标原点到m,n距离的比值.解答:解:(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p点A到准线l的距离,∵△ABD的面积S△ABD=,∴=,解得p=2,∴圆F的方程为x2+(y﹣1)2=8.(2)由题设,则,∵A,B,F三点在同一直线m上,又AB为圆F的直径,故A,B关于点F对称.由点A,B关于点F对称得:得:,直线切点直线坐标原点到m,n距离的比值为.点评:本题考查抛物线与直线的位置关系的综合应用,具体涉及到抛物线的简单性质、圆的性质、导数的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.21.(12分)(2012•黑龙江)已知函数f(x)满足;(1)求f(x)的解析式及单调区间;(2)若,求(a+1)b的最大值.考点:导数在最大值、最小值问题中的应用;利用导数研究函数的单调性.专题:综合题;探究型;转化思想.分析:(1)对函数f(x)求导,再令自变量为1,求出f′(1)得到函数的解析式及导数,再由导数求函数的单调区间;(2)由题意,借助导数求出新函数的最小值,令其大于0即可得到参数a,b 所满足的关系式,再研究(a+1)b的最大值解答:解:(1)令x=1得:f(0)=1∴令x=0,得f(0)=f'(1)e﹣1=1解得f'(1)=e故函数的解析式为令g(x)=f'(x)=e x﹣1+x∴g'(x)=e x+1>0,由此知y=g(x)在x∈R上单调递增当x>0时,f'(x)>f'(0)=0;当x<0时,有f'(x)<f'(0)=0得:函数的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0)(2)得h′(x)=e x﹣(a+1)①当a+1≤0时,h′(x)>0⇒y=h(x)在x∈R上单调递增x→﹣∞时,h(x)→﹣∞与h(x)≥0矛盾②当a+1>0时,h′(x)>0⇔x>ln(a+1),h'(x)<0⇔x<ln(a+1)得:当x=ln(a+1)时,h(x)min=(a+1)﹣(a+1)ln(a+1)﹣b≥0,即(a+1)﹣(a+1)ln(a+1)≥b ∴(a+1)b≤(a+1)2﹣(a+1)2ln(a+1),(a+1>0)令F(x)=x2﹣x2lnx(x>0),则F'(x)=x(1﹣2lnx)∴当时,即当时,(a+1)b的最大值为点评:本题考查导数在最值问题中的应用及利用导数研究函数的单调性,解题的关键是第一题中要赋值求出f′(1),易因为没有将f′(1)看作常数而出错,第二题中将不等式恒成立研究参数关系的问题转化为最小值问题,本题考查了转化的思想,考查判断推理能力,是高考中的热点题型,难度较大,计算量也大,易马虎出错四、请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22.(10分)(2012•黑龙江)选修4﹣1:几何证明选讲如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:(1)CD=BC;(2)△BCD~△GBD.考点:综合法与分析法(选修).专题:证明题.分析:(1)根据D,E分别为△ABC边AB,AC的中点,可得DE∥BC,根据等弧对等角,即可得到结论;(2)证明两组对应角相等,即可证得△BCD~△GBD.解答:证明:(1)∵AB∥CF,∴∠DAE=∠ECF.根据等弧对等角可知,,∴∠BDC=∠ADF.∵D,E分别为△ABC边AB,AC的中点∴DE∥BC∴∠ADF=∠DBC.∴∠BDC=∠DBC∴CD=BC.(2)由(1)知,所以.所以∠BGD=∠DBC.因为GF∥BC,所以∠BDG=∠ADF=∠DBC=∠BDC.所以△BCD~△GBD.点评:本题考查几何证明选讲,考查平行四边形的证明,考查三角形的相似,属于基础题.23.选修4﹣4;坐标系与参数方程已知曲线C1的参数方程是,以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(1)求点A,B,C,D的直角坐标;(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.考点:椭圆的参数方程;简单曲线的极坐标方程;点的极坐标和直角坐标的互化.专题:综合题.分析:(1)确定点A,B,C,D的极坐标,即可得点A,B,C,D的直角坐标;(2)利用参数方程设出P的坐标,借助于三角函数,即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围.解答:解:(1)点A,B,C,D的极坐标为点A,B,C,D的直角坐标为(2)设P(x0,y0),则为参数)t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ∵sin2φ∈[0,1]∴t∈[32,52]点评:本题考查极坐标与直角坐标的互化,考查圆的参数方程的运用,属于中档题.24.选修4﹣5:不等式选讲已知函数f(x)=|x+a|+|x﹣2|(1)当a=﹣3时,求不等式f(x)≥3的解集;(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.考点:绝对值不等式的解法;带绝对值的函数.专题:计算题.分析:(1)不等式等价于,或,或,求出每个不等式组的解集,再取并集即得所求.(2)原命题等价于﹣2﹣x≤a≤2﹣x在[1,2]上恒成立,由此求得求a的取值范围.解答:解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即①,或②,或③.解①可得x≤1,解②可得x∈∅,解③可得x≥4.把①、②、③的解集取并集可得不等式的解集为{x|x≤1或x≥4}.(2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立,等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立.故当1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0,故a的取值范围为[﹣3,0].点评:本题主要考查绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了分类讨论的数学思想,属于中档题.参与本试卷答题和审题的老师有:吕静;qiss;席泽林;邢新丽;刘长柏;xintrl;caoqz;minqi5;zlzhan(排名不分先后)菁优网2013年5月30日。
2012年全国统一高考数学试卷(理科)(新课标)

2012年全国统一高考数学试卷(理科)(新课标)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x﹣y∈A},则B中所含元素的个数为()A.3 B.6 C.8 D.102.(5分)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种 D.8种3.(5分)下面是关于复数z=的四个命题:其中的真命题为(),p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p44.(5分)设F1、F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.5.(5分)已知{a n}为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=()A.7 B.5 C.﹣5 D.﹣76.(5分)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a n,输出A,B,则()A.A+B为a1,a2,…,a n的和B.为a1,a2,…,a n的算术平均数C.A和B分别是a1,a2,…,a n中最大的数和最小的数D.A和B分别是a1,a2,…,a n中最小的数和最大的数7.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.188.(5分)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于点A和点B,|AB|=4,则C的实轴长为()A.B.C.4 D.89.(5分)已知ω>0,函数f(x)=sin(ωx+)在区间[,π]上单调递减,则实数ω的取值范围是()A.B.C. D.(0,2]10.(5分)已知函数f(x)=,则y=f(x)的图象大致为()A.B.C.D.11.(5分)已知三棱锥S﹣ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为()A.B.C.D.12.(5分)设点P在曲线上,点Q在曲线y=ln(2x)上,则|PQ|最小值为()A.1﹣ln2 B.C.1+ln2 D.二.填空题:本大题共4小题,每小题5分.13.(5分)已知向量夹角为45°,且,则=.14.(5分)设x,y满足约束条件:;则z=x﹣2y的取值范围为.15.(5分)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为.16.(5分)数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC ﹣ccosA.(1)求A;(2)若a=2,△ABC的面积为,求b,c.18.(12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:日需求量n14151617181920频数10201616151310以100天记录的各需求量的频率作为各需求量发生的概率.(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.19.(12分)如图,直三棱柱ABC﹣A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD(1)证明:DC1⊥BC;(2)求二面角A1﹣BD﹣C1的大小.20.(12分)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;(1)若∠BFD=90°,△ABD的面积为,求p的值及圆F的方程;(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.21.(12分)已知函数f(x)满足f(x)=f′(1)e x﹣1﹣f(0)x+x2;(1)求f(x)的解析式及单调区间;(2)若,求(a+1)b的最大值.四、请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22.(10分)如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:(1)CD=BC;(2)△BCD∽△GBD.23.选修4﹣4;坐标系与参数方程已知曲线C1的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,).(1)求点A,B,C,D的直角坐标;(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.24.已知函数f(x)=|x+a|+|x﹣2|(1)当a=﹣3时,求不等式f(x)≥3的解集;(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.2012年全国统一高考数学试卷(理科)(新课标)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.(5分)(2012•新课标)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y ∈A,x﹣y∈A},则B中所含元素的个数为()A.3 B.6 C.8 D.10【分析】由题意,根据集合B中的元素属性对x,y进行赋值得出B中所有元素,即可得出B中所含有的元素个数,得出正确选项【解答】解:由题意,x=5时,y=1,2,3,4,x=4时,y=1,2,3,x=3时,y=1,2,x=2时,y=1综上知,B中的元素个数为10个故选D2.(5分)(2012•新课标)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种 D.8种【分析】将任务分三步完成,在每步中利用排列和组合的方法计数,最后利用分步计数原理,将各步结果相乘即可得结果【解答】解:第一步,为甲地选一名老师,有=2种选法;第二步,为甲地选两个学生,有=6种选法;第三步,为乙地选1名教师和2名学生,有1种选法故不同的安排方案共有2×6×1=12种故选A3.(5分)(2012•新课标)下面是关于复数z=的四个命题:其中的真命题为(),p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p4【分析】由z===﹣1﹣i,知,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,由此能求出结果.【解答】解:∵z===﹣1﹣i,∴,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,故选C.4.(5分)(2012•新课标)设F1、F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.【分析】利用△F2PF1是底角为30°的等腰三角形,可得|PF2|=|F2F1|,根据P为直线x=上一点,可建立方程,由此可求椭圆的离心率.【解答】解:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|∵P为直线x=上一点∴∴故选C.5.(5分)(2012•新课标)已知{a n}为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=()A.7 B.5 C.﹣5 D.﹣7【分析】由a4+a7=2,及a5a6=a4a7=﹣8可求a4,a7,进而可求公比q,代入等比数列的通项可求a1,a10,即可【解答】解:∵a4+a7=2,由等比数列的性质可得,a5a6=a4a7=﹣8∴a4=4,a7=﹣2或a4=﹣2,a7=4当a4=4,a7=﹣2时,,∴a1=﹣8,a10=1,∴a1+a10=﹣7当a4=﹣2,a7=4时,q3=﹣2,则a10=﹣8,a1=1∴a1+a10=﹣7综上可得,a1+a10=﹣7故选D6.(5分)(2012•新课标)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a n,输出A,B,则()A.A+B为a1,a2,…,a n的和B.为a1,a2,…,a n的算术平均数C.A和B分别是a1,a2,…,a n中最大的数和最小的数D.A和B分别是a1,a2,…,a n中最小的数和最大的数【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出a1,a2,…,a n中最大的数和最小的数.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知,该程序的作用是:求出a1,a2,…,a n中最大的数和最小的数其中A为a1,a2,…,a n中最大的数,B为a1,a2,…,a n中最小的数故选:C.7.(5分)(2012•新课标)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.18【分析】通过三视图判断几何体的特征,利用三视图的数据求出几何体的体积即可.【解答】解:该几何体是三棱锥,底面是俯视图,三棱锥的高为3;底面三角形斜边长为6,高为3的等腰直角三角形,此几何体的体积为V=×6×3×3=9.故选B.8.(5分)(2012•新课标)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于点A和点B,|AB|=4,则C的实轴长为()A.B.C.4 D.8【分析】设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,由C与抛物线y2=16x的准线交于A,B两点,,能求出C的实轴长.【解答】解:设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,∵C与抛物线y2=16x的准线l:x=﹣4交于A,B两点,∴A(﹣4,2),B(﹣4,﹣2),将A点坐标代入双曲线方程得=4,∴a=2,2a=4.故选C.9.(5分)(2012•新课标)已知ω>0,函数f(x)=sin(ωx+)在区间[,π]上单调递减,则实数ω的取值范围是()A.B.C. D.(0,2]【分析】法一:通过特殊值ω=2、ω=1,验证三角函数的角的范围,排除选项,得到结果.法二:可以通过角的范围,直接推导ω的范围即可.【解答】解:法一:令:不合题意排除(D)合题意排除(B)(C)法二:,得:.故选A.10.(5分)(2012•新课标)已知函数f(x)=,则y=f(x)的图象大致为()A.B.C.D.【分析】考虑函数f(x)的分母的函数值恒小于零,即可排除A,C,由f(x)的定义域能排除D,这一性质可利用导数加以证明【解答】解:设则g′(x)=∴g(x)在(﹣1,0)上为增函数,在(0,+∞)上为减函数∴g(x)<g(0)=0∴f(x)=<0得:x>0或﹣1<x<0均有f(x)<0排除A,C,又f(x)=中,,能排除D.故选B11.(5分)(2012•新课标)已知三棱锥S﹣ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为()A.B.C.D.【分析】根据题意作出图形,利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积.【解答】解:根据题意作出图形:设球心为O,过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,延长CO1交球于点D,则SD⊥平面ABC.∵CO1==,∴OO1==,∴高SD=2OO1=,∵△ABC是边长为1的正三角形,=,∴S△ABC∴V==.三棱锥S﹣ABC故选:C.12.(5分)(2012•新课标)设点P在曲线上,点Q在曲线y=ln(2x)上,则|PQ|最小值为()A.1﹣ln2 B.C.1+ln2 D.【分析】由于函数与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数上的点到直线y=x的距离为的最小值,设g(x)=,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求.【解答】解:∵函数与函数y=ln(2x)互为反函数,图象关于y=x对称,函数上的点到直线y=x的距离为,设g(x)=(x>0),则,由≥0可得x≥ln2,由<0可得0<x<ln2,∴函数g(x)在(0,ln2)单调递减,在[ln2,+∞)单调递增,∴当x=ln2时,函数g(x)min=1﹣ln2,,由图象关于y=x对称得:|PQ|最小值为.故选B.二.填空题:本大题共4小题,每小题5分.13.(5分)(2012•新课标)已知向量夹角为45°,且,则=3.【分析】由已知可得,=,代入|2|====可求【解答】解:∵,=1∴=∴|2|====解得故答案为:314.(5分)(2012•新课标)设x,y满足约束条件:;则z=x﹣2y的取值范围为.【分析】先作出不等式组表示的平面区域,由z=x﹣2y可得,y=,则﹣表示直线x﹣2y﹣z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围【解答】解:作出不等式组表示的平面区域由z=x﹣2y可得,y=,则﹣表示直线x﹣2y﹣z=0在y轴上的截距,截距越大,z越小结合函数的图形可知,当直线x﹣2y﹣z=0平移到B时,截距最大,z最小;当直线x﹣2y﹣z=0平移到A时,截距最小,z最大由可得B(1,2),由可得A(3,0)∴Z max=3,Z min=﹣3则z=x﹣2y∈[﹣3,3]故答案为:[﹣3,3]15.(5分)(2012•新课标)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为.【分析】先根据正态分布的意义,知三个电子元件的使用寿命超过1000小时的概率为,而所求事件“该部件的使用寿命超过1000小时”当且仅当“超过1000小时时,元件1、元件2至少有一个正常”和“超过1000小时时,元件3正常”同时发生,由于其为独立事件,故分别求其概率再相乘即可【解答】解:三个电子元件的使用寿命均服从正态分布N(1000,502)得:三个电子元件的使用寿命超过1000小时的概率为设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时时,元件3正常}C={该部件的使用寿命超过1000小时}则P(A)=,P(B)=P(C)=P(AB)=P(A)P(B)=×=故答案为16.(5分)(2012•新课标)数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为1830.【分析】由题意可得a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97,变形可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a7=2,a12+a10=40,a13+a15=2,a16+a14=56,…利用数列的结构特征,求出{a n}的前60项和+(﹣1)n a n=2n﹣1,【解答】解:∵a n+1∴有a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97.从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a11=2,a16+a14=56,…从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.∴{a n}的前60项和为15×2+(15×8+)=1830,故答案为:1830.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)(2012•新课标)已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC﹣ccosA.(1)求A;(2)若a=2,△ABC的面积为,求b,c.【分析】(1)由正弦定理有:sinAsinC﹣sinCcosA﹣sinC=0,可以求出A;(2)有三角形面积以及余弦定理,可以求出b、c.【解答】解:(1)c=asinC﹣ccosA,由正弦定理有:sinAsinC﹣sinCcosA﹣sinC=0,即sinC•(sinA﹣cosA﹣1)=0,又,sinC≠0,所以sinA﹣cosA﹣1=0,即2sin(A﹣)=1,所以A=;(2)S=bcsinA=,所以bc=4,△ABCa=2,由余弦定理得:a2=b2+c2﹣2bccosA,即4=b2+c2﹣bc,即有,解得b=c=2.18.(12分)(2012•新课标)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:日需求量n14151617181920频数10201616151310以100天记录的各需求量的频率作为各需求量发生的概率.(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.【分析】(1)根据卖出一枝可得利润5元,卖不出一枝可得赔本5元,即可建立分段函数;(2)(i)X可取60,70,80,计算相应的概率,即可得到X的分布列,数学期望及方差;(ii)求出进17枝时当天的利润,与购进16枝玫瑰花时当天的利润比较,即可得到结论.【解答】解:(1)当n≥16时,y=16×(10﹣5)=80;当n≤15时,y=5n﹣5(16﹣n)=10n﹣80,得:(2)(i)X可取60,70,80,当日需求量n=14时,X=60,n=15时,X=70,其他情况X=80,P(X=60)===0.1,P(X=70)=0.2,P(X=80)=1﹣0.1﹣0.2=0.7,X的分布列为X607080P0.10.20.7EX=60×0.1+70×0.2+80×0.7=76DX=162×0.1+62×0.2+42×0.7=44(ii)购进17枝时,当天的利润的期望为y=(14×5﹣3×5)×0.1+(15×5﹣2×5)×0.2+(16×5﹣1×5)×0.16+17×5×0.54=76.4∵76.4>76,∴应购进17枝19.(12分)(2012•新课标)如图,直三棱柱ABC﹣A1B1C1中,AC=BC=AA1,D 是棱AA1的中点,DC1⊥BD(1)证明:DC1⊥BC;(2)求二面角A1﹣BD﹣C1的大小.【分析】(1)证明DC1⊥BC,只需证明DC1⊥面BCD,即证明DC1⊥DC,DC1⊥BD;(2)证明BC⊥面ACC1A1,可得BC⊥AC取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,C1H,可得点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角,由此可求二面角A1﹣BD﹣C1的大小.【解答】(1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°同理:∠A1DC1=45°,∴∠CDC1=90°∴DC1⊥DC,DC1⊥BD∵DC∩BD=D∴DC1⊥面BCD∵BC⊂面BCD∴DC1⊥BC(2)解:∵DC1⊥BC,CC1⊥BC,DC1∩CC1=C1,∴BC⊥面ACC1A1,∵AC⊂面ACC1A1,∴BC⊥AC取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,OH∵A1C1=B1C1,∴C1O⊥A1B1,∵面A1B1C1⊥面A1BD,面A1B1C1∩面A1BD=A1B1,∴C1O⊥面A1BD而BD⊂面A1BD∴BD⊥C1O,∵OH⊥BD,C1O∩OH=O,∴BD⊥面C1OH∴C1H⊥BD,∴点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角设AC=a,则,,∴sin∠C1DO=∴∠C1DO=30°即二面角A1﹣BD﹣C1的大小为30°20.(12分)(2012•新课标)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;(1)若∠BFD=90°,△ABD的面积为,求p的值及圆F的方程;(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.【分析】(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p点A到准线l的=,知距离,由△ABD的面积S△ABD=,由此能求出圆F的方程.(2)由对称性设,则点A,B关于点F对称得:,得:,由此能求出坐标原点到m,n距离的比值.【解答】解:(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p点A到准线l的距离,=,∵△ABD的面积S△ABD∴=,解得p=2,所以F坐标为(0,1),∴圆F的方程为x2+(y﹣1)2=8.(2)由题设,则,∵A,B,F三点在同一直线m上,又AB为圆F的直径,故A,B关于点F对称.由点A,B关于点F对称得:得:,直线,切点直线坐标原点到m,n距离的比值为.21.(12分)(2012•新课标)已知函数f(x)满足f(x)=f′(1)e x﹣1﹣f(0)x+x2;(1)求f(x)的解析式及单调区间;(2)若,求(a+1)b的最大值.【分析】(1)对函数f(x)求导,再令自变量为1,求出f′(1)得到函数的解析式及导数,再由导数求函数的单调区间;(2)由题意,借助导数求出新函数的最小值,令其大于0即可得到参数a,b 所满足的关系式,再研究(a+1)b 的最大值【解答】解:(1)令x=1得:f(0)=1∴令x=0,得f(0)=f'(1)e﹣1=1解得f'(1)=e故函数的解析式为令g(x)=f'(x)=e x﹣1+x∴g'(x)=e x+1>0,由此知y=g(x)在x∈R上单调递增当x>0时,f'(x)>f'(0)=0;当x<0时,有f'(x)<f'(0)=0得:函数的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0)(2)得h′(x)=e x﹣(a+1)①当a+1≤0时,h′(x)>0⇒y=h(x)在x∈R上单调递增,x→﹣∞时,h(x)→﹣∞与h(x)≥0矛盾②当a+1>0时,h′(x)>0⇔x>ln(a+1),h'(x)<0⇔x<ln(a+1)得:当x=ln(a+1)时,h(x)min=(a+1)﹣(a+1)ln(a+1)﹣b≥0,即(a+1)﹣(a+1)ln(a+1)≥b∴(a+1)b≤(a+1)2﹣(a+1)2ln(a+1),(a+1>0)令F(x)=x2﹣x2lnx(x>0),则F'(x)=x(1﹣2lnx)∴当时,即当时,(a+1)b的最大值为四、请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22.(10分)(2012•新课标)如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:(1)CD=BC;(2)△BCD∽△GBD.【分析】(1)根据D,E分别为△ABC边AB,AC的中点,可得DE∥BC,证明四边形ADCF是平行四边形,即可得到结论;(2)证明两组对应角相等,即可证得△BCD~△GBD.【解答】证明:(1)∵D,E分别为△ABC边AB,AC的中点∴DF∥BC,AD=DB∵AB∥CF,∴四边形BDFC是平行四边形∴CF∥BD,CF=BD∴CF∥AD,CF=AD∴四边形ADCF是平行四边形∴AF=CD∵,∴BC=AF,∴CD=BC.(2)由(1)知,所以.所以∠BGD=∠DBC.因为GF∥BC,所以∠BDG=∠ADF=∠DBC=∠BDC.所以△BCD~△GBD.23.(2012•新课标)选修4﹣4;坐标系与参数方程已知曲线C1的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,).(1)求点A,B,C,D的直角坐标;(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.【分析】(1)确定点A,B,C,D的极坐标,即可得点A,B,C,D的直角坐标;(2)利用参数方程设出P的坐标,借助于三角函数,即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围.【解答】解:(1)点A,B,C,D的极坐标为点A,B,C,D的直角坐标为(2)设P(x0,y0),则为参数)t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ∵sin2φ∈[0,1]∴t∈[32,52]24.(2012•新课标)已知函数f(x)=|x+a|+|x﹣2|(1)当a=﹣3时,求不等式f(x)≥3的解集;(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.【分析】(1)不等式等价于,或,或,求出每个不等式组的解集,再取并集即得所求.(2)原命题等价于﹣2﹣x≤a≤2﹣x在[1,2]上恒成立,由此求得求a的取值范围.【解答】解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即①,或②,或③.解①可得x≤1,解②可得x∈∅,解③可得x≥4.把①、②、③的解集取并集可得不等式的解集为{x|x≤1或x≥4}.(2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立,等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立.故当1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0,故a的取值范围为[﹣3,0].。
2012年全国高考理科数学试题及答案-新课标1
2012年普通高等学校招生全国统一考试理科数学 第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,)|,,}B x y x A y A x y A =∈∈-∈,则B 中所含元素的个数为 (A ) 3 (B ) 6 (C ) 8 (D ) 10(2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组有1名教师和2名学生组成,不同的安排方案共有(A ) 12种 (B ) 10种 (C ) 9种 (D )8种 (3)下面是关于复数21z i=-+的四个命题 1p :||2z = 2p : 22z i = 3p :z 的共轭复数为1i + 4p :z 的虚部为1-其中真命题为(A ) 2p , 3p (B ) 1p , 2p (C ) 2p ,4p (D ) 3p , 4p(4)设12,F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上的一点,21F PF ∆是底角为30的等腰三角形,则 E 的离心率为(A) 12 (B) 23 (C) 34 (D) 45(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=(A) 7 (B) 5 (C) 5- (D) 7- (6)如果执行右边的程序图,输入正整数(2)N N ≥和实数12,,...,N a a a 输入,A B ,则 (A)A B +为12,,...,N a a a 的和 (B )2A B+为12,,...,N a a a 的算式平均数 (C )A 和B 分别是12,,...,N a a a 中最大的数和最小的数(D )A 和B 分别是12,,...,N a a a 中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A )6 (B)9 (C )12 (D )18(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于,A B 两点,||43AB =,则C 的实轴长为(A )2 (B )22 (C )4 (D )8 (9)已知0ω>,函数()sin()4f x x πω=+在,2ππ⎛⎫⎪⎝⎭单调递减,则ω的取值范围 (A) 15[,]24 (B) 13[,]24 (C) 1(0,]2(D)(0,2](10)已知函数1()ln(1)f x x x=+-,则()y f x =的图像大致为(11)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为O的直径,且2SC =,则此棱锥的体积为(A)26 (B)36 (C)23 (D)22(12)设点P 在曲线12xy e =上,点Q 在曲线ln(2)y x =上,则||PQ 的最小值为 (A)1ln 2- (B)2(1ln 2)- (C)1ln 2+ (D)2(1ln 2)+第Ⅱ卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密*启用前
2012年普通高等学校招生全国统一考试
理科数学
注息事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.
3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·
4.考试结束后.将本试卷和答且卡一并交回。
第一卷
一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1) 已知集合
个数为
(A )3 (B )6 (C) 8 (D )10
(2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名
学生组成,不同的安排方案共有
(A )12种 (B )10种 (C) 9种 (D )8种
(3)下面是关于复数
的四个命题为:
P 1:|z|=2, P 2:z 2=2i,
P 3:z 的共轭复数为1+I, p 4:z 的虚部为-1, 期中的真命题为
(A )p 2,p 3 (B)P 1,P 2 (C)P 2,P 4 (D)P 3,P 4
(4)设12F F 是椭圆E :22
22(0)x y a b a b
+=>>的左、右焦点,P 为直线32a x =上一点,
21F PF 是底角为30 的等腰三角形,则E 的离心率为()
(A )
12 (B )23 (C )34 (D )4
5
(5)已知{}
n a 为等比数列,332a a +=,568a a =-,则110a a +=() (A )7 (B )5 (C )-5 (D )-7
(6)如果执行右边的程序框图,输入正整数(2)N N ≥和市属12,,...,n a a a ,
输出A,B,则
(A )A+B 为12,,...,n a a a 的和 (B )
2
A B
+为12,,...,n a a a 的算术平均数 (C )A 和B 分别是12,,...,n a a a 中最大的数和最小的数 (D )A 和B 分别是12,,...,n a a a 中最小的数和最大的数 (7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,
则此几何体的体积为
(A )6 (B )9 (C )12 (D )18
(8)等轴双曲线 C 的中心在原点,检点在X 轴上,C 与抛物线的准线交于A ,B 两点,
,则
C 的
实轴长为
(A ) (B )
(C )4
(D )
8
(9)已知w>0,函数f(x)=sin(wx+)在(,π)单调递减。
则△t的取值范围是
(10) 已知函数f(x)= ,则y=f(x)的图像大致为
(11)已知三棱锥S-ABC的所有顶点都在球O的求面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为
(12)设点P在曲线y=e x 上,点Q在曲线y=ln(2x)上,则|pQ|最小值为
(A)1-ln2 (B)(C)1+ln2 (D)(1+ln2)
第Ⅱ卷
本卷包括必考题和选考题两部分。
第13题-第21题为必考题,每个试题考生都必须作答,第22-24题为选考题,考生根据要求作答。
二.填空题:本大题共4小题,每小题5分。
(13)已知向量a,b夹角为450 ,且|a|=1.|2a-b|=,则|b|=
(14) 设x,y满足约束条件则z=x-2y的取值范围为
(15)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(100,,5),且各个部件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为
(16)数列满足=2n-1,则的前60项和为
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知a.b.c分别为△ABC三个内角A,B,C的对边
(1)求A
(2)若a=2,△ABC的面积为求b,c
18.(本小题满分12分)
某花店每天以每枝5元的价格从农场购进若干只玫瑰花,然后以每枝10元的价格出售,乳沟当天卖不完,剩下的玫瑰花做垃圾处理。
(I)看花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,)的函数解析式。
(II)花点记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率。
(i)若花店一天购进16枝玫瑰花,x表示当天的利润(单位:元),求x的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?
(19)(本小题满分12分)
如图,之三棱柱D是棱的中点,
(I)证明:
(II)求二面角的大小。
(20)(本小题满分12分)
设抛物线的交点为F,准线为L,A为C上的一点,已知以F为圆心,FA为半径的圆F交L于B,D两点。
(I)若,的面积为求P的值及圆F的方程;
(II)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点m,n 距离的比值。
(21)(本小题满分12分)
已知函数满足
(I)求的解析式及单调区间;
(II)若求的最大值
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若,证
明:
(I)CD=BC;
(II)△BCD∽△GBD
(23)(本小题满分10分)选修4—4;坐标系与参数方程
已知曲线C1的参数方程是以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是,正方形ABCD的顶点都在C2上,且A、B、C、D以逆时针次序排列,点A的
极坐标为
(I)求点A、B、C、D 的直角坐标;
(II)设P为C1上任意一点,求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围。
(24)(本小题满分10分)选修4—5:不等式选讲
已知函数f(x) = |x + a| + |x - 2|.
(I)当a = -3时,求不等式f(x) ≥3的解集;
(II)若f(x)≤|x - 4|的解集包含[1,2],求a的取值范围。
