(整理)经典雷达资料-第6章__反射面天线 (2)
第六章 面天线

s
S b a
z
1 1 kb sin 2 1 2 ka sin 2
(1 cos ) sin 1 FE 2 1 (1 cos ) sin 2 FH 2 2
y ds(xs , ys ) x R r y M(r , , ) x
s
S b a
dEH j
z
1 2 r
(1 cos ) E y e jkr dse
Im I O
4、惠更斯源辐射场
dEE j dEH j
1 2 r 1 2 r
(1 cos ) E y e jkr dse (1 cos ) E y e jkr dse
1 FE ( ) FH ( ) (1 cos ) 2
dse
dEH j
1 2 r
(1 cos ) E y e jkr dse
y ds(xs , ys ) x R r
y
M(r , , ) x
s
S O
z
二、平面口径辐射
当观察点很远时,可认为R与r近似平行,R可表示为
R r s er r xs sin cos ys sin sin
( E y dy )dx 2 r
e jkr ea
4、惠更斯源辐射场
在研究天线的方向性时,通常更关注两个主平面的情况, 所以只讨论面元在两个主平面的辐射。H平面(xOz平面) Il jkr
面内,电基本振子产生的辐射场为 2 r
H j
sin e
I l 1 jkr 60 Il jkr m jkr dse E j dEH j e (1 E E y e sin e sin cos ) j 2 r 2 r r y x H E E 0 Hr I ml1 x 0 jkr jkr r H j j dEe dx E y esin e r dse 2H r 0 J r dE E 2
第6讲 雷达天线、雷达显示器

2.4 雷达显示器
雷达终端显示器主要包括:
距离显示器 B型显示器(平面显示器) E型显示器(高度显示器) 平面位置显示器 情况显示器和综合显示器
2.4.1 距离显示器
距离显示器主要显示目标距离,它可以绘出接收机输
出幅度和距离的曲线关系。
Ae a A
显然,波长一定时,天线增益与Ae和A都成正比。天线有效孔径体现为面积 的量纲,它与入射电磁波功率密度Pi相乘后即可得到天线的接收功率Pr, 即 Pr= Pi·Ae
2.3.1 天线的方向性和增益 3.天线辐射方向图 天线辐射的电磁能量在三维空间中的分布变时成相对(归一化)基础上 的曲线(曲面)时,称为天线辐射方向图,通常称为天线方向图。 天线方向图通常用 F , 表示,θ和φ表示方位角和俯仰角,电场强 度记为E( θ , φ ),Emax为最大辐射方向上的电场强度,则有
E ex Ex ey E y
其中 Ex Exm cos t kz x
E y E ym cos t kz y
极化是指电场强度E的矢量端在空间固定点上随时间的变化所描绘的轨迹。 1.若矢量端轨迹是一条直线,称该波为线极化波。 2.若矢量端轨迹是圆,称该波为圆极化波。 3. 若矢量端轨迹为椭圆,称该波为椭圆极化波。
2.3 雷达天线 雷达天线的参数:
(1)增益:天线将辐射能量集中照射在某个方向的能力。增益与天线的孔
径面积成正比,与工作波长的平方成正比。 (2)天线的有效孔径面积:雷达天线接收时,其收集目标回波的能力用天 线的有效孔径面积表示。大的有效孔径面积等效于高的天线增益。 (3)方向性:天线都具有方向性,即天线向不同方向辐射的功率密度不同,
雷达天线学习资料——精.doc

雷达天线1雷达天线的简介雷达中用以辐射和接收电磁波并决定其探测方向的设备。
雷达天线具有将电磁波聚成波束的功能,定向地发射和接收电磁波。
雷达的重要战术性能,如探测距离、探测范围、测角(方位、仰角)精度、角度分辨力和反干扰能力均与天线性能有关。
雷达天线在空间聚成的立体电磁波束,通常用波束的水平截面图(即水平方向图)和垂直截面图(即垂直方向图)来描述。
方向图呈花瓣状,又称为波瓣图。
常规的天线方向图有一个主瓣和多个副瓣。
主瓣用于探测目标。
副瓣又称旁瓣,是无用的,愈小愈好。
雷达的战术用途不同,所要求的天线波束形状也不相同。
常规雷达的发射波束和接收波束是相同的,一些特殊体制的雷达,发射波束和接收波束不同。
脉冲雷达多数是发射和接收共用一个天线,靠天线收发开关进行发射和接收工作状态的转换。
有些雷达(如多基地雷达和连续波雷达),其发射天线和接收天线是分开的。
2雷达天线的种类雷达天线类型很多,按其结构形式,主要有反射面天线和阵列天线两大类。
按天线波束的扫描方式,雷达天线可分为机械扫描天线、电扫描天线和机电扫描结合的天线反射面天线由反射面和辐射器组成。
辐射器又称馈源、辐射元、照射器,它向反射面辐射电磁波,经反射形成波束。
典型的反射面天线是旋转抛物面天线,切割抛物面天线、抛物柱面天线、卡塞格伦天线、单脉冲天线、叠层波束天线、赋形波束天线和偏馈天线等多种形式。
机械扫描天线通过机械的方法驱动天线转动,实现天线波束在方位和仰角二维的扫描,扫描的速度较慢。
电扫描天线,天线固定不动,波束在方位和仰角二维的扫描,都是用电子技术控制阵列天线上各辐射单元的馈电相位或工作频率来实现,波束扫描的速度很快。
机电扫描结合的天线一般是方位扫描由机械驱动天线旋转进行,仰角扫描由电子技术控制各辐射单元的馈电相位或工作频率来实现,因此其方位扫描较慢, 仰角扫描很快。
有时也把机电扫描结合的天线叫一维电扫描天线。
雷达天线的主要性能指标雷达天线主要目的是更好地接受和发送数据,采用不同种类的天线拥有不同的指标,但雷达天线主要的性能指标有波瓣宽度、有效面积、增益、副瓣电平、极化方式、频带宽度、天线转速和抗风力等。
雷达知识点总结

雷达知识点总结一、雷达的基本原理雷达是利用无线电波进行探测的设备,其工作原理基于无线电波的发射和接收。
雷达基本原理包括以下几个关键环节:1. 无线电波的发射雷达发射机产生高频的无线电波,并将这些无线电波转化为一束射向待测目标的电磁波。
雷达发射机工作时,关键是通过天线把电能转换成电磁波,并辐射出去。
2. 无线电波的传播和反射发射出的无线电波在空间中传播,当遇到目标时部分被目标表面反射回来,这些反射回来的波被雷达的接收天线接收到。
3. 无线电波的接收和处理接收天线捕捉到反射回来的波,雷达接收机将这些波进行放大、滤波、解调处理,提取出有用的信息。
4. 目标信息的测量和分析通过分析接收到的信号的时间延迟、频率变化等信息,雷达系统可以确定目标的距离、速度、方位角等参数。
5. 显示和报警最后,雷达系统将分析得到的目标信息显示在操作员的监视屏幕上,同时进行报警和跟踪。
以上就是雷达基本的工作原理,根据这些原理,雷达系统可以实现对目标的探测和识别。
二、雷达的工作方式雷达可以根据工作方式的不同分为主动雷达和被动雷达两种类型。
1. 主动雷达主动雷达是指雷达发射机和接收机分开的雷达系统,发射机发射的信号由发送天线发射出去,接收机则由接收天线接收目标反射回来的信号,该方式下,雷达系统不需要等待传感器的使用权就能发射信号和接收目标信息。
2. 被动雷达被动雷达是指发射机和接收机是同一部分,这种雷达系统利用目标本身辐射的电磁波进行探测,通常是利用目标自身的雷达反射特性进行探测。
雷达的工作方式直接影响着其使用场景、性能和应用对象。
三、雷达系统的组成雷达系统是由多个部分组成的,主要包括以下几个组成部分:1. 发射和接收天线:发射和接收天线是雷达系统的核心部件,用于发射和接收电磁波。
2. 雷达发射机:雷达发射机负责产生和放大载频的高频信号,并将其送到发射天线。
3. 雷达接收机:雷达接收机负责接收目标反射回来的信号,并进行放大、解调、滤波等处理。
雷达天线原理

雷达天线原理引言:雷达(Radar)是一种利用电磁波进行探测和测距的技术。
而雷达天线作为雷达系统的核心组成部分,起着接收和发射电磁波的重要作用。
本文将介绍雷达天线的原理及其工作过程。
一、雷达天线的基本原理雷达天线的基本原理是利用电磁波与物体相互作用的特性,实现对目标的探测和定位。
雷达天线主要包括发射天线和接收天线两部分。
1. 发射天线:雷达系统通过发射天线向周围空间发射一定频率的电磁波。
发射天线将电能转换为电磁波能量,然后将其辐射到空间中。
发射天线的特性决定了雷达系统发射的电磁波的频率、功率和辐射方向等参数。
2. 接收天线:雷达系统的接收天线用于接收目标反射回来的电磁波信号。
接收天线将接收到的电磁波能量转化为电能,并通过接收机进行信号放大和处理。
接收天线的性能决定了雷达系统对目标反射信号的接收能力,包括接收灵敏度、方向性和波束宽度等参数。
二、雷达天线的工作过程雷达天线在雷达系统中起到了发射和接收电磁波的重要作用。
下面将介绍雷达天线的工作过程。
1. 发射过程:雷达系统通过发射天线向周围空间发射一定频率的电磁波。
发射天线产生并辐射出电磁波的过程中,会受到发射天线的结构和参数的影响。
发射天线的形状、尺寸和辐射功率等参数决定了电磁波的发射特性,如辐射方向性和波束宽度等。
2. 接收过程:雷达系统的接收天线用于接收目标反射回来的电磁波信号。
接收天线将接收到的电磁波能量转化为电能,并通过接收机进行信号放大和处理。
接收天线的性能决定了雷达系统对目标反射信号的接收能力。
接收天线的灵敏度、方向性和波束宽度等参数决定了雷达系统对目标的探测范围和精度。
3. 天线特性:雷达天线的性能指标主要包括天线增益、方向图、波束宽度和频率响应等。
天线增益是指天线辐射或接收电磁波的能力,方向图描述了天线在空间中的辐射或接收特性,波束宽度表示天线主瓣的角度范围,频率响应则是天线在不同频率下的工作特性。
4. 天线匹配:雷达天线的匹配是指将天线与雷达系统之间的阻抗进行匹配,以提高雷达系统的性能。
2_雷达导论—天线

单脉冲天线
14பைடு நூலகம்
刀形波束天线
AN/SPS-59(美国)
15
■ 按照大小尺寸分类
小天线(口径远小于波长) 共振天线(口径约等于波长的一半) 大天线(口径远大于波长)
6
天线的分类(续)
7
抛物球面天线
8
抛物球面天线举例
MISA 近地空间探测雷达(美国)
9
抛物柱面天线
10
抛物柱面天线举例
AN/TPS-63(美国)
11
多波束天线
12
多波束天线举例
AN/TPS-43(美国)
雷达系统导论
第二讲:雷达天线
1
天线的基本要求
■ 低旁瓣 ■ 高增益 ■ 大带宽 ■ 快速的空间覆盖能力(搜索雷达) ■ 精准的波束指向(跟踪雷达) ■ 接收信噪比高 ■ 可维护性好, 具备自检能力, 。。。
2
远场和近场的概念
■ 近场(Fresnel Region)
天线测试
■ 远场(Fraunhofer Region)
球面波以及平面波假设
3
天线的性能指标
■ 方向性(Directivity) ■ 增益(Gain) ■ 波束宽度(Beamwidth) ■ 旁瓣高度(Sidelobe) ■ 系统损耗
4
天线的波束类型
■ 笔(针)形波束 ■ 刀形波束(余切波束)
5
天线的分类
■ 按照物理特性分类
反射面天线 微波透镜天线 阵列天线
相控阵天线和反射面天线主要技术指标

相控阵天线和反射面天线主要技术指标下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!相控阵天线和反射面天线主要技术指标引言在现代通信领域,相控阵天线和反射面天线是两种重要的天线技术。
雷达天线
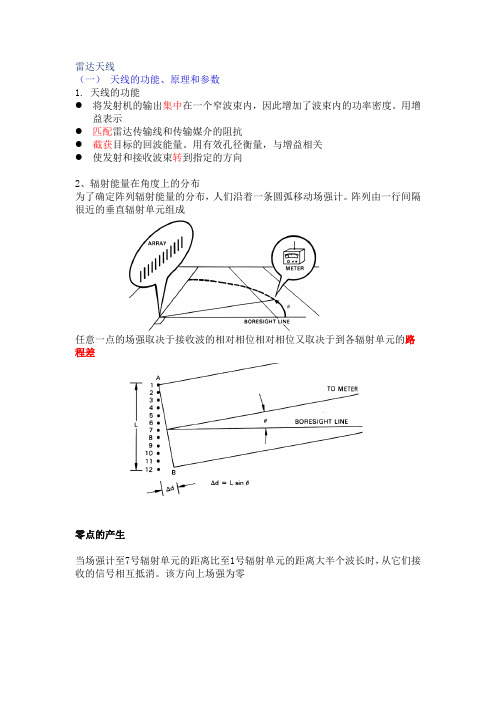
雷达天线(一)天线的功能、原理和参数1. 天线的功能●将发射机的输出集中在一个窄波束内,因此增加了波束内的功率密度。
用增益表示●匹配雷达传输线和传输媒介的阻抗●截获目标的回波能量。
用有效孔径衡量,与增益相关●使发射和接收波束转到指定的方向2、辐射能量在角度上的分布为了确定阵列辐射能量的分布,人们沿着一条圆弧移动场强计。
阵列由一行间隔很近的垂直辐射单元组成任意一点的场强取决于接收波的相对相位相对相位又取决于到各辐射单元的路程差零点的产生当场强计至7号辐射单元的距离比至1号辐射单元的距离大半个波长时,从它们接收的信号相互抵消。
该方向上场强为零旁瓣的产生当场强计到阵列两端的距离差接近1.5个波长时,只有3到10号辐射单元的信号相互抵消。
达到另一个峰值3. 天线参数•波束方向图:天线的发射和接收响应,它是偏离轴线的俯仰角和方位角的函数由天线的尺寸形状照射和频率决定• 波束宽度:主天线响应(主瓣)的角宽度,是长度、频率和照射的函数对电器特性的大天线,波束宽度与天线长度和波长有关为了抑制旁瓣,大的天线表面并不是均匀利用而是渐进照射,使得周边区域比中心使用效率低,因此有效尺寸比实际尺寸小• 有效口径:有效捕获电磁波的投影面积。
天线作为接收设备截获信号的面积。
随偏离天线轴线的方向变化。
一个有效的孔径指标通常是指在天线最大响应的方向。
由天线的投影面积和照射函数决定•增益:天线所指方向上能量集中程度的度量。
天线增益等于在某一特定方向上单位立体角内所辐射的功率与同样总功率在所有方向上即等方向均匀辐射时单位立体角内所辐射的功率之比• 辐射效率:天线总的接收功率中被辐射的(发射)或是转换到天线终端(接收)的部分• 旁瓣:主瓣以外其它方向的响应✓除了主瓣方向以外其它方向产生的响应✓以旁瓣的增益低于主瓣峰值增益的量(分贝表示)作为指标✓是EMI、ECM和杂波的主要进入通道天线的副瓣出现在所有方向上,甚至出现在后部,增加了雷达被敌方发现的敏感性和易受到干扰的脆弱性旁瓣缩减,旁瓣是由靠近孔径边缘部分的辐射产生的,因此可以利用照锥化低副瓣 aperture孔径• 场区:当离天线远处或近处观测时,描述天线的不同响应。
(整理)经典雷达资料-第1章 雷 达 概 论

第1章雷达概论Merrill I. Skolnik1.1 雷达描述雷达的基本概念相对简单,但在许多场合下它的实现并不容易。
它以辐射电磁能量并检测反射体(目标)反射的回波的方式工作。
回波信号的特性提供有关目标的信息。
通过测量辐射能量传播到目标并返回的时间可得到目标的距离。
目标的方位通过方向性天线(具有窄波束的天线)测量回波信号的到达角来确定。
如果是动目标,雷达能推导出目标的轨迹或航迹,并能预测它未来的位置。
动目标的多普勒效应使接收的回波信号产生频移,因而即使固定回波信号幅度比动目标回波信号幅度大多个数量级时,雷达也可根据频移将希望检测的动目标(如飞机)和不希望的固定目标(如地杂波和海杂波)区分开。
当雷达具有足够高的分辨力时,它能识别目标尺寸和形状的某些特性。
雷达可在距离上、角度上或这两方面都获得分辨力。
距离分辨力要求雷达具有大的带宽,角度分辨力要求大的电尺寸雷达天线。
在横向尺度上,雷达获得的分辨力通常不如其在距离上获得的分辨力高。
但是当目标的各个部分与雷达间存在相对运动时,可运用多普勒频率固有的分辨力来分辨目标的横向尺寸。
虽然人们通常认为SAR是通过在存储器中存储接收到的信号,从而产生大的“合成”天线,但是用于成像(如地形成像)的合成孔径雷达在横向尺度上获得的分辨力仍可解释为,是由于利用了多普勒频率分辨力的结果。
这两种观点(多普勒分辨力和合成天线)是等效的。
展望用于目标成像的ISAR所能得到的横向分辨力的途径,理所当然应该是多普勒频率分辨力。
雷达是一种有源装置,它有自己的发射机而不像大多数光学和红外传感器那样依赖于外界的辐射。
在任何气象条件下,雷达都能探测或远或近的小目标,并精确测量它们的距离,这是雷达和其他传感器相比具有的主要优势。
雷达原理已在几兆赫兹(高频或电磁频谱的高频端)到远在光谱区外(激光雷达)的频率范围内得到应用。
这范围内的频率比高达109:1。
在如此宽的频率范围内,为实现雷达功能而应用的具体技术差别巨大,但是基本原理是相同的。
雷达原理知识点汇总

雷达原理知识点汇总第一章绪论1、雷达概念(Radar):radar的音译,“Radio Detection and Ranging ”的缩写。
原意是“无线电探测和测距”,即用无线电方法发现目标并测定它们在空间的位置。
2、雷达工作原理:发射机在定时器控制下,产生高频大功率的脉冲串,通过收发开关到达定向天线,以电磁波形式向外辐射。
在天线控制设备的控制下,天线波束按照指定方向在空间扫描,当电磁波照射到目标上,二次散射电磁波的一部分到达雷达天线,经收发开关至接收机,进行放大、混频和检波处理后,送到雷达终端设备,能判断目标的存在、方位、距离、速度等。
3、雷达的任务:利用目标对电磁波的反射来发现目标并对目标进行定位。
随着雷达技术的发展,雷达的任务不仅仅是测量目标的距离、方位和仰角,而且还包括测量目标的速度,以及从目标回波中获取更多有关目标的信息。
4、从雷达回波中可以提取目标的哪些有用信息,通过什么方式获取这些信息?斜距R : 雷达到目标的直线距离OP。
方位角α: 目标斜距R在水平面上的投影OB与某一起始方向(正北、正南或其它参考方向)在水平面上的夹角。
俯仰角β:斜距R与它在水平面上的投影OB在铅垂面上的夹角,有时也称为倾角或高低角。
5、雷达工作方式连续波和脉冲波6、雷达测距原理R=(C∆t)/2式中,R为目标到雷达的单程距离,∆t为电磁波往返于目标与雷达之间的时间间隔,C为电磁波的传播速率(3×108米/秒)7、影响雷达性能指标脉冲宽度(窄),天线尺寸(大),波束(窄),方向性。
8、距离测量分辨力两个目标在距离方向上的最小可区分距离:Δr c=c/2(τ+d/υn)∆rc=c/2(τ+d/υn)或者Δr c=c/2∙1/B∆rc=c/2∙1/B其中,d为光点直径,υnυn为光点扫面速度;B为有效相关带宽。
9、雷达由哪几个主要部分,各部分的功能是什么?同步设备:雷达整机工作的频率和时间标准。
发射机:产生大功率射频脉冲。
(整理)经典雷达资料-第1章 雷 达 概 论

第1章雷达概论Merrill I. Skolnik1.1 雷达描述雷达的基本概念相对简单,但在许多场合下它的实现并不容易。
它以辐射电磁能量并检测反射体(目标)反射的回波的方式工作。
回波信号的特性提供有关目标的信息。
通过测量辐射能量传播到目标并返回的时间可得到目标的距离。
目标的方位通过方向性天线(具有窄波束的天线)测量回波信号的到达角来确定。
如果是动目标,雷达能推导出目标的轨迹或航迹,并能预测它未来的位置。
动目标的多普勒效应使接收的回波信号产生频移,因而即使固定回波信号幅度比动目标回波信号幅度大多个数量级时,雷达也可根据频移将希望检测的动目标(如飞机)和不希望的固定目标(如地杂波和海杂波)区分开。
当雷达具有足够高的分辨力时,它能识别目标尺寸和形状的某些特性。
雷达可在距离上、角度上或这两方面都获得分辨力。
距离分辨力要求雷达具有大的带宽,角度分辨力要求大的电尺寸雷达天线。
在横向尺度上,雷达获得的分辨力通常不如其在距离上获得的分辨力高。
但是当目标的各个部分与雷达间存在相对运动时,可运用多普勒频率固有的分辨力来分辨目标的横向尺寸。
虽然人们通常认为SAR是通过在存储器中存储接收到的信号,从而产生大的“合成”天线,但是用于成像(如地形成像)的合成孔径雷达在横向尺度上获得的分辨力仍可解释为,是由于利用了多普勒频率分辨力的结果。
这两种观点(多普勒分辨力和合成天线)是等效的。
展望用于目标成像的ISAR所能得到的横向分辨力的途径,理所当然应该是多普勒频率分辨力。
雷达是一种有源装置,它有自己的发射机而不像大多数光学和红外传感器那样依赖于外界的辐射。
在任何气象条件下,雷达都能探测或远或近的小目标,并精确测量它们的距离,这是雷达和其他传感器相比具有的主要优势。
雷达原理已在几兆赫兹(高频或电磁频谱的高频端)到远在光谱区外(激光雷达)的频率范围内得到应用。
这范围内的频率比高达109:1。
在如此宽的频率范围内,为实现雷达功能而应用的具体技术差别巨大,但是基本原理是相同的。
第6章 面天线

(6―2―16)
第6章 面天线
则两主平面的方向函数为
F (1c2os)si 1n1 (6―2―17)
FH()(1c2os)1c(o2s22) (6―2―18)
第6章 面天线
图6―2―3绘出了a=2λ,b=3λ的矩形口径的主平面方 向图,由于口径在E平面的尺寸较大,因此E面方向图 比H面方向图主瓣窄,并且E面波瓣个数多于H面波瓣 个数。又因为余弦分布只体现在x坐标上,所以对应的 方向图只在H面上主瓣变宽,而E面方向图维持不变。
相应的等效磁基本振子磁流的方向沿x轴方向,其长 度为dx,数值为
ImJx m dyEydy
(6―1―4)
于是,惠更斯元的辐射即为此相互正交放置的等效电 基本振子和等效磁基本振子的辐射场之和。
第6章 面天线
在研究天线的方向性时,通常更关注两个主平面 的情况,所以下面也只讨论面元在两个主平面的辐射。
E平面(yOz平面)如图6―1―3所示,在此平面 内,根据式(1―1―4),电基本振子产生的辐射场为
第6章 面天线
6.2.3 同相平面口径方向图参数
如果统一引入
A
j e jkr
r
E0
则平面口径的主平面辐射场可统一表示为
E ( ) A SF ( )
(6―2―28) (6―2―29)
第6章 面天线
第6章 面天线
E M j2 1 r ( 1 c o s)sE y ( x s ,y s ) e j k R d x (s d 6y ―s 2―1)
y ds(xs , ys)
x R
y
M(r, , )
s
S O
r
x
z
图6―2―1 平面口径坐标系
第6章 面天线
雷达复习资料
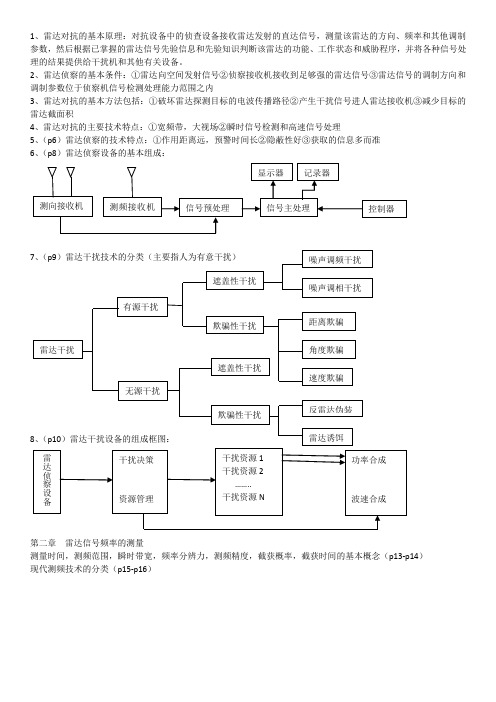
只与侦察机定向天线的扫描有关。输助支路B不仅能够消除雷
达天线扫描对测向的影响也能够消除发射信号起伏的影响,还
能用于旁瓣匿影。只有当A支路信号电平高于B支路信号电平
时才进行测向处理。
13、(p53)多波束测向技术的基本原理(罗特曼透镜)
为了清除由于雷达天线扫描等因素引起的信号幅度起伏对角度测量的影响,可以增加一个参考支路,它采用无方向性天线,对定向支路中的信号起伏进行对消处理。假设Fr(t),Fa(t)分别为侦察天线和雷达天线的扫描函数,A(t)为脉冲包络函数,则两支路收到的信号分别为Sa(t)=Fa(t)Fr(t)A(t)cosωt;Sb(t)=Fa(t)A(t)cosωt
17、对雷达旁瓣信号的侦察
一般雷达天线主瓣很窄,又处于空间搜索状态,侦察机接收到雷达天线主瓣的辐射信号概率很低,往往需要较长时间,通过提高侦察系统灵敏度,实现对雷达天线旁瓣信号的侦收。旁瓣侦察的作用距离为Rr=[PtGsaveGrλ²/(4π)²Prmin10°`]½Gsave是雷达天线的平均旁瓣增益。实现旁瓣侦察时,侦察接收机的灵敏度需要提高35-40dB
现代测频技术的分类(p15-p16)
2、(p19)射频调谐晶体视频接收机
检波器视放
微波预选器
3、(P19)频率搜索形式:连续搜索(分为单程搜索和双程搜索),步进搜索
4、(P20)频率慢速可靠搜索
Tf≤τn=ZnTr(τn为脉冲群宽度)
满足f2-f1≤(Zn/Z)△fr公式的搜索概率为1,故称为可靠搜索,Z为满足处理机所需的脉冲个数,Tr为脉冲重复周期。频率快速可靠搜索(它与慢速可靠搜索一样,都为全概率搜索)。在脉冲宽度τ内,要搜索完整个侦察频段,即Tf≤τ,故搜索速度应满的扫频速度不宜过大,否则会引起输出幅度的严重下降,导致接收机灵敏度降低
雷达天线学习资料——精

雷达天线 1 雷达天线的简介雷达中用以辐射和接收电磁波并决定其探测方向的设备。
雷达天线具有将电磁波聚成波束的功能,定向地发射和接收电磁波。
雷达的重要战术性能,如探测距离、探测范围、测角(方位、仰角)精度、角度分辨力和反干扰能力均与天线性能有关。
雷达天线在空间聚成的立体电磁波束,通常用波束的水平截面图(即水平方向图)和垂直截面图(即垂直方向图)来描述。
方向图呈花瓣状,又称为波瓣图。
常规的天线方向图有一个主瓣和多个副瓣。
主瓣用于探测目标。
副瓣又称旁瓣,是无用的,愈小愈好。
雷达的战术用途不同,所要求的天线波束形状也不相同。
常规雷达的发射波束和接收波束是相同的,一些特殊体制的雷达,发射波束和接收波束不同。
脉冲雷达多数是发射和接收共用一个天线,靠天线收发开关进行发射和接收工作状态的转换。
有些雷达(如多基地雷达和连续波雷达),其发射天线和接收天线是分开的。
2 雷达天线的种类雷达天线类型很多,按其结构形式,主要有反射面天线和阵列天线两大类。
按天线波束的扫描方式,雷达天线可分为机械扫描天线、电扫描天线和机电扫描结合的天线反射面天线由反射面和辐射器组成。
辐射器又称馈源、辐射元、照射器,它向反射面辐射电磁波,经反射形成波束。
典型的反射面天线是旋转抛物面天线,切割抛物面天线、抛物柱面天线、卡塞格伦天线、单脉冲天线、叠层波束天线、赋形波束天线和偏馈天线等多种形式。
机械扫描天线通过机械的方法驱动天线转动,实现天线波束在方位和仰角二维的扫描,扫描的速度较慢。
电扫描天线,天线固定不动,波束在方位和仰角二维的扫描,都是用电子技术控制阵列天线上各辐射单元的馈电相位或工作频率来实现,波束扫描的速度很快。
机电扫描结合的天线一般是方位扫描由机械驱动天线旋转进行,仰角扫描由电子技术控制各辐射单元的馈电相位或工作频率来实现,因此其方位扫描较慢,仰角扫描很快。
有时也把机电扫描结合的天线叫一维电扫描天线。
雷达天线的主要性能指标雷达天线主要目的是更好地接受和发送数据,采用不同种类的天线拥有不同的指标,但雷达天线主要的性能指标有波瓣宽度、有效面积、增益、副瓣电平、极化方式、频带宽度、天线转速和抗风力等。
天线基础知识与应用之雷达

天线基础知识与应用之雷达一、天线基本概念与分类天线是在无线电收发系统中,向空间辐射或从空间接收电磁波的装置,是无线电通信系统中必不可少的部分。
通常有以下几种分类方法:1)按用途分类:可分为通信天线、电视天线、雷达天线等;2)按工作频段分类:可分为短波天线、超短波天线、微波天线等;3)按方向性分类:可分为全向天线、定向天线等;4)按外形分类;可分为线状天线、面状天线等。
二、天线基本参数天线有如下几个基本参数:波瓣宽度、方向性系数、天线效率、增益系数、辐射电阻和天线有效高度等。
这些参数是衡量天线质量好坏的重要指标。
【波瓣宽度】有时也称波束宽度。
指方向性图的主瓣宽度,用来描述天线向一定方向辐射电磁波的能力。
一般是指半功率波瓣宽度。
当L/λ数值不同时,其波瓣宽度也不同。
L/λ比值增加时,方向图越尖锐,但当(L/λ)>0.5时,除了与振子轴垂直的方向有最大的主瓣外,还可能出现副瓣。
因此,波瓣宽度越小,其方向性越强,保密性也强,干扰邻台的可能性小。
所以,对于超短波,微波等所用的天线,主瓣宽度这一指标,是十分重要的。
【方向性系数】方向性系数是用来表示天线向某一个方向集中辐射电磁波程度(即方向性图的尖锐程度)的一个参数。
为了确定定向天线的方向性系数,通常以理想的非定向天线作为比较的标准。
任一定向天线的方向性系数是指在接收点产生相等电场强度的条件下,非定向天线的总辐射功率对该定向天线的总辐射功率之比。
按照上面的定义,由于定向天线在各个方向上的辐射强度不等,故天线的方向性系数也随着观察点的位置而不同,在辐射电场最大的方向,方向性系数也最大。
通常如果不特别指出,就以最大辐射方向的方向性系数作为定向天线的方向性系数。
在中波和短波波段,方向性系数约为几到几十;在米波范围内,约为几十到几百;而在厘米波波段,则可高达几千,甚至几万。
【辐射电阻】发射天线的辐射功率与馈电点的有效电流平方之比,称为天线的辐射电阻。
采用辐射电阻这个概念,可以简化天线的有关计算。
现代雷达系统分析与设计(陈伯孝)第6章

6.2.1 面杂波
面杂波包括地杂波和海杂波,又被称为区域杂波。在机 载雷达下视模式下,区域杂波会十分明显。对于地基雷达, 当搜索低擦地角目标时,杂波是影响目标检测的主要因素。 擦地角ψg是地表与波束中心之间的夹角,如图6.1所示。
12
图6.1 擦地角的定义
13
影响雷达杂波散射系数的因素主要有:擦地角、表面粗 糙度及其散射特性、雷达波长。一般来说,波长越短,杂波 散射系数σ0越大。σ0与擦地角有关,图6.2描述了σ0与擦地角 的关系示意图。根据擦地角的大小分为三个区域:低擦地角 区、平坦区和高擦地角区。低擦地角区又称干涉区,在这个 区域一般情况下散射系数随着擦地角的增加而迅速增加。在 平坦区,杂波变化基本是缓慢的,以非相干散射为主,散射 系数随擦地角的变化较小。高擦地角区,也称为准镜面反射 区。该区域以相干的镜向反射为主,散射系数随擦地角增大 而快速增大,并且与地面的状况(如粗糙度和介电常数)等特 性有关。
43
对散射特性处于瑞利区的雨滴,可以用理想小球的瑞利近似 式来估计雨滴的RCS。若不考虑传播媒介的折射系数,雨滴 的RCS的瑞利近似为
(6.2.24) k=2π/λ,r为雨滴的半径。 设η为每单位体积的RCS,它可用单位体积内所有独立散 射体RCS的和来进行计算,
解 由式(6.2.10)知,SCR为(SCR)c=
因此,为了可靠地检测目标,雷达应该增加其SCR至少到(32 +X)dB,其中X值一般为13 dB至15 dB,或者更高的量级。
27
2.地基雷达区域杂波的雷达方程
地基雷达的杂波包括从主瓣和旁瓣进入的杂波,因此 RCS的计算可描述为
(6.2.11) σMBc是主瓣杂波RCS,σSLc是旁瓣杂波RCS,如图 6.6所示。
反射面天线

当Ds/Dm0.2时,一般按照式(2-5)选取D s ;
若Ds/Dm0.1,可取 Ds 0.1Dm,以使馈源
副面最小遮挡口径
小些。只要 Dm/Ds 0.1,副面遮挡损失将小于0.1dB,但它随 D s 的增大迅速增大。
当D m,Fm / Ds以及D s 选定后,需要选择Fm以确定馈源位置和大小。这需要作两方面权衡:
又有2a等于边缘点H到两焦点距离之差,即
2 a O 2 H H 1 s D O s/ i 2 2 m n s D s/ i 1 2 m n D 2 ss si 1 m i 2 m n s n si 1 i m 2 m n n
将上面两式相除,得
e2 2a cssiin1 n m 1m ( si2n m2)m 即
根据抛物线的上述性质可得抛物面的下述两个重要性质: (1)从焦点出发的任一根射线经过抛物面反射,得到的反射线 都与抛物面的轴线平行,反之亦然。 (2)从焦点发出的射线经过抛物面任一点反射后到达的口径面 的距离相等,即口径面为一等相面。因此置于焦点的馈源所辐 射的球面波经过抛物面反射后变成沿抛物面轴线+z方向传播的 平面波。 这两条重要性质可以用来形成具有尖锐波瓣的天线即抛物面天 线。如果在焦点F放置一个波瓣较宽的馈源,并且焦点与抛物面 的距离远大于波长,则照射在抛物面上的是馈源的远区场,其 波阵面近似为球面,如果抛物面半径也远大于波长,则在局部 区域内此球面波可看成是局部平面波,从而可根据均匀平面波 在无穷大导电平面上的反射特性决定抛物面上的电流及反射波。 根据抛物面的性质可知,反射波的传播方向是+z方向,并在抛 物面口径上形成等相场分布。把口径上的场分布看成是等效场 源,如果口径半径远大于波长,则可得到主瓣最强方向在+z方 向的尖锐波瓣,如果几何光学是一个严格解,则辐射波束的宽 度为零。
第6讲雷达天线、雷达显示器

2 目标回波
目标回波2。 通常在R扫掠线上所显示的
移动距标
那一段距离在A扫掠线上以缺口方式、加
亮显示方式或其它方式显示出来, 以便使
用人员观测。
2.4.2 B型显示器
距离
平面显示器既可以用极坐标显示距离和方
位, 也可以用直角坐标来显示距离和方位, 若
为后者,则其画面如图4.4所示, 称为B式显示
器, 它以横坐标表示方位, 纵坐标表示距离。
2.4 雷达显示器
雷达终端显示器主要包括: ➢ 距离显示器 ➢ B型显示器(平面显示器) ➢ E型显示器(高度显示器) ➢ 平面位置显示器 ➢ 情况显示器和综合显示器
2.4.1 距离显示器
距离显示器主要显示目标距离,它可以绘出接收机输 出幅度和距离的曲线关系。
常用的距离显示器有A型显示器、A/R型显示器。 距离显示器显示目标的斜距坐标, 它是一度空间显示 器, 用光点在荧光屏上偏转的振幅来表示目标回波的大小, 所以又称为偏转调制显示器。
2.4.1 距离显示器
在A型显示器上, 我们可以控制移动距标去对准目标回波, 然后根据控制 元件的参量(电压或轴角)而算得目标的距离数据。 由于人的固有惯性, 在测量中不可能做到使移动距标完全和目标重合, 它们之间总会有一定 的误差Δl, 这个误差我们称为重合误差。
对于不同的量程, 重合误差Δl对应的距离误差ΔR将不同。例如, A型 显示器扫描线长度为100mm, 重合误差Δl=1 mm, 当其量程Rm为100km 时, Δl引起的误差为1km, 如果量程为1 km, 则Δl引起的距离误差只有10 m。但减小量程后,不能达到有效地监视雷达全程的目的。
通常方位角不是取整个360°, 而是取其中的
某一段, 即雷达所监视的一个较小的范围。如
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章反射面天线Helmut E. SchrankGary E. EvansDaniel Davis6.1 引言天线的作用雷达天线的基本作用是实现电磁波的自由空间传播和导波传播之间的转换。
发射期间天线的特定功能是将辐射能集中到具有某种形状的定向波束内,以照射指定方向的目标。
接收期间天线收集目标反射的回波信号能量并将之送往接收机。
因此,在以发射方式和接收方式工作时,雷达天线起到互易的,然而是相互关联的作用。
在两种方式或者作用中主要的目的都是要精确确定目标的方向角。
为实现此目的,需要有高度定向的(窄的)波束,从而不仅达到所需的角精度,而且能够分辨相互靠得很近的目标。
雷达天线的这一重要特性可以定量的用波束宽度来表示,也可以表示为发射增益和有效接收孔径。
后两个参量相互成正比,并且与检测距离和角精度有直接关系。
许多雷达都设计成工作在微波频率,这时用适当物理尺寸的天线就能获得窄的波束宽度。
以上雷达天线的功能性描述意味着一副天线既用于发射,又用于接收。
虽然大多数雷达系统都是这样工作的,但是也有例外,如一些单基地雷达采用收发分离的天线,当然,双基地雷达按定义必定是收发分离的天线。
在这一章中,重点介绍较常用的单部天线,特别是广泛使用的反射面天线。
相控阵天线的内容参见第7章。
波束扫描与目标跟踪由于雷达天线一般具有定向波束,大范围的角度覆盖要求窄波束快速往复地在空域内扫描,以保证不论目标在哪个方向上都能探测到。
这就是警戒雷达或搜索雷达的功能。
有些雷达系统设计成一旦探测到目标便可进行跟踪,这种跟踪功能要求专门设计与警戒雷达天线不同的天线。
在某些雷达系统中,特别是在机载雷达中,将天线设计成既具有搜索又有跟踪的功能。
测高大多数警戒雷达都是二维坐标的,只测定目标的距离和方位坐标。
在早期的雷达系统中,另外的测高天线通过机械俯仰摆动来测量第三个坐标,即仰角,由此计算出空中目标的高度。
现在设计的3D雷达采用一副天线测量所有三个坐标,例如,一部天线在接收方式工作时在俯仰方向形成多个堆积波束,而在发射方式工作时形成宽覆盖的垂直波束。
这些波束在水平方向同样窄,但垂直堆积接收波束可以用两个相邻的交叠波束测量回波振幅来确定目标的仰角。
天线的分类雷达天线可以分为两大类,光学天线和阵列天线。
顾名思义,光学天线是基于光学原理的,它包含两个子类,即反射面天线和透镜天线。
反射面天线仍然广泛应用于雷达中,而透镜天线虽然仍用于一些通信和电子战(EW)场合,但已经不再用于现代雷达系统中。
为了减少篇幅,透镜天线将不在本书中详细讨论。
但第一版中关于透镜天线的参考资料仍保留在本章末的参考资料中。
6.2 基本原理和参量本节简述天线的基本原理,着重介绍对雷达系统设计师有用的术语的定义。
为了给雷达系统选择最佳类型的天线,系统设计师应该对将要选择的各种类型天线的基本性能特征有清楚的认识[1],包括反射面天线(在本章讨论)和相控阵天线(在第7章讨论)之间的选择,还有用相控阵列馈电的反射面天线。
虽然本章着重讨论反射面天线,但是本节讨论的许多基本原理适用于所有的天线。
对任何天线,必须考虑的三个基本参量包括:∙增益(和有效孔径)∙辐射方向图(包括波束宽度、副瓣)∙阻抗(电压驻波比或VSWR)其他的基本考虑还有互易性和极化,它们将在本节做简要介绍。
互易性大多数雷达系统都采用一副天线,既用于发射,又用于接收,而且大部分这样的天线都是互易性设备,其含义是它们的性能参量(增益、方向图、阻抗)在两种工作方式下是一样的。
这一互易性原理[2]允许天线既可以看成是发射设备,又可看成是接收设备,由具体讨论时哪个更方便而定。
这也允许在任何一种工作方式下测试天线(参见6.10节)。
非互易雷达天线的例子是使用了非互易的铁氧体元件的相控阵天线,收发模块中含放大器的有源阵列天线和3D(距离、方位和仰角)雷达的测高天线。
后者的代表是AN/TPS—43雷达[3],它在接收时采用在仰角上堆积的几个交叠波束,在发射时采用一个宽仰角波束。
在水平方向上波束都一样窄。
必须分别测试这些非互易天线的发射特性和接收特性。
增益、方向性系数和有效孔径术语天线增益用来描述一副天线将能量聚集于一个窄的角度范围(方向性波束)的能力。
天线增益的两个不同却相关的定义是,方向增益和功率增益。
前者通常称做方向性系数,后者常称为增益。
清楚地理解两者之间的区别是非常重要的。
方向性系数(方向性增益)定义为最大辐射强度(每立体弧度内的瓦数)与平均辐射强度之比,即π==4/辐射的总功率率每立体弧度内的最大功平均辐射强度最大辐射强度D G (6.1) 也可以用远场距离R 处的最大辐射功率密度(每平方米的瓦数)与同一距离上的平均密度之比表示,即2max 24/4/RP P R G t D π=π=辐射的总功率最大辐射功率密度 (6.2) 因此,方向性系数定义就是指,实际的最大辐射功率密度比辐射功率为各向同性分布时的功率密度强多少倍。
注意,这个定义不包含天线中的耗散损耗,只与辐射功率的集中有关。
增益(功率增益)包含天线的损耗,并且用天线输入端收到的功率P 0来定义,而不用辐射功率P t ,即20max 24/4/RP P R G π=π=收到的总功率最大辐射功率密度 (6.3) 对于实际的(非理想的)天线,辐射功率P t 等于收到功率P 0乘以天线辐射效率因子η,0P P t η= (6.4)例如,若一个典型天线的耗散损耗为1.0 dB ,则79.0=η,即输入功率的79%被辐射。
其余部分)1(η-或21%,被转化为热能。
对反射面天线,大部分的损耗都发生在连接到馈源的传输线上,并能够做到小于1 d B 。
比较式(6.2)、式(6.3)和式(6.4),求得增益和方向性系数之间有如下的简单关系:D G G η= (6.5)因此,除理想无耗天线(η=1.0, G =G D )外,天线增益总是小于方向性系数。
方向性系数-波束宽度间的近似关系天线方向性系数与波束宽度间有如下近似的且非常有用的关系(参见2.3节):elaz 40000B B G D ≈ (6.6) 式中,B az 和B el 分别为主平面内的方位和俯仰半功率波束宽度(单位为︒)。
这一关系与方向性系数为46 dB 的1︒×1︒笔形波束等价。
由这一基本组合,其他天线的近似方向性系数可以很快求出,例如,与1︒×2︒波束对应的方向性系数是43 dB ,因为波束宽度加倍对应的方向性系数下降3 d B 。
类似地,2︒×2︒波束对应40 dB ,1︒×10°波束对应36 dB 的方向性系数,依次类推。
将每次波束宽度的变化都转换成分贝,方向性系数也做相应的调整。
但这一关系不适用于赋形(如余割平方)波束。
有效孔径天线的孔径是它在与主波束方向垂直平面上的投影的实际面积。
有效孔径的概念在分析天线工作于接收方式时是很有用的。
对面积为A ,工作波长为λ的理想(无耗)、均匀照射孔径,方向性增益为2/4λA G D π= (6.7)上式表示孔径A 可提供的最大增益,并意味着天线有理想的同相位、等振幅的分布。
为了减小方向图的副瓣,天线通常并不是均匀照射,而是渐变照射(孔径中心最大,边缘较小)的。
这时,天线的方向性增益比式(6.7)给出的要小,即2/4λe D A G π= (6.8)式中,A e 是天线的有效孔径或捕获面积,等于几何孔径与一个小于1的因子ρa (称为孔径效率)的乘积:A A a e ρ= (6.9)最好将孔径效率称为孔径效能,因为它不包括转化为热能的RF 功率,也就是说,它不含耗散效应,而只是给定孔径被利用的有效程度的量度。
比如说,孔径效率为50%(ρa =0.5)的天线比均匀照射孔径的增益低3 d B ,但并不是耗散了一半的功率。
有效孔径表示一个均匀照射孔径,该孔径比实际的非均匀照射孔径小,但具有相同的增益。
有效孔径是一个面积,与入射功率密度相乘后可给出天线的接收功率:e i r A P P = (6.10)辐射方向图电磁能在三维角空间中的分布表示成相对(归一化)基础上的曲线时,称为天线辐射方向图。
这种分布可用各种方式绘制成曲线,如极坐标或直角坐标、电压强度或功率密度、单位立体角内功率(辐射强度)等。
图6.1所示为典型的圆孔径天线的方向图,该图将等距离上的对数功率密度(垂直坐标用分贝计)与方位角和俯仰角的关系绘制在直角坐标系中。
方向图的主瓣(或主波束)是笔形波束(圆截面),四周是较小的瓣,通常称为副瓣。
角坐标的原点取在主瓣峰值方向,通常称为天线的电基准轴。
电基准轴可与天线的机械轴(即对称轴,有时称为视轴)重合,也可以不重合。
若两者不重合(常常是无意的),其角度差称为视轴误差,在测量目标方向时必须考虑这种误差。
图6.1(a )所示为天线方向图的三维特性,以这种形式绘制方向图需要大量的数据。
同样的数据也能够绘制成等功率电平轮廓线图,如图6.1(c )所示。
这些轮廓线图是一系列水平面与三维方向图在不同的功率电平处的交线,对显示功率的角空间分布是很有用的。
在大多数情况下,用二维方向图就足够了,且测量和绘制起来比较方便。
例如,如果将图6.1(a )的方向图与通过波束峰值和0︒方位的垂直面相截,则得到方向图的二维切片或“切割”,称为主平面垂直方向图,如图6.1(b )所示。
用与第一个平面垂直或正交的平面(含峰值和0︒仰角)做类似的切割,得到所谓的方位方向图,它也是一个主平面截面,因为其中包含波束峰值,也包含一个角坐标轴。
这些主平面有时也称为基本平面。
其他通过波束峰值的所有垂直平面则称为基本间平面。
为了描述天线的方向性能,有时需要测量和绘制±45︒基本间平面内的方向图,然而对于大多数情形只需绘制方位和俯仰方向图就足够了,或者说用两个包含波束轴的平面切割对三维方向图采样就足够了(且经济得多)。
术语方位和俯仰意味着以地面为参考坐标,这并不总是可行的,尤其是对机载或天基(星基)系统。
通常,天线的更通用的一对主平面是线性极化天线的所谓E 面和H 面。
其中,E 面方向图是包含天线辐射的E 场(电矢量)方向的主平面,由于H 面与之正交,故包含H 场(磁矢量)方向。
这两个主平面不依赖基于地面的方向(如方位和俯仰),故被广泛应用。
图6.1 典型的笔形波束方向图:(a)整个方向图的三维直角坐标曲面图;(b)主平面垂直方向图;(c )等强度(等照射)线(由美国海军研究实验室的D. Dhoward 提供)应该注意的是,对三维方向图的采样不限于上述平面切割。
从测量技术的观点看,有时取锥形切割是有意义且方便的,也就是用以天线的电轴(或机械轴)为中心取不同角宽度的角锥来截三维方向图。
图6.1(b )中所示的典型的二维方向图常常绘制在直角坐标系中,垂直轴用分贝表示。
