格兰杰检验流程
格兰杰因果检验(正式版)

一.北京的存款增长对北京的人均GDP增长的格兰杰因果检验(一)单根检验1.A1(北京的存款增长)的单根检验Null Hypothesis: A1 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -4.218621 0.0029 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A1)Method: Least SquaresDate: 10/25/11 Time: 10:04Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A1(-1) -0.835841 0.198131 -4.218621 0.0003C 19.33463 5.072943 3.811324 0.0008R-squared 0.415844 Mean dependent var 0.105185 Adjusted R-squared 0.392477 S.D. dependent var 14.84304 S.E. of regression 11.56922 Akaike info criterion 7.805761 Sum squared resid 3346.172 Schwarz criterion 7.901749 Log likelihood -103.3778 F-statistic 17.79676 Durbin-Watson stat 2.021836 Prob(F-statistic) 0.0002822.A2(北京人均GDP增长)的单根检验(1)未滞后Null Hypothesis: A2 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.648793 0.0960 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2)Method: Least SquaresDate: 10/25/11 Time: 10:08Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-1) -0.479685 0.181096 -2.648793 0.0138C 6.910332 2.804785 2.463765 0.0210R-squared 0.219143 Mean dependent var -0.148148 Adjusted R-squared 0.187909 S.D. dependent var 5.045590 S.E. of regression 4.546889 Akaike info criterion 5.937951 Sum squared resid 516.8550 Schwarz criterion 6.033939 Log likelihood -78.16234 F-statistic 7.016106 Durbin-Watson stat 1.735513 Prob(F-statistic) 0.013795(2).A2(-1)单根检验Null Hypothesis: A2(-1) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.962731 0.0519 Test critical values: 1% level -3.7114575% level -2.98103810% level -2.629906*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2(-1))Method: Least SquaresDate: 10/25/11 Time: 10:11Sample (adjusted): 1984 2009Included observations: 26 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-2) -0.540309 0.182368 -2.962731 0.0068C 8.050071 2.860246 2.814468 0.0096R-squared 0.267797 Mean dependent var -0.019231 Adjusted R-squared 0.237288 S.D. dependent var 5.099962 S.E. of regression 4.453969 Akaike info criterion 5.899272 Sum squared resid 476.1083 Schwarz criterion 5.996049 Log likelihood -74.69054 F-statistic 8.777775 Durbin-Watson stat 1.776754 Prob(F-statistic) 0.006779(3).A2(-2)单根检验(效果不好)Null Hypothesis: A2(-2) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=5)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.862298 0.0642 Test critical values: 1% level -3.7240705% level -2.98622510% level -2.632604*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2(-2))Method: Least SquaresDate: 10/25/11 Time: 10:13Sample (adjusted): 1985 2009Included observations: 25 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-3) -0.505189 0.176498 -2.862298 0.0088C 7.816925 2.752981 2.839440 0.0093R-squared 0.262649 Mean dependent var 0.328000 Adjusted R-squared 0.230590 S.D. dependent var 4.881386 S.E. of regression 4.281757 Akaike info criterion 5.823222 Sum squared resid 421.6692 Schwarz criterion 5.920732 Log likelihood -70.79028 F-statistic 8.192747 Durbin-Watson stat 1.790508 Prob(F-statistic) 0.0088093.A3(A2的对数化)单根检验(1)未滞后Null Hypothesis: A3 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.611346 0.1031 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A3)Method: Least SquaresDate: 10/25/11 Time: 10:16Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A3(-1) -0.533566 0.204326 -2.611346 0.0150C 1.387300 0.542896 2.555371 0.0171R-squared 0.214309 Mean dependent var -0.020242 Adjusted R-squared 0.182882 S.D. dependent var 0.372695 S.E. of regression 0.336896 Akaike info criterion 0.733104 Sum squared resid 2.837478 Schwarz criterion 0.829092 Log likelihood -7.896903 F-statistic 6.819130 Durbin-Watson stat 1.623005 Prob(F-statistic) 0.015031(2)A3(-1)单根检验Null Hypothesis: A3(-1) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.411417 0.0198 Test critical values: 1% level -3.7114575% level -2.98103810% level -2.629906*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A3(-1))Method: Least SquaresDate: 10/25/11 Time: 10:17Sample (adjusted): 1984 2009Included observations: 26 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A3(-2) -0.662217 0.194118 -3.411417 0.0023C 1.756069 0.518899 3.384223 0.0025R-squared 0.326557 Mean dependent var -0.002080 Adjusted R-squared 0.298497 S.D. dependent var 0.367688 S.E. of regression 0.307960 Akaike info criterion 0.556109 Sum squared resid 2.276143 Schwarz criterion 0.652886 Log likelihood -5.229419 F-statistic 11.63777 Durbin-Watson stat 1.773706 Prob(F-statistic) 0.002292(二)格兰杰因果检验。
格兰杰因果关系检验

格兰杰因果关系检验因果关系的判断:因果关系的判断分成两类:一类是没有介入因素的情况,另一类是有介入因素的判断。
1. 没干预因素的推论步骤(1)第一步——判断因果关系的前提:行为人的行为给法益制造、升高了法所不允许风险。
(2)第二步——危害结果就是表明出现的结果。
刑法中因果关系中的实害结果,就是指现实出现的结果,不包含假设的结果。
假设的结果与犯罪行为之间的因果关系被称作假设(假设)的因果关系,这种因果关系不是表明的因果关系,不被接纳。
(3)第三步——危害结果是规范保护范围内的结果。
每一个罪名、罪状规范都在保护一种法益,防止一种实害结果。
(4)第四步——危害结果就是行为人统辖范围内的结果。
因果关系探讨的就是还结果,就是行为人统辖内的结果,即为行为人自己存有责任和义务避免出现的结果。
如果避免结果的出现就是他人的统辖范围,则该结果无法免责于行为人。
2. 有介入因素的判断步骤:两步走不异常:引起关系先前犯罪行为与结果存有因果关系介入因素导致(阻断关系)干预因素与否异常先前行为导致异常:单一制关系谁的危害引致结果二者共同导致(叠加关系)3. 干预因素的种类(1)自然时间(2)被害人的特定体质先前行为引发被害人疾病发作,死亡结果与先前行为有因果关系。
先前犯罪行为没引起被害人疾病发作,丧生结果与先前犯罪行为没因果关系。
(3)被害人自身的行为(4)第三人的犯罪行为(5)阻断救助的行为在救助犯罪行为具备救活的可能性时,丧生结果归属于切断救助的犯罪行为,而不归属于先前犯罪行为。
无法查明的案件一、行为人就是一个人(一)一个人实施一个行为这一犯罪行为可能将形成重罪,可能将形成刑事犯罪,可能将不构成犯罪,无法查明到底就是哪种事实。
对此根据难以确定时有助于被告原则,挑选有助于被告的事实予以判定。
(二)一个人实施两个行为二、行为人就是两个人(一)两个人构成共同犯罪根据“部分实行,全部负责管理”原则,无法查明,二人均与结果存有因果关系。
格兰杰因果关系检验
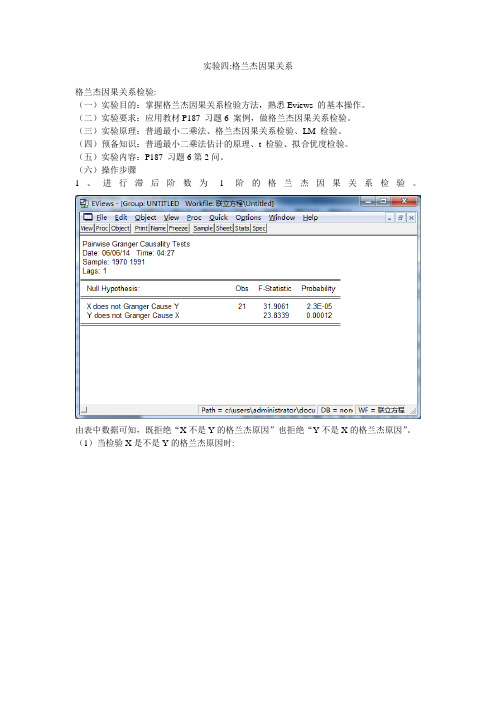
实验四:格兰杰因果关系格兰杰因果关系检验:(一)实验目的:掌握格兰杰因果关系检验方法,熟悉Eviews 的基本操作。
(二)实验要求:应用教材P187 习题6 案例,做格兰杰因果关系检验。
(三)实验原理:普通最小二乘法、格兰杰因果关系检验、LM 检验。
(四)预备知识:普通最小二乘法估计的原理、t 检验、拟合优度检验。
(五)实验内容:P187 习题6第2问。
(六)操作步骤1、进行滞后阶数为1阶的格兰杰因果关系检验。
由表中数据可知,既拒绝“X不是Y的格兰杰原因”也拒绝“Y不是X的格兰杰原因”。
(1)当检验X是不是Y的格兰杰原因时:X(-1)的P值为0.0000小于0.05则拒绝原假设。
此时X是Y的格兰杰原因。
AIC值为6.839780下面检验方程的序列相关性:拉格朗日检验如下:拉格朗日检验的LM=0.426186,P值为0.513866大于0.05,则存在严重的序列相关性。
(2)当检验Y是不是X的格兰杰原因时:Y(-1)的P值为0.0001小于0.05则拒绝原假设。
此时Y是X的格兰杰原因AIC值为:5.990657下面检验序列相关性:拉格朗日检验如下:拉格朗日检验的LM=04.504551,P值为0.033805小于0.05,则不存在严重的序列相关性。
2、进行滞后阶数为2阶的格兰杰因果关系检验。
由表中数据可知,既拒绝“X不是Y的格兰杰原因”也拒绝“Y不是X的格兰杰原因”。
(1)当检验X是不是Y的格兰杰原因时:X(-1)的P值为0.0281小于0.05,X(-2)的P值为0.4565小于0.05 则拒绝原假设。
此时X是Y的格兰杰原因。
AIC值为6.804851下面检验方程的序列相关性:拉格朗日检验如下:拉格朗日检验的LM=3.232597,P值为0.1986小于0.05,则不存在序列相关性。
(2)当检验Y是不是X的格兰杰原因时:Y(-1)的P值为0.0003小于0.05, Y(-1)的P值为0.1996小于0.05 则拒绝原假设。
bootstrap滚动格兰杰因果检验法

bootstrap滚动格兰杰因果检验法Bootstrap滚动格兰杰因果检验法又称滚动时间序列检验法,是一种基于偏相关系数的序列检验方法,适用于寻找时间序列之间的因果关系。
该方法通过对时间序列进行滚动,并对每一个时期的数据进行偏相关和t检验,以求得因果关系的显著性。
具体步骤如下:第一步,确定要进行因果检验的时间序列,这些序列需要在时间上有明确的先后关系,通常包括一个自变量序列(即潜在的“因素”序列)和一个因变量序列(即需要被检验影响的“响应”序列)。
第二步,将数据样本分成若干个时间段,对于每个时间段都进行滚动,即将时间点从头到尾依次滑动一个固定的步长,比如每隔一年或一个季度。
这样就得到了许多子样本,每个子样本包括一段时间序列中的数据和其对应的偏相关系数和t值。
第三步,对每个子样本进行偏相关和t检验。
通过偏相关分析确定两个序列是否存在“短期因果”的显著性,再通过t检验确定这种因果关系是否统计显著。
第四步,将所得到的偏相关和t值合并起来,得出整个时间序列的检验结果,并检验是否达到了所设定的显著性水平。
如果整个时间序列中的偏相关和t值表明潜在的“因素”序列对“响应”序列的影响是显著的,则可得出这两个序列之间的因果关系。
需要注意的是,在使用Bootstrap滚动格兰杰因果检验法时,还需要考虑时间序列中的一些其他因素,如趋势、季节性等。
比如,如果时间序列中存在明显的季节性因素,那么就需要先进行季节性调整,否则可能得出的结论不能代表真实情况。
总的来说,Bootstrap滚动格兰杰因果检验法是一种能够很好应对某些复杂数据序列的检验方法,能够帮助研究人员找到序列之间的因果关系,从而更好地理解数据的本质。
格兰杰因果关系检验的步骤

格兰杰因果关系检验的步骤(1)将当前的y对所有的滞后项y以及别的什么变量(如果有的话)做回归,即y对y 的滞后项yt—1,yt-2,…,yt-q及其他变量的回归,但在这一回归中没有把滞后项x包括进来,这是一个受约束的回归。
然后从此回归得到受约束的残差平方和RSSR。
(2)做一个含有滞后项x的回归,即在前面的回归式中加进滞后项x,这是一个无约束的回归,由此回归得到无约束的残差平方和RSSUR。
(3)零假设是H0:α1=α2=…=αq=0,即滞后项x不属于此回归。
(4)为了检验此假设,用F检验,即:它遵循自由度为q和(n-k)的F分布。
在这里,n是样本容量,q等于滞后项x的个数,即有约束回归方程中待估参数的个数,k是无约束回归中待估参数的个数。
(5)如果在选定的显著性水平α上计算的F值超过临界值Fα,则拒绝零假设,这样滞后x项就属于此回归,表明x是y的原因。
(6)同样,为了检验y是否是x的原因,可将变量y与x相互替换,重复步骤(1)~(5)。
首先将选定指标(xxx,xxx)对上证指数收益率及标志性股票收益率进行格兰杰因果检验,确定指标与收益率之间是否有因果关系,并以此作为筛选指标的标准。
为了排除其他其他有效变量对残差的影响,将股票收益率预测的几个常用指标(波动率,var,市净率,巴拉巴拉)加入通过格兰杰因果检验的市场情绪指标,一并进行主成分分析(选择主成分分析的原因是这些常用市场预测指标与市场情绪有符合常识的相关性),并选出解释度高的主成分,推算出关于选定指标的回归方程。
即为情绪指标的预测模型。
将预测模型对一千天的数据进行回顾测试,用方差分析检验二者之间是否存在显著差异;再选择市场情绪发生重大波动的特殊时段进行测试,方差分析检验二者是否存在显著差异。
若存在显著差异,考虑滞后影响和变量形态(比如变量的平方),进一步调整模型,直到得到满意的结果(比如置信度99。
99%)。
var格兰杰因果关系检验

var格兰杰因果关系检验格兰杰因果关系检验(Granger causality test)是一种经济计量学中常用的统计方法,用于判断两个时间序列之间是否存在因果关系。
本文将对格兰杰因果关系检验的原理、步骤和实际应用进行详细解析。
一、原理格兰杰因果关系检验是基于向量自回归模型(Vector Autoregressive, VAR)的思想发展而来的。
VAR模型用于描述多个时间序列之间的动态关系,其中涉及到滞后阶数(Lag Order)的选择和残差截断的问题。
而格兰杰因果关系检验则通过比较两个VAR模型的残差的方差来判断两个时间序列之间的因果关系。
二、步骤1. 数据准备:收集两个时间序列的观测数据,并确保两个序列具有相同的时间粒度和起始时间。
2. 建立VAR模型:使用计量经济学软件(如EViews、Stata等)建立两个时间序列的VAR模型。
在建模过程中,需要选择合适的滞后阶数和包含的控制变量。
3. 检验格兰杰因果关系:首先,检验VAR模型的残差是否满足正态性和独立同分布的假设。
如果残差不满足这些假设,则需进行适当的转换或修正。
然后,比较两个VAR模型的残差方差,通过统计检验确定是否存在因果关系。
4. 排除外生因素:如果检验结果表明存在因果关系,但在实际应用中无法解释或存在外生因素的干扰,则需要进行进一步的分析和调整。
三、实际应用格兰杰因果关系检验在实际应用中具有广泛的用途,以下列举几个常见的应用场景:1. 宏观经济研究:用于分析经济指标之间的因果关系,如GDP与消费、投资、进出口等之间的关系。
2. 金融市场预测:用于判断某个金融资产价格变动的因果关系,如利率、股票价格、汇率等之间的关系。
3. 商业决策分析:用于评估市场因素对产品销量的影响,如广告投入、竞争对手销售额等与产品销量之间的关系。
4. 自然灾害预测:用于分析自然灾害事件与其他气象因素之间的因果关系,如降雨量、地震活动等之间的关系。
格兰杰因果关系检验的优势是在不需要知道因果关系的具体方向的前提下,能够判断两个时间序列之间是否存在因果关系。
格兰杰因果检验步骤

格兰杰因果检验步骤引言:格兰杰因果检验是一种常用的统计方法,用于确定两个变量之间是否存在因果关系。
本文将介绍格兰杰因果检验的步骤和应用。
一、确定研究模型在进行格兰杰因果检验之前,首先需要确定研究模型。
研究模型是描述研究变量之间关系的理论框架,可以基于已有理论或实证研究构建。
二、收集数据收集数据是进行格兰杰因果检验的重要步骤。
数据可以通过实地调查、问卷调查、实验等方式获得。
收集的数据应涵盖研究模型中的所有变量,并确保数据的可靠性和有效性。
三、数据预处理在进行格兰杰因果检验之前,需要对收集到的数据进行预处理。
数据预处理包括数据清洗、缺失值处理、异常值处理等。
通过数据预处理,可以提高数据的质量和可靠性,减少误差的影响。
四、计算格兰杰因果检验统计量格兰杰因果检验的核心是计算格兰杰因果检验统计量。
格兰杰因果检验统计量可以通过计算变量之间的相关系数得到。
相关系数衡量了两个变量之间的线性关系强度,可以用来判断是否存在因果关系。
五、设定显著性水平在进行格兰杰因果检验之前,需要设定显著性水平。
显著性水平是判断研究结果是否具有统计学意义的标准。
通常,显著性水平设定为0.05或0.01。
六、进行格兰杰因果检验在设定显著性水平之后,可以进行格兰杰因果检验。
格兰杰因果检验以零假设和备择假设为基础。
零假设认为两个变量之间不存在因果关系,备择假设认为存在因果关系。
七、计算P值进行格兰杰因果检验后,可以得到一个P值。
P值是判断研究结果是否显著的指标。
如果P值小于设定的显著性水平,就可以拒绝零假设,认为存在因果关系;如果P值大于设定的显著性水平,就接受零假设,认为不存在因果关系。
八、解释研究结果根据计算得到的P值,可以解释研究结果。
如果P值小于设定的显著性水平,可以得出结论:存在因果关系。
如果P值大于设定的显著性水平,可以得出结论:不存在因果关系。
九、结果的解释和讨论在解释研究结果时,需要结合研究背景和理论知识进行综合分析。
分析结果时应注意避免歧义和错误信息的产生,确保结果的准确性和严谨性。
格兰杰因果检验步骤

格兰杰因果检验步骤格兰杰因果检验是一种用于判断两个二分类变量之间是否存在因果关系的统计方法。
它可以帮助我们确定一个变量是否能够预测另一个变量的状态,并且排除其他变量的干扰。
下面将介绍格兰杰因果检验的步骤。
1. 确定研究问题和变量在进行格兰杰因果检验之前,首先需要明确研究问题和要分析的变量。
例如,我们想要研究某种药物对于治疗某种疾病的效果,那么药物的使用与疾病的发展就是我们要分析的两个变量。
2. 收集数据接下来,我们需要收集关于这两个变量的数据。
数据可以通过实验、调查或观察等方式获得。
确保数据的收集过程严谨可靠,以保证后续的分析结果的可靠性。
3. 构建列联表格兰杰因果检验需要基于二分类变量的列联表进行计算。
列联表是一种将两个变量的不同取值组合成的表格,用于描述两个变量之间的关系。
表格的行表示一个变量的不同取值,列表示另一个变量的不同取值,交叉点则表示两个变量同时取某个值的频数。
4. 计算列联表的卡方值格兰杰因果检验使用卡方检验来判断两个变量之间是否存在因果关系。
卡方值是通过计算观察频数与期望频数之间的差异而得到的。
观察频数是指在实际数据中两个变量同时取某个值的频数,而期望频数是指在假设没有因果关系的情况下,两个变量同时取某个值的频数。
5. 计算自由度和临界值计算完卡方值后,需要根据列联表的自由度和显著性水平来确定临界值。
自由度是指列联表中独立的自由变量的个数。
临界值是在给定显著性水平下,用于判断卡方值是否显著的参考值。
6. 比较卡方值和临界值将计算得到的卡方值与临界值进行比较。
如果卡方值大于临界值,则可以得出结论:两个变量之间存在因果关系。
反之,如果卡方值小于临界值,则不能得出因果关系的结论。
7. 解释结果根据比较的结果来解释两个变量之间的关系。
如果卡方值大于临界值,说明药物的使用与疾病的发展之间存在因果关系。
如果卡方值小于临界值,则说明药物的使用与疾病的发展之间不存在因果关系。
同时,还可以进一步分析其他变量对于药物治疗效果的影响,以获得更全面的结论。
格兰杰因果关系检验的步骤

格兰杰因果关系检验的步骤1.收集数据:首先需要收集两个时间序列的数据,分别记为X和Y。
这两个时间序列可以是连续的,也可以是离散的,但要求它们均为平稳的时间序列。
2. 拟合模型:接下来,需要为X和Y拟合合适的模型。
常用的模型包括自回归模型(Autoregressive model, AR)、移动平均模型(Moving Average model, MA)和自回归移动平均模型(Autoregressive Moving Average model, ARMA)。
根据数据的特性进行模型的选择。
3. 确定滞后阶数:通过计算自相关函数(Autocorrelation Function, ACF)和偏自相关函数(Partial Autocorrelation Function, PACF),可以确定X和Y的滞后阶数。
滞后阶数表示因果关系所涉及的时间间隔。
4. 拟合向量自回归模型:通过将X和Y的滞后值作为自变量,建立一个向量自回归模型(Vector Autoregressive model, VAR)。
公式形式为:Y = c + A1*Y(lag1) + ... + An*Y(lagN) + B1*X(lag1) + ... +Bn*X(lagN) + ε,其中c为常数项,Ai和Bi为系数矩阵,N为滞后阶数。
5.检验格兰杰因果关系:对于VAR模型,可以通过计算向量自回归残差的协方差矩阵来检验X对Y的格兰杰因果关系。
设VAR模型的残差为e,如果存在一个时间滞后,称之为k,使得滞后残差e(k)与Y的现值Y(t)相关显著,那么就可以认为X对Y具有格兰杰因果关系。
6.计算p值:通过计算格兰杰因果关系检验的统计量,可以得到一个p值。
如果p值小于设定的显著性水平(通常为0.05),则可以拒绝原假设,认为X对Y具有格兰杰因果关系。
7.解释结果:根据检验结果,可以解释变量X对Y的因果关系的方向和强度。
如果X对Y具有正向影响且显著,可以认为X的变动可以导致Y的变动。
3.2格兰杰因果关系检验(计量经济学-武汉大学刘伟)

(2)建立变量序列并输入样本数据。
在工作文件建立后,应创建待分析处理的数据序列。在主窗口 的菜单选项或者工作文件窗口的工具栏中选择Objects/New Object,并在屏幕出现的对象定义对话框(New Object)左侧 的Type of Object一栏选择Series,在右侧Name for Object一 栏分别输入vol和ra表示水库流量与降水量两个序列。然后在 工作文件(Workfile)窗口分别双击vol或ra,在屏幕出现的 Series窗口工具栏上选择Edit+/-按钮,进入编辑状态,可以输 入样本数据。录入数据完毕后再次点击Edit+/-按钮,恢复只读 状态。或者,也可以在Excel中先建立一个工作表,将有关变 量的数据录进去;然后在EViews的工作文件窗口选择 procs/Import/Read Text-lotus-Excel,将其读入Eviews。
格兰杰因果关系检验的结果
Pairwise Granger Causality Tests Date: 07/10/04 Time: 20:14 Sample: 1 78 Lags: 9
Null Hypothesis:
VOL does not Granger Cause RA RA does not Granger Cause VOL
(3)进行Granger因果关系检验。
在工作文件窗口中,同时选中序列vol和ra,单击鼠标右键,在 弹出的菜单中选择Open/as Group,生成一个群对象 (Group);然后,在群对象观测值窗口的工具栏中选择View / Granger Causality,在屏幕出现的对话框(Lag Specification)中Lags to include一栏后面输入最大滞后期数 k=9,点击OK,即可得到格兰杰因果检验的结果。
r语言格兰杰因果关系检验

r语言格兰杰因果关系检验格兰杰因果关系检验(Granger causality test)是由Nobel经济学奖得主格兰杰(Clive W. J. Granger)提出的一种时间序列分析方法,用于检验一个时间序列是否因果影响另一个时间序列的变化。
格兰杰因果关系检验在经济学、金融学、计量经济学等领域得到广泛应用。
格兰杰因果关系检验的基本思想是:如果一个时间序列的过去值能够提供关于另一个时间序列未来值的额外信息,那么可以认为前者对后者存在因果关系。
因此,格兰杰因果关系检验的核心问题是,在控制了其他可能的因素之后,一个时间序列的延迟值是否能够预测另一个时间序列的当前值。
具体来说,格兰杰因果关系检验的步骤如下:1. 确定研究的两个时间序列。
假设我们有两个时间序列X和Y。
2. 建立一个基准模型。
基准模型仅包括Y的当前值的自回归模型,没有包含X序列。
基准模型的目的是为了提供对比。
3. 添加X序列到基准模型。
将X序列的延迟值添加到基准模型中,形成一个扩展模型。
4. 使用统计方法对基准模型和扩展模型进行比较。
常用的统计方法有F统计量、卡方统计量等。
如果扩展模型的统计显著性水平小于某个给定的阈值(通常取0.05),则可以认为X序列对Y序列存在因果关系。
需要注意的是,格兰杰因果关系检验的结果并不能确定因果关系的方向,即无法确定X序列是引起Y序列变化的原因,还是Y序列是引起X序列变化的原因。
为了确定因果关系的方向,通常需要进行额外的分析和判断。
此外,格兰杰因果关系检验要求序列之间是平稳的,否则结果可能出现错误。
格兰杰因果关系检验的优点是简单易行、易于解释和使用,对于两个时间序列之间的因果关系提供了一种经验检验的方法。
然而,它也存在一些限制。
首先,格兰杰检验忽略了可能存在的其他潜在因素,可能导致结果的偏误。
其次,格兰杰检验只能检验两个时间序列之间的因果关系,而不能检验多个时间序列之间的复杂关系。
综上所述,格兰杰因果关系检验是一种重要的时间序列分析方法,通过比较基准模型和扩展模型,判断一个时间序列是否对另一个时间序列存在因果影响。
格兰杰因果关系检验

• 考察X是否影响变量Y的问题,主要看当期的Y能够 在多大程度上被过去的X所解释,在Yt方程中加入X 的滞后值是否使解释程度显著提高。如果X有助于 Y预测效果的提高,就可以认为X是Y的格兰杰原因。
将式(5.4.2)和式(5.4.4)结合,得到一个一般的自回 归移动平均过程ARMA(p,q)
X t 1 X t 1 2 X t 2 p X t p t 1 t - 1 q t - q
(5.4.5)
• 式(5.4.5)表明,一个随机时间序列可以通过一个自 回归移动平均过程生成,即该序列可以由其自身 的过去或滞后值以及随机扰动项来解释。如果该 序列是平稳的,即它的行为不会随着时间的推移 而变化,那么就可以通过该序列过去的行为来预 测它的未来。
• 结构向量自回归模型(SVAR)
• 结构向量自回归模型中包含了变量间的当期关系。 变量间的当期关系揭示了变量之间的相互影响,实 质上是对向量自回归模型施加了基于经济理论分析 的限制性条件,从而识别变量之间的结构关系。结 构向量自回归模型每个方程左边是内生变量,右边 是自身的滞后和其他内生变量的当期和滞后。
• 格兰杰因果关系检验是通过受约束的F检验完成的。 以X不是Y 的格兰杰原因这一假设为例,即假设 (5.4.7)式中X各滞后项前的参数整体为零,分别做 包含与不包含X各滞后项的回归,记前者残差平方 和为RSSU,后者残差平方和为RSSR,再计算F统计
FRRSRSSU S/RnSUkS/m
式中,m为X的滞后项的个数,n为样本容量,k为 包含可能存在的常数项及其他变量在内的无约束 回归模型的待估参数的个数。
格兰杰因果关系检验

年份
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999
CONS
9113.2 10315.9 12459.8 15682.4 20809.8 26944.5 32152.3 34854.6 36921.1 39334.4
GDP
18319.5 21280.4 25863.7 34500.7 46690.7 58510.5 68330.4 74894.2 79003.3 82673.1
判断:=5%,临界值F0.05(2,17)=3.59
拒绝“GDP不是CONS的格兰杰原因”的假设,不 拒绝“CONS不是GDP的格兰杰原因”的假设。
因此,从2阶滞后的情况看,GDP的增长是居民 消费增长的格兰杰原因,而相反不是。
中国GDP与居民消费CONS的格兰杰因果检验
判断结果是:GDP与CONS有双向的格兰杰因果关系, 即相互影响。
年份
1978 1979 1980 1981 1982 1983 1984 1985 1986 1987
CONS
1759.1 2005.4 2317.1 2604.1 2867.9 3182.5 3674.5 4589 5175 5961.2
GDP
3605.6 4074 4551.3 4901.4 5489.2 6076.3 7164.4 8792.1 10132.8 11784.7
但究竟是GDP的增长导致了M2的增加,还是M2
增加促进了GDP的增长,或者两者互为因果关系,
从理论和实践两方面来回答这个问题,就不是很
简单的问题
二、格兰杰因果关系检验
(一)格兰杰检验的基本思想是“过去可以预测现在”
如果X是Y变化的原因,则 X的变化应当发生在 Y
格兰杰因果检验详细步骤

格兰杰因果检验详细步骤
嘿,朋友们!今天咱来聊聊格兰杰因果检验的详细步骤,这可有意思啦!
你想想看,就像我们在生活中找原因一样,格兰杰因果检验就是帮我们在一堆数据里找出谁是因谁是果。
那到底咋弄呢?
首先啊,咱得有数据,这就好比做饭得有食材呀!把相关的数据都准备好,整整齐齐地放那。
然后呢,开始计算啦!看看这些数据之间有没有啥特别的关系。
这就好像侦探在找线索,一点点地分析。
接下来,要进行统计检验咯!这就像是给这些线索做个鉴定,看看是不是真的靠谱。
再然后呀,根据检验的结果来判断啦!如果通过了,那就说明可能有因果关系哦。
举个例子吧,就好比说你发现每次下雨前家里的湿度都会升高,那是不是可以说下雨是湿度升高的原因呢?当然啦,这只是个简单的类比,实际的格兰杰因果检验可比这复杂多啦!
但咱别怕呀,一步一步来,就像爬山一样,慢慢往上爬,总能到山顶的。
在这个过程中,可能会遇到一些小挫折,数据不太听话啥的,可别灰心!就当是和数据玩个小游戏,斗智斗勇呗。
而且哦,学会了这个格兰杰因果检验,那可牛啦!你就能在很多领域大显身手啦,经济呀、统计呀,都能用上。
总之呢,格兰杰因果检验虽然有点复杂,但只要咱有耐心,有决心,肯定能把它拿下!大家加油呀!。
stata时间序列格兰杰单位根检验操作流程

stata时间序列格兰杰单位根检验操作流程格兰杰(Granger)单位根检验是一种常用的时间序列分析方法,用于判断一个变量是否是平稳的。
在Stata中,我们可以使用"dfuller"命令来进行格兰杰单位根检验。
以下是Stata中进行格兰杰单位根检验的操作流程:步骤1:准备数据首先,我们需要准备要进行单位根检验的时间序列数据。
在Stata中,可以将数据导入为一个数据集,确保数据按照时间顺序排列。
步骤2:加载数据使用"use"命令加载准备好的数据集。
步骤3:执行格兰杰单位根检验在Stata的命令窗口中输入以下命令执行格兰杰单位根检验:```dfuller 变量名```其中,"变量名"是要进行单位根检验的变量名称。
执行该命令后,Stata将输出单位根检验的结果。
步骤4:解读结果单位根检验的结果通常包括统计值和p值。
统计值(Test statistic)用于判断变量是否是平稳的,p值(MacKinnon's approximate p-value)用于判断假设是否成立。
- 如果统计值小于临界值,且p值小于0.05(通常所用的显著性水平),则可以拒绝原假设,即变量是平稳的。
在这种情况下,可以进行进一步的时间序列分析。
- 如果统计值大于临界值,或者p值大于0.05,则不能拒绝原假设,即变量存在单位根,是非平稳的。
在这种情况下,需要对数据进行差分处理或采取其他方法来使其平稳。
注意事项:- 在进行格兰杰单位根检验时,需要考虑是否存在时间滞后项。
如果发现存在滞后项,则需要将滞后项加入检验模型中,以保证结果的准确性。
- 格兰杰单位根检验是一种经典方法,但并不适用于所有的时间序列数据。
在进行单位根检验前,建议对数据进行初步的探索性分析,确保其适用性。
综上所述,以上是在Stata中执行格兰杰单位根检验的操作流程。
通过这一流程,我们可以判断时间序列数据是否是平稳的,从而为后续的时间序列分析提供基础。
r语言格兰杰因果关系检验

r语言格兰杰因果关系检验格兰杰因果关系检验(Granger causality test)是一种用于分析时间序列数据的方法,用于确定两个变量之间是否存在因果关系。
该方法基于因果关系的定义,即一个变量的变化是否能够在未来预测另一个变量的变化。
本文将介绍格兰杰因果关系检验的原理、步骤以及相关实现方法。
格兰杰因果关系检验的原理基于时间序列的因果关系理论。
该理论认为,如果一个时间序列能够显著地预测另一个时间序列的变化,那么可以认为这两个序列之间存在因果关系。
格兰杰因果关系检验通过统计方法来判断这种关系的显著性。
格兰杰因果关系检验的步骤如下:1. 确定时间序列数据:首先需要确定需要研究的时间序列数据,并将其表示为向量。
通常情况下,这两个时间序列被称为Y和X。
2. 拟合线性回归模型:对于每个时间点,使用历史数据对Y和X分别进行线性回归分析。
即对于每个时间点t,使用t之前的历史数据来估计Y的回归方程和X的回归方程。
3. 检验Y是否能够预测X:根据拟合的回归模型,计算残差序列ε_Y和ε_X。
然后使用统计方法检验Y的回归模型对于X的预测能力是否显著。
常用的统计检验方法有F检验和t检验。
4. 检验X是否能够预测Y:类似地,根据拟合的回归模型,计算残差序列ε_X和ε_Y。
然后使用统计方法检验X的回归模型对于Y的预测能力是否显著。
5. 判断因果关系:通过比较上述两个检验的结果,可以得出结论是否存在因果关系。
如果Y的回归模型对于X的预测显著,而X的回归模型对于Y的预测不显著,则可以认为Y对于X有因果关系。
在R语言中,可以使用“vars”包进行格兰杰因果关系检验。
首先,需要安装并加载该包:```install.packages("vars")library(vars)```接下来,假设我们有两个时间序列数据Y和X,可以使用以下代码进行格兰杰因果关系检验:```# 将时间序列数据转换为矩阵形式data <- cbind(Y, X)# 构建VAR模型model <- VAR(data)# 进行格兰杰因果关系检验granger.test(model, p = 2)```这里的参数p表示使用的滞后阶数,可以根据实际情况进行调整。
E-view格兰杰检验步骤

以1978~2006年间实际可支配收入(X)和居民实际消费总支出(Y)之间的因果关系为例,做格兰杰检验
1.点击E-view主画面顶部按钮File/New/Workfile,如下图
弹出下图
2.在上图中的Workfile frequency中选择Annual,并输入Start date:1978 和End date:
2006,点击OK,如下图所示
3.再点击主画面中Objects/New Object,弹出如下窗口
4.选择Group,并在Name for Object框输入你要定义的名字如g1,得到下图
5.点击obs右边的单元格,此时该单元格下方所在列会变蓝,如图
在对话框中输入变量名称X,Y及其变量值
6.点击主页面Quick/Group Statistics/Granger Causality Test,得到下图
输入y x,点击Ok,得到下图,
将2改为1点击OK得到下图
武汉理工大学杨超上传。
格兰杰因果检验假设

格兰杰因果检验假设
格兰杰因果检验假设是指一种用来判断某个因素是否能够引起某
个现象的方法。
这个方法是在观察和试验的基础上建立起来的,通常
用于研究医学和公共卫生领域中的问题。
以下是详细的步骤解析:步骤一:假设提出
格兰杰因果检验的第一步是提出一个理论假设,即研究者提出了
某个因素可能会导致某个现象,如研究健康饮食是否能够预防某种疾病。
步骤二:实证观察
在提出假设之后,研究者需要进行实证观察,对现象进行详细的
描述和测量。
比如,研究者可以对一组人群进行调查,了解他们的饮
食习惯以及疾病发生情况。
步骤三:数据分析
经过实证观察后,研究者需要分析所得数据,以便判断某个因素
是否与某个现象存在相关性。
这一步通常通过统计学方法来实现,例
如使用卡方检验或另一种与之等价的方法——费舍尔确切概率检验等。
步骤四:因果关系评估
数据分析之后,研究者需要评估因果关系。
这一步可以采用双盲
试验等方法,一组人群饮用健康餐饮,另一组则不饮用,随着时间的
推移对两组人群进行跟踪检测,以便对其疾病发生情况进行对比分析。
步骤五:结论
最后,研究者需要根据所得结果进行结论。
如果健康饮食确实能
够预防某种疾病,那么研究结论就可以肯定地把它们之间的关系称为
因果关系,否则就不能。
总体来说,格兰杰因果检验假设是一个很复杂的过程,需要跨过
从假设提出到得出结论这些重要的步骤。
它可以帮助人们确定某个因
素是否与某个现象存在相关性,从而有助于更全面、准确地理解问题,为人们提供更好的治疗方案。
ex7Granger

ex7Granger格兰杰(Granger)因果检验【实验⽬的】掌握格兰杰(Granger)因果检验的基本原理及操作。
【实验内容】⼀、Granger因果检验原理;⼆、数据的输⼊;三、单位根检验;四、协整检验;五、格兰杰检验【实验步骤】⼀、理解Granger因果检验原理在经济学上确定⼀个变量的变化是否是另⼀个变量变化的原因,⼀般⽤格兰杰因果关系(Granger Test of Causality)检验。
⽽进⾏格兰杰因果检验⾸先必须证明随机变量是平稳序列,因此,⼀个完整的格兰杰因果检验过程可描述为时间序列的单位根检验、变量之间的协整和格兰杰因果关系检验。
时间序列分析的⼀个难点是变量的平稳性考察,因为⼤部分整体经济时间序列都有⼀个随机趋势,这些时间序列被称为“⾮平稳性”时间序列,当⽤于平稳时间序列的统计⽅法运⽤于⾮平稳的数据分析时,⼈们很容易做出安全错误的判断。
动态计量经济理论要求在进⾏宏观经济实证的分析时,⾸先必须进⾏变量的平稳性检验,否则分析时会出现“伪回归”现象,以此作出的结论很可能是错误的。
对于⾮0阶单整的序列,则可⽤协整检验进⾏分析,因为对于不同时间序列变量,只有在协整的情况下,才可能存在⼀个长期稳定的⽐例关系。
(⼀)单位根检验(unit root test)检验变量是否稳定的过程称为单位根检验。
平稳序列将围绕⼀个均值波动,并有向其靠拢的趋势,⽽⾮平稳过程则不具有这个性质。
⽐较常⽤的单位根检验⽅法是ADF(Augented Dickey-Fuller Test)检验,这是⽬前普遍应⽤的单整检验⽅法。
该检验法的基本原理是通过n次差分的办法将⾮平稳序列转化为平稳序列。
(⼆)协整检验(cointegration test)变量序列之间的协整关系是由Engle和Granger⾸先提出的。
其基本思想在于,尽管两个或两个以上的变量序列为⾮平稳序列,但它们的某种线性组合却可能呈现稳定性,则这两个变量之间便存在长期稳定关系即协整关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
