ABAQUS中Cohesive单元建模方法
abaqus复合材料薄壁圆筒建模流程
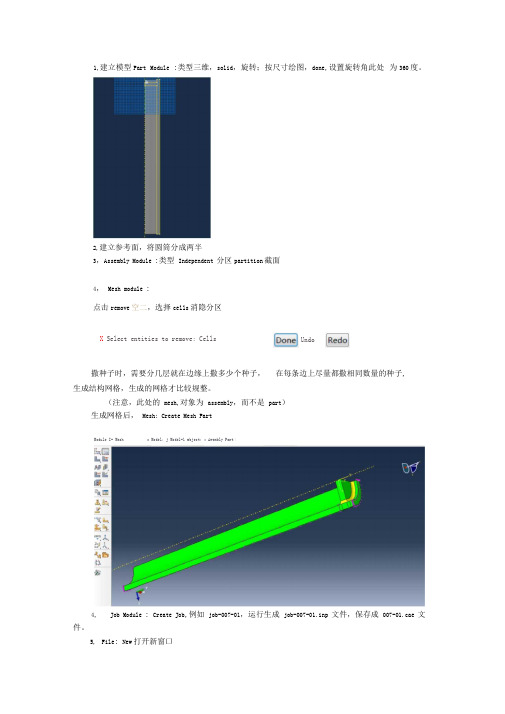
1,建立模型Part Module :类型三维,solid,旋转;按尺寸绘图,done,设置旋转角此处为360度。
2,建立参考面,将圆筒分成两半3,Assembly Module :类型Independent 分区partition截面4,Mesh module :点击remove空二,选择cells消隐分区X Select entities to remove: Cells Undo撒种子时,需要分几层就在边缘上撒多少个种子,在每条边上尽量都撒相同数量的种子,生成结构网格,生成的网格才比较规整。
(注意,此处的mesh,对象为assembly,而不是part)生成网格后,Mesh: Create Mesh PartModule I- Mesh * Model:j Model-1 abject: * Awembly Part「4,Job Module : Create Job,例如job-007-01,运行生成job-007-01.inp 文件,保存成007-01.cae 文件。
5,File: New打开新窗口6,File: Import : Model 选择job-007-01.inp 打开7,Mesh Module:Tools: Surface manager: create: by angle 定义surface 集合Tools: Set manager: create: Element: by angle 定义Element 集合用以下三个命令操作,选择恰当的面。
丄i Select the Entity Closest to the Screen,---- Select From Exterior En tities'包i 一J Select From Interior Entities (左键点击第二个图标不放拖出即可)注:定义Element集合时,可以从外到内,定以一层后,在display中--- -:把定义的那层remove掉再定义下面一层。
ABAQUS中Cohesive单元建模方法

复合材料模型建模与分析1. Cohesive单元建模方法几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive 的本构模型。
Cohesive 单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
ABAQUS中Cohesive单元建模方法

复合材料模型建模与分析1. Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation 描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive 单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive 的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive 的本构模型。
Cohesive 单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
Abaqus教程之cohesive单元损伤模拟全
然后我们结合具体的实例深入分析解读cohesive参数及设置,以及两种 不同的损伤演化准则之间的区别与联系
abaqus中 cohesive模型 的建立及设置
下面我们将给出abaqus不同模块下的实例设置步骤,方便快速理解和学习 Part模块:
Property模块:
Assembly模块:
Step模块:
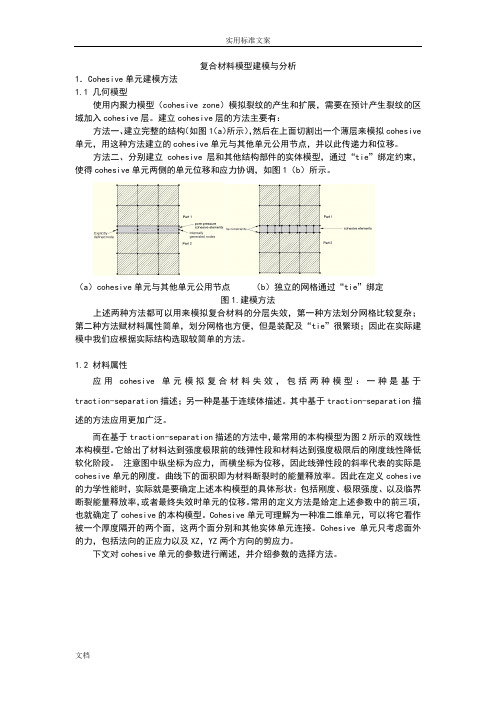
Cohesive element理论
abaqus6.14在线帮助文档 http://ivt-abaqusdoc.ivt.ntnu.no:2080/v6.14/books/usb/default.htm
cohesive element是基于损伤力学理论,自己去帮助文档补充相关基础知识
cohesive单元的理解起来其实并没有那么复杂,使用起来也是非常高效的,它可以 模拟分层失效,也可以通过在模型中相邻的实体单元间批量插入cohesive单元来模 拟裂纹的随机扩展。
单元由于很多人并不理解cohesive的参数,导致总是调不出想要的开裂效果,多次尝试无果 导致失去信心,其实如果你掌握了abaqus中所有的模拟方法后,你会发现abaqus做断裂其实
没那么难,无非就是断裂力学LEFM和损伤力学而已,下面我详细分析cohesive的本构 及参数设置,而且结合实例验证设置的参数,并分析损伤演化的位移准则和能量 准则的区别与联系,让你在10分钟内掌握cohesive。
Stress2-位移U2曲线
从Stress2与位移U2中发现,当达到100MPa时开始损伤,cohesive张开达到1e-5mm时, cohesive单元完全失效,此时的SDEG=1,此时的cohesive不能再承受力将被删除掉, 这个与我们开始的预期是完全一致的。
PS:如果有需要批量插入cohesive插件的可以联系qq1057593923或微信maliweizhiyuan 插入的具体内容见技术邻https:///content/post/418489
ABAQUS中Cohesive单元建模方法

ABAQUS中Cohesive单元建模方法复合材料模型建模与分析1、Coheive单元建模方法1、1几何模型使用内聚力模型(coheivezone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入coheive层。
建立coheive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟coheive单元,用这种方法建立的coheive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立coheive层和其他结构部件的实体模型,通过“tie”绑定约束,使得coheive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)coheive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1、建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1、2材料属性应用coheive单元模拟复合材料失效,包括两种模型:一种是基于traction-eparation描述;另一种是基于连续体描述。
其中基于traction-eparation描述的方法应用更加广泛。
而在基于traction-eparation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是coheive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义coheive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了coheive的本构模型。
Coheive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
ABAQUS中Cohesive单元建模方法分析

复合材料模型建模与分析1. Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation 描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
ABAQUS粘聚力模型(CohesiveModel)应用小结

ABAQUS粘聚⼒模型(CohesiveModel)应⽤⼩结关于Cohesive模型应⽤的⼀些⼩结学习粘聚⼒单元时从各种讨论中获益匪浅,现总结⾃⼰做过的⼀些练习模型,希望对⼤家有所帮助。
⾥⾯有很多是论坛中帖⼦⾥⾯的知识,在此对原作者⼀并谢过。
错误疏漏之处请⼤家多指正。
这⾥所有的粘聚⼒模型都是指Traction-separation-based modeling( The modeling of bonded interfaces in composite materials often involves situations where the intermediate glue material is very thin and for all practical purposes may be considered to be of zero thickness,帮助⽂献⽬录为32.5.1-2 )。
模型中参数仅作测试⽤,没有实际意义。
1.引⾔及⼀些讨论粘聚⼒模型( Cohesive Model )将复杂的破坏过程⽤两个⾯之间的‘相对分离位移-⼒’关系表达。
这种粘聚⼒关系很⼤程度上是宏观唯象的,有多种表达形式,如图1-1所⽰。
图1-1 常见的粘聚⼒关系Abaqus软件中⾃带的粘聚⼒模型为线性三⾓形(下降阶段可以为⾮线性)。
其它如指数、梯形等模型主要通过⽤户单元⼦程序(UEL/VUEL)实现。
粘聚⼒模型的形状对某些计算结果( 例如单纯的拉开分层)影响很⼤。
1.1 粘聚⼒单元及粘聚⼒接触粘聚⼒模型可以通过使⽤粘聚⼒单元( Cohesiev Elements )或者粘聚⼒接触( Cohesive Surfaces )来实现。
在模型和参数都⼀致的时候,两类⽅法得到的结果略有差别。
1.2粘聚⼒单元Abaqus中的粘聚⼒单元包括3D单元COH3D8,COH3D6;2D单元COH2D4;轴对称单元COHAX4;以及相应的孔压单元。
abaqus 插入cohesive element 原理

abaqus 插入cohesive element 原理Abaqus中的Cohesive Element(粘结元素)是一种用于模拟材料中裂纹扩展和断裂行为的元素。
它可以模拟材料中的粘结和剪切行为,并允许裂纹在材料中传播。
Cohesive Element的原理基于断裂力学理论和粘结力学理论。
它将材料中的断裂行为建模为两个相邻表面之间的相互作用。
在裂纹扩展过程中,材料的断裂面上会产生粘结应力和剪切应力。
Cohesive Element通过施加粘结和剪切应力来模拟这种相互作用。
Cohesive Element的工作原理如下:1. 定义材料的弹性行为:首先,需要定义材料的弹性行为,即材料在无裂纹时的应力-应变关系。
可以使用线性弹性模型或非线性弹性模型来描述材料的弹性行为。
2. 定义粘结行为:接下来,需要定义材料的粘结行为。
这包括定义材料的粘结强度、粘结刚度和粘结应力-开裂位移关系。
通常会使用一个或多个粘结模型来描述材料的粘结行为,如弹簧-剪切模型、弹簧-弹性模型或弹簧-塑性模型。
3. 插入Cohesive Element:将Cohesive Element插入到模型中,以模拟裂纹的扩展。
Cohesive Element通常插入到两个相邻的节点之间,其中一个节点代表裂纹的一个端点,另一个节点代表裂纹的另一个端点。
CohesiveElement的属性包括弹性刚度、粘结强度和粘结模型。
4. 定义断裂准则:定义断裂准则以确定何时发生裂纹扩展。
常见的断裂准则包括最大切应力准则、最大切应变准则和能量释放率准则。
这些准则根据材料的断裂特性来确定裂纹扩展的条件。
5. 模拟裂纹扩展:通过施加加载条件(如拉伸、剪切或弯曲)来模拟裂纹的扩展。
在加载过程中,CohesiveElement会根据定义的粘结行为和断裂准则来计算裂纹的扩展。
总之,Abaqus中的Cohesive Element通过模拟材料中的粘结和剪切行为来模拟裂纹的扩展和断裂行为。
利用Abaqus二维Cohesive单元和Tie constraint 进行分层模拟

e an dAl l t h 利用Abaqus 二维Cohesive 单元和Tie constraint 进行分层模拟第一步:建立三个part 分别为Top ,coh 和Bottom ,均为2D Planar ,Deformable ,Shell ,其具体尺寸如下(单位为国际单位kg-m-s-pa)TopCoh ,厚度为0.001Bottom第二步:建立两个材料属性,Steel 和Coh Steel Properties Value Elastic properties[Gpa]210Possion 0.3Coh PropertiesValueElastic properties[Gpa]Knn= 28,Kss= 14,Ktt=14Strength[Mpa]tn=75,ts=35,tt=35Fracture Energy250000第三步:截面属性定义第四步:Coh 单元方向定义,因为Coh 单元不同的方向具有不同的力学属性,所以要指定材料方向,进入Part 模块,如下图所示,指定单元堆叠方向为2方向第五步:分配截面属性给Top 、Bottom 和Coh 单元,在这一步中因为Top 和Bottom 各个方向的力学属性一样,不需要指定材料方向。
第六步:定义分析步参数如下所示,打开非线性,并将分析增量步设置为如下第七步:进入Assembly 模块,将上述三个部件生成部件实体,如下图所示,其中带孔的部位利用Partiton工具已经进行了自动分区第八步:创建两个Tie constraint :Top2coh 和Bottom2coh ,其中Coh 的表面为从表面,TOP 和Bottom 的主表面第九步:为了防止上下两个表明在挤压过程中出现穿透,创建上下两个表明的面面接触,如下图所示i n ga re go od fo rs o第十步:利用Coincident Point 约束将三个部件实体进行装配第十一步:网格划分,Top 和Bottom 单元类型为Plane Strain 单元,单元长度为1;Coh 为Cohesive 单元,方法为结构化网格,单元大小为0.5第十二步:编辑场输出变量,勾选STATUS 来观察coh 的失效第十三步:在Bottom 的底部施加边界条件,并在孔的四周施加向上的5个单位的位移,如下图所示第十四步:创建Job,提交分析,大功告成!。
abaqus中的cohesive element计算

在Abaqus中,Cohesive Element(粘聚单元)通常用于模拟材料界面的断裂行为。
这些单元特别适用于模拟复合材料层间断裂、焊接接头的断裂、粘合剂或涂层的失效等。
以下是在Abaqus中使用Cohesive Element进行计算的基本步骤:模型建立:首先,建立你的模型。
通常,你需要在界面区域插入一个额外的层来表示粘聚单元。
确保该层的厚度足够小,以便在模拟中不会显著影响整体结构的性能。
材料属性定义:为粘聚单元定义材料属性。
这通常包括断裂韧性、法向刚度、剪切刚度等。
你可能还需要定义损伤起始和损伤演化的准则,如最大应力、二次应力或能量准则。
单元类型选择:选择适当的粘聚单元类型。
Abaqus提供了多种适用于不同问题的粘聚单元,如COH2D4(二维四节点)、COH3D8(三维八节点)等。
网格划分:为模型划分网格,确保粘聚单元与相邻的实体单元正确相连。
边界条件和加载:应用适当的边界条件和加载。
这可能包括固定约束、位移、力或压力等。
分析设置:选择适当的分析类型,如静态分析、动态分析等。
设置分析步骤和输出要求。
运行分析:运行模拟。
Abaqus将使用你定义的粘聚单元属性和分析设置来计算模型的响应。
结果后处理:查看和分析模拟结果。
你可以查看应力、应变、损伤变量、断裂模式等。
使用Abaqus的可视化工具来更好地理解和解释结果。
迭代和优化:根据模拟结果调整粘聚单元的属性和分析设置。
重复上述步骤,直到得到满意的结果。
请注意,粘聚单元模拟的准确性高度依赖于你定义的粘聚行为、损伤准则和模型的其他参数。
因此,进行充分的验证和校准是非常重要的。
Cohesive经典讲解
复合材料模型建模与分析1.Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive 的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
ABAQUS中Cohesive单元建模方法

复合材料模型建模与分析1. Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive 的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
ABAQUS中Cohesive单元建模方法

复合材料模型建模与分析1、Cohesive单元建模方法1、1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生与扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive单元,用这种方法建立的cohesive单元与其她单元公用节点,并以此传递力与位移。
方法二、分别建立cohesive层与其她结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移与应力协调,如图1(b)所示。
(a)cohesive单元与其她单元公用节点(b)独立的网格通过“tie”绑定图1、建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但就是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1、2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种就是基于traction-separation描述;另一种就是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段与材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际就是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法就是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它瞧作被一个厚度隔开的两个面,这两个面分别与其她实体单元连接。
ABAQUS中Cohesive单元建模方法要点

复合材料模型建模与分析1. Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation 描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
Abaqus嵌入Cohesive单元插件POLARIS_INSERTCOHELEM使用说明书

POLARIS_INSERTCOHELEM使用说明书作者:星辰北极星目录POLARIS_INSERTCOHELEM使用说明书 (1)1 第一部分:星辰-北极星插件介绍:POLARIS_INSERTCOHELEM (2)1.1功能简介 (2)1.2插件的主要功能 (2)1.3插件使用方法: (2)1.3.1插件安装 (2)1.3.2插件界面 (3)1.3.3使用的常见问题 (4)1.4插件测试: (6)1.4.1测试模型:三维20*20*20立方体快 (6)1.4.2测试模型:二维100*100正方形 (6)1.5示例 (7)1.5.1球体全局嵌入有厚度Cohesive单元 (7)1.5.2纤维束嵌入有厚度Cohesive单元 (8)1.5.3混凝土细观骨料模型嵌入Cohesive单元 (8)1第一部分:星辰-北极星插件介绍:POLARIS_INSERTCOHELEM 1.1功能简介POLARIS-INSERTCOHELEM是星辰北极星团队开发的一款Abaqus插件,用于实体单元之间嵌入Cohesive单元功能,可实现复杂多裂缝的研究。
拓展软件原有功能,可实现全局、局部的零厚度或有厚度Coehsive单元的嵌入,可大大节约使用者的时间,提高工作效率。
1.2插件的主要功能1)支持二维(三角形、四边形单元)、三维(六面体、楔形体、四面体单元)实体单元之间嵌入Cohesive单元层;2)嵌入方式多样化,支持全局单元面、全局几何面、Set集合、手选几何面和手选单元面五种嵌入区域;3)支持零厚度和非零厚度Cohesive单元嵌入,(四面体单元除外);4)支持渗流和非渗流Cohesive单元嵌入,可实现复杂缝网压裂模拟。
1.3插件使用方法:1.3.1插件安装1、请解压插件包,生成一文件夹与本安装说明;2、打开我的电脑,并在文件路径处输入:%homepath%\abaqus_plugins3、将解压完成的文件夹放置到此路径下;4、重启Abaqus软件,在窗口的工具条中将新增工具条,点击图标即可激活插件。
abaquscohesive单元实例

abaquscohesive单元实例abaqus cohesive单元实例:建模和模拟断裂过程摘要:abaqus cohesive单元是一种用于模拟材料断裂和界面行为的元素类型。
本文将以一个具体的abaqus cohesive单元实例为例,介绍如何使用abaqus cohesive单元来建模和模拟断裂过程。
文章将逐步回答以下问题:什么是abaqus cohesive单元?如何定义材料参数和几何参数?如何生成和离散化几何模型?如何应用加载条件?如何进行模拟和分析结果?1. 引言断裂是材料结构力学中一个重要的问题,在工程实践中具有广泛的应用。
abaqus cohesive单元是一种用于模拟材料断裂行为的元素类型,适用于各种材料和应力条件。
abaqus cohesive单元模型能够准确地预测断裂面形状、力学性能和界面行为。
2. 定义材料参数和几何参数在开始模拟之前,我们需要定义材料参数和几何参数。
材料参数包括断裂准则、界面刚度和承载能力等。
几何参数包括断裂面的方向和位置等。
这些参数的选择取决于具体的应用需求和材料特性。
3. 生成和离散化几何模型使用abaqus软件生成几何模型,并对其进行离散化。
对于含有断裂接口的模型,我们需要定义和划分断裂面。
abaqus提供了丰富的工具和函数来操作几何模型,例如创建边界、划分网格等。
通过这些操作,可以生成符合实际需求的几何模型。
4. 应用加载条件加载条件是模拟中一个重要的因素。
我们需要定义在加载过程中施加在模型上的载荷和边界条件。
abaqus提供了丰富的加载条件类型,包括均布载荷、温度载荷、约束条件等。
根据应用需求选择合适的加载条件,并将其应用到模型中。
5. 模拟和分析结果模拟过程中,abaqus会自动计算每个离散化区域的力学响应和断裂行为。
根据所定义的材料参数和几何参数,abaqus会预测模型的断裂行为,并输出相应的力学曲线、断裂面形状等结果。
通过分析这些结果,我们可以评估模型的可靠性和性能。
(完整版)ABAQUS中Cohesive单元建模方法讲解
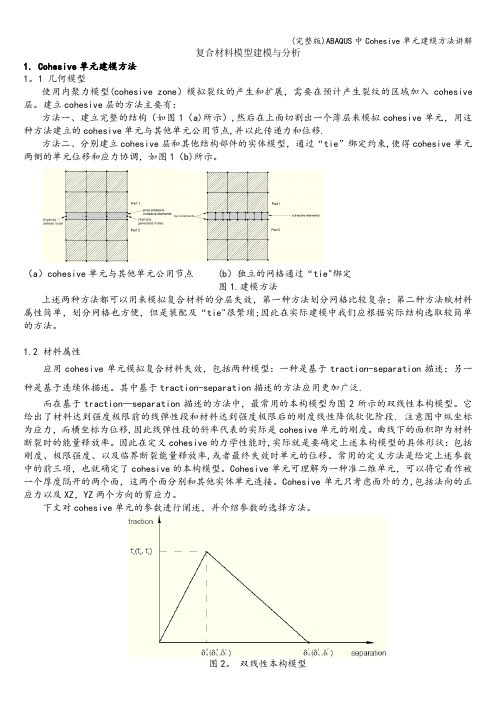
复合材料模型建模与分析1. Cohesive单元建模方法1。
1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive 层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移.方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点 (b)独立的网格通过“tie"绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie"很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛.而在基于traction—separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段. 注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复合材料模型建模与分析1. Cohesive单元建模方法几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation 描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
Cohesive单元只考虑面外的力,包括法向的正应力以及XZ,YZ两个方向的剪应力。
下文对cohesive单元的参数进行阐述,并介绍参数的选择方法。
图2. 双线性本构模型Cohesive 单元的刚度基于traction-separation 模型的界面单元的刚度可以通过一个简单杆的变形公式来理解PL AEδ= (1) 其中L 为杆长,E 为弹性刚度,A 为初始截面积,P 为载荷。
公式(1)又可以写成 S K δ=(2) 其中S P A =为名义应力,K E L =为材料的刚度。
为了更好的理解K ,我们把K E L =写成:1E E L E L K L L===' (3) 这里我们用L '来代替1,其中L 可以理解为建模厚度,即建模时cohesive interface 的几何厚度;L '为实际厚度,即cohesive interface 的真实厚度,这个厚度在cohesive section 中定义。
E L 可以理解为几何刚度,即模型中cohesive interface 所具有的刚度;E L L '为cohesive interface 的真实刚度。
当L '为1时,计算界面刚度就采用几何刚度E L ,当L '为时,计算时界面刚度变为1000E L 。
举个小例子,如果界面的实际厚度为,而在建模时就是按照这个厚度建立的,在定义material-section 时又specify 这层的厚度为,实际上就等于把界面刚度提高了2个数量级,模拟结果当然是不对的,这时定义section 时应采用默认厚度1。
ABAQUS 在cohesive 建模中使用了很“人性化”的设计,实际问题中界面可能很薄,有的只有0.001mm ,甚至更小。
有些问题cohesive 单元的interface 还可能是0厚度(比如crack 问题),而相对来说整体模型也许很大,如果不引入这两个厚度,我们就要在很大的模型中去创建这个很小的界面这是一个很麻烦的事情。
引入这两个厚度,在建模时我们就可以用有限的厚度来代替这个很小的界面厚度,只要在section 中定义这个L '就好了。
(注:以上大部分内容来自仿真论坛:再议cohesive 应用中对于一些参数的理解)一个解释“另外有个我的经验公式:大体上energy > *(damage initiation)^2/(stiffness)这个公式不难理解,就是锐角三角形的总面积大于一条侧边下的面积,将traction-separation law 画成图线你就一目了然了。
不过根据不同的法则,会稍微有些区别的。
”------以上的话引自dava 的个人空间,这里我想解释下这个不等式,有些新手可能一下还看不明白。
damage initiation为开始破坏时的应力,即三角形的高;stiffness 为刚度,也就是斜率,即tanq ;所以侧边三角形的底边为damage initiation/stiffness,*(damage initiation)^2/(stiffness)即为侧边下的三角形面积。
实际上能量还要大于这个侧边下三角形的面积很多,因为斜率一般都很大。
关于材料参数定义cohesive 的材料时,要填入材料的参数,这些材料参数是材料固有的特性,与几何没有关系,所以放心大胆的填入吧。
材料参数是由试验得到的,如果不能做实验(多数情况如此),就去查国际上相关的文献吧,数据甚至比你自己做试验都要详细,在填入数据时要注意单位的统一。
再说句,断裂能为单位面积上的能量,如你的单位选取N(力的单位)和M(长度单位),那么能量的单位为N/M。
下面举例来说明cohesive单元刚度的设置过程,以为例:进入property界面,点击Material→Creat,在弹出的Edit Material对话框中,可以编辑新创建的cohesive材料的名称,然后点击Mechanical→Elasticity→Elastic→Traction,在空格中输入相应的刚度。
图3. cohesive单元刚度的定义损伤准则初始损伤准则初始损伤对应于材料开始退化,当应力或应变满足于定义的初始临界损伤准则,则此时退化开始。
Abaqus的Damage for traction separation laws 中包括:Quade Damage、Maxe Damage、Quads Damage、Maxs Damage、Maxpe Damage、Maxps Damage六种初始损伤准则,其中前四种用于一般复合材料分层模拟,后两种主要是在扩展有限元法模拟不连续体(比如crack 问题)问题时使用。
使用图2所示的双线本构模型,其中:0n t 、0s t 及0t t 分别代表纯Ⅰ型、纯Ⅱ型或纯Ⅲ破坏的最大名义应力,0n ε、0s ε,0t ε代表相应的最大名义应变,当定义界面单元的初始厚度为1时,则名义应变等于与之相对应的相对位移n δ,s δ及t δ。
Quade Damage 为二次名义应变准则:当名义应变比的平方和等于1时,损伤开始。
2220001n s t n s t εεεεεε⎧⎫⎧⎫⎧⎫++=⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭ Maxe Damage 为最大名义应变准则:当任何一个名义应变的比值达到1时,损伤开始。
000max ,,1n s t ns t εεεεεε⎧⎫=⎨⎬⎭⎩ Quads Damage 为二次名义应力准则:当各个方向的名义应变比的平方和等于1时,损伤开始。
2220001n st n s t t t t t t t ⎧⎫⎧⎫⎧⎫++=⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭ Maxs Damage 为最大名义应力准则:当任何一个名义应力比值达到1时,损伤开始。
000max ,,1ns t n s t t t t t t t ⎧⎫=⎨⎬⎭⎩图4. 初始损伤准则定义Edit Material对话框中,点击Mechanical→Damage for Traction Separation Laws,然后根据自己的需要点击相应的损伤准则。
其中最常用是Quads Damage。
损伤演化规律选择了初始损伤准则之后,然后点击Suboptions→Damage Evolution,窗口如图5所示。
其中Type包括Displacement和Energy,Displacement为基于位移的损伤演化规律,而Energy 为基于能量的损伤演化规律。
Softening中包括Linear,Exponential及Tabular三种刚度退化方式……Damage Evolution中的所有的选项都是用来确定单元达到强度极限以后的刚度降阶方式。
一般常用:以能量来控制单元的退化,即Type→Energy;线性软化模型,即Softening→Linear,Degradation→Maximum;Mixed mode behavior→BK,Mode mix ratio→Energy,并选中Power。
图5.损伤演化规律定义1. 3 Cohesive单元界面属性还是在Property界面中,点击Section→Create,在弹出的Edit Section对话框中,选择Other→Cohesive。
图6. 定义材料的界面属性在Edit Section对话框中,在material的下拉菜单中选择刚才创建的cohesive材料,也可以点击右侧的create创建一组新的材料;Response选择traction separation。
Initial thickness为前文提到的L ,默认值为1,也可以在specify中指定一个特定的值。
将所创建的界面属性赋予几何实体点击Assign→Section,然后在视图中选中要赋的几何实体,点击左下角的Done,则弹出如下窗口,在窗口是Section中下拉选中所创建的Cohesive截面,点击OK,操作完成。
图7. 给实体赋截面属性Cohesive单元网格划分Cohesive单元网格的划分与其他单元基本一致,但是以下几点不同与其他单元,划分网格时应特别注意。
①网格密度,cohesive单元的网格尺寸不能太大,通常需要比较精细的网格,不然容易引起收敛性问题,甚至无法继续计算。
②必须使用sweep(扫掠)划分网格的方法,并且扫掠的方向垂直于cohesive面,即沿着cohesive单元的厚度方向。
③单元种类的选择图单元种类选择在单元库中选择cohesive,可以在Viscosity,specify中指定一粘性系数,来改善收敛性,但是粘性系数的设置不能太大,不然会影响计算结果,我们一般设置为;Element deletion:用于设置单元的删除情况,一般选yes,即当单元完全失效时被删除;max degradation:一般设置为1,即当SDEG=1时,认为单元失效。
