(完整版)勾股定理经典例题(教师版)
完整版勾股定理知识点及典型例题

(2)在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半。
(3 )在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角 等于30°。
5.勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3) 用于证明线段平方关系的问题。
(4) 利用勾股定理,作出长为j n 的线段6、2、勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法八下第18章《勾股定理》勾股定理知识点导航一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a 2+ b 2= C 2.即直角三角形两直角边的平方和等于斜边的平方勾:直角三角形较短的直角边 股:直角三角形较长的直角边 弦:斜边勾股定理的逆定理:如果三角形的三边长a ,b ,c 有下面关系:a 2+ b 2= c 2,那么这个三角形是直角三角形。
2.勾股数:满足 a 2+ b 2= C 2的三个正整数叫做勾股数(注意:若a ,b ,c 、为勾股数,那么 ka ,kb ,kc 同样也是勾股数组。
)* 附:常见勾股数:3,4,5 ; 6,8,10 ; 9,12,15 ; 5,12,13 如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为 C ); (2)若c 2= 3 +孑,则^ ABC 是以/ C 为直角的三角形;若a 2+ b 2< C 2,则此三角形为钝角三角形(其中若a 2+ b 2> C 2,则此三角形为锐角三角形(其中4. 注意:(1)直角三角形斜边上的中线等于斜边的一半a ,b ,斜边长为C ,那么3.判断直角三角形: 其他方法:(1) 有一个角为90°的三角形是直角三角形。
(完整版)勾股定理典型例题详解及练习(附答案)

典型例题知识点一、直接应用勾股定理或勾股定理逆定理例1:如图,在单位正方形组成的网格图中标有AB CD EF、GH四条线段, 其中能构成一个直角三角形三边的线段是()A.CD、EF、GHC. AB、CD GHB.AB、EF、GHD. AB、CD EF愿路分乐屮1)題意分析’本题考查幻股定理及勾股定理的逆定理.亠2)解題思器;可利用勾脸定理直接求出各边长,再试行判断•』解答过整屮在取DEAF中,Af=l, AE=2,根据勾股定理,得昇EF = Q抡於十£尸° = Q +F二艮同理HE = 2百* QH. = 1 CD = 2^5计算发现W十◎血尸=(鸥31即血+曲=GH2,根据勾股定理的逆宦理得到UAAE、EF\ GH为辺的三角形是直毎三角形.故选B. *縮題后KJ思专:*1.勾股定理只适用于直角三角形,而不适用于说角三角形和钝角三角形・因此」辭题时一宦妾认真分析题目所蛤■条件■,看是否可用勾股定理来解口*2.在运用勾股左理时,要正确分析题目所给的条件,不要习惯性地认为就是斜迫而“固执”地运用公式川二/十就其实,同样是S6"不一罡就等于餌,疋不一罡就昱斜辺,KABC不一定就是直角三祐3.直角三第形的判定条件与勾股定理是互逆的.区别在于勾股定理的运用是一个从卅形s—个三角形是直角三角形)到懺 y =沖十沪)的过程,而直角三角形的判定是一①从嗦(一个三角形的三辺满足X二护+酹的条件)到偲个三角形是直角三角形)的过程.a4•在应用勾股定理解题叭聲全面地琴虑间题.注意m题中存在的多种可能性,遊免漏辭.初例玉如圏,有一块直角三角形®椀屈U,两直角迫4CM5沁丸m・现将直角边AC沿直绘AD折蠡便它落在斜边AB上.且点C落到点E处, 则切等于(、*C/) "禎B. 3cm G-Icnin題童分析,本题着查勾股定理的应用刎:)解龜思路;車题若直接在△MQ中运用勾股定理是无法求得仞的长的,因为貝知遒一条边卫0的长,由题意可知,AACD和心迓门关于直线KQ对称.因而^ACD^hAED ・进一歩则有应RUm CZAED ED 丄AB,设UD=E2>黄泱,则在Rt A ABO中,由勾股定理可得^=^(^+^=^83=100,得AB=10cm,在松迟DE 中,W ClO-fl)2= d驚解得尸九4解龜后的思琴尸勾股定理说到底是一个等式,而含有未知数的等式就是方程。
完整版勾股定理典型例题详解及练习附答案

典型例题知识点一、直接应用勾股定理或勾股定理逆定理例1:如图,在单位正方形组成的网格图中标有 AB CD EF GH 四条线段, 其中能构成一个直角三角形三边的线段是( B. AB 、EF 、 D. AB 、G1) sa 倾 2) 解題患跖 解答过程=屮在gJ^EAF 中.Arm, AE=3,根据勾股定理,得EF = Q 苗十上尸'* =品+F =同理 AE = 2忑、CrjV= ^/13| ID = 2爲©计算发现(心r (2罷¥ =(届厂即血U E 严=閒士,根据 勾股定理的逆左理得到l^ADs ET, GH 为辺的三角形是直®三垢形•故选 B.屮解題后ffi 思专.*L 勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角形°因此5解题时一定更认真分析题目所给条皆,看是否可用匈股定理来解口 : 2. 在运用勾股定理时,要正确分析题目所给的条件,不要习惯性地认为 “匚"就是斜迫而“固执”地运用公式二/十迁 其冥,同样是厶, 丄C 不—定就等于g (K 疋不一定就是斜过,AA3C 不一定就是直®三® 孰*)GHCD EFA. CD 、EF 、GH C. AB 、CD GH +J本题考查幻股定理及勾股宦理的逆定理.4 可利用勾般定理直接求出各边长,再e 行判斷.43. 直角三角形的判定条件与勾股定理是S 逆的・区别在于勾股定理的运 用是一个从'「形''(一个三角形是直角三角形)到 嘟(十沪) 的过程,而直甬三«形的利定是一个从 懺段【一个三角影的三辺S 足 匚2 =亍+色询条件)到“形-1这个三甬形是直角三角形)的过程.44. 在应用勾股定理解题时,聲全®地琴虑间题.注意间题中存在的多种 可能性,避免漏辭.“W 1;如图,有一块直角三甬形紙椅屈C,两貢角迫月^孔皿3*沁. 现将直角边AC 沿直绘AD 折盞 便它落在斜边上.且点C 落到点E 处, fflCT 等于()4扎2 cm 1) SA 倾 本题着查勾股定理的应用仪:)龜思路,車题若直接在中运用勾股定理是无法求得仞a 匕的,因为貝知道一条边卫U 的长,由题意可知,△月CT 和△/£刀关于直 线KQ 对称,因而ZvlCD 竺△血Q ・进一歩则有 血TCMmh CL=ED, ED 丄AS,设则在Rt A ASC*中,由勾股定理可得TV A?月筋贋=1 皿,Aa=iacm,在 皿刃述中,Cio-fi ) 2= C S —X )$0 解得 益 4B.-IB 龜后的思肴:茫勾股定理说到底是一个等式,而含有未知数的等式就是方程。
勾股定理题型(很全面)

典型例题:一、利用勾股定理解决实际问题例题:水中芦苇梯子滑动1、有一个传感器控制的灯,安装在门上方,离地高4.5米的墙上,任何东西只要移至5米以内,灯就自动打开,一个身高1.5米的学生,要走到离门多远的地方灯刚好打开?2、如图,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=160米,点A 到公路MN 的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?3、如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我反走私A艇发现正东方向有一走私艇C以每小时6.4海里的速度偷偷向我领海开来,便立即通知正在MN在线巡逻的我国反走私艇B密切注意,反走私A艇通知反走私艇B时,A和C两艇的距离是20海里,A、B两艇的距离是12海里,反走私艇B测得距离C是16海里,若走私艇C的速度不变,最早会在什么时间进入我国领海?二、与勾股定理有关的图形问题1.已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是.2.如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是____ _____.3.在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4=______ ___.4.如图,△ABC中,∠C=90°,(1)以直角三角形的三边为边向形外作等边三角形(如图①),探究S1+S2与S3的关系;(2)以直角三角形的三边为斜边向形外作等腰直角三角形(如图②),探究S1+S2与S3的关系;(3)以直角三角形的三边为直径向形外作半圆(如图③),探究S1+S2与S3的关系.图①图②图③5.如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an=___ _____记正方形AB-CD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,……,S n(n为正整数),那么S n=____ ____.6、如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为.ABCDEFG1FE DAB CA B C D EG F F 三、关于翻折问题1、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠,使AD 落在对角线BD 上,得折痕DG ,若AB = 2,BC = 1,求AG.2、如图,把矩形纸片ABCD 沿对角线AC 折叠,点B 落在点E 处,EC 与AD 相交于点F. (1)求证:△FAC 是等腰三角形;(2)若AB=4,BC=6,求△FAC 的周长和面积.3、如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知cm CE 6=,cm AB 16=,求BF 的长.4、如图,一张矩形纸片ABCD 的长AD=9㎝,宽AB=3㎝。
勾股定理典型例题详解及练习(附答案)

典型例题知识点一、直接应用勾股定理或勾股定理逆定理例1:如图,在单位正方形组成的网格图中标有 AB CD EF 、GH 四条线段,其中能构成一个直角三角形三边的线段是()丄)題宜分斬’本题考查勾股定理及勾股定理的逆定理.心2)解題思路:可利用勾股定理直接求出各边快,再进行判斷."在段AEAF 中,AF=1, AE-2,根据勾股走理,得』EF = J 血 + 血==75P同理AR 二2晶GH 二届CD = 24计算发现(昉尸+(戈旋尸=(晅-即卫新+超戸=G0 ,根据 勾股定理的逆定理得到以AB 、EF. GH 为边的三角形是直角三角形.故选解题后的慝考’心1.勾股定理只适用于直甫三角形,而不适用于锐角三角形和純角三珀形.因此,解题时一定裝认真分析题目所给条件*看是否可用勾股定理来解-■2在运用勾股定理时,要正确分析题目所给的条件,不要习惯性地认海 化”就是斜边而“固执般地运用公式X 二’ +* 其实,同样是△朋0\ 三。
不一定就等于9叭亡不一定就是斜边,A ABC 不一定就是直角三甫 形.aA.CD C.AB CD EF 、GHGH B.AB 、EF 、GHD.AB CD EF3.直第三角形的判定条件2勾般定理是互逆的,区别在于勾股定理的运用是一个从水形"(一个三甫形是直甫三甫形)至I)噱(川=/ +护)的过程,而直第三角形的判定是一个从“数(一个三角形的三边満足八二卅+酹的条件)到“形”(这个三角形是直角三角形)的过程.松4.在应用勾股定理解题时,裝全面地若虑间题,注意问题中存在的多种可能性,瞳免漏解.初+>例2:如图,有一块直角三角形纸板肋C,两直角辺AC-6cm t BC=8cm, 现将直角边AC沿直竝AD折養,使它落在斜边虫迟上,且点<7落到点遐处, 则仞等于()祕A. 2cmB. 3cmC. 4cmD. Scm+J1)題意分析:本题肴查勾股走理的应用叙2)解題思路’本题若直接在△力仞中运用勾股定理是无法求得CD的长的,因为只知道一条边,卫<7册扶,由题意可知,△上仞和心劝关于直线对称,因而AACD^^AED.进一歩则W AE=AC=6cm> CD=ED, ED 丄AB.设dgg 则在Rt A-4BC中.由勾股定理可得J4^=40^8(^=^8^100,得AB=10cm,在取△乃DE 中,有应+ (1Q-6)》=(8—x)%解得—3.心解答逸BP解题諭朋= _____________________________________________________勾股定理说到底是一个等式,而含有未知数的等式就是方程。
勾股定理经典例题(全解版)

11类型一:勾股定理的直接用法1、在Rt △ABC 中,∠C=90°(1)已知a=6, c=10,求b , (2)已知a=40,b=9,求c ; (3)已知c=25,b=15,求a.思路点拨: 写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
解析:(1) 在△ABC 中,∠C=90°,a=6,c=10,b=(2) 在△ABC 中,∠C=90°,a=40,b=9,c=(3) 在△ABC 中,∠C=90°,c=25,b=15,a=举一反三【变式】:如图∠B =∠ACD =90°, AD =13,CD =12, BC =3,则AB 的长是多少? 【答案】∵∠ACD =90° AD =13, CD=12 ∴AC 2 =AD 2-CD 2 =132-122 =25 ∴AC =5又∵∠ABC=90°且BC =3 ∴由勾股定理可得 AB 2=AC 2-BC 2 =52-32 =16 ∴AB = 4∴AB 的长是4.类型二:勾股定理的构造应用 2、如图,已知:在中,,,. 求:BC 的长.思路点拨:由条件,想到构造含角的直角三角形,为此作于D ,则有,,再由勾股定理计算出AD 、DC 的长,进而求出BC 的长. 解析:作于D ,则因,∴(的两个锐角互余)∴(在中,如果一个锐角等于,那么它所对的直角边等于斜边的一半). 根据勾股定理,在中,.根据勾股定理,在中,22.∴ .举一反三【变式1】如图,已知:,,于P . 求证:.解析:连结BM ,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又∵ (已知),∴.在中,根据勾股定理有, ∴.【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD 的面积。
分析:如何构造直角三角形是解本题的关键,可以连结AC ,或延长AB 、DC 交于F ,或延长AD 、BC 交于点E ,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。
勾股定理典型例题【含答案】

勾股定理温习一、知识要点:一、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也确实是说:若是直角三角形的两直角边为a、b,斜边为c ,那么a2 + b2= c2。
公式的变形:a2 = c2- b2,b2= c2-a2 。
勾股定理在西方叫毕达哥拉斯定理,也叫百牛定理。
它是直角三角形的一条重要性质,揭露的是三边之间的数量关系。
它的要紧作用是已知直角三角形的两边求第三边。
勾股定理是一个大体的几何定理,它是用代数思想解决几何问题的最重要的工具之一,是数形结合的纽带之一。
二、勾股定理的逆定理若是三角形ABC的三边长别离是a,b,c,且知足a2 + b2= c2,那么三角形ABC 是直角三角形。
那个定理叫做勾股定理的逆定理.该定理在应历时,同窗们要注意处置好如下几个要点:①已知的条件:某三角形的三条边的长度.②知足的条件:最大边的平方=最小边的平方+中间边的平方.③取得的结论:那个三角形是直角三角形,而且最大边的对角是直角.④若是不知足条件,就说明那个三角形不是直角三角形。
3、勾股数知足a2 + b2= c2的三个正整数,称为勾股数。
注意:①勾股数必需是正整数,不能是分数或小数。
②一组勾股数扩大相同的正整数倍后,仍是勾股数。
4、最短距离问题:要紧运用的依据是两点之间线段最短。
二、知识结构:三、考点剖析考点一:利用勾股定理求面积求:(1) 阴影部份是正方形; (2) 阴影部份是长方形; (3) 阴影部份是半圆.2. 如图,以Rt △ABC 的三边为直径别离向外作三个半圆,试探讨三个半圆的面积之间的关系.考点二:在直角三角形中,已知两边求第三边例如图2,已知△ABC 中,AB =17,AC =10,BC 边上的高,AD =8,则边BC 的长为( )A .21B .15C .6D .以上答案都不对【强化训练】:1.在直角三角形中,若两直角边的长别离为1cm ,2cm ,则斜边长为.2.(易错题、注意分类的思想)已知直角三角形的两边长为3、2,则另一条边长的平方是3、已知直角三角形两直角边长别离为5和12, 求斜边上的高.(结论:直角三角形的两条直角边直角三角形 勾股定理应用判定直角三角形的一种方法的积等于斜边与其高的积,ab=ch)考点三:应用勾股定理在等腰三角形中求底边上的高例、如图1所示,等腰中,,是底边上的高,若,求①AD的长;②ΔABC的面积.考点四:应用勾股定明白得决楼梯上铺地毯问题例、某楼梯的侧面视图如图3所示,其中米,,,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为.分析:如何利用所学知识,把折线问题转化成直线问题,是问题解决的关键。
(完整版)勾股定理专题(附答案,全面、精选)

(6) 如图(1),图中的数字代表正方形的面积,则正方形A 的面积为。
3、运用勾股定理进行计算(重难点)(12)如图,一根旗杆在离地面9米处折断倒下,旗杆顶勾股定理一、探索勾股定理【知识点1】勾股定理定理内容:在RT△中,__________________________ 勾股定理的应用:在RT△中,知两边求第三边,关键在于确定斜边或直角典型题型(7)如图(2),三角形中未知边x与y的长度分别是x= ,y= 。
(8)在RtAABC 中,/ C= 90°,若AC= 6, BO 8,则AB的长为( )A、6B、8C、10(9)在直线l上依次摆放着七个正方形已知斜放置的三个正方形的面积分别是D、12(如图4所示)。
1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S I S2 S3 S4= ------------------------ 。
1、对勾股定理的理解(1)已知直角三角形的两条直角边长分别为a, b,斜边长c,则下列关于a,b,c的关系不成立的是( )A、c2- a2=b2C、a2- c2=b2(2) 在直角三角形中,/ 立的是( )A、BC2- AB2=AC2C、AB2+AC2= BC22、应用勾股定理求边长(3) 已知在直角三角形求AC的长.B、c2- b2=a2D、a2+b2= c2A=90°,则下列各式中不成B、BC2- AC2=AB2D、AC2+BC2= AB2AB=10 cm, BC=8 cm ABC中,(4)在直角△中,若两直角边长为a、b,且满足Va- 6a +9 + |b- 4| = 0,则该直角三角形的斜边长为__________3、利用勾股定理求面积(5)已知以直角△的三边为直径作半圆,其中两个半圆的面积为25兀,16兀,求另一个半圆的面积。
【知识点2】勾股定理的验证推导勾股定理的关键在于找面积相等,由面积之间的等量关系并结合图形利用代数式恒等变形进行推导。
(完整版)勾股定理典型例题详解及练习(附答案)

典型例题知识点一、直接应用勾股定理或勾股定理逆定理例1:如图,在单位正方形组成的网格图中标有 AB CD EF 、GH 四条线段, 其中能构成一个直角三角形三边的线段是( )1) 题意分析:本题考查勾照定理及勾股定理的逆定理./2) 解题思踏;可利用勾照定理直接求出各也长,再进行判断.卜 解答过程:#ai^AEAF 中,AF=h AE=2,根据勾股定理,得。
跻=J 招己'十』十F = 姊同理 = 2思* QH. = 1 CD = 2^5计算发现(右尸十0招”=(雁沪t 即/费+寥=奇,根据 勾股定理的迎定理得到以AE 、EF 、GH 为也的三角形是直角三角形.故选 B. *解题后B0思考、1.勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角形. 因此,解跑时一定要认真分析题目所蛤条件,看是否可用勾股定理来解n ,L 在运用勾股定理时,要正确分析题目所给的条件,不要习惯性地认为 七”就是斜诳而.固执"地运用公式"二/十舛 其实,同样是四"6 NC 不一定就等于叩幻I 不一定就是斜遮,A ABC 不一定就是直角三痢 形.卜A. CD 、EF 、GH C. AB 、CD GHB. AB 、EF 、GHD. AB 、CD EF3.直角三角形的判定条件与勾股定理是互逆的.区别在于勾股定理的运用是一个从"形胡(一个三角形是直角三角形)到板'3’ =疽十瑟)的辿程,而直角三角形的判定是一个从W〔一个三角形的三满是L = ^+广的条件)到胃形'这个三弟形是直急三甬形)的过程.甘1在应用勾股定理解题时,要全面地毒虑问题.注意m题中存在的多种可能性,避免漏解。
/例2-如图'有一块直角三角形舐板幽G两直角边ACMkm, BWg 现博直甬边AC沿直线AD折叠,庾它落在斜辿AB上,且点C落到点E处, 则CD等于(EC 。
A. 2cmB. 3cm C 4an D 5cm*" iiEMraZJ VI :『n暴意分析,本题考查勾股定理的应用,:)解题思路;本题若直接在△XOQ中运用勾股定理是无法求得® ffi 长的,因为只知道一条迫应。
(完整版)勾股定理经典题目及答案

勾股定理1.勾股定理是把形的特征(三角形中有一个角是直角),转化为数量关系(a 2+b 2=c 2),不仅可以解决一些计算问题,而且通过数的计算或式的变形来证明一些几何问题,特别是证明线段间的一些复杂的等量关系. 在几何问题中为了使用勾股定理,常作高(或垂线段)等辅助线构造直角三角形.2.勾股定理的逆定理是把数的特征(a 2+b 2=c 2)转化为形的特征(三角形中的一个角是直角),可以有机地与式的恒等变形,求图形的面积,图形的旋转等知识结合起来,构成综合题,关键是挖掘“直角”这个隐含条件.△ABC 中 ∠C =Rt ∠a 2+b 2=c 2⇔3.为了计算方便,要熟记几组勾股数:①3、4、5; ②6、8、10; ③5、12、13; ④8、15、17;⑤9、40、41.4.勾股定理的逆定理是直角三角形的判定方法之一.一般地说,在平面几何中,经常利用直线间的位置关系,角的相互关系而判定直角,从而判定直角三角形,而勾股定理则是通过边的计算的判定直角三角形和判定直角的. 利用它可以判定一个三角形是否是直角三角形,一般步骤是:(1)确定最大边;(2)算出最大边的平方,另外两边的平方和;(3)比较最大边的平方与另外两边的平方和是否相等,若相等,则说明是直角三角形; 5.勾股数的推算公式①罗士琳法则(罗士琳是我国清代的数学家1789――1853)任取两个正整数m 和n(m>n),那么m 2-n 2,2mn, m 2+n 2是一组勾股数。
②如果k 是大于1的奇数,那么k, ,是一组勾股数。
212-k 212+k ③如果k 是大于2的偶数,那么k, ,是一组勾股数。
122-⎪⎭⎫ ⎝⎛K 122+⎪⎭⎫⎝⎛K ④如果a,b,c 是勾股数,那么na, nb, nc (n 是正整数)也是勾股数。
典型例题分析例1 在直线l 上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4=____ 依据这个图形的基本结构,可设S 1、S 2、S 3、S 4的边长为a 、b 、c 、d 则有a 2+b 2=1,c 2+d 2=3,S 1=b 2,S 2=a 2,S 3=c 2,S 4=d 2 S 1+S 2+S 3+S 4=b 2+a 2+c 2+d 2=1+3=4例2 已知线段a ,求作线段 a5分析一:a ==525a 224a a +∴a 是以2a 和a 为两条直角边的直角三角形的斜边。
勾股定理经典例题(附答案)
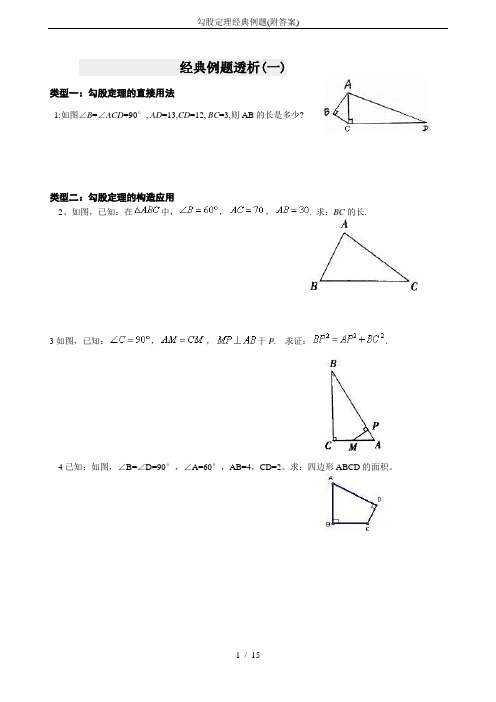
经典例题透析(一)类型一:勾股定理的直接用法1:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型二:勾股定理的构造应用2、如图,已知:在中,,,. 求:BC的长.3如图,已知:,,于P. 求证:.4已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
类型三:勾股定理的实际应用(一)用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
(二)用勾股定理求最短问题如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.利用勾股定理作长为的线段5、作长为、、的线段。
举一反三【变式】在数轴上表示的点。
经典例题透析(二)类型一:勾股定理及其逆定理的基本用法1、若直角三角形两直角边的比是3:4,斜边长是20,求此直角三角形的面积。
【变式2】直角三角形周长为12cm,斜边长为5cm,求直角三角形的面积。
【变式3】若直角三角形的三边长分别是n+1,n+2,n+3,求n。
【变式4】以下列各组数为边长,能组成直角三角形的是()A、8,15,17B、4,5,6C、5,8,10D、8,39,40类型二:勾股定理的应用2、如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m。
假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?如图学校有一块长方形花园,有极少数人为了避开拐角而走“捷径”,在花园内走出了一条“路”。
勾股定理经典例题(含答案)
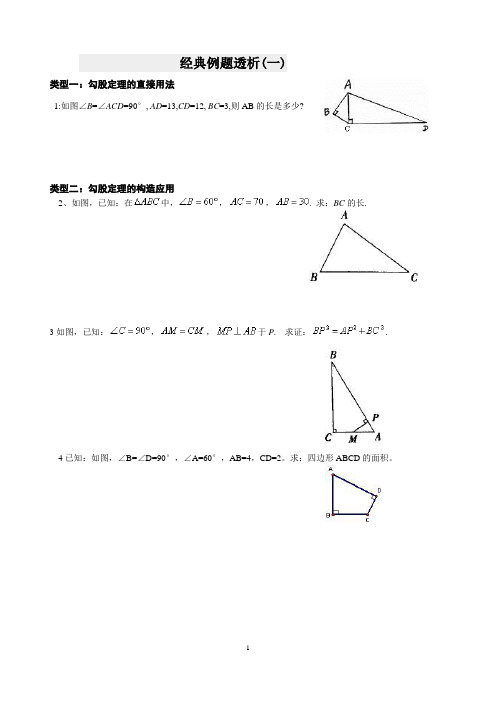
经典例题透析(一)类型一:勾股定理的直接用法1:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型二:勾股定理的构造应用2、如图,已知:在中,,,. 求:BC的长.3如图,已知:,,于P. 求证:.4已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
类型三:勾股定理的实际应用(一)用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
(二)用勾股定理求最短问题如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.利用勾股定理作长为的线段5、作长为、、的线段。
举一反三【变式】在数轴上表示的点。
经典例题透析(二)类型一:勾股定理及其逆定理的基本用法1、若直角三角形两直角边的比是3:4,斜边长是20,求此直角三角形的面积。
【变式2】直角三角形周长为12cm,斜边长为5cm,求直角三角形的面积。
【变式3】若直角三角形的三边长分别是n+1,n+2,n+3,求n。
【变式4】以下列各组数为边长,能组成直角三角形的是()A、8,15,17B、4,5,6C、5,8,10D、8,39,40类型二:勾股定理的应用2、如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m。
假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?如图学校有一块长方形花园,有极少数人为了避开拐角而走“捷径”,在花园内走出了一条“路”。
勾股定理经典例题(含答案)

勾股定理经典例题(含答案)勾股定理经典例题类型⼀:勾股定理的直接⽤法1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨: 写解的过程中,⼀定要先写上在哪个直⾓三⾓形中,注意勾股定理的变形使⽤。
举⼀反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型⼆:勾股定理的构造应⽤2、如图,已知:在中,,,. 求:BC的长.1、某市在旧城改造中,计划在市内⼀块如图所⽰的三⾓形空地上种植草⽪以美化环境,已知这种草⽪每平⽅⽶售价a元,则购买这种草⽪⾄少需要()A、450a元B、225a 元C、150a元D、300a元举⼀反三【变式1】如图,已知:,,于P. 求证:.150°20m 30m【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的⾯积。
类型三:勾股定理的实际应⽤(⼀)⽤勾股定理求两点之间的距离问题3、如图所⽰,在⼀次夏令营活动中,⼩明从营地A点出发,沿北偏东60°⽅向⾛了到达B 点,然后再沿北偏西30°⽅向⾛了500m到达⽬的地C点。
(1)求A、C两点之间的距离。
(2)确定⽬的地C在营地A的什么⽅向。
举⼀反三【变式】⼀辆装满货物的卡车,其外形⾼2.5⽶,宽1.6⽶,要开进⼚门形状如图的某⼯⼚,问这辆卡车能否通过该⼯⼚的⼚门?(⼆)⽤勾股定理求最短问题4、如图,⼀圆柱体的底⾯周长为20cm,⾼AB为4cm,BC是上底⾯的直径.⼀只蚂蚁从点A出发,沿着圆柱的侧⾯爬⾏到点C,试求出爬⾏的最短路程.类型四:利⽤勾股定理作长为的线段5、作长为、、的线段。
作法:如图所⽰举⼀反三【变式】在数轴上表⽰的点。
解析:可以把看作是直⾓三⾓形的斜边,,为了有利于画图让其他两边的长为整数,⽽10⼜是9和1这两个完全平⽅数的和,得另外两边分别是3和1。
完整版勾股定理习题含解析

勾股定理习题1. 赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的 赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一 个大正方形,设直角三角形较长直角边长为 a ,较短直角边长为b ,若(a+b ) 2=21,大正方形的面积为13,则小正方形的面积为(【解答】解:如图所示:•••( a+b ) 2=21, ••• a 2+2ab+b 2=21,•••大正方形的面积为13,2ab=21 - 13=8,•••小正方形的面积为13-8=5.2.直角三角形有一条直角边为6,另两条边长是连续偶数,则该三角形周长为A . 20B . 22C . 24D . 26【解答】解:•••两条边长是连续偶数,可设另一直角边为 X ,则斜边为(x+2),根据勾股定理得:(X+2) 2 - x 2=62,解得 x=8,.・. x+2=10,•••周长为:6+8+10=24.故选C5 D . 63. 在下列四组数中,不是勾股数的一组数是(A .a=15, b=8, c=17B .a=9, b=12, c=15C .a=7, b=24, c=25D .a=3, b=5, c=7【解答】解:由题意可知,在A 组中,152+82=172=289,在 B 组中,92+122=152=225,在 C 组中,72+242=252=625,而在 D 组中,32+52工72,6, 8, 10 ② 13, 5, 12 ③ 1, 2,3④9, 40, 41⑤3, 4, 5•其中能构成直角三角形的有()组. A .2B .3C . 4D .5 【解答】解:因为①62+82=102,②132=52+122,④92+402=412,符合勾股定理的7. △ ABC 的三边长分别为a, b, C ,下列条件:/ C=3: 4: 5:③a 2= ( b+c ) (b - c );④a :逆定理,所以能构成直角三角形的有三组.故选B .故选 D .4. 下列各组数,可以作为直角三角形的三边长的是(2, 3, 4 B .7, 24, 25C .8, 12, 20D .5, 13, 15 【解答】解:A 、T 22+32工42,二不能构成直角三角形;••• 72+242=252,二能构成直角三角形;A .B 、C 、 ••• 82+122工202,A 不能构成直角三角形;D 、 ••• 52+132工152,A 不能构成直角三角形.故选 B .5. 下列各组数中,能构成直角三角形的是(4, 5, 6 B .1, 1, 2C .6, 8, 11 【解答】解:A 、T 42+52工62,A 不能构成直角三角形,故 A 错误;B 、T 12+12=,二能构成直角三角形,故 B 正确;••• 62+82工112,A 不能构成直角三角形,故 ••• 52+122工232,A 不能构成直角三角形,故 A . C 、 D 、 D .5, 12, 23 C 错误;D 错误.故选: B .分别以下列五组数为一个三角形的边长:① 6. ①/ A=/ B-/ C ;②/A : / B : b : c=5: 12: 13,其中能判断△ABC 是直角三角形的个数有()A . 1 个B . 2 个C . 3 个D .4 个 【解答】解;①/ A=/ B-/ C,/ A+/ B+/ C=180,解得/ B=90°,故①是直角 三角形; ②/ A : / B : / C=3:4:5, / A+/ B+/ C=180,解得/ A=45 , / B=6ff , / C=75, 故②不是直角三角形;③ ••• a 2= (b+c ) (b - c), ••• a 2+c 2=b 2,符合勾股定理的逆定理,故③是直角三角形;④ ••• a : b : c=5: 12: 13,Aa 2+b 2=c 2,符合勾股定理的逆定理,故④是直角三角 形.能判断△ ABC 是直角三角形的个数有3个;故选:C .8. 下列三角形中,是直角三角形的是(A .三角形的三边满足关系 a+b=c B.三角形的三边比为1: 2: 3 C •三角形的一边等于另一边的一半 D .三角形的三边为9, 40, 41 【解答】解:A 、不能判定是直角三角形,此选项错误;B 、 由于12+22工32,所以不是直角三角形,此选项错误;C 、D 、不能判定是直角三角形,此选项错误; 由于 92+402=412,是直角三角形,此选项正确.故选 D . 9. 一个木工师傅测量了一个等腰三角形木板的腰、底边和高的长,但他把这三 个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.13,12,12B . 12,12,8 C . 13,10,12D . 5,8,4 【解答】解:A 、132工122+62,错误;B 、122工82+62,错误;C 、 确; A . 132=122+52,正D . 82工52+22,错误.故选C.10.下列说法正确的有()①如果/ A+/B=/ C,那么△ ABC是直角三角形;②如果/ A:/ B:/ C=1: 2:3,则三角形是直角三角形;③如果三角形的三边长分别为4、4、6,那么这个三角形不是直角三角形;④有一个角是直角的三角形是直角三角形.A. 1个B. 2个C. 3个D. 4个【解答】解:①•••/ A+/ B=/ C,且/ A+/B+/C=180,得/ C=90,:.△ ABC是直角三角形,故①正确;②设/ A=x,/ B=2x,/ C=3x,则/ A+/ B=/ C,由①知,该三角形是直角三角形,故②正确;③42=16, 62=36,显然42+42工62,不符合勾股定理的逆定理,该三角形不是直角三角形,故③正确;④符合直角三角形的判定方法,故④正确;所以4个结论都正确,故选D.11.若等边△ ABC的边长为A. 1cm2B. 2cm2C. 2cm,那么△ ABC的面积为( 3cm2D. 4cm2【解答】故选A.12.如图,四边形ABCD中,AD// BC, / ABO/DCB=90, 且BC=2AD 以ABBC DC为边向外作正方形,其面积分别为Si、S2、S3, 若S=3, 9=9,则9D. 48【解答】V S=3 , 3=9 , A AB=CD=3,过A作AE// CD交BC于E,则/ AEB=/DCB V AD // BC, A四边形AECD是平行四边形,A CE=AD AE=CD=3V/ ABC+Z DCB=90,.・./ AEB F/ABC=9O,•••/ BAE=9O,•••BE==2 V BC=2AD二BC=2BE=4 A◎二(4) 2=48,故选D.13. 一个三角形的三边的长分别是 3 , 4 , 5 ,则这个三角形最长边上的高是14.已知直角三角形两边的长为3和4 ,则此三角形的周长为【解答】解:设RtAABC的第三边长为x, ①当4为直角三角形的直角边时,x为斜边,由勾股定理得,x=5,此时这个三角形的周长=3+4+5=12;②当4为直角三角形的斜边时,x为直角边,由勾股定理得,x=,此时这个三角形的周长=3+4+77 ,15.女口图所示,AB=BC=CD=DE=1AB丄BC, AC丄CD, AD丄DE,贝U AE=16.如图,在四边形 ABCD 中,AB=1, BC=1, CD=2, DA=且/ ABC=90,则四边形ABCD 的面积是17. 已知一个Rt △的两边长分别为3和4,则第三边长的平方是18. 等腰三角形的腰长为10,底长为12,则其底边上的高为19. 如图字母B 所代表的正方形的面积是【解答】解:由题可知,在直角三角形中,斜边的平方=169, —直角边的平方=25, 根据勾股定理知,另一直角边平方=169-25=144,即字母B 所代表的正方形的面 积是144.21. 一直角三角形的三边分别为 2、3、X ,那么以x 【解答】解:当2和3都是直角边时,则X 2=4+9=13; 4=5.故选C.20.直角三角形的两条直角边的长分别为5, 12, 则斜边上的高线的长为 为边长的正方形的面积为当3是斜边时,则X 2=9-22.如图,在△ ABC 中,AD 丄BC 于 D,AB=17,BD=15,DC=6,J 则 AC 的长为 D . 8 【解答】解:女口图,V AD 丄BC, •••/ ADB=/ ADC=90. 又 v AB=17, BD=15,DC=6 •••在直角△ ABD 中,由勾股定理得到:AD 2=AB^ - BD 2=64.在直角△ ACD 中,由勾股定理得到:AC===10即AC=1Q 故选:B.23.如图,校园内有两棵树,相距 8米,一棵树树高13米,另一棵树高7米, 一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 __________ 。
勾股定理10题

勾股定理10题
以下是10道关于勾股定理的题目:
1.已知直角三角形的两条直角边分别为3和4,求斜边的长度。
2.在一个直角三角形中,斜边长为5,一条直角边长为3,求另一条直角边的长度。
3.一个直角三角形的斜边长为13,其中一条直角边长为5,求另一条直角边的长度。
4.一个直角三角形的两条直角边分别为6和8,求斜边上的高。
5.已知直角三角形的斜边长为10,一条直角边与斜边的夹角为30°,求另一条直角边
的长度。
6.一个直角三角形的斜边长为17,其中一条直角边长为8,求这个直角三角形的面
积。
7.一个直角三角形的两条直角边分别为a和b,斜边长为c,且a ️c = 3:4:5,求这个
直角三角形的面积。
8.已知直角三角形的斜边长为13,且两条直角边的比为3:4,求这个直角三角形的面
积。
9.一个直角三角形的斜边长为25,其中一条直角边长为15,求这个直角三角形的一
个锐角的正切值。
10.一个直角三角形的两条直角边分别为6和8,求这个直角三角形的外接圆半径。
这些题目涵盖了勾股定理的基本应用,包括求斜边长度、求直角边长度、求高、求面积、求角度正切值以及求外接圆半径等。
通过练习这些题目,可以加深对勾股定理的理解和掌握。
(完整版)勾股定理经典例题(教师版)

勾股定理全章知识点和典型例习题一、基础知识点: 1.勾股定理内容:表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下:3.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则 ②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题 4.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边 ①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若 ,时,以a ,b ,c 为三边的三角形是钝角三角形;若 ,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形 5.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用c b a H G F EDC B Ab ac b a ccab c a b a bc c b aE D C B A勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.6、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理全章知识点和典型例习题一、基础知识点:1•勾股定理内容:____________________________________________________________表示方法:如果直角三角形的两直角边分别为 a , b,斜边为c,那么__________________2 •勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:3 •勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC中,C 90 ,则 __________________________________________ ②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题4. 勾股定理的逆定理如果三角形三边长a , b , c满足a2 b2c,那么这个三角形是直角三角形,其中c为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和a2 b2与较长边的平方c2作比较,若它们相等时,以 a , b , c为三边的三角形是直角三角形;若 _________ ,时,以a , b , c为三边的三角形是钝角三角形;若__________________ ,时,以a ,b , c为三边的三角形是锐角三角形;②定理中a , b , c及a2 b2 c2只是一种表现形式,不可认为是唯一的,如若三角形三边长 a , b , c满足a2 c2 b2,那么以a , b , c为三边的三角形是直角三角形,但是b为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形5. 勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即a2 b2 c2中,a , b , c为正整数时,称a , b , c为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5 ; 6,8,10 ; 5,12,13; 7,24,25等③用含字母的代数式表示n组勾股数:2 2n 1,2n,n 1 (n 2, n 为正整数);2n 1,2n2 2n,2n2 2n 1 (n为正整数)m2 n2,2mn,m2 n2(m n, m , n为正整数)7 .勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题•在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.6、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
类型一:勾股定理的直接用法1 在Rt△ ABC 中,/ C=90 °(1) 已知a=6, c=10,求b, (2)已知a=40, b=9,求c;(3)已知c=25, b=15,求a. 思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
举一反三【变式】:如图/ B=Z ACD=90 ° , AD=13,CD=12, BC=3,则AB的长是多少【答案I:/ ACD =90 °AD=13, CD=12••• AC2 =AD 2-CD2=132- 122=25•AC=5又•••/ ABC=90 ° 且BC=3•••由勾股定理可得AB2=AC2-BC2=52- 32=16•AB= 4•AB的长是4.类型二:勾股定理的构造应用^=30.求BC的长.2、如图,已知:在丄:二-中,一二v,二-■匚-〔-A思路点拨:由条件--=--L,想到构造含丄「角的直角三角形,为此作上-—上匸于D,则有BD=-AB^■',: ,再由勾股定理计算出AD、DC的长,进而求出BC的长•解析:作于D,则因—二•(芒上的两个锐角互余)B D ~C-.45 = 15 2 (在他中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半) 根据勾股定理,在-中,加-⑹=3-15* = 1 久疗.根据勾股定理,在中,3二 J AC 2- AD 2 =—占乜三心....更二 ED + DC 仝5 +15 = 80 .举一反三 【变式1】如图,已知: —— _,一】二-丄吕二于p.求证:二’I -:l -BC A解析:连结BM ,根据勾股定理,在 見丄刃存中, BP 2 = BM 2-PM 2. 而在中,则根据勾股定理有 胚"二恥-亦. .———:…■ .:-.■-]——:•「.■ ■,! I 2又•••=•・---1 (已知), ...加=磁"肱? +肿. 在中,根据勾股定理有妝—W 二亦 ...加二肘 + AF\【变式2】已知:如图,/ B= / D=90 °,/ A=60 ° , AB=4 , CD=2。
求:四边形 ABCD 的面积。
分析:如何构造直角三角形是解本题的关键,可以连结 AC ,或延长AB 、DC 交于F ,或延长AD 、BC 交于点E ,根 据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。
解析:延长AD 、BC 交于E 。
• / A= / 60°,/ B=90 ° ,.Z E=30°。
.AE=2AB=8 , CE=2CD=4 ,A.BE 2=AE 2-AB 2=82-42=48 , BE=时4匕=4^/1。
类型三:勾股定理的实际应用BD =•/ DE 2= CE 2-CD 2=42-22=12,2...S 四边形 ABCD =S △ABE -S ^CDE= J AB用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了I二到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
解析:(1)过B点作BE//AD•••/ DAB= / ABE=60 °•/ 30° + / CBA+ / ABE=180 °•••/ CBA=90 °即厶ABC为直角三角形由已知可得:BC=500m , AB= =由勾股定理可得:二'—十所以「■■ - --- ..'■■■+ T I, -:■ I . I.(2)在Rt△ ABC 中,■/ BC=500m , AC=1000m•••/ CAB=30 °•••/ DAB=60 °•••/ DAC=30 °即点C在点A的北偏东30°的方向举一反三【变式】一辆装满货物的卡车,其外形高 2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?【答案】由于厂门宽度是否足够卡车通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD丄AE, 与地面交于H .解:OC= 1米(大门宽度一半),OD= 0.8米(卡车宽度一半)在Rt △ OCD中,由勾股定理得:CD八…亠」-…・.6米,C H=0 .6 + 2 .3 = 2 . 9(米)>2 .5(米).因此高度上有0.4米的余量,所以卡车能通过厂门.(二)用勾股定理求最短问题4、国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进行电网改造,某地有四个村庄B、C、D,且正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分•请你帮助计算一下,哪种架设方案最省电线.思路点拨:解答本题的思路是:最省电线就是线路长最短,通过利用勾股定理计算线路长,然后进行比较,得出结论.解析:设正方形的边长为1,则图(1)、图(2)中的总线路长分别为AB+BC+CD = 3, AB+BC+CD = 3图(3)中,在Rt △ ABC中AC = 莆¥肘=罷同理丄丄•一 "-•••图(3)中的路线长为--——;-图(4)中,延长EF交BC于H,贝U FH丄BC, BH = CH址砒=19由/ FBH = -及勾股定理得:EA = ED = FB = FC =-;• EF = 1 —2FH = 1—-•此图中总线路的长为4EA+EF = H ''-':■ 3 > 2.828>2.732•图(4)的连接线路最短,即图(4)的架设方案最省电线.举一反三【变式】如图,一圆柱体的底面周长为20cm,高AE为4cm, BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.••• AC =丄丄.’上- !=:丁=】;」2 ^10.77( cm)(勾股定理).答:最短路程约为1 0.77 cm.Ml —貝码致如杲沿狡力怵的表面从A 点至卩Q V,解么岀稣条路迪駁行銀血;■■你镰刑它找田来吗¥如图O厨那,梃倉林的为15 CTrt,宽为IO ge崗为2°eif点B与离C的ffE刚冷5 cm.类型四:利用勾股定理作长为肮的线段5、作长为°、宀、宀的线段。
思路点拨:由勾股定理得,直角边为1的等腰直角三角形,斜边长就等于,直角边为」…和1的直角三角形斜边长就是」•,类似地可作J:'。
作法:如图所示I *(1) 作直角边为1 (单位长)的等腰直角△ ACB,使AB为斜边;.•一、■i・. ----------- --- —■协■B A BA O AB(2) 以AB为一条直角边,作另一直角边为1的直角'-''。
斜边为'-';(3) 顺次这样做下去,最后做到直角三角形"'-,这样斜边心吕、国\、、7 :的长度就是、、、。
举一反三【变式】在数轴上表示'的点。
解析:可以把・、看作是直角三角形的斜边,为了有利于画图让其他两边的长为整数,解:作法:如图所示在数轴上找到A点,使0A=3,作AC丄OA且截取AC=1,以0C为半径,以0为圆心做弧,弧与数轴的交点B即为。
类型五:逆命题与勾股定理逆定理6、写出下列原命题的逆命题并判断是否正确1 •原命题:猫有四只脚.(正确)2. 原命题:对顶角相等(正确)3 •原命题:线段垂直平分线上的点,到这条线段两端距离相等. (正确)4•原命题:角平分线上的点,到这个角的两边距离相等. (正确)思路点拨:掌握原命题与逆命题的关系。
