清华大学数学科学系本科课程浏览
数学系本科课程

数学系本科课程数学是一门抽象而又实用的学科,在现代社会中发挥着重要的作用。
作为一位数学系的学生,本科课程对于我来说至关重要。
本文将介绍数学系本科课程的设置和重要性,并探讨数学系本科课程对学生综合素质的培养和未来职业发展的影响。
1. 基础课程在数学系的本科课程中,基础课程占有重要地位。
这些课程包括微积分、线性代数、概率统计等。
微积分是数学的基石,它贯穿了整个数学领域。
通过学习微积分,我们能够理解函数、曲线和变化率等概念,为后续高级课程的学习奠定坚实的基础。
线性代数则涉及向量空间、矩阵和线性变换等内容,为数学系学生提供了解决实际问题的工具和方法。
概率统计则帮助我们理解随机现象和数据分析方法,对于实际问题的应用至关重要。
2. 高级课程除了基础课程外,数学系本科课程还包括了一系列的高级课程。
这些课程涉及到了更加深入和专业的数学领域,如数值计算、拓扑学、实变函数等。
数值计算是数学在计算机科学中的应用,它运用了数值方法解决了很多实际问题,例如求解微分方程和优化问题等。
拓扑学研究的是空间和连续性的性质,对于理论研究和应用都有很大的意义。
实变函数则探讨了实数轴上的函数性质,为分析学的学习打下基础。
3. 应用课程在数学系本科课程中,应用课程的设置也非常重要。
这些课程将数学理论与实际问题相结合,培养了学生的问题解决能力和创新思维。
应用课程包括金融数学、运筹学、统计学等。
金融数学运用了数学方法与金融领域的问题相结合,例如建模金融市场和风险管理等。
运筹学则研究了如何最优化决策,可以应用于物流和生产等实际问题。
统计学是一门关于数据分析和推断的学科,对于科学研究和社会决策都有很大的帮助。
数学系本科课程的设置不仅为学生提供了一系列系统的数学知识,更重要的是培养了学生的逻辑思维和问题解决能力。
通过学习数学,我们能够锻炼自己的思维方式,培养出良好的数学建模和推理能力。
这些能力对于未来职业发展至关重要,无论是从事科学研究还是从事金融和数据分析等工作,数学知识都是必不可少的。
数学科学系数学与应用数学专业本科培养方案-Tsinghua

数学科学系数学与应用数学专业本科培养方案一、培养目标培养德才兼备并且具有强烈的社会责任感、使命意识和创新精神的学生。
通过基础课程的严格训练、专业课程的深入与提高以及科研训练等以达成如下的培养目标:1.使学生具有坚实的数学基础、宽广的自然科学知识、强烈的创新意识和优良的综合素质,具备在现代数学及相关学科继续深造并成为学术领军人才的潜力;2.使学生具备扎实的数学基础、从事交叉学习和研究的能力、强烈的创新意识和服务社会的综合素质,满足社会不同职业对数学人才的需求。
二、培养成效a.了解数学学科发展的特点,掌握大学数学的核心思想和技巧;b.对严格的数学证明有深刻的理解,具有逻辑思维的习惯和问题求解的分析技巧与丰富经验,能够写出条理清晰、逻辑合理的数学论证;c.能体会和欣赏数学的抽象性和一般性的魅力,并具有对具体问题进行抽象思维、提出恰当数学问题并进行适当的定性或者定量分析的能力;d.对基础数学、应用数学、概率论与数理统计、计算数学、运筹学与控制论中的至少一个专业方向有较为深入的了解,掌握其专业基础知识并了解其发展现状;e.具备开展自学、文献调研、论文写作、学术报告等方面的综合能力;f.具有进行定量分析所必需的计算机、软件和算法的知识;g.具有有效沟通能力,善于和不同学科方向的专业人员进行学术交流;h.具有良好的团队意识和协作精神,能够在团队中发挥积极作用。
三、学制与学位授予学制:按本科四年学制进行课程设置及学分分配。
本科最长学习年限专业学制加两年。
授予学位:理学学士学位。
四、基本学分学时本科培养总学分156学分,其中通识教育课程44学分,专业教育课程102学分,自由发展课程学分10学分。
五、课程设置与学分分布1.通识教育44学分(1) 思想政治理论课 14学分10610183 思想道德修养与法律基础 3学分10610193 中国近现代史纲要 3学分10610204 马克思主义基本原理 4学分10610224 毛泽东思想和中国特色社会主义理论体系概论 4学分(2) 体育 4学分第1-4学期的体育(1)-(4)为必修,每学期1学分;第5-8学期的体育专项不设学分,其中第5-6学期为限选,第7-8学期为任选。
清华本科 高数教材

清华大学本科高等数学教材,历来以其严谨性、系统性和前沿性而著称,在国内外享有盛誉。
清华大学本科高等数学教材,从清华大学数学系第一任系主任熊庆来教授亲自编写的《高等数学讲义》开始,历经几代数学家和教育工作者的不断修订和完善,形成了具有清华特色的高等数学教材体系。
清华大学本科高等数学教材,主要包括《高等数学上下册》、《线性代数》、《复变函数》、《概率论与数理统计》、《微分几何》、《偏微分方程》、《积分变换》、《数值分析》、《计算数学》等。
这些教材,既涵盖了高等数学的基础知识,也涵盖了高等数学的最新进展,能够满足清华大学本科生在数学方面的学习需求。
清华大学本科高等数学教材,不仅在清华大学内部使用,而且在国内外其他高校和科研机构中也广为流传。
这些教材,为我国的数学教育和科研事业做出了巨大的贡献。
清华大学本科高等数学教材,具有以下几个特点:1. 严谨性。
清华大学本科高等数学教材,在内容上十分严谨,对每一个概念、定理和公式的表述都十分精确,并给出详细的证明。
这使得学生能够对高等数学有深刻的理解,并能够将高等数学的知识应用到实际问题中去。
2. 系统性。
清华大学本科高等数学教材,在内容上十分系统,各章各节之间联系紧密,环环相扣,形成一个完整的体系。
这使得学生能够对高等数学有一个全面的了解,并能够掌握高等数学的整体结构。
3. 前沿性。
清华大学本科高等数学教材,在内容上十分前沿,涵盖了高等数学的最新进展。
这使得学生能够了解高等数学的最新成果,并能够站在学术前沿进行研究。
4. 适用性。
清华大学本科高等数学教材,在内容上十分适用,既适合于清华大学本科生的学习,也适合于其他高校和科研机构的研究人员的学习。
这使得清华大学本科高等数学教材在国内外广为流传,成为高等数学领域的一部经典教材。
清华大学本科高等数学教材,在我国的数学教育和科研事业中发挥着重要的作用。
这些教材,为我国培养了大批优秀的数学人才,为我国的数学研究做出了巨大的贡献。
清华大学网络课程列表(55门课程
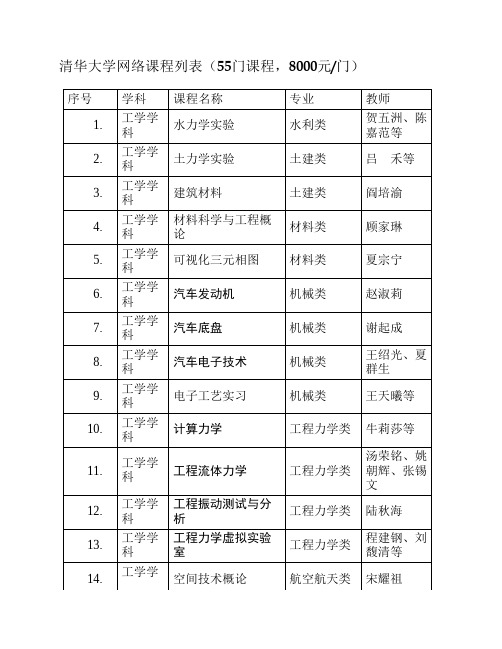
工程力学类 陆秋海
工程力学类
程建钢、刘 馥清等
航空航天类 宋耀祖
科
15.
工学学 科
反应堆热工水力学
能源动力类 俞冀阳
16.
工学学 科
核电厂系统及设备
能源动力类 藏希年
17.
工学学 科
反应堆原理
能源动力类 王侃
18.
工学学 科
核医学仪器与方法
能源动力类 金永杰
19.工学学 科源自工程热力学能源动力类 张冠忠
力学类
李万琼、贾 书惠等
39.
理学学 科
材料力学
力学类
蔡乾煌、崔 玉玺
40.
理学学 科
理论力学情景教学
力学类
贾书惠
41.
理学学 理论力学讨论式辅
科
导
力学类
薛克宗
42.
理学学 弹性力学 科
力学类
杨卫
43.
法学学 马克思主义政治经
科
济学原理
马克思主义 刘美洵、吴
理论类
娅茹等
44. 法学学 中国社会主义(邓 政治学类
20.
工学学 科
化学工程基础
化工与制药 类
林爱光
21.
工学学 科
仪器分析
化工与制药 刘密新、童
类
爱军等
22.
工学学 科
高电压工程实验
电机学类 徐光宝等
23.
工学学 科
电子技术
电气信息类 唐庆玉
24.
工学学 科
电路原理
电气信息类 陆文娟
25.
工学学 面向对象分析设计
科
与编程
电气信息类 吴炜煜
26.
清华大学本科课程及教材
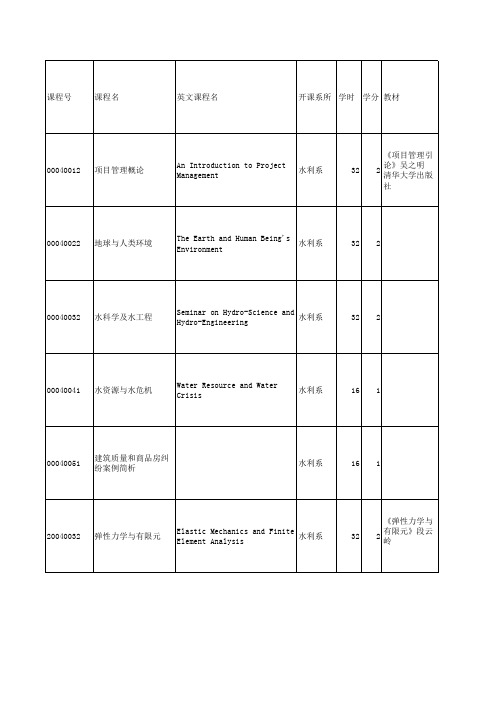
40040092
航运工程
Navigation Engineering
水利系
32
2
《航运工程》 (讲义)聂孟喜
40040102
公路工程
Highway Engineering
水利系
32
《道路工程》 2 杨富华 人民 交通出版社
40040112
环境水利
Environmental Hydraulic Engineering
水利系
64
《流体力学泵 与风机》周谟 4 仁 建筑工业 出版社
20040113
计算流体力学
Computational Fluid Mechanics
水利系
48
3
20040122
流体力学(2)
Fluid Mechanics(2)
水利系
32
《工程流体力 学》(水力学) 2 闻德荪 高等 教育出版社
30040012
Hydro-Power Station
水利系
48
《水电站建筑 3 物》清华大学 出版社 1992
40040212
水泵站及水电站
Hydro-Power Station and Pump 水利系 Station
32
《水电站建筑 2 物》清华大学 出版社 1992
40040222
抽orage
40040142
波浪理论与海洋水文
Theory of Water Wave and Ocean Hydrology
水利系
32
1.《工程水文 》(下)人民交 通出版社 2. 2 《水力学》 (下)高等教育 出版社 1.《水利工程 地质》 2.《 2 土木工程地质 》崔冠英 水 利水电出版社
清华大学本科生课程及教材列表
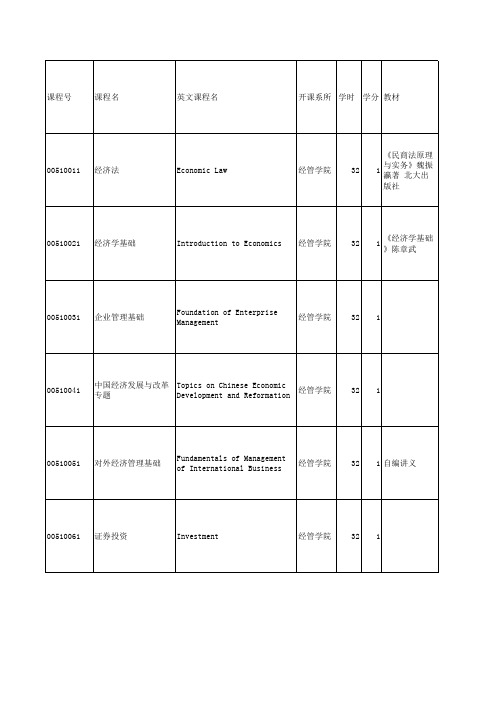
00510112 运筹学基础
Introduction to Operations Research
经管学院
32
2
《运筹学-规 划论及网络》
00510122 C语言程序设计
C Language and Programming 经管学院
32
2
《C程序设计 》谭浩强
00510133 会计学原理
Accounting Principles
Political Economics(2)
经管学院
《生产关系原
32
2
理及其应用讲 义》(讲义)吴
栋
20510032 工程经济学
Engineering Economics
经管学院
《工业技术经 济学》(第三 32 2 版)傅家骥 清华大学出版 社
20510044 运筹学(1)
Operations Research (1)
经管学院
《博弈论基础
48
3
》吉本斯著, 中国社会科学
出版社1999。
10510012 法律基础
Fundamentals of Law
经管学院 32 2
10510024 强化英语
Intensive English
经管学院 64 4
10510032 强化英语
Intensive English
经管学院
32
30510173 审计学
Auditing
30510182 投资学
Investment
经管学院 48 3
经管学院
2
《listen To This》(2)
10510042 英语听说(1)
English Listening and Speaking(1)
清华数理基础科学专业

清华数理基础科学专业 1. 数学基础:
- 离散数学
- 微积分
- 线性代数
- 概率论与数理统计
- 经典物理学
- 电磁学
- 量子力学
- 热力学与统计物理
- 程序设计与数据结构
- 计算机组成原理
- 算法设计与分析
- 操作系统
- 编译原理
4. 天文学与地球与空间科学:
- 宇宙学
- 材料化学
- 材料制备与表征技术
6. 数值计算方法:
- 偏微分方程数值解
- 数值优化方法
- 科学计算与模拟
- 多尺度模拟方法
7. 应用数学与计算科学:
- 数据科学与分析
- 图论与网络分析
- 复杂系统建模与仿真
8. 实验与研究项目:
- 实验室基础操作与安全
- 学术研究方法与论文写作
- 科学论文阅读与批判性思维
请注意,真实的清华大学数理基础科学专业课程可能与上述内容有所不同。
以上只是一个虚构的清华大学数理基础科学专业课程概览,仅供参考。
数学系本科生课程设置与简介

数学系本科生课程设置与简介01101011 数学分析(1) mathematical analysis课程性质:专业基础课课内学时:112 学分:7简介:“数学分析”是数学专业最重要的一门专业课。
第一学期主要内容是分析基础。
第一章函数、第二章极限、第三章连续函数、第四章实数的连续性、第五章导数与微分、第六章微分基本定理及其应用、第七章不定积分、第八章定积分。
先修课要求:无教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:秋01101021 数学分析(2) mathematical analysis课程性质:专业基础课课内学时:144 学分:8简介:本学期将在此基础上继续学习级数和多元函数微分学。
级数是数学分析的重要组成部分,它分为数值级数和函数级数。
数值级数是函数级数的特殊情况,也是函数级数的基础;函数级数是表示非初等函数的一个重要的数学工具,它在自然科学、工程技术和数学本身都有广泛的应用。
多元函数微分学是一元函数微分学的推广,隐函数、反常积分与含参变量的积分、重积分和曲线积分与曲面积分。
并且对某些概念和定理作了进一步的发展。
先修课要求:数学分析(1)教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:春01101031 数学分析(3) mathematical analysis课程性质:专业基础课课内学时:40 学分:2简介:本学期将在此基础上继续学习级数和多元函数积分学。
多元函数积分学是一元函数积分学的推广,隐函数、反常积分与含参变量的积分、重积分和曲线积分与曲面积分。
并且对某些概念和定理作了进一步的发展。
先修课要求:数学分析(1) 、数学分析(2)教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:秋01101041 数学分析选讲 Selected Topics of Analysis课程性质:专业选修课课内学时:48 学分:2简介:数学分析教材自身科学规律概述、数学分析的思想方法与表达方式浅析、数学分析解题方法概述、关于数学分析中何种类型习题宜于用反证法证明的问题、形式逻辑与辩证逻辑方面易出现的错误及其分析、函数、数列极限、函数极限、函数的连续性、导数、中值定理与导数的应用、实数的基本定理、不定积分、定积分、数项级数、函数列与函数项级数、含参量正常积分、黎曼积分概念与性质,重积分的计算、曲线积分、曲面积分、各类积分间的联系、非正常积分、含参量非正常积分。
清华大学数学系简介

清华大学数学科学系介绍清华大学数学科学系有着辉煌而悠久的历史。
其前身,是创建于1927年的清华大学数学系和前工程力学数学系计算数学专业以及1979年恢复建立的应用数学系。
从1927年创建至今,清华数学共经历了三个不同的发展阶段:1927年至1952年从创建到辉煌发展的阶段、1952年至1979年从院系调整到复建的特殊发展阶段、1979年至今蓬勃发展的新阶段。
可以说,在每个发展阶段清华数学系都为中国数学科学之发展和中国杰出科技人才之培养做出了很大的贡献。
从1927年创立到1952年院系调整前的25年间,先后担任过清华数学系主任的著名数学家有郑之番、熊庆来、杨武之、江泽涵、赵访熊、段学复等。
他们不仅积极引进和采用当时世界上最先进的数学教学体系,而且力倡学术研究、广泛罗致人才,在短短二十五年里就使清华数学从创建走向辉煌。
在这期间有许多国内知名数学家先后来清华数学系任教,其中包括孙光远、曾远荣、胡坤升、许宝禄、陈省身、华罗庚、庄圻泰、闵嗣鹤、徐利治、程民德、吴新谋、万哲先、冯康、周毓麟等。
1935年还聘请了法国数学家、当时的世界算学会副会长J.Hadamard和美国数学家、现代控制论创始人N.Wiener担任客座教授。
这期间也涌现出了不少的数学人才,如陈省身、华罗庚、吴大任、庄圻泰、许宝禄、柯召等。
可以说国际著名数学家陈省身、华罗庚等就是从清华数学系走向世界的,他们的辉煌成就对当代数学的发展产生了深远的影响。
由于提倡教学与研究兼重,当时取得了一批颇有影响的研究成果。
如熊庆来在亚纯函数方面所建立的无穷亚纯函数论;杨武之在我国现代数论研究方面的开创性工作“棱锥数的华林问题”;华罗庚在解析数论方面关于素数变换的Waring问题的研究以及变数之素数的方程组的研究;陈省身对微分几何中高斯—波内公式的研究以及拓扑学、Finsler 几何的研究等。
1941年华罗庚的“堆垒素数论”获得教育部颁发的首届学术研究及著作发明国家一等奖,许宝禄的“数理统计”论文获二等奖。
清华大学课程表

清华大学本科培养方案和本科指导性教学计划
化学工程系 高分子材料与工程专业本科培养方案
一、培养目标
为高分子材料领域培养具有扎实基础知识、较强的实践能力和创新精神的高层次高素质科学技术和 管理人才。本科毕业后应能胜任高分子材料领域的新工艺、新产品、新技术的研究、生产及技术管理工 作。
二、基本要求
高分子材料与工程专业本科毕业生应达到如下知识、能力和素质的要求: 掌握坚实的自然科学、人文社会科学、工程技术基础理论,具备高分子材料专业知识和高级专门知 识,较强的实践能力;具有较强的创新意识和创新能力;具有强烈的社会责任感、良好的工程职业道德 和职业行为规范;具有较强的求知欲,以及终身学习能力。实现通识教育基础上的宽口径专业教育,厚 基础、宽专业。
理论体系概论
4
体育(4)
1
英语(4)
2
物理实验A(2)
2
物理化学A(2)
4
有机化学实验A(2)
2
电工与电子技术
4
数学实验
4
高分子化学
3
文化素质选修课
合计:
24
周学时 考核方式 说明及主要先修课
3
考试
2
考查
2
考试
2
考查
先修物理实验A(1)
4
考试
先修物理化学B(1)
4
考查
4
考试
4
考试
3
考试
课程编号 30340292 40340282
三、学制与学位授予
学制:本科学制四年,按照学分制管理机制,实行弹性学习年限。 授予学位:工学学士学位。
四、基本学分学时
本科培养总学分174,其中春、秋季学期课程总学分144,夏季学期实践环节15学分,综合论文训 练15学分。
数学科学系数学与应用数学专业本科培养方案清华大学本科招生网

数学科学系数学与应用数学专业本科培养方案清华大学本科招生网一、引言在当今世界,数学科学与技术已经渗透到人类生活的各个领域,从自然科学的深度研究,到社会科学的高度复杂计算,数学都在无声无息中改变着我们的世界。
为了培养更多具备坚实数学基础,优秀科研素养,以及卓越创新能力的优秀人才,清华大学数学科学系致力于提供世界一流的本科教育。
本文将详细介绍数学科学系数学与应用数学专业的本科培养方案,以帮助更多的学生了解和接触这一极具前景的学科。
二、培养目标清华大学数学科学系的本科培养目标旨在培养具有深厚数学基础、广阔视野和高度社会责任感的人才。
通过系统的数学学习和实践,学生将掌握数学的基本理论和方法,培养独立思考和解决问题的能力,形成严谨的科学态度和批判性思维。
同时,该培养方案也注重培养学生的创新精神和实践能力,以适应社会发展的需要。
三、课程设置数学科学系的课程设置以严谨的学术性和广泛的应用性为特点。
学生在校期间将学习基础数学、应用数学、概率统计、计算机科学等核心课程,同时还有机会选修各种跨学科课程,如经济学、物理学、生物学、计算机科学等。
该系还特别注重国际化的教育理念,为学生提供多种外语和国际交流机会,以帮助学生更好地适应全球化的社会环境。
四、科研与实践清华大学数学科学系鼓励并支持学生在科研和实践方面的发展。
学生可以通过参加各种科研项目、学术研讨会、学术交流活动等,提高自己的研究能力和创新精神。
同时,该系还与国内外众多企业和研究机构建立了紧密的合作关系,为学生提供丰富的实践机会和职业发展前景。
五、招生与录取为了确保招收和培养最优秀的学生,清华大学数学科学系的录取标准非常严格。
在招生过程中,该系会全面评估学生的学术成绩、科研经历、社会活动、领导力等多方面的能力和素质。
同时,对于特别优秀的学生,该系还会提供各类奖学金和奖励计划以鼓励他们在数学领域的发展。
六、总结清华大学数学科学系的数学与应用数学专业本科培养方案是一套既严谨又全面的教育体系。
清华大学本科计算机课程介绍

课号:00240013 学分: 3 课程名称 中文 课程属性:全校任选 英文 开课学期:秋、春 Fundamentals of Computer-aided Design 出版社 清华大学出版社 出版年月 2002 年 8 月
计算机辅助设计技术基础 书名 作者
使用教材
计算机辅助设计技术基 础教程
本课程是计算机科学与技术系为全校本科生开设的一门重要的计算机专业基础 课,目的是培养学生的软件工程素质,提高学生的软件开发能力。 本课程以软件生命周期的主要活动为主线,从软件及软件工程的历史和发展、软 件开发过程、需求分析、软件设计、程序编码、软件测试、软件维护、软件项目管理、 标准及规范等方面全面介绍软件工程的基本理论、方法、技术和工具。
课号: 30240273 课程名称
学分: 3 中文
课程属性:本科必修 开课学期: 春季 数据结构 书名 作者 英文 Data Structure 出版社 出版年月 1997
使用教材 参考书 讲课对象 课 程 简 介
数据结构(C 语言版)
严蔚敏,吴伟民 清华大学出版社
[1] Kruse, et.al. Data Structures & Program Desing in C. [2] Knuth. The Art of Computer Programming. Volume 1. 本科生 适用专业 工业工程系 先修课 C 语言程序设计
This course focuses on the basic concepts, principles, algorithms and applications of computer-aided design(CAD), it mainly consists of the following topics: software and hardware system of CAD, two-dimensional transformations, line clipping, raster display of 2D graphics, curves Introduction and surfaces, solid modeling, three-dimensional transformations, three-dimensional viewing, visible-surface determination, basic illumination models, and introductions to AutoCAD, 3DMAX 5.0 and OpenGL. It is an ideal choice for students who want to learn the rudiments of this dynamic and exciting CAD technology. 姓 名 讲 课 教 师 职称 主要教学和科研领域 主要教学领域: (1)承担全校计算机辅助设计技术基础 课教学; (2)承担研究生的小波分析及其应用课教学; 主要研究领域:小波分析及其应用,科学计算可视化, 计算机图形学,几何造型和图象处理。 (1)承担全校计算机辅助设计技术基础课教学
清华大学数学科学系[1]
![清华大学数学科学系[1]](https://img.taocdn.com/s3/m/465c2f65eef9aef8941ea76e58fafab069dc449f.png)
统计学博士生培养方案一、适用学科统计学(Statistics),一级学科,理学门类,学科代码:0714二、培养目标培养德智体全面发展,掌握扎实统计学基础理论和系统深入的专门知识,具有独立从事统计学原创性研究和应用能力的统计学人才。
使得学生掌握学术规范,独立开展学术研究和进行学术交流,指导学生应用统计学、数学和计算机知识解决实际问题,在有关的研究方向上做出有重要理论或者实际应用的创新性成果。
毕业以后,适合于在高等学校、科研机构、政府部门、企事业单位中从事统计学与其相关领域的教学、科研、管理等方面的研究和工作。
三、主要研究方向1.数理统计学2.概率论3.生物与医学统计4.时间序列分析与随机过程统计5.金融统计6.大数据处理与分析7.工业统计四、培养方式1、博士研究生实行导师负责制。
必要时可设副导师,鼓励组成指导小组集体指导。
跨学科或交叉领域培养博士生时,应从相关学科中聘请副导师协助指导。
2、建立规范化的学术交流和学术报告制度,按期检查培养环节的完成情况。
3、博士生应在导师指导下,学习有关课程,查阅文献资料,参加专题讨论班和国内外学术会议,选择统计学的重要理论或者应用问题作为研究课题,独立从事科学研究并取得创新性成果。
四、课程学习的基本要求1、普博生普博生在学期间需获得学位要求的总学分不少于22,其中必修环节学分7。
课程设置见附录一。
2、直博生(包括提前攻博生)直博生(包括提前攻博生)在学期间需获得学位要求的总学分不少于40,其中必修环节学分7,考试学分不少于30。
课程设置见附录一。
五、培养环节与有关要求1、制定个人培养计划博士生入学并确定导师以后,在导师指导下制定个人培养计划,内容包括:研究方向、课程学习、文献综述、开题报告、科学研究、学术交流、学位论文与实践环节等方面的要求和进度计划。
在执行计划过程中,如因特殊情况需要变动,须在每学期选课期间修改。
修改后的课程计划,经导师签字后送系研究生主管部门备案。
清华大学高等数学教材

f ( x) − g ( x) = x + 2 x + u ∴ x + 2 x + u为最大公因式。
2 2
x +2x+u x + tx + u 3 2 x + 2 x + ux
2 3 2
x + (t − 2)
(t −2)x2 −ux 2 (t − 2)x + 2(t − 2)x +u(t − 2)
引理2:实系数多项式f ( X )的复根总是成共轭对 出现。 若α是其根, 则α 也是根。
n
设
f ( x ) = a n x + ⋯ + a1 x + a 0 f (α ) = a nα + ⋯ + a1α + a 0 = 0
n
则
f (α ) = a nα + ⋯ + a1α + a 0
n
= a nα + ⋯ + a1α + a 0 = 0.
试 证 : β 1 ,⋯ , β t 线 性 无 关 ⇔ r ( A) = t 证 ,β ⋯ t t 线 无关 ⇔ 故 : β 11,,⋯ , ,ββ线 性性 无 关 ⇔ A x = 0 只 有 零 解 x1 β 1 + ⋯ + x t β t = 0 仅 当 x1 = ⋯ = x t = 0 成 立
i =1
15
这种记法满足: (1)(e1,⋯, en ) A]B = e1,⋯, en ) AB [ ( ′ ( ′ ′ (2) e1,⋯, en ) A + e1,⋯, en ) A = e1 + e1,⋯, en + en ) A ( (′ (3) e1,⋯, en )(A + B) = e1,⋯, en ) A + e1,⋯, en )B. ( ( (
数学科学系数学与应用数学专业第二学士学位培养方案-清华大学

清华大学本科培养方案数学科学系数学与应用数学专业第二学士学位培养方案一、培养目标本着通识教育基础上的“厚基础,宽专业”的办学理念,培养具有扎实的数学基础知识和较强的数学应用能力的复合型人才。
使学生受到严格的科学思维训练,掌握数学学科的基本思想方法并有敏锐的应用意识。
二、基本要求数学与应用数学专业本科二学位毕业生应达到如下知识、能力和素质的要求:在学习并掌握微分方程、测度与积分、复分析、概率论(1)四门核心基础课程后,选修数学与应用数学方向的其他核心课程,参加相应的科研训练。
要求初步了解数学与应用数学方向基础知识和发展状况,具备开展自学、文献调研、论文写作、学术报告等各方面的综合能力。
三、学制与学位授予学制:第二学士学位学制二年,按学分制管理。
授予学位:理学第二学士学位。
四、学分要求选本专业为第二学位的学生必须修满培养方案规定的40学分,其中课程30学分,综合论文训练10学分。
五、课程设置1.专业必修课程 15学分30420023 微分方程(1) 3学分30420334 测度与积分4学分40420624 概率论(1) 4学分先修测度与积分30420464 复分析4学分2.专业选修课 15学分30420384 抽象代数4学分40420614 泛函分析(1) 4学分40420664 偏微分方程4学分先修微分方程(1) 40420644 微分几何4学分30420444 统计推断4学分先修概率论(1)30420433 线性回归3学分40420054 数值分析4学分40420534数学规划4学分清华大学本科培养方案3.综合论文训练 10学分综合论文训练10学分。
清华大学数学专业所学课程

数学科学系00420033 数学模型3学分48学时Mathematical Modelling建立数学模型是用数学方法解决实际问题的关键步骤。
本课程从日常生活的有趣问题入手,介绍数学模型的一般概念、方法和步骤,通过实例研究介绍一些用机理分析方法建立的非物理领域的模型及常用的建模数学方法,培养同学用建模方法分析和解决实际问题的意识和能力。
00420152 数学建模引论2学分32学时Introduction of Mathematical Modelling本课程以案例分析的方式组织教学,主要面向低年级的学生,各个学期根据对学生数学基础的不同要求,选择案例。
我们这里所选择的都是实际应用价值非常突出的案例。
00420163 数理科学与人文3学分48学时Mathematical and Physical Sciences and Humanities本课程旨在加强学生以通识教育为目标的思维和训练,提高学生的科学素质。
该课程虽然以知识为载体,却并不以传授理论知识为主要目的,而是以启迪思想,养成思考的习惯,以提升学生的创新意识。
00420172 数学与人类文明2学分32学时Mathematics and Civilization本课程不以讲述数学专门知识为目标,着重讲述数学发展对人类文明发展的地位、作用和影响,人类认识客观世界的能力,非数学专业学者如何理解和看待和欣赏数学。
10420095 微积分(1) 5学分80学时Calculus(1)内容包括:实数,函数,极限论,连续函数,导数与微分,微分中值定理,L'Hospital法则,极值与凸性,Taylor公式,不定积分与定积分,广义积分,积分应用,数项级数,函数级数,幂级数,Fourier级数。
10420115 微积分(2) 5学分80学时Calculus(2)n维空间中的距离、邻域、开集与闭集,多元函数的极限与连续,多元函数微分学,空间曲线与曲面,重积分、曲线与曲面积分、向量分析,常微分方程、初等积分法、高阶线性方程、线性常微分方程组。
清华大学数学科学系本科课程浏览

清华大学数学科学系本科课程浏览课程号课程名课时学分00420033数学模型Mathematical Models 48 3 00420073应用近世代数Applied abstract algebra 48 3 10420213几何与代数(1) Geometry and Algebra(1) 64 4 10420243随机数学方法Stochastic Mathematical Methods 48 3 10420252复变函数引论Introduction to Functions of One Complex Variable 32 2 10420262数理方程引论Introduction to Equations of Mathematical Physics 32 2 10420454高等分析Advanced Analysis 64 4 10420672初等数论与多项式Elementary Number Theory 32 2 10420684几何与代数(1) Geometry and Algebra 64 4 10420692几何与代数(2) Geometry and Algebra(2) 32 2 10420743微积分(I)Calculus(I)48 3 10420746微积分(III)Calculus(III)64 4 10420753微积分(II)Calculus(II)48 3 10420803概率论与数理统计Probability and Statistics 48 3 10420844文科数学Mathematics for Liberal Arts 64 4 10420845大学数学2(社科类) College Mathematics II (For Social Science)48 3 10420854数学实验Mathematical Experiments 48 4 10420874一元微积分Calculus of One Variable 64 4 10420884多元微积分Calculus of Several Variables 64 4 10420892高等微积分B Advanced Calculus B 32 2 10420894高等微积分Advanced Calculus 64 4 10420925数学分析(1)Mathematical Analysis 80 5 10420935数学分析(2)Mathematical Analysis II 80 5 10420944线性代数(1)Linear algebra 64 4 10420946线性代数Linear algebra 32 2 10420963大学数学(1)(社科类)48 3 10420984大学数学(3)(社科类) Collegiate mathematics (3) for social science students 64 4 10420994大学数学(4) Undergraduate Mathematics (4) 64 4 10421692几何与代数(2) Geometry and Algebra(2) 32 2 30420023微分方程(1) Differential Equations (1)48 3 30420033微分方程(2)Differential Equations (2)48 3 30420083复分析Complex analysis 48 3 30420095高等微积分(1)Mathematical analysis (I) 80 5 30420124高等代数与几何(1) Advanced Algebra and Geometry (1) 64 4 30420134高等代数与几何(2) Advanced Algebra and Geometry (2) 64 4 30420224高等微积分(3)Advanced Calculus(3) 64 4 30420334测度与积分Measure and Integration 64 4 30420352概率论介绍A First Course in Probability 32 2 30420364拓扑学Topology 64 4 30420384抽象代数Abstract Algebra 64 4 30420394高等微积分(2)Mathematical analysis (II) 64 4 40420093数理统计Mathematical Statistics 48 3 40420193数理方程与特殊函数Equations in Mathematical Physics and Special Function 48 3 40420534数学规划Mathematical Programming 64 4 40420583概率论(1)Introduction to Stochastics 48 3 40420593数据结构 Data Structures 48 3 40420603集合论Set Theory 48 3 40420614泛函分析(1)Functional Analysis 64 4 40420632数理统计介绍Introduction to Statistics 32 2 40420644微分几何 Differential Geometry#Mathematics。
数学科学系数学与应用数学专业、信息与计算科学专业本科-清华大学

(2) 体育 4学分 第 1-4 学期的体育(1)-(4)为必修,每学期 1 学分;第 5-8 学期的体育专项不设学分,其中第 5-6
学期为限选,第 7-8 学期为任选。
(3) 外语 8学分 英语课程共计 8 学分(其中至少 4 学分为英语必修课组课程),安排在前四个学期完成。夏季学期
设置 2 学分外语实践,为各专业必修环节,学生可以在 1-3 年级完成。外语实践是指学生在本科阶段,
以报名参加。
日语、德语、法语、俄语等小语种学生入学后直接进入课程学习,本科毕业需完成三学期的课程,
取得 6 学分。
2.文化素质课 13学分
文化素质教育课程体系包括文化素质教育核心课、新生研讨课、文化素质教育讲座课和一般文化 素质教育课,除文化素质教育讲座和新生研讨课外,其它所有课程划分为八个课组:①哲学与伦理、 ②历史与文化、③语言与文学、④艺术与审美、⑤环境、科技与社会、⑥当代中国与世界、⑦人生与 发展、⑧数学与自然科学。要求在本科学习阶段修满 13 学分,其中文化素质教育讲座课程为必修, 1-2 学分;文化素质教育核心课程和新生研讨课为限选,至少 5 门或 8 学分,建议其中 1 门为新生研 讨课;一般文化素质课程为任选。
三、学制与学位授予
学制:本科学制四年,按照学分制管理机制,实行弹性学习年限。 授予学位:理学学士学位。
四、基本学分学时
本科培养总学分 170 学分,其中春、秋季学期课程总学分 141 学分;夏季学期实践环节 14 学分, 综合论文训练 15 学分。
五、专业核心课程
本专业所有方向的基础核心课程 10 门,41 学分 数学分析(1)(5 学分)、数学分析(2)(5 学分)、数学分析(3)(4 学分)、高等代数与几何(1) (4 学 分)、高等代数与几何(2) (4 学分)、微分方程(1)(3 学分)、抽象代数(4 学分)、复分析(4 学分)、测 度与积分(4 学分)、概率论(1)(4 学分)。 基础数学方向的其他本科核心课程 4 门,16 学分 泛函分析(1)(4 学分)、拓扑学(4 学分)、偏微分方程(4 学分)、微分几何(4 学分)。 应用数学方向的其他本科核心课程 4 门,16 学分 泛函分析(1) (4 学分)、偏微分方程(4 学分)、数值分析(4 学分)、应用分析(4 学分)。 概率统计方向的其他本科核心课程 4 门,15 学分 统计推断(4 学分)、线性回归(3 学分)、应用随机过程(4 学分)、数值分析(4 学分)。 计算数学的其他本科核心课程 4 门,16 学分 泛函分析(1) (4 学分)、偏微分方程(4 学分)、 数值分析(4 学分)、偏微分方程数值解(4 学分)。 运筹学与控制论方向的其他本科核心课程 4 门,16 学分 泛函分析(1) (4 学分)、数值分析(4 学分)、数学规划(4 学分)、离散数学(4 学分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
清华大学数学科学系本科课程浏览
课程号课程名课时学分00420033数学模型Mathematical Models 48 3 00420073应用近世代数Applied abstract algebra 48 3 10420213几何与代数(1) Geometry and Algebra(1) 64 4 10420243随机数学方法Stochastic Mathematical Methods 48 3 10420252复变函数引论Introduction to Functions of One Complex Variable 32 2 10420262数理方程引论Introduction to Equations of Mathematical Physics 32 2 10420454高等分析Advanced Analysis 64 4 10420672初等数论与多项式Elementary Number Theory 32 2 10420684几何与代数(1) Geometry and Algebra 64 4 10420692几何与代数(2) Geometry and Algebra(2) 32 2 10420743微积分(I)Calculus(I)48 3 10420746微积分(III)Calculus(III)64 4 10420753微积分(II)Calculus(II)48 3 10420803概率论与数理统计Probability and Statistics 48 3 10420844文科数学Mathematics for Liberal Arts 64 4 10420845大学数学2(社科类)College Mathematics II (For Social Science)48 3 10420854数学实验Mathematical Experiments 48 4 10420874一元微积分Calculus of One Variable 64 4 10420884多元微积分Calculus of Several Variables 64 4 10420892高等微积分B Advanced Calculus B 32 2 10420894高等微积分Advanced Calculus 64 4 10420925数学分析(1)Mathematical Analysis 80 5 10420935数学分析(2)Mathematical Analysis II 80 5 10420944线性代数(1)Linear algebra 64 4 10420946线性代数Linear algebra 32 2 10420963大学数学(1)(社科类)48 3 10420984大学数学(3)(社科类) Collegiate mathematics (3) for social science students 64 4 10420994大学数学(4) Undergraduate Mathematics (4) 64 4 10421692几何与代数(2) Geometry and Algebra(2) 32 2 30420023微分方程(1)Differential Equations (1)48 3 30420033微分方程(2)Differential Equations (2)48 3 30420083复分析Complex analysis 48 3 30420095高等微积分(1)Mathematical analysis (I) 80 5 30420124高等代数与几何(1) Advanced Algebra and Geometry (1) 64 4 30420134高等代数与几何(2) Advanced Algebra and Geometry (2) 64 4 30420224高等微积分(3)Advanced Calculus(3) 64 4 30420334测度与积分Measure and Integration 64 4 30420352概率论介绍A First Course in Probability 32 2 30420364拓扑学Topology 64 4 30420384抽象代数Abstract Algebra 64 4 30420394高等微积分(2)Mathematical analysis (II) 64 4 40420093数理统计Mathematical Statistics 48 3 40420193数理方程与特殊函数Equations in Mathematical Physics and Special Function 48 3 40420534数学规划Mathematical Programming 64 4 40420583概率论(1)Introduction to Stochastics 48 3 40420593数据结构Data Structures 48 3 40420603集合论Set Theory 48 3 40420614泛函分析(1)Functional Analysis 64 4 40420632数理统计介绍Introduction to Statistics 32 2 40420644微分几何Differential Geometry
#Mathematics。
