数据结构实验3.2:以邻接矩阵为存储结构的图的深度、宽度优先遍历
数据结构实验报告图的遍历讲解

数据结构实验报告图的遍历讲解一、引言在数据结构实验中,图的遍历是一个重要的主题。
图是由顶点集合和边集合组成的一种数据结构,常用于描述网络、社交关系等复杂关系。
图的遍历是指按照一定的规则,挨次访问图中的所有顶点,以及与之相关联的边的过程。
本文将详细讲解图的遍历算法及其应用。
二、图的遍历算法1. 深度优先搜索(DFS)深度优先搜索是一种常用的图遍历算法,其基本思想是从一个顶点出发,沿着一条路径向来向下访问,直到无法继续为止,然后回溯到前一个顶点,再选择此外一条路径继续访问。
具体步骤如下:(1)选择一个起始顶点v,将其标记为已访问。
(2)从v出发,选择一个未被访问的邻接顶点w,将w标记为已访问,并将w入栈。
(3)如果不存在未被访问的邻接顶点,则出栈一个顶点,继续访问其它未被访问的邻接顶点。
(4)重复步骤(2)和(3),直到栈为空。
2. 广度优先搜索(BFS)广度优先搜索是另一种常用的图遍历算法,其基本思想是从一个顶点出发,挨次访问其所有邻接顶点,然后再挨次访问邻接顶点的邻接顶点,以此类推,直到访问完所有顶点。
具体步骤如下:(1)选择一个起始顶点v,将其标记为已访问,并将v入队。
(2)从队首取出一个顶点w,访问w的所有未被访问的邻接顶点,并将这些顶点标记为已访问,并将它们入队。
(3)重复步骤(2),直到队列为空。
三、图的遍历应用图的遍历算法在实际应用中有广泛的应用,下面介绍两个典型的应用场景。
1. 连通分量连通分量是指图中的一个子图,其中的任意两个顶点都是连通的,即存在一条路径可以从一个顶点到达另一个顶点。
图的遍历算法可以用来求解连通分量的个数及其具体的顶点集合。
具体步骤如下:(1)对图中的每一个顶点进行遍历,如果该顶点未被访问,则从该顶点开始进行深度优先搜索或者广度优先搜索,将访问到的顶点标记为已访问。
(2)重复步骤(1),直到所有顶点都被访问。
2. 最短路径最短路径是指图中两个顶点之间的最短路径,可以用图的遍历算法来求解。
数据结构中图的建立与深度优先、广度优先遍历

数据结构中图的建立与深度优先、广度优先遍历《数据结构》实验报告实验内容:图的建立(邻接矩阵)及其深度优先、广度优先遍历学号:姓名:一、上机实验的问题和要求(需求分析):[ 题目]二、程序设计的基本思想,原理和算法描述:设计一个程序,建立图的邻接矩阵,并且进行图的广度优先遍历。
三、调试和运行程序过程中产生的问题及采取的措施:(略)四、源程序及注释[ 源程序] 程序名:9.cpp#include"stdio.h"#include"stdlib.h"#define INFINITY 100#define MAX_VERTEX_NUM 20#define MAX 100#define OK 1#define ERROR 0#define NULL 0typedef int VRType;typedef int VertextType;typedef int Status;typedef enum {DG,DN,UDG,UDN}GraphKind;typedef struct ArcCell{VRType adj;}ArcCell,AdjMatrix[MAX_VERTEX_NUM ][MAX_VERTEX_NUM ]; typedef struct{int vexs[MAX_VERTEX_NUM ];int arcs[4][4] ;int vexnum,arcnum;GraphKind Kind;}MGraph;int LocateVex(MGraph G,int v1){ int i;for(i=0;i<g.vexnum;i++)< p="">if(G.vexs[i]==v1)printf("%d\n",i);return i;}Status CreateUDN(MGraph &G){ int v1,v2;int i,j,k,w;printf("输入图的顶点数和弧数:");scanf("%d,%d",&G.vexnum,&G.arcnum); printf("输入顶点:");for(i=0;i<g.vexnum;i++)< p="">scanf("%d",&G.vexs[i]);for(i=0;i<g.vexnum;i++)< p="">for(j=0;j<g.vexnum;j++)< p="">G.arcs[i][j]=INFINITY ;printf("输入顶点关系:");for(k=0;k<g.arcnum;k++)< p="">{scanf("%d%d%d",&v1,&v2,&w);i=LocateVex(G,v1);j=LocateVex(G,v2);G.arcs[i][j]=w;G.arcs[j][i]=G.arcs[i][j];printf("%d\n%d\n",G.arcs[i][j],G.arcs[j][i]);}printf("图的邻接矩阵图是:\n");for(i=0;i<g.vexnum;i++)< p="">{for(j=0;j<g.vexnum;j++)< p="">printf("%d",G.arcs[i][j]);printf("\n");}return OK;}Status Visit(int e){//输出函数printf("%d\n",e);return OK;}//PrintElement//Status(*VisitFunc)(char v);int visited[MAX];void DFS(MGraph G,int v){ int j;Visit (v);visited[v]=1;for(j=1;j<g.vexnum;j++)< p="">if(!visited[j]&&G.arcs[v][j]!=INFINITY)DFS(G,j); } void DFSTraverse(MGraph G){ int v;for(v=0;v<g.vexnum;++v)< p="">visited[v]=0;for(v=0;v<g.vexnum;++v)< p="">if(!visited[v])DFS(G,v);/* 有关队列的操作*/#define MAX SIZE 100#define QElemType int#define OVERFLOW 0typedef struct{QElemType *base;int front;int rear;}SqQueue;Status InitQueue(SqQueue &Q){ Q.base=(QElemType*)malloc(MAXSIZE* sizeof(QElemType)); if(!Q.base)exit(OVERFLOW);Q.front=Q.rear=0;return 0;}Status EnQueue(SqQueue &Q,QElemType e){if(Q.rear+1==Q.front)return ERROR;Q.base[Q.rear]=e;Q.rear=Q.rear+1;return OK;}Status DeQueue(SqQueue &Q,QElemType &e){if(Q.front==Q.rear)return ERROR;e=Q.base[Q.front];Q.front=Q.front+1;return OK;}Status QueueEmpty(SqQueue Q){if(Q.front==Q.rear)return OK;else return ERROR;void BFSTraverse(MGraph &G){ int v,u,j;SqQueue Q;for(v=0;v<g.vexnum;v++)< p=""> visited[v]=0;InitQueue(Q);for(v=0;v<g.vexnum;++v)< p="">if(!visited[v]){visited[v]=1;Visit(v);EnQueue(Q,v);while(!QueueEmpty(Q)){ DeQueue(Q,u);for(j=1;j<g.vexnum;j++)< p="">if(!visited[j]&&G.arcs[v][j]!=INFINITY) { visited[j]=1;Visit(j);EnQueue(Q,j);}} }}void main(){ MGraph G;CreateUDN(G);printf("建图成功!");printf("深度优先遍历的结果:\n"); DFSTraverse(G);printf("广度优先遍历的结果:\n"); BFSTraverse(G);}五、运行结果运行结果:上一页下一页</g.vexnum;j++)<></g.vexnum;++v)<></g.vexnum;v++)<></g.vexnum;++v)<> </g.vexnum;++v)<> </g.vexnum;j++)<> </g.vexnum;j++)<> </g.vexnum;i++)<> </g.arcnum;k++)<> </g.vexnum;j++)<> </g.vexnum;i++)<> </g.vexnum;i++)<> </g.vexnum;i++)<>。
数据结构图的存贮与遍历

一、实验目的掌握图这种复杂的非线性结构的邻接矩阵和邻接表的存储表示,以及在此两种常用存储方式下深度优先遍历(DFS)和广度优先遍历(BFS)操作的实现。
二、实验内容与实验步骤题目1:对以邻接矩阵为存储结构的图进行DFS 和BFS 遍历问题描述:以邻接矩阵为图的存储结构,实现图的DFS 和BFS 遍历。
基本要求:建立一个图的邻接矩阵表示,输出顶点的一种DFS 和BFS 序列。
测试数据:如图所示题目2:对以邻接表为存储结构的图进行DFS 和BFS 遍历问题描述:以邻接表为图的存储结构,实现图的DFS 和BFS 遍历。
基本要求:建立一个图的邻接表存贮,输出顶点的一种DFS 和BFS 序列。
测试数据:如图所示三、附录:#include <stdio.h>#include <malloc.h>#include <stdlib.h>#define M 5typedef struct node⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=010*******010101000100010A{int vex[M];int edge[M][M];int n,e;}Graph;typedef struct Node{int vertex;struct Node *next;}edgenode;typedef struct{int vex;edgenode *first;}Vexnode;Graph GA;Vexnode GL[M];Graph CreateGA(){int i,j,k;printf("请输入图的顶点数n及边数e:");scanf("%d,%d",&GA.n,&GA.e);printf("请输入顶点信息:");for(i=0;i<GA.n;i++)scanf("%d",&GA.vex[i]);printf("请输入边所对应的两顶点序号:");for(k=0;k<GA.e;k++){scanf("%d,%d",&i,&j);GA.edge[i][j]=1;}return GA;}Vexnode CreateGL(){int i,j,k,n,e;edgenode *p;printf("请输入顶点数n及边数e:");scanf("%d,%d",&n,&e);printf("请输入顶点信息:");for(i=0;i<n;i++){scanf("%d",&GL[i].vex);GL[i].first=NULL;}printf("请输入边所对应的两顶点序号:");for(k=0;k<e;k++){scanf("%d,%d",&i,&j);p=(edgenode*)malloc(sizeof(edgenode));p->vertex=j;p->next=GL[i].first;GL[i].first=p;}return GL[M];}void DFS1(Graph GA,int v,int visited[]){int i;printf("%3d\n",GA.vex[v]);visited[v]=1;for(i=0;i<GA.n;i++)if(GA.edge[v][i]!=0&&visited[i]==0)DFS1(GA,i,visited);}void traver1(Graph GA){int i;static int visited[M];for(i=0;i<GA.n;i++)visited[i]=0;for(i=0;i<GA.n;i++)if(visited[i]==0)DFS1(GA,i,visited);}void BFS1(Graph GA,int v,int visited[]){ int Q[M],f,r;int i,k;f=r=-1;printf("%3d\n",GA.vex[v]); visited[v]=1;r++; Q[r]=v;while(f!=r){ f++; k=Q[f];for(i=0;i<GA.n;i++)if(GA.edge[k][i]!=0&&visited[i]==0){ printf("%3d\n",GA.vex[i]); visited[i]=1; r++; Q[r]=i; } }}void DFS2(Vexnode GL[],int v,int visited[]){ int k;edgenode *p;printf("%3d\n",GL[v].vex);visited[v]=1;p=GL[v].first;while(p!=NULL){ k=p->vertex;if(visited[k]==0)DFS2(GL,k,visited);p=p->next;}}void traver2(Vexnode GL[],int n){int i;static int visited[M];for(i=0;i<n;i++)visited[i]=0;for(i=0;i<n;i++)if(visited[i]==0)DFS2(GL,i,visited);}void BFS2(Vexnode GL[],int v,int visited[]){ int Q[M],f,r;int i,k;edgenode *p;f=r=-1;printf("%3d\n",GL[v].vex);visited[v]=1;r++; Q[r]=v;while(f!=r){ f++; k=Q[f];p=GL[k].first;while(p!=NULL){ i=p->vertex;if(visited[i]==0){ printf("%3d\n",GL[i].vex); visited[i]=1; r++; Q[r]=i; }p=p->next;}}}void GAss(){int v,j,t=1;static int visited[M];while(t){printf(" |**************操作菜单****************|\n");printf(" |***********1.创建邻接矩阵************|\n");printf(" |***********2.DFS ************|\n");printf(" |***********3.BFS ************|\n");printf(" |***********4.退出************|\n");printf("Please input a number from 1 to 4 :");scanf("%d",&j);switch(j){ case 1: CreateGA();break;case 2: traver1(GA);break;case 3: for(v=0;v<GA.n;v++)if(visited[v]==0)BFS1(GA,v,visited);break;case 4: t=0;}}}void GLss(){int j,n,v,t=1;static int visited[M];while(t){printf(" |**************操作菜单****************|\n");printf(" |***********1.创建邻接表************|\n");printf(" |***********2.DFS ************|\n");printf(" |***********3.BFS ************|\n");printf(" |***********4.退出************|\n");printf("Please input a number from 1 to 4 :");scanf("%d",&j);switch(j){ case 1: CreateGL();break;case 2: printf("请输入顶点数n:");scanf("%d",&n);traver2(GL,n);break;case 3: for(v=0;v<M;v++)if(visited[v]==0)BFS2(GL,v,visited);break;case 4: t=0;}}}void main(){int j,t=1;while(t){printf(" |**************操作菜单****************|\n");printf(" |***********1.创建邻接矩阵************|\n");printf(" |***********2.创建邻接表************|\n");printf(" |***********3.退出************|\n");printf("Please input a number from 1 to 3 :");scanf("%d",&j);switch(j){ case 1: GAss();break;case 2: GLss();break;case 3: t=0;}}}四、运行结果:五、心得体会:最后一个实验有点难啊!。
数据结构试验报告-图的基本操作

中原工学院《数据结构》实验报告学院:计算机学院专业:计算机科学与技术班级:计科112姓名:康岩岩学号:201100814220 指导老师:高艳霞2012-11-22实验五图的基本操作一、实验目的1、使学生可以巩固所学的有关图的基本知识。
2、熟练掌握图的存储结构。
3、熟练掌握图的两种遍历算法。
二、实验内容[问题描述]对给定图,实现图的深度优先遍历和广度优先遍历。
[基本要求]以邻接表为存储结构,实现连通无向图的深度优先和广度优先遍历。
以用户指定的结点为起点,分别输出每种遍历下的结点访问序列。
【测试数据】由学生依据软件工程的测试技术自己确定。
三、实验前的准备工作1、掌握图的相关概念。
2、掌握图的逻辑结构和存储结构。
3、掌握图的两种遍历算法的实现。
四、实验报告要求1、实验报告要按照实验报告格式规范书写。
2、实验上要写出多批测试数据的运行结果。
3、结合运行结果,对程序进行分析。
【设计思路】【代码整理】#include "stdafx.h"#include <iostream>#include <malloc.h>using namespace std;typedef int Status;#define OK 1#define ERROR 0#define OVERFLOW -1#define MAX_SIZE 20typedef enum{DG,DN,UDG,UDN}Kind;typedef struct ArcNode{int adjvex; //顶点位置struct ArcNode *nextarc; //下一条弧int *info; //弧信息};typedef struct{char info[10]; //顶点信息ArcNode *fistarc; //指向第一条弧}VNode,AdjList[MAX_SIZE];typedef struct{AdjList vertices;int vexnum,arcnum; //顶点数,弧数int kind; //图的种类,此为无向图}ALGraph;//这是队列的节点,仅用于广度优先搜索typedef struct Node{int num;struct Node* next;};//队列的头和尾typedef struct{Node * front;Node *rear;}PreBit;int LocateV ex(ALGraph G,char info[]);//定位顶点的位置Status addArcNode(ALGraph &G,int adjvex); //图中加入弧Status CreatGraph(ALGraph&G);//创建图的邻接表Status DFSTraverse(ALGraph G);//深度优先搜索Status BFSTraverse(ALGraph G);//广度优先搜索Status DFS(ALGraph G,int v);//深度优先搜索中的数据读取函数,用于递归bool visited[MAX_SIZE]; // 访问标志数组//初始化队列Status init_q(PreBit&P_B){P_B.front=P_B.rear=(Node*)malloc(sizeof(Node));if(!P_B.front){exit(OVERFLOW);}P_B.front->next=NULL;}//将数据入队Status en_q(PreBit & P_B,int num){Node *p=(Node*)malloc(sizeof(Node));if(!p){exit(OVERFLOW);}p->num=num;p->next=NULL;P_B.rear->next=p;P_B.rear=p;return OK;}//出队Status de_q(PreBit & P_B){if(P_B.front==P_B.rear){return ERROR;}Node* p=P_B.front->next;P_B.front->next=p->next;if(P_B.rear==p){P_B.rear=P_B.front;}free(p);return OK;}Status CreatGraph(ALGraph&G){cout<<"请输入顶点数目和弧数目"<<endl;cin>>G.vexnum>>G.arcnum;//依次输入顶点信息for(int i=0;i<G.vexnum;i++){cout<<"请输入顶点名称"<<endl;cin>>G.vertices[i].info;G.vertices[i].fistarc=NULL;}//依次输入弧信息for(int k=1;k<=G.arcnum;k++){char v1[10],v2[10]; //用于表示顶点名称的字符数组int i,j; //表示两个顶点的位置BACK: //返回点cout<<"请输入第"<<k<<"条弧的两个顶点"<<endl;cin>>v1>>v2;i=LocateV ex(G,v1); //得到顶点v1的位置j=LocateV ex(G,v2); //得到顶点v2的位置if(i==-1||j==-1){ //头信息不存在则返回重输cout<<"不存在该节点!"<<endl;goto BACK; //跳到BACK 返回点}addArcNode(G,i); //将弧的顶点信息插入表中addArcNode(G,j);}return OK;}//倒序插入弧的顶点信息Status addArcNode(ALGraph &G,int adjvex){ArcNode *p; //弧节点指针p=(ArcNode*)malloc(sizeof(ArcNode));p->adjvex=adjvex;p->nextarc=G.vertices[adjvex].fistarc;//指向头结点的第一条弧G.vertices[adjvex].fistarc=p; //头结点的第一条弧指向p,即将p作为头结点的第一条弧return OK;}//定位顶点的位置int LocateV ex(ALGraph G,char info[]){for(int i=0;i<G.vexnum;i++){if(strcmp(G.vertices[i].info,info)==0){ //头结点名称与传入的信息相等,证明该头节点存在return i; //此时返回位置}}return -1;}//深度优先搜索Status DFSTraverse(ALGraph G){for(int v=0;v<G.vexnum;v++){visited[v]=false;}char v1[10];int i;BACK:cout<<"请输入首先访问的顶点"<<endl;cin>>v1;i=LocateV ex(G,v1);if(i==-1){cout<<"不存在该节点!"<<endl;goto BACK;}DFS(G,i);return OK;}//深度优先搜索递归访问图Status DFS(ALGraph G,int v){visited[v]=true;cout<<G.vertices[v].info<<" ";//输出信息ArcNode *p;p=G.vertices[v].fistarc; //向头节点第一条while(p) //当弧存在{if(!visited[p->adjvex]){DFS(G,p->adjvex); //递归读取}p=p->nextarc;}return OK;}//广度优先搜索Status BFSTraverse(ALGraph G){for(int v=0;v<G.vexnum;v++){visited[v]=false;}char v1[10];int v;BACK:cout<<"请输入首先访问的顶点"<<endl;cin>>v1;v=LocateV ex(G,v1);if(v==-1){cout<<"不存在该节点!"<<endl;goto BACK;}PreBit P_B;init_q(P_B);ArcNode *p;visited[v]=true;cout<<G.vertices[v].info<<" ";//输出信息en_q(P_B,v); //将头位置v入队while(P_B.front!=P_B.rear){//当队列不为空时,对其进行访问int w=P_B.front->next->num;//读出顶点位置de_q(P_B);//顶点已经访问过,将其出队列p=G.vertices[w].fistarc;//得到与顶点相关的第一条弧while(p){if(!visited[p->adjvex]){en_q(P_B,p->adjvex);//将弧入队,但不读取,只是将其放在队尾}p=p->nextarc;}}return OK;}int _tmain(int argc, _TCHAR* argv[]){ALGraph G;CreatGraph(G);cout<<"深度优先搜索图:"<<endl;DFSTraverse(G);cout<<endl;cout<<"广度优先搜索图:"<<endl;BFSTraverse(G);cout<<endl;system("pause");return 0;}。
数据结构实验报告-图的遍历

数据结构实验报告实验:图的遍历一、实验目的:1、理解并掌握图的逻辑结构和物理结构——邻接矩阵、邻接表2、掌握图的构造方法3、掌握图的邻接矩阵、邻接表存储方式下基本操作的实现算法4、掌握图的深度优先遍历和广度优先原理二、实验内容:1、输入顶点数、边数、每个顶点的值以及每一条边的信息,构造一个无向图G,并用邻接矩阵存储改图。
2、输入顶点数、边数、每个顶点的值以及每一条边的信息,构造一个无向图G,并用邻接表存储该图3、深度优先遍历第一步中构造的图G,输出得到的节点序列4、广度优先遍历第一部中构造的图G,输出得到的节点序列三、实验要求:1、无向图中的相关信息要从终端以正确的方式输入;2、具体的输入和输出格式不限;3、算法要具有较好的健壮性,对错误操作要做适当处理;4、程序算法作简短的文字注释。
四、程序实现及结果:1、邻接矩阵:#include <stdio.h>#include <malloc.h>#define VERTEX_MAX 30#define MAXSIZE 20typedef struct{intarcs[VERTEX_MAX][VERTEX_MAX] ;int vexnum,arcnum;} MGraph; void creat_MGraph1(MGraph *g) { int i,j,k;int n,m;printf("请输入顶点数和边数:");scanf("%d%d",&n,&m);g->vexnum=n;g->arcnum=m;for (i=0;i<n;i++)for (j=0;j<n;j++)g->arcs[i][j]=0;while(1){printf("请输入一条边的两个顶点:\n");scanf("%d%d",&i,&j);if(i==-1 || j==-1)break;else if(i==j || i>=n || j>=n){printf("输入错误,请重新输入!\n");}else{g->arcs[i][j]=1;g->arcs[j][i]=1;}}}void printMG(MGraph *g) {int i,j;for (i=0;i<g->vexnum;i++){for (j=0;j<g->vexnum;j++)printf(" %d",g->arcs[i][j]);printf("\n");}printf("\n");}main(){int i,j;int fg;MGraph *g1;g1=(MGraph*)malloc(sizeof(MGraph));printf("1:创建无向图的邻接矩阵\n\n");creat_MGraph1(g1);printf("\n此图的邻接矩阵为:\n"); printMG(g1);}2、邻接链表:#include<stdio.h>#include<malloc.h>#define MAX_SIZE 10typedef struct node{int vertex;struct node *next;}node,adjlist[MAX_SIZE];adjlist g;int visited[MAX_SIZE+1];int que[MAX_SIZE+1];void creat(){int n,e;int i;int start,end;node *p,*q,*pp,*qq;printf("输入无向图的顶点数和边数:");scanf("%d%d",&n,&e);for(i = 1; i <= n ; i++){visited[i] = 0;g[i].vertex = i;g[i].next = NULL;}printf("依次输入边:\n");for(i = 1; i <= e ; i++){scanf("%d%d",&start,&end);p=(node *)malloc(sizeof(node));p->vertex = end;p->next = NULL;q = &g[start];while(q->next)q = q->next;q->next = p;p1=(node*)malloc(sizeof(node));p1->vertex = start;p1->next = NULL;q1 = &g[end];while(qq->next)q1 = q1->next;q1->next = p1;}}void bfs(int vi){int front,rear,v;node *p;front =0;rear = 1;visited[vi] = 1;que[0] = vi;printf("%d ",vi);while(front != rear){v = que[front];p = g[v].next;while(p){if(!visited[p->vertex]){visited[p->vertex]= 1;printf("%d",p->vertex);que[rear++] = p->vertex;}p = p->next;}front++;}}int main(){creat();bfs(1);printf("\n");return 0;}五.实验心得与体会:(1)通过这次实验,使我基本上掌握了图的存储和遍历,让我弄清楚了如何用邻接矩阵和邻接链表对图进行存储(2)深度优先遍历和广度优先遍历都有着各自的优点,通过程序逐步调试,可以慢慢的理解这两种遍历方法的内涵和巧妙之处。
数据结构课程实验(图的存储与遍历)

实验五图的存储与遍历1、实验目的掌握图这种复杂的非线性结构的邻接矩阵和邻接表的存储表示,以及在此两种常用存储方式下深度优先遍历(dfs)和广度优先遍历(BFS)操作的实现。
2、实验预备知识(1)图的存储结构:邻接矩阵表示法和邻接表表示法。
邻接矩阵表示法除了要用一个二维数组存储用于表示顶点间相邻关系的邻接矩阵外,还需用一个一维数组来存储顶点信息,另外还有图的顶点数和边数。
邻接表表示法类似于树的孩子链表表示法。
(2)图的遍历方法有深度优先遍历(Depth-First Traersal)和广度优先遍历(Breadth-First Traversal),简称 DFS和BFS。
DFS对图遍历时尽可能先对纵深方向进行搜索;BFS是类似于树的按层次遍历。
3、实验内容题目1对以邻接矩阵为存储结构的图进行 DFS和 BFS遍历(1) 问题描述:以邻接矩阵为图的存储结构,实现图的DFS和BFS遍历。
(2) 基本要求:建立一个图的邻接矩阵表示,输出顶点的一种DFS和BFS序列。
(3) 测试数据:如图4.18所示。
(4) 实现提示:图的DFS遍历可通过递归调用或用栈来实现。
其思想是:只要当前结点未访问过,就访问该结点,沿着其一条分支深入下去,每深入一个未访问过的结点,就访问这个结点,然后从这个结点继续进行DFS遍历。
在这一过程中,若深入时遇到一个已访问过的结点,则查找是否有与这个结点相邻的下一个未访问过的结点。
若有则继续深人,否则将退回到这个结点的前一个结点,再找下一个相邻的本访问过的结点,……如此进行下去,直到所有的结点都被访问过。
BFS遍历可利用队列来帮助实现,也可以用栈。
实现方法与二叉树的层次遍历类似。
题目2对以邻接表为存储结构的图进行DFS和BFS遍历(1) 问题描述:以邻接表为存储结构,实现图的DFS和BFS遍历。
(2) 基本要求:建立一个图的邻接表存储,输出顶点的一种DFS和BFS序列。
(3) 测试数据:如图4.19所示:(4) 实现提示:以邻接表为存储结构的图的DFS和BFS算法的实现思想与以邻接矩阵为存储结构的实现是一样的。
数据结构实训实验报告

一、实验背景数据结构是计算机科学中一个重要的基础学科,它研究如何有效地组织和存储数据,并实现对数据的检索、插入、删除等操作。
为了更好地理解数据结构的概念和原理,我们进行了一次数据结构实训实验,通过实际操作来加深对数据结构的认识。
二、实验目的1. 掌握常见数据结构(如线性表、栈、队列、树、图等)的定义、特点及操作方法。
2. 熟练运用数据结构解决实际问题,提高算法设计能力。
3. 培养团队合作精神,提高实验报告撰写能力。
三、实验内容本次实验主要包括以下内容:1. 线性表(1)实现线性表的顺序存储和链式存储。
(2)实现线性表的插入、删除、查找等操作。
2. 栈与队列(1)实现栈的顺序存储和链式存储。
(2)实现栈的入栈、出栈、判断栈空等操作。
(3)实现队列的顺序存储和链式存储。
(4)实现队列的入队、出队、判断队空等操作。
3. 树与图(1)实现二叉树的顺序存储和链式存储。
(2)实现二叉树的遍历、查找、插入、删除等操作。
(3)实现图的邻接矩阵和邻接表存储。
(4)实现图的深度优先遍历和广度优先遍历。
4. 算法设计与应用(1)实现冒泡排序、选择排序、插入排序等基本排序算法。
(2)实现二分查找算法。
(3)设计并实现一个简单的学生成绩管理系统。
四、实验步骤1. 熟悉实验要求,明确实验目的和内容。
2. 编写代码实现实验内容,对每个数据结构进行测试。
3. 对实验结果进行分析,总结实验过程中的问题和经验。
4. 撰写实验报告,包括实验目的、内容、步骤、结果分析等。
五、实验结果与分析1. 线性表(1)顺序存储的线性表实现简单,但插入和删除操作效率较低。
(2)链式存储的线性表插入和删除操作效率较高,但存储空间占用较大。
2. 栈与队列(1)栈和队列的顺序存储和链式存储实现简单,但顺序存储空间利用率较低。
(2)栈和队列的入栈、出队、判断空等操作实现简单,但需要考虑数据结构的边界条件。
3. 树与图(1)二叉树和图的存储结构实现复杂,但能够有效地表示和处理数据。
数据结构与算法实验报告图的深度优先与广度优先遍历
w=NextAdj(g,v);
}
}
}
void Travel_BFS(源自Node g[],int visited[],int n){
int i;
for(i=0;i<n;i++){
visited[i]=0;
}
for(i=0;i<n;i++){
if(visited[i]==0)
BFS(g,i,visited);
vertexType data;
Arcnode *firstarc;
}VNode;
irstarc=NULL;
}
for(i=0;i<n;i++){
printf("create the edges for the %dth vertex\n",i);
scanf("%d",&e);
while(e!=-1){
二、实验题目与要求
图的遍历
利用邻接矩阵或邻接表作为存储结构建立一个无向图,每个顶点中存放一种水果名(例如apple、orange、banana等,并要求从键盘输入),顶点数不少于5个。要求分别以深度优先搜索(DFS)和广度优先搜索(BFS)进行遍历,输出遍历结果。
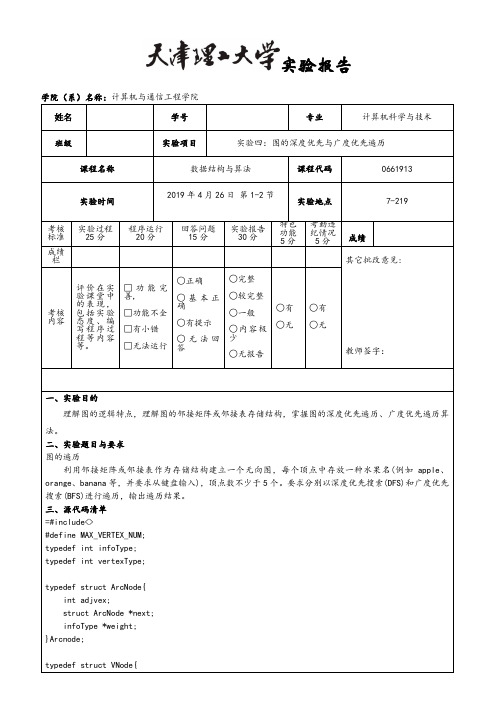
3、源代码清单
=#include<>
p=(Arcnode *)malloc(sizeof(Arcnode));
p->next=NULL;
p->adjvex=e;
if(G[i].firstarc==NULL){
G[i].firstarc=p;
}else{
q->next=p;
}
q=p;
邻接矩阵的深度优先遍历算法

邻接矩阵的深度优先遍历算法简介邻接矩阵是一种常用的图表示方法,它使用一个二维数组来表示图中各个节点之间的关系。
深度优先遍历(Depth First Search,DFS)是一种常用的图遍历算法,它通过递归或栈的方式依次访问图中的所有节点。
本文将介绍邻接矩阵的深度优先遍历算法,并提供相应的代码实现。
邻接矩阵邻接矩阵是一种二维数组,它的行和列分别代表图中的各个节点。
如果两个节点之间存在边,则对应位置上的元素为1;否则为0。
对于无向图来说,邻接矩阵是对称的;而对于有向图来说,邻接矩阵不一定对称。
下面是一个示例的邻接矩阵:A B C DA 0 1 0 1B 1 0 1 1C 0 1 0 0D 1 1 0 0深度优先遍历算法算法思想深度优先遍历算法从起始节点开始,递归或使用栈的方式依次访问与当前节点相邻的未访问过的节点,直到所有节点都被访问过为止。
算法步骤1.创建一个栈,并将起始节点入栈;2.创建一个数组,用于记录已经访问过的节点;3.当栈不为空时,执行以下操作:–从栈顶弹出一个节点,标记为已访问,并输出该节点;–遍历该节点的邻居节点,如果邻居节点未被访问,则将其入栈;4.重复步骤3,直到栈为空。
算法实现def dfs(adj_matrix, start_node):stack = [start_node]visited = [False] * len(adj_matrix)while stack:node = stack.pop()visited[node] = Trueprint(node)for i in range(len(adj_matrix)):if adj_matrix[node][i] == 1 and not visited[i]:stack.append(i)示例假设有以下图的邻接矩阵:A B C DA 0 1 0 1B 1 0 1 1C 0 1 0 0D 1 1 0我们以A作为起始节点进行深度优先遍历,那么遍历的顺序将会是A、B、C、D。
图的深度和广度优先遍历

数据结构课程实验报告课程名称数据结构班级计算123 实验日期2014年6月1日--3日姓名学号实验成绩实验名称实验四图的深度和广度优先遍历实验目的及要求【实验目的】熟练掌握图的邻接表存储结构及其图的建立方法和深度和广度优先遍历的方法。
【实验要求】1.图的存储可采用邻接矩阵或邻接表2.GraphCreate(): 按从键盘的数据建立图3.GraphDFS():深度优先遍历图4.GraphBFS():广度优先遍历图5.编写完整程序完成下面的实验内容并上机运行6.整理并上交实验报告实验环境硬件平台:普通的PC机软件平台:Windows 7 操作系统编程环境:VisualC++ 6.0实验内容1.以邻接矩阵或邻接表为存储结构,以用户指定的顶点为起始点,实现图的深度优先及广度优先搜索遍历,并输出遍历的结点序列。
算法描述及实验步骤算法:1)定义图的邻接表存储结构2)实现图的邻接表存储,即建立图的存储结构3)实现图的深度优先遍历4)定义队列的顺序存储结构,并实现队列的基本操作如初始化队列、入队、出对、判断队列是否为空等。
利用队列实现图的广度优先遍历。
伪代码:1)定义邻接矩阵和队列的存取结构;2)创建图L:1.置空图L->num=0;2.输入顶点数目num;3.i++,输入结点L->vexs[i]直到L->num;3)输出图L的各顶点;4)深度优先遍历图g中能访问的各个顶点1.输入起点的下标qidian;2.标志数组初始化mark[v]=0;3.for(v=qidian;v<g.num+qidian;v++) //{v1=v%g.num;if(mark[v1]==0)DFS(g,v1,mark); //从第v1个点出发深度优先遍历图g中能访问的各个顶点(算法描述里的流程图很详细)}5)广度优先周游图g中能访问的各个顶点。
1.构造空队列;2.入队a[0];3.a[0]出队,a[0]的邻接点入队,遍历a[0];4.队首出队,重复3直到队列为空;5.判断是否全遍历完了;6.输出广度优先遍历序列流程图:开始访问V 0,置标志求V 0邻接点有邻接点w求下一邻接点w V 0W 访问过结束NYN YDFS开始标志数组初始化V i =1Vi 访问过DFSV i =V i +1V i ==Vexnums结束NNYY调试过程及实验结果总结本次试验采用的是邻接表的方式实现图的深度优先遍历和广度优先遍历。
邻接矩阵和邻接表 深度遍历和广度遍历原理

邻接矩阵和邻接表是图论中用于表示图结构的两种常见方式,而深度遍历和广度遍历则是图论中常用的两种图遍历算法。
本文将从简介、原理和应用三个方面探讨这四个主题。
一、邻接矩阵和邻接表1.邻接矩阵邻接矩阵是一种使用二维数组来表示图中顶点之间关系的方法。
如果图中有n个顶点,那么对应的邻接矩阵就是一个n*n的矩阵,其中元素a[i][j]表示顶点i和顶点j之间是否有边,通常用0和1表示。
邻接矩阵适用于稠密图,其存储结构简单,可以直观地展示图的结构,但对于稀疏图来说可能会造成存储空间的浪费。
2.邻接表邻接表是一种使用链表来表示图中顶点之间关系的方法。
对于图中的每一个顶点,都维护一个相邻顶点的列表,图中所有顶点的列表再组合成一个链表,用于表示整个图的结构。
邻接表适用于稀疏图,其存储结构灵活,可以有效地节省存储空间,但查找任意两个顶点之间的关系可能会比较耗时。
二、深度遍历和广度遍历原理1.深度遍历深度遍历是一种用于遍历或搜索图中节点的算法,其原理是从图的某一顶点出发,沿着一条路径不断向下遍历直到末端,然后回溯到上一个节点继续遍历。
深度遍历使用栈来实现,可以通过递归或迭代来进行。
2.广度遍历广度遍历是一种用于遍历或搜索图中节点的算法,其原理是从图的某一顶点出发,依次访问其所有相邻节点,然后再依次访问这些相邻节点的相邻节点,以此类推。
广度遍历使用队列来实现。
三、深度遍历和广度遍历的应用1.深度遍历的应用深度遍历常用于求解图的连通分量、拓扑排序、解决迷宫问题等。
在连通分量中,深度遍历可以帮助我们找到图中的所有连通分量,并对其进行标记,用于进一步的算法运算。
在拓扑排序中,深度遍历可以帮助我们找到一个合理的顺序,用以处理依赖关系问题。
在解决迷宫问题时,深度遍历可以帮助我们找到一条从起点到终点的路径。
2.广度遍历的应用广度遍历常用于求解最短路径、解决迷宫问题等。
在求解最短路径中,广度遍历可以帮助我们找到起点到终点的最短路径,从而解决了许多实际问题。
图的遍历(深度优先遍历和广度优先遍历)

遍历规则 从图中某结点v0出发,深度优先遍历(DFS: Depth First Search)图的规则为: 访问v0; 对v0的各个出点v01,v02,…,v0m,每次从它们中按一定方式(也可任选)选取一个未被访问过的结点,从该结点出发按深度优先遍历方式遍历。 然,因为我们没有规定对出点的遍历次序,所以,图的深度优先遍历结果一般不唯一。
20.2 深度优先遍历
例如,对图 20‑1给出的有向图与无向图,一些遍历结果(结点访问次序)为: 左图:从1出发:1,2,4,5;或1,5,2,4 从2出发:2,1,5,4;或2,4,1,5 右图:从a出发:a,b,c,d;或a,b,d,c; … …
A 如果不想让visited或top做为函数参数,也可以在函数中将其定义为static型量。但是,这样的程序是不可再入的,即函数再次被调用时,static型的量也不重新初始化,造成错误!
上面函数中的参数visited和top实质上是中间变量,只是为了避免在递归调用时重新初始化而放在参数表中,造成使用的不方便,为此,做个包装程序: long DFS1(int g[][CNST_NumNodes], long n, long v0, long *resu ) { char *visited; long top=0; visited = new char[n]; for (long i=0; i<n; i++) visited[i]=0; long num=DFS1( g, n, v0, visited, resu, top ); delete visited; return num; }
深度优先遍历非递归算法的一般性描述。
long DFS_NR(图g,结点v0)
单击此处可添加副标题
邻接矩阵的深度优先遍历算法

邻接矩阵的深度优先遍历算法简介邻接矩阵是一种常见的图存储结构,它使用二维数组来表示图中各个顶点之间的关系。
而深度优先遍历算法是一种常用的图遍历算法,用于遍历和搜索图的各个顶点。
本文将介绍邻接矩阵的深度优先遍历算法,包括其基本思想、实现步骤以及应用场景等内容。
基本思想深度优先遍历算法(Depth-First Search,DFS)是一种针对图和树的遍历算法,它通过从起始顶点开始,逐个探索图中的顶点,并沿着某一条路径一直深入,直到无法继续为止,然后回溯到前一顶点继续探索其它路径,直到所有顶点都被访问过为止。
邻接矩阵是一种常见的图表示方法,它通过一个二维数组来表示图中各个顶点之间的关系。
邻接矩阵中的每个元素表示两个顶点之间是否存在一条边,具体而言,如果顶点i和顶点j之间存在一条边,则邻接矩阵中下标为(i, j)和(j, i)的元素值为1;否则,它们的元素值为0。
邻接矩阵的深度优先遍历算法是通过对邻接矩阵进行遍历,找出与起始顶点相连接的顶点,并依次对这些顶点进行深度优先遍历。
实现步骤邻接矩阵的深度优先遍历算法可以使用递归或迭代的方式来实现。
下面分别介绍这两种实现方法的具体步骤。
递归实现1.创建一个数组visited,用来记录每个顶点是否已被访问过,初始时所有元素都设为0。
2.选择一个起始顶点v,并将visited[v]设置为1,表示该顶点已被访问过。
3.遍历邻接矩阵中与v相连的所有顶点w,如果visited[w]为0,则递归调用深度优先遍历函数,将w作为新的起始顶点。
4.重复步骤3,直到所有顶点都被访问过为止。
迭代实现1.创建一个数组visited,用来记录每个顶点是否已被访问过,初始时所有元素都设为0。
2.创建一个栈,用来存储待访问的顶点。
3.选择一个起始顶点v,并将visited[v]设置为1,表示该顶点已被访问过。
4.将v入栈。
5.当栈不为空时,执行以下操作:–出栈一个顶点u,访问它。
–遍历邻接矩阵中与u相连的所有顶点w,如果visited[w]为0,则将w入栈,并将visited[w]设置为1。
基于java数据结构实验 基于邻接矩阵和邻接表的深度广度优先遍历图

基于邻接表:基于基于邻接矩阵:实验总结(结论或问题分析):通过这次实验,我掌握了无向图的建立,一种基于邻接表,一种基于邻接矩阵,然后分别实现深度广度优先遍历。
广度优先遍历类似于数的层序遍历,它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域。
深度优先遍历是从图的某个顶点出发,访问这个顶点,然后从v的没访问过的邻接点出发深度优先遍历图,直到图中所有和v有路径相通的顶点都被访问到。
实验成绩任课教师签名附:源程序:参考:基于邻接表的深度广度遍历package graph;import java.util.*;public class ALgraph{static class Vertex<T> {private T date;private Edge frist;public T getDate() {return date;}public void setDate(T date) {this.date = date;}public Edge getFrist() {return frist;}public void setFrist(Edge frist) {this.frist = frist;}}static class Edge {private int vertexIndex;private Edge next;public int getVertexIndex() {return vertexIndex;}public void setVertexIndex(int vertexIndex) {this.vertexIndex = vertexIndex;}public Edge getNext() {//System.out.println(next);if(next==null){return null;}return next;}public void setNext(Edge next) {this.next = next;}}public static Vertex[] set(int x,int y){//参考输入数据 1 2 3 4 5//1 3 1 2 1 4 1 5 2 5 2 4Scanner sc=new Scanner(System.in);Vertex[]arr=new Vertex[x];Vertex<String> v=null;System.out.println("请依次输入顶点的信息空格分开");for(int i=0;i<x;i++){String str=sc.next();v=new Vertex<String>();v.setDate(str);v.setFrist(null);arr[i]=v;}System.out.println("请依次输入边的信息空格分开 (根据你输入的顶点信息来)");Edge e=null;int str1,str2;//System.out.println(y);for(int j=0;j<y;j++){str1=sc.nextInt();str2=sc.nextInt();//System.out.println("str1:"+str1+"str2:"+str2);e=new Edge();e.setVertexIndex(str2-1);if(arr[str1-1].getFrist()==null){arr[str1-1].setFrist(e);}else{Edge e2=arr[str1-1].getFrist();while(e2.getNext()!=null){e2=e2.getNext();}//System.out.println(e.getVertexIndex());e2.setNext(e);}}return arr;}public static void dfs(Vertex[] arr) {boolean[] b = new boolean[arr.length];System.out.println();for (int j = 0, len = arr.length; j < len; j++) { //如果这个顶点没有被访问过;if (!b[j]) {fun(arr, j, b);}}System.out.println();}private static void fun(Vertex[] arr,int i,boolean[] b){ b[i]=true;//System.out.println(i);System.out.print(arr[i].getDate()+"\t");Edge e=arr[i].getFrist();while(e!=null){//对i的第一条边的顶点进行访问if(!b[e.getVertexIndex()]){fun(arr, e.getVertexIndex(), b);}e=arr[e.getVertexIndex()].getFrist();// if(b[e.getVertexIndex()]){// break;// }}e=arr[i].getFrist();if(e!=null&&e.getNext()!=null){ //对i坐标的顶点剩下的顶点进行访问e=e.getNext();}//1 2 1 3 2 4 3 5 5 4 4 6 6 7 7 5while(e!=null){if(!b[e.getVertexIndex()]){fun(arr, e.getVertexIndex(), b);}e=e.getNext();if(e==null||b[e.getVertexIndex()]){break;}}return;}public static void bfs(Vertex[] arr) {Queue<Vertex<String>> q = new LinkedList<Vertex<String>>();boolean[] b = new boolean[arr.length];for (int i = 0, len = arr.length; i < len; i++) {//如果该顶点没被访问过if (!b[i]) {System.out.print(arr[i].getDate()+"\t");b[i] = true;//将该顶点入队列q.add(arr[i]);//如果队列不是空while (!q.isEmpty()) {//v等于出队的顶点Vertex<String>v= q.poll();//e等于v的第一条连接的边Edge e = v.getFrist();//如果e不是空while (e != null) {//如果e所连接的顶点没被访问过if(!b[e.getVertexIndex()]){//该顶点入队q.add(arr[e.getVertexIndex()]);//输出该顶点的值System.out.print(arr[e.getVertexIndex()].getDate()+"\t");b[e.getVertexIndex()]=true;}//寻找改顶点的下一条边e=e.getNext();}}}}System.out.println();}public static void main(String[] args) {Vertex<Integer>[]arr=set(6, 6);System.out.println();System.out.println("深度优先遍历");dfs(arr);System.out.println("宽度优先遍历");bfs(arr);}}基于邻接矩阵:package graph;import java.util.*;public class Matrixgraph {private int[][] edges;private int num;//图的结点数量private boolean[] visited ;//结点是否被访问过private Vertex[] vertex ;private int pre;//用来记录前一个public void createGraph(){Scanner in = new Scanner(System.in);System.out.print("please input the info:");String str = in.next();String[] temp = str.split(",");System.out.print(temp.length);this.num = temp.length;System.out.print(num);visited = new boolean[num];vertex = new Vertex[num];for(int i=0;i<num;i++){Vertex v = new Vertex(i,temp[i]);vertex[i]=v;visit(vertex[i]);System.out.println();}edges = new int[num][num];for(int i=0;i<num;i++){for(int j=0;j<num;j++){Scanner in1 = new Scanner(System.in);System.out.print("input the value:");int k = in1.nextInt();/* System.out.print(k);*/edges[i][j] =k;}}}public void visit(Vertex v){if(v!=null){System.out.print( v.no+" "+);System.out.println();}}public void dFS(int i){visit(vertex[i]);visited[i]=true;for(int j=i+1;j<num;j++){if(!visited[j]&&edges[i][j]!=0){dFS(j);} } }public void dFSTrave(){//深度遍历是在邻接矩阵的基础上进行的for(int i=0;i<num;i++){visited[i]=false;//默认情况下所有顶点是没有被访问过的}for(int i=0;i<num;i++){if(!visited[i]){//还需要考虑一个条件就是必须可达dFS(i);}}}public void bFSTrave(){for(int i=0;i<num;i++){visited[i]=false;//默认情况下所有顶点是没有被访问过的}Vertex v=null;Queue queue = new LinkedList();for(int i=0;i<num;i++){if(!visited[i]){visit(vertex[i]);visited[i]=true;//访问完成后入队queue.add( vertex[i]);while(!queue.isEmpty()){v = (Vertex) queue.poll();if(v!=null){int k = v.no;for(int j=k+1;j<num;j++){if(!visited[j]&&edges[k][j]!=0){visit(vertex[j]);visited[j]=true;queue.add( vertex[j]);}}}}}}}public static void main(String[] args) {Matrixgraph graph = new Matrixgraph();graph.createGraph();graph.dFSTrave();// graph.bFSTrave();}class Vertex {//图的顶点信息public int no;//顶点的标号public String info;//顶点的信息public Vertex(int i,String info){this.no = i; = info;}}}参考程序1:public class Graph {private int[] vertexs;private int vertexsize;private int[][] matrix;private boolean[] isvisited;private static final int MAX_WEIGHT=1000;public Graph(int vertexsize){this.vertexsize=vertexsize;matrix=new int[vertexsize][vertexsize];vertexs=new int[vertexsize];for(int i=0;i<vertexsize;i++){vertexs[i]=i;}isvisited=new boolean[vertexsize];}public int[] getVertexs() {return vertexs;}public void setVertexs(int[] vertexs) {this.vertexs = vertexs;}public int getweight(int v1,int v2){return matrix[v1][v2]==0?0:(matrix[v1][v2]==MAX_WEIGHT?-1:matrix[v1][v2]); }public int getdegree(int index){int degree=0;for(int j=0;j<matrix[index].length;j++){int weight=matrix[index][j];if(weight!=0&&weight!=MAX_WEIGHT){degree++;}}return degree;}//找某个顶点的第一个邻接点public int getfirstadj(int index){for(int j=0;j<vertexsize;j++){if(matrix[index][j]>0&&matrix[index][j]<MAX_WEIGHT){return j;}}return -1;}public int getnextadj(int v,int index){for(int j=index+1;j<vertexsize;j++){if(matrix[v][j]>0&&matrix[v][j]<MAX_WEIGHT){return j;}}return -1;}public void depthfirstsearch(int i){isvisited[i]=true;int w=getfirstadj(i);while(w!=-1){if(!isvisited[w]){System.out.println("访问"+w+"顶点");depthfirstsearch(w);}w=getnextadj(i,w);}}public void depthfirstsearch(){}public static void main(String[] args) {Graph graph=new Graph(5);int [] a1=new int[]{0,45,28,10,MAX_WEIGHT};int [] a2=new int[]{45,0,12,MAX_WEIGHT,21};int [] a3=new int[]{28,12,0,17,26};int [] a4=new int[]{10,MAX_WEIGHT,17,0,15};int [] a5=new int[]{MAX_WEIGHT,21,26,15,0};graph.matrix[0]=a1;graph.matrix[1]=a2;graph.matrix[2]=a3;graph.matrix[3]=a4;graph.matrix[4]=a5;//System.out.println("权值"+graph.getweight(0, 3));//System.out.println("v0的度:"+graph.getdegree(2));graph.depthfirstsearch();}}。
数据结构图实验报告

数据结构图实验报告一、实验目的本次实验的主要目的是深入理解和掌握数据结构图的基本概念、原理和操作方法,通过实际编程和操作,提高对数据结构的应用能力和解决问题的能力。
二、实验环境本次实验使用的编程语言为C++,开发环境为Visual Studio 2019。
三、实验内容(一)线性表1、顺序表实现顺序表的创建、插入、删除、查找等基本操作。
分析顺序表在不同操作下的时间复杂度。
2、链表实现单链表、双向链表的创建、插入、删除、查找等基本操作。
比较单链表和双向链表在操作上的优缺点。
(二)栈和队列1、栈实现顺序栈和链式栈。
用栈解决表达式求值问题。
2、队列实现顺序队列和链式队列。
用队列模拟银行排队问题。
(三)树1、二叉树实现二叉树的创建、遍历(前序、中序、后序)。
计算二叉树的深度和节点数。
2、二叉搜索树实现二叉搜索树的插入、删除、查找操作。
分析二叉搜索树的性能。
(四)图1、图的存储实现邻接矩阵和邻接表两种图的存储方式。
比较两种存储方式的优缺点。
2、图的遍历实现深度优先遍历和广度优先遍历算法。
用图的遍历解决最短路径问题。
四、实验步骤(一)线性表1、顺序表定义一个数组来存储顺序表的元素,并使用一个变量记录当前表的长度。
插入操作时,需要判断插入位置是否合法,如果合法则将插入位置后的元素依次向后移动一位,然后将新元素插入指定位置。
删除操作时,先判断删除位置是否合法,合法则将删除位置后的元素依次向前移动一位,并更新表的长度。
查找操作通过遍历数组来实现。
分析不同操作的时间复杂度,插入和删除操作在最坏情况下为O(n),查找操作在平均情况下为 O(n/2)。
2、链表对于单链表,定义一个节点结构体,包含数据域和指向下一个节点的指针域。
通过操作指针来实现插入、删除和查找操作。
双向链表则在节点结构体中增加指向前一个节点的指针,使得操作更加灵活,但也增加了空间复杂度。
比较单链表和双向链表在插入、删除操作中指针的调整过程,得出双向链表在某些情况下更方便,但空间开销较大的结论。
基于邻接矩阵存储的图的深度优先遍历和广度优先遍历

基于邻接矩阵存储的图的深度优先遍历和⼴度优先遍历图的存储结构相⽐较线性表与树来说就复杂很多,对于线性表来说,是⼀对⼀的关系,所以⽤数组或者链表均可简单存放。
树结构是⼀对多的关系,所以我们要将数组和链表的特性结合在⼀起才能更好的存放。
那么我们的图,是多对多的情况,另外图上的任何⼀个顶点都可以被看作是第⼀个顶点,任⼀顶点的邻接点之间也不存在次序关系。
仔细观察以下⼏张图,然后深刻领悟⼀下:因为任意两个顶点之间都可能存在联系,因此⽆法以数据元素在内存中的物理位置来表⽰元素之间的关系(内存物理位置是线性的,图的元素关系是平⾯的)。
如果⽤多重链表来描述倒是可以做到,但在⼏节课前的树章节我们已经讨论过,纯粹⽤多重链表导致的浪费是⽆法想像的(如果各个顶点的度数相差太⼤,就会造成巨⼤的浪费)。
邻接矩阵(⽆向图)考虑到图是由顶点和边或弧两部分组成,合在⼀起⽐较困难,那就很⾃然地考虑到分为两个结构来分别存储。
顶点因为不区分⼤⼩、主次,所以⽤⼀个⼀维数组来存储是狠不错的选择。
⽽边或弧由于是顶点与顶点之间的关系,⼀维数组肯定就搞不定了,那我们不妨考虑⽤⼀个⼆维数组来存储。
图的邻接矩阵(Adjacency Matrix)存储⽅式是⽤两个数组来表⽰图。
⼀个⼀维数组存储图中顶点信息,⼀个⼆维数组(称为邻接矩阵)存储图中的边或弧的信息。
我们可以设置两个数组,顶点数组为vertex[4]={V0,V1,V2,V3},边数组arc[4][4]为对称矩阵(0表⽰不存在顶点间的边,1表⽰顶点间存在边)。
对称矩阵:所谓对称矩阵就是n阶矩阵的元满⾜a[i][j]=a[j][i](0<=i,j<=n)。
即从矩阵的左上⾓到右下⾓的主对⾓线为轴,右上⾓的元与左下⾓相对应的元全都是相等的。
有了这个⼆维数组组成的对称矩阵,我们就可以很容易地知道图中的信息:1. 要判定任意两顶点是否有边⽆边就⾮常容易了;2. 要知道某个顶点的度,其实就是这个顶点Vi在邻接矩阵中第i⾏(或第i列)的元素之和;3. 求顶点Vi的所有邻接点就是将矩阵中第i⾏元素扫描⼀遍,arc[i][j]为1就是邻接点咯。
2-深度优先遍历以邻接表存储的图-实验报告

《数据结构与关系数据库(本科)》实验报告姓名班级学号实验日期课程名称数据结构与关系数据库(本科)指导教师成绩实验名称:深度优先遍历以邻接表存储的图一、实验目的1、掌握以邻接表存储的图的深度优先遍历算法;二、实验环境1、硬件环境:微机2、软件环境:Windows XP,VC6.0三、实验内容、步骤及结果1、实验内容:基于图的深度优先遍历编写一个算法,判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i≠j)。
2、代码:#include <stdio.h>#include <stdlib.h>#define MaxVertexNum 100 /*最大顶点数为100*/typedef char VertexType;typedef struct node{ /*边表结点*/int adjvex; /*邻接点域*/struct node * next; /*指向下一个邻接点的指针域*//*若要表示边上信息,则应增加一个数据域info*/}EdgeNode;typedef struct vnode{ /*顶点表结点*/VertexType vertex; /*顶点域*/EdgeNode * firstedge; /*边表头指针*/}VertexNode;typedef VertexNode AdjList[MaxVertexNum]; /*AdjList 是邻接表类型*/typedef struct{AdjList adjlist; /*邻接表*/int n,e; /*顶点数和边数*/}ALGraph; /*ALGraph 是以邻接表方式存储的图类型*/bool visited[MaxVertexNum];void CreateTestALGraph(ALGraph *G){/*建立有向图的邻接表存储*/int i,j;EdgeNode * s;G->n=8;G->e=9;for (i=0;i<G->n;i++) /*建立有n 个顶点的顶点表*/{G->adjlist[i].vertex='1'+i;//转换为字符型G->adjlist[i].firstedge=NULL; /*顶点的边表头指针设为空*/}{i=0,j=1;s=(EdgeNode*)malloc(sizeof(EdgeNode)); /*生成新边表结点s*/s->adjvex=j; /*邻接点序号为j*/s->next=G->adjlist[i].firstedge; /*将新边表结点s 插入到顶点Vi 的边表头部*/ G->adjlist[i].firstedge=s;i=0,j=2;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; ///*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=1,j=3;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=1,j=4;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=2,j=0;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=2,j=6;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=3,j=4;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;i=4,j=3;s=(EdgeNode*)malloc(sizeof(EdgeNode)); //*生成新边表结点ss->adjvex=j; //*邻接点序号为js->next=G->adjlist[i].firstedge; //*将新边表结点s 插入到顶点Vi 的边表头部G->adjlist[i].firstedge=s;}///*CreateALGraph}void DFSTraverseAL(ALGraph *G){/*深度优先遍历以邻接表存储的图G*/int i;for (i=0;i<G->n;i++)visited[i]=false; /*标志向量初始化*/for (i=0;i<G->n;i++)if (!visited[i]) DFSAL(G,i); /*vi 未访问过,从vi 开始DFS 搜索*/ }/*DFSTraveseAL*///int level=1;//递归进行的层数int exist_path_DFS(ALGraph *G,int i,int j)//深度优先判断有向图G中顶点i到顶点j是否有路径,是则返回1,否则返回0{EdgeNode *p;int k;if(i==j) return 1; //i就是jelse{visited[i]=true;//for(p=G->adjlist[i].firstedge;p;p=p->next,level--)for(p=G->adjlist[i].firstedge;p;p=p->next){//level++;k=p->adjvex;if(!visited[k] && exist_path_DFS(G,k,j)){printf("V%d ",k+1);return 1;//i下游的顶点到j有路径}}//forreturn 0;}//else//if (level==1) return 0;}//exist_path_DFSvoid main(){ALGraph *G;G=(ALGraph *)malloc(sizeof(ALGraph));CreateTestALGraph(G);int i,j;printf("请输入i和j的值格式:i,j\n");scanf("%d,%d",&i,&j);i=i-1;j=j-1;if(i==j){printf("i不能等于j\n");}else{if(exist_path_DFS(G,i,j)){printf("该路径存在。
图的深度和广度遍历-实验报告

实验报告一、实验目的和内容1. 实验目的掌握图的邻接矩阵的存储结构;实现图的两种遍历:深度优先遍历和广度优先遍历。
2. 实验内容1.图的初始化; 2.图的遍历:深度优先遍历和广度优先遍历。
二、实验方案程序主要代码:/// <summary>/// 邻接矩阵的节点数据/// </summary>public struct ArcCell{public int Type; // 顶点的关系类型,对无权图,用 1或0表示相邻;// 对带权图,则为权值类型。
public object Data; // 该弧相关信息public ArcCell( int type, object data){Type = type;Data = data;}}/// <summary>/// 图的类型/// </summary>public enumGKind {DG,DN,UDG,UDN}; // 有向图,有向网,无向图,无向/// <summary>/// 图类/// </summary>public class Graph{public static int Max_Vertex_Num = 20; // 最大顶点数private object [] Vexs; // 顶点数据数组private ArcCell [,] Arcs; // 邻接矩阵private GKind Kind; // 图的种类private int VexNum,ArcNum; // 当前顶点数和弧数/// <summary>/// 图的初始化方法/// </summary>Ill VParam n ame="vex num">顶点数v∕param>III VParam n ame="arc num">弧数<∕param>Ill VParam name="k">图的类型<∕param> public Graph( int vexnum,int arcnum,GKind k) {VexNum = vexnum;ArcNum = arcnum;Kind = k;Vexs = new object [Max_Vertex_Num];Arcs = newArcCell[Max_Vertex_Num,Max_Vertex_Num];}III Vsummary>III设置v1, v2之间的弧的权值,顶点的关系类型,对无权图,用表示相邻;III 对带权图,则为权值类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:以实验3.1所示邻接矩阵为存储结构,编写程序,实现图的深度、宽度优先遍历。
部分代码:邻接矩阵的单一顶点DFS://邻接矩阵的单一顶点DFSvoid DFS(int v,int visited[],mGraph g){int j;printf("%d ",v); //访问顶点vvisited[v] = 1; //为顶点v打上访问标记for(j = 0;j < g.n; j++){ //遍历v的邻接点if(!visited[j] && g.a[v][j] > 0){ //当未被访问且有权值DFS(j,visited,g);}}}邻接矩阵的全图DFS://邻接矩阵的全图DFSvoid DFSGraph(mGraph g){int i;int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成标记数组vistedfor(i = 0;i < g.n;i ++){visited[i] = 0; //visted数组初始化} //visted数组初始化for(i = 0;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用DFS if(!visited[i]){ //当未被访问且有权值DFS(i,visited,g);}}free(visited); //释放visted数组}邻接矩阵的单一顶点BFS://邻接矩阵的单一顶点BFSvoid BFS(int v,int visited[],mGraph g){Queue q;Create(&q,g.n); //初始化队列visited[v] = 1; //为顶点v打上访问标记printf("%d ",v); //访问顶点vEnQueue(&q,v); //将顶点v放入队列while(!IsEmpty(&q)){Front(&q,&v);DeQueue(&q); //队首顶点出队列for(int i = 0;i < g.n;i ++){ //遍历v的每一项if(!visited[i] && g.a[v][i] > 0){ //若未被访问且有权值,则将其访问并放入队列,注意这里判断的是g.a[v][i]二维数组visited[i] = 1;printf("%d ",i);EnQueue(&q,i);}}}}邻接矩阵的全图BFS://邻接矩阵的全图BFSvoid BFSGraph(mGraph g){int i;int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成visited数组for(i = 0;i < g.n;i ++){ //初始化visited数组visited[i] = 0;}for(i = 0 ;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用BFSif(!visited[i]){BFS(i,visited,g);}}free(visited);}完整程序:#include<stdio.h>#include<stdlib.h>#include<math.h>#include<windows.h>#include<queue>#define ERROR 0#define OK 1#define Overflow 2 //表示上溢#define Underflow 3 //表示下溢#define NotPresent 4 //表示元素不存在#define Duplicate 5 //表示有重复元素typedef int ElemType;typedef int Status;//邻接矩阵的结构体定义typedef struct{ElemType **a; //邻接矩阵int n; //图的当前顶点数int e; //图的当前边数ElemType noEdge; //两顶点间无边时的值}mGraph;//循环队列的结构体定义typedef struct{int front;int rear;int maxSize; //最大容量ElemType *element;}Queue;//创建一个能容纳mSize个单元的空队列void Create(Queue *Q,int mSize){Q->maxSize=mSize;Q->element=(ElemType*)malloc(sizeof(ElemType)*mSize);Q->front=Q->rear=0;}//判断队列是否为空,若是,则返回TRUE;否则返回FALSEBOOL IsEmpty(Queue *Q){return Q->front==Q->rear;}//判断队列是否已满,若是,则返回TRUE,否则返回FALSEBOOL IsFULL(Queue *Q){return (Q->rear+1)%Q->maxSize==Q->front;}//获取队头元素,并通过x返回.若操作成功,则返回TRUE,否则返回FALSE BOOL Front(Queue *Q,ElemType *x){if(IsEmpty(Q)) //空队列处理return FALSE;*x=Q->element[(Q->front+1)%Q->maxSize];return TRUE;}//入队.在队列Q的队尾插入元素x(入队操作)。
操作成功,则返回TRUE,否则返回FALSEBOOL EnQueue(Queue *Q,ElemType x){if(IsFULL(Q)) //溢出处理return FALSE;Q->rear=(Q->rear+1)%Q->maxSize;Q->element[Q->rear]=x;return TRUE;}//出队.从队列Q中删除队头元素(出队操作)。
操作成功,则返回TRUE,否则返回FALSEBOOL DeQueue(Queue *Q){if(IsEmpty(Q)){ //空队列处理return FALSE;}Q->front=(Q->front+1)%Q->maxSize;return TRUE;}//邻接矩阵的初始化Status Init(mGraph *mg,int nSize,ElemType noEdgeValue){int i,j;mg->n = nSize; //初始化顶点数mg->e = 0; //初始化时没有边mg->noEdge = noEdgeValue; //初始化没有边时的取值mg->a = (ElemType**)malloc(nSize*sizeof(ElemType *)); //生成长度为n的一维指针数组if(!mg->a) return ERROR;for(i = 0;i < mg->n;i ++){ //动态生成二维数组mg->a[i] = (ElemType*)malloc(nSize*sizeof(ElemType));for(j = 0;j < mg->n;j ++){mg->a[i][j] = mg->noEdge;}mg->a[i][i] = 0; //自回路设置为0}return OK;}//邻接矩阵的撤销(改成了int型,有返回值),先释放一维数组,再释放指针数组int Destory(mGraph *mg){int i;for(i = 0;i < mg->n;i ++){free(mg->a[i]); //释放n个一维数组的存储空间}free(mg->a); //释放一维数组的存储空间return 1;}//邻接矩阵的边的搜索Status Exist(mGraph *mg,int u,int v){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v||mg->a[u][v] == mg->noEdge) return ERROR;return OK;}//邻接矩阵的边的插入Status Insert(mGraph *mg,int u,int v,ElemType w){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;if(mg->a[u][v] != mg->noEdge) return Duplicate; //若待插入边已存在,则返回出错信息mg->a[u][v] = w; //插入新边mg->e ++; //增加一条边return OK;}//邻接矩阵的边的删除Status Remove(mGraph *mg,int u,int v){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;if(mg->a[u][v] == mg->noEdge) return NotPresent; //若待删除边不存在,则返回出错信息mg->a[u][v] = mg->noEdge; //删除边mg->e --;return OK;}//邻接矩阵的单一顶点DFSvoid DFS(int v,int visited[],mGraph g){int j;printf("%d ",v); //访问顶点vvisited[v] = 1; //为顶点v打上访问标记for(j = 0;j < g.n; j++){ //遍历v的邻接点if(!visited[j] && g.a[v][j] > 0){ //当未被访问且有权值DFS(j,visited,g);}}}//邻接矩阵的全图DFSvoid DFSGraph(mGraph g){int i;int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成标记数组vistedfor(i = 0;i < g.n;i ++){visited[i] = 0; //visted数组初始化} //visted数组初始化for(i = 0;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用DFS if(!visited[i]){ //当未被访问且有权值DFS(i,visited,g);}}free(visited); //释放visted数组}//邻接矩阵的单一顶点BFSvoid BFS(int v,int visited[],mGraph g){Queue q;Create(&q,g.n); //初始化队列visited[v] = 1; //为顶点v打上访问标记printf("%d ",v); //访问顶点vEnQueue(&q,v); //将顶点v放入队列while(!IsEmpty(&q)){Front(&q,&v);DeQueue(&q); //队首顶点出队列for(int i = 0;i < g.n;i ++){ //遍历v的每一项if(!visited[i] && g.a[v][i] > 0){ //若未被访问且有权值,则将其访问并放入队列,注意这里判断的是g.a[v][i]二维数组visited[i] = 1;printf("%d ",i);EnQueue(&q,i);}}}}//邻接矩阵的全图BFSvoid BFSGraph(mGraph g){int i;int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成visited数组for(i = 0;i < g.n;i ++){ //初始化visited数组visited[i] = 0;}for(i = 0 ;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用BFSif(!visited[i]){BFS(i,visited,g);}}free(visited);}int main(){mGraph g;int nSize,edge,u,v,i;ElemType w;printf("Please enter the size of the mgraph:");scanf("%d",&nSize);Init(&g,nSize,-1);printf("Please enter the number of the edges:");scanf("%d",&edge);printf("Now init the graph.\n");/*for(i = 0;i < nSize;i ++){for(j = 0;j < nSize;j ++){printf("Please enter the edge:");scanf("%d%d%d",&u,&v,&w);Insert(&g,u,v,w);}}*/for(i = 0;i < edge;i ++){printf("Please enter the edge:");scanf("%d%d%d",&u,&v,&w);Insert(&g,u,v,w);}printf("DFS:\n");DFSGraph(g);printf("\nBFS:\n");BFSGraph(g);return 0;}实验结果:。
