半角模型题
半角模型专题训练含解析

半角模型专题训练一、解答题1.(探索发现)如图①,四边形ABCD 是正方形,M ,N 分别在边CD 、BC 上,且45MAN=∠︒,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将ADM ∆绕点A 顺时针旋转90︒,点D 与点B 重合,得到ABE ∆,连接AM 、AN 、MN .(1)试判断DM ,BN ,MN 之间的数量关系,并写出证明过程.(2)如图②,点M 、N 分别在正方形ABCD 的边BC 、CD 的延长线上,45MAN=∠︒,连接MN ,请写出MN 、DM 、BN 之间的数量关系,并写出证明过程.(3)如图③,在四边形ABCD 中,AB=AD ,120BAD=∠︒,180B+D=∠∠︒,点N ,M 分别在边BC ,CD 上,60MAN=∠︒,请直接写出线段BN ,DM ,MN 之间的数量关系.2.如图,等腰直角三角形ABC 中,∠BAC = 90°,AB =AC ,点M ,N 在边BC 上,且∠MAN =45°.若BM = 1,CN =3,求MN 的长.3.问题背景:如图1,在四边形ABCD 中,90BAD ︒∠=,90BCD ︒∠=,BA BC =,120ABC ︒∠=,60MBN ︒∠=,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段,,AE CF EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BGF BEF △≌△,可得出结论,他的结论就是______________;探究延伸:如图2,在四边形ABCD 中,BA BC =,180BAD BCD ︒∠+∠=,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70°,试求此时两舰艇之间的距离.4.如图,AB AD BC DC ===,90C D ABE BAD ∠=∠=∠=∠=︒,点E 、F 分别在边BC 、CD 上,45EAF ∠=︒,过点A 作GAB FAD ∠=∠,且点G 在CB 的延长线上.(1)GAB ∆与FAD ∆全等吗?为什么?(2)若2DF =,3BE =,求EF 的长.5.如图,在四边形ABCD 中,90B D ∠=∠=︒,E ,F 分别是BC ,CD 上的点,连接AE ,AF ,EF .(1)如图①,AB AD =,120BAD ∠=︒,60EAF ∠=︒.求证:EF BE DF =+;(2)如图②,120BAD ∠=︒,当AEF 周长最小时,求AEF AFE +∠∠的度数; (3)如图③,若四边形ABCD 为正方形,点E 、F 分别在边BC 、CD 上,且45EAF ∠=︒,若3BE =,2DF =,请求出线段EF 的长度.6.如图,ABC 是边长为2的等边三角形,BDC 是顶角为120°的等腰三角形,以点D 为顶点作60MDN ∠=︒,点M 、N 分别在AB 、AC 上.(1)如图①,当//MN BC 时,则AMN 的周长为______;(2)如图②,求证:BM NC MN +=.7.问题背景如图①,在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒,点E ,F 分别是BC ,CD 上的点,且60EAF ∠=︒,连接EF ,探究线段BE ,EF ,DF 之间的数量关系.探究发现(1)小明同学的方法是将ABE △绕点A 逆时针旋转120︒至ADG 的位置,使得AB 与AD 重合,然后再证明AFE AFG △≌△,从而得出结论:______;拓展延伸(2)如图②,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,点E ,F 分别是边BC ,CD 上的点,且12EAF BAD ∠=∠,连接EF .(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图③,在正方形ABCD 中,点E ,F 分别是边BC ,CD 上的点,且45EAF ∠=︒,连接EF ,已知3BE =,2DF =,求正方形ABCD 的边长.8.如图,ABC 是边长为3的等边三角形,BDC 是等腰三角形,且120BDC ∠=︒,以D 为顶点作一个60︒角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长.9.如图,已知:正方形ABCD ,点E ,F 分别是BC ,DC 上的点,连接AE ,AF ,EF ,且45EAF ∠=︒,求证:BE DF EF +=.10.(1)如图1,在四边形ABCD 中,AB =AD ,∠BAD =100°,∠B =∠ADC =90°.E ,F 分别是BC ,CD 上的点.且∠EAF =50°.探究图中线段EF ,BE ,FD 之间的数量关系.小明同学探究的方法是:延长FD 到点G ,使DG =BE ,连接AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论是 (直接写结论,不需证明); (2)如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E ,F 分别是BC ,CD 上的点,且2∠EAF =∠BAD ,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)如图3,四边形ABCD 是边长为7的正方形,∠EBF =45°,直接写出△DEF 的周长.11.如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF =BE+DF”,请补充辅助线的作法,并写出证明过程.(1)延长CB到点G,使BG=,连接AG;(2)证明:EF=BE+DF12.(2019秋•东台市期末)在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC 的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时QL;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.参考答案1.(1)MN DM BN =+,证明见解析;(2)MN BN DM =-,证明见解析;(3)MN DM BN =+.【分析】(1)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;(2)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN BN DM =-;(3)根据正方形的性质和旋转的性质可证ADM ≌ABE ,利用SAS 可证AMN AEN ≌,则可得:MN DM BN =+;【详解】证明:(1)如图①,∵四边形ABCD 是正方形∴AB=AD ,ABC ADC BAD =90将ADM 绕点A 顺时针旋转90︒,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 90 ∵MAN 45EANMAN 45 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN∵EN EB BN DM BN =+=+,∴MN BN DM =+(2)如图②,将ADM 绕点A 顺时针旋转90,得到ABE∵四边形ABCD是正方形∴AB=AD,ABC ADC BAD=90∵ADM绕点A顺时针旋转90,得到ABE ∴ADM≌ABE∴AM AE,DM BE,MAD EABMAE BAD90,∵MAN45EAN MAN45在AMN和AEN中AM AEMAN EANAN AN≌AMN AEN SASMN EN∵BN EB EN DM MN,=-;即:MN BN DM(3)如图,∵AB AD =,BAD 120∠=,B D 180,将ADM 绕点A 顺时针旋转120,得到ABE∴ADM ≌ABE∴AM AE,DMBE,MAD EAB MAE BAD 120 MAN 60EANMAN 60 在AMN 和AEN 中AMAE MANEAN AN ANAMN AEN SAS ≌MN EN ENBE BN MN DM BN ;【点睛】本题主要考查正方形的性质及全等三角形的判定和性质等知识,利用旋转法构造全等三角形是解题的关键是学会.2【分析】过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .通过证明△ABM ≌△ACE (SAS )推知全等三角形的对应边AM =AE 、对应角∠BAM =∠CAE ;然后由等腰直角三角形的性质和∠MAN =45°得到∠MAN =∠EAN =45°,所以△MAN ≌△EAN (SAS ),故全等三角形的对应边MN =EN ;最后由勾股定理得到EN 2=EC 2+NC 2即MN 2=BM 2+NC 2.【详解】解:如图,过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.∵CE⊥BC,∴∠ACE=∠B=45°.在△ABM和△ACE中AB ACB ACE BM CE⎧∠⎪∠⎪⎨⎩===,∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.在△MAN和△EAN中AM AEMAN EAN AN AN⎪∠⎪⎩∠⎧⎨===,∴△MAN≌△EAN(SAS).∴MN=EN.在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.∵BM=1,CN=3,∴MN2=12+32,∴MN.【点睛】本题主要考查全等三角形的判定和性质、等腰直角三角形的性质以及勾股定理的综合应用,掌握三角形的全等的判定定理是解题关键.=+;探究延伸:成立,理由见解析;实际应用:210海里3.问题背景:EF AE CF【分析】问题背景:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,即可得出结论:EF=AE+CF;探究延伸1:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;探究延伸2:延长DC到H,使得CH=AE,连接BH,先证明△BCH≌△BAE,即可得到BE=HB,∠ABE=∠HBC,再证明△HBF≌△EBF,即可得出EF=HF=HC+CF=AE+CF;实际应用:连接EF,延长BF交AE的延长线于G,根据题意可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.再根据探究延伸2的结论:EF=AE+BF,即可得到两舰艇之间的距离.【详解】解:问题背景:如图1,延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论:EF=AE+CF;故答案为:EF=AE+CF;探究延伸1:上述结论仍然成立,即EF=AE+CF,理由如下:如图2,延长FC到G,使CG=AE,连接BG,∵CG=AE,∠BCG=∠A=90°,BC=BA,∴△BCG≌△BAE(SAS),∴BG=BE,∠ABE=∠CBG,∵∠ABC=2∠EBF,∴∠ABE+∠CBF=∠EBF,即∠CBG+∠CBF=∠EBF,∴∠GBF=∠EBF,又∵BF=BF,∴△BFG≌△BFE(SAS),∴GF=EF,即GC+CF=EF,∴AE+CF=EF∴可得出结论:EF=AE+CF;探究延伸2:上述结论仍然成立,即EF=AE+CF,理由:如图3,延长DC到H,使得CH=AE,连接BH,∵∠BAD+∠BCD=180°,∠BCH+∠BCD=180°,∴∠BCH=∠BAE,∵BA=BC,CH=AE,∴△BCH≌△BAE(SAS),∴BE=HB,∠ABE=∠HBC,∴∠HBE=∠ABC,又∵∠ABC=2∠MBN,∴∠EBF=∠HBF,∴△HBF≌△EBF(SAS),∴EF=HF=HC+CF=AE+CF;实际应用:如图4,连接EF,延长BF交AE的延长线于G,因为舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇乙在指挥中心南偏东70°的B处,所以∠AOB=140°,因为指挥中心观测两舰艇视线之间的夹角为70°,所以∠EOF=70°,所以∠AOB=2∠EOF.依题意得,OA=OB,∠A=60°,∠B=120°,所以∠A+∠B=180°,因此本题的实际的应用可转化为如下的数学问题:在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交AG,BG于E,F,求EF的长.根据探究延伸2的结论可得:EF=AE+BF,根据题意得,AE=75×1.2=90(海里),BF=100×1.2=120(海里),所以EF=90+120=210(海里).答:此时两舰艇之间的距离为210海里.【点睛】本题属于四边形综合题,主要考查了全等三角形的判定和性质,解题的关键是正确作出辅助线构造全等三角形,解答时注意类比思想的灵活应用.4.(1)△GAB≌△F AD,理由见解析;(2)EF=5【分析】(1)由题意可得∠ABG=∠D=90°,进一步即可根据ASA证得△GAB≌△F AD;(2)由(1)的结论可得AG=AF,GB=DF,易得∠BAE+∠DAF=45°,进而可推出∠GAE=∠EAF,然后利用SAS即可证明△GAE≌△F AE,可得GE=EF,进一步即可求出结果.解:(1)∵90D ABE ∠=∠=︒,点G 在CB 的延长线上,∴∠ABG =∠D =90°,在△GAB 和△F AD 中,∵GAB FAD ∠=∠,AB =AD ,∠ABG =∠D ,∴△GAB ≌△F AD (ASA );(2)∵△GAB ≌△F AD ,∴AG =AF ,GB =DF ,∵90BAD ∠=︒,45EAF ∠=︒,∴∠BAE +∠DAF =45°,∴∠BAE +∠GAB =45°,即∠GAE =45°,∴∠GAE =∠EAF ,在△GAE 和△F AE 中,∵AG =AF ,∠GAE =∠EAF ,AE =AE ,∴△GAE ≌△F AE (SAS ),∴GE =EF ,∵GE =GB +BE =DF +BE =2+3=5,∴EF =5.【点睛】本题主要考查了全等三角形的判定和性质,属于常考题型,熟练掌握全等三角形的判定和性质是解题的关键.5.(1)见解析;(2)AEF AFE +∠∠120=︒;(3)5EF =.【分析】(1)延长FD 到点G,使DG BE =,连接AG ,首先证明ABE ADG ≌,则有AE AG =,BAE DAG ∠=∠,然后利用角度之间的关系得出60EAF FAG ∠=∠=︒,进而可证明EAF GAF △≌△,则EF FG DG DF ==+,则结论可证;(2)分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F ,根据轴对称的性质有A E AE '=,A F AF ''=,当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值,然后利用AEF AFE EA A EAA FAD A ''''∠+∠=∠+∠+∠+∠求解即可;(3)旋转ABE △至ADP △的位置,首先证明PAF EAF ≌△△,则有EF FP =,最后利用EF PF PD DF BE DF ==+=+求解即可.【详解】(1)证明:如解图①,延长FD 到点G ,使DG BE =,连接AG ,在ABE △和ADG 中,,,,AB AD ABE ADG BE DG =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴≌.AE AG ∴=,BAE DAG ∠=∠,120BAD ∠=︒,60EAF ∠=︒,60BAE FAD DAG FAD ∴∠+∠=∠+∠=︒.60EAF FAG ∴∠=∠=︒,在EAF △和GAF 中,,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩()EAF GAF SAS ∴≌.EF FG DG DF ∴==+,EF BE DF ∴=+;(2)解:如解图,分别作点A 关于BC 和CD 的对称点A ',A '',连接A A ''',交BC 于点E ,交CD 于点F .由对称的性质可得A E AE '=,A F AF ''=,∴此时AEF 的周长为AE EF AF A E EF A F A A '''''++=++=.∴当点A '、E 、F 、A ''在同一条直线上时,A A '''即为AEF 周长的最小值.120DAB ∠=︒,18012060AA E A ''∴∠'︒︒+∠=-=︒.,EA A EAA FAD A ''''∠=∠∠=∠,,EA A EAA AEF FAD A AFE ''''∠+∠=∠∠+∠=∠, AEF AFE EA A EAA FAD A ''''∴∠+∠=∠+∠+∠+∠=()2260120AA E A '''∠+∠=⨯︒=︒;(3)解:如解图,旋转ABE △至ADP △的位置,90PAE DAE PAD DAE EAB ∴∠=∠+∠=∠+∠=︒,AP AE =,PAF PAE EAF ∠=∠-∠904545EAF =︒-︒=︒=∠.在PAF △和EAF △中,,,,AP AE PAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩()PAF EAF SAS ∴≌△△.EF FP ∴=.325EF PF PD DF BE DF ∴==+=+=+=.【点睛】本题主要考查全等三角形的判定及性质,轴对称的性质,掌握全等三角形的判定及性质是解题的关键.6.(1)4;(2)见解析【分析】(1)首先证明△BDM ≌△CDN ,进而得出△DMN 是等边三角形,∠BDM=∠CDN=30°,NC=BM=12DM=12MN ,即可解决问题; (2)延长AC 至点E ,使得CE BM =,连接DE ,首先证明BDM CDE △≌△,再证明MDN EDN △≌△,得出MN NE =,进而得出结果即可.【详解】解:(1)∵ABC 是等边三角形,//MN BC ,60AMN ABC ∴∠=∠=︒,60ANM ACB ∠=∠=︒∴AMN 是等边三角形,AM AN ∴=,则BM NC =,∵BDC 是顶角120BDC ∠=︒的等腰三角形,30DBC DCB ∴∠=∠=︒,90DBM DCN ∴∠=∠=︒,在BDM 和CDN △中,,,,BM CN MBD DCN BD CD =⎧⎪∠=∠⎨⎪=⎩()BDM CDN SAS ∴△≌△,DM DN ∴=,BDM CDN ∠=∠,∵60MDN ∠=︒,∴DMN 是等边三角形,30BDM CDN ∠=∠=︒,1122NC BM DM MN ∴===,MN MB NC ∴=+, ∴AMN 的周长4AB AC =+=.(2)如图,延长AC 至点E ,使得CE BM =,连接DE ,∵ABC 是等边三角形,BDC 是顶角120BDC ∠=︒的等腰三角形,60ABC ACB ∴∠=∠=︒,30DBC DCB ∠=∠=︒,90ABD ACD ∠∴∠==︒,90DCE ∴∠=︒,在BDM 和CDE △中,,,,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩()BDM CDE SAS ∴△≌△,MD ED ∴=,MDB EDC ∠=∠,120120MDE MDB EDC ∴∠=︒-∠+∠=︒,∵60MDN ∠=︒,60NDE ∴∠=︒,在MDN △和EDN △中,,60,,MD ED MDN NDE DN DN =⎧⎪∠=∠=︒⎨⎪=⎩()MDN EDN SAS ∴△≌△.MN NE ∴=,又∵NE NC CE NC BM =+=+,BM NC MN ∴+=.【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质,掌握全等三角形的性质与判定,等边三角形及等腰三角形的性质是解题的关键.7.(1)EF BE DF =+;(2)(1)中的结论EF BE DF =+仍然成立.证明见解析;(3)正方形ABCD 的边长为6.【分析】(1)证明AEF AGF ≌,可得EF FG =,即可得出结论;(2)要探究BE ,EF ,DF 之间的数量关系,方法同(1)即可得出结论;(3)根据(1)(2)的结论和勾股定理,即可求出正方形ABCD 的边长.【详解】(1)解:由旋转得:AE=AG ,∠BAE=∠DAG ,BE=DG ,∵120BAD ∠=︒,∴∠EAG=120°,∵60EAF ∠=︒,∴∠GAF=60EAF ∠=︒,又∵AF=AF ,∴AFE AFG △≌△,∴EF=GF ,∵GF=DG+DF ,∴EF BE DF =+,故答案为:EF BE DF =+;(2)解:(1)中的结论EF BE DF =+仍然成立.证明:如解图,将ABE △绕点A 逆时针旋转至ADG 的位置,使AB 与AD 重合.则ADG B ∠=∠,DG BE =,AG AE =,BAE DAG ∠=∠,又∵180B ADC ∠+∠=︒,∴180ADG ADC ∠+∠=︒,∴C ,D ,G 三点共线. ∵12FAD DAG FAD BAE BAD EAF BAD ∠+∠=∠+∠=∠-∠=∠,∴FAG EAF ∠=∠,又∵AF AF =,∴AEF AGF ≌,∴EF FG =,又∵FG DG DF BE DF =+=+,∴EF BE DF =+;(3)解:由(1)(2)可知325EF BE DF =+=+=.设正方形ABCD 的边长为x ,则3CE x =-,2CF x =-,在Rt CEF 中,222EF CE CF =+,∴()()222532x x =-+-,解得16x =,21x =-(不合题意,舍去),故正方形ABCD 的边长为6.【点睛】此题考查了旋转的性质,全等三角形的判定及性质,勾股定理的运用,正方形的性质,解题中注意类比方法的运用,同样的类型题可以运用同样的思路及方法进行证明.8.AMN 的周长为6.【分析】要求△AMN 的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB 至F ,使BF=CN ,连接DF ,通过证明△BDF ≌△CDN ,及△DMN ≌△DMF ,从而得出MN=MF ,△AMN 的周长等于AB+AC 的长.【详解】解:∵△BDC 是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC 是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB 至F ,使BF=CN ,连接DF ,在Rt △BDF 和Rt △CND 中,BF=CN ,DB=DC∴△BDF ≌△CDN ,∴∠BDF=∠CDN ,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN ,DM 为公共边 ∴△DMN ≌△DMF ,∴MN=MF∴△AMN 的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.【点睛】此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.9.见解析.【分析】将△ABE 绕点A 逆时针旋转90°得到△ADG ,根据旋转的性质可得GD=BE ,AG=AE ,∠DAG=∠BAE ,然后求出∠FAG=∠EAF ,再利用“边角边”证明△AEF 和△AGF 全等,根据全等三角形对应边相等可得EF=FG ,即可得出结论.【详解】如解图,将ABE △绕点A 逆时针旋转90︒至ADG 的位置,使AB 与AD 重合.∴AG AE =,,DAG BAE DG BE ∠=∠=.∵45EAF ∠=︒.∴904545GAF DAG DAF BAE DAF BAD EAF ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒, ∴EAF GAF ∠=∠.在AGF 和AEF 中,,AG AE GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AGF AEF SAS △≌△.∴EF GF =.∵GF DG DF BE DF =+=+,∴BE DF EF +=.【点睛】本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,难点在于利用旋转变换作出全等三角形.10.(1)EF =BE +DF ;(2)成立,理由详见解析;(3)14.【分析】(1)延长FD 到点G .使DG =BE .连结AG ,由“SAS ”可证△ABE ≌△ADG ,可得AE =AG ,∠BAE =∠DAG ,再由“SAS ”可证△AEF ≌△AGF ,可得EF =FG ,即可解题;(2)延长EB 到G ,使BG =DF ,连接AG ,即可证明△ABG ≌△ADF ,可得AF =AG ,再证明△AEF ≌△AEG ,可得EF =EG ,即可解题;(3)延长EA 到H ,使AH =CF ,连接BH ,由“SAS ”可证△ABH ≌△CBF ,可得BH =BF ,∠ABH =∠CBF ,由“SAS ”可证△EBH ≌△EBF ,可得EF =EH ,可得EF =EH =AE +CF ,即可求解.【详解】证明:(1)延长FD 到点G .使DG =BE .连结AG ,在△ABE 和△ADG 中,90AB AD ABE ADG BE DG ︒=⎧⎪∠=∠=⎨⎪=⎩,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠BAD =100°,∠EAF =50°,∴∠BAE +∠F AD =∠DAG +∠F AD =50°,∴∠EAF =∠F AG =50°,在△EAF 和△GAF 中,∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△GAF (SAS ),∴EF =FG =DF +DG ,∴EF =BE +DF ,故答案为:EF =BE +DF ;(2)结论仍然成立,理由如下:如图2,延长EB 到G ,使BG =DF ,连接AG ,∵∠ABC +∠D =180°,∠ABG +∠ABC =180°,∴∠ABG =∠D ,∵在△ABG 与△ADF 中,AB=AD ABG=D BG=DF ⎧⎪∠∠⎨⎪⎩,∴△ABG ≌△ADF (SAS ),∴AG =AF ,∠BAG =∠DAF ,∵2∠EAF =∠BAD ,∴∠DAF +∠BAE =∠BAG +∠BAE =12∠BAD =∠EAF , ∴∠GAE =∠EAF ,又AE =AE ,∴△AEG≌△AEF(SAS),∴EG=EF.∵EG=BE+BG.∴EF=BE+FD;(3)如图,延长EA到H,使AH=CF,连接BH,∵四边形ABCD是正方形,∴AB=BC=7=AD=CD,∠BAD=∠BCD=90°,∴∠BAH=∠BCF=90°,又∵AH=CF,AB=BC,∴△ABH≌△CBF(SAS),∴BH=BF,∠ABH=∠CBF,∵∠EBF=45°,∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,∴∠EBH=∠EBF,又∵BH=BF,BE=BE,∴△EBH≌△EBF(SAS),∴EF=EH,∴EF=EH=AE+CF,∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=14.【点睛】本题是四边形的综合题,考查了全等三角形的判定和性质,正方形的性质,添加恰当辅助线构造全等三角形是本题的关键.11.(1)DF;(2)见解析【分析】(1)由于△ADF 与△ABG 可以看作绕点A 旋转90°的关系,根据旋转的性质知BG=DF ,从而得到辅助线的做法;(2)先证明△ADF ≌△ABG ,得到AG=AF ,∠GAB=∠DAF ,结合∠EAF =45°,易知∠GAE=45°,再证明△AGE ≌△AFE 即可得到EF =GE=BE+GB=BE +DF【详解】解:(1)根据旋转的性质知BG=DF ,从而得到辅助线的做法:延长CB 到点G ,使BG=DF ,连接AG ;(2)∵四边形ABCD 为正方形,∴AB=AD ,∠ADF=∠ABE=∠ABG=90°,在△ADF 和△ABG 中AD AB ADF ABG DF BG =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴AF=AG ,∠DAF=∠GAB ,∵∠EAF=45°,∴∠DAF+∠EAB=45°,∴∠GAB+∠EAB=45°,∴∠GAE=∠EAF =45°,在△AGE 和△AFE 中0AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABG (SAS ),∴GE=EF ,∴EF =GE=BE+GB=BE +DF【点睛】本题属于四边形综合题,主要考查正方形的性质及全等三角形的判定和性质等知识,解题的关键是学会利用旋转方法提示构造全等三角形,属于中考常考题型.12.(1)BM +NC =MN ,23;(2)结论仍然成立,详见解析;(3)NC ﹣BM =MN ,详见解析【分析】(1)由DM=DN,∠MDN=60°,可证得△MDN是等边三角形,又由△ABC是等边三角形,CD=BD,易证得Rt△BDM≌Rt△CDN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系BM+NC=MN,此时23QL=;(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC﹣BM=MN.【详解】(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时23QL=.理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴23QL=;(2)猜想:结论仍然成立.证明:在NC的延长线上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴23QL=;(3)证明:在CN上截取CM1=BM,连接DM1.∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N.∴NC﹣BM=MN.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知等边三角形的性质及全等三角形的判定定理.。
半角模型经典例题

半角模型经典例题
摘要:
1.半角模型的概念和特点
2.半角模型的经典例题
3.半角模型的解题技巧和方法
4.半角模型在实际生活中的应用
正文:
【半角模型的概念和特点】
半角模型,是数学模型中的一种,主要用于解决一些角度或位置只有半角(即180 度)的问题。
半角模型的特点是,问题中给出的信息通常只有角度或位置的一半,需要我们通过逻辑推理和数学计算,找出另外一半的角度或位置。
这种模型需要我们具备较强的空间想象能力和逻辑思维能力。
【半角模型的经典例题】
例题一:一个长方体的三条边长分别是3 厘米、4 厘米和5 厘米,求这个长方体的体积。
例题二:一个球体的半径是3 厘米,求这个球体的表面积和体积。
例题三:在一个等腰三角形中,已知底边的一半是4 厘米,高是6 厘米,求这个等腰三角形的面积。
【半角模型的解题技巧和方法】
在解决半角模型的问题时,有以下几点技巧和方法:
1.建立模型:根据题目描述,建立起半角模型,明确已知和未知的信息。
2.转换角度:将问题中的半角信息转换为可以计算的角度或位置信息。
3.使用公式:根据已知信息,运用相关的数学公式进行计算。
4.检验答案:将计算出的答案代入原问题中,检验答案的合理性。
【半角模型在实际生活中的应用】
半角模型在实际生活中的应用非常广泛,比如在物理、化学、生物、地理等学科的研究中,都会涉及到半角模型的问题。
半角模型训练

半角模型半角模型: 指的是一个大角夹着一个度数为它一半的角。
条件: 四边形ABCD中, E、F分别在BC.CD(或延长线上), 具备下列三个条件:①AB=AD(共顶点等线段);①①BAD=2①EAF;(共顶点的倍半角)①①B+①ADC=180°(或①BAD+①BCD=180°)(对角互补四边形)结论: EF=BE+DF (延长线上为EF=BE-DF);AE平分∠BEF, AF平分∠EFD。
情形一: 角内含半角(补短)情形二: 角外含半角(截长)模型一: 90°夹45°例1.如图, 点E、F分别是正方形BC.CD上的点, ∠EAF=45°, 求证:(1)DF+BE=EF;(2)AE平分∠BEF, AF平分∠EFD证明: 延长CB至点G, 使得BG=DF(在CD上补BE亦可)△ABG≌△ADF(SAS)△AEG≌△AEF(SAS)90°外夹45°例 2.如图, 在正方形ABCD中, E、F为CB.DC延长线上点, 且∠EAF=45°, 探究线段EF、BE、DF之间的数量关系, 并证明。
类型二、120°角夹60°例3.如图, 在四边形ABCD中, AB=AD, ∠BAD=120°, E, F分别为BC, CD上的点, ∠EAF=∠C=60°, 求证(1)EF=BE+DF;(2)点A在∠BCD的平分线上.练习:1.如图, 四边形ABCD中, ∠A=∠BCD=60°, ∠ADC=60°, AB=BC, E、F分别在AD、DC延长线上, 且∠EBF=60°, 求证:AE=EF+CF例4.在等边△ABC的两边AB.AC所在直线上分别有两点M、N, D为△ABC 外一点, 且∠MDN=60°, ∠BDC=120°, BD=DC. 探究: 当M、N分别在直线AB.AC上移动时, BM、NC.MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1, 当点M、N边AB.AC上, 且DM=DN时, BM、NC.MN之间的数量关系是;此时/=;(2)如图2, 点M、N在边AB、AC上, 且当DM≠DN时, 猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3, 当M、N分别在边AB、CA的延长线上时, 探索BM、NC、MN之间的数量关系如何?并给出证明.任意角夹半角例5.已知, 如图, 在四边形ABCD中, ∠B+∠D=180°, AB=AD, E, F分别是线段BC, CD上的点, 且BE+FD=EF. 求证: ∠EAF=/∠BAD.练习(1)如图, 在四边形ABCD中, AB=AD, ∠B=∠D=90°, E、F分别是边BC.CD 上的点, 且∠EAF=/∠BAD.求证: EF=BE+FD;(2)如图, 在四边形ABCD中, AB=AD, ∠B+∠D=180°, E、F分别是边BC.CD上的点, 且∠EAF=/∠BAD, (1)中的结论是否仍然成立?(3)如图, 在四边形ABCD中, AB=AD, ∠B+∠ADC=180°, E、F分别是边BC.CD 延长线上的点, 且∠EAF=/∠BAD, (1)中的结论是否仍然成立?若成立, 请证明;若不成立, 请写出它们之间的数量关系, 并证明.例6.(1)如图1, 已知正方形ABCD中, ∠MAN=45°, 猜想线段MN、BM与DN之间有怎样的关系?并证明. (2)如图2, 已知四边形ABCD中, AB⊥BC于点B, AD⊥CD于点D, AB=AD, ∠BAD=120°, ∠MAN=60°, (1)中线段BM与DN之间的关系还成立吗?如果成立, 请证明;如果不成立, 请说明理由. (3)张大爷有一块五边形的土地, 如图3, 已知AB=AE=6, BC=4, DE=3, ∠BAE=2∠CAD, AB⊥BC于点B, AE⊥DE于点E, 请你帮助张大爷计算这块土地的面积.课后练习1. 如图, 等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合, 将此三角板绕点A旋转, 使三角板中该锐角的两条边分别交正方形的两边BC.DC于点E、F, 连结EF. 若EF=5, DF=2, 则BE的长为.(第1题) (第2题)2. 如图, △ABC为等边三角形, BD=CD, ∠BDC=120°, BC=2, M、N分别在边AB, AC上, 且∠MDN=60°, 则△AMN的周长等于.3. 在四边形ABCD中, ∠B+∠D=180°, CB=CD. 以点C为顶点的∠ECF在四边形ABCD的内部绕点C旋转, 角的两边分别与AB.AD交于点E、F, ∠ECF=/∠BCD.(1)若∠BCD=120°,①如图1, 当∠B=90°, ∠BCE=30时, 求证: EF=BE+DF;②如图2, 当∠B≠90时, ①中的结论是否仍然成立?若成立, 请证明;若不成立, 请说明理由;③在∠ECF绕点C旋转的过程中, ①中的结论是否仍然成立, 请直接写出你的结论;(2)如图3, 若∠BCD为任意的一个角(0°<∠BCD<180°), 在∠ECF绕点C旋转的过程中, ①中的三条线段BE, DF, EF之间的数量关系是否发生变化?若变化, 请说明理由;若不变, 请直接写出你的结论.4. 如图1, 四边形ABCD, 将顶点为A的∠EAF绕着顶点A顺时针旋转, 角的一条边与DC的延长线交于点F, 角的另一边与CB的延长线交于点E, 连接EF.(1)如果四边形ABCD为正方形, 当∠EAF=45°时, 有EF=DF﹣BE. 请你思考如何证明这个结论(只需思考, 不必写出证明过程);(2)如图2, 如果在四边形ABCD中, AB=AD, ∠ABC=∠ADC=90°, 当∠EAF=/∠BAD时, EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式(3)如图3, 如果在四边形ABCD中, AB=AD, ∠ABC与∠ADC互补, 当∠EAF=/∠BAD时, EF与DF、BE之间有怎样的数学关系?请写出它们之间的关系式并给予证明;(4)在(3)中, 若BC=4, DC=7, CF=2, 求△CEF的周长(直接写出结果即可).5. 已知正方形ABCD, 一等腰直角三角板的一个锐角顶点与A重合, 将此三角板绕A点旋转时, 两边分别交直线BC.CD于M、N.(1)当M、N分别在边BC.CD上时(如图1), 求证: BM+DN=MN;(2)当M、N分别在边BC.CD所在的直线上时(如图2), 线段BM、DN、MN之间又有怎样的数量关系, 请直接写出结论;(不用证明)(3)当M、N分别在边BC、CD所在的直线上时(如图3), 线段BM、DN、MN之间又有怎样的数量关系, 请写出结论并写出证明过程.6.问题背景:如图1: 在四边形ABCD中, AB=AD, ∠BAD=120°, ∠B=∠ADC=90°, E、F分别是BC.CD上的点, 且∠EAF=60°, 探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是, 延长FD到点G, 使DG=BE.连结AG, 先证明△ABE ≌△ADG, 再证明△AEF≌△AGF, 可得出结论, 他的结论应是;(2)探索延伸:如图2, 若在四边形ABCD中, AB=AD, ∠B+∠D=180°, E、F分别是BC.CD上的点, 且∠EAF=/∠BAD, 上述结论是否仍成立, 并说明理由;(3)实际应用:如图3, 在某次军事演习中, 舰艇甲在指挥中心(点O处)北偏西30°的A处, 舰艇乙在指挥中心南偏东70°的B处, 并且两舰艇到指挥中心的距离相等.接到行动指令后, 舰艇甲向正东方向以45海里/时的速度前进, 同时, 舰艇乙沿北偏东50°的方向以60海里/时的速度前进, 2小时后, 指挥中心观察到甲、乙两舰艇分别到达E、F处, 且两舰艇之间的夹角为70°, 试求此时两舰艇之间的距离.7. 如图, △ABC和△DEF是两个等腰直角三角形, ∠BAC=∠DFE=90°, AB=AC, FD=FE, △DEF的顶点E在边BC上移动, 在移动过程中, 线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.(1)如图1, 当E为BC中点, 且BP=CQ时, 求证: △BPE≌△CQE;(2)如图2, 当ED经过点A, 且BE=CQ时, 求∠EAQ的度数;(3)如图3, 当E为BC中点, 连接AE、PQ, 若AP=3, AQ=4, PQ=5, 求AC的长.11。
半角模型(初中数学最全半角模型专题)

变式练习
变式4.在平面直角坐标系中,已知A(x,y),点A作AB⊥y
轴,垂足为B.若在x轴正半轴上取一点M,连接BM并延长至
N,以BN为直角边作等腰Rt△BNE,∠BNE=90°,过点A作
AF∥y轴交BE于点F,连接MF,设OM=a,MF=b,AF=c,试
1 1
证明: + =
.
例2.如图所示,过正方形ABCD的顶点A在正方形ABCD的内
几何模型一:半角模型
类型一、正方形中夹半角模型(45°)
例1.如图,已知正方形ABCD中,E、F分别是BC、CD上
的点,且∠EAF=45°
求证:EF=BE+DF;
变式练习
变式1.如图,已知正方形ABCD的边长为6,E,F分别是AB、
BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋
转90°,得到△DCM.
∠BAD.证明:EF=BE﹣FD
变式练习
变式3.已知,如图,在四边形ABCD中,∠B+∠D=180°,
AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求
证:2∠EAF=∠BAD.
变式练习
变式4.已知△ABC中,AB=AC,∠BAC=120°.点M在BC上,
点N在BC的上方,且∠MBN=∠MAN=60°,
求证:MC=BN+MN;
则MN的长为
.
变式练习
变式2.如图,在△ABC中,AB=AC,点E,F是边BC所在直线
上与点B,C不重合的两点.∠BAC=90°,∠EAF=135°,
证明:EF2=EC2+BF2
类型三、其他半角模型
例4.在等边△ABC的两边AB,AC上分别有两点M,N,点D为
半角模型(正方形中的半角模型)

例题讲解
例5.如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在求证:AH=AB.
证明:将△ADF绕点A顺时针旋转90°得到△ABG, 由旋转的性质得,DF=BG,AF=AG,∠DAF=∠BAG. ∵∠FAG=∠BAG+∠BAF=∠DAF+∠BAF=∠BAD=90°, ∠EAF=45°, ∴∠EAF=∠EAG=45°. 在△AEF和△AEG中,
(2)解:如图,过点A作AF⊥MN, ∵由(1)中△EAM≌△NAM得: ∠AMB=∠AMF, 又∵∠ABM=∠AFM=90°,AM=AM, ∴△ABM≌△AFM(AAS) ∴AB=AF=5, 即点A到MN的距离为5.
例题讲解
例3.已知正方形ABCD的边长为1,点M、N分别是边BC、CD的两点,若△CMN的周长 为2,求:∠MAN的大小;
∴△NAM≌△EAM(SSS),
∴∠NAM=∠EAM=∠BAM+∠EAB=
∠BAM+∠DAN=
=45°;
变式练习
练习3.如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,求 △MAN的面积的最小值.
变式练习
练习4.如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别 交AM,AN于E,F,下面结论正确的是 . ①△CMN的周长等于正方形ABCD的边长的两倍; ②点A到MN的距离等于正方形ABCD的边长; ③EF2=BE2+DF2; ④△EMO与△FNO均为等腰直角三角形; ⑤S正方形ABCD:S△AMN=2AB:MN.
变式练习
练习5.如图4.在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE= 45°,若BD=1,EC=2,求DE的长.
半角模型

半角模型
1、产生条件:共顶点、等线段,一个小角等于大角的一半,对角互补的四边形。
2、常见形式:图形中,往往出现90°套45°的情况,或者120°套60°的情况,还有2α套α的情况。
求证的结论一般是“a+b=c 或者a -b=c ”。
3、解题方法: 通过辅助线“截长补短”,构造全等三角形,转移边角。
旋转移位造全等,翻折分割构全等。
4、经典题型:
4.1、正方形半角模型:90°→ 45°
例1、如图,正方形ABCD 中,∠EAF=45°。
求证: (1)EF=BE+DF . (2)∠EFC 周长 = 2AB (3)EA 平分∠BEF
变式训练:
如图,正方形ABCD 中,∠EAF=45°。
求证:EF=DF - BE
B
B
4.2、等腰直角三角形半角模型:90°→ 45°
例2、如图,等腰直角三角形中∠BAC=90°,∠EAF=45°,求证:BE 、EF 、CF 的数量关系。
变式训练:
如图,等腰直角三角形中∠BAC=90°,∠EAF=45°,求证:BE 2 + CF 2 = EF 2。
(完整版)半角模型专题专练
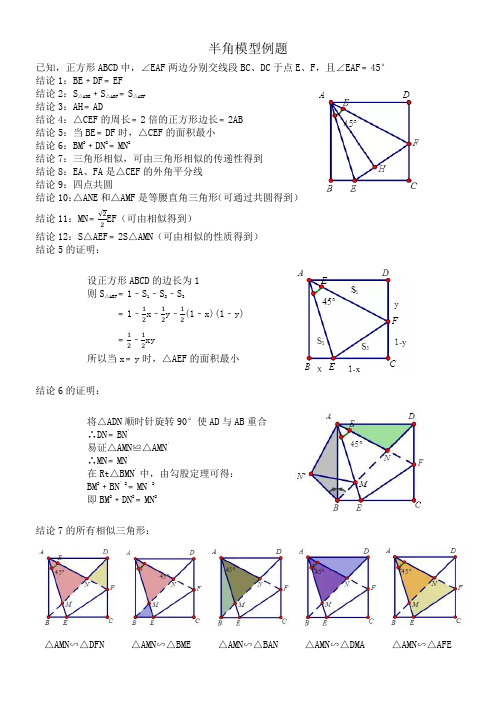
半角模型例题已知,正方形ABCD 中,∠EAF 两边分别交线段BC 、DC 于点E 、F ,且∠EAF ﹦45° 结论1:BE ﹢DF ﹦EF结论2:S △ABE ﹢S △ADF ﹦S △AEF 结论3:AH ﹦AD结论4:△CEF 的周长﹦2倍的正方形边长﹦2AB 结论5:当BE ﹦DF 时,△CEF 的面积最小 结论6:BM 2﹢DN 2﹦MN 2结论7:三角形相似,可由三角形相似的传递性得到 结论8:EA 、FA 是△CEF 的外角平分线 结论9:四点共圆 结论10:△ANE 和△AMF 是等腰直角三角形(可通过共圆得到) 结论11:MN ﹦√22EF (可由相似得到)结论12:S △AEF ﹦2S △AMN (可由相似的性质得到) 结论5的证明:设正方形ABCD 的边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3﹦1﹣12x ﹣12y ﹣12(1﹣x)(1﹣y) ﹦12﹣12xy所以当x ﹦y 时,△AEF 的面积最小结论6的证明:将△ADN 顺时针旋转90°使AD 与AB 重合 ∴DN ﹦BN ′易证△AMN ≌△AMN ′ ∴MN ﹦MN ′在Rt △BMN ′中,由勾股定理可得: BM 2﹢BN ′2﹦MN ′2 即BM 2﹢DN 2﹦MN 2结论7的所有相似三角形:△AMN ∽△DFN△AMN ∽△BME△AMN ∽△BAN△AMN ∽△DMA△AMN ∽△AFE结论8的证明:因为△AMN ∽△AFE ∴∠3=∠2因为△AMN ∽△BAN ∴∠3=∠4 ∴∠2=∠4 因为AB ∥CD ∴∠1=∠4 ∴∠1=∠2结论9的证明:因为∠EAN ﹦∠EBN =45°∴A 、B 、E 、N 四点共圆(辅圆定理:共边同侧等顶角)同理可证C 、E 、N 、F 四点共圆 A 、M 、F 、D 四点共圆 C 、E 、M 、F 四点共圆**必会结论-------- 图形研究正方形半角模型已知:正方形ABCD ,E 、F 分别在边BC 、CD 上,且︒=∠45EAF ,AE 、AF 分别交BD 于H 、G ,连EF .一、全等关系(1)求证:①EF BE DF =+;②DG 2﹢BH 2﹦HG 2;③AE 平分BEF ∠,AF 平分DFE ∠. 二、相似关系(2)求证:①DG CE 2=;②BH CF 2=;③HG EF 2=. (3)求证:④DH BG AB ⋅=2;⑤HG BG AG ⋅=2;⑥21=⋅CF DF CE BE . 三、垂直关系(4)求证:①EG AG ⊥;②FH AH ⊥;③BEAB HCF =∠tan . (5)、和差关系求证:①BE DG BG 2=-;②DH DF AD 2=+; ③||2||DG BH DF BE -=-.例1、在正方形ABCD 中,已知∠MAN ﹦45°,若M 、N 分别在边CB 、DC 的延长线上移动,①.试探究线段MN 、BM 、DN 之间的数量关系. ②.求证:AB=AH.例2、在四边形ABCD 中,∠B+∠D ﹦180°,AB=AD ,若E 、F 分别在边BC 、CD 上,且满足EF=BE +DF. 求证:∠EAF =12∠BAD例3、在△ABC 中,AB=AC ,∠BAC=2∠DAE=120°,若BD=5,CE=8,求DE 的长。
(完整版)半角模型专题专练.doc

半角模型例题已知,正方形 ABCD中,∠ EAF两边分别交线段 BC、 DC于点 E、F,且∠ EAF﹦45°结论 1:BE﹢ DF﹦EF结论 2:S△ABE﹢ S△ADF﹦S△AEF结论 3:AH﹦ AD结论 4:△ CEF的周长﹦ 2 倍的正方形边长﹦ 2AB结论 5:当 BE﹦DF时,△ CEF的面积最小22 2结论 6:BM﹢DN﹦MN结论 7:三角形相似,可由三角形相似的传递性得到结论 8:EA、 FA是△ CEF的外角平分线结论 9:四点共圆结论 10:△ANE和△ AMF是等腰直角三角形(可通过共圆得到)结论 11: MN﹦√2 EF(可由相似得到)2结论 12: S△ AEF﹦2S△ AMN(可由相似的性质得到)结论 5 的证明:设正方形 ABCD的边长为 1则S△AEF﹦1﹣S1﹣S2﹣ S3﹦1﹣1 x﹣1y﹣1 (1 ﹣x)(1 ﹣y)22 2﹦1﹣1 xy22所以当 x﹦y 时,△ AEF的面积最小结论 6 的证明:将△ ADN顺时针旋转 90°使 AD与 AB重合′∴DN﹦ BN′易证△ AMN≌△ AMN′∴MN﹦ MN′在 Rt△BMN中,由勾股定理可得:2′ 2′2BM﹢BN ﹦MN22 2即 BM﹢DN﹦MN结论 7 的所有相似三角形:△ AMN∽△ DFN△AMN∽△ BME△AMN∽△ BAN△ AMN∽△ DMA△AMN∽△ AFE结论 8 的证明:因为△ AMN∽△ AFE∴∠ 3=∠ 2因为△ AMN∽△ BAN∴∠ 3=∠ 4∴∠ 2=∠ 4因为 AB∥CD∴∠ 1=∠ 4∴∠ 1=∠ 2结论 9 的证明:因为∠ EAN﹦∠ EBN= 45°∴A、B、E、N 四点共圆(辅圆定理:共边同侧等顶角)同理可证 C、E、N、F 四点共圆A、M、 F、 D 四点共圆C、E、 M、 F 四点共圆**必会结论 -------- 图形研究正方形半角模型已知:正方形 ABCD ,E、F分别在边 BC 、 CD 上,且 EAF45 ,AE、AF分别交BD于H、 G ,连EF.一、全等关系()求证:① 2 2 2 平分,平分DF BE EF ;②DG﹢ BH﹦ HG;③AE BEF AF DFE .1二、相似关系(2)求证:①CE 2DG ;② CF 2 BH ;③ EF 2HG .(3)求证:④AB2 BG DH ;⑤ AG 2 BG HG ;⑥BEDF 1 . CE CF 2三、垂直关系(4)求证:①AG EG ;②AH FH ;③tan HCF AB .(5) 、和差关系BE 求证:① BG DG 2 BE ;② AD DF 2DH ;③ | BE DF | 2 | BH DG | .例1、在正方形 ABCD中,已知∠ MAN﹦ 45°,若 M、N 分别在边CB、 DC的延长线上移动,①.试探究线段 MN、BM 、 DN之间的数量关系 .②.求证: AB=AH.例2、在四边形 ABCD中,∠ B+∠ D﹦ 180°,AB=AD,若 E、F 分别在边 BC、 CD上,且满足 EF=BE +DF.求证:∠ EAF=1∠BAD2例3、在△ ABC中, AB=AC,∠ BAC=2∠ DAE=120°,若 BD=5,CE=8,求 DE的长。
专题06 半角模型(能力提升)(老师版)

专题06半角模型(能力提升)1.如图,点E、F分别在正方形ABCD的边CD,BC上,且∠EAF=45°,将△ADE绕点A顺时针旋转90°得到△ABG,连接BD交AF于点M,DE=2,BF=3,则GM=.【答案】2【解答】解:连接GE交AF于点O,∵四边形ABCD是正方形,∴∠BAD=∠ABF=∠ADE=∠C=90°,AB=AD=BC=DC,AD∥BC,∵∠EAF=45°,∴∠BAF+∠DAE=∠BAD﹣∠EAF=90°﹣45°=45°,由旋转得:AE=AG,∠ABF=∠ADE=90°,BG=DE=2,∠BAG=∠DAE,∴∠BAG+∠BAF=45°,∴∠GAF=∠EAF=45°,∵∠ABF=∠ABG=90°,∴∠GBC=∠ABG+∠ABF=180°,∴点G、B、F三点在同一条直线上,∵BF=3,∴FG=BG+BF=2+3=5,∴△GAF≌△EAF(SAS),∴FG=FE=5,设正方形ABCD的边长为x,∴CF=x﹣3,CE=x﹣2,在Rt△ECF中,FC2+EC2=EF2,∴(x﹣3)2+(x﹣2)2=52,∴x=6或x=﹣1(舍去),∴正方形ABCD的边长为6,在Rt△ABF中,AF===3,∵AD∥BC,∴∠DAM=∠MFB,∠ADM=∠MBF,∴△ADM∽△FBM,∴===2,∴AM=AF=2,在Rt△ADE中,AE===2,∵AG=AE,FG=FE,∴AF是EG的垂直平分线,∴∠AOE=90°,∵∠EAF=45°,∴AE=AO,∴AO=2,∴点M与点O重合,∴EG=2GM,在Rt△ECG中,EC=DC﹣DE=6﹣2=4,GC=BC+GB=6+2=8,∴EG===4,∴GM=2,故答案为:2.2.如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是.【答案】3﹣2【解答】解:∵四边形ABCD为正方形,∴∠B=∠D=90°,AB=AD,CD=CB;如图,将△ABN绕点A沿逆时针方向旋转90°得到△ADE,∴AE=AN,DE=BN,∠DAE=∠BAN;∴∠MAE=∠MAD+∠BAN,∵∠MAN=45°,∴∠MAD+∠BAN=90°﹣45°=45°,∴∠MAE=∠MAN;在△MAE与△MAN中,,∴△MAE≌△MAN(SAS),∴ME=MN,∴MD+BN=MN;∴△MCN的周长=CM+CN+MN=CM+ME+CN=CM+DM+CN+BN=CD+CB=2,而CD=CB,∴CD=CB=1;设DM=x,BN=y,△CMN的面积为s,则S==,整理得:x+y﹣xy=1﹣2S①;由勾股定理得:MN2=CM2+CN2,即(x+y)2=(1﹣x)2+(1﹣y)2,整理得:x+y+xy=1②,联立①②得:xy=s,x+y=1﹣s,∴x、y为方程z2﹣(1﹣s)z+s=0的两个根,∴△≥0,即[﹣(1﹣s)]2﹣4s≥0,解得:s或s(不合题意,舍去),故答案为3﹣2.3.旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且.(1)如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连结DF.①∠DAF=;②求证:DF=DE;(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.【解答】(1)①解:由旋转知,AF=AE,∠BAF=∠CAE,∠EAF=60°,∵∠DAE=α,∠BAC=α=60°,∴∠DAE=×60°=30°,∴∠CAE+∠BAD=∠BAC﹣∠DAE=30°,∴∠DAF=∠BAD+∠BAF=∠BAD+∠CAE=30°,故答案为:30°;②证明:由①知,AF=AE,∠DAF=∠DAE=30°,∵AB=AC,∴△DAF≌△DAE(SAS),∴DF=DE;(2)解:DE2=BD2+CE2,理由如下:如图,将△AEC绕点A顺时针旋转90°到△AFB的位置,连结DF,∴AF=AE,∠EAF=90°=∠BAC,∴∠BAF=∠CAE,∴△BAF≌△CAE(SAS),∴BF=CE,∠ABF=∠ACE,在Rt△ABC中,∠C=∠ABC=45°,∴∠ABF=45°,∴∠DBF=90°,根据勾股定理得,DF2=BD2+BF2,∴DF2=BD2+CE2,同(1)②的方法得,DF=DE,∴DE2=BD2+CE2.4.已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.(1)将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;(2)将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;(3)在(1)和(2)的条件下,若BF=4,AE=1,则CE=.【解答】(1)证明:∵△BEF为等边三角形,∴BE=EF=BF,∠EBF=60°,∴∠EBA+∠ABF=60°,∵∠MBN=60°,∴∠CBF+∠ABF=60°,∴∠EBA=∠CBF,在△ABE与△CBF中,,∴△ABE≌△CBF(SAS),∴AE=CF,∵CE=EF+CF,∴CE=BE+AE;(2)解:图②结论为CE=BE﹣AE,图③结论为CE=AE﹣BE,图②的理由如下:∵△BEF为等边三角形,∴BE=EF=BF,∠EBF=60°,∴∠EBA+∠ABF=60°,∵∠MBN=60°,∴∠CBF+∠ABF=60°,∴∠EBA=∠CBF,在△ABE与△CBF中,,∴△ABE≌△CBF(SAS),∴AE=CF,∵CE=EF﹣CF,∴CE=BE﹣AE,图③的利用如下:∵△BEF为等边三角形,∴BE=EF=BF,∠EBF=60°,∴∠EBA+∠ABF=60°,∵∠MBN=60°,∴∠CBF+∠ABF=60°,∴∠EBA=∠CBF,在△ABE与△CBF中,,∴△ABE≌△CBF(SAS),∴AE=CF,∵CE=CF﹣EF,∴CE=AE﹣BE;(3)解:在(1)条件下,CE=BE+AE=BF+AE=4+1=5;在(2)条件下,CE=BE﹣AE=BF﹣AE=4﹣1=3,综上所述,CE=3或5,故答案为:3或5.5.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.【解答】解:(1)如图①AH=AB,∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,在△ABM与△ADN中,,∴△ABM≌△ADN,∴∠BAM=∠DAN,AM=AN,∵AH⊥MN,∴∠MAH=MAN=22.5°,∵∠BAM+∠DAN=45°,∴∠BAM=22.5°,在△ABM与△AHM中,,∴△ABM≌△AHM,∴AB=AH;故答案为:AH=AB;(2)数量关系成立.如图②,延长CB至E,使BE=DN.∵ABCD是正方形,∴AB=AD,∠D=∠ABE=90°,在Rt△AEB和Rt△AND中,,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,,∴△AEM≌△ANM,∴S△AEM =S△ANM,EM=MN,∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH;(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,∴BM=2,DN=3,∠B=∠D=∠BAD=90°,分别延长BM和DN交于点C,得正方形ABCD,由(2)可知,AH=AB=BC=CD=AD,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,∴52=(x﹣2)2+(x﹣3)2,解得x1=6,x2=﹣1(不符合题意,舍去)∴AH=6.6.问题提出:如图1:在△ABC中,BC=10且∠BAC=45°,点O为△ABC的外心,则△ABC的外接圆半径是.问题探究:如图2,正方形ABCD中,E、F分别是边BC、CD两边上点且∠EAF=45°,请问线段BE、DF、EF有怎样的数量关系?并说明理由.问题解决:如图3,四边形ABCD中,AB=AD=4,∠B=45°,∠D=135°,点E、F分别是射线CB、CD上的动点,并且∠EAF=∠C=60°,试问△AEF的面积是否存在最小值?若存在,请求出最小值.若不存在,请说明理由.【解答】解:(1)如图1,作出△ABC的外接圆⊙O,∵∠A=45°,∴∠BOC=90°,∵BC=10,∴OB=sin45°×BC=,故答案为:5.(2)EF=BE+DF,理由如下:如图2,延长EB,使BG=DF,连接AG,∵四边形ABCD是正方形,∴AB=AD,∠ABG=∠D=90°,在△ABG和△ADF中,,∴△ABG≌△ADF(SAS),∴AG=AF,∠GAB=∠DAF,∵∠EAF=45°,∴∠DAF+∠BAE=45°,∴∠GAE=45°,在△GAE和△FAE中,,∴△GAE≌△FAE(SAS),∴EF=GE=DF+BE,(3)存在最小值,如图3,延长CB,使BG=DF,∵∠ABC=45°,∴∠ABG=135°,∴∠ABG=∠ADF,又∵AB=AD,∴△ABG≌△ADF(SAS),∴∠GAB=∠FAD,AG=AF,∵∠ABC=45°,∠D=135°,∠C=60°,∴∠BAD=120°,∵∠EAF=60°,∴∠BAE+∠DAF=60°,∴∠GAE=60°,∴△GAE≌△FAE(SAS),在△AEF中,∵∠EAF=60°,AH=4,∴EF边上的高AK=4,画△AEF的外接圆⊙O,作OM⊥EF于M,∵∠EAF=60°,∴∠EOM=60°,设OM=x,EM=,OE=2x,EF=2,∵OM+OA≥AK,∴x+2x≥4,∴x≥,∴EF的最小值为2×,∴S的最小值为.△AEF7.如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD 到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.【解答】解:(1)延长CB到G,使BG=FD,连接AG,∵∠ABG=∠D=90°,AB=AD,∴△ABG≌△ADF,∴∠BAG=∠DAF,AG=AF,∵∠EAF=∠BAD,∴∠DAF+∠BAE=∠EAF,∴∠EAF=∠GAE,∴△AEF≌△AEG,∴EF=EG=EB+BG=EB+DF.(2)结论不成立,应为EF=BE﹣DF,证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵AB=AD,∴△ABG≌△ADF.∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=∠BAD.∴∠GAE=∠EAF.∵AE=AE,∴△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD.8.已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连接MN,作AH⊥MN,垂足为点H(1)如图1,猜想AH与AB有什么数量关系?并证明;(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?【解答】(1)答:AB=AH,证明:延长CB至E使BE=DN,连接AE,∵四边形ABCD是正方形,∴∠ABC=∠D=90°,∴∠ABE=180°﹣∠ABC=90°又∵AB=AD,∵在△ABE和△ADN中,,∴△ABE≌△ADN(SAS),∴∠1=∠2,AE=AN,∵∠BAD=90°,∠MAN=45°,∴∠2+∠3=90°﹣∠MAN=45°,∴∠1+∠3=45°,即∠EAM=45°,∵在△EAM和△NAM中,,∴△EAM≌△NAM(SAS),又∵EM和NM是对应边,∴AB=AH(全等三角形对应边上的高相等);(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,∵AD是△ABC的高,∴∠ADB=∠ADC=90°∴∠E=∠F=90°,又∵∠BAC=45°∴∠EAF=90°延长EB、FC交于点G,则四边形AEGF是矩形,又∵AE=AD=AF∴四边形AEGF是正方形,由(1)、(2)知:EB=DB=2,FC=DC=3,设AD=x,则EG=AE=AD=FG=x,∴BG=x﹣2;CG=x﹣3;BC=2+3=5,在Rt△BGC中,(x﹣2)2+(x﹣3)2=52解得x1=6,x2=﹣1,故AD的长为6.9.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.(1)如图1,当∠MAN绕点A旋转到BM=DN时,有BM+DN=MN.当∠MAN绕点A旋转到BM≠DN时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.【解答】解:(1)图1中的结论仍然成立,即BM+DN=MN,理由为:如图2,在MB的延长线上截取BE=DN,连接AE,∵四边形ABCD是正方形,∴AD=AB,∠D=∠DAB=∠ABC=∠ABE=90°,∵在△ABE和△ADN中,∴△ABE≌△ADN(SAS).∴AE=AN;∠EAB=∠NAD,∵∠DAB=90°,∠MAN=45°,∴∠DAN+∠BAM=45°,∴∠EAM=∠BAM+∠EAB=45°=∠MAN,∵在△AEM和△ANM中,∴△AEM≌△ANM(SAS),∴ME=MN,∴MN=ME=BE+BM=DN+BM,即DN+BM=MN;(2)猜想:线段BM,DN和MN之间的等量关系为:DN﹣BM=MN.证明:如图3,在DN上截取DE=MB,连接AE,∵由(1)知:AD=AB,∠D=∠ABM=90°,BM=DE,∴△ABM≌△ADE(SAS).∴AM=AE;∠MAB=∠EAD,∵∠MAN=45°=∠MAB+∠BAN,∴∠DAE+∠BAN=45°,∴∠EAN=90°﹣45°=45°=∠MAN,∵在△AMN和△AEN中,∴△AMN≌△AEN(SAS),∴MN=EN,∵DN﹣DE=EN,∴DN﹣BM=MN.10.已知正方形ABCD,一等腰直角三角板的一个锐角顶点与A重合,将此三角板绕A点旋转时,两边分别交直线BC、CD于M、N.(1)当M、N分别在边BC、CD上时(如图1),求证:BM+DN=MN;(2)当M、N分别在边BC、CD所在的直线上时(如图2,图3),线段BM、DN、MN之间又有怎样的数量关系,请直接写出结论;(3)在图3中,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.【解答】解:(1)证明:作AE⊥AN交CB的延长线于E,∵∠EAB+∠BAN=90°,∠NAD+∠BAN=90°,∴∠EAB=∠NAD.又∵∠ABE=∠D=90°,AB=AD,∴△ABE≌△AND(ASA),∴AE=AN,BE=DN.∵∠EAM=∠NAM=45°,AM=AM,∴△AME≌△AMN.∴MN=ME=MB+BE=MB+DN.(2)图2的结论:MN+DN=BM;图3的结论:MN+BM=DN.(3)连接AC.∵MN=10,CM=8,在Rt△MNC中,根勾股定理得:MN2=CM2+CN2,即102=82+CN2,∴CN=6,如图3在ND上截取DG=BM,∵AD=AB,∠ABM=∠ADN=90°,∴△ADG≌△ABM,∴AG=AM,∠MAB=∠DAG,∵∠MAN=45°,∠BAD=90°,∴∠MAG=90°,△AMG为等腰直角三角形,∴AN垂直MG,∴AN为MG垂直平分线,所以NM=NG.∴DN﹣BM=MN,即MN+BM=DN,∴MN+CM﹣BC=DC+CN,∴CM﹣CN+MN=2BC,∴8﹣6+10=2BC,∴BC=6.∴AC=6.∵∠BAP+∠BAQ=45°,∠NAC+∠BAQ=45°,∴∠BAP=∠NAC.又∠ABP=∠ACN=135°,∴△ABP∽△CAN,∴==.∵在Rt△AND中,根据勾股定理得:AN2=AD2+DN2=36+144,解得AN=6.∴=,∴AP=3.。
半角模型经典例题

半角模型经典例题摘要:一、半角模型的概念与特点1.半角模型的定义2.半角模型的核心思想3.半角模型的应用场景二、半角模型的经典例题解析1.例题一:基本半角模型2.例题二:扩展半角模型3.例题三:半角模型的组合应用三、半角模型的解题方法与技巧1.识别半角模型的关键特征2.灵活运用半角模型解决实际问题3.总结半角模型的通用解题步骤正文:半角模型是计算机图形学中一种重要的模型,它以极坐标系为基础,描述了物体在二维空间中的位置和方向。
半角模型经典例题可以帮助我们更好地理解和掌握这一模型。
一、半角模型的概念与特点半角模型,顾名思义,是一个以极坐标系表示的模型。
它将一个物体在二维平面上的位置和方向表示为一个半径和一个角度。
半角模型的核心思想是将物体的局部坐标系与世界坐标系建立联系,从而实现对物体在世界坐标系中的位置和方向的描述。
半角模型的应用场景非常广泛,比如在计算机图形学中,可以用于表示物体的位置和方向;在机器人学中,可以用于描述机器人的关节运动;在物理模拟中,可以用于描述粒子的运动轨迹等。
二、半角模型的经典例题解析1.例题一:基本半角模型题目描述:给定一个物体在世界坐标系中的位置和方向,求物体在另一个坐标系中的位置。
解析:根据半角模型的定义,我们可以将物体的位置和方向表示为极坐标系下的一个半径和一个角度。
通过极坐标系的转换公式,可以轻松地求解物体在另一个坐标系中的位置。
2.例题二:扩展半角模型题目描述:给定一个物体在世界坐标系中的位置和方向,以及一个平移向量,求物体在另一个坐标系中的位置。
解析:在基本半角模型的基础上,我们需要考虑平移向量对物体位置的影响。
可以将平移向量表示为极坐标系下的一个半径和一个角度,然后将其与物体的位置和方向相加,即可求解物体在另一个坐标系中的位置。
3.例题三:半角模型的组合应用题目描述:给定多个物体的位置和方向,以及它们之间的相对位置和方向,求解这些物体在某个坐标系中的共同运动。
半角模型专题专练

半角模型例题F ,且∠ EAF= 45已知,正方形ABCDK∠ EAF两边分别交线段BG DC于点E、结论1: BE+ DF= EF结论2: S△ABE + S∆ ADF= AEF结论3: AH= AD结论4:A CEF的周长=2倍的正方形边长=2AB结论5:当BE= DF时,△ CEF的面积最小结论6: BM+ DN = MN结论7:三角形相似,可由三角形相似的传递性得到结论8: EA FA是厶CEF的外角平分线结论9:四点共圆结论10: △ ANE和厶AMF是等腰直角三角形(可通过共圆得到)结论11: MN= — EF (可由相似得到)结论12: S^AEF=2S A AMN(可由相似的性质得至U)结论5的证明:设正方形ABCD勺边长为1 则S∆ AEF= 1 —S —S2 —S B1—_ x ——y ——(1 —x)(1 —y)=一一一Xy所以当X = y时,△ AEF的面积最小结论6的证明:将厶ADN i时针旋转90°使AD与AB重合∙∙∙ DN= BN易证△ AMI⅛^ AMN∙∙∙ MN= MN在Rt△ BMN中,由勾股定理可得:BM + BN2= MN2即BM+DN= MN结论7的所有相似三角形:.J Q△ AMN^ DFN △ AMN^ BME △ AMN^ BAN △AMN^DMA △ AMN^ AFE结论8的证明:因为△ AMN P ^ AFE∙∙∙∠ 3=∠ 2因为△ AMF Φ^ BAN∙°∙∠ 3=∠ 4 ∙i ∠ 2=∠ 4因为AB// CD ∙∠1 = ∠ 4 ∙∠1 = ∠ 2结论9的证明:**必会结论 ------ 图形研究正方形半角模型一、 全等关系(1) 求证:① DF BE =EF :②DG+ BH= HG;③ AE 平分.BEF , 二、 相似关系(2) 求证:① CE= 2DG ; ® CF =J 2BH ; @ EF = J 2HG . (3) 求证:④ AB 2 =BG DH ; @ AG 2 =BG HG ; ® B E -DF =-.CE CF 2三、 垂直关系AB(4) 求证:① AG _ EG :② AH _ FH :③ tan HCF =A B .BE(5) 、和差关系求证:① BG -DG 「2 BE ; ® AD DF 「2DH ; ③ ∣BE-DF |=』2 | BH - DG |.已知:正方形 ZEAF =45, AE 、 ABCD , E 、F 分别在边BC 、CD 上,且 AF 分别交BD 于H 、G ,连EF .D因为∠ EAN=∠ EBN= 45° ∙ A 、B 、E 、N 四点共圆(辅圆定 理:共边同侧等顶角)同理可证C 、E 、N 、F 四点共圆 A M F 、D 四点共圆 C 、E 、M F 四点共圆AF 平分.DFE .B AOHDFE例1、在正方形ABCD中,已知∠ MAN= 45° ,若M N分别在边CB DC的延长线上移动,①•试探究线段MN BM、DN之间的数量关系.② .求证:AB=AH.例2、在四边形ABCD中∠ B+∠ D= 180°, AB=AD 若E、F 分别在边BC CD上,且满足EF=BE +DF.求证:∠ EAF^-∠ BAD例3、在厶ABC中,AB=AC ∠ BAC=∠ DAE=120 ,若BD=5CE=β求DE的长。
专题12 半角模型(原卷版)

专题12半角模型半角模型的概述:当一个角包含着该角的半角,如90°角包含着45°角,120°角包含着60°角,270°角包含着135°角,即出现12倍角关系,且这两个角共顶点,共顶点的两条边相等,则该模型为半角模型。
解题方法为:1)过公共点作旋转,2)截长补短的方法构造全等解题。
基本模型:1)90°的半角模型(常考)已知正方形ABCD中,E,F分别是BC、CD上的点,∠EAF=45°,AE、AF分别与BD相交于点O、P,则:①EF=BE+DF②AE平分∠BEF,AF平分∠DFE③C∆CEF=2倍正方形边长④S∆ABE+S∆ADF=S∆AEF⑤AB=AG=AD(过点A作AG⊥EF,垂足为点G)⑥OP2=OB2+OD2⑦若点E为BC中点,则点F为CD三等分点⑧∆APO∽∆AEF∽∆DPF∽∆BEO∽∆DAO∽∆BPA⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆⑩∆APE、∆AOF为等腰直角三角形(11)EF=2OP(12)S∆AEF=2S∆APO(13)AB2=BP×OD(14)CE•CF=2BE•DF(15)∆EPC为等腰三角形(16)PX=BX+DP(过点E作EX⊥BD,垂足为点X)证明:①思路:延长CD到点M,使DM=BE,连接AM先根据已知条件∆ABE≌∆ADM(SAS),由此可得AE=AM,∠BAE=∠DAM而∠BAE+∠FAD=45°,所以∠DAM+∠FAD=45°,可证明∆AEF≌∆AMF(SAS),由此可得EF=MF,而MF=DM+DF=BE+DF,因此EF=BE+DF②思路:∵∆AEF≌∆AMF(SAS)∴∠AFM=∠AFE,∠AMF=∠AEF∴AF平分∠DFE又∵∠AMF=∠AEB∴∠AEB=∠AEF∴AE平分∠BEF③思路:C∆CEF=EF+EC+FC=(BE+DF)+EC+FC=(BE+EC)+(DF+FC)=BC+DC=2BC④、⑤思路:过点A作AG⊥EF,垂足为点G根据②证明过程可知AFG=∠AFD,∠AEB=∠AEG因此可以证明:∆ABE≌∆AGE(AAS),∆AGF≌∆ADF(AAS)所以AB=AG=AD,S∆ABE=S∆AGE,S∆AGF=S∆ADF则S∆AEF=S∆AGE+S∆AGF=S∆ABE+S∆ADF⑥思路:绕点A将∆APD逆时针旋转90°得到∆ANB,使AD,AB重合因为∆APD≌∆ANB(AAS)所以AN=AP,BN=DP,∠NAB=∠PAD,∠ADP=∠ABN因为∠ADB=∠ABD=45°,所以∠NBO=90°因为∠BAE+∠PAD=45°所以∠NAB+∠BAE=45°则∆ANO≌∆APO(SAS)所以NO=OP在Rt∆NBO中,由勾股定理可知:ON2=OB2+NB2,则OP2=OB2+OD2⑦思路:已知tan∠EAB=BE AB=12,且∠EAB+∠FAD=45°∴tan∠FAD=13(“12345型”),∴DF:AD=1:3,即点F为CD的三等分点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半角模型题
Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998
半角模型
例1(海淀201405-8) 如图,点P 是以O 为圆心, AB 为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P 重合, 当此三角板绕点P 旋转时,它的斜边和直角边所在的直线与直径AB 分别
相交于C 、D 两点.设线段AD 的长为x ,线段BC 的长为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是
A B C D
例2.(海201311-24).已知在ABC △中, 90=∠ACB ,26==CB CA ,
AB CD ⊥于D ,点E 在直线CD 上,CD DE 2
1=,点F 在线段AB 上,M 是DB 的中点,直线AE 与直线CF 交于N 点.
(1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________,___________;
(2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证:
45=∠CNE ;
(3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得
45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由.
D
C
B
A
N
F
E
C
B
A
24. (本小题满分8分)
(1)AE ⊥CM ,AE =CM
(2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H .
∵ 90=∠ACB ,26==CB CA ,
∴∠CAB =∠CBA =45°,
12. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥,
∴CD=AD=BD =162
AB =. ∵ M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =,
∴4 2.AF DF ==,
∴+2+3=5.FM FD DM == ∵AG ⊥AF ,
∴FG =
∴.FG FM =
在△CAG 和△CBM 中, ∴△CAG ≌△CBM .
∴CG =CM ,ACG BCM ∠=∠.
∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=.在△FCG 和△FCM 中, ∴△FCG ≌△FCM . ∴FCG FCM ∠=∠. ∴45FCH ∠=.
由(1)知AE ⊥CM , ∴90CHN ∠= ∴ 45=∠CNE . (3)存在.
AF =8.
例3.(平谷201405-24)(1)如图1,点E 、F 分别是正方形ABCD 的边BC 、CD 上的点,∠EAF =45°,连接EF ,
则EF 、BE 、FD 之间的数量关系是:EF =BE +FD .连结BD ,交AE 、AF 于点M 、N ,且MN 、BM 、DN 满足222DN BM MN +=,请证明这个等量关系;
M'
A
B
C
D
E
F
M
N
(2)在△ABC 中, AB =AC ,点D 、E 分别为BC 边上的两点.
①如图2,当∠BAC =60°,∠DAE =30°时,BD 、DE 、EC 应满足的等量关系是__________________;
②如图3,当∠BAC =α,(0°<α<90°),∠DAE =α2
1时,BD 、DE 、EC 应满足
的等量关系是____________________.【参考:1cos sin 22=+αα】
24. (1) 在正方形ABCD 中,AB =AD ,∠BAD =90°,
∠ABM =∠ADN=45°.
把△ABM 绕点A 逆时针旋转90°得到M AD '∆. 连结M N '.则,,AM AM BM M D =='',
︒=∠='∠45ABM M AD ,BAM M DA ∠='∠.
∵∠EAF =45°,∴∠BAM +∠DAN =45°,
∠DAM′+∠DAF =45°, ︒=∠=∠45'MAN AN M . ∴N AM '∆≌AMN ∆. ∴N M '=MN .
在N DM '∆中,︒=∠+∠=∠90''ADM ADN DN M , ∴222BM DN MN +=
(2)① 222EC EC BD BD DE +⋅+=; - ② 222cos 2EC EC BD BD DE +⋅⋅+=α
例4.半角模型的应用: (2012西城期末改编).如图1,平面直角坐标系xOy 中,
抛物线21
2
y x bx c =++与x 轴交于A 、B 两点,点C 是AB 的中点,CD ⊥
AB 且CD =AB .直线BE 与y 轴平行,点F 是射线BE 上的一个动点,连接
AD 、AF 、DF .
(1)若点F 的坐标为(9
2
,1),AF
①求此抛物线的解析式;
②点P 是此抛物线上一个动点,点Q 在此抛物线的对称轴上,以点A 、
F 、P 、Q 为顶点构成的四边形是平行四边形,请直接写出点Q 的坐
标;
(2)若22b c +=-,2b t =--,且AB 的长为kt ,其中0t >.如图2,当∠
DAF =45°时,求k 的值和∠DFA 的正切值.。
