第十七届(2012年3月)华罗庚金杯少年数学邀请赛小学高年级组网上初赛试题及答案
第十七届华罗庚金杯少年数学邀请赛_试题及答案_小学高年级组

第十五届华罗庚金杯少年数学邀请赛初赛试卷(小学组)一、选择题(每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的()。
2.两条纸带,较长的一条为23cm,较短的一条为15 cm。
把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是()cm。
(A)6 (B)7 (C)8 (D)93.两个水池内有金鱼若干条,数目相同。
亮亮和红红进行捞鱼比赛,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3:4;捞完第二个水池内的金鱼时,亮亮比第一次多捞33条,与红红捞到的金鱼数目比是5:3。
那么每个水池内有金鱼()条。
(A)112 (B)168 (C)224 (D)3364.从中去掉两个数,使得剩下的三个数之和与最接近,去掉的两个数是()。
5.恰有20个因数的最小自然数是()。
(A)120 (B)240 (C)360 (D)4326.如图的大正方形格板是由81个1平方厘米的小正方形铺成,B,C是两个格点。
若请你在其它的格点中标出一点A,使得△ABC的面积恰等于3平方厘米,则这样的A点共有()个。
(A)6 (B)5 (C)8 (D)107.算式的值为,则m+n 的值是 。
8.“低碳生活”从现在做起,从我做起。
据测算,1公顷落叶阔叶林每年可吸收二氧化碳14吨。
如果每台空调制冷温度在国家提倡的26℃基础上调到27℃,相应每年减排二氧化碳21千克。
某市仅此项减排就相当于25000公顷落叶阔叶林全年吸收的二气化碳;若每个家庭按3台空调计,该市家庭约有 万户。
(保留整数)9.从0、1、2、3、4、5、6、7、8、9这十个数字中,选出九个数字,组成一个两位数、一个三位数和一个四位数,使这三个数的和等于2010,那么其中未被选中的数字是 。
第十七届华罗庚金杯少年数学邀请赛答案及解析过程(初一网络版)

word 专业资料-可复制编辑-欢迎下载第十七届华罗庚金杯少年数学邀请赛初赛试卷(初一网络版)一、选择题1. A 解析:根据题意可知,a 、b 异号,且a 为正,b 为负;2. C 解析:根据题意可知:B+D=9,A+C=13,根据竖式加法原理可知X=1,Y=3,则X+Y=43. D 解析:划过的面积为底边长为6,高为CD 的平行四边形的面积和ABC ∆的面积之和,在ADB ∆ 中,由勾股定理知:,3452222=-=-=AD AB BD 则CD=3+6=9,6646215496=⨯⨯+=+⨯=∆ABC S S 4. B 解析:第一个正方形为—,第二个正方形为X ,第三个正方形为+,第四个正方形为÷5. C 解析:32%2.6%5%8==+⨯+⨯乙甲乙甲乙甲,解得m m m m m m ,现在所求表达式为:%5.6%10032%561%83241%100%561%841=⨯+⨯⨯+⨯⨯=⨯+⨯⨯+⨯⨯乙乙乙乙乙甲乙甲m m m m m m m m 6. B 解析:设最小的一个数为a,则最大的那个数为a+n-1,根据连续n 个数的和的公式可知:20122)1=-++n n a a (,化简可知:2)1(2012--=n n a ,又503222012⨯⨯=,且a,n 均为正数,因此,(n-1)必须为偶数,故n 只能为奇数,且必须为2012的约数,所以n=503。
二、填空题7. 2010 解析:[][]=⨯⨯⨯=+⨯=+⨯⨯=2013-2013201220132010-201020122013-12012201220132010-2-201220122013-2012201220132010-20122-201222222323)()()(原式[]201020131-2012201320101-201222=⨯⨯⨯)()( 8. 0 解析:本题通过取特殊值法解题,发现当时,0====d c b a 等式成立,故0=+++d c b a9. 77 解析:取AG 中点I,因为,27)166(21)(21=+⋅⨯=+⋅=∆IC GH AB IC S ACG 解得1127=IC ,由IH BI GH AB GHI ABI =∆∆相似得与,解得:83=IH BI ,又113911276=-=-=IC BC BI ,所以1110438113938=⨯=⨯=BI IH ,7112711104=-=-=IE IH CH ,77)166(721)(21=+⨯⨯=+⨯⨯=HG CD CH S DHGC 10. 12,解析:令,32,6-=+=m a m b 则要使原式为整数,即要ab 为整数即可,又152=-a b ,两边同时处以1152+=b a 得:,为使取值如下:与只能为奇数,为整数,则m a a b 15 则。
2012年-2017年华罗庚金杯少年数学邀请赛初赛真题合集(小高组)附答案

目录第二十二届华罗庚金杯少年数学邀请赛 (1)第二十一届华罗庚金杯少年数学邀请赛 (3)第二十一届华罗庚金杯少年数学邀请赛 (5)第二十届华罗庚金杯少年数学邀请赛 (7)第二十届华罗庚金杯少年数学邀请赛 (9)第十九届华罗庚金杯少年数学邀请赛 (11)第十九届华罗庚金杯少年数学邀请赛 (13)第十八届华罗庚金杯少年数学邀请赛 (15)第十八届华罗庚金杯少年数学邀请赛 (17)第十七届华罗庚金杯少年数学邀请赛 (19)第十七届华罗庚金杯少年数学邀请赛 (21)第二十二届华罗庚金杯少年数学邀请赛答案 (23)第二十一届华罗庚金杯少年数学邀请赛答案 (24)第二十一届华罗庚金杯少年数学邀请赛答案 (25)第二十届华罗庚金杯少年数学邀请赛答案 (26)第二十届华罗庚金杯少年数学邀请赛答案 (27)第十九届华罗庚金杯少年数学邀请赛答案 (28)第十九届华罗庚金杯少年数学邀请赛答案 (29)第十八届华罗庚金杯少年数学邀请赛答案 (30)第十八届华罗庚金杯少年数学邀请赛答案 (31)第十八届华罗庚金杯少年数学邀请赛答案 (32)第十七届华罗庚金杯少年数学邀请赛答案 (33)第十七届华罗庚金杯少年数学邀请赛答案 (34)A B 第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间 2016 年 12 月 10 日 10:00-11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 两个有限小数的整数部分分别是 7 和 10,那么这两个有限小数的积的整数部分有( )种可能的取值.A .16B .17C .18D .192. 小明家距学校,乘地铁需要 30 分钟,乘公交车需要 50 分钟,某天小明因故先乘地铁,再换乘公交车,用了 40 分钟到达学校,其中换乘过程用了 6 分钟,那么这天小明乘坐公交车用了( )分钟. A .6 B .8 C .10 D .123. 将长方形 ABCD 对角线平均分成 12 段,连接成右图,长方形 ABCD 内部空白部分面积总和是 10 平方厘米,那么阴影部分面积总和是( )平方厘米.A .14B .16C .18D .204.请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是( ).A .2986B .2858C .2672D .27545. 在序列 20170……中,从第 5 个数字开始,每个数字都是前面 4 个数字和的个位数,这样的序列可以一直写下去.那么从第 5 个数字开始,该序列中一定不会出现的数组是( )A .8615B .2016C .4023D .20176. 从 0 至 9 选择四个不同的数字分别填入方框中的四个括号中,共有( )种填法使得方框中话是正确的.× 71 0 2罗华金杯ABG FHDEC二、填空题.(每小题 10 分,共 40 分)7. 若( 1 5 245 3— )× 9 2 5 7 ÷ 2 +2.25=4,那么A 的值是 .3 34 1A8. 右图中,“华罗庚金杯”五个汉字分别代表 1-5 这五个不同的数字,将各线段两端点的数字相加得到五个和,共有 种情况使得这五个和恰为五个连续自然数.9. 右图中,ABCD 是平行四边形,E 为 CD 的中点,AE 和 BD 的交点为 F ,AC 和 BE 的交点为 H ,AC 和BD 的交点为 G ,四边形 EHGF 的面积是 15 平方厘米,则 ABCD 的面积是平方厘米.10. 若 2017,1029 与 725 除以 d 的余数均为 r ,那么 d -r 的最大值是 .庚第二十一届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组A 卷) (时间:2015 年 12 月 12 日 10:00~11:00一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. 算式999 9 × 999 9 的结果中含有( )个数字 0.2016个92016个9A .2017B .2016C .2015D .20142. 已知 A ,B 两地相距 300 米.甲、乙两人同时分别从 A 、B 出发,相向而行,在距 A 地 140 米处相遇;如果乙每秒多行 1 米,则两人相遇处距 B 地 180 米.那么乙原来的速度是每秒( )米.A . 2 2B . 2 4C .3D . 3 15 5 53. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,则这个七位数最大是( )A .9981733B .9884737C .9978137D .98717734. 将 1,2,3,4,5,6,7,8 这 8 个数排成一行,使得 8 的两边各数之和相等,那么共有( )种不同的排法. A .1152B .864C .576D .2885. 在等腰梯形 ABCD 中,AB 平行于 CD ,AB =6,CD =14,∠AEC 是直角,CE =CB ,则 AE 2 等于( )A .84B .80C .75D .646. 从自然数 1,2,3,…,2015,2016 中,任意取 n 个不同的数,要求总能在这 n 个不同的数中找到 5个数,它们的数字和相等.那么 n 的最小值等于( ). A .109 B .110 C .111 D .112EABD C二、填空题.(每小题 10 分,共 40 分)AP M O7. 两个正方形的面积之差为 2016 平方厘米,如果这样的一对正方形的边长都是整数厘米,那么满足上述条件的所有正方形共有对.8. 如下图,O ,P ,M 是线段 AB 上的三个点,AO = 4 AB ,BP = 2AB ,M 是 AB 的中点,且 OM =2,那5 3么 PM 长为 .9. 设 q 是一个平方数.如果 q -2 和 q +2 都是质数,就称 q 为 p 型平方数.例如,9 就是一个 p 型平方数.那么小于 1000 的最大 p 型平方数是 .10. 有一个等腰梯形的纸片,上底长度为 2015,下底长度为 2016.用该纸片剪出一些等腰梯形,要求剪出的梯形的两底边分别在原来梯形的底边上,剪出的梯形的两个锐角等于原来梯形的锐角,则最多可以剪出 个同样的等腰梯形.第二十一届华罗庚金杯少年数学邀请赛初赛试卷 B (小学高年级组)(时间:2015 年 12 月 12 日 10:00~11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. “凑 24 点”游戏规则是:从一副扑克牌中抽去大小王剩下 52 张,(如果初练也可只用 1 至 10 这 40 张牌)任意抽取 4 张牌(称牌组),用加、减、乘、除(可加括号)把牌面上的数算成 24.每张牌必须用一次且只能用一次,并不能用几张牌组成一个多位数,如抽出的牌是 3,8,8,9,那么算式为(9- 8)×8×3 或(9-8÷8)×3 等.在下面 4 个选项中,唯一无法凑出 24 点的是( ). A .1,2,2,3 B .1,4,6,7 C .1,5,5,5 D .3,3,7,72. 有一种数,是以法国数学家梅森的名字命名的,它们就是形如 2n -1( n 为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如:22-1=3 就是一个梅森质数.第一个梅森合数是( ).A .4B .15C .127D .20473. 有一种饮料包装瓶的容积是 1.5 升.现瓶里装了一些饮料,正放时饮料高度为 20 厘米,倒放时空余部分的高度为 5 厘米,如下图.那么瓶内现有饮料( )升.A .1B .1.2C .1.25D .1.3754. 已知 a ,b 为自然数, 4 = 1 + 1,那么 a +b 的最小值是( ).15 a bA .16B .20C .30D .65. 如下图,平面上有 25 个点,每个点上都钉着钉子,形成 5×5 的正方形钉阵.现有足够多的橡皮筋,最多能套出( )种面积不同的正方形.A .4B .6C .8D .106. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,那么这个七位数最大是( ).A .9981733B .9884737C .9978137D .9871773二、填空题.(每小题 10 分,共 40 分)华 杯 赛 三 十 年× 杯 杯今 年 认 真 赛 好今 年 认 真 赛 好 三 十 年 华 杯 赛 好7. 计算:20152+20162-2014×2016-2015×2017= .8. 在下边的算式中,相同汉字代表相同数字,不同汉字代表不同数字.当杯代表 5 时,“华杯赛”所代表的三位数是 .9. 于 2015 年 10 月 29 日闭幕的党的十八届五中全会确定了允许普遍二孩的政策.笑笑的爸爸看到当天的新闻后跟笑笑说:我们家今年的年龄总和是你年龄的 7 倍,如果明年给妳添一个弟弟或妹妹,我们家 2020 年的年龄总和就是你那时年龄的 6 倍.那么笑笑今年 岁.10. 教育部于 2015 年 9 月 21 日公布了全国青少年校园足球特色学校名单,笑笑所在的学校榜上有名.为 了更好地备战明年市里举行的小学生足球联赛,近期他们学校的球队将和另 3 支球队进行一次足球友 谊赛.比赛采用单循环制(即每两队比赛一场),规定胜一场得 3 分,负一场得 0 分,平局两队各得 1分;以总得分高低确定名次,若两支球队得分相同,就参考净胜球、相互胜负关系等决定名次.笑笑学校的球队要想稳获这次友谊赛的前两名,至少要得 分.第二十届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 现在从甲、乙、丙、丁四个人中选出两个人参加一项活动,规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去,那么丁不去.最后去参加活动的两个人是( )A .甲、乙B .乙、丙C .甲、丙D .乙、丁2. 以平面上任意 4 个点为顶点的三角形中,钝角三角形最多有( )个.A .5B .2C .4D .33. 桌上有编号 1 至 20 的 20 张卡片,小明每次取出 2 张卡片,要求一张卡片的编号是另一张卡片的 2 倍多 2,则小明最多取出( )张卡片. A .12B .14C .16D .184. 足球友谊比赛的票价是 50 元,赛前一小时还有余票,于是决定降价,结果售出的票增加了三分之一, 而票房收入增加了四分之一,那么每张票售价降了( )元.A .10B . 25C . 50D .25235. 一只旧钟的分针和时针每重合一次,需要经过标准时间 66 分,那么,这只旧钟的 24 小时比标准时间的 24 小时( ).A .快 12 分B .快 6 分C .慢 6 分D .慢 12 分6. 在下图的 6×6 方格内,每个方格中只能填 A 、B 、C 、D 、E 、F 中的某个字母,要求每行、每列、每个标有粗线的 2×3 长方形的六个字母均不能重复.那么,第四行除了首尾两个方格外,中间四个方格填入的字母从左到右的顺序是( ).A .E 、 C 、 D 、 FB .E 、D 、C 、FC .D 、 F 、 C 、E D .D 、C 、F 、EB CA B D ABCE二、填空题(每小题 10 分,共 40 分) - - - = AFDPBEC7. 计算4811 + 265 1 + 904 129 41 55184160 7036 12 2030 42 568. 过正三角形 ABC 内一点 P ,向三边作垂线,垂足依次为 D 、E 、F ,连接 AP 、BP 、CP .如果正三角形ABC 的面积是 2028 平方厘米,三角形 PAD 和三角形 PBE 的面积都是 192 平方厘米,则三角形 PCF的面积为平方厘米.9. 自然数 2015 最多可以表示成 个连续奇数的和.10. 由单位正方形拼成的 15×15 网格,以网格的格点为顶点作边长为整数的正方形,则边长大于 5 的正方形有 个.第二十届华罗庚金杯少年数学邀请赛A BED H C 初赛 C 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:( 9 - 11 + 13 - 15 + 17 )×120- 1 ÷ 1=( )20 30 42 56 72 3 4A .42B .43C .15 1D .16 2332. 如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成 45 度角.最高的小树高 2.8 米,最低的小树高 1.4 米,那么从左向右数第 4 棵树的高度是( )米.A .2.6B .2.4C .2.2D .2.03. 春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生,事后,甲、乙、丙、丁 4 位同学有如下的对话: 甲:“丙、丁之中至少有 1 人捐了款.” 乙:“丁、甲之中至多有 1 人捐了款.” 丙:“你们 3 人中至少有 2 人捐了款.” 丁:“你们 3 人中至多有 2 人捐了款.” 已知这 4 位同学说的都是真话且其中恰有 2 位同学捐了款,那么这 2 位同学是( ).A .甲、乙B .丙、丁C .甲、丙D .乙、丁4. 六位同学数学考试的平均成绩是 92.5 分,他们的成绩是互不相同的整数,最高的 99 分,最低的 76分,那么按分数从高到低居第三位的同学的分数至少是( ). A .94 B .95 C .96D .975. 如图,BH 是直角梯形 ABCD 的高,E 为梯形对角线 AC 上一点;如果△DEH 、△BEH 、△BCH 的面积依次为 56、50、40,那么△CEH 的面积是( ).A .32B .34C .35D .366. 一个由边长为 1 的小正方形组成的n n 的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的 4 个角上的小正方形不全同色,那么正整数 n 的最大值是( ).A .3B .4C .5D .645°二、填空题(每小题10 分,共40 分)7.在每个格子中填入1 至6 中的一个,使得每行、每列及每个2×3 长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是3 月 1 4相约华杯8.整数n 一共有10 个约数,这些约数从小到大排列,第8 个数是n.那么整数n 的最大值是39.在边长为300 厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是厘米.(π取3.14)10.A 地、B 地、C 地、D 地依次分布在同一条公路上,甲、乙、丙三人分别从A 地、B 地C 地同时出发,匀速向D 地行进.当甲在C 地追上乙时,甲的速度减少40%;当甲追上丙时,甲的速度再次减少40%;甲追上丙后9 分钟,乙也追上了丙,这时乙的速度减少25%;乙追上丙后再行50 米,三人同时到D 地.已知乙出发时的速度是每分钟60 米,那么甲出发时的速度是每分钟米,A、D 两地间的路程是米.第十九届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 某次考试有 50 道试题,答对一道题得 3 分,答错一道题扣 1 分,不答题不得分.小龙得分 120 分,那么小龙最多答对了( )道试题.A .40B .42C .48D .503. 用左下图的四张含有 4 个方格的纸板拼成了右下图所示的图形.若在右下图的 16 个方格分别填入 1、3、5、7(每个方格填一个数),使得每行、每列的四个数都不重复,且每个纸板内四个格子里的数也不重复,那么 A 、B 、C 、D 四个方格中数的平均数是( ).A . 4B . 5C D .74. 小明所在班级的人数不足 40 人,但比 30 人多,那么这个班男、女生人数的比不可能是( ).A .2︰3B .3︰4C .4︰5D .3︰75. 某学校组织一次远足活动,计划 10 点 10 分从甲地出发,13 点 10 分到达乙地,但出发晚了 5 分钟, 却早到达了 4 分钟.甲、乙两地之间的丙地恰好是按照计划时间到达的,那么到达丙地的时间是( ). A .11 点 40 分 B .11 点 50 分 C .12 点 D .12 点 10 分6. 如图所示,AF =7cm ,DH =4cm ,BG =5cm ,AE =1cm .若正方形 ABCD 内的四边形 EFGH 的面积为78 平方厘米,则正方形的边长为( )cm .A .10B .11C .12D .13ABA EDHF BC二、填空题(每小题 10 分,共 40 分)甲 乙7. 五名选手 A 、B 、C 、D 、E 参加“好声音”比赛,五个人站成一排集体亮相.他们胸前有每人的选手编号牌,5 个编号之和等于 35.已知站在 E 右边的选手的编号和为 13;站在 D 右边的选手的编号和为 31;站在 A 右边的选手的编号和为 21;站在 C 右边的选手的编号和为 7.那么最左侧与最右侧的选手编号之和是 .8. 甲、乙同时出发,他们的速度如下图所示,30 分钟后,乙比甲一共多行走了米.9. 四个黑色 1×1×1 的正方体和四个白色 1×1×1 的正方体可以组成方体(经过旋转得到相同的正方体视为同一种情况).种不同的 2×2×2 的正10. 在一个圆周上有 70 个点,任选其中一个点标上 1,按顺时针方向隔一个点的点上标 2,隔两个点的点上标 3,再隔三个点的点上标 4,继续这个操作,直到 1,2,3,…,2014 都被标记在点上.每个点可 能不止标有一个数,那么标记了 2014 的点上标记的最小整数是分分5 10 15 202530 5 10 15 202530第十九届华罗庚金杯少年数学邀请赛初赛 B 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 在下列四个算式中: AB ÷ CD =2,E ×F =0,G -H =1,I +J =4,A ~J 代表 0~9 中的不同数字,那么两位数 AB 不可能是( ). A .54 B .58 C .92 D .963. 淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是( ).A .淘气的剪法利用率高B .笑笑的剪法利用率高C .两种剪法利用率一样D .无法判断4. 小华下午 2 点要到少年宫参加活动,但他的手表每个小时快了 4 分钟,他特意在上午 10 点时对好了表.当小华按照自己的表于下午 2 点到少年宫时,实际早到了( )分钟.A .14B .15C .16D .175. 甲、乙、丙、丁四个人今年的年龄之和是 72 岁.几年前(至少一年)甲是 22 岁时,乙是 16 岁.又知道,当甲是 19 岁的时候,丙的年龄是丁的 3 倍(此时丁至少 1 岁).如果甲、乙、丙、丁四个人的年龄互不相同,那么今年甲的年龄可以有( )种情况.A .4B .6C .8D .106. 有七张卡片,每张卡片上写有一个数字,这七张卡片摆成一排,就组成了七位数 2014315.将这七张卡片全部分给了甲、乙、丙、丁四人,每人至多分 2 张.他们各说了一句话: 甲:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 8 的倍数.” 乙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数仍不是 9 的倍数.” 丙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 10 的倍数.” 丁:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 11 的倍数.” 已知四个人中恰好有一个人说了谎,那么说谎的人是( ).A .甲B .乙C .丙D .丁甲 乙二、填空题(每小题 10 分,共 40 分)13 ÷ 3 + 3 ÷ 2 1 + 17. 算式 1007× 4 44 3 ÷19 的计算结果是 .(1 + 2 + 3 + 4 + 5)⨯ 5 - 228. 海滩上有一堆栗子,这是四只猴子的财产,它们想要平均分配,第一只猴子来了,它左等右等别的猴子都不来,便把栗子分成四堆,每堆一样多,还剩下一个,它把剩下的一个顺手扔到海里,自己拿走了四堆中的一堆.第二只猴子来了,它也没有等到别的猴子,于是它把剩下的栗子等分成四堆,还剩下一个,它又扔掉一个,自己拿走一堆.第三只猴子也是如此,等分成四堆后,把剩下的一个扔掉, 自己拿走一堆;而最后一只猴子来,也将剩下的栗子等分成了四堆,扔掉多余的一个,取走一堆.那 么这堆栗子原来至少有 个.9. 甲、乙二人同时从 A 地出发匀速走向 B 地,与此同时丙从 B 地出发匀速走向 A 地.出发后 20 分钟甲与丙相遇,相遇后甲立即掉头;甲掉头后 10 分钟与乙相遇,然后甲再次掉头走向 B 地.结果当甲走到 B 地时,乙恰走过 A 、B 两地中点 105 米,而丙离 A 地还有 315 米.甲的速度是乙的速度的 倍,A 、B 两地间的路程是 米.10. 从 1,2,3,…,2014 中取出 315 个不同的数(不计顺序)组成等差数列,其中组成的等差数列中包含 1 的有 种取法;总共有 种取法.第十八届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 2012.25×2013.75-2010.25×2015.75=( )A .5B .6C .7D .82. 2013 年的钟声敲响了,小明哥哥感慨地说:这是我有生以来第一次将要渡过一个没有重复数字的年份.已知小明哥哥出生的年份是 19 的倍数,那么 2013 年小明哥哥的年龄是( )岁.A .16B .18C .20D .223. 一只青蛙 8 点从深为 12 米的井底向上爬,它每向上爬 3 米,因为井壁打滑,就会下滑 1 米,下滑 1 米的时间是向上爬 3 米所用时间的三分之一.8 点 17 分时,青蛙第二次爬至离井口 3 米之处,那么青蛙从井底爬到井口时所花的时间为( )分钟.A .22B .20C .17D .164. 一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为 9︰7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为 7︰5,那么盒子里原有的黑子数比白子数多( )个.A .5B .6C .7D .85. 图 ABCD 是平行四边形,M 是 DC 的中点,E 和 F 分别位于 AB 和 AD 上,且 EF 平行于 BD .若三角形 MDF 的面积等于 5 平方厘米,则三角形 CEB 的面积等于( )平方厘米.A .5B .10C .15D .206. 水池 A 和 B 同为长 3 米,宽 2 米,深 1.2 米的长方体.1 号阀门用来向 A 池注水,18 分钟可将无水的A 池注满;2 号阀门用来从 A 池向B 池放水,24 分钟可将 A 池中满池水放入 B 池.若同时打开 1 号和2 号阀门,那么当 A 池水深 0.4 米时,B 池有( )立方米的水.A .0.9B .1.8C .3.6D .7.2D F MCAEB二、填空题(每小题 10 分,共 40 分)D E AFB7. 小明、小华、小刚三人分 363 张卡片,他们决定按年龄比来分.若小明拿 7 张,小华就要拿 6 张;若小刚拿 8 张,小明就要拿 5 张.最后,小明拿了 张;小华拿了张.张;小刚拿了8. 某公司的工作人员每周都工作 5 天休息 2 天,而公司要求每周从周一至周日,每天都至少有 32 人上班,那么该公司至少需要名工作人员.9. 如图,AB 是圆 O 的直径,长 6 厘米,正方形 BCDE 的一个顶点 E 在圆周上,∠ABE =45°.那么圆 O中非阴影部分的面积与正方形 BCDE 中非阴影部分面积的差等于 平方厘米(取 π=3.14)10. 圣诞老人有 36 个同样的礼物,分别装在 8 个袋子中.已知 8 个袋子中礼物的个数至少为 1 且各不相 同.现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给 8 个小朋友,恰好分完(每个小朋 友至少分得一个礼物).那么,共有 种不同的选择.第十八届华罗庚金杯少年数学邀请赛AB 初赛 B 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 一个四位数,各位数字互不相同,所有数字之和等于 6,并且这个数是 11 的倍数,则满足这种要求的四位数共有( )个.A .6B .7C .8D .92. 2+2×3+2×3×3+……+2× 3 ⨯ 3 ⨯⨯ 3 个位数字是( ). 9个3A .2B .8C .4D .63. 在下面的阴影三角形中,不能由下图中左面的阴影三角形经过旋转、平移得到的是图( )中的三角形.ABCD4. 某日,甲学校买了 56 千克水果糖,每千克 8.06 元.过了几日,乙学校也需要买同样的 56 千克水果糖,不过正好赶上促销活动,每千克水果糖降价 0.56 元,而且只要买水果糖都会额外赠送 5%同样的水果糖.那么乙学校将比甲学校少花( )元.A .20B .51.36C .31.36D .10.365. 甲、乙两仓的稻谷数量一样,爸爸、妈妈和阳阳单独运完一仓稻谷分别需要 10 天、12 天和 15 天.爸爸、妈妈同时开始分别运甲、乙两仓的稻谷,阳阳先帮妈妈,后帮爸爸,结果同时运完两仓稻谷.那么阳阳帮妈妈运了( )天. A .3B .4C .5D .66. 如图,将长度为 9 的线段 AB 分成 9 等份,那么图中所有线段的长度的总和是( ).A .132B .144C .156D .165二、填空题(每小题10 分,共40 分)7.将乘积0.2˙43˙×0.32˙5233˙化为小数,小数点后第2013 位的数字是.8.一只青蛙8 点从深为12 米的井底向上爬,它每向上爬3 米,因为井壁打滑,就会下滑1 米,下滑1 米的时间是向上爬3 米所用时间的三分之一.8 点17 分时,青蛙第二次爬至离井口3 米之处,那么青蛙从井底爬到井口时所花的时间为分钟.9.一个水池有三个进水口和一个出水口.同时打开出水口和其中的两个进水口,注满整个水池分别需要6 小时、5 小时和4 小时;同时打开出水口和三个进水口,注满整个水池需要3 小时.如果同时打开三个进水口,不打开出水口,那么注满整个水池需要小时.10.九个同样的直角三角形卡片,用卡片的锐角拼成一圈,可以拼成类似下图所示的平面图形.这种三角形卡片中的两个锐角中较小的一个的度数有种不同的可能值.(下图只是其中一种可能的情况)第十七届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2012 年 3 月 17 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:[(0.8+ 1 )×24+6.6]÷ 9-7.6=( ).5 14A .30B .40C .50D .602. 以平面上 4 个点为端点连接线段,形成的图形中最多可以有( )个三角形.A .3B .4C .6D .83. 一个奇怪的动物庄园里住着猫和狗,狗比猫多 180 只.有 20%的狗错认为自己是猫;有 20%的猫错认为自己是狗.在所有的猫和狗中,有 32%认为自己是猫,那么狗有( )只.A .240B .248C .420D .8424. 下图的方格纸中有五个编号为 1,2,3,4,5 的小正方形,将其中的两个涂上阴影,与图中阴影部分正好组成正方体的展开图,这两个正方形的编号可以是( )A .1,2B .2,3C .3,4D .4,55. 在下图所示的算式中,每个字母代表一个非零数字,不同的字母代表不同的数字,则和的最小值是( ) A .369B .396C .459D .5496. 下图是由相同的正方形和相同的等腰直角三角形构成,则正方形的个数为( )A .83B .79C .72D .651 253 4A B C + D E F H IJ二、填空题(每小题 10 分,共 40 分)百十个百 十 个A EC HFB7. 如图的计数器三个档上各有 10 个算珠,将每档算珠分成上下两部分,得到两个三位数.要求上面部分是各位数字互不相同的三位数,且是下面三位数的倍数,则上面部分的三位数是.8. 四支排球队进行单循环比赛,即每两队都要赛一场,且只赛一场.如果一场比赛的比分是 3:0 或 3:1.则胜队得 3 分,负队得 0 分;如果比分是 3:2,则胜队得 2 分,负队得 1 分.比赛的结果各队得分恰好是四个连续的自然数,则第一名的得分是 分.9. 甲、乙两车分别从 A 、B 两地同时出发,且在 A 、B 两地往返来回匀速行驶.若两车第一次相遇后,甲车继续行驶 4 小时到达 B ,而乙车只行驶了 1 小时就到达 A ,则两车第 15 次(在 A ,B 两地相遇次数不计)相遇时,它们行驶了 小时.10. 正方形 ABCD 的面积为 9 平方厘米,正方形 EFGH 的面积为 64 平方厘米.如图所示,边 BC 落在 EH上.己知三角形 ACG 的面积为 6.75 平方厘米,则三角形 ABE 的面积为 平方厘米.。
第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学高年级组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学高年级组)一、选择题(共6小题,每小题3分,满分18分)1.(3分)在如图所示的两位数的加法运算式中,已知A+B+C+D=22,则X+Y =()A.2 B.4 C.7 D.132.(3分)已知甲瓶盐水浓度为8%,乙瓶盐水浓度为5%,混合后浓度为6.2%,那么四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度为()A.7.5% B.5.5% C.6% D.6.5%3.(3分)两个数的最大公约数是20,最小公倍数是100,下面说法正确的有()个.(1)两个数的乘积是2000.(2)两个数都扩大10倍,最大公约数扩大100倍.(3)两个数都扩大10倍,最小公倍数扩大10倍.(4)两个数都扩大10倍,两个数乘积扩大100倍.A.1 B.2 C.3 D.44.(3分)将39、41、44、45、47、52、55这7个数重新排成一列,使得其中任意相邻的三个数的和都为3的倍数.在所有这样的排列中,第四个数的最大值是()A.44 B.45 C.47 D.525.(3分)如图所示,在5×8的方格中,阴影部分的面积为37cm2.则非阴影部分的面积为()cm2.A.43 B.74 C.80 D.1116.(3分)在由1、3、4、7、9组成的没有重复数字的数中,是9的倍数的有()个.A.1 B.2 C.3 D.4二、填空题(共4小题,每小题3分,满分12分)7.(3分)满足下列两个条件的四位数共有个.(1)任意相邻两位数字之和均不大于2;(2)任意相邻三位数字之和均不小于3.8.(3分)在17□17□17□17□17的四个□中填入“+”、“﹣”、“×”、“÷”运算符号各一个.所成的算式的最大值是.9.(3分)图中,ABC是一个钝三角形.BC=6厘米,AB=5厘米,BC边的高AD等于4厘米,若此三角形以每秒3厘米的速度沿DA的方向向上移动.2秒后,此三角形扫过的面积是平方厘米.10.(3分)一条公路上有A、O、B三个地点,O在A与B之间,A与O相距1360米.甲、乙两人同时分别从A点和O点出发向B点进行.出发后第10分钟,甲、乙两人离O点的距离相等:第40分钟甲与乙两人在B点相遇.那么O与B两点的距离是米.2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学高年级组)参考答案与试题解析一、选择题(共6小题,每小题3分,满分18分)1.(3分)在如图所示的两位数的加法运算式中,已知A+B+C+D=22,则X+Y =()A.2 B.4 C.7 D.13【分析】根据和的个位数字是9可得:B+D=9,则A+C=22﹣9=13,所以可得x=1,y=3,据此即可求出x+y的值.【解答】解:根据题干分析可得:B+D=9,则A+C=22﹣9=13,所以可得x=1,y=3,则x+y=1+3=4.故选:B.2.(3分)已知甲瓶盐水浓度为8%,乙瓶盐水浓度为5%,混合后浓度为6.2%,那么四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度为()A.7.5% B.5.5% C.6% D.6.5%【分析】我们分别设甲瓶盐水质量为a,乙瓶盐水的质量是b.根据它们混合后浓度为6.2%为等量关系求出ab之间的数量关系,然后再进一步求出四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度.【解答】解:设甲瓶盐水质量为a,乙瓶盐水的质量是b.(8%a+5%b)÷(a+b)=6.2%,解得:a=b;(a×8%+b×5%)÷(a+b),=(a+b)÷(b+b),=(b b)÷(b),=b×,=6.5%;故选:D.3.(3分)两个数的最大公约数是20,最小公倍数是100,下面说法正确的有()个.(1)两个数的乘积是2000.(2)两个数都扩大10倍,最大公约数扩大100倍.(3)两个数都扩大10倍,最小公倍数扩大10倍.(4)两个数都扩大10倍,两个数乘积扩大100倍.A.1 B.2 C.3 D.4【分析】根据“两个数的最大公约数是20,最小公倍数是100”,可知这两个数分别是20和100,据此逐项进行分析判断得解.【解答】解:根据题意,可知这两个数分别是20和100;(1)20×100=2000,所以两个数的乘积是2000,所以原说法正确的;(2)两个数都扩大10倍,最大公约数变为20×10=200,是扩大了10倍,所以原说法错误;(3)两个数都扩大10倍,最小公倍数变为100×10=1000,是扩大了10倍,所以原说法正确;(4)两个数都扩大10倍,变为200和1000,乘积变为200000,也即两个数乘积扩大100倍,所以原说法正确;正确的说法有3个.故选:C.4.(3分)将39、41、44、45、47、52、55这7个数重新排成一列,使得其中任意相邻的三个数的和都为3的倍数.在所有这样的排列中,第四个数的最大值是()A.44 B.45 C.47 D.52【分析】将给出的每个数分别除以3,余数分别是:0、2、2、0、2、1、1;把余数排列,相邻三个数的和都为3,则重新排列为:2、1、0、2、1、0、2;因为第四个数是2,余数为2的最大的数是47.【解答】解:因为39÷3=13,41÷3=13…2,44÷3=14…2,45÷3=15,47÷3=15…2,52÷3=17…1,55÷3=18…1,余数分别是:0、2、2、0、2、1、1;按相邻三个数的和都为3,把余数重新排列为:2、1、0、2、1、0、2;因为第四个数是2,余数为2的最大的数是47.故选:C.5.(3分)如图所示,在5×8的方格中,阴影部分的面积为37cm2.则非阴影部分的面积为()cm2.A.43 B.74 C.80 D.111【分析】如图所示,在5×8的方格中,阴影部分占了18.5个格,非阴影就分占21.5格;阴影面积为37cm2,据此可求出每格的面积,进而求出则非阴影部分的面积.【解答】解:如图,阴影部分占了18.5个格,面积为37cm2,每格的面积是:37÷18.5=2(cm2);非阴影就分占21.5格,其面积是:21.5×2=43(cm2);答:则非阴影部分的面积为43cm2;故选:A.6.(3分)在由1、3、4、7、9组成的没有重复数字的数中,是9的倍数的有()个.A.1 B.2 C.3 D.4【分析】一个数如果能被9整除那么这个数的各位数字和必须能被9整除,由此选择数字解答即可.【解答】解:如果能被9整除,那么这个数的各位数字和必须能被9整除,这样的组合可能是由一个数字9组成数是9,这样共有1种.故选:A.二、填空题(共4小题,每小题3分,满分12分)7.(3分)满足下列两个条件的四位数共有 1 个.(1)任意相邻两位数字之和均不大于2;(2)任意相邻三位数字之和均不小于3.【分析】由(1)可知,这个四位数每个数位上的数字只能是0,1,2,并且1与2,2与2不能相邻,再结合(2)可知,每个数位上的数字不能是0.综上可知每个数位上的数字只能是1,即这个四位数是1111.【解答】解:由分析可知,满足条件的四位数是1111,只有1个.故答案为:1.8.(3分)在17□17□17□17□17的四个□中填入“+”、“﹣”、“×”、“÷”运算符号各一个.所成的算式的最大值是305 .【分析】题目要求只填运算符号,不加括号;那么运算顺序是先算乘除,再算加减,要使运算的结果最大只要减的数最小即可.【解答】解:因为减号只能用一次,减数不能为0,那么17÷17=1做减数时,运算的结果最大:17×17+17﹣17÷17,=289+17﹣1,=305.故答案为:305.9.(3分)图中,ABC是一个钝三角形.BC=6厘米,AB=5厘米,BC边的高AD等于4厘米,若此三角形以每秒3厘米的速度沿DA的方向向上移动.2秒后,此三角形扫过的面积是66 平方厘米.【分析】平移时图形的每个点都在移动及整个图形沿同一方向移动同样的距离,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,就是沿高的方向移动了3×2=6cm,三角形扫过的面积应该是一个正方形的面积加上一个三角形的面积,再加上平行四边形ABFE的面积.【解答】解:扫过的面积应该是正方形BCDF的面积加上上面三角形的面积,再加上平行四边形ABFE的面积,因为AD=4,AB=5,且AB2﹣AD2=BD2,即52﹣42=32,所以DB=3厘米,3×2=6厘米,6×6+×6×4÷2+6×3,=36+12+18,=66(平方厘米).答:此三角形扫过的面积是66平方厘米.故答案为:66.10.(3分)一条公路上有A、O、B三个地点,O在A与B之间,A与O相距1360米.甲、乙两人同时分别从A点和O点出发向B点进行.出发后第10分钟,甲、乙两人离O点的距离相等:第40分钟甲与乙两人在B点相遇.那么O与B两点的距离是2040 米.【分析】第40分钟甲与乙两人在B点相遇,即此时甲行了1360米,则甲的速度为每分钟1360÷40米,所以10分钟甲行了1360÷40×10=340米,距0点1360﹣340=1020米,又出发后第10分钟,甲、乙两人离O点的距离相等,则乙每分钟行1020÷10=102米.由于第第40分钟甲与乙两人在B点相遇,此时乙行了2个0B,则O与B两点的距离是 102×40÷2米.【解答】解:(1360﹣1360÷40×10)÷10×40÷2=(1360﹣340)÷10×40÷2,=1020×40÷2,=2040(米).答:O与B两点的距离是 2040米.故答案为:2040.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:56:04;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第十七届华罗庚金杯少年数学邀请赛网上初赛试卷-中年级组.docx

第十七届华罗庚金杯少年数学邀请赛网上初赛试卷(小学中年级组)一、选择题(每小题10分,以下每题的四个选项中,仅有一个是正确的,请单击选择答案) 1•如图,适中上的表针从(1)转到(2)最少经过了( )A 、2小时30分B 、2小时45分C 、3小时30分D 、3小时45分【分析】:考点:钟表问题难度:★★ 解:表(1)显示的是12:45分,表(2)显示的是3: 30也可以表示为15:30分,两个表同 表示为下午的时间就是最近的。
15:30-22:45=2:45分答案:[B]2.在2012年,1月1日是星期口,并且( )【分析】: 考点:周期问题难度:★★★ 解:1月有31天,所以前三天所表示的星期数会出现5次,其它的出现4次,而1月份前 三天分别是星期日、一、二。
所以星期三只有4个。
这样1月最后一天就是星期二,而2 月第一天是星期三。
注意到2012年是闰年,2月份有29天。
所以,2月份的第一天表示的 星期数回出现5次。
所以2月份有4个星期三,2月份有5个星期三。
答案:[D]3•有大小不同的4个数,从中任取3个数相加,所得到的和分别是180,197,208和222,那 么,第二小的数所在的和一定不是( )A 、 180B 、 197C 、 208D 、 222【分析】:考点:推理难度:★★ 解:因为是三个数的和,所以可以看做是4个数的总和减去其中的一个。
那么和减去最小的 数一定是最大的222。
减去第二小的一定是第二大的,即208答案:[C]4.四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前而20米,这 时,跑在最前面的两位同学相差( )米 A 、 10 B 、 20 C 、 50 D 、60A 、 1月份有5个星期三,B 、 1月份有5个星期三,C 、 1月份有4个星期三,D 、 1月份有4个星期三, 2月份只有4个星期三 2月份也有5个星期三 2月份也有4个星期三 2月份有5个星期三【分析】:考点:推理问题难度:★★解:先根据中乙芮的位置关系容易得到下图內刼乙30 S 10 T所以,前两名甲与丁的距离是10米。
历届华杯赛初赛小高真题库

初赛试卷(小学高年级组)一、选择题(每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1.两个有限小数的整数部分分别是7和10,那么这两个有限小数的积的整数部分有()种可能的取值.(A)16 (B)17 (C)18 (D)192.小明家距学校,乘地铁需要30分钟,乘公交车需要50分钟.某天小明因故先乘地铁,再换乘公交车,用了40分钟到达学校,其中换乘过程用了6分钟,那么这天小明乘坐公交车用了()分钟.(A)6 (B)8 (C)10 (D)123.将长方形ABCD对角线平均分成12段,连接成右图,长方形ABCD内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是()平方厘米.(A)14 (B)16 (C)18 (D)204.请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是().(A)2986 (B)2858 (C)2672 (D)2754CD BA5. 在序列20170……中,从第5个数字开始,每个数字都是前面4个数字和的个位数,这样的序列可以一直写下去.那么从第5个数字开始,该序列中一定不会出现的数组是( ). (A )8615(B )2016(C )4023(D )20176. 从0至9中选择四个不同的数字分别填入方框中的四个括号中,共有( )种填法使得方框中话是正确的.(A )1(B )2(C )3(D )4二、填空题 (每小题 10 分, 共40分)7. 若15322.254553923444741A ⎛⎫-⨯÷+=⎪ ⎪ ⎪+ ⎪⎝⎭,那么A 的值是________. 8. 右图中,“华罗庚金杯”五个汉字分别代表1—5这五个不同的数字.将各线段两端点的数字相加得到五个和,共有 ________种情况使得这五个和恰为五个连续自然数.9. 右图中,ABCD 是平行四边形,E 为CD 的中点,AE 和BD 的交点为F ,AC 和BE 的交点为H ,AC 和BD 的交点为G ,四边形EHGF 的面积是15平方厘米,则ABCD 的面积是__________平方厘米.10. 若2017,1029与725除以d 的余数均为r ,那么d r -的最大值是________.第二十届华罗庚金杯少年数学邀请赛这句话里有( )个数大于1,有( )个数大于2,有( )个数大于3,有( )个数大于4. 罗华庚金 杯决赛试题B (小学高年级组)一、填空题(每小题10份,共80分)1. 计算:8184157.628.814.48012552⨯+⨯-⨯+=________.2. 甲、乙、丙、丁四人共植树60棵.已知,甲植树的棵数是其余三人的二分之一,乙植树的棵数是其余三人的三分之一,丙植树的棵数是其余三人的四分之一,那么丁植树________棵.3. 当时间为5点8分时,钟表面上的时针与分针成________度的角.4. 某个三位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,加4是6的倍数,那么这个数最小为________.5. 贝塔星球有七个国家,每个国家恰有四个友国和两个敌国,没有三个国家两两都是敌国.对于一种这样的星球局势,共可以组成________个两两都是友国的三国联盟.6. 由四个互不相同的非零数字组成的没有重复数字的所有四位数之和为106656,则这些四位数中最大的是________,最小的是________.7. 见右图,三角形ABC 的面积为1,3:1:=OB DO ,5:4:=OA EO ,则三角形DOE 的面积为________.8. 三个大于1000的正整数满足:其中任意两个数之和的个位数字都等于第三个数的个位数字,那么这3个数之积的末尾3位数字有________种可能数值.二、解答下列各题(每题10分,共40分,要求写出简要过程)9. 将1234567891011的某两位数字交换能否得到一个完全平方数?请说明理由.10. 如右图所示,从长、宽、高为15,5,4的长方体中切走一块长、宽、高为,5,y x 的长方体(,x y 为整数),余下部分的体积为120,求x 和y .yx515411. 圆形跑道上等距插着2015面旗子,甲与乙同时同向从某个旗子出发,当甲与乙再次同时回到出发点时,甲跑了23圈,乙跑了13圈.不算起始点旗子位置,则甲正好在旗子位置追上乙多少次?12. 两人进行乒乓球比赛,三局两胜制,每局比赛中,先得11分且对方少于10分者胜,10平后多得2分者胜.两人的得分总和都是31分,一人赢了第一局并且赢得了比赛,那么第二局的比分共有多少种可能?三、解答下列各题(每小题15分,共30分,要求写出详细过程)13. 如右图所示,点M 是平行四边形ABCD 的边CD 上的一点,且2:1: MC DM ,四边形EBFC 为平行四边形,FM 与BC 交于点G .若三角形FCG 的面积与三角形MED 的面积之差为13cm 2,求平行四边形ABCD 的面积.14. 设“一家之言”、“言扬行举”、“举世皆知”、“知行合一”四个成语中的每个汉字代表11个连续的非零自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数.如果每个成语中四个汉字所代表的数之和都是21,则“行”可以代表的数最大是多少?第十八届华罗庚金杯少年数学邀请赛 初赛试题C (小学高年级组) (时间: 2013 年3月23日)一、选择题 (每小题 10 分, 满分60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 如果mn=+⨯⨯20122014201420132013(其中m 与n 为互质的自然数), 那么m +n 的值是( ). (A )1243 (B )1343 (C )4025 (D )40292. 甲、乙、丙三位同学都把25克糖放入100克水中混合成糖水, 然后他们又分别做了以下事情:最终,( )得到的糖水最甜.(A )甲 (B )乙 (C )丙 (D )乙和丙3. 一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米,下滑1米的时间是向上爬3米所用时间的三分之一. 8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为( )分钟. (A )22 (B )20 (C )17 (D )164. 已知正整数A 分解质因数可以写成γβα532⨯⨯=A , 其中α、β、γ 是自然数. 如果A的二分之一是完全平方数, A 的三分之一是完全立方数, A 的五分之一是某个自然数的五次方, 那么 γβα++ 的最小值是( ).再加入50克含糖率20%的糖水.再加入20克糖和30克水.再加入100克糖与水的比是2:3的糖水.(A)10 (B)17 (C)23 (D)315.今有甲、乙两个大小相同的正三角形, 各画出了一条两边中点的连线. 如图, 甲、乙位置左右对称, 但甲、乙内部所画线段的位置不对称. 从图中所示的位置开始, 甲向右水平移动, 直至两个三角形重叠后再离开. 在移动过程中的每个位置, 甲与乙所组成的图形中都有若干个三角形. 那么在三角形个数最多的位置, 图形中有()个三角形.(A)9 (B)10 (C)11 (D)126.从1~11这11个整数中任意取出6个数, 则下列结论正确的有()个.①其中必有两个数互质;②其中必有一个数是其中另一个数的倍数;③其中必有一个数的2倍是其中另一个数的倍数.(A)3 (B)2 (C)1 (D)0二、填空题(每小题10 分, 满分40分)7.有四个人去书店买书, 每人买了4本不同的书, 且每两个人恰有2本书相同, 那么这4个人至少买了_______种书..8.每天, 小明上学都要经过一段平路AB、一段上坡路BC和一段下坡路CD (如右图). 已知AB:BC:CD =1:2:1, 并且小明在平路、上坡路、下坡路上的速度比为3:2:4. 那么小明上学与放学回家所用的时间比是.9.黑板上有11个1, 22个2, 33个3, 44个4. 做以下操作: 每次擦掉3个不同的数字,并且把没擦掉的第四种数字多写2个. 例如: 某次操作擦掉1个1, 1个2, 1个3, 那就再写上2个4. 经过若干次操作后, 黑板上只剩下3个数字, 而且无法继续进行操作, 那么最后剩下的三个数字的乘积是.10.如右图, 正方形ABCD被分成了面积相同的8个三角形, 如果DG = 5, 那么正方形ABCD面积是.第二十一届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间: 2015年12月12日10:00—11:00)一、选择题 (每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 算式43421Λ43421Λ个个2016201699999999⨯的结果中含有( )个数字0.(A )2017 (B )2016 (C )2015 (D )20142. 已知A , B 两地相距300米.甲、乙两人同时分别从A , B 两地出发, 相向而行, 在距A 地140米处相遇; 如果乙每秒多行1米, 则两人相遇处距B 地180米.那么乙原来的速度是每秒( )米.(A )532 (B )542(C )3 (D )513 3. 在一个七位整数中, 任何三个连续排列的数字都构成一个能被11或13整除的三位数, 则这个七位数最大是( ).(A )9981733 (B )9884737 (C )9978137 (D )98717734. 将1, 2, 3, 4, 5, 6, 7, 8这8个数排成一行, 使得8的两边各数之和相等, 那么共有( )种不同的排法.(A )1152 (B )864 (C )576 (D )2885. 在等腰梯形ABCD 中, AB 平行于CD , 6=AB , 14=CD , AEC ∠是直角, CE CB =, 则2AE 等于( ).(A )84 (B )80(C )75 (D )646. 从自然数1,2,32015,2016L ,,中, 任意取n 个不同的数, 要求总能在这n 个不同的数中找到5个数, 它们的数字和相等. 那么n 的最小值等于( ). (A )109 (B )110 (C )111 (D )112 二、填空题 (每小题 10 分, 共40分)7. 两个正方形的面积之差为2016平方厘米, 如果这样的一对正方形的边长都是整数厘米, 那么满足上述条件的所有正方形共有 对.8. 如下图, O , P , M 是线段AB 上的三个点, AB AO 54=, AB BP 32=, M 是AB 的中点, 且2=OM , 那么PM 长为 .9. 设q 是一个平方数. 如果2-q 和2+q 都是质数, 就称q 为P 型平方数. 例如, 9就是一个P 型平方数.那么小于1000的最大P 型平方数是 .10. 有一个等腰梯形的纸片, 上底长度为2015, 下底长度为2016. 用该纸片剪出一些等腰梯形, 要求剪出的梯形的两个底边分别在原来梯形的底边上, 剪出的梯形的两个锐角等于原来梯形的锐角, 则最多可以剪出 个同样的等腰梯形.第十七届华罗庚金杯少年数学邀请赛初赛试题A (小学高年级组)一、选择题1、计算:19+⨯+-=[(0.8)24]7.6(___)514(A)30 (B)40 (C)50 (D)602、以平面上4个点为端点连接线段,形成的图形中最多可以有()个三角形。
第17届“华杯赛”网上决赛试题以及答案(小中组)
3. 鸡兔同笼, 共有头 51 个, 兔的总脚数比鸡的总脚数的 3 倍多 4 只, 那么笼中 共有兔子 只.
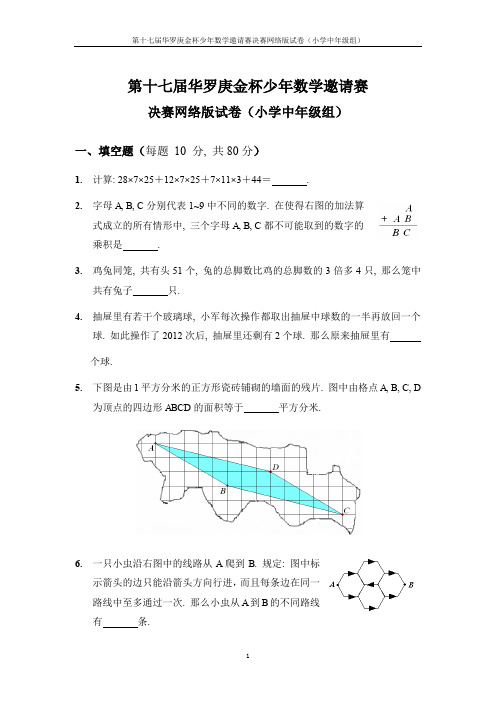
4. 抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个 球. 如此操作了 2012 次后, 抽屉里还剩有 2 个球. 那么原来抽屉里有 个球. 5. 下图是由 1 平方分米的正方形瓷砖铺砌的墙面的残片. 图中由格点 A, B, C, D 为顶点的四边形 ABCD 的面积等于 平方分米.
6. 一只小虫沿右图中的线路从 A 爬到 B. 规定: 图中标 示箭头的边只能沿箭头方向行进, 而且每条边在同一 路线中至多通过一次. 那么小虫从 A 到 B 的不同路线 有 条.
1
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷(小学中年级组)
7. 有一些自然数, 它们中的每一个与 7 相乘, 其积的末尾四位数都为 2012, 那 么在这些自然数中, 最小的数是 .
8. 将棱长为 1 米的正方体木块分割成棱长为 1 厘米的小正方体积木, 设想孙悟 空施展神力将所有的小积木一个接一个地叠放起来, 成为一根长方体 “神棒”, 直指蓝天. 已知珠穆朗玛峰的海拔高度为 8844 米, 则“神棒”的高度超过珠 穆朗玛峰的海拔高度 米.
二、回答下列各题(每题 10 分, 共 40 分, 写出答案即可)
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷(小学中年级组)
第十届华罗庚金杯少年数学邀请赛
决赛网络版试卷(小学中年级组)
一、填空题(每题 10 分, 共 80 分)
1. 计算: 28× 7× 25+12× 7× 25+7× 11× 3+44= .
2. 字母 A, B, C 分别代表 1~9 中不同的数字. 在使得右图的加法算 式成立的所有情形中, 三个字母 A, B, C 都不可能取到的数字的 乘积是 .
第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小中组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小中组)一、填空题(每题10分,共80分)1.(10分)计算:28×7×25+12×7×25+7×11×3+44=.2.(10分)字母 A,B,C 分别代表 1~9 中不同的数字.在使得如图的加法算式成立的所有情形中,三个字母 A,B,C 都不可能取到的数字的乘积是.3.(10分)鸡兔同笼,共有头51个,兔的总脚数比鸡的总脚数的3倍多4只,那么笼中共有兔子只.4.(10分)抽屉里有若干个玻璃球,小军每次操作都取出抽屉中球数的一半再放回一个球.如此操作了2012次后,抽屉里还剩有2个球.那么原来抽屉里有个球.5.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点 A,B,C,D 为顶点的四边形ABCD的面积等于多少平方分米?6.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?7.(10分)有一些自然数,它们中的每一个与7相乘,其积的末尾四位数都为2012,那么在这些自然数中,最小的数是.8.(10分)将棱长为1米的正方体木块分割成棱长为1厘米的小正方体积木,设想孙悟空施展神力将所有的小积木一个接一个地叠放起来,成为一根长方体“神棒”,直指蓝天.已知珠穆朗玛峰的海拔高度为8844米,则“神棒”的高度超过珠穆朗玛峰的海拔高度米.二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)已知被除数比除数大78,并且商是 6,余数是 3,求被除数与除数之积.10.(10分)今年甲、乙俩人年龄的和是70岁.若干年前,当甲的年龄只有乙现在这么大时,乙的年龄恰好是甲年龄的一半.问:甲今年多少岁?11.(10分)有三个连续偶数,它们的乘积是一个五位数,该五位数个位是0,万位是2,十位、百位和千位是三个不同的数字,那么这三个连续偶数的和是多少?12.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表 0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小中组)参考答案与试题解析一、填空题(每题10分,共80分)1.(10分)计算:28×7×25+12×7×25+7×11×3+44=7275 .【分析】根据乘法的结合律与分配律简算即可,注意计算中的11×25的乘法时根据“两边拉,中间加”巧算.【解答】解:28×7×25+12×7×25+7×11×3+44=7×25×(28+12)+11×21+11×4=7×(25×40)+11×(21+4)=7×1000+11×25=7000+275=7275故答案为:7275.2.(10分)字母 A,B,C 分别代表 1~9 中不同的数字.在使得如图的加法算式成立的所有情形中,三个字母 A,B,C 都不可能取到的数字的乘积是8 .【分析】首先分析出A是加上进位等于B,那么A比B小1,并且A与B 的和是有..进位的,枚举出所有情况排除即可.【解答】解:依题意可知:A加上进位等于B,那么这两个数字相差1,可以是A=5,B=6,C=1.A=6,B=7,C=3.A=7,B=8,C=5.A=8,B=9,C=7.那么A,B,C不可能取道的数字有2,4即2×4=8故答案为:83.(10分)鸡兔同笼,共有头51个,兔的总脚数比鸡的总脚数的3倍多4只,那么笼中共有兔子31 只.【分析】根据题意可知如果少一只兔子,则兔的总脚数是鸡的总脚数的3倍,因一只兔脚的只数是一只鸡脚只数的4÷2=2倍,所以当兔的只数是鸡的只数的3÷2=1.5倍时兔的总脚数是鸡的总脚数的3倍,据此可只鸡的头数是(51﹣1)÷(1.5+1)=20只,进而可求出兔子的只数.【解答】解:4÷2=2(51﹣1)÷(3÷2+1)=50÷2.5=20(只)51﹣20=31(只)答:笼子中共有兔子31只.故答案为:31.4.(10分)抽屉里有若干个玻璃球,小军每次操作都取出抽屉中球数的一半再放回一个球.如此操作了2012次后,抽屉里还剩有2个球.那么原来抽屉里有 2 个球.【分析】还原问题每次拿走一半再放回一个,倒推就是每次拿走一个再加一倍.2个拿走1个,剩下1个加一倍是2个.重复周期问题.【解答】解:还原问题的倒推图操作第一次:(2﹣1)×2=2(个)操作第二次:(2﹣1)×2=2(个)操作第三次:(2﹣1)×2=2(个)每一次结果都是2个,属于周期问题.无论操作多少次结果都是2个.故答案为:25.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点 A,B,C,D 为顶点的四边形ABCD的面积等于多少平方分米?【分析】这属于正方形格点问题,根据正方形格点毕克定理S=N﹣1+L÷2可以直接求出面积,其中N表示内部的格点数,L表示边界上的格点数.【解答】解:内部的格点数是12,边界点的数是6,根据公式列出算式是12﹣1+6÷2=14答:四边形ABCD的面积等于14平方分米.6.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?【分析】小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.【解答】解:小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.答:小虫从A到B的不同路线有10条.7.(10分)有一些自然数,它们中的每一个与7相乘,其积的末尾四位数都为2012,那么在这些自然数中,最小的数是1716 .【分析】首先分析本题可以反过来求解,想找到最小的乘数可以转换找到最小的乘积,2012不是7的倍数,那么需要在前面加上一位数字是最小的即可.【解答】解:首先发现2012不是7的倍数,那么要找到最小就需要看看在2012前加一个最小的数字组成7的倍数.在首位加上数字1,12012÷7=1716.那么最小就是1716.故答案为:1716.8.(10分)将棱长为1米的正方体木块分割成棱长为1厘米的小正方体积木,设想孙悟空施展神力将所有的小积木一个接一个地叠放起来,成为一根长方体“神棒”,直指蓝天.已知珠穆朗玛峰的海拔高度为8844米,则“神棒”的高度超过珠穆朗玛峰的海拔高度1156 米.【分析】1米=100厘米,则1立方米=1000000立方厘米,即1 米的正方体木块分割成棱长为 1 厘米的小正方体积1000000个,即可求解.【解答】解:1立方米=1000000立方厘米,即1米的正方体木块分割成棱长为1厘米的小正方体积1000000个;它们相互叠加组成“神棒”的高度=1000000×0.01=10000(米);即比珠穆朗玛峰的海拔高度高10000﹣8848=1156(米),故填1156.故答案为:1156.二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)已知被除数比除数大78,并且商是 6,余数是 3,求被除数与除数之积.【分析】被除数=除数×商+余数,所以被除数是除数的6倍多3,78就是除数的5倍多3.【解答】解:除数=(78﹣3)÷(6﹣1)=25,被除数=除数×商+余数=6×25+3=153,那么被除数与除数之积是153×25=3825.故答案为:3825.10.(10分)今年甲、乙俩人年龄的和是70岁.若干年前,当甲的年龄只有乙现在这么大时,乙的年龄恰好是甲年龄的一半.问:甲今年多少岁?【分析】根据题意,可得:若干年前乙的年龄等于今年乙的年龄的一半,所以今年甲的年龄等于若干年前甲的年龄的1.5(1+0.5=1.5)倍,所以今年甲的年龄等于今年乙的年龄的1.5倍,再根据今年甲、乙两人年龄的和是70岁.求出甲今年多少岁即可.【解答】解:因为当甲的年龄只有乙现在这么大时,乙的年龄恰好是甲年龄的一半,所以今年甲的年龄等于若干年前甲的年龄的:1+0.5=1.5倍,所以今年甲的年龄等于今年乙的年龄的1.5倍,70÷(1+1.5)×1.5=70÷2.5×1.5=28×1.5=42(岁)答:甲今年42岁.11.(10分)有三个连续偶数,它们的乘积是一个五位数,该五位数个位是0,万位是2,十位、百位和千位是三个不同的数字,那么这三个连续偶数的和是多少?【分析】26×26×26=17576,31×31×31=29791,所以三个连续偶数在24,26,28,30,32之间,考虑个位为0,应有因数2,5.【解答】解:26×26×26=17576,31×31×31=29791,所以三个连续偶数在24,26,28,30,32之间,考虑个位为0,应有因数2,5,26×28×30=21840,符合要求.28×30×32=26880,不合要求,30×32×34=32640,不符合要求.所以这三个连续偶数的和为26+28+30=84.故答案为:84.12.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表 0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?【分析】由题意,14×20×35+98=9898,即可得出结论.【解答】解:由题意,14×20×35+98=9898,∴当四位数北京精神最大时,厚德为98.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:49:20;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)一、填空题(每题10分,共80分)1.(10分)算式×[2×(1.875﹣)]÷[(0.875+1)÷3]的值为.2.(10分)小龙的妈妈比爸爸小3 岁,妈妈今年的年龄是小龙今年的9倍,爸爸明年的年龄是小龙明年的8倍,那么爸爸今年岁.3.(10分)某水池有A、B两个排水龙头.同时打开两个龙头排水,30分钟可将满池的水排尽;同时打开两个龙头排水10分钟,然后关闭A龙头,B龙头继续排水,30分钟后也可以将满池的水排尽.那么单独打开B龙头,需要分钟才能排尽满池的水.4.(10分)如图,圆O的面积为32,OC⊥AB,∠AOE=∠EOD,∠COF=∠FOD,则扇形EOF的面积为.5.(10分)算式+++++++++的值的整数部分为.6.(10分)如图中,正方形ABCD的面积为840平方厘米,AE=EB,BF=2FC,DF与EC 相交于G.则四边形AEGD的面积为平方厘米.7.(10分)一个自然数无论从左向右读或从右向左读都是一样的数称之为“回文数”,例如:909.那么所有三位回文数的平均数是.8.(10分)将七个连续自然数分别填在五个圆的交点A,B,C,D,E,F,G处,使得每个圆上的数的和都相等.如果所填的数都大于0且不大于10,则填在点G处的数是.二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?10.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点A,B,C,D为顶点的四边形ABCD的面积等于多少平方分米?11.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?12.(10分)求最小的自然数,它恰好能表示成4种不同的不少于两个的连续非零自然数之和.2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)参考答案与试题解析一、填空题(每题10分,共80分)1.(10分)算式×[2×(1.875﹣)]÷[(0.875+1)÷3]的值为5.【分析】根据分数的四则混合运算的运算顺序解答即可,注意把带分数化成假分数,小数化成分数有利于计算.【解答】解:×[2×(1.875﹣)]÷[(0.875+1)÷3]=××(﹣)÷[(+)×]=4×÷[(+)×]=÷[×]=÷=5故答案为:5.2.(10分)小龙的妈妈比爸爸小3 岁,妈妈今年的年龄是小龙今年的9倍,爸爸明年的年龄是小龙明年的8倍,那么爸爸今年39岁.【分析】设小龙今年的年龄是x岁,那么妈妈的年龄就是9x岁,小龙的妈妈比爸爸小3 岁,那么小龙爸爸的年龄就是9x+3岁,明年小龙爸爸的年龄就是9x+3+1岁;小龙明年的年龄就是x+1岁,它的8倍就是(x+1)×8,这与小龙爸爸明年的年龄相等,由此列出方程求出小龙今年的年龄,进而求出爸爸的年龄.【解答】解:设小龙今年的年龄是x岁,小龙爸爸的年龄就是9x+3岁,(x+1)×8=9x+3+18x+8=9x+49x﹣8x=8﹣4x=49x+3=9×4+3=39(岁)答:爸爸今年39岁.故答案为:39.3.(10分)某水池有A、B两个排水龙头.同时打开两个龙头排水,30分钟可将满池的水排尽;同时打开两个龙头排水10分钟,然后关闭A龙头,B龙头继续排水,30分钟后也可以将满池的水排尽.那么单独打开B龙头,需要45分钟才能排尽满池的水.【分析】设工作总量为1,A,B共同排水30分钟排尽,10分钟完成工程的,B完成剩下工程的,时间为30分钟,据此可求出B的工作效率,进而求解.【解答】解:设工作总量为1,A,B共同排水需要30分钟.两个水龙头的效率和为,合作10分钟,完成工作总量为×10=,但是B排水单独工作需要30分钟,工作总量为,B水龙头的效率为:,单独打开B需要时间:1÷=45(分).故答案为:45.4.(10分)如图,圆O的面积为32,OC⊥AB,∠AOE=∠EOD,∠COF=∠FOD,则扇形EOF的面积为4.【分析】可以利用弧度之间的关系先求得EOF的弧度,而EOF可以分EOC和COF两个弧度,再利用已知的弧度关系,不难求得EOF的弧度,面积也不难求得.【解答】解:根据分析,由图可知,∠AOE=∠EOD=∠FOD+∠COF+∠EOC;又∠AOE=90°﹣∠EOC,∠FOD=∠COF,∴90°﹣∠EOC=∠FOD+∠COF+∠EOC=2×∠COF+∠EOC,⇒2(∠EOC+∠COF)=90°⇒∠EOC+∠COF=45°⇒∠EOF=45°,又∵圆O的面积为32=πr2,∴EOF的面积===4.故答案是:4.5.(10分)算式+++++++++的值的整数部分为46.【分析】先把算式通过拆分变形为50﹣5×(++++…++),然后讨论括号里的和的取值,即可解答.【解答】解:设A=+++++++++=5×(+++++++++)=5×(1×10﹣﹣﹣…﹣)=50﹣5×(++++…++)括号里的:++++…++=(+++)+(+)+(++)所以,++++…++<5×(+)=则,A>50﹣5×≈46.5同理,++++…++=(+++)+(+)+(++)所以,++++…++>5×(+)=则,A<50﹣5×≈46.8所以,46.5<A<46.8所以,[A]=46即,原式的值的整数部分为46.故答案为:46.6.(10分)如图中,正方形ABCD的面积为840平方厘米,AE=EB,BF=2FC,DF与EC相交于G.则四边形AEGD的面积为510平方厘米.【分析】这图形,易让人想到求三角形BCE、CDF、CGF的面积,其中难求得是△CGF 的面积.根据所给的条件,我们应做做GM⊥BC交点为M,这样就形成了与△BCE、△CDF对应的2组相似三角形.再利用相似三角形面积之比等于相似比的平方,即可求得△CGF的面积.最后根据图形即可算出所求图形的面积.【解答】解:做GM⊥BC交点为M,∴△FMG∽△FCD⇒FM:FC=MG:CD,∵BF=2FC⇒BC=3FC,∴MG=3FM,∵△CGM:△CEB⇒CM:CB=GM:BE,BC=2BE,∴GM=CM=3FM⇒CM=6FM,∴FM:FC=1:7,CM:CB=2:7,S△BCE=□ABCD=210,S△CGM=4÷49×210=840÷49=120÷7,S△CDF=S□ABCD÷6=140,S△MGF=140×1÷49=140÷49=20÷7,S△CGM+△MGF=120÷7+20÷7=20,840﹣210﹣140+20=510(平方厘米).故:四边形AEGD的面积是510平方厘米.7.(10分)一个自然数无论从左向右读或从右向左读都是一样的数称之为“回文数”,例如:909.那么所有三位回文数的平均数是550.【分析】三位回文数是ABA的形式,共有90个,因此平均数=这些数的和÷90=[101×(1+2+…+9)×10+10×(0+1+2+…+9)×9]÷90,即可得出结论.【解答】解:三位回文数是ABA的形式A共有1到9共9种可能,即1B1、2B2、3B3…B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…共有9×10=90个因此平均数=这些数的和÷90=[101×(1+2+…+9)×10+10×(0+1+2+…+9)×9]÷90=(101×45×10+10×45×9)÷90=45×10×110÷90=5×110=550,故答案为550.8.(10分)将七个连续自然数分别填在五个圆的交点A,B,C,D,E,F,G处,使得每个圆上的数的和都相等.如果所填的数都大于0且不大于10,则填在点G处的数是6.【分析】首先分析这些数字之间的关系,相等的量和有倍数关系的量,枚举尝试即可.【解答】解:依题意可知:A+B=A+C+D=B+E+F=C+F+G=D+E+G.C+D=B,E+F=A.C+F+G+D+E+G=A+B+A+B2G=A+B.(和为偶数)字母G估算再中间数字5,6,7.字母A不能是1,2.字母B比较大.尝试A=3,B=9,G=6.E+F=3,C+D=9.相等数字和为12.所以F=1.C=5.E =2,D=4.满足条件.故答案为:6二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?【分析】小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.【解答】解:小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.答:小虫从A到B的不同路线有10条.10.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点A,B,C,D为顶点的四边形ABCD的面积等于多少平方分米?【分析】这属于正方形格点问题,根据正方形格点毕克定理S=N﹣1+L÷2可以直接求出面积,其中N表示内部的格点数,L表示边界上的格点数.【解答】解:内部的格点数是12,边界点的数是6,根据公式列出算式是12﹣1+6÷2=14答:四边形ABCD的面积等于14平方分米.11.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?【分析】由题意,14×20×35+98=9898,即可得出结论.【解答】解:由题意,14×20×35+98=9898,∴当四位数北京精神最大时,厚德为98.12.(10分)求最小的自然数,它恰好能表示成4种不同的不少于两个的连续非零自然数之和.【分析】从连续非零自然数的和的奇偶性切入进行分析:因为是连续非零自然数之和,那么两个数的和,奇数+偶数=奇数;三个数的和,偶数+奇数+偶数=奇数,并且是3的倍数;四个数的和一定是偶数,排除掉;五个数的和,奇数+偶数+奇数+偶数+奇数=奇数,并且是5的倍数;六个数时,三个奇数+三个偶数=奇数.3和5最小公倍数是15,这个最小自然数一定是15的倍数.通过试算可知45是符合条件的最小的自然数.【解答】解:两个数的和,奇数+偶数=奇数;三个数的和,偶数+奇数+偶数=奇数,并且是3的倍数;四个数的和一定是偶数,排除掉;五个数的和,奇数+偶数+奇数+偶数+奇数=奇数,并且是5的倍数;六个数时,三个奇数+三个偶数=奇数.3和5的最小公倍数是15,所以这个最小自然数一定是15的倍数.试算:45=22+23=14+15+16=7+8+9+10+11=5+6+7+8+9+10所以45是符合条件的最小的自然数.。
2012年第十七届华杯赛小高组初赛详解

老
第 3 页师兴趣是最的老师帅帅思维公众号:shuaiteacher
帅
2.以平面上 4 个点为端点连接线段,形成的图形中最多可以有( A.3 B.4 C.6 D.8 【考点】几何计数
老
第 1 页
师
)个三角形.
兴趣是最好的老师
学习有意思
快乐思维
4.图中的方格纸中有五个编号为 1,2,3,4,5 的小正方形,将其中的两个涂上阴影,与图中阴影部分正 好组成正方体的展开图,这两个正方形的编号可以是( ) . A.1,2 B.2,3 C.3,4 D.4,5 【考点】立体展开图 【难度】☆☆☆ 【答案】D 【解析】正方体的展开图,试着自己画一画.有 11 种, (6 种“141” ,3 种“231” , 1 种“33” ,1 种“222” .如图:
帅帅思维公众号:shuaiteacher
帅
6.右图由相同的正方形和相同的等腰直角三角形构成,则正方形的个数为( A.83 B.79 C.72 D.65
老
第 2 页
【解析】根据弃九法 ABC DEF HIJ 2HIJ 被 9 整除,所以 HIJ 被 9 整除,观察选项中只有 459 符合条 件,所以答案为 C.
【解析】 连接 EG , 根据三角形面积的等积代换得 S△AEC S△ACG 6.75 平方厘米,
帅
又因为 S△ ABC
S△ABE S△AEC S△ABC 6.75 4.5 2.25 平方厘米.
帅帅思维公众号:shuaiteacher
帅
1 SWABCD 4.5 平方厘米,所以 2
二、填空题(每小题 10 分,满分 40 分) 7.右图的计数器三个档上各有 10 个算珠,将每档算珠分成上下两部分,得到两个三位数,要求上面部分 是各位数字互不相同的三位数,且是下面三位数的倍数,那么上面部分的三位数是___________.
第十七届华罗庚金杯少年数学邀请赛小学高年级(B)试题与解析

第十七届华罗庚金杯少年数学邀请赛决赛笔试试题B (小学高年级组)--By 肖瑶如意一、填空题(每小题10分,共80分) 1. 算式4651112÷()75121555+-的值为() 【解析】4651112÷()75121555466012×7569558121555883616516552165+-=-=-=-= 这题我没考虑有没有简便算法,有那时间,直接做也做出来了2. 设a △b 和a ▽b 分别表示取a 和b 两个数的最小值和最大值,如,3△4=3,3▽4=4.那么对于不同的数x ,5▽(4▽(x △4))的取值共有(1)个。
【解析】4▽(x △4)这一步,不管x 取值如何,结果都是4,5▽4=5,取值只有1个或者分情况讨论:①x ≤4X △4=x4▽x=45▽4=5②x >4X △4=44▽4=45▽4=5所以取值只有1个3. 里山镇到省城的高速路全长189千米,途径县城,里山镇到县城54千米。
早上8:30,一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,11:00到达。
另有一辆客车于同天早上8:50从省城径直开往里山镇,每小时行驶60千米。
那么两车相遇的时间为(10:08)【解析】为叙述方便,称里山镇开出的客车为甲,省城开出的客车为乙甲到达县城前,平均时速为54÷45/60=72千米甲离开县城后,平均时速为(189-54)÷1.5=90千米/小时乙,从8:50到9:30,共行了60×40/60=40千米甲,从8:30到9:30,共行了54千米9:30,甲乙还相距189-40-54=95千米相遇还需95÷(90+60)=19/30小时=38分钟9:30+0:38=10:084. 有高度相同的一段方木和一段圆木,体积之比是1:1.如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱体体积和长方体的体积的比值为(π/8)【解析】高相同,体积比为1:1,则底面积比为1:1设方木底面边长为a,加工成的圆柱底面半径为m圆木底面半径为b,加工成的长方体的底面边长为na ²=πb ²,(a/b)²=πm ²=a ²/4n ²=2b ²所求比值为m ²:n ²=(a/b)²÷8=π/85. 用[x]表示不超过x 的最大整数,记{x}=x-[x],则算式20121201222012320122012{}{}{}...{}5555++++++++ 的值为()【解析】前两项,分别为3/5和4/5从第三项开始,5项一周期,分别为0/5,1/5,2/5,3/5,4/52012+2012=4024(4024-2014)÷5=402(一共402个周期)原式=(3+4)/5+(1+2+3+4)/5×402=805.46. 某个水池存有其容量的十八分之一的水。
第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)一、填空题(每题10分,共80分)1.(10分)算式×[2×(1.875﹣)]÷[(0.875+1)÷3]的值为.2.(10分)小龙的妈妈比爸爸小 3 岁,妈妈今年的年龄是小龙今年的9倍,爸爸明年的年龄是小龙明年的8倍,那么爸爸今年岁.3.(10分)某水池有A、B两个排水龙头.同时打开两个龙头排水,30分钟可将满池的水排尽;同时打开两个龙头排水10分钟,然后关闭A龙头,B 龙头继续排水,30分钟后也可以将满池的水排尽.那么单独打开B龙头,需要分钟才能排尽满池的水.4.(10分)如图,圆O的面积为32,OC⊥AB,∠AOE=∠EOD,∠COF=∠FOD,则扇形EOF的面积为.5.(10分)算式+++++++++的值的整数部分为.6.(10分)如图中,正方形ABCD的面积为840平方厘米,AE=EB,BF=2FC,DF与EC相交于G.则四边形AEGD的面积为平方厘米.7.(10分)一个自然数无论从左向右读或从右向左读都是一样的数称之为“回文数”,例如:909.那么所有三位回文数的平均数是.8.(10分)将七个连续自然数分别填在五个圆的交点A,B,C,D,E,F,G 处,使得每个圆上的数的和都相等.如果所填的数都大于0且不大于10,则填在点G处的数是.二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?10.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点 A,B,C,D 为顶点的四边形ABCD的面积等于多少平方分米?11.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表 0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?12.(10分)求最小的自然数,它恰好能表示成4种不同的不少于两个的连续非零自然数之和.2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小高组)参考答案与试题解析一、填空题(每题10分,共80分)1.(10分)算式×[2×(1.875﹣)]÷[(0.875+1)÷3]的值为 5 .【分析】根据分数的四则混合运算的运算顺序解答即可,注意把带分数化成假分数,小数化成分数有利于计算.【解答】解:×[2×(1.875﹣)]÷[(0.875+1)÷3]=××(﹣)÷[(+)×]=4×÷[(+)×]=÷[×]=÷=5故答案为:5.2.(10分)小龙的妈妈比爸爸小 3 岁,妈妈今年的年龄是小龙今年的9倍,爸爸明年的年龄是小龙明年的8倍,那么爸爸今年39 岁.【分析】设小龙今年的年龄是x岁,那么妈妈的年龄就是9x岁,小龙的妈妈比爸爸小3 岁,那么小龙爸爸的年龄就是9x+3岁,明年小龙爸爸的年龄就是9x+3+1岁;小龙明年的年龄就是x+1岁,它的8倍就是(x+1)×8,这与小龙爸爸明年的年龄相等,由此列出方程求出小龙今年的年龄,进而求出爸爸的年龄.【解答】解:设小龙今年的年龄是x岁,小龙爸爸的年龄就是9x+3岁,(x+1)×8=9x+3+18x+8=9x+49x﹣8x=8﹣4x=49x+3=9×4+3=39(岁)答:爸爸今年39岁.故答案为:39.3.(10分)某水池有A、B两个排水龙头.同时打开两个龙头排水,30分钟可将满池的水排尽;同时打开两个龙头排水10分钟,然后关闭A龙头,B 龙头继续排水,30分钟后也可以将满池的水排尽.那么单独打开B龙头,需要45 分钟才能排尽满池的水.【分析】设工作总量为1,A,B共同排水30分钟排尽,10分钟完成工程的,B完成剩下工程的,时间为30分钟,据此可求出B的工作效率,进而求解.【解答】解:设工作总量为1,A,B共同排水需要30分钟.两个水龙头的效率和为,合作10分钟,完成工作总量为×10=,但是B排水单独工作需要30分钟,工作总量为,B水龙头的效率为:,单独打开B需要时间:1÷=45(分).故答案为:45.4.(10分)如图,圆O的面积为32,OC⊥AB,∠AOE=∠EOD,∠COF=∠FOD,则扇形EOF的面积为 4 .【分析】可以利用弧度之间的关系先求得EOF的弧度,而EOF可以分EOC 和COF两个弧度,再利用已知的弧度关系,不难求得EOF的弧度,面积也不难求得.【解答】解:根据分析,由图可知,∠AOE=∠EOD=∠FOD+∠COF+∠EOC;又∠AOE=90°﹣∠EOC,∠FOD=∠COF,∴90°﹣∠EOC=∠FOD+∠COF+∠EOC=2×∠COF+∠EOC,⇒2(∠EOC+∠COF)=90°⇒∠EOC+∠COF=45°⇒∠EOF=45°,又∵圆O的面积为32=πr2,∴EOF的面积===4.故答案是:4.5.(10分)算式+++++++++的值的整数部分为46 .【分析】先把算式通过拆分变形为50﹣5×(++++…++),然后讨论括号里的和的取值,即可解答.【解答】解:设A=+++++++++=5×(+++++++++)=5×(1×10﹣﹣﹣…﹣)=50﹣5×(++++…++)括号里的:++++…++=(+++)+(+)+(++)所以,++++…++<5×(+)=则,A>50﹣5×≈46.5同理,++++…++=(+++)+(+)+(++)所以,++++…++>5×(+)=则,A<50﹣5×≈46.8所以,46.5<A<46.8所以,[A]=46即,原式的值的整数部分为46.故答案为:46.6.(10分)如图中,正方形ABCD的面积为840平方厘米,AE=EB,BF=2FC,DF与EC相交于G.则四边形AEGD的面积为510 平方厘米.【分析】这图形,易让人想到求三角形BCE、CDF、CGF的面积,其中难求得是△CGF的面积.根据所给的条件,我们应做做GM⊥BC交点为M,这样就形成了与△BCE、△CDF对应的2组相似三角形.再利用相似三角形面积之比等于相似比的平方,即可求得△CGF的面积.最后根据图形即可算出所求图形的面积.【解答】解:做GM⊥BC交点为M,∴△FMG∽△FCD⇒FM:FC=MG:CD,∵BF=2FC⇒BC=3FC,∴MG=3FM,∵△CGM:△CEB⇒CM:CB=GM:BE,BC=2BE,∴GM=CM=3FM⇒CM=6FM,∴FM:FC=1:7,CM:CB=2:7,S△BCE=□ABCD=210,S△CGM=4÷49×210=840÷49=120÷7,S△CDF=S□ABCD÷6=140,S△MGF=140×1÷49=140÷49=20÷7,S△CGM+△MGF=120÷7+20÷7=20,840﹣210﹣140+20=510(平方厘米).故:四边形AEGD的面积是510平方厘米.7.(10分)一个自然数无论从左向右读或从右向左读都是一样的数称之为“回文数”,例如:909.那么所有三位回文数的平均数是550 .【分析】三位回文数是ABA的形式,共有90个,因此平均数=这些数的和÷90=[101×(1+2+…+9)×10+10×(0+1+2+…+9)×9]÷90,即可得出结论.【解答】解:三位回文数是ABA的形式A共有1到9共9种可能,即1B1、2B2、3B3…B共有0到9共10种可能,即A0A、A1A、A2A、A3A、…共有9×10=90个因此平均数=这些数的和÷90=[101×(1+2+…+9)×10+10×(0+1+2+…+9)×9]÷90=(101×45×10+10×45×9)÷90=45×10×110÷90=5×110=550,故答案为550.8.(10分)将七个连续自然数分别填在五个圆的交点A,B,C,D,E,F,G 处,使得每个圆上的数的和都相等.如果所填的数都大于0且不大于10,则填在点G处的数是 6 .【分析】首先分析这些数字之间的关系,相等的量和有倍数关系的量,枚举尝试即可.【解答】解:依题意可知:A+B=A+C+D=B+E+F=C+F+G=D+E+G.C+D=B,E+F=A.C+F+G+D+E+G=A+B+A+B2G=A+B.(和为偶数)字母G估算再中间数字5,6,7.字母A不能是1,2.字母B比较大.尝试A=3,B=9,G=6.E+F=3,C+D=9.相等数字和为12.所以F=1.C =5.E=2,D=4.满足条件.故答案为:6二、回答下列各题(每题10分,共40分,写出答案即可)9.(10分)一只小虫沿如图中的线路从A爬到B.规定:图中标示箭头的边只能沿箭头方向行进,而且每条边在同一路线中至多通过一次.问:小虫从A到B的不同路线有多少条?【分析】小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.【解答】解:小虫从A到B,第一个六边形的分叉口上下均有2条,B所在的六边形也上下有2条,于是有2×2+2×2=8条,中间往回走的箭头有2条路线,一共有10条.答:小虫从A到B的不同路线有10条.10.(10分)如图是由1平方分米的正方形瓷砖铺砌的墙面的残片.问:图中由格点 A,B,C,D 为顶点的四边形ABCD的面积等于多少平方分米?【分析】这属于正方形格点问题,根据正方形格点毕克定理S=N﹣1+L÷2可以直接求出面积,其中N表示内部的格点数,L表示边界上的格点数.【解答】解:内部的格点数是12,边界点的数是6,根据公式列出算式是12﹣1+6÷2=14答:四边形ABCD的面积等于14平方分米.11.(10分)在等式“爱国×创新×包容+厚德=北京精神”中,每个汉字代表 0~9 的一个数字,爱、国、创、新、包、容、厚、德分别代表不同的数字.当四位数北京精神最大时,厚德为多少?【分析】由题意,14×20×35+98=9898,即可得出结论.【解答】解:由题意,14×20×35+98=9898,∴当四位数北京精神最大时,厚德为98.12.(10分)求最小的自然数,它恰好能表示成4种不同的不少于两个的连续非零自然数之和.【分析】从连续非零自然数的和的奇偶性切入进行分析:因为是连续非零自然数之和,那么两个数的和,奇数+偶数=奇数;三个数的和,偶数+奇数+偶数=奇数,并且是3的倍数;四个数的和一定是偶数,排除掉;五个数的和,奇数+偶数+奇数+偶数+奇数=奇数,并且是5的倍数;六个数时,三个奇数+三个偶数=奇数.3和5最小公倍数是15,这个最小自然数一定是15的倍数.通过试算可知45是符合条件的最小的自然数.【解答】解:两个数的和,奇数+偶数=奇数;三个数的和,偶数+奇数+偶数=奇数,并且是3的倍数;四个数的和一定是偶数,排除掉;五个数的和,奇数+偶数+奇数+偶数+奇数=奇数,并且是5的倍数;六个数时,三个奇数+三个偶数=奇数.3和5的最小公倍数是15,所以这个最小自然数一定是15的倍数.试算:45=22+23=14+15+16=7+8+9+10+11=5+6+7+8+9+10所以45是符合条件的最小的自然数.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:49:29;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
第十七届2012年华罗庚金杯

+
3 1 7 6 2 8 9 4 5 3 2 4 6 5 7 9 8 1 1 7 3 2 9 5 4 6 8
+
8+3+7
8+4+6
+
7+6+5
一、选择题(每题10分)
2、北京时间16时,小龙从镜子里看到挂在身后墙上的4个时 钟(如下图),其中最接近16时的是()
A
B
C
D
11 10
9 8 7
12
五边形 六边形 七边形 边长42,周长210 边长35,周长210 边长30,周长210
求圆的面积,古代人们也是由求的计算内接圆的多边形面积概算。
周长相等,比较平面图形的 面积、边长
4000
面积 圆 周长 3511 边长 210 0
3500
七边形 3270 210 30 六边形 3183 210 35 五边形 3040 210 42 四边形 2756 210 52.5 三角形 2105 210 70
共计
3a 3b+17
小计
a+2b
a+17
a+b
2012
二、填空题(每题10分,共40分)
8、下图的计数器三个档上各有10个算珠,将每档算珠分成上下两
部分,按数位得到两个三位数,要求上面的三位数的数字不同,且
是下面三位数的倍数,那么满足题意的上面三位数是()。
百 十 个
百
十
个
答案:925
n 1 2 3 4 5 6 7 8 9
厘米,面积都相等的小正方形纸片,最少能剪出()块,这种剪法剪成地
所有正方形纸片的周长之和是()厘米。
第十七届华罗庚金杯少年数学邀请赛初赛试卷小学中年级组

第十七届华罗庚金杯少年数学邀请赛初赛试卷(小学中年级组笔试版)〔吋间:2012年3月17日10:00-11:00 〕一、选择题(每小题10分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内)1.在右面的加法算式中,每个汉字代表一个非零数字,不同的汉字代表不同的数字.当算式成立吋,贺+新+春=().(A)24 〔B〕22 (C) 20 (D) 182.北京吋间16吋,小龙从镜子里看到挂在身后墙上的4个钟表(如下图),其中最接近16吋的是〔〕.3.平面上有四个点,任意三个点都不在-条直线上.以这四个点为端点连接六条线段,在所组成的图形中,最少可以形成()个三角形.(A)3 (B)4 (C) 6 (D) 84.在10口10口10口10口10的四个口中填入“+”“-”“×”“÷”运算符号各一个,所成的算式的最大值是〔〕.(A)104 〔B〕109 (C) 114 (D) 1195.牧羊人用15段每段长2米的篱笆,一面靠墙围成一个正方形或长方形羊圈,则羊圈的最大面积是〔〕平方米.(A)100 〔B〕108 (C) 112 (D) 1226.小虎在19x19的围棋盘的格点上摆棋子,先摆成了一个长方形的实心点阵.然后再加上45枚棋子,就正好摆成-边不变的较大的长方形的实心点阵.那么小虎最多用了〔〕枚棋子.(A)285 〔B〕171 (C) 95 (D)57二、填空题(每小题10分,满分40分)7.三堆小球共有2012颗,如杲从每堆取走相同数目的小球贩笫二堆还剩下17颗小球,并且笫一堆剩下的小球数是笫三堆剩下的2倍,那么笫三堆原有______颗小球.8.右图的计数器三个档上各有10个算珠,将每档算珠分成上下两部分,技数位得到两个三位数,要求上面的三位数的数字不同,且是下面三位数的倍数,那么满足题意的上面的三位数是________.9.把一块长90厘米,宽42厘米的长方形纸板恰无剩余地剪成边长都是整数厘米、面积都相等的小正方形纸片,最少能剪出_____块,这种剪法剪成的所有正方形纸片的周长之和是_______厘米.10.体育馆正在进行乒乓球单打、双打比赛,双打比赛的运动员比单打的运动员多4名,比赛的乒乓球台共有13张,那么双打比赛的运动员有________名.第十七届全国华罗庚金杯少年数学邀请赛初赛试题(小学中年级组笔试版)答案―、选择题(每小题10分,满分60分)二、填空理(每小题10分,满分40分)。
2012年第十七届华杯赛决赛真题及答案大全

第十七届华罗庚金杯少年数学邀请赛决赛笔试试题A及答案(小学中年级组)一、填空题(每小题10 分, 共80 分)1. 若将一个边长为6厘米的正方形盖在一个三角形上, 则两个图形重叠部分的面积占三角形面积的一半, 占正方形面积的三分之二.那么这个三角形的面积是________平方厘米.2. 右图是两个两位数的减法竖式, 其中A, B, C, D代表不同的数字.当被减数AB取最大值时,.A×B+(C+E)×(D+F) =_________。
3. 某水池有A,B两个水龙头.如果A,B同时打开需要30分钟可将水池注满.现在A和B同时打开10分钟,即将A关闭,由B继续注水80分钟,也可将水池注满. 如果单独打开B龙头注水, 需要_______分钟才可将水池注满.4. 将六个数1, 3, 5, 7, 9, 11 分别填入右图中的圆圈内(每个仅填一个数), 使每边上三个数的和都等于17, 则三角形点处的圆圈内所填三数之和为_______。
5.四年级一班用班费购买单价分别为3元、2元、1元的甲、乙、丙三种文具. 要求购买乙种文具的件数比购买甲种文具的件数多2件, 且购买甲种文具的费用不超过总费用的一半. 若购买的文具恰好用了66元, 则甲种文具最多可买__________件.6.如右图所示,一只蚂蚁从正方体的顶点A出发,沿正方体的棱爬到顶点B,要求行走的路线最短,那么蚂蚁有______种不同的走法.7. 一个车队以4米/秒的速度缓慢通过一座长298米的大桥, 共用115秒,已知每辆车长6米, 相临两车间隔20米, 则这个车队一共有________辆车.8.有一个长方形, 如果它的长和宽同时增加6厘米, 则面积增加了114平方厘米. 则这个长方形的周长等于_______厘米.二、简答题(每题15分, 共60分, 要求写出简要过程)9. 扑克牌的点数如图所示,最大是13, 最小是1. 现小明手里有3张点数不同的扑克牌,第一张和第二张扑克牌点数和是25, 第二张和第三张扑克牌点数和是13, 问: 第三张扑克牌的点数是多少?10.下图是一个净化水装置, 水流方向为从A先流向B, 再流到C.原来容器A-B之间有10个流量相同的管道, B-C之间也有10个流量相同的管道.现调换了A-B与B-C之间的一个管道后, 流量每小时增加了40立方米. 问: 通过调整管道布局, 从A到C的流量最大可增加多少立方米?11. 右图中的一个长方形纸板每个角上都被切掉了一个小长方形(含正方形), 如果被切掉的小长方形的8对对边的长度分别是一个1, 四个2, 两个3和一个4, 那么纸板剩下部分的面积最大是多少?12. 有20张卡片,每张上写一个大于0的自然数,且任意9张上写的自然数的和都不大于63. 若称写有大于7的自然数的卡片为“龙卡”,问:这20张卡片中“龙卡”最多有多少张?所有“龙卡”上写的自然数的和的最大值是多少?答案一、填空(每题10 分, 共80分)题号 1 2 3 4 5 6 7 8答案48 144 120 15 11 6 7 26二、解答下列各题(每题15 分, 共60分, 要求写出简要过程)9. 答案: 1.10.答案: 200.11.答案: 112.12.答案: 7, 61.第十七届华罗庚金杯少年数学邀请赛决赛笔试试题B及答案(小学中年级组)一、填空题(每小题10 分, 共80 分)1.若将一个边长为8厘米的正方形盖在一个三角形上, 则两个图形重叠部分的面积占三角形面积的一半, 占正方形面积的四分之三.那么这个三角形的面积是________平方厘米.2.右图的算式中,每个字母代表一个1至9之间的数,不同的字母代表不同的数字,则A+B+C=________3. 某水池有A,B两个水龙头.如果A,B同时打开需要30分钟可将水池注满.现在A和B同时打开10分钟,即将A关闭,由B继续注水40分钟,也可将水池注满. 如果单独打开B龙头注水, 需要_______分钟才可将水池注满.4. 将六个数1, 3, 5, 7, 9, 11 分别填入右图中的圆圈内(每个仅填一个数), 使每边上三个数的和都等于19, 则三角形点处的圆圈内所填三数之和为_______。
2012年第十七届“华罗庚金杯”奥数初赛试卷(小学中低年级组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学中低年级组)一、选择题(共6小题,每小题3分,满分18分)1.(3分)如图,时钟上的针从(1)转到(2)最少经过了( )A.2小时30分B.2小时45分C.3小时50分D.3小时45分2.(3分)在2012年,1月1日是星期日,并且( )A.1月份有5个星期三,2月份只有4个星期三B.1月份有5个星期三,2月份也有5个星期三C.1月份有4个星期三,2月份也有4个星期三D.1月份有4个星期三,2月份有5个星期三3.(3分)有大小不同的4个数,从中任取3个数相加,所得到的和分别是180、197、208和222.那么,第二小的数所在的和一定不是( )A.180B.197C.208D.2224.(3分)四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前面20米.这时,跑在前面的两位同学相差( )米.A.10B.20C.50D.605.(3分)在如图所示的两位数的加法运算式中,已知A+B+C+D=22,则X+Y=( )A.2B.4C.7D.136.(3分)小明在正方形的边上标出若干个点,每条边上恰有3个,那么所标出的点最少有( )个.A.12B.10C.8D.6二、填空题(共4小题,每小题3分,满分12分)7.(3分)如图,用一条线段把一个周长是30cm的长方形分割成一个正方形和一个小的长方形.如果小长方形的周长是16cm,则原来长方形的面积是 cm2.8.(3分)将10、15、20、30、40和60填入图中的圆圈中,使A,B,C三个小三角形顶点上的3个数的积都相等.那么相等的积最大为 .9.(3分)用3,5,6,18,23这五个数组成一个四则运算式,得到的结果是最小的非零自然数, .(要求列出该算式)10.(3分)里山镇到省城的高速路全长189千米,途径县城.县城离里山镇54千米.早上8:30一辆客车从里山镇开往县城,9:15到达.停留15分钟后开往省城,午前11:00能够到达.另有一辆客车于当日早上9:00从省城径直开往里山镇.每小时行驶60千米.两车相遇时,省城开往里山镇的客车行驶了 分钟.2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学中低年级组)参考答案与试题解析一、选择题(共6小题,每小题3分,满分18分)1.(3分)如图,时钟上的针从(1)转到(2)最少经过了( )A.2小时30分B.2小时45分C.3小时50分D.3小时45分【分析】先分别得到时钟上的表针的两个时刻,再用结束的时刻﹣开始的时刻即为中间的时间.【解答】解:表针(1)的时刻是0时45分,表针(2)的时刻是3时30分,最少经过的时间为:3时30分﹣0时45分=2小时45分.答:时钟上的秒针从(1)转到(2)最少经过了2小时45分.故选:B.2.(3分)在2012年,1月1日是星期日,并且( )A.1月份有5个星期三,2月份只有4个星期三B.1月份有5个星期三,2月份也有5个星期三C.1月份有4个星期三,2月份也有4个星期三D.1月份有4个星期三,2月份有5个星期三【分析】先分别推算出2012年1月,2012年2月的天数,然后用经过的天数除以7,求出一共是几周,还余几天,然后根据余数判断.【解答】解:因为2012年1月有31天,2月有29天,31÷7=4(星期)…3(天),29÷7=4(星期)…1(天),所以1月份有4个星期三,2月份有5个星期三.故选:D.3.(3分)有大小不同的4个数,从中任取3个数相加,所得到的和分别是180、197、208和222.那么,第二小的数所在的和一定不是( )A.180B.197C.208D.222【分析】设这四个不同的数分别为a,b,c,d.由题意可知,(a+b+c)+(a+c+d)+(b+c+d)+(a+b+d)=3(a+b+c+d)=180+197+208+222=807,则a+b+c+d=269.由此能求出第二小的数不在的和是哪个.【解答】解:设这四个不同的数分别为a,b,c,d.则(a+b+c)+(a+c+d)+(b+c+d)+(a+b+d)=3(a+b+c+d),=180+197+208+222,=807;所以,a+b+c+d=807÷3=269.因此最小数应为:269﹣222=47,第二小的数为:269﹣208=61.即第二小的数所在的和一定不是208.故选:C.4.(3分)四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前面20米.这时,跑在前面的两位同学相差( )米.A.10B.20C.50D.60【分析】根据题意画出线段图如下:跑在前面的两位同学是丁和甲,相差60﹣20﹣30=10米.【解答】解:由分析得出:跑在前面的两位同学是丁和甲,相差60﹣20﹣30=10(米).答:跑在前面的两位同学相差10米;故选:A.5.(3分)在如图所示的两位数的加法运算式中,已知A+B+C+D=22,则X+Y=( )A.2B.4C.7D.13【分析】根据和的个位数字是9可得:B+D=9,则A+C=22﹣9=13,所以可得x=1,y=3,据此即可求出x+y的值.【解答】解:根据题干分析可得:B+D=9,则A+C=22﹣9=13,所以可得x=1,y=3,则x+y=1+3=4.故选:B.6.(3分)小明在正方形的边上标出若干个点,每条边上恰有3个,那么所标出的点最少有( )个.A.12B.10C.8D.6【分析】要使每条边上所标出的点最少,则正方形的四个顶点处都要标点,由此利用正方形的四周点数=每边点数×4﹣4即可求出最少标出的点数.【解答】解:3×4﹣4,=12﹣4,=8(个),答:标出的点最少有8个.故选:C.二、填空题(共4小题,每小题3分,满分12分)7.(3分)如图,用一条线段把一个周长是30cm的长方形分割成一个正方形和一个小的长方形.如果小长方形的周长是16cm,则原来长方形的面积是 56 cm2.【分析】由大长方形到小长方形周长减少了:30﹣16=14(厘米),相当于减少了两条正方形的边长,所以正方形的边长是:14÷2=7(厘米),也就是原来长方形的宽是7厘米;那么原来长方形的长为:16÷2﹣7+7=8(厘米),面积是:8×7=56cm2.【解答】解:根据分析可得,30﹣16=14(厘米),正方形的边长:14÷2=7(厘米),原来长方形长:16÷2﹣7+7=8(厘米),面积:8×7=56(平方厘米);答:原来长方形的面积是56cm2.故答案为:56.8.(3分)将10、15、20、30、40和60填入图中的圆圈中,使A,B,C三个小三角形顶点上的3个数的积都相等.那么相等的积最大为 18000 .【分析】设A,B,C三个小三角形顶点上的3个数的积是S,那么中间3个数被计算了两次,设这三个数的积是d,则(10×15×20×30×40×60)×d=S3,把每个因数分解质因数即29×56×33×d=S3,由于29、56、33都是立方数,所以d也应是立方数,由于要使积d最大,必须有60这个因数,60=22×3×5,要使d是立方数,还需要1个2、2个3、2个5,即2×32×52=15×30,由此,可知d=60×15×30,经过调整可得A,B,C三个小三角形顶点上的3个数的积是:60×20×15=60×30×10=15×30×40=18000;据此解答.【解答】解:根据分析可得,设A,B,C三个小三角形顶点上的3个数的积是S,那么中间3个数被计算了两次,设这三个数的积是d,则(10×15×20×30×40×60)×d=S3,29×56×33×d=S3,由于29、56、33都是立方数,所以d也应是立方数,由于要使积d最大,必须有60这个因数,60=22×3×5,要使d是立方数,还需要1个2、2个3、2个5,即2×32×52=15×30,由此,可知d=60×15×30,经过调整可得A,B,C三个小三角形顶点上的3个数的积是:60×20×15=60×30×10=15×30×40=18000;.9.(3分)用3,5,6,18,23这五个数组成一个四则运算式,得到的结果是最小的非零自然数, 23﹣18+5﹣6﹣3或(23﹣3)÷5﹣18÷6 .(要求列出该算式)【分析】最小的非零自然数是1,看能否算出1,转化为跟算24类似的问题;化繁为简,先用最大的二个数相减:23﹣18=5;进一步转化为3,5,6,5四个数要算出来是1即可.【解答】解:由分析可得:23﹣18+5﹣6﹣3=1;或:(23﹣3)÷5﹣18÷6=1.故答案为:23﹣18+5﹣6﹣3或(23﹣3)÷5﹣18÷6.10.(3分)里山镇到省城的高速路全长189千米,途径县城.县城离里山镇54千米.早上8:30一辆客车从里山镇开往县城,9:15到达.停留15分钟后开往省城,午前11:00能够到达.另有一辆客车于当日早上9:00从省城径直开往里山镇.每小时行驶60千米.两车相遇时,省城开往里山镇的客车行驶了 72 分钟.【分析】先求出从8:30到9:15,客车行驶的时间,依据速度=路程÷时间,求出客车从里山镇到县城时的速度,再求出客车从县城出发时,以及到达省城时的时间,依据速度=路程÷时间,求出此时客车的速度;客车9:15到达.停留15分钟后开往省城,相当于客车是从9:30分开车,根据路程=速度×时间,求出另一辆客车30分钟行驶的路程,再求出两车共同行驶的路程,最后根据时间=路程÷速度,求出两车的相遇时间,再加30分钟即可解答.【解答】解:9:15+15分钟=9:30,11:00﹣9:30=1.5小时,30分钟=0.5小时,(189﹣54)÷1.5,=135÷1.5,=90(千米),189﹣54﹣60×0.5,=189﹣54﹣30,=135﹣30,=105(千米),105÷(60+90),=105÷150,=0.7(小时)=42(分钟),42+30=72分钟,答:省城开往里山镇的客车行驶了72分钟,故应填:72.11。
2012年十七届华杯赛初赛中年级组详解(网络版含笔试公开题)

第十七届华罗庚金杯少年数学邀请赛初赛试卷详细解答(小学中年级组网络版)(时间: 2012 年 3 月8 日19:30 ~ 20:30 )一、选择题(每小题10分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.如下图,时钟上的表针从(1)转到(2)最少经过了().(A)2小时30分(B)2小时45分(C)3小时30分(D)3小时45分【解答】(1)中表所示时间是12:45,(2)表时间为15:30,经历了2小时45分2.在2012年,1月1日是星期日,并且().(A)1月份有5个星期三,2月份只有4个星期三(B)1月份有5个星期三,2月份也有5个星期三(C)1月份有4个星期三,2月份也有4个星期三(D)1月份有4个星期三,2月份有5个星期三【解答】1月份一共有31天,7天一个星期,周期为7,那么1月4日,1月11日,1月18日,1月25日,都是星期三,共4个,1月32日即2月1日,2月9日,2月169Y X D C B A + 日,2月23日,2月30日都是星期三,共5个3. 有大小不同的4个数,从中任取3个数相加,所得到的和分别是180, 197, 208和222. 那么,第二小的数所在的和一定不是( ).(A )180 (B )197 (C )208 (D )222【解答】四个数中任取3个,一共有4中取法,分别加起来得到和从小到大排列,那么缺少的数分别对应最小数,第二小数,第三小数和最大数,所以是2084. 四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前面20米. 这时,跑在最前面的两位同学相差( )米.(A )10 (B )20 (C )50 (D )60【解答】丙 乙 甲 丁可以从图中看出在最前面的是甲和丁,相距10米5. 在右图所示的两位数的加法算式中, 已知22=+++D C B A , 则=+Y X ( ).(A )2 (B )4 (C )7 (D )13 和180 197 208 222 缺少数 最大数 第三小数 第二小数 第一小数【解答】B+D=9,不可能是19,所以A+C=22-9=13,那么X=1,Y=3,X+Y=1+3=46.小明在正方形的边上标出若干个点,每条边上恰有3个,那么所标出的点最少有()个.(A)12 (B)10 (C)8 (D)6【解答】如图所示二、填空题(每小题10 分,满分40分)7.如右图,用一条线段把一个周长是30 cm的长方形分割成一个正方形和一个小的长方形. 如果小长方形的周长是16 cm,则原来长方形的面积是cm2.【解答】大长方形与小长方形的高相等高:(30-16)÷2=7厘米长:30÷2-7=8厘米面积:7×8=56平方厘米8.将10,15,20,30,40和60填入右图的圆圈中,使A, B, C三个小三角形顶点上的3个数的积都相等. 这相等的积最大为【解答】10=2×515=3×520=2×2×530=2×3×540=2×2×2×560=2×2×3×5因数2一共9个;因数3一共3个;因数5一共6个,中间三个圈里面的数,各乘了2次,三个乘积再相乘,等于原来6个数的乘积再乘上其中的三个数,结果是一个立方数因数5最多增加3个,有9个因数3最多增加3个,有6个因数2最多增加3个,有12个乘积最大为53×32×24=180009.用3, 5, 6, 18,23这五个数组成一个四则运算式,得到的非零自然数最小是 .【解答】(23-3)÷5-18÷6=110.里山镇到省城的高速路全长189千米,途经县城. 县城离里山镇54千米. 早上8:30一辆客车从里山镇开往县城,9:15到达,停留15分钟后开往省城,午前11:00能够到达. 另有一辆客车于当日早上9:00从省城径直开往里山镇,每小时行驶60千米. 那么两车相遇时, 省城开往里山镇的客车行驶了分钟.【解答】8:30—9:15,一共45分钟=0.75小时9:30—11:00,一共1.5小时9:00—9:30,一共30分钟=0.5小时县城与省城相距:189-54=135千米第一辆客车从县城出发以后的速度为每小时:135÷1.5=90千米第一辆客车从县城出发时,省城开出的客车已经行了0.5小时,行程为:60×0.5=30千米两车相遇还需: (135-30)÷(90+60)×60=42分钟省城开出的客车一共行了:42+30=72分钟11.(笔试公开题)北京时间16时, 小龙从镜子里看到挂在身后墙上的4块表, 如下图,其中最接近16时的是().(A)(B)(C)(D)【解答】从镜中看到的时间与原来钟表中时间左右对称,时间分别为:。
