图学 CH03 基本投影几何学
投影基础—基本几何元素投影(机械制图课件)

例:已知四边形ABCD的水平投影abcd及正面 投影a′b′c′,试 完成其正面投影。
模块二 投影基础
任务一 基本几何元素的投影
模块二 投影基础
任务一 基本几何元素的投影
➢投影法和三视图
一、投影法和三视图
1、投影法分类 1)中心投影法
2)平行投影法
斜投影法:投射线倾斜于投影面,所得的投影称为斜投影。 正投影法:投射线垂直于投影面,所得的投影称为正投影。
c.三视图与物体方位的关系 主视图反映物体的上、下和左、右的相对位置关系; 俯视图反映物体的前、后和左、右的相对位置关系; 左视图反映物体的前、后和上、下的相对位置关系。
2. 投影面平行面 正平面:平行于V面并与H、W面垂直的平面; 水平面:平行于H面并与V、W面垂直的平面; 侧平面:平行于W面并与V、H面垂直的平面。
3. 一般位置平面 与三个投影面都倾斜的平面。
4、平面上的点 点在平面上的一直线上,则点一定在该平面上。
例:已知属于△ABC平面的点E的正面投影e′和 点F的水平投影f,试求它们的另一面投影。
2、正投影法基本性质 1)真实性 2)积聚性 3)类似性
3. 三视图
1)三视图的形成 物体的正面投影称为主视图; 物体的水平投影称为俯视图; 物体的侧面投影称为左视图。
为了作图方 便,规定正 面不动
2)三视图之间的关系 a、三视图间的位置关系 b、三视图间的投影关系:长对正,高平齐,宽相等。
模块二 投影基础
任务一 基本几何元素的投影
点的投影
二、 点、直线、平面的投影
2.1 点的投影 1. 点的投影规律 (1)s′s⊥OX (2)s′s″⊥OZ (3)ssX=s″sZ
Hale Waihona Puke 2. 点的投影与直角坐标的关系
投影基础—投影法及三视图(化工制图课件)

俯视图
主视图
用正投影法向各投影 面投射所得到的投影 图,称为视图。
Y 左视图
三投影面展开
三视图的投影规律 1.长对正、高平齐、宽相等
高
平
宽相等
齐
长对正
①主视图、俯视图长对正 ②主视图、左视图高平齐 ③俯视图、左视图宽相等
三视图的投影规律
上
上
2.俯、左视图
靠近主视图的
一边,表示物
左
右后
前 体的后面,
投影法及三视图
阳光或灯光照射物体时, 在地面或墙面上会产生影像, 这种投射线(如光线)通过 物体,向选定的面(如地面 或墙面)投射,并在该面上 得到图形(影像)的方法, 称为投影法。
根据投影法所得到的图 形称为投影图,简称投影。
放置投影的面称为投影面。
投影法分类
中心投影法 投影方法
斜投影法 平行投影法
正投影
投影面
斜投影
正投影的基本性质
1.显实性:平面图形(或直线)平行于投影面时,其投影 反映实形(或实长)
A F E
B C
fa
b
e
P
c
正投影的基本性质
2.积聚性:平面图形(或直线)垂直于投影面时,其投影 积聚为一条直线(或实长)
E
A
B
FD
C
e (f) d a P
cb
正投影的基本性质
3.类似性:平面图形(或直线)倾斜于投影面时,其投影 为类似的多边形(或比实长短的直线)
反之,表示物
下
下
体的前面
后
上
后
左
右
右 左
前
前
下
画三视图的方法和步骤
第三章投影的基本知识精品PPT课件

• 多面投影图多面投影图来自形成增加投影图W1投影
V投影 H投影
W投影 H方向
V1方向
V1投影 W1方向
W方向
V方向
§3-3 基本形体的投影
常见的基本形体
平面立体
曲面立体
一、平面体的投影图
轮廓线:表面之间的交线。
y1
y
y y1
六棱柱
三棱锥
y1 y3
y1 y3
二、曲面体的投影 注意:曲面立体的转向轮廓线。
本章内容
第三章 投影的基本知识
§3.1 投影的概念及分类 §3.2 正投影及其特性 §3.3 基本形体的投影 §3.4 组合体的投影
§3-1 投影的概念及分类
投影法:使几何形体在平面上产生图象的方法
一、投影法分类: 1 、中心投影法
投影中心、物 体、投影面三者之 间的相对距离对投 影的大小有影响。
演讲人:XXXXXX 时 间:XX年XX月XX日
示例1 示例2
动画
1、形体分析: 有圆筒、支承板、肋、底板。
各部分之间 的组合关系
圆筒表面与支承板左右两侧面? 相切
圆筒表面与肋左右侧面? 相交
肋、支承板、底板? 叠合
加粗
加粗
支承板与圆筒相切时 的画法
支承板与圆筒相交时
相切
相交
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量
圆柱体:
1、投影 ① 画轴线 ② 画底面和顶面 的投影 ③ 画轮廓转向线 正面转向线 侧面转向线
利用投影 的积聚性
圆锥体: 投影:
a
球体:
投影:
三个投影分别为 三个和圆球的直径相 等的圆,它们分别是 圆球三个方向转向轮 廓线的投影。
投影理论的基础知识(4点的投影)

投影保持点到直线的距离不变。即对于任意点A和直线L,点A 到直线L的距离等于点A在直线L上的投影点到直线L的距离。
投影的分类
正交投影
正交投影是将一个向量或更高维度的几何对象正交地映射到另一个向量或低维 度空间的线性变换。正交投影保持了原始向量的长度和方向不变。
非正交投影
非正交投影是一种将一个向量或更高维度的几何对象映射到另一个向量或低维 度空间的线性变换,但不保持原始向量的长度和方向不变。在实际应用中,非 正交投影的应用更为广泛。
02 投影的几何意义
投影的几何解释
投影是光源照射物体 时,在某个平面上留 下的影子。
投影可分为中心投影 和平行投影。
投影线与投影面之间 的夹角称为投影角。
投影的几何应用
01
在建筑设计、工程制图等领域, 投影理论被广泛应用于绘制三维 物体的二维图形表示。
02
通过投影,可以将三维空间中的 物体转换为二维平面上的图形, 便于分析和表达。
投影理论的基础知识
目录
• 投影的定义与性质 • 投影的几何意义 • 投影变换 • 投影的应用
01 投影的定义与性质
投影的基本定义
投影的基本定义
投影是将一个向量或更高维度的几何对象映射到另一个向量或低维度空间的线性变换。在数学和物理中,投影被广泛 应用于解决各种问题。
投影的数学表示
在数学中,投影通常用矩阵或线性变换来表示。给定一个向量空间和目标子空间,投影矩阵将原始向量映射到目标子 空间。
三视图
三视图是正投影的一种应用,通过从三个不同的角度观察物体,将物体
的主视图、俯视图和左视图分别绘制在三个不同的平面上,从而完整地
描述物体的结构和形状。
投影在计算机图形学中的应用
几何图形的投影与视图

几何图形的投影与视图几何图形是研究物体形状及其性质的一门数学学科,是我们理解和描述三维空间中的物体的重要工具。
为了更好地理解和分析几何图形,我们经常需要使用投影和视图等方法来展示物体在二维平面上的表示。
在本文中,我们将探讨几何图形的投影与视图的概念、分类和应用。
一、投影的概念和分类1.1 投影的概念投影是指将一个物体映射到另一个平面上的过程。
在几何学中,我们通常将物体在垂直于该物体的平面上的投影称为正投影。
正投影是一种保持物体形状和大小的投影方式,常用于建筑学、机械工程等领域的工程绘图中。
1.2 投影的分类根据投影方式的不同,我们可以将投影分为平行投影和中心投影两种类型。
1.2.1 平行投影平行投影是指物体与投影平面平行的投影方式。
在平行投影中,投影线与物体平行,因此,所有物体的投影都是平行的,即保持物体的形状和大小不发生变化。
常见的平行投影方式有正射投影和斜投影。
1.2.2 中心投影中心投影是指物体与投影平面不平行的投影方式。
在中心投影中,物体与投影平面相交,投影线不平行,因此物体的形状和大小会发生变化。
常见的中心投影方式有透视投影。
二、视图的概念和应用2.1 视图的概念在几何学中,视图是指通过不同的角度观察物体,所得到的物体在平面上的投影。
视图可以用于描述物体的外形和内部结构,是实际工程和设计中非常常用的展示方式。
2.2 视图的应用视图广泛应用于建筑设计、工程绘图、机械制图等领域。
通过不同角度的视图,我们可以更清晰地了解和分析物体的形状、尺寸以及各个部分之间的关系。
在实际工程中,使用视图可以减少误差和理解的困难,提高工作效率。
三、几何图形的投影与视图案例分析为了更好地理解几何图形的投影与视图的应用,我们以一个简单的长方体为例进行分析。
3.1 长方体的正投影对于长方体来说,正投影是将长方体映射到与其垂直的投影平面上。
因为长方体的六个面都是平行的,所以投影的形状和大小与原长方体相同。
通过正投影,我们可以得到长方体的俯视图、前视图和侧视图等不同视图。
几何图形的投影与视图

几何图形的投影与视图在我们的日常生活和学习中,几何图形无处不在。
无论是建筑设计、工程制图,还是艺术创作、科学研究,都离不开对几何图形的理解和运用。
而几何图形的投影与视图,作为描述和理解几何图形的重要手段,更是具有十分重要的意义。
首先,让我们来了解一下什么是几何图形的投影。
简单来说,投影就是光线照射在物体上,在某个平面上形成的影子。
当我们把光线看作是平行的直线时,这种投影被称为平行投影;而当光线从一个点发出,就像手电筒的光一样,这样的投影被称为中心投影。
平行投影又可以分为正投影和斜投影。
正投影是指光线垂直于投影面的投影,这种投影能够准确地反映出物体的形状和大小。
比如,我们在绘制工程图纸时,通常使用的就是正投影。
通过正投影,我们可以从不同的方向观察物体,并将其在图纸上清晰地表现出来。
斜投影则是光线倾斜于投影面的投影,它在某些情况下可以更直观地展示物体的立体感。
中心投影则有着独特的特点。
由于光线是从一个点发出的,所以物体离光源越近,投影就越大;离光源越远,投影就越小。
这种投影在我们日常生活中的应用也不少,比如夜晚的灯光下,物体的影子就是中心投影的结果。
在摄影和绘画中,艺术家们也常常利用中心投影的原理来营造出独特的视觉效果。
接下来,我们再说说几何图形的视图。
视图是指从不同的方向观察物体所得到的平面图形。
通常,我们会从正面、左面和上面三个方向来观察一个物体,分别得到主视图、左视图和俯视图。
主视图反映了物体的长度和高度;左视图反映了物体的宽度和高度;俯视图反映了物体的长度和宽度。
通过这三个视图,我们就能够比较全面地了解一个物体的形状和结构。
比如,在制造一个零件时,工人师傅就需要根据零件的视图来进行加工。
为了更清楚地理解视图,我们可以通过一个简单的例子来感受一下。
假设我们有一个长方体,长为 5 厘米,宽为 3 厘米,高为 2 厘米。
从正面看,我们看到的是一个长为 5 厘米,高为 2 厘米的长方形,这就是主视图;从左面看,看到的是一个宽为 3 厘米,高为 2 厘米的长方形,即左视图;从上面看,看到的是一个长为 5 厘米,宽为 3 厘米的长方形,也就是俯视图。
基本形体的投影图

平脊
两条脊线相交,则过该交点必然且至少还有第三条脊线。
斜脊
屋檐
整理课件 10
【例1】求同坡屋顶的各脊线的水平投影。
斜沟
平脊
斜脊
屋檐
整理课件 11
【例1】求同坡屋顶的水平投影.
23
25 2
56 26
3 35
5
12
16 6
34 4
45
斜沟
1
斜脊
整理课件 12
平脊
屋檐
【例2】求同坡屋顶的正面投影.
整理课件 13
c 1
a b
c 1
a b
y
a
c
y
b1
整理课件 26
§4-2 曲面体的投影
曲面体的投影
3 圆球
整理课件 27
§4-2 曲面体的投影
曲面立体的投影
3 圆球 在球表面上取点
m
m
M
m
整理课件
注 纬圆法求点。
28
§4-2 曲面体的投影
曲面体的投影
3 圆球 在球表面上取点
m
m
M
m
整理课件
注 纬圆法求点。
29
c
1
a
b
c
1
a b
y
y
a
c
1
b
整理课件 20
§4-2 曲面体的投影
曲面立体的投影
2 圆锥
整理课件 21
§4-2 曲面体的投影
二、曲面立体的投影
2 圆锥 在圆锥表面上取点
S
s
s
E
e
(e)
s
e
方法之一 :
素线法
投影的基本知识

投影显示技术的分类
根据投影显示技术的原理和应用,可 以分为前投式、背投式、内投式和外 投式等多种类型。
背投式投影机则将图像投射到一块特 殊的屏幕上,通常用于高端家庭影院 和商业展示。
前投式投影机通常将图像投射到一个 大屏幕上,广泛应用于商务、教育、 家庭等领域。
内投式和外投式投影机则分别将图像 投射到室内和室外的屏幕上,常用于 大型活动和户外广告等场合。
交互式游戏
通过投影技术将游戏场景与实体环境相结合,实 现游戏与现实世界的交互。
虚拟现实游戏
通过投影技术将虚拟游戏场景投射到头戴式设备 上,为玩家提供沉浸式的游戏体验。
THANKS FOR WATCHING
感谢您的观看
艺术创作
在艺术创作中,投影用于将三 维物体或场景转换为二维图像 ,以便进行绘画和摄影等创作
。
02 投影几何学
投影线与投影面
投影线
连接投射中心和投影表面的线段 ,表示光线在投射过程中经过的 路径。
投影面
接受投影的平面或曲面,通常是 一个垂直于投影中心的平面。
正投影与斜投影
正投影
投影线与投影面垂直的投影方式,能够真实反映物体的形状 和大小。
斜投影是指投影面与投影线倾斜,物 体的图像会产生变形。斜投影常用于 地形图、地图和透视图等领域。
投影的应用场景
工程设计
在工程设计中,投影用于将三 维模型转换为二维图纸,方便
施工和制造。
建筑设计
在建筑设计中,投影用于制作 建筑图纸和效果图,以便更好 地展示建筑物的外观和内部结 构。
地理信息系统
在地理信息系统中,投影用于 将地球表面的信息转换为地图 上的二维图像,方便分析和可 视化。
投影显示技术的基本原理是将图像或视 频信息投射到一个大屏幕上,通过改变 光线投射的角度和强度,形成可见的图
工程制图投影的基本知识课件

contents
目录
• 投影的基本概念 • 正投影法 • 三视图 • 点、线、面的投影 • 立体投影 • 工程制图实践
01
投影的基本概念
投影的定义
投影
根据几何图形通过投影中心,将三维空间的 物体转换到二维平面上的一种方法。
投影面
投影结果的承载面,通常为平面或曲面。
投影中心
基本几何体的绘制
掌握基本几何体
掌握常见基本几何体的绘制方法,如直线、圆、椭圆、多边形等,熟悉 其性质和绘制技巧。
了解几何体的投影规律,如长对正、高平齐、宽相等,能够准确绘制出 基本几何体的三视图。
组合体的绘制
01
掌握组合体绘制
02
掌握组合体的绘制方法,包括叠加、切割等,能够根据组合体
的构成方式选择合适的视图进行表达。
建筑设计
在建筑设计中,利用投影 原理绘制建筑物的平面图 、立面图和剖面图等。
机械制图
在机械设计中,利用投影 原理绘制零件图和装配图 等。
02
正投影法
正投影法的定义
正投影法是一种将三维物体通过特定的投影方式转换为二维图像的方法。
在正投影法中,物体的投影线与投影面是垂直的,因此也被称为“垂直投影法”。
物体与投影面之间的连接点,也称为投影点 。
投影的分类
斜投影
物体在投影面上的投影与其真实形状存在一 定的角度差异。
正投影
物体在投影面上的投影与其真实形状完全一 致。
中心投影
物体通过投影中心在投影面上形成的投影。
投影的应用
01
02
03
工程制图
在工程设计中,通过投影 将三维物体转换为二维平 面图,便于设计和施工。
几何图形的投影与展开图

几何图形的投影与展开图几何图形在三维空间中可以有不同的投影形式,而在二维平面上可以通过展开图来展示其真实形状。
投影与展开图是几何学中的基本概念和工具,可以帮助我们更好地理解和研究各种几何图形。
一、投影图形在现实生活中,我们经常可以见到物体在地面上的阴影。
这个阴影就是物体的投影。
在几何学中,投影是指将三维空间中的图形投射到二维平面上的过程。
1. 平行投影平行投影是指光线与投影面平行的情况下的投影。
在平行投影中,图形的大小和形状不会发生改变,只是产生了一个平行于投影面的投影。
2. 中心投影中心投影是指光线从一个点向外辐射的情况下的投影。
在中心投影中,图形的大小和形状会发生变化,与光线的距离越近,投影的图形越大。
3. 斜投影斜投影是指光线与投影面不平行的情况下的投影。
在斜投影中,图形既可能会发生大小形状的变化,也可能会出现倾斜的投影形式。
二、展开图展开图是将一个三维图形展开成二维平面上的各个面,并按照一定的规则进行排列,以便更直观地展示几何图形的真实形状。
1. 注意要领在制作展开图时,需要注意一些要领。
首先,需要确保展开图的各个面之间不发生交叉和重叠。
其次,需要保持各个面之间连接的正确性,即确保边与边、面与面之间的对应关系准确。
2. 制作步骤制作展开图的步骤可以分为以下几个部分:(1)选择一种合适的展开方式,根据几何图形的特点和需要,可以选择不同的展开方式,如平面展开、圆柱展开、锥体展开等。
(2)将几何图形的各个面分解、剪开,并保证它们在同一平面上。
(3)按照一定的次序,将各个面依据对应关系进行排列。
(4)在展开图上标注各个面的名称和相应的边长、角度等重要信息。
三、应用投影与展开图在实际生活和工程中有着广泛的应用。
1. 工程设计在工程设计中,投影与展开图被广泛应用于建筑、机械、电子等领域。
通过投影和展开图,设计师可以更好地理解和分析三维物体的形状、结构以及与其他部件之间的连接关系,从而指导设计和制造过程。
《投影理论基础》课件

透视变换
透视变换是投影的一种特殊形式,它模拟了人眼 看物体的方式,通过透视变换可以将一个几何图 形映射到一个视平面。
射影几何学与投影
射影几何的基本概念
射影几何是研究图形在射影变换下不变性质的几何学分支 ,它为投影提供了理论基础。
投影的应用
投影在计算机图形学中广泛应用于游戏开发、电影制作、建筑设计等领 域。通过投影,可以将三维模型渲染到屏幕上,实现逼真的视觉效果。
图像的投影
图像投影原理
图像投影是指将三维场景中的光线投射到二维图像平面上,生成最终的图像。这个过程涉及到光线追踪、阴影生成等 技术。
投影质量
投影质量取决于多种因素,如光源的位置、物体的材质、摄像机的角度等。高质量的投影能够提供更加逼真的图像效 果,而低质量的投影则可能导致图像失真或模糊。
投影的应用场景
三维可视化
在三维可视化中,投影技 术可以将三维数据转换为 二维图像,便于观察和分 析。
地理信息系统
地理信息系统中的地图投 影是将地球表面信息转换 为地图平面的过程,是地 理信息系统的基础。
工程设计
在工程设计中,投影技术 可以将三维模型转换为二 维图纸,便于施工和制造 。
02
投影的几何基础
面上得到保持。
垂直性
在中心投影下,物体上相互垂 直的线段在投影面上仍相互垂
直。
03
投影的数学基础
线性代数与投影
线性变换与矩阵
投影可以视为线性变换的一种,通过矩阵表示投影变换,理解投影在数学中的形式化表达 。
向量空间与投影
向量空间中的投影可以看作是一种特殊的线性变换,它把一个向量映射到另一个子空间上 。
投影及三视图(第一课时)

建筑设计
在建筑设计中,通过正投 影可以将建筑物的三维模 型转换为二维图纸,方便 施工和规划。
机械制图
在机械制图中,通过正投 影可以将机械零件的三维 模型转换为二维图纸,方 便生产和装配。
艺术创作
在艺术创作中,投影可以 用来表现三维物体的形态 和质感,增强画面的立体 感和层次感。
02
三视图的形成原理
根据观察到的形状,将物体绘制在所 选的观察方向上。
三视图的特点与作用
特点
三视图是从三个不同方向观察物体的结果 ,每个视图都有其特定的表达方式和特点 。
作用
三视图是工程设计和制造中常用的表达方 式,用于描述物体的形状、大小和相对位 置,以便进行准确的制造和施工。
主视图
表达物体的长度和宽度,通常放置在图纸 的中央。
三视图的形成原理
讲解了如何通过中心投影法将 三维物体转换为三视图,即主 视图、俯视图和左视图。
三视图的绘制方法
详细介绍了如何根据物体的实 际尺寸和角度,在图纸上绘制 出物体的三视图。
三视图的识读
讲解了如何通过三视图来还原物 体的实际形状和尺寸,以及如何
通过三视图进行尺寸标注。
三视图在实际应用中的展望
投影与三视图在工程设计中的应用
在工程设计中,设计师需要利用 投影和三视图来表达物体的形状
和尺寸。
通过三视图,设计师可以详细描 述物体的各个面、孔洞、凸起等
特征,以便制造者准确制造。
在复杂的设计中,设计师可能还 需要利用剖面图、局部视图等辅 助视图来表达物体的内部结构和
细节。
投影与三视图在机械制图中的应用
三视图的基本概念
定义
三视图是从三个不同的方向观察 同一个物体,并将所观察到的图 形绘制在同一个平面上所得到的 图形。
投影基础—几何元素的投影(化工制图课件)
投影面平行线:
平行于一个投影面,倾斜于另两个投影面
投影面垂直线:
垂直于一个投影面,平行于另二个投影面
投影面平行线
平行于水平面H的投影面平行线———水平线
投影特性:1. 在H面的投影反映实形 2. V面、W面的投影为类似形,分别平行于X、Y轴
投影面平行线
平行于正平面V的投影面平行线——正平线
投影面垂直线
垂直于侧平面W的投影面垂直线——侧垂线
投影特性:1. 在W面的投影积聚为一点 2. H面、V面的投影反映实形,分别垂直于Y、Z轴,同时平 行于X轴
投影面垂直线的投影特性:
在所垂直的投影面上积聚为一点 ,在其它投影面上的投影反映实形 ; 其它两投影分别垂直于相应的投 影轴,同时平行于相对的投影轴。
投影特性:1. 在V面的投影反映实形 2. H面、W面的投影为类似形,分别平行于X、Z轴
投影面平行线
平行于侧平面W的投影面平行线——侧平线
投影特性:1. 在W面的投影反映实形 2. H面、V面的投影为类似形,分别平行于Y、Z轴
投影面平行线的投影特性:
在所平行的投影面上的投影反映 实长; 其它两投影分别平行于相应的投 影轴,同时垂直于相对的投影轴, 且小于实长。
几何元素的投影
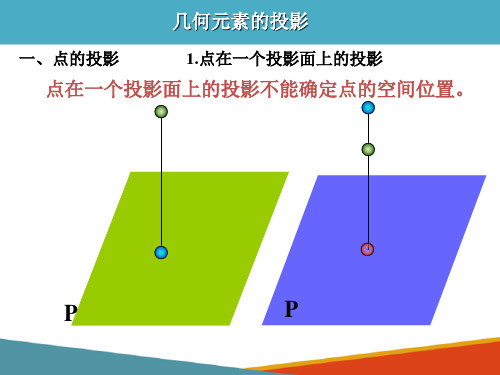
一、点的投影
1.点在一个投影面上的投影
点在一个投影面上的投影不能确定点的空间位置。
P
P
点在三个投影面上的投影
a 点A的正面投影
a 点A的水平投影
a'
a 点A的侧面投影
a"
A
O
A 空间点
a
aa X轴
a'
aaZ轴
X ax
aax = aaz
几何形的投影和展开

几何形的投影和展开在几何学中,投影和展开是两个重要的概念。
投影是指将一个立体物体在不同的平面上产生的影子或图像,展开则是将一个立体物体展开成为一个平面图形。
这两个概念对于理解和研究几何形体的性质和关系有着重要的作用。
一、投影投影可以分为正投影和斜投影两种形式。
1. 正投影正投影是指在投影过程中,投影线垂直于投影面的情况。
在正投影中,投影的图像几何形状与实际物体的形状完全相同。
我们常见的在地面上的阴影就是正投影的一种形式。
2. 斜投影斜投影是指投影线与投影平面不垂直的情况。
在斜投影中,投影的图像几何形状与实际物体的形状不完全相同,会出现形变和尺寸变化。
斜投影的角度和方向决定了投影的图像效果。
二、展开展开是将一个立体物体展开成为平面图形的过程。
通过展开,我们可以更直观地观察和研究立体物体的各个面、边和角的关系。
以正四面体为例,正四面体有四个三角形面。
我们可以将每个面按照一定的方式展开,并通过连接边的方式,将展开后的各个平面图形组合起来,得到一个展开图。
这个展开图可以还原成与原来正四面体形状相同的立体。
展开图的制作需要一定的技巧和方法。
通常,我们可以根据立体物体的各个面的相互关系和角度关系来确定展开图的形状和位置。
对于复杂的立体物体,展开图的制作也需要一定的计算和构造技巧。
三、应用投影和展开在日常生活和实际应用中有广泛的应用。
以下是一些例子。
1. 工程制图在工程制图中,投影是一种重要的手段,用于绘制三维物体的投影图。
工程师需要通过投影图来描述和表达物体的形状、尺寸和位置关系,以便进行设计、制造和施工。
2. 游戏开发在游戏开发中,展开图常常用于构建游戏场景和角色模型。
开发人员可以将三维模型展开成为平面图,然后进行贴图和纹理处理,最终在游戏中呈现出逼真的三维效果。
3. 裁剪和包装在制作衣物、纸箱和包装盒等产品时,常常需要通过展开图来确定材料的形状和尺寸,以便进行裁剪和包装。
通过合理地制作展开图,可以最大限度地节省材料并提高产品的质量和效益。
画法几何之投影基础知识

济 南 大 学 图 学 教 研 中 心
1.中心投影法
S 投射中心 投射线 形体
a
物体的中 心投影
b
a
济 南 大 学 图 学 教 研 中 心
2 .
投 射 线 方 向
a c
90°
b
平 行 投 (影 1 法 ) 斜 投 影 法
济 南 大 学 图 学 教 研 中 心
投 射 线 方 向
90°
a
c
( 2 ) 正 投 影 法
25 20 1 5 25 20 1 5
25
20 1 5
济 南 大 学 图 学 教 研 中 心
4.透视投影图
济 南 大 学 图 学 教 研 中 心
3-2 正投影的基本性质
一、实形性(不变性)
济 南 大 学 图 学 教 研 中 心
二、积聚性
济 南 大 学 图 学 教 研 中 心
三、类似性
济 南 大 学 图 学 教 研 中 心
济 南 大 学 图 学 教 研 中 心
第三章 投影基础知识
第一节 第二节 第三节
投影概念及其分类 正投影的基本性质 三面投影的形成及其规律
济 南 大 学 图 学 教 研 中 心
3-1 投影概念及其分类
3.1.1 投影法 投射线
b a 投影
济 南 大 学 图 学 教 研 中 心
3.1.2 投影法分类 1. 中心投影法 2. 平行投影法 (1)斜投影法 (2)正投影法 3.1.3 工程上常用用的几种投影图 1. 多面正投影图 (1) 问题的提出 (2) 多面正投影图 2. 轴测投影图 3. 标高投影图 4. 透视投影图
V
W
V
W
H
H
济 南 大 学 图 学 教 研 中 心
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本投影幾何學
❑投影幾何學為十八世紀法國數學家兼軍事工程師孟奇Gaspard Monge)所創,是一門闡述投影原理的科(Gaspard
學,主要為應用投影原理,探討如何在2D平面圖上表達空間物體的形狀、大小及其相互間的關係。
❑投影原理提供了繪製與閱讀工程圖的理論基礎,因此,研習工程圖者須熟悉投影幾何學,以奠定工程圖學的基礎。
2
投影的基本觀念
所謂投影,即是利用一假想的透明平面(稱為投影面),置於物體與觀察者間,或放置於物體的後方,以設定的投影方法,將此物體各部分的輪廓,用點投影投射到此假想平面上,用線條將投影面上的各點連接而成的圖形,稱為該物體在假想平面上的投影。
❑視點SP(Sight Point):為光源或觀察者眼睛所在位置。
❑視線(Line of Sight):視點與物體間的連線。
❑投影線PL(Projection Lines):視點、物體與投影面間的連線,或相當於投射的光線。
❑投影面PP(Projection Plane):呈現投影圖(視圖)的平面。
投影的分類
投影原理分為平行投影(Parallel projection)與透視投影(Perspective projection):
④平行投影:平行投影乃假想觀察者站在無窮遠處看物體,由
觀察者的眼睛至物體上各點的連線(即視線)彼此互相平行,如此在投影面上所呈現此物體外型的投影,謂平行投影。
♦斜投影。
♦正投影。
④透視投影:透視投影係指當觀察者站在有限的距離內看物體
,故視線交於一點(即觀察者的視點-眼睛),因此,其投影線互不平行,所得投影的圖形,其大小會隨觀察者、畫面或物體三者間距離不同而變。
平行投影
透視投影
斜投影:投影線彼此平行但不垂直於投影面。
正投影:投影線彼此平行且垂直於投影面。
最常用三個互相垂直相交的投影面。
④置於水平方位,稱為水平投影面(Horizontal plane
of projection,HP)或H面
④置於垂直方位,稱為直立投影面(Vertical plane of
projection,VP)或V面
④置於與前兩者皆垂直位置的投影面,稱為側投影面
(Profile plane of projection,PP)或P面。
在側投影面(Profile plane)左側,可以看到水平投影面(Horizontal plane)與直立投影面(Frontal plane or Vertical plane)相互垂直相交,且將空間區分成四個部分,每一部分稱為一個「象限」:
④第一象限。
④第二象限。
④第三象限。
④第四象限。
象限與投影
工程製圖中的正投影,依被投影物體不同的放置位置,分成「第一角投影」、「第二角投影」、「第三角投影」與「第四角投影」等四種投影方法。
❑V面與H面的交線稱為基線(Ground line,GL)
❑P面與V面或H面的交線稱為副基線,簡稱GL1。
❑物體投影完成後,將水平投影面以基線為軸旋轉,使水平投影面與直立投影面共平面。
❑水平投影面係依順時針方向旋轉,即直立投影面前方的部份向前下方旋轉,直立投影面後方的部份則向後上方旋轉。
第一角投影法
將被投影的物體置於第一象限,並依箭頭A與B所示的方向作垂直投影(a)【觀察者、物體、投影面】,而所得的視圖沿基線(Ground line)以順時針方向展開,其投影圖排列如(b)所示。
第一角投影展開
左側視圖由左邊看物體,
所繪出的視圖
第三角投影
將被投影的物體置於第一象限,並依箭頭A 與B 所示的
方向作垂直投影(a )【觀察者、投影面、物體】,而 所得的視圖沿基線以順時針方向展開,其投影圖排列
如(
b )所示。
看到物體,所繪出的視圖
第二、四象限視圖重疊
❑物體如置於第二、四象限,旋轉水平投影後,將會產生視圖重疊的現象。
❑工程圖所用之投影僅限於將物體置於一或三象限。
