算术编码的C实现
算术编码

实现算术编码及其译码一、实验内容借助C++编程来实现对算术编码的编码及其译码算法的实现二、实验环境1.计算机2.VC++6.0三、实验目的1.进一步熟悉算术编码的原理,及其基本的算法;2.通过编译,充分对于算术编码有进一步的了解和掌握;3.掌握C++语言编程(尤其是数值的进制转换,数值与字符串之间的转换等)四、实验原理算术编码算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔,消息越长,编码表示它的间隔就越小,表示这一间隔所需的二进制位就越多。
算术编码用到两个基本的参数:符号的概率和它的编码间隔。
信源符号的概率决定压缩编码的效率,也决定编码过程中信源符号的间隔,而这些间隔包含在0到1之间。
编码过程中的间隔决定了符号压缩后的输出。
给定事件序列的算术编码步骤如下:(1)编码器在开始时将“当前间隔”设置为[0,1)。
(2)对每一事件,编码器按步骤(a)和(b)进行处理(a)编码器将“当前间隔”分为子间隔,每一个事件一个。
(b)一个子间隔的大小与下一个将出现的事件的概率成比例,编码器选择子间隔对应于下一个确切发生的事件相对应,并使它成为新的“当前间隔”。
(3)最后输出的“当前间隔”的下边界就是该给定事件序列的算术编码。
编码过程假设信源符号为{A, B, C, D},这些符号的概率分别为{ 0.1, 0.4, 0.2,0.3 },根据这些概率可把间隔[0, 1]分成4个子间隔:[0, 0.1], [0.1, 0.5],[0.5, 0.7], [0.7, 1],其中[x,y]表示半开放间隔,即包含x不包含y。
上面的信息可综合在表03-04-1中。
下表为信源符号,概率和初始编码间隔如果二进制消息序列的输入为:C A D A C D B。
编码时首先输入的符号是C,找到它的编码范围是[0.5,0.7]。
由于消息中第二个符号A的编码范围是[0,0.1],因此它的间隔就取[0.5, 0.7]的第一个十分之一作为新间隔[0.5,0.52]。
自适应算术编码的原理实现与应用

自适应算术编码的原理实现与应用简介自适应算术编码(Adaptive Arithmetic Coding)是一种无损数据压缩算法,用于将输入数据流转换为更短的编码表示形式。
相对于固定长度编码,自适应算术编码能够更好地利用数据的统计特性,从而达到更高的压缩比。
本文将介绍自适应算术编码的原理实现与应用,并对其进行详细的解释与示例。
原理自适应算术编码的原理非常简单,主要分为以下几个步骤:1.定义符号表:首先,需要将输入数据中的符号进行编码,因此需要定义一个符号表,其中包含了所有可能的符号及其概率。
符号可以是字符、像素、或者任意其他离散的数据单元。
2.计算累积概率:根据符号表中每个符号的概率,计算出累积概率。
累积概率用于将输入数据中的符号映射到一个区间上。
3.区间编码:将输入数据中的符号通过区间编码进行压缩。
每个符号对应一个区间,区间的大小与符号的概率成比例。
4.更新概率模型:在每次编码过程中,根据已经编码的符号,可以得到新的概率模型。
根据这个模型,可以动态地调整符号表中每个符号的概率。
这样,在下一次编码中,就能更好地适应数据的统计特性。
实现步骤与示例1.定义符号表假设我们要对一个字符串进行压缩,其中包含的符号为’a’、’b’、’c’、’d’和’e’。
我们可以根据经验或者统计数据,估计每个符号的概率。
例如:’a’的概率为0.2,’b’的概率为0.15,’c’的概率为0.3,’d’的概率为0.25,’e’的概率为0.1。
2.计算累积概率根据符号表中每个符号的概率,计算出累积概率。
累积概率可以通过累计每个符号的概率得到。
在本示例中,累积概率为:’a’的概率为0.2,’b’的概率为0.35,’c’的概率为0.65,’d’的概率为0.9,’e’的概率为1.0。
3.区间编码使用累积概率对输入数据中的符号进行区间编码。
假设我们要对字符串’abecd’进行编码。
–第一个符号为’a’,其累积概率为0.2。
因此,我们将区间[0,1.0)划分为5个小区间,每个小区间对应一个符号:•’a’对应的区间为[0,0.2);•’b’对应的区间为[0.2,0.35);•’c’对应的区间为[0.35,0.65);•’d’对应的区间为[0.65,0.9);•’e’对应的区间为[0.9,1.0)。
信息论算术编码实验报告

实验三算术编码一、实验目的1.进一步学习C++语言概念和熟悉VC 编程环境。
2.学习算术编码基本流程, 学会调试算术编码程序。
3. 根据给出资料,自学自适应0 阶算术编、解码方法。
二、实验内容与原理(一)实验原理:1.算术编码基本原理这是将编码消息表示成实数0 和1 之间的一个间隔,消息越长,编码表示它的间隔就越小,表示这一间隔所需的二进制位就越多。
算术编码用到两个基本的参数:符号的概率和它的编码间隔。
信源符号的概率决定压缩编码的效率,也决定编码过程中信源符号的间隔,而这些间隔包含在0到1之间。
编码过程中的间隔决定了符号压缩后的输出。
首先借助下面一个简单的例子来阐释算术编码的基本原理。
考虑某条信息中可能出现的字符仅有a b c 三种,我们要压缩保存的信息为bccb。
在没有开始压缩进程之前,假设对a b c 三者在信息中的出现概率一无所知(采用的是自适应模型),暂认为三者的出现概率相等各为1/3,将0 - 1 区间按照概率的比例分配给三个字符,即a 从0.0000 到0.3333,b 从0.3333 到0.6667,c 从0.6667 到1.0000。
进行第一个字符b编码,b 对应的区间0.3333 -0.6667。
这时由于多了字符b,三个字符的概率分布变成:Pa = 1/4,Pb = 2/4,Pc = 1/4。
按照新的概率分布比例划分0.3333 - 0.6667 这一区间,划分的结果可以用图形表示为:+-- 0.6667 Pc = 1/4 | +-- 0.5834 | | Pb = 2/4 | | | +-- 0.4167 Pa = 1/4 | +-- 0.3333 接着拿到字符c,现在要关注上一步中得到的c 的区间0.5834 -0.6667。
新添了c 以后,三个字符的概率分布变成Pa = 1/5,Pb = 2/5,Pc = 2/5。
用这个概率分布划分区间0.5834 - 0.6667:+-- 0.6667 | Pc = 2/5 | +-- 0.6334 | Pb = 2/5 || +-- 0.6001 Pa = 1/5 | +-- 0.5834 输入下一个字符c,三个字符的概率分布为:Pa = 1/6,Pb = 2/6,Pc = 3/6。
算术编码

二、算术编码的编码过程:
1、从信源符号全序列出发,将各信源序列依累 积概率分布函数的大小映射到[0,1]区间,将 [0,1]区间分成许多互不重叠的小区间。
2、此时每个符号序列均有一个小区间与之对 应,因而可在小区间内取点来代表该符号序列。
二、算术编码的编码过程:
1、累积分布函数递推公式与信源符号序列所对应的区间宽 度的递推公式的求得:
② 将F(S)的十进制小数形式换算成二进制小数C,取小数点 后 L 位,就可以得到序列的码字。
注:如果第L+1有尾数,就进位。
三、算术编码的特点
① 因为C≥F(S)
2L
由码字长度的计算公式可知,p(a)≥ 。 令S+1为按顺序正好在S后面的一个序列,则:
2 F(S 1) F(S) p(a) F(S) L C
① 累积分布函数的定义
设信源符号集A={a1 ,a2 ,,aq
P(ai ), P(ai ) 0(i 1,2,,q)
k 1
F(ak ) P(ai ) i 1
},其相应的概率分布为 ,累积分布函数:
a(i ,ak A )
② 以二元无记忆信源为例,将结果推广到一般情况。
无失真信源编码-------
算术编码
参考资料:《信息论与编码》傅祖芸 《信息论与编码》曹雪虹
一、算术编码简介
1、非分组码,它是从全序列出发,考虑符号之间的 依赖关系。
2、经香农-费诺-埃利斯编码推广而来的,直接对信 源符号序列进行编码输出。
3、即时码,信源符号序列对应的累积概率区间是不 重叠的。肯定也可以唯一译码。
如下图所示其累积分布函数F(S ) 的对应区间及一般多元
序列的累积函数的推导公式的得出:
python算术编码

python算术编码算术编码是一种常用的数据压缩算法,其主要原理是将数据转化为一个数值范围内的小数,然后将其储存下来。
在数据解压时,根据压缩时使用的转化方法,就能将原始数据准确地还原出来。
算术编码在实际应用中已经被广泛地运用在文件压缩、图像压缩和语音压缩等方面。
本文将从算术编码的原理、实现方式以及应用场景三个层面进行详细介绍。
一、算术编码的原理算术编码的原理是将一个字符串转化为一个小数,该小数对应的是一个数值范围内的一段连续区间。
这个小数的值越接近1,表示原始字符串中的内容就越靠近该区间的顶端,而值越接近0,表示原始字符串的内容越靠近该区间的底端。
在解码时,将该小数从第一位开始与不同的区间进行匹配,就能够还原出原始的字符串。
二、算术编码的实现方式算术编码是一种非常灵活的编码方式,因此在实现方式上也存在多种不同的方法。
其中一种常见的实现方法是基于概率模型的顺序算术编码。
它的具体流程如下:1. 对于每一个字符,统计其在原始字符串中出现的概率。
2. 将每一个字符的概率映射到数值范围内的一个小数区间。
3. 依次将每个字符的小数区间叠加起来,形成一个新的数值范围。
4. 当一个字符对应的小数区间完全包含在新的数值范围内时,就将新的数值范围作为编码结果储存。
5. 重复步骤4,直到所有字符都被编码。
6. 解码时,根据编码结果以及字符串中每个字符对应的概率,重新定位原始字符串中的每个字符。
三、算术编码的应用场景算术编码在实际的应用场景中已经被广泛地使用,其主要优点是可以实现更高的压缩比,以及更加精确的拟合,从而能够表现出更好的压缩效果。
在文件压缩方面,算术编码可以实现更好的压缩效果,并且不需要占用太多的存储空间。
在图像压缩方面,算术编码能够准确地描述图像的数据内容,从而实现更好的压缩效果。
在语音压缩方面,算术编码的灵活性和高效性使其成为了一种不可替代的压缩方式。
总之,算术编码作为一种常用的数据压缩算法,其原理清晰、实现方式多样,并且拥有广泛的应用场景。
算术编码c语言课程设计

算术编码c语言课程设计一、课程目标知识目标:1. 学生能理解算术编码的基本原理和算法流程。
2. 学生能掌握C语言实现算术编码的关键技术,包括浮点数的运算和位操作。
3. 学生能了解算术编码在数据压缩中的应用及其优势。
技能目标:1. 学生能运用C语言编写出完整的算术编码程序,实现对给定数据的编码和解码。
2. 学生能够分析算术编码程序的性能,并进行简单的优化。
3. 学生通过实际操作,培养编程解决问题的能力,提高逻辑思维能力。
情感态度价值观目标:1. 学生在课程中培养对编程的兴趣,激发主动学习和探索的精神。
2. 学生通过合作学习,培养团队协作精神和沟通能力。
3. 学生认识到算术编码在现实生活中的应用价值,激发对信息科技领域的学习热情。
课程性质:本课程为选修课,侧重于C语言编程实践和算法应用。
学生特点:学生具备一定的C语言基础,对编程有较高的兴趣,具备一定的逻辑思维能力。
教学要求:注重理论与实践相结合,强调动手实践,鼓励学生思考、提问和讨论,提高学生的编程能力和问题解决能力。
将课程目标分解为具体的学习成果,便于在教学过程中进行有效指导和评估。
二、教学内容1. 算术编码原理介绍:包括编码的基本思想、算法流程和关键概念(如概率分布、码区间划分)。
相关教材章节:第3章“数据压缩”,第2节“算术编码”。
2. C语言实现算术编码:讲解如何利用C语言实现算术编码,涉及浮点数的运算、位操作等。
相关教材章节:第4章“C语言编程技巧”,第3节“位操作及应用”。
3. 算术编码程序设计:引导学生分析算术编码的需求,逐步完成编码和解码程序的编写。
教学内容安排:分阶段进行,包括程序框架搭建、编码模块编写、解码模块编写及测试。
4. 算术编码性能分析及优化:分析影响算术编码性能的因素,探讨优化方法。
相关教材章节:第6章“程序性能优化”,第1节“性能分析”。
5. 实践项目:设计一个简单的算术编码实现案例,要求学生独立完成编码、解码及性能优化。
编程实现算术编码算法

编程实现算术编码算法算术编码是一种无损数据压缩算法,它能够对输入的数据进行高效的压缩,减小数据的存储空间。
本文将介绍如何使用Python编程实现算术编码算法。
算术编码的基本思想是将整个输入数据流转化为一个大整数,并将该整数表示为一个小数,该小数的小数部分表示输入数据的编码。
算术编码的核心过程包括初始化和更新编码上下文、计算符号的概率范围、更新编码上下文的概率模型和输出编码结果等。
在开始编程实现算术编码算法之前,我们需要先准备一些辅助函数。
首先,我们需要实现一个函数,将概率转化为范围,并计算累积概率。
以下是该函数的实现示例:```pythondef get_range(prob, symbol):"""将概率转化为范围,并计算累积概率:param prob: 符号的概率:param symbol: 符号:return: 符号的范围和累积概率"""range_start = 0range_end = 0freq = 0for p, s in zip(prob, symbol):range_start = range_endrange_end += pif s == symbol:freq = preturn range_start, range_end, freq```接下来,我们需要实现一个函数,用于更新编码上下文模型。
以下是该函数的实现示例:```pythondef update_context_model(ctx_model, symbol):"""更新编码上下文模型:param ctx_model: 编码上下文模型:param symbol: 当前符号:return: 更新后的编码上下文模型"""#增加符号的频率for i in range(len(ctx_model)):if ctx_model[i][0] == symbol:ctx_model[i][1] += 1#对符号频率进行归一化total_freq = sum([x[1] for x in ctx_model])for i in range(len(ctx_model)):ctx_model[i][1] /= total_freqreturn ctx_model```然后,我们可以实现算术编码的核心过程。
算术编码

为[0.0624,0.0688)
输入第五个符号a4后,对序列a1a2a3a3 a4进行编码,编码区
间为[0.06752,0.0688)
在区间[0.06752,0.0688)内的任何数字都可以表示消息
a1a2a3a3a4,例0.06752
7
无失真编码
算术编码—编码过程
步骤 1 2 3 4 5 6 输入 a1 a2 a3 a3 a4 编码间隔 [0,0.2) [0.04,0.08) [0.056,0.072) [0.0624,0.0688) [0.06752,0.0688)
输入第二个符号a2后,编码区间由[0,0.2)变为[0.04,0.08),当前区间 长度length=0.08-0.04=0.04
6
无失真编码
算术编码—编码过程
输入第三个符号a3后,对序列a1a2 a3进行编码,编码区间
为[0.056,0.072)
输入第四个符号a3后,对序列a1a2a3a3进行编码,编码区间
4
无失真编码
5
无失真编码
算术编码—编码过程
根据每个符号出现的概率将半开区间[0,1)分成四个区域
[0,0.2) [0.2,0.4) [0.4,0.8) [0.8,1)
对输入的第一个符号a1编码
symbol_high(a1)=0.2
symbol_low(a1)=0
high=0+1.0×0.2=0.2
无失真编码
算术编码
算术编码并不是将单个信源符号映射成一个码字,
而是把整个信源表示为实数线上0到1之间的一个 区间,其长度等于该序列的概率。 制作为实际的编码输出
在该区间内选择一个代表性的小数,转换为二进 消息序列中的每个元素都要用来压缩这个区间 消息序列中元素越多,所得到的区间就越小,当
算术编码(Arithmeticcoding)的实现
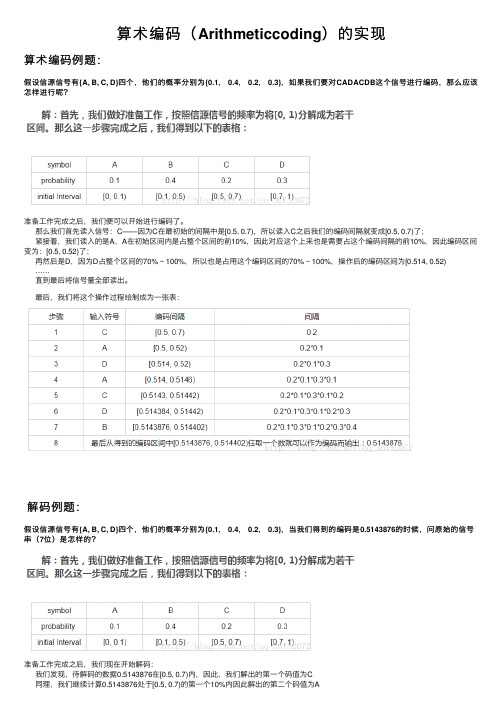
算术编码(Arithmeticcoding)的实现算术编码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},如果我们要对CADACDB这个信号进⾏编码,那么应该怎样进⾏呢?准备⼯作完成之后,我们便可以开始进⾏编码了。
那么我们⾸先读⼊信号:C——因为C在最初始的间隔中是[0.5, 0.7),所以读⼊C之后我们的编码间隔就变成[0.5, 0.7)了; 紧接着,我们读⼊的是A,A在初始区间内是占整个区间的前10%,因此对应这个上来也是需要占这个编码间隔的前10%,因此编码区间变为:[0.5, 0.52)了; 再然后是D,因为D占整个区间的70% ~ 100%,所以也是占⽤这个编码区间的70% ~ 100%,操作后的编码区间为[0.514, 0.52) …… 直到最后将信号量全部读出。
最后,我们将这个操作过程绘制成为⼀张表:解码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},当我们得到的编码是0.5143876的时候,问原始的信号串(7位)是怎样的?准备⼯作完成之后,我们现在开始解码: 我们发现,待解码的数据0.5143876在[0.5, 0.7)内,因此,我们解出的第⼀个码值为C 同理,我们继续计算0.5143876处于[0.5, 0.7)的第⼀个10%内因此解出的第⼆个码值为A …… 这个过程持续直到执⾏七次全部执⾏完为⽌。
那么以上的过程我们同样可以列表表⽰:作业:对任⼀概率序列,实现算术编码,码长不少于16位,不能固定概率,语⾔⾃选。
基于Python实现:from collections import Counter #统计列表出现次数最多的元素import numpy as npprint("Enter a Sequence\n")inputstr = input()print (inputstr + "\n")res = Counter(inputstr) #统计输⼊的每个字符的个数,res是⼀个字典类型print (str(res))# print(res)#sortlist = sorted(res.iteritems(), lambda x, y : cmp(x[1], y[1]), reverse = True)#print sortlistM = len(res)#print (M)N = 5A = np.zeros((M,5),dtype=object) #⽣成M⾏5列全0矩阵#A = [[0 for i in range(N)] for j in range(M)]reskeys = list(res.keys()) #取字典res的键,按输⼊符号的先后顺序排列# print(reskeys)resvalue = list(res.values()) #取字典res的值totalsum = sum(resvalue) #输⼊⼀共有⼏个字符# Creating TableA[M-1][3] = 0for i in range(M):A[i][0] = reskeys[i] #第⼀列是res的键A[i][1] = resvalue[i] #第⼆列是res的值A[i][2] = ((resvalue[i]*1.0)/totalsum) #第三列是每个字符出现的概率i=0A[M-1][4] = A[M-1][2]while i < M-1: #倒数两列是每个符号的区间范围,与输⼊符号的顺序相反A[M-i-2][4] = A[M-i-1][4] + A[M-i-2][2]A[M-i-2][3] = A[M-i-1][4]i+=1print (A)# Encodingprint("\n------- ENCODING -------\n" )strlist = list(inputstr)LEnco = []UEnco = []LEnco.append(0)UEnco.append(1)for i in range(len(strlist)):result = np.where(A == reskeys[reskeys.index(strlist[i])]) #满⾜条件返回数组下标(0,0),(1,0) addtollist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],3]))addtoulist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],4]))LEnco.append(addtollist)UEnco.append(addtoulist)tag = (LEnco[-1] + UEnco[-1])/2.0 #最后取区间的中点输出LEnco.insert(0, " Lower Range")UEnco.insert(0, "Upper Range")print(np.transpose(np.array(([LEnco],[UEnco]),dtype=object))) #np.transpose()矩阵转置print("\nThe Tag is \n ")print(tag)# Decodingprint("\n------- DECODING -------\n" )ltag = 0utag = 1decodedSeq = []for i in range(len(inputstr)):numDeco = ((tag - ltag)*1.0)/(utag - ltag) #计算tag所占整个区间的⽐例for i in range(M):if (float(A[i,3]) < numDeco < float(A[i,4])): #判断是否在某个符号区间范围内decodedSeq.append(str(A[i,0]))ltag = float(A[i,3])utag = float(A[i,4])tag = numDecoprint("The decoded Sequence is \n ")print("".join(decodedSeq))Arithmetic coding Code参考:。
python算术编码

python算术编码
Python 中的算术编码 (Arithmetic Encoding) 是一种常用的图像压缩方法,可以将原始图像转换为压缩后的图像,从而减少图像的存储空间和传输时间。
算术编码的基本原理是将图像像素值转换为二进制数,然后用这些二进制数来表示图像像素值。
下面是一个简单的 Python 实现算术编码的示例代码:
```python
import numpy as np
# 创建一个包含 10 个像素的 3x3 大小的图像
image = np.array([[1, 1, 1], [2, 2, 2], [3, 3, 3]], dtype=np.float32)
# 将图像转换为二进制数
bits = np.binary_repr(image, 2)
# 将二进制数转换为字符串
string = np.str_fmt(bits, "08b")
# 打印结果
print(string)
```
输出结果为:
```
"01100100 01100100 01100100"
```
在这个示例中,我们首先创建一个包含 10 个像素的 3x3 大小的图像。
然后,我们将图像像素值转换为二进制数,并使用
np.binary_repr() 函数将二进制数转换为字符串。
最后,我们将字符串打印出来。
算术编码的压缩效果取决于图像的像素数量和大小,以及输入的二进制数的位数。
一般来说,当二进制数的位数增加时,压缩效果会变得更好,但是二进制数的长度也会增加,因此需要权衡压缩效果和二进制数长度。
python算术编码

python算术编码算术编码是一种常用的无损压缩算法,可以对数据进行高效的编码和解码,以达到数据压缩的目的。
本文将介绍算术编码的原理和实现,以及其在实际应用中的一些注意事项。
1. 算术编码原理算术编码将数据编码为一个区间,该区间表示数据的概率分布。
编码过程中,每个符号根据其出现的概率被分配一个子区间。
编码最后输出的是包含所有符号的区间的编码值。
解码过程则是根据编码值将其映射回原始数据。
2. 算术编码步骤算术编码主要包含以下几个步骤:- 确定每个符号的概率分布。
- 计算每个符号所对应的区间。
- 编码:根据符号和区间,将数据编码为一个编码值。
- 解码:根据编码值和符号的概率分布,将编码值解码为原始数据。
3. 算术编码的实现算术编码的实现需要对概率进行建模,并进行区间的计算。
下面是一个简单的算术编码的实现示例:```pythondef arithmetic_encode(data, symbol_list, probability_list):low = 0high = 1result = 0for symbol in data:symbol_index = symbol_list.index(symbol)symbol_low = low + (high - low) *sum(probability_list[:symbol_index])symbol_high = low + (high - low) *sum(probability_list[:symbol_index + 1])low = symbol_lowhigh = symbol_highresult = (low + high) / 2return resultdef arithmetic_decode(encoded_data, symbol_list, probability_list, length):low = 0high = 1result = []for _ in range(length):for i in range(len(symbol_list)):symbol_low = low + (high - low) * sum(probability_list[:i]) symbol_high = low + (high - low) * sum(probability_list[:i + 1])if symbol_low <= encoded_data < symbol_high:result.append(symbol_list[i])low = symbol_lowhigh = symbol_highbreakreturn result```以上代码中,`arithmetic_encode`函数用于将数据编码为编码值,`arithmetic_decode`函数用于将编码值解码为原始数据。
算术编码c语言

算术编码c语言算术编码(Arithmetic Coding)是一种无损数据压缩算法,它通过对数据流中的符号进行区间映射来实现压缩。
以下是一个简单的算术编码的示例,使用C语言编写。
请注意,这只是一个基本的演示,实际的算术编码实现可能更为复杂和优化。
```c#include <stdio.h>// 符号结构体,用于存储符号和其概率typedef struct {char symbol;double probability;} Symbol;// 编码函数void arithmeticEncode(char* input, Symbol* symbols, int numSymbols) {double low = 0.0;double high = 1.0;double range = 1.0;for (int i = 0; input[i] != '\0'; i++) {char currentSymbol = input[i];// 查找当前符号的概率double currentProbability = 0.0;for (int j = 0; j < numSymbols; j++) {if (symbols[j].symbol == currentSymbol) {currentProbability = symbols[j].probability;break;}}// 更新区间high = low + range * currentProbability;low = low + range * currentProbability - range;range = high - low;}// 输出压缩后的区间printf("Encoded range: [%lf, %lf)\n", low, high);}int main() {char input[] = "ABBACAB";Symbol symbols[] = {{'A', 0.5},{'B', 0.25},{'C', 0.125}// 可根据需要添加更多的符号和对应的概率};int numSymbols = sizeof(symbols) / sizeof(symbols[0]);// 进行算术编码arithmeticEncode(input, symbols, numSymbols);return 0;}```在这个简单的示例中,我们假设输入是字符串"ABBACAB",并定义了三个符号'A'、'B'、'C',以及它们的概率。
算术编码用C++的实现

算术编码在图象数据压缩标准(如jpeg,jbig)中扮演了重要的⾓⾊。
在算术编码中,消息⽤0到1之间的实数进⾏编码。
算术编码⽤到了两个基本的参数:符号的概率和它的编码间隔。
信源符号的概率决定压缩编码的效率,也决定编码过程中信源符号的间隔,⽽这些间隔包含在0到1之间。
编码过程中的间隔决定了符号压缩后的输出。
算术编码需要输⼊的是符号,各个符号的概率还有需要编码的符号序列,根据概率可以算出初始编码间隔,先设⼏个变量在后⾯可⽤:High——当前编码的上限,Low——当前编码的下限,high——中间变量,⽤来计算下⼀个编码符号的当前间隔的上限,low——中间变量,⽤来计算下⼀个编码符号的当前间隔的下限,d——当前间隔之间的距离。
第1个编码符号的当前间隔为其初始的编码间隔,第i个编码符号的当前间隔为第i-1个编码后的[Low,High),第i+1个编码符号的当前间隔算法如下:high=Low+d*第i+1个初始编码符号对应的上限,low=Low+d*第i+1个编码符号对应的下限,然后High=high,Low=low,d=d*第i个编码符号的概率。
编码程序如下:#include#define M 100#define N 4class suanshu{int count,length;char number[N],n;long double chance[N],c;char code[M];long double High,Low,high,low,d;public:suanshu(){High=0;Low=0;}void get_number();void get_code();void coding();~suanshu(){}};void suanshu::get_number(){cout<for(int i=0;i{cin>>n>>c;number[i]=n;chance[i]=c;}if(i==20)cout<count=i;}。
算术编码ArithmeticCoding-高质量代码实现详解

算术编码ArithmeticCoding-⾼质量代码实现详解关于算术编码的具体讲解我不多细说,本⽂按照下述三个部分构成。
两个例⼦分别说明怎么⽤算数编码进⾏编码以及解码(来源:ARITHMETIC CODING FOR DATA COIUPRESSION);接下来我会给出算术编码的压缩效果接近熵编码的证明⽅法(这⼀部分参考惠普公司的论⽂:Introduction to Arithmetic Coding - Theory and Practice);最后我会详细说明⼀下算数编码的实现代码(代码来源:ACM87 ARITHMETIC CODING FOR DATA COIUPRESSION);⼀, 直观上去认识算术编码编码过程:将字符映射到 [0,1) 的区间的⼀个数稍微说明⼀下,⼀开始将区间分为好⼏段,每⼀段表⽰⼀个字符。
编码字符e的时候,就把原先区间表⽰e的那⼀段放⼤,对这个区间进⾏划分获得⼦区间,每个⼦区间也是代表⼀个字符。
依次进⾏下去。
编码结束的时候获得的那个区间就是我们要的,我们可以在这中间取个数就好了。
伪代码是这样的:解码过程:将编码得到的数还原成字符串。
⼤概思路是这样的,就是每次看那个数处落在哪个⼦区间段,然后输出这个区间段所表⽰的字符。
之后,调整区间以及这个数,递归知道输出所有编码字符为⽌。
⼆,证明算术编码的压缩效率⾸先我们得确切知道我们到底编码出来的是什么,然后我们才能去进⼀步去证明。
经过上⼀步的直观认识,我们应该知道编码结束的时候我们获得⼀个最终的区间,然后取这个区间中的⼀个值来表⽰最终的编码。
在实践中,我们是输出⼦区间上下界中的共同位。
⽐如我们最终得到的区间是[0.1010011,0.1010000)那么共同位就是0.10100,当然喽,⽅便起见,我们就只保存10100就好了,⽽把⼩数点什么的去掉。
接下来就是证明了。
三,实现代码详解着重讲⼀下编码过程中字符编码的实现,先看⼀下代码。
c++ 算术编码译码

算术编码是一种用于无损数据压缩的熵编码方法。
与更常见的基于符号频率的方法不同,算术编码是基于输入数据流的概率分布。
以下是C++中算术编码和解码的基本实现:```cpp#include <iostream>#include <cmath>using namespace std;// 输入概率分布double P[4] = {0.25, 0.35, 0.15, 0.25};// 编码函数double encode(int symbol) {double low = 0.0, high = 1.0;double range = high - low;for (int i = 0; i < symbol; i++) {low = high;high *= P[i];range *= P[i];}return low + (rand() / (double)RAND_MAX) * range;}// 解码函数int decode(double probability) {int s = 0;while (probability > P[s]) {probability -= P[s];s++;}return s;}int main() {srand(time(NULL)); // 初始化随机数生成器int data[] = {1, 2, 3, 0, 2, 1, 0, 1, 3, 2}; // 输入数据流for (int i = 0; i < 10; i++) {double encoded = encode(data[i]); // 编码数据流 cout << "Encoded value for symbol " << data[i] << " is " << encoded << endl; // 输出编码值}double encoded_data = encode(3); // 编码一个随机符号(这里假设是3)cout << "Encoded value for symbol 3 is " << encoded_data << endl; // 输出编码值int decoded_data = decode(encoded_data); // 解码数据流cout << "Decoded value is " << decoded_data << endl; // 输出解码值return 0;}```这个程序首先定义了一个概率分布数组,然后定义了两个函数:一个用于编码,另一个用于解码。
C语言中的编解码技巧

C语言中的编解码技巧编解码是计算机科学中非常重要的概念,它涉及到将数据从一种形式转换为另一种形式。
在C语言中,编解码技巧是开发者必备的技能之一。
本文将介绍C语言中常用的编解码技巧,包括字符编码、数值转换、位操作等方面。
1. 字符编码在C语言中,字符编码是将字符表示为二进制数据的过程。
常用的字符编码方式包括ASCII码、Unicode和UTF-8等。
ASCII码是美国标准信息交换码,用于表示英语字符和控制字符。
Unicode是一种国际字符集,几乎包含了所有的字符。
UTF-8是对Unicode的一种变长编码方式。
在使用字符编码时,需要注意以下几点:- 确保字符集的一致性,避免出现乱码现象。
- 要正确处理特殊字符,如换行符、制表符等。
- 对于不支持的字符,需要进行适当的处理,如显示为占位符或进行字符转义。
2. 数值转换在C语言中,经常需要进行数值的转换,例如将整型转换为浮点型、字符型转换为整型等。
2.1 整型转换整型转换是将一个整数表示为不同数据类型的过程。
C语言中提供了强制类型转换的方式来实现整型转换。
例如,使用 `(float)` 可将整型转换为浮点型,使用 `(int)` 可将浮点型转换为整型。
在进行整型转换时,需要注意数据范围的限制,避免溢出或损失精度。
2.2 字符转换字符转换是将一个字符表示为整数的过程。
在C语言中,每个字符都对应一个ASCII码值。
可以通过强制类型转换将字符转换为整型。
例如,使用`(int)`可以将字符'A'转换为对应的ASCII码值65。
3. 位操作位操作是对二进制位进行操作的技巧,常用的位操作运算符包括按位与(`&`)、按位或(`|`)、按位取反(`~`)以及位移操作(`<<`和`>>`)。
3.1 按位与运算按位与运算可以将两个二进制数的对应位进行与操作,并返回结果。
在C语言中,可以使用`&`运算符来实现按位与运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算术编码的C++实现#include <iostream>#include <string>#include <cstring>#include <vector>using namespace std;#define N 50 //输入的字符应该不超过50个struct L //结构用于求各字符及其概率{char ch; //存储出现的字符(不重复)int num; //存储字符出现的次数double f;//存储字符的概率};//显示信息void disp();//求概率函数,输入:字符串;输出:字符数组、字符的概率数组;返回:数组长度;int proba(string str,char c[],long double p[],int count);//求概率的辅助函数int search(vector<L> arch,char,int n);//编码函数,输入:字符串,字符数组,概率数组,以及数组长度;输出:编码结果long double bma(char c[],long double p[],string str,int number,int size);//译码函数,输入:编码结果,字符串,字符数组,概率数组,以及它们的长度;输出:字符串//该函数可以用于检测编码是否正确void yma(string str,char c[],long double p[], int number,int size,long double input);int main(){string str; //输入要编码的String类型字符串int number=0,size=0; //number--字符串中不重复的字符个数;size--字符串长度char c[N]; //用于存储不重复的字符long double p[N],output; //p[N]--不重复字符的概率,output--编码结果disp();cout<<"输入要编码的字符串:";getline(cin,str); //输入要编码的字符串size=str.length(); //字符串长度number=proba(str,c,p,size);//调用求概率函数,返回不重复字符的个数cout.setf(ios::fixed); //“魔法配方”规定了小数部分的个数cout.setf(ios::showpoint); //在此规定编码结果的小数部分有十个cout.precision(10);output=bma( c, p, str, number, size);//调用编码函数,返回编码结果yma(str,c, p, number, size, output); //调用译码函数,输出要编码的字符串,//以验证编码是否正确return 0;}//显示信息void disp(){cout<<endl;cout<<"********************算术编码*********************\n";cout<<"*****************作者:heiness******************\n";cout<<endl;cout<<"此程序只需要输入要编码的字符串,不需要输入字符概率\n";cout<<endl;}//求概率函数int proba(string str,char c[],long double p[], int count){cout.setf(ios::fixed); //“魔法配方”规定了小数部分位数为三位cout.setf(ios::showpoint);cout.precision(3);vector<L>pt; //定义了结构类型的向量,用于同时存储不重复的字符和其概率L temp; //结构类型的变量temp.ch = str[0]; //暂存字符串的第一个字符,它的个数暂设为1temp.num=1;temp.f=0.0;pt.push_back(temp); //将该字符及其个数压入向量for (int i=1;i<count;i++)//对整个字符串进行扫描{temp.ch=str[i]; //暂存第二个字符temp.num=1;temp.f=0.0;for (int j=0;j<pt.size();j++) //在结构向量中寻找是否有重复字符出现{ //若重复,该字符个数加1,并跳出循环int k; //若不重复,则压入该字符,并跳出循环k=search(pt,str[i],pt.size());if(k>=0){pt[k].num++;break;}else{pt.push_back(temp);break;}}}for (i=0;i<pt.size();i++) //计算不重复字符出现的概率{pt[i].f=double(pt[i].num)/count;}int number=pt.size(); //计算不重复字符出现的次数cout<<"各字符概率如下:\n";for (i=0;i<number;i++) //显示所得的概率,验证是否正确{if (count==0){cout<<"NO sample!\n";}else{c[i]=pt[i].ch;p[i]=pt[i].f;cout<<c[i]<<"的概率为:"<<p[i]<<endl;}}return number; //返回不重复字符的个数}//求概率的辅助函数//若搜索发现有重复字符返回正数//否则,返回-1int search(vector<L> arch,char ch1,int n){for (int i=0;i<n;i++)if(ch1==arch[i].ch) return i;return -1;}//编码函数long double bma(char c[],long double p[],string str,int number,int size){long double High=0.0,Low=0.0,high,low,range;//High--下一个编码区间的上限,Low--下一个编码区间的下限;//high--中间变量,用来计算下一个编码区间的上限;//low--中间变量,用来计算下一个编码区间的下限;//range--上一个被编码区间长度int i,j=0;for(i=0;i<number;i++)if(str[0]==c[i]) break; //编码第一个字符while(j<i)Low+=p[j++]; //寻找该字符的概率区间下限range=p[j]; //得到该字符的概率长度High=Low+range; //得到该字符概率区间上限for(i=1;i<size;i++) //开始编码第二个字符for(j=0;j<number;j++) //寻找该字符在c数组中的位置{if(str[i]==c[j]){if(j==0) //若该字符在c数组中的第一个字符{low=Low; //此时该字符的概率区间下限刚好为零high=Low+p[j]*range;High=high;range*=p[j]; //求出该字符的编码区间长度}else //若该编码字符不是c数组中的第一个{float proba_next=0.0;for(int k=0;k<=j-1;k++)proba_next+=p[k]; //再次寻找字符的概率区间下限low=Low+range*proba_next; //编码区间下限high=Low+range*(proba_next+p[j]);//编码区间上限Low=low; //编码区间下限High=high; //编码区间上限range*=p[j]; //编码区间长度}}else continue; //i++,编码下一个字符}cout<<endl;cout<<"输入字符串的编码为:"<<Low<<endl;return Low;}//译码函数void yma(string str,char c[],long double p[], int number,int size,long double input){vector<char> v; //定义char类型向量vlong double temp; //中间变量long double sum[N]; //存储不重复字符概率区间的下限sum[0]=0.0; //数组第一个元素为0for (int i=1;i<number+1;i++) //计算数组各元素的值{sum[i]=sum[i-1]+p[i-1];}for (int j=0;j<size;j++){for (int k=0;k<number;k++){ //确定被编码字符的下限属于【0,1】之间的哪一段if ((input>sum[k])&&(input<sum[k+1])) //发现在哪就将属于该段的字符压入向量v{v.push_back(str[j]);temp=(input-sum[k])/(sum[k+1]-sum[k]);//计算下一个被编码字符的下限input=temp;break;}elsecontinue;}}cout<<endl;cout<<"译码输出为:"; //将译码结果输出for (int m=0;m<v.size();m++){cout<<v[m];}cout<<endl;}。
