matlab所有实验及答案
MATLAB)课后实验答案[1]
![MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/60464e2a366baf1ffc4ffe4733687e21af45ffcc.png)
MATLAB)课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值,然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。
(1) 0122sin851z e =+(2) 221ln(1)2z x x =++,其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ?≤=-≤,其中t =0:0.5:2.5 解: M ⽂件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5]; z2=1/2*log(x+sqrt(1+x^2)) a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建⽴⼀个字符串向量,删除其中的⼤写字母。
解:(1) 结果:m=100:999;n=find(mod(m,21)==0);length(n)ans =43(2). 建⽴⼀个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch =实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵,试通过数值计算验证22E R RS A O S +??=。
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、 已知⎪⎭⎫⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
matlab上机实验答案-整理版

第一次实验答案1. 设要求以0.01秒为间隔,求出y 的151个点,并求出其导数的值和曲线。
clcclearx=0:0.01:1.5;y=sqrt(3)/2*exp(-4*x).*sin(4*sqrt(3)*x+pi/3)y1=diff(y)subplot(2,1,1)plot(x,y)subplot(2,1,2)plot(x(1:150),y1)2绘制极坐标系下曲线(a,b,n 自定数据)clccleara=10;b=pi/2;n=5;theta=0:pi/100:2*pi;rho=a*cos(b+n*theta);polar(theta,rho)3. 列出求下列空间曲面交线的程序clcclearx=[-5:0.5:5];[X,Y]=meshgrid(x);z1=X.^2-2*Y.^2;z2=X.*2-Y.*3;xlabel('x')ylabel('y')zlabel('z')surf(X,Y,z1)hold onsurf(X,Y,z2)k=find(abs(z1-z2)<0.5);x1=X(k)y1=Y(k)z3=x1.^2-2*y1.^2hold onplot3(x1,y1,z3,'*')⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t ()θρn b a +=cos 2212y x z -=y x z 322-=4、设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线,要求有图形标注。
clcclearx=-2*pi:0.1: 2*pi;y=cos(x).*(0.5+sin(x)*3./(1+x.^2));plot(x,y,'b*-');title('绘图');xlabel('x 坐标');ylabel('y 坐标');legend('原函数')gtext('y=cos(x)(0.5+3*sin(x)/(1+x^2))')5、求下列联立方程的解81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y x clccleara=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10];b=[4,-3,9,-8];c=b/a;x=c(1,1)y=c(1,2)z=c(1,3)w=c(1,4)6. 假设一曲线数据点为x = 0:2:4*pi;y = sin(x).*exp(-x/5);试将x 的间距调成 0.1,采用不同插值方法进行插值,并通过子图的形式将不同插值结果和原始数据点绘制在同一图形窗口。
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
MATLAB)课后实验答案

实验一 MATLAB 运算基础1、 先求下列表达式得值,然后显示MATLAB 工作空间得使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0、5:2、5 解:4、 完成下列操作:(1) 求[100,999]之间能被21整除得数得个数。
(2) 建立一个字符串向量,删除其中得大写字母。
解:(1) 结果:(2)、 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果就是:实验二 MATLAB 矩阵分析与处理1、 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵与对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5、 下面就是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程得解。
(2) 将方程右边向量元素b 3改为0、53再求解,并比较b 3得变化与解得相对变化。
(3) 计算系数矩阵A 得条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1、 求分段函数得值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5、0,-3、0,1、0,2、0,2、5,3、0,5、0时得y 值。
MATLAB)课后实验答案

3. 硅谷公司员工的工资计算方法如下: (1) 工作时数超过120小时者,超过部分加发15%。 (2) 工作时数低于60小时者,扣发700元。 (3) 其余按每小时84元计发。 试编程按输入的工号和该号员工的工时数,计算应发工资。 解:M文件下
实验四 循环结构程序设计 1. 根据2222211116123nL,求π的近似值。当n分别取100、1000、10000时,结果是多少? 要求:分别用循环结构和向量运算(使用sum函数)来实现。 解:M文件如下:
实验一 MATLAB运算基础 1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。 (1) 0122sin851ze (2) 221ln(1)2zxx,其中2120.455ix (3) 0.30.330.3sin(0.3)ln,3.0,2.9,,2.9,3.022aaeeazaaL (4) 2242011122123ttzttttt,其中t=0:0.5:2.5 解: M文件: z1=2*sin(85*pi/180)/(1+exp(2)) x=[2 1+2*i;-.45 5]; z2=1/2*log(x+sqrt(1+x^2)) a=-3.0:0.1:3.0; z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) t=0:0.5:2.5; z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)
clc; h=6:2:18; t1=[18.0 20.0 22.0 25.0 30.0 28.0 24.0]; t2=[15.0 19.0 24.0 28.0 34.0 32.0 30.0]; T1=interp1(h,t1,'spline')%室内的3次样条插值温度 T2=interp1(h,t2,'spline')%室外的3次样条插值温度 运行结果: 4. 已知lgx在[1,101]区间10个整数采样点的函数值如实验表2所示。 实验表2 lgx在10个采样点的函数值 x 1 11 21 31 41 51 61 71 81 91 101 lgx 0 1.0414 1.3222 1.4914 1.6128 1.7076 1.7853 1.8513 1.9085 1.9510 2.0043 试求lgx的5次拟合多项式p(x),并绘制出lgx和p(x)在[1,101]区间的函数曲线。 解: M文件: x=1:10:101; y=lg10(x); P=polyfit(x,y,5) y1=polyval(P,x); plot(x,y,':o',x,y1,'-*') 5. 有3个多项式P1(x)=x4+2x3+4x2+5,P2(x)=x+2,P3(x)=x2+2x+3,试进行下列操作: (1) 求P(x)=P1(x)+P2(x)P3(x)。 (2) 求P(x)的根。 (3) 当x取矩阵A的每一元素时,求P(x)的值。其中 : 11.21.40.7523.5052.5A (4) 当以矩阵A为自变量时,求P(x)的值。其中A的值与第(3)题相同。 解:M文件: clc;clear; p1=[1,2,4,0,5]; p2=[1,2]; p3=[1,2,3]; p2=[0,0,0,p2]; p3=[0,0,p3]; p4=conv(p2,p3); %p4是p2与p3的乘积后的多项式 np4=length(p4); np1=length(p1);
MATLAB)课后实验答案[1]
![MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/adaedec65727a5e9846a61d9.png)
实验一 MATLAB 运算基础1。
先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解:4. 完成下列操作:(1)求[100,999]之间能被21整除的数的个数. (2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2)。
建立一个字符串向量例如:ch=’ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5。
下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ch =123d4e56g9(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0。
53再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1. 求分段函数的值.2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5.0,—3.0,1.0,2。
matlab实验指导答案详解(非常详细正确)

实验一MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条(Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-52⨯2-70)÷3 >>(365-52*2-70)/3 ans = 63.6667(2)>>area=pi*2.5^2 area = 19.6350(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= >>x=3 >>y=4>>z = x ^2 * y ^3 / (x - y) ^2 z = 576(4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1 =[16 2 3 13 ; 5 11 10 8 ; 9 7 6 12 ; 4 14 15 1 ] >>m1( 2 , 3 ) ans = 10 >>m1( 11 ) ans = 6>>m1( : , 3 ) ans =3 10 6 15>>m1( 2 : 3 , 1 : 3 ) ans =5 11 10 9 7 6>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) ans = 34(5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) (6)执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
MATLAB数学实验100例题解
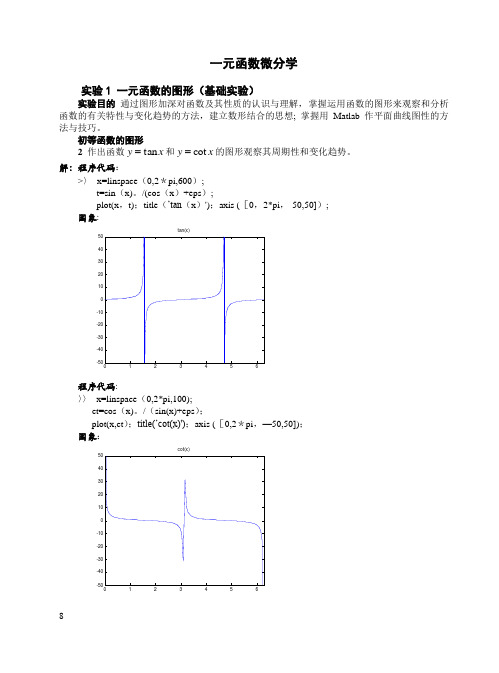
一元函数微分学实验1 一元函数的图形(基础实验)实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧。
初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势。
解:程序代码:>〉 x=linspace (0,2*pi,600); t=sin (x)。
/(cos (x )+eps );plot(x ,t);title (’tan (x )');axis ([0,2*pi ,-50,50]); 图象:程序代码: 〉〉 x=linspace (0,2*pi,100); ct=cos (x)。
/(sin(x)+eps ); plot(x,ct );title(’cot(x)');axis ([0,2*pi ,—50,50]); 图象:cot(x)4在区间]1,1[-画出函数xy 1sin =的图形。
解:程序代码:>> x=linspace (-1,1,10000);y=sin(1。
/x ); plot (x,y ); axis ([-1,1,—2,2]) 图象:二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形:解:程序代码:>〉 t=linspace(0,2*pi,100); plot(cos(t ).*cos (5*t ),sin(t )。
*cos(3*t)); 图象:极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解:程序代码:〉〉 t=0:0.01:2*pi ; r=exp (t/10);polar(log(t+eps ),log (r+eps)); 图象:90270分段函数作图10 作出符号函数x y sgn =的图形。
MATLAB数学实验答案(全)

第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin limx mx mxx →∞- syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算2211x y edxdy +⎰⎰dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +⎰ syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//高阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
MATLAB相关的实验以及答案

y=zeros(size(x)); i=numel(x); for j=1:i if (x(j)>=0) y(j)=-3*x(j)^2+5; else y(j)=3*x(j)^2+5; end end x y
4. 编写一程序,求出 编写一程序,求出[100 1000]以内的全部素数。 以内的全部素数。 以内的全部素数 num=[ ]; i=1; for k1=100:1000 k2=fix(sqrt(k1)); sign=1; for k3=2:k2 if mod(k1,k3)==0 sign=0; break end end if sign==1 num(i)=k1; i=i+1; end end num
6. 建立函数count(x),其中x为一个班的学生成绩,统 建立函数 ,其中 为一个班的学生成绩, 为一个班的学生成绩 计该班学生成绩,其中优秀:成绩≥90,良好:80≤ 计该班学生成绩,其中优秀:成绩 ,良好: 成绩<90,中等:70≤成绩 成绩<80,及格:60≤成绩 成绩<70, 成绩 ,中等: 成绩 ,及格: 成绩 , 不及格:成绩<60,分别输出优秀、良好、中等、不 不及格:成绩 ,分别输出优秀、良好、中等、 及格的人数,要求有输入、输出提示语句。例如: 及格的人数,要求有输入、输出提示语句。例如: >> count 请输入该班学生成绩: %输出提示 请输入该班学生成绩: 输出提示 [34 67 98 89 78] %输入成绩 输入成绩 成绩优秀: %输出结果 成绩优秀:1 输出结果 成绩良好: 成绩良好:1 成绩中等: 成绩中等:1 成绩及格: 成绩及格:1 成绩不及格: 成绩不及格:1
2. 输入三角形的三条边,求三角形的面积。如果输入 输入三角形的三条边,求三角形的面积。 的三个数不能构成三角形,要求输出“ 的三个数不能构成三角形,要求输出“不能构成一个 三角形”这样的提示信息。 三角形”这样的提示信息。 提示: 提示: area = s(s −a)(s −b)(s −c) s = (a +b + c) / 2 a=input('a='); b=input('b='); c=input('c='); if (a+b>c)&(a+c>b)&(b+c>a) s=(a+b+c)/2; area=sqrt(s*(s-a)*(s-b)*(s-c)) else fprintf(‘不能构成一个三角形 不能构成一个三角形\n’) 不能构成一个三角形 end
MATLAB实验答案

实验一:变量和矩阵的赋值、矩阵的初等运算实验目的:1. 熟悉MATLAB的工作环境2. 掌握变量的赋值、矩阵的创建。
3. 掌握矩阵和数组的初等运算。
4. 熟悉和掌握inv、mean、var、randn、rand、ones、zeros、magic、eye函数的使用。
实验内容:1. 菜单栏File→Preferences→Command Window→Font and Colors修改字体,选择Use custom font改为24。
同样方法File→Preferences→Editor/Debugger→Font and Colors 修改字体,选择Use custom font改为24。
点击Apply,OK即可。
2. 在内产生均匀分布的200个点,形成1×200向量赋给变量X。
(结果不必记录)X=linspace(0,2*pi,200);3. 在内每间隔3产生向量Y。
Y=[0:3:10];4. 给矩阵赋值,,打开workspace查看矩阵的赋值。
使用save data A B语句存储到data.mat数据文件中。
输入Clear all命令清空所有变量,再使用load data加载矩阵A 和B。
A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 18];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7];save data A B;clear all;load data;5. 产生8*6阶的正态分布随机数矩阵R,求其各列的平均值和方差,并求全体的平均值和方差。
R=randn(8,6);a=mean(R);b= var(R);c=mean(R(:));d=var(R(:));6. 模拟选号程序,现有10000人,按顺序编号为1,2,…10000号,一次随机选出一个编号,要求随机数均匀分布。
R=round(ceil(rand(10000,1)*10000));7. 产生4*6阶的均匀分布随机数矩阵R,要求其元素在1~16之间取整数值,并求此矩阵前四列组成的方阵的逆阵。
Matlab上机实验答案

Matlab 上机实验答案实验一MATLAB运算基础1.先求以下表达式的值,尔后显示 MATLAB 工作空间的使用状况并保存所有变量。
2sin850(1)z11 e2>>z1=2*sin(85*pi/180)/(1+exp(2)) z1 =(2) z21 1 x2212iln( x) ,此中x5 2>>x=[2 1+2i;-0.45 5];>>z2=1/2*log(x+sqrt(1+x^2))z2 =(3) z3e0.3a e sin(a0.3) ln0.3 a22>>a=-3.0:0.1:3.0;>>z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) (>> z33=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2)可以考据 z3==z33 ,能否都为 1)z3 =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 20 Columns 21 through 25 Columns 26 through 30 Columns 31 through 35 Columns 36 through 40Columns 41 through 45 Columns 46 through 50 Columns 51 through 55 Columns 56 through 60Column 61t 20 t1(4) z4t 211t 2 ,此中t 22t 1 2t3>>t=0:0.5:2.5;>>z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3).*(t.^2-2.*t+1)z4 =002.已知:12344131A 34787, B2033657327求以下表达式的值:(1)A+6*B 和 A-B+I (此中 I 为单位矩阵)(2)A*B 和 A.*B(3)A^3 和 A.^3(4)A/B 及 B\A(5) [A,B] 和[A([1,3],:);B^2]>>A=[12 34 -4;34 7 87;3 65 7];>>B=[1 3 -1; 2 0 3;3 -2 7];>>A+6*Bans =1852-10467105215349>>I=eye(3);>>A-B+Ians =1231-3328840671(2)>> A*Bans =684462309-72596154-5241>>A.*Bans =1210246802619-13049(3)>> A^3ans =372262338244860424737014918860076678688454142118820>>A.^3ans =172839304-643930434365850327274625343 (4)>> A/Bans =>>B\Aans =(5)>>[A,B]ans =1234-413-13478720336573-27 >>[A([1,3],:);B^2]ans =1234-436574511101920-5403.设有矩阵 A和B1234530166789101769A 1112131415, B02341617181920970212223242541311(1)求它们的乘积 C。
matlab所有实验及答案李楠资料

第二章 习题1、 矩阵Y= ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3472123100451150425,给出元素1的全下标和单下标,求出元素100的存储位置。
取出子矩阵⎥⎦⎤⎢⎣⎡21301,并求该矩阵的维数。
解:命令为:Y=[5,2,4;0,15,1;45,100,23;21,47,3] Y(2,3) Y(10)find(Y==100) sub2ind([4 3],3,2)B=Y(2:2:4,3:-2:1) 或 B=Y([2 4],[3 1]) [m n]=size(Y)2、已知矩阵A=[1 0 -1 ;2 4 1; -2 0 5],B=[0 -1 0;2 1 3;1 1 2] 求2A+B 、A 2-3B 、A*B 、B*A 、A .*B ,A/B 、A\B 解:命令为:A=[1 0 -1 ;2 4 1; -2 0 5] B=[0 -1 0;2 1 3;1 1 2] E=2*A+B F=A^2-3*B G=A*B H=B*A I=A.*B J=A/B K=A\B3、 利用函数产生3*4阶单位矩阵和全部元素都为8的4*4阶矩阵,并计算两者的乘积。
解:命令为: A=eye(3,4) B=8*ones(4) C=A*B4、创建矩阵a=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------7023021.5003.120498601,取出其前两列构成的矩阵b ,取出前两行构成矩阵c ,转置矩阵b 构成矩阵d ,计算a*b 、c<d ,c&d, c|d ,~c|~d 解:命令为:a=[-1,0,-6,8;-9,4,0,12.3;0,0,5.1,-2;0,-23,0,-7] b=a(:,[1 2]) c=a([1 2],:) d=b ’ e=a*b f=c<d g=c&d h=c|d i=~c|~d5、 使用函数,实现A 到B 、C 、D 、E 的转换A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡129631185210741 B=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡321654987121110 C=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡101112789456123,D=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡369122********* E=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡126311521041 解:命令为:A=[1 4 7 10;2 5 8 11;3 6 9 12] B=rot90(A) C=rot90(A,3) D=fliplr(A) A(:,3)=[] E=A7. 矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-410091021.5823.1204450002,用函数取出列向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100845和矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡410091001.582004450002 解:命令为:A=[2 0 0 0;45 4 0 12.3;2 8 5.2 -2;0 91 100 4] B=diag(A)C=tril(A)8.建立5阶魔方矩阵,求该矩阵的行列式和逆矩阵、秩以及any 和all 运算结果。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/d27ebaa958fb770bf78a55b8.png)
实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5. 下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0.53再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下: 123d4e56g9实验三 选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 40 98 80 7 14 16 73 55 57 64 41 4 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 34 17 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37P 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1]; >> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]'; >> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95]; >> x1=a*x, x2=a^2*x, x10=a^10*x >> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i -0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000 -41.0000 25.0000 10.0000 -6.0000 -17.0000 10.0000 5.0000 -3.0000 10.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286 -0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771 -0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628 -0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\b ans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);1 6*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小,x(2)最大。
Matlab实验习题集答案

1:用以上两种形式计算36sin 5e ++π算术运算结果。
>> 5^6+sin(pi)+exp(3)ans =1.5645e+004>> x=5^6+sin(pi)+exp(3)x = 1.5645e+0042:已知矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2211,2121B A ,对它们做简单的关系与逻辑运算C=(A<B)&(A= =B)>> A=[1 2;1 2];>> B=[1 1;2 2];>> C=(A<B)&(A==B) C =0 00 03:对数7sin 5+=a 用五位定点、十五位定点以及有理数形式表示出来。
>> a=5+sin(7);format short,aa =5.6570>> a=5+sin(7);>> format long,aa =5.6569865987187894:直接输入创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=98760154321A>> A=[1 2 3;4 15 60;7 8 9]A =1 2 34 15 607 8 95:输入矩阵111111111⎛⎫ ⎪ ⎪ ⎪⎝⎭。
%利用MATLAB 命令直接输入矩阵OneMatrix=ones(3,3,1)OneMatrix =1 1 1 1 1 1 1 1 16:输入矩阵00000 00000⎛⎫ ⎪⎝⎭>> OneMatrix=ones(2,5,1);ZeroMatrix=zeros(size(OneMatrix))ZeroMatrix =0 0 0 0 00 0 0 0 07:生成3阶魔方矩阵。
>> magic(3)ans =8 1 63 5 74 9 28:操作符冒号”:”的应用a)步长为1的等差数列b)步长为2的等差数列c)步长为-2的等差、递减数列>> 0:1:10ans =0 1 2 3 4 5 6 7 8 9 10 >> 0:2:10ans =0 2 4 6 8 10>> 10:(-2):0ans =10 8 6 4 2 09:已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=162ln973sin56231A,抽取与修改矩阵A的一些元素.a)求矩阵A的第二行第三列元素b)求矩阵A的第四个元素c)取矩阵A的A(2),A(3),A(4)d)取矩阵A的第一行e)取矩阵A的第三列f)把矩阵A的第一行第三列元素赋值给变量g)把矩阵A的第二行第一列元素修改为100>> A=[1 23 56;sin(3) 7 9;log(2) 6 1] >> A(2,3)ans =9>> A(4)ans =23>> A(2),A(3),A(4)ans =0.141120008059867ans =0.693147180559945ans =23>> A(1,:)ans =1 23 56>> A(:,3)ans =5691>> x=A(1,3)x =56>> A(2,1)=100A =1.0000 23.0000 56.0000 100.0000 7.0000 9.00000.6931 6.0000 1.000010:已知矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=851,9631BA,利用A与B生成矩阵13100690C⎛⎫= ⎪⎝⎭,() D A B=,AAAB⎛⎫= ⎪⎝⎭。
MATLAB课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+(2) 221ln(1)2z x x =++,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=-- (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解: M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5]; z2=1/2*log(x+sqrt(1+x^2)) a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:m=100:999;n=find(mod(m,21)==0);length(n)ans =43(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 习题1、 矩阵Y= ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3472123100451150425,给出元素1的全下标和单下标,并用函数练习全下标和单下标的转换,求出元素100的存储位置。
取出子矩阵⎥⎦⎤⎢⎣⎡21301,并求该矩阵的维数。
解:命令为:Y=[5,2,4;0,15,1;45,100,23;21,47,3] Y(2,3) Y(10)sub2ind([4 3],2,3) [i,j]=ind2sub([4 3],10)find(Y==100) sub2ind([4 3],3,2)B=Y(2:2:4,3:-2:1) 或 B=Y([2 4],[3 1]) [m n]=size(Y)2、 建立一个数值范围为0—100内4*5的整数随机矩阵。
求出大于50的元素的位置。
解:命令为:G=int8(100*rand(4,5)) find(G>50)3、 已知矩阵A=[1 0 -1 ;2 4 1; -2 0 5],B=[0 -10;2 1 3;1 1 2] 求2A+B 、A 2-3B 、A*B 、B*A 、A .*B ,A/B 、A\B 解:命令为:A=[1 0 -1 ;2 4 1; -2 0 5] B=[0 -1 0;2 1 3;1 1 2] E=2*A+B F=A^2-3*B G=A*B H=B*A I=A.*B J=A/B K=A\B4、 利用函数产生3*4阶单位矩阵和全部元素都为8的4*4阶矩阵,并计算两者的乘积。
解:命令为: A=eye(3,4) B=8*ones(4) C=A*B5、 创建矩阵a=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------7023021.5003.120498601,取出其前两列构成的矩阵b ,取出前两行构成矩阵c ,转置矩阵b构成矩阵d ,计算a*b 、c<d ,c&d, c|d ,~c|~d 解:命令为:a=[-1,0,-6,8;-9,4,0,12.3;0,0,5.1,-2;0,-23,0,-7] b=a(:,[1 2]) c=a([1 2],:) d=b ’ e=a*b f=c<d g=c&d h=c|d i=~c|~d6、 使用函数,实现A 到B 、C 、D 、E 的转换A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡129631185210741 B=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡321654987121110 C=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡101112789456123,D=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡369122*********E=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡126311521041 解:命令为:A=[1 4 7 10;2 5 8 11;3 6 9 12] B=rot90(A) C=rot90(A,3) D=fliplr(A) A(:,3)=[] E=A7. 矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-410091021.5823.1204450002,用函数取出列向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100845和矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡410091001.582004450002 解:命令为:A=[2 0 0 0;45 4 0 12.3;2 8 5.2 -2;0 91 100 4] B=diag(A) C=tril(A)8.建立5阶魔方矩阵,求该矩阵的行列式和逆矩阵、迹以及any 和all 运算结果。
建立一个M 文件保存起来并练习调用。
解:命令文件为: A=magic(5) x=det(A) B=inv(A) C=trace(A) D=any(A) E=all(A)实验三 习题1. 创建2*2元胞数组A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡i 2189241001abc ’‘,并求出1001;创建结构数组student ,要求包含三个属性名:姓名,学号,年龄,分别存放 张三,10021、20 李四、10022、18王五、10023、19,并写出取得李四学号的操作。
解:命令为:A={'abc',[1001;24];89,1+2i} x=A{1,2}(1,1)student=struct('name',{'张三';'李四';'王五'},'number',{10021;10022;10023},'age',{20;18;19}) student(2,1).number2. 求多项式10235x p(x)235++-=x x ,在3.12=x 时的值,和p(x)=0时候的根。
解:命令为: p=[5,0,-3,2,0,10]; poly2sym(p)x=polyval(p,12.3) y=roots(p)3.已知矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----73220250453.12049826101, 求A 的特征值,特征向量。
解:命令为:A=[-1 10 26 8;-9 4 0 12.3;45 0 5 -2;0 -2 32 -7] [X,D]=eig(A) t=eig(A)并求拟合多项式系数向量。
解:命令为: x=[21 22 23 24] format longy=[0.35537 0.37461 0.39073 0.40674] interp1(x,y,21.5,'nearest') [P,S]=polyfit(x,sin(x),3)(P 是一个长度为N+1的向量,代表N 次多项式,S 是采样点的误差向量。
)5.将10个学生5门功课的成绩存入矩阵P 中,进行 (1)求每门课的最高分,最低分,平均分, (2)求5门课总分的最高分、最低分 解:命令为:Y=[90 89 91 82 75;88 82 85 89 95;79 89 93 82 76;91 89 87 79 85;90 79 78 91 82;86 85 84 89 88;89 91 79 90 94;75 85 95 90 87;85 78 75 90 89;98 89 87 86 80] a=max(Y) b=min(Y) c=mean(Y,1) format short f=mean(Y ,2)*5 t=max(f) h=min(f) 或n=sum(Y ,2) a=max(n) b=min(n)6. 用数值方法解线性方程组⎪⎪⎩⎪⎪⎨⎧=+-=-++=-+--=+-+1129312243134945256u y x u z y x u z y x u z y x 解:命令为:A=[6 5 -2 5;9 -1 4 -1;3 4 2 -2;3 -9 2 0] b=[-4 13 1 11]' X=A\b7、 求方程,1025=+x x x 在x=1附近的根。
解:命令为:fsolve('x*5^x+2*x-10',1)实验四:程序设计注意:要用M 文件实现,一道题,一个M 文件,命令文件或者函数文件自选 1. 求!201∑=n n解:命令文件为 sum=0; s=1;for n=1:20 s=n*s;sum=sum+s; end sum2. 求a aa aaa aa a S n ++++=得值,其中a 是一个数字,由键盘输入,表达式中位数最多项a 的个数,也由键盘输入。
例如:输入a=3,n=4, 则s4=3+33+333+3333 解:命令文件为sum=0; s=0;a=input('请输入a 的值:') n=input('请输入n 的值:') for i=1:ns=s+a*10^(i-1); sum=sum+s;end sum3. 计算下列分段函数的值:⎪⎩⎪⎨⎧>≤<-≤=1021054350)(x xx x x x f解:命令文件为x=input('输入x 的值:') if x<=5 f=0;elseif x>5&x<=10 f=(x-3)/4.0; elsef=2*x; endf4. 有一群鸡和兔子,加在一起头的数量是36,脚的数量是100,编程序解答鸡和兔子数量各是多少? 解:命令文件为 for x=0:36for y=0:36-xif (x+y==36)&(2*x+4*y==100) disp('鸡有:') disp(x)disp('兔子有') disp(y) end end end5. 产生20个两位随机整数,输出其中小于平均值的奇数。
解:命令文件为disp('随机矩阵为:') A=randint(1,20,[10,99]) Aver=mean(A)disp('小于平均值的奇数为:') for k=Aif (k<aver)&rem(k,2)==1 disp(k) end end实验五:符号计算 1.(1)化简表达式2cos22sin f x x =+ (2)对表达式624--x x 进行因式分解。
解:命令文件为 syms xf1=cos(2*x)+(sin(x))^2 f2=x^4-x^2-6 t1=simple(f1) t2=factor(f2) 2.求下列极限值 (1)0sin 2limsin 5x x x -> (2)x →∞解:命令文件为 syms xf1=sin(2*x)/sin(5*x)f2=sqrt(x^2+x)-sqrt(x^2-x) t1=limit(f1,x,0) t2=limit(f2,x,inf) 3.分别计算表达式42220(1)1(2)(31)x dx x x x dx+-+⎰⎰解:命令文件为: syms xf1=x^4/(1+x^2) f2=3*x^2-x+1 t1=int(f1,x)t2=int(f2,x,0,2) 4.分别求cos x x 得一阶导数、二阶导数和三阶导数 解:命令文件为: syms x f=x*cos(x) t1=diff(f,'x') t2=diff(f,'x',2) t3=diff(f,'x',3) 5.求下列级数之和(提示:利用symsum(s,v,n,m)函数 或者编程实现)23(1)123(2)21491610000n s x x x nx s =+++=++++解:命令文件为: syms x n m s1=n*x^n s2=n^2t1=symsum(s1,n,1,n) t2=symsum(s2,n ,1,100)6. 求表达式322311x x x +-+ 在x=1.723处的,精度为20位的代数值 解:命令文件为: syms xf=(3*x^3+x^2-1)/(x^2+1) t1=subs(f,'x','1.723') t2=vpa(t1,20) 7.求方程组222602x y z x xz z y x y z z ++=⎧⎪-+=⎨⎪+-=⎩的解 解:命令文件为: syms x y z s1=x+6*y+zs2=x^2-2*x*z+z-y s3=x^2+y-z-z^2[x,y,z]=solve(s1,s2,s3)实验六 绘图21.绘制行向量( 1 8 6 5 4)的图形。
