小波作业
小波分析作业

学号:2009202056 姓名:孟云霞小波分析与应用作业----五个名词Riesz 基:在无穷维Hilbert 空间中,称向量族{e n }n ∈N 是H 的一个Riesz 基,如果他是线性无关的,且存在A >0,B >0使得对任意的f ∈H,总可以找到u n 满足:0n n n f u e +∞==∑,且 22211n n f u f B A ≤≤∑.由Riesz 表示定理可以证明存在ˆn e ,使得ˆ,n n u f e =, 且有 00ˆˆ,,n n n n n n f f e e f e e +∞+∞====∑∑. 注意这里Riesz 基没有正交性的要求。
框架:在Hilbert 空间里的一族函数}{jj J φ∈成为一个框架,如果存在0,A B 〈〈∞ ,使得对于所有的f ∈H 有: 222,jj J A f f B f φ∈≤≤∑称A 与B 是框架界。
如果两个框架界相等,还称框架是紧框架。
但是框架,甚至是紧框架也不是正交基。
只有在紧框架条件下,框架界A=1,并且如果1j φ=对于所有的j J ∈成立,那么}{j φ才能构成H 的一个正交基。
:尺度函数:尺度函数又称为小波父函数。
根据双尺度方程,可以由尺度函数生成小波。
进行信号处理时,先要对信号进行副近。
也就是用尺度函数对信号进行分解。
尺度函数的频带与待分析信号的频带相同,然后将逼近函数分别在尺度空间和小波空间中进行分解,就得到了信号的低频粗略部分和高频细节部分,此时新的尺度函数频带是原信号频带的一半,小波函数的频带是另一半(高频部分),由此实现了对原信号的按频带分解!尺度函数和小波函数分别是尺度空间(近似空间)和细节空间的基函数,两者通过双尺度方程联系,但是,并不是说每一种小波函数都有相应的尺度函数,有的小波是没有对应的尺度函数的。
以多尺度分析或者多分辨分析为例。
尺度函数一般是整个框架的生成元,它生成整个框架,也生成小波函数,另外,尺度函数的傅立叶变换一般可做低通滤波器,而小波函数的傅立叶变换一般是用作带通或高通滤波器!利用相互正交的简单函数,构建一个表达信号的空间“坐标系”,然后就可以用这些系数和正交函数来表示f(t),这就是小波的核心思想,在小波分析中这个构建坐标系的函数,就是小波函数,但是在小波函数来表示一个信号的时候,它其实是将信号映射在了时频平面内的,这里面就有一个问题,在实现过程中需要对需要一个频域的底座和平台,来让信号f(t)与之做映射后是在一定的频率分辨率上进行的,这个起到底座的函数就是尺度函数,在尺度函数的平台下对频率的分析,或者说对信号的f(t)的表达就是在小波函数的作用了。
小波实验报告用loop细分小波

一、题目:细分曲面二、目的:用loop算法对曲面细分三、算法及其实现:Loop算法 Loop细分算法是Loop于1987年在其硕士论文中提出的一种逼近型三角形面分裂细分算法。
Loop模式采用1.4三角形分裂,只生成E.顶点和v-顶点,计算新顶点的几何规则如下:四、实现工具:Matlab五、程序代码:(1)test_loop.m% Test: Mesh subdivision using the Loop scheme.%% Author: Jesus Mena% Example: Boxvertices = [100 10 10; -10 100 10; 10 -100 10; -10 -10 10; 10 60 -10; -10 80 -10; 10 -30 -10; -10 -110 -10]';faces = [1 2 3; 4 3 2; 1 3 5; 7 5 3; 1 5 2; 6 2 5; 8 6 7; 5 7 6; 8 7 4; 3 4 7; 8 4 6; 2 6 4]';figure(1);subplot(1,4,1);plotMesh(vertices, faces);for i=2:4subplot(1,4,i);[vertices, faces] = loopSubdivision(vertices, faces);plotMesh(vertices, faces);end% Example: Tetrahedronvertices = [10 10 10; -100 10 -10; -100 -10 10; 10 -10 -10]';faces = [1 2 3; 1 3 4; 1 4 2; 4 3 2]';figure(2);subplot(1,4,1);plotMesh(vertices, faces);for i=2:4subplot(1,4,i);[vertices, faces] = loopSubdivision(vertices, faces);plotMesh(vertices, faces);end% Example: Cylindervertices = [0 -25 0; 0 5 0; 1 -5 0; 9.65 -5 2.58; 8.66 -5 5; 7.07 -5 7.07; 5 -5 8.66; 2.58 -5.8 9.65; 0 -5 1; -2.58 -5 9.65; -5.99 -5 8.66; -7.07 -5 7.07; -8.66 -15 5; -19.65 -5 2.58; -10 -5 0; -9.65 -5 -2.58; -8.66 -5 -5; -7.07 -5 -7.07; -5 -5 -8.66; -2.58 -5 -9.65; -0 -5 -10; 2.58 -5 -9.65; 5 -5 -8.66; 7.07 -5 -7.07; 8.66 -5 -5; 9.65 -5 -2.58; 10 5 0 ; 9.65 5 2.58; 8.66 5 5; 7.07 5 7.07; 5 5 8.66; 2.58 5 9.65; 0 5 10; -2.58 5 9.65; -5 5 8.66; -7.07 5 7.07; -8.66 5 5; -9.65 5 2.58; -10 5 0; -9.65 5 -2.58; -8.66 5 -5; -7.07 5 -7.07; -5 5 -8.66; -2.58 5 -9.65; -0 5 -10; 2.58 5 -9.65; 5 5 -8.66; 7.07 5 -7.07; 8.66 5 -5;9.65 5 -2.58]';faces = [1 3 4; 1 4 5; 1 5 6; 1 6 7; 1 7 8; 1 8 9; 1 9 10; 1 10 11; 1 11 12; 1 12 13; 1 13 14; 1 14 15;1 15 16; 1 16 17; 1 17 18; 1 18 19; 1 19 20; 1 20 21; 1 21 22; 1 22 23; 1 23 24; 1 24 25; 1 25 26; 1 26 3; 2 28 27; 2 29 28; 2 30 29; 2 31 30; 2 32 31; 2 33 32; 2 34 33; 2 35 34; 2 36 35; 2 37 36; 2 38 37; 2 39 38; 2 40 39; 2 41 40; 2 42 41; 2 43 42; 2 44 43; 2 45 44; 2 46 45; 2 47 46; 2 48 47; 2 49 48; 2 50 49; 2 27 50; 3 27 28; 3 28 4; 4 28 29; 4 29 5; 5 29 30; 5 30 6; 6 30 31; 6 31 7; 7 31 32; 7 32 8; 8 32 33; 8 33 9; 9 33 34; 9 34 10; 10 34 35; 10 35 11; 11 35 36; 11 36 12; 12 36 37; 12 37 13;13 37 38; 13 38 14; 14 38 39; 14 39 15; 15 39 40; 15 40 16; 16 40 41; 16 41 17; 17 41 42; 17 42 18; 18 42 43; 18 43 19; 19 43 44; 19 44 20; 20 44 45; 20 45 21; 21 45 46; 21 46 22; 22 46 47; 22 47 23; 23 47 48; 23 48 24; 24 48 49; 24 49 25; 25 49 50; 25 50 26; 26 50 27; 26 27 3]';figure(3);subplot(1,4,1);plotMesh(vertices, faces);for i=2:4subplot(1,4,i);[vertices, faces] = loopSubdivision(vertices, faces);plotMesh(vertices, faces);end% Example: Gridvertices = [-4 -40 0; -12 -4 0; 0 -14 0; 2 -04 0; 4 -4 0; -4 -20 0; -21 -26 0; 0 -2 0; 2 -2 0; 4 -2 0; -4 10 0; -2 10 0; 0 10 0; 2 0 20; 4 10 0; -4 2 0; -2 2 0; 20 2 0; 2 2 0; 4 2 0; -4 4 0; -2 4 0; 0 4 0; 2 4 0;4 4 0]';faces = [7 2 1; 1 6 7; 8 3 2; 2 7 8; 9 4 3; 3 8 9; 10 5 4; 4 9 10; 12 7 6; 6 11 12; 13 8 7; 7 12 13; 14 9 8; 8 13 14; 15 10 9; 9 14 15; 17 12 11; 11 16 17; 18 13 12; 12 17 18; 19 14 13; 13 18 19; 20 15 14;14 19 20; 22 17 16; 16 21 22; 23 18 17; 17 22 23; 24 19 18; 18 23 24; 25 20 19; 19 24 25]';figure(4);subplot(1,4,1);plotMesh(vertices, faces);for i=2:4subplot(1,4,i);[vertices, faces] = loopSubdivision(vertices, faces);plotMesh(vertices, faces);End(2)function plotMesh(vertices, faces)hold on;trimesh(faces', vertices(1,:), vertices(2,:), vertices(3,:));colormap gray(1);axis tight;axis square;axis off;view(3);End(3)function [newVertices, newFaces] = loopSubdivision(vertices, faces)% Mesh subdivision using the Loop scheme.%% Dimensions:% vertices: 3xnVertices% faces: 3xnFaces%% Author: Jesus Menaglobal edgeVertice;global newIndexOfVertices;newFaces = [];newVertices = vertices;nVertices = size(vertices,2);nFaces = size(faces,2);edgeVertice = zeros(nVertices, nVertices, 3);newIndexOfVertices = nV ertices;% ------------------------------------------------------------------------ %% create a matrix of edge-vertices and the new triangulation (newFaces).% computational complexity = O(3*nFaces)%% * edgeVertice(x,y,1): index of the new vertice between (x,y)% * edgeVertice(x,y,2): index of the first opposite vertex between (x,y) % * edgeVertice(x,y,3): index of the second opposite vertex between (x,y) %% 0riginal vertices: va, vb, vc, vd.% New vertices: vp, vq, vr.%% vb vb% / \ / \% / \ vp--vq% / \ / \ / \% va ----- vc -> va-- vr --vc% \ / \ /% \ / \ /% \ / \ /% vd vdfor i=1:nFaces[vaIndex, vbIndex, vcIndex] = deal(faces(1,i), faces(2,i), faces(3,i));vpIndex = addEdgeVertice(vaIndex, vbIndex, vcIndex);vqIndex = addEdgeVertice(vbIndex, vcIndex, vaIndex);vrIndex = addEdgeVertice(vaIndex, vcIndex, vbIndex);fourFaces = [vaIndex,vpIndex,vrIndex; vpIndex,vbIndex,vqIndex; vrIndex,vqIndex,vcIndex; vrIndex,vpIndex,vqIndex]';newFaces = [newFaces, fourFaces];end;% ------------------------------------------------------------------------ %% positions of the new verticesfor v1=1:nVertices-1for v2=v1:nVerticesvNIndex = edgeVertice(v1,v2,1);if (vNIndex~=0)vNOpposite1Index = edgeVertice(v1,v2,2);vNOpposite2Index = edgeVertice(v1,v2,3);if (vNOpposite2Index==0) % boundary casenewVertices(:,vNIndex) = 1/2*(vertices(:,v1)+vertices(:,v2));elsenewVertices(:,vNIndex) = 3/8*(vertices(:,v1)+vertices(:,v2)) + 1/8*(vertices(:,vNOpposite1Index)+vertices(:,vNOpposite2Index));end;end;end;end;% ------------------------------------------------------------------------ %% adjacent vertices (using edgeVertice)adjVertice{nVertices} = [];for v=1:nVerticesfor vTmp=1:nVerticesif (v<vTmp && edgeVertice(v,vTmp,1)~=0) || (v>vTmp && edgeVertice(vTmp,v,1)~=0)adjVertice{v}(end+1) = vTmp;end;end;end;% ------------------------------------------------------------------------ %% new positions of the original verticesfor v=1:nVerticesk = length(adjVertice{v});adjBoundaryVertices = [];for i=1:kvi = adjVertice{v}(i);if (vi>v) && (edgeVertice(v,vi,3)==0) || (vi<v) && (edgeVertice(vi,v,3)==0)adjBoundaryVertices(end+1) = vi;end;end;if (length(adjBoundaryVertices)==2) % boundary casenewVertices(:,v) = 6/8*vertices(:,v) + 1/8*sum(vertices(:,adjBoundaryVertices),2);elsebeta = 1/k*( 5/8 - (3/8 + 1/4*cos(2*pi/k))^2 );newVertices(:,v) = (1-k*beta)*vertices(:,v) + beta*sum(vertices(:,(adjVertice{v})),2);end;end;end% ---------------------------------------------------------------------------- %function vNIndex = addEdgeVertice(v1Index, v2Index, v3Index)global edgeVertice;global newIndexOfVertices;if (v1Index>v2Index) % setting: v1 <= v2vTmp = v1Index;v1Index = v2Index;v2Index = vTmp;end;if (edgeVertice(v1Index, v2Index, 1)==0) % new vertexnewIndexOfVertices = newIndexOfVertices+1;edgeVertice(v1Index, v2Index, 1) = newIndexOfVertices;edgeVertice(v1Index, v2Index, 2) = v3Index;elseedgeVertice(v1Index, v2Index, 3) = v3Index;end;vNIndex = edgeVertice(v1Index, v2Index, 1);return;end六、运行结果:七、结果分析:曲面的细分是徐徐逼近得到图形,并且更改坐标的数字,或更改曲面的顺序,所得到的图形是不同的。
小波分析作业

( )
2
d
满足容许性条件的小波变换一定存在着相应的逆变换。
5
对应的小波逆变换公式为:
f (t )
其中
1 C
1 [ W ( a , b ) ( t ) db ] da f ab R R a
(2-5)
C
( )
2
d
(2-6)
上式中 ( ) 为 (t ) 的傅里叶变换。 把满足 C 条件的函数 (t ) L 2.3 离散小波变换 在实际应用中,为了计算的简便,小波窗函数 ab (t ) 中的连续的 a、b 值通常取为一系列离散的整数值,这样 ab (t ) 可表示为:
3
第二章 小波分析的基础知识
小波分析是 20 世纪 80 年代中期发展起来的一门数学理论和方 法, 由法国科学家 Grossman 和 Morlet 在进行地震信号分析时提出 的,随后迅速发展。1985 年 Meyer 在一维情形下证明了小波函数的 存在性 , 并在理论上作了深入研究。 Mallat 基于多分辨分析思想, 提出了对小波应用起重要作用的 Mallat 算法,它在小波分析中的地 位相当于 FFT 在经典 Fourier 变换中的地位。小波分析理论的重要 性及应用的广泛性引起了科技界的高度重视。如今,小波分析已经广 泛地应用于数学理论、信号分析、图像处理和分析、模式识别和通信 系统等领域。 2.1 傅里叶变换 傅里叶变换在实际信号领域广泛应用, 可以将一个非周期的函数 f(t)进行傅里叶变换。傅里叶积分变换公式:
平移得到的小波函数,其中 a 为尺度因子,b 为平移因子,它们分别 代表时频局部窗中的频率参数和时间参数。 小波变换是用来进行时间-尺度分析的积分变换,需要在处理后 利用其逆变换来恢复原信号,也就是说这样的小波变换一定要存在相 应的逆变换。 要使小波变换存在逆变换需要满足的条件为: 该条件称为容许性条件。
小波变换及其应用

小波变换及其应用
小波变换是一种多尺度分析的信号处理技术,可以将信号分解为不同
频率和时间尺度的小波分量,从而提供了更全面的信息,具有很广泛的应用。
以下为小波变换的主要应用:
1.信号压缩:小波变换具有如同离散余弦变换(DCT)、小波重构等
变换可压缩性,可以通过选取一定的小波基,剔除高频噪声等方法将信号
压缩到较小的尺寸。
2.信号去噪:小波变换能够将信号分解为多个尺度和频段的小波系数,因而,小波变换可以应用于信号去噪。
在小波域中对噪声尺度和频段进行
分析和滤波,可有效地去除噪声,使信号更加真实。
3.图像处理:小波变换可以将图像分为低频和高频两个部分,分别表
示图像中大面积变化和微小变化的部分。
图像压缩往往采用这种特性进行
处理。
4.音频处理:小波变换也是音频处理领域中广泛应用的技术。
对语音
信号进行小波分析,可以提取其频率、语气、声调信息等,为音频处理提
供更多信息。
5.金融数据分析:小波变换也被广泛应用于金融领域中,用于对金融
数据进行分析和预测。
通过小波分解,可以提取出不同的时间尺度和频率
对应的信息,进一步了解金融市场的趋势和波动情况。
总之,小波变换在信号处理、图像处理、音频处理、金融领域等方面
都具有广泛的应用。
小波实验报告

小波实验报告小波实验报告引言小波分析是一种数学工具,可以将信号分解成不同频率的成分。
它在信号处理、图像处理、数据分析等领域有着广泛的应用。
本实验旨在通过对小波变换的实际应用,探索其在信号处理中的效果和优势。
一、实验背景小波分析是一种基于频域的信号分析方法,与传统的傅里叶变换相比,小波分析可以更好地捕捉信号的瞬时特性和局部特征。
它通过将信号与一组基函数进行卷积运算,得到信号在不同尺度和位置上的频谱信息。
二、实验目的1. 了解小波变换的基本原理和概念;2. 掌握小波变换的实现方法和工具;3. 分析小波变换在不同信号处理任务中的应用效果。
三、实验步骤1. 选择适当的小波基函数和尺度参数;2. 将待处理信号进行小波变换;3. 分析小波变换后的频谱信息;4. 根据实际需求,选择合适的尺度和位置,重构信号。
四、实验结果与分析本实验选择了一段音频信号进行小波变换。
首先,选择了Daubechies小波作为基函数,并调整尺度参数。
经过小波变换后,得到了信号在不同频率上的能量分布图。
通过分析能量分布图,可以清晰地观察到信号的频率成分和时域特征。
进一步分析小波变换的结果,可以发现小波变换具有良好的局部化特性。
不同于傅里叶变换将整个信号分解成各个频率的正弦波,小波变换可以将信号分解成不同频率的局部波包。
这种局部化特性使得小波变换在信号分析和处理中更加灵活和精确。
五、实验应用1. 信号去噪小波变换可以将信号分解成不同频率的成分,通过滤除高频噪声成分,实现信号的去噪。
在音频处理和图像处理中,小波去噪已经成为一种常用的方法。
2. 图像压缩小波变换可以将图像分解成不同频率的局部波包,通过保留重要的低频成分,可以实现对图像的压缩。
小波压缩在数字图像处理和视频编码中有着重要的应用。
3. 时频分析小波变换可以提供信号在不同时间和频率上的分布信息,通过时频分析,可以更好地理解信号的时域和频域特性。
在语音识别、心电图分析等领域,时频分析是一种常用的方法。
小波变换作业

小波变换作业小波转换在分析化学中的应用摘要:小波变换是80年带发展起来的一种新的数学分支,因为小波变换具有许多其他信号出路方法所不具备的优良特征,如可变的时频分辨率和可调节的局部支持等,所以使它成为信号处理的一种强有力的工具。
本文介绍了小波分析的发展,现状和它在分析化学中的应用,对其可能运用的领域进行了探讨。
关键词:小波:信号;傅立叶变换;分析化学Abstract: Because of the fine properties of flexible time---frequency windows and governedlocalized support, the wavelet transform is a useful tool in signal processing. The text introduced the development and present of Wavelet Analysis. A review of application of Wavelet Analysis in Analytical Chemistry has been presented.Key words: wavelet; signals; Fourier Transform; analytical chemistry小波(又叫子波 )变换的理论是最近发展起来的新的数学方法, 被认为是傅里叶分析理论的重大突破。
小波变换同时在时域和频域中具有较好的局部特性, 将时频统一于一体来研究信号。
而傅里叶变换则与此不同, 它把信号完全变换到频域中研究, 对频率的分辨率是无穷, 但对时间的分辨率是零; 传统的时域分析则完全在时域中分析信号, 它对时间的分辨率是无穷, 但对频率的分辨率为零。
虽然加窗傅里叶变换能部分克服傅里叶变换的不足, 但其窗口大小固定不变, 在应用中也存在它的局限性。
小波变换则同时对时间和频率具有较好的分辨率, 目前已经在若干领域取得了突破性的成果。
2023年教师资格之幼儿综合素质通关题库(附答案)

2023年教师资格之幼儿综合素质通关题库(附答案)单选题(共60题)1、小波很贪玩,经常不完成作业。
一天,他又没做作业,班主任张老师很生气,放学后让他单独在教室里补作业。
这时,张老师突然想起家里有事要办,看见小波还没有补完作业,就说:“补完作业才能回家,我一会儿回来检查”。
为了防止小波偷偷跑了,临走时张老师把教室的门上了锁。
张老师的做法()。
A.正确,有利于小波按时完成作业B.错误,侵犯了小波的受教育权C.错误,侵犯了小波的人身自由权D.正确,有利于小波养成良好的行为习惯【答案】 C2、学校举办“给自己喜爱的作家写信”的活动,并给了每个班五个名额。
可以帮助学生把他们写的信寄给他们喜爱的作家,其他班级都是抽签决定这五个名额给谁,但是三班的王老师认为只有作文写得好的学生才有资格把信寄出,因此她把名额给了她认为写作能力强的五名学生,王老师的做法()。
A.符合因材施教的原则B.符合公平竞争的要求C.违背平等待生的理念D.违背民主互助的理念【答案】 C3、我国面积最大的咸水湖是()。
A.青海湖B.鄱阳湖C.太湖【答案】 A4、几个幼儿正趴在树下兴致勃勃地观察着什么,一个老师看到他们满身是灰的样子,生气地走过去问:“你们在做什么”幼儿头也不抬地说:“听知了唱歌呢。
”为了激发幼儿的学习动机和对知识的兴趣,教师正确的说法是()。
A.胡说,知了怎么会唱歌B.那你们想知道知了是怎么唱歌的吗C.快回教室做作业D.那你们继续听吧【答案】 B5、下列选项中说法错误的一项是()。
A.学校应当建立、健全安全制度和应急机制,对学生进行安全教育,加强管理,及时消除隐患,预防发生事故B.县级以上地方人民政府定期对学校校舍安全进行检查;对需要维修、改造的,及时予以维修、改造C.学校不得违反国家规定收取费用,不得以向学生推销或者变相推销商品、服务等方式谋取利益D.学校可以根据需要聘用曾经因故意犯罪被依法剥夺政治权利或者其他不适合从事义务教育工作的人担任工作人员【答案】 D6、“教育有法可依,但无定法可抄”,这说明教师劳动具有()。
小波分解和重构算法作业
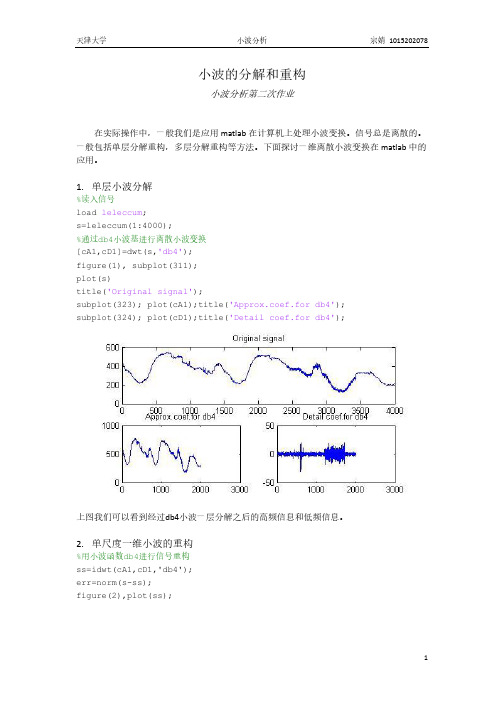
小波的分解和重构小波分析第二次作业在实际操作中,一般我们是应用matlab在计算机上处理小波变换。
信号总是离散的。
一般包括单层分解重构,多层分解重构等方法。
下面探讨一维离散小波变换在matlab中的应用。
1.单层小波分解%读入信号load leleccum;s=leleccum(1:4000);%通过db4小波基进行离散小波变换[cA1,cD1]=dwt(s,'db4');figure(1), subplot(311);plot(s)title('Original signal');subplot(323); plot(cA1);title('Approx.coef.for db4');subplot(324); plot(cD1);title('Detail coef.for db4');上图我们可以看到经过db4小波一层分解之后的高频信息和低频信息。
2.单尺度一维小波的重构%用小波函数db4进行信号重构ss=idwt(cA1,cD1,'db4');err=norm(s-ss);figure(2),plot(ss);重构完成后的误差为3.53e-10。
重构完成后的函数与分解前的函数相同,仅仅存在很小很小可以忽略为0的误差。
3.多层小波分解上文是使用单层小波分解,下面使用wavedec函数进行多层小波分解,并显示分解后的低频高频信息。
%通过db4小波基进行三尺度小波分解[c,l]=wavedec(s,3,'db4');a1=appcoef(c,l,'db4',1);%提取尺度1的低频系数a2=appcoef(c,l,'db4',2);%提取尺度2的低频系数a3=appcoef(c,l,'db4',3);%提取尺度3的低频系数figure(3);subplot(321);plot(a1);title('尺度1的低频系数');subplot(323);plot(a2);title('尺度2的低频系数');subplot(325):plot(a3):title('尺度3的低频系数');d1=detcoef(c,l,1);d2=detcoef(c,l,2);d3=detcoef(c,l,3);figure(3);subplot(322);plot(d1);title('尺度1的高频系数');figure(3);subplot(324);plot(d2);title('尺度2的高频系数');figure(3);subplot(326);plot(d2);title('尺度3的高频系数');由上图可以清晰的看出低频的信息和高频的信息。
小波实验报告

小波实验报告
《小波实验报告》
小波分析是一种用于信号处理和数据分析的强大工具。
在本次实验中,我们将探索小波分析的基本原理,并通过实验验证其在信号处理中的有效性。
首先,我们介绍了小波分析的基本概念和原理。
小波分析是一种基于窗口函数的信号分析方法,它可以将信号分解成不同频率和时间尺度的成分。
与傅里叶变换不同,小波分析可以同时提供频域和时域的信息,因此在处理非平稳信号和非线性系统时具有独特优势。
接下来,我们进行了一系列实验,验证了小波分析在信号处理中的应用。
我们首先使用小波分析对一段包含多个频率成分的信号进行了分解,并成功地提取出了各个频率成分的时域和频域信息。
接着,我们对一个非平稳信号进行了小波变换,并观察到了小波分析在处理非平稳信号时的优越性。
最后,我们还利用小波分析进行了信号去噪和压缩,结果表明小波分析在这些应用中具有良好的效果。
通过本次实验,我们深刻理解了小波分析的原理和应用,并验证了其在信号处理中的有效性。
小波分析不仅可以帮助我们更好地理解信号的时频特性,还可以在实际工程中发挥重要作用。
我们相信,在未来的研究和应用中,小波分析将会得到更广泛的应用和发展。
小波变换期末大作业

研究生“小波变换”课程期末大作业2010/06/17说明:下述四道题中可任选两道一、结合MATLAB中的数据文件leleccum (1-D),研究小波去噪的原理和方法。
1.综述用小波去除噪声的原理。
包括:(1)去噪阈值的种类,各种阈值形成的原理,阈值风险函数;(2)阈值使用的方法;2.MATLAB 6.5中与1-D信号去噪相关的m 文件有14个,结合所给数据的去噪,讨论这些文件的应用;3.对上述数据实现去噪;参考文献:1.M Jansen, Noise Reduction by Wavelet Threshold, 2001.2. D L Donoho. De-noiseing by soft-thresholding. IEEE Tran on Info Theory 1995(见附件)请自己在EI 或IEEE全文库上给定相应的关键词,查找其他去噪相关文献。
二、研究利用小波变换检测信号中的奇异点及由模最大重建信号的原理与方法。
内容包括:1.信号中的突变点在小波变换中的行为;2.由模最大重建信号的原理与方法;3.下载ecg文件(见附件),用open_ecg打开该文件实现对该信号的峰值(R波)检测。
该信号的抽样频率为360Hz;4.令j=1~6, 试用各尺度下的模最大重建原信号;参考文献:1.S Mallat. Singularity Detection and Processing with Wavelet. IEEE Tran on IF, 1992(见附件)2.S Mallat. Signal Characterization from Multiscale Edges. 1990(见附件)请自己在EI 或IEEE全文库上给定相应的关键词,查找其他相关文献。
三、结合MATLAB W A VELET TOOLBOX 中有关小波包的文件(不包括两个2-D文件),研究:1.小波包最佳分解层(即尺度j)的选择原理;2.最佳小波包选择的原理;3.上述13个文件的功能及相关关系;4.利用MATLAB中的数据文件leleccum(1-D),按最佳分解层及最佳小波包进行分解。
小波分析课程作业

基于小波分析的齿轮故障诊断方法摘要:齿轮传动是机械传动中最常用的方式。
本文阐述了三种基于小波理论的齿轮故障诊断方法。
其中,小波包和BP网络识别的方法能较好地抑制干扰,从复杂振动信号中分离出故障特征,对齿轮故障模式进行准确识别,是一种有效的齿轮故障在线诊断方法。
高斯复小波变换利用高斯小波基函数从相位的角度提取齿轮振动信号的故障信息,可突出边频带结构,有效识别故障模式。
复解析小波变换将Hilbert 变换与小波分析紧密结合在一起,具有自适应分析能力。
该方法能有效地诊断齿轮局部故障,且与传统的频域方法相比具有更好的分析效果。
关键词:齿轮故障诊断小波包BP 网络复小波变换复解析小波变换Methods of Gear Fault Diagnosis Based on Wavelet Analysis Abstract:Gear transmission is the most common way in mechanical transmission. In this paper, three kinds of wavelet theory-based gear fault diagnosis method are presented. As an effective method for gear fault diagnosis, the method of wavelet packet and BP neural network identification can suppress the interference and separate the fault feature from complex vibration signals to make an accurate identification of the gear fault pattern. By using the Gaussian wavelet function to extract the fear fault vibration signals from the phase aspect, Gaussian complex wavelet transform can prominent the structure of sideband and identify the failure modes. The complex analytic wavelet transformation combines the Hilbert transformation and the wavelet analysis to get the capability of Adaptive analysis. This method can effectively detect partial failure of gear. Thus, it has got a better effectiveness compared with traditional frequency domain methods.Key words:Gear fault diagnosis Wavelet packet BP neural network Complex wavelet transform Complex Analytical Wavelet Transform0 引言齿轮具有结构紧凑、效率高、工作可靠等优点,齿轮及齿轮箱作为机械设备中一种必不可少的连接和传递动力的通用零部件,在现代工业设备中得到了广泛的应用。
小波分析考试题及答案

一、叙述小波分析理论发展的历史和研究现状答:傅立叶变换能够将信号的时域和特征和频域特征联系起来,能分别从信号的时域和频域观察,但不能把二者有机的结合起来。
这是因为信号的时域波形中不包含任何频域信息,而其傅立叶谱是信号的统计特性,从其表达式中也可以看出,它是整个时间域内的积分,没有局部化分析信号的功能,完全不具备时域信息,也就是说,对于傅立叶谱中的某一频率,不能够知道这个频率是在什么时候产生的。
这样在信号分析中就面临一对最基本的矛盾——时域和频域的局部化矛盾。
在实际的信号处理过程中,尤其是对非常平稳信号的处理中,信号在任一时刻附近的频域特征很重要。
如柴油机缸盖表明的振动信号就是由撞击或冲击产生的,是一瞬变信号,单从时域或频域上来分析是不够的。
这就促使人们去寻找一种新方法,能将时域和频域结合起来描述观察信号的时频联合特征,构成信号的时频谱,这就是所谓的时频分析,亦称为时频局部化方法。
为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并开发了一系列新的信号分析理论:短时傅立叶变换、时频分析、Gabor 变换、小波变换Randon-Wigner变换、分数阶傅立叶变换、线形调频小波变换、循环统计量理论和调幅—调频信号分析等。
其中,短时傅立叶变换和小波变换也是因传统的傅立叶变换不能够满足信号处理的要求而产生的。
短时傅立叶变换分析的基本思想是:假定非平稳信号在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。
但从本质上讲,短时傅立叶变换是一种单一分辨率的信号分析方法,因为它使用一个固定的短时窗函数,因而短时傅立叶变换在信号分析上还是存在着不可逾越的缺陷。
小波变换是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨率分析(Multi-resolution)的特点,而且在时频两域都具有表征信号局部特征的能力,使一种窗口大小固定不变,但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法。
小波分析作业(含自编程序)

地球科学学院小波分析课程作业课程名称:小波分析指导老师:学生姓名:学号:几种时频分析方法1 短时傅里叶变换为了研究信号在局部时间范围内的瞬时频率特性,1946年,D.GABOR 引进了短时傅氏变换或窗口傅氏变换的概念,其基本原理是取一个称为(t)g 窗口的函数,使它在有限的区间范围外恒等于零或趋于零。
设任意信号(t)f ,并假设该信号在一个以时间τ为中心,且范围有限的窗口函数)-(t τg 内是稳定的,这样,窗口内函数)-(t)g(t τf 的傅氏变换就定义为短时傅氏变换,表示为dt e T t i STFT ωτωτ--)-f(t)g(t ),(⎰∞∞=STFT 是通过滑动时窗来计算其频谱,因而它的时间分辨率和频率分辨率受Heisenberg 测不准原理约束。
因此利用短窗口有较高的时间分辨率,但是频率分辨率差。
2 小波变换常见的小波变换有连续、二进制以及离散小波变换等。
在连续小波变换中,仅要求小波函数满足容许条件即可,这使得在选择小波函数时具有很大的自由度。
对任意地震信号函数)((t)2R L f ∈,其连续小波变换定义为 )f(t)dt a b -t (a 1(t)f(t)dt b)(a,-*-b a,⎰⎰∞∞∞∞==ϕψw T 式中,a为尺度因子,b为平移参数,函数ψ(t)称为母小波。
小波分析具有可调的时频窗口,被广泛地应用于地震信号处理中,但是也存在着一定的局限性,主要表现在难以选择小波基、固定的基函数、恒定的多分辨率,信号的能量—时间—频率分布也很难定量给出。
3 S 变换为了解决短时傅氏变换只能以一种分辨率进行时频分析及小波变换不能直接与频率对应的缺陷,1996年美国地球物理学家Stockwell 在前人的基础上提出了S 变换。
S 变换中,基本小波是由简谐波与高斯函数的乘积构成的,基本小波中的简谐波在时间域仅作伸缩变换,而高斯函数则进行伸缩和平移。
这一点与连续小波变换不同,在连续小波变换中,简谐波与高斯函数进行同样的伸缩和平移。
小波作业

小波分析基本理论及在信号去噪中的应用摘要:小波分析由于在时域、频域同时具有良好的局部化性质和多分辨率分析的特点,因此不仅能满足各种去噪要求,如低通、高通、陷波、随机噪音的去除等,而且与传统的去噪方法相比较,有着无可比拟的优点,成为信号分析的一个强有力的工具。
尤其是其中的小波阈值去噪方法,由于计算简单而得到了广泛的应用。
本文首先阐述了小波分析的基本理论,随后阐述了小波变换的计算过程,然后研究了小波分析在信号去噪问题中的应用,主要对小波阈值去噪的原理及其实现方法进行了分析,特别是软、硬阈值函数的优、缺点。
关键词:小波分析;母小波;信号去噪;阈值函数Basic Theory Of Wavelet Analysis And Its Application In SignalDemisingAbstract:Wavelet has good localizing quality at time domain and frequency simultaneously and the characteristic of multi-resolution ratio analysis, so it can fulfill all kinds of wave-filtering needs such as low-pass,high-pass, sink wave, random noise demising. Compare with traditional wave- filtering methods,wavelet has incomparable advantage, wavelet has become an effective means of signal analysis. The paper comprehensively expound the fundamental theory of Wavelet Transform, then the paper introduce the Wavelet Transform computing progress, then the application of wavelet in signal demising is studied.Keywords: Wavelet Analysis; Mother Wavelet; Signal demising; Threshold Function1 小波变换基本理论小波变换[1](Wavelet Transform) 的基本思想和传统的傅里叶变换是一致的,它也是用一族函数来表示信号或函数,这一族函数称之为小波函数系,但是小波函数系与其它两种方法所用的简谐函数系不同,它是由一基本小波函数平移和伸缩构成的。
小波分析结课作业——小波理论发展及应用综述

摘要摘要小波分析是一门正在迅速发展的新兴学科,目前,它在实际中得到了广泛的应用。
研究小波的新理论、新方法以及新应用具有重要的理论意义和实用价值。
本文在简述了小波发展历史和小波的基本理论知识后,对以小波为工具进行数字图像处理进行了有益的探索。
最后详细介绍了基于阈值的小波分析的图像去噪算法及其在信号处理中的应用。
关键字:小波分析研究现状应用图像去噪阈值ABSTRACTABSTRACTWavelet analysis is a rapidly developing and novel subject. Nowadays,it has been widely used in practical applications. To study the new theory,methods and applications of wavelet is of great theoretical significance and practical value.After a brief description of the history of wavelet development and the basic theoretical knowledge of wavelet,this paper makes valid probe towards digital image processing using wavelet. Finally,this paper analysis and study of the classical thresholding denoising methods and the new scopes of wavelet applications.key word: Wavelet Analysis , Research Status , Application , Signal Denoising, Thresholding目录i目录第一章绪论 (1)1.1小波发展简史 (1)1.2 小波变换及应用 (1)1.3 论文的主要工作 (3)第二章小波及小波分析的理论基础 (5)2.1 小波分析 (5)2.2 正交小波 (6)第三章小波分析的应用 (9)3.1 小波分析的应用现状 (9)3.2 小波阈值去噪研究 (11)3.2.1 小波去噪算法的研究概况 (11)3.2.2 小波阈值去噪的算法原理 (12)3.2.3 小波去噪的应用及发展 (13)第四章总结和展望 (15)致谢 (17)参考文献 (19)ii目录第一章绪论1第一章绪论1.1小波发展简史小波分析是时频发展的新理论,是80年代后期发展起来的。
(完整版)整数小波变换作业

小波变换:S 整数变换作业1. 题目:用整数小波的S 或2/6变换对256*256 Lena 灰度图像进行非标准方法的3级分解与重构。
2. 总体设计:本题目的意义在于通过实验体会整数小波变换,由于MA TLAB 自身对矩阵操作的方便性,以及其丰富的库函数(如可以用来直接显示图象),我决定用MATLAB 编程完成本次作业。
要说明的是,这里并不是直接利用MATLAB 中的wavelet 工具箱中的已有小波函数对图象进行整数小波分解,而是用下面的已知分解公式进行小波分解和重构。
分解公式:1,,21,21,,21,[]j k j k j kj k j k j k d s s s s d -+--=-=+ 重构公式:,21,1,,211,,2[]j k j k j k j k j k j k s s d s d s --+-=-=+ ,其中[ ]表示取整。
进行非标准小波分解,即交替进行3次行变换和3次列变换,程序对每次变换后的结果都保存为位图文件,运行后可以在程序所在路径下看到保存的6个分解位图文件和6个重构位图文件。
最后还会在一个图像中显示每次分解后的图像,以便于对比。
3. 实现方法:编写S 变换的分解和重构子程序,分别对图像数据进行一次行列分解和列行重构,程序返回该次变换后的行列矩阵,在主程序中可以连续三次调用行列变换,即完成对原始图像的3级分解和重构,这里的变换是完全可逆的,也就是能够完全恢复原图像数据。
通过对比3次重构后返回的数据与原图像数据后发现它们完全相同。
主要用的MA TLAB 工具函数有:imread( )---------读取图像数据,为uint8类型,需变为double 类型才能进行各种运算 imwrite()---------用于保存图像,这里用它来保存每一级变换后的图像image( )----------显示图像,需要给出色谱表colormap ,这里是灰度图,用colormap =gray (256)即可subplot( )--------用于分开绘图,即在一个窗口下绘制多个图像,在这里用于输出变换后的图像,以便对比。
课程作业-杭电研究生-小波变换-第三次作业
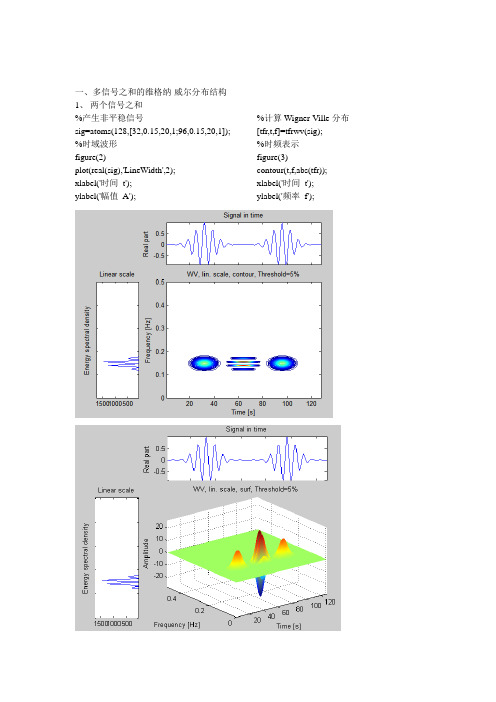
一、多信号之和的维格纳-威尔分布结构 1、 两个信号之和 %产生非平稳信号sig=atoms(128,[32,0.15,20,1;96,0.15,20,1]); %时域波形 figure(2)plot(real(sig),'LineWidth',2); xlabel('时间 t'); ylabel('幅值 A');%计算Wigner-Ville 分布 [tfr,t,f]=tfrwv(sig); %时频表示 figure(3)contour(t,f,abs(tfr)); xlabel('时间 t'); ylabel('频率f');2、 三个信号之和 %产生非平稳信号sig=atoms(128,[32,0.35,20,1;96,0.15,20,1;96,0.35,20,1]); %时域波形 figure(2)plot(real(sig),'LineWidth',2); xlabel('时间 t'); ylabel('幅值 A');%计算Wigner-Ville 分布 [tfr,t,f]=tfrwv(sig); %时频表示 figure(3) tfrwv(sig);xlabel('时间 t'); ylabel('频率 f');二、比较跳频信号的STFT 变换与Wigner-Ville 分布的频谱图 clear close all clc %产生跳频信号 n=0:383; ts=1/(80*10^3);%采样时间 f=4.21*10^3; delta_f=8000;%频偏 f1=f; f2=f+delta_f; f3=f2+delta_f; y1=cos(2*pi*f1*ts*n).*[ones(1,128),zeros(1,128*2)]; y2=cos(2*pi*f2*ts*n).*[zeros(1,128),ones(1,128),zeros(1,128)]; y3=cos(2*pi*f3*ts*n).*[zeros(1,128*2),ones(1,128)]; sig=y1+y2+y3; figure(1); plot(n,sig); title('跳频信号'); sig=sig'; %计算短时傅立叶变换 sig=hilbert(sig); %计算短时傅立叶变换 [tfr,t,f]=tfrstft(sig); %短时傅立叶变换时频表示 figure(2); tfrstft(sig); xlabel('时间 t'); ylabel('频率 f'); %计算Wigner-Ville 分布 [tfr,t,f]=tfrwv(sig); %时频表示 figure(3) tfrwv(sig); xlabel('时间 t'); ylabel('频率 f');三、四个高斯信号构成的Wigner-Ville分布与伪Wigner-Ville分布%产生非平稳信号sig=atoms(128,[32,0.15,20,1;96,0.15,20,1;32, 0.35,20,1;96,0.35,20,1]);%时域波形figure(2)plot(real(sig),'LineWidth',2);xlabel('时间t');ylabel('幅值A');%计算Wigner-Ville分布[tfr,t,f]=tfrwv(sig);%时频表示figure(3)tfrwv(sig);xlabel('时间t');ylabel('频率f');%计算伪Wigner-Ville分布sig=hilbert(sig);[tfr,t,f]=tfrpwv(sig);%时频表示figure(4) tfrpwv(sig); xlabel('时间t'); ylabel('频率f');。
2021年哈工大小波实验报告

小波理论试验汇报院(系)专业学生学号日期12月试验汇报一一、 试验目1. 利用傅立叶变换知识对常见基础函数做基础变换。
2. 加深对因果滤波器了解, 并会判定因果滤波器类型。
3. 利用卷积公式对基础信号做滤波处理并分析, 以加深了解。
4. 熟悉Matlab 中相关函数使用方法。
二、 试验原理1.利用傅立叶正、 反变换基础公式:()ˆ()() ()(),11ˆ()(),22i x i t i ti t i t f f x e dx f t e dt f t e f t fe df t e ωωωωωωωωππ∞∞---∞-∞∞--∞=====⎰⎰⎰及其性质, 对所要处理信号做对应傅里叶变换和逆变换。
2.利用卷积定义式:1212()()()()+∞-∞*=-⎰f t f t f f t d τττ对所求信号做滤波处理。
三、 试验步骤与内容1.试验题目:Butterworth 滤波器, 其冲击响应函数为,0()0,0若若α-⎧≥=⎨<⎩t Ae t h t t 1. 求()h ω2. 判定是否因果; 是低通、 高通、 带通还是带阻?3. 对于信号3()(sin22sin40.4sin2sin40),-=++t f t e t t t t 0π≤≤t ,画出图形()f t4. 画出滤波后图形()*f h t , 比较滤波前后图形, 你会发觉什么, 这里取10α==A 5. 取()(sin5sin3sin sin40),-=+++t f t e t t t t 采取不一样变量值α=A (初始设定A=α=10) 画出原信号图形与滤波后图形, 比较滤波效果。
2.试验步骤及分析过程:1.求()h ω由傅里叶变换定义式可得:()0ˆαϖαϖωαω+∞+∞-----∞=⋅=⋅=+⎰⎰t i t t i t Ah Ae e dt Ae e dt i (1) 故该滤波器幅频特征为: ()ω==H , 转折频率τα=;假定1,2A α==, 绘制该滤波器幅频特征曲线以下:图1.1滤波器幅频特征曲线2. 判定是否因果; 是低通、 高通、 带通还是带阻?(1)观察滤波器响应函数可知, 只有在输入信号抵达后, 该滤波器才会有输出响应, 另外实际应用滤波器均是因果滤波器, 所以, 题中滤波器是因果滤波器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小波分析基本理论及在信号去噪中的应用摘要:小波分析由于在时域、频域同时具有良好的局部化性质和多分辨率分析的特点,因此不仅能满足各种去噪要求,如低通、高通、陷波、随机噪音的去除等,而且与传统的去噪方法相比较,有着无可比拟的优点,成为信号分析的一个强有力的工具。
尤其是其中的小波阈值去噪方法,由于计算简单而得到了广泛的应用。
本文首先阐述了小波分析的基本理论,随后阐述了小波变换的计算过程,然后研究了小波分析在信号去噪问题中的应用,主要对小波阈值去噪的原理及其实现方法进行了分析,特别是软、硬阈值函数的优、缺点。
关键词:小波分析;母小波;信号去噪;阈值函数Basic Theory Of Wavelet Analysis And Its Application In Signal DemisingAbstract:Wavelet has good localizing quality at time domain and frequency simultaneously and the characteristic of multi-resolution ratio analysis, so it can fulfill all kinds of wave-filtering needs such as low-pass,high-pass, sink wave, random noise demising. Compare with traditional wave- filtering methods,wavelet has incomparable advantage, wavelet has become an effective means of signal analysis. The paper comprehensively expound the fundamental theory of Wavelet Transform, then the paper introduce the Wavelet Transform computing progress, then the application of wavelet in signal demising is studied.Keywords: Wavelet Analysis; Mother Wavelet; Signal demising; Threshold Function1 小波变换基本理论小波变换[1](Wavelet Transform) 的基本思想和传统的傅里叶变换是一致的,它也是用一族函数来表示信号或函数,这一族函数称之为小波函数系,但是小波函数系与其它两种方法所用的简谐函数系不同,它是由一基本小波函数平移和伸缩构成的。
它是一种窗口面积恒定,窗口形状可变(时域窗口和频域窗口均可变) 的时- 频局域化分析方法。
1.1连续小波变换理论设函数为一平方可积函数, 即∈L2 ( R) , 其傅里叶变换满足允许条件:(1.1.1)则称为一个基小波(或小波母函数) ,我们称上式为小波函数的容许条件。
将母函数经伸缩和平移后,就可以得到一个小波序列。
对于连续的情况,小波序列为:(1.1.2)其中, , ∈R, ≠0 。
为伸缩因子,为平移因子, 我们称为依赖于参数, 的小波基函数。
将任意L2 ( R) 空间里的函数在小波基下展开, 称这种展开为函数的连续小波变换( Continue Wavelet Transform ,简称CWT) 其表达式为:(1.1.3)由以上定义,我们可以看出小波变换和傅里叶变换一样,也是一种积分变换,为小波变换系数。
但它不同于傅里叶变换的地方是,小波基具有尺度和平移两个参数,所以函数一经小波变换, 就意味着将一个时间函数投影到二维的时间——尺度相平面上, 这样有利于提取信号函数的某些本质特征[2]。
1.2 离散二进小波变换在实际应用中,为了方便计算机进行分析、处理,信号都要离散化成离散序列, 和也必须离散化,成为离散小波变换, 记为DWT (Discrete Wavelet Transform) 。
在对连续小波离散化的过程中,连续小波变换的伸缩因子和进行采样,选取a = 2 - j , b = 2 - j kb c,则可得到离散的二进小波变换:(1.1.4)这里, ∈ Z ,采样率> 0.由于离散二进小波变换是对连续小波变换的伸缩因子和平移因子按一定规则采样而得到的,任一函数∈L2( R) ,经二进离散小波变换, 得到了一个连续降半频带上的时间信息。
从算法上, 二进离散小波变换分为一般二进离散小波变换和快速二进离散小波变换。
.1.3 连续小波变换的一些性质连续小波变换是一种线性变换,它具有以下几方面的性质:(1)叠加性设空间,为任意常数,且的CWT为,且的CWT为,则的CWT为(1.3.1)(2)时移不变性设的CWT为,则的CWT为,即延时后的信号的的小波系数可将原信号的小波系数在轴上进行同样时移得到。
(3)尺度转换(伸缩共变性)设的CWT为,则的CWT为(1.3.2)此性质表明,当信号在时域作某一倍数的伸缩时,其小波变换在轴上也作同一倍数的伸缩,形状不变。
(4)内积定理设空间,它们的CWT分别为,,即则有Moyal定理:(1.3.3)其中证明由傅里叶积分的乘积定理可知则有(1.3.4)(1.3.5)由小波函数的定义得,,则有(1.3.6)(1.3.7)将式(1.3.7)代入式(1.3.4),(1.3.5),再将式(1.3.4),(1.3.5)代入式(1.3.3)。
则式(1.3.3)左边为因为又由于小波函数满足可容许性条件(即中括号内的积分值存在),其一般情况下我们取,所以可容许性条件改为则式(1.3.3)左边最后成为内积定理得证。
由上述定理的证明过程得知,内积定理的成立是以为条件的。
当时,由Moyal公式可推出:(1.3.8)由于小波变换幅度平方的积分同信号的能量成正比,我们又称式(1.3.3)为能量关系。
(5)自相关性:对应不同尺度参数a和不同平移参数b的连续小波变换之间是自相关的。
(6)冗余性:连续小波变换把一维信号变换到二维空间,因此在连续小波变换中存在信息表述的冗余度(redundancy)。
小波变换的逆变换公式不是唯一的。
2小波去噪原理我们知道,一个含噪声的一维信号的模型可表示为: (2.1)式中,为真实信号, 为噪声信号, 为含噪信号。
这里以一个简单的噪声模型加以说明,即为高斯白噪声N (0 ,1) ,噪声级为1 ,通常表现为高频信号,在实际工程中,有用信号通常表现为低频信号或较平稳的信号,所以消噪过程可按以下方法进行处理:首先对实际信号进行小波分解, 选择小波并确定分解层次为N ,则噪声部分通常包含在高频中;然后对小波分解的高频系数进行门限阈值量化处理; 最后根据小波分解的第N 层低频系数和经过量化后的1~ N 层高频系数进行小波重构,达到消除噪声的目的,对信号降噪实质上是抑制信号的噪声,在实际信号中恢复真实信号的过程。
小波收缩去噪方法的关键步骤是如何选择阈值和如何进行门限阈值处理,在某种程度上,它关系到信号去噪的质量。
在对小波系数作门限阈值处理操作时, 可以使用软阈值处理方法或硬阈值处理方法。
硬阈值是把信号的绝对值与指定的阈值进行比较, 小于或等于阈值的点变为0 ,大于阈值的点保持不变[3]。
(2.2)软阈值是把信号的绝对值与指定的阈值进行比较, 小于或等于阈值的点变为0 ,大于阈值的点变为该点值与阈值的差:(2.3)一般来说,硬阈值比软阈值处理后的信号更粗糙一些。
2.1 小消躁处理的方法首先对信号进行小波分解,由于噪声信号多包含在具有较高频率的细节中,我们可以利用门限、阈值等形式对分解所得的小波系数进行处理,然后对信号进行小波重构即可达到对信号的消躁目的。
波分析去噪处理一般有下述三种方法:(1)默认阈值去噪处理。
该方法利用函数ddencmp生成信号的默认阈值,然后利用函数wdencmp进行去噪处理。
(2)给定阈值去噪处理。
在实际的去噪处理过程中,阈值往往可通过经验公式获得,这种阈值比默认的阈值可信度高。
在进行阈值量化处理时,可利用函数wthresh。
(3)强制去噪处理。
该方法是将小波分解结构中的高频系数全部置为零,即滤掉所有高频部分,然后对信号进行小波重构。
这种方法比较简单,且去噪的信号比较平滑,但是容易丢失信号中的有用成分。
2.2信号降噪的准则1.光滑性:在大部分情况下,降噪后的信号应该至少和原信号具有同等的光滑性。
2.相似性:降噪后的信号和原始信号的方差估计应该是最坏情况下的方差最小。
2.3.一维信号消躁的步骤:(1) 一维信号的小波分解。
选择一个小波并确定分解的层次,然后进行分解计算。
(2)小波分解高频系数的阈值量化。
对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理。
(3)一维小波重构。
根据小波分解的最低层系数和各层高频系数进行一维小波重构。
关键:如何选择阈值和进行阈值量化。
在某种程度上,它关系到信号消躁的质量。
2.4消躁阈值选取规则上式为硬阀值法(2.4.1)上式为软阀值法(2.4.2)图(a)硬阀值图 (b) 软阈值图(a)和(b)表明了软阈值和硬阈值法的区别,图中横坐标表示小波分解系数,纵坐标表示由阈值法得到的小波系数估计值,为阈值。
可以看出,硬阈值法的函数在点处不连续,这会给重构信号带来震荡;软阈值法虽然函数连续性较好,但其导数并不连续,这就限制了它的进一步应用。
并且当时,由软阈值法得出的估计值与小波系数存在着恒定的偏差。
这些分析表明,软阈值法通常会使去噪后的信号平滑一些,但是也会丢掉某些特征;而硬阈值可以保留信号的特征,但是在平滑方面有所欠缺。
一般来说,去噪中软阈值的作用会更多一些,但是到底选取哪种处理方法,还应视具体情况而定。
3 小波去噪的MA TLAB 仿真3.1应用一维小波分析进行信号消躁处理的MATLAB 函数1.利用小波分析对含躁正弦波进行消躁。
分析:(1)消躁后的信号大体上恢复了原信号的形状,并明显去除了噪声所引起的干扰。
(2)恢复后的信号与原信号相比有明显的改变。
主要原因是,在进行消躁处理的过程中所用的分析小波和细节系数阈值不恰当。
2. 在电网电压值监测过程中,由于监测设备出现了一点故障,致使所采在电网电压值监测过程中,由于监测设备出现了一点故障,致使所采集到的信号受到噪声的污染。
现在利用小波分析对污染信号进行消躁处理以恢复原始信号。
下面将利用小波分析对污染信号进行去噪处理以恢复原始信号,仿真结果如下:图3.2信号去噪从图3.2得到的结果来看,应用强制去噪处理后的信号较为光滑,但是它很有可能丢了信号中的一些有用的成分,默认阈值去噪和给定阈值去噪这两种处理方法在实际中应用的更为广泛一些。
