三年级奥数巧数图形
三年级奥数--第六讲--巧数图形(三)

新速度教育三年级奥数
第六讲——巧数图形(三)
1. 温故知新。
2. 无规则图形的数法:分类法。
从小到大,从左到右,从上到下数。
3. 请小朋友们数一数下列图形有多少个。
4. 巧数图形在实际生活中的应用。
5. 有10个小朋友,每2个人照一张合影,一共要照多少张照片? 思路导航:这道题可以用数线段的方法来解答。
6.分析:根据题意,画出线段图,每一个点代表一个小朋友:
从图上可以看出,第1个小朋友要与其余9个小朋友合影,要照9张照片;第2个小朋友还要与其余8个小朋友合影,再照8张照片……以此类推,第9个小朋友只要再与1个小朋友合影,再照1张照片。
所以,一共要照9+8+7+6+5+4+3+2+1=45张照片。
I H G
F E D C B
A
1098743
10.小朋友们,我们一起来练一练吧!!
1,三年级有6个班,每两个班要比赛拔河一次,这样一共要组织多少场比赛?
2,有红、黄、蓝、白四只气球,如果每两只气球扎成一束,共有多少种不同的扎法?
3,有1——6六个数字,能组成多少个不同的两位数?
4,数一数下图有多少个三角形。
三年级 数学奥数拓展培优 第3讲 巧数图形(学生版)
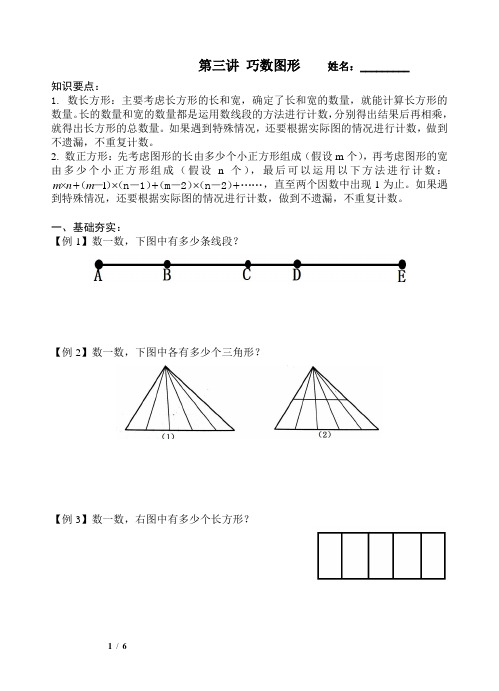
第三讲巧数图形姓名:_________
知识要点:
1. 数长方形:主要考虑长方形的长和宽,确定了长和宽的数量,就能计算长方形的数量。
长的数量和宽的数量都是运用数线段的方法进行计数,分别得出结果后再相乘,就得出长方形的总数量。
如果遇到特殊情况,还要根据实际图的情况进行计数,做到不遗漏,不重复计数。
2. 数正方形:先考虑图形的长由多少个小正方形组成(假设m个),再考虑图形的宽由多少个小正方形组成(假设n个),最后可以运用以下方法进行计数:(-)(n-1)(m-2)(n-2)……,直至两个因数中出现1为止。
如果遇+⨯+⨯+
×1
m n m
到特殊情况,还要根据实际图的情况进行计数,做到不遗漏,不重复计数。
一、基础夯实:
【例1】数一数,下图中有多少条线段?
【例2】数一数,下图中各有多少个三角形?
【例3】数一数,右图中有多少个长方形?
1/ 6。
三年级奥数巧数图形

第2讲 巧数图形知识要点同学们,我们经常会遇到数图形的问题,对于较复杂的图形,经常会出现数重复或数漏掉的错误。
怎样才能不重复也不遗漏地数出图形的个数呢?这节课,我们将一起来寻找好的方法。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
精典例题例1:数出下图中有多少条线段?模仿练习数一数,每种图形有多少个?有( )条线段 有( )个三角形有( )个角 有( )个长方形 有( )个正方形例2:数出图中共有多少个三角形?从短的线段入手,再两条两条拼接起来数,你发现规律了吗?EABCDODC B A FEDC B A模仿练习数一数,每幅图里有多少个三角形? (1) (2)有( )个三角形有( )个三角形例3:下面的图形中有多少个三角形?(第九届中国青少年数学论坛趣味数学解题技能展示大赛试题)模仿练习数一数,图中共有几个正方形?(2010武汉明心数学资优生水平测试题)精典例题例4:数出下图中有多少个长方形?多少个正方形?还能用刚才的方法来数吗?三角形很多,可以尝试按三角形的方向和大小尝试分类数。
KG I H G FEDC B A模仿练习1.数一数,图中有多少个长方形?2.数一数图中有多少个正方形?家庭作业1.数一数每幅图里面图形的个数(能计算的写出算式)。
(1) (2)前面学习的数长方形的方法还有用吗?怎么能用上呢?DCBA D CBA有( )条线段 有( )个角2.右图中有多少个三角形?3.图中有多少个长方形?(把你的想法分享给你的爸爸妈妈听,你能教会他们吗?分享后让爸爸妈妈给你打星,最多5颗星)4.数一数,右图中有多少个正方形?5.(20XX 年“陈省身杯”国际青少年数学邀请赛试题)。
巧数图形详细讲解小学三年级奥数(课堂PPT)

知识回顾 Knowledge Review
总共:10+10+4= 24 个
Page 19
拓展12:数出下图中所有三角形的个数。
(3+2+1)×55=25
5个 5个
小五边形外侧组合三角形有(3+2+1)×5-5=25个三角形。 以大五边形边为底边的等腰三角形有5个。 以小五边形顶角为顶角的等腰三角形有5个。
总共:25+5+5= 35 个。
Page 20
5个组合 1
总计
15
可见,整齐单排长方形个数的算法与线段计算相同。
Page 4
例3.数出图中共有多少三角形。
A
三角形个数: 4+3+2+1=10
1 2 34
B C DE F
数三角形有时也可以用数线段的方法;有的图形要用 编号数图形的方法,还有的图形先要分成几部分分别 去数,再考虑几部分拼合起来看看有没有产生新三角 形。
巧数图形
Page 1
白汀水
例1、数线段
31542
共5+4+3+2+1= 15条线段
Page 2
练习1、数线段
1 23 4
5
67
共 7+6+5+4+3+2+1=28 条线段
Page 3
例2、下面图中有几个长方形?
数一数:
总计: 5+4+3+2+1=15
单个
5
2个组合 4
3个组合 3
4个组合 2
Page 22
拓展15. 数一数,图中有多少个长方形?
三年级奥数--第五讲--巧数图形(二)
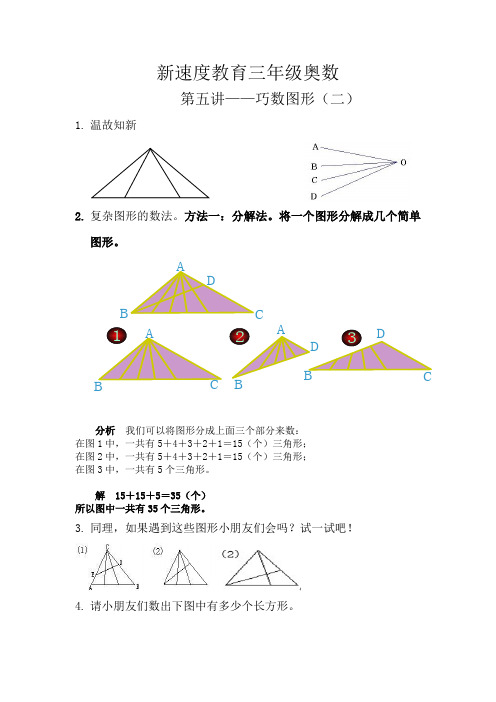
新速度教育三年级奥数
第五讲——巧数图形(二)
1. 温故知新
2. 复杂图形的数法。
方法一:分解法。
将一个图形分解成几个简单图形。
B C
分析 我们可以将图形分成上面三个部分来数:
在图1中,一共有5+4+3+2+1=15(个)三角形;
在图2中,一共有5+4+3+2+1=15(个)三角形;
在图3中,一共有5个三角形。
解 15+15+5=35(个)
所以图中一共有35个三角形。
3. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
4. 请小朋友们数出下图中有多少个长方形。
分析:数图形中有多少个长方形和数三角形的方法一样,长方形是由长宽两对线段围成,线段CD 上有3+2+1=6条线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6个长方形;而AC 上共2+1=3条线段也就有6×3=18个长方形。
它的计算公式为:
5. 方法二:长方形的总数=长边线段的总数×宽边线段的总数
6. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
7. *请小朋友们数出下图中有多少个正方形。
分析:一个小正方形有9个,四个小正方形组成有4个,9个小正方形有1个,所以一共有1+4+9=15个
8.*方法三:公式法。
1*1+2*2+3*3+..+N*N=。
N 是一行正方形的个数。
9.练一练:
D B C
A。
小学三年级奥数之难点:巧数图形

小学三年级奥数之难点:巧数图形李正堂—2008—12—25 图形问题说来一直是三年级的一个难点,很多学生第一次接触这种题型的时候总是喜欢去数,可是如果只仅仅是靠数,我相信那不是你所想要的,大家一定要学会在掌握规律的同时学会分析。
下面我们一起来剖析一些题目,希望对大家有些帮助:【铺垫】:【分析】:具体推理过程不详述,大家一定要记住:总的长方形数目解答过程:宽的基本线段数3,长的基本线段数2(1+2+3)×(1+2)=18所以共有18个长方形【巩固】:【分析】:方法很清楚,也很明确,关键是它是一个不规则图形,可以先将该图分为两部分:通过图形可以帮助我们理解:第一个图形中有长方形(1+2+3+4)×(1+2+3+4)=100个第二个图形中有长方形(1+2)×(1+2+3+4+5+6)=63个而它们重复的图形中有长方形(1+2)×(1+2+3+4)=30个所以原图中共有:100+63-30=133个长方形【拓展】含有两个★在内的由小正方形组成的长方形(含正方形)共有_____个【分析】:采用间接的方法也许会比较困难,不妨采用直接法进行求解。
(1)两层的情况长为2个正方形边长:1长为3个正方形边长:22层的情况长为4个正方形边长:3 共12个长为5个正方形边长:3长为6个正方形边长:2长为7个正方形边长:1(2)三层的情况三层的情况有两种,所以只需要考虑一种情况就可以求解了:长为2个正方形边长:1长为3个正方形边长:23层的情况长为4个正方形边长:3 共12个(2个)长为5个正方形边长: 3长为6个正方形边长:2长为7个正方形边长:1三层的情况共有12×2=24个(3)4层的情况长为2个正方形边长:1长为3个正方形边长:24层的情况长为4个正方形边长:3 共12个(2个)长为5个正方形边长: 3长为6个正方形边长:2长为7个正方形边长:1四层的情况共有12×2=24个(4)5层的情况长为2个正方形边长:1长为3个正方形边长:25层的情况长为4个正方形边长:3 共12个长为5个正方形边长:3长为6个正方形边长:2长为7个正方形边长:1所以总共有12+24+24+12=72个【总结】我想大家通过这样的讲解也可以找到一些规律了,分了层之后其实边长分法都一样,所以只需要看宽的情况,宽的情况(层的情况)共有(1+2+2+1)=6种情况,故总共有6×12=72大家一定要学会采用适当的方法进行求解!。
三年级奥数巧数图形精编版

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯第 2讲巧数图形知识重点同学们,我们常常会碰到数图形的问题,关于较复杂的图形,常常会出现数重复或数遗漏的错误。
如何才能不重复也不遗漏地数出图形的个数呢?这节课,我们将一同来找寻好的方法。
要正确数出图形的个数,重点是要从基本图形下手。
第一要弄清图形中包括的基本图形是什么,有多少个,而后再数出由基本图形构成的新的图形,并求出它们的和。
精典例题例 1: 数出下列图中有多少条线段?A B C D E从短的线段下手,再两条两条拼接起来数,你发现规律了吗?模拟练习A数一数,每种图形有多少个?B C D EF有()条线段有()个三角形ABCOD有()个角有()个长方形有()个正方形例 2: 数出图中共有多少个三角形?⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯还可以用方才的方法来数吗?AKGH I GB CD E F模拟练习数一数,每幅图里有多少个三角形?(1)(2)有()个三角形有()个三角形例 3: 下边的图形中有多少个三角形?(第九届中国青少年数学论坛兴趣数学解题技术展现大赛试题)三角形好多,能够试试按三角形的方向和大小试试分类数。
模拟练习数一数,图中共有几个正方形?(2010 武汉明心数学资优生水平测试题)精典例题例 4:数出下列图中有多少个长方形?多少个正方形?⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯前方学习的数长方形的方法还实用吗?怎么能用上呢?A BC D模拟练习1.数一数,图中有多少个长方形?A BDC2.数一数图中有多少个正方形?家庭作业1.数一数每幅图里面图形的个数(能计算的写出算式)。
(1)(2)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯有()条线段有()个角2.右图中有多少个三角形?3.图中有多少个长方形?(把你的想法分享给你的爸爸妈妈听,你能教会他们吗?分享后让爸爸妈妈给你打星,最多 5 颗星)4.数一数,右图中有多少个正方形?5.数一数,此中共有多少个包括“”的三角形?(2011年“陈省身杯”国际青少年数学邀请赛试题)。
小学奥数--巧数图形

第5讲 巧数图形一、知识要点小朋友,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,其次再数出由基本图形组成的新的图形,最后求出它们的和。
二、精讲精练【例题1】数一数,下图中有几条线段?练习1:(1)数出下图中有多少条线段?(2)数出下图中有几个长方形?【例题2】数出图中有几个角?E A B C D D A B C O DC BA练习2:数出图中有几个角?(1) (2)【例题3】数出下图中共有多少个三角形?练习3:数出图中共有多少个三角形?(1)(2)O C B A EDO C B A PDC B A FE D C B A KGI H G FE D C B A【例题4】数出下图中有多少个长方形?练习4:(1)数出下图中有多少个长方形?(2)数出下图中有多少个正方形?【例题5】有5个同学,每两个人握手一次,一共要握手多少次?练习5:(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?DC B AD C BA(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?三、课后作业1、数一数下图中各有多少条线段?(2)(3)2、数一数下图中有多少个锐角。
3、下列各图中各有多少个锐角?4、数一数下面图中各有多少个三角形。
5、数一数下面各图中分别有多少个长方形。
6、数一数,下面各图中分别有几个长方形?7、数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)。
小学三年级奥数巧数图形知识点与习题教学内容

第11讲巧数图形数出某种图形的个数是一类有趣的图形问题。
由于图形千变万化,错综复杂,所以要想准确地数出其中包含的某种图形的个数,还真需要动点脑筋。
要想有条理、不重复、不遗漏地数出所要图形的个数,最常用的方法就是分类数。
例1数出下图中共有多少条线段。
分析与解:我们可以按照线段的左端点的位置分为A,B,C三类。
如下图所示,以A为左端点的线段有3条,以B为左端点的线段有2条,以C为左端点的线段有1条。
所以共有3+2+1=6(条)。
我们也可以按照一条线段是由几条小线段构成的来分类。
如下图所示,AB,BC,CD是最基本的小线段,由一条线段构成的线段有3条,由两条小线段构成的线段有2条,由三条小线段构成的线段有1条。
所以,共有3+2+1=6(条)。
由例1看出,数图形的分类方法可以不同,关键是分类要科学,所分的类型要包含所有的情况,并且相互不重叠,这样才能做到不重复、不遗漏。
例2 下列各图形中,三角形的个数各是多少?分析与解:因为底边上的任何一条线段都对应一个三角形(以顶点及这条线段的两个端点为顶点的三角形),所以各图中最大的三角形的底边所包含的线段的条数就是三角形的总个数。
由前面数线段的方法知,图(1)中有三角形1+2=3(个)。
图(2)中有三角形1+2+3=6(个)。
图(3)中有三角形1+2+3+4=10(个)。
图(4)中有三角形1+2+3+4+5=15(个)。
图(5)中有三角形1+2+3+4+5+6=21(个)。
例3下列图形中各有多少个三角形?分析与解:(1)只需分别求出以AB,ED为底边的三角形中各有多少个三角形。
以AB为底边的三角形ABC中,有三角形1+2+3=6(个)。
以ED为底边的三角形CDE中,有三角形1+2+3=6(个)。
所以共有三角形6+6=12(个)。
这是以底边为标准来分类计算的方法。
它的好处是可以借助“求底边线段数”而得出三角形的个数。
我们也可以以小块个数作为分类的标准来计算:图中共有6个小块。
三年级奥数--第四讲--巧数图形(一)教学教材

新速度教育三年级奥数
第四讲——巧数图形(一)
1. 小故事:
晚饭过后,妈妈给小小出了一道“试眼力”的题目:数数窗户上一共有多少个正方形。
小小一看,立即回答:“窗户上一共有6个正方形。
”妈妈笑了,爸爸在一旁也笑了,小小给弄了个“丈二和尚莫不着头脑”。
小朋友,你知道小小的爸爸妈妈为什么笑吗?小小数得难道不对吗?如果不对,那么窗户上究竟有几个正方形呢?下面我们就一起来研究数图形的问题。
2.
3. 数出下图中有几条线段。
数一数,找规律。
D C B A
4. 5. 方法:如果线段有N 段的话,就一共有1+2+3..+N 段。
(1)B A F (2)E B A
4. 数出下图中有几个角。
数一数,找规律。
D C
B
A
O E D C B A O
6. 7. 方法:如果有N 个最小的角,就一共有1+2+3+..+N 个角。
8.
9. 数出下图中有几个三角形。
数一数,找规律。
10.
11.
12.
13. 方法:如果有N 个最小的三角形,就一共有1+2+3+..+N 个三
角形。
15.
16. 想一想,如果换成全都是长方形,结果会怎样呢?
18.方法:如果有N个最小的长方形,就一共有1+2+3+..+N个长方形。
19.
20.
21.
23.
24.总结:线段,角,简单的三角形组合(只有一层),简单的长
方形组合(只有一层)。
计算数量的方法都是1+2+3+..+N。
26.
28.
29.练一练:
(3)(4)(5)。
第3讲--巧数图形--奥数个性化辅导(三年级)
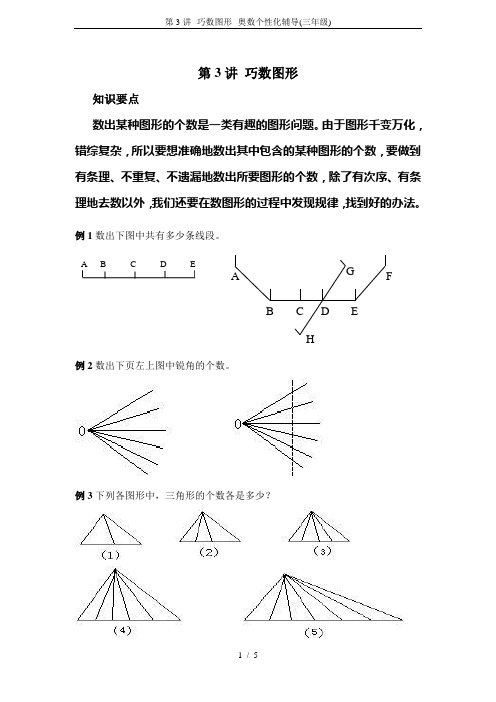
第3讲 巧数图形
知识要点
数出某种图形的个数是一类有趣的图形问题。
由于图形千变万化,错综复杂,所以要想准确地数出其中包含的某种图形的个数,要做到有条理、不重复、不遗漏地数出所要图形的个数,除了有次序、有条理地去数以外,我们还要在数图形的过程中发现规律,找到好的办法。
例1数出下图中共有多少条线段。
例2数出下页左上图中锐角的个数。
例3下列各图形中,三角形的个数各是多少?
A
B
C D
E
F
G H A
B
C
D
E
例4下列图形中各有多少个三角形?
例5右图中有多少个三角形?
例6数一数下图中共有多少个正方形。
例7数一数下图中共有多少个长方形
练习
1、下列图形中各有多少条线段?
2、下列图形中,各有多少个小于180°的角?
3、下列图形中各有多少个三角形?
E
F
D A
B
C O
A B C D E F
A B C D E F
F G H
I
4、下图中各有多少个长方形?
(3)
5、下图中有多少个正方形?
拓展延伸
1、下列图形中,包含“*”号的正方形有多少?
3、右图中有多少个正方形?
4、数一数下图中有多少个平行四边形?
5、数一数下图中有多少个梯形?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲 巧数图形
知识要点
同学们,我们经常会遇到数图形的问题,对于较复杂的图形,经常会出现数重复或数漏掉的错误。
怎样才能不重复也不遗漏地数出图形的个数呢?这节课,我们将一起来寻找好的方法。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
精典例题
例1: 数出下图中有多少条线段?
模仿练习
数一数,每种图形有多少个?
有( )条线段 有( )个三角形
有( )个角 有( )个长方形 有( )个正方形
例2: 数出图中共有多少个三角形?
从短的线段入手,再两条两条拼接起来数,你发现规律了吗?
E
A
B
C
D
O
D
C B A A
模仿练习
数一数,每幅图里有多少个三角形? (1) (2)
有( )个三角形 有( )个三角形
例3:下面的图形中有多少个三角形?(第九届中国青少年数学论坛趣味数学
解题技能展示大赛试题)
模仿练习
数一数,图中共有几个正方形?(2010武汉明心数学资优生水平测试题)
精典例题
例4: 数出下图中有多少个长方形?多少个正方形?
还能用刚才的方法来数吗?
三角形很多,可以尝试按三角形的方向和大小尝试分类数。
K
G I H G D
C B A
模仿练习
1.数一数,图中有多少个长方形?
2.数一数图中有多少个正方形?
家庭作业
1.数一数每幅图里面图形的个数(能计算的写出算式)。
(1) (2)
前面学习的数长方形的方法还有用吗?怎么能用上呢?
D
C
B
A D C
B
A
有( )条线段 有( )个角
2.右图中有多少个三角形?
3.图中有多少个长方形?(把你的想法分享给你的爸爸妈妈听,你能教会他们吗?分享后让爸爸妈妈给你打星,最多5颗星)
4.数一数,右图中有多少个正方形?
5.数一数,其中共有多少个包含“
(2011年“陈省身杯”国际青
少年数学邀请赛试题)。
