用MATLAB计算复数的实部、虚部、模、辐角,共轭复数、简单复数方程根及复数的极限
matlab 复数运算指令

matlab 复数运算指令Matlab是一种功能强大的数学软件,其提供了丰富的复数运算指令,使得对复数的运算变得更加便捷。
本文将介绍几个常用的复数运算指令及其应用。
一、复数的定义与表示在Matlab中,复数可以通过使用虚数单位i来表示。
例如,我们可以使用1+2i表示一个复数,其中1为实部,2为虚部。
Matlab还提供了另一种表示复数的方式,即使用complex函数。
例如,complex(1,2)也表示一个实部为1,虚部为2的复数。
二、复数的基本运算1. 加法运算复数的加法可以通过使用加号来实现。
例如,对于两个复数a和b,可以使用c = a + b来计算它们的和。
需要注意的是,Matlab中的加法运算是按照分量进行的,即实部与实部相加,虚部与虚部相加。
2. 减法运算复数的减法可以通过使用减号来实现。
例如,对于两个复数a和b,可以使用c = a - b来计算它们的差。
同样地,减法运算也是按照分量进行的。
3. 乘法运算复数的乘法可以通过使用乘号来实现。
例如,对于两个复数a和b,可以使用c = a * b来计算它们的积。
在Matlab中,复数的乘法运算是按照规定的乘法法则进行的。
4. 除法运算复数的除法可以通过使用除号来实现。
例如,对于两个复数a和b,可以使用c = a / b来计算它们的商。
需要注意的是,除法运算中的除数不能为0。
三、复数的其他运算1. 模运算复数的模可以通过使用abs函数来计算。
例如,对于一个复数z,可以使用m = abs(z)来计算其模。
2. 幅角运算复数的幅角可以通过使用angle函数来计算。
例如,对于一个复数z,可以使用theta = angle(z)来计算其幅角。
3. 共轭运算复数的共轭可以通过使用conj函数来计算。
例如,对于一个复数z,可以使用w = conj(z)来计算其共轭复数。
四、复数的应用举例1. 极坐标形式与直角坐标形式的转换在Matlab中,我们可以使用polar函数将复数从直角坐标形式转换为极坐标形式。
MATLAB学习(4)——复数及其运算

MATLAB学习(4)——复数及其运算MATLAB学习(4)——复数及其运算复数及其运算A)复数的表⽰(1).x=a+bi,其中a称为实部,b称为虚部(2)或写成复指数的形式:x=re^(iθ)其中r称为复数的模,⼜记为 |x| ;θ称为复数的幅度,⼜记为Arg(x) 。
且满⾜r=√(a^2+b^2) ,tanθ=b/a第⼀种⽅式适合处理复数的代数运算,第⼆种⽅式适合处理复数旋转等涉及幅⾓改变的问题复数的构造:(1)直接构造法将复数看做完整的表达式输⼊例:x1=-1+i%实部虚部形式x2=sqrt(2)*exp(i*(3*pi/4))%复指数形式(2)符号函数构造法将复数看做函数形式,将实部和虚部看做⾃变量,⽤syms来构造,⽤subs对符号函数中的⾃变量赋值例:syms a b real%声明a b为实数型x3=a+b*i%实部虚部形式复数的符号表达subs(x3,{a,b},{-1,1})%代⼊具体值syms r ct real;%声明r ct为实数型x4=r*exp(ct*i);%复指数形式复数的符号表达subs(x4,{r,ct},{sqrt(2),3*pi/4})%代⼊具体值以上例⼦中复数均为 -1+1i复数矩阵的构造:(1)由复数元素构造例:a1=[sqrt(2)*exp((pi/4)*i) 1+2i 1+3i;sqrt(2)*exp((-pi/4)*i) 1-2i 1-3i](2)由实矩阵构造例:a2re=[1 1 1;1 1 1];%实部实矩阵a2im=[1 2 3;-1 -2 -3];%虚部实矩阵a2=a2re+a2im*i%由实矩阵构造以上两例中的复数矩阵均为1.0000 + 1.0000i 1.0000 +2.0000i 1.0000 +3.0000i1.0000 - 1.0000i 1.0000 -2.0000i 1.0000 -3.0000iB)复数的绘图(1)直⾓坐标图plot函数(2)极坐标图Polar函数调⽤格式:polar(theta,rho)其中theta为极坐标极值,rho为极坐标⽮径例:做出y=t+i*rsin(t) 的坐标图t=0:0.01:2*pi;y=t+i*t.*sin(t); %直⾓坐标表⽰r=abs(y);delta=angle(y);%极坐标表⽰subplot(2,1,1)plot(y)%绘制直⾓坐标图title('直⾓坐标图');subplot(2,1,2)polar(delta,r)%绘制极坐标图title('极坐标图')C)复数的操作函数常⽤矩阵分解函数转⾃博客:。
复变函数中MATLAB的应用

MATLAB在复变函数中的应用复变函数的运算是实变函数运算的一种延伸,但由于其自身的一些特殊的性质而显得不同,特别是当它引进了“留数”的概念,且在引入了Taylor级数展开Laplace 变换和Fourier变换之后而使其显得更为重要了。
使用MATLAB来进行复变函数的各种运算;介绍留数的概念及MAT–LAB的实现;介绍在复变函数中有重要应用的Taylor展开(Laurent展开Laplace变换和Fourier变换)。
1 复数和复矩阵的生成在MATLAB中,复数单位为)1ji,其值在工作空间中都显示为=sq rt=(-0+。
.1i00001.1 复数的生成复数可由iz+=。
a=语句生成,也可简写成biaz*+b另一种生成复数的语句是)exp(i=,也可简写成)rz*=,thetaexp(theta*irz*其中theta为复数辐角的弧度值,r为复数的模。
1.2 创建复矩阵创建复矩阵的方法有两种。
(1)如同一般的矩阵一样以前面介绍的几种方式输入矩阵例如:)]iA*ii*=+3[i*-+*2523exp(336),exp(3,,9(2)可将实、虚矩阵分开创建,再写成和的形式例如:re=;rand)2,3(im i re com *+=]5466.07271.05681.02897.07027.05341.08385.03420.03704.03412.03093.06602.0[i ii i ii com ++++++=注意 实、虚矩阵应大小相同。
2 复数的运算1.复数的实部和虚部复数的实部和虚部的提取可由函数real 和imag 实现。
调用形式 )(x real返回复数x 的实部)(x imag返回复数x 的虚部2.共轭复数复数的共轭可由函数conj 实现。
调用形式)(x conj返回复数x 的共轭复数3.复数的模和辐角复数的模和辐角的求解由功能函数abs 和angle 实现。
调用形式 )(x abs 复数x 的模)(x angle复数x 的辐角例:求下列复数的实部与虚部、共轭复数、模与辐角 (1)i231+ (2)i i i --131 (3)ii i 2)52)(43(-+(4)i i i +-2184由MATLAB 输入如下:]21^48^,2/)52()43(),1/(3/1),23/(1[i i i i i i i i i i a +*--*=--+==ai iii0000.30000.10000.135000.35000.25000.11538.02308.0-----)(a real %实部=ans0.23081.5000 –3.50001.0000)(a imag%虚部=ans–0.1538–2.5000 –13.0000 –3.0000)(a conj%共轭复数=ans0.2308+0.1538i 1.5000+2.5000i–3.5000+13.0000i1.0000+3.0000i)(a abs%模=ans0.27742.9155 13.4629 3.1623)(a angle%辐角=ans–0.5880–1.0304–1.8228-1.24904.复数的乘除法复数的乘除法运算由“/”和“*”实现。
matlab复数数组

matlab复数数组Matlab是一种强大的数学软件,可以进行复数计算和操作。
复数是由实部和虚部组成的数,可以用a+bi的形式表示,其中a是实部,b是虚部。
在Matlab中,复数数组可以用一个一维数组来表示,每个元素都是一个复数。
复数数组在Matlab中的使用非常方便,可以进行各种复数运算和操作。
下面我们来介绍一些常见的复数数组操作。
1. 创建复数数组我们可以使用complex函数来创建复数数组。
例如,我们可以创建一个包含5个复数的数组:```z = complex([1 2 3 4 5], [6 7 8 9 10]);```这个数组中的第一个元素是1+6i,第二个元素是2+7i,以此类推。
2. 访问复数数组的元素我们可以使用索引来访问复数数组的元素。
例如,我们可以访问数组z的第3个元素:```z(3)```这将返回数组z的第3个元素。
3. 复数数组的运算在Matlab中,我们可以对复数数组进行各种运算,包括加法、减法、乘法和除法。
例如,我们可以计算两个复数数组的和:```a = complex([1 2 3], [4 5 6]);b = complex([7 8 9], [10 11 12]);c = a + b;```这将返回一个新的复数数组c,其中的元素是a和b对应元素的和。
4. 复数数组的函数计算Matlab提供了许多函数来计算复数数组的各种属性,如绝对值、相位、共轭等。
例如,我们可以计算复数数组z的绝对值:```abs(z)```这将返回一个新的数组,其中的元素是z中对应元素的绝对值。
5. 复数数组的切片和索引我们可以使用切片和索引来访问复数数组的子数组。
例如,我们可以访问数组z的前三个元素:```z(1:3)```这将返回一个包含z的前三个元素的新数组。
6. 复数数组的图表绘制Matlab提供了丰富的绘图函数,可以用来绘制复数数组的图表。
例如,我们可以使用plot函数来绘制复数数组的实部和虚部:```plot(real(z), imag(z))```这将绘制出一个以实部为x轴,虚部为y轴的散点图。
Matlab中的复数运算基础教程

Matlab中的复数运算基础教程引言:在科学计算和工程领域中,复数运算是一项非常重要的技术。
Matlab作为一种强大的数值计算软件,提供了灵活而高效的复数运算工具。
本文将介绍Matlab中的复数运算基础知识,涵盖了复数的表示、基本运算、共轭和幅角的计算等。
1. 复数的表示复数是由实数和虚数组成的数。
在Matlab中,复数可以用a + bi的形式表示,其中a是实部,b是虚部。
例如,3 + 2i就是一个复数。
在Matlab中,可以直接输入复数,例如:z = 3 + 2i;这样就定义了一个复数变量z。
2. 基本运算Matlab中的复数运算基本与实数一致。
支持加法、减法、乘法和除法等运算。
例如,可以使用"+"运算符计算两个复数的和:z1 = 3 + 2i;z2 = 1 + 4i;z = z1 + z2;这样,z的值将是4 + 6i。
3. 共轭运算在复数运算中,共轭运算是一个重要的概念。
复数的共轭是将虚部的符号取反得到的结果。
在Matlab中,可以使用conj函数对复数进行共轭运算。
例如:z = 3 + 2i;w = conj(z);这样,w的值将是3 - 2i。
4. 幅角运算在复数的表示中,幅角是指复数与正实轴之间的夹角。
在Matlab中,可以使用angle函数计算复数的幅角。
angle函数的结果以弧度形式表示。
例如:z = 3 + 2i;theta = angle(z);这样,theta的值将是0.5880弧度。
5. 赋值运算在进行复数运算时,经常需要将结果赋值给一个变量。
在Matlab中,可以使用等号将计算结果赋值给一个变量。
例如:z1 = 3 + 2i;z2 = 1 + 4i;z = z1 + z2;在这个例子中,z1和z2分别是两个复数,将它们相加的结果赋值给z。
6. 数值计算与绘图Matlab中的复数运算不仅支持基本的数值计算,还能与绘图功能结合。
通过使用plot函数和复数运算,可以绘制出复平面上的曲线。
matlab中如何处理复数,matlab中复数的处理函数

matlab中如何处理复数,matlab中复数的处理函数matlab中复数的处理函数MATLAB 中复数的处理函数要说明复数的运算,先从解以下的⼆次⽅程式的复数根谈起上式的根有实部 (-2) 及虚部 (±3),我们就这个复数的表⽰法来说明 MATLAB的复数功能。
MATLAB 是以 i或 j字元来代表虚部,其它的复数相关函数有real, imag, conj, abs, angle等等,详见线上说明 lookfor complex。
如果复数表⽰为 x=a+bi共轭复数 = , 复数⼤⼩ r = , 复数向量的夹⾓ θ= tan -1 (b/a)复数实部 a = r cosθ, 复数虚部 b = r sinθ, 复数指数表⽰法 x=r ei上述各函数对应 MATLAB的复数指令为a=real(x), b=imag(x), =conj(x),r=abs(x), =angle(x), x=r*exp(i*angle(x))以下是⼏个复数表⽰式的例⼦:>> x=1-2*i; % 注意是 2*i 不是 2i>> real(x) % 列出实部ans=1>> imag(x) % 列出虚部ans =-2>> conj(x) % 计算共轭复数ans =1.0000 + 2.0000i>> abs(x) % 计算复数的⼤⼩ans =2.2361>> angle(x) % 计算复数向量的夹⾓(以径度表⽰)ans =-1.1071>> a=1; b=4; c=13;>> x1=(-b+sqrt(b^2-4*a*c))/(2*a) % 以解⼆次⽅程式根的公式计算复数根x1 =-2.0000 + 3.0000i>> x2=(-b-sqrt(b^2-4*a*c))/(2*a)x2 =-2.0000 - 3.0000i>> y=exp(i) % 以复数指数⽅式表⽰⼀个复数y =0.5403 + 0.8415i>> y=exp(i*pi*0.75)y =-0.7071 + 0.7071i和复数有关的图以极座标来表⽰会⽐⼀般的卡⽒座标要合适,polar 指令可以将数据以极座标⽅式加以绘图, 其语法为 polar(theta,r),(theta,r)分别代表极座标上的⾓度及半径值。
利用MATLAB进行复变函数的主要运算

利用MATLAB进行复变函数的主要运算摘要复变函数与积分变换理论性较强,又是解决实际问题的强有力的工具.该课程已深入到数学的各个分支,如微分方程、积分方程、概率论和数论等多个学科.然而该课程的很多内容比较抽象,学起来比较枯燥且难学.本文利用MATLAB讨论了复变函数与积分变换中的复数运算、泰勒级数的展开、留数、有理函数展开、Fourier变换、Laplace变换和复变函数图形绘制等几个问题.这样不仅提高和完善复变函数与积分变换方法的实用性,同时可以培养学习者运用MATLAB语言编程的能力,对学习者以后的专业课及工作中使用数学软件进行数据处理有很大帮助.关键词:MATLAB; 复变函数; 积分变换1.复数的生成:Z= a + b*I;z = r*exp(i*theta);2.复数的运算:Real(z)imag(z);3.共轭复数复数的共轭可由函数conj 实现。
调用形式conj(x) 返回复数x 的共轭复数4.复数的模和辐角复数的模和辐角的求解由功能函数abs和angle实现。
调用形式abs(x)复数x 的模angle(x)复数x的辐角5.复数的乘除法复数的乘除法运算由“/”和“ ”实现。
6.复数的平方根复数的平方根运算由函数sqrt实现。
调用形式sqrt(x)返回复数x的平方根值。
7.复数的幂运算复数的幂运算的形式为x^ n结果返回复数x的n次幂。
8.复数的指数和对数运算复数的指数和对数运算分别由函数exp和log实现。
调用形式exp(x)返回复数x的以e为底的指数值log( x) 返回复数x的以e为底的对数值。
9.复数方程求根复数方程求根或实方程的复数根求解也由函数solve实现。
10.留数在MATLAB中可用如下方法:假设以知奇点a和m重数,则用下面的MATLAB 语句可求出相应的留数Limit(f*(x-a),x,a) %返回x=a的一级极点的留数Limit(diff(f*(x-a)^m,x,m-1)/prod(1:m-1),z,a %返回x=a的m级极点的留数11. taylor 泰勒级数展开taylor( f )返回f 函数的五次幂多项式近似。
matlab常用函数

一、MATLAB常用的基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
当x<0时,sign(x)=-1;当x=0时,sign(x)=0;当x>0时,sign(x)=1。
rem(x,y):求x除以y的馀数gcd(x,y):整数x和y的最大公因数lcm(x,y):整数x和y的最小公倍数exp(x):自然指数pow2(x):2的指数log(x):以e为底的对数,即自然对数或log2(x):以2为底的对数log10(x):以10为底的对数二、MATLAB常用的三角函数sin(x):正弦函数cos(x):馀弦函数tan(x):正切函数asin(x):反正弦函数acos(x):反馀弦函数atan(x):反正切函数atan2(x,y):四象限的反正切函数sinh(x):超越正弦函数cosh(x):超越馀弦函数tanh(x):超越正切函数asinh(x):反超越正弦函数acosh(x):反超越馀弦函数atanh(x):反超越正切函数三、适用於向量的常用函数有:min(x): 向量x的元素的最小值max(x): 向量x的元素的最大值mean(x): 向量x的元素的平均值median(x): 向量x的元素的中位数std(x): 向量x的元素的标准差diff(x): 向量x的相邻元素的差sort(x): 对向量x的元素进行排序(Sorting)length(x): 向量x的元素个数norm(x): 向量x的欧氏(Euclidean)长度sum(x): 向量x的元素总和prod(x): 向量x的元素总乘积cumsum(x): 向量x的累计元素总和cumprod(x): 向量x的累计元素总乘积dot(x, y): 向量x和y的内积cross(x, y): 向量x和y的外积四、MATLAB的永久常数i或j:基本虚数单位(即)eps:系统的浮点(Floating-point)精确度inf:无限大,例如1/0nan或NaN:非数值(Not a number),例如0/0 pi:圆周率p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargin: 函数的输出引数个数五、MATLAB基本绘图函数plot: x轴和y轴均为线性刻度(Linear scale)loglog: x轴和y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度六、plot绘图函数的叁数字元颜色字元图线型态y 黄色 . 点k 黑色o 圆w 白色x xb 蓝色+ +g 绿色* *r 红色- 实线c 亮青色: 点线m 锰紫色-. 点虚线-- 虚线七、注解xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线八、二维绘图函数bar 长条图errorbar 图形加上误差范围fplot 较精确的函数图形polar 极座标图hist 累计图rose 极座标累计图stairs 阶梯图stem 针状图fill 实心图feather 羽毛图compass 罗盘图quiver 向量场图----------------------------附录1 常用命令附录1.1 管理用命令函数名功能描述函数名功能描述addpath 增加一条搜索路径rmpath 删除一条搜索路径demo 运行Matlab演示程序type 列出.M文件doc 装入超文本文档version 显示Matlab的版本号help 启动联机帮助what 列出当前目录下的有关文件lasterr 显示最后一条信息whatsnew 显示Matlab的新特性lookfor 搜索关键词的帮助which 造出函数与文件所在的目录path 设置或查询Matlab路径附录1.2管理变量与工作空间用命令函数名功能描述函数名功能描述clear 删除内存中的变量与函数pack 整理工作空间内存disp 显示矩阵与文本save 将工作空间中的变量存盘length 查询向量的维数size 查询矩阵的维数load 从文件中装入数据who,whos 列出工作空间中的变量名附录1.3文件与操作系统处理命令函数名功能描述函数名功能描述cd 改变当前工作目录edit 编辑.M文件delete 删除文件matlabroot 获得Matlab的安装根目录diary 将Matlab运行命令存盘tempdir 获得系统的缓存目录dir 列出当前目录的内容tempname 获得一个缓存(temp)文件! 执行操作系统命令附录1.4窗口控制命令函数名功能描述函数名功能描述echo 显示文件中的Matlab中的命令more 控制命令窗口的输出页面format 设置输出格式附录1.5启动与退出命令函数名功能描述函数名功能描述matlabrc 启动主程序quit 退出Matlab环境startupMatlab自启动程序附录2 运算符号与特殊字符附录2.1运算符号与特殊字符函数名功能描述函数名功能描述+ 加 ... 续行标志- 减, 分行符(该行结果不显示)* 矩阵乘; 分行符(该行结果显示).* 向量乘% 注释标志^ 矩阵乘方! 操作系统命令提示符.^ 向量乘方' 矩阵转置kron 矩阵kron积 . 向量转置\ 矩阵左除= 赋值运算/ 矩阵右除== 关系运算之相等.\ 向量左除~= 关系运算之不等./ 向量右除< 关系运算之小于: 向量生成或子阵提取<= 关系运算之小于等于() 下标运算或参数定义> 关系运算之大于[] 矩阵生成>= 关系运算之大于等于{} & 逻辑运算之与. 结构字段获取符| 逻辑运算之或. 点乘运算,常与其他运算符联合使用(如.\) ~ 逻辑运算之非xor 逻辑运算之异成附录2.2逻辑函数函数名功能描述函数名功能描述all 测试向量中所用元素是否为真is*(一类函数)检测向量状态.其中*表示一个确定的函数(isinf)any 测试向量中是否有真元素*isa 检测对象是否为某一个类的对象exist 检验变量或文件是否定义logical 将数字量转化为逻辑量find 查找非零元素的下标附录3 语言结构与调试附录3.1编程语言函数名功能描述函数名功能描述builtin 执行Matlab内建的函数global 定义全局变量eval 执行Matlab语句构成的字符串nargchk 函数输入输出参数个数检验feval 执行字符串指定的文件script Matlab语句及文件信息function Matlab函数定义关键词附录3.2控制流程函数名功能描述函数名功能描述break 中断循环执行的语句if 条件转移语句case 与switch结合实现多路转移otherwise 多路转移中的缺省执行部分else 与if一起使用的转移语句return 返回调用函数elseif 与if一起使用的转移语句switch 与case结合实现多路转移end 结束控制语句块warning 显示警告信息error 显示错误信息while 循环语句for 循环语句附录3.3交互输入函数名功能描述函数名功能描述input 请求输入menu 菜单生成keyboard 启动键盘管理pause 暂停执行附录3.4面向对象编程函数名功能描述函数名功能描述class 生成对象isa 判断对象是否属于某一类double 转换成双精度型superiorto 建立类的层次关系inferiorto 建立类的层次关系unit8 转换成8字节的无符号整数inline 建立一个内嵌对象附录3.5调试函数名功能描述函数名功能描述dbclear 清除调试断点dbstatus 列出所有断点情况dbcont 调试继续执行dbstep 单步执行dbdown 改变局部工作空间内存dbstop 设置调试断点dbmex 启动对Mex文件的调试sbtype 列出带命令行标号的.M文件dbquit 退出调试模式dbup 改变局部工作空间内容dbstack 列出函数调用关系附录4 基本矩阵与矩阵处理附录4.1基本矩阵函数名功能描述函数名功能描述eye 产生单位阵rand 产生随机分布矩阵linspace 构造线性分布的向量randn 产生正态分布矩阵logspace 构造等对数分布的向量zeros 产生零矩阵ones 产生元素全部为1的矩阵: 产生向量附录4.2特殊向量与常量函数名功能描述函数名功能描述ans 缺省的计算结果变量non 非数值常量常由0/0或Inf/Inf获得computer 运行Matlab的机器类型nargin 函数中参数输入个数eps 精度容许误差(无穷小) nargout 函数中输出变量个数flops 浮点运算计数pi 圆周率i 复数单元realmax 最大浮点数值inf 无穷大realmin 最小浮点数值inputname 输入参数名varargin 函数中输入的可选参数j 复数单元varargout 函数中输出的可选参数附录4.3时间与日期函数名功能描述函数名功能描述calender 日历eomday 计算月末clock 时钟etime 所用时间函数cputime 所用的CPU时间now 当前日期与时间date 日期tic 启动秒表计时器datenum 日期(数字串格式) toc 读取秒表计时器datestr 日期(字符串格式) weekday 星期函数datevoc 日期(年月日分立格式)附录4.4矩阵处理函数名功能描述函数名功能描述cat 向量连接reshape 改变矩阵行列个数diag 建立对角矩阵或获取对角向量rot90 将矩阵旋转90度fliplr 按左右方向翻转矩阵元素tril 取矩阵的下三角部分flipud 按上下方向翻转矩阵元素triu 取矩阵的上三角部分repmat 复制并排列矩阵函数附录5 特殊矩阵函数名功能描述函数名功能描述compan 生成伴随矩阵invhilb 生成逆hilbert矩阵gallery 生成一些小的测试矩阵magic 生成magic矩阵hadamard 生成hadamard矩阵pascal 生成pascal矩阵hankel 生成hankel矩阵toeplitz 生成toeplitz矩阵hilb 生成hilbert矩阵wilkinson 生成wilkinson特征值测试矩阵附录6 数学函数附录6.1三角函数函数名功能描述函数名功能描述sin/asin 正弦/反正弦函数sec/asec 正割/反正割函数sinh/asinh 双曲正弦/反双曲正弦函数sech/asech 双曲正割/反双曲正割函数cos/acos 余弦/反余弦函数csc/acsc 余割/反余割函数cosh/acosh 双曲余弦/反双曲余弦函数csch/acsch 双曲余割/反双曲余割函数tan/atan 正切/反正切函数cot/acot 余切/反余切函数tanh/atanh 双曲正切/反双曲正切函数coth/acoth 双曲余切/反双曲余切函数atan2 四个象限内反正切函数附录6.2指数函数函数名功能描述函数名功能描述exp 指数函数log10 常用对数函数log 自然对数函数sqrt 平方根函数附录6.3复数函数函数名功能描述函数名功能描述abs 绝对值函数imag 求虚部函数angle 角相位函数real 求实部函数conj 共轭复数函数附录6.4数值处理函数名功能描述函数名功能描述fix 沿零方向取整round 舍入取整floor 沿-∞方向取整rem 求除法的余数ceil 沿+∞方向取整sign 符号函数附录6.5其他特殊数学函数函数名功能描述函数名功能描述airy airy函数erfcx 比例互补误差函数besselh bessel函数(hankel函数) erfinv 逆误差函数bessili 改进的第一类bessel函数expint 指数积分函数besselk 改进的第二类bessel函数gamma gamma函数besselj 第一类bessel函数gammainc 非完全gamma函数bessely 第二类bessel函数gammaln gamma对数函数beta beta函数gcd 最大公约数betainc 非完全的beta函数lcm 最小公倍数betaln beta对数函数log2 分割浮点数elipj Jacobi椭圆函数legendre legendre伴随函数ellipke 完全椭圆积分pow2 基2标量浮点数erf 误差函数rat 有理逼近erfc 互补误差函数rats 有理输出-----------------------------A aabs 绝对值、模、字符的ASCII码值acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割align 启动图形对象几何位置排列工具all 所有元素非零为真angle 相角ans 表达式计算结果的缺省变量名any 所有元素非全零为真area 面域图argnames 函数M文件宗量名asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦assignin 向变量赋值atan 反正切atan2 四象限反正切atanh 反双曲正切autumn 红黄调秋色图阵axes 创建轴对象的低层指令axis 控制轴刻度和风格的高层指令B bbar 二维直方图bar3 三维直方图bar3h 三维水平直方图barh 二维水平直方图base2dec X进制转换为十进制bin2dec 二进制转换为十进制blanks 创建空格串bone 蓝色调黑白色图阵box 框状坐标轴break while 或for 环中断指令brighten 亮度控制C ccapture (3版以前)捕获当前图形cart2pol 直角坐标变为极或柱坐标cart2sph 直角坐标变为球坐标cat 串接成高维数组caxis 色标尺刻度cd 指定当前目录cdedit 启动用户菜单、控件回调函数设计工具cdf2rdf 复数特征值对角阵转为实数块对角阵ceil 向正无穷取整cell 创建元胞数组cell2struct 元胞数组转换为构架数组celldisp 显示元胞数组内容cellplot 元胞数组内部结构图示char 把数值、符号、内联类转换为字符对象chi2cdf 分布累计概率函数chi2inv 分布逆累计概率函数chi2pdf 分布概率密度函数chi2rnd 分布随机数发生器chol Cholesky分解clabel 等位线标识cla 清除当前轴class 获知对象类别或创建对象clc 清除指令窗clear 清除内存变量和函数clf 清除图对象clock 时钟colorcube 三浓淡多彩交叉色图矩阵colordef 设置色彩缺省值colormap 色图colspace 列空间的基close 关闭指定窗口colperm 列排序置换向量comet 彗星状轨迹图comet3 三维彗星轨迹图compass 射线图compose 求复合函数cond (逆)条件数condeig 计算特征值、特征向量同时给出条件数condest 范-1条件数估计conj 复数共轭contour 等位线contourf 填色等位线contour3 三维等位线contourslice 四维切片等位线图conv 多项式乘、卷积cool 青紫调冷色图copper 古铜调色图cos 余弦cosh 双曲余弦cot 余切coth 双曲余切cplxpair 复数共轭成对排列csc 余割csch 双曲余割cumsum 元素累计和cumtrapz 累计梯形积分cylinder 创建圆柱D ddblquad 二重数值积分deal 分配宗量deblank 删去串尾部的空格符dec2base 十进制转换为X进制dec2bin 十进制转换为二进制dec2hex 十进制转换为十六进制deconv 多项式除、解卷delaunay Delaunay 三角剖分del2 离散Laplacian差分demo Matlab演示det 行列式diag 矩阵对角元素提取、创建对角阵diary Matlab指令窗文本内容记录diff 数值差分、符号微分digits 符号计算中设置符号数值的精度dir 目录列表disp 显示数组display 显示对象内容的重载函数dlinmod 离散系统的线性化模型dmperm 矩阵Dulmage-Mendelsohn 分解dos 执行DOS 指令并返回结果double 把其他类型对象转换为双精度数值drawnow 更新事件队列强迫Matlab刷新屏幕dsolve 符号计算解微分方程E eecho M文件被执行指令的显示edit 启动M文件编辑器eig 求特征值和特征向量eigs 求指定的几个特征值end 控制流FOR等结构体的结尾元素下标eps 浮点相对精度error 显示出错信息并中断执行errortrap 错误发生后程序是否继续执行的控制erf 误差函数erfc 误差补函数erfcx 刻度误差补函数erfinv 逆误差函数errorbar 带误差限的曲线图etreeplot 画消去树eval 串演算指令evalin 跨空间串演算指令exist 检查变量或函数是否已定义exit 退出Matlab环境exp 指数函数expand 符号计算中的展开操作expint 指数积分函数expm 常用矩阵指数函数expm1 Pade法求矩阵指数expm2 Taylor法求矩阵指数expm3 特征值分解法求矩阵指数eye 单位阵ezcontour 画等位线的简捷指令ezcontourf 画填色等位线的简捷指令ezgraph3 画表面图的通用简捷指令ezmesh 画网线图的简捷指令ezmeshc 画带等位线的网线图的简捷指令ezplot 画二维曲线的简捷指令ezplot3 画三维曲线的简捷指令ezpolar 画极坐标图的简捷指令ezsurf 画表面图的简捷指令ezsurfc 画带等位线的表面图的简捷指令F ffactor 符号计算的因式分解feather 羽毛图feedback 反馈连接feval 执行由串指定的函数fft 离散Fourier变换fft2 二维离散Fourier变换fftn 高维离散Fourier变换fftshift 直流分量对中的谱fieldnames 构架域名figure 创建图形窗fill3 三维多边形填色图find 寻找非零元素下标findobj 寻找具有指定属性的对象图柄findstr 寻找短串的起始字符下标findsym 机器确定内存中的符号变量finverse 符号计算中求反函数fix 向零取整flag 红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 矩阵沿指定维翻转floor 向负无穷取整flops 浮点运算次数flow Matlab提供的演示数据fmin 求单变量非线性函数极小值点(旧版)fminbnd 求单变量非线性函数极小值点fmins 单纯形法求多变量函数极小值点(旧版)fminunc 拟牛顿法求多变量函数极小值点fminsearch 单纯形法求多变量函数极小值点fnder 对样条函数求导fnint 利用样条函数求积分fnval 计算样条函数区间内任意一点的值fnplt 绘制样条函数图形fopen 打开外部文件for 构成for环用format 设置输出格式fourier Fourier 变换fplot 返函绘图指令fprintf 设置显示格式fread 从文件读二进制数据fsolve 求多元函数的零点full 把稀疏矩阵转换为非稀疏阵funm 计算一般矩阵函数funtool 函数计算器图形用户界面fzero 求单变量非线性函数的零点G ggamma 函数gammainc 不完全函数gammaln 函数的对数gca 获得当前轴句柄gcbo 获得正执行"回调"的对象句柄gcf 获得当前图对象句柄gco 获得当前对象句柄geomean 几何平均值get 获知对象属性getfield 获知构架数组的域getframe 获取影片的帧画面ginput 从图形窗获取数据global 定义全局变量gplot 依图论法则画图gradient 近似梯度gray 黑白灰度grid 画分格线griddata 规则化数据和曲面拟合gtext 由鼠标放置注释文字guide 启动图形用户界面交互设计工具H hharmmean 调和平均值help 在线帮助helpwin 交互式在线帮助helpdesk 打开超文本形式用户指南hex2dec 十六进制转换为十进制hex2num 十六进制转换为浮点数hidden 透视和消隐开关hilb Hilbert矩阵hist 频数计算或频数直方图histc 端点定位频数直方图histfit 带正态拟合的频数直方图hold 当前图上重画的切换开关horner 分解成嵌套形式hot 黑红黄白色图hsv 饱和色图I iif-else-elseif 条件分支结构ifft 离散Fourier反变换ifft2 二维离散Fourier反变换ifftn 高维离散Fourier反变换ifftshift 直流分量对中的谱的反操作ifourier Fourier反变换i, j 缺省的"虚单元"变量ilaplace Laplace反变换imag 复数虚部image 显示图象imagesc 显示亮度图象imfinfo 获取图形文件信息imread 从文件读取图象imwrite 把imwrite 把图象写成文件ind2sub 单下标转变为多下标inf 无穷大info MathWorks公司网点地址inline 构造内联函数对象inmem 列出内存中的函数名input 提示用户输入inputname 输入宗量名int 符号积分int2str 把整数数组转换为串数组interp1 一维插值interp2 二维插值interp3 三维插值interpn N维插值interpft 利用FFT插值intro Matlab自带的入门引导inv 求矩阵逆invhilb Hilbert矩阵的准确逆ipermute 广义反转置isa 检测是否给定类的对象ischar 若是字符串则为真isequal 若两数组相同则为真isempty 若是空阵则为真isfinite 若全部元素都有限则为真isfield 若是构架域则为真isglobal 若是全局变量则为真ishandle 若是图形句柄则为真ishold 若当前图形处于保留状态则为真isieee 若计算机执行IEEE规则则为真isinf 若是无穷数据则为真isletter 若是英文字母则为真islogical 若是逻辑数组则为真ismember 检查是否属于指定集isnan 若是非数则为真isnumeric 若是数值数组则为真isobject 若是对象则为真isprime 若是质数则为真isreal 若是实数则为真isspace 若是空格则为真issparse 若是稀疏矩阵则为真isstruct 若是构架则为真isstudent 若是Matlab学生版则为真iztrans 符号计算Z反变换J j , K kjacobian 符号计算中求Jacobian 矩阵jet 蓝头红尾饱和色jordan 符号计算中获得Jordan标准型keyboard 键盘获得控制权kron Kronecker乘法规则产生的数组L llaplace Laplace变换lasterr 显示最新出错信息lastwarn 显示最新警告信息leastsq 解非线性最小二乘问题(旧版)legend 图形图例lighting 照明模式line 创建线对象lines 采用plot 画线色linmod 获连续系统的线性化模型linmod2 获连续系统的线性化精良模型linspace 线性等分向量ln 矩阵自然对数load 从MAT文件读取变量log 自然对数log10 常用对数log2 底为2的对数loglog 双对数刻度图形logm 矩阵对数logspace 对数分度向量lookfor 按关键字搜索M文件lower 转换为小写字母lsqnonlin 解非线性最小二乘问题lu LU分解M mmad 平均绝对值偏差magic 魔方阵maple &nb, sp; 运作Maple格式指令mat2str 把数值数组转换成输入形态串数组material 材料反射模式max 找向量中最大元素mbuild 产生EXE文件编译环境的预设置指令mcc 创建MEX或EXE文件的编译指令mean 求向量元素的平均值median 求中位数menuedit 启动设计用户菜单的交互式编辑工具mesh 网线图meshz 垂帘网线图meshgrid 产生"格点"矩阵methods 获知对指定类定义的所有方法函数mex 产生MEX文件编译环境的预设置指令mfunlis 能被mfun计算的MAPLE经典函数列表mhelp 引出Maple的在线帮助min 找向量中最小元素mkdir 创建目录mkpp 逐段多项式数据的明晰化mod 模运算more 指令窗中内容的分页显示movie 放映影片动画moviein 影片帧画面的内存预置mtaylor 符号计算多变量Taylor级数展开N nndims 求数组维数NaN 非数(预定义)变量nargchk 输入宗量数验证nargin 函数输入宗量数nargout 函数输出宗量数ndgrid 产生高维格点矩阵newplot 准备新的缺省图、轴nextpow2 取最接近的较大2次幂nnz 矩阵的非零元素总数nonzeros 矩阵的非零元素norm 矩阵或向量范数normcdf 正态分布累计概率密度函数normest 估计矩阵2范数norminv 正态分布逆累计概率密度函数normpdf 正态分布概率密度函数normrnd 正态随机数发生器notebook 启动Matlab和Word的集成环境null 零空间num2str 把非整数数组转换为串numden 获取最小公分母和相应的分子表达式nzmax 指定存放非零元素所需内存O oode1 非Stiff 微分方程变步长解算器ode15s Stiff 微分方程变步长解算器ode23t 适度Stiff 微分方程解算器ode23tb Stiff 微分方程解算器ode45 非Stiff 微分方程变步长解算器odefile ODE 文件模板odeget 获知ODE 选项设置参数odephas2 ODE 输出函数的二维相平面图odephas3 ODE 输出函数的三维相空间图odeplot ODE 输出函数的时间轨迹图odeprint 在Matlab指令窗显示结果odeset 创建或改写ODE选项构架参数值ones 全1数组optimset 创建或改写优化泛函指令的选项参数值orient 设定图形的排放方式orth 值空间正交化pack 收集Matlab内存碎块扩大内存pagedlg 调出图形排版对话框patch 创建块对象path 设置Matlab搜索路径的指令pathtool 搜索路径管理器pause 暂停pcode 创建预解译P码文件pcolor 伪彩图peaks Matlab提供的典型三维曲面permute 广义转置pi (预定义变量)圆周率pie 二维饼图pie3 三维饼图pink 粉红色图矩阵pinv 伪逆plot 平面线图plot3 三维线图plotmatrix 矩阵的散点图plotyy 双纵坐标图poissinv 泊松分布逆累计概率分布函数poissrnd 泊松分布随机数发生器pol2cart 极或柱坐标变为直角坐标polar 极坐标图poly 矩阵的特征多项式、根集对应的多项式poly2str 以习惯方式显示多项式poly2sym 双精度多项式系数转变为向量符号多项式polyder 多项式导数polyfit 数据的多项式拟合polyval 计算多项式的值polyvalm 计算矩阵多项式pow2 2的幂ppval 计算分段多项式pretty 以习惯方式显示符号表达式print 打印图形或SIMULINK模型printsys 以习惯方式显示有理分式prism 光谱色图矩阵procread 向MAPLE输送计算程序profile 函数文件性能评估器propedit 图形对象属性编辑器pwd 显示当前工作目录quad 低阶法计算数值积分quad8 高阶法计算数值积分(QUADL)quit 推出Matlab 环境quiver 二维方向箭头图quiver3 三维方向箭头图R rrand 产生均匀分布随机数randn 产生正态分布随机数randperm 随机置换向量range 样本极差rank 矩阵的秩rats 有理输出rcond 矩阵倒条件数估计real 复数的实部reallog 在实数域内计算自然对数realpow 在实数域内计算乘方realsqrt 在实数域内计算平方根realmax 最大正浮点数realmin 最小正浮点数rectangle 画"长方框"rem 求余数repmat 铺放模块数组reshape 改变数组维数、大小residue 部分分式展开return 返回ribbon 把二维曲线画成三维彩带图rmfield 删去构架的域roots 求多项式的根rose 数扇形图rot90 矩阵旋转90度rotate 指定的原点和方向旋转rotate3d 启动三维图形视角的交互设置功能round 向最近整数圆整rref 简化矩阵为梯形形式rsf2csf 实数块对角阵转为复数特征值对角阵rsums Riemann和S ssave 把内存变量保存为文件scatter 散点图scatter3 三维散点图sec 正割sech 双曲正割semilogx X轴对数刻度坐标图semilogy Y轴对数刻度坐标图series 串联连接set 设置图形对象属性setfield 设置构架数组的域setstr 将ASCII码转换为字符的旧版指令sign 根据符号取值函数signum 符号计算中的符号取值函数sim 运行SIMULINK模型simget 获取SIMULINK模型设置的仿真参数simple 寻找最短形式的符号解simplify 符号计算中进行简化操作simset 对SIMULINK模型的仿真参数进行设置simulink 启动SIMULINK模块库浏览器sin 正弦sinh 双曲正弦size 矩阵的大小slice 立体切片图solve 求代数方程的符号解spalloc 为非零元素配置内存sparse 创建稀疏矩阵spconvert 把外部数据转换为稀疏矩阵spdiags 稀疏对角阵spfun 求非零元素的函数值sph2cart 球坐标变为直角坐标sphere 产生球面spinmap 色图彩色的周期变化spline 样条插值spones 用1置换非零元素sprandsym 稀疏随机对称阵sprank 结构秩spring 紫黄调春色图sprintf 把格式数据写成串spy 画稀疏结构图sqrt 平方根sqrtm 方根矩阵squeeze 删去大小为1的"孤维"sscanf 按指定格式读串stairs 阶梯图std 标准差stem 二维杆图step 阶跃响应指令str2double 串转换为双精度值str2mat 创建多行串数组str2num 串转换为数strcat 接成长串strcmp 串比较strjust 串对齐strmatch 搜索指定串strncmp 串中前若干字符比较strrep 串替换strtok 寻找第一间隔符前的内容struct 创建构架数组struct2cell 把构架转换为元胞数组strvcat 创建多行串数组sub2ind 多下标转换为单下标subexpr 通过子表达式重写符号对象subplot 创建子图subs 符号计算中的符号变量置换subspace 两子空间夹角sum 元素和summer 绿黄调夏色图superiorto 设定优先级surf 三维着色表面图surface 创建面对象surfc 带等位线的表面图surfl 带光照的三维表面图surfnorm 空间表面的法线svd 奇异值分解svds 求指定的若干奇异值switch-case-otherwise 多分支结构sym2poly 符号多项式转变为双精度多项式系数向量symmmd 对称最小度排序symrcm 反向Cuthill-McKee排序syms 创建多个符号对象T ttan 正切tanh 双曲正切taylortool 进行Taylor逼近分析的交互界面text 文字注释tf 创建传递函数对象tic 启动计时器title 图名toc 关闭计时器trapz 梯形法数值积分treelayout 展开树、林treeplot 画树图tril 下三角阵trim 求系统平衡点trimesh 不规则格点网线图trisurf 不规则格点表面图triu 上三角阵try-catch 控制流中的Try-catch结构type 显示M文件U uuicontextmenu 创建现场菜单uicontrol 创建用户控件uimenu 创建用户菜单unmkpp 逐段多项式数据的反明晰化unwrap 自然态相角upper 转换为大写字母V vvar 方差varargin 变长度输入宗量varargout 变长度输出宗量vectorize 使串表达式或内联函数适于数组运算ver 版本信息的获取view 三维图形的视角控制voronoi Voronoi多边形vpa 任意精度(符号类)数值W wwarning 显示警告信息what 列出当前目录上的文件whatsnew 显示Matlab中Readme文件的内容which 确定函数、文件的位置while 控制流中的While环结构white 全白色图矩阵whitebg 指定轴的背景色who 列出内存中的变量名whos 列出内存中变量的详细信息winter 蓝绿调冬色图。
关于MATLAB在复数方面的应用–MATLAB中文论坛

关于MATLAB在复数方面的应用–MATLAB中文论坛最近,看到有不少朋友问MATLAB在复数方面的应用问题,特此发个帖子,给大家分享点资料.matlab在复数中的应用1.复数的生成复数生成语句(其中theta为复数辐角的弧度值,r为复数的模)z=a+b*i,z=a+bi。
z=r*exp(i*theta),z=r*exp(thetai)。
2.创建复矩阵创建复矩阵的方法有两种。
(1)如同一般的矩阵一样以前面介绍的几种方式输入矩阵例如:A=[3+5*i,-2+3i,9*exp(i*6),23*exp(33i)](2)可将实、虚矩阵分开创建,再写成和的形式例如:re=rand(3,2)im=rand(3,2)com=re+i*im注意实、虚矩阵应大小相同。
3.复数的运算real(x)返回复数x的实部imag(x)返回复数x的虚部conj(x)返回复数x的共轭复数angle(x)返回复数x的辐角abs(x)返回复数x的模复数的乘除法运算由“*”和“/”实现。
ex.x=4*exp(pi/3i)y=4*exp(pi/(3i))z=4*exp(pi/3*i)>>x =2.0000 - 3.4641iy =2.0000 - 3.4641iz =2.0000 + 3.4641isprt(x)返回复数x的平方根值x^n返回复数x的n次幂exp(x)返回复数x的以e为底的指数值log(x)返回复数x的以e为底的对数值4.复数三角函数运算sin(x)返回复数x的正弦函数值,asin(x)返回复数x的反正弦值cos(x)返回复数x的余弦函数值,acos(x)返回复数x的反余弦值tan(x)返回复数x的正切函数值,atan(x)回复数x的反正切值cot(x)返回复数x的余切函数值,acot(x)返回复数x的反余切值sec(x)返回复数x的正割函数值,asec(x)返回复数x的反正割值csc(x)返回复数x的余割函数值,acsc(x)返回复数x的反余割值sinh(x)返回复数x的双曲正弦值,coth(x)返回复数x的双曲余切值cosh(x)返回复数x的双曲余弦值,sech(x)返回复数x的双曲正割值tanh(x)返回复数x的双曲正切值,sech(x)返回复数x的双曲余割值5.复数方程求根复数方程求根或实方程的复数根求解由函数solve实现ex.solve('x^3+1=0')或solve('x^3=-1')>>ans =[ -1][ 1/2-1/2*i*3^(1/2)][ 1/2+1/2*i*3^(1/2)]6.留数及其应用[R,P,K]=residue(B,A)s=2*pi*i*sum(R)----找出满足条件的R,求积分值ex1.求f(z)=(z+1)/(z^2-2z)的奇点处的留数[R,P,K]=residue([1,1],[1,-2,0])>>R =1.5000-0.5000P =2K =[]ex2.求积分,f(z)=z/(z^4-1),C为正向圆周abs(z)=2 [R,P,K]=residue([1,0],[1,0,0,0,-1])s=2*pi*i*sum(R)%此处均符合>>R =0.25000.2500-0.2500 + 0.0000i-0.2500 - 0.0000iP =-1.00001.00000.0000 + 1.0000i0.0000 - 1.0000iK =[]s =7.Taylor级数展开taylor(f) 返回函数的五次幂多项式近似taylor(f,n)返回n-1次幂多项式taylor(f,a)返回a点附近的幂多项式近似taylor(r,x)使用独立变量代替函数findsym(f)place变换及其逆变换(1)Laplace变换L=laplace(F)返回以默认独立变量T对符号函数F的Laplace变换。
MATLAB常用的基本数学函数

grid on; % 显示格线
我们可用subplot来同时画出数个小图形於同一个视窗之中:
subplot(2,2,1); plot(x, sin(x));
subplot(2,2,2); plot(x, cos(x));
subplot(2,2,3); plot(x, sinh(x));
一、 MATLAB常用的基本数学函数
abs(x):纯量的绝对值或向量的长度
angle(z):复数z的相角(Phase angle)
sqrt(x):开平方
real(z):复数z的实部
imag(z):复数z的虚部
conj(z):复数z的共轭复数
round(x):四舍五入至最近整数
当x<0时,sign(x)=-1;
当x=0时,sign(x)=0;
当x>0时,sign(x)=1。
rem(x,y):求x除以y的馀数
gcd(x,y):整数x和y的最大公因数
lcm(x,y):整数x和y的最小公倍数
exp(x):自然指数
pow2(x):2的指数
六、MATLAB的永久常数
i或j:基本虚数单位(即)
eps:系统的浮点(Floating-point)精确度
inf:无限大, 例如1/0
nan或NaN:非数值(Not a number),例如0/0
pi:圆周率 p(= 3.1415926...)
realmax:系统所能表示的最大数值
stem 针状图
fill 实心图
Hale Waihona Puke feather 羽毛图 compass 罗盘图
quiver 向量场图
matlab 实部的表示方法

matlab 实部的表示方法在MATLAB中处理复数数据时,实部与虚部是两个核心概念。
实部表示复数的实数部分,而虚部表示复数的虚数部分。
本文将详细介绍在MATLAB中表示实部的方法。
MATLAB(矩阵实验室)提供多种方式来表示和处理复数。
实部作为复数的一部分,可以通过以下几种方式来表示:1.直接赋值:在MATLAB中,可以直接给复数变量指定实部和虚部。
实部通过数值直接赋予,虚部通过字母“i”或“j”来表示。
例如:```matlabz = 3 + 4i; % 或者z = 3 + 4j;```在上述代码中,数字3是复数z的实部。
2.使用实部和虚部函数:MATLAB内置了实部和虚部函数`real`和`imag`,它们可以分别提取复数的实部和虚部。
```matlabz = 3 + 4i;realPart = real(z); % 获取实部```上述代码将变量`realPart`设置为3,即复数z的实部。
3.构造函数:如果你想创建一个只有实部的复数,可以使用`complex`函数,它允许你指定实部和虚部。
```matlabrealPart = 5;complexNumber = complex(realPart, 0); % 创建只有实部的复数```在这个例子中,我们给`complex`函数传递了实部5和虚部0,从而创建了一个实部为5的复数。
4.数组操作:当处理包含复数的数组时,可以应用数组运算来获取实部。
```matlabcomplexArray = [1+2i; 3+4i; 5+6i];realArray = real(complexArray); % 获取数组中每个复数的实部```在上面的例子中,`realArray`会包含第一行的1,第二行的3,以及第三行的5。
5.矩阵提取:如果你的实部是矩阵的一部分,可以使用矩阵索引来提取。
```matlabmatrix = [1+2i, 3+4i; 5+6i, 7+8i];realPartOfFirstRow = real(matrix(1, :)); % 获取第一行的实部```通过上述方法,你可以在MATLAB中方便地表示和操作复数的实部。
MATLAB常用的基本数学函数

一、MATLAB常用的基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
当x<0时,sign(x)=-1;当x=0时,sign(x)=0;当x>0时,sign(x)=1。
rem(x,y):求x除以y的馀数gcd(x,y):整数x和y的最大公因数lcm(x,y):整数x和y的最小公倍数exp(x):自然指数pow2(x):2的指数log(x):以e为底的对数,即自然对数或log2(x):以2为底的对数log10(x):以10为底的对数二、MATLAB常用的三角函数sin(x):正弦函数cos(x):馀弦函数tan(x):正切函数asin(x):反正弦函数acos(x):反馀弦函数atan(x):反正切函数atan2(x,y):四象限的反正切函数sinh(x):超越正弦函数cosh(x):超越馀弦函数tanh(x):超越正切函数asinh(x):反超越正弦函数acosh(x):反超越馀弦函数atanh(x):反超越正切函数三、变数也可用来存放向量或矩阵,并进行各种运算,如下例的列向量(Row vector)运算:x = [1 3 5 2];y = 2*x+1y =3 7 11 5四、变数命名的规则1.第一个字母必须是英文字母2.字母间不可留空格3.最多只能有19个字母,MATLAB会忽略多馀字母五、适用於向量的常用函数有:min(x): 向量x的元素的最小值max(x): 向量x的元素的最大值mean(x): 向量x的元素的平均值median(x): 向量x的元素的中位数std(x): 向量x的元素的标准差diff(x): 向量x的相邻元素的差sort(x): 对向量x的元素进行排序(Sorting)length(x): 向量x的元素个数norm(x): 向量x的欧氏(Euclidean)长度sum(x): 向量x的元素总和prod(x): 向量x的元素总乘积cumsum(x): 向量x的累计元素总和cumprod(x): 向量x的累计元素总乘积dot(x, y): 向量x和y的内积cross(x, y): 向量x和y的外积五、图像绘制:1、基本绘图函数plot 绘制二维线性图形和两个坐标轴plot3 绘制三维线性图形和两个坐标轴fplot 在制定区间绘制某函数的图像。
matlab解含复数的方程

matlab解含复数的方程【原创版】目录1.MATLAB 简介2.复数方程的表示方法3.使用 MATLAB 解复数方程4.常见问题与解决方法5.总结正文一、MATLAB 简介MATLAB(Matrix Laboratory)是一款强大的数学软件,广泛应用于科学计算、数据分析、可视化等领域。
它基于矩阵计算,可以高效地处理各种数学问题,是科研和工程技术领域的重要工具。
二、复数方程的表示方法复数方程是指包含复数的等式,通常用 a+bi 的形式表示复数,其中a 和 b 是实数,i 是虚数单位(满足 i^2=-1)。
复数方程在科学研究和工程技术中有着广泛的应用,例如,电路分析、信号处理等领域。
三、使用 MATLAB 解复数方程MATLAB 提供了丰富的函数和命令用于解决复数方程。
以下是使用MATLAB 解复数方程的基本步骤:1.创建复数方程:在 MATLAB 中,可以使用符号运算直接创建复数方程。
例如,创建一个复数方程:2+3i=5-2i。
2.求解复数方程:MATLAB 提供了`solve`函数用于求解复数方程。
例如,对上述复数方程进行求解:`x = solve(2+3i=5-2i)`。
3.显示解:使用`disp`函数可以显示求解结果。
例如,`disp(x)`。
四、常见问题与解决方法在使用 MATLAB 解复数方程时,可能会遇到一些问题。
以下是一些常见问题及其解决方法:1.复数方程中包含复数函数:如果复数方程中包含复数函数,可以使用 MATLAB 的符号运算功能进行求解。
2.复数方程的系数为复数:MATLAB 可以处理复数系数的复数方程,但在求解过程中可能需要进行一些转换。
3.复数方程的解为复数:MATLAB 可以求解复数方程的复数解,但需要注意在显示解时使用正确的格式。
五、总结MATLAB 作为一款强大的数学软件,可以方便地解决复数方程问题。
通过创建复数方程、求解方程和显示解等步骤,可以有效地处理复数方程问题。
MATLAB中关于复数的相关函数
Isstr
参量为一个字符串,返回真值
Isstudent
MATLAB为学生版,返回真值
Isunix
计算机为UNIX系统,返回真值
函数句柄的操作函数
函数名称
函数功能
Functions(funhandle)
返回一个结构体,存储了函数的名称、函数类型(simple或overloaded),以及函数M文件的位置
Isempty
参量有限,返回真值
Isglobal
参量为全局变量,返回真值
Ishold
当前绘图保持状态是“ON”,返回真值
Isieee
计算机执行IEEE算术运算,返回真值
Isinf
元素无穷大,返回真值
Isletter
元素为字母,返回真值
Isnan
元素为不定值,返回真值
Isreal
参量无虚部,返回真值
Isspace
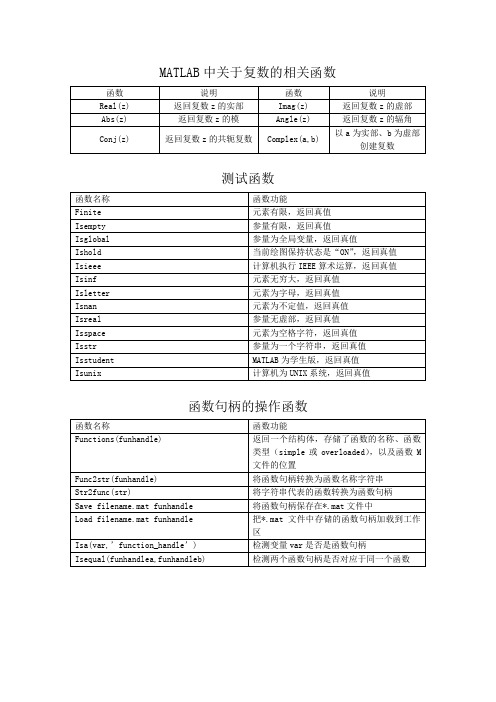
MATLAB中关于复数的相关函数
函数
说明
函数
说明
Real(z)
返回复数z的实部
Imag(z)
返回复数z的虚部
Abs(z)
返回复数z的模
Angle(z)
返回复数z的辐角
Conj(z)
返回复数z的共轭复数
Complex(a,b)
以a为实部、b为虚部创建复数
测试函数
函数名称
函数功能
Finite
元素有限,返回真值
Isa(var,’function_handle’)
检测变量var是否是函数句柄
Isequal(funhandlea,funhandleb)
检测两个函数句柄是否对应于同一个函数
Func2str(funhandle)
matlab解含复数的方程

matlab解含复数的方程
用MATLAB求解复数方程
MATLAB是一种用于数值计算和科学工程的高级编程语言和环境。
它提供了许多功能强大的工具和函数,可以用于解决各种数学问题,包括求解复数方程。
复数方程是指方程中包含复数的方程。
一般来说,复数方程可以表示为a+bi=0,其中a和b分别表示实部和虚部,i表示虚数单位。
为了求解复数方程,我们可以使用MATLAB中的solve函数。
该函数可以用来解决各种类型的方程,包括复数方程。
下面是一个使用MATLAB求解复数方程的示例:
```matlab
% 求解方程 z^2 - 4 = 0
syms z
eqn = z^2 - 4 == 0;
sol = solve(eqn, z);
% 输出解
disp(sol);
```
在上面的示例中,我们定义了一个复数方程z^2 - 4 = 0,并使用
solve函数求解该方程。
最后,我们使用disp函数输出解。
运行上述代码,我们可以得到以下结果:
```
-2
2
```
这意味着复数方程z^2 - 4 = 0的解为-2和2。
使用MATLAB求解复数方程非常简单和方便。
只需定义方程,并使用solve函数即可得到解。
matlab解复数方程组

matlab解复数方程组
在MATLAB中,解复数方程组的过程需要使用到符号计算工具箱,如sym、solve等。
以下是一个示例,演示了如何使用MATLAB符号计算工具箱来解复数方程组。
1. 首先,确保已经安装了MATLAB的符号计算工具箱。
可以通过以下命令安装:
```
install_symbolab -desktop
```
2. 创建一个新的MATLAB脚本,并添加以下代码:
```matlab
% 导入符号计算工具箱
syms a b c d e f g h;
% 定义符号变量
x = solve('a*x^2 + b*x + c = 0', 'x = x');
y = solve('d*y^2 + e*y + f = 0', 'y = y');
z = solve('g*z^2 + h*z + i = 0', 'z = z');
% 输出结果
disp(x);
disp(y);
disp(z);
```
3. 运行脚本,将输出解复数方程组的结果。
在这个示例中,我们假设有以下复数方程组:```
a*x^2 + b*x + c = 0
d*y^2 + e*y + f = 0
g*z^2 + h*z + i = 0
```
这个示例仅用于演示MATLAB解复数方程组的基本方法。
在实际应用中,可能需要处理更复杂的方程组。
MATLAB可视化方法和技巧13复数的计算和图示

复数的计算和图示表3 MATLAB关于复数运算的函数{范例3_1}复数的加减法设有两个复数z1 = 1 + 2i和z2 = 4 + 3i,其中i是虚数单位求两个复数的和z1 + z2和差z2–z1。
[解析]复数有三种表示形式(1)代数式z = x + i y(3_1_1)(2)三角式z = r(cosθ + isinθ) (3_1_2) 其中r是复数的模,θ是复角。
代数式与三角式的换算关系是r=arctan yθ(3_1_3)xx = r cosθ,y = r sinθ(3_1_4)(3)指数式z = r e iθ(3_1_5) 其中利用了欧拉公式e iθ= cosθ + isinθ(3_1_6)设有两个复数z1 = x1 + i y1,z2 = x2 + i y2(3_1_7) 复数加法是z= z1 + z2 = (x1 + x2) + i(y1 + y2) (3_1_8) 复数减法是z= z1 - z2 = (x1 - x2) + i(y1 - y2) (3_1_9) [程序]P3_1plus.m如下。
%复数的加减法clear %清除变量z1=1+2i; %第1个复数(1)x1=real(z1); %取第1个复数的实部(2)y1=imag(z1); %取第1个复数的虚部(2)x2=4; %第2个复数的实部y2=3; %第2个复数的虚部z2=x2+i*y2; %形成第2个复数(3)z=z1+z2; %两复数之和(4)x=real(z); %取复数的实部y=imag(z); %取复数的虚部figure %创建图形窗口quiver(0,0,x1,y1,0) %在复平面画第1个复数(5)hold on%保持图像quiver(0,0,x2,y2,0) %画第2个复数(5)quiver(0,0,x,y,0) %画复数之和(5)plot([x1,x],[y1,y],'--') %画虚线(6)plot([x2,x],[y2,y],'g--') %画虚线(6)axis equal%使坐标刻度相等(7)grid on%加网格r=abs(z); %求模(8)theta=angle(z)*180/pi; %求复角(9)text(0,0,num2str(theta),'FontSize',16) %显示复角(10)text(x,y,num2str(r),'FontSize',16) %显示模(10)title('两复数之和','FontSize',16) %显示标题z=z2-z1; %两复数之差x=real(z); %取复数的实部y=imag(z); %取复数的虚部figure %创建图形窗口quiver(0,0,x1,y1,0) %在复平面画第1个复数(11)hold on%保持图像quiver(0,0,x2,y2,0) %画第2个复数quiver(x1,y1,x,y,0) %画复数之差axis equal%使坐标刻度相等grid on%加网格title('两复数之差','FontSize',16) %标题[说明](1)变量i表示虚数单位,可用于形成复数。
matlab求复数的相角函数

matlab求复数的相角函数复数的相角函数是指复数在复平面上的角度表示。
在数学中,复数可以用实部和虚部表示,即z=a+bi,其中a和b分别表示实部和虚部。
而相角函数则是指求解复数z的角度的函数。
在Matlab中,可以使用函数angle(z)来计算复数z的相角。
这个函数的返回值是一个角度值,表示复数z相对于正实轴的角度。
为了更好地理解复数的相角函数,我们可以通过一个具体的例子来说明。
假设有一个复数z=3+4i,我们想要求解它的相角。
首先,我们可以使用Matlab中的angle函数来计算,代码如下:z = 3 + 4i;theta = angle(z);运行这段代码后,我们可以得到复数z的相角theta的值。
在本例中,theta的值为0.9273,表示复数z与正实轴的夹角为约53.13度。
除了使用angle函数,Matlab还提供了其他方法来计算复数的相角。
例如,可以使用atan2函数来计算复数z的相角,代码如下:z = 3 + 4i;theta = atan2(imag(z), real(z));这里,imag(z)表示复数z的虚部,real(z)表示复数z的实部。
通过计算虚部与实部的比值,再使用反正切函数,我们可以得到复数z的相角。
在实际应用中,复数的相角函数具有广泛的应用。
例如,在信号处理中,可以使用相角函数来计算信号的相位信息。
在控制系统中,相角函数可以用来分析系统的稳定性和性能。
总结起来,复数的相角函数是指求解复数在复平面上的角度表示的函数。
在Matlab中,可以使用angle函数或者atan2函数来计算复数的相角。
复数的相角函数在数学和工程领域具有重要的应用价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、用 MATLAB 计算复数方程的根及极限
例 6 求方程 z 8 0 的根. >> solve('z^3+8=0') ans = -2 1+i*3^(1/2) 1-i*3^(1/2) 例 8 对复变函数 f ( z ) z , 取 z 0 1 2i syms z z0 >> f=z^2; >> z0=1+2i z0 = 1.0000 + 2.0000i >> limit(f,z,z0) ans = -3+4*i
2
3
求极限 lim f ( z ) .
z z0
3
>> conj([z1,z2,z3,z4]) ans = 0.2308 + 0.1538i 例 4 >> z=log(-i) z = 0 - 1.5708i >> z=log(5+7i)
2
1.5000 + 2.5000i -3ቤተ መጻሕፍቲ ባይዱ5000 +13.0000i
1.0000 + 3.0000i 1.2.4
实验一
用 MATLAB 计算复数的实部、虚部、模、
辐角,共轭复数、简单复数方程根及复数的极限
一、用 MATLAB 计算复数的实部、虚部、模、辐角,共轭复数 1、在 MATLAB 中,复数单位为 i=j=sqrt(-1),其值显示为 0+1.0000i 复数可由 z=a+b*i 生成,也可简写成 z=a+bi z=r*exp(i*theta) 或 z=r*exp(theta i) 2、复数的实部与虚部的提取可由函数 real 和 imag 实现 3、复数的模和幅角的求解由功能函数 abs 和 angle 实现 4、复数的共轭可由函数 conj 实现 5、复数的乘除法通过“*”和“/”实现 注意:y 和 y1 的不同,MATLAB 中(„)/5i 和(„)/5*i 不相等。 6、 复数的平方根运算由函数 sprt 实现 7、复数的幂运算的形式为 x^n 8、复数的指数和对数运算分别由函数 exp 和 log 实现
例 3 求下列复数的实部、虚部、共轭复数、模与辐角 (1)
1 1 3i (3 4i)(2 5i) , (2) , (3) , (4) i 8 4i 21 i 3 2i i 1 i 2i
由 MATLAB 输入如下 >> z1=1/(3+2i);z2=1/i-3i/(1-i);z3=(3+4i)*(2-5i)/(2i);z4=i^8-4*i^21+i; >> real([z1,z2,z3,z4]) ans = 0.2308 1.5000 -3.5000 1.0000
>> imag([z1,z2,z3,z4]) ans = -0.1538 -2.5000 -13.0000 -3.0000
>> abs([z1,z2,z3,z4]) ans = 0.2774 2.9155 13.4629 3.1623
>> angle([z1,z2,z3,z4]) ans = -0.5880 -1.0304 -1.8338 -1.2490
z = 2.1520 + 0.9505i
二、复数的三角函数运算同实数的三角函数运算
三角函数运算函数为 sin(x),cos(x),tan(x),cot(x),sec(x),csc(x),sinh(x),cosh(x),tanh(x),coth(x),sech( x),csch(x) 反三角函数运算函数为 asin(x),acos(x),atan(x),acot(x),asec(x),acsc(x), 例 5 求复数 3+4i 的三角函数 >> z=3+4i; >> sin(z) ans = 3.8537 -27.0168i
例 1:求复数 12 2i 的实部、虚部、模、共轭复数和辐角 >> z=-sqrt(12)-2i; >> x=real(z) x = -3.4641 >> y=imag(z) y = -2 >> abs(z) ans = 4.0000 >> conj(z) ans =
1
-3.4641 + 2.0000i >> angle(z) ans = -2.6180 例 2 imag([5-8j,3+4j]) ans = -8 4
