第15届中环杯三年级决赛

合集下载

15届中环杯三年级决赛试题

第十五届“中环杯”小学生思维能力训练活动
三年级决赛
得分:
三尧动手动脑题:(每题10分,共20分)
13.5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米。

求:单个长方形的面积。

14.D 老师将分别写有1、2、……、13这13个数字的13张牌按从小到大的顺序顺时针放在一个圆周上,开始的时候所有牌都是牌面朝上,每次翻动可以将一张牌翻成牌面朝下(一旦变成牌面朝下,这张牌就不能再翻动了)。

D 老师翻牌的规则为:若一张牌面朝上的牌上数字为A ,并且与这张牌相隔2张的牌也是牌面朝上的,那么D 老师就可以翻动写有数字A 的这张牌。

比如:只要写有数字9或者2的牌是牌面朝上,那么D 老师就可以翻动写有数字12的牌(当然,前提是写有数字12的牌还是牌面朝上的)。

最后,只要D 老师将12张牌翻成牌面朝下,那么就算D 老师成功了。

为了获得成功,D 老师有多少种不同的翻牌顺序
?
三年级第3页三年级第4
页答案详解，敬请关注唯课数学公众号vclassedu。

2015年第十五届“中环杯”小学生思维能力训练活动初赛试卷(五年级答案及解析

2015年第十五届“中环杯”小学生思维能力训练活动初赛试卷（五年级）-学生用卷一、填空题共20题，共100 分1、已知，其中，是两个互质的正整数，则。

2、老师家里有五个烟囱，这五个烟囱正好从矮到高排成一排，相邻两个烟囱之间的高度差为厘米，其中最高的烟囱又正好等于最矮的两个烟囱的高度之和，则五个烟囱的高度之和是厘米。

3、已知，其中、、、是四个正整数，请你写出满足条件的一个乘法算式：。

4、一个长方体的长、宽分别为厘米、厘米，其体积的数值与表面积的数值相等，则它的高为厘米。

5、一次中环杯比赛，满分为分，参赛学生中，最高分为分，最低分为分（所有的分数都是整数），一共有个学生参加，那么至少有个学生的分数相同。

6、对个蛋黄月饼进行打包，一共有两种打包规格：大包装里每包有个月饼，小包装里每包有个月饼。

要求不能剩下月饼，那么一共打了个包。

7、小明和小红在米的环形跑道上跑步，两人从同一起点同时出发，朝相反方向跑，第一次和第二次相遇时间间隔秒，已知小红的速度比小明慢米/秒，则小明的速度为米/秒。

8、、、的因数个数相同，那么在具有这样性质的三个连续自然数、、中，的最小值是。

9、图中的正三角形与正六边形的周长相等，已知正三角形的面积是，则正六边形的面积为。

10、甲、乙、丙在猜一个两位数。

甲说：“它的因数个数为偶数，而且它比大。

”乙说：“它是奇数，而且它比大。

”丙说：“它是偶数，而且它比大。

”如果他们三个人每个人都只说对了一半，那么这个数是。

11、如图，正方形和正方形，他们的四对边互相平行，连接并延长交于点。

已知，三角形面积，三角形，则的长度为。

12、将个桃子分给若干个孩子，这些孩子得到的桃子数量是一些连续的正整数，则获得桃子数量最多的那个孩子最多可以得到个桃子。

13、定义，比如，若（其中为正整数，且）是完全平方数，比如时，，就是一个完全平方数，则所有满足条件的的和为。

14、小明将若干枚棋子放入如图所示的方格的小正方形内，每个小正方形内可以不放棋子，也可以放等于或多于枚的棋子。

二年级上册数学试题-第十五届中环杯初赛详解全国通用版(含答案)PDF版

第十五届“1.计算：302928--答案：0考点：巧算（分组法）解析：按符号“＋－－＋为0。

2.两个奥特曼一起打怪兽可以攻击12次，另一个每那么_________分钟后可答案：5考点：加减乘除应用解析：两个奥特曼一起，100÷20＝5（分钟）3.观察前两个天平，衡。

A. B.答案：D考点：等量代换解析：1圆＝2五角星，个五角星。

4.小胖、小丁丁、小亚游乐场玩。

游乐场门票元；10人及以上可以买答案：800考点：付钱策略解析：若家长全买成人票（元）；若所有人全买团体票每位少付了30元，儿童每“中环杯”小学生思维能力训练活动二年级选拔赛272625242322212019++--++--+=－＋”四个为一组进行分组，每组结果为0，打怪兽，怪兽可以承受100次攻击。

其中一个奥一个每分钟可以攻击8次。

如果两个奥特曼一起钟后可以将怪兽打倒。

，每分钟可攻击12＋8＝20（次）。

那么，第3个天平的“？”处应放上_________，才能C. D.，所以1菱形＝6－2＝4五角星，答案中的小亚、小巧四个家庭共8个家长和4个小朋友场门票的收费标准是：成人票每人100元；儿童可以买团体票，每人70。

他们最少要花______人票，小朋友全买儿童票，则需：100×8＋团体票，则需70×（8＋4）＝840（元），此时儿童每位多付了20元。

要使花的钱最少，则成练活动，所以最后结果一个奥特曼每分钟曼一起开始攻击，，一共需要攻击才能使得天平平中的D 相当于4朋友，他们结伴去儿童票每人50____元购买门票。

50×4＝1000此时相当于成人则成人尽可能买团体票，儿童尽可能买儿童人（8个成人＋2个儿童）＋50×2＝800（元）5.到了冰雪宫殿开放的日梯，爱丽丝走20级台阶180秒，正好走完所有阶答案：30级考点：乘除法应用解析：20级台阶用了秒可以走：180÷6＝30（6.右图中的每个小正方形米。

第十五届中环杯中小学生思维能力训练活动五年级决赛试卷及解析

第15届中环杯决赛试题解析（五年级）一、填空题A （本大题共8小题，每题6分，共48分）：1. 计算：1331649113157112015157++⨯+⨯=++________. 【答案】2 【解答】133164911315711201515731313199315711201515711311130571151331157231231++⨯+⨯+++++=⨯++⎛⎫⨯++ ⎪⎝⎭=⨯⨯⨯++=⨯= 2. 老师布置了一些数学回家作业。

由于小明基础不好，所以小明收到的题目数量比小王收到的题目数量多20道。

若两人收到的题目数量之比为4:3，则小明回家需要完成________道题目。

【答案】80【解答】设小明收到了4x 道题目，则小王收到了3x 道题目，根据题意432020x x x -=⇒=，所以小明需要完成442080x =⨯=道题目。

3. 如图，正八边形的边长为1，将其进行下图的切割，切割后灰色部分面积与斜线部分面积之差为________（大减小）。

【答案】14【解答】如下图，,A B 与,C D 抵消，剩下的中间的正方形可以切割为四个等腰直角三角形，其中三个与灰色部分抵消，留下的一个面积就是14【说明】考察等腰直角三角形用斜边表示的面积公式4. 在一组英文字母串中，第一个字母串1a A =、第二个字母串2a B =，之后每个字母串()3n a n ≥都是由1n a -后面跟着2n a -的反转构成的。

比如321a a a BA ==（我们用i a 表示i a 的反转，就是从右往左读这个字母串得到的结果，比如ABB BBA =、AABA ABAA =），432a a a BAB ==，543a a a BABAB ==，654a a a BABABBAB ==。

那么，这组字母串的前1000个中，有________个是回文字母串（所谓的回文字母串，就是指从左往右读与从右往左读相同，比如ABA 、AABAA ）【答案】667【解答】通过尝试，我们发现只有3a 、6a 、9a 、、999a 不是回文字母串，别的都是，那么可以直接得到答案：一共只有333个非回文字母串，剩下的1000333667-=个都是回文字母串。

第15届中环杯七年级决赛

3 5z 改为 3 54 并不会影响“不能构成倍数”这个关系。由于 20 31 54 已经被选出了，那么剩下的 2a 3b 54 （ a,b 不同时为 0）中只能再选一个 21 30 54 （2 的指数增加，则 3 的指数要减小），也就是说剩下的 18 个数的 z 都从 0、1、2、3 中选。与前面步骤相同，可以推出矛盾；
第 15 届中环杯决赛试题解析（七年级）一、填空题（本大题共 10 小题，每题 6 分，共 60 分）：
1. 已知 A 2 4 6 2014 1 3 5 2013 ，将 A 表示为最简分数 m ，则
1 3 5 2013 2 4 6 2014
“不能构成倍数”这个关系）
综上所述，如果要使得最后的“中环数”数量大于等于 20，就不能选 0,0 、 0,1 、 1,0 、 4,3 、 3, 4 、 4,4 。由于一共只有 25 种选择，不选这 6 种，最多也就 19 种
了
二、动手动脑（本大题共 4 小题，每题 10 分，共 40 分）：
11. 已知 a,b,c, x, y, z 都是非零实数，满足 x2 y z y2 x z z2 x y xyz 1，求证：
【解答】我们先研究一下，如果题目的条件是 2x3y 0 x, y 4 ，那么可以选几个出
来。如果选出 2a3b 与 2c3d ，显然 a c ，否则 b, d 总有一个大小关系，会使得其中一个
是另一个的倍数。不妨设 a c ，此时我们必须有 b d ，否则 2a3b | 2c3d 。将所有选出
（2）如果最下面那行不是间隔染色（一共 210 2 种染色方法），如下左图所示，则倒数第 2 行只有唯一的染色方法，如下右图所示。此时倒数第 2 行也不符合间隔染色的情况，那么倒数第 3 行有一种选择；依次类推，这种情况下一共有 210 2 种染色方法；

第十五届“中环杯”初赛五年级试题解析

第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++，其中 m,，n 是两个互质的正整数，则10______m n +=。

【考点】分数计算【答案】110 分析：2016910920110162020=-=⨯+=原式。

2、D 老师家里有五个烟囱，这五个烟囱正好从矮到高排成一排，相邻两个烟囱之间的高度差为 2 厘米，其中最高的烟囱又正好等于最矮的两个烟囱的高度之和，则五个烟囱的高度之和是________厘米。

【考点】等差数列，方程【答案】50分析：设这五个烟囱分别为 x-4，x-2，x ，x+2，x+4，则 x+4=x-2+x-4，x=10，和为 5x=50。

3、已知()()22332014a b c d =+⨯-，其中 a 、b 、c 、d 是四个正整数，请你写出满足条件的一个乘法算式：___________。

【考点】数的拆分，分解质因数【答案】答案不唯一分析：2014=1×2014=2×1007=19×106=38×53()()22335932+⨯-4、一个长方体的长、宽分别为 20 厘米、15 厘米，其体积的数值与表面积的数值相等，则它的高为______厘米（答案写为假分数）。

【考点】立体几何，方程【答案】6023分析：设高为 h ，则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=，则。

5、一次中环杯比赛，满分为 100 分，参赛学生中，最高分为 83 分，最低分为 30 分（所有的分数都是整数），一共有 8000 个学生参加，那么至少有_____个学生的分数相同。

【考点】抽屉原理【答案】149分析：833015480005414881481149-+=÷=+=，…,。

6、对 35个蛋黄月饼进行打包，一共有两种打包规格：大包袋里每包有9 个月饼，小包装里每包有 4个月饼。

第十三届“中环杯”小学生思维能力训练活动三年级决赛答案版

第十三届“中环杯”小学生思维能力训练活动三年级决赛一、填空题（5’×10=50’）1.计算：12345+23451+34512+45123+51234=（166665）。

速算巧算：原式=（1+2+3+4+5）×11111=1666652.水果店原来有156箱苹果和84箱橘子。

苹果和桔子各卖出相等的箱数后，剩下的苹果箱数比橘子箱数多2倍。

苹果和桔子各卖出（48）箱。

和差倍：156-84=72,72÷2=364,84-36=483.在一次学科测试中，小芳的语文、数学、英语、科学4门学科的平均分是88分，前2门的平均分是93分，后3门的平均分为87分，小芳的英语测试成绩是（95）分。

（本题英语成绩无法确定，疑为求数学的成绩）平均数：93×2=186,87×3=261，88×4=352,186+261-352=954.星期天，小军帮助妈妈做一些家务。

各项家务花的时间为：叠被子3分钟，洗碗8分钟，用洗衣机洗衣服30分钟，晾衣服5分钟，拖地板10分钟，削土豆皮12分钟。

经过合理安排，小军至少要用（38）分钟才能完成这些家务。

统筹规划：洗衣机一边洗衣服，小军一边完成其他任务，3+8+5+10+12=385.图中共有16个方格，要把A、B、C、D四个不同的棋子放在四个不同的方格里，并使每行，每列只能出现一个棋子。

共有（576）种不同的放法。

棋盘问题：4！×4！=576或16×9×4×1=5766.如图，正方体的每个角上有一个小圆圈。

请你把2至9这8个数分别填入小圆圈内，使正方体6个面每一面上的4个数之和都相等。

数阵图：2+3+...+9=44，44÷2=22，22=2+3+8+9=2+4+7+9=2+5+7+8=2+5+6+9，结果如图7.如图是某地区所有街道的平面图。

甲、乙两人同时分别从A、B出发，以相同的速度行进。

小晨精品2015第十五届中环杯三年级决赛解析【XCJP】

第15 届中环杯决赛试题解析（三年级）一、填空题A （本大题共8小题，每题6分，共48分）：1. 计算：2513 2 15137 ________.【答案】2015【解答】2513 2 1513 751310 513 2151310 2151331 20152. 在一场上海队与北京队的篮球比赛中，姚明得到了30 分，带领上海队以10 分的优势战胜了北京队。

上海队与北京队的总得分比姚明得分的5 倍少10 分，那么上海队获得______分【答案】75分【解答】根据题意，上海队与北京队的总得分为30510 140 分，而上海队减去北京队的得分为10 分，根据和差问题，我们有：上海队得了140 10 2 75分3. 一个数只包含两种数字：3或者4 ，而且3或者4 都至少出现一个。

这个数既是3的倍数，又是4 的倍数。

这样的数最小为______.【答案】3444【解答】为了使得它是4 的倍数，最后两位只能是44 。

如果只有两个数字4 ，这个数无法成为3的倍数，所以很容易得到其最小值为34444. 我们有27个111的小立方体，将其拼成一个333的大立方体，其中的一些小立方体的某些面被涂成了灰色，最后拼成的大立方体如下图所示。

那么，六个面都是白色的小立方体最多有________个【答案】15【解答】我们可以数一下，发现含有灰色面的小立方体有12 个，而一共有27个小立方体，所以六个面都是白色的小立方体最多有27 12 15个5. 如图，一个大三角形ABC 被三条线段分成了七部分，其中四部分是三角形，另外三部分是四边形。

三个四边形的周长之和为25厘米，四个三角形的周长之和为20厘米，三角形ABC 的周长为19 厘米。

那么AD BE CF ______厘米AFEB D C【答案】13【解答】如果我们将三个四边形的周长之和与四个三角形的周长之和相加，那么中间的线段都被加了两次。

比如下图中的GH ，它既是四边形GFBH 的一条边、又是的一条边。

小学奥数习题版三年级其他乘车坐船学生版

知识要点乘车1. 四年级共有三个班级，其中四（1）班有48人，四年级（2）班有47人。

如果四年级组织一次秋游，要求每个班级有1个带队老师。

现在要用载客数为50人的大巴士3辆，且发现总共有3个空位。

请问四（3）班有多少人？在日常生活中，人们要外出学习、工作或活动，就要乘车或坐船。

在城市里，一个人外出乘车，有的一天中要乘几次车。

在乘车、坐船活动中，怎样来合理安排座位，我们常常会遇到一系列这样的问题。

解决这一类实际问题，关键是要从生活实际出发，弄清题意，从条件或问题入手，进行合乎情理的分析推理，从而找到解决问题的方法。

最后求出的结果，要检查是否符合实际。

1. 乘车问题关键在于确定车子的实际载客量以及实际乘客数量，也就是有无司机或者领队人等。

2. 坐船问题的解题关键同样在于确定船的实际一次运客量，也就是判断船上是否有船夫：（1）如果有船夫，那么所有人可根据船的载客量平均分配计算乘船次数；（2）如果没有船夫，那么需要先挑出一人做船夫往返划船，因此最后一次最多能运的人数比前面几次最多能运的人数多1人（被挑出来的船夫）。

（3）解决坐船问题还需要注意“运送次数”与“渡河次数”的区别。

3. 碰到“最划算”问题时可用列表的方法来计算得出最佳方案。

4. 另外常用到行程的基本公式：路程=速度⨯时间。

乘车坐船2.二(1)班和二(2)班的同学坐两辆大巴汽车去参观科技博物馆，每车（除司机）各坐了52人。

两班男同学共有50人，带队老师每车有1名．那么两班女同学共多少人？3.旅行社组织一个团去三峡旅游，共包了两种不同型号的轮船，大轮船共2艘，每艘可载客坐30人，快艇共5艘，每艘可载客坐7人。

最后大轮船和快艇还剩5个座位未坐满。

这个旅行团一共有多少人？4.某校三年级一共三个班，三（1）班有45人，三（2）班有51人，三（3）班有49人。

如果三年级组织春游活动，并要求每个班级需要有2名带队老师，请问需要载客数为52的大巴士多少辆？5.丁丁到外公家来回乘车只需要18分钟。

2016年中环杯获奖名单（三年级组）

准考证号姓名奖项0130006⾦洛⽻⼀等奖0130056佟松翼⼀等奖0130069杨元睿⼀等奖0130072纪皓天⼀等奖0130099祝明睿⼀等奖0130137李昊扬⼀等奖0130140周睿阳⼀等奖0130185王旭扬⼀等奖0130190徐⼦晨⼀等奖0130254黄⼤卫⼀等奖0130315张成浩⼀等奖0130361诸哲⾔⼀等奖0130384张书笑⼀等奖0130394卫星⼀等奖0130473杨镇⼀等奖0130523陈⽅旭⼀等奖0130536阮欣妍⼀等奖0130547贾丁⼀等奖0130548王淇瞻⼀等奖0130550孟钰轩⼀等奖0130647姚越⼀等奖0130706⾦鑫渝⼀等奖0130708陈栩越⼀等奖0130721陆宇⼀等奖0130766陈修毅⼀等奖0130769张在贺⼀等奖0130787陈奕鑫⼀等奖0130788郭⽂赋⼀等奖0130877吴星宇⼀等奖0130907黄崇瑞⼀等奖0130926周昀朗⼀等奖0430026朱⼀青⼀等奖0430069蒋昕灏⼀等奖0430071徐邦杰⼀等奖0430108许皓然⼀等奖0430113邓瑞宁⼀等奖0430120黄⾸鑫⼀等奖0530042林光濠⼀等奖0530227潘嘉诚⼀等奖1230004孟浩然⼀等奖1630051杨⼦⽥⼀等奖1630052刘棋騵⼀等奖2930025吕锐⼀等奖2930026张黛凝⼀等奖2930059曹鸿⽣⼀等奖0130004李尚荣⼆等奖0130015舒胤嘉⼆等奖0130024庄⼦涵⼆等奖0130029李嘉安⼆等奖0130036陈⼀臻⼆等奖0130065薛睿涵⼆等奖0130066季庄喆⼆等奖0130074王舒涵⼆等奖0130079王淳稷⼆等奖0130157黄瀚卿⼆等奖0130165黄⽂远⼆等奖0130222周路耘⼆等奖0130229黄静轩⼆等奖0130242⽂韬⼆等奖0130243汪悠旎⼆等奖0130245郁浩⽂⼆等奖0130257孔韵颖⼆等奖0130298吴翔宇⼆等奖0130321何熠菲⼆等奖0130322蔡晟杰⼆等奖0130327袁弈⼆等奖0130333王⼤为⼆等奖0130349全佳乐⼆等奖0130366盛昱皓⼆等奖0130399祁翊博⼆等奖0130427傅予珩⼆等奖0130433瞿⼒扬⼆等奖0130439⽯昊轩⼆等奖0130478宋⽞烨⼆等奖0130491马煜轩⼆等奖0130508朱叶蓁⼆等奖0130513胡⽴杨⼆等奖0130521王志涵⼆等奖0130522孙诚⼆等奖0130526秦嘉牧⼆等奖0130527管毅⼆等奖0130553郭⼀诺⼆等奖0130556周睿康⼆等奖0130563张皓然⼆等奖0130567邓乐⾔⼆等奖0130576王静⾬⼆等奖0130584唐笑添⼆等奖0130585周骐⼆等奖0130598虞诗⽻⼆等奖0130614罗傲然⼆等奖0130618庄鲲涵⼆等奖0130641陈博宇⼆等奖0130642沈奕轩⼆等奖0130646汤逸悠⼆等奖0130650亓⾟瑞⼆等奖0130659⽥知闲⼆等奖0130663王陈哲⼆等奖0130670张楚然⼆等奖0130680朱汶宣⼆等奖0130693杨昀铮⼆等奖0130695王乐洋⼆等奖0130698王乐天⼆等奖0130704张乐俊⼆等奖0130719阙开城⼆等奖0130727胡恒嘉⼆等奖0130728张廷瑞⼆等奖0130729忻运⼆等奖0130731王谦雪⼆等奖0130740严皓天⼆等奖0130746褚⼦萱⼆等奖0130807余凯宣⼆等奖0130810钱晨灏⼆等奖0130843朱⼦川⼆等奖0130868陈思充⼆等奖0130869范艺洋⼆等奖0130874奚雯俐⼆等奖0130882李宇祺⼆等奖0130884徐晨喆⼆等奖0130887张天悦⼆等奖0130889杜思宸⼆等奖0130893周⽂菁⼆等奖0130897陈孝丰⼆等奖0130898周天涯⼆等奖0130920严昱淇⼆等奖0130929孟繁全⼆等奖0130935廉涪钦⼆等奖0130938龚威宇⼆等奖0130946吴⼦恒⼆等奖0130973陆亦铭⼆等奖0130975陈嘉熙⼆等奖0130977黄易晨⼆等奖0130998李云帆⼆等奖0230011马逸然⼆等奖0230015李泽霖⼆等奖0230016顾冉阳⼆等奖0330025顾希妍⼆等奖0330036蔡翔宇⼆等奖0330045孙嘉诺⼆等奖0430037徐乐宜⼆等奖0430054刘启源⼆等奖0430055吴豫成⼆等奖0430063李⾠迈⼆等奖0430068张悠涵⼆等奖0430072杨智捷⼆等奖0430073王俊哲⼆等奖0430078陈浩然⼆等奖0430080陈奕涵⼆等奖0430083李肖彤⼆等奖0430092上官英杰⼆等奖0430103汤济铭⼆等奖0430114蒋天佑⼆等奖0430149张英宁⼆等奖0430150沈朗⼆等奖0530005⾕元杰⼆等奖0530019王泽⼈⼆等奖0530046莫竣淇⼆等奖0530119张宸铭⼆等奖0530150潘柏桦⼆等奖0530172朱饶杰⼆等奖0530180杜建纬⼆等奖0530184黄俊豪⼆等奖0530187简⼠翔⼆等奖0530211郑浩阳⼆等奖0630001顾济海⼆等奖1730011潘兆轩⼆等奖2230001丁睿桐⼆等奖2930020韩晨⽵⼆等奖2930024徐⼦坤⼆等奖2930056陈家宇⼆等奖2930058杨伯伦⼆等奖0130001张奕瑶三等奖0130002韩澍三等奖0130005周馨悦三等奖0130009唐晨峻三等奖0130010宋飞⾠三等奖0130018戴⼦涵三等奖0130032浦睿胤三等奖0130033张洲铭三等奖0130037赵浩峰三等奖0130038闵欣睿三等奖0130042潘鸣⽲三等奖0130043章宇洲三等奖0130061陈⼼⾬三等奖0130067沈致远三等奖0130070张楚乔三等奖0130078刘⽂宇三等奖0130080叶泓飞三等奖0130081郁思琪三等奖0130083朱胤诚三等奖0130088尹紫菡三等奖0130089罗嘉涵三等奖0130090曹哲三等奖0130092贺成超三等奖0130093吴旖瑄三等奖0130100顾偲仪三等奖0130101周千翔三等奖0130103⽑思源三等奖0130104王⼈可三等奖0130113韩岩三等奖0130114王堃三等奖0130118韦景元三等奖0130121谭鸿儒三等奖0130125马令翔三等奖0130127王圣博三等奖0130142李哲彦三等奖0130150袁⼀鸣三等奖0130152李溯⾈三等奖0130153周允皓三等奖0130156陈吾扬三等奖0130170顾⼀凡三等奖0130172杨逸萱三等奖0130175董知微三等奖0130181吴睿三等奖0130182狄睿天三等奖0130186陆晓涵三等奖0130200周承开三等奖0130203吕越飞三等奖0130204叶容轩三等奖0130210傅⽂睿三等奖0130260林睿海三等奖0130262⾦奕萱三等奖0130265郭笑涵三等奖0130272顾⼀帆三等奖0130275葛梦琪三等奖0130299张诣泓三等奖0130302吴晏申三等奖0130303陈奕珲三等奖0130314倪为三等奖0130316刘厚安三等奖0130323王⾬桐三等奖0130330吴彦翔三等奖0130335朱雅馨三等奖0130337曾宣宁三等奖0130343童⼼婕三等奖0130346赵⼀阳三等奖0130350梁钰容三等奖0130354徐⼷菲三等奖0130362周睿三等奖0130363张默晗三等奖0130371何煦冉三等奖0130375薛杰锐三等奖0130383殷超三等奖0130388谢祥和三等奖0130404苏悠然三等奖0130405傅睿鸿三等奖0130411王缪三等奖0130423许宗桓三等奖0130443刘泽川三等奖0130448孙绮诗三等奖0130460卓功亦三等奖0130462马锐三等奖0130470黄睿杰三等奖0130484诸徐旎三等奖0130494王喆三等奖0130495熊恒三等奖0130500董思⾬三等奖0130501徐若菡三等奖0130506段思成三等奖0130510孙欣妍三等奖0130516杨⼀帆三等奖0130525周啸林三等奖0130530王思齐三等奖0130531黄钰涵三等奖0130539庾昊晨三等奖0130541王⾠睿三等奖0130544吴梓渲三等奖0130557⾼天宇三等奖0130565黄鑫三等奖0130571卢欣祺三等奖0130575曾梓越三等奖0130578何彦峰三等奖0130579徐⽴恒三等奖0130580陈泽豪三等奖0130622杨镒铭三等奖0130626隋棂译三等奖0130635鲁谦元三等奖0130636俞轲三等奖0130640贾钰涵三等奖0130648许丁三等奖0130652叶如沃三等奖0130656刘镓铭三等奖0130657汪玥莹三等奖0130658王⼦依三等奖0130671吴天⼀三等奖0130672郑智⼼三等奖0130677秦楚涵三等奖0130685赵熠谦三等奖0130689魏⼦卿三等奖0130690张轶越三等奖0130702屈天卓三等奖0130710周皓洋三等奖0130714郭景融三等奖0130726邓凌熠三等奖0130735周昕朋三等奖0130743杨幼芸三等奖0130749顾楒桤三等奖0130755符敦栎三等奖0130758李⽻轩三等奖0130760索乐岩三等奖0130790杨明昊三等奖0130799李思齐三等奖0130808王⼀尧三等奖0130819陈泉三等奖0130839张翔宇三等奖0130840王⼦祺三等奖0130849王奕帆三等奖0130852王优嘉三等奖0130853范俊逸三等奖0130873曹景熠三等奖0130875顾梓杰三等奖0130879陈思宇三等奖0130885严依朵三等奖0130888钱秉⾠三等奖0130892郭焕琨三等奖0130895韩李宣三等奖0130922刘亦宁三等奖0130930杨凯晨三等奖0130937王思轩三等奖0130939翁爽钧三等奖0130940王炜诚三等奖0130941孙霖铃三等奖0130951王跃阳三等奖0130953李天椋三等奖0130957黄俊元三等奖0130965姜君三等奖0130971赵敏⾏三等奖0130985刘奕冰三等奖0330002杜⾬泽三等奖0330020向伊俐三等奖0330026李泽源三等奖0330033周奕菲三等奖0330041汪⼼可三等奖0330046沈⼦程三等奖0330047易⾠耘三等奖0330051罗雪松三等奖0430012孙禹尧三等奖0430031赵晨皓三等奖0430039丁宇轩三等奖0430044姚嘉昊三等奖0430075刘思齐三等奖0430084王晗三等奖0430096周魏巍三等奖0430102王浩宸三等奖0430104袁从周三等奖0430111孔思涵三等奖0430115温天乐三等奖0430124韩诚骏三等奖0430139李丹妮三等奖0430156秦宇轩三等奖0430158李哲睿三等奖0530007贺佳三等奖0530012谯致洋三等奖0530018王承熙三等奖0530031陈凇玮三等奖0530035葛⽂璟三等奖0530040⾦尚明三等奖0530049王俊奇三等奖0530053叶昱⾠三等奖0530054张怀江三等奖0530071齐思远三等奖0530074宋宇轩三等奖0530085吴睿阳三等奖0530091於哲宇三等奖0530099周彦婷三等奖0530107郭默涵三等奖0530109林乐遥三等奖0530113王若熙三等奖0530123仲雯三等奖0530124邹明悦三等奖0530130陈仕卿三等奖0530131陈笑瞻三等奖0530132陈奕恺三等奖0530136郭翰星三等奖0530140胡⼼恬三等奖0530142李姝隽三等奖0530167张安泊三等奖0530169周灵朗三等奖0530182范奕成三等奖0530197钱鹏宇三等奖0530200宋思睿三等奖0530206熊天娇三等奖0630002陈霖逸三等奖0630009鲍康迪三等奖0630018袁梦三等奖0730007范稼好三等奖0730010王念劬三等奖1130004陆楚玥三等奖1130010徐颖妍三等奖1130019吴越三等奖1230011孔德恕三等奖1230013严承明三等奖1430003陈博宇三等奖1430005董鲁备三等奖1430011诸宸霖三等奖1630008王静怡三等奖1630014郭曦彤三等奖1630022谢钟傲三等奖1630025吴俊豪三等奖1630028朱培尧三等奖1630031庄⼦涵三等奖1630035杭鹏昊三等奖1630038李元卿三等奖1630053陶悦祺三等奖1730006徐浩林三等奖1730017张许智三等奖1730020黄瑜亮三等奖1730021沈思捷三等奖1830001张洪程三等奖2030001林天悦三等奖2230003吕钦唐三等奖2230011程⾀泽三等奖2330004骆爽三等奖2930035章兴翯三等奖2930036龚梓涵三等奖2930051蒋相⾠三等奖2930054吕惟乔三等奖。

15届中环杯二年级决赛试题

二、填空题B :(每题8分,共32分)9.如图所示,花花被邪恶的巫师关在了由26个正方形房间组成的迷宫里,边与边相邻的房间是互通的。

已知:黑色房间里有怪物,不能进;斜纹房间里住着巫师,只能进,不能出;灰色房间有机关,只能走一次;白色房间是安全的,可以重复走。

巫师告诉花
花,走遍所有灰色房间,然后进入斜纹房间就可以离开。

花花只有从(填“A 、B 、C 、D 、E 、F 、G ”中的一个)房间开始走,才能
成功离开迷宫。

10.甲、乙、丙、丁四人年龄之和是100岁。

甲32岁,他与乙的年龄之和是另外两个人年龄之和的3倍。

丙比丁大3岁。

那么,这四个人中,年龄最大的人与年龄最小的人,他们的年龄之和是。

11.如图所示,每个小图形代表一个数字(大方框只是起到分割行、列的作用),右边和下边的数字代表该行或者该列所有数之和(每行、每列均有6个数)。

如果“○”代表6,那么,△=。

12.数一数,图中共有个梯形。

三、动手动脑题:(每题10分,共20分)
13.如图,把图形分成大小、形状都相同的三部分,并且每部分中都带有一个圆点,请你在图中画出分割线。

14.将1~10分别填入图中的空格内,每个数字只能使用一次。

要求“□”内的数等于它左上角和右上角两个数的差(大减小),“○”里的数等于它左上角和右上角两个数的和。

求:A 的值。

题
得分:第十五届“中环杯”小学生思维能力训练活动
二年级决赛。

第15届二年级中环杯决赛真题(2015年)

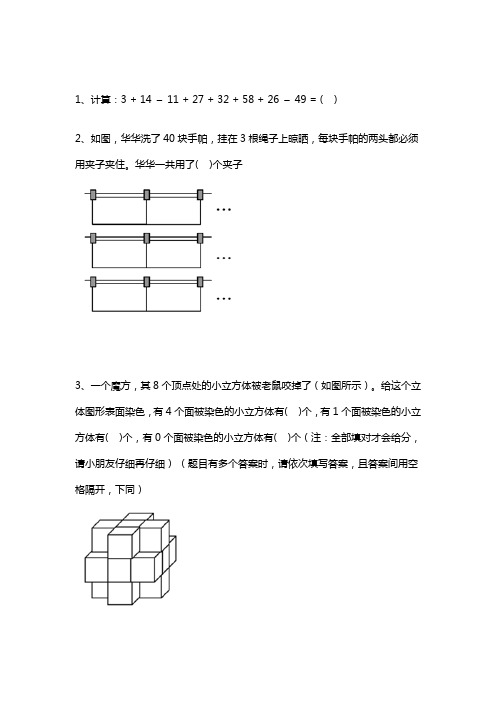
1、计算：3 + 14 –11 + 27 + 32 + 58 + 26 –49 = ( )2、如图，华华洗了40块手帕，挂在3根绳子上晾晒，每块手帕的两头都必须用夹子夹住。

华华一共用了( )个夹子3、一个魔方，其8个顶点处的小立方体被老鼠咬掉了（如图所示）。

给这个立体图形表面染色，有4个面被染色的小立方体有( )个，有1个面被染色的小立方体有( )个，有0个面被染色的小立方体有( )个（注：全部填对才会给分，请小朋友仔细再仔细）（题目有多个答案时，请依次填写答案，且答案间用空格隔开，下同）4、有两根一样长的绳子，第一根用去42 米，第二根用去12 米，第二根剩下来的绳子长度刚好是第一根剩下来绳子长度的4 倍。

原来两根绳子共长( )米。

5、甲、乙、丙三人中有一人是牧师，有一人是骗子，还有一人是赌徒。

牧师从不说谎，骗子总是说谎，赌徒有时说真话有时说谎话。

甲说：“我是牧师。

”乙说：“我是骗子。

”丙说：“我是赌徒。

”那么，三人中，( )是牧师。

6、小明在电脑上玩一种新型飞行棋，如果骰子掷到黑色数字，代表需要后退，掷到红色数字，代表需要前进（例如：黑色2代表后退2步，红色3代表前进3步）。

他掷了5 次，分别是黑色5、红色4、红色2、黑色3、红色1。

走完后发现自己在第6 格。

在第一次掷骰子前，他在第( )格7、一个盒子里有一些大小相同的球，其中白的有8个，黑的有9个，黄的有7个。

不许看球，每次拿一个，至少拿( )次才能保证三种颜色的球都有。

8、阿拉丁在藏宝库里发现了20条项链，其中有的项链只镶有2颗钻石，有的项链镶有5颗钻石，一共有79颗钻石。

那么镶有5颗钻石的项链有( )条9、如图所示，花花被邪恶的巫师关在了由26个正方形房间组成的迷宫里，边与边相邻的房间是互通的。

已知：黑色房间里有怪物，不能进；斜纹房间里住着巫师，只能进，不能出；灰色房间有机关，只能走一次；白色房间是安全的，可以重复走。

巫师告诉花花，走遍所有灰色房间，然后进入斜纹房间就可以离开。

第十三届中环杯中小学生思维能力训练活动三年级决赛试卷及解析

渊1冤请你把这 8 块拼板剪下并拼成图 1 所示大的正三角形袁且小三角形间的黑尧白两种颜色必须相间遥请在图 1 中用粗线条直接画出拼法袁并标上每块拼板的标号遥
图1
第十三届“中环杯”中小学生思维能力训练活动三年级决赛答案
第十三届“中环杯”中小学生思维能力训练活动
三年级决赛答案
一、填空题 1. 答：166665
4. 答：本题方法不唯一，但最少要移动 3 根。下图为一种移动方法。
2/3
第十三届“中环杯”中小学生思维能力训练活动三年级决赛答案
5. 答：（1）如图
（2）45 分两种情况。第一种是竖着的，一共有 1＋2＋3＋4＋5＝15（个）；第二种是横着的，有 2＋4＋6＋8＋10＝30（个）。所以总共有 15＋30＝45（个）。（3）不存在
6. 答：本题填法不唯一，符合题目要求即可。下图为一种填法。
7 4
5 6
2
8
9
3
7. 答：甲此题为一笔画问题。A、D 是奇点，其他点都是偶点，因此从 A 或 D 出发可完成一笔画。所以甲能先走遍所有街道，而乙必有重复路线。
8. 答：144，81 因为要构成方阵，所以大方阵和小方阵的人数都是完全平方数。 15 行15 列的方阵由1515 225 （人）组成，则大方阵人数应大于 225÷2＝
4. 答：38 晾衣服必须要等洗衣机洗完后才能进行，而在用洗衣机洗衣服的同时。可先后完成洗碗、拖地板和削土豆皮，正好 8＋10＋12＝30（分钟）。之后再完成叠被子和晾衣服。所以共用 30＋3＋5＝38（分钟）。
5. 答：576 由于每放入一个棋子就有 1 行 1 列不可以再放入其他棋子，所以第一个棋子有 4×4＝16（格）可以放，第二个棋子有 3×3=9(格)可以放，第三个子只有 2×2=4(格)可以放，最后一个棋子就只有 1 格可以放。所以共有 16×9× 4×1=576(种)种不同的放法。

2014年中环杯三年级7期至12期---学生版

2014年第十五届“中环杯”青少年科技报思维训练营三年级7期至12期--王洪福老师加减法数字谜例1、下列算式中，每个字母都代表了0～9中一个数字，并且计算过程中无进位，那么XYZ有多少种可能？例2、下列算式中A～I分别代表1～9这9个数字，写出一个GHI取最小值时的算式。

分类枚举例1、用0、1、2、3四个数字能组成多少个不同的三位数？例2、现有1元、2元和5元的硬币各4枚，用其中的一些硬币支付23元钱，一共有多少种不同的支付方法？和差倍问题例1、在书架上摆放着三层书共275本，第三层的书比第二层的3倍多8本,第一层比第二层的2倍少3本。

第三层上摆放着多少本书？例2、水果店原来有156箱苹果和84箱橘子。

苹果和橘子各卖出相等的箱数后，剩下的苹果箱数比橘子箱数多2倍。

苹果和橘子各卖出多少箱？植树问题例1、小朋友们在路的一边植树。

先植一棵树，以后每隔3米植一棵。

已经植了9棵，第一棵树和第九棵树相距多少米？例2、在一个长方形池塘的四边种树，每边种5棵树，四边一共种多少棵树（长方形四个顶角上都要种树）？图形计数例1、数一数，图中有多少个三角形？例2、如图，在方格纸上的14个格点处有14枚钉子，用橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等几何图形。

那么，一共可以构成几个不同的正方形？鸡兔同笼问题例1、小梅数她家的鸡与兔，数头有16个，数脚有44只，那么小梅家的鸡与兔各有多少只？例2、某场乒乓球比赛售出30元、40元、50元的门票共200张，收入7800元。

其中40元和50元的票的张数相等。

每种票各售出多少张？“中环杯”模拟题精选例1、超市促销规定：用3只空汽水瓶可以换一瓶汽水，而不用另外付钱。

小李给自己小组的同学买了10瓶汽水，不用再花钱，他们最多能喝上几瓶汽水？。

第十五届中环杯初赛(三年级)解析

第十五届“中环杯”小学生思维能力训练活动三年级选拔赛1.计算：3×995＋4×996＋5×997＋6×998＋7×999－4985×3＝__________【答案】9980【解析】考点：巧算方法一：3×995+4×996+5×997+6×998+7×999-4985×3=（3+4+5+6+7）×997-3×2-4×1+6×1+7×2-5×997×3=25×997-6-4+6+14-15×997=(25-15)×997+10=9970+10=9980方法二：3×（1000－5）＋4×（1000－4）＋5×（1000－3）＋6×（1000－2）＋7×（1000－1）－（5000－15）×3＝3000－15＋4000－16＋5000－15＋6000－12＋7000－7－15000＋45＝25000－15000－30－28－7＋45＝10000＋15－35＝10000－20＝99802.一个数除以20的商是10，余数是10，这个数为__________【答案】210【解析】考点：除法运算被除数÷20=10 (10)则：被除数=20×10+10=2103.如图是一个美术馆的俯视图，每个“×”表示A 、B 、C 、D 四人中的一个人，在美术馆中央是一根大石柱。

已知A 看不到任何人，B 只能看到C ，C 既可以看到B 也可以看到D ，D 只能看到C 。

那么，__________在P 点（填A 、B 、C 或D ）【答案】C 【解析】考点：逻辑推理由A 看不到任何人，则A 应该在最上面（如图1）由B 只能看到C ，则B 应该在右下方（如图2）由C 既可以看到B 也可以看到D ，则C 应该在左下方（如图3）由D 只能看到C ，则D 在左边（如图4）A B B A AA B C CD如图1如图2如图3如图4则：P点为C4.甲、乙两人相约去餐厅吃饭，由于这家餐厅生意火爆，所以甲到了之后就先去拿了一个等位号码，顺便等乙。

巧算速算练习题

巧算速算练习题巧算速算练习题1．计算2011×990+2011×11=_____。

（第九届走美杯三年级初赛）★2．2012×9+2012×8-2012×7=_____。

（第十届走美杯三年级初赛A卷）★3．计算23×98-37×23+23×38+23=_____。

（第十一届走美杯四年级决赛）★4．计算25×13×2+15×13×7=_____。

（第十五届中环杯三年级决赛）★5．算式5×13×（1+2+4+8+16）的计算结果是_____。

（2015年数学花园探秘中年级组决赛）★6．计算2011-（9×11×11+9×9×11-9×11）=_____。

（2011年数学解题能力展示中年级复赛）★★7．在下面的□中填入一个相同的数字，使算式成立。

97+□×（19+91÷□）=321, □=_____。

（第十三届小机灵杯三年级决赛）★★8．计算2×（999999+5×379×4789）=_____。

（第十三届走美杯上海赛区三年级决赛）★★9．计算13+73+132+145+255+274+326+368+427=_____。

（第十四届中环杯三年级选拔赛）★★10．计算2015-123-125-127-129-131=_____。

（第十三届小机灵杯三年级初赛）★★11．计算1+3+5+7+…+97+99-2014=_____。

（第十三届走美杯三年级初赛）★★12．101-99+97-…-7+5-3+1=_____。

（第十一届走美杯三年级决赛）★★13．计算2014-37×13-39×21=_____。

（第十四届中环杯三年级决赛）★★★14．123×8+82×9+41×7-2009=_____。

第十五届“中环杯”初赛各年级试题

遥
20 个 2
7. 一个物体从高空落下袁已知第一秒下落距离是 5 米袁以后每秒落下的距离都比前一
秒多 10 米袁10 秒末物体落地遥则物体最初距离地面的高度为
米遥
8. 小明父亲每天上班需要先骑 10 分钟山地自行车袁然后乘坐 40 分钟的地铁遥有一天袁
地铁坏了袁所以他直接骑车上班袁一共花了 3 个半小时遥那么袁地铁的速度是山地自行车的
这个人有一个头两条腿袁普通狼有一个头四条腿袁变异狼有两个头三条腿遥所有的人和
狼加起来有 21 个头 57 条腿袁则所有的狼渊包括变异狼冤有
头遥
11. 如图袁从 A 走到 B袁每次走一格袁只能向下或者
向右走遥将一路上的数字全部相加渊如果走到黑格袁就直
接加 5冤袁最后的总和为 51遥不同的走法有
种遥
每人 70 元遥他们最少要花
元购买门票遥
5. 到了冰雪宫殿开放的日子袁小朋友们相约一同前往避暑遥冰雪宫殿
前有个阶梯袁爱丽丝走 20 级台阶用了 120 秒遥用同样的速度走台阶袁爱丽丝
共走了 180 秒袁正好走完所有阶梯遥到达冰雪宫殿的台阶一共有
级遥
6. 右图中的每个小正方形边长为 5 厘米袁那么这个图形的周长是厘米遥
3
7 9 12
16 18 21 噎
246
11 13 15
20 噎
1
5 8 10
14 17 19 噎
第 13 题
A
B
棒中 7
+1杯环中
1中杯环
第 14 题
D
C
第 15 题
影部分面积为
平方厘米遥
16. 将 1~6 填入右图的三个算式中袁每个数恰好使

中环杯第11-16届三年级初赛真题

第十一届“中环杯”小学生思维能力训练活动三年级组选拔赛一、填空题1.计算：666×111+222×667 =（）。

2.找规律：179，278，377，476，（），（），773，872 。

3.有7个数的平均数是11，前四个数的平均数是8，后四个平均数是13，第四个数是（）。

4.把一张长为30厘米，宽为20厘米的长方形纸片，剪成一个面积最大的正方形（不允许拼接），这个正方形的面积是（）平方厘米。

5.有甲、乙两支人数相等的运动队，由于训练需要，从甲队调10人到乙队，这时乙队的人数正好是甲队人数的3倍。

甲队原有（）人。

6.小巧站在铁路边，一列火车从她身边开过用了3分钟。

已知这列火车长360米，以同样的速度通过一座大桥，用了6分钟。

这座大桥长（）米。

7.一条公路全长2010米。

现在公路的两边分别种上一些树，要求从公路一端开始，每相邻两棵树相距3米。

这样共需要植树（）棵。

8.小花猫和小白猫一起吃鱼。

小花猫每分钟吃一条鱼，但每吃1分钟要休息3分钟；小白猫每分钟吃2条鱼，但每吃1分钟要休息1分钟。

它们吃完30条鱼需要（）分钟。

二、动手动脑题：9.如图，一个牧童从甲地出发，赶着羊群先到河边饮水，再将羊群赶到乙地吃草。

已知从甲地到河边饮水点，以及从饮水点到乙地都是直线路程，请问应该怎么选择河边饮水点的位置，使羊群所走的路程为最短？请在图上表示出来并作文字说明。

甲10.超市向某食品厂订购一批食品，在付款总数和付款时间都相同的情况下，可以有以下两种付款方法：第一种：第一个月付款13万元，以后每月付3万元；第二种：前一半时间每月付6万元，后一半时间每月付2万元。

问超市的付款总数是多少？11.一个四口之家，由爸爸、妈妈、大儿子和小儿子组成，他们的年龄之和为68岁。

爸爸比妈妈大2岁。

3年前，这个家庭成员的年龄之和为57岁。

5年前，这个家庭的成员年龄之和为52岁。

请问这个家庭每个成员现在的年龄是多少？12.有6个边长为2厘米的等边三角形，2个边长同为2厘米的正方形，如图。