运算放大器噪声
运算放大器电路固有噪声的分析与测量(三)
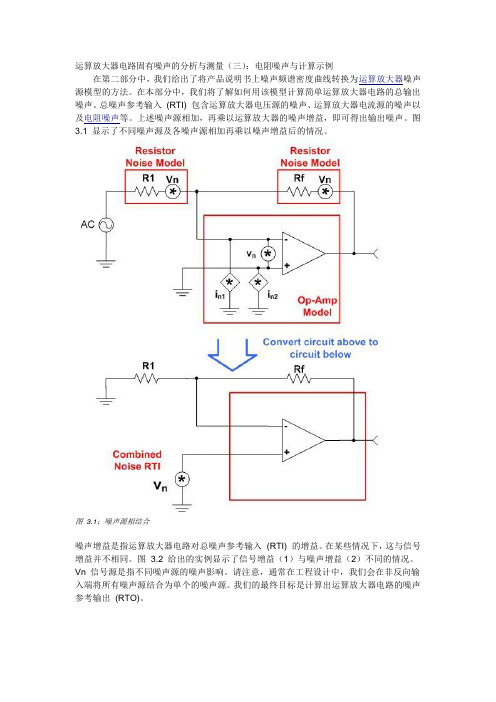
运算放大器电路固有噪声的分析与测量(三):电阻噪声与计算示例在第二部分中,我们给出了将产品说明书上噪声频谱密度曲线转换为运算放大器噪声源模型的方法。
在本部分中,我们将了解如何用该模型计算简单运算放大器电路的总输出噪声。
总噪声参考输入(RTI) 包含运算放大器电压源的噪声、运算放大器电流源的噪声以及电阻噪声等。
上述噪声源相加,再乘以运算放大器的噪声增益,即可得出输出噪声。
图3.1 显示了不同噪声源及各噪声源相加再乘以噪声增益后的情况。
图 3.1:噪声源相结合噪声增益是指运算放大器电路对总噪声参考输入(RTI) 的增益。
在某些情况下,这与信号增益并不相同。
图 3.2 给出的实例显示了信号增益(1)与噪声增益(2)不同的情况。
Vn 信号源是指不同噪声源的噪声影响。
请注意,通常在工程设计中,我们会在非反向输入端将所有噪声源结合为单个的噪声源。
我们的最终目标是计算出运算放大器电路的噪声参考输出(RTO)。
图 3.2:噪声增益与信号增益。
方程式 3.1:简单运算放大器电路的噪声增益在上一篇文章中,我们了解到如何计算电压噪声输入,不过我们如何将电流噪声源转换为电压噪声源呢?一种办法就是对每个电流源进行独立的节点分析,并用叠加法将结果求和。
这时我们要注意,要用和的平方根(RSS) 对每个电流源的结果进行求和。
通过方程式 3.2 和 3.3,我们可将简单运算放大器电路的电流噪声转换为等效电压噪声源。
图 3.3 给出了有关图示。
附录 3.1 给出了该电路的整个演算过程。
方程式 3.2与3.3:将简单运算放大器的电流噪声转换为电压噪声(RTI)图 3.3:将电流噪声转换为电压噪声(等效电路)。
我们还必须考虑的另一因素是运算放大器电路中电阻器的热电压噪声。
我们可用节点分析法来独立分析电压源。
我们可用叠加法与RSS 添加法将结果相结合。
通过方程式 3.4 与3.5,我们可将所有热噪声源相结合,从而得到单个的噪声源参考输入。
不可不知的运算放大器的噪声

不可不知的运算放大器的噪声
1 为何最近又强调低噪声放大问题? 低噪声放大的部分问题与信噪比(SNR)有关。 2 我们谈论的噪声究竟是哪一种? 这种噪声是放大器本身固有的,或者由相应的无源器件所产生并放大 的。 外部噪声则是系统级的问题。 3 这ቤተ መጻሕፍቲ ባይዱ噪声的来源是什幺? 热噪声来源于输入和反馈电阻(e n,R2)、放大器的固有电压噪声(e n) 和电流噪声(i n)(图 1)。如图 1 所示,折合到输入端的噪声方程(N o i s e R T I)
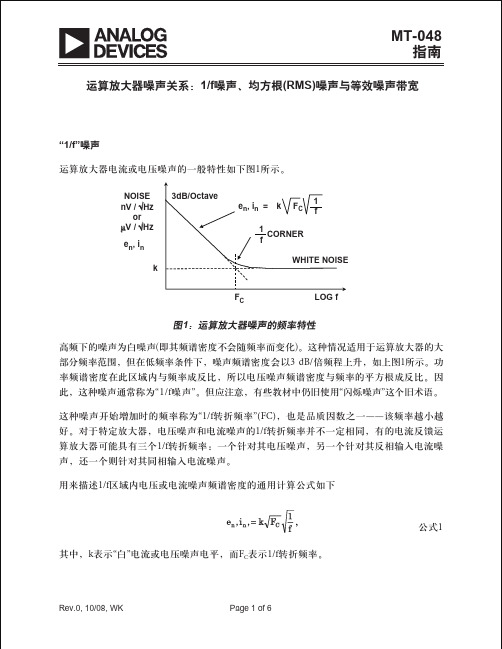
上述公式中,e n,w 是宽带白噪声,F C 是 1/f 拐角频率,FL 和 FH 定 义了感兴趣的待测带宽。 一般来说,比其它任何一个噪声分量高 4~5 倍的任何噪声分量都会 成为主导噪声,而其余的分量则可以忽略不计。因此,在更高的频率上,F C l n(F H/F L)的影响不再显着,而总的 rms 噪声就等于白噪声乘以频率差的平 方根。事实上,如果 FH 远远高于 FL,总的 rms 噪声即等于白噪声乘以 F H 的平方根。另一方面,当器件工作在 1/f 噪声区中,总的 rms 噪声是拐角频 率点的噪声水平(即白噪声水平)乘以拐角频率的平方根再乘以 ln(FH/FL)。
显示了所有的噪声源的贡献。表达式的电阻噪声中的 k 因子是波尔兹曼常 数。T 是绝对温度、R 是以欧姆为单位的电阻。一个经验法则是, 1kΩ的电阻在室温下产生的噪声为 4nV/ Hz,这比某些现代运放的噪 声还高。 4 如何表示噪声? 为了让所有的噪声源能够以先平方和再求平方根的方式简单地组合起 来,基带噪声指标以 nV(或者 pA)/ Hz 来表示。只要噪声源是不相关的,这一 表示就是可行的,于是在整个频谱上,出现任何给定的信号幅值的概率满足 正态(高斯)分布。 5 噪声在所有的频率上并非真正是恒定? 的确不是。e n 和 i n 有两个分量( 图 2a):低频的 1/f 噪声,其频谱密 度随着频率降低而以 3dB/倍频程的速率上升,具有分布在更高频率上平坦化 频谱分布的白噪声。对于 1/f 噪声有着重要影响的应用来说,在产品手册中 可找到有限带宽上的峰-峰值噪声指标,例如 0.1~10Hz(图 2b)。 6 什幺是拐角频率?它为何具有重要性?
第二部分:运算放大器噪声介绍

第二部分:运算放大器噪声介绍作者:TI高级应用工程师Art Kay噪声的重要特性之一就是其频谱密度。
电压噪声频谱密度是指每平方根赫兹的有效(RMS) 噪声电压(通常单位为nV/rt-Hz)。
功率谱密度的单位为W/Hz。
在上一篇文章中,我们了解到电阻的热噪声可用方程式 2.1 计算得出。
该算式经过修改也可适用于频谱密度。
热噪声的重要特性之一就在于频谱密度图较平坦(也就是说所有频率的能量相同)。
因此,热噪声有时也称作宽带噪声。
运算放大器也存在宽带噪声。
宽带噪声即为频谱密度图较平坦的噪声。
方程式2.1:频谱密度——经修改后的热噪声方程式图2.1:运算放大器噪声频谱密度除了宽带噪声之外,运算放大器常还有低频噪声区,该区的频谱密度图并不平坦。
这种噪声称作1/f 噪声,或闪烁噪声,或低频噪声。
通常说来,1/f 噪声的功率谱以1/f 的速率下降。
这就是说,电压谱会以1/f(1/2 ) 的速率下降。
不过实际上,1/f 函数的指数会略有偏差。
图2.1 显示了典型运算放大器在1/f 区及宽带区的频谱情况。
请注意,频谱密度图还显示了电流噪声情况(单位为fA/rt-Hz)。
我们还应注意到另一点重要的情况,即1/f 噪声还能用正态分布曲线表示,因此第一部分中介绍的数学原理仍然适用。
图2.2 显示了1/f 噪声的时域情况。
请注意,本图的X 轴单位为秒,随时间发生较慢变化是1/f 噪声的典型特征。
图2.2:时域所对应的1/f 噪声及统计学分析结果图2.3 描述了运算放大器噪声的标准模型,其包括两个不相关的电流噪声源与一个电压噪声源,连接于运算放大器的输入端。
我们可将电压噪声源视为随时间变化的输入偏移电压分量,而电流噪声源则可视为随时间变化的偏置电流分量。
图2.3:运算放大器的噪声模型运算放大器噪声分析方法运算放大器噪声分析方法是根据运放数据表上的数据计算出运放电路峰峰值输出噪声。
在介绍有关方法的时候,我们所用的算式适用于最简单的运算放大器电路。
运算放大器的噪声分析

运算放大器的噪声分析07-06-04 10:37 发表于:《活石家园》分类:未分类问:有关运算放大器的噪声我应该知道些什么?答:首先,必须注意到运算放大器及其电路中元器件本身产生的噪声与外界干扰或无用信号并且在放大器的某一端产生的电压或电流噪声或其相关电路产生的噪声之间的区别。
干扰可以表现为尖峰、阶跃、正弦波或随机噪声而且干扰源到处都存在:机械、靠近电源线、射频发送器与接收器、计算机及同一设备的内部电路(例如,数字电路或开关电源)。
认识干扰,防止干扰在你的电路附近出现,知道它是如何进来的并且如何消除它或者找到对干扰的方法是一个很大的题目。
如果所有的干扰都被消除,那么还存在与运算放大器及其阻性电路有关的随机噪声。
它构成运算放大器的控制分辨能力的终极限制。
我们下面的讨论就从这个题目开始。
问:好,那就请你讲一下有关运算放大器的随机噪声。
它是怎么产生的?答:在运算放大器的输出端出现的噪声用电压噪声来度量。
但是电压噪声源和电流噪声源都能产生噪声。
运算放大器所有内部噪声源通常都折合到输入端,即看作与理想的无噪声放大器的两个输入端相串联或并联不相关或独立的随机噪声发生器。
我们认为运算放大器噪声有三个基本来源:★一个噪声电压发生器(类似失调电压,通常表现为同相输入端串联)。
★两个噪声电流发生器(类似偏置电流,通过两个差分输入端排出电流)。
★电阻噪声发生器(如果运算放大器电路中存在任何电阻,它们也会产生噪声。
可把这种噪声看作来自电流源或电压源,不论哪种形式在给定电路中都很常见)。
运算放大器的电压噪声可低至3 nV/Hz。
电压噪声是通常比较强调的一项技术指标,但是在阻抗很高的情况下电流噪声常常是系统噪声性能的限制因素。
这种情况类似于失调,失调电压常常要对输出失调负责,但是偏置电流却有真正的责任。
双极型运算放大器的电压噪声比传统的FET运算放大器低,虽然有这个优点,但实际上电流噪声仍然比较大。
现在的FET运算放大器在保持低电流噪声的同时,又可达到双极型运算放大器的电压噪声水平。
运放的噪声特性和放大电路的噪声分析

也只规定 了 电压 噪声 的参 数 作 为电压性 噪声 的参数在数
21年 第1 期 <6 00 1 、 ◇
域.分别用下面的方法换算成有效值。然后再用两个有效
值的平方 和开平 方根 的方法 求 出总噪声 。
lN = . / O 1 2 、 9x 0 2  ̄ s2 、 l5 = . /9 1 2 - 2
E ̄ Gn・ o = Vn
五 、 目标 信 噪 比特 性 的噪 声 电平
表2 相对 于基 准信 号 电平 1r s Vm 一般 的线 是 V m 和2 r s(
路输出电平)在达到一定 的信噪比 (N )时,信噪比与 SR
噪声 电压 有效值 之间 的对应关 系 由表 中的数值 可知 .希 望得到 的信噪 比的数值 不同 .要求 的输入 端噪声 电压有效 值 的数值 也完 全 不 同。例 如以2 r s Vm 的信 号为例 .信 噪 比 为10 B 的噪声 电压容许 值2 1 rs 0d 时 0 V m 在S = 2d  ̄样 x / 10 B l N i 的超低噪 声特性 时噪声 电压 的容许 值为2 Vm 1 rs  ̄ 对 于一般 的音 频用运 算放 大器 来说 .要 实现 10 B 0d 的
运放的噪声特性和放大电路的噪声分析
口张
运算 放 大 器集 成 电路 是 在模 拟 电路 中 .包 括音 频 应
用 电路 在 内应 用最 为广 泛 、普及 度很 高的放 大器件 由于
达
据表 中有两种 表示方 法 ,一种 是噪声 频谱密 度 .另一种 是 噪声 有效 值 表 1 是集 成运 算放 大 器噪声 参数 的表 示方 法 的例 子 。在 该 表 中对 噪 声频 谱 密 度 和噪 声有 效 电压 都 同 时做 了规 定 。但 是对 于 一些 不针 对音 频应 用 的型号来 说 . 有的并不 规定 噪声有效 值 只给出噪声 频谱密 度
2-4(6)运算放大器的噪声特性

Fa = F +
+
4kTRs B
2 2 I a = I n + 4kTB / R f 低噪声电阻 的1/f噪声可 Rs 忽略 Fa = F + Rf
负反馈电阻增加了电路的热噪声。
By TianGJ,YanshanUniv
2.74 反馈电路
2.7.4 反馈电路 负反馈不会改善放大器的内部固有噪声,负反馈 电阻增加了电路的热噪声。通过串并联电阻的方 法进行阻抗匹配是 不可取的。 However,只要反馈电阻增加的阻抗与源电阻相 比可以忽略,而且并联反馈阻抗足够大,那么加 入负反馈后热噪声特性可保持基本不变。 •在必须改变放大器输入阻抗的场合,可以考虑利用 负反馈解决问题。
R1
R2 200k uA741 + R2 200k
R2 2 R2 2 2 2 2 Vno = 2( ER1 ) + 2ER2 + En (1 + ) + 2( I n R2 )2 R1 R1
ER1 = 4kTR1 B ER2 = 4kTR2 B
1k R1 1k
•功率增益等于电压增益的平方
Vno≈177uV
= 20 2 × [(100 − 0.01) + 200 × ln( ≈ 0.88μV
类似地,计算电流噪声
100 = 0.552 ×[(100− 0.01) + 2000× ln( )], ( pA) 0.01 ≈ 75pA
By TianGJ,YanshanUniv
2.6.2 运算放大器的噪声性能计算
f E = e [( f B − f A ) + f ce ln( B )] fA
运算放大器噪声增益

运算放大器噪声增益
在我们平常的设计中很少用到噪声增益这个概念,由于它通常并不是多么的重要,忽视它对我们的设计也不会造成太大的影响,所以我们很少考虑它。
但是有些时候我们经常在这个问题上出错,这时我们就要仔细考虑一下了。
来看这样的一个电路:
首先我们把两个开关都拨到上面的时候称为CASE1,都拨到下面的时候称为CASE2。
这也就是我们平常所说的同相放大电路和反向放大电路。
在CASE1的状况下,信号增益为1+R1/R2,在CASE1的状况下,信号增益为-R1/R2,这两个电路的反馈是一样的,反馈系数都是R2/(R1+R2),所以他们的噪声增益都是(R1+R2)/R2。
而增益带宽积的表达式为GBP=Gn*B,所以两种状况下的带宽是一样的。
这里我们可以看出,这对反向放大器是很不利的。
信号放大了R1/R2倍,带宽却减小了1+R1/R2倍。
所以当我们在设计运放电路时,在增益带宽积的问题上只考虑电路的噪声增益就可以了,而与电路的放大模式无关。
分析模拟电路必需熟悉到:什么增益、稳定性、带宽之类,都是电路自身的内因,而输入信号一类的是外因。
所以同相放大器和反相放大器其实是一个电路,两者的带宽其实应当完全一样,那一点点
差异是别的缘由。
同相放大器和反相放大器归一,才有了所谓的噪声增益。
电路中的运算放大器如何抑制噪声

电路中的运算放大器如何抑制噪声在电路设计中,噪声是一个常见的问题,它可以干扰信号的传输和处理。
在运算放大器中,抑制噪声是至关重要的。
本文将介绍电路中的运算放大器如何抑制噪声,并探讨一些常用的方法。
一、噪声的来源噪声可以来自于多个方面,例如电源线、元件本身以及热噪声等。
这些噪声会被引入到运算放大器中,影响信号的准确性和质量。
二、共模抑制比共模抑制比(Common Mode Rejection Ratio,CMRR)是衡量运算放大器抑制共模噪声能力的指标。
它表示在输入信号有共模分量时,运算放大器输出信号中的共模信号与共模输入信号之比。
CMRR越高,运算放大器抑制共模噪声的能力越强。
常用的提高CMRR的方法包括采用差分输入电路、使用抵消电路等。
差分输入电路可以将共模信号抵消,从而提高抑制共模噪声的能力。
抵消电路则可以通过引入一个与输入信号反向相等的噪声信号来消除共模噪声。
三、反馈电阻的选择反馈电阻也对抑制噪声起着重要的作用。
反馈电阻越大,运算放大器的放大倍数越高,信号与噪声的比例也越大,从而抑制噪声的效果也越好。
但是,过大的反馈电阻会导致电路的幅频特性受到影响,影响放大器的性能。
因此,在选择反馈电阻时需要综合考虑信号放大倍数和噪声抑制的需求,以及电路的幅频特性。
四、降低输入噪声输入噪声可以通过一些方法来降低。
一种常用的方法是使用低噪声元件,例如低噪声电阻、低噪声电容等。
这些低噪声元件可以减少噪声引入到电路中的概率。
此外,还可以通过合理布线和屏蔽等方法来降低输入噪声。
合理布线可以减少信号线与干扰源的接触,从而减少干扰信号的引入。
屏蔽则可以通过遮挡干扰源的辐射信号,达到降噪的目的。
五、电源滤波电源线是常见的噪声来源之一。
为了抑制来自电源线的噪声,可以采用电源滤波的方法。
电源滤波可以通过添加滤波电容、滤波电感等元件来消除电源线中的噪声。
滤波电容可以将高频噪声短路到地,从而减少其传播到运算放大器的可能性。
滤波电感则可以通过孤立输入和输出电路与电源线之间的电流,进一步提高噪声抑制能力。
运算放大器电路中固有噪声的分析与测量(七)

运算放大器电路的固有噪声分析与测量(七)本文将讨论决定运算放大器 (op amp) 固有噪声的基本物理关系。
集成电路设计人员在噪声和其他运算放大器参数之间进行了一些性能折衷的设计,而电路板和系统级设计人员将从中得到一些启发。
另外,工程师们还能了解到,如何根据产品说明书的典型规范在室温及超过室温时估算最坏情况下的噪声。
最坏情况下的噪声分析和设计的 5 条经验法则大多数运算放大器产品说明书列出的仅仅是一个运算放大器噪声的典型值,没有任何关于噪声温度漂移的信息。
电路板和系统级设计人员希望能根据典型值找出一种可以估算最大噪声的方法,此外,这种方法应该还可以有效地估算出随着温度变化的噪声漂移。
这里给出了一些有助于进行这些估算的基本的晶体管噪声关系。
但是为了能准确地利用这些关系,我们有必要对内部拓扑结构(如偏置结构和晶体管类型等等)进行一些了解。
不过,如果我们考虑到最坏情况下的结构,也可以做一些包括大多数结构类型的概略性说明。
本节总结了最坏情况下的噪声分析和设计的 5 条经验法则。
下一节给出了与这些经验法则相关的详细数学计算方法。
经验法则 1:对半导体工艺进行一些改变,不会影响到宽带电压噪声。
这是因为运算放大器的噪声通常是由运算放大器偏置电流引起的。
一般说来,从一个器件到另一个器件的偏置电流是相对恒定的。
在一些设计中的噪声主要来自输入 ESD 保护电阻的热噪声。
这样的话,宽带噪声的变化超过典型值的 10% 是非常不可能的。
事实上,许多低噪声器件的这种变化一般都低于 10%。
请参见图 7.1 示例。
宽带电流噪声要比电压噪声更容易受影响(主要是对双极工艺而言)。
这是因为电流噪声与基极电流密切相关,而基极电流又取决于晶体管电流增益 (beta)。
通常来说,宽带电流噪声频谱密度的变化不到 30%。
图 7.1 基于典型值估算的室温条件下的宽带噪声经验法则 2:放大器噪声会随着温度变化而变化。
对于许多偏置方案 (bias scheme) 来说(如,与绝对温度成正比的方案,PTAT),噪声以绝对温度的平方根成正比地增大,因此在大范围的工业温度内噪声的变化相对很小(如,在25℃ 至125 ℃之间仅发生 15% 的变化)。
运算放大器噪声

Page 5 of 7
MT-047
NOISE nV / √Hz or µV / √Hz en, in k
3dB/Octave
en, in = k
FC
1 f
1 CORNER f WHITE NOISE
FC
LOG f
1/f Corner Frequency is a figure of merit for op amp noise performance (the lower the better) Typical Ranges: 2Hz to 2kHz Voltage Noise and Current Noise do not necessarily have the same 1/f corner frequency
Page 3 of 7
MT-047
EXAMPLE: OP27 Voltage Noise = 3nV / √ Hz Current Noise = 1pA / √ Hz T = 25°C
+ R OP27 – R2 Neglect R1 and R2 Noise Contribution
CONTRIBUTION FROM AMPLIFIER VOLTAGE NOISE AMPLIFIER CURRENT NOISE FLOWING IN R JOHNSON NOISE OF R
1. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 9780750687034. Chapter 1. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 1.
运算放大器总输出噪声计算

运算放大器总输出噪声计算 我们已经指出,噪声比一些较大噪声源少三分之一至五分之一的任何噪声源都可以忽略,几乎不会有误差。
此时,两个噪声电压必须在电路内的同一点测量。
要分析运算放大器电路的噪声性能,必须评估电路每一部分的噪声贡献,并确定以哪些噪声为主。
为了简化后续计算,可以用噪声频谱密度来代替实际电压,从而带宽不会出现在计算公式中(噪声频谱密度一般用nV/Hz表示,相当于1 Hz带宽中的噪声)。
如果考虑下图1中的电路由一个运算放大器和三个电阻组成的放大器(R3代表节点A处的源阻抗),可以发现六个独立噪声源:三个电阻的约翰逊噪声、运算放大器电压噪声和运算放大器各输入端的电流噪声。
每个噪声源都会贡献一定的放大器输出端噪声。
噪声一般用RTI来规定,或折合到输入端,但计算折合到输出端(RTO)噪声往往更容易,然后将其除以放大器的噪声增益(非信号增益)便得到RTI噪声。
下图2详细分析了图1中的各噪声源是如何反映到运算放大器输出端的。
有关反相输入端的电流噪声效应,还需要进一步讨论。
此电流IN–不会按预期流入R1放大器周围的负反馈可使得反相输入端的电位保持不变,因此从该引脚流出的电流在负反馈强制作用下仅能流入R2,从而产生IN– R2输出端电压。
也可以考虑IN–流入R1和R2并联组合产生的电压,然后通过放大器的噪声增益放大,但结果是一样的,计算反而更复杂。
请注意,与三个电阻相关的约翰逊噪声电压已包括在图2的表达式中。
所有电阻的约翰逊噪声为(4kTBR),其中k是玻尔兹曼常数(1.38&TImes;10–23 J/K),T是绝对温度,B是带宽(单位为Hz),R是电阻(单位为-)。
一个很容易记住的简单关系是:1000 -电阻在25ºC时产生的约翰逊噪声为4 nV/Hz。
以上分析假设是单极点系统,其中反馈网络为纯阻性,且噪声增益与频率关系曲线平坦。
2-3集成运算放大器的噪声

2.1 带宽校正系数
低通滤波器的宽带区域进行积分计算。 理想情况下,曲线的低通滤波器部分是一条直线,为理 想滤波器 。 由于理想滤波器情况下的曲线下方区域为矩形,因此这 一区域的问题比较好解决,长乘宽即可。 在实际情况下,不可能实现理想的滤波器。 不过,可用一组常量来将实际情况下的滤波器带宽转换 为等效的理想滤波器带宽,以满足噪声计算的需要。 这就是带宽校正系数
1、集成运算放大器的噪声
1/ƒ 噪声 (热 宽噪 带声 噪 声 )
表征噪声特性:
频谱密度。 电压噪声频谱密度:
每平方根赫兹的有效 ( RMS) 噪声电压 (单位为nV/Hz1/2)
功率谱密度单位为 W/ Hz1/2
集成运算放大器噪声频谱密度曲线
1.1
热噪声
热噪声的重要特性之一:白噪声 频谱密度图较平坦即所有频率的能量相同。 因此,热噪声有时也称作宽带噪声。 运算放大器也存在热噪声:
计算噪声增益: 噪声增益 = Rf/R1 + 1 = 100k/1k + 1 = 101 信号带宽受到运算放大器的闭环带宽的影响。 根据产品说明书中的单位增益带宽, 可用下式 来确定闭环带宽。
Closed_Loop_Bandwidth=Unitity_Gain_Bandwidth/Noise_Gain
3.4 运算放大器电路中电阻的噪声
还必须考虑的另一因素: 运算放大器电路中电阻的热噪声电压。 用节点分析法来独立分析电压源。 用叠加法与 RSS 添加法将结果相结合。
运算放大器电路的 电阻热噪声 (等效电路) 通过方程式 Req=R1||Rf
en _ R 4k TReq f
将所有电阻热噪声源 相结合,得到电阻热 噪声源参考输入。 乘以噪声增益得到输出端电阻热噪声
运算放大器电路固有噪声的分析与测量

和 用叠 加将 两个分 析结果 整合 。放 大器 来 ,把图 1 图 2中最 终传递函数 的
的上半部分是一个简单 的反相放 大器 , 结 果整 合。请注 意所有 的增益 都位于 增益为 一 :0 =- 1v V t 第一个级 ,第二 个级将 第一个 级 的差 动输 出转 换成 了一个 单端信 号。参考 电压直 接添加 到 了输 出端 ( 考信号 参
归并 在一起 。图 5显示了具有一 个或
增益 变化下 降。输出噪 声将 随着增益
两 噪 源 简 噪模 。 个 声 的化 声 型
l
i
的提 高而一 直增加。因此正 确的结论 是输入 级和输 出级在低增益 时都会 引 起 噪声 ,但 在高增益 时输入级 是带来
噪声 的主要原 因。由于在高增益 时噪
运算放大器 电路固有噪声的 分析与测量
An lssa dMe s r me t fn r scNos ay i n a u e n I tn i ie i OpAmp C r ut o i n i i c s
— —
● 德 州仪器 ( 1公司高级应用工程师 A t a T) rK y
图 5顶 部 的两 级模 型 具 有 一个 输 入 级 ( n i)电压 噪 声 源 和 一 个 V _n 输 出 级 (n ot V _ u)电压 噪 声 源。Vn
—
增益
1 2 5 1 O 10 0 10 00
一 m一 “ []n u 1 I t p 脚
向放大器每一半输 出端的转移 。
仪表 放大器 ( A 对 小差动信 号 I ) N
进 行 了放 大。大 多数 I A 都 包 括 若 N 干个 电阻 和运 算 放大 器 (pa s 。 o mp ) 虽然 可 以使 用分 立 组件 来 构 建 这 些 IA,但是 使用 单片 集成 电路 IA 的 N N
关于运算放大器电路噪声特性的简析

关于运算放大器电路噪声特性的简析【摘要】噪声是广播电视设备中的重要技术指标,“如何运用好噪声”对广播电视技术有着重要的意义。
本文简要介绍了运算放大器电路包含的噪声类型。
运用标准的电路理论和噪声模型,计算运算放大器电路的噪声。
最后,给设计人员提供了有关噪声设计的建议和方法。
【关键词】运算放大器;噪声;功率谱密度;噪声源1.引言早期的噪声研究,把具体电路中这种电流和电压的自然波动比作布朗运动。
1928年,J.B.John-son的研究证明,噪声对电子工程师设计精密放大器具有很大影响,一个电子线路灵敏度的极限,必须设置在信噪比刚好要下降到可接受限度的临界点上。
和是噪声谱密度,通常用来表征噪声参数。
它的出现简单地说是噪声功率会随着带宽的增加(每)而增加,因此,噪声电压或噪声电流会随着带宽平方根的增加(每Hz)而增加。
这种确定噪声源的参数等效总是与频率相结合的,表明谱密度是表征噪声源的天然形式。
2.运算放大器电路的噪声类型运算放大器电路中存在5种噪声源:散粒噪声(Shot Noise)热噪声(Thermal Noise)闪烁噪声(Flicker Noise)爆裂噪声(Burst Noise)雪崩噪声(Avalanche Noise)爆裂噪声和雪崩噪声在运算放大器电路中通常没有太大影响,即使有,也能够消除,在噪声分析中可以不予考虑。
下面逐一介绍各种噪声源。
2.1 散粒噪声散粒噪声总是与电流流动相联系的。
无论何时电荷流过势垒(如pn结),导体不再处于热平衡状态,都会导致散粒噪声产生。
流过势垒纯粹是随机事件,因此,大量随机、独立的电流脉冲的平均值iD就形成了瞬时电流i。
散粒噪声是白噪声(某一频率范围内谱密度保持常数的噪声信号),它的频谱是平坦的(作一条相对于频率的散粒噪声曲线时,噪声值始终恒定),即功率密度是均匀的。
此外,散粒噪声与温度无关。
2.2 热噪声热噪声是由于导体内部载流子(电子或空穴)的无规则热运动产生的。
运放噪声计算公式

运放噪声计算公式运放噪声是在电子电路设计中一个比较重要的概念,特别是在对精度要求较高的模拟电路中。
要搞清楚运放噪声的计算公式,咱们得先从噪声的基本概念说起。
噪声这玩意儿,就像是电路里的“小捣蛋鬼”,总是在你不注意的时候出来捣乱,影响电路的性能。
比如说,在音频放大器中,噪声可能会让你听到“沙沙”的声音;在测量仪器中,噪声可能会导致测量结果不准确。
运放的噪声主要来源于两个方面:一是内部的热噪声,二是闪烁噪声。
热噪声就像是一群调皮的孩子在教室里乱跑乱撞,是由电子的随机运动产生的。
而闪烁噪声呢,则像是一个神秘的“隐身侠”,在低频时特别活跃,它的产生机制比较复杂,咱先不深究。
那运放噪声的计算公式是啥呢?一般来说,运放的总噪声电压可以用下面这个公式来计算:\(V_{n,tot} = \sqrt{V_{n1}^2 + V_{n2}^2 + V_{n3}^2 + ...... +V_{nn}^2}\)这里面,\(V_{n1}\)、\(V_{n2}\) 等等分别是不同噪声源的噪声电压。
我记得有一次,我在设计一个用于传感器信号放大的电路时,就因为没有充分考虑运放的噪声,结果出来的数据总是有一些莫名其妙的波动。
我当时那叫一个郁闷啊,反复检查电路的连接,确定没有接错线。
然后又开始怀疑是不是传感器出了问题,把传感器换了一个新的,还是不行。
最后,经过一番仔细的分析和计算,才发现原来是运放的噪声在作祟。
要计算每个噪声源的噪声电压,那又得用到不同的公式。
比如热噪声的电压可以用下面这个公式计算:\(V_{n,thermal} = \sqrt{4kTRB}\)这里的 \(k\) 是玻尔兹曼常数,\(T\) 是绝对温度,\(R\) 是电阻值,\(B\) 是带宽。
而闪烁噪声的电压通常可以表示为:\(V_{n, flicker} = K / \sqrt{f}\)其中 \(K\) 是一个与器件相关的常数,\(f\) 是频率。
在实际应用中,我们还得考虑运放的增益对噪声的影响。
运算放大器电路固有噪声的分析与测量(六)

运算放大器电路的固有噪声分析与测量(六):噪声测量实例在第 5 部分我们介绍了不同类型的噪声测量设备。
我们将在第 6 部分讨论与噪声测量相关的参数和操作模式。
在这里我们将列举一些实际应用的例子,来说明如何使用该设备对第3 部分及第 4 部分所描述的电路进行测量。
屏蔽:测量固有噪声时,消除外来噪声源是很重要的。
常见的外来噪声源有:电源线路“拾取”(“拾取”是指引入外来噪声,比如60Hz 噪声)、监视器噪声、开关电源噪声以及无线通信噪声。
通常利用屏蔽外壳将所测电路放置于其中。
屏蔽外壳通常由铜、铁或铝制成,而重要的是屏蔽外壳应与系统接地相连。
一般来说,电源线缆和信号线缆是通过外壳上的小孔连接到屏蔽外壳内电路的。
这些小孔尽可能地小,数量也要尽可能地少,这一点非常重要。
实际上,解决好接缝、接合点以及小孔的(电磁)泄露,就可以实现较好的屏蔽效果。
[1]图6.1 举例显示了一种极易构建且非常有效的屏蔽外壳,该屏蔽外壳是采用钢漆罐制成的(这些材料可从绝大多数五金商店买到,而且价格也不高)。
漆罐有紧密的接缝,并且罐盖的设计可以使我们方便地接触到所测电路。
请注意,I/O 信号是采用屏蔽式同轴线缆进行连接的,该同轴线缆采用BNC 插孔-插孔式连接器将其连接到所测试的电路;BNC 插孔-插孔式连接器壳体与漆罐进行电气连接。
外壳唯一的泄露路径是将电源连接到所测电路的三个香蕉插头(banana connector)。
为了实现最佳的屏蔽效果,应确保漆罐密封紧固。
图6.2 为测试用漆罐装配示意图图6.1:使用钢漆罐进行测试。
图6.2:测试用漆罐装配示意图。
检测噪声底限一个常见的噪声测量目标是测量低噪声系统或组件的输出噪声。
通常的情况是,电路输出噪声太小,以至于绝大多数的标准测试设备都无法对其进行测量。
通常,会在所测试电路与测试设备之间放一个低噪声升压放大器(boost amplifier)(见图 6.3)。
采用该种配置的关键是升压放大器的噪声底限要低于所测电路的输出噪声,从而使得所测电路噪声能在测量中反映出来。
运算放大器的噪声分析

运算放大器的噪声分析运算放大器的噪声分析2010年11月02日星期二16:24问:有关运算放大器的噪声我应该知道些什么?答:首先,必须注意到运算放大器及其电路中元器件本身产生的噪声与外界干扰或无用信号并且在放大器的某一端产生的电压或电流噪声或其相关电路产生的噪声之间的区别。
干扰可以表现为尖峰、阶跃、正弦波或随机噪声而且干扰源到处都存在:机械、靠近电源线、射频发送器与接收器、计算机及同一设备的内部电路(例如,数字电路或开关电源)。
认识干扰,防止干扰在你的电路附近出现,知道它是如何进来的并且如何消除它或者找到对干扰的方法是一个很大的题目。
如果所有的干扰都被消除,那么还存在与运算放大器及其阻性电路有关的随机噪声。
它构成运算放大器的控制分辨能力的终极限制。
我们下面的讨论就从这个题目开始。
问:好,那就请你讲一下有关运算放大器的随机噪声。
它是怎么产生的?答:在运算放大器的输出端出现的噪声用电压噪声来度量。
但是电压噪声源和电流噪声源都能产生噪声。
运算放大器所有内部噪声源通常都折合到输入端,即看作与理想的无噪声放大器的两个输入端相串联或并联不相关或独立的随机噪声发生器。
我们认为运算放大器噪声有三个基本来源:★一个噪声电压发生器(类似失调电压,通常表现为同相输入端串联)。
★两个噪声电流发生器(类似偏置电流,通过两个差分输入端排出电流)。
★电阻噪声发生器(如果运算放大器电路中存在任何电阻,它们也会产生噪声。
可把这种噪声看作来自电流源或电压源,不论哪种形式在给定电路中都很常见)。
运算放大器的电压噪声可低至3 nV/Hz。
电压噪声是通常比较强调的一项技术指标,但是在阻抗很高的情况下电流噪声常常是系统噪声性能的限制因素。
这种情况类似于失调,失调电压常常要对输出失调负责,但是偏置电流却有真正的责任。
双极型运算放大器的电压噪声比传统的FET 运算放大器低,虽然有这个优点,但实际上电流噪声仍然比较大。
现在的FET运算放大器在保持低电流噪声的同时,又可达到双极型运算放大器的电压噪声水平。
运算放大器电路固有噪声的分析与测量

运算放大器电路中固有噪声的分析与测量第一部分:引言与统计数据评论作者:德州仪器公司高级应用工程师 Art Kay我们可将噪声定义为电子系统中任何不需要的信号。
噪声会导致音频信号质量下降以及精确测量方面的错误。
板级与系统级电子设计工程师希望能确定其设计方案在最差条件下的噪声到底有多大,并找到降低噪声的方法以及准确确认其设计方案可行性的测量技术。
噪声包括固有噪声及外部噪声,这两种基本类型的噪声均会影响电子电路的性能。
外部噪声来自外部噪声源,典型例子包括数字交换、60Hz 噪声以及电源交换等。
固有噪声由电路元件本身生成,最常见的例子包括宽带噪声、热噪声以及闪烁噪声等。
本系列文章将介绍如何通过计算来预测电路的固有噪声大小,如何采用 SPICE 模拟技术,以及噪声测量技术等。
热噪声热噪声由导体中电子的不规则运动而产生。
由于运动会升高温度,因此热噪声的幅度会随温度的上升而提高。
我们可将热噪声视为组件(如电阻器)电压的不规则变化。
图 1.1 显示了标准示波器测得的一定时间域中热噪声波形,我们从图中还可看到,如果从统计学的角度来分析随机信号的话,那么它可表现为高斯分布曲线。
我们给出分布曲线的侧面图,从中可以看出它与时间域信号之间的关系。
图 1.1: 在时间域中显示白噪声以及统计学分析结果热噪声信号所包含的功率与温度及带宽直接成正比。
请注意,我们可简单应用功率方程式来表达电压与电阻之间的关系(见方程式1.1),根据该表达式,我们可以估算出电路均方根 (RMS) 噪声的大小。
此外,它还说明了在低噪声电路中尽可能采用低电阻元件的重要性。
e n4kTR∆f where e is the rms noise voltageT is Temperature in Kelvin (K)R is Resistance in Ohms (Ω)f is noise bandiwdth frequency in Hertz (Hz)k is Boltzmann's Constant 1.381E-23 joule/KNote to convert degrees Celsius to KelvinT K = 273.15o C + T C方程式 1.1:热电压方程式 1.1 中有一点值得重视的是,根据该表达式我们还可计算出 RMS 噪声电压。
运放噪声计算

运放噪声计算引言:运放(Operational Amplifier,简称Op Amp)是一种常用的电子器件,广泛应用于模拟电路中。
然而,在实际应用中,我们常常会遇到运放噪声的问题。
本文将介绍运放噪声的概念、分类和计算方法,帮助读者更好地理解和解决运放噪声问题。
一、运放噪声概述运放噪声是指运放内部电子元件运动导致的电压或电流的随机变化,表现为输出信号中的杂散噪声。
它由多种因素引起,包括热噪声、互模干扰、电流噪声等。
二、运放噪声分类根据引起噪声的原因和特性,运放噪声可分为以下几类:1. 热噪声:也称为白噪声,是由于温度引起的电子元件的随机热运动所产生的噪声。
在运放中,热噪声主要源自电阻、电容和晶体管等元件。
2. 互模干扰:也称为互调噪声,是由于不同信号在运放内部进行非线性混频而产生的干扰。
互模干扰会导致不同频率的信号相互干扰,降低运放的性能。
3. 电流噪声:是由于电子元件内部的电流随机变化引起的噪声。
电流噪声主要源自晶体管的随机电流涨落,对运放的放大性能产生影响。
三、运放噪声计算方法运放噪声的计算可以帮助我们评估运放的性能,并选择合适的运放器件。
下面介绍几种常用的运放噪声计算方法。
1. 热噪声计算:运放的热噪声主要由电阻引起。
根据热噪声的公式,可以计算出运放的等效输入噪声电压和输出噪声电压。
2. 电流噪声计算:运放的电流噪声主要由晶体管引起。
通过测量运放的输入等效电压噪声和输入电阻,可以计算出运放的等效输入噪声电流。
3. 互模干扰计算:互模干扰的计算相对复杂,需要考虑不同信号频率的非线性混频效应。
一种常用的方法是通过频谱分析来评估互模干扰的影响。
四、运放噪声优化方法为了降低运放噪声,我们可以采取以下几种方法:1. 选择低噪声运放器件:市场上有许多低噪声运放器件可供选择,选择合适的器件可以降低运放噪声。
2. 降低运放的温度:热噪声是温度相关的,降低运放的工作温度可以减小热噪声。
3. 优化电路布局:合理的电路布局可以减少电路中的干扰,降低噪声。
运算放大器噪声关系1f噪声、均方根(RMS)
MT-048
GAUSSIAN NOISE
SOURCE
SINGLE POLE LOWPASS FILTER, fC
IDENTICAL LEVELS
GAUSSIAN NOISE
SOURCE
BRICK WALL LOWPASS
FILTER, 1.57fC
SAME RMS NOISE
Page 6 of 6
6.6 × rms**
0.10%
7 × rms
0.046%
8 × rms
0.006%
**Most often used conversion factor is 6.6
图5:均方根-峰峰值比
Page 5 of 6
MT-048
因此,峰峰值噪声规格必须写上时间限制。6.6乘以均方根值较为合适,即该值仅在0.1% 的时间内被超过。 参考文献
均方根噪声考虑
如上所述,噪声频谱密度与频率成函数关系。为了获得均方根噪声,噪声频谱密度曲线必 须在整个目标带宽上积分。
在1/f区域中,带宽FL至FC内的均方根噪声由下式给出
公式2
其中,vnw表示“白”区域内的电压噪声频谱密度,FL表示1/f区域中的最低目标频率,而FC表 示1/f转折频率。
下一目标区域是从FC至FH的“白”噪声区。该带宽内的均方根噪声由下式给出
0.1Hz to 10Hz VOLTAGE NOISE
25
20
1/F CORNER
FC = 0.7Hz
15
vnw (WHITE) 10
200nV
5
0.1
1
10
100
FREQUENCY (Hz)
TIME - 1sec/DIV.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
– VN +
Input Voltage Noise is bandwidth dependent and measured in nV/√Hz (noise spectral density) Normal Ranges are 1nV/√ Hz to 20nV/√Hz
图1:输入电压噪声
电压噪声因运算放大器而异,可能不到1 nV/√Hz,也可能高达20 nV√Hz,甚至更高。双 极性运算放大器的电压噪声往往低于JFET运算放大器;虽然也可以使JFET运算放大器具 有低电压噪声(如 AD743/AD745),但涉及的输入器件非常大,因而输入电容也就相当 高。数据手册中会给出电压噪声,该值无法从其它参数中预测。
1 1k 10k 10 100 1k 10k
RS = 1MΩ
All Horizontal Scales Hz
100 10 100 1k 10k
图5:源阻抗不同时最佳放大器也不同
电压和电流噪声的频率特性 前面我们都假设噪声为“白噪声”(即其频谱密度不会随频率而变化)。这种情况适用于运算 放大器的大部分频率范围,但在低频率条件下,噪声频谱密度会以3 dB/倍频程上升,如 下面图6所示。功率频谱密度在此区域内与频率成反比,因此电压噪声频谱密度与频率的 平方根成反比。因此,这种噪声通常称为“1/f噪声”。但应注意,有些教材中仍旧使用 “闪 烁噪声”这个旧术语。 这种噪声开始增加时的频率称为“1/f转折频率(FC)”,也是品质因数之一——该频率越小越 好。对于特定放大器,电压噪声和电流噪声的1/f转折频率并不一定相同,有的电流反馈 运算放大器可能具有三个1/f转折频率:一个针对其电压噪声,另一个针对其反相输入电 流噪声,还一个则针对其同相输入电流噪声。
Page 4 of 7
MT-047
100
741 795 744 OP07 743
100 RS = 100Ω
744 OP27, 795 741
RS = 10kΩ
10
10
OP27 OP07, 743
1 10 100 10k All Vertical Scales nV /√ Hz 1k
744பைடு நூலகம்743 795 741 OP27 OP07
图6:运算放大器噪声的频率特性
用来描述1/f区域内电压或电流噪声频谱密度的通用计算公式如下 公式 1 其中,k表示“白”电流或电压噪声电平,而FC表示1/f转折频率。 最佳低频率、低噪声放大器的转折频率位于1-10 Hz范围内,而JFET器件和更为通用的运 算放大器则位于1-100 Hz范围内。不过,超高速放大器可能会在处理能力上做出让步以便 实现高速性能,从而导致1/f转折频率特性相当差,高达数百Hz,甚至1-2 kHz。对于此类 器件所针对的宽带应用,这点通常并不是很重要,但可能会影响其在音频条件下使用, 尤其是在均衡电路中。 “爆米花”噪声 “爆米花噪声”之名源于通过音频系统播放时,它听起来像炒爆米花。该噪声由失调电压的 随机阶跃变化组成,发生间隔为10+毫秒时间范围内的随机值。此类噪声由硅片表面存在 严重污染及晶格移位所导致,而这是工艺技术不合适或原材料品质欠佳而造成的。
Page 2 of 7
MT-047
IN – IN+ +
Normal Ranges: 0.1fA/√ Hz to 10pA/√Hz In Voltage Feedback op amps the current noise in the inverting and non-inverting inputs is uncorrelated (effectively) but roughly equal in magnitude. In simple BJT and JFET input stages, the current noise is the shot noise of the bias current and may be calculated from the bias current. In bias-compensated input stages and in current feedback op amps, the current noise cannot be calculated. The current noise in the two inputs of a current feedback op amp may be quite different. They may not even have the same 1/f corner.
Page 6 of 7
MT-047
上世纪60年代首次推出单芯片运算放大器时,爆米花噪声是主要噪声源。不过,如今人 们已经充分认识到爆米花噪声的成因,再加上原材料纯度高、污染程度低且生产测试可 靠,对任何运算放大器制造商来说,生产基本上没有爆米花噪声的产品应该不是什么难 事。因此,多数现代运算放大器教材中甚至不会提到该噪声。 参考文献
VALUES OF R 0 3kΩ 300kΩ
3 0 0
3 3 7
3 300 70
R1
RTI NOISE (nV / √ Hz) Dominant Noise Source is Highlighted
图4:源阻抗不同时主要噪声源也不同
从上例可以看出,选择低噪声运算放大器时主要取决于信号的源阻抗,而在高阻抗条件 下,电流噪声始终占据主导地位。 从下面的图5可以明显看出,源阻抗不同时,最佳放大器也不同。对于低阻抗电路,明显 应该选择OP27等低电压噪声放大器,因为这类放大器价格低廉,并且相对较高的电流噪 声不会对应用造成影响。在阻抗处于中等水平时,电阻的约翰逊噪声占据主导地位,而 在源阻抗非常高的情况下,则必须尽可能选择电流噪声最小的运算放大器,如AD549或 AD795。 目前,BiFET放大器往往具有相对较高的电压噪声(不过电流噪声极低),因此更适合低噪 声应用中的高阻抗电路,而不是低阻抗电路。AD795、AD743和AD745具有极低的电压 噪声和电流噪声。10 kHz时,AD795的电压噪声和电流噪声分别为10 nV/√Hz和 0.6 fA/√Hz,而AD743/AD745则分别为2.9 nV/√Hz和6.9 fA/√Hz。利用这些器件可以设计 在宽源阻抗范围内具有低噪声性能的低噪声放大器电路。
1. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 9780750687034. Chapter 1. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 1.
Page 5 of 7
MT-047
NOISE nV / √Hz or µV / √Hz en, in k
3dB/Octave
en, in = k
FC
1 f
1 CORNER f WHITE NOISE
FC
LOG f
1/f Corner Frequency is a figure of merit for op amp noise performance (the lower the better) Typical Ranges: 2Hz to 2kHz Voltage Noise and Current Noise do not necessarily have the same 1/f corner frequency
图3:输入电流噪声
只有在阻抗中流动并进而产生噪声电压时,才需要考虑电流噪声。在运算放大器电路的 输入端保持相对较低的阻抗,可以显著降低电流噪声的影响(就像相同操作也有助于将失 调电压降至最低一样)。 因此,低噪声运算放大器的最佳选择理所当然地取决于其周围的阻抗。下面将通过一些 阻抗示例进一步说明。 合并噪声源 不相关的噪声电压(如均方根噪声电压V1、V2、V3)以“方和根”形式相加,即可得到√(V12 + V22 + V32)。当然,噪声功率照常相加。因此,大小是任何其他噪声电压3-5倍的噪声电压 占据主导地位,而其他噪声电压通常可以忽略不计。这样可以简化复杂电路中的噪声评 估。 确定主要噪声源 以OP27为例,该运算放大器具有低电压噪声(3 nV/√Hz),但电流噪声却相当高(1 pA/√Hz)。 在无源阻抗条件下,电压噪声是主要噪声源,如下面图4所示(左边一栏)。当源阻抗为3 kΩ( 中间一栏)时,流经3 kΩ的1 pA/√Hz电流噪声就等于电压噪声,但3 kΩ电阻的约翰逊噪声 为7 nV/√Hz,占据主导地位。当源阻抗为300 kΩ(右边一栏)时,电流噪声部分增长100倍, 达到300 nV/√Hz,电压噪声继续保持不变,而约翰逊噪声(与电阻“平方根”成比例)则增长十 倍。电流噪声占据主导地位。
图2:电阻的约翰逊噪声
运算放大器输入电流噪声 电流噪声的变化范围远大于电压噪声;视输入结构而定,从大约0.1 fA/√Hz(JFET静电计运 算放大器中)到数pA/√Hz(高速双极性运算放大器中)不等。数据手册中不一定会给出该项 数据,但在简单的BJT或JFET等器件中却可以计算得出,因为在这类情况下,所有偏置电 流均流入输入结点,电流噪声就是偏置电流的肖特基噪声(或称散粒噪声)。 散粒噪声频谱密度就是√(2IBq)/√Hz,其中IB表示偏置电流(放大器内),而q表示电子电荷 量(1.6 × 10–19 C)。在偏置补偿或电流反馈运算放大器中,外部偏置电流是两个内部电流之 间的“差值”,因此无法计算出电流噪声。简单电流噪声模型如下面图3所示。
