第六章流体力学题库5-1-8
流体力学课后习题答案第六章

6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l /s ,水温为10oC ,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-= 由214Q nd v π= ①及临界雷诺数R e 2300vdν== ② 联立有 14d m m = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510ggJ 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510ggJ 1.0109.80.20147Pa 2l22τρρ-⨯===⨯⨯⨯⨯=2'3r1010gJ 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯=6.9为了确定圆管内径,在管内通过ν为0.013 cm 2/s 的水,实测流量为35cm 3/s ,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gdlQgdl gd l d h f πνυνυυν===11441281280.013150035 1.949802f lQ d cm ghνππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Qd 层流6-18 利用圆管层流Re64=λ,紊流光滑区25.0Re3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v∝f h ,光滑区75.1v∝f h ,粗糙区0.2v∝f h ;(2) 在不计局部损失h m 的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失h f 不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失h m 的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失h f 减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几? 解:(1)由R e vdν=,22f l vh d gλ=有1232f l h v gdν=即在层流 1.0f h v∝由0.250.3164R eλ=得0.251.752 1.250.1582f lvh dgν=光滑区 1.752f h v∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505sf k lh v dg=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为14128f lQh d gνπ=Q 变为16倍0.251.752 4.751.750.7898f lQh dg νπ=Q 变为6.56倍0.2523 5.2520.808sf k lQh dg π=Q 变为6.17倍(3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比h f 圆/h f 方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少? 解:(1)2214d a π=224a dπ=当量直径de a = 层流时 226464R e 22f l vlv h d gd gν==22220.7854f h de a h ddπ====圆方紊流粗糙区22f l vh d gλ=,λ相等0.886f h de a h dd====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 l/s ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
流体力学课后习题答案第六章

6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l /s ,水温为10oC ,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-=由214Q nd v π= ① 及临界雷诺数Re 2300vdν== ②联立有 14d mm = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510g g J 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510g g J 1.0109.80.20147Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=2'3r 1010g J 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯= 6.9为了确定圆管内径,在管内通过ν为0.013 cm 2/s 的水,实测流量为35cm 3/s ,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gd lQ gd l g d l d h f πνυνυυν===11441281280.013150035 1.949802f lQ d cm gh νππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Q d 层流 6-18 利用圆管层流Re 64=λ,紊流光滑区25.0Re 3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v ∝f h ,光滑区75.1v ∝f h ,粗糙区0.2v ∝f h ;(2) 在不计局部损失h m 的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失h f 不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失h m 的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失h f 减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几?解:(1)由Re vdν=,22f l v h d g λ=有1232f lh v gd ν=即在层流 1.0f h v ∝由0.250.3164Re λ= 得0.25 1.752 1.250.1582f lv h d g ν=光滑区 1.752f h v∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505s f k l h v d g=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为 14128f lQh d gνπ=Q 变为16倍0.25 1.7524.75 1.750.7898f lQ h d g νπ= Q 变为6.56倍0.25235.2520.808s f k lQ h d g π= Q 变为6.17倍 (3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比h f 圆/h f 方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少?解:(1) 2214d a π= 224a d π=当量直径de a =层流时 226464Re 22f l v lv h d g d gν==22220.7854f h de a h d d π====圆方紊流粗糙区22f l v h d gλ=,λ相等0.886f h de a h d d ====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 l/s ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
李玉柱流体力学课后题答案 第六章

第六章 孔口、管嘴出流与有压管流6-1 在水箱侧壁上有一直径50mm d =的小孔口,如图所示。
在水头H 的作用下,收缩断面流速为 6.86m/s C V =,经过孔口的水头损失0.165m w h =,如果流量系数0.61μ=,试求流速系数ϕ和水股直径c d 。
解:根据伯努利方程:22.51m 2c w V H h g=+= 流速系数0.9672c cV V V gHϕ=== 2c c Q A gH AV μ==,39.71mm cd = 6-2 图示一船闸闸室,闸室横断面面积2800m A =,有一高2m h =、宽4m b =的矩形放水孔。
该孔用一个速度0.05m/s v =匀速上升的闸门开启。
假设初始水头15m H =,孔口流量系数0.65μ=,孔口出流时下游水位保持不变。
试求(1)闸门开启完毕时闸室中水位降低值y ;(2)闸室水位与下游平齐所需要的总时间T 。
解:(1)闸门完全开启所用的时间:40s ht v== 此段时间内孔口的面积可用孔的平均面积来表示:24m A =因为40s T ==所以:2 3.796m H =,12 1.204m y H H =-=(2)闸门完全打开后,防水孔的面积:28m A bh '== 液面降到与下游液面平齐所需要的时间因为135.41s T '==所以175.41s T t T '=+=6-3 贮液箱中水深保持为 1.8m h =,液面上的压强070kPa p =(相对压强),箱底开一孔,孔直径50mm d =。
流量系数0.61μ=,求此底孔排出的液流流量。
解:根据伯努利方程:202p V h g gρ+= 215.9L/s 4Q d V πμ==6-4 用隔板将矩形水池中的水体分成左右两部分,如图所示,右半部分水面保持恒定,隔板上有直径10.1m d =的圆形孔口,位于右半部液面下1 4.8m H =处。
在左半部分的侧面与前一孔口相同的高度处开有直径20.125m d =的圆形孔口,当水池两半部分的水面稳定后,试求左半部水面高度计孔口出流流量。
《流体力学》徐正坦主编课后答案第6、7、8章

第六、七、八章习题简答6-1 假设自由落体的下落距离s与落体的质量m,重力加速度g及下落时间t有关,试用瑞利法导出自由落体下落距离的关系式。
解:首先将关系式写成指数关系:s=Km a g b t c其中,K为无量纲量,也称无量系数。
各变量的量纲分别为:dim s=L,dim W=MLT-2,dim t= T,dim g=LT-2。
将上式指数方程写成量纲方程:L=( MLT-2) a ( LT-2) b ( T) c根据物理方程量纲一致性原则得到M:0=aL:1=a+bT:0=-2a-2b+c得出a=0 b=1 c=2代入原式,得s=Km0gt2即s=Kgt2注意:式中重量的指数为零,表明自由落体距离与重量无关。
其中系数K须由实验确定。
6-7已知矩形薄壁堰的溢流量Q与堰上水头H、堰宽b、水的密度ρ和动力粘滞系数μ,重力加速度g 有关,试用π定理推导流量公式。
题6-7图解:首先将函数关系设为 F(Q ,H ,b ,ρ,μ,g )=0其中变量数n=6,选取基本变量H 、ρ、g ,这3个变量包含了L 、T 、M 三个基本量纲。
根据π定理,上式可变为 f (π1,π2,π3)=0 式中Q g H c b a 1111ρπ=b g Hc b a 2222ρπ=μρπ3333c b a g H =将各数方程写成量纲形式:)()()(dim 132********---==T L LT ML L T L M c b a π根据量纲的一致性,有: L :a 1-3b 1+c 1+3=0 T :-2c 1-1=0 M :b 1=0得a 1=-5/2,b 1= 0,c 1= -1/2所以 gHQ Q g H 2521251==--π同理可得Hb b H ==-12πgH g H ρμμρπ23211233==---这样原来的函数关系可写成0(2325=),,gH H b g H Q f ρμ 即),gH H b f gHQ ρμ23125(=则5252312((H g Hb f H g g H H b f Q )),==ρμ 6-8 加热炉回热装置冷态模型试验,模型长度比尺λl =5,已知回热装置中烟气的运动粘滞系数为ν=0.7×10-4m 2/s ,流速为υ=2.5m/s ,试求20℃空气在模型中的流速为多大时,流动才能相似。
流体力学第六章边界层流动5

层流与紊流、雷诺数
在不同的初始和边界条件下,粘性流体质点的运动会出现两种不同
的运动状态,一种是所有流体质点作定向有规则的运动,另一种是
作无规则不定向的混杂运动。前者称为层流状态,后者称为湍流状 态(别称紊流状态)。首先是英国物理学家雷诺在1883年用实验证
明了两种流态的存在,确定了流态的判别方法。
u???????????????????????用量纲分析的方程分析法可得一般二维流动无量纲方程组用量纲分析的方程分析法可得一般二维流动无量纲方程组621平板层流边界层微分方程精确解0??????yuxuyxre12222yuxuxpeuyuuxuuxxxyxx???????????????1121?11?11?11???2?2015112924忽略第二方程最后一项第三方程除压强项的其他项
vc d Re c
Re c
vc d
Re 2320时,管中是层 流; Re 2320时,管中是紊 流。
2018/10/31 13
根据实验结果可知,同管流一样,边界层内也存在着层流和紊流两种 流动状态,若全部边界层内部都是层流,称为层流边界层;若全部边界层 内部都是湍流,称为湍流边界层;若在边界层起始部分内是层流,而在 其余部分内是紊流,称为混合边界层。如图所示,在层流变为紊流之间 有一过渡区。在紊流边界层内紧靠壁面处也有一层极薄的层流底层。
dp dU U dx dx
②第二式右边得到简化(x方向二阶偏导数消失),有利于数值计算。 利用该方程就可计算壁切应力和流动阻力,具有里程碑式意义。
2018/10/31 25
布拉修斯利用相似性解法,引入无量纲坐标:
Rex
*
*
流体力学课后题

第一章 绪论1-6.图示为一水平方向运动的木板,其速度为1m s,平板浮在油面上,油深 1mm δ=,油的0.09807Pa s μ=,求作用于平板单位面积上的阻力?⎡⎤⎣⎦解10.0980798.070.001du Pa dy τμ==⨯= 1-7. 温度为20℃的空气,在直径为2.5cm 管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的粘滞切应力为多少? 解: f=m N dyduA/103.410/1031105.2100183.053223-----⨯=⨯⨯⨯⨯⨯⨯=πμ 1-8.一底面积为4045cm ⨯,高为1cm 的木板,质量为5kg ,沿着涂有润滑油的斜面等速向下运动,1m v s=,1mm δ=,求润滑油的动力黏度?⎡⎤⎣⎦解0T GSin α-=55255131313T GSin G g g α==⋅=⨯⨯=所以 10.400.451800.001du T A dy μμμ==⨯=但 259.8070.10513180Pa s μ⨯==⋅⨯所以5第二章 流体静力学2-6.封闭容器水面的绝对压强20107.7KNp m=,当地大气压强298.07a KNp m =,试求〔1〕水深0.8h m =的A 点的绝对压强和相对压强?〔2〕假设容器水面距基准面高度5Z m =,求A 点的测压管高度和测压管水头。
并图示容器液体各点的测压管水头线;〔3〕压力表M 和酒精〔27.944KNm γ=〕测压计h 的读数值?hh 1AM p 0⎡⎤⎣⎦解〔1〕201107.79.8070.8115.55A KN p p h m γ'=+=+⨯= 2115.5598.0717.48A A a KN p p p m '=-=-=〔2〕217.481.789.807Ap h m γ=== 25 1.78 6.78n A H Z h m =+=+=〔3〕20107.798.079.63M a KNp p p m =-=-=9.631.217.944Mp h m γ=== 2-16. 水箱真空表M 的读数为0.98kPa ,水箱与油箱的液面差H =1.5m ,水银柱差m 2.02=h ,3m /kg 800=油ρ,求1h 为多少米?解:取等压面1-1,那么()()()()()12122211332800.29809800 1.50.2 5.610008009.8a a Hg Hg P P g H h h P gh gh gh P g H h h gmρρρρρρρ-+++=+++-+=-⨯+-⨯+==-⨯油油2-20.图为倾斜水管上测定压差的装置,cm 20=z ,压差计液面之差cm 12=h ,求当〔1〕31kg/m 920=ρ的油时;〔2〕1ρ为空气时;A 、B 两点的压差分别为多少?解:〔1〕取等压面1-1 PaghgZ gh P P ghgZ P gh P A B B A 92.1865)12.02.0(980012.08.992011=-⨯+⨯⨯=-+=---=-ρρρρρρ〔2〕同题〔1〕可得Pagh gZ P P gZP gh P A B B A 784)12.02.0(9800=-⨯=-=--=-ρρρρ2-36.有一圆滚门,长度10l m =,直径4D m =,上游水深14H m =,下游水深22H m =,求水作用于圆滚门上的水平和铅直分压力?⎡⎤⎣⎦解2212121()2x x x p p p l H H γ=-=- 2219.80710(42)5902KN =⨯⨯⨯-=23439.8074109204z p V Al R lKN γγγππ==•==⨯⨯⨯=2-44.一洒水车以等加速度2/98.0s m a =在平地上行驶,水车静止时,B 点位置m x 5.11=,m h 1=,求运动后该点的静水压强。
流体力学题库

名词解释1。
粘性:在外力作用下,流体微元间出现相对运动时,随之产生阻抗相对运动的内摩擦力2。
压缩系数:在一定温度下,密度的变化率与压强的变化成正比3。
膨胀系数:在一定压强下,体积的变化率与温度的变化成正比4.表面张力:通常是指液体与气体交界面上的张应力( 单位长度所受拉力(N/m) )5.接触角:当液体与固体壁面接触时, 在液体,固体壁面作液体表面的切面, 此切面与固体壁在液体内部所夹部分的角度θ称为接触角,当θ为锐角时, 液体润湿固体,当θ为钝角时,液体不润湿固体。
6。
时变导数:固定点物理量A随时间变化率,反映流场的不定常性。
7。
位变导数:不同位置上物理量的差异引起的变化率,反映流场的不均匀性8.流管:在液流中取一封闭的曲线,通过这一封闭曲线上每一点可以引出一条流线,这些流线形成一个封闭的管状体,称为流管。
9.总流:过流断面为有限大小的流束,它由无数元流构成10.涡管:在给定瞬时,在涡量场中取一不是涡线得封闭曲线,通过曲线上每点做涡线,这些涡线形成一个管状表面,称为涡管,涡管中充满着做旋转运动的流体。
11。
漩涡强度:面积dA,dA上流体质点的旋转角速度向量为ω,n为dA的法线方向,微元面积上的漩涡强度用dI表示,公式为:对整个表面积A积分,总的漩涡强度为:12.速度环量:假定某一瞬时,流场中每一点的速度是已知的,AB曲线上任一点的速度为V,在该曲线上取一微元段ds,V与ds之间的夹角为α,则称dГ=V·ds=V cos αds为沿微元线段ds上的环量。
简答题拉格朗日法与欧拉法的区别与联系:区别:拉格朗日法是以研究单个流体质点运动过程作为基础,综合所有质点的运动,构成整个流体的运动.——质点法欧拉法是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法.——流场法 它不直接追究质点的运动过程,而是以充满运动液体质点的空间--流场为对象。
联系:拉格朗日法和欧拉法只不过是描述流体运动的两种不同的方法,本质上是一样的。
第6章-流体流动微分方程-例题
0 0 0
θ:
2 v ∂v v v ∂vθ ∂v ⎡ ∂ ⎛1 ∂ 1 1 ∂p ⎞ 1 ∂ vθ 2 ∂vr ⎤ + ν ⎢ ⎜ (rvθ) + + vr θ + θ θ + r θ = fθ − + ⎟ 2 ρ r ∂θ r r ∂θ r
∂r ⎝ r ∂r ∂t ∂r ∂θ 2 r 2 ∂θ ⎥ ⎠ ⎣ ⎦
工程流体力学——第六章 流体流动微分方程——例题
CH6-5
r:
2 ⎡ ∂ ⎛1 ∂ ∂vr ∂v v ∂v v 2 1 ∂p ⎞ 1 ∂ vr 2 ∂vθ ⎤ + vr r + θ r − θ = f r − + − 2 + ν ⎢ ⎜ (rvr) ⎥ ⎟ 2 2 r r ∂ r ∂θ ⎦ θ r N ρ ∂r ∂t ∂ ∂r ⎝ r ∂r ⎠ r ∂θ ⎣
∂vz dv =μ z ∂r dr
由此可知:(a)不可压缩一维稳态层流每点各方向正应力=-p,因此分析 相应问题时微元体表面正应力可直接以压力标注;(b)管内流体既有沿 z 方向 的切应力,同时也伴随有 r 方向的切应力。 ⑤ 因 ∂p*/ ∂z = ∂p / ∂z =const 且 vz =vz (r ) ,故 z 方向运动方程为常微分方程, 其边界条件为 vz r = R = 0 、 (dvz /dr ) r =0 = 0 ;积分运动方程并以 −Δp /L 替代 ∂p / ∂z 可得 速度分布,进而得到切应力分布,其结果为:
CH6-7
对于内筒转动外筒固定的情况, 由于离心 力与压差力均指向外壁, 两者都促使流体向外 层运动, 故流体沿切向的层流流动难以保持稳 定。该条件下,雷诺数定义及过渡雷诺数分别 为:
第六章 流体力学课后答案

第六章 液体力学6-1 有一个长方体形的水库,长200 m ,宽150 m ,水深10 m ,求水对水库底面和侧面的压力。
解:水对水库底面的压力为:()()391 1.0109.810150200 2.910F ghS N ρ==⨯⨯⨯⨯⨯=⨯侧面的压力应如下求得:在侧面上建立如图所示的坐标系,在y 处取侧面窄条dy ,此侧面窄条所受的压力为:dF glydy ρ=整个侧面所受的压力可以表示为:2012hF glydy glh ρρ==⎰对于10h m =、200l m =的侧面:()2721'9.8102F glh N ρ==⨯ 对于10h m =、150l m =的侧面:()2721''7.4102F glh N ρ==⨯侧面的总压力为:()82222'2'' 3.410F F F N =+=⨯6-2 有三个底面积相同但形状各异的容器,分别盛上高度相同的水,如题图所示,根据静止流体压强的概念,三个容器底面的压强是相同的,所以每个容器底面所受的水的压力也是相同的,水对底面压力是由水的重量引起的,但是三个容器中所盛的水的重量显然不等,请对这个似乎矛盾的结果作出解释。
答:三个容器底面的压强是相同的,但流体对容器内壁的压强并不是容器对其支撑面的压强,容器对其支撑面的压力等于水与容器本身重量之和。
因此,容器对其支撑面的压强是不同的。
如蓝球内壁的压强要比蓝球对支撑面的压强要大得多。
6-3 在35.010s ⨯的时间内通过管子截面的二氧化碳气体(看作为理想流体)的质量为0.51 kg 。
已知该气体的密度为37.5kg m -⋅ ,管子的直径为2.0 cm ,求二氧化碳气体在管子里的平均流速。
解: 单位时间内流过管子截面的二氧化碳气体的体积,即流量为:53130.511.36107.5 5.010V m Q m s t ρ--===⨯⋅⨯⨯平均流速为:()521221.3610 4.3103.14 1.010V Q v m s S ----⨯===⨯⋅⨯⨯ 6-4 当水从水笼头缓慢流出而自由下落时,水流随位置的下降而变细,何故?如果水笼头管口的内直径为d ,水流出的速率为0v ,求在水笼头出口以下h 处水流的直径。
流体力学-势流理论(精品)

第六章势流理论本章内容:1.势流问题求解的思路2.库塔----儒可夫斯基条件3. 势流的迭加法绕圆柱的无环绕流,绕圆柱的有环绕流4.布拉休斯公式5.库塔----儒可夫斯基定理学习这部分内容的目的有二:其一,获得解决势流问题的入门知识,即关键问题是求解速度势。
求出速度势之后,可按一定的步骤解出速度分布、压力分布,以及流体和固体之间的作用力。
其二,明确两点重要结论:1)园柱体在理想流体中作等速直线运动时,阻力为零(达朗贝尔疑题);升力也为零。
2)园柱本身转动同时作等速直线运动时,则受到升力作用(麦格鲁斯效应)。
本章重点:1、平面势流问题求解的基本思想。
2、势流迭加法3、物面条件,无穷远处条件4、绕圆柱有环流,无环流流动的结论,即速度分布,压力分布,压力系数分布,驻点位置,流线图谱,升力,阻力,环流方向等。
5、四个简单势流的速度势函数,流函数及其流线图谱。
6、麦马格鲁斯效应的概念7、计算任意形状柱体受流体作用力的卜拉修斯定理8、附加惯性力,附加质量的概念本章难点:1.绕圆柱有环流,无环流流动的结论,即速度分布,压力分布,压力系数分布,驻点位置,流线图谱,升力,阻力,环流方向等。
2.任意形状柱体受流体作用力的卜拉修斯定理3.附加惯性力,附加质量的概念§6-1 几种简单的平面势流平面流动:平面上任何一点的速度、加速度都平行于所在平面,无垂直于该平面的分量;与该平面相平行的所有其它平面上的流动情况完全一样。
例如:1)绕一个无穷长机翼的流动,2)船舶在水面上的垂直振荡问题,由于船长比宽度及吃水大得多,且船型纵向变化比较缓慢,可以近似认为流体只在垂直于船长方向的平面内流动,如图6-2所示。
如果我们在船长方向将船分割成许多薄片,并且假定绕各薄片的流动互不影响的话,则这一问题就可以按平面问题处理。
这一近似方法在船舶流体力学领域内称为切片理论。
一、均匀流流体质点沿x轴平行的均匀速度V o ,如图6-5所示,V x=V o , V y =0平面流动速度势的全微分为dx V dy V dx V dy ydx x d y x 0=+=∂∂+∂∂=ϕϕϕ 积分:φ=V ox (6-4) 如图6-3 流函数的全微分为,dy V dy V dx V dy ydx x d o x y =+-=∂∂+∂∂=ψψψ 积分:ψ=V o y (6-5) 如图6-4 由(6-4)和(6-5)可得:流线:y=const ,一组平行于x轴的直线,如图6-3中的实线。
流体力学习题及答案

2-9有一半封闭容器,左边三格为水,右边一格为油(比重为0.9)。试求A、B、C、D四点的相对压力。
2-10一小封闭容器放在大封闭容器中,后者充满压缩空气。测压表A、B的读数分别为8.28kPa和13.80kPa,已知当地大气压为100kPa,试求小容器内的绝对压力。
题2-10图题2-11图
题2-30图题2-31图
2-31有一三角形闸门,可绕AB轴旋转,油液的重度为γ,求液体对闸门的总压力及总压力对AB轴的力矩。
2-32倾斜的矩形平板闸门,长为AB,宽b=2m,设水深h=8m,试求作用在闸门上的静水总压力及其对端点A的力矩。
题2-32图题2-33图
2-33矩形平板闸门,宽b=0.8m,高h=1m,若要求箱中水深h1超过2m时闸门即可自动开启,铰链的位置y应设在何处?
1-16空气中水滴直径为0.3mm时,其内部压力比外部大多少?
1-17在实验室中如果用内径0.上升高度各为多少?
1-18两块竖直的平行玻璃平板相距1mm,求其间水的毛细升高值。
《流体力学》习题(二)
2-1质量为1000kg的油液(S=0.9)在有势质量力 (N)的作用下处于平衡状态,试求油液内的压力分布规律。
1-4图示为一水暖系统,为了防止水温升高时体积膨胀将水管胀裂,在系统顶部设一膨胀水箱,使水有膨胀的余地。若系统内水的总体积为8m3,加温前后温差为50℃,在其温度范围内水的膨胀系数为βT=9×10-41/℃,求膨胀水箱的最小容积。
题1-4图题1-5图
1-5图示为压力表校正器。器内充满压缩系数为βp=4.75×10-101/Pa的油液,器内压力为105Pa时油液的体积为200mL。现用手轮丝杆和活塞加压,活塞直径为1cm,丝杆螺距为2mm,当压力升高至20MPa时,问需将手轮摇多少转?
流体输配管网习题集第六章
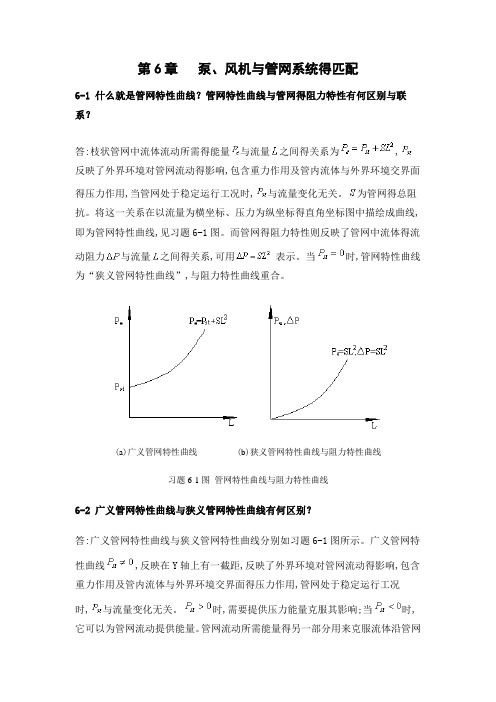
第6章泵、风机与管网系统得匹配6-1 什么就是管网特性曲线?管网特性曲线与管网得阻力特性有何区别与联系?答:枝状管网中流体流动所需得能量与流量之间得关系为,反映了外界环境对管网流动得影响,包含重力作用及管内流体与外界环境交界面得压力作用,当管网处于稳定运行工况时,与流量变化无关。
为管网得总阻抗。
将这一关系在以流量为横坐标、压力为纵坐标得直角坐标图中描绘成曲线,即为管网特性曲线,见习题6-1图。
而管网得阻力特性则反映了管网中流体得流动阻力与流量之间得关系,可用表示。
当时,管网特性曲线为“狭义管网特性曲线”,与阻力特性曲线重合。
(a)广义管网特性曲线(b)狭义管网特性曲线与阻力特性曲线习题6-1图管网特性曲线与阻力特性曲线6-2 广义管网特性曲线与狭义管网特性曲线有何区别?答:广义管网特性曲线与狭义管网特性曲线分别如习题6-1图所示。
广义管网特性曲线,反映在Y轴上有一截距,反映了外界环境对管网流动得影响,包含重力作用及管内流体与外界环境交界面得压力作用,管网处于稳定运行工况时,与流量变化无关。
时,需要提供压力能量克服其影响;当时,它可以为管网流动提供能量。
管网流动所需能量得另一部分用来克服流体沿管网流动产生得阻力,与流量得平方成正比。
当泵或风机得工况沿广义管网特性曲线变化时(如调节泵或风机得转速,不改变管网特性曲线),工况点之间不满足泵或风机得相似律。
而具有狭义管网特性曲线得管网,流动所需得全部能量为流体沿管网流动产生得阻力,与流量得平方成正比,当泵或风机得工况沿管网特性曲线变化时遵守相似泵或风机得相似律。
6-3 分析影响管网特性曲线得因素。
答:影响管网特性曲线得形状得决定因素就是管网得阻抗S。
S值越大,曲线越陡。
当流量采用体积流量单位时,管段阻抗S得计算式为:kg/m7根据S得计算式可知,影响S值得参数有:摩擦阻力系数、管段长度、直径(或当量直径)、局部阻力系数、流体密度。
其中取决于流态。
由流体力学知,当流动处于阻力平方区时,仅与 (管段得相对粗糙度)有关。
大学物理学第六章流体力学基础习题

第六章 流体力学基础一、测验题1. 在水池边上装有宽为b =1.0m 的小门,其下边与水池底相平,并用铰链与池壁联结.试问,当池内的水深为h =2.0m 时,门受到的水压力对铰链的力矩有多大?A. 1.1⨯104N ⋅m B. 1.3⨯104 N ⋅m C. 1.5⨯104N ⋅m D. 1.7⨯104 N ⋅m2. 注射器活塞面积为S ,针管内部截面积为s .以力F 推动活塞使药液从针管射出.不考虑流体阻力,活塞的移动速度为多大?A. v =ρF 2S 22s S s -B. v =ρF S22sS s -C. v =SF ρ222s S s -D. v =ρ4F S22sS s -二、讨论题1. 根据伯努利原理简要解释火车站月台上为什么要设置黄色警戒线?2. 为何刮大风时,迎风会出现呼吸困难? 三、计算题1. 如图倒T 字型容器,上部细管横截面积S 1=5.00 cm 2, 下部横截面积S 2=100 cm 2,高度h 2= 5.00cm .容器总高h 1+h 2=100 cm .注满水( ρ=1.00⨯103kgm -3).求:(1)水对容器底部的作用力. (2)此装置内水的重量.(3)解释(1)、(2)的结zbhxOz d zS 2S 1h 2h 1果为何不同?2. 一圆柱形水桶,横截面的直径为D = 60 cm ,桶底有一直径为d = 10 cm 的圆孔。
开始时桶内水的深度为h =100 cm ,求:此时水从桶底孔中流出的速率v 和流量Q 。
3. (课后习题6-3)粗圆筒内盛有水,水的深度为H ,在圆筒的侧壁上开一个小孔。
(1)孔与水面的距离为多大时,水流的水平射程最大;(2)水流的最大水平射程为多少?4. (课后习题6-8)如图,文丘里(Venturi)流量计的两种管径的截面积分别为1S 和2S ,流体的密度为ρ,并由U 形管液柱高度差h 可计算出压强差为p ∆,试推导流体的体积流量为()1222122V p Q S S S S ρ∆=-5.(课后习题6-10)内径为2.5 cm 进水管将水送到地下室,管内水的流速为10.90m s -⋅、压强为170 kPa 。
李玉柱流体力学课后题答案 第六章

第六章 孔口、管嘴出流与有压管流6-1 在水箱侧壁上有一直径50mm d =的小孔口,如图所示。
在水头H 的作用下,收缩断面流速为 6.86m/s C V =,经过孔口的水头损失0.165m w h =,如果流量系数0.61μ=,试求流速系数ϕ和水股直径c d 。
解:根据伯努利方程:22.51m 2c w V H h g=+= 流速系数0.9672c cV V V gHϕ=== 2c c Q A gH AV μ==,39.71mm cd = 6-2 图示一船闸闸室,闸室横断面面积2800m A =,有一高2m h =、宽4m b =的矩形放水孔。
该孔用一个速度0.05m/s v =匀速上升的闸门开启。
假设初始水头15m H =,孔口流量系数0.65μ=,孔口出流时下游水位保持不变。
试求(1)闸门开启完毕时闸室中水位降低值y ;(2)闸室水位与下游平齐所需要的总时间T 。
解:(1)闸门完全开启所用的时间:40s ht v== 此段时间内孔口的面积可用孔的平均面积来表示:24m A =因为40s T ==所以:2 3.796m H =,12 1.204m y H H =-=(2)闸门完全打开后,防水孔的面积:28m A bh '== 液面降到与下游液面平齐所需要的时间因为135.41s T '==所以175.41s T t T '=+=6-3 贮液箱中水深保持为 1.8m h =,液面上的压强070kPa p =(相对压强),箱底开一孔,孔直径50mm d =。
流量系数0.61μ=,求此底孔排出的液流流量。
解:根据伯努利方程:202p V h g gρ+= 215.9L/s 4Q d V πμ==6-4 用隔板将矩形水池中的水体分成左右两部分,如图所示,右半部分水面保持恒定,隔板上有直径10.1m d =的圆形孔口,位于右半部液面下1 4.8m H =处。
在左半部分的侧面与前一孔口相同的高度处开有直径20.125m d =的圆形孔口,当水池两半部分的水面稳定后,试求左半部水面高度计孔口出流流量。
《流体力学》课后习题答案详解

习题【1】1-1 解:已知:120t =℃,1395p kPa '=,250t =℃ 120273293T K =+=,250273323T K =+= 据p RT ρ=,有:11p RT ρ'=,22p RT ρ'= 得:2211p T p T '=',则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解:受到的质量力有两个,一个是重力,一个是惯性力。
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-3 解:已知:V=10m 3,50T ∆=℃,0.0005V α=℃-1根据1V V V Tα∆=⋅∆,得:30.000510VVV Tα∆=⋅⋅∆=⨯⨯1-4 解:已知:419.806710Pa p '=⨯,52 5.884010Pa p '=⨯,150t =℃,278t =℃得:1127350273323T t K=+=+=,G =mg自由落体: 加速度a =g2227378273351T t K =+=+=根据mRTp V=,有:111mRT p V '=,222mRT p V '=得:421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯,即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解:已知:40mm δ=,0.7Pa s μ=⋅,a =60mm ,u =15m/s ,h =10mm根据牛顿内摩擦力定律:uT Ayμ∆=∆ 设平板宽度为b ,则平板面积0.06A a b b =⋅=上表面单位宽度受到的内摩擦力:1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ,方向水平向左下表面单位宽度受到的内摩擦力: 2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ,方向水平向左平板单位宽度上受到的阻力:12216384N τττ=+=+=,方向水平向左。
流体力学第6章(1-6节)

全微分的充分必要条件。
即
d v x dx v y dy v z dz
d dx dy dz x y z
函数Φ的全微分为
比较两式,得到
vx , vy , vz x y z
函数Φ(x, y, z)称为速度势函数,无旋流动又称为有 势流动 。
复速度的三角函数 式和指数式:
dW v (cos i si n ) v e i dz
α O vx
V
vx-ivy
W(z)共轭复变数:
W i f ( z )
z x iy
dW i v x ivy V dz x x
dW dW 2 2 2 vx vy v dz dz
证明: 取微元线段 d s ,过微元线段的速度为 v ,
则单位厚度的微元流量dq的表达式为
dq v d s v x dy v y dx d
通过线段AB的流量为
q dq d B A
A A
B
B
q 2 1
特性3
证明:对于平面势流,有
v x v y 0 x y v y v x x y
由数学分析知,上式正是 v y dx v x dy 成为某一函 数Ψ(x, y)全微分的充分必要条件。
即
d v y dx v x dy
d dx dy x y
函数ψ的全微分为
比较两式,得到
证明:不可压缩流体的连续性方程为 v x v y v z 0 x y z 对于有势流动 得到
vx , vy , vz x y z
2 2 2 2 0 2 2 x y z
船舶流体力学测验第六章

船舶流体力学测验第六章1.求解势流问题,首先要在一定边界条件和初始条件下求解(A)。
A.拉普拉斯方程B.欧拉方程C.拉格朗日方程D.伯努利方程2.理想流体的无旋流动称为(D)。
A.定常流动B.均匀流动C.不可压缩流动D.势流3.关于势流问题,下列错误的是(B)。
A.势流为无旋流B.基本方程为伯努利方程C.势函数满足拉普拉斯方程D.波浪问题可以用势流理论求解4.流体由平面上各个方向流过来汇聚于一点,这种流动称为(B)。
A.源B.汇C.偶极子D.点涡5.关于偶极子流,说法错误的是(B)。
A.是一种极限流动B.有大小,没有方向C.是一对特殊状态下的源、汇D.大小用偶极矩来表达6.流场中坐标原点处有一根无穷长的直涡线,强度为,方向垂直于图平面,则该涡线与图平面的交点即为一个点涡。
(对)7.绕圆柱体有环量流动中,单位长圆柱体所受升力大小与(D)无关。
A.来流密度B.来流速度C.环量D.圆柱体长度8.流体由平面上坐标原点流出,流向各个方向,这种流动称为(A)。
A.源B.汇C.偶极子D.点涡9.平面无环量圆柱绕流可以视为下列哪种流动的叠加(D)。
A.点源+点汇B.点源+均匀流C.点汇+均匀流D.偶极子+均匀流10.下列哪项不是流场中达朗贝尔缪理成立的条件(C)。
A.理想流体B.物体周围流场是无边际的C.物体做变速直线运动D.物体表面上没有分离11.绕圆柱体有环量流动可由下列(ABD)叠加得到。
A.均匀流B.点涡C.点汇D.偶极子12.物体在静止流体中做加速运动引起的附加质量,比在非定常流体中固定物体的绕流流动所引起的附加质量小,因而所受的流体作用力也小。
(对)13.在非匀速运动中,物体和流体存在相互作用。
流体会使物体产生附加惯性力的作用。
它是流体对物体的一种反作用力,表现为附加质量。
(对)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章流体力学题库
5-1-8
问题:
[单选]图示并联管路,已知两支管的比阻比,管长比,则两支管的流量比()。
A.['12
B.
C.
D.2
问题:
[单选]图示压力供水箱水位恒定,顶部压力表读数,水深H=2m,水平供水管长l=100m,管径d=200mm,沿程阻力系数λ=0.02,若忽略局部水头损失,则管道通过的流量Q=()Ls。
A.47.4
B.59.3
C.83.8
D.196.5
问题:
[单选]下列渠道中,可能产生均匀流的是()。
A.平坡棱柱形渠道
B.逆坡棱柱形渠道
C.正坡棱柱形渠道
D.正坡非棱柱形渠道
/ 西甲赛程
问题:
[单选]欲使水力最优梯形断面渠道的水深和底宽相等,则渠道的边坡系数m应为()。
A.1
B.34
C.12
D.14
问题:
[单选]图示半圆形断面长直渠道,半径r0=2m,底坡i=0.0004,渠壁粗糙系数n=0.01,则渠道的断面平均流速为()ms。
A.1
B.2
C.2.5
D.3
问题:
[单选]有一条养护良好的矩形断面长直渠道,底坡i=0.0008,底宽b=1.0m,均匀流动水深h=0.5m,粗糙系数n=0.025,则渠道通过的流量Q=()m3s。
A.0.10
B.0.15
C.0.23
D.0.35
问题:
[单选]矩形断面长直渠道通过流量Q=5m3s,渠壁粗糙系数n=0.016,底坡i=0.001,按水力最优断面设计,渠道底宽b应为()m。
A.2.60
B.3.60
C.4.60
D.5.60。
