Scilab在高等数学二维图形绘制中的应用
MATLAB图形可视化方法及其在高等数学中的应用共3页

MATLAB图形可视化方法及其在高等数学中的应用高等数学课程是一门研究自然科学和工程技术的重要工具,它服务于各专业课,是学好专业课程的必要保障。
作为一门科学,高等数学有其固有的特点,这就是高度的抽象性、严密的逻辑性和广泛的应用性。
高等数学是高职高专学生必修的一门重要基础课程,课时少,内容多,学生基础相对薄弱,学习耐性相对差。
而高等数学的很多内容都比较抽象,学生理解起来比较困难。
因此,能否将一些抽象不易理解的数学知识在教学过程中进行科学有序的、深入浅出地讲解描述,就显得至关重要。
根据人类的认识从具体到抽象的规律可知,在学习中若能借助几何图形从直观上理解数学中抽象的概念,无法观察的现象以及多维空间中的函数,则能使学生的学习收到事半功倍的效果。
但实际上这类图形的绘制往往很复杂,仅凭手工绘制也难以达到精确的效果。
而Mat1ab强大的图形输出功能使我们能较容易地解决上述问题,方便、快速地绘出各种图形。
MATLAB软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。
MATLAB计算软件具有强大的图形输出功能,在高等数学领域中有关图形方面的应用,无论是初等函数图形、还是极坐标图形、统计图,对于MATLAB而言都是完全可以胜任的。
在高等数学课程的教学过程中借助MATLAB简单的命令能够绘制出许多几何图形,对于学生直观地理解高等数学中抽象的概念和培养良好的空间思维能力非常有帮助。
以下通过几个实例来具体分析讨论MATLAB图形可视化的方法及其在高等数学中的作用。
一、利用MATLAB画几何图形理解极限的概念高等数学中有许多概念都很抽象,往往又非常重要,例如极限是微积分的基本概念,高等数学中的一系列重要概念,如函数的连续性、导数以及定积分等等都是借助于极限来定义的。
通过MATLAB绘制几何图形能够很好的体现这些概念内涵,加深学生对抽象概念的理解。
根据图象可以从直观上很容易地看出x→+∞时,f(x)=0,而当x→1时,g(x)左右极限不等,故不存在极限。
利用Matlab来解决高等数学中的二维图形问题

5 绘制统计图
例 5 下面是 100 名学生体重的频数表
3 绘制饱和非线性特性方程
例 3 绘制出饱和非线性特性方程 可以用下面的语句绘制出分段函数的曲线: x=[- 2:0.02:2];
收稿日期: 2007- 02- 25
的曲线。
在显著水平 $=0.05 下能否认为这些体重服从正态分布? 绘出 统计数据的直方图。
参考文献: [1]邓定华,等.如何在 网 页 上 实 现 Java 3D 绘 制 图 像[J].计 算 机 与现代化, 2006( 2) : 91- 95. [2]朱 晓 明.网 络 数 控 插 补 教 学 软 件 的 开 发 与 研 究[D].哈 尔 滨: 哈尔滨工业大学, 2002:37. [3]冯 乔 生 等.Java 3D 中 的 Text2D 的 扩 展 与 应 用[J].计 算 机 工 程与应用, 2003; 39(20): 122- 125. [4]张杰.Java 3D 交互式三维图形编程[M].北京: 人民邮电出版 杜, 1999. [5]都志辉.Java3D 编程实 践— ——网 络 上 的 三 维 动 画[M].北 京 : 清华大学出版社, 2002.
分 析 : H=LILLIEST(X,ALPHA) [H,P,LSTAT,CV] = LILLIEST(X, ALPHA)
(下转第 1689 页)
1677
本栏目责任编辑: 谢媛媛
开发研究与设计技术
new Point3f(0.lf,- 0.1f,0.02f), //new Point3f(0.1f,0.0f,0.01f), //new Point3f(- 0.lf,- 0.1f,0.0f), new Point3f(0.0f,0.0f,0.0f)}; //设置方向 //t3d.setTranslation(new Vector3f(1.0f,0.0f,0.0f)); //t3d.setTranslation(new Vector3f(0.0f,0.0f,1.0f)); // Alpha alpha=new Alpha(- 1,A1pha.INCREASING_ENABLE+ A1pha.DECREASING_ENABLE,0,0,2000,0,1000,2000,0,1000); PositionPathlnterpolator posPathInt=new PositionPathInterpolator(alpha,objMove,t3d,knots,positions); posPathInt.setSchedulingBounds(bounds); //////////////////////// t3d.setTranslation(new Vector3f(- 1.0f,0.0f,- l.0f); TransformGroup objMovePos=new TransformGroup(t3d); objRoot.addChild(objMovePos); //objMovePos.addChild(objMove); //objMove.addChild(new ColorCube(0.2f)); trans.addChild(g1); objMove.addChild(g2); objMove.addChild(g3); trans2.addChild(objMove); objRoot.addChild(posPathInt);
MATLAB绘图功能在高等数学教学中的应用

摘要本文利用matlab 软件在作图上的优势,结合高等数学和matlab 软件的特点,以高等数学教学中隐函数图像、三维曲线、三维曲面等图像的绘制,阐述了matlab软件中的绘图功能在高等数学课程教学中的一些应用。
关键词 matlab绘图高等数学教学中图分类号:g424 文献标识码:a doi:10.16400/ki.kjdkx.2016.06.0330 引言高等数学课程是高等学校各专业学生必修的一门非常重要的基础课程。
但是高等数学课程十分抽象,对于该课程的学习,学生普遍感到非常困难。
传统的高等数学教学,一般情况下都是教员按照教学大纲的要求对定义、定理、推论等在课堂上给同学进行理论上的推导和计算。
这种以教员教授、学员被动接受为主的教学方式在传授系统知识的时候具有比较好的效果,但忽视了学员的主体地位,不利于学员获取知识能力的培养,学员缺乏创新能力。
为克服这些不足,可以将matlab软件引入到高等数学课程的教学中。
1 隐函数的图像在高等数学课程的教学中,我们经常会遇到各种比较抽象的函数,或者多维的函数。
这些函数从形式上不能直接看出函数的特性。
但是通过matlab软件绘图,我们就可以利用比较简单的语句,将这些抽象函数的图像描绘出来。
通过函数图像我们可以非常容易理解函数的内在关系和特点。
比如隐函数() = ( + ) + + ( + ) = 0,从函数形式上看起来非常抽象,我们下面通过命令把函数可视化。
绘图命令:ezplot('x^2*sin(x+y^2)+exp(x+y)+ y^2*cos(x^2+y)')通过上面简单的一行命令,就可用绘制出所给隐函数的图像,如图1所示。
上面的语句自动选择x轴范围,如果想改变定义域,直接在后面加上定义域即可。
ezplot('x^2*sin(x+y^2)+exp(x+y)+ y^2*cos(x^2+y)',[-10,10])即可绘制x,y在(-10,10)直接的图形,如图2所示。
浅谈matlab的绘图功能在高等数学教学中的应用_于丽妮
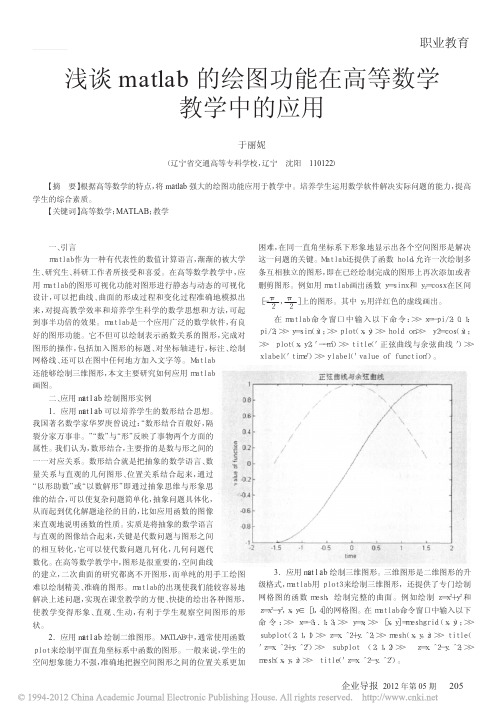
三、结论 利用 matlab 的绘图功能辅助高等数学教学,静态与动态 的三维演示,将抽象问题具体化,提高教学质量,激发学生的学 习热情,使教学方式由传统的板书式教学向多样化发展。 本文所有源代码在 matlab6.1 中调试通过。
参考文献
函数
y=sinx
和
y2=cosx
在区间[-
π 2
,π 2
]上的图形。在
[4] 牛秀敏等. 几种常规综合评价方法的比较 [J]. 统计与决策. 2006,21(3):142~143 [5]Editiorial.In search of European model for the Information Society[J]. Telematics andInformatics.2000,11(17):1~7 [6]Anders Henten,Thomas Myrup rmation society visions in the Nordiccountries [J].Telematics and Informatics.2000,14(17): 77~103 [7] 王其荣等. 综合评价方法之评价 [J]. 统计与决策,2006,4(6): 137~138 [8]王少卫等.数字化车间布局模糊层次评价研究[J].计算机仿真. 2009,22(7):290~293 [9]徐绪堪.基于模糊理论的毕业设计质量评估模型的构建[J].实验 室技术与管理.2007,24(6):117~ 119 [10]马莉,孙延明等.企业信息化评价指标体系及其评价方法的研究 [J].现代制造工程.2005,22(3):41~44 [11]朱海荣,傅铅生.企业信息化水平模糊评价模型的研究[J].科技 情报开发与经济.2005,15(15):110~ 111 项目基金:本文系甘肃省教育厅科研项目(1102- 05)。
MATLAB的图形和动画功能在高等数学教学中的应用

MATLAB的图形和动画功能在高等数学教学中的应用牛海微(辽宁理工学院公共教学部,辽宁锦州121000)摘要:本文通过MATLAB直观灵活的语言和强大的绘图工具,将高等数学中一些抽象的函数图形、空间曲线的形成过程等难以理解的内容动态、直观地演示出来,有利于学生理解概念,激发学生的学习兴趣,增强其空间想象力,提高教学质量。
关键词:高等数学;MATLAB;作图功能;动画功能DOI:10.16083/ki.22-1296/g4.2021.07.026中图分类号:G642.0文献标识码:A文章编号:1671—1580(2021)07—0056—03收稿日期:2021—01—15作者简介:牛海微(1986—),女,吉林公主岭人。
辽宁理工学院公共教学部,讲师,硕士,研究方向:应用数学。
高等数学是高等院校大部分专业的一门重要基础课,对后续课程的学习影响深远。
但相对于初等数学而言,高等数学的内容更加抽象,对理论的要求更高,导致大一学生普遍感到迷茫、抽象、难懂、无所适从。
因此,在教学过程中将抽象、不易理解的数学知识进行科学、有效、深入浅出的讲解,调动学生的学习兴趣,提高学生的整体素质是至关重要的。
由美国Mathworks公司推出的MATLAB软件有着强大的图形可视化、数值计算和动画功能,可以作出非常精致的图形。
近几年,MATLAB 软件在各高校和研究单位应用广泛,因其编程语言简单易学,在高等数学课的教学中有很大的辅助作用。
对于常用的数学问题可直接调用软件的函数和文件,通过程序编写可实现复杂函数的图像、动画演示和体积可视化。
一、MATLAB的绘图功能在高等数学中的应用大多数学生缺乏空间想象力,对空间立体图形很难想象出来,而黑板也难以将空间关系描述清楚,但在高等数学中很多章节内容都需要借助多元函数的图形来理解,这就导致学生对所学内容感到迷茫、困惑。
利用MATLAB的绘图功能可以方便快捷地建立空间函数图形,同时还可以从不同角度观察图形,增加其渲染效果,使学生能够直观、全面地理解图形,建立空间思维模型,从而解决问题。
利用MATLAB绘制二维函数图形

《MATLAB语言》课程论文利用MATLAB绘制二维函数图形姓名:海燕学号:***********专业:通信工程班级:通信一班指导老师:***学院:物理电气信息学院成日期:2011年12月5利用MATLAB绘制二维函数图形(海燕12010245375 2010级通信1班)[摘要]大学高等数学中涉及许多复杂的函数求导绘图极值及其应用的问题,例如二维绘图,对其手工绘图因为根据函数的表达式的难易程度而不易绘制,而MATLAB语言正是处理这类的很好工具,既能简易的写出表达式,又能绘制有关曲线,非常方便实用。
另外,利用其可减少工作量,节约时间,加深理解,同样可以培养应用能力。
本文将探讨利用matlab来解决高等数学中的二维图形问题,并对其中的初等函数、极坐标、进行实例分析,对于这些很难用手工绘制的图形,利用matlab则很轻易地解决。
[关键词]高等数学一元函数二元函数MATLAB语言图形绘制一、问题的提出MATLAB 语言是当今国际上科学界(尤其是自动控制领域) 最具影响力、也是最有活力的软件。
它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、便捷的与其他程序和语言接口的功能。
中学数学中常见到的是二维平面图形,由于概念抽象,学生不好理解,致使学生对学习失去信心,导致学习兴趣转移。
在传统的教学中,教师在黑板上应用教具做图,不能保证所做图形的准确性,曲线的光滑度不理想,教学过程显得枯燥无味,教学质量难以保证。
Matlab是集数值计算、符号计算和图形可视化三大基本功能于一体的大型软件,广泛应用于科学研究、工程计算、动态仿真等领域。
Matlab是一种集成了计算功能、符号运算、数据可视化等强大功能的数学工具软件。
其代码的编写过程与数学推导过程的格式很接近,所以使编程更为直观和方便,应用于教学就更加容实现Matlab软件尤其在简单的绘图中有较强的编辑图形界面功能,在中学的数学教学中的抽象函数变得直观形象、容易实现,同时也激发学生的学习兴趣,学生通过数形结合,更好地理解题意高等数学是一门十分抽象的学科,对于一些抽象的函数,我们可以借助于几何图形来理解,但这类图形的绘制往往很复杂,仅凭手工绘制也难以达到精确的效果,这时如果使用Matlab 来解决所遇到的图形问题,则能达到事半功倍的效果。
MATLAB在二维三维绘图中简单应用

《MATLAB语言》课程论文MATLAB在二维三维绘图中简单应用姓名:石磊学号:12011243923专业:通信工程班级:11级通信工程1班指导老师:汤全武学院:物理电气信息学院完成日期:2012年12月20日MATLAB在二维三维绘图中的简单应用(石磊 12011243923 2011级通信1班)[摘要]MATLAB提供了一系列的绘图函数,用户不仅不许考虑绘图细节,只需给出一些基本的参数就能得到所需要的图形,这一类函数称为高层绘图函数。
除此之外,MATLAB还提供了直接对句柄进行操作的一系列的低层的绘图操作。
这类操作将图形的每个元素看做是一个独立的对象,系统给每个对象独立的分配一个句柄,以后可以通过该句柄对改图元素进行操作,而不影响图形的其他部分。
高层绘图操作简单明了,方便高效,使用户最常使用的绘图方法,而低层绘图操作控制和表现图形的能力更强,为用户自主绘图创造了条件。
其实MATLAB的高层绘图函数都是利用低层绘图函数建立起来的。
所以MATLAB的计算准确、效率高、使用快捷等优点常被广泛应用于科学和工程领域.[关键字]MATLAB语言二维图形三维图形图像处理绘制一、问题的提出MATLAB语言是当前国际学科界应用很广泛的一种软件,强大的绘图功能是MATLAB的特点之一。
MATLAB提供了一系列的绘图函数,利用它强大的图像处理来绘制二维三维图形既简单而且也很方便。
在绘制二维三维图形的过程中也用到了MATLAB语言的其他功能,绘制二维三维图形时用到了它提供的一些函数,利用这些函数可以方便的生成一些特殊矩阵,因此可生成一个坐标平面,三维图形的绘制也离不开绘制二维图形的一些函数,例如绘制三维图形的前视图和侧视图等的时候可以利用而为函数对其进行操作和处理,进而达到绘制三维图形的三视图的目的。
类似的问题也产后应用在软件开发类的编程中。
MATLAB语言强大的功能也在二维三维绘图中的得到了很广泛的应用,利用它所提供的精细的图像处理功能,如MATLAB还提供了直接对句柄进行操作的一系列的低层的绘图操作。
MATLAB在二维绘图中的应用

《MATLAB语言》课程论文MATLAB在二维绘图中的应用姓名:郭露学号:12012241985专业:电气工程与自动化班级:12级电气1班指导老师:李虹学院:物理电气信息学院完成日期:2013年12月10日MATLAB在二维绘图中的应用(姓名:郭露12012241985 12级电气1班)【摘要】二维图形是将平面坐标上的数据点连接起来的平面图形。
可以采用不同的坐标系,如直角坐标、对数坐标、极坐标等。
二维图形的绘制是其他绘图操作的基础。
强大的绘图功能是MATLAB的特点之一。
MATLAB提供了一系列的绘图函数,用户不仅不许考虑绘图细节,只需给出一些基本的参数就能得到所需要的图形,这一类函数称为高层绘图函数。
除此之外,MATLAB还提供了直接对句柄进行操作的一系列的低层的绘图操作。
这类操作将图形的每个元素(如坐标轴、曲线、文字等)看做是一个独立的对象,系统给每个对象独立的分配一个句柄,以后可以通过该句柄对改图元素进行操作,而不影响图形的其他部分。
高层绘图操作简单明了,方便高效,使用户最常使用的绘图方法,而低层绘图操作控制和表现图形的能力更强,为用户自主绘图创造了条件。
其实MATLAB的高层绘图函数都是利用低层绘图函数建立起来的。
所以MATLAB的计算准确、效率高、使用快捷等优点常被广泛应用于科学和工程领域.【关键字】MATLAB语言二维绘图图像处理【引言】MATLAB语言是当前国际学科界应用很广泛的一种软件,强大的绘图功能是MATLAB 的特点之一。
MATLAB提供了一系列的绘图函数,利用它强大的图像处理来绘制二维图形既简单而且也很方便。
在绘制二维图形的过程中也用到了MATLAB语言的其他功能,比如说它提供的一些函数,利用这些函数可以方便的生成一些特殊矩阵,因此可生成一个坐标平面。
MATLAB语言强大的功能也在二维绘图中的得到了很广泛的应用,利用它所提供的精细的图像处理功能还可以对所绘制的二维图形作一个修饰的处理。
高中数学里,scilab 的辅助应用
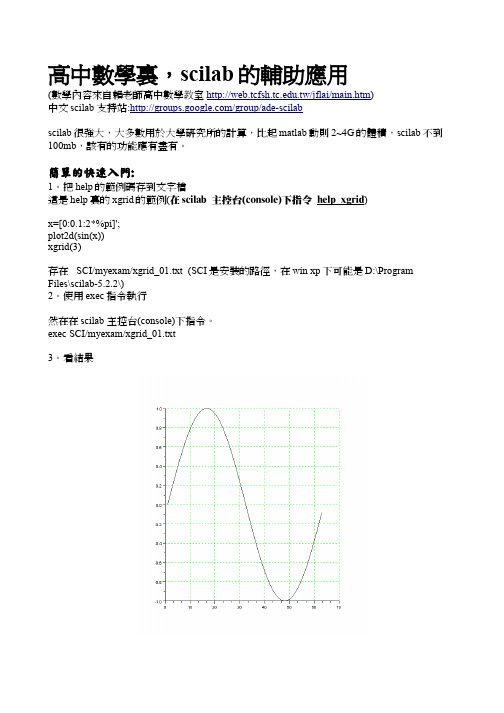
簡單的快速入門:
1。把 help 的範例碼存到文字檔 這是 help 裏的 xgrid 的範例(在 scilab 主控台(console)下指令 help xgrid) x=[0:0.1:2*%pi]'; plot2d(sin(x)) xgrid(3) 存在 SCI/myexam/xgrid_01.txt (SCI 是安裝的路徑,在 win xp 下可能是 D:\Program Files\scilab-5.2.2\) 2。使用 exec 指令執行 然在在 scilab 主控台(console)下指令。 exec SCI/myexam/xgrid_01.txt 3。看結果
執行後輸出 ym = 1.5 xm = 0.5
二。求極限的輔助:
將 scilab 當電子計算機使用,拿來求極限,極限常常是逼近於 0,小數點的計算對一般人筆 算很吃力,交給電腦算完後,畫成圖,快速抓到感覺 題目: sin(x)/x 在 x=0 的極限 指令如下 x=[-0.1 -0.01 -0.001 -0.0001 0.0001 0.001 0.01 ] y=sin(x) z=y./x 輸出如下 x = – 0.1 - 0.01 - 0.001 - 0.0001 0.0001 0.001 0.01 y = column 1 to 6 - 0.0998334 - 0.0099998 - 0.0010000 - 0.0001 0.0001 0.0010000 column 7 0.0099998 z = column 1 to 6 0.9983342 0.9999833 0.9999998 1. 1. 0.9999998 column 7 0.9999833 雖然是很尋常的事,但是想想,當 x 趨進於 0,其實 有 x^2(次方) ,x^3, x^1/2(平方根)也趨 進於 0,但是就是沒有像 sin(x)和 x 趨近的速度那麼一致,舉 x^1/2(平方根,sqrt(x))為例: x=[0.0001 0.001 0.01 0.1] y=sqrt(x) z=y./x 計算結果為 y=0.01 0.0316228 0.1 0.3162278 z=100. 31.622777 10. 3.1622777 (發散的結果) 再舉 x^2(次方) 為例: x=[-0.1 -0.01 -0.001 -0.0001 0.0001 0.001 0.01 0.1] y=x^2 z=y./x 計算結果為 y=0.01 0.0001 0.000001 1.000D-08 1.000D-08 0.000001 0.0001 z=- 0.1 - 0.01 - 0.001 - 0.0001 0.0001 0.001 0.01 0.1 (趨進於 0)
scilab指令及应用

18. 图形文件及图形文字
3
xsave 将图形存储为文件 xload 从磁盘中读出图形文件 xbasimp 将图形按PS文件 打印或存储为文件 xs2fig 将图形生成Xfig 格式文件 xbasc 取消图形窗及其相关内 容 xclear 清空图形窗 driver 选择图形驱动器 xinit 图形驱动器初始化 xend 关闭 图形 xbasr 图形刷新 replot 更改显示范围后的图形刷新 xdel 关闭图形 xname 改变当前图形窗名称
17. 图形颜色及图形文字 colormap 应用颜色图 getcolor 交互式选择颜色图 addcolor 增加新色于颜色图 graycolormap 线性灰度图 hotcolormap 热色(红到黄色)颜色图 xset 图形显示方 式设定 xget 读当前图形显示方式设定 getsymbol 交互式选择符号和尺寸
scilab指令及应用

5.基本矩阵函数和操作 eye 单位阵 zeros 全零矩阵 ones 全1 矩阵 rand 均匀分布随机阵 genmarkov 生成随机Markov矩阵 linspace 线性等分向量 logspace 对数等分向量 logm 矩阵 对数运算 cumprod 矩阵元素累计乘 cumsum 矩阵元素累计和 toeplitz Toeplitz 矩阵 disp 显示矩阵和文字内容 length 确定向量的长度 size 确定矩阵的维数 diag 创建对角阵或抽取对角向量 find 找出非零元素1的下标 matrix 矩阵变维 rot90 矩 阵逆时针旋转90度 sub2ind 据全下标换算出单下标 tril 抽取下三角阵 triu 抽取上 三角阵 conj 共轭矩阵 companion 伴随矩阵 det 行列式的值 norm 矩阵或向量 范数 nnz 矩阵中非零元素个数 null 清空向量或矩阵中的某个元素 orth 正交基 rank 矩阵秩 trace 矩阵迹 cond 矩阵条件数 rcond 逆矩阵条件数 inv 矩阵的逆 lu LU分解或高斯消元法 pinv 伪逆 qr QR分解 givens Givens变换 linsolve 求解 线性方程 lyap Lyapunov方程 hess Hessenberg 矩阵 poly 特征多项式 schur Schur 分解 expm 矩阵指数 expm1 矩阵指数的Pade逼近 expm2 用泰勒级数求 矩阵指数 expm3 通过特征值和特征向量求矩阵指数 funm 计算一般矩阵函数 logm 矩阵对数 sqrtm 矩阵平方根
17. 图形颜色及图形文字 colormap 应用颜色图 getcolor 交互式选择颜色图 addcolor 增加新色于颜色图 graycolormap 线性灰度图 hotcolormap 热色(红到黄色)颜色图 xset 图形显示方 式设定 xget 读当前图形显示方式设定 getsymbol 交互式选择符号和尺寸
MATLAB原理及应用2b绘图

使用基本画图函数
创建一幅图(用MATLAB画图函数来创建和修改图形)
函数plot(y) 产生分断线性图,y向量对y中元素的标号(下标) 函数plot(x,y) y对x
一简单例子画正弦信号 x = 0:pi/100:2*pi; y = sin(x); plot(x,y) xlabel('x = 0:2\pi') ylabel('Sine of x') title('Plot of the Sine Function')
设置坐标系的高宽比
设置栅格线
加坐标标签和标题
用xlabel、ylabel和zlabel命令添加x、y、z轴标签 用title命令在图形窗口顶部添加标题 用text在图形窗口任意位置添加文本
例子: t = -pi:pi/100:pi; y = sin(t); plot(t,y) axis([-pi pi -1 1]) xlabel('-\pi \leq {\itt} \leq \pi') ylabel('sin(t)') title('Graph of the sine function') text(1,-1/3,'{\itNote the odd symmetry.}')
一个图形窗口中显示多个坐标系
பைடு நூலகம்
命令subplot 可以在一个图形窗口内显示多个坐 标系。
subplot(m,n,p)将图形窗口分成了m*n个坐标系,并选 中第p个坐标系作为当前操作对象,这些坐标系是按行 编号的,先第一行,后第二行等。
t = 0:pi/10:2*pi; [X,Y,Z] = cylinder(4*cos(t)); subplot(2,2,1); mesh(X) subplot(2,2,2); mesh(Y) subplot(2,2,3); mesh(Z) subplot(2,2,4); mesh(X,Y,Z)
MATLAB在高等数学实验中的应用

MATLAB在高等数学实验中的应用在高等数学实验中,MATLAB是一种广泛应用的计算软件,它具有强大的数学计算能力和可视化处理功能。
本文将探讨MATLAB在高等数学实验中的应用,并展示其在解决实际问题和学习数学概念中的优势。
一、MATLAB在函数绘图中的应用函数绘图是高等数学实验中常见的任务之一。
MATLAB提供了丰富的绘图函数和图形工具箱,可以方便地绘制各种函数的图像,并进行定量分析。
使用MATLAB绘制函数图像的基本步骤如下:1. 定义函数表达式:通过MATLAB的符号计算工具箱或直接使用符号表达式来定义函数。
2. 创建绘图窗口:使用MATLAB的绘图函数,如plot、scatter等来创建绘图窗口,并设置绘图参数。
3. 绘制函数图像:将定义好的函数表达式作为参数传递给绘图函数,即可绘制函数图像。
4. 添加坐标轴、标题和图例:通过MATLAB的绘图函数设置坐标轴、标题和图例等信息,以增强图像的可读性。
除了基本的函数绘图,MATLAB还可以绘制等高线图、三维曲面等复杂的图形,帮助学生更直观地理解数学概念和解决实际问题。
二、MATLAB在求解微分方程中的应用微分方程是高等数学中的重要内容,解微分方程需要进行数值计算。
MATLAB具有强大的数值计算能力和求解微分方程的工具箱,可以高效地求解各种类型的微分方程。
MATLAB中求解微分方程的基本步骤如下:1. 定义微分方程:使用MATLAB的符号计算工具箱来定义微分方程。
可以采用符号表达式或匿名函数的形式定义微分方程。
2. 设置初值条件:对于常微分方程,需要给出初值条件。
通过定义符号变量或直接赋值的方式,设置初值条件。
3. 调用求解函数:使用MATLAB的求解微分方程工具箱中的函数,如ode45、ode23等,传入定义好的微分方程和初值条件,即可求解微分方程。
4. 绘制解曲线:将求解得到的数值解通过MATLAB的绘图功能进行可视化展示,以增加对解的理解和分析。
matlab在高等数学中的应用

matlab在高等数学中的应用Matlab是一种强大的数学软件工具,广泛应用于高等数学的教学和研究中。
它提供了丰富的功能和工具,可以帮助学生和研究人员更好地理解和应用高等数学的概念和方法。
本文将介绍Matlab在高等数学中的应用,并分别从微积分、线性代数和概率论三个方面进行探讨。
Matlab在微积分中的应用非常广泛。
微积分是高等数学中的重要分支,研究函数的极限、导数、积分等概念和方法。
Matlab提供了丰富的函数和工具,可以进行符号计算、求解微分方程、绘制函数图像等。
例如,可以使用Matlab计算函数的导数和积分,从而得到函数的极值、拐点和定积分等重要信息。
此外,Matlab还可以用于求解微分方程,例如常微分方程、偏微分方程等。
通过Matlab的求解器,可以得到微分方程的近似解或精确解,进一步深入理解微积分的概念和方法。
Matlab在线性代数中的应用也非常重要。
线性代数是高等数学中的另一个重要分支,研究向量、矩阵、线性方程组等概念和方法。
Matlab提供了丰富的矩阵运算和线性代数函数,可以进行矩阵的加减乘除、转置、逆矩阵、特征值和特征向量等计算。
例如,可以使用Matlab求解线性方程组,通过矩阵的消元和回代,得到方程组的解析解或数值解。
此外,Matlab还可以进行矩阵的特征值分解和奇异值分解,从而得到矩阵的特征值、特征向量和奇异值等重要信息。
通过Matlab的计算和可视化功能,可以帮助学生更好地理解线性代数的概念和方法。
Matlab在概率论中的应用也非常突出。
概率论是高等数学中的重要分支,研究随机变量、概率分布、概率论等概念和方法。
Matlab提供了丰富的统计和概率函数,可以进行概率分布的计算、随机变量的模拟和统计分析等。
例如,可以使用Matlab计算正态分布的概率密度函数和累积分布函数,从而得到随机变量的概率分布和统计特性。
此外,Matlab还可以进行随机变量的模拟,通过生成随机数样本,估计概率分布的参数和进行假设检验等。
MATLAB二维图形及其应用

MATLAB绘制二维、三维图形例2-1在子图形窗口中画出上正弦、余弦曲线。
x=0:0.1*pi:2*pi;%按步长赋值生成x向量y=sin(x); z=cos(x);%生成正弦、余弦函数值y、z向量subplot(2,1,1)%分图形窗口为2行1列,并在第一个子窗中绘图plot(x,y,x,z)%在第一个子窗中画出正弦、余弦曲线subplot(2,1,2)%在第二个子窗中绘图plot(x,y,'k:',x,z,'r-')%在第二个子窗中用不同颜色画两条曲线hold on%保持第二个子窗中绘图plot(x,y,'bo',x,z,'k+')%用'o'和'+'标记曲线上分点hold off%取消图形保持例2-2画出上正弦、余弦曲线并对线型加粗、点型加大,重新定置坐标系以及加注相说明和注释。
x=0:0.1*pi:2*pi;%按步长赋值生成x向量y=sin(x); %生成正弦、余弦函数值y、z向量z=cos(x);plot(x,y, 'b-', x,z, 'k .-','linewidth',3, 'markersize',15)axis([-0.2*pi 2*pi -1.2 1.2])%重新设置图形窗口坐标轴范围grid%加注坐标网格xlabel('Variable \it{x}')%标记横坐标轴, \it{x}表示x为斜体ylabel('Variable \it{y}')%标记纵坐标轴title('Sine and Cosine Cruves')%标记图名text(2.5,0.7,'Sin(x)')%在(2.5,0.7)位置,标记曲线名称text(1.5,0.1,'Cos(x)')%在(1.5,0.1)位置,标记曲线名称hold on%图形保持,在同一图形窗口中叠加图形plot([0,2*pi],[0,0], 'r-.')%叠加一条红色的点划直线 0,0)到(2pi,0)hold off%图形保持取消,再画图时将另辟窗口例2-3分别在两个图形窗口画出填充一正方形和极坐标方程的图形。
scilab-使用教程

与MATLAB的互操作性
01
SCILAB可以与MATLAB进行互 操作,允许用户在SCILAB中调 用MATLAB函数或编辑器中的 脚本。
02
互操作性可以通过MATLAB Engine API for Scilab实现, 该API提供了与MATLAB的接 口,以便在SCILAB中执行 MATLAB代码。
图像处理
SCILAB提供了图像处理和分析的功能,可以用 于图像处理和计算机视觉等领域。
ABCD
工程仿真
SCILAB可以用于工程设计和仿真的数值计算和 分析,如流体动力学、结构力学等。
系统控制
SCILAB可以用于控制系统设计和分析,如控制 系统仿真和优化等。
02 SCILAB基础操作
启动与退出SCILAB
易用性
SCILAB的用户界面友好,易于学 习和使用,支持多种编程语言接 口,方便用户进行编程和开发。
开放性
SCILAB是开源软件,用户可以自 由获取和使用源代码,并根据自 己的需求进行定制和开发。
SCILAB的应用领域
科学计算
SCILAB广阵元素
使用单引号或双引号将元素索引括起来,例如 `A(1,1)`或`A"[1,1]"`。
矩阵运算
支持常见的矩阵运算,如加法、减法、乘法 等。
03 SCILAB编程基础
控制流语句
顺序执行
SCILAB中的代码按照从上到下的顺序 执行,无需使用特定的控制流语句。
循环语句
使用`for`循环重复执行特定代码块, 例如`for i=1:10, statements, endfor`。
初值条件
求解常微分方程时需要指定初值条件,可以使用"="指定初值。例如, y(t0)=y0将指定在t0时刻的初值。
利用MATLAB作图在高数中的应用

利用MATLAB作图在高数中的应用高等数学是大学教育中重要的基础理论课之一,在教学的过程中要教给学生基本的理论、学习方法、分析问题和解决问题的能力,高等数学又是一门比较抽象的课程,尤其对于非数学专业的学生,在教学的过程中,很难通过简单的语言将复杂的问题表述清楚,因此图形是高等数学学习过程中离不开的重要手段之一。
图形所能传达的信息远远大于文字,因此,将MATLAB的图形处理应用在高等数学的教学过程中,可起到事半功倍的作用.1 在泰勒公式中的应用泰勒公式是一个用函数在某点的信息描述其附近取值的公式。
如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,可以用这些导数值做系数构建一个泰勒多项式来近似函数在这一点的邻域中的值。
泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
但是在实际的教学过程中,学生对泰勒公式的理解一直不够深入,常常对泰勒公式打着一个大大的问号,大多数学生只能停留在如何展开方面,对于它的实际意义理解不透彻。
例1函数y=sinx的麦克劳林展开式为:下面,我们将绘制出原函数与它的一阶、三阶、五阶和七阶展开式的图形。
在MATLAB 的命令窗口输入如下命令:>> x=0:0.01:10;>> y=sin(x);>> y1=x;>> y2=x-x.^3/factorial(3);>> y3=x-x.^3/factorial(3)+x.^5/factorial(5);>> y4=x-x.^3/factorial(3)+x.^5/factorial(5)-x.^7/factorial(7);>> plot(x,y,x,y1,x,y2,x,y3,x,y4);>> axis([0,10,-5,5]);>>legend('y=sinx','y=x','y=x-x^3/3!','y=x-x^3/3!+x^5/5!','y=x-x^3/3!+ x^5/5!-x^7/7!');显示图形如图1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 为向量或实数矩阵,若 y 为向量,则以 y 元素值为纵坐标,以相应元素下标为横坐标
图 1:limx → 0(sinx/x) 的图形
图 2:函数 f(x) 的图像
值绘制连线图;若 y 为实数矩阵,则按每行为 纵坐标值,以对应列下标为横坐标值绘制连线 图。
的图像,观察当 x → 0 时此函数的极限(如 图 2)。
e.g2. 代码:
-->x=-2*%pi:0.01:0; // 定义自变量 x 的值
-->x1=0:0.01:2*%pi;
-->z=[x;x1]';
-->y=[x-1;x1+1]';
// 确定函数 y 的
值
-->plot(z,y,[0],[0],'.');
Scilab 计算软件用于绘制二维图形常用的 函数指令主要有 plot、plot2di、champ 等。我 们可以根据不同的需要,采用相应的绘图命令 来实现图形的绘制。
2 绘图格式及应用
2.1 Plot
Plot 是最基本的二维图形绘制指令,它属 于 Scilab 内部函数。它是根据对向量或矩阵的 列来绘制连线图形,在高等数学中二维图形绘 制常用的命令格式为: 2.1.1 命令调用格式 [3]
是同维矩阵,则以 x,y 对应行元素为横纵坐标 分别绘制曲线,曲线条数等于矩阵的列数。
以 上 两 种 格 式 中,LineSpec 与 GlobalProperty 均 为 可 选 参 数, 可 通 过 LineSpec 可以为每个点设置其线型,颜色,标 记形式;通过 GlobalProperty 定义适用于所有 由该 plot 指令创建曲线的全局对象的属性。 2.1.2 绘图实例
计 算 功 能、 绘 图 功 能 以 及 直 观 动
态 的 演 示 功 来 体 现, 引 导
学 生 逐 步 探 源 理 论 的 本 质, 提 高
学生学习兴趣。
【关键词】SCILAB 高等数学 二维图形
1 引言
科学计算自由软件 Scilab 是由法国国家信 息与自动化研究院(INRIA)所开发的科学与 工程计算软件,作为著名的开源科学计算软件 之一,它以其开放的源代码形式,在数值计算 和计算结果可视化方面,广受人们的重视与喜 爱。Scilab 具有丰富的数据类型,使用者可以 非常方便地实现各种矩阵与数组计算。同时他 又有很强的图形显示能力,基本上实现了常规 计算结果到图形显示的无缝链接,满足了高校 师生、科研工作者和工程技术人员关于可视化 直观平台的需要。与商业科学计算软件 Matlab 的相比,Scilab 是完全免费的,其源代码以公 开形式发布,使用者完全可以参与软件的开发 与优化,并具有运行稳定、语言简单、绘图方 便等诸多特点。
题
从图中可能看出,当 x → 0 时,
limn → 0-f(x)=limn → 0-(x-1)=-1;
limn → 0+f(x)=limn → 0+(x+1)=1;
左极限与右极限虽然都存在,但不相等,
所以极限 limn → 0f(x) 不存在,故点 x=0 是函
数 f(x) 的 间 断 点, 因 y=f(x) 的 图 形 在 x=0 处
产生跳跃现象,故称 x=0 为函数 f(x) 的跳跃间
断点。通过函数 f(x) 的几何图形,对间断点的
理解更加直观了。
plot2d 函数同样也为 Scilab 最基本的二维 图形绘制指令但它提供了功能更为强大的二维 曲线绘制方法,并可以对线型,坐标轴,标记 等进行控制。 2.2.1 命令格式
(2)格式 2:plot(x,y,<LineSpec>,<Globa lProperty>)
若 x 和 y 是 两 个 向 量, 则 其 中 y 是 x 的 函数,在 x 没有给定的情况下,用向量 [1: size(y,‘*’)] 代替横坐标值;若 y 是一个实数 矩阵,则按行绘制每行元素的连线图;若 x,y
// 绘制函数 f(x)
的图形
-->xgrid;
// 为图形绘制网格线
-->a=gca();
-->a.x_location="origin";
-->a.y_location="origin"; // 设 置 x 和 y
坐标轴均位于原点
-->xtitle(" 函数 f(x) 的图形 ") // 加注标
例 1:使用 plot 函数绘制高等数学中重要
●基金项目:贵州师范学院校级课题《Scilab 在高校数学教学中的辅助应用研究》(项目编号:GZSY201107)阶段性成果。
Electronic Technology & Software Engineering 电子技术与软件工程 • 81
• 软件应用 Software Application
2.2 plot2d函数
图 3:函数
(左)与
(右)的图像
图 4:向量场(左)向量场及等高线(右)
极限之一的 limx → 0(sinx/x)=1 的图形,观察 当 x → 0 时此函数的极限(如图 1)。
e.g1. 代码: -->x=-10*%pi:0.01:10*%pi; // 定 义 自 变 量 x 的值 -->y=sin(x)./x; // 确定函数 y 的值 -->plot(x,y); // 绘制函数 y=sin(x)/x 的图形 -->xgrid; // 为图形绘制网格线 -->xtitle("y=sin(x)/x") // 加 注 标 题“y= sin(x)/x” 从 图 1 中 可 以 很 容 易 的 看 出, 函 数 y=sin(x)/x,当 x → 0 时此函数极限等于 1。意 义在于准确的画出几何图形,能帮助学生迅速 明确定理的题设和结论的意义,提高学生的观 察能力、分析能力和理解能力,促进学生对理 论的理解掌握。 例 2:绘制函数
• Software Application 软件应用
Scilab 在高等数学二维图形绘制中的应用
文/左欣
摘
随 着 科 学 技 术 的 飞 速 发 展,
科学计算软件越来越多的应用到 要 教育教学中,成为各科研领域众
多学者、教师和学生的必备工具。
本文探讨在高等数学教学实践中,
运用科学计算自由软件 Scilab 的
