医学统计学知识点梳理图文稿
医学统计学

实用文档
一、医学统计学的意义
3.统计学方法的特点: (1)用数量反映质量 1)体格检查(量血压、脉搏…) →个 体健康质量 2)考试分数→个体学习质量
3)期望寿命——反映人群健康状况的指标 4) 婴儿死亡率——反映卫生服务质量的指 标
1、研究单位(观察单位、unit)和 变量
(variable)、变量值(value of variable)
(1)、 研究单位(unit) :研究中的个 体(individual),是根据研究目的确定的。
实用文档
二、统计学中的几个基本概念
例如:研究7岁男孩身高的正常值范围
一
个人
一只眼睛
研究大学生视力
• 研究单位:一个人
• 变量:红细胞数
• 同质:同某地、同2002年、同成年男子、
同正常。
总体:1)某地所有的正常成年男子
年男子的
2)某地所有的正常成 红细胞数
实用文档
二、统计学中的几个基本概念
• 1)有限总体(finite population): 研究单位数是有限的
• 例如:调查某地2002年正常成年男子的 红细胞数的正常值范围
第十一章 多因素试验资料的方差分析 第十二章 重复测量设计资料的方差分析 第十五章 多元线性回归分析 第十六章 logistic回归分析 第十七章 生存分析 第十八章 判别分析 第十九章 聚类分析 第二十三章 常用综合评价方法 第二十四章 量表研制与量表资料的统计分析方法
“非常痛心地看到,因为数据分析的缺陷和错误,那 么多好的生物研究工作面临着被葬送的危险” 。
一毫升水
医用统计学思维导图
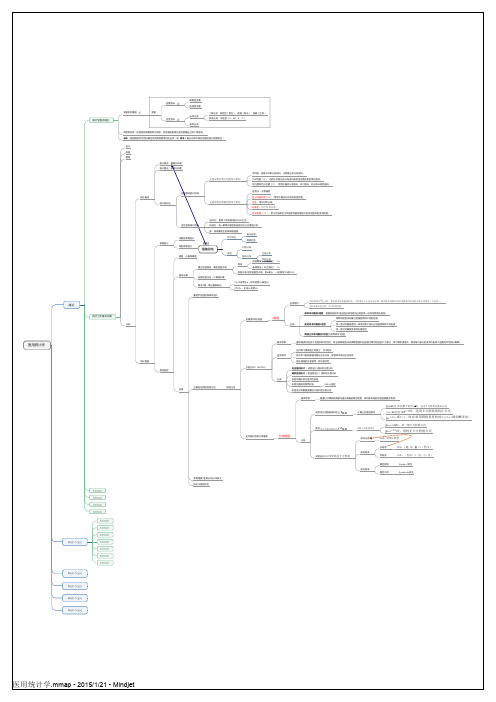
统计推断
假设检验
应用
正确选定假设检验方法
检验方法
方差分析(ANOVA)
应用条件
任何两个观察值之间独立,互不相关 各水平下的观察值均服从正态分布,即各样本来自正态总体 各处理组的方差相等,即方差齐性
分类
完全随机设计 (成组设计)资料的方差分析
随机区组设计 (配伍组设计)资料的方差分析
多组均数比较方差齐性检验
多组均数间的两两比较
SNK-q检验
析因设计和重复测量设计资料的方差分析
基本思想
是通过计算实际频数与理论频数的吻合程度,来判断所给的处理因数是否有效。
争取理解 ”差异无统计学意义 “ 结论不能绝对化
成组设计四格表资料的 χ 2
计算公式使用条件
当n≥40,且所以格子的T≥5时,选用卡方检验的基本公式 当n≥40,但有1≤T<5时,选用卡方检验的校正公式 当n<40,或T<1,时必须用四格表资料的Fisher确切概率法。
t检验
分类
单样本均数的t检验 :是推断该样本来自的总体均数与已知的某一总体均数有无差别。
两种同质受试对象分别接受两种不同的处理
配对样本均数的t检验
同一受试对象或者同一样本的两个部分分别接受两种不同处理
同一受试对象接受某种处理前后
两独立样本均数的 t检验 又称两样本T检验
基本思想
是根据资料的设计类型和研究目的,将全部观察值总的离散程度和自由度分解为相应的几个部分,除了随机误差外,其余每个部分的变异可由某个因素的作用加以解释。
均数的参数估计 率的参数估计
率:某现象发生的频率或强度。 两个特征
集中趋势 离散趋势
查表法
频正数态近分似布法
医学统计学知识点梳理

医学统计学知识点梳理医学统计学:?是用统计学原理和方法研究生物医学问题的一门学科。
他包括了研究设计、数据收集、整理、分析以及分析结果的正确解释和表达。
统计描述:用统计指标、统计图表对资料的数量特征及分布规律进行客观的描述和表达。
统计推断:在一定的置信度和概率保证下,用样本信息推断总体特征:? ①参数估计:用样本的指标去推断总体相应的指标? ②假设检验:由样本的差异推断总体之间是否可能存在的差异同质:一个总体中有许多个体,他们之所以共同成为人们研究的对象,必定存在共性,我们说一些个体处于同一总体,就是指他们大同小异,具有同质性。
总体(population)是根据研究目的确定的同质的观察单位的全体,更确切的说,是同质的所有观察单位某种观察值(变量值)的集合。
总体可分为有限总体和无限总体。
总体中的所有单位都能够标识者为有限总体,反之为无限总体。
样本:从总体中随机抽取部分观察单位,其测量结果的集合称为样本(sample)。
样本应具有代表性。
所谓有代表性的样本,是指用随机抽样方法获得的样本。
随机抽样:随机抽样(random sampling)是指按照随机化的原则(总体中每一个观察单位都有同等的机会被选入到样本中),从总体中抽取部分观察单位的过程。
随机抽样是样本具有代表性的保证。
变异:在自然状态下,个体间测量结果的差异称为变异(variation)。
变异是生物医学研究领域普遍存在的现象。
严格的说,在自然状态下,任何两个患者或研究群体间都存在差异,其表现为各种生理测量值的参差不齐。
(1)计量资料:对每个观察单位用定量的方法测定某项指标量的大小,所得的资料称为计量资料(measurement data)。
计量资料亦称定量资料、测量资料。
.其变量值是定量的,表现为数值大小,一般有度量衡单位。
(2)计数资料:将观察单位按某种属性或类别分组,所得的观察单位数称为计数资料(count data)。
计数资料亦称定性资料或分类资料。
医学统计知识点整理

医学统计学知识点整理第一节统计学中基本概念一、同质与变异同质:统计研究中,给观察单位规定一些相同的因素情况。
如儿童的生长发育,规定同性别、同年龄、健康的儿童即为同质的儿童。
变异:同质的基础上个体间的差异。
“同质”是相对的,是客观事物在特定条件下的相对一致性,而“变异”则是绝对的μ.δ.πX.S.p1.2.变量:确定总体之后,研究者应对每个观察单位的某项特征进行观察或测量,这种特征能表现观察单位的变异性,称为变量。
一、数值变量资料又称为计量资料、定量资料:观测每个观察单位某项指标的大小而获得的资料。
表现为数值大小,带有度、量、衡单位。
如身高(cm)、体重(kg)、血红蛋白(g)等。
二、无序分类变量资料又称为定性资料或计数资料:将观察对象按观察对象的某种类别或属性进行分组计数,分组汇总各组观察单位后得到的资料。
分类:二分类:+ -;有效,无效;多分类:ABO血型系统特点:没有度量衡单位,多为间断性资料【例题单选】某地A、B、O、AB血型人数分布的数据资料是( )A.定量资料B.计量资料C.计数资料D.等级资料分组统计描述:是利用统计指标、统计表和统计图相结合来描述样本资料的数量特征及分布规律。
统计推断:是使用样本信息来推断总体特征。
统计推断包括区间估计和假设检验。
第四节统计表与统计图★一、统计表统计表的基本结构与要求标题:高度概括表的主要内容,时间、地点、研究内容,位于表的上方,居中摆放,左侧加表的序号。
标目:横标目和纵标目。
线条:通常采用三线表和四线表的形式。
没有竖线或斜线。
数字:表内数字一律用阿拉伯数字。
同一指标,小数位数应一致,位次对齐。
无数字用“—”表示。
暂缺用“…”表示。
“0”为确切值。
备注:位于表的下面,通常是对表内数字的注解和说明,必要时可以用“*”等标出。
一张统计表的备注不宜太多。
二、制表原则1.(7理分布。
【例题填空】描述某地十年间结核病死亡率的变化趋势宜绘制_________图。
医学统计学-知识梳理

均数±2.58标准差: 表示集中位置、离散程度均数±2.58标准误: 表示平均水平、抽样误差大小P75一、标准差的主要作用是估计正常值的范围实际应用中, 估计观察值正常值范围应该用标准差(s), 表示为“Mean ±SD”。
此写法综合表达一组观察值的集中和离散特征的变异情况, 说明样本平均数对观察值的代表性。
s 的大或小说明数据取值的分散或集中。
s与样本均数合用, 主要是在大样本调查研究中, 对正态或近似正态分布的总体正常值范围进行估计。
如果不是为了正常值范围估计, 一般不用。
当数据与正态分布相差很大, 或者虽为正态分布, 但样本容量太小(小于30 或100), 也不宜用估计正常值范围。
二、标准差还可用来计算变异系数(CV)当两组观察值单位不同, 或两均数相差较大时, 不能直接用标准差比较其变异程度的大小, 须用变异系数系数来做比较。
:2.2 标准误的正确使用一、标准误用来衡量抽样误差的大小和了解用样本平均数来推论总体平均数的可靠程度。
在抽样调查中, 往往通过样本平均数来推论总体平均数, 样本标准误适用于正态或近似正态分布的数据, 是主要描述小样本试验中, 样本容量相同的同质的多个样本平均均数间的变异程度的统计量。
即如果多次重复同一个试验, 它们之间的变异程度用。
显然它越小, 样本平均数变异越小, 越稳定, 用样本平均数估计总体均数越可靠。
因此, 为说明它的稳定性、可靠性或通过几个对几组数据进行比较(这是科研论文中最常见的), 应当用描述数据。
实际应用中应该写成“平均数±标准误”或而英文表示为“Mean ±SE”的形式。
二、标准误还可以进行总体平均数的区间估计与点估计(置信区间)。
根据正态分布原理, 与合用还可以给出正态总体平均数的可信区间估计即推论总体平均数的可靠区间, 例如常用(其中t0.05 (n-1) 为样本容量是n的t界值)表示总体均值的95%可信区间, 意指总体平均数有95%的把握在所给范围内。
医学统计学基础知识课件

48
48
47
42
53
49
45
50
48
52
49
57
46
48
46
42
49
51
50
51
56
42
59
49
48
52
42
49
55
53
51
45
47
47
47
50
48
51
51
53
46
47
57
45
46
51
46
51
47
51
55
47
52
47
48
54
47
54
49
44
53
54
45
48
44
48
42
47
48
50
55
50
53
56
49
50
56
41
53
53
49
44
49
48
45
52
52
46
54
50
44
53
49
47
48
45
51
45
50
53
•医学统计学基础知识
•37
表 2.2 某医院产科某月顺产婴儿出生身长频数分布
组段(cm) 频数 f 相对频数(%) 累计频数 累计相对频数(%)
41~
6
6.0
6
6.0
43~
4
4.0
10
10.0
45~
•医学统计学基础知识
•9
• 第二节
2024版图文《医学统计学》PPT课件

图文《医学统计学》PPT课件目录•医学统计学概述•医学统计学基本概念•描述性统计方法•推断性统计方法•实验设计与分析•临床医学中的统计学应用01医学统计学概述定义与特点定义医学统计学是应用数理统计学的原理和方法,在医学领域中研究数据的收集、整理、分析和解释的一门科学。
特点以医学为背景,以数据为基础,运用统计学方法揭示医学现象的数量特征和规律。
发展历程及现状发展历程医学统计学经历了从描述性统计到推断性统计,再到现代多元统计分析的发展历程。
现状随着计算机技术的发展和大数据时代的到来,医学统计学在医学研究和实践中发挥着越来越重要的作用。
研究对象与任务研究对象医学统计学的研究对象包括生物医学数据、临床医学数据、公共卫生数据等。
任务医学统计学的任务包括描述医学数据的分布特征、比较不同组别间的差异、分析影响医学现象的因素、预测医学现象的发展趋势等。
02医学统计学基本概念总体样本样本量从总体中随机抽取的一部分个体所构成的集合。
样本中所包含的个体数目。
0302 01总体与样本研究对象的全体个体所构成的集合。
随机抽样与非随机抽样随机抽样按照随机原则从总体中抽取样本的方法,保证每个个体被抽中的机会相等。
非随机抽样根据研究者的主观意愿或方便性选择样本的方法,可能导致选择偏倚。
变量与数据类型变量研究中观察或测量的特征或属性。
数据类型根据变量的性质可分为定量数据和定性数据。
定量数据包括连续型数据和离散型数据,定性数据包括分类数据和顺序数据。
统计量与参数统计量描述样本特征的量,如样本均数、样本标准差等。
参数描述总体特征的量,如总体均数、总体标准差等。
通常情况下参数是未知的,需要通过样本统计量进行估计。
03描述性统计方法频数分布表直方图应用场景频数分布表与直方图用于展示数据的分布情况,包括各组数据的频数、频率、累计频数和累计频率。
用矩形的面积表示各组频数,矩形的高度表示每一组的频数密度,宽度则表示组距。
适用于连续变量,可直观地展示数据的分布规律,如偏态、峰态等。
医学统计学重点图表总结

描述内容 指 标 意 义 适 用 场 合平均水平均 数 个体的平均值 对称分布几何均数 平均倍数 取对数后对称分布中 位 数 位次居中的观察值 ①非对称分布;②半定量资料;③末端开口资料;④分布不明众 数 频数最多的观察值 不拘分布形式,概略分析 调和均数 基于倒数变换的平均值正偏峰分布资料 变 异 度全 距 观察值取值范围 不拘分布形式,概略分析 标 准 差 (方 差) 观察值平均离开均数的程度对称分布,特别是正态分布资料四分位数间距 居中半数观察值的全距①非对称分布;②半定量资料;③末端开口资料;④分布不明变异系数标准差与均数的相对比①不同量纲的变量间比较;②量纲相同但数量级相差悬殊的变量间比较4. 常用统计图有哪些?分别适用于什么分析目的? 常用统计图的适用资料及实施方法 图 形 适 用 资 料 实 施 方 法条 图 组间数量对比 用直条高度表示数量大小直 方 图 定量资料的分布 用直条的面积表示各组段的频数或频率百分条图 构成比 用直条分段的长度表示全体中各部分的构成比 饼 图 构成比用圆饼的扇形面积表示全体中各部分的构成比 线 图 定量资料数值变动 线条位于横、纵坐标均为算术尺度的坐标系半对数线图 定量资料发展速度 线条位于算术尺度为横坐标和对数尺度为纵坐标的坐标系 散 点 图 双变量间的关联 点的密集程度和形成的趋势,表示两现象间的相关关系 箱 式 图 定量资料取值范围 用箱体、线条标志四分位数间距及中位数、全距的位置 茎 叶 图 定量资料的分布用茎表示组段的设置情形,叶片为个体值,叶长为频数定性资料统计描述常用的统计指标及其适用场合指标 计算公式适用场合频率 n/N估计总体中某一结局发生的概率 频率分布 n 1/N ,n 2/N,…..,n k /N 估计总体中所有可能结局发生的概率强度 阳性人数/总观察人时数 估计总体中单位时间内某一结局发生的概率 比A/B估计两个指标的相对大小4。
卫生统计学知识框架图
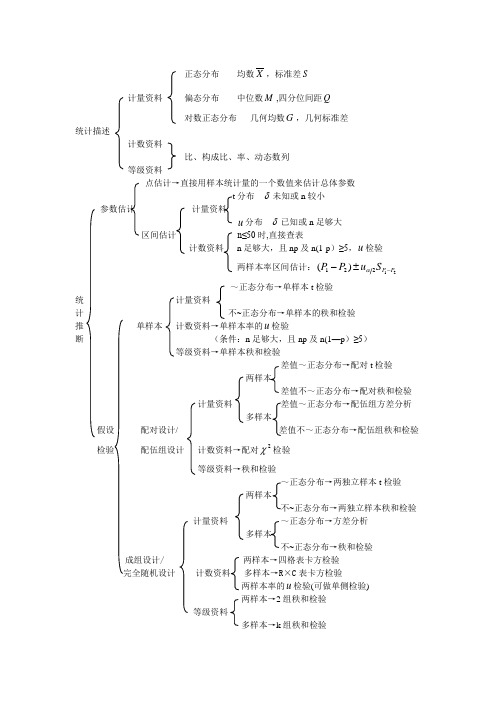
正态分布 均数X ,标准差S 计量资料 偏态分布 中位数M ,四分位间距Q
对数正态分布 几何均数G ,几何标准差
统计描述
计数资料
比、构成比、率、动态数列
等级资料
点估计→直接用样本统计量的一个数值来估计总体参数
t 分布 δ未知或n 较小
参数估计 计量资料
u 分布 δ已知或n 足够大
区间估计 n≤50时,直接查表
计数资料 n 足够大,且np 及n(1-p )≥5,u 检验
两样本率区间估计:2
1221)(P P S u P P -±-α ~正态分布→单样本t 检验
统 计量资料
计 不~正态分布→单样本的秩和检验
推 单样本 计数资料→单样本率的u 检验
断 (条件:n 足够大,且np 及n(1—p )≥5)
等级资料→单样本秩和检验
差值~正态分布→配对t 检验 两样本
差值不~正态分布→配对秩和检验 计量资料 差值~正态分布→配伍组方差分析 多样本
假设 配对设计/ 差值不~正态分布→配伍组秩和检验 检验 配伍组设计 计数资料→配对2χ检验
等级资料→秩和检验
~正态分布→两独立样本t 检验 两样本
不~正态分布→两独立样本秩和检验 计量资料 ~正态分布→方差分析
多样本
不~正态分布→秩和检验 成组设计/ 两样本→四格表卡方检验
完全随机设计 计数资料 多样本→R ×C 表卡方检验
两样本率的u 检验(可做单侧检验)
两样本→2组秩和检验
等级资料
多样本→k 组秩和检验。
医学统计学知识点

实用标准文案精彩文档第一章绪论1、统计学,是关于数据收集、整理、分析、表达和解释的普遍原理和方法。
2、研究对象:具有不确定性结果的事物。
3、统计学作用:能够透过偶然现象来探测其规律性,使研究结论具有科学性。
4、统计分析要点:正确选用统计分析方法,结合专业知识作出科学的结论。
5、医学统计学基本内容:统计设计、数据整理、统计描述、统计推断。
6、医学统计学中的基本概念(1) 同质与变异同质,指根据研究目的所确定的观察单位其性质应大致相同。
变异,指总体内的个体间存在的、绝对的差异。
统计学通过对变异的研究来探索事物。
(2) 变量与数据类型变量,是反映实验或观察对象生理、生化、解剖等特征的指标。
变量的观测值,称为数据分为三种类型:定量数据,也称计量资料,指对每个观察单位某个变量用测量或其他定量方法准确获得的定量结果。
(如身高、体重、血压、温度等)定性数据,也称计数资料,指将观察单位按某种属性分组计数的定性观察结果。
包括二分类、无序多分类。
(进一步分为二分类和多分类,如性别分为男和女,血型分为A、B、O、AB等)有序数据,也称半定量数据或等级资料,指将观察单位按某种属性的不同程度或次序分成等级后分组计数的观察结果,具有半定量性质。
统计方法的选用与数据类型有密切的关系。
(3)总体与样本总体,指根据研究目的确定的所有同质观察单位的全体,包括所有定义范围内的个体变量值。
样本,是从研究总体中随机抽取部分有代表性的观察单位,对变量进行观测得到的数据。
抽样,是从研究总体中随机抽取部分有代表性的观察单位。
参数,指描述总体特征的指标。
统计量,指描述样本特征的指标。
(4)误差误差,指观测值与真实值、统计量与参数之间的差别。
可分为三种:系统误差,也称统计偏倚,是某种必然因素所致,不是偶然机遇造成的,误差的大小通常恒定,具有明确的方向性。
随机测量误差,是偶然机遇所致,误差没有固定的大小和方向。
抽样误差,是抽样引起的统计量与参数间的差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
医学统计学知识点梳理集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)医学统计学知识点梳理医学统计学:是用统计学原理和方法研究生物医学问题的一门学科。
他包括了研究设计、数据收集、整理、分析以及分析结果的正确解释和表达。
统计描述:用统计指标、统计图表对资料的数量特征及分布规律进行客观的描述和表达。
统计推断:在一定的置信度和概率保证下,用样本信息推断总体特征:①参数估计:用样本的指标去推断总体相应的指标②假设检验:由样本的差异推断总体之间是否可能存在的差异同质:一个总体中有许多个体,他们之所以共同成为人们研究的对象,必定存在共性,我们说一些个体处于同一总体,就是指他们大同小异,具有同质性。
总体(population)是根据研究目的确定的同质的观察单位的全体,更确切的说,是同质的所有观察单位某种观察值(变量值)的集合。
总体可分为有限总体和无限总体。
总体中的所有单位都能够标识者为有限总体,反之为无限总体。
样本:从总体中随机抽取部分观察单位,其测量结果的集合称为样本(sample)。
样本应具有代表性。
所谓有代表性的样本,是指用随机抽样方法获得的样本。
随机抽样:随机抽样(random sampling)是指按照随机化的原则(总体中每一个观察单位都有同等的机会被选入到样本中),从总体中抽取部分观察单位的过程。
随机抽样是样本具有代表性的保证。
变异:在自然状态下,个体间测量结果的差异称为变异(variation)。
变异是生物医学研究领域普遍存在的现象。
严格的说,在自然状态下,任何两个患者或研究群体间都存在差异,其表现为各种生理测量值的参差不齐。
(1)计量资料:对每个观察单位用定量的方法测定某项指标量的大小,所得的资料称为计量资料(measurement data)。
计量资料亦称定量资料、测量资料。
.其变量值是定量的,表现为数值大小,一般有度量衡单位。
(2)计数资料:将观察单位按某种属性或类别分组,所得的观察单位数称为计数资料(count data)。
计数资料亦称定性资料或分类资料。
其观察值是定性的,表现为互不相容的类别或属性。
(3)等级资料:将观察单位按测量结果的某种属性的不同程度分组,所得各组的观察单位数,称为等级资料(ordinal data)。
概率:概率(probability)又称几率,是度量某一随机事件A发生可能性大小的一个数值,记为P(A),P(A)越大,说明A事件发生的可能性越大。
0﹤P(A)﹤1。
频率:在相同的条件下,独立重复做n 次试验,事件A 出现了m 次,则比值m/n 称为随机事件A 在n 次试验中出现的频率(freqency)。
当试验重复很多次时P(A)= m/n。
随机误差(random error)又称偶然误差,是指排除了系统误差后尚存的误差。
它受多种因素的影响,使观察值不按方向性和系统性而随机的变化。
误差变量一般服从正态分布。
随机误差可以通过统计处理来估计。
抽样误差(sampling error )是指样本统计量与总体参数的差别。
在总体确定的情况下,总体参数是固定的常数,统计量是在总体参数附近波动的随机变量。
系统误差:系统误差(systematic error)是指由于仪器未校正、测量者感官的某种偏差、医生掌握疗效标准偏高或偏低等原因,使观察值不是分散在真值的两侧,而是有方向性、系统性或周期性地偏离真值。
系统误差可以通过实验设计和完善技术措施来消除或使之减少。
随机变量:随机变量(random variable)是指取指不能事先确定的观察结果。
随机变量的具体内容虽然是各式各样的,但共同的特点是不能用一个常数来表示,而且,理论上讲,每个变量的取值服从特定的概率分布。
参数:参数(paramater)是指总体的统计指标,如总体均数、总体率等。
总体参数是固定的常数。
多数情况下,总体参数是不易知道的,但可通过随机抽样抽取有代表性的样本,用算得的样本统计量估计未知的总体参数。
统计量:统计量(statistic)是指样本的统计指标,如样本均数、样本率等。
样本统计量可用来估计总体参数。
总体参数是固定的常数,统计量是在总体参数附近波动的随机变量。
频数表(frequency table)用来表示一批数据各观察值或在不同取值区间的出现的频繁程度(频数)。
算术均数(arithmetic mean)描述一组数据在数量上的平均水平。
总体均数用μ表示,样本均数用X 表示。
几何均数(geometric mean)用以描述对数正态分布或数据呈倍数变化资料的水平。
记为G。
中位数(median)Md将一组观察值由小到大排列,n 为奇数时取位次居中的变量值;为偶数时,取位次居中的两个变量的平均值。
反映一批观察值在位次上的平均水平。
极差(range)亦称全距,即最大值与最小值之差,用于资料的粗略分析,其计算简便但稳定性较差。
百分位数(percentile)是将n 个观察值从小到大依次排列,再把它们的位次依次转化为百分位。
百分位数的另一个重要用途是确定医学参考值范围。
四分位数间距(inter-quartile range)是由第3 四分位数和第1 四分位数相减计算而得,常与中位数一起使用,描述偏态分布资料的分布特征,较极差稳定。
方差(variance):方差表示一组数据的平均离散情况,由离均差的平方和除以样本个数得到。
标准差(standard deviation)是方差的正平方根,使用的量纲与原量纲相同,适用于近似正态分布的资料,大样本、小样本均可,最为常用。
变异系数(coefficient of variation)用于观察指标单位不同或均数相差较大时两组资料变异程度的比较。
用CV 表示。
计算:标准差/均数*100%统计推断:通过样本指标来说明总体特征,这种从样本获取有关总体信息的过程称为统计推断(statistical inference)。
抽样误差:由个体变异产生的,抽样造成的样本统计量与总体参数的差异,称为抽样误差(sampling error)。
标准误及X s :通常将样本统计量的标准差称为标准误(standard error of mean,SEM ),它反映了样本均数间的离散程度,也反映了样本均数与总体均数的差异,说明均数抽样误差的大小。
可信区间:按预先给定的概率确定的包含未知总体参数的可能范围。
该范围称为总体参数的可信区间(confidence interval,CI)。
参数估计:指用样本指标值(统计量)估计总体指标值(参数)。
假设检验中P 的含义:指从H0 规定的总体随机抽得等于及大于(或等于及小于)现有样本获得的检验统计量值的概率。
I?型错误(type I error ),指拒绝了实际上成立的H0,这类“弃真”的错误称为I 型错误,其概率大小用α表示。
II?型错误(type II error),指接受了实际上不成立的H0,这类“存伪”的误称为II 型错误,其概率大小用β表示。
检验效能:1-β称为检验效能(power of test),它是指当两总体确有差别,按规定的检验水准a 所能发现该差异的能力。
率(rate)又称频率指标,说明一定时期内某现象发生的频率或强度。
计算公式为:发生某现象的观察单位数/可能发生某现象的观察单位总数*100%,表示方式有:百分率(%)、千分率(‰)等。
构成比(proportion)又称构成指标,说明某一事物内部各组成部分所占的比重或分布。
计算公式为:某一组成部分的观察单位数/同一事物各组成部分的观察单位总数*100%,表示方式有:百分数等。
比(ratio)又称相对比,是A、B 两个有关指标之比,说明A 是B 的若干倍或百分之几。
计算公式为:A/B ,表示方式有:倍数或分数等。
非参数统计:针对某些资料的总体分布难以用某种函数式来表达,或者资料的总体分布的函数式是未知的,只知道总体分布是连续型的或离散型的,用于解决这类问题的一种不依赖总体分布的具体形式的统计分析方法。
参数统计:通常要求样本来自总体分布型是已知的(如正态分布),在这种假设的基础上,对总体参数(如总体均数)进行估计和检验,称为参数统计(parametric statistics)秩次:变量值按照从小到大顺序所编的秩序号称为秩次(rank)。
秩和:各组秩次的合计称为秩和(rank sum),是非参数检验的基本统计量。
直线回归(linear regression)建立一个描述应变量依自变量变化而变化的直线方程,并要求各点与该直线纵向距离的平方和为最小。
直线回归是回归分析中最基本、最简单的一种,故又称简单回归(simple regression)。
回归系数(regression coefficient )即直线的斜率(slope),在直线回归方程中用b 表示,b 的统计意义为X每增(减)一个单位时,Y平均改变b 个单位。
相关系数r:用以描述两个随机变量之间线性相关关系的密切程度与相关方向的统计指标。
二相关概念医学科研数据统计分析大致分以下4个步骤。
1.1 数据整理1.2 统计描述1.3 统计推断1.4 结果表达频数表的制作求全距R找到资料中的最大值A和最小值B计算全距R,划分组段确定组数确定组距确定各组段的上下限下限(lower limit)上限(upper limit)第一组段,其下限可取小于最小观察值得数半开半闭区间 [ -- ,-- )画表频数分布表和频数分布图的用途揭示频数分布的特征集中趋势集中趋势是指一组数据向某一个位置聚集或集中的倾向。
离散趋势离散趋势反映的是一组数据的分散性和变异度,即各个数据离开集中位置的程度。
便于观察数据的分布类型正态分布?集中趋势的指标:均数离散趋势的指标:标准差偏态分布集中趋势的指标:中位数离散趋势的指标:四分位间距算术平均数几何平均数中位数符号X G M含义各观察值相加除以观察值的个数所得之商。
N各观察值的乘积开n次方所得之根一组观察值按顺序排列,居中者。
应用条件正态或近似正态分布对数正态分布极偏态或分布不清的资料计算公式说明加权法计算中X值的含义中位数为百分位数的特例标准差的意义和用途0.说明资料的离散趋势(或变异程度),标准差的值越大,说明变异程度越大,均数的代表性越差.标准差与原始数据的单位一致,在科技论文报告中,均数与标准差经常被同时用来描述资料的集中趋势与离散趋势。
0.用于计算变异系数1.用于计算标准误2.结合均值与正态分布的规律,估计参考值的范围。
变异系数(coefficient of variation)适用范围1观察指标单位不同,如身高、体重——不同单位资料2均数相差悬殊变异系数的特点及相应的用途没有单位n 反映标准差占均数的百分比或标准差是均数的几倍n 可用来比较度量衡单位不同的资料的变异度不受平均水平的影响n 反映的是以均数为基数的相对变异的大小n 比较均数相差悬殊的资料的变异度变异指标小结1.极差较粗,适合于任何分布2.标准差与均数的单位相同,最常用,适合于近似正态分布3.变异系数主要用于单位不同或均数相差悬殊资料4.平均指标和变异指标分别反映资料的不同特征,常配套使用如——正态分布:均数、标准差;偏态分布:中位数、四分位间距相对数使用应注意的问题1.根据需要正确选择相对数,常见错误是以构成比代率。
