通信原理基于matlab的计算机仿真资料

合集下载

通信原理matlab实验

二进制信号传输时的眼图只有一只“眼睛”，当传输三元码时，会显示两只“眼睛”。眼图是由各段码元波形叠加而成的，眼图中央的垂直线表示最佳抽样时刻，位于两峰值中间的水平线是判决门限电平。
在无码间串扰和噪声的理想情况下，波形无失真，每个码元将重叠在一起，最终在示波器上看到的是迹线又细又清晰的“眼睛”，“眼”开启得最大。当有码间串扰时，波形失真，码元不完全重合，眼图的迹线就会不清晰，引起“眼”部分闭合。若再加上噪声的影响，则使眼图的线条变得模糊，“眼”开启得小了，因此，“眼”张开的大小表示了失真的程度，反映了码间串扰的强弱。由此可知，眼图能直观地表明码间串扰和噪声的影响，可评价一个基带传输系统性能的优劣。另外也可以用此图形对接收滤波器的特性加以调整，以减小码间串扰和改善系统的传输性能。
从以上分析可知，眼图可以定性反映码间串扰的大小和噪声的大小，眼图还可以用来指示接受滤波器的调整，以减少码间串扰，改善系统性能。
使用了随机数，产生的基带信号也是随机的，经过加白噪声，产生的眼图也是不一样的。选取的采样频率也影响着最后的博兴和眼图。一开始的时候，提示加噪声的部分有问题，通过调试，发现工作空间设置的不准确，相加会出现错误，将工作空间加大，语法没错了，但是眼图出不来。后来经过仔细观察，发现做卷积的时候把一个元素弄错了，经过修改，最终成功运行。
2015年6月25日
基于MATLAB的第一类部分响应系统的
基带信号及其眼图实现
摘要
所谓眼图，是指通过用示波器观察接收端的基带信号波形，从而估计和调整系统性能的一种方法。这种方法具体做法是：用一个示波器跨接在抽样判决器的输入端，然后调整示波器水平扫描周期，使其与接受码元的周期同步。此时可以从示波器显示的图形上，观察码间干扰和信道噪声等因素影响的情况，从而估计系统性能的优劣程度。因为在传输二进制信号波形时，示波器显示的图像很像人的眼睛，故名“眼图”。

（完整版）基于matlab的通信系统仿真毕业论文

（完整版）基于matlab的通信系统仿真毕业论文创新实践报告报告题目：学院名称：姓名：基于 matlab 的通信系统仿真信息工程学院余盛泽班级学号：指导老师：温靖二 O 一四年十月十五日目录一、引言 (3)二、仿真分析与测试 (4)2.1 随机信号的生成 ............................................................................................................... 4 2.2 信道编译码........................................................................................................................4 2.2.1 卷积码的原理 ........................................................................................................ 4 2.2.2 译码原理 ................................................................................................................5 2.3 调制与解调 (5)2.3.1 BPSK 的调制原理 .................................................................................................. 5 2.3.2 BPSK 解调原理 (6)2.3.3 QPSK 调制与解调................................................................................................. 7 2.4 信道 .......................................................................................................................... . (8)2.4.1 加性高斯白噪声信道 ............................................................................................ 8 2.4.2 瑞利信道 ................................................................................................................ 8 2.5 多径合并 .......................................................................................................................... .. 8 2.5.1 MRC 方式 (8)2.5.2 EGC 方式................................................................................................................ 9 2.6 采样判决 .......................................................................................................................... .. 9 2.7 理论值与仿真结果的对比 (9)三、系统仿真分析 (11)3.1 有信道编码和无信道编码的的性能比较...................................................................... 11 3.1.1 信道编码的仿真 ................................................................................................... 11 3.1.2 有信道编码和无信道编码的比较 .......................................................................12 3.2 BPSK 与QPSK 调制方式对通信系统性能的比较...................................................... 13 3.2.1 调制过程的仿真 ................................................................................................... 13 3.2.2 不同调制方式的误码率分析 ...............................................................................14 3.3 高斯信道和瑞利衰落信道下的比较 .............................................................................. 15 3.3.1 信道加噪仿真 ....................................................................................................... 15 3.3.2 不同信道下的误码分析 ....................................................................................... 15 3.4 不同合并方式下的对比 .. (16)3.4.1 MRC 不同信噪比下的误码分析 ......................................................................... 16 3.4.2 EGC 不同信噪比下的误码分析 .......................................................................... 16 3.4.3 MRC、EGC 分别在2 根、4 根天线下的对比 . (17)3.5 理论数据与仿真数据的区别 (17)四、设计小结.............................................................................................................. 19 参考文献......................................................................................................................20一、引言现代社会发展要求通信系统功能越来越强，性能越来越高，构成越来越复杂；另一方面，要求通信系统技术研究和产品开发缩短周期，降低成本，提高水平。

通信原理基于matlab的计算机仿真

通信原理基于matlab的计算机仿真通信原理基于matlab的计算机仿真已经成为通信领域中一项重要的研究工具。

此类仿真软件通过模拟现实情形，能够极大地加快通信设备的开发进程，并且可以帮助工程师进行实验，发现并解决通讯中可能存在的问题。

同时，matlab的通信仿真功能也成为了相关教材和教学实验的首选，许多大学，尤其是通信工程专业的学生要通过matlab的仿真来更好地理解通信原理和通信设备的工作原理。

由于matlab的专业性，无论是对于传输介质的模型计算，还是信号的传输过程的计算仿真，都非常适合。

通信原理的matlab仿真可以有效地帮助工程师分析各种信号，包括模拟信号、数字信号及混合信号。

这种仿真可用于计算机网络、通信系统设计以及无线通信和移动通信等领域。

在matlab中，通信原理的仿真重点是信号的传输与接收。

目前，通信设备主要采用数字信号的传输方式，而matlab中也能够实现该方式的仿真。

通过模拟数字信号的传输过程，可以帮助工程师分析此类信号在不同媒介下的传输效果。

所以，在进行数字信号的仿真时，matlab会考虑到以下几个因素：1.噪声在数字通信中，噪声是一个常见的问题。

因此，在matlab 的仿真中也要考虑到噪声的影响因素。

matlab能够对噪声进行建模，模拟各种环境下的噪声对数字信号的影响程度。

2.数据传输速率数据传输速率也会影响数字信号的仿真结果。

matlab可以模拟数字信号传输的速率以及不同速率下的传输效果。

3.差错率差错率也是数字信号传输中的一个显著因素，matlab在通信原理仿真中也会进行模拟。

除数字信号外，模拟信号的仿真也是通信原理仿真领域的一项重要工作。

在matlab的仿真中，通常对模拟信号的传输和接收会更加复杂。

通信原理的matlab仿真的一个重要应用就是误码率和比特误差率测试。

误码率和比特误差率都是评估数字信号传输质量的指标。

通信系统的设计旨在在受到最小干扰时保持误差率的最小化。

通信原理实验Matlab程序(软件仿真)

num=0; % 计数器清零 yz(k)=1*yz(k-4); % 让0000的最后一个0改变为与前一个非零符号相同极性的符号 V(k)=yz(k); % V 脉冲位置记录 if yz(k)==sign % 如果当前V符号与前一个V符号的极性相同 yz(k)=-1*yz(k); % 则让当前V符号极性反转,以满足V符号间相互极性反转要求 yz(k-3)=yz(k); % 添加B符号,与V符号同极性 B(k-3)=yz(k); % B脉冲位置记录 V(k)=yz(k); % V 脉冲位置记录 yz(k+1:length(yw))=-1*yz(k+1:length(yw)); % 并让后面的非零符号从V符号开始再交替变化 end sign=yz(k); % 记录前一个V符号的极性 end else num=0; % 当前输入为“1”则连“0”计数器清零 end end % 编码完成 %re=[xn',yw',yz',V',B']; % 结果输出: xn AMI HDB3 V&B 符号 yn=yz;% 输出yn初始化 num=0;% 计数器初始化 for k=1:length(yz) if yz(k)==1 num=num+1; % "1" 计数器 if num/2 == fix(num/2) % 奇数个1时输出-1,进行极性交替 yn = [yn gt1]; else yn = [yn -1*gt1]; end else yn = [yn gt2]; end end yh=yn; fft_se1 = fftshift(fft(yh)); % 求序列的频谱 PE1 = 10 * log10(abs(fft_se1) .^ 2 / (N * Ts)); % 公式法求概率谱密度 PEL1 = (-length(fft_se1) / 2 : length(fft_se1) / 2 - 1) / 10; % 求区间长度 subplot(2,1,1);stairs([0:length(yn)-1],yn);axis([0 length(yn) -2 2]);

通信原理-基于Matlab的计算机仿真 (19)

• 2PAM、FSK、PSK
第二十三讲：幅相调制
• 矩形星座QAM、APSK • 接收机及性能*
第二十四讲：载波恢复、相位模糊
• 锁相环 • Costas环、平方环
第二十五、六讲：连续相位数字调制*
• MSK信号及其原理 • GMSK信号 • PI/4－OQPSK
第二十七讲：信源和信源编码
通信原理
本学期讲授内容及学时安排参考书习题、考试、成绩
内容及学时安排
第一讲：概述
• 通信简史、通信系统概念（模拟、数字）、信号与系统知识复习（傅氏变换）、信号量（功率、能量）、信号特性（自相关、功率谱密度、能谱密度）、线性系统、信号通过线性系统
第二讲：Hilbert变换和等效基带
樊昌信等，通信原理（第五版），国防工业出版社）曹志刚等，现代通信原理，清华大学出版社。
成绩及作业
成绩构成
• 平时课外作业（10－15％） • 期中测试（25－35％） • 期末测试（50－65％）
• 图象编码
• JPEG
• 视频编码
• MPEG
参考书（精读一本）
周炯磐等，通信原理（上、下），2004年6月第四次印刷，北邮出版社。
Leon W.Couch, 数字与模拟通信系统，电子工业出版社。（中文翻译版、英文版）
John G.Proakis,Digital Communications，电子工业出版社（影印版，第三版或第四版）
第十八讲：数字基带信号同步
• 锁相环* • 数字基带同步方法
第十九讲：数字频带信号及其传输
• 频谱搬移（MPAM、BPSK、OOK） • 调频：2FSK、MFSK • 调相：BPSK、QPSK、OQPSK、MPSK

通信原理基于matlab的计算机仿真

例1-1%周期信号（方波）的展开,fb_jinshi.mclose all;clear all;N=100; %取展开式的项数为2N＋1项T=1;fs=1/T;N_sample=128; %为了画出波形，设置每个周期的采样点数dt = T/N_sample;t=0:dt:10*T-dt;n=-N:N;Fn = sinc(n/2).*exp(-j*n*pi/2);Fn(N+1)=0;ft = zeros(1,length(t));for m=-N:Nft = ft + Fn(m+N+1)*exp(j*2*pi*m*fs*t);endplot(t,ft)例 1-2利用FFT计算信号的频谱并与信号的真实频谱的抽样比较。

脚本文件T2F.m定义了函数T2F，计算信号的傅立叶变换。

function [f,sf]= T2F(t,st)%This is a function using the FFT function to calculate a signal's Fourier %Translation%Input is the time and the signal vectors,the length of time must greater %than 2%Output is the frequency and the signal spectrumdt = t(2)-t(1);T=t(end);df = 1/T;N = length(st);f=-N/2*df:df:N/2*df-df;sf = fft(st);sf = T/N*fftshift(sf);脚本文件F2T.m定义了函数F2T，计算信号的反傅立叶变换。

通信原理MATLAB仿真教程第8章

B 2 AS K 2 B s
2 Tb
2 fb
（8-8）
（3）因为系统的传码率 R B 1 T b（Baud），故2ASK系统的频带利用率为
1 Tb 2 Tb
这意味着用2ASK方式传送码元速率为 R B 的二进制数字信号时，要求该系统的带宽至少为 2 R B（Hz）。 19

2
数字信息有二进制和多进制之分，因此，数字调制可分为二进制调制和多进制调制。在二进制调制中，信号参量只有两种可能的取值；在多进制（如M进制，M>2）调制中，信号参量可能有M中取值。
3
本章知识要点
●
●
二进制数字调制
多进制数字调制
4
8.1 二进制数字调制
用数字基带信号控制载波，把数字基带信号变换为数字
10
图8-3 2ASK信号波形
11
三、解调方法
2ASK信号解调的常用方法主要有两种：包络检波法和相干检测法。包络检波法的原理方框图如图8-4所示。带通滤波器（ BPF）恰好使2ASK信号完整地通过，经包络检测后，输出其包络。低通滤波器（LPF）的作用是滤除高频杂波，使基带信号（包络）通过。抽样判决器包括抽样、判决及码元形成器。定时抽样脉冲（位同步信号）是很窄的脉冲，通常位于每个码元的中央位置，其重复周期等于码元的宽度。不计噪声影响时，带通滤波器输出为2ASK信号，即
图8-1 2ASK信号产生方法与波形示例
8
二、MATLAB实现以数字信号序列10110010为例，给出产生2ASK 信号的MATLAB程序如下（函数文件askdigital.m），流程图如图8-2所示。
开始为变量赋初值生成2ASK信号画出原始二进制代码波形画出2ASK信号波形结束

通信原理及MATLAB-Simulink仿真通信原理--ch2

当k(t)=常数，称为恒(定)参(量)信道例如，同轴电缆
当k(t)常数，称为随(机)参(量)信道
例如，移动蜂窝网通信信道
10
二、编码信道模型
★ 二进制信号、无记忆信道：
P(0/0) 0 P(0/1) 1 P(1/1) P(1/0) 0
1
11
二、编码信道模型
★ 四进制编码信道模型：
0 1 2 3 0 1
5
调制信道和编码信道
编码器调制器发转换器传输媒质收转换器解调器译码器
调制信道编码信道
狭义信道信道广义信道有线信道：如明线、对称电缆、同轴电缆、光纤等
无线信道：如短波电离层反射、对流层散射等
调制信道恒参信道：如明线、对称电缆、同轴电缆、光纤随参信道：如短波电离层反射、对流层散射等
26
2.5 典型随参信道
一、电离层反射信道
27
多径传播的几种主要形式
28
2.5 典型随参信道
二、对流层散射信道
29
2.6 恒参信道特性及其对信号影响
随参信道的特点多径效应导致信号瑞利衰落
（频率扩散）
多径效应引起频率选择性衰落
30
一、随参信道的特点
信号的衰耗随时间随机变化信号传输的时延随时间随机变化
第 2章
信道与噪声
【第1章测试】一通信系统同时传送语音、
文字和图像，语音按常规8kHz抽样量化，假设图像数字化（720×576像素）压缩60 倍，按电视速率传送。语音、图像采用8bit 二进制编码每抽样点。文字用ASCII编码，
假设传送方式是打字，打字速度为6字符/s。
请问通信10min，系统传送文字、语音和图像的数据量各是多少？比例是多少？

通信原理课程设计基于MATLAB的DSB系统的仿真设计

课程设计原理班级：姓名：学号：指导教师：成绩：电子与信息工程学院信息与通信工程系课程设计评分标准目录摘要Ⅲ关键词Ⅲ第一章引言11.1 课程设计目的和意义11.2 课程设计容 1第二章 Matlab和Simulink的相关介绍12.1 Matlab简介 12.1.1 Matlab的功能 12.1.2 学习Matlab需要掌握的基本知识 12.2 Simulink简介 22.2.1 Simulink功能 22.2.2 特点 2第三章 DSB信号调制、解调原理 33.1 DSB信号调制原理 33.2 DSB信号解调原理 43.2.1 时域分析 43.2.2 频域分析 5第四章基于Matlab编程DSB系统的仿真 54.1 DSB调制 54.1.1 DSB调制仿真代码 54.1.2 DSB调制仿真波形 (6)4.2 高斯白噪声信道64.2.1 高斯白噪声信道仿真代码64.2.2 高斯白噪声信道仿真波形 84.3 DSB解调 84.3.1 DSB解调仿真代码 8第五章基于Simulink对系统建模与仿真 95.1 DSB系统调制建模实现 95.1.1 DSB调制模块设计 95.1.2 DSB信号调制波形 115.2 高斯白噪声信道建模实现 115.2.1 高斯白噪声模块设计 115.2.2 高斯白噪声信道传输波形 12 5.3 DSB系统解调模实现 125.3.1 DSB解调模块设计 135.3.2 DSB解调模块波 145.4总体模型与波形 145.4.1 总体模型 145.4.2 系统各关键点波形 15第六章结果分析 15第七章心得体会 16第八章参考文献 16基于MATLAB的DSB系统的仿真摘要在当前飞速发展的信息时代，随着数字通信技术计算机技术的发展，以与通信网络与计算机网络的相互融合，信息技术已成为21世纪社会国际化的强大动力。

Matlab软件包含众多的功能各异的工具箱，涉与领域包括：数字信号处理、通信技术、控制系统、神经网络、模糊逻辑、数值统计、系统仿真和虚拟现实技术等。

通信原理Matlab仿真实验报告

通信原理Matlab仿真实验报告学号：姓名：实验一1、利用Matlab实现矩形信号串信号分解与合成⑴ Matlab程序代码：①矩形信号串信号分解与合成函数rectexpd()：function rectexpd(T1,T0,m)%矩形信号串信号分解与合成%T1：矩信号区间为（-T1/2，T1/2）%T0：矩形矩信信号串周期%m:傅里叶级数展开项次数t1=-T1/2:0.01:T1/2;t2=T1/2:0.01:(T0-T1/2); t=[(t1-T0)';(t2-T0)';t1';t2';(t1+T0)'];n1=length(t1);n2=length(t2); %根据周期矩形信号函数周期,计算点数f=[ones(n1,1);zeros(n2,1);ones(n1,1);zeros(n2 ,1);ones(n1,1)]; %构造周期矩形信号串y=zeros(m+1,length(t));y(m+1,:)=f';figure(1);plot(t,y(m+1,:)); %绘制周期矩形信号串axis([-(T0+T1/2)-0.5,(T0+T1/2)+0.5,0,1.2]); set(gca,'XTick',[-T0,-T1/2,T1/2,T0]);set(gca,'XTickLabel',{'-T0','-T1/2','T1/2','T0'}) ;title('矩形信号串');grid on; a=T1/T0;pause; %绘制离散幅度谱freq=[-20:1:20];mag=abs(a*sinc(a*freq)); stem(freq,mag);x=a*ones(size(t));for k=1:m %循环显示谐波叠加图形pause;x=x+2*a*sinc(a*k)*cos(2*pi*t*k/T0);y(k,:)=x;plot(t,y(m+1,:));hold on;plot(t,y(k,:));hold off;grid on;axis([-(T0+T1/2)-0.5,[T0+T1/2]+0.5,-0.5,1.5]) ;title(strcat(num2str(k),'次谐波叠加')); xlabel('t');endpause;plot(t,y(1:m+1,:));grid on;axis([-T0/2,T0/2,-0.5,1.5]);title('各次谐波叠加');xlabel('t');②在命令窗口调用rectexpd()函数：T1=5;T0=10;m=5;rectexpd(T1,T0,m)⑵Matlab仿真结果：1次谐波叠加t3次谐波叠加tt2次谐波叠加t4次谐波叠加tt2、利用Matlab实现连续信号卷积运算⑴ Matlab程序代码：①连续信号卷积运算的通用函数sconv()：function [f,k]=sconv(f1,f2,k1,k2,p) f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:p:k3*p; subplot(2,2,1); plot(k1,f1); title('f1(t)'); xlabel('t'); ylabel('f1(t)');subplot(2,2,2);plot(k2,f2);title('f2(t)'); xlabel('t'); ylabel('f2(t)'); subplot(2,2,3); plot(k,f); title('f(t)=f1(t)*f2(t)'); xlabel('t'); ylabel('f(t)');h=get(gca,'position'); h(3)=2.5*h(3);set(gca,'position',h);②在命令窗口调用sconv ()函数： p=0.01; k1=0:p:2; f1=exp(-k1); k2=0:p:3;f2=ones(1,length(k2)); [f,k]=sconv(f1,f2,k1,k2,p)⑵Matlab 仿真结果：0.511.5200.51f1(t)tf 1(t )01230.511.52f2(t)tf 2(t )00.51 1.522.533.544.550.51f(t)=f1(t)*f2(t)tf (t )实验二1、用Matlab模拟图形A律解码⑴Matlab程序代码：①建立函数ADecode()function y=ADecode(code,n) codesize=size(code);cr_len=codesize(1);cl_len=codesize(2);ca=zeros(1,cl_len-1);for i=1:cr_lenca=code(i,2:n);s=0;for j=1:n-1s=s+ca(j)*2^(n-1-j);enda=code(i,1);y(i)=s*((-1)^(a+1)); endy=y/(2^(n-1));A=87.6;A1=1+log(A); for j=1:length(y)if(y(j)>=0)if(y(i)<=1/A1)y(j)=y(j)*A1/A;elsey(j)=exp(y(j)*A1-1/A);endelsetemp=-y(j);if(temp<=1/A1)y(j)=-temp*A1/A;elsey(j)=-exp(temp*A1-1)/A;endendend②建立函数APCM()function code=APCM(x,n)xmax=max(abs(x));x=x/xmax;xlen=length(x);y=zeros(1,xlen);A=87.6;A1=1+log(A);for i=1:xlenif x(i)>=0if x(i)<=1/Ay(i)=(A*x(i))/A1;elsey(i)=(1+log(A*x(i)))/A1;endelsex1=-x(i);if x1<=1/Ay(i)=-(A*x1)/A1;elsey(i)=-(1+log(A*x1))/A1;endendendy1=y*(2^(n-1)-1);y1=round(y1);code=zeros(length(y1),n); c2=zeros(1,n-1);for i=1:length(y1)if(y1(i)>0)c1=1;elsec1=0;y1(i)=-y1(i);endfor j=1:n-1r=rem(y1(i),2);y1(i)=(y1(i)-r)/2;c2(j)=r;endc2=fliplr(c2);code(i,:)=[c1 c2];end③在新函数中调用前两个函数 t=0:0.01:1; x=sin(2*pi*t); code=APCM(x,7); y=ADecode(code,7); subplot(2,1,1) plot(t,x);title('原函数的图形'); subplot(2,1,2) plot(t,y);title('解码后函数的图形');⑵Matlab 仿真结果：00.10.20.30.40.50.60.70.80.91-1-0.500.51原函数的图形00.10.20.30.40.50.60.70.80.91-1-0.50.5解码后函数的图形2、用Matlab 模拟DSB 调制及解调过程 ⑴Matlab 程序代码： close all; clear all;dt=0.001;%采样时间间隔 fm=1; %信源最高频率 fc=10; %载波中心频率 N=4096;T=N*dt; t=0:dt:T-dt;mt=sqrt(2)*cos(2*pi*fm*t);%信源s_dsb=mt.*cos(2*pi*fc*t); %DSB-SC 双边带抑制载波调幅B=2*fm;figure(1); subplot(311) plot(t,s_dsb,'b-');hold on; %画出DSB 信号波形plot(t,mt,'r--');%画出m(t)信号波形 title('DSB 调制信号'); xlabel('t'); grid on;%DSB demodulation rt=s_dsb.*cos(2*pi*fc*t); rt=rt-mean(rt); [f,rf]=T2F(t,rt); [t,rt]=lpf(f,rf,B); subplot(312) plot(t,rt,'k-'); hold on;plot(t,mt/2,'r--');title('相干解调后的信号波形与输入信号的比较'); xlabel('t'); grid on; subplot(313)[f,sf]=T2F(t,s_dsb); %求调制信号的频谱psf=(abs(sf).^2)/T; %求调制信号的功率谱密度 plot(f,psf);axis([-2*fc 2*fc 0 max(psf)]); title('DSB 信号功率谱'); xlabel('f'); grid on;⑵Matlab 仿真结果：00.51 1.52 2.53 3.54 4.5-22DSB 调制信号t0.511.522.533.544.5-101相干解调后的信号波形与输入信号的比较t-20-15-10-5051015200.5DSB 信号功率谱f实验三1、用Matlab模拟双极性归零码⑴ Matlab程序代码：function y=drz(x)t0=300;x=[1 0 0 1 1 0 0 0 0 1 0 1];t=0:1/t0:length(x);for i=1:length(x);if(x(i)==1)for j=1:t0/2y(t0/2*(2*i-2)+j)=1;y(t0/2*(2*i-1)+j)=0;endelsefor j=1:t0/2y(t0/2*(2*i-2)+j)=-1;y(t0/2*(2*i-1)+j)=0;endendendy=[y,x(i)];M=max(y);m=min(y); subplot(211)plot(t,y);grid on;axis([0,i,m-0.1,M+0.1]);title('1 0 0 1 1 0 0 0 0 1 0 1 ');⑵Matlab仿真结果：2、用Matlab产生2FSK信号⑴ Matlab程序代码：①建立函数fskdigital()function fskdigital(s,f1,f2) t=0:2*pi/99:2*pi;m1=[];c1=[];b1=[];for n=1:length(s)if s(n)==0;m=ones(1,100);c=sin(f2*t);b=zeros(1,100) else s(n)==1;m=ones(1,100);c=sin(f1*t);b=ones(1,100)endm1=[m1 m]; c1=[c1 c]; b1=[b1 b]; endfsk=c1.*m1;subplot(211);plot(b1,'r')title('原始信号');axis([0 100*length(s) -0.1 1.1]);grid on;subplot(212);plot(fsk)title('2FSK信号');grid on;②在命令窗口调用函数fskdigital() >> s=[1 0 1 1 0 0 1 0]; f1=200; f2=100;fskdigital(s,f1,f2)⑵Matlab 仿真结果：10020030040050060070080000.20.40.60.81原始信号100200300400500600700800-1-0.500.512FSK 信号3、用Matlab 的simulink 模块模拟三角波的分解与还原 ⑴模块图⑵仿真结果：①三角波原图②用矩形波近似的冲击函数③分解后的三角波④经低通还原的三角波。

基于Matlab(Simulink)《通信原理》实验仿真(模拟部分)

基于Matlab（Simulink）《通信原理》实验仿真（模拟部分）基于Matlab(Simulink)《通信原理》实验仿真(模拟部分)摘要模拟通信在通信系统中的使用非常广泛，而MATLAB(Simulink)是用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，它可以解决包括信号和图像处理、通讯等众多应用领域中的问题。

利用MATLAB集成环境下的M文件和Simulink工具箱可以完成通讯系统设计与仿真，本文主要是利用MATLAB集成环境下的M文件，编写程序来实现AM、FM、VSB调制与解调过程，并分别绘制出其信号波形。

再通过Simulink工具箱对模拟通信系统进行建模仿真。

Simulation of communication in a communication system is very extensive, and the use of MATLAB (Simulink) is used to algorithm development, data visualization, data analysis and numerical calculation of the senior technical calculation language and interactive environment, it can solve the including signal and image processing, communicationetc many applications in question. MATLAB integration environment Mfiles and Simulink tool box can complete communication system design and simulation, this paper is mainly use of MATLAB integration environment, programming of the M files to achieve AM, FM, VSB modulation and demodulation process, and separately plot its signal waveform. Again through Simulink communication system toolbox of simulation modeling simulation .关键词模拟信号;AM;FM;VSB;调制解调;MATLAB(Simulink)目录:第一章绪论第二章理论与方法2.1 matlab简介2.2 Simulink简介2.3 通信原理概述第三章设计方案3.1用 MATLAB的M文件进行模拟调制3.1.1 基于MATLAB的AM信号调制与解调3.1.2 基于MATLAB的FM信号调制与解调3.1.3 基于MATLAB的VSB信号调制与解调3.2用Simulink对模拟通信系统进行建模仿真3.2.1频分复用和超外差接收机的仿真模型3.2.2调频立体声接收机模型第四章小结参考文献致谢附录1:程序清单第一章绪论调制在通信系统中的作用至关重要。

通信原理实验的MATLAB仿真讲义(一、二)

数据通信原理实验的MATLAB仿真讲义MATLAB原意为“矩阵实验室—MA-TrixLABoratory”，它是目前控制界国际上最流行的软件，它除了传统的交互式编程之外，还提供了丰富可靠的矩阵运算、图形绘制、数据和图象处理、Windows编程等便利工具。

MATLAB还配备了大量工具箱，特别是还提供了仿真工具软件SIMULINK。

SIMULINK这一名字比较直观地表明了此软件的两个显著的功能：SIMU(仿真)与LINK(连接)，亦即可以利用鼠标在模型窗口上“画”出所需的系统模型，然后利用SIMULINK提供的功能对控制系统进行仿真和线性化分析。

MATLAB在80年代一出现，首先是在控制界得到研究人员的瞩目。

随着MA T-LAB软件的不断完善,特别是仿真工具SIMULINK的出现，使MA TLAB的应用范围越来越广。

MATLAB的仿真环境(simulink)提供的系统模型库包括以下几个子模型库：Sources(输入源)、Sinks(输出源)、Discrete(离散时间系统)、Linear(线性环节)、Non-linear(非线性环节)、Connections(连接及接口)、Extras(其它环节)。

打开子模型库,你会发现每个模型库都包含许多个子模块，比如Sources模型库里含有阶跃函数、正弦函数、白噪声函数、MATLAB空间变量、信号发生器等子模块。

另外在Extras子模型库下还有一个BlockLibrary，集中了子模型库中最常用及其它常用的子模块,使用起来特别方便。

通信系统一般都可以建立数学模型,在数学模型中,主要包括乘法器、加法器、信号发生器、滤波器等，而这些在上述的simulink 系统模型库中一般都可找到，对于没有的模块(如伪随机信号发生器),可自己根据掌握的技术生成所需的子模块，随时调用。

这样就可根据数学模型，建立通信系统的仿真模型。

应用MA TLAB下的SIMULINK仿真工具可以很方便地进行通信系统仿真，利用SIMULINK仿真工具下的现有子模块进行仿真。

通信原理-基于Matlab的计算机仿真教学设计

通信原理-基于Matlab的计算机仿真教学设计引言计算机仿真教学是一种相对于传统教学方法而言比较“新生”的教学方法，随着计算机技术的进一步发展，计算机仿真教学的方法也越来越被教育领域所接受。

在通信原理这一门课程中，计算机仿真教学也得到了广泛的应用，特别是基于Matlab的计算机仿真教学，更是让学生更好地理解和掌握课程内容。

本文以通信原理-基于Matlab的计算机仿真教学设计为主题，探讨在这种教学环境下如何更好地进行教学设计和实践。

Matlab在通信原理教学中的应用Matlab是一款针对科学和工程领域的数学软件，它提供了基本的数学函数、图形绘制工具、语言结构等等，可以大大简化工程和科学计算中的重复计算过程。

在通信原理课程中，学生通过Matlab软件，可以更加深入地理解到通信原理与实际应用的关系，同时也能够更加通俗地解释课程中一些比较难以理解的概念。

下面我们来介绍一些Matlab在通信原理教学中的具体应用实例：模拟数字调制解调过程学生可以通过Matlab软件实现数字调制解调过程的模拟，通过实际操作，学生能够更加深入地理解数字调制解调实际过程的基本原理及相关的参数设置等等。

这样不仅能够锻炼学生的实际操作技能，还能够更加深入地理解课程内容。

模拟数字信号调制过程Matlab可以帮助学生更加清晰地了解数字信号调制过程，学生可以通过Matlab软件实现数字信号调制器的设计，比如正弦波频率的设置、载频的设置等等，再通过对波形的观察和参数的调节，进一步理解数字信号调制的全过程。

模拟数字信号的解调过程学生也可以通过Matlab软件实现数字信号解调过程的模拟，这样不仅能够更加直观地感受到数字信号的解调过程，还能够进一步理解解调器的设计、整体结构等等。

基于Matlab的计算机仿真教学实践在通信原理的教学中，计算机仿真教学已经成为了教学中必不可少的一部分，因此如何进行基于Matlab的计算机仿真教学实践，便成为了一种切实可行的教学方法。

MATLAB仿真实例(通信原理)

T T T 我们把 s( t ) 按区间 , 截短为 sT ( t ) ，再对 sT ( t ) 按时间间隔 Biblioteka 均匀取样得到个样 t 2 2
值。仿真时我们用这个样值集合来表示信号 s( t ) 。显然 t 反映了仿真系统对信号波形的分辨率， t 越小则仿真的精确度越高。据通信原理所学，信号被取样以后的频谱是频率的周 1 1 期函数，其重复周期是。如果信号的最高频率为 f H ，那么必须有 f H 才能保证不 t 2 t 1 发生混叠失真。我们称 Bs 为仿真系统的系统带宽。如果我们的仿真程序中设定的采 2 t 样间隔是 t ，那么我们不能用此仿真程序来研究带宽大于 Bs 的信号或系统。此外，信号 s( t ) 的频谱 S f 通常来说也是定义在频率区间 , 上的连续函数，所以仿真频域特性时，我们也必须把 S f 截短并取样。考虑到系统带宽是 Bs ，我们把频域的截短
三、实验内容
3.1 傅里叶变换与傅里叶反变换对于确定信号 f (t ) ，其傅里叶变换为：
F( f )
F ( f ) 傅里叶反变换为：

f (t )e 2 j ft dt
f (t ) F ( f )e2 j ft df

在通信原理仿真中，傅里叶变换与傅里叶反变换会经常用到，我们可以利用 MATLAB 的快速傅里叶变换函数 fft 与快速傅里叶反变换函数 ifft 编写傅里叶变换子程序与傅里叶反变换子程序。其程序代码如下：
傅里叶变换子程序：
%傅里叶变换子程序 function X=t2f(x) global dt df N t f T %X=t2f(x) %x 为时域的取样值矢量 %X 为 x 的傅氏变换 %X 与 x 长度相同,并为 2 的整幂。

用MatLab仿真通信原理系列实验

用MatLab仿真通信原理系列实验一、引言通信原理是现代通信领域的基础理论，通过对通信原理的研究和仿真实验可以更好地理解通信系统的工作原理和性能特点。

MatLab作为一种强大的数学计算软件，被广泛应用于通信原理的仿真实验中。

本文将以MatLab为工具，介绍通信原理系列实验的仿真步骤和结果。

二、实验一：调制与解调1. 实验目的通过MatLab仿真，了解调制与解调的基本原理，并观察不同调制方式下的信号特征。

2. 实验步骤（1）生成基带信号：使用MatLab生成一个基带信号，可以是正弦波、方波或任意复杂的波形。

（2）调制：选择一种调制方式，如调幅（AM）、调频（FM）或相移键控（PSK），将基带信号调制到载波上。

（3）观察调制后的信号：绘制调制后的信号波形和频谱图，观察信号的频谱特性。

（4）解调：对调制后的信号进行解调，还原出原始的基带信号。

（5）观察解调后的信号：绘制解调后的信号波形和频谱图，与原始基带信号进行对比。

3. 实验结果通过MatLab仿真，可以得到不同调制方式下的信号波形和频谱图，观察到调制后信号的频谱特性和解调后信号的还原效果。

可以进一步分析不同调制方式的优缺点，为通信系统设计提供参考。

三、实验二：信道编码与解码1. 实验目的通过MatLab仿真，了解信道编码和解码的基本原理，并观察不同编码方式下的误码率性能。

2. 实验步骤（1）选择一种信道编码方式，如卷积码、纠错码等。

（2）生成随机比特序列：使用MatLab生成一组随机的比特序列作为输入。

（3）编码：将输入比特序列进行编码，生成编码后的比特序列。

（4）引入信道：模拟信道传输过程，引入噪声和干扰。

（5）解码：对接收到的信号进行解码，还原出原始的比特序列。

（6）计算误码率：比较解码后的比特序列与原始比特序列的差异，计算误码率。

3. 实验结果通过MatLab仿真，可以得到不同编码方式下的误码率曲线，观察不同信道编码方式对信号传输性能的影响。

通信原理MATLAB仿真实验设计

2. 本实验中，高斯噪声信号序列长度为�� 1024，自相关序列长度为�� 512；
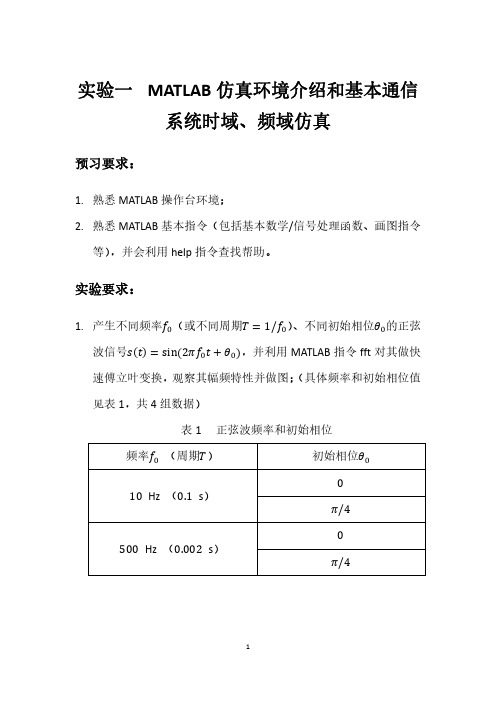
3. 步骤 3 中，当调用函数 dft 时，输入参数中采样周期可以设为1s；
6
4. 画图时，时间和频率范围、过零点、幅度、周期等重要信息要标识清楚。
7
实验四模拟调制系统的 AM 调制仿真
预习要求：
图；（具体周期和幅度值见表 2，共 4 组数据）
表 2 方波周期和幅度
周期��
幅度
1 0.3 s
2.5
1 1s
2.5
3. 产生不同周期 �� 、不同幅度 �� 的三角波信号 ��
��,
0 ��
，并利用 MATLAB 指令 fft 对其做傅立叶
1s
方波
幅度��
1
三角波
周期��
0.25 s
幅度��
1
4
实验说明：
1. 为了计算�� ，函数 dft 需要以下输入参数：输入信号序列�� , �� 0.1, ⋯ , �� 1。注意：MATLAB 中，一维
数组或序列长度可以由指令 length 在函数内得到，因此无需将��
cos �� 图 3 DSB‐SC 调制器模型 2. 利用实验一中程序产生两个周期长度的正弦信号（频率�� 为100Hz，初始相位�� 0）； 3. 利用实验三中程序产生标准正态分布的噪声信号�� ，并利用公式�� 10 �� 将�� 转变为另一正态分布的噪声信号�� ，其均值和方差分别为0和10 ； 4. 将�� 叠加到信号�� 上，从而生成信号�� ，并将其输入至 DSB‐SC 调制器中产生调制信号�� _ �� ； 5. 利用实验四中函数 amdemod 解调�� _ �� ，从而得到解调信号 �� ，比较调制器输入信号和解调输出信号并做图。

通信原理-基于Matlab的计算机仿真 (8)

AWGN信道
x(t) n(t)
带宽为 B的 y(t) x(t) nB (t)
滤波器
当B无限宽时，为理想AWGN信道。
f
而
( y(t)
|
x(t))
(2
1 N0B)N /2
1 Ts ( y (t )x(t ))2 dt
e N0 0
二进制情况
假设发送端，消息空间U的取值只有两种可能（即0、1），经过调制后将0、1一一对应成信号空间中的两个信号 x0 (t), x1 (t) ，经过信道后，在某个码元间隔时间内，接收到的信号 y(t) xi (t) n(t) ；
根据ML准则 f ( y | X 0 )P( X 0 ) f ( y | X1)P( X1) 判为0；
反之判为1
二进制
即
f f
(y | (y |
X0) X1)
1
e n0
Ts 0
y
(
t
)
x0
(
t
)
2
dt
1
e n0
Ts 0
y
(
t
)
x1
(
t
)
2
dt
1
e n0
Ts 0
{
y
(
t
)
x0
(
t
)
2
y
(
t
• zn是均值为0，方差为N0B的高斯变量； • an取值＋A，－A
如果选取判决规则：
yn>0,判为1；反之，判为0。
则系统的平均误码率为
Pe=P(yn>0|an=-A)P(an=-A) +P(yn<0|an=+A)P(an=+A)

通信原理MATLAB仿真实验指导书V1.1

leansmall@
表 5 MATLAB 特殊运算符号：；，（） [] {} 5.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式指令格式 A(r,c) A(r,:) A(:,c) A(:) A(i) A(r,c)=Sa A(:)=D(:) 指令功能数组A中r指定行、c指定列之元素组成的子数组数组A中r指定行对应的所有列之元素组成的子数组数组A中c指定列对应的所有行之元素组成的子数组数组A中各列元素首尾相连组成的“一维长列”子数组 "一维长列"子数组中的第i个元素数组A中r指定行、c指定列之元素组成的子数组的赋值数组全元素赋值，保持A的行宽、列长不变，A、D两组元素总合应相同构成向量、矩阵构成单元数组功能说明示例 1:1:4;1:2:11 分隔行分隔列符号 . .. … % ！ = 注释调用操作系统命令用于赋值功能说明示例
4.MATLAB变量与运算符变量命名规则如下：（1）变量名可以由英语字母、数字和下划线组成
Leansmall Lin
第 3 页
2013-4-26
通信原理 Matlab 仿真实验指导书 V1.1
leansmall@
（2）变量名应以英文字母开头（3）长度不大于 31 个（4）区分大小写 MATLAB中设置了一些特殊的变量与常量，列于下表。表1 MATLAB的特殊变量与常量变量名 ANS i或j pi eps realmax 功能说明默认变量名，以应答最近一次操作运算结果虚数单位圆周率浮点数的相对误差最大的正实数变量名 realmin INF(inf) NAN(nan) nargin nargout 功能说明最小的正实数无穷大不定值（0/0）

通信原理MATLAB仿真自修课(伟)

三、MATLAB基本操作基本操作， M文件程序设计。
基于MATLAB的通信系统仿真
四、MATLAB在通信系统中的应用
基于MATLAB的通信系统仿真
标准调幅 1．实验目的 (1)学习线性调制的基本原理； (2)通过MATLAB 编程实现AM调制信号及其功率谱密度。 2．实验原理标准调幅又称常规双边带调幅。标准调幅中的调制信号m(t)带
有直流分量，设s(t)是载波，即：
其中，为载波频率，为起始相位，A0为载波的幅度。那么，已调信号为
st 0 cosc t 0
c
0
s AM t A0 mt cosc t 0
基于MATLAB的通信系统仿真
m(t)
O
t
A0 m(t)
O
t
cosc(t)
调幅信号的时间波形
已调信号的包络确实与调制信O 号呈线性对应关系。因此，
%Power Spectrum Density [f,Xf]=FFT_SHIFT(t,s_am); PSD=(abs(Xf).^2)/T;
%调制信号频谱 %调制信号功率谱密度
基于MATLAB的通信系统仿真
figure(1)
subplot(211);பைடு நூலகம்plot(t,s_am);hold on;
%画出AM信号波形
plot(t,A+mt,'r--');
%标示AM的包络
title('AM调制信号及其包络');
xlabel('t');
subplot(212); %画出功率谱图形
plot(f,PSD);
axis([-2*fc 2*fc 0 1.5*max(PSD)]); title('AM信号功率谱');

用MatLab仿真通信原理系列实验

实验二：扰码与解扰……………………………………………..……13
实验三：低通信号的抽样定理…………………………….………….16
第四章小结……………………………………………...18
致谢………………………………………………………18
参考文献…………………………………………………18
摘要:本毕业设计用Matlab中的建模仿真工具Simulink对通信原理实验进行仿真。作为系列实验的第一部分，包括模拟信号的线性调制解调(AM、DSB、SSB)过程、扰码与解扰实验和低通信号的抽样定理实验。论文中讲述了Matlab的基础知识、Simulink仿真操作方法以及在通信系统中的应用，对被仿真实验的基本原理也进行了简要介绍。通过本设计对构造通信原理虚拟实验室这一课题进行了初步的探索。
MATLAB系统共有5个主要部分构成：
1)MATLAB语言；
2)MATLAB工作环境；
3)MATLAB数学函数库；
4)MATLAB图形处理系统；
5)MATLAB应用程序接口。
1．MATLAB语言
MATLAB语言是一种面向对象的高级语言，正如前面所述，它以矩阵作为最基本的数据结构。MATLAB语言由自己独特的数据结构、输入输出功能、流程控制语句和函数。MATLAB在工程计算方面具有其他高级语言无法比拟的优越性，它集计算、数据可视化、程序设计于一体，并能将数学问题和解决方案以用户熟悉的数学符号表示出来。
(1)实现了可视化建模，用户通过简单的鼠标操作就可建立起直观的系统模型，并进行仿真；
(2)实现了多工作环境间文件互用和数据交换,如Simulink与MATLAB、FORTRAN以及C的工作环境的信息交换都可以方便的实现；
(3)把理论研究和工程实现有机地结合在一起。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例1-1%周期信号（方波）的展开,fb_jinshi.mclose all;clear all;N=100; %取展开式的项数为2N＋1项T=1;fs=1/T;N_sample=128; %为了画出波形，设置每个周期的采样点数dt = T/N_sample;t=0:dt:10*T-dt;n=-N:N;Fn = sinc(n/2).*exp(-j*n*pi/2);Fn(N+1)=0;ft = zeros(1,length(t));for m=-N:Nft = ft + Fn(m+N+1)*exp(j*2*pi*m*fs*t);endplot(t,ft)例1-2利用FFT计算信号的频谱并与信号的真实频谱的抽样比较。

脚本文件T2F.m定义了函数T2F，计算信号的傅立叶变换。

function [t st]=F2T(f,sf)%This function calculate the time signal using ifft function for the input %signal's spectrumdf = f(2)-f(1);Fmx = ( f(end)-f(1) +df);dt = 1/Fmx;N = length(sf);T = dt*N;%t=-T/2:dt:T/2-dt;t = 0:dt:T-dt;sff = fftshift(sf);st = Fmx*ifft(sff);另写脚本文件fb_spec.m如下：%方波的傅氏变换, fb_spec.mclear all;close all;T=1;N_sample = 128;dt=T/N_sample;t=0:dt:T-dt;st=[ones(1,N_sample/2), -ones(1,N_sample/2)]; %方波一个周期subplot(211);plot(t,st);axis([0 1 -2 2]);xlabel('t'); ylabel('s(t)');subplot(212);[f sf]=T2F(t,st); %方波频谱plot(f,abs(sf)); hold on;axis([-10 10 0 1]);xlabel('f');ylabel('|S(f)|');%根据傅氏变换计算得到的信号频谱相应位置的抽样值sff= T^2*j*pi*f*0.5.*exp(-j*2*pi*f*T).*sinc(f*T*0.5).*sinc(f*T*0.5);plot(f,abs(sff),'r-')例1-3%信号的能量计算或功率计算,sig_pow.mclear all;close all;dt = 0.01;t = 0:dt:5;s1 = exp(-5*t).*cos(20*pi*t);s2 = cos(20*pi*t);E1 = sum(s1.*s1)*dt; %s1(t)的信号能量P2 = sum(s2.*s2)*dt/(length(t)*dt); %s2(t)的信号功率s[f1 s1f]= T2F(t,s1);[f2 s2f]= T2F(t,s2);df = f1(2)-f1(1);E1_f = sum(abs(s1f).^2)*df; %s1(t)的能量,用频域方式计算df = f2(2)-f2(1);T = t(end);P2_f = sum(abs(s2f).^2)*df/T; %s2(t)的功率，用频域方式计算figure(1)subplot(211)plot(t,s1);xlabel('t'); ylabel('s1(t)');subplot(212)plot(t,s2)xlabel('t'); ylabel('s2(t)');例1-4%方波的傅氏变换，sig_band.mclear all;close all;T=1;N_sample = 128;dt=1/N_sample;t=0:dt:T-dt;st=[ones(1,N_sample/2) -ones(1,N_sample/2)];df=0.1/T;Fx = 1/dt;f=-Fx:df:Fx-df;%根据傅氏变换计算得到的信号频谱sff= T^2*j*pi*f*0.5.*exp(-j*2*pi*f*T).*sinc(f*T*0.5).*sinc(f*T*0.5);plot(f,abs(sff),'r-')axis([-10 10 0 1]);hold on;sf_max = max(abs(sff));line([f(1) f(end)],[sf_max sf_max]);line([f(1) f(end)],[sf_max/sqrt(2) sf_max/sqrt(2)]); %交点处为信号功率下降3dB处Bw_eq = sum(abs(sff).^2)*df/T/sf_max.^2; %信号的等效带宽例1-5%带通信号经过带通系统的等效基带表示，sig_bandpass.mclear all;close all;dt = 0.01;t = 0:dt:5;s1 = exp(-t).*cos(20*pi*t); %输入信号[f1 s1f]= T2F(t,s1); %输入信号的频谱s1_lowpass = hilbert(s1).*exp(-j*2*pi*10*t); %输入信号的等效基带信号[f2 s2f]=T2F(t,s1_lowpass); %输入等效基带信号的频谱h2f = zeros(1,length(s2f));[a b]=find( abs(s1f)==max(abs(s1f)) ); %找到带通信号的中心频率h2f( 201-25:201+25 )= 1;h2f( 301-25:301+25) = 1;h2f = h2f.*exp(-j*2*pi*f2); %加入线性相位，[t1 h1] = F2T(f2,h2f); %带通系统的冲激响应h1_lowpass = hilbert(h1).*exp(-j*2*pi*10*t1); %等效基带系统的冲激响应figure(1)subplot(521);plot(t,s1);xlabel('t'); ylabel('s1(t)'); title('带通信号');subplot(523);plot(f1,abs(s1f));xlabel('f'); ylabel('|S1(f)|'); title('带通信号幅度谱');subplot(522)plot(t,real(s1_lowpass));xlabel('t');ylabel('Re[s_l(t)]');title('等效基带信号的实部');subplot(524)plot(f2,abs(s2f));xlabel('f');ylabel('|S_l(f)|');title('等效基带信号的幅度谱');%画带通系统及其等效基带的图subplot(525)plot(f2,abs(h2f));xlabel('f');ylabel('|H(f)|');title('带通系统的传输响应幅度谱'); subplot(527)plot(t1,h1);xlabel('t');ylabel('h(t)');title('带通系统的冲激响应');subplot(526)[f3 hlf]=T2F(t1,h1_lowpass);plot(f3,abs(hlf));xlabel('f');ylabel('|H_l(f)|');title('带通系统的等效基带幅度谱');subplot(528)plot(t1,h1_lowpass);xlabel('t');ylabel('h_l(t)');title('带通系统的等效基带冲激响应');%画出带通信号经过带通系统的响应及等效基带信号经过等效基带系统的响应tt = 0:dt:t1(end)+t(end);yt = conv(s1,h1);subplot(529)plot(tt,yt);xlabel('t');ylabel('y(t)');title('带通信号与带通系统响应的卷积')ytl = conv(s1_lowpass,h1_lowpass).*exp(j*2*pi*10*tt);subplot(5,2,10)plot(tt,real(yt));xlabel('t');ylabel('y_l(t)cos(20*pi*t');title('等效基带与等效基带系统响应的卷积×中心频率载波')例1-6%例：窄带高斯过程，文件 zdpw.mclear all; close all;N0=1; %双边功率谱密度fc=10; %中心频率B=1; %带宽dt=0.01;T=100;t=0:dt:T-dt;%产生功率为N0*B的高斯白噪声P = N0*B;st = sqrt(P)*randn(1,length(t));%将上述白噪声经过窄带带通系统，[f,sf] = T2F(t,st); %高斯信号频谱figure(1)plot(f,abs(sf)); %高斯信号的幅频特性[tt gt]=bpf(f,sf,fc-B/2,fc+B/2); %高斯信号经过带通系统glt = hilbert(real(gt)); %窄带信号的解析信号，调用hilbert函数得到解析信号glt = glt.*exp(-j*2*pi*fc*tt);[ff,glf]=T2F( tt, glt );figure(2)plot(ff,abs(glf));xlabel('频率(Hz)'); ylabel('窄带高斯过程样本的幅频特性')figure(3)subplot(411);plot(tt,real(gt));title('窄带高斯过程样本')subplot(412)plot(tt,real(glt).*cos(2*pi*fc*tt)-imag(glt).*sin(2*pi*fc*tt))title('由等效基带重构的窄带高斯过程样本')subplot(413)plot(tt,real(glt));title('窄带高斯过程样本的同相分量')subplot(414)plot(tt,imag(glt));xlabel('时间t(秒)'); title('窄带高斯过程样本的正交分量')%求窄带高斯信号功率;注：由于样本的功率近似等于随机过程的功率，因此可能出现一些偏差P_gt=sum(real(gt).^2)/T;P_glt_real = sum(real(glt).^2)/T;P_glt_imag = sum(imag(glt).^2)/T;%验证窄带高斯过程的同相分量、正交分量的正交性a = real(glt)*(imag(glt))'/T;用到的子函数function [t,st]=bpf(f,sf,B1,B2)%This function filter an input at frequency domain by an ideal bandpass filter %Inputs:% f: frequency samples% sf: input data spectrum samples% B1: bandpass's lower frequency% B2: bandpass's higher frequency%Outputs:% t: frequency samples% st: output data's time samplesdf = f(2)-f(1);T = 1/df;hf = zeros(1,length(f));bf = [floor( B1/df ): floor( B2/df )] ;bf1 = floor( length(f)/2 ) + bf;bf2 = floor( length(f)/2 ) - bf;hf(bf1)=1/sqrt(2*(B2-B1));hf(bf2)=1/sqrt(2*(B2-B1));yf=hf.*sf.*exp(-j*2*pi*f*0.1*T);[t,st]=F2T(f,yf);例1-7%显示模拟调制的波形及解调方法DSB，文件mdsb.m %信源close all;clear all;dt = 0.001; %时间采样间隔fm=1; %信源最高频率fc=10; %载波中心频率T=5; %信号时长t = 0:dt:T;mt = sqrt(2)*cos(2*pi*fm*t); %信源%N0 = 0.01; %白噪单边功率谱密度%DSB modulations_dsb = mt.*cos(2*pi*fc*t);B=2*fm;%noise = noise_nb(fc,B,N0,t);%s_dsb=s_dsb+noise;figure(1)subplot(311)plot(t,s_dsb);hold on; %画出DSB信号波形plot(t,mt,'r--'); %标示mt的波形title('DSB调制信号');xlabel('t');%DSB demodulationrt = s_dsb.*cos(2*pi*fc*t);rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);subplot(312)plot(t,rt); hold on;plot(t,mt/2,'r--');title('相干解调后的信号波形与输入信号的比较'); xlabel('t')subplot(313)[f,sf]=T2F(t,s_dsb);psf = (abs(sf).^2)/T;plot(f,psf);axis([-2*fc 2*fc 0 max(psf)]);title('DSB信号功率谱');xlabel('f');function [t st]=lpf(f,sf,B)%This function filter an input data using a lowpass filter %Inputs: f: frequency samples% sf: input data spectrum samples% B: lowpass's bandwidth with a rectangle lowpass%Outputs: t: time samples% st: output data's time samplesdf = f(2)-f(1);T = 1/df;hf = zeros(1,length(f));bf = [-floor( B/df ): floor( B/df )] + floor( length(f)/2 ); hf(bf)=1;yf=hf.*sf;[t,st]=F2T(f,yf);st = real(st);例1-8%显示模拟调制的波形及解调方法AM,文件mam.m%信源close all;clear all;dt = 0.001; %时间采样间隔fm=1; %信源最高频率fc=10; %载波中心频率T=5; %信号时长t = 0:dt:T;mt = sqrt(2)*cos(2*pi*fm*t); %信源%N0 = 0.01; %白噪单边功率谱密度%AM modulationA=2;s_am = (A+mt).*cos(2*pi*fc*t);B = 2*fm; %带通滤波器带宽%noise = noise_nb(fc,B,N0,t); %窄带高斯噪声产生%s_am = s_am + noise;figure(1)subplot(311)plot(t,s_am);hold on; %画出AM信号波形plot(t,A+mt,'r--'); %标示AM的包络title('AM调制信号及其包络');xlabel('t');%AM demodulationrt = s_am.*cos(2*pi*fc*t); %相干解调rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm); %低通滤波subplot(312)plot(t,rt); hold on;plot(t,mt/2,'r--');title('相干解调后的信号波形与输入信号的比较'); xlabel('t')subplot(313)[f,sf]=T2F(t,s_am);psf = (abs(sf).^2)/T;plot(f,psf);axis([-2*fc 2*fc 0 max(psf)]);title('AM信号功率谱');xlabel('f');例1-9%显示模拟调制的波形及解调方法SSB，文件mssb.m%信源close all;clear all;dt = 0.001; %时间采样间隔fm=1; %信源最高频率fc=10; %载波中心频率T=5; %信号时长t = 0:dt:T;mt = sqrt(2)*cos(2*pi*fm*t); %信源%N0 = 0.01; %白噪单边功率谱密度%SSB modulations_ssb = real( hilbert(mt).*exp(j*2*pi*fc*t) ); B=fm;%noise = noise_nb(fc,B,N0,t);%s_ssb=s_ssb+noise;figure(1)subplot(311)plot(t,s_ssb);hold on; %画出SSB信号波形plot(t,mt,'r--'); %标示mt的波形title('SSB调制信号');xlabel('t');%SSB demodulationrt = s_ssb.*cos(2*pi*fc*t);rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);subplot(312)plot(t,rt); hold on;plot(t,mt/2,'r--');title('相干解调后的信号波形与输入信号的比较');xlabel('t')subplot(313)[f,sf]=T2F(t,s_ssb);psf = (abs(sf).^2)/T;plot(f,psf);axis([-2*fc 2*fc 0 max(psf)]);title('SSB信号功率谱');xlabel('f');例2-0%显示模拟调制的波形及解调方法VSB，文件mvsb.m%信源close all;clear all;dt = 0.001; %时间采样间隔fm=5; %信源最高频率fc=20; %载波中心频率T=5; %信号时长t = 0:dt:T;mt = sqrt(2)*( cos(2*pi*fm*t)+sin(2*pi*0.5*fm*t) ); %信源%VSB modulations_vsb = mt.*cos(2*pi*fc*t);B=1.2*fm;[f,sf] = T2F(t,s_vsb);[t,s_vsb] = vsbpf(f,sf,0.2*fm,1.2*fm,fc);figure(1)subplot(311)plot(t,s_vsb);hold on; %画出VSB信号波形plot(t,mt,'r--'); %标示mt的波形title('VSB调制信号');xlabel('t');%VSB demodulationrt = s_vsb.*cos(2*pi*fc*t);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);subplot(312)plot(t,rt); hold on;plot(t,mt/2,'r--');title('相干解调后的信号波形与输入信号的比较');xlabel('t')subplot(313)[f,sf]=T2F(t,s_vsb);psf = (abs(sf).^2)/T;plot(f,psf);axis([-2*fc 2*fc 0 max(psf)]);title('VSB信号功率谱');xlabel('f');function [t,st]=vsbpf(f,sf,B1,B2,fc)%This function filter an input by an residual bandpass filter %Inputs: f: frequency samples% sf: input data spectrum samples% B1: residual bandwidth% B2: highest freq of the basedband signal%Outputs: t: frequency samples% st: output data's time samplesdf = f(2)-f(1);T = 1/df;hf = zeros(1,length(f));bf1 = [floor( (fc-B1)/df ): floor( (fc+B1)/df )] ;bf2 = [floor( (fc+B1)/df )+1: floor( (fc+B2)/df )];f1 = bf1 + floor( length(f)/2 ) ;f2 = bf2 + floor( length(f)/2 ) ;stepf = 1/length(f1);hf(f1)=0:stepf:1-stepf;hf(f2)=1;f3 = -bf1 + floor( length(f)/2 ) ;f4 = -bf2 + floor( length(f)/2) ;hf(f3)=0:stepf:(1-stepf);hf(f4)=1;yf=hf.*sf;[t,st]=F2T(f,yf);st = real(st);例2-1%显示模拟调制的波形及解调方法AM、DSB、SSB, %信源close all;clear all;dt = 0.001;fm=1;fc=10;t = 0:dt:5;mt = sqrt(2)*cos(2*pi*fm*t);N0 = 0.1;%AM modulationA=2;s_am = (A+mt).*cos(2*pi*fc*t);B = 2*fm;noise = noise_nb(fc,B,N0,t);s_am = s_am + noise;figure(1)subplot(321)plot(t,s_am);hold on;plot(t,A+mt,'r--');%AM demodulationrt = s_am.*cos(2*pi*fc*t);rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);title('AM信号');xlabel('t');subplot(322)plot(t,rt); hold on;plot(t,mt/2,'r--');title('AM解调信号');xlabel('t');%DSB modulations_dsb = mt.*cos(2*pi*fc*t);B=2*fm;noise = noise_nb(fc,B,N0,t);s_dsb=s_dsb+noise;subplot(323)plot(t,s_dsb);hold on;plot(t,mt,'r--');title('DSB信号');xlabel('t');%DSB demodulationrt = s_dsb.*cos(2*pi*fc*t);rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);subplot(324)plot(t,rt); hold on;plot(t,mt/2,'r--');title('DSB解调信号');xlabel('t');%SSB modulations_ssb = real( hilbert(mt).*exp(j*2*pi*fc*t) );B=fm;noise = noise_nb(fc,B,N0,t);s_ssb=s_ssb+noise;subplot(325)plot(t,s_ssb);title('SSB信号');xlabel('t');%SSB demodulationrt = s_ssb.*cos(2*pi*fc*t);rt = rt-mean(rt);[f,rf] = T2F(t,rt);[t,rt] = lpf(f,rf,2*fm);subplot(326)plot(t,rt); hold on;plot(t,mt/2,'r--');title('SSB解调信号');xlabel('t');function [out] = noise_nb(fc,B,N0,t)%output the narrow band gaussian noise sample with single-sided power spectrum N0 %at carrier frequency equals fc and bandwidth euqals Bdt = t(2)-t(1);Fmx = 1/dt;n_len = length(t);p = N0*Fmx;rn = sqrt(p)*randn(1,n_len);[f,rf] = T2F(t,rn);[t,out] = bpf(f,rf,fc-B/2,fc+B/2);%FM modulation and demodulation，mfm.mclear all;close all;Kf = 5;fc = 10;T=5;dt=0.001;t = 0:dt:T;%信源fm= 1;%mt = cos(2*pi*fm*t) + 1.5*sin(2*pi*0.3*fm*t); %信源信号mt = cos(2*pi*fm*t); %信源信号%FM 调制A = sqrt(2);%mti = 1/2/pi/fm*sin(2*pi*fm*t) -3/4/pi/0.3/fm*cos(2*pi*0.3*fm*t); %mt的积分函数mti = 1/2/pi/fm*sin(2*pi*fm*t) ; %mt的积分函数st = A*cos(2*pi*fc*t + 2*pi*Kf*mti);figure(1)subplot(311);plot(t,st); hold on;plot(t,mt,'r--');xlabel('t');ylabel('调频信号')subplot(312)[f sf] = T2F(t,st);plot(f, abs(sf));axis([-25 25 0 3])xlabel('f');ylabel('调频信号幅度谱')%FM 解调for k=1:length(st)-1rt(k) = (st(k+1)-st(k))/dt;endrt(length(st))=0;subplot(313)plot(t,rt); hold on;plot(t,A*2*pi*Kf*mt+A*2*pi*fc,'r--');xlabel('t');ylabel('调频信号微分后包络')%数字基带信号的功率谱密度 digit_baseband.mclear all; close all;Ts=1;N_sample = 8; %每个码元的抽样点数dt = Ts/N_sample; %抽样时间间隔N = 1000; %码元数t = 0:dt:(N*N_sample-1)*dt;gt1 = ones(1,N_sample); %NRZ非归零波形gt2 = ones(1,N_sample/2); %RZ归零波形gt2 = [gt2 zeros(1,N_sample/2)];mt3 = sinc((t-5)/Ts); % sin(pi*t/Ts)/(pi*t/Ts)波形，截段取10个码元gt3 = mt3(1:10*N_sample);d = ( sign( randn(1,N) ) +1 )/2;data = sigexpand(d,N_sample); %对序列间隔插入N_sample-1个0st1 = conv(data,gt1); %Matlab自带卷积函数st2 = conv(data,gt2);d = 2*d-1; %变成双极性序列data= sigexpand(d,N_sample);st3 = conv(data,gt3);[f,st1f] = T2F(t,[st1(1:length(t))]);[f,st2f] = T2F(t,[st2(1:length(t))]);[f,st3f] = T2F(t,[st3(1:length(t))]);figure(1)subplot(321)plot(t,[st1(1:length(t))] );gridaxis([0 20 -1.5 1.5]);ylabel('单极性NRZ波形');subplot(322);plot(f,10*log10(abs(st1f).^2/T) );gridaxis([-5 5 -40 10]); ylabel('单极性NRZ功率谱密度(dB/Hz)');subplot(323)plot(t,[st2(1:length(t))] );axis([0 20 -1.5 1.5]);gridylabel('单极性RZ波形');subplot(324)plot(f,10*log10(abs(st2f).^2/T));axis([-5 5 -40 10]);gridylabel('单极性RZ功率谱密度(dB/Hz)');subplot(325)plot(t-5,[st3(1:length(t))] );axis([0 20 -2 2]);gridylabel('双极性sinc波形');xlabel('t/Ts');subplot(326)plot(f,10*log10(abs(st3f).^2/T));axis([-5 5 -40 10]);gridylabel('sinc波形功率谱密度(dB/Hz)');xlabel('f*Ts');function [out]=sigexpand(d,M)%将输入的序列扩展成间隔为N-1个0的序列N = length(d);out = zeros(M,N);out(1,:) = d;out = reshape(out,1,M*N);例2-4%数字基带信号接收示意 digit_receive.mclear all;close all;N =100;N_sample=8; %每码元抽样点数Ts=1;dt = Ts/N_sample;t=0:dt:(N*N_sample-1)*dt;gt = ones(1,N_sample); %数字基带波形d = sign(randn(1,N)); %输入数字序列a = sigexpand(d,N_sample);st = conv(a,gt); %数字基带信号ht1 = gt;rt1 = conv(st,ht1);ht2 = 5*sinc(5*(t-5)/Ts);rt2 = conv(st,ht2);figure(1)subplot(321)plot( t,st(1:length(t)) );axis([0 20 -1.5 1.5]); ylabel('输入双极性NRZ数字基带波形'); subplot(322)stem( t,a);axis([0 20 -1.5 1.5]); ylabel('输入数字序列')subplot(323)plot( t,[0 rt1(1:length(t)-1)]/8 );axis([0 20 -1.5 1.5]);ylabel('方波滤波后输出');subplot(324)dd = rt1(N_sample:N_sample:end);ddd= sigexpand(dd,N_sample);stem( t,ddd(1:length(t))/8 );axis([0 20 -1.5 1.5]);ylabel('方波滤波后抽样输出');subplot(325)plot(t-5, [0 rt2(1:length(t)-1)]/8 );axis([0 20 -1.5 1.5]);xlabel('t/Ts'); ylabel('理想低通滤波后输出');subplot(326)dd = rt2(N_sample-1:N_sample:end);ddd=sigexpand(dd,N_sample);stem( t-5,ddd(1:length(t))/8 );axis([0 20 -1.5 1.5]);xlabel('t/Ts'); ylabel('理想低通滤波后抽样输出');例2-5%部分响应信号眼图示意,pres.mclear all; close all;Ts=1;N_sample=16;eye_num = 11;N_data=1000;dt = Ts/N_sample;t = -5*Ts:dt:5*Ts;%产生双极性数字信号d = sign(randn(1,N_data));dd= sigexpand(d,N_sample);%部分响应系统冲击响应ht = sinc((t+eps)/Ts)./(1- (t+eps)./Ts);ht( 6*N_sample+1 ) = 1;st = conv(dd,ht);tt = -5*Ts:dt:(N_data+5)*N_sample*dt-dt;figure(1)subplot(211);plot(tt,st);axis([0 20 -3 3]);xlabel('t/Ts');ylabel('部分响应基带信号'); subplot(212)%画眼图ss=zeros(1,eye_num*N_sample);ttt = 0:dt:eye_num*N_sample*dt-dt;for k=5:50ss = st(k*N_sample+1:(k+eye_num)*N_sample);drawnow;plot(ttt,ss); hold on;end%plot(ttt,ss);xlabel('t/Ts');ylabel('部分响应信号眼图');例2-6%2ASK,2PSK，文件名binarymod.mclear all;close all;A=1;fc = 2; %2Hz;N_sample = 8;N = 500; %码元数Ts = 1; %1 baud/sdt = Ts/fc/N_sample; %波形采样间隔t = 0:dt:N*Ts-dt;Lt = length(t);%产生二进制信源d = sign(randn(1,N));dd = sigexpand((d+1)/2,fc*N_sample);gt = ones(1,fc*N_sample); %NRZ波形figure(1)subplot(221); %输入NRZ信号波形(单极性）d_NRZ = conv(dd,gt);plot(t,d_NRZ(1:length(t)));axis([0 10 0 1.2]); ylabel('输入信号');subplot(222); %输入NRZ频谱[f,d_NRZf]=T2F( t,d_NRZ(1:length(t)) );plot(f,10*log10(abs(d_NRZf).^2/T));axis([-2 2 -50 10]);ylabel('输入信号功率谱密度(dB/Hz)');%2ASK信号ht = A*cos(2*pi*fc*t);s_2ask = d_NRZ(1:Lt).*ht;subplot(223)plot(t,s_2ask);axis([0 10 -1.2 1.2]); ylabel('2ASK');[f,s_2askf]=T2F(t,s_2ask );subplot(224)plot(f,10*log10(abs(s_2askf).^2/T));axis([-fc-4 fc+4 -50 10]);ylabel('2ASK功率谱密度(dB/Hz)');figure(2)%2PSK信号d_2psk = 2*d_NRZ-1;s_2psk = d_2psk(1:Lt).*ht;subplot(221)plot(t,s_2psk);axis([0 10 -1.2 1.2]); ylabel('2PSK');subplot(222)[f,s_2pskf] = T2F(t,s_2psk);plot( f,10*log10(abs(s_2pskf).^2/T) );axis([-fc-4 fc+4 -50 10]);ylabel('2PSK功率谱密度(dB/Hz)');% 2FSK% s_2fsk = Acos(2*pi*fc*t + int(2*d_NRZ-1) );sd_2fsk = 2*d_NRZ-1;s_2fsk = A*cos(2*pi*fc*t + 2*pi*sd_2fsk(1:length(t)).*t );subplot(223)plot(t,s_2fsk);axis([0 10 -1.2 1.2]);xlabel('t'); ylabel('2FSK')subplot(224)[f,s_2fskf] = T2F(t,s_2fsk);plot(f,10*log10(abs(s_2fskf).^2/T));axis([-fc-4 fc+4 -50 10]);xlabel('f');ylabel('2FSK功率谱密度(dB/Hz)');例2-7%QPSK & OQPSKclear all;close all;M = 4;Ts= 1;fc= 10;N_sample = 16;N_num = 100;dt = 1/fc/N_sample;t = 0:dt:N_num*Ts-dt;T = dt*length(t);py1f = zeros(1,length(t)); %功率谱密度1py2f = zeros(1,length(t)); %功率谱密度2for PL=1:100 %输入100段N_num个码字的波形，为了使功率谱密度看起来更加平滑，%可以取这100段信号功率谱密度的平均d1 = sign(randn(1,N_num));d2 = sign(randn(1,N_num));gt = ones(1,fc*N_sample);%QPSK调制s1 = sigexpand(d1,fc*N_sample);s2 = sigexpand(d2,fc*N_sample);b1 = conv(s1,gt);b2 = conv(s2,gt);s1 = b1(1:length(s1));s2 = b2(1:length(s2));st_qpsk = s1.*cos(2*pi*fc*t) - s2.*sin(2*pi*fc*t);s2_delay= [-ones(1,N_sample*fc/2) s2(1:end-N_sample*fc/2)];st_oqpsk= s1.*cos(2*pi*fc*t) - s2_delay.*sin(2*pi*fc*t);%经过带通后，再经过非线性电路[f y1f] = T2F(t,st_qpsk);[f y2f] = T2F(t,st_oqpsk);[t y1] = bpf(f,y1f,fc-1/Ts,fc+1/Ts);[t y2] = bpf(f,y2f,fc-1/Ts,fc+1/Ts);subplot(221);plot(t,y1); xlabel('t'); ylabel('QPSK波形');axis([5 15 -1.6 1.6]);title('经过带通后的波形');subplot(222)plot(t,y2); xlabel('t'); ylabel('OQPSK波形');axis([5 15 -1.6 1.6]);title('经过带通后的波形');%经过非线性电路y1 = 1.5*tanh(2*y1);y2 = 1.5*tanh(2*y2);[f y1f] = T2F(t,y1);[f y2f] = T2F(t,y2);py1f = py1f + abs(y1f).^2/T; %QPSK不同段信号功率谱密度相加 py2f = py2f + abs(y2f).^2/T; %OQPSK不同段信号功率谱密度相加endpy1f = py1f/100; %QPSK 100段功率谱密度平均py2f=py2f/100; %OQPSK 100段功率谱密度平均subplot(223);plot(f,10*log10(py1f)); xlabel('f');ylabel('QPSK功率谱密度(dB/Hz)'); title('经过非线性电路后的功率谱密度');axis([ -15 15 -30 10]);subplot(224)plot(f,10*log10(py2f));xlabel('f');ylabel('OQPSK功率谱密度(dB/Hz)'); title('经过非线性电路后的功率谱密度');axis([ -15 15 -30 10]);figure(2)x = -2:0.1:2;y=1.5*tanh(2*x);plot(x,y); title('非线性电路的输入输出函数');例2-8%demo for u and A law for quantize，filename: a_u_law.m%u=255 y=ln(1+ux)/ln(1+u)%A=87.6 y=Ax/(1+lnA) (0<x<1/A) y=(1+lnAx)/(1+lnA)clear allclose alldx=0.01;x=-1:dx:1;u=255;A=87.6;%u Lawyu=sign(x).*log(1+u*abs(x))/log(1+u);%A Lawfor i=1:length(x)if abs(x(i))<1/Aya(i)=A*x(i)/(1+log(A));elseya(i)=sign(x(i))*(1+log(A*abs(x(i))))/(1+log(A));endendfigure(1)plot(x,yu,'k.:');title('u Law')xlabel('x');ylabel('y');grid onhold onxx=[-1,-127/255,-63/255,-31/255,-15/255,-7/255,-3/255,-1/255,1/255,3/255,7/255 ,15/255,31/255,63/255,...127/255,1];yy=[-1,-7/8,-6/8,-5/8,-4/8,-3/8,-2/8,-1/8,1/8,2/8,3/8,4/8,5/8,6/8,7/8,1];plot(xx,yy,'r');stem(xx,yy,'b-.');legend('u律压缩特性','折线近似u律');figure(2)plot(x,ya,'k.:');title('A Law')xlabel('x');ylabel('y');grid onhold onxx=[-1,-1/2,-1/4,-1/8,-1/16,-1/32,-1/64,-1/128,1/128,1/64,1/32,1/16,1/8,1/4,1/ 2,1];yy=[-1,-7/8,-6/8,-5/8,-4/8,-3/8,-2/8,-1/8,1/8,2/8,3/8,4/8,5/8,6/8,7/8,1];plot(xx,yy,'r');stem(xx,yy,'b-.');legend('A律压缩特性','折线近似A律');例2-9%show the pcm encode and decodeclear allclose allt=0:0.01:10;vm1=-70:1:0; %输入的正弦信号幅度不同vm = 10.^(vm1/20);figure(1)for k=1:length(vm)for m=1:2x=vm(k)*sin(2*pi*t+2*pi*rand(1));v=1;xx=x/v; %normalizesxx = floor(xx*4096);y = pcm_encode(sxx);yy = pcm_decode(y,v);nq(m)=sum((x-yy).*(x-yy))/length(x); sq(m)=mean(yy.^2);snr(m)=(sq(m)/nq(m));drawnowsubplot(211)plot(t,x);title('sample sequence');subplot(212)plot(t,yy)title('pcm decode sequence');endsnrq(k)=10*log10( mean(snr) );endfigure(2)plot(vm1,snrq);axis([-60 0 0 60]);grid;function [out]=pcm_encode(x)%x encode to pcm coden=length(x);%-4096<x<4096for i=1:nif x(i)>0out(i,1)=1;elseout(i,1)=0;endif abs(x(i))>=0 & abs(x(i))<32out(i,2)=0;out(i,3)=0;out(i,4)=0;step=2;st=0;elseif 32<=abs(x(i)) & abs(x(i))<64out(i,2)=0;out(i,3)=0;out(i,4)=1;step=2;st=32;elseif 64<=abs(x(i)) & abs(x(i))<128out(i,2)=0;out(i,3)=1;out(i,4)=0;step=4;st=64;elseif 128<=abs(x(i)) & abs(x(i)) <256out(i,2)=0;out(i,3)=1;out(i,4)=1;step=8;st=128;elseif 256<=abs(x(i)) & abs(x(i))<512out(i,2)=1;out(i,3)=0;out(i,4)=0;step=16;st=256;elseif 512<=abs(x(i)) & abs(x(i))<1024out(i,2)=1;out(i,3)=0;out(i,4)=1;step=32;st=512;elseif 1024<=abs(x(i)) & abs(x(i))<2048out(i,2)=1;out(i,3)=1;out(i,4)=0;step=64;st=1024;elseif 2048<=abs(x(i)) & abs(x(i))<4096out(i,2)=1;out(i,3)=1;out(i,4)=1;step=128;st=2048;elseout(i,2)=1;out(i,3)=1;out(i,4)=1;step=128;st=2048;endif(abs(x(i))>=4096)out(i,2:8) = [1 1 1 1 1 1 1];elsetmp = floor( (abs(x(i))-st)/step );t = dec2bin(tmp,4) - 48; %函数dec2bin输出的是ASCII字符串，48对应0 out(i,5:8) =t(1:4);endendout=reshape(out',1,8*n);function [out]= pcm_decode(in,v)%decode the input pcm code%in : input the pcm code 8bit/sample%v: quantized leveln=length(in);in = reshape(in',8,n/8)';slot(1) = 0;slot(2) = 32;slot(3) = 64;slot(4) = 128;slot(5) = 256;slot(6) = 512;slot(7) = 1024;slot(8) = 2048;step(1) = 2;step(2) = 2;step(3) = 4;step(4) = 8;step(5) = 16;step(6) = 32;step(7) = 64;step(8) = 128;for i=1:n/8ss = 2*in(i,1)-1;tmp= in(i,2)*4+in(i,3)*2+in(i,4)+1;st = slot(tmp);dt = (in(i,5)*8+in(i,6)*4+in(i,7)*2+in(i,8))*step(tmp) + 0.5*step(tmp); out(i)=ss*(st+dt)/4096*v;end例3-0%信道失真示意，clear all;close all;Ts=1;N_sample = 8; %每个码元的抽样点数dt = Ts/N_sample; %抽样时间间隔N = 1000; %码元数t = 0:dt:(N*N_sample-1)*dt;gt1 = ones(1,N_sample); %NRZ非归零波形gt2 = ones(1,N_sample/2); %RZ归零波形gt2 = [gt2 zeros(1,N_sample/2)];mt3 = sinc((t-5)/Ts); % sin(pi*t/Ts)/(pi*t/Ts)波形，截段取10个码元gt3 = mt3(1:10*N_sample);d = ( sign( randn(1,N) ) +1 )/2;data = sigexpand(d,N_sample); %对序列间隔插入N_sample-1个0st1 = conv(data,gt1);st2 = conv(data,gt2);d = 2*d-1; %变成双极性序列data= sigexpand(d,N_sample);st3 = conv(data,gt3);xt = st1;%无失真信道[f,xf] = T2F(t,xt);hf1 = exp(-j*pi*f);yf1 = xf.*hf1;[t1,yt1] = F2T(f,yf1);%幅频失真信道hf2 = sinc(f).*exp(-j*pi*f);yf2 = xf.*hf2;[t2,yt2] = F2T(f,yf2);%相频失真、群时延无失真信道%hf3 = exp(j*pi*f+j*0.1*pi);f1 = find(f<0);hf3 = exp( -j*pi*f+j*pi );hf3(f1) = exp( -j*pi*f(f1)-j*pi );yf3 = xf.*hf3;[t3,yt3]=F2T(f,yf3);%相频、群时延失真信道hf4 = exp(-j*pi*f.*f-j*pi*f+j*pi);yf4 = xf.*hf4;[t4,yt4]=F2T(f,yf4);sfigure(1)subplot(221)plotyy(f,abs(hf1),f,angle(hf1)/pi);ylabel('幅频、相频特性'); title('线性无失真信道');grid on;subplot(222)plot(t1,real(yt1) );title('经过信道后的输出信号');axis([0,20,-1.2 1.2]);grid on;subplot(223)plotyy(f,abs(hf2),f,angle(hf2)/pi);ylabel('幅频、相频特性'); title('幅频失真信道');grid on; xlabel('f')subplot(224)plot(t2,real(yt2));axis([0,20,-1.2 1.2]);grid on;xlabel('t');figure(2)subplot(221);plotyy(f,abs(hf3),f,angle(hf3)/pi);ylabel('幅频、相频特性');title('相频失真、群时延无失真信道');grid on;subplot(222);plot(t3,real(yt3));title('经过信道后的输出信号');axis([0,20,-1.2 1.2]);grid on;subplot(223)plotyy(f,abs(hf4),f,angle(hf4)/pi);ylabel('幅频、相频特性');title('相频失真、群时延失真信道');grid on;xlabel('f');subplot(224);plot(t4,real(yt4));axis([0,20,-1.2 1.2]);grid on;xlabel('t');例3-1clear all;close all;Ts=1;N_sample = 8; %每个码元的抽样点数dt = Ts/N_sample; %抽样时间间隔N = 1000; %码元数t = 0:dt:(N*N_sample-1)*dt;dLen = length(t);gt1 = ones(1,N_sample); %NRZ非归零波形d = ( sign( randn(1,N) ) +1 )/2;data = sigexpand(d,N_sample); %对序列间隔插入N_sample-1个0st1 = conv(data,gt1);[f sf1] = T2F(t,st1(1:dLen));%3径信道m=[0.5 0.707 0.5];tao =[ 0 1 2];hf = m(1)*exp(-j*2*pi*f*tao(1)) +m(2)* exp(-j*2*pi*f*tao(2))+...m(3)* exp(-j*2*pi*f*tao(3));%信号经过3径信道yt1 = m(1)*st1(1:dLen)+m(2)*[zeros(1,N_sample), st1(1:dLen-N_sample)]+... m(3)*[zeros(1,2*N_sample), st1(1:dLen-2*N_sample)];[f yf1] = T2F(t,yt1);figure(1)subplot(221)plot(t,st1(1:dLen),'LineWidth',2);。