一类分式函数最小值的求导处理及推广
常见分式函数的研究

03 分式函数的运算与变换
分式函数的加减法
分式函数的加减法可以通过通分实现,将分母统一后再进行加减运算。 在进行分式函数的加减法时,需要注意分母不能为零的情况,避免出现无意义的情况。 对于分式函数的加减法,需要注意运算的顺序,先进行乘除运算再进行加减运算。 在进行分式函数的加减法时,可以利用等价无穷小替换简化计算过程。
分式函数的极限与连续性
分式函数的极限:研究分式函数在某点的极限值,以及极限的运算法则
分式函数的连续性:探讨分式函数在某点的连续性,以及连续性的性质和判定方法
分式函数极限与连续性的关系:分析极限与连续性之间的联系,以及在数学分析中的应 用
分式函数极限与连续性的应用:举例说明分式函数极限与连续性在解决实际问题中的应 用
分式函数极值的几 何意义
分式函数极值在实 际问题中的应用
分式函数的凹凸性及拐点问题
分式函数的凹凸性 定义
拐点及其判定条件
分式函数凹凸性的 判别方法
分式函数拐点的求 法
06 分式函数的综合题解析
分式函数的解析几何问题
涉及直线与圆的位 置关系
涉及点到直线的距 离公式
涉及直线的斜率公 式
涉及圆的半径和弦 长公式
分式函数的优化问题
分式函数的极值条件 分式函数的单调性分析 分式函数的凹凸性判断 分式函数的最值求解方法
分式函数的极值问题
分式函数的极值条件 分式函数的极值计算方法 分式函数的极值应用场景 分式函数的极值与连续性的关系
分式函数的最大值与最小值问题
分式函数的极值条 件
分式函数的最大值 与最小值的求解方 法
04 分式函数的应用
分式函数在物理中的应用
力学中速度与时间的关系
电学中电流与电压的关系
求导法则与基本求导公式

求导法则与基本求导公式导数是微积分中的重要概念,用来描述函数的变化率。
在求导的过程中,可以用一些基本的求导公式和求导法则来简化计算。
下面将详细介绍一些基本求导公式和求导法则。
1.常数函数的导数对于常数函数y=a,其中a为常数,导函数为y'=0。
这是因为常数函数不随自变量的改变而改变,所以导数为0。
2.幂函数的导数对于幂函数y = x^n,其中n为实数,导函数为y' = nx^(n-1)。
这可以通过对幂函数进行逐项求导证明。
3.指数函数的导数对于指数函数y = a^x,其中a为正实数且a≠1,导函数为y' =a^x * ln(a)。
这可以通过对指数函数进行逐项求导证明。
4.对数函数的导数对于对数函数y = loga(x),其中a为正实数且a≠1,导函数为y' = 1 / (x * ln(a))。
这可以通过对对数函数进行逐项求导证明。
5.三角函数的导数(1)sine函数的导数:y = sinx,导函数为y' = cosx。
(2)cosine函数的导数:y = cosx,导函数为y' = -sinx。
(3)tangent函数的导数:y = tanx,导函数为y' = sec^2x。
(5)secant函数的导数:y = secx,导函数为y' = secx * tanx。
(6)cosecant函数的导数:y = cscx,导函数为y' = -cscx * cotx。
6.反三角函数的导数(1)arcsine函数的导数:y = arcsinx,导函数为y' = 1 / √(1 - x^2)。
(2)arccosine函数的导数:y = arccosx,导函数为y' = -1 /√(1 - x^2)。
(3)arctangent函数的导数:y = arctanx,导函数为y' = 1 / (1 + x^2)。
(4)arccotangent函数的导数:y = arccotx,导函数为y' = -1 / (1 + x^2)。
分式导数公式

分式导数公式一、分式导数的定义在微积分中,分式函数是指形如f(x) = g(x)/h(x)的函数,其中g(x)和h(x)均为多项式函数。
分式导数就是指这样的函数的导数。
二、分式导数的求解方法为了求解分式函数的导数,我们可以使用分式导数公式。
具体而言,对于一个分式函数f(x) = g(x)/h(x),它的导数可以通过以下公式计算:f'(x) = (g'(x)h(x) - g(x)h'(x)) / (h(x))^2其中,g'(x)表示g(x)的导数,h'(x)表示h(x)的导数。
三、分式导数的应用分式导数在实际问题中有着广泛的应用。
以下是一些常见的应用场景:1. 物理学中的应用在物理学中,许多问题可以建模为分式函数。
例如,弹簧振子的运动可以用分式函数来描述,通过对这个分式函数求导,我们可以得到弹簧振子的速度和加速度,从而进一步研究其运动规律。
2. 经济学中的应用经济学中的供给曲线和需求曲线通常可以用分式函数表示。
通过对这些分式函数求导,我们可以研究市场的均衡点、价格变化对供需关系的影响等经济现象。
3. 工程学中的应用在工程学中,分式函数常常用于建模和优化问题。
例如,在电路设计中,电流和电压可以用分式函数表示,通过对这些分式函数求导,我们可以研究电路的稳定性和效率。
四、总结本文介绍了分式导数的定义、求解方法以及应用。
分式导数是微积分中的重要概念,它在物理学、经济学和工程学等领域有着广泛的应用。
通过对分式函数求导,我们可以研究函数的变化率、优化问题等。
分式导数的求解方法是通过分式导数公式进行计算。
希望本文能够帮助读者理解分式导数的概念和应用,并在实际问题中灵活运用。
导数与函数单调性和最小值的关系

导数与函数单调性和最小值的关系导数是微积分中的重要概念,它与函数的单调性和最小值之间存在着密切的关系。
本文将探讨导数与函数单调性以及最小值之间的相互关系。
一、导数与函数的单调性函数的单调性是指函数在定义域上的增减性质。
导数的存在性和符号可以揭示函数的单调性。
1.1 导数的存在性函数在某一点处的导数存在意味着函数在该点处的变化率存在。
如果函数在某一点处的导数存在,则说明函数在该点处具有切线,即函数在该点处局部近似为一条直线。
1.2 导数的符号导数的符号可以揭示函数在某一区间上的增减性。
假设函数在某一区间上的导数大于零,即导数为正,那么函数在该区间上是递增的;反之,如果导数小于零,即导数为负,那么函数在该区间上是递减的。
通过导数的符号,我们可以判断函数在不同区间上的单调性。
二、导数与函数的最小值函数的最小值是指函数在定义域上的最小取值。
导数可以帮助我们找到函数的最小值。
2.1 导数的零点函数在导数为零的点处可能存在最小值。
这是因为导数为零意味着函数在该点处的变化率为零,即函数在该点处的斜率为零。
这样的点可以是函数的最低点。
2.2 导数的符号变化函数在导数发生符号变化的点处可能存在最小值。
如果函数在某一点的导数由正变为负,那么函数在该点处可能具有最小值。
因为导数由正变为负,说明函数在该点的斜率从正向变为负向,即函数在该点附近由增加转为减少,可能达到了最小值。
综上所述,导数与函数的单调性和最小值之间存在着紧密的关系。
通过导数的存在性和符号,我们可以判断函数的单调性。
而导数的零点和符号变化可以帮助我们找到函数的最小值。
在微积分中,导数的应用不仅可以帮助我们理解函数的性质,还可以用来解决各种实际问题。
参考资料:1. Stewart, ___(2011). Calculus: ___.2. Anton, H., Bivens, I., & Davis, S. (2009). Calculus. WileyGlobal ___.。
用导数解决函数的单调性、极值、最值的方法步骤

用导数解决函数的单调性、极值、最值的方法步骤极值是一个局部概念 由定义,极值只是某个点的函数值与它附近点的函数值比较是并不意味着它在函数的整个的定义域内最大或最小函数的极值不是唯一的 即一个函数在某区间上或定义域内极大值或极小值可以不止一个极大值与极小值之即一个函数的极大值未必大于极小值. 函数的极值点一定出现在区间的内部,区间的端点不能成为极值点 而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点用导数判别f (x 0)是极大、极小值的思路: 若0x 满足0)(0='x f ,且在0x 的两侧)(x f 的导数异号,则0x 是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在0x 两侧满足“左正右负”,则0x 是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在0x 两侧满足“左负右正”,则0x 是)(x f 的极小值点,)(0x f 是极小值求函数f (x )的极值的步骤: (1)确定函数的定义区间,求导数f ′(x ) (2)求方程f ′(x )=0的根 (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f ′(x )在方程根左右的值的符号,如果左正右负,那么f (x )在这个根处取得极大值;如果左负右正,那么f (x )在这个根处取得极小值;如果左右不改变符号即都为正或都为负,则f (x )在这个根处无极值在闭区间[]b a ,上连续的函数)(x f 在[]b a ,上必有最大值与最小值;在开区间(,)a b 内连续的函数)(x f 不一定有最大值与最小值. 函数的最值是比较整个定义域内的函数值得出的,函数的极值是比较极值点附近函数值得出的. 函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个利用导数求函数的最值步骤:⑴求)(x f 在(,)a b 内的极值;⑵将)(x f 的各极值与)(a f 、)(b f 比较得出函数)(x f 在[]b a ,上的最值例1 求列函数的极值:(1)22)2()1(--=x x y ;(2)2122-+=x x y解:(1)2/22)2)(75)(1()(,)2()1()(---=∴--=x x x x f x x x f令0)(/=x f ,得驻点2,57,1321===x x x0)1(=∴f 是函数的极大值;3125108)57(-=f 是函数的极小值. (2)22222/2)1()1)(1(2)1(22)1(2)(,212)(x x x x xx x x f x x x f ++-=+⋅-+=∴-+=令0)(/=x f ,得驻点121,1x x =-=∴当1-=x 时,f极小=-3;当1=x 时,f极大=-1值。
待定系数法求一类函数的最小值

生的求简意识相矛盾. 我把文仁 1 」 中的例 1 、 例3 、 例 4 、 例5 、 例6 及文「 2 」 中的例2 作为练习题在我校高 三实验班中进行试验, 结果大多数同学能正确解答
了, 一万+了 一一 万 +丁一 一 下
1十x 1 +y - 1+z
1 1
=1 . 而不必像文【 1 〕 那样通
〕「
文「 1 」 利用6 个例题从6 个方面谈了如何培养
学生的 求简意识, 文〔 2 」 谈了 从问题结构特征来选
择解题策略, 读后颇受启发, 同时又感觉到有话要
、 止 易 得 ( x 2 + 2 1 ) - 1
说. 我们在平时的数学教学中, 应坚持通性通法, 反
对过份强调技巧, 而文【 1 」 中的4 个例题的解法不 是通法, 我们很难想到, 这与文〔 1 ] 所倡导的培养学
即 产布七 + - 1 2 + 尸 六 1+x 1+y 一 1+z
1 十 z
e * 当二 , y , z > 0 时, 丁 三 下十 十了 一 尸z 2 1 + X-
2
作者简介
侯小华, 男, 1 9 7 9 年出生, 硕士, 讲师.
万方数据
这 西问 题, 但没有一个同 学选择文〔 1 ] 所介绍的 方
法.
1 1 过构造三棱锥来得到了一 , 文 -  ̄ 万 +丁 一一 万 +了一一 万 =1 1 +x 1 +y 1+: -
例 1已 知 二 . , . : , 0 日 , 三 共一才 去 +  ̄ . . 宜
由( 1 ) 、
+d
一 d , 代 人 ( 3 ) 得 p =
+ b一 2 犷- 4
bd 一 2
对 X式两边平方得: 4 a 2 + 4 a 2 b x + a 2 b 2 = 4 d 2 ' : X 2
用导数解决函数的单调性极值最值的方法步骤

用导数解决函数的单调性极值最值的方法步骤导数是微积分中非常重要的概念,它可以通过求取函数的斜率来提供关于函数的很多信息。
通过导数,我们能够判断函数的单调性、极值和最值。
下面,我将详细介绍使用导数进行函数分析的方法步骤。
一、函数的单调性分析:函数的单调性指的是函数在定义域上的递增或递减特性。
使用导数可以判断函数在不同区间上的单调性。
1.求出函数的导数:根据函数的定义,求出函数的导数。
若函数在其中一点存在导数,则说明函数在该点是可导的。
2.导数的符号变化:对求得的导数进行符号变化的分析,即导数求值时,符号的正负变化。
假设导数的结果是f’(x)。
通过求解f’(x)=0的解集,得到导数的零点集合。
3.导数零点的意义:对于导数零点集合中的每一个点进行分析。
如果导数在其中一点处的零点是一个正的极值点,则说明函数在该点是递增的;如果导数在其中一点处的零点是一个负的极值点,则说明函数在该点是递减的。
4.极值点的判定:在求得导数零点的基础上,通过导数的符号变化来判定函数在区间上的单调性。
当导数从正数变为负数时,说明函数在该区间上是递减的;当导数从负数变为正数时,说明函数在该区间上是递增的。
二、函数的极值分析:函数的极值是指函数在其中一点处取得的最大值或最小值。
通过导数可以判断函数的极值点。
1.求出函数的导数:根据函数的定义,求出函数的导数。
2.导数零点的极值分析:计算导数的零点,并求出零点对应的函数值,在零点处求得导数的值,在零点前后进行符号判定。
3.极值点的判定:若导数从负数增加到正数,则说明函数在该点处取得极小值;若导数从正数减小到负数,则说明函数在该点处取得极大值。
三、函数的最值分析:函数的最值是函数在定义域上取得的最大值或最小值。
通过导数可以判断函数的最值点。
1.求出函数的导数:根据函数的定义,求出函数的导数。
2.导数的变化性:通过计算导数的值和导数的符号变化来判断函数的最值。
3.导数的非零点分析:计算函数的定义域上的导数,找出导数等于零的点的集合。
导数法求最大最小值PPT课件

.
4
(3)函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且 极大值(极小值)不一定就是最大值(最小值),但除端点 外在区间内部的最大值(或最小值),则一定是极大值 (或极小值).
(4)如果函数不在闭区间[a,b]上可导,则在确定函数的最 值时,不仅比较该函数各导数为零的点与端点处的值, 还要比较函数在定义域内各不可导的点处的值.
.
7
延伸1:大设值32 为a1,最1 ,函小数值为f(x )6 x,3求常2 3a数2x a,b b(.1x1)的最
2
解:令 f(x)3x23a x0得x=0或a.
当x变化时, f (x),f(x)的变化情况如下表:
x -1
(-1,0) 0 (0,a) a (a,1) 1
f’(x)
+0-
0
+
f(x) -1-3a/2+b ↗ b ↘ -a3/2+b ↗ 1-3a/2+b
令 f(x)0,得 x 1 1 2 ,x 2 1 2 ,且 x 1 ,x 2 [ 1 ,3 ].
相应的函数值为: f(12)752,f(12)752.
2
2
又f(x)在区间端点的函数值为:f(-1)=6,f(3)=0
比较得,
f(x)在点x1 1
2处取得最大值
7
5 2
2;
75 2 在点 x2 1 2处取得最小值 2 .
答案:最大值为f(4)=142,最小值为f(1)=7.
练习2:求函数f(x)=p2x2(1-x)p(p是正数)在[0,1]上的最 大值.
解: f(x ) p 2 x (1 x )p 1 [2 (2 p )x ].
分式函数知识点总结

分式函数知识点总结分式函数的定义分式函数的一般形式如下所示:\[f(x) = \frac{P(x)}{Q(x)}\]其中P(x)和Q(x)分别代表分子和分母的多项式函数。
值得注意的是,分母函数Q(x)不能为零,因为分式函数的定义域是所有使得分母不为零的x值的集合。
当Q(x)为零时,分式函数的值无意义。
分式函数的图像分式函数的图像通常表现为一条曲线,其性质和形态受到分子和分母的多项式函数的影响。
在进行分式函数图像的分析时,我们可以先考察分式函数的分母的零点和分子的零点,并利用它们来确定函数的极值点和渐近线。
当分母函数的零点不等于分子函数的零点时,分式函数的图像将展现出横轴方向的渐近线。
若分子函数次数小于分母函数次数,则图像会有一个水平渐近线;若分子函数次数等于分母函数次数减1,则图像会有一个斜率不为零的斜渐近线。
而当分子函数的次数大于等于分母函数的次数时,分式函数的图像将有一个斜率不为零的斜渐近线和一个水平渐近线。
根据这些渐近线,我们可以初步掌握分式函数的图像性质和形态。
另外,我们还可以通过一阶导数和二阶导数的求导分析来了解分式函数图像的凸凹性以及拐点的位置,进一步掌握其曲线的性状。
分式函数的性质分式函数有一系列独特的性质,主要体现在定义域、值域、零点及极限的方面。
1. 定义域作为一个分式函数,其定义域是所有使得分母函数值不为零的x值的集合。
当分母函数有n个零点时,分式函数的定义域将为实数集合减去这n个零点的集合,即:\[D = \{x|x∈R, Q(x) ≠ 0\}\]2. 值域分式函数的值域会受分子和分母函数的次数、系数等的影响。
通过对分式函数的分析,我们可以得到其值域所处的范围。
3. 零点分式函数的零点是指当f(x) = 0时,对应的x值。
通过求解分子函数和分母函数的交点,我们可以得到分式函数的零点的位置。
4. 极限当x趋向于某个值时,分式函数的值也可能会趋向于某个值或者无穷大。
利用极限的方法,我们可以研究分式函数在定义域内的行为,包括渐近线、极值点,以及曲线的凸凹性等特性。
导数的应用--函讲义数的最大值与最小值

价格p与产量q的函数关系式为 p 25 1 q.求产量
q为何值时,利润L最大?
8
分析:利润L等于收入R减去成本C,而收入R等于产量乘价格.由 此可得出利润L与产量q的函数关系式,再用导数求最大利润.
解:收入 Rqpq251 8q25q1 8q2
利润
L R C 2 5 q 1 8 q 2 ( 1 0 0 4 q ) 1 8 q 2 2 1 q 1 0 0
(0q100)
L 1 q 21
令
L
,0 即
4
1 4
q
21
,0 求得唯一的极值点
q 84
答:产量为84时,利润L最大。
课堂练习
1.下列说法正确的是( D )
A.函数的极大值就是函数的最大值
B.函数的极小值就是函数的最小值
C.函数的最值一定是极值
D.在闭区间上的连续函数一定存在最值
⑶函数 f ( x)在闭区间 a,b上连续,是 f (x)在闭区 间 a,b上有最大值与最小值的充分条件而非必要条
件.
(4)函数在其定义区间上的最大值、最小值最多各有 一个,而函数的极值可能不止一个,也可能没有一个。
2、设函数f (x)在[a,b]上连续, f (x)在(a,b)在内 可导,求f (x)在闭区间[a,b]上的最值的步骤:
0两侧的导数异号是x
为极值点的充要条件。
0
新课讲授
1.函数的最大值和最小值
观察图中一个定义在闭区间 a,b上的函数 f (x)
的 图 象 . 图 中 f (x1与) f ( x 3是) 极 小 值 , f ( x 2 )是 极 大
值.函数 f (x) 在 a,b上的最大值是 f (b) ,最小值
一类分式函数最小值的求导处理及推广

江苏省 常 熟 市中 学
2 50 150
蔡祖 才
2 ~
=
函数 )=. l + _ ( 6, d ∈ R+, < 一 了6 0 c, c
,
戈 一 C
f 一 z
仅 : 二 时g ) 最 值 ( : 当 三 , 取 小 g ) (
一 , 2
一 /
o—c 二 ~
一
因 , = 为 当 ;
1 l
时g = ; ,( 0 ,)
当 C< < ——T———— — , )<0, ( 时 g( g )递
n 46 -
c + dn 6 T
L
减; 当
( ,,, ∈ R 0 b cd ,
< < d时 , , g ( >0, ( ) g )递 1 时 , 最 小 值 取
+
) :
b
’
眠当= 案
c +d
+
时 , )=O; c< , ( 当
[ 一( ] 一 1)
时 /( < ) 减 当 , 。 递 ; )
由 广 可 ,且 当 { 时 推 l 知当 仅 = ,
g x 的最小值为g =(a+ ), () () U
函数最小值为 汀 + - ) 4 ( 5 + :6.
t
+ + + + 的最小值. y ÷ —I Z_
解
2
+
所 , 仅 y÷ , + + 以当 当 == 时“ 1 且 = 18
<
l l
中学数学杂志 20 年第 1 期 09 1
雹
<
6 舅 一跪 g
, —
一 (
d 二 ) c 一一
求 d~ 导 一 得 一d 厂 一
解决函数导数问题的常用方法PPT课件

考点三、求解函数的最值问题
考点四、函数与导数综合问题
导数是研究函数的工具,导数进入新教材之后 ,拓展了高考对函数问题的命题空间。对研究函数 的目标也不仅限于求定义域,值域,单调性,奇偶 性,对称性,周期性等,而是把高次多项式函数, 分式函数,指数型,对数型函数,以及初等基本函 数的和、差、积、商都成为命题的对象,试题的命 制往往融函数,导数,不等式,方程等知识于一体 ,通过演绎证明,运算推理等理性思维,解决单调 性,极值,最值,切线,方程的根,参数的范围等 问题,这类题难度比较大,综合性强,内容新,背 景新,方法新,是高考命题的热点。解题中需用到 函数与方程思想、分类讨论思想、数形结合思想、 转化与划归思想。
【典型例题分析】
考点一、利用导数求解函数的单调性问题
考点二、求函数的极值问题
极值点的导数一定为0(连续可导函数), 但导数为0的点不一定是极值点,同时不可 导的点可能是极值点.因此函数的极值点只能 在导数为0的点解析式求极值; (2)根据函数的极值求解参数问题.解答时要 注意准确应用利用导数求极值的原理求解.
【突破方法技巧】
1.讨论函数的性质时,必须坚持 定义域优先的原则.对于函数实际应 用问题,注意挖掘隐含在实际中的 条件,避免忽略实际意义对定义域 的影响.
2.运用函数的性质解题时,注意 数形结合,扬长避短.
3.对于含参数的函数,研究其性质 时,一般要对参数进行分类讨论,全 面考虑.如对二次项含参数的二次函 数问题,应分a=0和a≠0两种情况讨 论,指、对数函数的底数含有字母参 数a时,需按a>1和0<a<1分两种 情况讨论. 4.解答函数性质有关的综合问题时 ,注意等价转化思想的运用.
类分式函数最小值问题讨论

中学数学杂志2009年第3期
名z,且zz∈[寺,1).再由z在(e一,1)范围内变化时,
关于u的方程戈“=//,的根C(X)是连续变化的,且z
=e1时C(x):土,当z一+1时,G(x)=u=正“一
C
l,所以此时得G(石)的值域是[土,1).
C
(3)当咒=l时,名‘4’=l,limx‘4’=l最口G(1)
此时,等号成立的条件是atan20=bcot20,即
tan4p=鱼,因而有tan20a
=√’、『鱼a,从而石=c。s2p=
矗丽=去=忐旭就是说,邹、= 1讹n2p 1+压石+万~”“一”一。、
0忑n等+q—b看时,函数八戈)“=詈+1r一 笔“(口,6∈R+,o<
石<1)有最小值(扛+√i)2.由于这里只使用了一
小值,此时最小值八聋)mi。=八等)=i81.
例2求函鳓茹)=丽3+r笔(÷<聋<
求函数八。z), =磊麟 兰‘一+丁C当忑口(口一,,珑b,c,d,m,n E
R+,旦<z<旦)的最小值,我们可以借助上面的类
旦
鱼
型3,把它先变成以茗)=—与+了旦^,即可用类
互一一 一一石
/'t/,
n
型3来求解.
了3)的最小值.
,j
,’
解法1 原函数可变为八石)=—彳+
互一虿
广1,因为÷<髫<了3,且(聋一÷)+(÷一髫)=
1‘3
÷,所以可设戈一12=-三-COS2口,手一石=÷sin2口,其
中p∈(o,要),则原问题可化为求函数八口)=
__CO2日笔。S+jsin2毛p叫的最“小_’值曲 . m/(o)=丽6+丽4=6(tan2p+1)+
分式的求导公式范文

分式的求导公式范文
1.基本法则:如果f(x)=u(x)/v(x)是一个分式函数,其中u(x)和
v(x)均可导,则其导数可以通过以下公式计算:
f'(x)=[u'(x)*v(x)-u(x)*v'(x)]/[v(x)]^2
2.乘法法则:如果f(x)=g(x)*h(x)是一个分式函数,其中g(x)和
h(x)均可导,则其导数可以通过以下公式计算:
f'(x)=g'(x)*h(x)+g(x)*h'(x)
3.除法法则:如果f(x)=g(x)/h(x)是一个分式函数,其中g(x)和
h(x)均可导,并且h(x)≠0,则其导数可以通过以下公式计算:f'(x)=[h(x)*g'(x)-g(x)*h'(x)]/[h(x)]^2
4.倒数法则:如果f(x)=1/g(x)是一个分式函数,其中g(x)可导且g(x)≠0
f'(x)=-[g'(x)]/[g(x)]^2
5.幂函数法则:如果f(x)=[g(x)]^n是一个幂函数的分式形式,其中g(x)可导且n是一个实数,则可以使用以下公式计算导数:
f'(x)=n*g(x)^(n-1)*g'(x)
这些公式可以帮助我们计算分式函数的导数。
通过应用这些公式,可以更轻松地求解含有分式的微分方程和优化问题。
当使用这些公式时,需要确保函数满足适用条件,例如分母不为零等。
函数在区间的最小值

函数在区间的最小值
要找到一个函数在给定区间上的最小值,可以使用以下方法之一:
1. 求导法:如果函数是可导的,首先求出函数的导数。
然后找到导数为零或不存在的点。
对于一个可导函数,这些点是可能的最小值或最大值。
然后,检查这些点以确定哪一个对应于最小值。
如果区间开头或结尾处的导数为零,也要将这些点考虑在内。
2. 区间取值法:在给定区间上将函数的值计算出来,并找到其中的最小值。
这个方法适用于在离散集合上定义的函数。
3.使用计算机算法:使用计算机算法,如穷举法或优化算法,来找到函数在给定区间上的最小值。
这些算法可以通过对函数进行计算和优化来找到最小值。
浅谈利用导数知识求解函数的最值题

浅谈利用导数知识求解函数的最值题
求函数的最大值和最小值可以通过7种方法:1、配方法;2、判别式法;3、利用函
数的单调性;4、利用均值不等式;5、换元法;6、数形结合法;7、利用导数求函数最值。
1、配方法:形如的函数,根据二次函数的极值点或边界点的取值确定函数的最值。
2、判别式法:形似的分式函数,将其化为系数所含y的关于x的二次方程。
由于,所以≥0,算出y的最值,此种方法极易产生增根,因而必须对获得最值时对应的x值
与否存有求解检验。
3、利用函数的单调性:首先明确函数的定义域和单调性,再求最值。
4、利用均值不等式,形似的函数,特别注意正、定等的应用领域条件,即为: a,b均为正数,就是定值, a=b的等号与否设立。
5、换元法:形如的函数,令,反解出x,代入上式,得出关于t的函数,注意t
的定义域范围,再求关于t的函数的最值。
还有三角换元法,参数换元法。
6、数形结合法:形似将式子左边看作一个函数,右边看作一个函数,在同一坐标
系做出它们的图象,观测其边线关系,利用解析几何科学知识谋最值。
谋利用直线的
斜率公式谋形似的最值。
7、利用导数求函数最值。
函数最小值公式范文

函数最小值公式范文函数的最小值可以通过求导数和判别法来计算。
首先,我们需要了解一些基本的导数和最小值的概念。
导数是描述函数在其中一点上的变化率的概念。
如果函数y=f(x)在点x处可导,那么函数在该点的导数就是f'(x)。
导数可以理解为函数的斜率,它告诉我们函数在其中一点上是上升还是下降。
最小值是函数在一定范围内取得的最小值。
如果函数y=f(x)在其中一点x处的导数为0,并且在该点的导数从正变为负,那么该点就是函数的极小值点。
也就是说,最小值出现在导数为零的点,并且在该点的导数从正变为负。
有一些基本的规则可以帮助我们计算函数的导数,这些规则包括求导法则、链式法则和求导数的基本公式。
求导法则:-常数规则:常数的导数为零。
-幂函数规则:对于函数f(x)=x^n,其导数为f'(x)=n*x^(n-1)。
-和差法则:对于函数f(x)=g(x)+h(x),其导数为f'(x)=g'(x)+h'(x)。
-乘法法则:对于函数f(x)=g(x)*h(x),其导数为f'(x)=g'(x)*h(x)+g(x)*h'(x)。
-除法法则:对于函数f(x)=g(x)/h(x),其导数为f'(x)=(g'(x)*h(x)-g(x)*h'(x))/h(x)^2链式法则:-对于函数f(g(x)),其导数为f'(g(x))*g'(x)。
求导数的基本公式:-导数的加减法:如果函数f(x)和g(x)的导数都存在,那么它们的和(差)的导数等于它们的导数的和(差)。
-导数的乘法法则:如果函数f(x)和g(x)的导数都存在,那么它们的乘积的导数等于f'(x)*g(x)+f(x)*g'(x)。
-导数的除法法则:如果函数f(x)和g(x)的导数都存在,并且g(x)不等于零,那么它们的商的导数等于(f'(x)*g(x)-f(x)*g'(x))/g(x)^2求解函数的最小值的步骤如下:1.求函数的导数。
导数和微分知识的应用1建立函数关系式,求函数的最大值和最小值
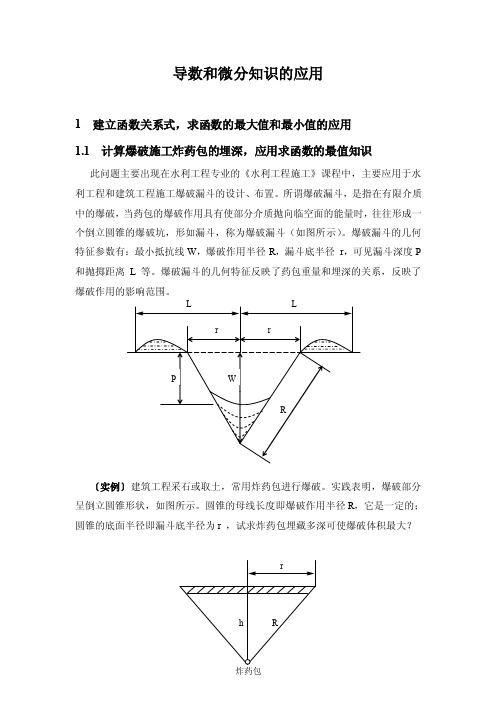
导数和微分知识的应用1 建立函数关系式,求函数的最大值和最小值的应用1.1 计算爆破施工炸药包的埋深,应用求函数的最值知识此问题主要出现在水利工程专业的《水利工程施工》课程中,主要应用于水利工程和建筑工程施工爆破漏斗的设计、布置。
所谓爆破漏斗,是指在有限介质中的爆破,当药包的爆破作用具有使部分介质抛向临空面的能量时,往往形成一个倒立圆锥的爆破坑,形如漏斗,称为爆破漏斗(如图所示)。
爆破漏斗的几何特征参数有:最小抵抗线W,爆破作用半径R,漏斗底半径r,可见漏斗深度P 和抛掷距离L等。
爆破漏斗的几何特征反映了药包重量和埋深的关系,反映了〔实例〕建筑工程采石或取土,常用炸药包进行爆破。
实践表明,爆破部分呈倒立圆锥形状,如图所示。
圆锥的母线长度即爆破作用半径R,它是一定的;圆锥的底面半径即漏斗底半径为r ,试求炸药包埋藏多深可使爆破体积最大?分析:首先根据圆锥的体积公式V=31πr 2h,建立函数关系式。
然后运用求函数最值的方法、步骤,即可求得炸药包的埋深h. 解答:(计算过程略) 当炸药包埋深为h=R 33时,爆破体积最大. 1.2 研究梁的抗弯截面模量,应用求函数的最值知识此问题主要出现在水利工程专业的《工程力学》课程,主要应用于梁的弯曲强度的计算、研究。
所谓梁的抗弯截面模量,是反映梁的弯曲强度的一个指标。
其值取决于梁截面的形状和尺寸,其值越大梁的强度就越好。
从弯曲强度方面考虑,最合理的截面形状是能用最少的材料获得最大的抗弯截面模量。
在截面面积相同的条件下,矩形截面比方形截面好,方形截面比圆形截面好。
〔实例1〕把一根直径为d 的圆木锯成截面为矩形的梁。
问矩形截面的高h 和宽b 应如何选择才能使梁的抗弯截面模量最大?(矩形梁的抗弯截面模量216w b h =)解答:(计算过程略)当矩形截面的宽b =,而高h =时,才能使梁的抗弯截面模量最大。
〔实例2〕已知矩形断面横梁的强度与它的宽和高的平方之积成正比。
分式高阶求导公式

分式高阶求导公式分式是代数函数中常用的一种形式,对于分式的求导也可以应用链式法则和两个函数的商的求导法则。
下面列举了一些常用的分式求导的公式。
1.基本规则- 对于任意常数a,有$\frac{d}{dx}(af(x))=a\frac{d}{dx}f(x)$,其中f(x)是x的任意函数。
- $\frac{d}{dx}(x^n)=nx^{n-1}$,其中n是任意实数。
2.一次函数- $\frac{d}{dx}(\frac{1}{x})=-\frac{1}{x^2}$- $\frac{d}{dx}(\frac{a}{x})=-\frac{a}{x^2}$,其中a是任意常数。
- $\frac{d}{dx}(ax+b)=a$,其中a和b是任意常数。
3.幂函数- $\frac{d}{dx}(\frac{1}{x^n})=-\frac{n}{x^{n+1}}$,其中n是任意实数。
- $\frac{d}{dx}(\frac{a}{x^n})=-\frac{an}{x^{n+1}}$,其中a是任意常数,n是任意实数。
- $\frac{d}{dx}(x^{\frac{m}{n}})=\frac{m}{n}x^{\frac{m}{n}-1}$,其中m和n为任意有理数。
4.指数函数- $\frac{d}{dx}(\frac{1}{b^x})=-\frac{\ln b}{b^x}$,其中b是任意正实数。
- $\frac{d}{dx}(e^x)=e^x$- $\frac{d}{dx}(a^x)=a^x\ln a$,其中a是任意正实数。
5.对数函数- $\frac{d}{dx}(\ln x)=\frac{1}{x}$- $\frac{d}{dx}(\log_b x)=\frac{1}{x\ln b}$,其中b是任意正实数。
- $\frac{d}{dx}(\ln f(x))=\frac{1}{f(x)}\cdot\frac{d}{dx}(f(x))$,其中f(x)是x的任意函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以口,b,c)=(口+b+C)(b+c—fi)(口+C一6)(口 +b—c),(口,b,c为三角形三条边)
因为以a,b,c)=(口+b+C)(b+C一口)(口+c —b)(a+b—c)=4a2b2一(口2+b2一c2)2=
参考文献 [1] 刘超.海伦公式证明之史海钩沉[J].中学数学杂志,
2008,(10).
z十菇
x+'
v+z
z+x
x+
3\ 4- z}
+瓦2i万2巧1 +瓦i万2 +琵忑3万
由算,y,z>0,3x+4),+5z=I,可知(戈+Y)+
2(z+z)+3(y+z)=1 设石+Y=m,2(z+戈)=,l,贝0 3(y+彳)=1一
+i2+熹 因为z,Y,彳>0,所以m,rt,1一m—n>0
构造函数F(m,n)=i1
若n E N+,%b∥∈R+,bj<zj<c,∑bi<
南b+南b+…+南b+ c,i=1,2,…,,l,求函数H(xl,算2,…,善。) =
_————旦——可的最小值.读者可自行研 (舅l— I)7
Байду номын сангаас
(石2— 2)7
(菇。一 。)’
Lc—zl—X2一…一xn J
究,不再赘述.
总之,一类分式函数最小值问题的研究过程,它
次,这类导数题首先都应有共同的一步,即先求导,
然后求解导数等于0这个方程,再结合具体题目进
行分析.所以解导数等于0这个方程几乎是解答导
数所有题通向成功的一座独木桥.正如一首歌词里 唱得“让所有问题,都自己扛”,于是乎,就出现了这
样一个问题:当导数等于0解不了怎么办?
我们先来看2009年浙江高考数学参考卷最后
万方数据
减;当尘娑n‘+1+br+l <石 <d时,g,(石) >o,g(髫)递
增;所以,当且仅当菇:尘罕埤时,取最小值
gg((膏膏)面)n血2:万土与(‘口口鬲鬲1++66击鬲))r”+-1
应用1 设口,6∈R+,I石l<号,求函数以石)
解设小)=尚+己舞= =√^石/1({生+ 2x百2)+石(1一 {L2x可)2的~最一小。值一 .
q +0b 时以z)取最小值“≠一。 ‘(石+万)2的结
论.他山之石,可以攻玉.笔者在高中数学教学中,把
它作为研究性学习素材,让学生进行实践探究,收到
良好的教学效果.现将学生研究性学习得到的求导
证明及推广结论整理如下.
导函数是求函数最值的有效方法,学生利用求
导来研究函数性质,思路清晰,较易操作,这类分式
推广l 若函数g(茗) =zjL百+
百与‘口,”∈R+,c,d∈R“茗<d),则当且
仅当菇:生罕±穹翌时,g(z)取最小值g(石)血。:
口r+1+b,+1
百b(茹+6叫I“
简证
对函数g(x)求导得:g’(z)=
石i可+面刁 —.ar
br
因为,当z=尘军埤时,gt(算)=0;
口7+1+b’+I
当c<算<≮上军时,g‰)<o,g(z)递
一题: 例1
。2
已知函数以石)=e。一等一口z一1,其中 二
1
口为实数,(1)当口=一÷时,求曲线Y=以石)在点 二
(1以1))处的切线方程;
海伦公式的一个简洁证明
4a262【l一(警)2】=4a262(-…s2c)= 石河子大学师范学院数学系832003
刘超
若已知任一AABC的三边长为fi,b,c,则其面
万方数据
中学数学杂志2009年第11期
当导数等于0解不了怎么办
——从2009浙江高考数学参考卷最后一题谈起
浙江上虞城南中学
312300
王永平
导数是高中新课标教材中的重要内容,它既是 研究函数的有力工具,又是对学生进行理性思维训 练的良好素材.自导数进入新教材之后,给函数问题 注入了生机和活力,开辟了许多解题新途径,拓展了 高考对函数问题的命题空间.导数的考题一般分基 础层次与提高层次,基础层次是导数的简单应用,包 括求函数的单调性,极值,最值等,提高层次是导数 的综合应用,将导数内容与传统内容中解证不等式, 方程根的分布,参数的范围等问题结合起来,这类题 难度很大,综合性强,内容新,是高考命题的丰富宝 藏.解题中还常需用到函数与方程思想、分类讨论思 想、数形结合思想、转化与化归思想,所以颇得高考 命题者的青睐.但是,无论是基础层次,还是提高层
函数的最小值也不例外.
对函数八茗)=上+jjL一(口,b,c,d∈R+,c
。
并一C
口一石
<z<∽求导得/,(旬2石二三备+西芒了
一垒(兰二12:二堡(生二苎2:
(算一c)2(d一石)2
一[巫(兰二12±矗(生二苎2][拯苎二!!=正(生二兰U
(髫一c)2(d一茹)2
一[拯苎=!)±亟垡二纠[(正±亟苎:(!垣±垡固]
应用3 设x,y,z E R+,算+Y+z=1,求H=
三+与+要的最小值.
万南,申推广2可知, 解 构造二元函数G(童,),):T1+了1+
汀
当 j且且’仅队当j
弧+弧+
汀
),=
弧+源+
l
4
时,
l
4
函数最小值为击(汀+汀+洒)3=64.
所以,当且仅当石:Y:{时,M:与+丢+导
.'
玉
j,
五
的最小值为64.
=生警,此即海伦公式.关于海伦公式的证明, 积可表示为A=,/s(s一口)(s—b)(s—c),其中s 二
笔者已在文[1]中给出了中外数学史上的有关证明 方法.分析发现,历史上的证法均为几何证法(添加 辅助线,利用全等三角形的边、角关系或者相似三角 形中的比例关系进行推导),各种方法堪称精巧美 妙,但略显复杂.本文拟给出海伦公式的一个代数 证法.
中学数学杂志2009年第1 1期
d口鬲
d),则当且仅当
口 上川 +
}击
诗腑 时
y 2—丁———丁———丁
口鬲+6鬲+C,-Zi
函数有 最
,J、值G(石,),)面。:与(口击+6鬲1+c者)7+l
简证 分式函数自变量从一元推广到两元,可 以用最小两乘法思想求解,由推广1可知,当Y看成
常量时,当z:垒年』且#时函数有最小值;当算看
中学数学杂志2009年第11期
霓舞夤噎4舾I彩雹;%酚裼。趸弘跷己埽£。为哆
一类分式函数最小值的求导处理及推广
江苏省常熟市中学
215500
蔡祖才
函数以石)=—生+j—堡一(口,b,c,d∈R+,c<
石一C
口一石
z<d),求其最小值,文[1][2]采用均值不等式或
筹a三角换元变换去求解,并得到当且仅当石=
(算一c)2(d一茗)2
显然有c<垫笪±虫丝</----d
因为,当髫=q丛B+辫qn时,f,(石)=o;当c<
名<垫辫时,f,(石) √口十√0
<o以石)递减;当
型鳟<q石a+<q dD 时,f,(菇)>o以算)递增;
√a所+√以D ,当且仅当写:型鳟时,以茁)有最小
≈Q+0b
值八等警)=士(,/-d+∥.
ar+l+cr+l
成常量时,当y:型#兰翠时函数有最小值;
dn鬲
上川
口
+
+ 上川
alr+_l_i忑4-C 联立解得当 y2
诗腑
时 G 石y 有
+6…
r+1
最小值为{(口士+6击+c鬲I)川. d
应用2 设x,),,z>o,3石+4y+5z=l,求7毛
+—L+—L的最小值.
解而1+再1+鬲1=鬲1 Y+南Y ),十孑
体现了最小两乘法思想及函数求导思想,是学生研
究性学习的好材料,值得我们借鉴应用.
参考文献 [1] 郭晓泉.一类分式函数最小值讨论[J].中学数学杂
志.2009,(3). [2] 李春雷.双根式和或差的函数求最值方法[J].数学通
报,2008,(12).
作者简介 蔡祖才,1965年8月出生,中学高级教师.发 表论文多篇.主要从事高中数学教学研究,学术主持省、市级 课题若干.
[髫一(一扣2。‘丁1一石)2’
由推广l可知,当且仅当菇=麦糕时,
2赫.Ta g(茗)的最小值为g(戈)耐。=(拓+拓)3,
所以当且仅当石2
时以旬取最小
。
( +√6)
值污+拓
推广2 对函数G(石,),):_a+_b+
石
Y
万j可(口,6,c,如“+,0<“d,0<y<
万方数据
舅.署娩镌貔泓拣5霸绲I高私焉£壕g叠§岁
构造多项式:
16(1absinC)=16A2
又八a,b,c)=2s·2(s—d)·2(s j 6)·2(5一 c)=16s(s一口)(s一6)(5一c),
两者比较得,16A2=16s(s—fit)(s一6)(s—c), 故A=石(s—a)(s—b)(s—c),公式得证. 该证法较之历史上的几何证法,所用知识简单, 证明过程直观、自然,巧而不烦,且对于运用“构造 多项式”方法证明几何命题也有一定的启发作用.
由推广 2 可知,
当且仅当
1
l 瓜’压 点 瓜’压 +矗
2∽牡志’ r万而 +五 +万)2
H
l
即
V■T V厶T VJ
3算+4),+5z=1
解得{…y=嬲6+3√芝一2 43 石=————=■——==——■= 12(√l+√互+√3)
一6+3√2+2 43
●一
12(√1十√2+√3)
此时,鬲1 +歹l_+_毛有最小值为(汀+厄+万)2.
