现代控制理论大作业

合集下载

现代控制理论大作业

现代控制理论直流电动机模型的分析姓名：李志鑫班级：测控1003学号：20100203030921直流电动机的介绍1.1研究的意义直流电机是现今工业上应用最广的电机之一，直流电机具有良好的调速特性、较大的启动转矩、功率大及响应快等优点。

在伺服系统中应用的直流电机称为直流伺服电机，小功率的直流伺服电机往往应用在磁盘驱动器的驱动及打印机等计算机相关的设备中，大功率的伺服电机则往往应用在工业机器人系统和CNC铣床等大型工具上。

[1]1.2直流电动机的基本结构直流电动机具有良好的启动、制动和调速特性，可以方便地在宽范围内实现无级调速，故多采用在对电动机的调速性能要求较高的生产设备中。

直流伺服电机的电枢控制：直流伺服电机一般包含3个组成部分：-图1.1①磁极：电机的定子部分，由磁极N—S级组成，可以是永久磁铁（此类称为永磁式直流伺服电机），也可以是绕在磁极上的激励线圈构成。

②电枢：电机的转子部分，为表面上绕有线圈的圆形铁芯，线圈与换向片焊接在一起。

③电刷：电机定子的一部分，当电枢转动时，电刷交替地与换向片接触在一起。

直流电动机的启动电动机从静止状态过渡到稳速的过程叫启动过程。

电机的启动性能有以下几点要求：1）启动时电磁转矩要大，以利于克服启动时的阻转矩。

2）启动时电枢电流要尽可能的小。

3）电动机有较小的转动惯量和在加速过程中保持足够大的电磁转矩，以利于缩短启动时间。

直流电动机调速可以有：（1）改变电枢电源电压；（2）在电枢回路中串调节电阻；（3）改变磁通，即改变励磁回路的调节电阻Rf以改变励磁电流。

本文章所介绍的直流伺服电机，其中励磁电流保持常数，而有电枢电流进行控制。

这种利用电枢电流对直流伺服电机的输出速度的控制称为直流伺服电机的电枢控制。

如图1.2Bm电枢线路图1.2——定义为电枢电压（伏特）。

——定义为电枢电流（安培）。

——定义为电枢电阻（欧姆）。

——定义为电枢电感（亨利）。

——定义为反电动势（伏特）。

现代控制理论大作业课件

总结词
自适应控制设计需要建立合适的自适应算法和控制器结构。
详细描述
自适应控制设计需要建立合适的自适应算法和控制器结构，以确保控制器能够实时地调整自身参数并保证系统的最优性能。此外，还需要对算法和控制器结构进行充分的验证和测试，以确保其在实际应用中的可靠性和有效性。
06
非线性系统理论
非线性系统的基本性质
齐次性
线性系统的输出与输入成正比，即当输入信号乘以一个常数时，输出信号也乘以相同的常数。
叠加性
对于线性系统的多个输入信号，其输出信号等于各个输入信号单独作用于系统所产生的输出信号之和。
时不变性
线性系统的输出信号与输入信号在不同时刻的比值保持恒定，即系统特性不随时间变化。
线性系统的状态空间表示
平衡点稳定性
分析非线性系统平衡点的稳定性，可以通过求解系统的线性化方程来获得。
动态稳定性
动态稳定性是指非线性系统在受到扰动后恢复稳定的能力。
非线性系统的控制设计
状态反馈控制
通过测量系统的状态变量，并使用状态反馈控制器来控制非线性系统的输出。
滑模控制
滑模控制是一种变结构控制方法，通过设计滑模面和滑模控制器来实现对非
最优控制问题的描述
01
最优控制问题是在给定初始和终端状态约束下，寻找一个控制输入，使得系统状态在满足约束条件下，某个性能指标达到最优。
02
性能指标通常包括系统状态和控制输入的能量、时间和成本等。
03
约束条件可以是系统状态、控制输入或性能指标的限制。
极小值原理
极小值原理是求解最优控制问题的一种方法，它基于动态规划的思想，通过求解一系列的子问题来找到最优解。
状态方程
描述系统内部状态变量随时间变化的数学方程，通常表示为矩阵形式。

现代控制理论大作业

2019/11/21
2
课题背景
系统工作原理
Accelerometer gyroscope 遥控器
电源
左轮软件编码
AD 采样
滤波
MCU
驱动器1 驱动器2
无线模块
软件编码右轮
减速机构左电机
右电机减速机构
2019/11/21
3
系统工作原理前进（后仰）
后退（前倾）
2019/11/21
课题背景
后退（纠正后仰）前进（纠正前倾）
Matlab计算程序:
pole=[-1,-2,-3,-4]; K=place(A,B,pole) A1=A-B*K; pole=[-3,-4,-5,-6]; K=place(A,B,pole) A2=A-B*K; pole=[-8,-9,-10,-11]; K=place(A,B,pole) A3=A-B*K;
figure; hold on; plot(curve1(:,2),'color','blue'); plot(curve2(:,2),'color','red'); plot(curve3(:,2),'color','green'); xlabel(‘时间（s）'); ylabel(‘摆动角度（rad）'); hold off
2019/11/21
N C,CA,CA2 ,CA3
计算结果：
rankc = 4 ranko = 4
结论： k（M）=4 系统完全能控 Rank（N）=4 系统完全能观
稳定性分析
运用Matlab解出矩阵A的特征值如下：

现代控制理论大作业

现代控制理论大作业“现代控制理论”课本质上是一门工学理论基础课，它在电气工程领域众多研究工作中也有着广泛的应用，例如发电机励磁控制、发电机调速控制、电力电子装置控制等。

“现代控制理论”课立足于近年来控制理论与工程应用的最新进展，旨在实现以下两个目的：一是将控制与系统理论的前沿领域介绍给研究生，使之理解基本思想并掌握基本设计方法；二是在工程实践（主要是电力系统）与先进理论之间架设一座桥梁，使研究生能正确地运用有关理论和方法解决实际工程问题。

通过实现上述目标，本课程可拓宽研究生的专业基础知识，了解和掌握学科前沿动态，培养和提高研究生独立从事科研的能力。

课程内容本课程的教学理念是“用生动鲜活的例子诠释复杂的控制理论，用教师的研究经历点亮学生思考的火炬”。

“现代控制理论”立足于近年来控制理论与工程应用的最新进展，紧紧围绕鲁棒控制和非线性系统控制两个重点，主要讲述以下内容：①线性最优控制系统理论。

②非线性最优控制系统设计——微分几何方法。

③线性H∞控制设计原理。

④非线性控制系统H∞设计原理。

课程教学方式本课程采用教师讲授、学生课外阅读、习题练习和研究型大作业相结合的教学模式。

为加强理论联系实际，避免过分理论化，课程结合控制工程特别是电力系统工程实际，设置了下述专题研究：a. 汽轮机汽门开度系统非线性控制器设计b. 可控串联补偿鲁棒控制器设计c. 水轮机调速非线性鲁棒控制器设计d. 静止无功补偿器非线性控制器设计e. 直流输电系统非线性控制器设计f. 倒立摆控制器设计（购置2级和3级倒立摆各1台）g. 电力巡线机器人越障控制上述专题研究的目的是：在基本掌握现代控制理论主要设计方法的基础上，让研究生开展某一专题的研究，以培养学生的综合能力和素质。

这一部分内容可以代替课程的期末考试（笔试闭卷）。

教师事先就专题研究的要求、选题、难度等方面进行指导；专题研究一般由个人独立完成，内容较多的题目可以两个人作为一组来完成。

现代控制理论作业

现代控制理论大作业要求：（1）自选一实际物理对象进行研究，建立实际物理系统的状态空间模型；（2）进行原系统的定性分析，包括稳定性、能控性、能观性分析；（3）根据系统提出的性能指标要求（如超调量、超调时间、调节时间等动态性能指标以及稳态误差等稳态性能指标），进行原系统的仿真分析，和要求的性能指标做对比；（4）对不稳定系统且能镇定的系统，进行镇定控制；（5）对未达到性能指标要求的系统进行状态反馈控制设计，满足系统性能指标要求；（6）设计状态观测器观测所有状态；（7）设计降阶状态观测器；（可选）（8）最优控制；（9）体会及对课程建议。

1实际物理模型：如图1所示，为一交接车前后连接振动简化模型。

设计一个调节器系统使得在无扰动的情况下，系统保持在零位置上（y1=0）。

其中m1=1，m2=2，k=36，b=0.62系统的描述方程：)()(m )()(m 212122121211y y b y y k yu y y b y y k y-+-=+-+-= 其空间状态模型为：设：。

,,,24132211y x yx y x y x ====[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡432121432143210001u 01003.03.018186.06.0-3636-10000100x x x x y y x x x x x x x x 3分析与求解过程：由根轨迹和特征根（a = -0.4500 + 7.3347i -0.4500 - 7.3347i -0.000 0 ）知虽实根都为负数但都靠近零轴，是李雅普诺夫定义下的稳定，但存在震荡，所以把希望闭环极点配置在10-s ,10-s ，32-2-s ，322-s ===+=和把最小阶观测器希望极点配置在16-s ,15-s ==来改善系统的性能。

北航-现代控制理论结课大作业

1. 控制系统任务的物理描述为了满足飞机品质的要求，飞机的纵向运动和横侧向运动都需要有能够连续工作的阻尼器，以用来调整飞机的飞行姿态，避免其出现不必要的俯仰和倾斜。

维持飞机纵向运动的阻尼器称为俯仰阻尼器，维持飞机横侧向运动的阻尼器称为偏航阻尼器。

本次课程大作业旨在通过运用Matlab 的经典控制系统设计工具对某型飞机偏航阻尼器进行控制系统的设计。

2. 控制系统对象的数学模型巡航状态下，某型飞机侧向运动的状态空间模型为：111121314111222122232421221313233343132234142434441424()1()()()()2()()()3()()4t x t a a a a b b t x t a a a a b b u t a a a a b b u t x t t a a a a b b x t t x x x x ••••⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 1111213141221222324234()()()()()()x t c c c c y t x t c c c c y t x t x t ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦式中： 1()x t ：侧滑角（单位为rad ）2()x t ：偏航角速度（单位为/rad s ）3()x t ：滚转角速度（单位为/rad s ）4()x t ：倾斜角（单位为rad ）输入向量及输出向量分别为：1()u t ：方向舵偏角（单位为rad ）2()u t ：副翼偏角（单位为rad ）1()y t ：偏航角速度（单位为/rad s ）2()y t ：倾斜角（单位为rad ）设飞机巡航飞行时的速度为0.8马赫，高度为40000英尺，此时模型的参数为：0.055800.99680.08020.04150.598000.11500.031803.050000.38800.4650000.0805 1.00000A --⎡⎤⎢⎥--⎢⎥=⎢⎥--⎢⎥⎣⎦ 0.007290.00000.475000.007750.15300.1430000B ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦0 1.000000 1.0C ⎡⎤=⎢⎥⎣⎦0000D ⎡⎤=⎢⎥⎣⎦首先输入飞机状态空间模型参数。

现代控制理论结课大作业

现代控制理论结课大作业一、引言现代控制理论是现代科学技术的重要组成部分，广泛应用于工程控制系统中。

在控制理论课程的学习过程中，结课大作业是一项重要的任务。

本文将介绍现代控制理论结课大作业的相关要求和设计思路。

二、研究背景现代控制理论是控制理论的一个重要分支，它主要研究控制系统的建模、分析和设计方法。

通过运用数学和工程技术知识，利用现代控制理论可以对各种系统进行精确的描述和控制。

因此，现代控制理论在自动控制领域具有广泛的应用。

三、大作业要求现代控制理论结课大作业要求学生能够独立选择一个控制系统并进行详细的研究和设计。

具体要求如下： 1. 选择一个真实的控制系统作为研究对象；2. 系统建模：根据实际情况，选择合适的建模方法，将系统转化为数学模型；3. 系统分析：通过分析系统模型，对系统的稳定性、鲁棒性等进行评估； 4. 系统设计：基于现代控制理论的设计思想，设计适合该系统的控制器； 5. 系统仿真：利用仿真软件对设计的控制系统进行验证和优化； 6. 结果分析和总结：对仿真结果进行分析，总结设计过程和经验教训。

四、设计思路在完成现代控制理论结课大作业时，需要有清晰的设计思路和步骤。

以下是一个可能的设计思路供参考： 1. 选择合适的控制系统：可以选择一个典型的工业控制系统，或者选择一个与个人兴趣相关的系统； 2. 进行系统建模：根据系统的实际情况，选择适合的建模方法，如状态空间法、传递函数法等；3. 系统分析：利用控制理论的知识和工具，分析系统的稳定性、鲁棒性，确定系统的可控性和可观性等性能指标；4. 系统设计：基于现代控制理论，设计一个合适的控制器结构，并选择适当的控制参数；5. 系统仿真：利用仿真软件，对设计的控制系统进行仿真验证，观察系统的响应特性和控制性能； 6.结果分析和总结：根据仿真结果，分析系统的优点和不足之处，并总结设计过程中的经验教训。

五、实例分析下面以一个简单的倒立摆系统为例，介绍如何完成现代控制理论结课大作业。

现代控制理论课程设计(大作业)

现代控制理论课程设计报告题目打印机皮带驱动系统能控能观和稳定性分析项目成员史旭东童振梁沈晓楠专业班级自动化112指导教师何小其分院信息分院完成日期2014-5-28目录1. 课程设计目的 (5)2.课程设计题目描述和要求 (5)3.课程设计报告内容 (6)3.1 原理图 (6)3.2 系统参数取值情况 (6)3.3 打印机皮带驱动系统的状态空间方程 (7)4. 系统分析 (10)4.1 能控性分析 (10)4.2 能观性分析 (10)4.3 稳定性分析 (11)5. 总结 (13)项目组成员具体分工打印机皮带驱动系统能控能观和稳定性分析课程设计的内容如下：1.课程设计目的综合运用自控现代理论分析皮带驱动系统的能控性、能观性以及稳定性，融会贯通并扩展有关方面的知识。

加强大家对专业理论知识的理解和实际运用。

培养学生熟练运用有关的仿真软件及分析，解决实际问题的能力，学会应用标准、手册、查阅有关技术资料。

加强了大家的自学能力，为大家以后做毕业设计做很好的铺垫。

2.课程设计题目描述和要求(1)环节项目名称：能控能观判据及稳定性判据(2)环节目的：①利用MATLAB分析线性定常系统的可控性和客观性。

②利用MATLAB进行线性定常系统的李雅普诺夫稳定性判据。

(3)环节形式：课后上机仿真(4)环节考核方式：根据提交的仿真结果及分析报告确定成绩。

(5)环节内容、方法：①给定系统状态空间方程，对系统进行可控性、可观性分析。

②已知系统状态空间方程，判断其稳定性，并绘制出时间响应曲线验证上述判断。

3.课程设计报告内容3.1 原理图在计算机外围设备中，常用的低价位喷墨式或针式打印机都配有皮带驱动器。

它用于驱动打印头沿打印页面横向移动。

图1给出了一个装有直流电机的皮带驱动式打印机的例子。

其光传感器用来测定打印头的位置，皮带张力的变化用于调节皮带的实际弹性状态。

图1打印机皮带驱动系统3.2 系统参数取值情况表1打印装置的参数3.3 打印机皮带驱动系统的状态空间方程图2打印机皮带驱动模型状态空间建模及系统参数选择。

现代控制理论大作业1

Harbin Institute of Technology现代控制理论基础上机实验报告之一亚微米超精密车床振动控制系统的状态空间法设计课程名称：现代控制理论院系：航天学院自动化班号：1104103作者：皮永江学号：1110410228指导教师：刘杨、井后华哈尔滨工业大学2014年6月5日1.工程背景介绍超精密机床是实现超精密加工的关键设备，而环境振动又是影响超精密加工精度的重要因素。

为了充分隔离基础振动对超精密机床的影响，目前国内外均采用空气弹簧作为隔振元件，并取得了一定的效果，但是这属于被动隔振，这类隔振系统的固有频率一般在2Hz左右。

2.实验目的通过本次上机实验，使同学们熟练掌握：a)控制系统机理建模b)时域性能指标与极点配置的关系c)状态反馈控制律设计d)MATLAB语言的应用3.给定的实际参数与数学建模3.0参数与物理模型机床的已知参数上图表示了亚微米超精密车床隔振控制系统的结构原理，其中被动隔振元件为空气弹簧，主动隔振元件为采用状态反馈控制策略的电磁作动器。

床身质量的运动方程为：(1)空气弹簧所产生的被动控制力作动器所产生的主动控制力假设空气弹簧内为绝热过程，则被动控制力可以表示为：(2)标准压力下的空气弹簧体积相对位移（被控制量）空气弹簧的参考压力参考压力下单一弹簧的面积参考压力下空气弹簧的总面积绝热系数电磁作动器的主动控制力与电枢电流、磁场的磁通量密度及永久磁铁和电磁铁之间的间隙面积有关，这一关系具有强非线性。

由于系统工作在微振动状况，且在低于作动器截止频率的低频范围内，因此主动控制力可近似线性化地表示为：(3)力-电流转换系数电枢电流其中，电枢电流满足微分方程：(4)控制回路电枢电感系数控制回路电枢电阻控制回路反电动势控制电压综上得到如下方程组：3.1如果忽略非线性部分数学建模设状态变量为：得到状态方程：状态空间表达式：代入数据：那么状态空间表达式为：显然系统能控，可以采用状态反馈进行任意配置极点。

现代控制理论大作业

专业综合调研报告电气工程与智能控制专业分类号：TH89 单位代码：10110学号：中北大学综合调研报告题目: 磁盘驱动器读写磁头的定位控制系别: 计算机科学与控制工程学院专业年级: 电气工程与智能控制2014级姓名: 何雨贾晨凌朱雨薇贾凯张钊中袁航学号: 14070541 39/03/04/16/33/47指导教师: 靳鸿教授崔建峰讲师2017年5月7日摘要硬盘驱动器作为当今信息时代不可缺少的存储设备，在人们日常生活中正扮演着越来越重要的角色，同时它也成为信息时代科学技术飞速发展的助推器。

然而，随着信息量的日益增长，人们对硬盘驱动器存储容量的要求越来越高。

但另一方面由于传统硬盘驱动器的低带宽、低定位精度，导致磁头很难准确地定位在目标磁道中心位置，从而限制了存储容量的持续增加。

自IBM公司于1956年向全球展示第一台磁盘存储系统R.AMAC以来，随着存储介质、磁头、电机及半导体芯片等相关技术的不断发展，硬盘的存储容量成倍增长、读写速度不断提高。

要保证可靠的读写性能，盘片的转速控制和磁头的定位控制问题具有重要意义。

其中磁头的定位控制主要包括寻道控制与定位跟踪控制两个问题，如PID控制、自适应控制、模态切换控制等，这些控制方法大大提高了硬盘磁头伺服系统的性能。

为达到更高的精度，磁头双级驱动模型成近年的研究热点，多种控制策略已有相关报道，但目前仍处于实验水平。

关键词：磁盘驱动器；磁头；定位；控制AbstractHard disk drive (HDD), acted as requisite storage equipment in current information age,plays a more and more vital role in people’s daily life, and it becomes a roll booster in rapid development of science and technology. However, with the increase of information capacity, we put forward a severe request for HDD data storage capacity. Unfortunately, due to the low bandwidth, low positioning accuracy in conventional HDD, magnetic head is hard to be positioned onto the destination track center, thus it limits the continuing increase in storage capacity.Since IBM brought the first disk-the random access memory accounting machine(RAMAC) to market in 1956, the storage capacity and read/write speed have continuously increased along with the development of the techniques of media,read/write head, actuators and semiconducting chips. The problems of R/W head's settling control is definitely important in order to ensure the reliability of read and write performance. Track seeking and track following are two main stages of the hard disk servo system. Researchers have developed kinds of control strategies to implement the servo control from PID control to advanced controlmethods.Dual-stage actuator has attracted many researchers and engineers for its broaderbandwidth compared with single-stage actuator.Key Words：Hard Disk Drive;Heads; Location; Control专业综合调研报告电气工程与智能控制专业第1章磁盘驱动器的介绍自上世纪50年代计算机发明以来，随着科技的进步，软硬件技术都获得了相当大的发展。

现代控制理论大作业-北科

现代控制理论大作业分析对象：汽车悬架系统指导老师：周晓敏专业：机械工程姓名：白国星学号：S2*******1.建模悬架是车轮或车桥与汽车承载部分之间具有弹性的连接装置的总称，具有传递载荷、缓和冲击、衰减振动以及调节汽车行驶中的车身位置等作用。

传统汽车悬驾系统是被动悬驾，其参数不能改变，无法控制其对不同路面激励的响应，因此对不同路面的适应性较差。

为提高汽车的行驶平顺性、操纵稳定性和制动性等性能，人们开始用主动悬架系统来代替传统的被动悬架系统。

主动悬架系统能根据路面的情况通过一个动力装置改变悬挂架的参数，改善汽车的各方面性能。

对悬驾系统进行仿真计算首先要建立悬驾系统动力学模型，随后对所建立的模型进行仿真分析。

为了简化模型，取汽车的一个车轮的悬驾系统进行研究，该模型可简化为一维二自由度的弹簧阻尼质量系统，图1所示为该模型的模拟图。

图1 悬架系统模型的模拟图其中u为动力装置的作用力，w为路面位移，x1为车身位移，x2为悬驾位移，用车身位移来度量车身的振动情况，并视为系统的输出。

路面状况以w为尺度，并视为系统的一个干扰输入。

当汽车从平面落入坑时，w可用一个阶跃信号来模拟。

u为主动悬架的作用力，它是系统的控制量。

进行受力分析，由牛顿第二规律可得车身悬架系统的动力学方程为:()()()()()1121212212122s s t m x K x x b x x um x K x x b x x u K w x ⎧=-+-+⎪⎨=-+--+-⎪⎩ 设系统状态变量为:[]1212x x x x x =则上面系统动力学方程可改写为状态空间表达式:x Ax Buy Cx Du=+⎧⎨=+⎩ 其中:()1111222200100001sss t s K K b b A m m m m K K K b b m m m m ⎡⎤⎢⎥⎢⎥⎢⎥--=⎢⎥⎢⎥-+⎢⎥-⎢⎥⎣⎦1220000101t B m K m m ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦[]1000C = []00D = u u w ⎡⎤=⎢⎥⎣⎦Matlab 系统模型程序代码： m1=800;m2=320;ks=10000;b=30000; kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1; ks/m2 -(ks+kt)/m2 b/m2 -b/m2]; b=[0 0;0 0;1/m1 0;-1/m2 kt/m2]; c=[1 0 0 0];d=[0 0];G=ss(a,b,c,d)[num,den]=ss2tf(a,b,c,d,1); tfsys=tf(num,den)eig(a)figure(1)impulse(G)figure(2)step(G)系统状态空间模型：:系统传递函数：系统矩阵特征值：系统矩阵特征值都在左半平面，故系统稳定。

现代控制理论大作业

现代控制理论大作业现代控制理论大作业1．解：（1）.选取状态变量为：x1=y, x2=y’，x3=y’’由题可得：a2=1 , a1=4, a0=5所以x3’=-5x1-4x2-x3+3u系统的状态方程为：x1’=x2x2’=x3x3’=-5x1-4x2-x3+3u输出方程为：y=x1将微分方程表达为矩阵形式即得其状态空间表达式：[x1’; x2’; x3’]=[0,1,0;0,0,1;-5, -4, -1][x1;x2;x3]+[0;0;3]uy=[1, 0, 0][x1;x2;x3]（2）.选取系统的状态变量为：x1=y-h0ux2=x1’-h1u=y’-h0u’-h1ux3=x2’-h2u=y’’-h0u’’-h1u’-h2u 由题可得：a0=0, a1=3/2, a2=0b0=-1/2, b1=0, b2=1/2, b3=0所以：[h0;h1;h2;h3]=[1 0 0 0;0 1 0 0;3/2 0 1 0;0 3/2 0 1]^-1*[0 ;1/2;0 ;-1/2]=[0;1/2;0;-5/4]取状态变量为：x1=y-h0u=yx2=x1’-h1u=x1’-1/2ux3=x2’-h2u=x2’所以该系统的状态空间表达式为：[x1’;x2’;x3’]=[0 1 0;0 0 1;0 -3/2 0][x1;x2;x3]+[0;1/2;0;-5/4]uy=[1 ,0, 0][x1;x2;x3](3)由题可得：a2=2, a1=3, a0=5;b3=5, b2=0, b1=0, b0=7所以[h0;h1;h2;h3]=[1 0 0 0;2 1 0 0;3 2 1 0;5 3 2 1]^-1*[5;0;0;7] =[5;-10;5;2]取状态变量为：x1=y-h0u=y-5ux2=x1’-h1u=x1’x3=x2’-h2u=x2’所以该系统的状态空间表达式为：[x1’;x2’;x3’;]=[0 1 0;0 0 1;-5 -3 -2][x1;x2;x3]+[5;-10;5;2]u2.经典控制理论是建立在常微分方程稳定性理论和以拉普拉斯变换为基础的根轨迹和奈奎斯特判断理论之上。

现代控制理论大作业

控制理论：控制理论是讲述系统控制科学中具有新观念、新思想的理论研究成果及其在各个领域中，特别是高科技领域中的应用研究成果，但是在民用领域即实际生活中有很严重的脱节。

飞行器控制技术的进步是与自动控制理论的发展密切相关的。

控制理论在飞行器控制技术方面获得了广泛的应用，取得了许多重要成果。

现代控制理论：建立在状态空间法基础上的一种控制理论，是自动控制理论的一个主要组成部分。

在现代控制理论中，对控制系统的分析和设计主要是通过对系统的状态变量的描述来进行的，基本的方法是时间域方法。

现代控制理论比经典控制理论所能处理的控制问题要广泛得多，包括线性系统和非线性系统，定常系统和时变系统，单变量系统和多变量系统。

它所采用的方法和算法也更适合于在数字计算机上进行。

现代控制理论还为设计和构造具有指定的性能指标的最优控制系统提供了可能性。

发展过程：现代控制理论是在20世纪50年代中期迅速兴起的空间技术的推动下发展起来的。

空间技术的发展迫切要求建立新的控制原理，以解决诸如把宇宙火箭和人造卫星用最少燃料或最短时间准确地发射到预定轨道一类的控制问题。

这类控制问题十分复杂，采用经典控制理论难以解决。

1958年，苏联科学家Л.С.庞特里亚金提出了名为极大值原理的综合控制系统的新方法。

在这之前，美国学者R.贝尔曼于1954年创立了动态规划，并在1956年应用于控制过程。

他们的研究成果解决了空间技术中出现的复杂控制问题，并开拓了控制理论中最优控制理论这一新的领域。

1960～1961年，美国学者R.E.卡尔曼和R.S.布什建立了卡尔曼-布什滤波理论，因而有可能有效地考虑控制问题中所存在的随机噪声的影响，把控制理论的研究范围扩大，包括了更为复杂的控制问题。

几乎在同一时期内，贝尔曼、卡尔曼等人把状态空间法系统地引入控制理论中。

状态空间法对揭示和认识控制系统的许多重要特性具有关键的作用。

其中能控性和能观测性尤为重要，成为控制理论两个最基本的概念。

现代控制理论大作业资料

现代控制理论(主汽温对象模型)班级:学号:姓名:目录一. 背景及模型建立1.火电厂主汽温研究背景及意义2.主汽温对象的特性3.主汽温对象的数学模型二.分析1.状态空间表达2.化为约当标准型状态空间表达式并进行分析3.系统状态空间表达式的求解4.系统的能控性和能观性5.系统的输入输出传递函数6.分析系统的开环稳定性7.闭环系统的极点配置8.全维状态观测器的设计9.带状态观测器的状态反馈控制系统的状态变量图10.带状态观测器的闭环状态反馈控制系统的分析三.结束语1.主要内容2.问题及分析3.评价一.背景及模型建立1.火电厂主汽温研究背景及意义火电厂锅炉主汽温控制决定着机组生产的经济性和安全性。

由于锅炉的蒸汽容量非常大、过热汽管道很长，主汽温调节对象往往具有大惯性和大延迟，导致锅炉主汽温控制存在很多方面的问题，影响机组的整个工作效率。

主汽温系统是表征锅炉特性的重要指标之一，主汽温的稳定对于机组的安全运行至关重要。

其重要性主要表现在以下几个方面：(1) 汽温过高会加速锅炉受热面以及蒸汽管道金属的蠕变，缩短其使用寿命。

例如，12CrMoV 钢在585℃环境下可保证其应用强度的时间约为10万小时，而在 595℃时，其保证应用强度的时间可能仅仅是 3 万小时。

而且一旦受热面严重超温，管道材料的强度将会急剧下降，最终可能会导致爆管。

再者，汽温过高也会严重影响汽轮机的汽缸、汽门、前几级喷嘴和叶片、高压缸前轴承等部件的机械强度，从而导致设备损坏或者使用年限缩短。

(2) 汽温过低，会使得机组循环热效率降低，增大煤耗。

根据理论估计可知：过热汽温每降低10℃，会使得煤耗平均增加0.2%。

同时，汽温降低还会造成汽轮机尾部的蒸汽湿度增大，其后果是，不仅汽轮机内部热效率降低，而且会加速汽轮机末几级叶片的侵蚀。

此外，汽温过低会增大汽轮机所受的轴向推力，不利于汽轮机的安全运行。

(3) 汽温变化过大会使得管材及有关部件产生疲劳，此外还将引起汽轮机汽缸的转子与汽缸的胀差变化，甚至产生剧烈振动，危及机组安全运行。

现代控制理论课程设计(大作业)

加强大家对专业理论知识的理解和实际运用。

培养学生熟练运用有关的仿真软件及分析，解决实际问题的能力，学会应用标准、手册、查阅有关技术资料。

加强了大家的自学能力，为大家以后做毕业设计做很好的铺垫。

2.课程设计题目描述和要求(1)环节项目名称：能控能观判据及稳定性判据(2)环节目的：①利用MATLAB分析线性定常系统的可控性和客观性。

②利用MATLAB进行线性定常系统的李雅普诺夫稳定性判据。

(3)环节形式：课后上机仿真(4)环节考核方式：根据提交的仿真结果及分析报告确定成绩。

(5)环节内容、方法：①给定系统状态空间方程，对系统进行可控性、可观性分析。

②已知系统状态空间方程，判断其稳定性，并绘制出时间响应曲线验证上述判断。

3.课程设计报告内容3.1 原理图在计算机外围设备中，常用的低价位喷墨式或针式打印机都配有皮带驱动器。

它用于驱动打印头沿打印页面横向移动。

图1给出了一个装有直流电机的皮带驱动式打印机的例子。

其光传感器用来测定打印头的位置，皮带张力的变化用于调节皮带的实际弹性状态。

现代控制理论大作业—弹簧系统

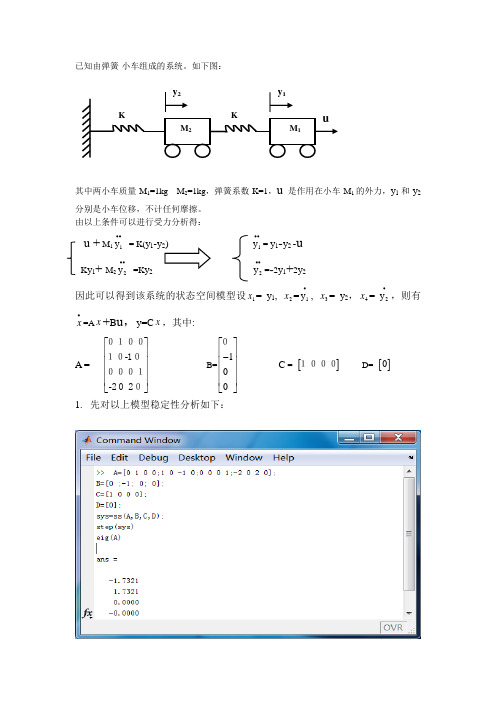
已知由弹簧-小车组成的系统。

如下图：其中两小车质量M 1=1kg M 2=1kg ，弹簧系数K=1，u 是作用在小车M 1的外力，y 1和y 2分别是小车位移，不计任何摩擦。

由以上条件可以进行受力分析得： u + M 11y ••= K(y 1-y 2)1y ••= y 1-y 2 -uK y1+ M 22y ••=K y 2 2y ••=-2y 1+2y 2因此可以得到该系统的状态空间模型设1x = y 1, 2x =1y •, 3x = y 2，4x = 2y •，则有x •=A x +B u ，y=C x ，其中:A = --⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦０１００１０1００００１202０ B=100⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦０ C = []１０００ D= []01. 先对以上模型稳定性分析如下：M 2M 1KKy 2y 1u从图中可知矩阵A 的特征值为-1.732 ，1.732, 0，0，有正值，因此开环系统是不稳定的。

2. 判断系统可控性与可观性可见系统是可控和可观的。

3. 状态反馈控制器设计有步骤1可知系统是能控的。

因此，可以通过状态反馈来任意配置闭环系统的极点。

特别是将闭环极点配置在左半开复平面可以保证闭环系统是渐进稳定的。

因此可以设计一个状态反馈控制器u= -K x ,使得闭环系统极点是-2，-1，-1+j ，-1-j ，期望的闭环特征多项式为（λ+2）（λ+1）（λ+1+j ）(λ+1-j)= 432510104λλλλ++++而状态反馈控制器所到出的闭环系统特征多项式为det{()I A BK λ--}= det{I λ- 1⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦２３４０　１　０　０１+k ｋ　ｋ　ｋ　０　０　０　１－２　２　０　０} =2431k 2k k λλλλ-+４３２-ｋ-２其中K=[]2１３４ｋ　k ｋ　ｋ。

由以上两个多项式的相等，可得１ｋ=4 2k = -5 ３ｋ= -5 ４ｋ= -5。