现代控制理论习题解答..
现代控制理论习题解答(第一章)

Ra
La
i f = 常数
ua
f ia D J
ω
ML
【解】: 设状态变量为:
题 1-2 图
⎡ x1
⎢ ⎣
x
2
⎤ ⎥ ⎦
=
⎡ia ⎢⎣ω
⎤ ⎥ ⎦
其中 ia 为流过电感上的电流, ω 电动机轴上的角速度。 电动机电枢回路的电压方程为:
eb 为电动机反电势。 电动机力矩平衡方程为
•
ua = La ia + Ra ⋅ ia + eb
(4) y (4) + 3y + 2y = −3u + u
【解】:
5
在零初始条件下,方程两边拉氏变换,得到传递函数,再根据传递函数求状态空间 表达式。 此题多解,一般写成能控标准型、能观标准型或对角标准型,以下解法供参考。 (1)传递函数为:
状态空间表达式为:
G(s) =
2
s3 + 2s2 + 4s + 6
1⎤
R 2 C1 −1
R2C2
⎥ ⎥ ⎥
⎡ ⎢ ⎣
x1 x2
⎥⎦
⎤ ⎥ ⎦
+
⎡ ⎢ ⎢ ⎣
1
R1C1 0
⎤ ⎥⎥u i ⎦
y = u0 = [0
1]⎢⎡
⎣
x1 x2
⎤ ⎥ ⎦
(2)
设状态变量: x1 = iL 、 x2 = uc 而
1
根据基尔霍夫定律得: 整理得
•
iL = C uc
•
ui = R ⋅ iL + LiL + uc
•
M D = J ω + fω + M L
现代控制理论课后题及答案

第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
1图P2.2解 这是一个物理系统,采用机理分析法求状态空间表达式会更为方便。
令()f t 为输入量,即u f =,1M ,2M 的位移量1y ,2y 为输出量, 选择状态变量1x =1y ,2x = 2y ,3x =1dy dt,24dyx dt =。
现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解:()()22232321s s s s s s s++ =++ ? ?D S N S ; ()3r 2,1,2E -:223381s s s s s s ??++ ?-- ? ???;()3r 2,3,3E :223051s s s s s ??++ ?- ? ???;()3r 1,3,2E s --:01051s s ?? ?- ? ;()3r 2,1,5E s -:01001s ?? ?;()3r 3,1,1E -:01000s ?? ? ? ???;()1r 2,3E :01000s ?? ? ? ???;()1r 1,2E :00100s ?? ?;所以⼀个gcrd 为001s ??;取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ,根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ,根据C-H 有限项展开法求解转移矩阵t A e 。
解:(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -,得1,233,1λλ== 对1,23λ=,可以计算1,2()2rank λ=A I -,所以该特征值的⼏何重数为1。
《现代控制理论》第三版_.习题答案

K1
0 0 K1
K p
B 0 0 0 0 0
K1
T
K p
C 1 0 0 0 0 0;
1-3.
图
1-29
机械系统。M1
M
受外力
2
作用 f1 f2作用,求M1 M 2运动速度输出的
状态空间表达式。
解:微分方程 M1 y1 f1 K1(c1 c2 ) B1( y1 y2 )
M 2 y2 f2 K2c2 B2 y2 K1(c1 c2 ) B1( y1 y2 )
第一章 作业
参考答案
1-1. 求模拟结构图,并建立其状态空间 表达式。 解:状态方程:
x1 x2
x2
Kb J2
x3
x3
1 J1
x5 K p x6 x3 x4
Kp J1
x3
1 J1
x4
1 J1
x5
Kp J1
x6
x4 Kn x3 x5 K1(x6 x3 ) K1x3 K1x6
x 6
设状态变量 x = c1 c2 y1 y2 T
y y1 y2 T ,u f1 f2 T
令 x1 c1, x2 c2, x3 y1, x4 y2
x1 x3 x2 x4
x3
K1 M1
x1
K1 M1
x2
B1 M1
x3
B1 M1
x4
1 M1
f1
x4
K1 M2
x1
K1 K2 M2
第二章 作业
参考答案
2-4. 用三种方法计算eAt (定义法,约 当标准型,拉氏反变换,凯莱哈密顿)
(1)
A
0 4
1 0
直接法(不提倡使用,除非针对一些特
《现代控制理论》第三版_.习题答案

1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
现代控制理论习题解答(第三章)

第三章 线性控制系统的能控性和能观性3-3-1 判断下列系统的状态能控性。
(1)⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=01,0101B A (2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=111001,342100010B A (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A (4)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1110,0000000011111B A λλλλ 【解】:(1)[]2,1011==⎥⎦⎤⎢⎣⎡-==n rankU AB BU c c ,所以系统完全能控。
(2)[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==7111111010012B A ABBU c 前三列已经可使3==n rankU c ,所以系统完全能控(后续列元素不必计算)。
(3)A 为约旦标准型,且第一个约旦块对应的B 阵最后一行元素全为零,所以系统不完全能控。
(4)A 阵为约旦标准型的特殊结构特征,所以不能用常规标准型的判别方法判系统的能控性。
同一特征值对应着多个约旦块,只要是单输入系统,一定是不完全能控的。
可以求一下能控判别阵。
[]2,111321031211312113121121132=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡==c c rankU B A BA AB BU λλλλλλλλλλλ,所以系统不完全能控。
3-3-2 判断下列系统的输出能控性。
(1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=xy u x x 011101020011100030013 (2) []⎪⎪⎩⎪⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x y u x x 0011006116100010【解】: (1)已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A ,⎥⎦⎤⎢⎣⎡-=011101C ,⎥⎦⎤⎢⎣⎡=0000D []⎥⎦⎤⎢⎣⎡--=111300002B CA CAB CB D前两列已经使[]22==m B CA CAB CB D rank ,所以系统输出能控。
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)

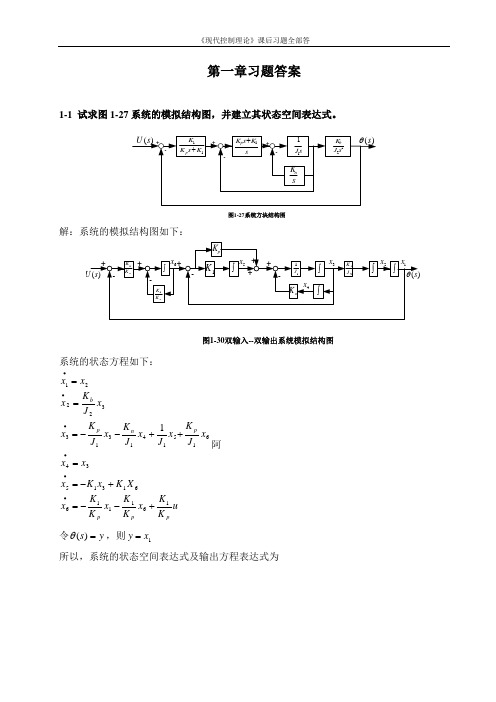
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论习题附答案

现代控制理论习题附答案现代控制理论习题附答案现代控制理论是控制工程领域中的重要分支,它研究如何利用数学模型来描述和分析控制系统的行为,并设计出相应的控制算法。
掌握现代控制理论对于提高控制系统的性能和稳定性至关重要。
在这篇文章中,我们将介绍一些现代控制理论的习题,并附上相应的答案,希望能够帮助读者更好地理解和应用这一理论。
1. 问题:给定一个连续时间域的线性时不变系统,其传递函数为G(s) = (s + 1)/(s^2 + 3s + 2),试求该系统的单位阶跃响应。
答案:单位阶跃响应是指当输入信号为单位阶跃函数时,系统的输出响应。
对于连续时间域的系统,单位阶跃函数可以表示为u(t) = 1,其中t >= 0。
根据系统的传递函数,我们可以使用拉普拉斯变换来求解单位阶跃响应。
首先,将传递函数G(s)进行部分分式分解,得到G(s) = 1/(s + 1) - 1/(s + 2)。
然后,对每一项进行拉普拉斯反变换,得到g(t) = e^(-t) - e^(-2t)。
因此,该系统的单位阶跃响应为g(t) = e^(-t) - e^(-2t)。
2. 问题:给定一个离散时间域的线性时不变系统,其传递函数为G(z) = (0.5z + 0.3)/(z^2 - 0.7z + 0.1),试求该系统的单位脉冲响应。
答案:单位脉冲响应是指当输入信号为单位脉冲函数时,系统的输出响应。
对于离散时间域的系统,单位脉冲函数可以表示为δ(n),其中n为整数。
根据系统的传递函数,我们可以使用z变换来求解单位脉冲响应。
首先,将传递函数G(z)进行部分分式分解,得到G(z) = 0.3/(z - 0.5) + 0.2/(z - 0.1)。
然后,对每一项进行z反变换,得到g(n) = 0.5^n - 0.1^n。
因此,该系统的单位脉冲响应为g(n) = 0.5^n - 0.1^n。
3. 问题:给定一个连续时间域的线性时不变系统,其状态空间表示为dx/dt =Ax + Bu,y = Cx + Du,其中A = [[-1, -2], [3, -4]],B = [[1], [0]],C = [[1, 0], [0, 1]],D = [[0], [0]],试求该系统的零输入响应。
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)
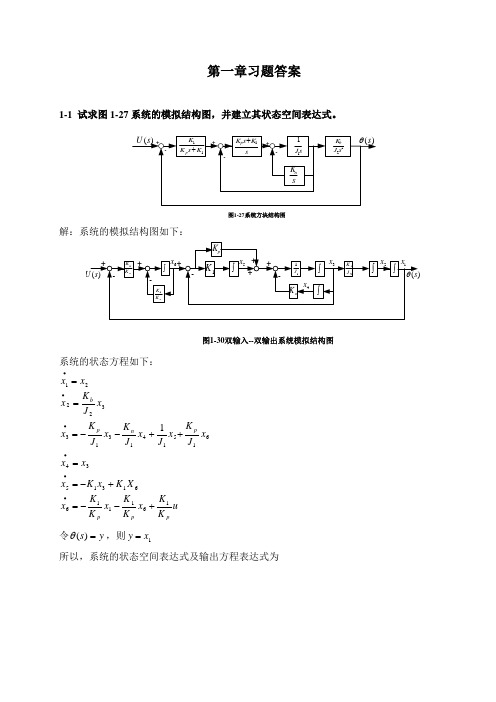
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:uKK x KK x KK x X K x K x x x x J Kx J x J K x J Kx x J K x x x ppppn pb 1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙65432116543211111111265432100000100000000000000010010000000000010x x x x x x y uK K x x x xx x K K K K K K J K J J K J KJ K x x x x x xp p pp n pb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x Cx Cx x L x L R x uL x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000010111010x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)
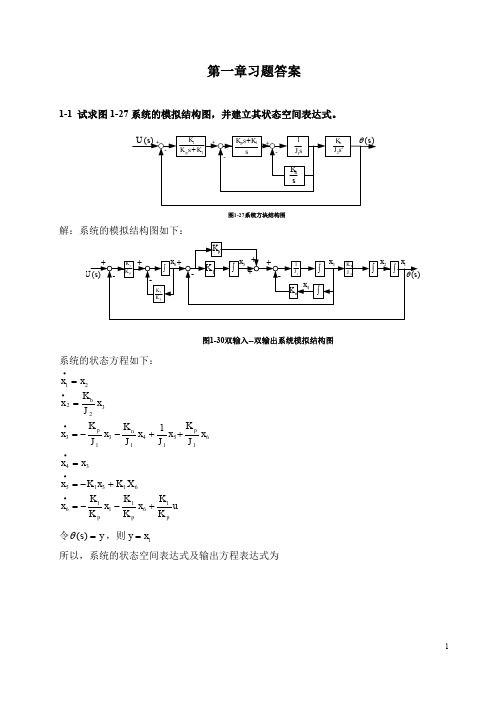
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论习题解答(第四章)

第四章 控制系统的稳定性3-4-1 试确定下列二次型是否正定。
(1)3123212322212624)(x x x x x x x x x x v --+++= (2)232123222126410)(x x x x x x x x v ++---= (3)312321232221422410)(x x x x x x x x x x v --+++= 【解】: (1)04131341111,034111,01,131341111<-=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数不定。
(2)034101103031,0110331,01,4101103031<-=--->=--<-⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=P 二次型函数为负定。
(3)017112141211003941110,010,1121412110>=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数正定。
3-4-2 试确定下列二次型为正定时,待定常数的取值范围。
312321231221211242)(x x x x x x x c x b x a x v --+++=【解】:312321231221211242)(x x x x x x x c x b x a x v --+++=x c b a x T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1112121110212111,011,0111111>---->>c b a b a a 满足正定的条件为:⎪⎩⎪⎨⎧++>+>>1111111114410ca b c b a b a a3-4-3 试用李亚普诺夫第二法判断下列线性系统的稳定性。
;1001)4(;1111)3(;3211)2(;1110)1(x x x x x x x x ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=【解】: (1)设22215.05.0)(x x x v +=⎩⎨⎧≠≤==-=--=+=)0(0)0(0222221212211)(x x x x x x x x x x x x x v为半负定。
(完整word版)《现代控制理论》第3版课后习题答案
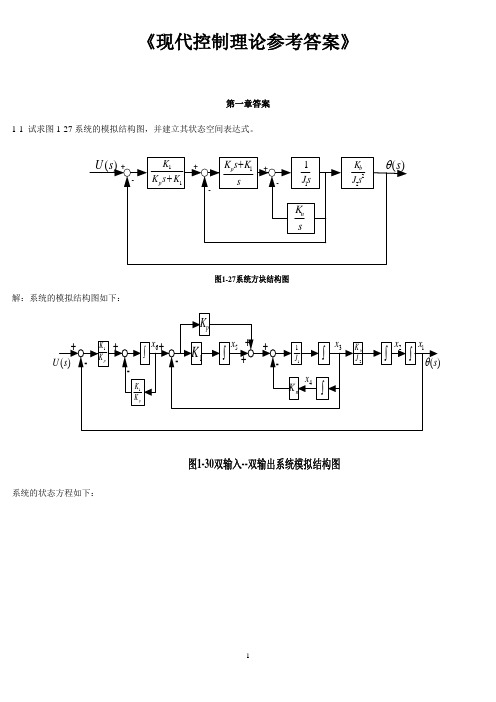
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》第3版课后习题答案.
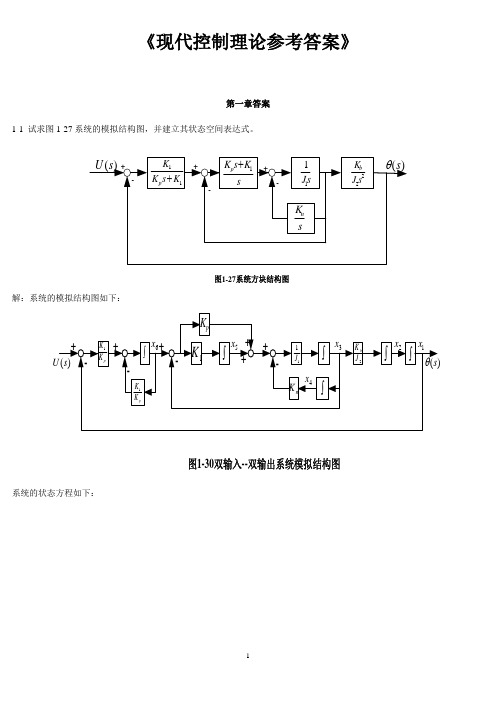
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》课后习题答案1

G ( s) =
每一个环节的状态空间模型分别为:
1 2s + 5 ⋅ s+3 s+5
2 = −5 x 2 + u1 ⎧x ⎩ y = −5 x 2 + 2u1
1 = −3x1 + u ⎧x ⎨ ⎩ y1 = x1
又因为 y1 = u1 , 所以
和 ⎨
1 = −3 x1 + u ⎧x ⎨ 2 = x1 − 5 x 2 ⎩x y = 2 x1 − 5 x 2
由此得到的 d 就是状态空间实现中的直接转移项 D 。 1.6 在例 1.2.2 处理一般传递函数的状态空间实现过程中,采用了如图 1.12 的串联分解, 试问:若将图 1.12 中的两个环节前后调换,则对结果有何影响? 答: 将图 1.12 中的两个环节调换后 y a(s)
5
1.10
已知单输入单输出时不变系统的微分方程为:
(t ) + 3 y (t ) = u ( t ) + 6u ( t ) + 8u ( t ) y (t ) + 4 y
试求:(1)建立此系统状态空间模型的对角线标准形; (2)根据所建立的对角线标准形求系统的传递函数。 答: (1)由微分方程可得:
s 2 + 6s + 8 2s + 5 G(s) = 2 = 1+ 2 s + 4s + 3 s + 4s + 3
记
G 1 (s) =
其中,
c c 2s + 5 2s + 5 = = 1 + 2 , s + 4 s + 3 ( s + 1)( s + 3) s + 1 s + 3
《现代控制理论》刘豹著(第3版)课后习题答案

第一章习题答案1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x C C L L R L L R x x x 。
1-5系统的动态特性由下列微分方程描述u u u y y y y 23375)2(......++=+++列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡321321321132100573100010x x x y u x x x x x x 。
相应的模拟结构图如下:573⎰⎰⎰uy+++---31x 2x 3x 211-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡432143214321313310411100000020*********x x x x y u x x x x x x x x1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W )1)(2)(3()3(2)3(2+++=+++=-s s s s s s A sI()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=--)2)(1(150)3()3(2033)1)(2)(3(1)(21s s s s s s s s s s s s A sI ()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=-=-)3)(12()3()3()1)(2)(3(1210)2)(1(150)3()3(2033)1)(2)(3(1)()(21s s s s s s s s s s s s s s s s s s s s B A sI s W ux[])1)(2()12()1)(2)(3(1)3)(12()3()3(100)()(1+++=+++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++=-=-s s s s s s s s s s s B A sI C s W uy 1-9将下列状态空间表达式化成约旦标准型(并联分解)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x (2)解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 1,332,1==λλ当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得 3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101201011T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-1102112101T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-4325183572131102112101B T⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=302413101201011110021CT约旦标准型x ~y ux ~x ~⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=302413432518100030013 1-12 已知差分方程为)(3)1(2)(2)1(3)2(k u k u k y k y k y ++=++++试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1:21112332)(2+++=+++=z z z z z z W)(11)(2001)1(k u k x k x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=+ [])(11)(k x k y =解法2:)(2)(3)()(3)(2)1()()1(2121221k x k x k y u k x k x k x k x k x +=+--=+=+ [])(23)()(10)(3210)1(k x k y k u k x k x =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=+ 求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡=-15041011321010111AT T [][]13101123-=⎥⎦⎤⎢⎣⎡-=CT 所以,状态空间表达式为[])(13)()(11)(1504)1(k z k y k u k z k z -=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡---=+第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论课后习题答案

前言本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答,可帮助同学学习和理解教材的内容。
由于习题数量较多,难易程度不同,虽然主要对象是研究型大学自动化专业本科学生,但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答;第4、7 章由井元伟教授组织编选和解答,第1、2章由郑艳副教授组织编选和解答。
由于时间比较仓促,可能存在错误,请读者批评、指正。
另外有些题目解法和答案并不唯一,这里一般只给出一种解法和答案。
编者 2005年5月第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
(完整word版)现代控制理论习题解答

(完整word版)现代控制理论习题解答《现代控制理论》第1章习题解答1.1 线性定常系统和线性时变系统的区别何在?答:线性系统的状态空间模型为:xAx Bu y Cx Du=+=+&线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和D 中的各分量均为常数,⽽对线性时变系统,其系数矩阵A ,B ,C 和D 中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的⼀类系统,⽽线性时变系统的参数则随时间的变化⽽变化。
1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别?答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪⼏种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对⾓线标准型。
对于n 阶传递函数1212101110()n n n n n n n b s b s b s b G s d s a s a s a ------++++=+++++L L ,分别有⑴能控标准型: []012101210100000100000101n n n xx u a a a a y b b b b x du---=+??----????=+LL &M M M O M M L LLb a b y xdu ---?--=-+?????-????=+??L L &%%L M M M M M M L %L ⑶对⾓线标准型: []1212001001001n n p p x x u p y c c c x du=+??????=+?L L &M M O M M L L 式中的12,,,n p p p L 和12,,,n c c c L 可由下式给出,12121012111012()n n n n n n n n nb s b s b s bc c c G sd d s a s a s a s p s p s p ------++++=+=++++++++---L L L 能控标准型的特点:状态矩阵的最后⼀⾏由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分⼦多项式系数,输⼊矩阵中的元素除了最后⼀个元素是1外,其余全为0。
《现代控制理论》课后习题全部答案(最完整打印版)
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
刘豹 现代控制理论 习题解答

天津大学刘豹主编《现代控制理论》习题解答R O n e i (李荣辉)完成,仅供参考非卖品
2007.04.03
NUAA 李荣辉
李 荣
辉数字签名人 李 荣辉DN :cn=李 荣辉,c=<无
>,o=NUAA ,ou=NUAA ,
email=ROnei@126.
com 原因:我是该文档的作
者
日期:2007.04.03
21:28:51 +08'00'
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品
R O n e i (李荣辉)完成,仅供参考非卖品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《现代控制理论》第1章习题解答1.1 线性定常系统和线性时变系统的区别何在? 答:线性系统的状态空间模型为:x Ax Buy Cx Du=+=+线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和D 中的各分量均为常数,而对线性时变系统,其系数矩阵A ,B ,C 和D 中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别? 答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于n 阶传递函数1212101110()n n n n n n n b s b s b s b G s d s a s a s a ------++++=+++++,分别有⑴ 能控标准型: []012101210100000100000101n n n x x u a a a a y b b b b x du---⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪----⎣⎦⎣⎦⎪=+⎪⎩⑵ 能观标准型: []00112211000100010001001n n n b a b a x a x u b a b y x du ---⎧-⎡⎤⎡⎤⎪⎢⎥⎢⎥-⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=-+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪-⎣⎦⎣⎦⎪=+⎪⎩ ⑶ 对角线标准型: []1212001001001n n p px x u p y c c c x du⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎪=+⎩ 式中的12,,,n p p p 和12,,,n c c c 可由下式给出,12121012111012()n n n n nn n n nb s b s b s bc c c G sd d s a s a s a s p s p s p ------++++=+=++++++++--- 能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1外,其余全为0。
能观标准型的特点:能控标准型的对偶形式。
对角线标准型的特点:状态矩阵是对角型矩阵。
1.4 对于同一个系统,状态变量的选择是否惟一?答:对于同一个系统,状态变量的选择不是惟一的,状态变量的不同选择导致不同的状态空间模型。
1.5 单输入单输出系统的传递函数在什么情况下,其状态空间实现中的直接转移项D 不等于零,其参数如何确定?答: 当传递函数)(s G 的分母与分子的阶次相同时,其状态空间实现中的直接转移项D 不等于零。
转移项D 的确定:化简下述分母与分子阶次相同的传递函数1110111)(a s a s a s b s b s b s b s G n n nn n n n ++++++++=---- 可得:d a s a s a s c s c s c s G n n n n n ++++++++=----01110111)( 由此得到的d 就是状态空间实现中的直接转移项D 。
1.6 在例1.2.2处理一般传递函数的状态空间实现过程中,采用了如图1.12的串联分解,试问:若将图1.12中的两个环节前后调换,则对结果有何影响?答: 将图1.12中的两个环节调换后的系统方块图为:图中,3221011()a s s a s a s a =+++,2210()b s b s b s b =++。
由于3s y -相当于对y 作3次积分,故1()y m a s =可用如下的状态变量图表示:因为2s b 相当于对b 作2次微分,故()mb s u=可用如下的状态变量图表示:因此,两个环节调换后的系统状态变量图为进一步简化,可得系统状态变量图为u取3y x =,2y x =,1y x =,可以得到两个环节调换后的系统的状态空间模型为001122001001[001]a b x a x b ua b y x-⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦=两个环节调换前的状态空间模型是:012012010000101[]x x u a a a y b b b x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦=显然,调换前后的状态空间实现是互为对偶的。
1.7 已知系统的传递函数2()6()56Y s s U s s s +=++ 试求其状态空间实现的能控标准形和能观标准形。
答: 系统的能控标准形为:[]01065161x x u y x⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥--⎣⎦⎣⎦⎨⎪=⎩系统的能观标准形为:[]06615101x x u y x⎧-⎡⎤⎡⎤=+⎪⎢⎥⎢⎥-⎣⎦⎣⎦⎨⎪=⎩1.8 考虑由下图描述的二阶水槽装置,图1.18二阶水槽装置图该装置可以看成是由两个环节串联构成的系统,它的方块图是:图1.19 二阶水槽系统的方块图试确定其状态空间模型。
答:图1.19中两个环节的状态空间模型分别为:⎩⎨⎧=+-=2222222x y u b x a x和 ⎩⎨⎧=+-=11111x y u b x a x又因为21x u u +=,所以1121111u b x b x a x++-= 22222u b x a x+-= 1x y =进一步将其写成向量矩阵的形式,可得:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21212121121000u u b b x x a b a x x []⎥⎦⎤⎢⎣⎡=2101x x y1.9 考虑以下单输入单输出系统:61166+++=y y y y u试求该系统状态空间模型的对角线标准形。
答: 由微分方程可得:321)3)(2)(1(661166)(32123+++++=+++=+++=s c s c s c s s s s s s s G 其中,3)3)(2(6lim11=++=-→s s c s6)3)(1(6lim22-=++=-→s s c s3)2)(1(6lim 33=++=-→s s c s故该系统状态空间模型的对角线标准形为:u x x x x x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111300020001321321 []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321363x x x y1.10 已知单输入单输出时不变系统的微分方程为:()4()3()()6()8()++=++y t y t y t u t u t u t试求:(1)建立此系统状态空间模型的对角线标准形;(2)根据所建立的对角线标准形求系统的传递函数。
答: (1)由微分方程可得:345213486)(222++++=++++=s s s s s s s s G记12122525()(1)(3)1343c c s s G s s s s s s s ++===+++++++, 其中,23352lim11=++=-→s s c s ,21152lim 32=++=-→s s c s 。
从输入通道直接到输出通道上的放大系数1=d ,由此可得:u x x x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡1130012121 u x x y +⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=212123 (2) 由于⎥⎦⎤⎢⎣⎡--=3001A ,⎥⎦⎤⎢⎣⎡=11B ,⎥⎦⎤⎢⎣⎡=2123C ,1=D ,因此 1()()3011311011(1)(2)221.50.5113G s C sI A B Ds s s s s s -=-++⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦=++++ 1.11 已知系统的传递函数为25()(3)(5)+=++s G s s s(1) 采用串联分解方式,给出其状态空间模型,并画出对应的状态变量图; (2) 采用并联分解方式,给出其状态空间模型,并画出对应的状态变量图。
答:(1)将()G s 重新写成下述形式:125()35s G s s s +=⋅++ 每一个环节的状态空间模型分别为:⎩⎨⎧=+-=11113x y u x x和 ⎩⎨⎧+-=+-=12122255u x y u x x又因为11y u =, 所以⎩⎨⎧-=+-=2121153x x x u x x2152x x y -=因此,若采用串联分解方式,则系统的状态空间模型为:u x x x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡0151032121 []⎥⎦⎤⎢⎣⎡-=2152x x y对应的状态变量图为:(2)将()G s 重新写成下述形式:0.5 2.5()35S G s s -=+++ 每一个环节的状态空间模型分别为:111130.5x x uy x =--⎧⎨=⎩ ⎩⎨⎧=+-=22225.25x y u x x又由于⎩⎨⎧+-=--=u x x u x x5.255.032211 1212y y y x x =+=+⎰52x x -1x ⎰31x -因此,若采用并联分解方式,则系统的状态空间模型为:u x x x x ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡5.25.050032121 []⎥⎦⎤⎢⎣⎡=2111x x y对应的状态变量图为:1.12 已知系统的状态空间模型为,x Ax Bu y Cx =+=,写出该系统的特征多项式和传递函数矩阵。
答: 系统的特征多项式为det()sI A -, 传递函数为1()()G s C sI A B -=-。
1.13 一个传递函数的状态空间实现是否惟一?由状态空间模型导出的传递函数是否惟一?答: 一个传递函数的状态空间实现不惟一;而由状态空间模型导出的传递函数是惟一的。
1.14 已知系统的状态空间模型为Cx y Bu Ax x=+=, ,写出其对偶状态空间模型。
答: 其对偶状态空间模型为:⎩⎨⎧=+=xB y uC x A x T T T ~~~ 1.15 两个对偶状态空间模型之间的特征多项式和传递函数有什么关系?答: 对于互为对偶的 ⎩⎨⎧=+=Cxy Bu Ax x与⎩⎨⎧=+=xB y uC x A x T T T ~~~ ,它们对应的特征多项式分别为det()sI A -和det()T sI A -。
由于一个矩阵和其装置的特征多项式是相同的,故互为对偶的两个状态空间模型具有相同的特征多项式。
它们对应的传递函数分别为--5⎰1x ⎰2x x11()()()det()C sI A BG s C sI A B sI A *--=-=-12()()()det()T T TTT TT B sI A C G s B sI A C sI A *--=-=-由于det()det()TsI A sI A -=-,()()()TT T T C sI A BB sI AC **-=-,故对偶状态空间模型之间的传递函数关系为12()()TG s G s =,即互为转置。
