材料力学基础—结构力学弯矩图
材料力学4-弯矩图剪力图 PPT课件
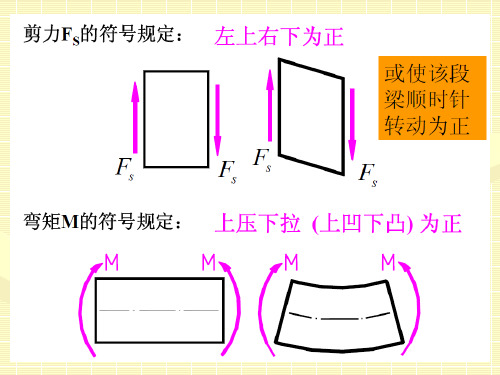
梁上最大弯矩可能发生在Fs(x) = 0 的截面上或梁段边界 的截面上。最大剪力发生在全梁或梁段的界面。
在集中力作用处剪力图有突变,其突变值等于集中力的 值。弯矩图的相应处形成尖角。
在集中力偶作用处弯矩图有突变,其突变值等于集中力 偶的值,但剪力图无变化。
矩就等于梁在各项荷载单独作用下同一 横截面上弯矩的代数和。
叠加原理:由几个外力共同作用时所引起的某一参数 (内力、应力、位移),就等于每个外力单独作用时 所引起的该参数值的代数和。
• 5.4 内力与分布荷载间的关系及其应用
剪力图上某点处的切线斜率 等于该点处荷载集度的大小
弯矩图上某点处的切线斜率 等于该点处剪力的大小。
q(x)、Fs (x)图、M(x)图三者间的关系
梁上有向下的均布荷载,即 q(x) < 0 Fs (x)图为一向右下方倾斜的 直线 M(x)图为一向下凸的二次抛 物线
• 5.3 剪力方程与弯矩方程 剪力图与弯矩图
一、剪力和弯矩方程: 剪力和弯矩沿梁长度方向的表达式,表示的是剪力和
弯矩沿轴线长度方向的分布情况
二、剪力图和弯矩图 以X轴表示横截面位置,以纵坐标表示相应截面
上的剪力Fs 、弯矩M,称为剪力图、弯矩图。 剪力图为正值画在x 轴上侧,负值画在x 轴下侧 弯矩图为正值画在x 轴下侧,负值画在x 轴上侧
作剪力图和弯矩图的几条规律
梁上集中力作用处左、右两侧横截面上,剪 力值(图)有突变,其突变值等于集中力的 数值。在此处弯矩图则形成一个尖角。
梁上集中力偶作用处左、右两侧横截面上 的弯矩值(图)也有突变,其突变值等于 集中力偶矩的数值。但在此处剪力图没有 变化。
作剪力图和弯矩图的几条规律
梁上的最大剪力发生在全梁或各梁段的边界 截面处;梁上的最大弯矩发生在全梁或各梁 段的边界截面,或Fs = 0的截面处。
经典材料力学结构力学弯矩图课件
L
L
(25)
(2(53)5)
L
L
L
L
(24) (24)
qa 2
qa
qa
1
qa
q 2q
8
1 qa2 2
a a
(26) ((2366))
aa
2L2L
qa
q
与杆件轴 线相切
qa
qa 2
q
qa 2 qa2
1 qa2 2
a
(27)
(37)
a/2
a/2பைடு நூலகம்
2a
q
1 qa2
2
1 qa2 2
q
qa 2
a
a
(28)
(38)
利用L反对称性q 作LM/图4 :
(15)1 M 2q
qq L
L
(L1211M)
LL(7)
P=qL L PP==qqLL
2PL L L PP
PL L L PL
(((22166PP)0))
L
L
从右向左作M图:
LL
LL (2) LL
PL ((66)) q
P=qL
q qq L q
(9)
PL
PP==qqLL
PL 2 3PL 2
M=PL
300 P
2qa2
2a
4a
用“局部悬臂梁法”直接作M 图,P力通过截面弯矩为0
L/2
PL
2
PL 2
PL 2
P
L/2
3PL 3PL 2
L
(19)
(27)
PL
PL
L/2
L/2
(20)
(28)
q
结构力学必会100种结构弯矩图,一定要收藏!

结构力学必会100种结构弯矩图,一定要收藏!
素材:筑龙论坛如有侵权,请联系删除
实际工作中,有时候要对软件(MIDAS、SAP2000、PKPM)的计算结果进行判断,那就要对结构的弯矩和剪力图有个大概的判断。
下面总结各种结构弯矩图的绘制及图例:
一、方法步骤1、确定支反力的大小和方向(一般情况心算即可计算出支反力)●悬臂式刚架不必先求支反力;●简支式刚架取整体为分离体求反力;●求三铰式刚架的水平反力以中间铰的某一边为分离体;●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、观察检验M图的正确性1、观察各个关键点和梁段的M图特点是否相符●铰心的弯矩一定为零;●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;●集中力作用点的弯矩有折角;●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有节点的杆端弯矩必须符合平衡特点。
各种结构弯矩图如下:
(手机横屏显示更清楚)【投稿及合作咨询】。
材料力学结构力学弯矩图 ppt课件

q2qP
MM==PqLPL2=qL
L
LL L L/2
(((1190))()1)
P作用下的M图: qL2
2PL
qP
PL
q M=qL2 q
P=qL
P=qL
LL
L
P=2qL
LL
L
((21)1()2)
P作用下的M图:
(((313) 2))
P作用下的M图: 4qL2
/2 L/2
L
M=qL2 q
q作用q下的M图:
30
3
30
(16)
(17)
先计算支反力,再作M图: 直接作M图:
Fa
qa2
1 Fa 3
1F
3
9 qa2 8
(18)
直接作M图:
10
60
20
(19)
CD段直接作M图, AC段采用叠加法:
qa2
1 qa2 2
相切
(20)
力偶只影响BD段,直 接用叠加法作M图:
qa2 qa2
ppt课件
(21)
力偶只影响BC段,力
L
MM(8)
P
L/2
P
LL L
LL L
(((888()))4)
利用反L 对称性q 作LM/4图:
(15)1 M 2q
qq L
L
LLp((Lp7121t)1课M)件 L
P=qL PP==qqLL
2PL L L PP
PL L L PL
(((22616PP) 0))
从LL 右L向LL左(2作) MLL图L :
(6)
1.6 0.6kN
1.6 2.4 0.1
1.4kN
材料力学4-弯矩图剪力图
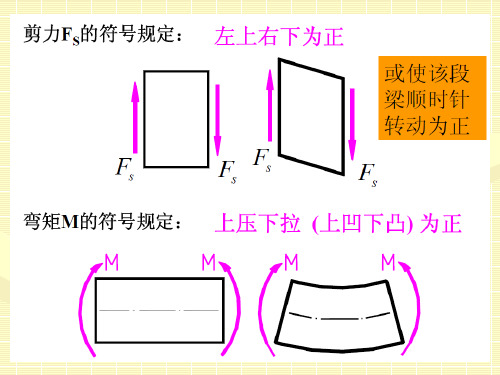
由(2),(4)式可知, AC,CB 两段梁的弯矩 图各是一条斜直线
作剪力图和弯矩图的几条规律
取梁的左端点为坐标原点,x 轴向右为正;剪 力图向上为正;弯矩图向下为正。
以集中力、集中力偶作用处,分布荷载开始或 结束处,及支座截面处为界点将梁分段。分段 写出剪力方程和弯矩方程,然后绘出剪力图和 弯矩图。
例2 图a 所示坐标原点取在梁 的左端,写出梁的剪力 方程和弯矩方程 :
根据方程画剪力图、弯矩图(注意正负号画的方向)
例3 图a 所示悬臂梁,在全梁上受集度为q 的均布荷 载作用 。试作此梁的的剪力图和弯矩图。
解:为计算方便,将坐标原 点取在梁的右端,得梁的剪 力方程和弯矩方程:
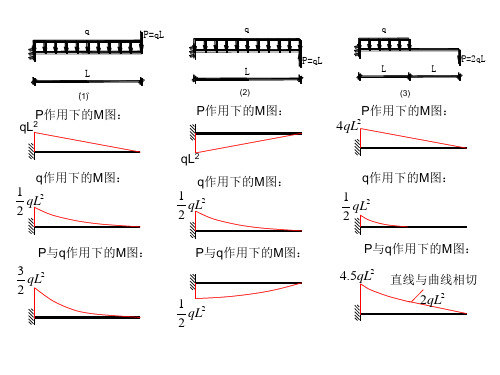
梁上最大弯矩可能发生在Fs(x) = 0 的截面上或梁段边界 的截面上。最大剪力发生在全梁或梁段的界面。 在集中力作用处剪力图有突变,其突变值等于集中力的 值。弯矩图的相应处形成尖角。
在集中力偶作用处弯矩图有突变,其突变值等于集中力 偶的值,但剪力图无变化。
叠加原理:当梁上受几项荷载共同作用时,某一横 截面上的弯矩就等于梁在各项荷载单独作用下同一 横截面上弯矩的代数和。
例4 图a 所示的简支梁,在全梁上受集度为q的均布 荷载作用。试作此梁的的剪力图和弯矩图。
解:由Σy =0求得两个支反力 取距左端为x的任意横截面。写出剪力方程和弯矩方程。
由式(1)可知,剪力图为一倾斜直线。由
由式(2)知,弯矩图为一条二次抛物线。由
由(1),(3)两 式可知,AC,CB 两段梁的剪力图各 是一条平行于 x轴 的直线。
• 5.3 剪力方程与弯矩方程 剪力图与弯矩图
一、剪力和弯矩方程: 剪力和弯矩沿梁长度方向的表达式,表示的是剪力和 弯矩沿轴线长度方向的分布情况
经典__材料力学结构力学弯矩图

a a/2 L
Pa
Pa
2
2
Pa Pa
2 Pa
P
2
P
2Pa
a
a
((4335) )
三 、 简 支 式 刚 架
15qa2 4
21qa2 qa8 2qa2
PL
P
PL
L ( (4346) )
qa2
q
qa2
支座B无反力,AB段无变形 不用计算支反力, 直接作M图
计算A支座水平反力, 即可作M图
a
2m 2m
1 qa 2 2
q
qa 2
a
a
( 2 8 )
(38)
10010kN/m
P=40kN
60
100
80 40kN
2m 2m 2m 2m (30)
(39)
2m 2m
qL2+2cqoLs 22 α
qL2
2cos2αq
L
L
(33)
(40)
q
aa
q qa2 2
2
qa
qa
qa2
2
a
a
((4314))
15 3
3
计算A处支反力为0,直接作 M图
Pa/2 P Pa/2
A
a a/2 a/2
(55)
(65)
q=20kN/m
A
(54)
(47)
B、A处无水平支反力,直接 作M图
q=20kN/m
25kN.m
25kN.m q
65kN.m 50kN50kN
25kN.m 25kN.m
0.5m
0.5m
(48)
B、A处无水平支反力,AC、 DB无弯曲变形,EC、ED也 无弯曲变形
结构力学中必须掌握的弯矩图

作为一名又土又木的工程师,离不开弯矩图,现在把它汇总起来,用以怀念当年的苦逼生活……
各种结构弯矩图的绘制及图例:
一、?方法步骤
1、确定支反力的大小和方向(一般情况心算即可计算出支反力)
●悬臂式刚架不必先求支反力;
●简支式刚架取整体为分离体求反力;
●求三铰式刚架的水平反力以中间铰C的某一边为分离体;
●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;
●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、?观察检验M图的正确性
1、观察各个关键点和梁段的M图特点是否相符
●铰心的弯矩一定为零;
●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;
●集中力作用点的弯矩有折角;
●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;
2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有结点的杆端弯矩必须符合平衡特点。
各种结构弯矩图例如下:。
结构力学必会100种结构弯矩图,一定要收藏!

结构力学必会100种结构弯矩图,一定要收藏!
素材:筑龙论坛
如有侵权,请联系删除
实际工作中,有时候要对软件(MIDAS、SAP2000、PKPM)的计算结果进行判断,那就要对结构的弯矩和剪力图有个大概的判断。
下面总结各种结构弯矩图的绘制及图例:
一、方法步骤
1、确定支反力的大小和方向(一般情况心算即可计算出支反力)
●悬臂式刚架不必先求支反力;
●简支式刚架取整体为分离体求反力;
●求三铰式刚架的水平反力以中间铰的某一边为分离体;
●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;
●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、观察检验M图的正确性
1、观察各个关键点和梁段的M图特点是否相符
●铰心的弯矩一定为零;
●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;
●集中力作用点的弯矩有折角;
●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;
2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有节点的杆端弯矩必须符合平衡特点。
各种结构弯矩图如下:
(手机横屏显示更清楚)
【投稿及合作咨询】。
结构力学必会100种结构弯矩图,一定要收藏!

结构力学必会100种结构弯矩图,一定要收藏!
素材:筑龙论坛
如有侵权,请联系删除
实际工作中,有时候要对软件(MIDAS、SAP2000、PKPM)的计算结果进行判断,那就要对结构的弯矩和剪力图有个大概的判断。
下面总结各种结构弯矩图的绘制及图例:
一、方法步骤
1、确定支反力的大小和方向(一般情况心算即可计算出支反力)
●悬臂式刚架不必先求支反力;
●简支式刚架取整体为分离体求反力;
●求三铰式刚架的水平反力以中间铰的某一边为分离体;
●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;
●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、观察检验M图的正确性
1、观察各个关键点和梁段的M图特点是否相符
●铰心的弯矩一定为零;
●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;
●集中力作用点的弯矩有折角;
●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;
2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有节点的杆端弯矩必须符合平衡特点。
各种结构弯矩图如下:
(手机横屏显示更清楚)
【投稿及合作咨询】。
《材料力学》课件4-2梁的剪力和弯矩.剪力图和弯矩图
F
B
FCs F FCs F
M C Fl M C Fl
l
l
FCs
MA FA
A
M C 2Fl Fl 0
FDs F
F
B
l
FCs
C
MA
MC
MC 2 Fl
D
MD 0
FDs
F
D
C
l
MD
B
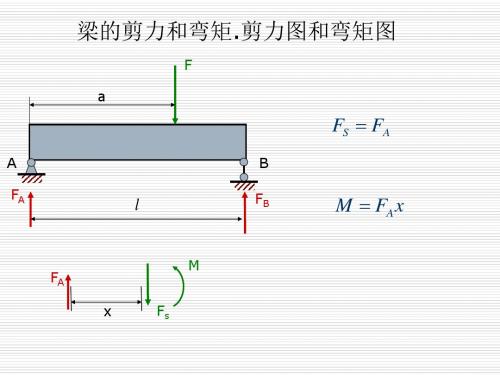
截开后取左边为示力对象:
向上的外力引起正剪力,向下的外力引起负剪力;
向上的外力引起正弯矩,向下的外力引起负弯矩;
图示外伸梁,,试作剪力图和弯矩图.
10kN m
X2
40 kN m
A
35kN
B
FS x1 20kN
M x1 20 x1
0 x1 1 0 x1 1
1m
15
4m
2.5
25kN
FS x2 25 10 x2
25
2 x2 M x2 25 x2 10 2
突变,顺下逆上,大小与M 同,FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN
D
4.5kN m
A
2kN m
B E
C
FA 10kN 1m 2m
2m
FB 2kN 1m
7
kN
3 3
x 1.56
2 2
kNm
2.44
2
例题
4.10
4kN m
6kN
2kN m
1m
1m
2m
4.5 kN 1.5
x
l
FB
ql FS qx 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q 2 q P
MM == P q L P L 2 =qL
L L L L L/2
( ( (1 19 0 )) ( ) 1)
P作用下的M图: qL2
2PL
qP
PL
qM=qL 2 q P=qL
LL
P=qL L
P=2qL
LL
L
( (21)1 () 2)
P作用下的M图:
( (( 31 3 )2 ))
先计算支反M= 力qL 2,再q作MP 图=q:L
(15) 1 M
(13)
2
L
q q qL
( L 1211 M)
L L (7)
P=qL
1 qL LP P= =q qL L 4
L M M L= =q qL L 142 2( qM L12 2q q )L81LqLP P= 2=q qL L
L L (8)L L
P作用下的M图:
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图:
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图:
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图:
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图:
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q LL L q q
(7)
L L L L L L
L ( ( (77 7 )) )
利(1用4)对称性2P作M图M= :L P/ L4
1 2
qL L 2
81(1 q2 2 L0 P P) 2 12LqL
2
M M= =P PL L
L L
L L
L
L
( ( M 2 2 = ) ) qL 2 qq
一 、 梁
P=qL
q
与杆件轴 线相切
q L 2 2
L
( (2 32 0) )
用“局部悬臂梁法”直接作M图:用“局部悬臂梁法”直接作M图:
从L L右L 向L L 左(2 作)ML L 图L:
PL ( (6 6) ) q
P=qL
q 1 qL 2
L2
L
M M(8)
P
q q q Lq
(9)
PL
P P= =q qL L
L LL
P L LL
L/2
L L L
L
( ((8 8 8( ) ) )4)
利用反L对称性q作ML/4 图:
( ( L 9 9) )((5 9) )
P=qL
5qL 2 L/432
q
qL 2 2
3qL 2 2
q P=qL
L/2
5qL 2
qL2M=qL 232
LqL 22
L
8
(12)
L
L/4
(24)
(25)
(( 21 65 ))
所对应简支梁为:
q
q
q
L/2
qL2 8 L
(13)
qL2 8 L
(14)
5qL 2 L/432
qL 2 8
L
5qL 2 32
L
L
( (3 P 3) ) 2P 2
(( 51 )(2 5) q q )
从右向左L作ML 图/2:
5 qL 2 2
L L ( ( ( 231 5 5) ) q)LM2 L L81 qL 2
2PL LL P L LLPL
P P ( (( 2 2 616 P )P 0) )
2PL
P q PL
L L
L L
(( 1( 2 05 ) ))
叠加法作M图: 1.先考虑力偶作用
2.再叠加M P的q作用
PL
2PL L
L
L 14(P8L) L
(5)
qP 2P
P=2qL LL L LL
(1( ( 13 6 )) )
(12)
先计算支反力,再作M图: 先计算支反力,再作M图:
q P 2P
P L 2
P L 2
P
L L/2 L/2
3 P L 3 P L 2
L (19) (27)
P L
P L
L/2 L/2 (20)
(28)
q
L
3 P L 3 P L
L
2
(19)
用“局部悬臂梁法”直接作M 图,P力通过截面弯矩为0
P L
P L
P L
(( 22 91 ) )
L/2 L/2
(20)
用“局部悬臂梁法”直接作M 图
P=qL
4P 3
4 L3
PL
(9 LL )53 PL
5P L3
(6)
1.6 0.6k N
1.6 2.4 0.1
1.4k N
(13q )M
作M图,只需计算C P=qL 截面弯L矩 L L
1 Fl ( ( 1 8 1 ) ) 2
M=q q L 2 q
(14)
P P = = q q L L
作M图,只需计算C
q作q用下的M图:
1 qL 2 L L L
2
(6)
L/2
P与q作用下的M图:
4.5qL2L 直线q 与曲L线/4相切P=qL (15) 2 qL 2
L
(9)
L L/2
( (1 1) ) q P
P
P=qL
LL L
( (( 41 )4 1 ) )
P P
从右L L向左作P PML L 图:
PL
( (P4 4 q) )L
L/4
3a
a
2a
2a a a
1 5 q a2 1 6 q a2
(18)
用“局部悬臂梁法”直接作M 图,P力通过截面以上部分还 二 、 有悬 力臂 偶式 ,刚 所架 以弯矩不为0:
3 P L 2
P L 2
M=P L
300 P
2a
2 q a2 4a
用“局部悬臂梁法”直接作M 图,P力通过截面弯矩为0
P L 2
15 qa 2 16 qa 2
4 a
1 q4a 2
8
(11)
qL 2 2
qL2 2
L
L
LL L
斜梁各截面弯矩值与所对应简支梁一样(8 ,)作M图:
L (9)
(7)
q
q
pL 2P M=PL
qL2 L 8 L pL
L (10)
(13)
q
qL2 2
qL2
8 qL 2
L
L8
(11) (14)
5qL 2 2
截面弯L矩
L
1
(1 92 ))2
L
qa 21
qa
2
8
曲线在B点与水平线相切
(15)
不用计算支反力, 可快速作M图
30
30
(16)
(17)
先计算支反力,再作M图: 直接作M图:
Fa
qa 2
1 Fa 3
1F
3
9 qa 2 8
(18)
直接作M图:
10
60
20
(19)
CD段直接作M图, AC段采用叠加法:
a aa
a
2 a
a
( 1 7 )
m
q
m
P = q a M = q a 2
P = 2 q a
m
q
3 a
a 2 a
2 a a a 2 a
(23) ( 1 8 )
从附属部分开始,用“局部悬臂梁法”直接作M图:
1 q 3a 2
8
8.5qa2
8 qa 2
4 qa 2 相切
二 、 悬 臂 式 刚 架
M = P L
qa 2
1 qa 2 2
相切
(20)
力偶只影响BD段,直 接用叠加法作M图:
qa 2 qa 2
(21)
力偶只影响BC段,力
只影响AC段,作M图:
qa 2
qa 2
2
不与水平线相切
mq = 1 0 a
2 m
6 0
1 5
aa a
2 m
2 m
2 m
( 1 6 )
(22)
从附属部分开始,直接作M图:
m
q
M = 2 q a
