有源低通滤波电路
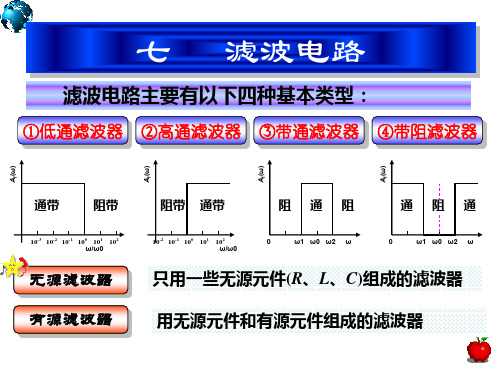
滤波电路主要有以下四种基本类型
U jC Ui 1 R jC 1 Ui 1 jRC
R
R
R
f
1
+
U
o
U
i
C
传递函数
Aup Rf 1 A 1 R 1 jRC 1 1 j
(1)当ω<<ω0时,Af(ω)/Af=1, 即20lg[Af(ω)/Af]=0dB (2)当ω=ω0时,Af(ω)/Af= 1 / 2 幅值下降了3dB,ω0是电路的通 带截止角频率
Q
1 2
-40dB/十倍频
10-3 0.01 0.1
1
10
ω/ω0
(3)当ω=10ω0时, Af ( ) 1 1 Af 992 2 102 100 说明阻带区内Af(ω0)以每十倍频 40dB(100倍)的速率衰减。
简单二阶低通滤波 电路的幅频特性
由幅频特性可见ω>>ω0时衰减 的斜率为-40dB/十倍频。但在 ω0附近,其幅频特性与理想的 低通滤波特性相差较大。
0 -3dB
20 lg
Af ( ) / dB Af
-40dB/十倍 频
0.1 0.37 1
10
ω/ω0
改进
R
1
R
U
2
f
将电容C1的接 地端改接到集成 运放的输出端。
R U R
M
U
oUBiblioteka +i
C
1
C
只要参数合适
R
1
R
U
2
f
(1)该电路在f0附近形 成正反馈,不致造 成自激振荡,使f0附 近的电压放大倍数 得到提高。
一阶低通有源滤波电路的截止频率fh

一阶低通有源滤波电路的截止频率fh在电子电路中,滤波器是一种常用的电路元件,它能够通过选择性地传递或阻止特定频率范围内的信号。
而有源滤波电路则是一种利用有源元件(例如运放)来实现的滤波器,具有较好的增益和频率特性。
其中,一阶低通有源滤波电路的截止频率fh是一个重要的参数,它决定了电路对高频信号的抑制能力。
在本文中,我们将深入探讨一阶低通有源滤波电路的截止频率fh,并探讨其在电路设计和应用中的重要性。
1. 一阶低通有源滤波电路的原理和结构1.1 电压跟随器1.2 电容C和电阻R构成的RC低通滤波器在一阶低通有源滤波电路中,常见的电路结构包括由电压跟随器和电容C、电阻R构成的RC低通滤波器。
电压跟随器能够实现输入电压的跟随和转移,并提供给RC滤波器更好的输入阻抗,从而改善电路的性能。
而RC低通滤波器则通过电容和电阻的组合,实现对低频信号通路和高频信号阻断。
2. 一阶低通有源滤波电路的截止频率fh及其计算公式2.1 截止频率fh概念解释2.2 截止频率fh的计算公式在一阶低通有源滤波电路中,截止频率fh是一个十分重要的参数,它代表了电路对高频信号的抑制能力。
截止频率fh通常是通过电容C和电阻R的数值来计算的,具体公式为fh=1/2πRC。
通过这个公式,可以清晰地计算出截止频率fh与电容和电阻的关系,从而方便电路设计和性能调整。
3. 一阶低通有源滤波电路的应用和调试3.1 天然频率和调整方法3.2 应用案例分析在实际电路设计和应用中,一阶低通有源滤波电路具有广泛的应用场景。
而在调试过程中,需要特别关注电路的天然频率以及调整方法,以确保电路能够稳定地工作。
通过应用案例的分析,可以更好地理解一阶低通有源滤波电路在实际应用中的优劣势和调试技巧。
4. 结语在本文中,我们对一阶低通有源滤波电路的截止频率fh进行了深入的探讨,从其原理结构到计算公式和应用案例,全面展现了该参数在电路设计和应用中的重要性。
通过深入理解截止频率fh,我们可以更好地设计和调试有源滤波电路,提高电路的性能和稳定性。
简单二阶有源低通滤波器电路及幅频特性

简单二阶有源低通滤波器电路及幅频特性为了使输出电压在高频段以更快的速率下降,以改善滤波效果,再加一节RCo(1)通带增益当f=0时,各电容器可视为开路,通带内的增益为低通滤波环节,称为二阶有源滤波电路。
它比一阶低通滤波器的滤波效果更好二阶LPF的电路图如图6所示,幅频特性曲线如图7所示。
1-(2)二阶低通有源滤波器传递函数根据图8-2.06可以写出丄“盘斗丄〕俯二一礎通常有,联立求解以上三式,可得滤波器的传递函数臥)—九…(3)通带截止频率将s 换成j 3,令3 0 = 2n f o=1/(RC)可得当f=fp时,上式分母的模="丿厶I VoZ与理想的二阶波特图相比,在超过fO以后,幅频特性以-40 dB/dec的速率下降,比一阶的下降快。
但在通带截止频率fp -fO之间幅频特性下降的还不够快。
摘要设计一种压控电压源型二阶有源低通滤波电路,并利用MultisimIO仿真软件对电路的频率特性、特征参量等进行了仿真分析,仿真结果与理论设计一致,为有源滤波器的电路设计提供了EDA手段和依据。
关键词二阶有源低通滤波器;电路设计自动化;仿真分析;MultisimIO滤波器是一种使用信号通过而同时抑制无用频率信号的电子装置,在信息处理、数据传送和抑制干扰等自动控制、通信及其它电子系统中应用广泛。
滤波一般可分为有源滤波和无源滤波,有源滤波可以使幅频特性比较陡峭,而无源滤波设计简单易行,但幅频特性不如有源滤波器,而且体积较大。
从滤波器阶数可分为一阶和高阶,阶数越高,幅频特性越陡峭。
高阶滤波器通常可由一阶和二阶滤波器级联而成。
采用集成运放构成的RC有源滤波器具有输入阻抗高,输出阻抗低,可提供一定增益,截止频率可调等特点。
压控电压源型二阶低通滤波电路是有源滤波电路的重要一种,适合作为多级放大器的级联。
本文根据实际要求设计一种压控电压源型二阶有源低通滤波电路,采用EDA仿真软件Multisim1O对压控电压源型二阶有源低通滤波电路进行仿真分析、调试,从而实现电路的优化设计。
有源低通滤波器的设计

有源低通滤波器的设计有源滤波器是一种使用有源元件(如运放)来构成的滤波器。
有源滤波器具有较低的输出阻抗和较高的增益,并且能够提供较大的增益和较低的失真。
有源低通滤波器是一种能够通过滤除高频信号而传递低频信号的滤波器。
它可以应用于音频信号处理、视频信号处理和通信系统中,用于去除噪音、改善信号品质等。
本文将介绍有源低通滤波器的设计原理和步骤,以供读者参考。
1.确定滤波器的截止频率:首先,根据需要滤除的高频信号范围,确定滤波器的截止频率。
截止频率是决定滤波器的性能的重要参数之一,它决定了滤波器在不同频率范围内的衰减特性。
2.选择合适的滤波器类型:根据应用场景和信号要求,选择合适的有源滤波器类型。
常见的有源滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
不同的滤波器类型具有不同的性能和设计要求,需要根据具体情况选择。
3.设计滤波器的电路结构:根据选择的滤波器类型和截止频率,设计滤波器的电路结构。
有源低通滤波器通常由运放、电阻和电容组成。
根据电路结构设计电容和电阻的数值,以满足滤波器的要求。
4.计算反馈电阻和输入电阻:根据电路结构和信号要求,计算滤波器的反馈电阻和输入电阻的数值。
反馈电阻决定了滤波器的增益和频率响应,输入电阻影响了滤波器的输入阻抗和信噪比。
5.选择适当的运放:根据滤波器的增益要求和频率响应,选择合适的运放器件。
不同的运放器件具有不同的增益、带宽和失真等特性,需要根据具体要求选择。
6.绘制电路图并进行仿真:根据设计的滤波器电路结构和参数,绘制电路图,并进行仿真分析。
通过仿真可评估滤波器的性能,如增益、相位延迟和截止频率等。
7.电路实现和调试:根据仿真结果,实现电路并进行调试。
调试过程中需要注意电路的稳定性和可靠性,同时还需要进行频率响应测试和输出波形观察,以验证设计结果。
总结:有源低通滤波器是一种常见的滤波器类型,其设计步骤包括确定截止频率、选择滤波器类型、设计电路结构、计算反馈电阻和输入电阻、选择适当的运放器件、绘制电路图并进行仿真分析,最后实现电路和调试。
低通有源滤波电路

低通有源滤波电路由集成运放与RC低通电路一起组成,可以提高通带电压放大倍数和带负载能力。
低通滤波器(LPF)最简单的低通滤波器由电阻和电容元件构成,实际上这是一个最简单的RC低通电路,一般称为无源低通滤波器。
该低通电路的电压放大倍数为:•当频率高于截止频率时,随着频率的升高,电压放大倍数将降低,因此电路具有“低通”的特性。
•这种无源RC低通滤波器的主要缺点是电压放大倍数低,由Au 的表达式可知,通带电压放大倍数只有l。
•同时带负载能力差,若在输出端并联一个负载电阻,除了使电压放大倍数降低以外,还将影响通带截止频率fo的值。
有源滤波电路

(a) 图6-12 【例6-2】电路图
(b)
Vo Vn VP 0
该电路在频率低时有输出,频率高时无输出,因此电路(a)是低通滤波器。
在电路(b)中,在频率低时无输出,频率高时有输出,因此电路(b)是 高通滤波器。
(2) 电路(a)的通带增益为
Avp 1
Rf R1
电路(b)的通带增益为 Avp
【例6-2】电路如图6-12所示。已知集成运放均为理想运放; (1)分别说明各电路是低通滤波器还是高通滤波器,简述理由; (2)分别求出各电路的通带增益。
解: (1)在电路(a)中,若输入电压频率趋于零,则C1和C2相当于开路,集成运放构成 电压跟随器, 输出电压为 Vo Vi 若输入电压频率趋于无穷大,则C1和C2相当于短路,输出电压为
通带宽度 B
品质因数
Q
1 3 Avf
Avf 1
Rf R1
f0 Q
通带电压增益
Avp
Avf 3 Avf
上限截止频率
f p2
B f0 2
B 下限截止频率 f p1 f 0 2
【例6-3】图6-13(a)所示电路中,R=796kΩ,C=0.01μF,R1=243kΩ,
6.2 有源滤波电路
6.2.1 6.2.2 6.2.3 6.2.4 有源低通滤波器 有源高通滤波电路 有源带通滤波电路 有源带阻滤波电路
6.2.1 有源低通滤波器
低通滤波器的主要技术指标如下: (1)通带增益Aup 通带增益是指滤波器在通频带内的电压放大倍数。理想的 LPF通带内的幅频特性曲线是平坦的,阻带内的电压放大倍数 为零,如图6-1中虚线所示。 (2)通带截止频率fp 截止频率是滤波器通带与阻带的界限频率。低通滤波器 的截止频率指随着工作频率的提高,滤波器的传递函数的模 下降到0.707Aup时所对应的频率。 (3)衰减速率 实际滤波器的通带与阻带之间称为过渡带,如图6-1所 示。过渡带越窄,说明滤波器的选择性越好。通常用滤波器 在通带外每十倍频衰减了多少来表示。
第五章(二)有源滤波电路

模 : A uf
Au
1
2 2 1 ( L)
通 带 内 C 1视 为 短 路 : 电 压 放 大 倍 数 Au
滤波电路—使有用的频率信号通过,同时抑制无用频率成分的电路。 分类: 按处 按处理 按构成 理信 方法 器件分 号分 按频率特性分 低 通 滤 波 器 高 通 滤 波 器 带 通 滤 波 器 带 阻 滤 波 器 一 阶 滤 波 器 按传递函数分 二 阶 滤 波 器 N 阶 …… 滤 波 器
Au 1 (
Auf fn f ) j
2
fn Qf
对于二阶低通、高通电路, Auf 3时 , Q 电 路 产 生 自 激 振 荡 。 为防止自激,应使: Auf<3
3 Auf
三、有源带通滤波电路(BPF—Band Pass Filter)
电路只允许某一频段内信号通过,有上限和下限两个截止频 率,将高通滤波电路与低通滤波电 路进行适当组合,就可获得 带通滤波电路。下图为二阶有源带通滤波电路,图中R、C组成低 通电成路,C1、R3组成高通电路,要求RC<R3C1,故低通电路的上 限截止频率fH大于高通电路的下限截止频率fL,两 者之间形成了 一个通带,从而构成了带通滤波电路。
6
2 160 10 0.01 10 Rf 100 1 1 1.588 R1 170 1 3 Auf 1 3 1.588
99.5 H Z
0.708
Q 0.707时 : f H f n 上 限 截 止 频 率 : fH 99.5 H Z
2.内部电路:由输入级、中间级和输出级等组成。输入级有V2、V4组成双端输入 单端输出差分电路;V3、V5是其恒流源负载;V1、V6是射级跟随器,高 Ri;V7 V12为功率放大电路;V7 为驱动级(I0 为恒流源负载);V11、V12 用于消除交越失 真 ;V8、V10 构成 PNP 准互补对称 ;1、 8 开路时,负反馈最强,整个 电路的电压放大倍数Au = 20 ,若在1、 8 间外接旁路电容,以短路R5两 端的 交流压降,可使电压放大倍数提高到200;调整RP(典型应用电路图),可使集 成功放电压放大倍数在20~200之间变化;管脚7与地之间外接电解电容C5(典 型应用电路图),C5可与R2组成直流电源去耦电路。
滤波电路主要有以下四种基本类型

它们的截止角频率是
o
1 RC
无源滤波电路存在的问题
(1)电路的增益小,最大为1 (2)带负载能力差
R
U i
C
(a)
Au
1 0.707
0
o
(c)
C
U i
R
U o
(b)
Au
1 0.707
0 o
(d )
如在无源滤波电路输
R
C
出端接一负载电阻RL, 则其截止频率和增益
U i
C
RLU o U i
C2 C
解得
其中
Af
1 Rf R1
o
1 RC
令 p 为通带截止角频率
1
p o
2
j3 p o
2
p
0.37 RC
p
53 2
7o
0.37o
简单二阶低通滤波 电路的幅频特性
由幅频特性可见ω>>ω0时衰减 的斜率为-40dB/十倍频。但在 ω0附近,其幅频特性与理想的 低通滤波特性相差较大。
20lg Af () / dB Af
0 -3dB
-40dB/十倍 频
0.1 0.37 1 10
ω/ω0
改进
R1
Rf
-
Uo
将电容C1的接 地端改接到集成
Ui
R UM R U +
C1
C2
运放的输出端。
只要参数合适
(1)该电路在f0附近形 成正反馈,不致造
成自激振荡,使f0附 近的电压放大倍数
有源低通滤波器电路

有源低通滤波器电路
有源低通滤波器电路是一种电子电路,用于滤除高频信号并保留低频信号。
它由一个放大器和一个低通滤波器组成。
该电路被广泛应用于音频放大器、通信电路和信号处理系统中。
有源低通滤波器电路的原理是利用放大器的增益来放大输入信号,并通过低通滤波器将高频信号滤除。
放大器的增益可由放大器电路的设计来确定,而低通滤波器则由电容和电阻来构成。
在有源低通滤波器电路中,放大器通常采用运算放大器(Op-Amp)作为放大器。
这是因为Op-Amp具有高增益、低失真和高输入阻抗的特点,非常适合用于放大器电路。
低通滤波器的设计需要考虑电容和电阻的大小。
电容的大小决定了滤波器的截止频率,而电阻则决定了放大器的增益。
在设计电路时,需要根据需要的截止频率和增益来确定电容和电阻的大小。
有源低通滤波器电路的优点是具有高增益、低失真和良好的滤波效果。
它可以有效地滤除高频噪声和干扰信号,从而保证输出信号的质量。
此外,该电路还具有较小的占用空间和较低的成本,非常适合用于电子设备中。
总之,有源低通滤波器电路是一种非常实用的电子电路,在音频放大器、通信电路和信号处理系统等领域都有广泛应用。
通过正确的设计和优化,它可以有效地滤除高频噪声和干扰信号,从而提高系统的性能和可靠性。
- 1 -。
二阶低通有源滤波电路

二阶低通有源滤波电路二阶低通有源滤波电路是一种常见的电子电路,它能够对输入信号进行滤波,去掉高频噪声,输出较为纯净的信号。
这种电路由一个二阶低通滤波器和一个放大器组成,具有良好的滤波效果和稳定性。
电路原理图二阶低通有源滤波电路的原理图如下所示。
它由一个二阶低通滤波器和一个放大器组成。
输入信号X(t)经过二阶低通滤波器滤波后,输出信号Y(t),然后经过放大器放大,输出最终的滤波结果。
在电路中,R1、C1和R2、C2组成了二阶低通滤波器,其中R1和R2为电阻器,C1和C2为电容器。
这些元件的组合决定了滤波器的截止频率和带宽,从而影响滤波效果。
放大器采用运算放大器,它可以提供足够的增益和输出电流,保证滤波器的稳定性和精度。
滤波器的截止频率为:f=1/(2π√(R1C1)×(R2C2))带宽为:fL=√(R1C1/R2C2)×f根据实际需要,可以选择不同的元件值来调整截止频率和带宽。
优点1. 滤波效果稳定,可以有效地去掉高频噪声,输出纯净的信号;2. 放大器可以提供足够的增益和输出电流,保证滤波器的精度和稳定性;3. 电路简单,易于实现。
缺点1. 对于不同的输入信号,需要重新调整电路参数,以获得最佳的滤波效果;2. 二阶低通滤波器的截止频率和带宽相对较低,可能无法处理高频信号。
应用领域1. 音频处理:在音频系统中,可以使用二阶低通有源滤波电路来降低高频噪声和回声的影响;2. 传感器信号处理:在传感器信号处理中,可以使用二阶低通有源滤波电路来去掉高频干扰;3. 电源滤波:在电源滤波中,可以使用二阶低通有源滤波电路来去掉高频噪声和电磁干扰。
总结二阶低通有源滤波电路是一种简单而有效的电子电路,可以用于对输入信号进行滤波和处理。
它由一个二阶低通滤波器和放大器组成,可以提供稳定的滤波效果和良好的精度。
然而,对于不同的输入信号,需要重新调整电路参数以获得最佳的滤波效果。
在音频处理、传感器信号处理和电源滤波等领域中广泛应用。
二阶低通有源滤波电路

二阶低通有源滤波电路二阶低通有源滤波电路是一种常见的电路,其主要作用是滤除高频信号,使得输出信号更加平滑。
在实际应用中,二阶低通有源滤波电路有着广泛的应用,例如在音频处理、通信系统等领域中都有着重要的作用。
二阶低通有源滤波电路由放大器、电容和电阻等组成。
其中,放大器是电路中最重要的部分,它能够对输入信号进行放大和处理。
电容则起到存储电荷和滤波的作用,电阻则是为了限制电流和阻抗匹配等。
在电路中,放大器的类型和电容的取值会对电路的性能产生影响。
二阶低通有源滤波电路的工作原理是基于滤波器的原理。
在电路中,输入信号首先通过一个电容,然后进入放大器。
放大器对信号进行放大和处理后,再通过第二个电容进行滤波。
最终,输出的信号就是经过滤波后的平滑信号。
由于二阶低通有源滤波电路具有比一阶滤波器更好的滤波效果,因此在实际应用中更加常见。
在设计二阶低通有源滤波电路时,需要注意以下几点:1. 放大器的增益和稳定性。
放大器的增益和稳定性对电路的性能有着重要的影响。
在选择放大器时,需要考虑其增益和稳定性等因素。
2. 电容的取值。
电容的取值会对电路的性能产生影响。
一般来说,电容的值越大,滤波器的截止频率就越低,滤波效果就越好。
3. 电阻的取值。
电阻的取值对电路的性能也有一定的影响。
一般来说,电阻的值越小,电路的带宽就越大,但是滤波效果会变差。
4. 滤波器的截止频率。
滤波器的截止频率是指滤波器能够滤除高频信号的最大频率。
在设计电路时,需要根据实际需求来确定滤波器的截止频率。
二阶低通有源滤波电路在实际应用中有着广泛的用途。
例如,在音频处理中,二阶低通滤波器可以用于去除高音部分的杂音,使得音质更加清晰。
在通信系统中,二阶低通滤波器可以用于滤除高频信号,提高信号的可靠性和稳定性。
二阶低通有源滤波电路是一种重要的电路,其在实际应用中有着广泛的应用。
在设计电路时,需要考虑各个因素的影响,以达到滤波效果最佳的目的。
低通有源负反馈滤波电路

低通有源负反馈滤波电路
低通有源负反馈滤波电路是一种电子滤波器,它使用有源元件(如运放)和负反馈回路来实现对特定频率范围的信号的滤波功能。
这类滤波器通常设计用于让低频信号通过而抑制高频信号。
以下是低通有源负反馈滤波电路的基本组成部分和工作原理:
1. 运放(Operational Amplifier,简称为Op-Amp):运放是这种电路的核心元件,它具有高输入阻抗、低输出阻抗和大增益的特性。
常见的运放有正反馈输入端和负反馈输入端。
2. 电容(Capacitor):电容用于构建低通滤波特性。
通过选择适当的电容值,可以确定滤波器的截止频率,即高频信号开始被抑制的频率。
3. 电阻(Resistor):电阻用于调整运放的增益和负反馈网络的性质。
4. 负反馈网络:这是连接运放输出和反馈输入的网络。
它通过向运放的反馈输入引入一部分输出信号,从而实现负反馈。
这有助于稳定运放的增益,并影响滤波器的频率响应。
5. 截止频率:通过选择适当的电容值,可以确定低通滤波器的截止频率。
截止频率是指在该频率以下的信号通过,而在该频率以上的信号被滤除。
一种常见的低通有源负反馈滤波电路是使用运放和电容构建的Sallen-Key滤波器。
这种电路的设计允许通过调整电阻和电容的数值来实现不同的截止频率和滤波特性。
需要注意的是,具体的电路设计取决于应用的要求,截止频率和滤波特性的需求。
设计电路时,工程师通常会考虑到电源电压、输入输出阻抗、相位失真等因素。
因此,电路的详细设计需要根据具体的应用和性能要求进行调整。
有源低通滤波器的实现100KHZ

电子线路设计(论文)说明书题目:有源低通滤波器的设计院(系):信息与通信学院专业:电子信息工程学生姓名:黄翔学号:1100220514指导教师:王娇职称:讲师2013年11月16日摘要低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
理想滤波器电路的频响在通带内应具有一定幅值和线性相移,而在阻带内其幅值应为零。
有源滤波器是指由放大电路及RC网络构成的滤波器电路,它实际上是一种具有特定频率响应的放大器。
滤波器的阶数越高,幅频特性衰减的速率越快,但RC网络节数越多,元件参数计算越繁琐,电路的调试越困难。
关键词:低通;放大器;阶数AbstractLow pass filter allows low frequency signal to pass through and suppresses the high frequency components of signals. Ideal filter circuit should have certain amplitude frequency response in the passband and linear phase shift, and its amplitude should be zero in the stopband. Active filter is one that is composed of RC network and amplifying circuit. It is actually a kind of specific frequency response amplifier. The higher the order number of the filter, the faster the amplitude frequency attenuation rate.But the RC network node number is associated with the components parameter calculation and the debugging of the circuit.Key words: low pass; Amplifier; Order number目录引言 (1)1 原理及设计方案 (1)1.1滤波器的介绍 (1)1.2 有源滤波器的设计 (2)1.3方案选择 (4)2 硬件介绍 (6)3 仿真及结果 (7)4 测量结果 (8)5 实验心得与体会 (9)谢辞 (11)参考文献 (12)引言课程设计是理论联系实际的重要实践教学环节,是对学生进行的一次综合性专业设计训练。
有源二阶低通滤波器工作原理

有源二阶低通滤波器工作原理
有源二阶低通滤波器是一种电子电路,通常由一个运放、电容器和电阻器组成。
其主要作用是将输入信号中高于截止频率的部分滤除,只保留低于截止频率的部分。
它的工作原理基于运放的反馈放大作用,通过调整电容器和电阻器的阻抗比,将信号频率进行滤波。
当输入信号通过输入电容器后,运放的反馈回路会将一部分信号再次输入到输入电容器形成相互补偿的作用,从而限制输出信号的频率范围。
以下是有源二阶低通滤波器的一些关键参考内容:
1. 截止频率:有源二阶低通滤波器的截止频率取决于输入电容器和输出电容器以及电阻器的阻值和阻抗比,一般可以通过调整这些参数来控制截止频率。
2. 放大倍数:滤波器放大倍数的大小也可以通过调整运放的增益来控制,通常情况下,增益越高,滤波器的放大倍数也越高。
3. 电容器类型:在选择电容器的类型和值时需要注意,不同的电容器会对滤波器的性能产生不同的影响,例如铝电解电容器具有较大的电感和电阻,会对滤波器的性能产生负面影响。
4. 运放选择:有源二阶低通滤波器中使用的运放可以是单个运放也可以是双电源运放,双电源运放在设计中可以提高滤波器的性能。
5. 滤波器的稳定性:滤波器的稳定性是设计时需要考虑到的因素之一,在电源电压或温度变化时,滤波器的性能可能会发生变化,需要选择较为稳定的元器件来保证滤波器的稳定性。
有源低通滤波器(LPF)

有源低通滤波器(LPF)1 低通滤波器的主要技术指标(1)通带增益Avp通带增益是指滤波器在通频带的电压放大倍数,如图3所示。
性能良好的LPF通带的幅频特性曲线是平坦的,阻带的电压放大倍数基本为零。
(2)通带截止频率fp其定义与放大电路的上限截止频率相同,见图3。
通带与阻带之间称为过渡带,过渡带越窄,说明滤波器的选择性越好。
图3 LPF的幅频特性曲线2 简单一阶低通有源滤波器一阶低通滤波器的电路如图4所示,其幅频特性见图5,图中虚线为理想的情况,实线为实际的情况。
特点是电路简单,阻带衰减太慢,选择性较差。
图4 一阶LPF 图5 一阶LPF的幅频特性曲线当f = 0时,电容器可视为开路,通带的增益为一阶低通滤波器的传递函数如下,其中该传递函数式的样子与一节RC低通环节的增益频率表达式差不多,只是缺少通带增益Avp这一项。
3 简单二阶低通有源滤波器为了使输出电压在高频段以更快的速率下降,以改善滤波效果,再加一节RC低通滤波环节,称为二阶有源滤波电路。
它比一阶低通滤波器的滤波效果更好。
二阶LPF的电路图如图6所示,幅频特性曲线如图7所示。
图6 二阶LPF图7 二阶LPF的幅频特性曲线(1)通带增益当f = 0时,各电容器可视为开路,通带的增益为(2)二阶低通有源滤波器传递函数根据图8-2.06可以写出通常有,联立求解以上三式,可得滤波器的传递函数(3)通带截止频率将s换成jω,令ω0=2πf0=1/(RC)可得当f=fp 时,上式分母的模解得截止频率:与理想的二阶波特图相比,在超过f0以后,幅频特性以-4 0 dB/dec的速率下降,比一阶的下降快。
但在通带截止频率fp →f0之间幅频特性下降的还不够快。
4 二阶压控型低通有源滤波器(1)二阶压控型LPF二阶压控型低通有源滤波器如图8所示。
其中的一个电容器C1原来是接地的,现在改接到输出端。
显然,C1的改接不影响通带增益。
图8 二阶压控型LPF 图9 二阶压控型LPF的幅频特性(2)二阶压控型LPF的传递函数对于节点N,可以列出下列方程联立求解以上三式,可得LPF的传递函数上式表明,该滤波器的通带增益应小于3,才能保障电路稳定工作。
滤波电路主要有以下四种基本类型

C R
(b)
RL Uo
式中 可见
有源滤波电路特点:
(1)电路的增益得到提高 (3)带负载能力强
(2)运放本身对RC网络影响小 (4)运放工作在线性区
一、低通滤波器
低通滤波器用来通过低频信号,抑制或衰减高频信号。 称为滤波电路增益或电压传递函数。
(一)一阶电路
输出电压为
Rf
R1
•
R
-
Uo
•
+
Ui
C
传递函数
结论
0 -3dB
3dB -40dB/十倍频源自10-3 0.01 0.1 1 10
ω/ω0
Q=2时幅
频特性。
将电容C1接地的一端改接到运放的输出端,形成 正反馈后,可使Uo的幅值在ω≈ω0范围内得到加强, 如果Q值合适,其幅频特性比较接近理想情况 。
二、高通滤波器
Af(ω)
理想的高通滤波器幅频特性
阻带
通带电压放大倍数
通带截止角频率
幅频特性为
20lg A Aup
1
20lg A Aup
1 0.707
0
1
(a)理想特性
o
0
(b)实际幅频特性 o
结论
1.改变电阻Rf和R1的阻值可调节通带电压放大倍数 2.改变截止频率,应调整RC
一阶电路缺点
当ω≥ ωo时,幅频特性衰减太慢,以-20dB/10 倍频程的速率下降,与理想的幅频特性相差甚远。
-40dB/十倍 频
0.1 0.37 1 10
ω/ω0
改进
R1
Rf
•
•
•-
Uo
将电容C1的接 地端改接到集成
•
Ui
三阶有源低通滤波器工作原理

三阶有源低通滤波器工作原理
三阶有源低通滤波器是一种常用的电路,主要用于对输入信号进行滤波处理,以去除高频噪声或对低频信号进行增强。
其基本结构由三极管、电容和电阻组成。
在工作时,输入信号经过第一级RC滤波
电路进行初步滤波,然后进入三极管的共射放大电路中进行放大,并通过第二级RC滤波电路进行进一步的低通滤波。
最后,输出信号经
过第三级RC滤波电路进行最终的滤波处理,并输出到外部载荷电路中。
其工作原理基于三极管的放大特性和RC滤波电路的滤波原理。
在三极管的共射放大电路中,输入信号经过电容耦合到三极管的基极,通过微小的信号变化引起三极管的集电极电流的变化,实现对信号的放大。
同时,通过合适的偏置电路设置,使得三极管处于放大状态,能够提供充足的放大增益。
在RC滤波电路中,电容和电阻的组合可
以实现对特定频率范围的信号进行滤波处理,将高频信号滤除,只保留低频信号。
通过三级RC滤波电路的串联,可以实现更精细的滤波
处理。
最终输出的信号可经过放大器等电路进行增强,以满足实际应用需求。
综上所述,三阶有源低通滤波器具有滤波效果好、增益高、可调性强等优点,在各种电路设计中得到广泛应用。
- 1 -。
有源低通滤波器的实现100KHZ讲解

电子线路设计(论文)说明书题目:有源低通滤波器的设计院(系):信息与通信学院专业:电子信息工程学生姓名:黄翔学号:1100220514指导教师:王娇职称:讲师2013年11月16日摘要低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
理想滤波器电路的频响在通带内应具有一定幅值和线性相移,而在阻带内其幅值应为零。
有源滤波器是指由放大电路及RC网络构成的滤波器电路,它实际上是一种具有特定频率响应的放大器。
滤波器的阶数越高,幅频特性衰减的速率越快,但RC网络节数越多,元件参数计算越繁琐,电路的调试越困难。
关键词:低通;放大器;阶数AbstractLow pass filter allows low frequency signal to pass through and suppresses the high frequency components of signals. Ideal filter circuit should have certain amplitude frequency response in the passband and linear phase shift, and its amplitude should be zero in the stopband. Active filter is one that is composed of RC network and amplifying circuit. It is actually a kind of specific frequency response amplifier. The higher the order number of the filter, the faster the amplitude frequency attenuation rate.But the RC network node number is associated with the components parameter calculation and the debugging of the circuit.Key words: low pass; Amplifier; Order number目录引言 (1)1 原理及设计方案 (1)1.1滤波器的介绍 (1)1.2 有源滤波器的设计 (2)1.3方案选择 (4)2 硬件介绍 (6)3 仿真及结果 (7)4 测量结果 (8)5 实验心得与体会 (9)谢辞 (11)参考文献 (12)引言课程设计是理论联系实际的重要实践教学环节,是对学生进行的一次综合性专业设计训练。
有源低通滤波电路

If R1=R2=R ,C1=C2=C, and RC=τ ,then
So, 1= j2Aτ2ω2/k+jA (3τω /k - τω)+A/k That is,
sin(ω t)= A sin(ωt+φ+π)· τ2ω2/k + A sin(ωt+φ+π/2)·(3τω /k - τω)+ A sin(ωt+φ)·/k
UC2
QC2
i2
Vi
Vm
i1
i2
i
i
数学模型
i2 Vi i
Vm
V+
VVo
i1
AC1ω sin(ω t+φ +π /2)/k +ω [AR2C1ω sin(ω t+φ +π )/k +Asin(ω t+φ +π /2)/k - Asin(ω t+φ +π /2)]C2
输入输出特性
AR2C1 ω sin(ω t+φ +π /2)/k sinω t AC1sin(ω t+φ )/k Asin(ω t+φ )/k Asin(ω t+φ ) AC1 ω sin(ω t+φ +π /2)/k
电路形式
信号源
From low_filter1.ms10
二阶有源低通滤波电路
电路分析
i2
Vi Vm V+
VVo
i
已知量:Vi
i1
待求量:Vo
中间量:Vm , V+,V目标:寻找这些量之间的关系
电路分析:从相对独立的模块入手
i2
Vi Vm V+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iR1
Vm
iC2
iR2
Vo
iC1 iR3
利用剥笋子的方法进行追寻: (1)要想得到Vo,只要得到iC1即可; (2)要想得到iC1 或 iR2 ,只要得到Vm即可; (3)要想得到Vm,只要得到iR1即可; (4)要想得到iR1,要得到iR2 、 iR2 、 iC2 ,而这些均可得到了
Vo
Vi UR1 iR2 iR1 QC2 Vm iC1 QC1 UR3 UC1 iR3
iC2
From low_filter2.mdl
方波信号的滤波推导
From low_filter1.mdl
方波信号的滤波分析
问题:
1、方波信号含有哪些频率的信号,它们的幅值分别是多少,怎 么计算?
2、通过滤波系统后,哪些信号的幅值增加,哪些信号的幅值降 低了,这些指标从哪里来?怎么计算?
3、如何设计,让输出只有一个频率信号的输出,其他频率信号 的幅值几乎将为0;
If R1=R2=R ,C1=C2=C, and RC=τ ,then
So, 1= j2Aτ2ω2/k+jA (3τω /k - τω)+A/k That is,
sin(ω t)= A sin(ωt+φ+π)· τ2ω2/k + A sin(ωt+φ+π/2)·(3τω /k - τω)+ A sin(ωt+φ)·/k
电路分析:从相对独立的模块入手
i2
Vi Vm V+
VVo
i
建立Vm与V+的关系, 并得到i1与它们的关系
i1
建立Vo与V-的关系
电路分析
i2
Vi
(1)V+与Vm之关系,与i1 之关系
Vm V+ VVo
(2)V-与Vo之关系 (3)V-与V+之关系 (4)i2与Vm、Vo之关系 (5)i与i1、i2之关系 (6)Vm与i、Vi之关系
12= A2[(1-τ2ω2)/k]2 + A2 (3τω /k – τω)2
A=?
什么情况下,A无穷大
The phase of sum is 0, the augend and addend are φ 、 φ +π /2,
obviously, φ <0. it is easy to prove, Φ =-atan { (3τω /k – τω)/ [(1-τ2ω2)/k] }
V-
Vo
Vm Vo
UC2
QC2
i2
Vi i1 i2 i i UR1
Vm
电路分析:模型整理、化简
i2 Vi i
Vm
V+
V-
Vo
i1
From low_filter1.mdl
Vm
UR2
i1
QC1
V+
V-
Vo
Vm Vo
UC2
QC2
i2
Vi
Vm
i1
i2
i
i
数学模型
i2 Vi i
Vm
V+
VVo
i1
AC1ω sin(ω t+φ +π /2)/k +ω [AR2C1ω sin(ω t+φ +π )/k +Asin(ω t+φ +π /2)/k - Asin(ω t+φ +π /2)]C2
有源低通滤波电路
作用
• 消除高频噪声信号 • 保留直流与低频响应信号 • 比RC滤波电路具有更强的抑制高频能力与 更高的响应速度
电路形式
信号源
From low_filter1.ms10
二阶有源低通滤波电路
电路分析
i2
Vi Vm V+
VVo
i
已知量:Vi
i1
待求量:Vo
中间量:Vm , V+,V目标:寻找这些量之间的关系
公式整理技巧与验证原则
• 从单位换算的角度来看公式正确与否?即 电压与电压相加;电流只能与电流相加。 • 注意RC可以认为是时间单位、ω 可以认为 是时间倒数,即S-1,正好与RC相反 • 从ω 所处位置与相位的关系看公式正确与 否? ω 是分子,则是微分环节,超前π /2, ω 2则超前π ; ω 是分母,则是积分环节, 滞后π /2, 1/ω 2则滞后π 。
4、————频率下,输出信号幅值是输入信号幅值的一半
其他滤波电路的推导:必考题
From low_filter2
From low_filter3
From low_filter4
iR1
Vm
iC2
iR2
Vo
iC1
iR3
利用剥笋子的方法进行追寻: (1)要想得到Vo,只要得到iC1即可; (2)要想得到iC1 或 iR2 ,只要得到Vm即可; (3)要想得到Vm,只要得到iR1即可; (4)要想得到iR1,要得到iR2 、 iR2 、 iC2 ,而这些均可得到了
输入输出特性
AR2C1 ω sin(ω t+φ +π /2)/k sinω t AC1sin(ω t+φ )/k Asin(ω t+φ )/k Asin(ω t+φ ) AC1 ω sin(ω t+φ +π /2)/k
AR2C1 ω sin(ω t+φ +π /2)/k+Asin(ω t+φ )/k
AR2C1 ωsin(ω t+φ +π /2)/k+Asin(ω t+φ )/k - Asin(ω t+φ ) [AR2C1 ω sin(ω t+φ +π /2)/k+Asin(ω t+φ )/k - Asin(ω t+φ )]C2 ω [AR2C1ω sin(ω t+φ +π )/k+Asin(ω t+φ +π /2)/k - Asin(ω t+φ +π /2)]C2 AC1ω sin(ω t+φ +π /2)/k +ω [AR2C1ω sin(ω t+φ +π )/k +Asin(ω t+φ +π /2)/k - Asin(ω t+φ +π /2)]C2
Simulation comes from low_filter5
整理公式
Vi = Vm + i R1 求解A,划出A与ω 的关系曲线,用EXCEL划出曲线图,从曲线中 得到什么样的结论。 A是输出对输入幅值的放大倍数 结论:
1、如果输入信号频率很大,输出信号幅值降低很大;
2、如果是直流信号,输出信号是输入信号的k倍; 3、如果频率为————,输出对输出的幅值放大倍数最大;
Where,1 represents sin(ω t)
输入输出特性
jAR2C1 ω/k jAC1 ω /k
AC1/k A/k
jA represents Asin(ω t +φ +π /2)
A represents Asin(ω t +φ )
A
1
jAR2C1 ω/k+A/k
j2AR1R2C1C2ω2/k+jA R1ωC2 /k -j A R1ω C2 +jAR1C1ω/k
j2AR2C1C2ω2/k+jA ωC2 /k -j A ω C2+ jAC1ω/k
jAR2C1 ω/k+A/k - A
[jAR2C1 ω /k+A/k - A]C2
j2AR2C1C2ω2/k+jA ωC2 /k -j A ω C2
Ask: j2A represents
__----------------
i
②
④ i =C dUc/dt ⑤ 干流与支 流 ⑥ Vm=Vi – i * R1
From low_filter.mdl Vo
Vm
UR2
i1
QC1
V+
V-
Vm Vo
UC2
QC2
i2
Vi i1 i2 i i
Vm
电路分析:数学模型
④
Vi i2
⑥
Vm V+
⑤
① ③ Vi1
Vo
i
②
Vm
UR2
i1
QC1
V+
Simulation conclusions
1、同频率的信号相加,频率不变; 2、相差90度的两个同频率信号相加,和信号的幅值与原信号的幅值满足勾股关系; 3、和信号的相位靠近幅值大的那一个信号,且和信号的相位夹在两个原信号之间。 sin(ω t)= A sin(ωt+φ)· [(1-τ2ω2)/k] + A sin(ωt+φ+π/2)·(3τω /k – τω)
sin(ω t)= A sin(ωt+φ)· [(1-τ2ω2)/k] + A sin(ωt+φ+π/2)·(3τω /k – τω) The phase difference between sin(ωt+φ) and sin(ωt+φ+π/2) is 90o, simulation Simulation comes from low_filter5
R C 模 型 框 图
(1)电流的累加成电量; (2)电量除以电容 = 输出电位;
i
VO Q
(3)电流= 电阻两端电压除以电阻; (4)电阻两端电压 = 输入电位减去 输出电位.
① ③
i
UR
Ui
累加 除以R
UR
