多目标遗传算法代码
MATLAB多目标优化计算

MATLAB多目标优化计算多目标优化是指在一个优化问题中同时优化多个目标函数,这些目标函数往往存在冲突,不能同时达到最优。
MATLAB提供了许多工具和函数,可以帮助解决多目标优化问题。
在MATLAB中,多目标优化问题可以用以下形式表示:min f(x)s.t.g(x)≤0h(x)=0lb ≤ x ≤ ub其中,f(x)表示待优化的多个目标函数,g(x)和h(x)分别表示不等式约束和等式约束条件,lb和ub分别表示x的下界和上界。
1. paretofront函数:可以用来判断一组给定解的非支配解集合。
```index = paretofront(F)```其中,F是一个m×n矩阵,每一行表示一个解的m个目标函数值。
index是一个逻辑向量,长度为n,表明对应位置的解是否为非支配解。
2. paretofun函数:可以用来对非支配解集进行排序。
```rank = paretofun(F)```其中,F同样是一个m×n矩阵,每一行表示一个解的m个目标函数值。
rank表示对应位置的解在非支配解集中的排序。
3. gamultiobj函数:使用遗传算法进行多目标优化。
```[x, fval, exitflag, output, population] = gamultiobj(fun, nvars, A, b, Aeq, beq, lb, ub)```其中,fun是一个函数句柄,表示待优化的目标函数。
nvars表示决策变量的个数。
A、b、Aeq、beq、lb和ub分别表示不等式约束、等式约束、下界和上界。
x是优化后的决策变量值,fval是优化后的目标函数值。
exitflag是优化器的退出标志,output包含了优化算法的输出结果,population包含了所有迭代过程中的解集。
4.NSGA-II函数:使用非支配排序遗传算法进行多目标优化。
```[x, fval, exitflag, output, population] = nsga2(fun, nvars, A, b, Aeq, beq, lb, ub)```参数和返回结果的含义同gamultiobj函数相似。
多目标遗传算法NSGA-II

在NSGA-II中,我们计算两个属性Sp 和np来帮助我们识别更好的个体。
快速非支配排序
假设种群大小为P,该算法需要计算每个个体p的被支配个数np和该个体支配的解的集合Sp 这两个参数。 遍历整个种群
该算法的伪代码如下:
拥挤度
• 为了使得到的解在目标空间中更加均匀,引入了拥挤度的概念
•为所有个体的拥挤距离初始化零。 •审视所有的个人和目标值。通过用Inf值分配绑定解决方案 来选择它们。 •计算每个目标的第m个最大值和最小值,得到归一化的分 母。 •对第i个个体的m个目标的拥挤距离求和
计算拥挤度是为了保存下来相似程度较低的解,保持解空间的多样性
精英保留策略
1 首先将父代种群Pt和子代种群Qt合成种群Rt 2 根据以下规则从种群Rt生成新的父代种群Rt+1
(1)根据Pareto等级从低到高的顺序,将整层种 群放入父代种群Rt+1中,真到某一层个体不能 全部放入父代种群Rt+1。 (2)将该层个体根据拥挤度从大到小排列,依次 放入父代种群Rt+1中,直到父代种群Rt+1f填满。
单目标优化——》多目标优化
NSGA-II 在常规遗传算法上的改进
• 1 快速非支配算子设计 • 多目标优化问题的设计关键在于求取Pareto最优解集。
• 2 通过优先选择拥挤距离较大的个体
• 3 精英策略选择算子
• NAS中的性能评估也可以是一个多目标问题 • 测试集上的准确率 • 参数数量
遗传算法解决多目标优化问题
多目标优化问题:
• 包含多个可能有冲突的目标函数
NSGA-Ⅱ算法,即带有精英保留策略的快 速非支配多目标优化算法,是一种基于 Pareto最优解的多目标优化算法。
(完整版)遗传算法c语言代码

}
}
}
//拷贝种群
for(i=0;i<num;i++)
{
grouptemp[i].adapt=group[i].adapt;
grouptemp[i].p=group[i].p;
for(j=0;j<cities;j++)
grouptemp[i].city[j]=group[i].city[j];
{
group[i].p=1-(double)group[i].adapt/(double)biggestsum;
biggestp+=group[i].p;
}
for(i=0;i<num;i++)
group[i].p=group[i].p/biggestp;
//求最佳路劲
bestsolution=0;
for(i=0;i<num;i++)
printf("\n******************是否想再一次计算(y or n)***********************\n");
fflush(stdin);
scanf("%c",&choice);
}while(choice=='y');
return 0;
}
遗传算法代码
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define cities 10 //城市的个数
遗传算法解释及代码(一看就懂)

遗传算法( GA , Genetic Algorithm ) ,也称进化算法。
遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ):包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。
适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。
那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。
这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取);首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。
这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。
多目标优化python代码

多目标优化python代码多目标优化(multi-objective optimization)是一个在优化问题中存在多个目标函数的情况下,同时优化多个目标的方法。
在Python中,我们可以利用各种优化算法和工具来实现多目标优化。
多目标优化在实际问题中非常常见,例如在供应链管理中,我们可能需要同时考虑成本最小化和服务水平最大化;在工程设计中,我们可能需要同时优化性能和可靠性等。
传统的单目标优化方法往往只能找到单个最优解,无法同时考虑多个目标。
而多目标优化则能够为决策者提供一系列不同的解决方案,形成一个解集(Pareto set),其中每个解都是在某种意义上是最优的。
在Python中,有几个常用的库和工具可以用于多目标优化。
下面将介绍其中的几个。
1. PyGMO:PyGMO是一个基于Python的开源优化库,它提供了多种多目标优化算法,如NSGA-II、MOEA/D等。
PyGMO的优势在于其丰富的算法库和灵活的接口,可以方便地在多种问题上进行实验。
2. DEAP:DEAP也是一个Python的开源优化库,它提供了多种遗传算法和进化策略的实现。
DEAP的特点是简单易用,适合初学者使用。
3. Platypus:Platypus是一个Python的多目标优化库,它提供了多种多目标优化算法的实现,如NSGA-II、SPEA2等。
Platypus的特点是速度快、易用性好,适合处理中小规模问题。
4. Scipy.optimize:Scipy是一个Python的科学计算库,其中的optimize模块提供了一些基本的优化算法,如COBYLA、SLSQP等。
虽然Scipy.optimize主要用于单目标优化,但也可以通过一些技巧来实现多目标优化。
在使用这些工具进行多目标优化时,我们需要定义适应度函数(fitness function),也就是衡量解决方案好坏的指标。
对于多目标优化问题,适应度函数通常是一个向量,其中每个维度对应一个目标函数。
多目标多约束优化问题算法

多目标多约束优化问题算法多目标多约束优化问题是一类复杂的问题,需要使用特殊设计的算法来解决。
以下是一些常用于解决这类问题的算法:1. 多目标遗传算法(Multi-Objective Genetic Algorithm, MOGA):-原理:使用遗传算法的思想,通过进化的方式寻找最优解。
针对多目标问题,采用Pareto 前沿的概念来评价解的优劣。
-特点:能够同时优化多个目标函数,通过维护一组非支配解来表示可能的最优解。
2. 多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization, MOPSO):-原理:基于群体智能的思想,通过模拟鸟群或鱼群的行为,粒子在解空间中搜索最优解。
-特点:能够在解空间中较好地探索多个目标函数的Pareto 前沿。
3. 多目标差分进化算法(Multi-Objective Differential Evolution, MODE):-原理:差分进化算法的变种,通过引入差分向量来生成新的解,并利用Pareto 前沿来指导搜索过程。
-特点:对于高维、非线性、非凸优化问题有较好的性能。
4. 多目标蚁群算法(Multi-Objective Ant Colony Optimization, MOACO):-原理:基于蚁群算法,模拟蚂蚁在搜索食物时的行为,通过信息素的传递来实现全局搜索和局部搜索。
-特点:在处理多目标问题时,采用Pareto 前沿来评估解的质量。
5. 多目标模拟退火算法(Multi-Objective Simulated Annealing, MOSA):-原理:模拟退火算法的变种,通过模拟金属退火的过程,在解空间中逐渐减小温度来搜索最优解。
-特点:能够在搜索过程中以一定的概率接受比当前解更差的解,避免陷入局部最优解。
这些算法在解决多目标多约束优化问题时具有一定的优势,但选择合适的算法还取决于具体问题的性质和约束条件。
多目标优化实例和matlab程序

NSGA-II 算法实例目前的多目标优化算法有很多, Kalyanmoy Deb 的带精英策略的快速非支配排序遗传算法(NSGA-II) 无疑是其中应用最为广泛也是最为成功的一种。
本文用的算法是MATLAB 自带的函数gamultiobj ,该函数是基于NSGA-II 改进的一种多目标优化算法。
一、 数值例子多目标优化问题424221*********422421221211212min (,)10min (,)55..55f x x x x x x x x x f x x x x x x x x x s t x =-++-=-++-≤≤⎧⎨-≤≤⎩二、 Matlab 文件1. 适应值函数m 文件: function y=f(x) y(1)=x(1)^4-10*x(1)^2+x(1)*x(2)+x(2)^4-x(1)^2*x(2)^2;y(2)=x(2)^4-x(1)^2*x(2)^2+x(1)^4+x(1)*x(2);2. 调用gamultiobj 函数,及参数设置:clearclcfitnessfcn=@f; %适应度函数句柄nvars=2; %变量个数lb=[-5,-5]; %下限ub=[5,5]; %上限A=[];b=[]; %线性不等式约束Aeq=[];beq=[]; %线性等式约束options=gaoptimset('paretoFraction',,'populationsize',100,'ge nerations',200,'stallGenLimit',200,'TolFun',1e-100,'PlotFc ns',@gaplotpareto);% 最优个体系数paretoFraction 为;种群大小populationsize 为100,最大进化代数generations 为200,% 停止代数stallGenLimit 为200, 适应度函数偏差TolFun 设为1e-100,函数gaplotpareto :绘制Pareto 前端[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)3. 计算结果-40-35-30-25-20-15-10-5-505101520253035Objective 1O b j e c t i v e 2Pareto front图1. 实例1对应的Pareto 前沿图从图1可以看出Pareto 前分布较均匀,多样性较好。
遗 传 算 法 详 解 ( 含 M A T L A B 代 码 )

遗传算法入门(上)代码中的进化学说与遗传学说写在之前算法所属领域遗传算法的思想解析为什么要用遗传算法?科研现状应用现状遗传算法入门系列文章:(中篇)遗传算法入门(中)实例,求解一元函数最值(MATLAB版)(下篇)遗传算法入门(下)实例,求解TSP问题(C++版)写在之前说明:本想着用大量篇幅写一篇“关于遗传算法的基本原理”作为本系列入门的第一篇,但是在找寻资料的过程中,看到网络上有大量的关于遗传算法的介绍,觉得写的都挺好,所以本文我就简单写点自己的理解。
推荐几篇关于遗传算法的介绍性文章:遗传算法详解(GA)(个人觉得很形象,很适合初学者)算法所属领域相信每个人学习一门知识之前,都会想知道这门知识属于哪一门学科范畴,属于哪一类技术领域?首先对于这种问题,GA是没有绝对的归属的。
算法的定义是解决问题的一种思想和指导理论。
而遗传算法也是解决某一问题的一种思想,用某一编程语言实现这种思想的程序具有很多特点,其中一个便是智能性和进化性,即,不需要大量的人为干涉,程序本身能够根据一定的条件自我筛选,最终得出令人满意的结果。
所以按照这种特性,把它列为人工智能领域下的学习门类毫无疑问是可以的。
遗传算法的思想是借鉴了达尔文的进化学说和孟德尔的遗传学说,把遗传算法说成是一门十足的仿生学一点都不过分。
然而从应用的角度出发,遗传算法是求最优解问题的好方法,如信号处理中的优化、数学求解问题、工业控制参数最优解、神经网络中的激活函数、图像处理等等,所以把遗传算法说成优化范畴貌似也说的过去。
为了方便理解,我们可以暂时将其定位为人工智能–智能优化,这也是很多书中描述遗传算法的惯用词汇。
遗传算法的思想解析遗传算法(gentic algorithms简称GA)是模拟生物遗传和进化的全局优化搜索算法我们知道,在人类的演化中,达尔文的进化学说与孟德尔的遗传学说起着至关重要的理论指导。
每个人作为一个个体组成一个人类种群,正是经历着物竞天择,才会让整个群体慢慢变的更好,即更加适应周围的环境。
函数优化的遗传算法代码实现

2 . 1 个 体编 码及初 始种 群设定
映 射 即 编 码 工 作 。 由 于仿 照 基 因编 码 的工 作 很 复 杂 , 我 们
往 往 进 行 简化 , 如二 进 制 编 码 , 初代种群产生之后 , 按 照 适 者生存和优胜劣汰的原 理 , 逐代 ( G e n e r a t i o n ) 演化 产生 出
c o d i n g ) , 可 以 作 为 问题 近 似最 优解 。
遗 传 算法 的基 本 运 算 过 程 如 下 : ( 1 ) 初始化 : 设置进化代数计数器 t z0 , 设 置 最 大进 化
代 数 丁, 随机 生 成 M 个 个 体 作 为 初 始群 体 P( O ) 。
进化规律 ( 适者生存 、 优胜劣汰遗传机制) 演 化 而 来 的 随 机
函数 优 化 的遗 传 算 法 源程 序 , 该 源 程 序 可 以 直接 运 行 。
关键词 : 遗传算法 ; Ma t l a b ; 函数 优 化
中 图分 类 号 : TP 3 1 2
文 献标 识码 : A
文章 编 号 : 1 6 7 2 — 7 8 0 0 ( 2 0 1 3 ) 0 0 2 — 0 0 4 0 — 0 3
规 则 。遗 传算 法 的这 些 性 质 已 被 人 们 广 泛 地 应 用 于 组 合
( 2 ) 个体评价 : 计算群体 P ( ) 中各 个 体 的 适 应 度 。
( 3 ) 选 择 运算 : 将 选 择 算 子 作 用 于 群 体 。选 择 的 目的 是 把 优 化 的 个 体 直 接 遗 传 到 下 一 代 或 通 过 配 对 交 叉 产 生 新 的个 体 再 遗 传 到 下 一 代 。选 择 操 作 是 建 立 在 群 体 中 个 体 的适 应 度 评 估 基 础 之 上 的 。 ( 4 ) 交叉运算 : 将 交 叉 算 子 作 用 于 群 体 。所 谓 交 又 是 指 把 两 个 父 代 个 体 的 部 分 结 构 加 以替 换 重 组 而 生 成 新 个 体 的操 作 。遗 传 算 法 中起 核 心 作 用 的 就 是 交 叉 算 子 。 ( 5 ) 变异运算 : 将 变 异 算 子 作 用 于 群 体 。 即 是 对 群 体
多目标遗传算法------NSGA-II(部分源码解析)拥挤距离计算crowddist.c
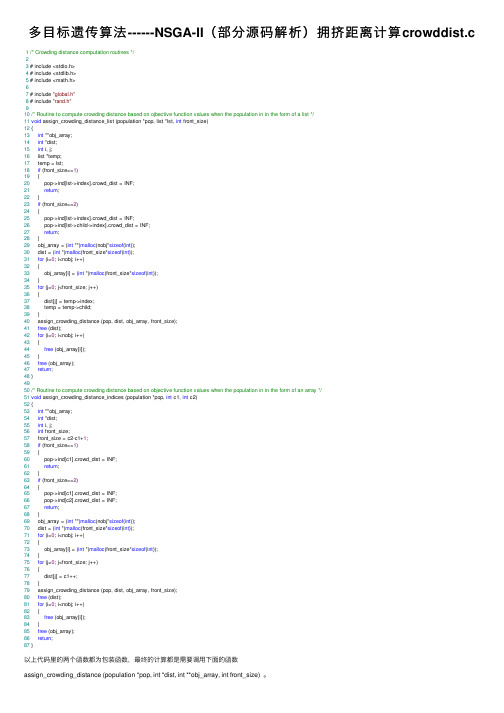
多⽬标遗传算法------NSGA-II(部分源码解析)拥挤距离计算crowddist.c 1/* Crowding distance computation routines */23 # include <stdio.h>4 # include <stdlib.h>5 # include <math.h>67 # include "global.h"8 # include "rand.h"910/* Routine to compute crowding distance based on ojbective function values when the population in in the form of a list */11void assign_crowding_distance_list (population *pop, list *lst, int front_size)12 {13int **obj_array;14int *dist;15int i, j;16 list *temp;17 temp = lst;18if (front_size==1)19 {20 pop->ind[lst->index].crowd_dist = INF;21return;22 }23if (front_size==2)24 {25 pop->ind[lst->index].crowd_dist = INF;26 pop->ind[lst->child->index].crowd_dist = INF;27return;28 }29 obj_array = (int **)malloc(nobj*sizeof(int));30 dist = (int *)malloc(front_size*sizeof(int));31for (i=0; i<nobj; i++)32 {33 obj_array[i] = (int *)malloc(front_size*sizeof(int));34 }35for (j=0; j<front_size; j++)36 {37 dist[j] = temp->index;38 temp = temp->child;39 }40 assign_crowding_distance (pop, dist, obj_array, front_size);41free (dist);42for (i=0; i<nobj; i++)43 {44free (obj_array[i]);45 }46free (obj_array);47return;48 }4950/* Routine to compute crowding distance based on objective function values when the population in in the form of an array */51void assign_crowding_distance_indices (population *pop, int c1, int c2)52 {53int **obj_array;54int *dist;55int i, j;56int front_size;57 front_size = c2-c1+1;58if (front_size==1)59 {60 pop->ind[c1].crowd_dist = INF;61return;62 }63if (front_size==2)64 {65 pop->ind[c1].crowd_dist = INF;66 pop->ind[c2].crowd_dist = INF;67return;68 }69 obj_array = (int **)malloc(nobj*sizeof(int));70 dist = (int *)malloc(front_size*sizeof(int));71for (i=0; i<nobj; i++)72 {73 obj_array[i] = (int *)malloc(front_size*sizeof(int));74 }75for (j=0; j<front_size; j++)76 {77 dist[j] = c1++;78 }79 assign_crowding_distance (pop, dist, obj_array, front_size);80free (dist);81for (i=0; i<nobj; i++)82 {83free (obj_array[i]);84 }85free (obj_array);86return;87 }以上代码⾥的两个函数都为包装函数,最终的计算都是需要调⽤下⾯的函数assign_crowding_distance (population *pop, int *dist, int **obj_array, int front_size) 。
用遗传算法求解多目标函数优化c++程序

遗传算法是一种优化搜索方法,它模拟了自然选择和遗传学中的一些概念,如基因突变、交叉和选择。
这种方法可以用于解决多目标优化问题,其中多个目标之间可能存在冲突。
以下是一个使用C++和OpenCV库实现遗传算法的基本示例。
这个例子解决的是一个简单的多目标优化问题,目标是找到一个最优的图像分割方案,使得两个目标(分割的精度和计算的效率)同时最大化。
注意:这个示例是为了演示遗传算法的基本概念,并不一定适用于所有问题。
你可能需要根据你的具体需求来调整遗传算法的参数和约束条件。
```cpp#include <iostream>#include <vector>#include <algorithm>#include <opencv2/opencv.hpp>// 多目标函数优化struct ObjectiveFunction {std::vector<double> values;void operator()(const std::vector<double>& x) const {// 这里应该根据你的具体问题来定义函数的具体形式// 这里只是一个简单的示例,只考虑了分割精度和计算效率两个目标values.resize(x.size(), 0); // 初始化所有目标值为0values[0] = 1.0; // 精度目标values[1] = 1.0; // 效率目标}};class GeneticAlgorithm {public:GeneticAlgorithm(int populationSize, int generations, double crossoverRate, double mutationRate) : populationSize(populationSize), generations(generations), crossoverRate(crossoverRate), mutationRate(mutationRate) {} std::vector<std::vector<double>> optimize(const std::vector<std::vector<double>>& inputs) {std::vector<std::vector<double>>bestSolution(inputs.size(),std::vector<double>(populationSize, 0)); // 初始化最优解double bestScore = -1; // 初始最佳分数为-1,通常需要先运行一次算法以找到初始最佳分数for (int generation = 0; generation <generations; ++generation) {std::vector<std::vector<double>>population(populationSize,std::vector<double>(populationSize, 0)); // 初始化种群for (int i = 0; i < populationSize; ++i) { std::vector<double>randomSolution(inputs.size(), 0); // 随机生成解for (int j = 0; j < inputs.size(); ++j) {randomSolution[j] = inputs[j][rand() % inputs[j].size()]; // 在输入范围内随机选择一个数作为解}population[i] = randomSolution; // 将随机解加入种群}while (!population.empty()) { // 当种群不为空时继续迭代std::sort(population.begin(), population.end(), [](const std::vector<double>& a, const std::vector<double>& b) { // 对种群进行排序,根据适应度进行排序(这里适应度是解的分数)return ObjectiveFunction()(a) > ObjectiveFunction()(b); // 如果分数更高,则适应度更好,优先选择这个解作为下一代解的一部分});std::vector<double>nextGeneration(population[0]); // 选择当前种群中的第一个解作为下一代解的一部分for (int j = 1; j < populationSize; ++j) { // 对剩余的解进行交叉和变异操作,生成下一代解if (rand() / double(RAND_MAX) < crossoverRate) { // 如果满足交叉条件,则进行交叉操作for (int k = 0; k < inputs.size(); ++k) { // 将两个解的部分基因进行交叉操作,生成新的基因序列nextGeneration[k] = population[j][k]; // 将两个解的部分基因复制到下一代解中if (rand() / double(RAND_MAX) < mutationRate) { // 如果满足变异条件,则对部分基因进行变异操作,增加种群的多样性nextGeneration[k] = nextGeneration[k] * (1 - mutationRate) + population[j][k] * mutationRate; // 对部分基因进行变异操作,增加种群的多样性}}} else { // 如果不满足交叉条件,则直接复制当前解作为下一代解的一部分for (int k = 0; k < inputs.size(); ++k) { // 将当前解的部分基因复制到下一代解中 nextGeneration[k] = population[。
遗传算法介绍并附上Matlab代码
1、遗传算法介绍遗传算法,模拟达尔文进化论的自然选择和遗产学机理的生物进化构成的计算模型,一种不断选择优良个体的算法。
谈到遗传,想想自然界动物遗传是怎么来的,自然主要过程包括染色体的选择,交叉,变异(不明白这个的可以去看看生物学),这些操作后,保证了以后的个基本上是最优的,那么以后再继续这样下去,就可以一直最优了。
2、解决的问题先说说自己要解决的问题吧,遗传算法很有名,自然能解决的问题很多了,在原理上不变的情况下,只要改变模型的应用环境和形式,基本上都可以。
但是遗传算法主要还是解决优化类问题,尤其是那种不能直接解出来的很复杂的问题,而实际情况通常也是这样的。
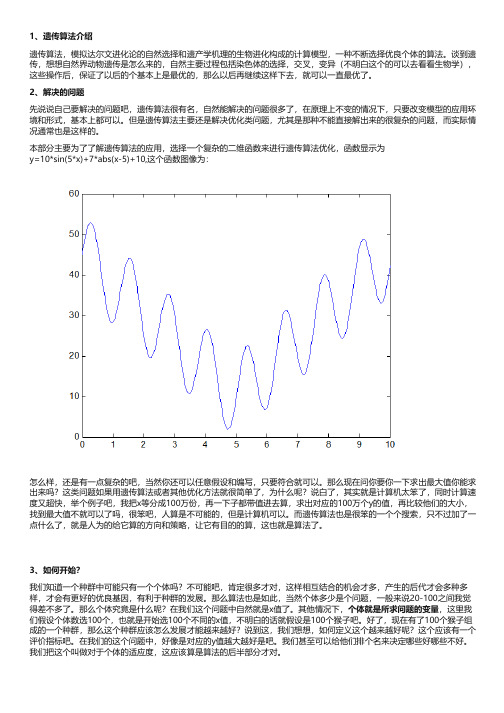
本部分主要为了了解遗传算法的应用,选择一个复杂的二维函数来进行遗传算法优化,函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为:怎么样,还是有一点复杂的吧,当然你还可以任意假设和编写,只要符合就可以。
那么现在问你要你一下求出最大值你能求出来吗?这类问题如果用遗传算法或者其他优化方法就很简单了,为什么呢?说白了,其实就是计算机太笨了,同时计算速度又超快,举个例子吧,我把x等分成100万份,再一下子都带值进去算,求出对应的100万个y的值,再比较他们的大小,找到最大值不就可以了吗,很笨吧,人算是不可能的,但是计算机可以。
而遗传算法也是很笨的一个个搜索,只不过加了一点什么了,就是人为的给它算的方向和策略,让它有目的的算,这也就是算法了。
3、如何开始?我们知道一个种群中可能只有一个个体吗?不可能吧,肯定很多才对,这样相互结合的机会才多,产生的后代才会多种多样,才会有更好的优良基因,有利于种群的发展。
那么算法也是如此,当然个体多少是个问题,一般来说20-100之间我觉得差不多了。
那么个体究竟是什么呢?在我们这个问题中自然就是x值了。
其他情况下,个体就是所求问题的变量,这里我们假设个体数选100个,也就是开始选100个不同的x值,不明白的话就假设是100个猴子吧。
遗传算法 c语言代码

以下是一个简单的遗传算法的C语言代码示例:c#include <stdio.h>#include <stdlib.h>#include <time.h>#include <math.h>#define POPULATION_SIZE 100#define GENE_LENGTH 10#define MAX_GENERATIONS 1000#define MUTATION_RATE 0.01#define CROSSOVER_RATE 0.8typedef struct Individual {char genes[GENE_LENGTH];double fitness;} Individual;double calculate_fitness(Individual* individual) {// 计算适应度函数,这里使用简单的二进制字符串中1的个数作为适应度 int count = 0;for (int i = 0; i < GENE_LENGTH; i++) {if (individual->genes[i] == '1') {count++;}}return count;}void initialize_population(Individual* population) {// 初始化种群for (int i = 0; i < POPULATION_SIZE; i++) {for (int j = 0; j < GENE_LENGTH; j++) {population[i].genes[j] = rand() % 2 ? '0' : '1';}population[i].fitness = calculate_fitness(&population[i]); }}void selection(Individual* population, Individual* parents) {// 选择操作,采用轮盘赌算法选择两个父代个体double total_fitness = 0;for (int i = 0; i < POPULATION_SIZE; i++) {total_fitness += population[i].fitness;}double rand1 = rand() / (double)RAND_MAX * total_fitness;double rand2 = rand() / (double)RAND_MAX * total_fitness;double cumulative_fitness = 0;int parent1_index = -1, parent2_index = -1;for (int i = 0; i < POPULATION_SIZE; i++) {cumulative_fitness += population[i].fitness;if (rand1 < cumulative_fitness && parent1_index == -1) {parent1_index = i;}if (rand2 < cumulative_fitness && parent2_index == -1) {parent2_index = i;}}parents[0] = population[parent1_index];parents[1] = population[parent2_index];}void crossover(Individual* parents, Individual* offspring) {// 交叉操作,采用单点交叉算法生成两个子代个体int crossover_point = rand() % GENE_LENGTH;for (int i = 0; i < crossover_point; i++) {offspring[0].genes[i] = parents[0].genes[i];offspring[1].genes[i] = parents[1].genes[i];}for (int i = crossover_point; i < GENE_LENGTH; i++) {offspring[0].genes[i] = parents[1].genes[i];offspring[1].genes[i] = parents[0].genes[i];}offspring[0].fitness = calculate_fitness(&offspring[0]);offspring[1].fitness = calculate_fitness(&offspring[1]);}void mutation(Individual* individual) {// 变异操作,以一定概率翻转基因位上的值for (int i = 0; i < GENE_LENGTH; i++) {if (rand() / (double)RAND_MAX < MUTATION_RATE) {individual->genes[i] = individual->genes[i] == '0' ? '1' : '0'; }}individual->fitness = calculate_fitness(individual);}void replace(Individual* population, Individual* offspring) {// 替换操作,将两个子代个体中适应度更高的一个替换掉种群中适应度最低的一个个体int worst_index = -1;double worst_fitness = INFINITY;for (int i = 0; i < POPULATION_SIZE; i++) {if (population[i].fitness < worst_fitness) {worst_index = i;worst_fitness = population[i].fitness;}}if (offspring[0].fitness > worst_fitness || offspring[1].fitness > worst_fitness) {if (offspring[0].fitness > offspring[1].fitness) {population[worst_index] = offspring[0];} else {population[worst_index] = offspring[1];}}}。
邻域培植多目标遗传算法ncga简介

邻域培植多目标遗传算法ncga简介下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!邻域培植多目标遗传算法(Neighborhood Cultivation Multi-Objective Genetic Algorithm, NCGA)是一种结合了邻域搜索技术和多目标优化方法的进化算法。
nsga2算法 python代码

nsga2算法 python代码NSGA-II(Nondominated Sorting Genetic Algorithm II)是一种多目标优化算法,适用于解决具有多个决策变量和目标函数的优化问题。
该算法引入了非支配排序和拥挤度距离的概念,能够在不依赖问题特定知识的情况下高效地搜索多目标优化问题的解集。
在NSGA-II中,算法的核心部分包括:选择、交叉和变异。
首先,通过使用快速非支配排序将种群划分为不同的前沿,并计算每个个体的拥挤度距离。
然后,通过轮盘赌选择方法,选择与给定前沿相同数量的个体作为下一代的父代。
接下来,对选择的父代进行交叉和变异操作产生新的个体,并将其添加到子代中。
最后,通过混合父代和子代的方式生成下一代种群,并重复以上步骤直到满足停止条件。
下面是一个简单的NSGA-II算法的Python实现:```pythonimport random#定义目标函数def obj_func(x):return [x[0]**2, (x[0]-2)**2]#定义个体类class Individual:def __init__(self, x):self.x = xself.obj_values = obj_func(x)self.rank = Noneself.crowding_distance = None#初始化种群def init_population(pop_size, n_var):population = []for _ in range(pop_size):x = [random.uniform(0, 5) for _ in range(n_var)]population.append(Individual(x))return population#计算个体之间的非支配关系def non_dominated_sort(population):fronts = [[]]for ind in population:ind.domination_count = 0ind.dominated_set = []for other_ind in population:if ind.obj_values[0] < other_ind.obj_values[0] and ind.obj_values[1] < other_ind.obj_values[1]:ind.dominated_set.append(other_ind)elif ind.obj_values[0] > other_ind.obj_values[0] and ind.obj_values[1] > other_ind.obj_values[1]:ind.domination_count += 1if ind.domination_count == 0:ind.rank = 0fronts[0].append(ind)curr_front = 0while len(fronts[curr_front]) > 0: next_front = []for ind in fronts[curr_front]:for other_ind in ind.dominated_set: other_ind.domination_count -= 1if other_ind.domination_count == 0: other_ind.rank = curr_front + 1 next_front.append(other_ind)curr_front += 1fronts.append(next_front)return fronts#计算个体的拥挤度距离def crowding_distance_assignment(front):n = len(front)for ind in front:ind.crowding_distance = 0for m in range(len(front[0].obj_values)):front.sort(key=lambda x: x.obj_values[m])front[0].crowding_distance = float('inf')front[n-1].crowding_distance = float('inf')for i in range(1, n-1):front[i].crowding_distance += (front[i+1].obj_values[m] - front[i-1].obj_values[m])#选择操作def selection(fronts, pop_size):new_population = []for front in fronts:crowding_distance_assignment(front)front.sort(key=lambda x: x.crowding_distance, reverse=True)new_population += frontif len(new_population) >= pop_size:breakreturn new_population[:pop_size]#交叉操作def crossover(parent1, parent2):n_var = len(parent1.x)child1 = Individual([0]*n_var)child2 = Individual([0]*n_var)#生成交叉点cxpoint1 = random.randint(0, n_var-1)cxpoint2 = random.randint(0, n_var-1)if cxpoint1 > cxpoint2:cxpoint1, cxpoint2 = cxpoint2, cxpoint1#执行交叉child1.x = parent1.x[:cxpoint1] +parent2.x[cxpoint1:cxpoint2] + parent1.x[cxpoint2:] child2.x = parent2.x[:cxpoint1] +parent1.x[cxpoint1:cxpoint2] + parent2.x[cxpoint2:] return child1, child2#变异操作def mutation(individual):n_var = len(individual.x)mutant = Individual(individual.x[:])#选择变异位点mutation_point = random.randint(0, n_var-1)#执行变异mutant.x[mutation_point] = random.uniform(0, 5) return mutant# NSGA-II算法主函数def nsga2(pop_size, n_var, n_gen):population = init_population(pop_size, n_var) for _ in range(n_gen):fronts = non_dominated_sort(population) population = selection(fronts, pop_size)for i in range(pop_size):if random.random() < 0.9:parent1 = random.choice(population)parent2 = random.choice(population)child1, child2 = crossover(parent1, parent2)population[i] = mutation(child1)else:population[i] = mutation(random.choice(population))return population#测试population = nsga2(100, 1, 100)for ind in population:print(ind.x, ind.obj_values)```该例子实现了一个目标函数为两个二次函数的一维优化问题。
遗传算法matlab代码0304190947

tmpind=tmprnd if ~any(difind) difind(1)=1; end
difind=[0,diff(tmpieind(logical(difind)); fatherrand=fatherrand(:,childind); generation=generation+1; end % score maxV=max(score,[],2); minV=11*300-maxV; plot(minV,'*');title('各代的目标函数值'); F4=D(:,4); FF4=F4-fatherrand(:,1); FF4=max(FF4,1); D(:,5)=FF4; save DData D function D=code load youhua.mat % properties F2 and F3 F1=A(:,1); F2=A(:,2); F3=A(:,3); if (max(F2)>1450)||(min(F2)<=900) error('DATA property F2 exceed it''s range (900,1450]') end % get group property F1 of data, according to F2 value F4=zeros(size(F1)); for ite=11:-1:1 index=find(F2<=900+ite*50); F4(index)=ite; end D=[F1,F2,F3,F4]; function ScoreN=scorefun(fatherrand,D) F3=D(:,3); F4=D(:,4); N=size(fatherrand,2); FF4=F4*ones(1,N); FF4rnd=FF4-fatherrand; FF4rnd=max(FF4rnd,1); ScoreN=ones(1,N)*300*11; % 这里有待优化 for k=1:N FF4k=FF4rnd(:,k); for ite=1:11
多目标优化遗传算法

多目标优化遗传算法多目标优化遗传算法(Multi-objective Optimization Genetic Algorithm, MOGA)是一种通过模拟生物进化过程,寻找多个最优解的优化算法。
其主要应用于多目标决策问题,可以在多个决策变量和多个目标函数之间找到最优的平衡点。
MOGA算法的基本原理是模拟自然界的进化过程,通过交叉、变异和选择等操作,生成并更新一组候选解,从中筛选出一组最优解。
具体步骤如下:1. 初始化种群:随机生成一组初代候选解,称为种群。
种群中的每个个体都是决策变量的一组取值。
2. 评估适应度:针对每个个体,通过目标函数计算其适应度值。
适应度值代表了个体在当前状态下的优劣程度,可以根据具体问题进行定义。
3. 交叉和变异:通过交叉和变异操作,生成一组新的个体。
交叉操作模拟了个体之间的交配,将两个个体的染色体进行交叉,生成两个新个体。
变异操作模拟了个体基因的变异,通过对个体的染色体进行随机改变,生成一个新个体。
4. 选择:从种群中选择适应度较高的个体,作为下一代种群的父代。
常用的选择策略包括轮盘赌选择、锦标赛选择等。
5. 重复执行步骤2~4,直到满足停止条件。
停止条件可以是达到指定的迭代次数,或达到一定的收敛程度等。
MOGA算法的优点在于可以同时找到多个最优解,而不仅限于单目标优化问题。
它可以通过调整交叉和变异的概率来平衡个体的多样性和收敛性。
然而,MOGA算法也存在一些局限性。
首先,算法的性能高度依赖于目标函数的设计和参数的选择。
不同的问题需要采用不同的适应度函数、交叉变异操作和选择策略。
此外,MOGA算法在处理高维问题时,容易受到维度灾难的困扰,导致搜索效果较差。
总之,多目标优化遗传算法是一种有效的优化算法,可以用于解决多目标决策问题。
通过模拟生物进化过程,寻找多个最优解,找到问题的多个最优平衡点。
不过,在应用中需要根据具体问题进行参数调整,以及避免维度灾难的影响。
多目标遗传算法

多目标遗传算法多目标遗传算法(MOGA)是一种基于遗传算法的优化算法,专门用于解决具有多个目标的优化问题。
与单目标遗传算法不同的是,MOGA可以同时优化多个目标函数,找到多个满足一定条件的优化解。
MOGA的基本思想是利用遗传算法的进化过程来搜索解空间中的非劣解集合。
它采用一种特殊的个体编码方式,即每个个体都有多个目标函数值。
在每一代进化中,通过选择、交叉和变异等操作,产生新的个体,并计算它们的目标函数值。
然后根据非劣解排序的原则,选择出一部分优秀的个体作为父代,并从中产生下一代个体。
通过不断重复这个过程,逐渐逼近最佳解集合。
MOGA的核心操作是选择、交叉和变异。
选择操作是根据个体的适应度值来确定被选择的概率。
一般来说,适应度值越好的个体被选择的概率越大。
交叉操作是将两个个体的染色体按照一定的规则进行交换,生成新的个体。
变异操作是对个体的染色体进行随机的变异,增加个体的多样性。
通过这些操作,逐渐产生具有更优的目标函数值的个体。
MOGA的优点是能够找到多个满足优化条件的解,并且这些解构成了一个非劣解集合,可以为决策者提供多个选择的方案。
另外,MOGA还具有较强的鲁棒性和全局搜索能力,能够较好地处理复杂的多目标优化问题。
MOGA的应用范围非常广泛。
例如,在工程设计中,可以用MOGA来寻找多个满足设计要求的最优结构;在生产调度中,可以用MOGA来寻找多个平衡的生产方案等。
总之,多目标遗传算法是一种有效的优化算法,通过遗传算法的进化过程,能够同时优化多个目标函数,找到多个满足一定条件的优化解。
它具有较强的鲁棒性和全局搜索能力,并且在工程设计、生产调度等领域有着广泛的应用。
(完整版)遗传算法简介及代码详解

遗传算法简述及代码详解声明:本文内容整理自网络,认为原作者同意转载,如有冒犯请联系我。
遗传算法基本内容遗传算法为群体优化算法,也就是从多个初始解开始进行优化,每个解称为一个染色体,各染色体之间通过竞争、合作、单独变异,不断进化。
遗传学与遗传算法中的基础术语比较染色体:又可以叫做基因型个体(individuals)群体/种群(population):一定数量的个体组成,及一定数量的染色体组成,群体中个体的数量叫做群体大小。
初始群体:若干染色体的集合,即解的规模,如30,50等,认为是随机选取的数据集合。
适应度(fitness):各个个体对环境的适应程度优化时先要将实际问题转换到遗传空间,就是把实际问题的解用染色体表示,称为编码,反过程为解码/译码,因为优化后要进行评价(此时得到的解是否较之前解优越),所以要返回问题空间,故要进行解码。
SGA采用二进制编码,染色体就是二进制位串,每一位可称为一个基因;如果直接生成二进制初始种群,则不必有编码过程,但要求解码时将染色体解码到问题可行域内。
遗传算法的准备工作:1) 数据转换操作,包括表现型到基因型的转换和基因型到表现型的转换。
前者是把求解空间中的参数转化成遗传空间中的染色体或者个体(encoding),后者是它的逆操作(decoding)2) 确定适应度计算函数,可以将个体值经过该函数转换为该个体的适应度,该适应度的高低要能充分反映该个体对于解得优秀程度。
非常重要的过程。
遗传算法基本过程为:1) 编码,创建初始群体2) 群体中个体适应度计算3) 评估适应度4) 根据适应度选择个体5) 被选择个体进行交叉繁殖6) 在繁殖的过程中引入变异机制7) 繁殖出新的群体,回到第二步实例一:(建议先看实例二)求 []30,0∈x 范围内的()210-=x y 的最小值1) 编码算法选择为"将x 转化为2进制的串",串的长度为5位(串的长度根据解的精度设 定,串长度越长解得精度越高)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.% function nsga_2(pro)%% Main Function% Main program to run the NSGA-II MOEA.% Read the corresponding documentation to learn more about multiobjective % optimization using evolutionary algorithms.% initialize_variables has two arguments; First being the population size % and the second the problem number. '1' corresponds to MOP1 and '2' % corresponds to MOP2.%inp_para_definition=input_parameters_definition;%% Initialize the variables% Declare the variables and initialize their values% pop - population% gen - generations% pro - problem number%clear;clc;tic;pop = 100; % 每一代的种群数gen = 100; % 总共的代数pro = 2; % 问题选择1或者2,见switchswitch procase 1% M is the number of objectives.M = 2;% V is the number of decision variables. In this case it is% difficult to visualize the decision variables space while the % objective space is just two dimensional.V = 6;case 2M = 3;V = 12;case 3 % case 1和case 2 用来对整个算法进行常规验证,作为调试之用;case 3为本工程所需;M = 2; %(output parameters 个数)V = 8; %(input parameters 个数)K = 10;end% Initialize the populationchromosome = initialize_variables(pop,pro);%% Sort the initialized population% Sort the population using non-domination-sort. This returns two columns % for each individual which are the rank and the crowding distance% corresponding to their position in the front they belong. 真是牛 X了。
chromosome = non_domination_sort_mod(chromosome,pro);%% Start the evolution process..% The following are performed in each generation% Select the parents% Perfrom crossover and Mutation operator% Perform Selectionfor i = 1 : gen% Select the parents% Parents are selected for reproduction to generate offspring. The % original NSGA-II uses a binary tournament selection based on the % crowded-comparision operator. The arguments are% pool - size of the mating pool. It is common to have this to be half the% population size.% tour - Tournament size. Original NSGA-II uses a binary tournament % selection, but to see the effect of tournament size this is kept% arbitary, to be choosen by the user.pool = round(pop/2);tour = 2;%下面进行二人锦标赛配对,新的群体规模是原来群体的一半parent_chromosome = tournament_selection(chromosome,pool,tour);% Perfrom crossover and Mutation operator% The original NSGA-II algorithm uses Simulated Binary Crossover (SBX) and% Polynomial crossover. Crossover probability pc = 0.9 and mutation % probability is pm = 1/n, where n is the number of decision variables. % Both real-coded GA and binary-coded GA are implemented in the original % algorithm, while in this program only the real-coded GA is considered. % The distribution indeices for crossover and mutation operators as mu = 20% and mum = 20 respectively.mu = 20;mum = 20;% 针对对象是上一步产生的新的个体parent_chromosome%对parent_chromosome 每次操作以较大的概率进行交叉(产生两个新的候选人),或者较小的概率变异(一个新的候选人)操作,这样%就会产生较多的新个体offspring_chromosome =genetic_operator(parent_chromosome,pro,mu,mum);% Intermediate population% Intermediate population is the combined population of parents and % offsprings of the current generation. The population size is almost 1 and% half times the initial population.[main_pop,temp]=size(chromosome);[offspring_pop,temp]=size(offspring_chromosome);intermediate_chromosome(1:main_pop,:)=chromosome;..intermediate_chromosome(main_pop+1:main_pop+offspring_pop,1:M+V)=offs pring_chromosome;%intermediate_chromosome=inter_chromo(chromosome,offspring_chromo some,pro);% Non-domination-sort of intermediate population% The intermediate population is sorted again based on non-domination sort% before the replacement operator is performed on the intermediate % population.intermediate_chromosome = ...non_domination_sort_mod(intermediate_chromosome,pro);% Perform Selection% Once the intermediate population is sorted only the best solution is% selected based on it rank and crowding distance. Each front is filled in% ascending order until the addition of population size is reached. The% last front is included in the population based on the individuals with% least crowding distancechromosome = replace_chromosome(intermediate_chromosome,pro,pop); if ~mod(i,10)fprintf('%d\n',i);endend%% Result% Save the result in ASCII text format.save solution.txt chromosome -ASCII%% Visualize% The following is used to visualize the result for the given problem. switch procase 1plot(chromosome(:,V + 1),chromosome(:,V + 2),'y+');title('MOP1 using NSGA-II');xlabel('f(x_1)');ylabel('f(x_2)');case 2plot3(chromosome(:,V + 1),chromosome(:,V + 2),chromosome(:,V + 3),'*');title('MOP2 using NSGA-II');xlabel('f(x_1)');ylabel('f(x_2)');zlabel('f(x_3)');end%disp('run time is:')%toc; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f = initialize_variables(N,problem)..% function f = initialize_variables(N,problem)% N - Population size% problem - takes integer values 1 and 2 where,% '1' for MOP1% '2' for MOP2%% This function initializes the population with N individuals and each % individual having M decision variables based on the selected problem. % M = 6 for problem MOP1 and M = 12 for problem MOP2. The objective space % for MOP1 is 2 dimensional while for MOP2 is 3 dimensional.% Both the MOP's has 0 to 1 as its range for all the decision variables. min = 0;max = 1;switch problemcase 1M = 6;K = 8; % k=决策变量(M=6)+目标变量(K-M=2)=8case 2M = 12;K = 15;case 3 % case 1和case 2 用来对整个算法进行常规验证,作为调试之用;case3为本工程所需;M = 8; %(input parameters 个数)K = 10;endfor i = 1 : N% Initialize the decision variablesfor j = 1 : Mf(i,j) = rand(1); % i.e f(i,j) = min + (max - min)*rand(1);end% Evaluate the objective functionf(i,M + 1: K) = evaluate_objective(f(i,:),problem);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f = evaluate_objective(x,problem)% Function to evaluate the objective functions for the given input vector % x. x has the decision variablesswitch problemcase 1f = [];%% Objective function onef(1) = 1 - exp(-4*x(1))*(sin(6*pi*x(1)))^6;sum = 0;..for i = 2 : 6sum = sum + x(i)/4;end%% Intermediate functiong_x = 1 + 9*(sum)^(0.25);%% Objective function onef(2) = g_x*(1 - ((f(1))/(g_x))^2);case 2f = [];%% Intermediate functiong_x = 0;for i = 3 : 12g_x = g_x + (x(i) - 0.5)^2;end%% Objective function onef(1) = (1 + g_x)*cos(0.5*pi*x(1))*cos(0.5*pi*x(2));%% Objective function twof(2) = (1 + g_x)*cos(0.5*pi*x(1))*sin(0.5*pi*x(2));%% Objective function threef(3) = (1 + g_x)*sin(0.5*pi*x(1));case 3f = [];%% Objective function onef(1) = 0;%% Objective function onef(2) = 0;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Non-Donimation Sort %按照目标函数最小了好% This function sort the current popultion based on non-domination. All the% individuals in the first front are given a rank of 1, the second front % individuals are assigned rank 2 and so on. After assigning the rank the % crowding in each front is calculated.function f = non_domination_sort_mod(x,problem)[N,M] = size(x);switch problemcase 1M = 2;V = 6;case 2M = 3;V = 12;case 3 % case 1和case 2 用来对整个算法进行常规验证,作为调试之用;case 3为本工程所需;..M = 2; %(output parameters 个数)V = 8; %(input parameters 个数)K = 10;endfront = 1;% There is nothing to this assignment, used only to manipulate easily in % MATLAB.F(front).f = [];individual = [];for i = 1 : N% Number of individuals that dominate this individual 支配i的解的个数individual(i).n = 0;% Individuals which this individual dominate 被i支配的解individual(i).p = [];for j = 1 : Ndom_less = 0;dom_equal = 0;dom_more = 0;for k = 1 : Mif (x(i,V + k) < x(j,V + k))dom_less = dom_less + 1;elseif (x(i,V + k) == x(j,V + k))dom_equal = dom_equal + 1;elsedom_more = dom_more + 1;endend% 这里只要考虑到求取得是函数的最小值就可以了,此时支配的概念就会变为谁的函数值小,谁去支配别的解%——————————————————————if dom_less == 0 & dom_equal ~= M % 举个例子,其中i=a,b; j= c,d; 如果i中的a,b全部大于individual(i).n = individual(i).n + 1; % 或者部分大于j中的c,d(但没有小于的情况),则称为i优于j,elseif dom_more == 0 & dom_equal ~= M % 当i优于j的时候,则此时把individual(i)_n加1individual(i).p = [individual(i).p j]; %如果i中的a,b全部小于或者部分小于j中的c,d(但没有大于的情况),则end %则称为j优于i, 则把此时的j放入individual(i)_P中;end %总之,就是说两个目标变量必须全部大于或者全部小于才能对individual有效。
