第四章 光学仪器
第四章光学仪器显微镜望远镜的放大本领
詹姆斯· 格雷戈里在1663年提出一种方案:利用一面主 镜,一面副镜,它们均为凹面镜,副镜置于主镜的焦点之外, 并在主镜的中央留有小孔,使光线经主镜和副镜两次反射后 从小孔中射出,到达目镜。这种设计的目的是要同时消除球 差和色差,这就需要一个抛物面的主镜和一个椭球面的副镜, 这在理论上是正确的,但当时的制造水平却无法达到这种要 求,所以格雷戈里无法得到对他有用的镜子。
• 光路图:如上图示。可适当调节物镜和目镜的距离,使Q’刚好在视镜的 物方焦平面上,使出射光束为平行光束。
• 由于场镜的物为实物,所以可用其对物镜所成的像进行测量。分划板应配 置于FQ处,由于分划板同物FQ一样既对场镜,也对视镜成像,所以,场 镜的消像差作用起作用,因而,可在大范围内清晰成像,测量精度高。
' '
O
S’
l'
Q P
即:M等于两视角之比
U
O
l
③由上式可看出:助视仪器的作用就是增大人眼视角,从而改善和扩展视野。
u' ④注意放大本领 与角放大率 的区别。 u u , u ' : 是 对 一 个 光 具 组 的 入 、 出 射 线 的 倾 角, 是 一 对 共 轭 量 ;
U' M U
未使用望远镜时,无穷远处物体对眼睛的张角为:
''
U'
y y
'
'
y U
'
f2
f
' 2
U '' f1' 伽利略望远镜的放大本领: M U f 2'
说明:
f1'
① f1`为正值,f2`为负值,故放大本领M为正值,望远镜成正立的像;
光学仪器的基本原理

{
的光学系统成的象。
出射光瞳——限制出射光线,有效光阑被它后面
的光学系统成的象。
既可以为实物,也可以为象。
分析有效光阑、入射光瞳、出射光瞳的思路:
(1)明确考虑的物点P; (2)所有光阑(包括透镜)对它前面透镜成象; (3)由确定物点对所有像做张角,比较所得的张角, 张角最小者所对应的物就是有效光阑; (4)张角最小的象即是入射光瞳; (5)有效光阑对其右边的光学系统成象得到出射 光瞳。
(sr为球面度)
五、照度和出射度
照度E——单位面积上接收的光通量。
E d dS
单位:勒克斯(lux), lm/m2
点光源
E Id I cosdS
dS
dS
R2
I
cos
R2
α
R
dS
面光源 出射度M——单位面积上辐射出来的光通量。
M d dS
单位:勒克斯(lux), lm/m2
六、亮度
亮度L——辐射面上单位投影面积,在单位 立体角内辐射的光通量。
y1 f1'
放大本领:
M
tan u' tan u
y1' y1'
f
' 2
f1'
f1' f2'
∴
M
f1'
f
' 2
M<0,倒立象
有限远的物
物镜
目镜
u
F1•'
F2
-u'
放大本领:
M
tan u' tan u
y1' y1'
f2' s1'
s1' f2'
现代光学基础课件:第四章 光学仪器的基本原理

• 放大镜放大率的公式,通常采用以下形式
M 250 f'
• 放大镜的放大率仅由放大镜的焦距f ′ 所决定,焦 距越大则放大率越小。
§4-3 目 镜
放大镜是一种通过直接放大实物达到增大视角的助视仪器。下面将介绍 一种放大像的助视仪器——目镜。 一、目镜
• 由于场镜的物为虚物,所以这种目镜无法对物镜所成的像进行测量。
• 此目镜的视角较大(可达400),在250范围内像更清晰。而且结构 紧凑,适用于生物显微镜。
2、冉斯登目镜 1
Q 'Q
2
⑴ 结构:如图示 3
⑵ 特点:
F2 F
o1
• 场镜、视镜均为同种材
3
F1' 3
o2
2
2
料的平凸透镜,二镜凸 面相向,平面朝外。
网膜 脉络膜 黄斑中心凹
前室
晶状体
盲斑
总能将像成在网膜上。
后室
角膜和晶状体之间的空间称为前室;充满1.336的水状液;
晶状体和网膜所包围的空间称为后室;充满1.336的玻状体
人眼的构造剖视图
瞳孔 虹膜 角膜
1.376
前室
1.336
晶状体
巩膜
网膜 脉络膜 黄斑中心凹
视轴
光轴
盲斑
后室 1.336
眼睛的像方节点与中心凹的连线为眼睛的视轴, 在观察物 体时眼睛本能地把物体瞄准在这根轴上。
x'
f1' f1'
• 物镜的像被目镜放大,其放大率为
Me
250 f2 '
• 式中: f2' 为目镜的焦距。由此,显微镜系统的
《光学教程》姚启钧原著第四章光学仪器基本基本原理

《光学教程》姚启钧原著第四章光
7
学仪器基本基本原理
(四)、像面弯曲
1.现象:对较大物平面经透镜后成的像是抛物面。 2. 消除方法:采用组合系统,适当的选配各透镜
的焦距和折射率。
《光学教程》姚启钧原著第四章光
8
学仪器基本基本原理
(五)、畸变
物平面
枕形畸变
桶形畸变
1、现象:像和物不能保持几何相似。
2、成因:由于物点离主轴的距离不同,而使得横 向放大率不同所引起。
Q
说明:
P
O
l
U
① 须将物放在同一特定位置比较两像大小。
② 放大镜和显微镜:明视距离处(25cm);
望远镜:无穷远《处光。学教程》姚启钧原著第四章光
23
学仪器基本基本原理
三、放大镜
Q`
最简单的放大镜--凸透镜:
L
U‘
y`
Q
使用放大镜的视角:
P`
y
O
FP
l'
U `
y`
s`
y
f
y f`
Q
-s`
-f U‘
一、目镜
1、定义:用于放大其它光具组所成像的助视仪器。 要求:A、放大本领高;
B、能校正像差、色差。 2、结构:场镜+视镜+分划板(刻度尺)
• 场镜: 面向物体的透镜(或透镜组)
• 视镜: 接近人眼的透镜(或透镜组)
• 分划板:包含透明刻度尺,用于提高测量精度。
《光学教程》姚启钧原著第四章光
27
学仪器基本基本原理
未用放大镜的视角: y
P
U y 25
放大镜的放大本领:
25cm
O
光学仪器的基本原理 光度学的基本概念

正常眼明视距离为25cm
一.放大本领定义
l ' tgu' u '
M
l tgu u
二.简单放大镜的放大本领
M
y s
y 25
y f 25
y 25 f
以cm为单位
一般3~5×复式放大镜可达20× ,物放在焦点内侧,成一放大正立虚象
三.显微镜的放大本领
书上导出方法可得 M
1
2
三.光源较远时物镜的聚光本领·相对孔径
E
d ds
B0n2
sin 2
u
代换 sin u
sin u
d x
2 x p
x xp
f
x f
x p f
f
p
∵ x
f
为物象的横向放大率 E' B0n'2 sin 2 u' B0n'2
4
d pd
1 4
B0 n' 2
2 p
d
第四章 光学仪器的基本原理
教学目的:
本章围绕衡量光学仪器特性的三个本领进行教学。通过本章的 学习,使学生掌握仪器常用的放大本领。了解仪器的震光本领及其 相关因素。使学生了解光度学中的一些基本概念,了解相差的一些 类型及成因 .
重点:放大本领和分辨本领 难点:光度学中的概念 教学方法:课堂讲授、结合仪器演示
d/ f'
显微镜物镜:象分辨本领 y' 1.22 s'
d
yn sin u y'n'sin u'
y 1 0.61 小y小
n sin u
三.分光仪器的色分辨本领
1.棱镜光谱仪 角色散率
第4章光学仪器的基本原理(第1讲)

为f ’: 1 1 1 f ' 2(m)
f ' s' s
光焦度 : 1 0.5(D)
f'
50度的近视眼镜。
§4.1 人的眼睛
第四章 光学仪器的基本原理
2、远视眼的矫正
方法:使放在明视距离处的物体经 凸透镜成像在被矫正眼的近点上。
例子 某人的近点为50cm。应戴 的凸透镜的焦距f ’ 为:
放大本领 、聚光本领、分辨本领
§4.1 人的眼睛
一、人眼的构造
1、从前到后,角膜前 房虹膜(中心为瞳 孔)晶状体玻璃 体视网膜。
2、眼睛有视觉暂留作用, 时间一般为简化眼模型
人眼可视为只有一个折射球面的简化眼。曲率半径为 5.7 mm;眼折射率为4/3;光焦度为58.48 m-1;物方焦距为17.1 mm;像方焦距为22.8 mm。
§4.1 人的眼睛
第四章 光学仪器的基本原理
三、非正常眼的矫正
睫状肌完全放松时,眼睛看清楚的最远点,称远点;肌 肉最紧张时看清的最近点,称近点。
远点为无穷远处,近点则为25 cm。
1、近视眼的矫正
方法:戴凹透镜,使无穷远处的
物体经凹透镜发散成一虚像在有限
远处,从而看清远物
例子 如某人近视眼的远点在2m,则应戴凹透镜,其焦距
1 1 1 f ' 50(cm) f ' s' s
光焦度: 1 2(D) 即200度的远视眼镜。
f'
3、散光眼
散光眼轴上的物点将成为两条像线,矫正的方法是戴一 柱状透镜,使其与眼的像散作用相反而相互抵消。
§4.1 人的眼睛
第四章 光学仪器的基本原理
第四章 光学仪器的基本原理
光学仪器的基本基本原理

1、近点、远点、明视距离
幼年 中年 老年
近点 7—8厘米 25厘米 1—2米
远点 无限远
几米
明视距离:25厘米
第四章光学仪器的基本基本原理
2、人眼的矫正
近视眼:远点不在∞,变近了 远视眼(老花眼):近点大于明视距离
矫正:戴一凹透镜将∞处的物 矫正:戴一凸透镜将明视距离上
成像于其能看到的远点。
的物成像于其能看到的近点上。
电子: 0.1A 1A (10 -2 10 -1 nm)
所以电子显微镜分辨本领很高,可观察物质 的结构。
1981年联邦德国宾尼格和瑞士罗雷尔 发明了遂道效应电子显微镜,并获1986年 诺贝尔物理奖。
第四章光学仪器的基本基本原理
例题
1、在迎面驶来的汽车上,两盏前灯相 120cm。 试问汽车离人多远的地方,眼睛恰能分辩这 两盏前灯?设夜间人眼瞳孔直径为 5.0mm , 入射光波长为 550nm,而且仅考虑人眼瞳孔的 衍射效应。
Q 1、物 Q距 F1很近,从而得到尽量大的实像 Q 。
2、目镜最后成的像 Q( 虚像)处于明视距离上。
因为f1′ 、f2′要求第很四章小光学, 仪器的故基s本′基≈本原x理′≈ ≈l(镜筒长)
二、显微镜的放大本领
s ≈ f1 、
y y
s s
≈
s f1
( -sf1)
s -
f1
y
≈- y
s f1
、f1要尽量小
(-U′′)= -
fy1′sf′2′、M
U U
25s f1 f2
s ≈x ≈ ≈l(镜筒长)
M
≈(- 25l)(f1 f2
xf1第四)章光(学仪2器f5的2基)本≈基本原物理 M目
光学仪器的基本原理

f2
f1'
Q P U O1
'
Q" U O U"
'
O2 U
F1` F2
使用望远镜: U '' U '
y y
f2
'
y'
Q
26
y 不用望远镜: U
f1'
f 2'
3、放大本领
'' ' U U 使用望远镜后,视角:
y y
远点变近:幼年—无限远;老年—数米
近点: 10cm; 远点:无穷远 定义: 明视距离: 25cm
4
(2) 人眼的缺陷及矫正——被动调节:外加辅助仪器改变焦距的过程。
① 近视眼:远点在有限远处的人眼。
特点:晶状体曲率半径比正常眼小,外形凸出;像方焦点在视网膜 前,焦距短。
矫正前
P 远点 O F‘ O
B、折射式望远镜:物镜为 透镜。 ② 按目镜种类分: A、开普勒望远镜:目镜为 会聚透镜; B、伽利略望远镜:目镜为 发散透镜。
23
三、开普勒望远镜 1、结构特点: 2、光路原理:
• 物镜、目镜均为会聚透镜; • 物镜 像方焦点与目镜物方焦点重合
无穷远处的物体PQ发出的平行光, 入射物镜,成实象PQ于象方焦平面 上;物镜的象方焦平面与目镜的物方焦平面重合,故最终由目镜 出射的光为平行光,成倒立象于无穷远处。
明视 距离 P’’ y
25 l 25 M ' ' ' ' f1 f 2 f1 f 2
Q
' l s1
F1
光学 第四章

成像的高度为: y s y 20 4 20cm s4
凹透镜经凸透镜所成的像对物点所张的孔径角uL2为:
uL2
arctg
y / 2 s 6
arctg
10 26
凸透镜对物点所张的孔径角 uL1
:uL1
arctg
y/2 6
arctg
2 6
uL2 uL1 所以凸透镜为同轴光具组的有效光阑。20
视角 U U ,由图知: U y f2
物镜的横向放大率为:
y s s s s y y s
y s f1 ( f1) f1
f1
U ys
f1f 2
8
不用显微镜直接看位于明视距离的物体,视角U:
U y 25cm
通过数码变焦,拍摄的景物放大了,但它的清晰度会有一 定程度的下降,所以数码变焦并没有太大的实际意义。
33
§4-10 助视仪器的像分ห้องสมุดไป่ตู้本领
★ 分辨本领 几何光学观点:对无像差系统,由于物像共轭,每一物点 都能成一个清晰的像点,即:物面上任何 微小的细节都能在像面上清晰反映出来。 波动光学观点:光束总会受到系统的有效光阑的限制,像 点应是物点的衍射图样,所以,在像面上 清晰的反映物面的细节是不可能的。
物点所成像点就是衍射图样中的中央亮斑。
34
中央亮斑的范围由第一个暗环的角半径1决定:
1
0.61
R
当两发光点较远时,像面上两像点可清晰区分;随
着距离的缩小,两像点将逐渐发生重叠。到达某一距离
(一个中央亮斑的最大值位置与另一个中央亮斑的最小
值位置重合),两像点刚能被分辨,之后,两像点就难
光学 第4章 光学仪器的基本原理

解:已知 s 0.25m,s' 1.25m, 由空气中的透镜的物象公式得: 光焦度:Φ 1 1 1 1 1 3.2(D) 凸透镜。 f ' s' s 1.25 0.25 凸透镜的度数 3100 300(度)
12
四.人眼的视角
③ 此目镜的视角大(可达40°),结构紧凑,适用于生物显微镜。
20
4.冉斯登目镜 (目标:最终的出射光线为平行光束) (1) 结构:由两个同种平凸透镜同向共轴而组成,两者的凸面相向,平面相背。
两透镜的间距等于透镜焦距的2/3倍,即 f1': d : f2' =1: 2/3 :1。
Q'
1
Q
2 3
F2 F
3 脉络膜—不透光暗褐色 膜,起遮光作用使眼内成 一暗房。
视神经
7 视网膜—含有许多 对光线敏感的细胞, 能感受到光的刺激。 当外面物体发出的光 束进入眼内在视网膜 上成像,由视神经传 到大脑而形成视觉。
2 角膜—巩膜在眼球前 凸出透明的部分,呈椭 圆形。有外物接触角膜, 眼睑便会由自主地合上 保护眼睛眼。
放大镜是可以帮助人眼看清微小物体及其细节的一种助视仪器。 凸透镜是最简单的放大镜。
14
1.放大本领
表达式:M l' l
l'
l s
s' tanU s'U ' tanU ' s'U '
M l' U' lU
又称视角放大率
Q
U
O
P
l
25cm
P'
s'
Q
U'
第4章光学仪器基本原理习题及解答

第四章 光学仪器的基本原理4.1.眼睛的构造简单地可用一折射球面来表示,其曲率半径为5.55mm ,内部为折射率等于43的液体,外部是空气,其折射率近似地等于1,试计算眼球的两个焦距。
用肉眼观察月球时月球对眼的张角为01,问视网膜上月球的像多大?解:眼睛的构造简单地可用一折射球面时,其物方焦点为'1 5.551.67413nr f cm n n⨯=-=-=---其像方焦点为'''43 5.55 2.22413n r f cm n n ==⨯=-- 根据折射定律有关系式''''''sin sin sin sin n n n nθθθθθθθθθ=≈≈≈因为很小,所以,''''''11tan 2.220.02941803n y d f f cm n θθθ=≈≈=⨯⨯=4.2.把人眼的晶状体看成距视网膜2cm 的一个简单透镜。
有人能看清楚距离在100cm 到300cm 间的物体,试问:(1)此人看清远点和近点时,眼睛透镜的焦距是多少?(2)为看清25cm 远的物体,需配戴怎样的眼镜?解:根据透镜的物像公式''111s s f -= (1)远点对应的焦距 将'2s cm = 300s cm =-代入上式''1112300300 1.987151f f cm-=-==近点对应的焦距将'2s cm = 100s cm =-代入上式''1112100100 1.96151f f cm-=-==(2)此人的近点为100cm ,要看清楚25cm 的物体,需要配戴眼镜使的25cm 的物体成虚象在100cm 处,所以应该配戴凸透镜(远视镜),根据透镜的物像公式''111s s f-= 其中'100s cm =- 25s cm =-'1110.10.25f =--- '1143300D f Φ==-+==(度)4.3.一照相机对准远物时,底片距物镜18cm ,当透镜拉至最大长度时,底片与物镜相距20cm ,求目的物在镜前的最近距离?解:根据透镜的物像公式''111s s f-= 当照相机对准远物时, 1s =-∞''11111s s f -= 所以 ''118s f cm ==当照相机对准最近物时,要成像必须把底片与物镜的距离拉到最大''22111s s f-= '220s cm =''21111112018s f s -=== 2180s cm =-目的物在镜前的最近距离为180厘米4.4.两星所成的视角为'4,用望远镜物镜照相,所得两像点相距1mm ,问望远镜物镜的焦距是多少?解:根据视角与透镜焦距的关系''1y U f -=, ''1185.987460180y f cm U π-===⨯ 4.5.一显微镜具有三个物镜和两个目镜。
最新第四章--光学仪器课件ppt

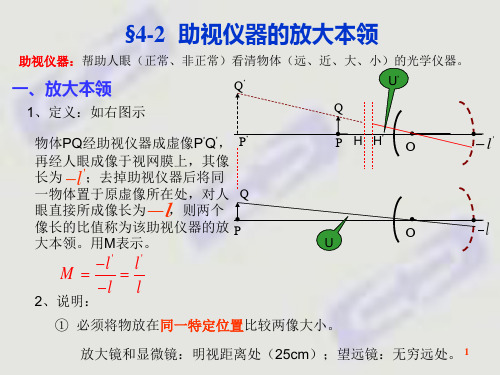
§4.2 助视仪器的放大本领
助视仪器: 帮助人眼(正常、非正常)看清物体(远、近、大、小)的光学仪器。
一、放大本领的概念 Q’
U’
1、定义:如右图示
Q
物体PQ经助视仪器成虚象P ’Q ’ , 再经人眼成像于视网膜上,其像长 P‘
为 l ';去掉助视仪器后将同一
物体置于原虚像所在处,对人眼直
接所成像长为 l,则两个像长 Q
的比值称为该助视仪器的放大本领。
用M表示。 M l '
P
2、说明:
l
P H H’ O
l'
O
l
U
① 必须将物放在同一特定位置比较两像大小。
放大镜和显微镜:明视距离处(25cm);望远镜:无穷远处。
② 在近轴条件下
Q’
l s 'tgU s 'U
l ' s 'tgU ' s 'U ' P‘
特点:晶状体曲率半径比正常眼小,外形凸出;像方焦点在视网膜 前,焦距短。
矫正前
P
O
F‘
远点
O
F‘
远物
P‘
O
远点
F‘
矫正后
[例4-1] 一个远点为0.2m的近视眼戴上眼镜后远点可恢复到无穷远。 求所戴眼镜的光焦度。
[解]:已知ss' 0.2m 由空气中的1高 1斯 1公式 s' s f'
有:f1' s1' 1ss1' 01.25(D)50(0屈光) 度
第四章--光学仪器
7. 了解光通量、发光强度、光照度和光亮度的概念及 其单位,特别是作为七个基本物理量之一的发光强度 的单位-坎德拉;
第四章光学仪器

解:因最后形成的象在无穷远处,说明
物镜成的象在目镜的物方焦平面上。
已知:f2'=2cm、f1'=0.5cm、L=22cm
物镜所成象的象距:s1'= L-f2'=20cm
第四章-光学仪器
———————————————————————————————— 作者:
———————————————————————————————— 日期:
第四章光学仪器的基本原理
1 眼睛的构造简单地可用一折射球面来表示,其曲率半径为5.55mm,内部为折射率等于4/3的液体,外部是空气,其折射率近似等于1,试计算眼球的两个焦距。用肉眼来观察月球时,月球对眼睛的张角为10,问视网膜上月球的象有多大?
毫米
(2)显微镜的放大本领
由 和 及物镜的横向放大率公式可得
而目镜的放大本领为
所以显微镜的放大本领为
12 一架伽利略望远镜,物镜和目镜之间距离为12厘米。若该望远镜的放大本领为4,试求物镜和目镜的焦距各是多少?
解:伽里略望远镜是用发散透镜来做目镜的,且物镜的象方焦点和目镜的物方焦点相重合。故由已知条件可得
附:若简单计算,
2 把人眼的晶状体看成距视网膜2cm的一个简单透镜,有人能看清距离在100cm到300cm间的物体。试问:(1)此人看清远点和近点时,眼睛透镜的焦距是多少?(2)为看清25cm远的物体,需配戴怎样的眼镜?
解:(1)设看清近点100cm处的物体,眼睛的焦距为f1',
此时,物距:s=-100cm、象距:s'=2cm
由: 解出:f1'=1.961cm
第四章光学仪器2011

返回
4.11.1 棱镜光谱仪
• (1). 角色散率:
• 或 D • 在最小偏向角 附近的角色散率的数值为: d d d dn D d d dn d
0
0 0
d D lim 0 d
• 而
n
sin
A
0
2 A sin 2
• (2). 分辨本领:u 0.610 1
R
• 式中 u 是两个发光点在光具组入射光瞳中心 所张的视角,θ 1 是各衍射图样第一暗环半径 的衍射角,R是入射光瞳的半径。 u 1 时,两点的像分辨得开; • u 1 时,则分辨不开。 • u 1 时的这个极限角成为光具组的分辨 • 极限,而它的倒数称为分辨本领。 • 此外,也可用像面上或物面上能够分辨的 两点之间的距离来表示分辨极限。
4.3
目 镜
4.3.1 目镜的作用 • (1). 作用: • 用来放大其它光具组(物镜)所成的像。 • (2). 构成: • 由不相接触的两个薄透镜组成。
场镜:面向物体的透镜 视镜:接近眼睛者
4.3.2 两种目镜
2 U 30 (
)
(1)惠更斯目镜: 两个同种玻璃的平凸透镜组成, 凸面都向着物镜。
• 视网膜上分布着视网膜上分布着光敏细胞, 光敏细胞分为两种: 圆柱细胞和圆锥细胞。 • 视锥细胞(core,C): 6.5百万/单眼,光敏 感度低,强光刺激才能引起兴奋,但具有 分辨颜色的能力。鸽子只有视锥细胞。 • 视杆细胞(rod, R):1.25亿/单眼,对弱光敏 感,不能分辨颜色。猫头鹰只有视杆细胞。
y 0.610
• •
n sin u
1932年,鲁斯卡—电子显微镜; 1982年,宾尼希、罗雷尔—扫描 隧穿电子显微镜; • 1986年,三人同获诺贝尔奖。
第四章 光学仪器的基本原理

返
回 上一页
第四章 光学仪器的基本原理
习
一对双星的角间隔为0.05〃。
5-4
题
4.1 (1)需要多大口径的望远镜才能分辨它们? (2)此望远镜的角放大率应设计为多少才比较合理? 4.2 一台天文望远镜的口径为2.16米,由这一数据你能进一步获得关于它在光学性能方面 的哪些知识? 4.3 一台显微镜,已知其N· A=1.32,物镜焦距f0 = 1.9mm,目镜焦距f = 50mm,求 (1)最小分辨距离; (2)有效放大率; (3) 光学筒长。 4.4 用一架照相机在离地面200公里的高空拍摄地面上的物体,如果要求它能分辨出地面 上相距1m的两点,照相机的镜头至少要多大?设镜头的几何象差已很好地消除,感 光波长4.000×10-5cm。 4.5 已知地月距离约为3.8×105公里,用口径为1m的天文望远镜能分辨月球表面两点的最 小距离是多少? 4.6 已知日地距离约为1.5×108公里,要求分辨太阳表面相距20公里的两点,望远镜的口 径至少需有多大?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 光学仪器的基本原理1 眼睛的构造简单地可用一折射球面来表示,其曲率半径为 5.55mm ,内部为折射率等于4/3的液体,外部是空气,其折射率近似等于1,试计算眼球的两个焦距。
用肉眼来观察月球时,月球对眼睛的张角为10,问视网膜上月球的象有多大?解:(1)根据单球面折射系统焦距的计算公式:r n n n f -''=' r nn n f -'-= 已知:n=1、n '=4/3、r=5.55mm ,代入公式,得:象方焦距:f '=22.2mm 物方焦距:f=-16.7mm(2)月球对眼睛的张角:U=10,在眼睛内,张角为U '在角度不太大时,折射定律:nsinU=n 'sinU '可近似写为:nU=n 'U ' 视网膜上的象长:cm n n Uf U f L 031.01801432.2200=⨯⨯⨯=''=''='π附:若简单计算,cm U f L 029.018012.2200=⨯⨯='='π2 把人眼的晶状体看成距视网膜2cm 的一个简单透镜,有人能看清距离在100cm 到300cm 间的物体。
试问:(1)此人看清远点和近点时,眼睛透镜的焦距是多少?(2)为看清25cm 远的物体,需配戴怎样的眼镜?解:(1)设看清近点100cm 处的物体,眼睛的焦距为f 1', 此时,物距:s=-100cm 、象距:s '=2cm由:f s s '=-'111 解出:f 1'=1.961cm 设看清远点300cm 处的物体,眼睛的焦距为f 2', 此时,物距:s=-300cm 、象距:s '=2cm 由:f s s '=-'111 解出:f 2'=1.987cm (2) 为看清25cm 处的物体,设需配戴眼镜的焦距为f ' 在成象时,物距: s=-25cm 、象距:s '=-100cm由:f s s '=-'111 解出:f 2'=1/3cm 光焦度:Φ=1/ f 2'=3屈光度=300度,即此人应佩戴300度的凸透镜。
3 一照相机对准远物时,底片距物镜18cm ,当镜头拉至最大长度时,底片与物镜相距20cm ,求目的物在镜前的最近距离。
解:当照相机对准远物时,物距为:s 1=-∞,象距为:s 1'=18cm设照相机镜头的焦距为f ',有:f s s '=-'11111解出焦距为:f '=18cm当镜头拉至最大长度成象时,象距为:s 2'=20cm ,设物距为s 2, 代入:f s s '=-'11122解出:s 2=-180cm 即物到镜头的最近距离为1.8m 。
4 两星所成的视角为4',用望远镜物镜照相,所得两象点相距1mm ,问望远镜物镜的焦距是多少?解:根据题意做出光路图。
已知:U=4'、y '=1mm由图得到:f y U ''≈/ cm Uy f 95.8518060141=⨯⨯'='='π5 一显微镜具有三个物镜和两个目镜,三个物镜的焦距分别为16mm 、4mm 、1.9mm ,两个目镜的放大本领分别为5和10倍。
设三个物镜形成的象都能落在象距160mm 处,问这显微镜的最大和最小放大本领为多少?解:因三个物镜形成的象都能落在象距160mm 处,且知道物镜的焦距,根据:f s f x ''-≈''-=β,分别计算得到物镜的横向放大率:β1=-10 β2=-40 β3=-84.2已知目镜的放大本领:M 1=5× M 2=10× 由:M=β物M 目 可得到:显微镜的最大放大本领:M 大=β物3M 目2=-842× 最小放大本领:M 小=β物1M 目1=-50×6 一显微镜物镜焦距为0.5cm ,目镜焦距为2cm ,两镜间距为22cm 。
观察者看到的象在无穷远处,试求物到物镜的距离和显微镜的放大本领。
解:因最后形成的象在无穷远处,说明 物镜成的象在目镜的物方焦平面上。
已知:f 2'=2cm 、f 1'=0.5cm 、L=22cm 物镜所成象的象距:s 1'= L-f 2'=20cm 由:f s s '=-'11111 解出物体到物镜的距离:s 1=-0.51cm 因显微镜的放大本领:''-=''=212112525f f L f f s M代入数据解出显微镜的放大本领:M=-550×7 眼睛的构造可简化为一折射球面,其曲率半径为5.55毫米,内部为折射率等于34的液体,外部是空气。
计算其两个焦距。
若月球在眼睛的节点所张的角为10,试问网膜上月球的象有多大?解:眼睛的物方焦距和象方焦距分别为65.1655.51341-=⨯--=-'-=r nn n f 毫米=-1.665厘米20.255.513434=⨯-=-''-='r nn n f 毫米=2.22厘米若月球的张角为10,考虑到折射定律,则θθn nd d y '⋅='⋅='将2.2,34,1,1801=='==︒=d n n πθ厘米代入上式,得29.01803412.2=⋅='πy 毫米8 冉斯登目镜由两个同种玻璃的平凸透镜组成,两者焦距均为36毫米,若两透镜间的距为28毫米。
求此目镜的焦距和放大本领,并问分划板应放置在何处?解:根据空气中薄透镜组的公式,已知3621='='f f 毫米,28=d 毫米,则由公式得冉斯登目镜的焦距为毫米45.29 36443628362111222121='=-=''-'+'='f f f d f f f 冉斯登目镜的物方主平面位置由公式可知9.2228363628)36(11=+---=∆==d f H H p 毫米 分划板应放在冉斯登目镜的物方焦点处,即p f -',离场镜左方6.55毫米处,其放大本领为49.84529250250=⋅='=f M9 惠更斯目镜是由两个同种玻璃的凸透镜组成,场镜的焦距是视镜焦距的三倍,两者相隔的距离等于视镜焦距的两倍。
若要制造一个放大本领为10的惠更斯目镜,所用的玻璃材料的折射率为5136.1=n ,试求两块透镜的距离及其曲率半径。
解:根据惠更斯目镜的放大本领可得其焦距为 5.2102525==='M f 厘米又由空气中的薄透镜组的焦距公式可知5.223 )3(21311112222222121='=''''-'+'=''-'+'='f f f f f f f f f d f f f352='f 厘米 5321='='f f 厘米 31022='=f d 厘米 应用透镜焦距公式,已知∞==2 ,5163.1r n 。
故场镜凸面的半径r 由下列方程:)1)(0000.15163.1(51r-= 解得 5815.2=r 厘米 视镜凸面半径r '满足下列方程)1)(0000.15163.1(51r '-= 解得 8605.0='r 厘米故两块透镜的距离为310厘米,其曲率半径分别为 2.5815厘米和0.8605厘米。
10 一显微镜具有三个物镜,两个目镜。
三个物镜的焦距分别16、4、1.9毫米,两个目镜的放大本领分别为5、10倍。
设三物镜所成之象都能落在象距160毫米处,问这显微镜的最大和最小的放大本领各为多少?解:由显微镜放大本领公式得842109.1160)(-=⨯-='''-='=最大最大最大最大最大M f s M M β 50516160)(-=⨯-='''-='=最小最小最小最小最小M f s M M β11 一显微镜物镜和目镜相距200毫米,物镜的焦距0.71='f 毫米,目镜的焦距0.52='f 毫米。
若最后观察到的象在无穷边,试求:(1)被观察物到物镜的距离;(2)显微镜的放大本领为多少?解:(1)因为最后观察到的象在无穷远,所以经由物镜成象必定在目镜的物方焦平面上。
已知目镜的焦距为5毫米,故第一次成象的象距19552001=-='s 毫米。
根据物镜焦距71='f 毫米和象距1951='s 毫米,由公式计算物到物镜的距离为261.71957195711111-=-⨯='-''⋅'=s f s f s 毫米 (2)显微镜的放大本领由1s 和1s '及物镜的横向放大率公式可得 86.26261.719511-=-='=s s β 而目镜的放大本领为 5052502502=='=f M 目 所以显微镜的放大本领为 1343-==目M M β12 一架伽利略望远镜,物镜和目镜之间距离为12厘米。
若该望远镜的放大本领为4,试求物镜和目镜的焦距各是多少?解:伽里略望远镜是用发散透镜来做目镜的,且物镜的象方焦点和目镜的物方焦点相重合。
故由已知条件可得1221=-'f f 厘米421=''=f f M ∴ 4 4 16221-='=='f f f 即厘米厘米厘米13 有一光阑孔径为2.5厘米,位于透镜前1.5厘米,透镜焦距为3厘米,孔径4厘米,物长1厘米。
位于光阑前6厘米处,试求:(1)入射光瞳和出射光瞳的位置及大小;(2)象的位置,并作图表示。
解:(1)因光阑前面没有透镜,直接比较光阑及透镜对物的张角,光阑即入射光瞳。
出射光瞳是这光阑为其后面透镜所成的象。
设此象离透镜的位置为s ',象的大小为y '。
已知5.1-=s 厘米,3='f 厘米,代入:f s s '=-'111,得3-='s 厘米。
由横向放大率 25.13=--=-='=x f y y β 得 : 525.2=⨯=='βy y 厘米(2)象的位置的计算:已知5.7)5.16(-=+-=s 厘米,3='f 厘米,代入物象公式:f s s '=-'111 5.71311-='s 得5='s 厘米14 证明望无镜光具组的放大本领等于入射光瞳与出射光瞳直径之比。
解:开普勒望远镜,入镜光瞳为其物镜,出射光瞳为物镜被目镜所成的象。
