南京邮电大学 数值代数实验
南邮数据结构实验一

实验报告(2014 / 2015 学年第一学期)课程名称数据结构实验名称二叉树基本操作以及哈夫曼编码译码系统实验时间年月日指导单位指导教师学生姓名班级学号学院(系) 专业二叉树的基本运算:一、问题描述1.设计递归算法,实现二叉树的运算:删除一棵二叉树,求一棵二叉树的高度,求一棵二叉树中叶子节点数,复制一棵二叉树,交换一棵二叉树的左右子树2.设计算法,自上而下,自左向右即按层次遍历一棵二叉树3.设计main函数,测试上述每个运算二、系统分析和概要设计首先用maketree构造一棵二叉树,然后遍历二叉树,然后交换每个结点的左右子树,接着算出输得高度和叶子节点,最后删除。
三、详细设计2. 核心算法建立二叉树的void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right)和计算叶子节点的int Size();3. 算法分析删除一棵二叉树,求一棵二叉树的高度,求一棵二叉树中叶子节点数,复制一棵二叉树等都是用递归的方法实现。
四、程序代码流程图#include<iostream.h>template<class T>struct BTNode{BTNode(){lChild=rChild=NULL;}BTNode(const T &x){element=x;lChild=rChild=NULL;}BTNode(const T &x,BTNode<T>* l,BTNode<T>* r){element=x;lChild=l;rChild=r;}T element;BTNode<T>* lChild,* rChild;};template<class T>class BinaryTree{public:BinaryTree(){root=NULL;}~BinaryTree(){Clear();}void Copy(BinaryTree<T> &r) const;bool IsEmpty()const{return root == NULL;}void Clear();void Exchange();bool Root(T& x)const;int GetHeight();void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right);void BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right);void PreOrder(void (*Visit)(T &x));void LevelOrder(void (*Visit)(T& x));int Size();BinaryTree<T>(BinaryTree<T> &t)root=Copy(t.root);}// void InOrder(void (*Visit)(T &x));// void PostOrder(void (*Visit)(T &x));BTNode<T>* Copy(BTNode<T>* t);protected:BTNode<T> * root;private:static int number;void Clear(BTNode<T>* &t);void Exchange(BTNode<T>* t);int GetHeight(BTNode<T>* t);int Size(BTNode<T>* t);void PreOrder(void (*Visit)(T &x),BTNode<T>* t);void LevelOrder(void (*Visit)(T& x),BTNode<T>* t); // void InOrder(void (*Visit)(T &x),BTNode<T>* t);// void PostOrder(void (*Visit)(T &x),BTNode<T>* t); };template <class T>bool BinaryTree<T>::Root(T &x)const{if(root){x=root->element;return true;}elsereturn false;}template <class T>void BinaryTree<T>::Clear(){Clear(root);}template <class T>void BinaryTree<T>::Clear(BTNode<T>* &t){if(t)Clear(t->lChild);Clear(t->rChild);delete t;t=NULL;}}template <class T>void BinaryTree<T>::MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(root||&left==&right)return;root=new BTNode <T>(x,left.root,right.root);left.root=right.root=NULL;}template <class T>void BinaryTree<T>::BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(!root||&left==&right||left.root||right.root)return;x=root->element;left.root=root->lChild;right.root=root->rChild;delete root;root=NULL;}template <class T>BTNode<T>* BinaryTree<T>::Copy(BTNode<T>* t){if(!t)return NULL;BTNode<T>*q=new BTNode<T>(t->element);q->lChild=Copy(t->lChild);q->rChild=Copy(t->rChild);return q;}template <class T>void Visit(T &x){cout<<x<<" ";}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x)){PreOrder(Visit,root);}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x),BTNode<T>* t) {if(t){Visit(t->element);PreOrder(Visit,t->lChild);PreOrder(Visit,t->rChild);}}template <class T>void BinaryTree<T>::Exchange(){Exchange(root);}template <class T>void BinaryTree<T>::Exchange(BTNode<T>* t){if(!t)return;BTNode<T>* temp;temp=t->lChild;t->lChild=t->rChild;t->rChild=temp;Exchange(t->lChild);Exchange(t->rChild);}template <class T>int BinaryTree<T>::GetHeight(){return GetHeight(root);}int BinaryTree<T>::GetHeight(BTNode<T>* t){int templ;int tempr;if(!t)return 0;templ=GetHeight(t->lChild);tempr=GetHeight(t->rChild);if(templ++>tempr++)return templ;elsereturn tempr;}template <class T>int BinaryTree<T>::number=0;template <class T>int BinaryTree<T>::Size(){Size(root);return number;}template <class T>int BinaryTree<T>::Size(BTNode<T>* t){if(t!=NULL){Size(t->lChild);if(t->lChild ==NULL&&t->rChild ==NULL)number++;Size(t->rChild);}return number;}template <class T>void BinaryTree<T>::LevelOrder(void (*Visit)(T& x)) {PreOrder(Visit,root);}void BinaryTree<T>::LevelOrder(void (*Visit)(T& x),BTNode<T>* t) {BTNode *quene[50],*p;int pre=1,rear=1;quene[++pre]=t;while(pre!=0){p=quene[++rear];cout<<p->element<<" ";if(p->lChild !=NULL)quene[++pre]=p->rChild ;if(p->rChild !=NULL)quene[++pre]=p->lChild ;}}void main(){BinaryTree <char> a,b,x,y,z;y.MakeTree('E',a,b);z.MakeTree('F',a,b);x.MakeTree('C',y,z);y.MakeTree('D',a,b);z.MakeTree('B',y,x);cout<<"二叉树z的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;cout<<"层次遍历二叉树:";z.LevelOrder(Visit);cout<<endl;BinaryTree<char> q(z);cout<<"复制的二叉树q的先序遍历:"<<endl;q.PreOrder(Visit);cout<<endl;cout<<"树的高度:";cout<<z.GetHeight()<<endl;cout<<"叶子节点数量:";cout<<z.Size()<<endl;z.Exchange();cout<<"二叉树左右子树交换后的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;}五、测试用例和运行结果测试用例如main函数中所示,结果如下图所示。
资料:数学实验(南邮)答案2

第二次题库1、 设⎪⎩⎪⎨⎧=+=+32/)7(11x x x x n n n ,数列}{n x 是否收敛?若收敛,其值为多少?精确到6位有效数字。
>> f=inline('(x+7/x)/2'); syms x; x0=3; for i=1:1:20 x0=f(x0);fprintf('%g,%g\n',i,x0); end 1,2.66667 2,2.64583 3,2.64575 4,2.64575 5,2.64575 6,2.64575 7,2.64575 8,2.64575 9,2.64575 10,2.64575 11,2.64575 12,2.64575 13,2.64575 14,2.64575 15,2.64575 16,2.64575 17,2.64575 18,2.64575 19,2.64575 20,2.64575本次计算运行到第三次结果稳定,可得: 数列}{n x 收敛,收敛到2.645752、 设 ,131211pp p n n x ++++= }{n x 是否收敛?若收敛,其值为多少?精确到17位有效数字。
学号为单号,取7=p >> s=0; for i=1:1:200 s=s+1/i^7;fprintf('%g,%20.17f\n',i,s); end1, 1.00000000000000000 2, 1.00781250000000000 3, 1.00826974737082750 4, 1.00833078252707750 5, 1.00834358252707750 6, 1.00834715477216210 7, 1.00834836903784100 8, 1.00834884587499920 9, 1.00834905495015730 10, 1.00834915495015730 …………………………… 181, 1.00834927738191870 182, 1.00834927738191890 183, 1.00834927738191920 184, 1.00834927738191940 185, 1.00834927738191960 186, 1.00834927738191980 187, 1.00834927738192000 188, 1.00834927738192030 189, 1.00834927738192050190, 1.00834927738192070 191, 1.00834927738192070 192, 1.00834927738192070 193, 1.00834927738192070 194, 1.00834927738192070 195, 1.00834927738192070 196, 1.00834927738192070 197, 1.00834927738192070 198, 1.00834927738192070 199, 1.00834927738192070 200, 1.00834927738192070运行至第190次后稳定,值为1.00834927738192070书上题库:(实验四) 1,2,4,7(1),8,12(改为:对例2,取 120,55,25,5.4=a 观察图形有什么变化.),13,14 。
南邮数据结构上机实验一线性表的基本运算和多项式的基本运算资料

实验报告(2015 / 2016学年第二学期)课程名称数据结构A实验名称线性表的基本运算和多项式的基本运算实验时间2016 年 3 月10 日指导单位计算机科学与技术系指导教师骆健学生姓名班级学号学院(系) 管理学院专业信息管理与信息系统实习题名:线性表的基本运算班级姓名学号日期2016.03.10一、问题描述深入理解线性表数据结构,熟练掌握顺序表的各种基本操作。
在顺序表类SeqList 中增加成员函数void Reverse(),实现顺序表的逆置;在顺序表类SeqList中增加成员函数bool DeleteX(const T &x),删除表中所有元素值等于x元素。
若表中存在这样的元素,则删除之,且函数返回true,否则函数返回false。
二、概要设计文件Inverse.cpp中定义了Linearlist类, SeqList类继承Linearlist类。
在顺序表类SeqList中通过函数void Reverse()实现顺序表的逆置,通过函数boolDeleteX(const T &x),删除表中所有元素值等于x元素。
三、详细设计1.类和类的层次设计程序使用了两个类, 线性表Linearlist类和顺序表SeqList类和一个主函数mian。
Linearlist类里包括常见的线性表运算,在类SeqList里面新增成员函数void Reverse()和bool DeleteX(const T &x)。
TLinearlist#int n+virtual bool IsEmpty() const = 0;+virtual int Length() const = 0;+virtual bool Find(int i,T& x) const = 0;+virtual int Search(T x) const = 0;+virtual bool Insert(int i,T x) = 0;+virtual bool Delete(int i) = 0;+virtual bool Update(int i,T x) = 0;+virtual void Output(ostream& out) const = 0;TSeqList-int maxLength;-T *elements;+IsEmpty() const;+Length() const;+Find(int i,T& x) const;+Search(T x) const;+Insert(int i,T x);+Delete(int i);+Update(int i,T x);+Output(ostream& out) const;+Reverse();+DeleteX(const T& x);2.核心算法顺序表SeqList类中,私有段封装了两个私有数据成员maxLength和elements,公有段封装了构造、析构、查找、删除、逆置等函数。
南邮电工电子实验复习与试卷

蒆南京邮电大学电工电子实验复习资料与试卷薃一、实验操作莄1、信号与系统操作实验请复习所做的实验。
膂主要掌握的要点:葿①由所给的电路转换出该电路的电压传输函数H(s)=V2(s)/V1(s),并能把传输函数化成Multisim所需的标准形式:薃(A)算子S在分子的幂次不高于分母的幂次。
薁(B)因需用积分器仿真,算子S应化成1/S。
蚀(C)分母的常数项化成1。
芈②能画出完整的系统模拟框图。
蚃③运用Multisim的模拟器件库中的积分器、比例放大器、加法器等模块组构系统模拟电路。
应遵循以下几个原则:羂(1)系统模拟电路输入端必用加法器模块对输入信号和反馈信号求和,加法器输出送积分器模块莁(2)根据S的最高幂次n,取出n个积分器模块串接。
羆(3)算子S的系数使用比例放大器模块肇(4)传输函数H(S)的分子是输出项,分子中各项比例放大器模块的输出用加法器求和后成为系统输出。
分母是负反馈项,其系数正、负异号后送输入端加法器。
莂(5)分母中为1的常数项不用任何运算模块蝿例如1:聿画出幅频和相频图膇例如2:螃画出幅频和相频图薁2、操作题如下图所示,写出该图的传输函数H(S)(V1是输入信号、V2是输出信号)。
画出题中电路对应的系统模拟框图。
(20分)螈写出传输函数H(S)(10分)芇画出题中电路对应的系统模拟框图(10?分)膄在Multisim2001环境中,测试该系统模拟电路的幅频特性相关参数。
(10分)(需包含半功率点与谐振频率点)罿频率点薇3.147KHz 芇3.715KHz芁4.474KHz蚁电压比莆0.707 莆0.9999 蚂0.707腿根据测试数据作出该电路的幅频特性曲线图。
(10分)荿有波形5分,每个参数1分.蒆3、D/A转换器操作实验请复习所做的实验。
肃掌握的要点:袁①根据输出电压选定数字输入端。
膈设计由DAC0832完成。
根据实验课题的要求输出正负斜率锯齿波上升或下降的台阶数大于或等于16个台阶,可用4位二进制数,根据输出电压选定数字输入端。
南邮数据结构实验三

南邮数据结构实验三南京邮电大学数据结构实验三、链表的基本操作实验目的本次实验的主要目的是理解链表的概念,掌握链表的基本操作,包括链表的创建、插入、删除和遍历。
实验内容本次实验分为以下几个部分:1、链表的定义与创建1.1 链表的概念链表是一种常见的数据结构,由一系列节点组成,每个节点包含数据和指向下一个节点的指针。
链表可以分为单链表、双链表和循环链表等不同类型。
本次实验将创建一个单链表。
1.2 链表节点的定义链表节点包含两个成员变量,分别是数据域和指针域。
数据域用于存储节点的数据,指针域指向下一个节点。
1.3 链表的创建在主函数中创建一个空链表,并添加一些初始数据,用于后续的操作。
2、链表的插入操作2.1 插入节点的位置链表的插入操作需要指定节点插入的位置,可以在链表的头部、尾部或者中间插入新节点。
2.2 插入节点的操作根据所选位置,在链表中插入新节点,并更新相应的指针。
3、链表的删除操作3.1 删除节点的位置链表的删除操作需要指定节点删除的位置,可以删除头节点、尾节点或者中间节点。
3.2 删除节点的操作根据所选位置,删除链表中的节点,并更新相应的指针。
4、链表的遍历操作通过循环遍历链表的所有节点,并输出每个节点的数据。
附件说明本文档涉及以下附件:附件1:源代码附件2:实验报告法律名词及注释本文所涉及的法律名词及注释如下:1、数据结构:数据的存储方式和操作组成的集合。
在计算机科学中,数据结构是计算机中存储、组织数据的方式。
2、链表:链表是一种常见的数据结构,由一系列节点组成,每个节点包含数据和指向下一个节点的指针。
3、节点:链表中的一个元素,包含数据域和指针域。
4、数据域:节点中存储的数据。
5、指针域:节点中指向下一个节点的指针。
6、插入操作:在链表中插入一个新节点。
7、删除操作:从链表中删除一个节点。
8、遍历操作:按照一定的顺序访问链表中的所有节点。
全文结束。
南邮数学实验

第一次练习题1.求解下列各题:1)30sin lim x mx mx x ->->> limit((1834*x-sin(1834*x))/(x^3)) ans =3084380852/32)(10)cos ,1000.0xmx y e y =求>> diff(exp(x)*cos(1834*x/1000.0),10) ans =-4262767519435573449/9765625000000000*exp(x)*cos(917/500*x)+2969869727171403/1953125000000*exp(x)*sin(917/500*x)3)4224x dx m x+⎰ int(x^4/(1834^2+4*x^2),x) ans =1/12*x^3-840889/4*x+771095213/4*atan(1/917*x)40x =展开(最高次幂为8). >> taylor(sqrt(1834/1000.0+x),9,x) ans =1/50*4585^(1/2)+5/917*4585^(1/2)*x-625/840889*4585^(1/2)*x^2+156250/771095213*4585^(1/2)*x^3-48828125/7*4585^(1/2)*x^4+2441406250/92629354652051*4585^(1/2)*x^5-9/849411*4585^(1/2)*x^6+25177/5452373373*4585^(1/2)*x^7-10228125/499982363688330647123041*4585^(1/2)*x^82.求矩阵21102041A m -⎛⎫ ⎪= ⎪ ⎪-⎝⎭的逆矩阵1-A 及特征值和特征向量。
逆矩阵:>> A=[-2,1,1;0,2,0;-4,1,1834];inv(A) ans =-0.5005 0.2501 0.0003 0 0.5000 0 -0.0011 0.0003 0.0005 特征值:>> A=[-2,1,1;0,2,0;-4,1,1834];eig(A) ans =1.0e+003 * -0.0020 1.8340 0.0020 特征向量:>> A=[-2,1,1;0,2,0;-4,1,1834];[P,D]=eig(A) P =-1.0000 -0.0005 0.24250 0 0.9701 -0.0022 -1.0000 0.0000 D =1.0e+003 *-0.0020 0 0 0 1.8340 0 0 0 0.00203.已知221(),()2f x ex μσ=--分别在下列条件下画出)(x f 的图形: /600m σ=,μ分别为0,1,1-(在同一坐标系上作图);>> x=-2:1/50:2;y1=1/(sqrt(2*pi)*1834/600)*exp(-x.^2/(2*(1834/600)^2)); y2=1/sqrt(2*pi)*1834/600*exp(-(x+1).^2/(2*(1834/600)^2)); y3=1/sqrt(2*pi)*1834/600*exp(-(x-1).^2/(2*(1834/600)^2)); plot(x,y1,x,y2,x,y3)-6-4-20240.020.040.060.080.10.120.14xu=-1/u=1/u=04.画 (1)sin 020cos 02100x u t t y u t u t z m ⎧⎪=≤≤⎪=⎨≤≤⎪⎪=⎩>>t=0:pi/1000:20;u=0:pi/10000:2; x=u.*sin(t); y=u.*cos(t); z=100.*t/1834;plot3(x,y,z)(2)sin()03,03 z mxy x y=≤≤≤≤>>ezmesh('sin(1834*x*y)',[0,3],[0,3])(3)sin()(/100cos)02 cos()(/100cos)02 sinx t m uty t m uuz uππ=+⎧≤≤⎪=+⎨≤≤⎪=⎩>>[t,u]=meshgrid(0:.01*pi:2*pi,0:.01*pi:2*pi); x=sin(t).*(1834./100+cos(u));y=cos(t).*(1834./100+cos(u));z=sin(u);surf(x,y,z)5.对于方程50.10200mx x--=,先画出左边的函数在合适的区间上的图形,借助于软件中的方程求根的命令求出所有的实根,找出函数的单调区间,结合高等数学的知识说明函数为什么在这些区间上是单调的,以及该方程确实只有你求出的这些实根。
南京邮电大学算法设计实验报告——动态规划法

if(a[i]==b[j]) {
c[i][j]=c[i-1][j-1]+1; s[i][j]=1; } else if(c[i-1][j]>=c[i][j-1]) { c[i][j]=c[i-1][j]; s[i][j]=2; } else { c[i][j]=c[i][j-1]; s[i][j]=3; } } } return c[m][n]; //返回最优解值 }
算法分析与设计 A
动态规划法
2009
年 11 月 20 日
计算机学院软件工程系
张怡婷
学生姓名 学院(系)
丁力琪 班级学号 计算机学院 专 业
B07030907 软件工程
实验报告
实验名称
动态规划法
指导教师 张怡婷
实验类型
验证
实验学时 2×2 实验时间 2009-11-20
一、 实验目的和任务
目的:加深对动态规划法的算法原理及实现过程的理解,学习用动态
6
8、输入序列 X={x1,x2,……,xm}={a,b,c,b,d,a,b}和 Y={y1,y2,……,yn}={b,d,c,a,b,a}作为测 试数据,测试程序是否能够正确运行?输出结果是什么? 运行正确,实验结果显示:4
bcba
9、分析该动态规划算法的两个主要成员函数 int LCSLength()和 void CLCS()的时间复杂 性。
#include<iostream> #include<string> using namespace std; #define maxlength 11 class LCS { public:
南京邮电大学数值代数实验

数值代数实验数值线性代数实验一一、实验名称:矩阵的LU分解.二、实验目的:用不选主元的LU分解和列主元LU分解求解线性方程组Ax=b, 并比较这两种方法.三、实验内容与要求(1)用所熟悉的计算机语言将不选主元和列主元LU分解编成通用的子程序,然后用编写的程序求解下面的84阶方程组将计算结果与方程组的精确解进行比较,并就此谈谈你对Gauss消去法的看法.(2)写出追赶法求解三对角方程组的过程,并编写程序求该实验中的方程组Gauss消去法:用消去法解方程组的基本思想是用逐次消去未知数的方法把原来方程组Ax=b化为与其等价的三角方程组,而求解三角方程组就容易了。
换句话说,上述过程就是用行的初等变换将原方程组系数矩阵化为简单形式,从而将求解原方程组的问题转化为求解简单方程组的问题。
利用Gauss消去法对线性方程组Ax=b进行求解。
用MATLAB建立m文件DelGauss.m,程序如下:function x=DelGauss(a,b)[n,m]=size(a);nb=length(b);det=1;x=zeros(n,1);for k=1:n-1for i=k+1:nif a(k,k)==0returnendm=a(i,k)/a(k,k);for j=k+1:na(i,j)=a(i,j)-m*a(k,j);endb(i)=b(i)-m*b(k);enddet=det*a(k,k);enddet=det*a(n,n);for k=n:-1:1for j=k+1:nb(k)=b(k)-a(k,j)*x(j);endx(k)=b(k)/a(k,k);End在matlab中输入如下:结果如下:方程组的精确解为x 1=x 2=…=x 84=1.0000,与Gauss 消去法求得的解差距很大,所得结果不够准确,计算简单但其消元过程有时不能进行到底而使求解出现解失真的情况。
数值线性代数实验二一、实验名称:实对称正定矩阵的A的Cholesky分解.二、实验目的:用平方根法和改进的平方根方法求解线性方程组Ax=b.三、实验内容与要求用所熟悉的计算机语言将Cholesky分解和改进的Cholesky分解编成通用的子程序,然后用编写的程序求解对称正定方程组Ax=b,其中(1)b随机的选取,系数矩阵为100阶矩阵(2)系数矩阵为40阶Hilbert矩阵,即系数矩阵A的第i行第j列元素为,向量b的第i个分量为(3)用实验一的程序求解这两个方程组,并比较所有的计算结果,然后评价各个方法的优劣。
南京邮电大学-数值计算实践报告

数值计算实践I 、方程求根一、实验目的熟悉和掌握Newton 法,割线法,抛物线法的方法思路,并能够在matlab 上编程实现二、问题描述(1).给定一个三次方程,分别用Newton 法,割线法,抛物线法求解. 方程的构造方法:(a)根:方程的根为学号的后三位乘以倒数第二位加1再除以1000. 假设你的学号为B06060141,则根为141*(4+1)/1000=0.564(b)方程:以你的学号的后三位数分别作为方程的三次项,二次项,一次项的系数,根据所给的根以及三个系数确定常数项. 例如:你的学号是B06060141,则你的方程是x 3+4x 2+x+a 0=0的形式. 方程的根为0.564,因此有0.5643+4*0.5642+0.564+a0=0,于是a0=-2.015790144 你的方程为x 3+4x 2+x-2.015790144=0.(2)假设方程是sinx+4x 2+x+a0=0的形式(三个系数分别是学号中的数字),重新解决类似的问题(3)构造一个五次方程完成上面的工作.四次方程的构造:将三次多项式再乘以(x-p*)2得到对应的五次多项式(p*为已经确定的方程的根,显然,得到的五次方程有重根).(4)将(2)中的方程同样乘以(x-p*)得到一个新的方程来求解注:(1)Newton 法取0.5为初值,割线法以 0,1为初值,抛物线法以0,0.5,1为初值, (2)计算精度尽量地取高.终止准则:根据ε<--||1n n p p 来终止(3)可供研究的问题:(一)ε的取值不同对收敛速度有多大的影响(二)将注(1)中的初值该为其它的初值,对收敛性以及收敛速度有无影响 (三)能否求出方程的所有的根 (4)实验报告的撰写实验报告包含的内容:(一)实验目的(二)问题描述(三)算法介绍(包括基本原理)(四)程序(五)计算结果(六)结果分析(七)心得体会三、算法介绍在本问题中,我们用到了newton 法,割线法,抛物线法。
南邮数学实验答案

第一次练习题1、求032=-x e x 的所有根。
>>x=-5:0.01:5;y=exp(x)-3*x.^2;plot(x,y);grid on>> fsolve('exp(x)-3*x.^2',-1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =-0.4590>> fsolve('exp(x)-3*x.^2',1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =0.9100>> fsolve('exp(x)-3*x.^2',4)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =3.73312、求下列方程的根。
南邮 数学实验参考答案(选题版)

syms x y;>> a=int(int(exp(x^2+y^2),x,0,1),y,0,1) a =(pi*erfi(1)^2)/41.7、n=20;for i=1:(n-2)a(1)=1;a(2)=1;a(i+2)=a(i+1)+a(i);enda'ans =112358132134558914423337761098715972584418167651.8、>> A=[-2,1,1;0,2,0;-4,1,303/1000]; >> inv(A)0.0893 0.1027 -0.29460 0.5000 01.1786 -0.2946 -0.5893>> eig(A)ans =-0.8485 + 1.6353i-0.8485 - 1.6353i2.0000>> [p,D]=eig(A)p =0.2575 - 0.3657i 0.2575 + 0.3657i 0.24250 0 0.97010.8944 0.8944 0.0000D =-0.8485 + 1.6353i 0 00 -0.8485 - 1.6353i 00 0 2.0000 >> det(A)ans =6.7880>> A^6ans =45.0194 4.7452 -6.37180 64.0000 025.4870 -6.3718 30.3452>> A.^6ans =1.0e+003 *0.0640 0.0010 0.00100 0.0640 04.0960 0.0010 0.0000 1.9、M文件定义如下:function y=f(x)if x>=0&&x<=1/2y=2*x;else if x>1/2&&x<=1y=2-2*x;endend命令窗口执行:fplot(@f,[0,1])1.10、t=-8:0.1:8;x=cos(t);y=sin(t);z=t;plot3(x,y,z,'r');hold onx1=2*cos(t);y1=2*sin(t);z1=t;plot3(x1,y1,z1)grid on1.11、>> A=[4 -2 2;-3 0 5;1 5*303 3];>> B=[1 3 4;-2 0 -3;2 -1 -1];>> det(A)ans =-39418>> 2*A-Bans =7 -7 0-4 0 130 3031 7>> A*Bans =12 10 207 -14 -17-3023 0 -4544>> A.*Bans =4 -6 86 0 -152 -1515 -3>> A*B^-1ans =-0.4211 -1.4737 0.7368-1.0000 -2.0000 -3.0000637.7368 716.5789 398.2105>> A^-1*Bans =0.3467 0.5763 0.99950.0015 -0.0017 -0.0013-0.1920 0.3458 -0.0003>> A^2ans =24 3022 4-7 7581 9 -4538 4543 7586>> A'ans =4 -3 1-2 0 15152 5 31.12、syms x;fplot('(1/(sqrt(2*pi)*514/600))*exp(-((x)^2)/2)',[-3,3],'r') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x-1)^2)/2)',[-3,3],'b') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x+1)^2)/2)',[-3,3],'g') hold offlegend('u为0','u为-1','u为1')syms x;fplot('(1/(sqrt(2*pi)*1))*exp(-((x)^2)/2)',[-3,3],'r')hold onfplot('(1/(sqrt(2*pi)*2))*exp(-((x)^2)/2)',[-3,3],'b')hold onfplot('(1/(sqrt(2*pi)*4))*exp(-((x)^2)/2)',[-3,3],'--')hold onfplot('(1/(sqrt(2*pi)*5.14))*exp(-((x)^2)/2)',[-3,3],'g')hold off1.15、ezplot('exp(x)-3*303*x.^2',[-10,10]);grid onfsolve('exp(x)-3*303*x.^2',0)ans =-0.0326第二次练习:2.1、f=inline('(x+7/x)/2');syms x;x0=3;for i=1:1:15x0=f(x0);fprintf('%g,%g\n',i,x0);end结果如下:1,2.666672,2.645833,2.645754,2.645755,2.645756,2.645757,2.645758,2.645759,2.6457510,2.6457511,2.6457512,2.6457513,2.6457514,2.6457515,2.645752.2、同2.1的方法,把f=inline('(x+7/x)/2');把未知表达式改一下就可以了;2.3、f=inline('1-2*abs(x-1/2)');x=[];y=[];x(1)=rand;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,10]);axis([0,1,0,1]);hold off答案如下:2.4、以α=3.5为例;其他的把α改变就可以了;f=inline('3.5(是α的取值)*x*(1-x)');x=[];y=[];x(1)=0.5;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,1]);axis([0,1,0,1]);hold off结果如下:整体结果如下:3.3 3.5 3.56 3.568 3.6 3.84序列收敛情况不收敛循环周期为2不收敛循环周期为4不收敛循环周期为8混沌混沌不收敛循环周期为32.5、对着书上的代码先输入到M文件里,然后再在命令窗口输入执行命令如:Martin(303,303,303,5000);即可。
南邮 数字信号处理实验报告(带问题答案小结)

南京邮电大学实验报告实验名称熟悉MATLAB环境快速傅里叶变换(FFT)及其应用 IIR数字滤波器的设计FIR数字滤波器的设计课程名称数字信号处理A班级学号_ 12006311____ 姓名_______张文欣_____________开课时间 2014/2015学年,第二学期实验一熟悉MATLAB环境一、实验目的(1)熟悉MA TLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容(1) 数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3,4,5,6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B 。
并用stem语句画出A、B、C、D、E、F、G。
n = 0:1:3;A=[1 2 3 4];subplot(4,2,1)stem(n,A)xlabel('n')ylabel('A')B=[3,4,5,6];subplot(4,2,2)stem(n,B)xlabel('n')ylabel('B')C=A+B;subplot(4,2,3)stem(n,C)xlabel('n')ylabel('C')D=A-BSubplot(4,2,4)stem(n,D)xlabel('n')ylabel('D')E=A.*Bsubplot(4,2,5)stem(n,E)xlabel('n')ylabel('E')F=A./Bsubplot(4,2,6)stem(n,F) xlabel('n') ylabel('F')G=A.^B subplot(4,2, 7) stem(n,G) xlabel('n') ylabel('G')nAnBnCnDnEnFnG(2) 用MATLAB 实现下列序列: a) 08(). 0n 15nx n =≤≤ n=0:1:15; x1=0.8.^n; stem(n,x1) xlabel('n') ylabel('x(n)')title('2(a)')nx (n )b) 023(.)() 0n 15j nx n e+=≤≤ n=0:1:15;i=sqrt(-1); a = 0.2+3*i; x2=exp(a*n); figuresubplot(1,2,1) stem(n,real(x2)) xlabel('n')ylabel('x(n)实部') subplot(1,2,2) stem(n,imag(x2)) xlabel('n')ylabel('x(n)虚部')nx (n )实部nx (n )虚部2(b)c) 3012502202501()cos(..)sin(..)x n n n ππππ=+++ 0n 15≤≤ n=0:1:15;x3=3*cos(0.125*pi*n+0.2*pi) + 2*sin(0.25*pi*n+0.1*pi); stem(n,x3) xlabel('n') ylabel('x(n)') title('2(c)')nx (n )2(c)(4) 绘出下列时间函数的图形,对x 轴、y 轴以及图形上方均须加上适当的标注: a)2()sin() 0t 10s x t t π=≤≤t=0:0.001:10; x=sin(2*pi*t); plot(t,x,'r-')xlabel('t'),ylabel('x(t)'),title('sin(2\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )sin(2πt)b) 100()cos()sin() 0t 4s x t t t ππ=≤≤ t=0:0.001:4;x=cos(100*pi*t).*sin(pi*t); plot(t,x,'b-')xlabel('t'),ylabel('x(t)'),title('cos(100\pit)*sin(\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )cos(100πt)*sin(πt)(6)给定一因果系统12121106709()()/(..)H z z z z ----=++-+,求出并绘制H (z )的幅频响应和相频响应。
南京邮电大学实验课程安排表(2011-12-1)-最终稿
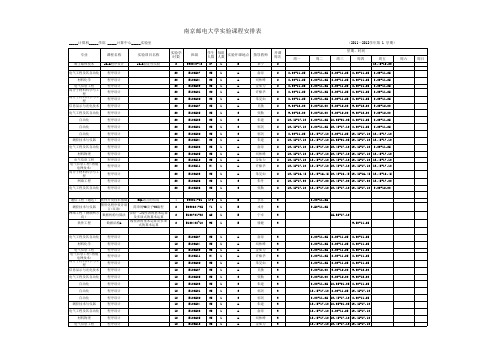
学生 每组 实验开课地点 人数 人数
87 35 35 35 32 35 35 35 35 35 35 35 35 35 35 34 35 35 35 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 B A A A A A A C C C C A A A A A A C C
13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-16:45 13:45-16:45 13:45-16:45 13:45-16:45 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 9:00-12:00 9:00-12:00 9:00-12:00 9:00-12:00
150 104 71 109 120 183
1 1 1 1 1 1
B B B B B B
B100408 B100405 B100402 B100403 B100401 B100407 B100409 33 30 40 37
1 1 1 1 1 1 1 1 1
A A A A A A C C C
李频 蒋凌云 张琳 肖甫 张迎周 王海艳 闵丽娟 李超 徐小龙
(2011~2012学年第 1 学期) 实验学 时数
2 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20
课程名称
南京邮电大学软件设计实验报告

软件设计报告( 2014 / 2015 学年第二学期)课程名称软件设计指导老师赵江实习时间第十八周学生XX学号____学院______专业软件设计课程编号:B0465011C适用专业:班级:一、所涉及的课程及知识点涉及的课程:第6学期之前的专业基础课程。
知识点:专业基础课程中所学的知识点。
二、目的与任务目的:通过软件设计,培养学生的实践能力和创新精神,加强学生对专业基础课程的理解和掌握,加强学生高级语言编程能力、应用软件以及仿真能力。
任务:选择以下任一模块进行设计:Matlab软件仿真、C语言及应用。
软件设计的内容题目1:如果给出两个矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=136782078451220124A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=087654321B ,执行下面的矩阵运算命令。
(1)B A *5+和I B A +-分别是多少(其中I 为单位矩阵)?(2)B A *⋅和B A *将分别给出什么结果,它们是否相同?为什么? 逻辑功能程序:function [ ] = EXP1()A=[4,12,20;12,45,78;20,78,136];B=[1,2,3;4,5,6;7,8,0];I=eye(3);disp('A+5*B=');disp(A+5*B);disp('A-B+I=')disp(A-B+I);disp('A.*B=');disp(A.*B)disp('A*B=');disp(A*B);End实验过程与结果打开matlab ,在命令窗口“mand Window ”中键入edit,启动程序编辑器。
输入完整程序后利用save as储存为M文件,文件名为EXP1。
返回主界面,在命令窗口“mand Window”中输入函数EXP1(),按下回车,得到程序运行结果如下:>> EXP1()A+5*B=9 22 3532 70 10855 118 136A-B+I=4 10 178 41 7213 70 137A.*B=4 24 6048 225 468140 624 0A*B=192 228 84738 873 3061284 1518 528实验结果分析(1)利用MATLAB提供的disp函数既可以输出表达式、数值,也可以输出字符串,其调用方式为:disp(表达式或数值)、disp(‘待显示字符串’);(2)在MATLAB的矩阵运算中,+、-运算符通用,表示矩阵相加、减;*与.*不同在于*表示矩阵乘法,而.*表示矩阵对应位置元素相乘,所以*要求两个矩阵的行、列数互为转置,而.*则要求两个矩阵行、列数要相同;(3)使用eye可以获得单位矩阵函数(矩阵对角线处元素为1,其余元素为0),矩阵的阶数由括号内的值决定,格式为eye(n),n为矩阵阶数。
南邮 数学实验 报告

@1.1>> syms x>> limit(((1+1514*x^2)^(1/2)-cos(1514*x))/x^2)ans =1146855>> syms x>> limit(((1+1514*x^2)^(1/2)-cos(1514*x))/x,inf)ans =1514^(1/2)@1.2>> syms x>> diff(exp(x)*cos(1514*x/1000),x,2)ans =-323049/250000*exp(x)*cos(757/500*x)-757/250*exp(x)*sin(757/500*x)>> syms x>> p=diff(exp(x)*cos(1514*x/1000),6);>> subs(p,x,0)ans =33.3859@1.3>> syms x>> int(exp(-1514*x^2),x,0,inf)ans =1/3028*1514^(1/2)*pi^(1/2)@1.4>> syms x>> taylor((1514/1000+x)^(1/3),5,0)ans =1/500*757^(1/3)*500^(2/3)+1/2271*757^(1/3)*500^(2/3)*x-500/5157441*757^(1/3)*500^(2/3 )*x^2+1250000/35137645533*757^(1/3)*500^(2/3)*x^3-1250000000/79797593005443*757^(1 /3)*500^(2/3)*x^4@1.5x=randint(1,2,[1,1515]);>> for n=3:1:10x(n)=x(n-1)+x(n-2);end>> disp(x)1033 575 1608 2183 3791 5974 9765 15739 25504 41243@1.6>> A=[4,-2,2;-3,0,5;1,5,3*1514];det(A)ans =-27392>> A=[4,-2,2;-3,0,5;1,5,3*1514];inv(A)ans =0.0009 -0.3320 0.0004-0.4976 -0.6632 0.00090.0005 0.0008 0.0002’>> A=[4,-2,2;-3,0,5;1,5,3*1514];eig(A)ans =1.0e+003 *0.0052-0.00124.5420>> A=[4,-2,2;-3,0,5;1,5,3*1514];B=[1,3,4;-2,0,-3;2,-1,1]; A/B ans =1.0e+003 *0 0 0.0020-0.0027 -0.0080 -0.0081-1.2944 -4.5360 -3.8883>> A=[4,-2,2;-3,0,5;1,5,3*1514];B=[1,3,4;-2,0,-3;2,-1,1]; A\B ans =0.6656 0.0024 1.00000.8306 -1.4938 0-0.0006 0.0014 0@1.7@1.8t=-1514/2:25:1514/2; >> x=(1514/20)*cos(t); >> y=(1514/20)*sin(t); >> z=t;>> plot3(x,y,z);grid ont=-1514/2:0.1:1514/2; x=cos(t)+(t.*sin(t));y=sin(t)-t.*cos(t);z=-t;plot3(x,y,z);grid on@1.9M:function y=f(x)if x>0y=(1000/1514)*exp((-1000/1514)*x);elseif x<=0y=0;endend>> hold on>> fplot('f(x)',[-8,8],'r -')>> fplot('g(x)',[-8,8],'b -')>> fplot('h(x)',[-8,8],'m -')>> fplot('z(x)',[-8,8],'y -')>> hold off@1.10ezplot('sin(x^2+(1514/1000)*y^2)-cos(x*y)',[-5,5,-5,5])x y22@1.11x=-5:0.2:5;y=x;[X Y]=meshgrid(x,y);Z=1514*X.^2+Y.^4;mesh(X,Y,Z);@1.12Syms xfplot('exp(x)-3*1514/1614*x^2',[-5,5]);grid on fsolve('exp(x)-3*1514/1614*x^2',-1)fsolve('exp(x)-3*1514/1614*x^2',1)fsolve('exp(x)-3*1514/1614*x^2',4)ans =-0.4710ans =0.9665ans =3.5922syms x>> diff(exp(x)-3*1514/1614)*x^2)ans =exp(x)-1514/269*xsyms xfplot('exp(x)-1514/269*x',[-5,5]);grid onfsolve('exp(x)-1514/269*x',0)ans =0.2218fsolve('exp(x)-1514/269*x',3)ans =2.7333体会:对应一个不甚了解的函数,先画出其图形,可增加我们对它的了解,再在了解的基础上进行其他运算,得到该函数的其他性质。
数学实验报告南邮

实验名称:线性方程组的求解方法实验目的:1. 理解线性方程组的概念及其解法。
2. 掌握高斯消元法和克拉默法则求解线性方程组的方法。
3. 通过实验验证不同方法的计算效率和适用范围。
实验时间:2023年X月X日实验地点:南京邮电大学计算机实验室实验器材:1. 计算机2. 数学软件(如MATLAB、Mathematica等)3. 纸张和笔实验步骤:一、实验准备1. 确定实验所需线性方程组,例如:\[\begin{cases}2x + 3y - z = 4 \\-x + 2y + 3z = -1 \\3x - 2y + 4z = 5\end{cases}\]2. 熟悉高斯消元法和克拉默法则的原理。
二、实验实施1. 高斯消元法求解(1)将线性方程组转化为增广矩阵:\[\begin{bmatrix}2 &3 & -1 & | &4 \\-1 & 2 & 3 & | & -1 \\3 & -2 &4 & | & 5\end{bmatrix}\](2)进行行变换,将增广矩阵转化为行最简形式:\[\begin{bmatrix}1 & 0 & 0 & | & 1 \\0 & 1 & 0 & | & 1 \\0 & 0 & 1 & | & 1\end{bmatrix}\](3)根据行最简形式得到方程组的解:\(x = 1, y = 1, z = 1\)。
2. 克拉默法则求解(1)计算系数矩阵的行列式:\[D = \begin{vmatrix}2 &3 & -1 \\-1 & 2 & 3 \\3 & -2 & 4\end{vmatrix}\](2)计算增广矩阵的行列式:\[D_x = \begin{vmatrix}4 & 3 & -1 \\-1 & 2 & 3 \\5 & -2 & 4\end{vmatrix}\](3)计算\(D_y\)和\(D_z\),分别对应\(x\)、\(y\)、\(z\)的系数矩阵和增广矩阵的行列式。
南邮_数学实验答案(全)

第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx→∞- 程序:syms xlimit((1001*x-sin(1001*x))/x^3,x,0) 结果:1003003001/6程序: syms xlimit((1001*x-sin(1001*x))/x^3,x,inf) 结果: 01.2 cos1000xmxy e =,求''y 程序: syms xdiff(exp(x)*cos(1001*x/1000),2) 结果:-2001/1000000*exp(x)*cos(1001/1000*x)-1001/500*exp(x)*sin(1001/1000*x)1.3 计算221100xy e dxdy +⎰⎰程序:dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) 结果:2.139350195142281.4 计算4224x dx m x+⎰ 程序: syms xint(x^4/(1000^2+4*x^2)) 结果:1/12*x^3-1002001/16*x+1003003001/32*atan(2/1001*x)1.5 (10)cos ,x y e mx y =求程序: syms xdiff(exp(x)*cos(1000*x),10) 结果:-1009999759158992000960720160000*exp(x)*cos(1001*x)-10090239998990319040000160032*exp(x)*sin(1001*x)1.6 0x =的泰勒展式(最高次幂为4).程序: syms xtaylor(sqrt(1001/1000+x),5) 结果:1/100*10010^(1/2)+5/1001*10010^(1/2)*x-1250/1002001*10010^(1/2)*x ^2+625000/1003003001*10010^(1/2)*x^3-390625000/1004006004001*10010^(1/2)*x^41.7 Fibonacci 数列{}n x 的定义是121,1x x ==,12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值代数实验
数值线性代数实验一
一、实验名称:矩阵的LU分解.
二、实验目的:用不选主元的LU分解和列主元LU分解求解线性方程组Ax=b, 并比较这
两种方法.
三、实验内容与要求
(1)用所熟悉的计算机语言将不选主元和列主元LU分解编成通用的子程序,然后用编写的程序求解下面的84阶方程组
将计算结果与方程组的精确解进行比较,并就此谈谈你对Gauss消去法的看法.
(2)写出追赶法求解三对角方程组的过程,并编写程序求该实验中的方程组
Gauss消去法:
用消去法解方程组的基本思想是用逐次消去未知数的方法把原来方程组Ax=b化为与其等价的三角方程组,而求解三角方程组就容易了。
换句话说,上述过程就是用行的初等变换将原方程组系数矩阵化为简单形式,从而将求解原方程组的问题转化为求解简单方程组的问题。
利用Gauss消去法对线性方程组Ax=b进行求解。
用MATLAB建立m文件DelGauss.m,程序如下:
function x=DelGauss(a,b)
[n,m]=size(a);
nb=length(b);
det=1;
x=zeros(n,1);
for k=1:n-1
for i=k+1:n
if a(k,k)==0
return
end
m=a(i,k)/a(k,k);
for j=k+1:n
a(i,j)=a(i,j)-m*a(k,j);
end
b(i)=b(i)-m*b(k);
end
det=det*a(k,k);
end
det=det*a(n,n);
for k=n:-1:1
for j=k+1:n
b(k)=b(k)-a(k,j)*x(j);
end
x(k)=b(k)/a(k,k);
End
在matlab中输入如下:
结果如下:
方程组的精确解为x1=x2=…=x84=1.0000,与Gauss消去法求得的解差距很大,所得结果不够准确,计算简单但其消元过程有时不能进行到底而使求解出现解失真的情况。
数值线性代数实验二
一、实验名称:实对称正定矩阵的A的Cholesky分解.
二、实验目的:用平方根法和改进的平方根方法求解线性方程组Ax=b.
三、实验内容与要求
用所熟悉的计算机语言将Cholesky分解和改进的Cholesky分解编成通用的子程序,然后用编写的程序求解对称正定方程组Ax=b,其中
(1)b随机的选取,系数矩阵为100阶矩阵
(2)系数矩阵为40阶Hilbert矩阵,即系数矩阵A的第i行第j列元素为
,向量b的第i个分量为
(3)用实验一的程序求解这两个方程组,并比较所有的计算结果,然后评价各个方法的优劣。
平方根法:
平方根法就是利用对称正定矩阵的三角分解而得到的求解对称正定方程组的一种有效方法。
平方根法递推公式可以证明对于对称正定矩阵A,可以唯一地分解成A=LL T,其中L是非奇异下三角形矩阵。
模型二:利用平方根法对线性方程组Ax=b进行求解。
用MATLAB建立m文件pingfg.m,程序如下:
function [x]=pingfg(A,b) %Cholesky分解
[n,n]=size(A);
L=zeros(n,n);%实际上不用为 L 申请空间,使用 A 即可
L(1,1)=sqrt(A(1,1));
for k=2:n
L(k,1)=A(k,1)/L(1,1);
end
for k=2:n-1
L(k,k)=sqrt(A(k,k)-sum(L(k,1:k-1).^2));
for i=k+1:n
L(i,k)=(A(i,k)-sum(L(i,1:k-1).*L(k,1:k-1)))/L(k,k);
end
end
L(n,n)=sqrt(A(n,n)-sum(L(n,1:n-1).^2));%解下三角方程组Ly=b
y=zeros(n,1);
for k=1:n
j=1:k-1;
y(k)=(b(k)-L(k,j)*y(j))/L(k,k);
end%解上三角方程组L'x=y
x=zeros(n,1);
U=L';
for k=n:-1:1
j=k+1:n;
x(k)=(y(k)-U(k,j)*x(j))/U(k,k);
End
模型三:利用改进的平方根法对线性方程组Ax=b进行求解。
用MATLAB建立m文件ave.m,程序如下:
function [x]=ave(A,b,n) %用改进平方根法求解Ax=b
L=zeros(n,n); %L为n*n矩阵
D=diag(n,0); %D为n*n的主对角矩阵
S=L*D;
for i=1:n %L的主对角元素均为1
L(i,i)=1;
end
for i=1:n
for j=1:n %验证A是否为对称正定矩阵
if (eig(A)<=0)|(A(i,j)~=A(j,i)) %A的特征值小于0或A非对称时,输出wrong disp('wrong');break;end
end
end
Hilbert矩阵用MATLAB建立m文件Hil.m,程序如下:
function b=Hil()
for k=1:40
for m=1:40
s=0;
t=s+1/(k+m-1);
s=t;
end
b(k,1)=s;
end
在matlab中输入如下:
输出结果如下:
在输入:输出为:
.....
问题3:
...
Gauss消去法所得的结果与平方根法和改进的平方根法求得的结果差距很大,而且Gauss消去法所得的结果大部分为零,显然平方根法和改进的平方根法求得的结果与方程的精确解比Gauss消去法的更接近,更准确。
但不管是哪一类算法都只能在预定的计算步骤内或给定的精度内得到近似解,有一定的误差。
数值线性代数实验三
一、实验名称:矩阵A 的QR 分解
二、实验目的:应用改进的Gram —Schmidt 方法和Householder 变换的方法计算矩阵A 的QR 分解. 其中),()(n m R a A n m ij ≥∈=⨯ rank A =n
三、实验内容与要求
输入:A 的各列),,1,],,[(,,,121n j a a a a a a T mj j j n ==
输出:Q 的各列元素(存放在A 的相应位置上)以及R 的元素
),,,,,1(n i j n i r ij ==
数值线性代数实验四
一、实验名称:用迭代法求解方程组及超松弛迭代和最佳松弛因子的确定.
二、实验目的:应用Jacobi 迭代法、Gauss -Seidel 迭代法和超松弛迭代方法求解线性方程组 Ax=b, 并选择不同的松弛因子ω,观察松弛因子对松弛迭代法计算效果的影响.
三、实验内容与要求
将常微分方程22(0)0,(1)1d y dy a dx dx y y ε⎧+=⎪⎨⎪==⎩
(01a <<)离散化得到差分方程Ax=b ,取
10.5,100,a n h n
===,应用Jacobi 迭代法、Gauss -Seidel 迭代法和超松弛迭代方法求解线性方程组,分别取1,0.1,0.01,0.0001ε=,用SOR 迭代法计算对应的数值解,并与精确解进行比较. 写出这三种迭代法求解线性方程组的步骤,并对计算结果进行分析.
四、实验原理
将[0,1]区间n 等分,方程离散化得差分方程
211()(2)i i i h y h y y ah εεε+-+-++=
差分方程对应的系数矩阵和右端项分别为
20222(1)(1)(1)1(2)(2)(2)(2)()n n n n h h ah y h h ah A b h h ah h ah h y εεεεεεεεεεεε-⨯--⨯⎛⎫-++-⎛⎫ ⎪ ⎪-++ ⎪ ⎪ ⎪ ⎪==-+ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪-+-+⎝⎭⎝
⎭
其中0(0),(1).n y y y y ==
SOR 迭代法的迭代矩阵和常数项分别为
11()[(1)],()B D L U D f D L b ωωωωωωω--=-+-=-
SOR 迭代法的迭代公式: 1k k y B y f ωω+=+
五、实验过程
利用Matlab 语言实现SOR 迭代公式的计算,分别对于1,0.1,0.01,0.0001ε=,松弛因子在(1,2)范围内,先按步长0.1搜索,在最少迭代步数附近按步长0.01再搜索.
算法终止准则:1410k k y y +--≤ 或者410k y y --≤或者迭代次数1000≥.
记录四种情况下的计算结果,并找出最佳松弛因子ω的值,并观察松弛因子ω与ε间的关系.。
