带通滤波器幅频相频分析
IIR数字滤波器设计实验报告

实验三IIR数字滤波器设计实验报告一、实验目的:1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求:1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号,并对其滤波,对比滤波前后波形和频谱三、基本原理:㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础,常用的类型分为巴特沃斯(Butterworth)、切比雪夫(Chebyshev)Ⅰ型、切比雪夫Ⅱ型、贝塞尔(Bessel)、椭圆等多种。
在MATLAB信号处理工具箱里,提供了这些类型的IIR数字滤波器设计子函数。
(二)性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段,滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB,双线性变换法中T取1s.四、实验步骤:1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波,并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性:101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中,采用的带通滤波器为6000-7000Hz ,换算成角频率为4.47-0.55,在上图中可以清晰地看出到达了题目的要求。
冲击响应不变法后的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性,而在在幅频曲线上几乎没有差别,都能达到相同的结果。
滤波器设计中的滤波器阻带和通带的幅频响应和相频响应的优化分析

滤波器设计中的滤波器阻带和通带的幅频响应和相频响应的优化分析在滤波器设计中,滤波器的阻带和通带的幅频响应以及相频响应的优化分析是非常重要的。
通过对滤波器的阻带和通带部分进行优化分析,可以实现滤波器对信号的滤波效果的优化。
首先,我们来讨论滤波器的阻带部分。
在滤波器设计中,阻带通常是指比滤波器设计要求的截止频率要大的频率范围。
阻带通常会引起滤波器的增益下降或者相位变化,从而对信号进行有效的抑制和阻断。
因此,优化阻带部分的幅频响应和相频响应对于滤波器的性能提升是至关重要的。
为了优化滤波器的阻带部分,可以采取以下措施。
首先,可以选择合适的滤波器类型和结构,如低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
不同的滤波器类型能够获得不同的阻带特性,因此根据具体需求选择适当的滤波器类型是至关重要的。
其次,可以通过调整滤波器的模拟或数字参数,如电容、电感、阻值或采样频率等,来改变滤波器的阻带幅频响应和相频响应。
此外,还可以采用滤波器的级联或并联方式,结合不同的滤波器,来进一步优化阻带部分的性能。
接下来,我们来讨论滤波器的通带部分。
滤波器的通带通常是指在滤波器设计要求的截止频率范围内的频率范围。
通带通常需要满足一定的增益要求或者相位要求,以保证滤波器对信号的有效传递和处理。
因此,优化通带部分的幅频响应和相频响应同样对于滤波器的性能提升具有重要作用。
为了优化滤波器的通带部分,可以采取以下策略。
首先,可以选择适当的通带增益或者滤波器增益,以满足所需的信号传递要求。
其次,可以对滤波器的通带幅频响应和相频响应进行优化,以获得更加平坦和稳定的响应特性。
这可以通过设计合理的滤波器参数,如截止频率、放大倍数或滤波器阶数等来实现。
另外,对于数字滤波器来说,还可以采用非线性滤波器设计方法来进一步优化通带部分的性能。
最后,需要注意的是,滤波器的幅频响应和相频响应的优化是一个综合考虑多个因素的过程。
需要根据具体的应用需求和设计要求,权衡滤波器的各项性能指标,如通带纹波、阻带抑制、群延时等,来进行综合设计和优化。
滤波器主要参数与特性指标-滤波器的主要性能参数

滤波器的主要参数(Definitions):之五兆芳芳创作中心频率(Center Frequency):滤波器通带的频率f0,一般取f0=(f1+f2)/2,f1、f2为带通或带阻滤波器左、右相对下降1dB或3dB边频点.窄带滤波器常以插损最小点为中心频率计较通带带宽.截止频率(Cutoff Frequency):指低通滤波器的通带右边频点及高通滤波器的通带左边频点.通常以1dB或3dB相对损耗点来尺度定义.相对损耗的参考基准为:低通以DC处插损为基准,高通则以未出现寄生阻带的足够高通带频率处插损为基准.通带带宽(BWxdB):指需要通过的频谱宽度,BWxdB=(f2-f1).f1、f2为以中心频率f0处拔出损耗为基准,下降X(dB)处对应的左、右边频点.通经常使用X=3、1、0.5即BW3dB、BW1dB、BW0.5dB 表征滤波器通带带宽参数.分数带宽(fractional bandwidth)=BW3dB/f0×100[%],也经常使用来表征滤波器通带带宽.拔出损耗(Insertion Loss):由于滤波器的引入对电路中原有信号带来的衰耗,以中心或截止频率处损耗表征,如要求全带内插损需强调.纹波(Ripple):指1dB或3dB带宽(截止频率)规模内,插损随频率在损耗均值曲线根本上动摇的峰-峰值.带内动摇(Passband Riplpe):通带内拔出损耗随频率的变更量.1dB带宽内的带内动摇是1dB.带内驻波比(VSWR):权衡滤波器通带内信号是否良好匹配传输的一项重要指标.理想匹配VSWR=1:1,失配时VSWR<1.对于一个实际的滤波器而言,满足VSWR<1 BWdBBWdBdiv>在入射波和反射波相位相同的地方,电压振幅相加为最大电压振幅Vmax ,形成波腹;在入射波和反射波相位相反的地方电压振幅相减为最小电压振幅Vmin ,形成波节.其它各点的振幅值则介于波腹与波节之间.这种分解波称为行驻波.驻波比是驻波波腹处的电压幅值Vmax与波节处的电压幅值Vmin之比.回波损耗(Return Loss):端口信号输入功率与反射功率之比的分贝(dB)数,也等于|20Log10ρ|,ρ为电压反射系数.输入功率被端口全部吸收时回波损耗为无穷大.回波损耗,又称为反射损耗.是电缆链路由于阻抗不匹配所产生的反射,是一对线自身的反射.从数学角度看,回波损耗为-10 lg [(反射功率)/(入射功率)].回波损耗愈大愈好,以削减反射光对光源和系统的影响.阻带抑制度:权衡滤波器选择性能黑白的重要指标.该指标越高说明对带外搅扰信号抑制的越好.通常有两种提法:一种为要求对某一给定带外频率fs抑制多少dB,计较办法为fs处衰减量As-IL;另一种为提出表征滤波器幅频响应与理想矩形接近程度的指标——矩形系数(KxdB<1),KxdB=BWxdB/BW3dB,(X可为40dB、30dB、20dB等).滤波器阶数越多矩形度越高——即K越接近理想值1,制作难度当然也就越大.延迟(Td):指信号通过滤波器所需要的时间,数值上为传输相位函数对角频率的导数,即Td=df/dv.带内相位线性度:该指标表征滤波器对通带内传输信号引入的相位失真大小.按线性相位响应函数设计的滤波器具有良好的相位线性度.特性指标1、特征频率:1)通带截频fp=wp/(2p)为通带与过渡带鸿沟点的频率,在该点信号增益下降到一团体为规则的下限;2)阻带截频fr=wr/(2p)为阻带与过渡带鸿沟点的频率,在该点信号衰耗下降到一人为规则的下限;3)转折频率fc=wc/(2p)为信号功率衰减到1/2(约3dB)时的频率,在良多情况下,常以fc作为通带或阻带截频;4)固有频率f0=w0/(2p)为电路没有损耗时,滤波器的谐振频率,庞杂电路往往有多个固有频率.2、增益与衰耗滤波器在通带内的增益并不是常数.1)对低通滤波器通带增益Kp一般指w=0时的增益;高通指w→∞时的增益;带通则指中心频率处的增益;2)对带阻滤波器,应给出阻带衰耗,衰耗定义为增益的倒数;3)通带增益变更量△Kp指通带内各点增益的最大变更量,如果△Kp以dB为单位,则指增益dB值的变更量.3、阻尼系数与品质因数阻尼系数是表征滤波器对角频率为w0信号的作用,是滤波器中暗示能量衰耗的一项指标.阻尼系数的倒数称为品质因数,是*价带通与带阻滤波器频率选择特性的一个重要指标,Q= w0/△w.式中的△w为带通或带阻滤波器的3dB带宽,w0为中心频率,在良多情况下中心频率与固有频率相等.品质因数电学和磁学的量.暗示一个储能器件(如电感线圈、电容等)、谐振电路中所储能量同每周期损耗能量之比的一种质量指标;串联谐振回路中电抗元件的Q值等于它的电抗与其等效串联电阻的比值;元件的Q值愈大,用该元件组成的电路或网络的选择性愈佳.在串联电路中,电路的品质因数Q有两种丈量办法,一是按照公式 Q=UL/U0=Uc/U0测定,Uc与UL辨别为谐振时电容器C与电感线圈L上的电压;另一种办法是通过丈量谐振曲线的通频带宽度△f=f2-f1,再按照Q=f0/(f2-f1)求出Q 值.式中f0为谐振频率,f2与f1是失谐时,亦即输出电压的幅度下降到最大值的1/√2(=0.707)倍时的上、下频率点.Q 值越大,曲线越锋利,通频带越窄,电路的选择性越好. 4、灵敏度滤波电路由许多元件组成,每个元件参数值的变更都会影响滤波器的性能.滤波器某一性能指标y对某一元件参数x 变更的灵敏度记作Sxy,定义为:Sxy=(dy/y)/(dx/x).该灵敏度与丈量仪器或电路系统灵敏度不是一个概念,该灵敏度越小,标记取电路容错能力越强,稳定性也越高. 5、群时延函数当滤波器幅频特性满足设计要求时,为包管输出信号失真度不超出允许规模,对其相频特性∮(w)也应提出一定要求.在滤波器设计中,经常使用群时延函数d∮(w)/dw*价信号经滤波后相位失真程度.群时延函数d∮(w)/dw越接近常数.。
滤波器设计中的频率响应分析

滤波器设计中的频率响应分析在电子电路领域中,滤波器是非常重要的组成部分,用于将特定频率范围内的信号滤除或放大。
在滤波器设计过程中,频率响应分析是一项关键任务,它帮助工程师评估滤波器对不同频率信号的响应能力。
本文将介绍滤波器频率响应分析的基本概念和常用方法。
一、滤波器频率响应的定义与分类滤波器的频率响应是指其输出信号随输入信号频率变化而发生的变化。
根据频率响应曲线特征,滤波器可分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四种基本类型。
低通滤波器用于将低于截止频率的信号通过,而高通滤波器则允许高于截止频率的信号通过。
二、频率响应分析方法1. 理想频率响应分析:理想频率响应是指在理想条件下滤波器对频率的响应情况。
在理想低通滤波器中,截止频率前的信号完全通过,而截止频率后的信号完全被滤除。
类似地,理想高通滤波器中,截止频率前的信号被滤除,而截止频率后的信号完全通过。
理想滤波器的频率响应可用数学函数表示,例如低通滤波器的频率响应为1,高通滤波器的频率响应为0,截止频率处的响应为0.5。
2. 实际频率响应分析:实际频率响应受到滤波器的非理想特性和电路元件的误差等因素的影响。
常用的分析方法包括Bode图分析、频率响应曲线绘制等。
Bode 图是描述滤波器频率响应的常用工具,它展示了滤波器增益和相位随频率变化的情况。
根据Bode图,可以直观地了解滤波器的截止频率、增益幅度和相位偏移等信息。
频率响应曲线则通过将输入信号的频率范围在横轴上表示,滤波器的增益在纵轴上表示,以图形方式呈现了滤波器的频率特性。
三、频率响应分析的应用频率响应分析在滤波器设计和实验中有着重要的应用价值。
通过分析滤波器的频率响应,可以确定滤波器的截止频率和增益特性,从而满足实际应用的要求。
例如,在音频处理中,低通滤波器用于去除杂音和高频噪声,而高通滤波器则可以突出音乐中的高频成分。
在射频领域,带通滤波器用于滤除特定频率范围外的信号,以避免干扰和频率重叠。
滤波器设计中的滤波器阻带和通带的滤波器阻带和通带的频率范围选择分析

滤波器设计中的滤波器阻带和通带的滤波器阻带和通带的频率范围选择分析滤波器设计中的滤波器阻带和通带的频率范围选择分析滤波器在电子系统中扮演着至关重要的角色,它能够滤除或增强特定频率范围的信号。
在滤波器设计中,选择合适的滤波器阻带和通带的频率范围对滤波器的性能至关重要。
本文将分析滤波器阻带和通带的频率范围选择的关键因素。
1. 了解滤波器的基本原理在深入讨论滤波器阻带和通带的频率范围之前,我们需要了解滤波器的基本原理。
滤波器可以根据其频率响应来分类为低通、高通、带通或带阻滤波器。
低通滤波器允许低频信号通过,而抑制高频信号。
相反,高通滤波器允许高频信号通过,而抑制低频信号。
带通滤波器允许特定范围内的频率信号通过,而抑制其他频率范围的信号。
带阻滤波器与带通滤波器相反,它抑制特定范围内的频率信号。
2. 确定滤波器的应用需求为了选择合适的滤波器阻带和通带的频率范围,我们首先需要确定滤波器的应用需求。
不同的应用场景对滤波器的要求不同。
例如,在音频系统中,滤波器需要去除杂音和频率扭曲,同时保留音频信号的精确性。
在无线通信系统中,滤波器需要滤除不同频率之间的干扰信号。
因此,了解滤波器的应用需求对滤波器设计至关重要。
3. 选择滤波器的阻带频率范围滤波器的阻带频率范围是指滤波器能够有效抑制信号的频率范围。
选择阻带频率范围的关键取决于所需的抑制程度和应用需求。
一般来说,阻带频率范围应包含需要抑制的信号频率。
例如,对于低通滤波器,阻带频率范围应包含高频信号。
通过正确选择阻带频率范围,可以保证滤波器能够有效地滤除不需要的信号。
4. 确定滤波器的通带频率范围滤波器的通带频率范围是指滤波器能够传递信号的频率范围。
选择通带频率范围的关键是确保所需的信号能够传递而不受到滤波器的影响。
对于带通滤波器或带阻滤波器,通带频率范围应包含所需频率范围。
例如,对于音频系统中的带通滤波器,通带频率范围应包含所需的音频频率范围。
5. 考虑滤波器的性能要求除了滤波器的应用需求和频率范围之外,滤波器的性能要求也应考虑在内。
带通滤波器分析
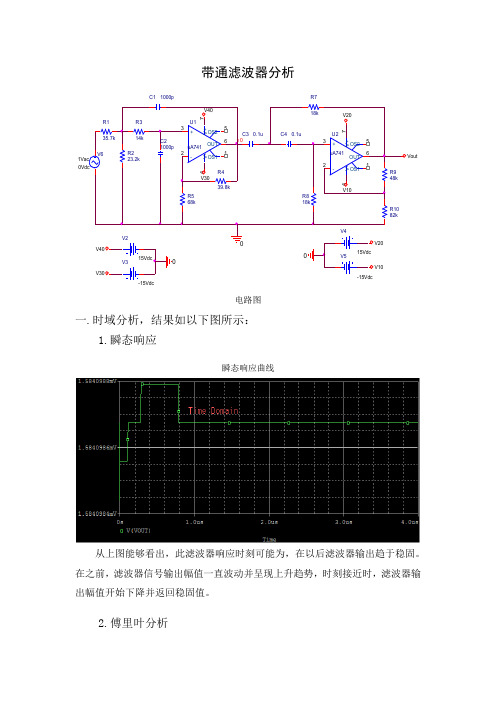
带通滤波器分析U2uA7413274615+-V+V-OUTOS1OS2V10R223.2kU1uA7413274615+-V+V-OUTOS1OS2V20R818kV215VdcR718kR439.8kV20R568kC40.1uVoutV415VdcV10R314k v0V30V40R948k V61Vac0VdcV5-15VdcC30.1uR135.7kC21000pR1082k V40V30C11000pV3电路图一.时域分析,结果如以下图所示:1.瞬态响应瞬态响应曲线从上图能够看出,此滤波器响应时刻可能为,在以后滤波器输出趋于稳固。
在之前,滤波器信号输出幅值一直波动并呈现上升趋势,时刻接近时,滤波器输出幅值开始下降并返回稳固值。
2.傅里叶分析参数设置如以下图,计算直流分量和从基波一直到九次谐波。
傅里叶分析结果如下:FOURIER COMPONENTS OF TRANSIENT RESPONSE V(VOUT)DC COMPONENT =HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 +01 +00 +01 +002 +02 +00 +01 +013 +02 +00 +01 +024 +02 +00 +01 +025 +02 +00 +01 +026 +02 +00 +01 +027 +02 +00 +01 +028 +02 +00 +01 +029 +02 +00 +01 +02TOTAL HARMONIC DISTORTION = +02 PERCENT由以上数据能够得出瞬态响应各次谐波的分量。
二.频域分析幅频特性相频特性由上图能够得出结论,此电路为带通滤波器,通带频率范围可能为100-10kHz。
由于鼓励信号的幅值为1,因此频率响应的幅值即为电压放大倍数,从图中能够看出,滤波器最大电压放大倍数为1,因此信号通过滤波器时,能够以原先的幅值正常的通过。
滤波器电路分析

图5-3 m推演型LPF的特性示例
图5-5
表2 m推演型低通滤波电路元件归一化参数表
续表2
(9) 将上式(6)~(9)带入电路中得下图m推演型低通滤波电路,陷波点为 130MHZ,截止频率为100MHZ。
m推演型低通滤波电路,在f=130MHZ处有一个陷波点
仿真结果
回波损耗频率特性曲线,当在陷波点f=130MHZ时,电路的回拨损 耗最大,信号反射最厉害
2A
63.66 V
u1 (t ) [63.66 42.44cos(t ) 8.488cos(2t ) 3.638cos(3t ) ...]V
2. 对于基波,先计算转移电压比
| H ( j ) | 1 1 C
2
1 1 10
设计RC二阶低通滤波器电路,可以通过将两个RC一阶低通滤波电路 级联等到,RC二阶低通滤波电路。
图 14-9
下面给出一个fc=200KHZ的RC二阶低通滤波电路的仿真电路图
仿真结果:RC二阶电路的幅频特性 曲线,截止频率为28.199KHZ,
RC二阶高通滤波电路相频特性曲线
3.3RC二阶高通滤波电路
RC一阶高通滤波电路仿真原理图
RC一阶高通滤波电路幅频特性曲线,从图中可以看 出电路在幅度增益下降3.232dB时,截止为 100.901KHZ,滤波电路的性能能满足设计指标。
RC一阶高通滤波电路相频特性曲线,从图中可任意看 出当f=100.697KHZ时,相角超前46.497 deg。
3.3RC二阶低通滤波电路
图10
RC二阶高通滤波电路幅度表达式
RC二阶高通滤波电路截止频率
RC滤波电路所实现的频率特性,也可由相应的 RL电路来实现。在低频率应用的条件下,由于
RC滤波原理简介

RC 无源滤波器电路及其原理
在测试系统中,常用RC 滤波器。
因为在这一领域中,信号频率相对来说不高。
而RC 滤波器电路简单,抗干扰性强,有较好的低频性能,并且选用标准的阻容元件易得,所以在工程测试的领域中最经常用到的滤波器是RC 滤波器。
1)一阶RC 低通滤波器
RC 低通滤波器的电路及其幅频、相频特性如下图所示。
设滤波器的输入电压为ex 输出电压为ey ,电路的微分方程为:
这是一个典型的一阶系统。
令 τ=RC ,称为时间常数,对上式取拉氏变换,有:
H y y x
y
x sE E E E E τ+=令(s )= H(s)是传递函数
或
其幅频、相频特性公式为:
分析可知,当f很小时,A(f)=1,信号不受衰减的通过;当f很大时,A(f)=0,信号完全被阻挡,不能通过。
2)一阶RC高通滤波器
RC高通滤波器的电路及其幅频、相频特性如下图所示。
设滤波器的输入电压为ex输出电压为ey,电路的微分方程为:
同理,令=RC,对上式取拉氏变换,有:
或
其幅频、相频特性公式为:
分析可知,当f很小时,A(f)=0,信号完全被阻挡,不能通过;当f很大时,A(f)=1信号不受衰减的通过. 3)RC带通滤波器
带通滤波器可以看作为低通滤波器和高通滤波器的串联,其电路及其幅频、相频特性如下图所示。
其幅频、相频特性公式为:H(s) = H1(s) * H2(s)
式中H1(s)为高通滤波器的传递函数,H2(s)为低通滤波器的传递函数。
有:。
四种滤波器的幅频特性

四种滤波器的幅频特性本次实验是观察四种滤波器(低通、高通、带宽、带阻)的幅频特性,以加强对各种滤波器的功能认知。
本次实验我们选用的放大器为324型,其功能图如下所示:下面我们来逐步观察一下四种滤波器的特性。
1.低通滤波器其电路图如下所示: 图中,电阻R1=R2=R=10KΩ,C1=C2=0.01uF,Ro=0.8R=8Ω,Vcc+=+12V , Vcc-=-12V ,低通滤波器的传递函数20022)(ωαωω++=s s K s H p ,,其中2221102121001111;1;1C R K R R C C C R R RRK K ff p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数据w 。
=10000rad/s ,Kp =1.8,α=1.2,()()2202202225/2425/78.1)(ωωωωω+-=j H ;当w =0时)(ωj H =1.8,;w 增加且w<4800rad/s 时,)(ωj H 增加;当>4800rad/s 时,)(ωj H 减小,;w 趋近无穷时,)(ωj H 趋近于0。
此时wc=1.17rad/s 。
对于不同的α,滤波器的幅频特性也不相同对于实验中的低通,α=1.2,与1.25的相似,我们对于实验数据的测量如下:输入为100mV范围10~6kHz 输出不失真 绘出的幅频特性图如下: 2、高通滤波器 其电路图如下:其中R1=R2=R=10K,C1=C2=0.01uF,Ro=0.8R=8K 高通的传递函数为20022)(ωαω++=s s s K s H p ,()()2022022)(ωαωωωωω+-=p K j H ,1121202121001111;1;1CR K C C R C C R R RR K K f f p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数值后,Kp =1.8,W=0时)(ωj H =0;w<4800rad/s 时)(ωj H 增加;w 趋近于无穷时,)(ωj H 保持不变。
带通滤波器的原理

带通滤波器的原理带通滤波器是一种常见的信号处理器件,其主要作用是滤除频率范围外的噪声和干扰信号,只保留特定的频率范围内的信号。
在实际应用中,带通滤波器广泛应用于音频、视频、通信等领域,具有重要的作用。
带通滤波器的原理是基于滤波器对频率的选择性,只有特定频率范围内的信号可以通过滤波器,而其他频率范围的信号则被滤除。
带通滤波器通常由一个低通滤波器和一个高通滤波器组成,低通滤波器可以将低于截止频率的信号通过,而高通滤波器可以将高于截止频率的信号通过,两者结合可以实现带通滤波。
带通滤波器的设计需要确定两个关键参数:截止频率和带宽。
截止频率是指在该频率以下或以上的信号将被滤除,而带宽则是指通过滤波器的频率范围。
根据这些参数,可以选择不同类型的滤波器来实现不同的滤波效果。
常见的带通滤波器包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
巴特沃斯滤波器具有平坦的幅频响应和良好的相位响应,但是在截止频率附近会出现较大的过渡带宽。
切比雪夫滤波器则可以实现更尖锐的截止边缘和更小的过渡带宽,但是会引入较大的纹波。
椭圆滤波器则综合了两者优点,但是设计较为复杂。
在实际应用中,带通滤波器可以用于多种信号处理任务。
例如,在音频处理中,可以使用带通滤波器来增强特定频率范围内的声音效果;在视频处理中,可以使用带通滤波器来去除视频中的噪声和干扰信号;在通信中,可以使用带通滤波器来选择特定频率范围内的信号进行解调和解码。
总之,带通滤波器是一种重要的信号处理器件,广泛应用于音频、视频、通信等领域。
其原理是基于滤波器对频率的选择性,通过选择不同类型的滤波器和确定关键参数来实现不同的滤波效果。
带通滤波器在实际应用中具有重要的作用,可以增强信号质量、去除噪声和干扰信号等。
带通滤波器相位特性讨论(new)

(带通信号通过带通系统的输出和不失真条件)
第
带通信号的复包络表示
s(t ) = a(t )cos[ωct +φ(t )]
2 页
基带信号: f s 基带信号: (t ) ⇔ F(ω) = 0 ω > ωH,经调制得 (t ): , 1 j [ωct +φ ( t )] − j[ωct +φ ( t )] = a(t ) e +e 2 1 1 jφ ( t ) jωct − jφ ( t ) − jωct e = a(t )e e + a(t )e 2 2 ∆ 1 1 ∗ jωct − jωc t jφ ( t ) , x(t ) = a(t )e = x(t )e + x (t )e 2 2 1 1 jωc t jωc t ∗ = x(t )e + x(t )e 2 2
7 页
固定相移 ct,则系统为: ω 则系统为: 如果在通带内附加一个 e = ke
− j ( ω−ωc )t0
= kce
− jωt
仍为常数,系统仍为无 失真传输。 仍为常数, 失真传输。
附加相移修正后, H 的幅频特性不变, 附加相移修正后, (ω )的幅频特性不变,相位
ω 点的负斜率直线, 在 特性变为过载频 c点的负斜率直线,系统 ωc附近的
{
}
[
]
x( t )= a( t )e jφ ( t )是基带带限信号,称为( t )的复包络; 是基带带限信号, s 的复包络; s( t )是高频带限信号,也称 是高频带限信号, 为带通信号。 为带通信号。 x 令: ( t ) ⇔ X(ω ) 有 ∗( t ) ⇔ X∗( −ω ) , x 1 S 则: (ω ) = X(ω −ωc ) + X∗( −ω −ωc ) = S(ω ) e jΨ( ω ) 2
滤波器的主要特性指标

滤波器的主要特性指标电子知识1、特征频率:①通带截频fp=wp/(2p)为通带与过渡带边界点的频率,在该点信号增益下降到一个人为规定的下限。
②阻带截频fr=wr/(2p)为阻带与过渡带边界点的频率,在该点信号衰耗(增益的倒数)下降到一人为规定的下限。
③转折频率fc=wc/(2p)为信号功率衰减到1/2(约3dB)时的频率,在很多情况下,常以fc作为通带或阻带截频。
④固有频率f0=w0/(2p)为电路没有损耗时,滤波器的谐振频率,复杂电路往往有多个固有频率。
2、增益与衰耗滤波器在通带内的增益并非常数。
①对低通滤波器通带增益Kp一般指w=0时的增益;高通指w→∞时的增益;带通那么指中心频率处的增益。
②对带阻滤波器,应给出阻带衰耗,衰耗定义为增益的倒数。
③通带增益变化量△Kp指通带内各点增益的最大变化量,如果△Kp以dB为单位,那么指增益dB值的变化量。
3、阻尼系数与品质因数阻尼系数是表征滤波器对角频率为w0信号的阻尼作用,是滤波器中表示能量衰耗的一项指标。
阻尼系数的倒数称为品质因数,是*价带通与带阻滤波器频率选择特性的一个重要指标,Q= w0/△w。
式中的△w为带通或带阻滤波器的3dB 带宽, w0为中心频率,在很多情况下中心频率与固有频率相等。
4、灵敏度滤波电路由许多元件构成,每个元件参数值的变化都会影响滤波器的性能。
滤波器某一性能指标y对某一元件参数x变化的灵敏度记作Sxy,定义为: Sxy=(dy/y)/(dx/x)。
该灵敏度与测量仪器或电路系统灵敏度不是一个概念,该灵敏度越小,标志着电路容错能力越强,稳定性也越高。
5、群时延函数当滤波器幅频特性满足设计要求时,为保证输出信号失真度不超过允许范围,对其相频特性∮(w)也应提出一定要求。
在滤波器设计中,常用群时延函数d∮(w)/dw*价信号经滤波后相位失真程度。
群时延函数d∮(w)/dw越接近常数,信号相位失真越小。
IBIS模型是一种基于V/I曲线对I/O BUFFER快速准确建模方法,是反映芯片驱动和接收电气特性一种国际标准,它提供一种标准文件格式来记录如驱动源输出阻抗、上升/下降时间及输入负载等参数,非常适合做振荡和串扰等高频效应计算与仿真。
带通滤波器幅频相频分析课件

仿真软件法
使用仿真软件对带通滤波 器进行仿真,得到其幅频 响应曲线。
03
波器相响分 析
相频响应的定义
相频响应
描述滤波器输出信号与输入信号 之间的相位差随频率变化的特性。
相移
表示输出信号与输入信号之间的 相位差,与频率相关。
群延时
描述相位差随频率变化的速率。
相频响应的特性
线性特性
在一定的频率范围内,相频响应 与频率呈线性关系。
设计参数选择
通带范围
阻带范围Βιβλιοθήκη 最大衰减群延迟根据系统需求,确定带 通滤波器通带的频率范围。
确定带通滤波器阻带的 频率范围,以保证信号
的隔离和防止干扰。
确定带通滤波器的最大 衰减,以保证信号的传
输质量和稳定性。
确定带通滤波器的群延 迟,以保证信号的时域
特性。
设计实现方法
使用MATLAB或Simulink等软 件工具进行建模和仿真,验证 设计的正确性。
通带和阻带
在幅频响应曲线中,增益 值较高的区域称为通带, 而增益值较低的区域称为 阻带。
带宽
带宽是指带通滤波器通带 范围内频率的范围,带宽 决定了滤波器对不同频率 信号的响应速度。
幅频响应的分析方法
实验测量法
通过实验测量带通滤波器 在不同频率下的输出信号 幅度,得到幅频响应曲线。
数值计算法
利用滤波器设计理论和数 值计算方法,计算出带通 滤波器的幅频响应。
它通常由电阻、电容、电感等电 子元件组成,通过调整元件的参 数,可以实现对不同频率信号的 抑制或通过。
带通滤波器的特性
带通滤波器具有频率选择性,即它只 允许特定频率范围内的信号通过。
带通滤波器还具有稳定性和高效性, 它可以对信号进行平滑处理,减少噪 声干扰,同时不会改变信号的幅度和 相位。
带通滤波器BPF知识讲解

0
( 0 ) 相频响应 f arctg0 3
2. RC串并联选频网络的选频特性
FV
1
32 ( 0 )2 0
( 0 )
f arctg0 3
0 .1
当 0R 1C 或ff02π1 RC
幅频响应有最大值
0.1
1 FVmax 3
相频响应 f 0
FV 0 .4 1
3 0 .3
0 .2
0 .1 0 1 (a ) f 90 60
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
带通滤波器BPF
复习
1. 滤波电路的功能
使指定频段的信号顺利通过,其它频率的信号被衰减。
2. 滤波电路的种类
低通滤波器(LPF)
通带放大倍数
理想幅频特性 无过渡带
通带截止频率
下降速率
用幅频特性描述滤波特性,要研究 Au p 、Au ( fP、下降速率)。
复习
3、理想滤波器的幅频特性
高通滤波器(HPБайду номын сангаас)
AVFV 1 稳幅
讨论
不符合相位条件 不符合幅值条件
1)是否可用共射放大电路? 2)是否可用共集放大电路? 3)是否可用共基放大电路? 4)是否可用两级共射放大电路?
输入电阻小、输出 电阻大,影响f0
可引入电压串联负反馈,使 电压放大倍数大于3,且Ri大、 Ro小,对f0影响小
应为RC 串并联网路配一个电压放大倍数略大于3、输入电 阻趋于无穷大、输出电阻趋于0的放大电路。
Z2 R C
Vi Vf
=
R1
热敏电阻的作用
-
Vo
Io
Rf 功耗 Rf 温度 Rf 阻值
带通滤波器(个人学习总结)

有源模拟带通滤波器的设计滤波器是一种具有频率选择功能的电路,它能使有用的频率信号通过。
而同时抑制(或衰减)不需要传送频率范围内的信号。
实际工程上常用它来进行信号处理、数据传送和抑制干扰等,目前在通讯、声纳、测控、仪器仪表等领域中有着广泛的应用。
1滤波器的结构及分类以往这种滤波电路主要采用无源元件R、L和C组成,60年代以来,集成运放获得迅速发展,由它和R、C组成的有源滤波电路,具有不用电感、体积小、重量轻等优点。
此外,由于集成运放的开环电压增益和输入阻抗都很高,输出阻抗比较低,构成有源滤波电路后还具有一定的电压放大和缓冲作用。
通常用频率响应来描述滤波器的特性。
对于滤波器的幅频响应,常把能够通过信号的频率范围定义为通带,而把受阻或衰减信号的频率范围称为阻带,通带和阻带的界限频率叫做截止频率。
滤波器在通带内应具有零衰减的幅频响应和线性的相位响应,而在阻带内应具有无限大的幅度衰减。
按照通带和阻带的位置分布,滤波器通常分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
文中结合实例,介绍了设计一个工作在低频段的二阶有源模拟带通滤波器应该注意的一些问题。
2二阶有源模拟带通滤波器的设计2.1基本参数的设定二阶有源模拟带通滤波器电路,如图1所示。
图中R1、C2组成低通网络,R3、C1组成高通网络,A、Ra、Rb组成了同相比例放大电路,三者共同组成了具有放大作用的二阶有源模拟带通滤波器,以下均简称为二阶带通滤波器。
根据图l可导出带通滤波器的传递函数为令s=jω,代入式(4),可得带通滤波器的频率响应特性为波器的通频带宽度为BW0.7=ω0/(2πQ)=f0/Q,显然Q值越高,则通频带越窄。
通频带越窄,说明其对频率的选择性就越好,抑制能力也就越强。
理想的幅频特性应该是宽度为BW0.7的矩形曲线,如图3(a)所示。
在通频带内A(f)是平坦的,而通带外的各种干扰信号却具有无限抑制能力。
各种带通滤波器总是力求趋近理想矩形特性。
滤波器的幅频特性与相频特性的关系分析

滤波器的幅频特性与相频特性的关系分析滤波器是一种常用的电子设备,用于将输入信号中的特定频率成分进行选择性的放大或抑制。
在滤波器的设计和应用过程中,幅频特性和相频特性是两个重要的指标。
本文将探讨滤波器的幅频特性与相频特性之间的关系,并分析它们在滤波器设计中的应用。
一、幅频特性幅频特性是指滤波器在不同频率下的传递函数的模的变化。
在滤波器的幅频特性曲线中,横轴代表输入信号的频率,纵轴代表输出信号的幅值。
根据幅频特性曲线,可以判断滤波器在不同频段的放大或衰减程度。
幅频特性通常由滤波器的增益-频率特性曲线表示。
滤波器的幅频特性可以分为低通、高通、带通和带阻四种类型。
低通滤波器允许低频分量通过,并衰减高频分量;高通滤波器则允许高频分量通过,并衰减低频分量;带通滤波器则将某一频率范围内的信号放大,其他频率信号衰减;带阻滤波器则将某一频率范围内的信号衰减,其他频率信号放大。
二、相频特性相频特性是指滤波器在不同频率下的传递函数的相位的变化。
相频特性曲线描述了输入信号和输出信号之间的相对时间延迟。
相频特性可以直观地反映滤波器对不同频率信号的相位响应。
滤波器的相频特性对于某些应用非常重要。
例如,在音频处理中,相频特性的失真可能导致声音的混叠和不自然的声音效果。
因此,在设计音频滤波器时,需要特别关注相频特性,以确保信号的相位保持一致。
三、幅频特性与相频特性的关系滤波器的幅频特性和相频特性之间存在密切的关系。
一些滤波器设计方法,如巴特沃斯滤波器设计,可以同时优化幅频特性和相频特性。
在某些情况下,滤波器的幅频特性和相频特性可能相互牵制。
例如,当滤波器的幅频特性要求具有非常陡峭的衰减特性时,可能会导致相频特性的失真。
因此,在实际滤波器设计中,需要在幅频特性和相频特性之间进行权衡,并选择最合适的设计方法。
四、幅频特性与相频特性的应用滤波器的幅频特性和相频特性在信号处理和通信系统中有着广泛的应用。
以下是一些常见的应用场景:1. 音频处理:在音频系统中,滤波器常用于去除噪声、修饰音频信号等。
带通滤波器的技术指标

带通滤波器的技术指标
带通滤波器是一种用于选择特定频率范围内信号的滤波器。
在设计和评估带通滤波器时,通常会考虑以下一些技术指标:
1. 通带范围(Passband Range):指定滤波器允许通过的频率范围。
通带范围通常由下限频率和上限频率来定义。
2. 通带波纹(Passband Ripple):描述在通带范围内信号增益的变化。
通带波纹通常以分贝(dB)为单位来表示。
3. 阻带范围(Stopband Range):指定滤波器阻止通过的频率范围。
阻带范围通常由下限频率和上限频率来定义。
4. 阻带衰减(Stopband Attenuation):描述在阻带范围内信号的衰减程度。
通常以分贝(dB)为单位来表示。
5. 通带边缘频率(Passband Edge Frequency):指定通带范围的边缘频率,即通带的上限或下限频率。
6. 阻带边缘频率(Stopband Edge Frequency):指定阻带范围的边缘频率,即阻带的上限或下限频率。
7. 带宽(Bandwidth):通常指通带范围的宽度,即上限频率和下限频率之间的差值。
8. 过渡带宽(Transition Bandwidth):描述从通带到阻带的过渡范围的宽度。
这些技术指标可以帮助工程师评估带通滤波器的性能和适用性,以确保它能够满足特定的信号处理需求。
在实际设计和应用中,还会考虑到滤波器的阶数、相位响应、群延迟等更多的指标和特性。
交流电路的频率特性

2.高通滤波电路 传递函数为
设
幅频特性和相频特性随角频率 变化的整体情况如图 所示,从图中看到,以 作为分界点,高频信号很容易通 过,而低频信号的幅值下降很快,表明该电路具有高频通 过而抑制低频的能力,所以此电路称之为高通滤波电路。
电流 值在等于最大值 之间宽度称为通频带,即
是下限频率。
的70.7 %处,频率的上下限 ,式中 是上限频率,
Q大
Q小
通频带与品质因数成反比。 值越大,谐振曲线愈尖锐, 选择性越好,但通频带越窄。
例 3-5 将一线圈(
,
)与电容串联,接在
,
的电源上,问 为何值时电路发生谐振?
并求谐振电流 、电容端电压 、线圈端电压 及品质
使电路发生谐振。
串联谐振电路具有下列特征: (1)串联谐振时外加电压与电路电流同相( ),因 此电路呈阻性。电源供给电路的能量全部消耗在电阻上,电 源与电路不存在能量交换,电感和电容之间相互交换能量, 以满足无功功率的需要。
即 与 在相位上相反, 相量模相等,互相抵消,外加 电压等于电阻电压,相量图如 图所示。
3.带通滤波电路 带通滤波器的传递函数
幅频特性
相频特性 设
由图可见,当
时,输出电压与输入电压同相,同时
输出也达到最大值
,并规定,当
等于最大值
的 70.7% 处之间频率的宽度称为通频带宽度,即
二、 谐振电路
对于任何含有电感和电容的电路,在一定频率下可以 呈现电阻性,即整个电路的总电压与总电流同相位,这种 现象称为正弦交流电路的谐振。
滤波器的频率响应和幅频特性分析

滤波器的频率响应和幅频特性分析滤波器是一种电子设备,广泛应用于信号处理、通信系统和音频设备等领域。
它可以根据频率的不同,将输入信号中的特定频段通过,而抑制其他频段的信号。
滤波器的频率响应和幅频特性是评估其性能的重要指标。
本文将对滤波器的频率响应和幅频特性进行详细分析。
一、滤波器的频率响应滤波器的频率响应是指滤波器对不同频率信号的响应程度。
频率响应通常用幅度响应和相位响应来表示。
1. 幅度响应幅度响应表示滤波器对不同频率信号的衰减或增益程度。
一般来说,滤波器在通带内的幅度响应应该尽量保持平坦,即对各个频率的信号均衡地衰减或增益。
而在阻带内,滤波器应该有较高的衰减能力,使该频率范围内的信号被有效抑制。
幅度响应可以用增益曲线或幅度频率特性曲线来表示,通常以对数坐标形式呈现。
2. 相位响应相位响应描述滤波器对不同频率信号的相位延迟。
不同频率信号在滤波器中传输时,会因为电路元件的特性而存在不同的延迟。
相位响应的平坦度是滤波器性能的重要指标之一,应尽量保持线性。
二、滤波器的幅频特性滤波器的幅频特性描述了滤波器对信号幅度的衰减或增益关系。
常见的幅频特性包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
1. 低通滤波器低通滤波器能够通过低频信号,而将高频信号衰减。
在幅频特性曲线上,低通滤波器的通带是从直流到截止频率,通常以增益值为0dB作为参考。
截止频率是指滤波器在该频率处的幅值衰减到-3dB的位置。
2. 高通滤波器高通滤波器能够通过高频信号,而将低频信号衰减。
在幅频特性曲线上,高通滤波器的通带是从截止频率开始,直到无穷大频率。
截止频率处的增益值通常为0dB。
3. 带通滤波器带通滤波器能够通过某个频率范围内的信号,而将其他频率的信号衰减。
在幅频特性曲线上,带通滤波器的通带是两个截止频率之间的频率范围。
通带内的增益应尽量保持平坦。
4. 带阻滤波器带阻滤波器能够衰减某个频率范围内的信号,而通过其他频率的信号。
在幅频特性曲线上,带阻滤波器的阻带是两个截止频率之间的频率范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h 2 ( t ) 1 [ H 2 ( s ) e ] t[c t o ss i t ] n e tA co t ) s(
其中: A 1()2, arctan
结论:H(s)的零点只影响h(t)的幅度和相位,而不影响形状。
系统的幅频、相频特性曲线
H (s)R 1(s s1/1)C 2(s 11/2)
-1/R1C1 -1/R2C2
H (s)R 1(s s1/1)C 2(s 11/2)
S平面上的负实轴的极点
H (s) 1 h(t) eatu(t) sa
冲激相应按指数规律衰减,为稳定的系统
H(s)零点的位置对系统的特性的影响
考虑如下两个系统:
H H2 1((ss)) ((ss s)s )2 2 2 2(s s h 1 )( 2 t ) 2 (1 s[H 1 ()s 2 ) ]e 2 tco ts
零极点分析:
左半s平面→h(t)衰减
极点:
右半s平面→h(t)增长
一阶极点→h(t) 等幅振荡或阶跃
虚轴上
二阶极点→h(t) 呈增长形式
h(t)衰减
稳定系统(极点在左半s平面)
h(t)增长
如果在虚轴上→
非稳定系统(极点在右半s平面)
一阶:阶跃或等幅振荡(临界稳定)
二阶:以上不稳定系统
零极点分析
o
H (j)
1
R 1 2 (1 /1)2C 2 2 (1 /2)2
1.000 0.500
0.100 0.050
0.010 0.005
0.001
0.001
0.01
0.1
1
10
100
1000
w
s
1
H (s)R 1(s1/1)C 2(s1/2)
9 a 0r1 c a tr g 2 ctg
信号频谱与系统的频域特性 ——以一实际的二阶电路为例
可编辑ppt
1
题目内容
求系统传递函数并作零、极点分析;大 致画出系统的幅频、相频特性曲线;从 一般意义上说明系统的滤波类型;
求传递函数
s
1
H (s)R 1(s1/1)C 2(s1/2)
其中τ1=R1C1, τ2=R2C2
传递函数是输出信号与输入信号的拉普拉斯变换的比
1.50
500
1000
1500
2000
系统的幅频、相频特性曲线
结论
当原件参数取合适值时为带通滤波 器,由传递函数看相当于一个高通 和一个低通滤波器串联
原件参数满足一定条件时可组成微 分电路、高通电路、积分电路、低 通电路或比例电路。
极点关系到系统的稳定性 零点影响系统冲激相应的幅值和相
