西方经济学(第四版)课后习题答案
西方经济学第四版章后习题参考答案

西方经济学——习题参考答案(第四版)第一章1.西方经济学的基本假设是:(1)经济人假设第一,在经济活动中,经济主体(居民户、厂商或政府)所追求的唯一目标是自身经济利益的最优化。
第二,经济主体所有的经济行为都是有意识的和理性的,不存在经验型的或随机的决策。
因此经济人又被称为理性人。
(2)产权明确在理想化的市场经济中,一切市场行为都必须以明确的产权为前提。
不同的产权界定会带来资源配置的不同效率。
(3)完全信息经济活动的所有当事人都拥有充分的和相同的信息,而且获取信息不需要支付任何成本。
(4)厂商是以利润最大化为唯一目标的整体。
上述基本假设与实际经济生活存在很大差距。
采用这些假设或者是因为实际情况多半是如此,或者是为了简化问题,而不是因为实际情况应该如此。
例如,采用经济人假设是因为现实生活中人们或多或少会考虑自己的利益,因而在分析时从经济人假设出发比较接近现实。
这并不意味着人们在考虑问题时必须从自身利益出发,或者意味着不从自身利益出发考虑问题的人(例如汶川地震时救学生的教师)是没有人性的。
2.微观经济学不是不研究宏观问题,而是把宏观看成微观(个量)的加总,用研究个量的方法研究宏观问题。
这样的研究在某些情况下是适用的,(例如研究个人需求与市场需求时)但在另外一些情况下就不适用。
(例如研究总就业时)3.静态分析不考虑时间因素,不考虑均衡达到和变动的过程,只在一定假设前提下分析均衡达到和变动的条件,因而静态分析是一种状态分析。
动态分析则引入时间因素,分析均衡达到和变动的过程,因而动态分析是一种过程分析。
动态分析又可以分成稳态分析和非稳态分析。
稳态分析承认经济变量随着时间的推移而变化,但同时假定变动的比率或幅度为常数。
非稳态分析则认为,动态分析和静态分析之间存在着质的差异,过去和未来是不相同的。
过去发生的事情是确定的,未来则具有不确定性。
过去发生的事情,现在无法更改,要更改也只能通过今后的步骤加以改变。
而现在所做的事情,对将来的影响无法确知。
西方经济学第四版完整答案高鸿业第四版课后答案

100?501?08yisr??yr?30?1的曲线为即10510525yisr?15?由2的已知条件可得2的曲线为50yisr?15?由3的已知条件可得3的曲线为402由1和2的投资函数比较可知2的投资行为对利率更为敏感而由1和2isis的is曲线方程和比较可知2的曲线斜率绝对值要小于的曲线斜率这说dis明在其他条件不变的情况下投资对利率越敏感即越大时曲线的斜率绝对值越小is即曲线更平坦一些
(5)题目中所给的结论是不完整的,原因如下:
①名义GDP的变动由两个因素造成的:一是所生产的物品和劳务的数量的变动,一是物品和劳务的价格的变动。由于价格变动导致的名义GDP变化并不反映实际产出的变动,故将名义GDP折算为实际GDP,通过实际GDP来比较GDP的变化.
②基期的选择不同,计算出来的实际GDP就不一样,但是GDP的变化趋势应该不变的,所以“GDP的变化取决于我们用哪一年的价格作衡量实际GDP的基期的价格”的说法只说出了后一个因素,是不正确的。
所以,如果甲乙两国合并成一个国家,对GDP总和会有影响。
4.某年发生了以下活动:(a)一银矿公司支付7.5万美元给矿工开采了50千克银卖给一银器制造商,售价10万美元;(b)银器制造商支付5万美元工资给工人造了一批项链卖给消费者,售价40万美元。
(1)用最终产品生产法计算GDP;
(2)每个生产阶段生产多少价值?用增值法计算GDP。
(2)可是,平均消费倾向就不一定总是大于零而小于1.当人们收入很低甚至是零时,也必须消费,哪怕借钱也要消费,这时,平均消费倾向就会大于1。
图13—2
例如,如图13-2所示,当收入低于y0时,平均消费倾向就大于1.这是因为,当收入低于y0时,消费曲线上任一点与原点相连的连线与横轴所形成的夹角总大于45°,因而这时 >1。
许纯祯西方经济学第4版课后习题详解

许纯祯《西方经济学》(第4版)课后习题详解目录第一章西方经济学的研究对象和方法第二章需求、供给和价格第三章效用论与消费者行为第四章生产和成本第五章市场结构与厂商均衡第六章寡头市场与博弈第七章生产要素定价理论第八章一般均衡、市场失灵与政府的微观经济政策第九章宏观经济核算第十章凯恩斯模型第十一章AS-AD模型第十二章通货膨胀和失业第十三章经济周期和经济增长第十四章宏观经济政策第十五章开放经济的宏观经济学本书是许纯祯《西方经济学》教材的学习辅导书,严格按照许纯祯《西方经济学》(第4版)教材内容进行编写,共分15章,参考大量相关辅导资料对许纯祯等三位教授编著的《西方经济学》(第4版)的课后“复习思考题”(除了“基本概念”未作答)进行了详细的分析和解答。
资料下载地址:/Ebook/155313.html来源:【弘博学习网】或关注公众号【hbky96】获取更多学习资料。
一、基本概念稀缺性微观经济学宏观经济学经济人价值中立原则实证经济学规范经济学经济理论模型内生变量和外生变量存量和流量均衡分析局部均衡分析、一般均衡分析静态分析动态分析比较静态分析边际分析答:略。
二、思考题1什么是西方经济学?如何看待它与马克思主义政治经济学的关系?答:(1)西方经济学是一个内容相当广泛而松散的名词,迄今在世界上尚不存在一个众所同意的定义。
它可以泛指大量与经济问题有关的各种不同的文献、资料和统计报告,其中包括教科书、官方文件、私营经济记录、专业或非专业著作、报刊杂志的文章和报道,等等。
包括有下列三种类别的内容:①企事业的经营管理方法和经验。
如行情研究、存货管理、产品质量控制、车间生产流程布局等。
②对一个经济部门或经济领域或经济问题的集中研究成果,如资源经济学、商业经济学、农业经济学、石油经济学,对税收、财政、通货膨胀问题的论述等。
③经济理论的研究和考察。
如微观经济学、宏观经济学、数理经济学、动态经济学、福利经济学、经济思想史等。
西方经济学_高鸿业(宏观部分)第四版课后答案

第十三章简单国民收入决定理论3、依据哪种消费理论,一个暂时性减税对消费影响最大?依据哪种消费理论,社会保障金的一个永久性上升对消费影响最大?依据哪种消费理论,持续较高的失业保险金对消费影响最大?解答:依据凯恩斯消费理论,一个暂时性减税会增加人们当前收入,因而对消费影响最大,凯恩斯认为消费是收入的函数,减税使得收入增加进而使得消费相应的增加。
其他的消费理论认为如果减税只是临时性的,则消费不会受到很大的影响,收入的变动对消费的影响是较小的。
依据生命周期理论,社会保障金的一个永久性上升可以减少老年时代的后顾之忧,减少当前为退休后生活准备的储蓄,因而会增加消费。
依据持久收入消费理论,持续较高的失业保险金等于增加了持久收入,因而可增加消费。
4、哪种消费理论预言总储蓄将依赖与人口中退休人员和年轻人的比例?这种关系是什么?哪种理论预言消费将不会随经济的繁荣与衰退做太大变化?为什么?解答:生命周期理论认为,年轻人要为自己年老生活作储蓄准备,因此,年轻人对退休人员比例提高时,总储蓄会增加.反之,退休人员对年轻人比例上升,总储蓄会下降,因为退休人员不储蓄,而消耗已有储蓄.持久收入假说认为,消费行为与持久收入紧密相关,而与当期收入较少有关联,即消费不会随经济的繁荣与衰退作太大变化。
相对收入消费理论认为消费不会随经济的繁荣和衰退做太大变化,这种理论认为消费者会受自己过去的消费水平的影响来决定消费,当期消费是相对固定的。
依照人们习惯,增加消费容易,减少消费很难。
因此从短期来看,在经济波动过程中,收入增加时低水平收入者的消费会增加,但收入减少时消费水平的降低则很有限。
5、假设你和你邻居的收入完全一样,不过你比她更健康从而预期有更长的寿命。
那么,你的消费水平将高于还是低于他的消费水平?为什么?解答:可以根据生命周期假说来分析此题.分两种情况讨论:(1)当你和你的邻居预期寿命小于工作年限WL ,即未到退休就已结束生命时,尽管你比邻居长寿写,但两人年年都可能把年收入YL 消费完,两人的消费会一样多。
陈承明---《简明西方经济学》(第四版)习题集答案

目录目录 (1)绪论 (2)【参考答案】 (4)第一章需求与供给 (6)【参考答案】 (10)第二章消费效用理论 (15)【参考答案】 (19)第三章生产与成本 (23)【参考答案】 (28)第四章完全竞争和完全垄断 (34)【参考答案】 (38)第五章垄断竞争与寡头竞争 (43)【参考答案】 (48)第六章要素价格与收入分配 (53)【参考答案】 (56)第七章一般均衡与福利经济学 (60)【参考答案】 (63)第八章影响微观经济的相关政策 (67)【参考答案】 (71)第九章国民收入核算 (74)【参考答案】 (77)第十章国民收入决定 (81)【参考答案】 (85)第十一章宏观经济政策 (89)【参考答案】 (92)第十二章商品市场与货币市场的均衡 (95)【参考答案】 (100)第十三章经济增长和经济周期 (107)【参考答案】 (108)第十四章西方经济学流派简介 (113)【参考答案】 (114)第十五章国际经济学理论概览 (118)【参考答案】 (119)绪论一、选择题1.经济学主要是研究()。
A.资源的拥有状况B.稀缺资源的配置C.政府行为D.企业行为2.下列物品中不稀缺的是()。
A.空气B.草地C.纸张D.小麦3.说“资源是稀缺的”是指()。
A.世界上大多数人生活在贫困中B.相对于需求而言,资源总是不足的C.资源必须留给下一代D.资源终将由于生产而消耗光4.经济资源用于生产一种产品而放弃生产其他产品所能取得的最大收益是生产这种产品的()。
A.短期成本B.经济成本C.机会成本D.长期成本5.表示在既定的经济资源和生产技术条件下所能达到的各种产品最大产量组合是()。
A.生产可能性曲线B.成本曲线C.收益曲线D.需求曲线6.以下哪一个不是微观经济学考察的问题()。
A.一个厂商的产出水平B.失业率的上升或下降C.联邦货物税对货物销售的影响D.某行业雇佣工人的数量7.()不是宏观经济学的内容。
高鸿业版西方经济学第四版课后习题答案

第二章练习题参考答案5 解:由以知条件M=100 Q2 可得Q=√M/100于是,有:进一步,可得:观察并分析以上计算过程即其结果,可以发现,当收入函数M=aQ2 (其中a>0为常数)时,则无论收入M为多少,相应的需求的点弹性恒等于1/2.6 解由以知条件可得:由此可见,一般地,对于幂指数需求函数Q(P)= MP-N而言,其需求的价格价格点弹性总等于幂指数的绝对值N.而对于线性需求函数Q(P)= MP-N而言,其需求的收入点弹性总是等于1.7 解: 另在该市场上被100个消费者购得的该商品总量为Q,相应的市场价格为P。
根据题意,该市场的1/3的商品被60个消费者购买,且每个消费者的需求的价格弹性都是3,于是,单个消费者i的需求的价格弹性可以写为;Edi=-(d Qi/d P)即d Qi/d P =-3P/Q2 (i=1,2……60) (1)且(2)相类似的,再根据题意,该市场1/3的商品被另外40个消费者购买,且每个消费者的需求的价格弹性都是6,于是,单个消费者j的需求的价格弹性可以写为: Edj=-(d Q/d P)*(P/Q)=6即d Qj/d P=-6Q j/P(j=1,2……40)(3)且(4)此外,该市场上100个消费者合计的需求的价格弹性可以写为:QP dPdQ dPdQ QP dPQQ d QP dPdQ E j ji i j ji i d ⋅+-=⋅+-=⋅-=∑∑∑∑====)()(401601401601将(1)式、(3)式代入上式,得:QP Q PQ PQP PQ PQ E i j j i j j i i d ⋅-+--=⋅-+--=∑∑∑∑====]63[])6()3([601401401601再将(2)式、(4)式代入上式,得: 5)41()32633(=⋅---=⋅⋅-⋅--=QPP Q Q P Q P Q P E d 所以,按100个消费者合计的需求的价格弹性系数是5。
西方经济学(宏观部分)第四版(高鸿业)课后答案(第十五章)

第十五章宏观经济政策分析1、选择题玞 .`鶝乴----------(1)C(2)C(3)A(4)D(5)C2.答:(1)情况<1>LM曲线:y=500+25r IS曲线:y=950-50r解得:r=6 y=650 i =140-10r=80情况<2>LM曲线:y=500+25r IS曲线:y=800-25r解得:r=6 y=650 i =110-5r=80(2)情况<1>求IS曲线:I+(G+△G)=S+T(140-10r)+(50+30)= -40+(1-0.8)(y-50)+50所以:y=1100-50rG增加,LM不变,LM仍为:y=500+25rIS曲线为:y=1100-50r解得:r=8 y=700情况<2>类似地求得:IS曲线:y=950-25rLM曲线:y=500+25r解得:r=9 y=725(3)因为情况<1>的投资利率乘数为10,情况<2>中为5,故:当△G使r上升时,情况<1>中,△i =(140-80)-(140-60)= -20情况<2>中,△i =(110-45)-(110-30)= -15由于KG=5,求挤出效应:情况<1>中,-20×5= -100情况<2>中,-15×5= -75可以求得无挤出效应时:△y=30×5= 150所以:情况<1>中,△y=150-100=50情况<2>中,△y=150-75= 75故:情况<1>中,y=650+50=700情况<2>中,y=650+75=7253.答案:(1)L=M 0.2Y=200Y=1000(LM方程)I+g=s+ t得140-5r+50=Yd-90-0.8Yd+508皠??p得Y=1150-25r(IS方程)IS=LM得Y=1000,r=8 代入I=140-5r=140-5×8得I=1000#嚭濝鬘?(2)当g=70美元得出Y=1300-25r(IS方程)IS=LM得Y=1000r=12 代入I=140-5r=140-5*12=80得I=80晳楬l@7NVB(3)存在挤出效应,因为LM垂直于横轴,即货币需求对利率弹性(h)为零,利率已高到人们再不愿为投机而持有货币。
厉以宁《西方经济学》(第4版)笔记和课后习题详解

目录第1章西方经济学概述1.1 复习笔记考点一:西方经济学相关定义★1经济学的定义关于经济学的定义,不存在一个被所有经济学家一致接受的说法,但是一种比较流行的定义是:经济学是研究各种稀缺资源在可供选择的用途中进行配置的科学。
2西方经济学相关概念(见表1-1)表1-1 西方经济学相关概念图1-1 机会成本图1-1横坐标表示军用品,纵坐标表示民用品。
图中的曲线为生产可能性边界,或称生产可能性曲线、产品转换曲线。
曲线表示一国在既定的资源与技术条件下所能够生产的最大数量的军用品与民用品的组合。
A点表示只生产民用品而不生产军用品;B点表示只生产军用品而不生产民用品。
增加一单位军用品生产的机会成本是所放弃的民用品生产的数量。
生产可能性曲线凹向原点的特征表明从一种产品的生产转换为另一种产品的生产所产生的机会成本递增。
考点二:西方经济学的基本假设及其质疑★★1西方经济学的基本假设(见表1-2)表1-2 西方经济学的基本假设2对基本假设的质疑(见表1-3)表1-3 对基本假设的质疑考点三:西方经济学的分析方法★★★1微观分析、宏观分析与结构分析(见表1-4)表1-4 微观分析、宏观分析与结构分析2静态分析与动态分析(见表1-5)表1-5 静态分析与动态分析3实证分析与规范分析(见表1-6)表1-6 实证分析与规范分析实证分析与规范分析较之定性分析与定量分析是两类不同的范畴,不应将这两类范畴相混淆。
定性分析并不一定带有价值判断,因此定性分析可能是一种实证分析。
例如,政府最低工资的政策是否会减少就业量,这是一种定性分折。
如果进一步研究政府最低工资政策使就业量减少了多少,则是定量分析。
考点四:经济量的有关概念(见表1-7)★表1-7 经济量的有关概念考点五:西方理论经济学分支(见表1-8)★表1-8 西方理论经济学分支1.2 课后习题详解1西方经济学有哪些基本假设?怎样看待这些基本假设?答:西方经济学的基本假设包括:(1)经济人假设经济人假设包括以下内容:①在经济活动中,经济主体(居民户、厂商或政府)所追求的唯一目标是自身经济利益的最优化。
西方经济学(第四版)课后习题答案

第五章练习题参考答案3。
假定某企业的短期成本函数是TC(Q)=Q3-5Q2+15Q+66:(1) 指出该短期成本函数中的可变成本部分和不变成本部分;(2) 写出下列相应的函数:TVC(Q ) AC(Q)A VC (Q) AFC (Q)和MC(Q)。
解(1)可变成本部分: Q3—5Q2+15Q不可变成本部分:66(2)TVC(Q )= Q3-5Q2+15QAC(Q)=Q2—5Q+15+66/QA VC(Q)= Q2—5Q+15AFC(Q )=66/QMC(Q)= 3Q2—10Q+154已知某企业的短期总成本函数是STC(Q)=0.04 Q3—0.8Q2+10Q+5,求最小的平均可变成本值。
解: TVC(Q)=0.04 Q3-0。
8Q2+10QA VC(Q)= 0。
04Q2—0.8Q+10令08.008.0=-='Q C AV得Q=10又因为008.0>=''C AV所以当Q=10时,6=MIN AVC5。
假定某厂商的边际成本函数MC=3Q2—30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值。
(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数。
解:MC= 3Q2—30Q+100所以TC(Q)=Q3—15Q2+100Q+M当Q=10时,TC=1000 M=500(1) 固定成本值:500(2) TC(Q)=Q3-15Q2+100Q+500TVC(Q)= Q3—15Q2+100QAC(Q)= Q2—15Q+100+500/QA VC(Q)= Q2-15Q+1009。
假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2—8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC 函数和A VC函数.解答:由总成本和边际成本之间的关系。
有STC(Q)= Q3—4 Q2+100Q+C= Q3—4 Q2+100Q+TFC2400=103-4*102+100*10+TFCTFC=800进一步可得以下函数STC(Q)= Q3—4 Q2+100Q+800SAC(Q)= STC(Q)/Q=Q2-4 Q+100+800/QA VC(Q)=TVC(Q)/Q= Q2-4 Q+100第六章练习题参考答案1、已知某完全竞争行业中的单个厂商的短期成本函数为STC=0。
高鸿业《西方经济学(微观部分)》(第4版)课后习题详解-非完全竞争的市场【圣才出品】
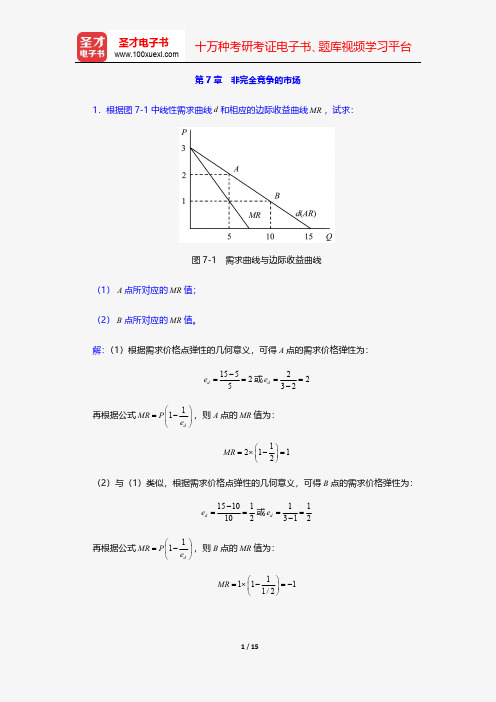
第 7 章 非完全竞争的市场 1.根据图 7-1 中线性需求曲线 d 和相应的边际收益曲线 MR ,试求:
图 7-1 需求曲线与边际收益曲线
(1) A 点所对应的 MR 值;
(2) B 点所对应的 MR 值。
解:(1)根据需求价格点弹性的几何意义,可得 A 点的需求价格弹性为:
2 / 15
圣才电子书 十万种考研考证电子书、题库视频学习平台
(3)长期均衡时的利润量由图中阴影部分的面积表示,即 AR Q0 SAC Q0 Q0 。
3.已知某垄断厂商的短期总成本函数为 STC 0.1Q3 6Q2 140Q 3000 ,反需求函数为 P 150 3.25Q 。
求:该垄断厂商的短期均衡产量与均衡价格。 解:由已知可得垄断厂商的利润函数为:
PQ STC 150 3.25Q Q 0.1Q3 6Q2 140Q 3000 0.1Q3 2.75Q 2 10Q 3 000
故要实现短期均衡,则令 d 0 ,即有: dQ d 0.3Q2 5.5Q 10 0 dQ
(3)通过(1)和(2)可知:将该垄断厂商实现利润最大化的结果与实现收益最大化
的结果相比较,该厂商实现利润最大化时的产量较低(因为 2.5 10 ),价格较高(因为 7 4 ),
收益较少(因为17.5 40 ),利润较大(因为 4.25 52 )。显然,理性的垄断厂商总是以利
4 / 15
圣才电子书 十万种考研考证电子书、题库视频学习平台
求:该厂商实现利润最大化时 Q 、 P 和 A 的值。
解:已知垄断者面临的反需求函数为 P 100 2Q 2 A ,则可得厂商的利润函数为:
PQ TC 100 2Q 2 A Q 3Q 2 20Q A 5Q 2 80 2 A Q A
高鸿业《西方经济学(微观部分)》(第4版)课后习题详解-引 论【圣才出品】

第1章引论1.回想你看到过或接触过的西方经济学著作。
它们各自属于本章所说的三种类别中的哪一种?答:第一类,企事业的经营管理方法和经验。
如行情研究、存货管理、产品质量控制、车间生产流程布局等内容。
著作有《现代企业财务管理》等。
第二类,对一个经济部门或经济问题的集中研究成果。
如资源经济学、商业经济学、农业经济学、石油经济学,对税收、财政和通货膨胀等问题的论述。
著作有《资源经济学》、《农业经济学》等。
第三类,经济理论的研究和考察。
如微观经济学、数理经济学、福利经济学、经济思想史等。
著作有《微观经济学》、《宏观经济学》、《经济思想史》等。
2.为什么我国学员学习西方经济学的目的不同于西方?答:由于西方经济学具有双重性质,它既是资本主义的意识形态,又是资本主义市场经济的经验总结,这就决定了我国学员学习西方经济学所应持有的态度:在整个理论体系上或整体倾向上对它持否定的态度,而在具体的内容上应该看到它的有用之处,是否真正有用还需要考虑到国情的差别,应结合我国的国情加以借鉴吸收,做到“弃其糟粕、取其精华、洋为中用”。
(1)我国学习西方经济学的主要目的在于从中得到对我国有用的知识,即“学以致用”。
对西方经济学而言,“为艺术而艺术”的学习目标是不适用的。
因为,如果不是为了“实用”而学习,那么还不如去从事其他的活动。
“经济学”这一名词的英文来源是希腊文的名词“家庭管理”,由此也可以看出西方经济学的“致用”性质。
(2)既然学习西方经济学的目的是为了“致用”,那么就必须注意到它涉及对西方“致用”的两个特点:其一,它宣扬西方国家的意识形态,以便巩固西方社会的共识或凝聚力,即增加西方学者所说的“社会无形资本”;其二,它总结西方市场运行的经验,以便为改善其运行提供对策。
西方经济学之所以能够存在于西方,其原因即在于此。
这就是说:它存在于西方的原因正是由于它对西方国家有用。
(3)在以上两个特点中,第一个特点显然对我国不但没有用处,反而会引起有害的作用。
厉以宁《西方经济学》(第4版)课后习题详解-产品市场均衡【圣才出品】

第14章产品市场均衡1.假设某经济社会的消费函数为C=1000+0.8Y,投资为500,单位为亿美元。
(1)求均衡产出、消费或储蓄。
(2)如果当实际产出(即收入)为8000,试求企业非意愿存货为多少。
(3)若投资增至1000,均衡产出增加多少?(4)若消费函数变为C=1000+0.9Y,投资仍为500,则均衡产出和储蓄各为多少?投资增至1000时,均衡产出增加多少?(5)消费函数变动后,乘数有何变化?解:(1)由两部门经济国民收入恒等式可得:Y=C+I=1000+0.8Y+500解得均衡产出为:Y*=7500(亿美元)。
此时消费为:C=1000+0.8Y=7000(亿美元),储蓄为:S=Y-C=Y-1000-0.8Y =500(亿美元)。
(2)若实际产出为8000,则非意愿存货量为:8000-(1000+0.8×8000)-500=100(亿美元)(3)投资增至1000,则:Y=C+I=1000+0.8Y+1000解得:Y=10000(亿美元),即均衡产出增加2500亿美元。
(4)当C=1000+0.9Y,投资I=500时,则由:Y=C+I=1000+0.9Y+500,可得Y*=15000(亿美元),S*=500(亿美元)。
投资增至1000时,Y*′=20000,产出增加5000亿美元。
(5)消费函数变化,即b发生变化,投资乘数∂Y/∂I=1/(1-b)发生变化,由5变为10。
2.假定某经济社会的消费函数为C=1000+0.8Y,投资I=500亿美元,政府购买支出G=2000亿美元,政府转移支付TR=625亿美元,边际税率t=0.25。
(1)求均衡收入。
(2)试求投资乘数、政府支出乘数、税收乘数、转移支付乘数、平衡预算乘数。
(3)假定社会达到充分就业所需要的国民收入为12000亿美元,试问:①增加政府购买;②减少税收;③增加政府购买和税收同一数额(以便预算平衡)。
这三种情况下,实现充分就业,各需多少数额?解:(1)根据收入恒等式得:Y=C+I+G=1000+0.8(Y-0.25Y+625)+500+2000解得:Y*=10000(亿美元)。
西方(微观)经济学第4版第四章习题答案
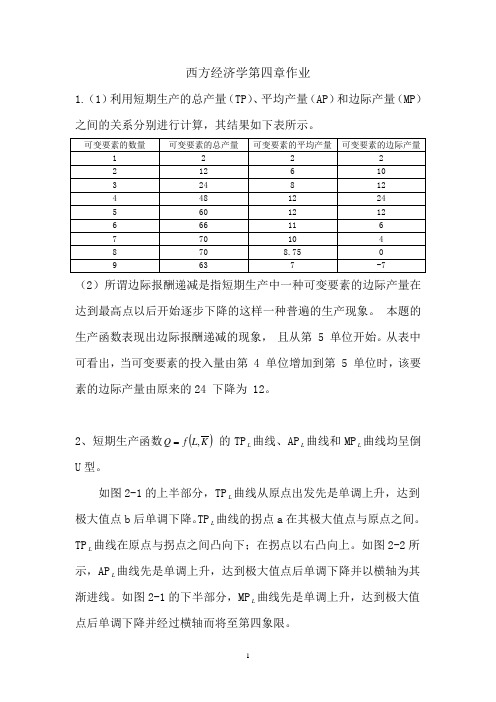
西方经济学第四章作业1.(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系分别进行计算,其结果如下表所示。
(2)所谓边际报酬递减是指短期生产中一种可变要素的边际产量在达到最高点以后开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,且从第 5 单位开始。
从表中可看出,当可变要素的投入量由第 4 单位增加到第 5 单位时,该要素的边际产量由原来的24 下降为 12。
2、短期生产函数()K L fQ,=的TPL 曲线、APL曲线和MPL曲线均呈倒U型。
如图2-1的上半部分,TPL曲线从原点出发先是单调上升,达到极大值点b后单调下降。
TPL曲线的拐点a在其极大值点与原点之间。
TPL曲线在原点与拐点之间凸向下;在拐点以右凸向上。
如图2-2所示,APL曲线先是单调上升,达到极大值点后单调下降并以横轴为其渐进线。
如图2-1的下半部分,MPL曲线先是单调上升,达到极大值点后单调下降并经过横轴而将至第四象限。
Q bcaTPLO LQOLMP L图2-1APLQTPLAPLOLMP O L 图2-2 图2-3MPL 与 TPL之间的主要关系是:,0,0<↓⇔=⇔>↑⇔LLLLLLMPTPMPTPMPTP极大从几何上看(图2-1),在TPL 递增的区间,MPL位于横轴上方;在TPL 取极大值处,MPL恰好经过横轴;在TPL递减的区间,MPL位于横轴下方。
MP L 与AP L 之间的主要关系是:L L AP ,AP ,<↓⇔=⇔>↑⇔L L L L L L L MP AP MP AP AP MP AP 极大从几何上看(图2-2),在AP L 递增的区间,MP L 位于AP L 上方;在AP L 取极大值处,MP L 恰好经过AP L ;在AP L 递减的区间,MP L 位于AP L 下方。
TP L 与AP L 之间的主要关系是:TP L 曲线上点与原点连线的斜率即为相应横坐标处的AP L (图2-3).3. (1)因为生产函数225.05.02),(K L KL K L f Q --==,且 K=10, 则劳动的总产量为505.020),(2--===L L K L f Q TP L 劳动的平均产量AP L = TP L /L=20-0.5L-50/L 劳动的边际产量MP L =dTP L /dL=20-L (2)①总产量的最大值令MP L =20-L=0,解得劳动的总产量TP L 达到极大值时厂商的劳动投入量L=20。
高鸿业《西方经济学(宏观部分)》(第4版)课后习题详解-西方经济学与中国【圣才出品】

高鸿业《西方经济学(宏观部分)》(第4版)课后习题详解-西方经济学与中国【圣才出品】答:在过去的几十年里,经济学家开始对把微观经济学与宏观经济学分割开来研究的这种分裂提出质疑。
经济学界已经逐渐认识到宏观经济行为必须与其背后的微观经济学原理联系在一起,只有一套经济学原理,而不是两套。
下面试举两例来说明微观经济学是如何应用于宏观经济分析:(1)卢卡斯供给曲线是以微观分析为基础推导的宏观总供给曲线。
卢卡斯假定整个经济由n个完全相同的厂商组成,只要推出代表性厂商i的供给曲线,然后进行加总就可以得出整个社会的总供给曲线。
(2)新凯恩斯主义学者的理论致力于构筑宏观经济学的微观基础。
在新凯恩斯主义关于工资和价格黏性的理论分析中用到了不完全竞争理论。
第23章西方经济学与中国说明:由于本章涉及到的西方经济学知识点非常少,因此,略去本章的课后习题详解。
但是,需要提醒大家注意的是,本章考试内容主要集中在西方经济学理论在我国的应用问题,尤其是结合我国乃至世界经济形势出题已经成了近年来众多高校命题的特点,一般都是分值较大的论述题。
所以,建议大家多留意热点经济问题,密切关注经济形势的变化和我国经济政策的改变,并经常思考经济政策背后所隐藏的经济学原理,真正做到学以致用。
附录:指定高鸿业《西方经济学》教材为考研参考书目的院校列表高鸿业主编的《西方经济学》(中国人民大学出版社)被列为普通高等教育“十一五”国家级规划教材,是我国众多高校采用的经济学优秀教材,也被众多高校(包括科研机构)指定为“经济类”专业考研参考书目,具体如下表所示。
高校(包括科研机构)对应学院(专业)清华大学公共管理学院北京大学马克思主义学院中国人民大学经济学院、财政金融学院、商学院、农业与农村发展学院、劳动人事学院、马克思主义学院、国际关系学院、社会与人口学院、环境学院、公共管理学院、农业与农村发展学院、汉青研究院北京师范大学经济与资源管理研究院、管理学院中央财经大学财政学院、金融学院、经济学院、文化与传媒学院、管理科学与工程学院、保险学院、统计学院、税务学院、中国发展和改革研究院、体育经济与管理学院、中国煤炭经济研究院、国防经济与管理研究院、政府管理学院对外经济贸易大学国际经济贸易学院、金融学院、保险学院、国际商学院(工商管理综合)、中国世界贸易组织研究院、国际经济研究院北京邮电大学经济管理学院北京理工大学管理与经济学院中国传媒大学政治与法律学院中国政法大学商学院北京第二外国语学院旅游管理学院北京工商大学经济学院北京化工大学经济管理学院(复试)北京林业大学经济管理学院北方工业大学经济管理学院财政部财政科学研究所财政学、会计学、国民经济学、企业管理中国青年政治学院经济系中共中央党校国际战略研究所外交学院国际经济系北京物资学院产业经济学、劳动经济学华北电力大学(北京)电气与电子工程学院、工商管理学院北京信息科技大学经管学院北京印刷学院出版传播与管理学院复旦大学经济学院上海财经大学马克思主义研究院华东理工大学商学院上海师范大学商学院上海理工大学管理学院上海外国语大学国际贸易学上海对外贸易学院金融管理学院、国际经贸学院南开大学经济学院、经济与社会发展研究院、日本研究院、商学院天津工业大学经济学院燕山大学经济管理学院河北大学经济学院南京航空航天大学经济与管理学院南京理工大学经济管理学院南京农业大学经济管理学院南京师范大学商学院南京财经大学国际经济与贸易学院、工商管理学院、会计学院、金融学院、经济学院、营销与物流管理学院、财政与税务学院、产业发展研究院宁波大学商学院浙江师范大学工商管理学院浙江工商大学经济学院、统计学院浙江理工大学经济管理学院浙江林学院经济管理学院浙江财经学院财政与公共管理学院、金融学院、经济与国际贸易学院武汉大学经济与管理学院华中科技大学经济学院经济学院、财政税务学院、新华金融保险学院、工商管理学院、中南财经政法大学公共管理学院、信息学院华中农业大学经济管理学院、土地管理学院华中师范大学经济学院湖北大学商学院中南大学商学院武汉科技大学管理学院、文法与经济学院湖南大学会计学院、统计学院、经济与贸易学院;政治与公共管理学院(复试)。
西方经济学(微观部分_高鸿业)第四版_课后部分习题答案

西方经济学(微观部分_高鸿业)第四版_课后部分习题答案需求的价格弹性在a点、b点和c点是相同的。
它们都是:ed = of/PE (2)需求的价格弹性是:eda =GB/OG f需求的价格弹性是:edf =GC/OG e需求的价格弹性是:ede =GD/ OG因此eda 5。
解决方案:Q=0.01M1/2,eM=(dQ/dM)(M/Q)=0.02M-1/2M/Q,当M=6400时,Q=8,因此eM=1/206.ed = N;eM=17。
解决方案:已知edi= -(dQi/dP)(P/Qi)=3,∑ Q I = QT/3 (I = 1,2,...,60),EDJ =-(DQJ/DP) (P/QJ) = 6,∑ QJ = 2QT/3 (J = 1,2,...,40)。
因此,存在DQi/dP =-3Qi/P;p;dQj /dP)= -6Qj /P市场需求价格弹性为ed =-(dqt/DP)(P/Qt)=-[(d∑Qi+d∑Qj)/DP]Qt/P =-[∑dqi/DP+∑dqj/DP]Qt/P =-[∑-3qi/P+∑-6Qj/P]Qt/P =-[(-3∑Qi 6∑Qj)/P]Qt/P =[(1)2.6%;(2)11%9。
(1)EdA = 3;EdB=5。
(2) eAB≈1.7。
(3)降价前销售收入为25,000元,降价后销售收入为35,200元。
降价是正确的。
第三部分问题答案(第4版)1。
MRSc,f=1/42。
(1)本人=60元;(2)P2=3元;(3)60=2X1+3X2,或:x2 = 20-2/3x 1;(4)-2/3;(5)MRS12=2/34。
预算约束为540 = 20x 1+30x 2;效用函数是:u = 3x1x2均衡:进入预算方程求解X1,x2将求解出的X1=9,X2=12代入效用函数,得到U=38886.X1 = 3M/(8P 1);X2=5M/(8P2)7。
如果:a>P1/P2,最佳组合为:(M/P1,0);If: a0)L=40,q=1880,W=180第9部分练习参考答案(第4版)8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章练习题参考答案3。
假定某企业的短期成本函数是TC(Q)=Q3-5Q2+15Q+66:(1) 指出该短期成本函数中的可变成本部分和不变成本部分;(2) 写出下列相应的函数:TVC(Q) AC(Q)A VC(Q) AFC(Q)和MC(Q)。
解(1)可变成本部分: Q3-5Q2+15Q不可变成本部分:66(2)TVC(Q)= Q3-5Q2+15QAC(Q)=Q2-5Q+15+66/QA VC(Q)= Q2-5Q+15AFC(Q)=66/QMC(Q)= 3Q2-10Q+154已知某企业的短期总成本函数是STC(Q)=0。
04 Q3-0。
8Q2+10Q+5,求最小的平均可变成本值。
解: TVC(Q)=0。
04 Q3-0。
8Q2+10QA VC(Q)= 0。
04Q2-0。
8Q+10令08.008.0=-='Q C AV得Q=10又因为008.0>=''C AV所以当Q=10时,6=MIN AVC5。
假定某厂商的边际成本函数MC=3Q2-30Q+100,且生产10单位产量时的总成本为1000。
求:(1) 固定成本的值。
(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数。
解:MC= 3Q2-30Q+100所以TC(Q)=Q3-15Q2+100Q+M当Q=10时,TC=1000 M=500(1) 固定成本值:500(2) TC(Q)=Q3-15Q2+100Q+500TVC(Q)= Q3-15Q2+100QAC(Q)= Q2-15Q+100+500/QA VC(Q)= Q2-15Q+1009。
假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC 函数和A VC函数。
解答:由总成本和边际成本之间的关系。
有STC(Q)= Q3-4 Q2+100Q+C= Q3-4 Q2+100Q+TFC2400=103-4*102+100*10+TFCTFC=800进一步可得以下函数STC(Q)= Q3-4 Q2+100Q+800SAC(Q)= STC(Q)/Q=Q2-4 Q+100+800/QA VC(Q)=TVC(Q)/Q= Q2-4 Q+100第六章练习题参考答案1、已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。
试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产?(3)厂商的短期供给函数。
解答:(1)因为STC=0.1Q3-2Q2+15Q+10dSTC=0.3Q3-4Q+15所以SMC=dQ根据完全竞争厂商实现利润最大化原则P=SMC,且已知P=55,于是有:0.3Q2-4Q+15=55整理得:0.3Q2-4Q-40=0解得利润最大化的产量Q*=20(负值舍去了)以Q*=20代入利润等式有:=TR-STC=PQ-STC=(55×20)-(0.1×203-2×202+15×20+10)=1100-310=790即厂商短期均衡的产量Q*=20,利润л=790(2)当市场价格下降为P小于平均可变成本A VC即P A VC时,厂商必须停产。
而此时的价格P 必定小于最小的可变平均成本A VC 。
根据题意,有:A VC=QQ Q Q Q TVC 1521.023+-==0.1Q2-2Q+15 令0=dQ dAVC ,即有:022.0=-=Q dQdAVC 解得 Q=10 且02.022>=dQ AVC d 故Q=10时,A VC (Q )达最小值。
以Q=10代入A VC (Q )有:最小的可变平均成本A VC=0.1×102-2×10+15=5于是,当市场价格P5时,厂商必须停产。
(3)根据完全厂商短期实现利润最大化原则P=SMC ,有:0.3Q2-4Q+15=p整理得 0.3Q2-4Q+(15-P )=0 解得6.0)15(2.1164P Q --±= 根据利润最大化的二阶条件C M R M '<'的要求,取解为:6.022.14-+=P Q 考虑到该厂商在短期只有在P>=5才生产,而P <5时必定会停产,所以,该厂商的短期供给函数Q=f (P )为:6.022.14-+=P Q ,P>=5 Q=0 P <52、已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q 。
试求:(1)当市场商品价格为P=100时,厂商实现MR=LMC 时的产量、平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)当市场的需求函数为Q=660-15P 时,行业长期均衡时的厂商数量。
解答:(1)根据题意,有:402432+-==Q Q dQdLTC LMC 且完全竞争厂商的P=MR ,根据已知条件P=100,故有MR=100。
由利润最大化的原则MR=LMC ,得:3Q2-24Q+40=100整理得 Q2-8Q-20=0解得Q=10(负值舍去了) 又因为平均成本函数4012)()(2+-==Q Q QQ STC Q SAC 所以,以Q=10代入上式,得:平均成本值SAC=102-12×10+40=20最后,利润=TR-STC=PQ-STC=(100×10)-(103-12×102+40×10)=1000-200=800因此,当市场价格P=100时,厂商实现MR=LMC 时的产量Q=10,平均成本SAC=20,利润为л=800。
(2)由已知的LTC 函数,可得:40124012)()(223+-=+-==Q Q QQ Q Q Q Q LTC Q LAC 令0)(=dQ Q dLAC ,即有:0122)(=-=Q dQQ dLAC ,解得Q=6 且02)(22>=dQQ LAC d 解得Q=6所以Q=6是长期平均成本最小化的解。
以Q=6代入LAC (Q ),得平均成本的最小值为:LAC=62-12×6+40=4由于完全竞争行业长期均衡时的价格等于厂商的最小的长期平均成本,所以,该行业长期均衡时的价格P=4,单个厂商的产量Q=6。
(3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线,且相应的市场长期均衡价格是固定的,它等于单个厂商的最低的长期平均成本,所以,本题的市场的长期均衡价格固定为P=4。
以P=4代入市场需求函数Q=660-15P ,便可以得到市场的长期均衡数量为Q=660-15×4=600。
现已求得在市场实现长期均衡时,市场均衡数量Q=600,单个厂商的均衡产量Q=6,于是,行业长期均衡时的厂商数量=600÷6=100(家)。
3、已知某完全竞争的成本递增行业的长期供给函数LS=5500+300P 。
试求:(1)当市场需求函数D=8000-200P 时,市场的长期均衡价格和均衡产量;(2)当市场需求增加,市场需求函数为D=10000-200P时,市场长期均衡加工和均衡产量;(3)比较(1)、(2),说明市场需求变动对成本递增行业的长期均衡价格个均衡产量的影响。
解答:(1)在完全竞争市场长期均衡时有LS=D,既有:5500+300P=8000-200P解得Pe=5,以Pe=5代入LS函数,得:Qe=5500+300×5=7000或者,以Pe=5代入D函数,得:Qe=8000-200*5=7000所以,市场的长期均衡价格和均衡数量分别为Pe=5,Qe=7000。
(2)同理,根据LS=D,有:5500+300P=10000-200P解得Pe=9以Pe=9代入LS函数,得:Qe=5500+300×9=8200或者,以Pe=9代入D函数,得:Qe=10000-200×9=8200所以,市场的长期均衡价格和均衡数量分别为Pe=9,Qe=8200。
(3)比较(1)、(2)可得:对于完全竞争的成本递增行业而言,市场需求增加,会使市场的均衡价格上升,即由Pe=5上升为Qe=9;使市场的均衡数量也增加,即由Qe=7000增加为Qe=8200。
也就是说,市场需求与均衡价格成同方向变动,与均衡数量也成同方向变动。
5、在一个完全竞争的成本不变行业中单个厂商的长期成本函数为LAC=Q3-40Q2+600Q ,g 该市场的需求函数为Qd=13000-5P 。
求:(1)该行业的长期供给函数。
(2)该行业实现长期均衡时的厂商数量。
解答:(1)由题意可得:600402+-==Q Q Q LTC LAC 6008032+-==Q Q dQdTC LMC 由LAC=LMC ,得以下方程:Q2-40Q+600=3Q2-80Q+600Q2-20Q=0解得Q=20(负值舍去)由于LAC=LMC ,LAC 达到极小值点,所以,以Q=20代入LAC 函数,便可得LAC 曲线的最低点的价格为:P=202-40×20+600=200。
因为成本不变行业的长期供给曲线是从相当与LAC 曲线最低点的价格高度出发的一条水平线,故有该行业的长期供给曲线为Ps=200。
(2)已知市场的需求函数为Qd=13000-5P ,又从(1)中得到行业长期均衡时的价格P=200,所以,以P=200代入市场需求函数,便可以得到行业长期均衡时的数量为:Q=13000-5×200=12000。
又由于从(1)中可知行业长期均衡时单个厂商的产量Q=20,所以,该行业实现长期均衡时的厂商数量为12000÷20=600(家)。
7.某完全竞争厂商的短期边际成本函数SMC=0.6Q-10,总收益函数TR=38Q ,且已知当产量Q=20时的总成本STC=260.求该厂商利润最大化时的产量和利润解答:由于对完全竞争厂商来说,有P=AR=MR AR=TR(Q)/Q=38,MR=dTR(Q)/dQ=38所以P=38根据完全竞争厂商利润最大化的原则MC=P0.6Q-10=38Q*=80 即利润最大化时的产量再根据总成本函数与边际成本函数之间的关系STC(Q)=0.3Q2-10Q+C=0.3Q2-10Q+TFC以Q=20时STC=260代人上式,求TFC,有260=0.3*400-10*20+TFCTFC=340于是,得到STC函数为STC(Q)=0.3Q2-10Q+340最后,以利润最大化的产量80代人利润函数,有π(Q)=TR(Q)-STC(Q)=38Q-(0.3Q2-10Q+340)=38*80-(0.3*802-10*80+340)=3040-1460=1580即利润最大化时,产量为80,利润为15808、用图说明完全竞争厂商短期均衡的形成极其条件。
