数字图像处理3赵建峰
《数字图像处理》课程教学大纲
二、课程章节主要内容及学时分配第一章、数字图像处理方法概述讲课3课时了解本课程研究的对象、内容及其在培养软件编程高级人才中的地位、作用和任务;了解数字图像处理的应用;了解数字图像的基本概念、与设备相关的位图(DDB)、与设备无关的位图(DIB);了解调色板的基本概念和应用;了解CDIB类与程序框架结构介绍;了解位图图像处理技术。
重点:CDIB类与程序框架结构介绍。
难点:调色板的基本概念和应用。
第二章、图像的特效显示讲课3课时、实验2学时了解扫描、移动、百叶窗、栅条、马赛克、渐显与渐隐、浮雕化特效显示。
重点:渐显与渐隐。
难点:马赛克。
第三章、图像的几何变换讲课2课时了解图像的缩放、平移、镜像变换、转置、旋转。
重点:镜像变换。
难点:旋转。
第四章、图像灰度变换讲课3课时、实验2学时了解非0元素取1法、固定阈值法、双固定阈值法的图像灰度变换;了解灰度的线性变换、窗口灰度变换处理、灰度拉伸、灰度直方图、灰度分布均衡化。
重点:灰度直方图。
难点:灰度分布均衡化。
第五章、图像的平滑处理讲课3课时了解二值图像的黑白点噪声滤波、消除孤立黑像素点、3*3均值滤波、N*N 均值滤波器、有选择的局部平均化、N*N中值滤波器、十字型中值滤波器、N*N最大值滤波器、产生噪声。
重点:消除孤立黑像素点、中值滤波器。
难点:有选择的局部平均化。
第六章、图像锐化处理及边缘检测讲课3课时、实验2学时了解梯度锐化、纵向微分运算、横向微分运算、双方向一次微分运算、二次微分运算、Roberts边缘检测算子、Sobel边缘检测算子、Krisch边缘检测、高斯-拉普拉斯算子。
重点:Roberts边缘检测算子、高斯-拉普拉斯算子。
难点:梯度锐化。
第七章、图像分割及测量讲课4课时了解图像域值分割、轮廓提取、轮廓跟踪、图像的测量。
重点:轮廓提取、轮廓跟踪。
难点:图像的测量。
包括:图像的区域标记、图像的面积测量及图像的周长测量。
第八章、图像的形态学处理讲课3课时了解图像腐蚀、图像的膨胀、图像开启与闭合、图像的细化、图像的粗化、中轴变化。
精品文档-数字图像处理(第三版)(何东健)-第1章

第1章 概论
5. 图像分析(Image Analysis 图像处理应用的目标几乎均涉及图像分析, 即对图像中 的不同对象进行分割、 特征提取和表示, 从而有利于计算机 对图像进行分类、 识别和理解。 在工业产品零件无缺陷且正确装配检测中, 图像分析是 把图像中的像素转化成一个“合格”或“不合格”的判定。 在医学图像处理中, 不仅要检测出异变(如肿瘤)的存在, 而且还要检查其尺寸大小。
第1章 概论 图像自动分割是图像处理中最困难的问题之一。 人类视 觉系统能够将所观察的复杂场景中的对象分开并识别出每个物 体。 但对计算机来说, 却是一个非常困难的问题。 由于解 决和分割有关的基本问题是特定领域中图像分析实用化的关键 一步, 因此, 将各种方法融合在一起并使用知识来提高处理 的可靠性和有效性是图像分割的研究热点。
第1章 概论 4. 图像分割(Image Segmentation 把图像分成区域的过程即图像分割。 图像中通常包含多 个对象, 例如, 一幅医学图像中显示出正常的或有病变的各 种器官和组织。 为达到识别和理解的目的, 必须按照一定的 规则将图像分割成区域, 每个区域代表被成像的一个物体 (或部分)。
第1章 概论
(4) 图像数据量庞大。 图像中包含有丰富的信息, 可以通过图像处理技术获取图像中包含的有用信息。 但是, 数字图像的数据量巨大。 一幅数字图像是由图像矩阵中的像 素(Pixel )组成的, 通常每个像素用红、 绿、 蓝三种颜 色表示, 每种颜色用8bit表示灰度级。 那么一幅1024×768 不经压缩的真彩色图像, 数据量达2.25 MB (1024×768×8×3/8), 一幅遥感图像的数据量达3240× 2340×4=30Mb 。 如此庞大的数据量给存储、 传输和处理 都带来巨大的困难。 如果再提高颜色位数及分辨率, 数据量 将大幅度增加。
数字图像处理第一章(国科大)

1Digital Image Processing数字图像处理课程简介本课程为计算机科学与技术、电子科学与技术、信息与通信工程、控制科学与工程以及电气工程等学科下研究生的专业基础课。
主要内容课程共分三大部分:第一部分:介绍数字图像处理的基础知识,包括绪论、图像与视觉系统、图像变换等;第二部分:介绍图像处理的基本方法,包括图像增强、图像复原及图像压缩等;第三部分:介绍图像分析的基本原理和技术,包括图像分割、图像描绘及特征提取等。
教学目标⏹基本:完成课程学习,通过考试,获得学分。
掌握数字图像处理的基本概念和研究方法,相关交叉学科的基本知识;⏹提高:能够将所学知识和内容用于课题研究;⏹再提高:通过数字图像处理课程的学习,改进思维方式。
教材及参考书第一章绪论绪论⏹前言⏹数字图像处理的起源⏹数字图像处理的基本概念与研究内容⏹数字图像处理与其他学科的关系⏹数字图像处理的主要应用⏹数字图像处理的发展动向前言“百闻不如一见”One picture is worth more than ten thousand words.在人类接受的信息中,听觉信息占约20%,视觉信息占约60%,其他如味觉、触觉等总起来不过占约20%。
所以,作为传递信息的重要手段—图像信息是十分重要的。
第一节数字图像处理的起源(1)世界上第一幅实景照片(1827)数字图像的应用之一是在报业,20世纪20年代的海底电缆使得伦敦与纽约之间图片的传输从过去的一个多星期缩短到3个小时以内。
1921年经编码后用电报打印机打印的图像1929年通过海底电缆从伦敦传输到纽约的一幅照片第一节数字图像处理的起源(2)二十世纪二十年代:图像远距离传输第一节数字图像处理的起源二十世纪五十年代:伴随着技术进步,数字计算机发展到一定水平,尤其是大规模的存储和显示系统的发展,数字图象处理引起巨大关注。
第一节数字图像处理的起源进实验室(Jet PropulsionLaboratory,JPL)运用计算机处理了由“旅行者7号”发回的月球表面照片。
精品文档-数字图像处理(第三版)(何东健)-第9章

第9章 图像编码
它将标量数据组织成一系列k维矢量, 根据一定的失真测 度(如均方误差、 lp范数、 极大范数等)在码书中搜索出 与输入矢量失真最小的码字的索引, 传输时仅传输相应码字 的索引,接收方根据码字索引在码书中查找对应码字, 再现 输入矢量。 矢量量化编码的核心是码书设计, 经典的码书设 计算法有LBG(Linde, Buzo和Gray三人的首字母) 算法(又称为K-means算法)。 码书设计过程就是寻求把M 个训练矢量分成N类(N<M)的一种最佳方案(如均方误差最 小), 并把各类的中心矢量作为码书中的码字。
第9章 图像编码 9.1.2
人们不断提出新的图像编码方法, 如基于人工神经网络 的编码、 子带编码(Sub band Coding)、 分形编码 (Fractal Coding)、 小波编码(Wavelet Coding)、 基 于模型的编码(Model based Coding)、 基于对象的编码 (Object based Coding)和基于语义的编码(Semantic Based Coding)等。
(2) 预测编码。 预测编码是基于图像数据的空间或时 间冗余特性, 它用相邻的已知像素(或像素块)来预测当 前像素(或像素块)的取值, 然后再对预测误差进行量化和 编码。 预测编码可分为帧内预测和帧间预测, 常用的预测编 码有差分脉码调制(DPCM, Differential Pulse Code Modulation)和运动补偿法。 图9-1和图9-2分别给出了无损 预测编码和有损预测编码系统的原理图,均包括编码器和解码 器, 其中符号编码器通常采用变长编码。
第9章 图像编码 信息熵是无损编码的理论极限, 当平均码长大于等于信 息熵时, 总可设计出一种无失真编码, 这是熵编码的理论基 础。 若使用相同长度的码字表示信源符号, 则称该编码方法 为等长编码, 否则称为变长编码。 变长编码的基本原理是给 出现概率较大的符号赋予短码字, 而给出现概率较小的符号 赋予长码字, 从而使得最终的平均码长很小。 哈夫曼编码和 香农-范诺编码就是两种变长编码方法。
数字图像处理(许录平着)课后答案(全)
+a
+b
−b +a −a
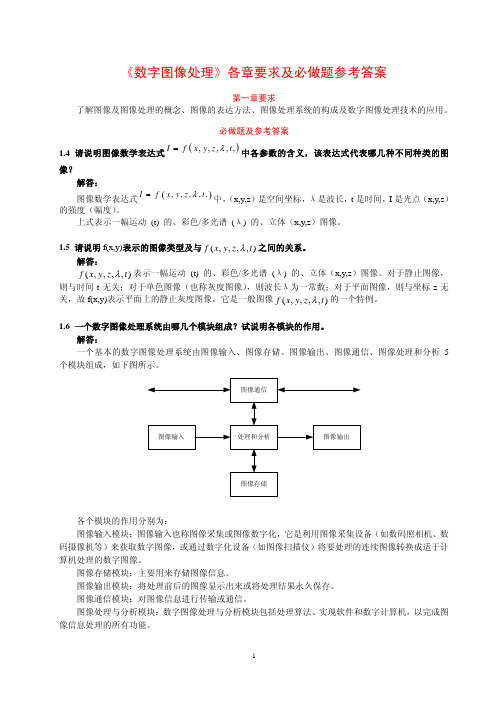
h ( x, y )e − jux e − jvy dxdy e − jux dx ∫ e − jvy dy
−b
jua
+b
− e e − jvb − e jvb − ju − jv sin ua sin vb = 4E uv =E e
(3) H (u, v ) =
− jua
图像通信
图像输入
处理和分析
图像输出
图像存储
各个模块的作用分别为: 图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数 码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计 算机处理的数字图像。 图像存储模块:主要用来存储图像信息。 图像输出模块:将处理前后的图像显示出来或将处理结果永久保存。 图像通信模块:对图像信息进行传输或通信。 图像处理与分析模块:数字图像处理与分析模块包括处理算法、实现软件和数字计算机,以完成图 像信息处理的所有功能。
《数字图像处理》各章要求及必做题参考答案
第一章要求 了解图像及图像处理的概念、图像的表达方法、图像处理系统的构成及数字图像处理技术的应用。 必做题及参考答案 1.4 请说明图像数学表达式 像? 解答:
I = f (x, y, z, λ , t,) 图像数学表达式 中, (x,y,z)是空间坐标,λ是波长,t 是时间,I 是光点(x,y,z) 的强度(幅度) 。 上式表示一幅运动 (t) 的、彩色/多光谱 (λ) 的、立体(x,y,z)图像。
⎡10 ⎢0 则 F1 = H 4 f1 H 4 = ⎢ ⎢0 ⎢ ⎣0 ⎡16 ⎢0 F3 = H 4 f 3 H 4 = ⎢ ⎢0 ⎢ ⎣0
数字图像处理的理论与方法

数字图像处理的理论与方法数字图像处理(Digital Image Processing)是指利用计算机对图像进行处理和分析的一种技术。
它涉及的理论与方法是指对图像进行数学建模和处理的一系列过程和方法。
下面将对数字图像处理的理论与方法进行详细介绍,并分点列出步骤。
一、数字图像处理的理论基础1. 数学基础:数字图像处理的理论与方法建立在一系列数学基础上,包括几何学、代数学、概率论、统计学等。
2. 图像重建理论:数字图像处理的核心目标是从原始图像中还原出最准确的信息,图像重建理论为实现这一目标提供了依据。
3. 信号处理理论:图像本质上是一个二维信号,所以信号处理理论对于数字图像处理至关重要,包括傅里叶分析、滤波器设计等。
二、数字图像处理的方法1. 图像获取:获得数字图像是数字图像处理的前提,方法包括数码相机、扫描仪、卫星遥感等。
2. 图像预处理:对原始图像进行预处理是为了去除噪声和改善图像质量。
常用的方法有平滑滤波、锐化、直方图均衡化等。
3. 图像增强:根据具体需求,对图像进行增强可以使图像更加鲜明和易于分析,常用方法有对比度增强、边缘增强等。
4. 图像恢复:通过数学模型和算法,重建被损坏的图像或以更好的方式表示图像是图像恢复的关键过程,常用方法有降噪、插值等。
5. 图像分割:将图像划分为具有特定特征的区域,常用方法有阈值分割、边缘检测、聚类等。
6. 特征提取:从分割后的图像中提取出与感兴趣的目标有关的特征,常用方法有形状分析、纹理分析等。
7. 目标识别与分类:根据提取的特征,利用模式识别算法对目标进行识别与分类,常用方法有神经网络、支持向量机等。
8. 图像压缩与编码:为了减少图像数据的存储空间和传输带宽,常使用图像压缩与编码技术,例如JPEG、PNG等。
三、数字图像处理的应用领域1. 医学影像处理:数字图像处理在医学影像诊断中起着重要作用,例如X光、磁共振成像、超声等。
2. 人脸识别:数字图像处理为人脸识别提供了基础技术,常用于安全、人机交互等领域。
数字图像处理2_赵建峰

F (u )e
x 0
N 1
j 2ux / N
式中:x,u=0, 1, 2, …, N-1,其中系数1/N可 以在正变换或逆变换中,也可在傅立叶正变换和逆 变换前分别乘以1 / N , 这是无关紧要的, 只要正 变换和逆变换前系数乘积等于1/N即可。
复数表示法
由欧拉公式可得:
e cos j sin
F [ f ( x, y )] F (u, v ) f ( x, y )e
x 0 y 0 j 2 ( M N )
1 F 1[ F (u, v )] f ( x, y ) MN
M 1 N 1 u 0 v 0
F ( u, v ) e
j 2 (
ux vy ) M N
| F (u, v ) | R 2 (u, v ) I 2 (u, v ) I ( u, v ) (u, v ) arctan R ( u, v ) E ( u, v ) R 2 ( u, v ) I 2 ( u, v )
式中,R(u, v)和I(u, v)分别是F(u, v)的实部 和虚部。
1、具有有限个间断点; 2、具有有限个极值点;
3、绝对可积。
连续函数傅立叶变换定义
一维:
F [ ( x )] F (u )
1
f ( x )e j 2ux dx F (u )e j 2ux du
F [ F (u )] f ( x )
式中: j 1 ,x称为时域变量,u称为频域 变量。 二维: F [ f ( x, y )] F (u, v) f ( x, y )e j 2 ( ux vy)dxdy
数字图像处理实验报告之数字图像的空间域滤波

数字图像处理实验报告学院:班级:学号:时间:2012.11.29实验三:数字图像的空间域滤波——锐化滤波1.实验目的1.掌握图像滤波的基本定义及目的。
2.理解空间域滤波的基本原理及方法。
3.掌握进行图像的空域滤波的方法。
2.实验基本原理1.空间域增强空间域滤波是在图像空间中借助模板对图像进行领域操作,处理图像每一个像素的取值都是根据模板对输入像素相应领域内的像素值进行计算得到的。
空域滤波基本上是让图像在频域空间内某个范围的分量受到抑制,同时保证其他分量不变,从而改变输出图像的频率分布,达到增强图像的目的。
空域滤波一般分为线性滤波和非线性滤波两类。
线性滤波器的设计常基于对傅立叶变换的分析,非线性空域滤波器则一般直接对领域进行操作。
各种空域滤波器根据功能主要分为平滑滤波器和锐化滤波器。
平滑可用低通来实现,平滑的目的可分为两类:一类是模糊,目的是在提取较大的目标前去除太小的细节或将目标内的小肩端连接起来;另一类是消除噪声。
锐化可用高通滤波来实现,锐化的目的是为了增强被模糊的细节。
结合这两种分类方法,可将空间滤波增强分为四类:线性平滑滤波器(低通)非线性平滑滤波器(低通)线性锐化滤波器(高通)非线性锐化滤波器(高通)空间滤波器都是基于模板卷积,其主要工作步骤是:1)将模板在图中移动,并将模板中心与图中某个像素位置重合;2)将模板上的系数与模板下对应的像素相乘;3)将所有乘积相加;4)将和(模板的输出响应)赋给图中对应模板中心位置的像素。
2.锐化滤波器图像平滑往往使图像中的边界、轮廓变得模糊,为了减少这类不利效果的影响,需要利用图像锐化技术,使图像的边缘变得清晰。
1)线性锐化滤波器线性高通滤波器是最常用的线性锐化滤波器。
这种滤波器的中心系数都是正的,而周围的系数都是负的,所有的系数之和为0。
对3×3 的模板来说,典型的系数取值为:[-1 -1 -1;-1 8 -1;-1 -1 -1]事实上这是拉普拉斯算子。
CH3数字图像处理技术-数字媒体技术基础-宗绪锋-清华大学出版社

3.2 数字图像处理应用领域
3.2.3 数字图像处理在工业生产中的应用 1. 射线照相检验。利用X射线或γ射线的众多特性(如感 光),通过观察记录在胶片上的有关X射线或γ射线在被检 材料或工件中发生的衰减变化,来判定被检材料和工件的内 部是否存在缺陷。
3.2 数字图像处理应用领域
3.2.3 数字图像处理在工业生产中的应用 2. 超声检测。超声波探伤比X射线探伤具有较高的探伤灵敏 度、够快速便捷、无损伤、精确地进行工件内部多种缺陷的 检测、定位、评估和诊断。
3.1 数字图像处理基础知识
3.1.3位图与矢量图 2. 矢量图形 矢量图形(Vector),也称为面向对象的图像或绘图图像, 在数学上定义为一系列由线连接的点。矢量图是以数学向量 方式记录图像的,其内容以线条和色块为主。 矢量图的优点是轮廓的形状更容易修改和控制,并且和分辨 率无关,它可以任意地放大且清晰度不变,也不会出现锯齿 状边缘。
3.2 数字图像处理应用领域
3.2.5 数字图像处理在通信中的应用 4.数字电视 数字电视就是指从演播室到发射、传输、接收的所有环节 都是使用数字电视信号或对该系统所有的信号传播都是通 过由0、1数字串所构成的数字流来传播的电视类型。数字 电视信号损失小,接收效果好。
3.2 数字图像处2.可视电话 可视电话业务是一种点到点的视频通 信业务。它能利用电话网双向实时传 输通话双方的图像和语音信号。由于 可视电话能收到面对面交流的效果, 实现人们通话时既闻其声、又见其人 的梦想。
3.2 数字图像处理应用领域
3.2.5 数字图像处理在通信中的应用 3.卫星通讯 卫星通信系统由卫星和地球站两部分 组成。卫星在空中起中继站的作用, 即把地球站发上来的电磁波放大后再 返送回另一地球站。地球站则是卫星 系统与地面公众网的接口,地面用户 通过地球站出入卫星系统形成链路。
《数字图像处理》课程教学大纲

数字图像处理课程教学大纲课程简介数字图像处理是计算机科学与技术领域的一门重要课程,它研究如何使用计算机和算法来处理和分析数字图像。
本课程旨在介绍数字图像处理的基本原理、方法和应用,并培养学生的图像处理能力和技巧。
课程目标本课程的主要目标是让学生掌握数字图像处理的基本理论和方法,具备图像处理算法设计、图像增强、图像分割、图像压缩等技术的基本能力。
同时,通过实践项目的实施,培养学生的问题解决能力和团队合作能力。
课程安排第一周:课程介绍与基本概念•课程介绍•数字图像的基本概念与特点•数字图像处理的基本步骤第二周:图像预处理•图像采集与获取•图像灰度变换•图像噪声模型与去噪方法第三周:图像增强•直方图均衡化•空域滤波与频域滤波•边缘增强与锐化第四周:图像压缩•图像压缩的基本概念与方法•离散余弦变换(DCT)与JPEG压缩算法•小波变换与JPEG2000压缩算法第五周:图像分割与边缘检测•阈值分割•基于边缘的图像分割•基于区域的图像分割第六周:实践项目1 - 图像识别•项目需求分析与设计•图像特征提取与选择•分类器的训练与测试第七周:实践项目2 - 图像恢复•项目需求分析与设计•图像模型与图像去模糊•图像去噪与图像修复第八周:实践项目3 - 图像处理工具开发•项目需求分析与设计•图像处理算法的实现•图形界面设计与用户交互评估方式•平时成绩:30%•作业与实验报告:30%•期末考试:40%参考教材•Rafael C. Gonzalez, Richard E. Woods. 数字图像处理(第三版). 清华大学出版社,2018.•Richard Szeliski. 计算机视觉:算法与应用. 电子工业出版社,2014.参考资源•MATLAB图像处理工具箱文档•OpenCV计算机视觉库官方文档以上是《数字图像处理》课程的教学大纲,希望通过本门课程的学习,能够让学生对数字图像处理有一个全面的了解,并具备实践应用的能力。
大学遥感数字图像处理教案

大学遥感数字图像处理教案大学遥感数字图像处理教案课程名称:遥感数字图像处理课时数:48学时课程设计:王老师教材:1. 《数字图像处理》(第3版) - 冈萨雷斯 / 伍兹2. 《数字遥感图像处理》 - Mather / Koch教学目标:1. 熟悉遥感数字图像处理的基本原理和流程,了解数字图像的基本概念和处理方法。
2. 掌握数字图像处理软件的使用,学习图像增强、分割、融合等处理方法。
3. 熟悉常用的遥感数据格式,能够读取、转换遥感数据。
4. 运用遥感数字图像处理技术,对不同类型的遥感数据进行处理,获得有用的信息。
教学内容:第一章数字图像基础知识1.1 数字图像的定义和特点1.2 图像采集和表示方法1.3 图像处理的基本概念和分类1.4 图像文件格式第二章数字图像增强2.1 空间域增强方法2.2 频域增强方法2.3 灰度变换2.4 直方图处理第三章数字图像分割3.1 基本概念和流程3.2 阈值分割3.3 区域分割3.4 模型分割第四章数字图像融合4.1 基本概念和流程4.2 像元级融合4.3 特征级融合4.4 决策级融合第五章遥感数据格式5.1 常用遥感数据格式5.2 遥感数据的读取和转换方法第六章遥感数字图像处理实例6.1 单波段图像处理实例6.2 多波段图像处理实例6.3 地物分类实例6.4 遥感图像融合实例教学方法:1. 讲授理论知识,辅以实例分析,使学生能够理解和掌握处理方法。
2. 实验操作,让学生在软件中进行图像处理和数据读取等相关操作,以加深理解和掌握处理技能。
3. 课堂讨论,通过分析学生操作的结果,针对处理方法中的问题进行讨论,促进学生思考和交流。
评估方法:1. 实验报告:学生根据作业布置的题目进行实验操作,提交一份实验报告。
2. 课堂讨论:对学生在课堂中的问题解答和参与情况进行评估。
3. 期末考试:对学生整个学期的知识掌握水平进行综合评估。
教学建议:1. 建议学生提前学习相关的数字图像处理和遥感知识,提高学习效果。
23887 《数字图像处理(第3版)》习题解答(上传)(1)

胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案目录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显示 (7)第4章图像变换与二维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应用 (31)第10章彩色图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animation)等视觉信息之间的联系和区别。
答:图像是用成像技术形成的静态画面;视频用摄像技术获取动态连续画面,每一帧可以看成是静态的图像。
图形是人工或计算机生成的图案,而动画则是通过把人物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再用摄影机连续拍摄成一系列画面,给视觉造成连续变化的图画。
数字图像处理1_赵建峰

五、数字图像处理的作用?
一般来数字图像处理与分析 数字图像处理与分析讲,对 图像进行处理(或加工、分析)的主要目的有三个方面: (1)提高图像的视感质量,如进行图像的亮度、彩色变 换,增强、抑制某些成分,对图像进行几何变换等,以改 善图像的质量。 (2)提取图像中所包含的某些特征或特殊信息,这些被 提取的特征或信息往往为计算机分析图像提供便利。提取 特征或信息的过程是模式识别或计算机视觉的预处理。提 取的特征可以包括很多方面,如频域特征、灰度或颜色特 征、边界特征、区域特征、纹理特征、形状特征、拓扑特 征和关系结构等。 (3)图像数据的变换、编码和压缩,以便于图像的存储 和传输。
46
86 86 84
5 处理 图像是可视化结果
35 46 52
45 64 46 47 64 65
77
36
4346 86源自123 45 104 88
56 77 100
42 42 140
114 90
122 99
86
84
二、图像的分类?
1、模拟图像 2、数字图像
三、图像的作用?
1、形象直观; 2、方便存储等。
四、什么是数字图像处理?
图像处理(image processing),用计算机对 图像进行分析,以达到所需结果的技术。 又称影像处理。 基本内容 图像处理一般指数字图像处理。 数字图像是指用数字摄像机、扫描仪等设 备经过采样和数字化得到的一个大的二维 数组,该数组的元素称为像素,其值为一 整数,称为灰度值。图像处理技术的主要 内容包括图像压缩,增强和复原,匹配、 描述和识别3个部分。
亮度分辨率测试
《数字图像处理》实验指导书

数字图像处理实验指导书电气信息工程系实验中心2008年8月目 录实验一、数字图像获取实验二、图像的傅立叶变换实验三、图像增强实验四、图像压缩实验一、数字图像获取一、实验目的1.掌握使用扫描仪等数字化设备以及计算机获取数字图像的方法;2.修改图像的存储格式。
二、实验仪器1.计算机;2.扫描仪(或数码相机、数字摄像机)及其驱动程序盘;3.图像处理软件(画图,photoshop, Microsoft photo edit等);4.记录用的笔、纸。
三、 实验内容用扫描仪获取图像也是图像的数字化过程的方法之一,扫描仪按种类可以分为手持扫描仪,台式扫描仪和滚筒式扫描仪(鼓形扫描仪)。
扫描仪的主要性能指标有x、y方向的分辨率、色彩分辨率(色彩位数)、扫描幅面和接口方式等。
各类扫描仪都标明了它的光学分辨率和最大分辨率。
分辨率的单位是dpi,dpi是英文Dot Per Inch的缩写,意思是每英寸的像素点数。
扫描仪工作时,首先由光源将光线照在欲输入的图稿上,产生表示图像特征的反射光(反射稿)或透射光(透射稿)。
光学系统采集这些光线,将其聚焦在CCD上,由CCD将光信号转换为电信号,然后由电路部分对这些信号进行A/D转换及处理,产生对应的数字信号输送给计算机。
当机械传动机构在控制电路的控制下,带动装有光学系统和CCD的扫描头与图稿进行相对运动,将图稿全部扫描一遍,一幅完整的图像就输入到计算机中去了。
图1.1扫描仪的工作原理扫描仪扫描图像的步骤是:首先将欲扫描的原稿正面朝下铺在扫描仪的玻璃板上,原稿可以是文字稿件或者图纸照片;然后启动扫描仪驱动程序后,安装在扫描仪内部的可移动光源开始扫描原稿。
为了均匀照亮稿件,扫描仪光源为长条形,并沿y方向扫过整个原稿;照射到原稿上的光线经反射后穿过一个很窄的缝隙,形成沿x方向的光带,又经过一组反光镜,由光学透镜聚焦并进入分光镜,经过棱镜和红绿蓝三色滤色镜得到的RGB三条彩色光带分别照到各自的CCD上,CCD将RGB光带转变为模拟电子信号,此信号又被A/D变换器转变为数字电子信号。
数字图像处理第三版中文答案解析冈萨雷斯

第二章2.1(第二版是0.2和1.5*1.5的矩形,第三版是0.3和1.5圆形)对应点的视网膜图像的直径x 可通过如下图题2.1所示的相似三角形几何关系得到,即()()01702302.x .d =解得x=0.06d 。
根据2.1 节内容,我们知道:如果把中央凹处想象为一个有337000 个成像单元的圆形传感器阵列,它转换成一个大小25327.⨯π成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为1.5 mm (直径) 的一条线上有655个成像单元和654个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s=[(1.5 mm)/1309]=1.1×10-6 m 。
如果在中央凹处的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说, 眼睛不能检测到以下直径的点:m .d .x 61011060-⨯<=,即m .d 610318-⨯<2.2 当我们在白天进入一家黑暗剧场时,在能看清并找到空座时要用一段时间适应。
2.1节描述的视觉过程在这种情况下起什么作用?亮度适应。
2.3 虽然图2.10中未显示,但交流电的却是电磁波谱的一部分。
美国的商用交流电频率是77HZ 。
问这一波谱分量的波长是多少?光速c=300000km/s ,频率为77Hz 。
因此λ=c/v=2.998 * 108(m/s)/77(1/s) = 3.894*106m = 3894 Km. 2.5根据图2.3得:设摄像机能看到物体的长度为x (mm),则有:500/x=35/14; 解得:x=200,所以相机的分辨率为:2048/200=10;所以能解析的线对为:10/2=5线对/mm. 2.7 假设中心在(x0,y0)的平坦区域被一个强度分布为:])0()0[(22),(y y x x Ke y x i -+--= 的光源照射。
为简单起见,假设区域的反射是恒定的,并等于1.0,令K=255。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章、图像处理基本技术
§3.1 几何变换 §3.2点处理
§3.1 几何变换
一、图像像素的属性 二、几何变换基础 三、图像基本变换 四、图像复合变换 五、图像透视变换
一、图像像素的属性
数字图像的基本构成单位是像素。 图像像素有两个重要的属性:
1、像素位置; 2、像素颜色或灰度。
按比例放大;当s=1时,图像大小不变。
三、图像基本变换
1、图像比例缩放 2、图像平移变换 3、图像镜像变换 4、图像旋转变换
1、图像比例缩放
图像比例缩放是指将给定的图像在x轴方向 按比例缩放fx倍, 在y轴方向按比例缩放fy 倍,从而获得一幅新的图像。如果fx=fy, 即在x轴方向和y轴方向缩放的比率相同,称 这样的比例缩放为图像的全比例缩放。如 果fx≠fy,图像的比例缩放会改变原始图像 的像素间的相对位置,产生几何畸变。
二维空间坐标点的规范化齐次坐标的前两个数没 有变化,仅在原坐标中增加了H=1的附加坐标。
由点的齐次坐标(Hx, Hy, H)求点的规范化齐次 坐标(x, y, 1),可按如下公式进行:
规范化齐次坐标的几何意义:点(x, y)落在3D空间 H=1的平面上。
若将XOY 平面内的三角形abc的各顶点表示成齐次 坐标(xi, yi, 1)(i=1, 2, 3)的形式,就变成H=1平面 内的三角形a1b1c1的各顶点。
设原图像中的点P0(x0,y0)比例缩放后,在新 图像中的对应点为P(x, y),则P0(x0,y0)和P(x, y)之间的对应关系如上图所示。
若用矩阵的形式表示,点P(x, y)的坐标为:
坐标点平移图示
上述变换若要使用一个变换矩阵来实现,则需要 使用2×3阶变换矩阵,其形式为:
此矩阵的第一、二列构成单位矩阵,第三列元素 为平移常量。
故对2D图像进行变换,只需要将图像的点集矩阵 乘以变换矩阵即可。
2D图像对应的点集矩阵是2×n阶的,而扩展后变 换矩阵是2×3阶的,这不符合矩阵相乘时要求前 者的列数与后者的行数相等的规则。
如果所处理的是一幅灰度图,这时f表示灰度值。
而且此时f、x、y都在整数集合中取值。
常见的图像几何变换可以通过与之对应的矩阵线 性变换来实现(除了插值运算)。
对于一些简单几何变换及变换中心在坐标 原点的比例缩放、 反射、 错切和旋转等变 换,可以用2×2的矩阵表示和实现。
但数字图像的平移以及绕任意点的比例缩
设变换矩阵T为: 则上述变换可以用公式表示为:
图像上各点的新齐次坐标规范化后的点集 矩阵为:
引入齐次坐标后,表示2D图像几何变换的 3×3矩阵的功能就完善了,可以用它完成 2D图像的各种几何变换。
下面讨论3×3阶变换矩阵中各元素在变换中的功 能。几何变换的3×3矩阵的一般形式为:
3×3的阶矩阵T可以分成四个子矩阵。其中,
子矩阵可使图像实现恒等、 比例、 镜像、 错切和 旋转变换。[p q] T这一列矩阵可以使图像实现平移 变换。 [l m] 矩阵可以使图像实现透视变换,但当 l=0,m=0时它无透视作用。[s]矩阵可以使图像实 现全比例变换。
例如:
将齐次坐标 规范化后,
。由此可见,
当s>1时,图像按比例缩小;当0<s<1时,整个图像
齐次坐标在二维图像中的另一个应用是:若点 S(60000,40000)在16位计算机上表示则大于 32767的最大坐标值。
将点S的坐标形式变成(Hx, Hy, H)形式的齐次坐标 ,则可解决这一问题。
在齐次坐标系中,设H=1/2,则
(60000,
40000)的齐次坐标为(1/2x, 1/2y, 1/2),那么所要
放、反射、错切和旋转等变换,。却不能
通过一个2×2变换矩阵
实现
为了使用统一的矩阵线性变换形式,表示 和实现这些常见的图像几何变换,需要引 入一种新的坐标,即齐次坐标。
利用齐次坐标,可使用统一的形式实现上 述二维图像的几何变换。
齐次坐标
现将点P0(x0, y0)平移到P(x, y),其中x方向的平移 量为Δx,y方向的平移量为Δy。则点P(x, y)的坐标 为:
因此在点的坐标列矩阵[x y]T中引入第三个元素,增加 一个附加坐标,扩展为3×1的列矩阵[x y 1]T。用三维 空间点(x, y, 1)来表示二维空间点(x, y),即采用一种 特殊的坐标,可以实现平移变换。
因此,利用这种特殊的坐标,可将2×3阶矩阵扩充为3×3 阶矩阵,以拓宽功能。由此可得平移变换矩阵:
验证一下点P (x, y)按照3×3的变换矩阵T平 移变换的结果:
可见,引入附加坐标后,扩充了矩阵的第3 行, 并没有使变换结果受到影响。这种ቤተ መጻሕፍቲ ባይዱn +1维向量表示n维向量的方法称为齐次坐 标表示法。
二维空间坐标(x, y)的齐次坐标可表示为(Hx, Hy, H) ,其中H表示任意非零实数。当H=1时,则(x, y, 1)就称为点(x, y)的规范化齐次坐标。
像素属性的改变会引起图像的变化。图像 像素位置属性有规律的变化,称为数字图 像的几何变换。
二、几何变换基础
图像的几何变换,是指通过改变像素的位 置,使图像产生大小、形状和位置的变化 ,来达到用户期望的图像。
从图像类型来分,图像的几何变换有二维 平面图像的几何变换和三维图像的几何变 换以及由三维向二维平面投影变换等。
从变换的性质分, 图像的几何变换有平移 、比例缩放、旋转、反射和错切等基本变 换,透视变换等复合变换,以及插值运算 等。
数字图像说明
二维数字图像就是把连续的二维(2D)图像在坐标 空间XOY和性质空间F都离散化了的图像,可用一 组二维(2D)数组f(x, y)来表示。
其中x和y表示2D空间XOY中一个坐标,f代表图像 在点(x, y)的某种性质F的数值。
表示的点变为(30000, 20000, 1/2),此点显然在
16位计算机上二进制数所能表示的范围之内。
图像几何变换矩阵形式
实现二维图像几何变换的一般过程为:将2×n阶的二 维点集矩阵
表示成齐次坐标
然后乘以相应的变换矩阵即可完成,即: 变换后的点集矩阵=变换矩阵T×变换前的点集矩阵。
(图像上各点的新齐次坐标)(图像上各点的原齐次坐标)
